Fortran计算实例培训讲学
Fortran-第一讲--第一章

1.3.1 声明部分
声明由不可执行语句组成 位于程序开头 定义程序名和程序引用的数据以及变量类型
PROGRAM语句用来指定程序的名字 程序名最长可达31个字符 由字母、数字和下划线任意组合而成 第一个字符必须是字母 如果存在PROGRAM语句,它必须是程序的第一个语句行 例:下列程序名是否有效,如无效则说明原因 new_program 3rd
无效的实数表示: -12.0E1.5
例
下列各组数在计算机里表示的值是否一样 4650. 4.65E+3 -12.71 -1.27E1 0.0001 1.0E4 3.14159E0 314.159E-3
1.5.3 字符类型
字符类型由字符串组成 字符常数是由单引号或双引号括住的字符串 在单引号或双引号之间括起来的部分称为字符文本, 字符文本可以采用任意计算机可以表示的字符,而 不受Fortran字符集限制 如果字符文本中含有单引号该怎么办?
这一转换仅仅是指参与操作的两个操作数类型 分别为实数和整数而言
表达式
1 2 3 1+1/4 1.0+1/4 1+1.0/4
结果
1 1.0 1.25
因为混合运算的情况是如此复杂,所以我们在程序中要尽量避免这种情 况发生
练习
下面的程序段的三个赋值语句是否正确,正 确写结果,错误说明原因 INTEGER :: i,j INTEGER, PARAMETER :: K=4 i = K **2 j = i/K K=i+j
简单地说:学完本章,你应该可以编写除函数以外的简单程序
1.1 Fortran字符集
正如英语的学习从abc开始,Fortran的学习 也是从字符集开始
fortran数值计算基础

数值计算基础目录实验一直接法解线性方程组的 (2)实验二插值方法 (11)实验三数值积分 (5)实验四常微分方程的数值解 (7)实验五迭代法解线性方程组与非线性方程 (9)实验一 直接法解线性方程组一、实验目的掌握全选主元消去法与高斯-塞德尔法解线性方程组。
二、实验内容分别写出Guass 列选主元消去法与追赶法的算法,编写程序上机调试出结果,要求所编程序适用于任何一解线性方程组问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
1、用Guass 列选主元消去法求解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--5.58.37.33.47.11.85.16.93.51.53.25.2321x x x2、用追赶法求解方程组⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----000010210000210000210000210000254321x x x x x 三、实验仪器设备与材料主流微型计算机四、实验原理1、Guass 列选主元消去法 对于AX =B1)、消元过程:将(A|B )进行变换为)~|~(B A ,其中A ~是上三角矩阵。
即:⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n nn nnn nnn n nn b a b a b a a b a a a b a a a b a a a0010122111221222221111211 k 从1到n-1a 、 列选主元选取第k 列中绝对值最大元素ik ni k a ≤≤max 作为主元。
b 、 换行ik ij kj b b n k j a a ⇔+=⇔,,1,c 、 归一化kkk k kj kk kj b a b n k j a a a ⇒+=⇒/,,1,/d 、 消元nk i b b a b n k j n k i a a a a i k ik i ij kj ik ij ,,1,,,1;,,1, +=⇒-+=+=⇒-2)、回代过程:由)~|~(B A 解出11,,,x x x n n -。
第2章 Fortran程序设计基础PPT课件
SUBRO UTINE 、MO NEY 、< = 都是非法的。
一般情况下,记号之间需留有空格。例如:100CONTINUE 是非法的, 因为标号100 和关键字 CONTINUE 是两个独立的记号。
有的记号间的空格是可选的,例如:END PROGRAM 和 ENDPROGRAM是 合法的。
四. 注释
END
注释行
注:其中处于同一水平位置的各语句之间没有严格的前后 顺序,而不同的行则表示了严格的在程序当中出现的前后 顺序。
语句顺序的一般原则:
程序段的段头语句,只能ຫໍສະໝຸດ 现在每个程序段开始的位置。如: PROGRAM、FUNCTION、SUBROUTINE、BLOCK、DATA、MODULE等;
如果出现USE语句,则只能出现在段头语句之后、其他语句之前; IMPLICIT NONE语句应紧跟在USE语句之后,在其他说明语句之前; FORMAT语句和DATA语句也可以放置在可执行语句中间,不过把DATA
* 固定格式是为配合早期使用穿孔卡片输入程序所发明的 格式, 这里介绍固定格式,只是让大家对 Fortran 77 程序有所了解,建议大家在编写程序时采用前述地自由 格式。
* 固定格式尽管有其过多的限制,但由于具有一定的规范 性,方便程序的编写和检查。
二、自由格式
自由格式是Fortran 90之后的新写法,是目前最流行的书写格 式,取消了许多限制。没有规定每行的第几个字符有什么作用。
固定格式说明:
一行共80列,分为4个区: 第1-5列,标号区,可以空白,也
可以出现符号;
第6列,续行标志区,可以空白( 无续行),非0字符(续行 );
第7-72列,语句区,语句区的书写 可以从任意一列开始,空白 编译时被忽略,一行只能书 写一个语句;
Fortran讲义 第七章

派生类 型的使 用
结构体的赋值
结构体成员单独赋值 用结构体构造函数赋值
结构体成员的引用:% 结构体成员的引用:
派生类 型的使 用
结构体的输入输出
整体操作时按派生类型定义的顺序 整体操作时不能包含可变大小的成员
exam_7_1
作为形参或函数的返回值
exam_7_2
BASIC_DATA.F90
派生类 型的使 用
结构体的声明
exam_7_1
变量声明语句中类型名用“type(派生类型名称) 变量声明语句中类型名用“type(派生类型名称)”替 换
结构体的初始化
派生类型定义时的初始化(缺省初始化) 派生类型定义时的初始化(缺省初始化) 结构体声明时用结构体构造函数初始化 显式初始化) 结构体构造函数初始化( 结构体声明时用结构体构造函数初始化(显式初始化) 语句中用结构体构造函数初始化 在data语句中用结构体构造函数初始化(显式初始化) 语句中用结构体构造函数初始化(显式初始化)
第七章 派生类型
派生类型 的基本概 念
派生类型用于表示包含不同类型 派生类型用于表示包含不同类型变量的集合 不同类型变量的集合
基本数据类型
指针类型
其它派生类型Leabharlann 派生类型的实例称为结构体派生类 型的定 义
type[[,<访问属性>]::]<派生类型名称> type[[,<访问属性>]::]<派生类型名称> [[,<访问属性>]::]<派生类型名称 [sequence] sequence] [private] private] {成员声明} 成员声明} end type [派生类型名称] 派生类型名称] <访问属性>→public|private 访问属性> public|
Fortran 第六讲

SUM (ARRAY,MASK) 计算ARRAY中MASK为真的元素的和。MASK为 可选的,如果不提供,计算数组中所有元素的和
TRANSPOSE(MATRIX) 将MATRIX转置后返回
更多的变换函数可以参考教材的附录A的数组函数 部分
这些函数都很有用,我们在以后的例程或习题会涉 及到一部分,请诸位养成查阅这一附录的习惯
说明: WHERE结构中的每个mask_expr是一个逻辑数组, 它应该确保和数组执行语句中处理的数组具有同 样的结构。 WHERE结构使得语句体1中的操作或操作集用于 mask_expr1为TRUE的所有数组元素上,语句体2 中则作用于mask_expr1为FALSE而mask_expr2为 TRUE的所有数组元素上,最后,语句体3作用于 mask_expr1和mask_expr2均为FALSE的所有数组 元素上
6.3 WHERE结构
6.1中,我们学习了如何操作部分数组 INTEGER :: a(10) a(3:5)=3 将a(3),a(4),a(5)赋值为3
如果我们要对满足某个条件的所有元素进行操作 WHERE (a<0) a=ABS(a) END WHERE 将a中所有小于0的元素取绝对值
一般形式 [name:] WHERE (mask_expr1) 数组操作语句体1 ELSEWHERE (mask_expr2) [name] 数组操作语句体2 ELSEWHERE [name] 数组操作语句体3 END WHERE [name]
动态分配一个二维数组 通过status返回分配状态 如果分配成功,status为0,否则不为0
总是使用STAT=status监视分配状态,以便准确知道 程序异常终止的原因
ALLOCATED()函数 ALLOCATED(array) 如果已经用ALLOCATE()给ARRAY分配了空间 那么函数返回值是.TRUE. 否则为.FALSE. 例: IF (ALLOCATED(array)) THEN array=1 ELSE WRITE(*,*) ‘Warning : Array not allocated!’ END IF
Fortran的讲义第五章共21页文档

ASSEM_FORCE.f90
<where语句>→wt;
<where语句>→[<标签>:]where(<屏蔽表达式>) {<赋值语句>}
else where(<屏蔽表达式>)[<标签>] {<赋值语句>}
{else where(<屏蔽表达式>)[<标签>] {<赋值语句>}}
给单个数组元素赋值
用数组构造器赋值(Fortran90)
两种格式:(/…/) 或 […] 只能给一维数组(或数组片段)赋值 可以是常量、表达式、三元组、隐式do循环或数组片段
用reshape语句给多维数组(或数组片段)赋值
数组元素赋值
exam_5_2
条件赋值(where)- Fortran90
第m次消元
m1,2,...n,
A (m ) AA mj
(m 1 ) mj
(m 1 ) mm
jm ,m 1 ,.n ..b ,m (m )b A m ( m (m m 1 1 )m )
pure函数(Fortran95): 确保函数不影响程序其它部分的状态
数组元素赋值
条件赋值(forall)- Fortran95
exam_5_2
<forall语句> → forall(<三元组>{, <三元组>}[,<屏蔽表达式>]) <赋值语句
>
<forall语句>→ [<标签>:]forall(<三元组>{, <三元组>} [,<屏蔽表达式>]) <赋值语句> {<赋值语句>} end forall[<标签>]
Fortran程式语言的编、译与执行简述培训课件.ppt

二、Fortran 程式語言編譯
將 c 磁碟的 mingw 目錄的 bin 子目錄的 g77.exe複製到 工作目錄下
來將 福傳檔案 *.for 編譯為 可執行檔 *.exe
二、Fortran 程式語言編譯
Fortran程式語言編譯指令(2) g77.exe 已經單獨複製到 C 碟之工作目錄 cjs 下
七、運算指令指令
電腦計算可使用之操作種類
加法運算:+ 減法運算: 乘法運算:* 除法運算:/ 冪次方運算:**;^
Ans = -(a+(b*c-d**3.)*25.+e*e*e)/2. 運算式中之運算次序依一般數學運算次序
八、控制指令
〔if ( ) goto no.〕 〔if ( ) then // else // endif〕 〔do no. // no. continue〕 〔call sub_name ( ) 〕
執行 〔t1 〕 結果 〔7〕
游標閃爍 - - 待 令狀態
四、MS-DOS 作業環境的瀏覽
執行 〔dir 〕 瀏覽工作目 錄下之檔案 與目錄
〔dir/p 〕 〔dir/w 〕 〔dir*.for 〕 〔dir*.* 〕
五、電腦語言漫談
電腦計算可使用之操作種類
一、檔案(文書)編輯
編輯完成 執行儲存
二、Fortran 程式語言編譯
在工作目錄cjs 下呼叫 c 磁碟的 mingw 目錄的 bin 子目錄的 g77.exe
來將 福傳檔案 *.for 編譯為 可執行檔 *.exe
二、Fortran 程式語言編譯
Fortran程式語言編譯指令(1)
加法運算:+ 減法運算: 乘法運算:* 除法運算:/ 冪次方運算:**;^
Fortran讲义 第四章

输入输 出的格 式
隐式格式(implicit 隐式格式(implicit format)
表控格式(list 表控格式(list directed) 名称列表(namelist 名称列表(namelist directed) * 不能用于内部记录
显式格式(explicit 显式格式(explicit format) 无格式(unformatted) 无格式(unformatted)
输入输出项的个数等于 输入输出项的个数等于格式编辑符个数 等于格式编辑符个数
输入输出项的个数大于 输入输出项的个数大于格式编辑符个数 大于格式编辑符个数
<输出语句>→ 输出语句>
[{<表达式 [{<表达式>}]| 表达式>}]| print <格式> [,{<表达式>}] 格式> [,{<表达式 表达式>}]
标准输入输出设备
write“ write“(”<设备>[, <格式>][, <状态和控制符>]“)” 设备>[, 格式>][, 状态和控制符>] >]“
exam_4_6
显式格式 输入输出
纵向走纸控制
格式说明的首字符 (空格) 空格) 0(数字 0(数字0) 数字0) 1(数字 1(数字1) 数字1) +(加号 +(加号) 加号) 其它字符 纵向间隔控制功能 移到下一行开头 移到下面第二行开头 移到下一页第一行开头 移到当前行开头 移到下一行开头
exam_4_7
无格式( 无格式(unformatted 二进制) 二进制)
输入输 出语句
<输入语句>→ 输入语句>
fortran教程.ppt
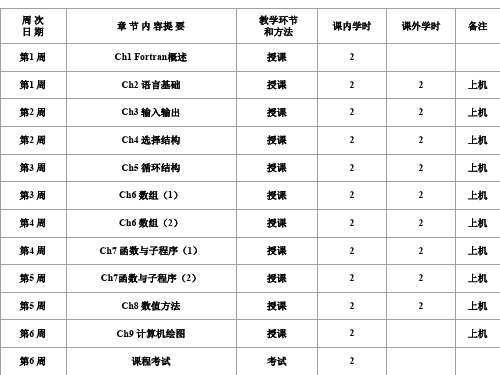
N-S 图——结构化流程图 S=0
例2 用N-S图表示
N=1
S+1/N= S
N+1= N
直到N>100为止
打印 S 值
例1 用N-S图表示
N=0 T=0
输入 A A+T →T N+1 →N 直到N≥100 为止 打印 T
例3
L=1
N=1
S=1
SUM = 1
L+2 → L
-S → S
N+1 → N
SUM+S/L →SUM
(3)输入一个数给“收入变量”A
(4)将A和T的值相加,其和值放在变量T中 A+TT;
(5)使N的值加1,即N+1 N(N的值表示已累加数据的个数)
(6)若N﹤100,则返回(3)继续执行以后各步,否 则转到执行(7)
(7)打印出总和T的值
以上算法体现“迭代”的思想—计算机算法的最大特 点
例2 求 1
将高级语言程序(源程序)转换为机器语言程序(目标程序)
的工作由“编译程序”来完成。 编译
执行
高级语言程序
机器指令目标程序
计算结果
编译程序 (预先存如电脑)
裸机
用户源程序
操作系统
高级语言编译系统
计算机系统与操作系统关系示意图
§ 1-2 算法(Algorithm)与程序设计(Programming)
1. 近50年的丰富积累,资源不浪费,对原有程 序向下兼容。而C语言与Matlab才20多年
2. FORTRAN书写和语法要求严格,更适合于 严谨的科学计算。而C对数组不提供越界检查, 容易出错,而且不容易查出
3. FORTRAN 90~95可以直接对矩阵和复数进行 运算。而C语言则要用多重循环
Fortran入门培训

(1) 采用fortran 进行计算的好处简单的计算,例如2/1-+=d k i s σσ,可以直接在origin 等里面计算;复杂的计算,例如 2220)()()(geo the or s σσσσσ∆+∆+∆+= 其中 Lbor μϕσ=∆,ρμησb the =∆,D b f m geo /εμβσ=∆又其中 2/14⎪⎪⎭⎫⎝⎛=fD L π,)1(12f D b fT -∆∆=αρ,怎么算??(2) fortran 语言 (以以上计算为例)REAL EM,EP,YSM,F,VM,YS (定义参量 REAL :实数,赋值时需要加.) REAL ROU REAL D,B,UM,DETAALFA,DETA T,YSINCROR,YSINCRTHE,YSINCRGEO,YSMINC This project is used to calculate the YIELD STRENGTH of AL-AMORPHOUSPARTICLES SL METHOD (说明这个程序的目的 开头C 决定了这一行是不运行的)OPEN(4,FILE='YS.DA T', STATUS='UNKNOWN') (建立数据文件.DAT ,存储数据) OPEN(5,FILE='YSINCROR.DA T', STATUS='UNKNOWN') OPEN(6,FILE='YSINCRTHE.DA T', STATUS='UNKNOWN')EM=50. (基体M 弹性模量赋值) VM=0.33 (基体M 泊松比赋值) UM=28. (基体M 剪切模量赋值) EP=95. (第二相P 弹性模量赋值)B=0.286 (基体Burges 矢量赋值) (注:为减小计算量,以上赋值均省去单位,最后一起核算)YSM=113. (基体屈服强度0σ赋值)D=100. (第二相颗粒直径赋值) DETAALFA=1.2E-5 (热膨胀系数差α∆赋值) DETAT=345. (热膨胀系数差T ∆赋值)DO 30 F=0.0001,0.8,0.0999 (DO CONTINUE 循环语句,对颗粒含量F 连续赋值) L=0.5*D*(4.188/F)**0.334 (求第二相颗粒间距L ) YSINCROR=UM*B/L (计算or σ∆)ROU=12.*DETAALFA*DETAT*F/(B*D*(1.-F)) (计算位错密度ρ) YSINCRTHE=1.4*UM*B*SQRT(1.E3*ROU) (计算the σ∆)YSINCRGEO=UM*SQRT(1.E-3*F*0.002*B/D) (计算geo σ∆) YS=YSM+SQRT(YSINCROR**2.+YSINCRTHE**2.+YSINCRGEO**2.) (计算s σ) WRITE (4,*)100.*F,YS (输出 F, s σ结算结果 )WRITE (5,*)100.*F,YSINCROR (输出 F, or σ∆结算结果 )WRITE (6,*)100.*F,YSINCRGEO,YSINCRTHE (输出 F, geo σ∆, the σ∆结算结果 )30 CONTINUE END (结束)(2) fortran 计算界面(i) compile 编辑,查错(ii) built建立文件关联(iii) go 运行计算程序存盘时必须是.f查看计算结果:(3) fortran 计算结果的输出 (origin)100120140160180Y i e l d s t r e n g t h (M P a )Volume fraction of particles (%)D=20 μm D=50 μm D=100 μm点击openAll filesF σS点击后找到相应文件附1:Al-Cu合金系析出强化计算程序涉及到的理论及公式请参考Liu et al., Materials Science and Engineering A 344(2003)113REAL R0,D,B,C0,CE,CP,P0,PM,W0,WM,G,B1,TM,FM,A0,FV1,FV2,FV,K,K1REAL D1,G1,BTIME,BTM,R0D1,T1,T2,F,G11,G12,G21,G22,A1,A2,R1,R,NINTEGER T,NOMBER,TIMEOPEN(4,FILE='AL-CU52-SHIYAN.dat')OPEN(3,FILE='AL-CU52-SHIYAN-N.OUT')R=8.31K=27.0READ(4,*) TM,A0,T,W0,NOMBERWRITE(3,*)NOMBERWRITE(3,*)KP0=8.93PM=2.6989CP=0.33WM=1.-W0C0=W0*PM/(W0*PM+WM*P0)CE=13.176*EXP(-41680./(R*T))FM=C0-CEB=0.625*FM/(K*(0.33-CE))FV1=CP*LOG(C0/CE)FV2=(1.-CP)*LOG((1.-C0)/(1.-CE))FV=R*T*(FV1+FV2)R0=8.7E3/FVD=6.0E-6*EXP(-119691./(R*T))D1=D*1.0E20BTM=(B*TM)**1.5R0D1=(R0*D1)**2.0K1=K**2.0G11=9.12E7*K1*BTM*SQRT(D)G12=R0D1*C0*TMG1=3.0*FM/(G11*G12)G=-R*T*LOG(G1)write(3,*)G/1000.DO 10 TIME=100,800,10T2=TIME/100.0T1=10.0**(T2)R1=0.666667*K*SQRT(D*B*T1)R=1.0E9*R1BTIME=(B*T1)**1.5G21=9.12E7*K1*BTIME*SQRT(D)G22=R0D1*C0*T1F=G21*G22*G1N=1.0E10*F*K/(2.5*6.28*R**3.)B1=0.286IF (0.079*R.LE.B1) THENA2=A0WRITE(3,300) T1,NELSE IF (T1.LE.TM) THENA1=1.61355E3*SQRT(K)/RA2=A0+A1*(SQRT(F)+0.75*SQRT(K)*F+0.14*K*(F)**1.5)*LOG(0.079*R/B1)WRITE(3,300) T1,NELSEF=3.0*FMA1=1.61355E3*SQRT(K)/RA2=A0+A1*(SQRT(F)+0.75*SQRT(K)*F+0.14*K*(F)**1.5)*LOG(0.079*R/B1)N=1.0E10*F*K/(2.5*6.28*R**3.)WRITE(3,300) T1,N300 FORMAT(1X,F18.6,2X,F18.6)END IF10 CONTINUECLOSE(3)CLOSE(4)END得到的结果举例:附2:复合材料应力应变曲线计算涉及到的理论及公式请参考Liu et al., Acta Materialia 57(2009)2029REAL KM,KP,KX,UMS,UM,UP,UX,VVM,VVPREAL STRESSM,STRAINM,STRAINMM,STRESSX,STRAINX,STRESSM0REAL STRESSP,STRESSPCRI,DIAM,FCRI,M,K,VOLFRREAL YS,EMS,EM,EP,EX,ALFA,N,NI,F,FF,FM,F1REAL A1,A2,A3,B1,B2,C1,C2,D1,D2,YIELDREAL STRESSX1R,STRAINXR,DETAINTEGER IC This project is used to calculate the strain-stress curves of compositesOPEN(4,FILE='STRAIN-STRESS-60%-70.DAT', STATUS='UNKNOWN') OPEN(5,FILE='STRAIN-STRESS-MATRIX.DAT', STA TUS='UNKNOWN') OPEN(6,FILE='YIELD.DA T', STATUS='UNKNOWN')OPEN(7,FILE='VOLFRA.DAT', STATUS='UNKNOWN')ALFA=0.42857N=0.03NI=1./NF=0.10F1=FFM=1.-FFF=F/FMDIAM=25.K=1200.C K=5600.STRESSPCRI=K/SQRT(DIAM)M=5.8EM=70.EP=115.EX=EM*(1.-F)+EP*FVVM=0.33VVP=0.22KM=EMUM=0.5*KM/(1.+VVM)KP=EPUP=0.5*KP/(1.+VVP)STRESSM0=205.STRESSM=0.VOLFR1=0.STRAINXR=0.STRESSXR=0.WRITE(4,*) 0,0WRITE(5,*) 0,0DO 30 I=1,400STRESSM=STRESSM+1.A1=STRESSM/STRESSM0A2=N/(1.-N)A3=1.+ALFA*(A1)**A2STRAINM=STRESSM/EM+ALFA*(STRESSM0/EM)*(A1)**NIEMS=EM/A3UMS=EMS/(3.-EMS/(3.*KM))B1=UMS*(9.*KM+8.*UMS)B2=6.*(KM+2.*UMS)YS=B1/B2YX=YSC1=3.*KP*KM*(1.+FF)+4.*UX*(KM+KP)C2=4.*UX*(1.+FF)+3.*(KP+FF*KM)KX=C1/C2D1=UMS*UP*(1.+FF)+YX*(UMS+FF*UP)D2=YX*(1.+FF)+UP+FF*UMSUX=D1/D2STRAINX=STRAINM*(3.*KM+4.*UMS)/(3.*KX+4.*UMS) STRESSX1=STRESSM*(KX/KM)*(3.*KM+4.*UMS)/(3.*KX+4.*UMS) STRESSX2=1.E3*EX*(1.E-3*STRAINX-0.002)STRESSX=STRESSX1-STRESSX2STRESSP=STRESSM*(KP/KM)*(3.*KM+4.*UMS)/(3.*KP+4.*UMS) VOLFR=1.-EXP(-(STRESSP/STRESSPCRI)**M)F=F1-F1*VOLFRFF=F/FMEM=70.*FM/(FM+F1*VOLFR)N=0.03*FM/(FM+F1*VOLFR)N1=1./NDETA=1.E3*(STRESSX1-STRESSXR)/(STRAINX-STRAINXR) WRITE (4,*)1.E-1*STRAINX,STRESSX1,DETA WRITE (5,*)1.E-1*STRAINM,STRESSM,STRESSX1,STRESSXR WRITE (7,*)1.E-1*STRAINX,VOLFR*100. STRAINXR=STRAINX STRESSXR=STRESSX1 IF(ABS(STRESSX).LT.5.) THEN YIELD=STRESSX1 ELSE ENDIF30 CONTINUEWRITE (6,*)YIELD END得到的结果举例:St r e s s (M P a )Strain (%)S t r e s s (M P a )Strain (%)。
fortran90简易教学教程

real(8):: x
double precision x
绝对值在 2.22e-308 和 1.79e+308 之间,还包括 0,有效位 15 位
complex :: x character(5) :: z=’abcde’
complex x chracter*5 z
logical :: x
logical x
(逻辑型,.true. 或 .false.)主要不要漏写.
注意以下几点 1.Integer(1)、integer(2)赋值溢出,编译器不报错 比如 Integer(1):: x
x=128 write (*,*)x 输出:-128
而 integer、real、double precision 都可以判断溢出
优化,一般来说,fortran 的程序比 c 程序的执行效率要高一些。当然目前的 fortran90 已 经提供了指针,我认为主要的作用是实现一些数据结构。 4. 变量采用的是静态存储变量,在调用子过程或函数时,参数传递通过引用方式传递,节 省了复制变量的时间
二、书写风格
fortran 的老版本是 fortran77,教材上面的程序就是 f77 格式,而新版本是 fortran90,是 f77 的一个超集,这两种标准我都讲一讲,主要是因为我们既要看得懂老程序,同时自己写 程序时最好还是按新标准去写。
end
2.数组作为形参可以进行局部传递 program main
implicit none integer,dimension(50) ::IA integer :: lbound=10 call input(IA(lbound)) end
subroutine(X) implict none integer,dimension(20) :: X X=1 Write (*,*) x
Fortran课件第一章

当型循环传统流程图
当型循环 N——S 图
b) 直到型循环——先执行循环体 A 块一次; P 为假 当 (F) 时,反复执行循环体 A 块;当 P 为真(T)时,退出循环 体 A 块,流程转到下面的语句。注:也可以让 P 为真时, 执行循环,P 为假时,退出循环。
三、结构化程序设计方法 结构化程序设计方法,就是结合计算机语言的特点,把算法结 构化的程序设计方法。具体说来,就是规定一些基本结构,由基 本结构来组织更复杂的算法。 结构化程序设计方法中的三种基本结构:1)顺序结构,2)选 择结构,3)循环结构。 1) 顺序结构——顺序执行 A 块和 B 块。
A B A B
例 fortest101.f90
! Free Format Demo program main writቤተ መጻሕፍቲ ባይዱ(*,*) „Hi‟ write(*,*)& „John‟ write(*,10) 10 format(„Fine!‟) stop end program main
注释:程序 fortest101.f90 中,第一行有感叹号“!,说明“! ” ” 之后且同行的文本为注释部分;第四行程序代码后面的“&” ,说 明第五行“„John‟”是它的继续行;第七行的格式语句的标号“10” 写在前面。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 . . . ... 72 73 C F I X E D F O R M A T p r o g r a m m a i n w r i t e ( * , * ) „ H i „ w r i t e ( * , * ) # „ J o h n „ w r i t e ( * , 1 0 ) 1 0 f o r m a t („ f i n e ! „ ) s t o p e n d Fortran 源程序必须包含且只能包含一个主函数(program 主 函数名…end 或 program 主函数名…end program 主函数名) 。 Fortran 程序由主函数开始执行,由主函数调用其他函数,最后返 回主函数结束。
Fortran的讲义第三章

选择结构
计算goto (Fortran 95废除)
goto(10, 20) (x .le. 0.0) + 2 10 y = 0.0
goto 30 20 y = 1.0 30 print *, ‘y = ‘, y
back3.for
选择结构
赋值goto (Fortran 90废除,Fortran95取消)
r .ne. 0
True
执行循环体
False
i = i + inc
r=r-1
i: 循环变量 e1:初值 e2: 终值 inc:步长 r: 循环次数
exam_3_2
循环结构
不允许改变循环变量i
允许改变表达式e1,e2,inc中变量的值,并且不 影响循环次数
退出循环后循环变量的值有意义
循环结构
{<执行语句>}
直到型 do
enddo [<标签>] 10 <执行语句>
{<执行语句>}
{<执行语句>}
if(<逻辑表达式>) exit if(<逻辑表达式>) goto 10
enddo
异常的程序流程
在选择和循环结构中不允许从结构外跳转到结 构内
goto 10 if(<逻辑表达式>) then 10 <执行语句> {<执行语句>} end if
优先级
1 2 3 4 5 6 7 8 9 10
选择结构
块if
<基本块if语句>→[<标签>:]if(<逻辑表达式>)then {<执行语句>} [else [<标签>] {<执行语句>}] endif [<标签>]
Fortran讲义第二章汇总课件

优先级(最好加括号) : ①括号 ②函数 ③** ④*、/ ⑤单目+、- 双目+、-
类型转换(向高看齐),int, nint, real, dble, cmplx
复数运算
exam_2_5
表达式和赋值语句
❖ 字符表达式 ①
子字符串 字符串的连接 相关内部函数
exam_2_6
❖ 关系表达式: ②
内部过程或模块过程
END
Fortran源程序的书写格式
❖ 固定格式(*.for或*.f)
Fortran源程序的书写格式
Fortran源程序的书写格式
lists.for
Fortran源程序的书写格式
❖ 自由格式(*.f90)和固定格式的比较
exam_2_1
固定格式
自由格式
每行字符数 80
132(VF 中几乎不限制)
Fortran的名称
❖ 用来标识程序中的实体(变量、子程序、函数…)
❖ <名称>→<英文字母>{<英文字母>|<数字>|_|$}
❖ 名称长度不能超过6(FORTRAN77) 31(Fortran90) 63(Visual Fortran)
Fortran的名称
program X-Y-Z Find_it 1A _program $total
注释
第一列: c *
任意位置: !
73-80列
任意位置:!(第六列除外)
每行语句数 多条,用;隔开
多条,用;隔开
(FORTRAN77只能有1条)
续行
第六列,非0非空格 最多续19行
& 最多续39行
Visual Fortran允许续511行
第一章FORTRAN程序设计基础精品PPT课件

FORTRAN程序设计基础
计算机是在“程序”的控制下进行自动工作 的,它解决任何实际问题都依赖于解决问题的程 序。
学习FORTRAN程序设计的目的,就是要学 会利用FORTRAN语言编写出适合自己实际需要 的程序,让计算机完成自己指定的任务。
本章将介绍:
• 程序设计的基本概念
• FORTRAN 语言的发展
1. 一般流程图
一般流程图是一种传统的算法描述方法,它 用不同的几何图形来代表不同性质的操作。例 如,用矩形框表示要进行的操作,用菱形框表 示判断,用流程线将各步操作连接起来并指示 算法的执行方向。一般流程图的主要优点是直 观性强,初学者容易掌握。缺点是对流程线的 使用没有严格限制,如毫无限制地使流程任意 转来转去,将使流程图变得毫无规律,难以阅 读。为了提高算法可读性和可维护性,必须限 制无规则的转移,使算法结构规范化。
例1.1 求 u x y x y
其中
a2 b2 ab xa2 b2 ab
这一题的算法并不难,可写成:
a b
y
a
4
b
a b
(1)从键盘输入a、b的值。
(2)如果a<b,则 xa2b2,yaa bb,
否则 xa2b2,y 4 。
(3)计算u的值。
ab
(4)输出u的值。
ab ab
例1.2 输入十个数,要求找出其中最大的数。
(3) 有效性。算法中的每一步操作必须是可执行 的。
(4) 要有数据输入。算法中操作的对象是数据, 因此应提供有关数据。
(5) 要有结果输出。算法的目的是用来解决一个 给定的问题,因此应提供输出结果,否则算法 就2没有实际意义。
1.2.2 算法的描述
算法的描述有许多方法,常用的有:自然语言、一般流 程图、N-S图等。前面例1.1~例1.3的算法是用自然语言── 汉语描述的,其优点是通俗易懂,但它不太直观,描述不够 简洁,且容易产生二义性。在实际应用中常用流程图表示算 法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主 体
do 50 i=2,im-1
部
d1(i)=0.5d0*(d(i-1)+d(i+1))-dt*(u(i)*(d(i+1)-d(i-1))/2.d0/dx+
分
+
d(i)*(u(i+1)-u(i-1))/2.d0/dx)
u1(i)= 0.5d0*(u(i-1)+u(i+1))-dt*(u(i)*(u(i+1)-u(i-1))/2.d0/dx+ 可考虑
+
(t(i+1)-t(i-1))/2.d0/dx +t(i)/d(i)*(d(i+1)-d(i-1))/2.d0/dx) 加入人 为耗散
t1(i)=0.5d0*(t(i-1)+t(i+1))-dt*(u(i)*(t(i+1)-t(i-1))/2.d0/dx+
50 +
(gamma-1.d0)*t(i)*(u(i+1)-u(i-1))/2.d0/dx)
可采用另一计时变量,如tp, 其初值为0, tp=tp+dt,待tp快接近0.02,dt=0.02-tp, 然后输出结果,并重新令tp=0.
实例之二
1. 建模
磁场扩散
磁场扩散方程(仅1D)
初条
B(x,0) BB 0, 0, xx00
B 2B
t
解析解 B(x,t)2B 0 x/ 4teu2du 0
d1 (1)= d (1)
u1(1)= u (1)
t1(1)= t (1)
d1 (im)= d (im)
主
u1(im)= u (im)
体
t1(im)= t (im)
部
tim=tim+dt
分
dt=1.d0
do 60 i=2,im-1
固定边界条件
局地无量 纲声速
由柯朗条件定 下一时间步长
60
dt=dmin1(dt,dx/(dsqrt(gamma*t1(i))+dabs(u1(i)))
பைடு நூலகம்
模型方程
u t
2u x 2
1
全隐格式
u i n 1 u i n x t 2u i n 1 1 2 u i n 1 u i n 1 1
精度:O(t,x2) 稳定条件:恒稳
u in 1 1 (2 x2 t)u in 1 u in 1 1 x2 tu in
c
a
do 30 i=(im+1)/2+1,im
d1(i)=1.d-1
u1(i)=0.d0
30
t1(I)=1.d0
划分网格 设定初值
tim=0.d0
初始时间
dt=0.9d0*dx
初始时间步长
999 continue
do 40 i=1,im
d (i)= d1 (i) u(i)= u1 (i)
赋新值
40
t(i)= t1(i)
4. 选取适当的差分格式
模型方程
u c u 0
t
x
Lax格式或Friedrichs格式
u i n 1 1 2 u i n 1 u i n 1 2 c x tu i n 1 u i n 1
精度:O(t, x2 ,x2) 稳定条件: t x
t
|c |
对流体力学问题,其稳定条件为
If(dt.le.1.e-9) then输出”dt太小”并goto 888
goto 999
888 close(10) End
停止运算的 无量纲时间
Subroutine output(tim,d1,u1,t1)
…..
If(tim.eq.0)open(10,…..form=‘unformatted’)
write(10)d,u,t Return end
a, b,c 系数
可将3个变量一起 放在一个2维数组
设定常数
dx=1./dble(im-1)
do 10 i=1,im
x(i)=dx*dble(im-1)
10
continue
do 20 i=2, im
20
b1(i)=1.d0
b1(1)=0.d0
划分网格 设定初值
tim=0.d0
dt=(x(2)-x(1))**2
Fortran计算实例
3. 确定解域、划分网格及设置边界条件
可划分为上 千个格点
1
模拟区域: 网 格:
边 条:
0
1x1
x
1
x(i)2 (i 1 )/N ( 1 ) 1 均匀网格(最好用自适应网格)
fn(1 )f0 (1 ); fn(N )f0 (N ),f其 ,u ,T 中
在激波传播至边界之前有效
b
s
5. 编程及调试
program diffusion parameter(im=1001) implicit double precision(a-h,o-z) dimension x(im),bb(im) dimension b1(im) Dimension a(im),b(im),c(im),s(im) b0=1.67d-5 t0=1.d5 L0=1.d5 ……
d: 密度; u: 速度;t: 温度
可将3个变量一起 放在一个2维数组
设定常数
dx=2.d0/dble(im-1)
do 10 i=1,im
x(i)=dx*dble(i-1)-1.
10
continue
do 20 i=1,(im+1)/2
d1(i)=1.d0
u1(i)=0.d0
20
t1(i)=1.d0
t
x cs | u |
5. 编程及调试
program shocktube parameter(im=1001) implicit double precision(a-h,o-z) dimension x(im),d(m),u(im),t(im) dimension d1(m),u1(im),t1(im) d0=1.67d-5 t0=3.d2 r=2.78d-2 v0=dsqrt(r*t0) L0=10 gamma=1.4d0 ……
Continue write(*,*)tim,dt
屏幕输出供调试
如0.02, 0.04, 0.06, 0.08,……。即每0.02 时间间隔则将结果输出到数据文件。
主
体
部
if(tim在某些时刻)call output(tim,d1,u1,t1)
分
if(输出结果的次数等于tend/0.02)goto 888
2. 无量纲化
B B0B*
x L0x*
t
L2 0
t*
B 2B t
3. 确定解域、划分网格及设置边界条件
B
可划分为上
1
千个格点
x
0
1
模拟区域: 网 格: 边 条:
0x1 x(i)(i1)/N (1)
B n(1 )0 ; B n(N )B 0(N )
扩散至边界之前有效
均匀网格
4. 选取适当的差分格式
