还款计算表(等本递减法)
等额本息法和等额本金法的两种计算公式

等额本息法和等额本金法的两种计算公式一:按等额本金还款法:贷款额为:a,月利率为:i,年利率为:I,还款月数:n,an第n个月贷款剩余本金:a1=a, a2=a-a/n, a3=a-2*a/n ...次类推还款利息总和为Y每月应还本金:a/n每月应还利息:an*i每期还款a/n +an*i支付利息Y=(n+1)*a*i/2还款总额=(n+1)*a*i/2+a等额本金法的计算等额本金(递减法):计算公式:每月本金=贷款额÷期数第一个月的月供=每月本金+贷款额×月利率第二个月的月供=每月本金+(贷款额-已还本金)×月利率申请贷10万10年个人住房商业性贷款,试计算每月的月供款额?(月利率:4.7925‰)计算结果:每月本金:100000÷120=833元第一个月的月供:833+100000×4.7925‰=1312.3元第二个月的月供:833+(100000-833)×4.7925‰=1308.3元如此类推……二:按等额本息还款法:设贷款额为a,月利率为i,年利率为I,还款月数为n,每月还款额为b,还款利息总和为Y 1:I=12×i2:Y=n×b-a3:第一月还款利息为:a×i第二月还款利息为:〔a-(b-a×i)〕×i=(a×i-b)×(1+i)^1+b第三月还款利息为:{a-(b-a×i)-〔b-(a×i-b)×(1+i)^1-b〕}×i=(a×i-b)×(1+i)^2+b第四月还款利息为:=(a×i-b)×(1+i)^3+b第n月还款利息为:=(a×i-b)×(1+i)^(n-1)+b求以上和为:Y=(a×i-b)×〔(1+i)^n-1〕÷i+n×b4:以上两项Y值相等求得月均还款:b=a×i×(1+i)^n÷〔(1+i)^n-1〕支付利息:Y=n×a×i×(1+i)^n÷〔(1+i)^n-1〕-a还款总额:n×a×i×(1+i)^n÷〔(1+i)^n-1〕注:a^b表示a的b次方。
房贷等额本金和等额本息的计算公式

计算公式:等额本息还款法:每月月供额=〔贷款本金×月利率×(1+月利率)^还款月数〕÷〔(1+月利率)^还款月数-1〕每月应还利息=贷款本金×月利率×〔(1+月利率)^还款月数-(1+月利率)^(还款月序号-1)〕÷〔(1+月利率)^还款月数-1〕每月应还本金=贷款本金×月利率×(1+月利率)^(还款月序号-1)÷〔(1+月利率)^还款月数-1〕总利息=还款月数×每月月供额-贷款本金贷款金额:150000元贷款年限:5年(60个月)按照商业贷款,等额本息计算年利率:6.9%(月利率5.75‰)每月月供:2963.11元总利息:27786.47元计算原则:银行从每月月供款中,先收剩余本金利息,后收本金;利息在月供款中的比例中随剩余本金的减少而降低,本金在月供款中的比例因增加而升高,但月供总额保持不变。
等额本金还款法:每月月供额=(贷款本金÷还款月数)+(贷款本金-已归还本金累计额)×月利率每月应还本金=贷款本金÷还款月数每月应还利息=剩余本金×月利率=(贷款本金-已归还本金累计额)×月利率每月月供递减额=每月应还本金×月利率=贷款本金÷还款月数×月利率总利息=〔(总贷款额÷还款月数+总贷款额×月利率)+总贷款额÷还款月数×(1+月利率)〕÷2×还款月数-总贷款额贷款金额:150000元贷款年限:5年(60个月)按照商业贷款,等额本金计算年利率:6.9%(月利率5.75‰)首月月供:3362.5元逐月递减:14.38元末月月供:2514.38元总利息:26306.25元提前还款计算公式其实等额本金还款法的提前还款计算方法比较简单,只要大家仔细阅读很快就可以掌握。
在我国,等额本金还款法的特定是:每月还相同的本金,同时把当月所还本金的利息也还了。
还款计算表(等本递减法)
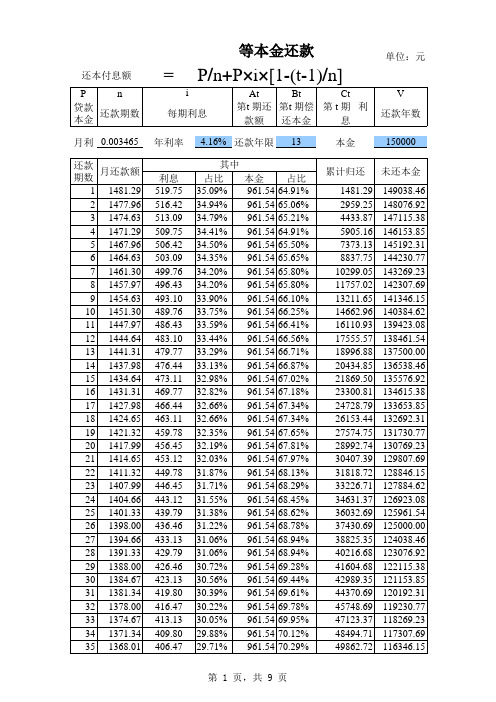
3 1474.63
4 1471.29
5 1467.96
6 1464.63
7 1461.30
8 1457.97
9 1454.63
10 1451.30
11 1447.97
12 1444.64
13 1441.31
14 1437.98
15 1434.64
16 1431.31
17 1427.98
18 1424.65
元pnatbtctv贷款本金还款期数第t期还款额第t期偿还本金第t期利息还款年数月利率0003465年利率416还款年限13本金150000利息5197551642513095097550642503094997649643493104897648643483104797747644473114697746644463114597845645453124497844645443124397943646433134297942646423134198041647413134098040647占比35093494347934413450343534203420339033753359334433293313329832823266326632353219320331873171315531383122310631063072305630393022300529882971本金961546491961546506961546521961546491961546550961546565961546580961546580961546610961546625961546641961546656961546671961546687961546702961546718961546734961546734961546765961546781961546797961546813961546829961546845961546862961546878961546894961546894961546928961546944961546961961546978961546995961547012961547029占比1234567891481291477961474631471291467961464631461301457971454631451301447971444641441311437981434641431311427981424651421321417991414651411321407991404661401331398001394661391331388001384671381341378001374671371341368011481292959254433875905167373138837751029905117570213211651466296161109317555571899688204348521869
等额还本计算公式(二)

等额还本计算公式(二)
等额还本计算公式
1. 等额本息计算公式
等额本息是指贷款人每月还款金额固定,包含本金和利息部分,
每月还款金额相同。
公式:
月还款金额 = 贷款本金 × [月利率 × (1 + 月利率)^还款月数] / [(1 + 月利率)^还款月数 - 1]
其中,月利率 = 年利率 / 12,还款月数为贷款期限(月)。
举例:
假设有一笔贷款本金为10万元,年利率为5%,贷款期限为36个月(3年)。
带入公式可得:
月利率 = 5% / 12 = %
月还款金额 = 10万元 × [% × (1 + %)^36] / [(1 + %)^36 - 1]≈ 3,元
因此,每月需还款约为3,元。
2. 等额本金计算公式
等额本金是指贷款人每月还款金额固定,主要包含本金部分,利息逐月递减。
公式:
每月本金还款金额 = 贷款本金 / 还款月数
每月利息还款金额 = 贷款本金 × 月利率
月还款金额 = 每月本金还款金额 + 每月利息还款金额
其中,月利率 = 年利率 / 12,还款月数为贷款期限(月)。
举例:
假设有一笔贷款本金为10万元,年利率为5%,贷款期限为36个月(3年)。
带入公式可得:
每月本金还款金额 = 10万元/ 36 ≈ 2,元
每月利息还款金额 = 10万元× % ≈ 元
月还款金额 = 2,元 + 元≈ 3,元
因此,首月需还款3,元,之后每月还款金额递减。
以上是等额还本计算公式的相关内容。
还款计划表计算公式算法优化

还款计划表计算公式算法优化1.还款计划表计算公式✧等额计算公式应还本利合计= 贷款金额×月利率×(1+月利率)总还款期数(1+月利率)总还款期数– 1应还本金=应还金额-应还利息应还本金金额= 贷款金额×月利率×(1+月利率)还款期数-1(1+月利率)总还款期数– 1应还利息=贷款金额×月利率应还利息金额= 贷款金额×月利率×[(1+月利率)总还款期数- (1+月利率)还款期数-1] (1+月利率)总还款期数– 1✧按年递增减计算公式按年递增(减)还款法有两个公式,公式A在贷款放款时使用,而公式B在提前还款、利率调整及调整贷款期限时使用公式A本息合计=P×I×(1+I)V×12[(1+I)12-(1+K)] [(1+I)12-1]×[(1+I)V×12-(1+K)V]其中:P为本金,I为月利率,V为贷款年限,贷款总期数n=12*V,K为每年递增(减)比率(K>0递增,K<0递减,K=0时,为等额还款法)。
公式B本息合计=P×I×(1+I)n(1+I)12×V×[(1+I)Wb-1]+(1+K)× [(1+I)12-1] ×[(1+I) 12×V-(1+K)V]/ [(1+I)12-(1+K)]应还利息=贷款金额×月利率应还本金=本息合计-应还利息其中:P为剩余贷款本金;n为剩余贷款期数;V为剩余贷款年数(本年除外);Wb为本年度尚未扣款的期数,n=12*V+Wb(因为提前还款后,剩余的期数不再是12的整除数,不能套用公式A,只能用公式B,将剩余的期数分为两个部分)说明:由于等额计算公式、按年递增减计算公式中均涉及到指数函数(1 + i)n的运算,这里i为日利率,n为还款周期,通常还款周期会有100或者更多,导致主机运行效率大幅度降低,为解决此问题进行算法分析,如下。
等额本金还款计算

等额本金还款计算等额本金是指一种贷款的还款方式,是在还款期内把贷款数总额等分,每月偿还同等数额的本金和剩余贷款在该月所产生的利息,这样由于每月的还款本金额固定,而利息越来越少,借款人起初还款压力较大,但是随时间的推移每月还款数也越来越少。
计算公式等额本金法最大的特点是每月的还款额不同,呈现逐月递减的状态;它是将贷款本金按还款的总月数均分,再加上上期剩余本金的利息,这样就形成月还款额,所以等额本金法第一个月的还款额最多,然后逐月减少,越还越少,计算公式为:每月还本付息金额=(本金/还款月数)+(本金-累计已还本金)×月利率每月本金=总本金/还款月数每月利息=(本金-累计已还本金)×月利率还款总利息=(还款月数+1)×贷款额×月利率/2还款总额=(还款月数+1)×贷款额×月利率/2+ 贷款额注意:在等额本金法中,人们每月归还的本金额始终不变,利息随剩余本金的减少而减少,因而其每月还款额逐渐减少。
适合人群等额本金法因为在前期的还款额度较大,而后逐月递减,所以比较适合在前段时间还款能力强的贷款人,当然一些年纪稍微大一点的人也比较适合这种方式,因为随着年龄增大或退休,收入可能会减少。
对比等额本息是在还款期内,每月偿还同等数额的贷款(包括本金和利息)。
每月还款金额= [贷款本金×月利率×(1+月利率)^还款月数]÷[(1+月利率)^还款月数-1]等额本息还款法特点:等额本息还款法本金逐月递增,利息逐月递减,月还款数不变;相对于等额本金还款法的劣势在于支出利息较多,还款初期利息占每月供款的大部分,随本金逐渐返还供款中本金比重增加。
但该方法每月的还款额固定,可以有计划地控制家庭收入的支出,也便于每个家庭根据自己的收入情况,确定还贷能力。
等额本金还款法特点:等额本金还款法本金保持相同,利息逐月递减,月还款数递减;由于每月的还款本金额固定,而利息越来越少,贷款人起初还款压力较大,但是随时间的推移每月还款数也越来越少。
WPS表格《等额本息法》还房贷模板

计算公式复杂每月还本付息金额本金月利率1月利率贷款月数1月利率还款月数1其中Байду номын сангаас月利息剩余本金贷款月利率每月本金每月月供额每月利息
WPS 表格《等额本息法》还房贷模板 按揭贷款,即以房产作为抵押的贷款。每月还款又称为月供。目前银行多采用等额本息法, 利息是递减的。 计算公式复杂, 每月还本付息金额 = [ 本金 × 月利率 ×(1+月利率)^贷款月 数 ] / [(1+月利率)^还款月数 - 1], 其中:每月利息 = 剩余本金 * 贷款月利率 ,每月本金 = 每月月供额 – 每月利息。注意上面的“^”是幂符号,“/”是除以。 由于其中涉及 N 次方 运算,手工无法实现,一般计算器也难以计算。但是用 WPS 表格可以轻松实现,因为有专 门的函数。下面介绍是如何实现的 1、打开 WPS 表格,新建一个空白表格,在 A1、B1、C1、D1 分别输入“期数”、“本金”、 “利息”、“月供”。 2、计算月供:在 D2 中输入“=PMT(0.0051,120,100000)”, 拖动填充柄向下复制到 D121(图 1)。
图3 这样一个详细的还款表就做成了,不仅能制作还款表,也能计算年金等投资。 公式讲解: 1、函数 PMT 基于固定利率及等额分期付款方式,返回贷款的每期付款额。 PMT(0.0051,120,100000),0.0051 为月利率,120 为贷款期限即 120 月(10 年),100000 为贷款额。 2、函数 PPMT 基于固定利率及等额分期付款方式,返回投资在某一给定期间内的本金 偿还额。 PPMT(0.0051,ROW()-1,120,100000),0.0051 为月利率, ROW()-1 为期数,ROW()为行数, 借助行数算出期数,120 为贷款期限即 120 月(10 年),100000 为贷款额。
银行贷款分期还贷计算表

贷款月数(月) 月利率
360 0.003958
等 额 本 金 还 款 法
银行贷款分期还款计算表
备 注 每月还本付息 每月还利息 每月还本金 剩余本金 还款总利息 贷款月利率 贷款日利率 还款总额 1877930.41 877930.41 5216.47
每月还本付息金额 每月本金 每月利息 还款总利息 还款总额
6736.11 第一个月还
714479.17 1714479.17
还款计算表
计 算 公 式 [贷款本金×月利率×(1+月利率)^还款月数]÷ [(1+月利率)^还款月数-1] 剩余本金x贷款月利率(第一个月的本金就是的贷款金额,逐月递减) 每月还款金额-每月还利息 上月剩余本金-本月偿还本金 贷款额*贷款月数*月利率*(1+月利率)^还款月数/[(1+月利率)^还款月数 贷款年利率/12 贷款年利率/360=贷款月利率/30
(本金/还款月数)+(本金-累计已还本金)×月利率 总本金/还款月数 (本金-累计已还本金)×月利率 (还款月数+1)*贷款额*月利率/2 (还款月数+1)*贷款额*月利率/2+贷款额
还款月数-1]
月递减)
率)^还款月数 - 1]-贷款额
等额本金算法公式表

等额本金算法公式表等额本金算法是一种常用的还款方式,也是银行和其他金融机构常用的一种贷款计算方法。
该算法主要用于计算贷款每期还款额度相等的案例,其计算公式如下:每期应还本金 = 贷款总额 / 还款期数每期应还利息 = 剩余贷款本金 ×月利率每期还款金额 = 每期应还本金 + 每期应还利息在等额本金算法中,每期还款的本金相等,而每期还款的利息则随着剩余贷款本金的减少逐渐减少。
这意味着前期每月要还的利息较高,后期逐渐减少,每月还款总额保持不变。
例如,假设有一个贷款总额为100,000元,贷款期限为12个月,年利率为5%的贷款案例,可以使用等额本金算法计算每月还款金额。
第一个月:每期应还本金 = 100,000元 / 12 = 8,333.33元每期应还利息 = 100,000元 × 5% ÷ 12 = 416.67元每期还款金额 = 8,333.33元 + 416.67元 = 8,750元第二个月:剩余贷款本金 = 100,000元 - 8,333.33元 = 91,666.67元每期应还本金 = 91,666.67元 / 12 = 7,638.89元每期应还利息 = 91,666.67元 × 5% ÷ 12 = 380.56元每期还款金额 = 7,638.89元 + 380.56元 = 8,019.44元通过以上计算,可以得到每个月的还款金额。
根据等额本金算法,每月还款金额逐渐减少,直至最后一期还款金额为最低。
等额本金算法的优点之一是,贷款总利息较少,因为随着每个月剩余贷款本金的减少,每月应还利息也相应减少。
相比之下,等额本息算法中每月还款金额相等,但总利息较高。
需要注意的是,在使用等额本金算法计算贷款时,还需要考虑月利率的计算方式。
通常,年利率除以12即可得到月利率。
但在某些特殊情况下,需要根据实际情况进行调整。
总之,等额本金算法是一种常用的贷款计算方法,适用于每期还款额度相等的贷款案例。
等额本金和等额本息逐月还款明细表(可修改)
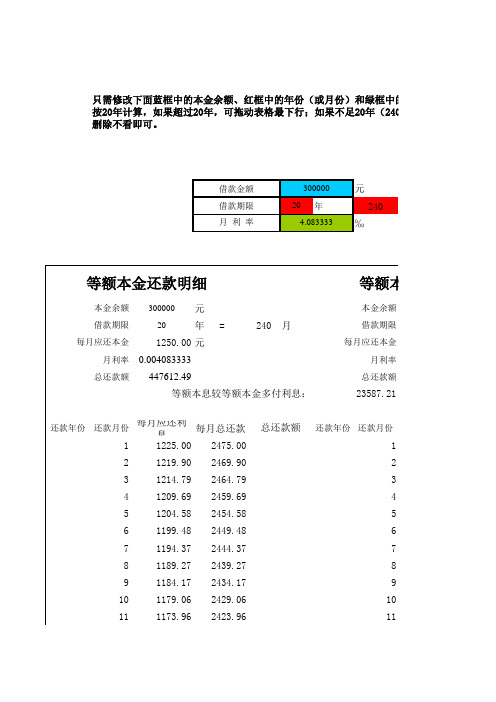
元20年240‰300000元20年 =240月1250.00元月利率0.004083333月利率总还款额447612.49总还款额还款年份还款月份每月应还利息每月总还款还款年份还款月份11225.002475.00121219.902469.90 231214.792464.79 341209.692459.69 451204.582454.58 561199.482449.48 671194.372444.37 781189.272439.27 891184.172434.17 9101179.062429.06 10 111173.962423.96 114.083333借款金额月 利 率借款期限等额本息较等额本金多付利息:23587.21总还款额只需修改下面蓝框中的本金余额、红框中的年份(或月份)和绿框中的利按20年计算,如果超过20年,可拖动表格最下行;如果不足20年(240月),表下半部出现行删除不看即可。
每月应还本金每月应还本金等额本金还款明细本金余额借款期限等额本息本金余额借款期限3000001121168.852418.85112 131163.752413.7513141158.652408.6514151153.542403.5415161148.442398.4416171143.332393.3317181138.232388.2318191133.122383.1219201128.022378.0220211122.922372.9221221117.812367.8122231112.712362.7123 2241107.602357.60224 251102.502352.5025261097.402347.4026271092.292342.2927281087.192337.1928291082.082332.0829301076.982326.9830311071.872321.8731321066.772316.7732331061.672311.6733341056.562306.5634351051.462301.4635 3361046.352296.35336 371041.252291.2537381036.152286.1538391031.042281.0439401025.942275.9440411020.832270.8341421015.732265.7342431010.622260.6243441005.522255.5244451000.422250.424546995.312245.314647990.212240.2147 448985.102235.10448 49980.002230.004950974.902224.905051969.792219.795152964.692214.695253959.582209.585354954.482204.485455949.372199.375556944.272194.275657939.172189.175758934.062184.065859928.962178.9659 560923.852173.85560 61918.752168.756162913.652163.656263908.542158.546364903.442153.446465898.332148.336566893.232143.236667888.122138.126768883.022133.026869877.922127.926970872.812122.817071867.712117.7171 672862.602112.60672 73857.502107.507374852.402102.407475847.292097.297576842.192092.197677837.082087.087778831.982081.987879826.872076.877980821.772071.778081816.672066.678182811.562061.568283806.462056.4683 784801.352051.35784 85796.252046.258586791.152041.158687786.042036.048788780.942030.948889775.832025.838990770.732020.739091765.622015.629192760.522010.529293755.422005.429394750.312000.319495745.211995.2195 896740.101990.10896 97735.001985.009798729.901979.909899724.791974.7999 100719.691969.69100 101714.581964.58101 102709.481959.48102 103704.371954.37103 104699.271949.27104 105694.171944.17105 106689.061939.06106 107683.961933.96107 9108678.851928.859108 109673.751923.75109 110668.651918.65110111663.541913.54111112658.441908.44112113653.331903.33113114648.231898.23114115643.121893.12115116638.021888.02116117632.921882.92117118627.811877.81118119622.711872.71119 10120617.601867.6010120 121612.501862.50121122607.401857.40122123602.291852.29123124597.191847.19124125592.081842.08125126586.981836.98126127581.871831.87127128576.771826.77128129571.671821.67129130566.561816.56130131561.461811.46131 11132556.351806.3511132 133551.251801.25133134546.151796.15134135541.041791.04135136535.941785.94136137530.831780.83137138525.731775.73138139520.621770.62139140515.521765.52140141510.421760.42141142505.311755.31142143500.211750.2114312144495.101745.1012144 145490.001740.00145146484.901734.90146147479.791729.79147148474.691724.69148149469.581719.58149150464.481714.48150151459.371709.37151152454.271704.27152153449.171699.17153154444.061694.06154155438.961688.96155 13156433.851683.8513156 157428.751678.75157158423.651673.65158159418.541668.54159160413.441663.44160161408.331658.33161162403.231653.23162163398.121648.12163164393.021643.02164165387.921637.92165166382.811632.81166167377.711627.71167 14168372.601622.6014168 169367.501617.50169170362.401612.40170171357.291607.29171172352.191602.19172173347.081597.08173174341.981591.98174175336.871586.87175176331.771581.77176177326.671576.67177178321.561571.56178179316.461566.46179 15180311.351561.3515180 181306.251556.25181182301.151551.15182183296.041546.04183184290.941540.94184185285.831535.83185186280.731530.73186187275.621525.62187188270.521520.52188189265.421515.42189190260.311510.31190191255.211505.21191 16192250.101500.1016192 193245.001495.00193194239.901489.90194195234.791484.79195196229.691479.69196197224.581474.58197198219.481469.48198199214.371464.37199200209.271459.27200201204.171454.17201202199.061449.06202203193.961443.96203 17204188.851438.8517204 205183.751433.75205206178.651428.65206207173.541423.54207208168.441418.44208209163.331413.33209210158.231408.23210211153.121403.12211212148.021398.02212213142.921392.92213214137.811387.81214215132.711382.71215 18216127.601377.6018216 217122.501372.50217218117.401367.40218219112.291362.29219220107.191357.19220221102.081352.0822122296.981346.9822222391.871341.8722322486.771336.7722422581.671331.6722522676.561326.5622622771.461321.46227 1922866.351316.3519228 22961.251311.2522923056.151306.1523023151.041301.0423123245.941295.9423223340.831290.8323323435.731285.7323423530.621280.6223523625.521275.5223623720.421270.4223723815.311265.3123823910.211260.21239447612.4920240 5.101255.1020240月总利息=总贷款数×月利率×(还款次数+1)÷2300000元20年 =240月1963.33元0.004083333471199.70元每月应还本金每月应还利息剩余本金总还款额738.331225.00299261.67741.351221.99298520.32744.371218.96297775.95747.411215.92297028.53750.471212.87296278.07753.531209.80295524.54756.611206.73294767.93759.701203.64294008.23762.801200.53293245.44765.911197.42292479.52769.041194.29291710.48框内内容不要修改!中的利率即可,其他部分不要修改。
等额本息法和等额本金法的两种计算公式

等额本息法和等额本金法的两种计算公式一:按等额本金还款法:贷款额为:a,月利率为:i,年利率为:I,还款月数:n,an第n个月贷款剩余本金:a1=a, a2=a-a/n, a3=a-2*a/n ...次类推还款利息总和为Y每月应还本金:a/n每月应还利息:an*i每期还款a/n +an*i支付利息Y=(n+1)*a*i/2还款总额=(n+1)*a*i/2+a等额本金法的计算等额本金(递减法):计算公式:每月本金=贷款额÷期数第一个月的月供=每月本金+贷款额×月利率第二个月的月供=每月本金+(贷款额-已还本金)×月利率申请贷10万10年个人住房商业性贷款,试计算每月的月供款额?(月利率:4.7925‰)计算结果:每月本金:100000÷120=833元第一个月的月供:833+100000×4.7925‰=1312.3元第二个月的月供:833+(100000-833)×4.7925‰=1308.3元如此类推……二:按等额本息还款法:设贷款额为a,月利率为i,年利率为I,还款月数为n,每月还款额为b,还款利息总和为Y 1:I=12×i2:Y=n×b-a3:第一月还款利息为:a×i第二月还款利息为:〔a-(b-a×i)〕×i=(a×i-b)×(1+i)^1+b第三月还款利息为:{a-(b-a×i)-〔b-(a×i-b)×(1+i)^1-b〕}×i=(a×i-b)×(1+i)^2+b第四月还款利息为:=(a×i-b)×(1+i)^3+b第n月还款利息为:=(a×i-b)×(1+i)^(n-1)+b求以上和为:Y=(a×i-b)×〔(1+i)^n-1〕÷i+n×b4:以上两项Y值相等求得月均还款:b=a×i×(1+i)^n÷〔(1+i)^n-1〕支付利息:Y=n×a×i×(1+i)^n÷〔(1+i)^n-1〕-a还款总额:n×a×i×(1+i)^n÷〔(1+i)^n-1〕注:a^b表示a的b次方。
