插值拟合数学建模算法
数学建模插值及拟合详解Word版

数学建模插值及拟合详解Word版插值和拟合实验⽬的:了解数值分析建模的⽅法,掌握⽤Matlab进⾏曲线拟合的⽅法,理解⽤插值法建模的思想,运⽤Matlab⼀些命令及编程实现插值建模。
实验要求:理解曲线拟合和插值⽅法的思想,熟悉Matlab相关的命令,完成相应的练习,并将操作过程、程序及结果记录下来。
实验内容:⼀、插值1.插值的基本思想·已知有n +1个节点(xj,yj),j = 0,1,…, n,其中xj互不相同,节点(xj, yj)可看成由某个函数 y= f(x)产⽣;·构造⼀个相对简单的函数 y=P(x);·使P通过全部节点,即 P (xk) = yk,k=0,1,…, n ;·⽤P (x)作为函数f ( x )的近似。
2.⽤MATLAB作⼀维插值计算yi=interp1(x,y,xi,'method')注:yi—xi处的插值结果;x,y—插值节点;xi—被插值点;method—插值⽅法(‘nearest’:最邻近插值;‘linear’:线性插值;‘spline’:三次样条插值;‘cubic’:⽴⽅插值;缺省时:线性插值)。
注意:所有的插值⽅法都要求x是单调的,并且xi不能够超过x的范围。
练习1:机床加⼯问题x035791112131415y0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6⽤程控铣床加⼯机翼断⾯的下轮廓线时每⼀⼑只能沿x⽅向和y⽅向⾛⾮常⼩的⼀步。
表3-1给出了下轮廓线上的部分数据但⼯艺要求铣床沿x⽅向每次只能移动0.1单位.这时需求出当x坐标每改变0.1单位时的y坐标。
试完成加⼯所需的数据,画出曲线.步骤1:⽤x0,y0两向量表⽰插值节点;步骤2:被插值点x=0:0.1:15; y=y=interp1(x0,y0,x,'spline');步骤3:plot(x0,y0,'k+',x,y,'r')grid on答:x0=[0 3 5 7 9 11 12 13 14 15 ];y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ];x=0:0.1:15;y=interp1(x0,y0,x,'spline');plot(x0,y0,'k+',x,y,'r')grid on0510150.511.522.53.⽤MATLAB 作⽹格节点数据的插值(⼆维) z=inte rp2(x0,y0,z0,x,y,’method’) 注:z —被插点值的函数值;x0,y0,z0—插值节点;x ,y —被插值点;method —插值⽅法(‘nearest’ :最邻近插值;‘linear’ :双线性插值; ‘cubic’ :双三次插值;缺省时:双线性插值)。
数学建模插值与拟合

数学建模插值与拟合数据插值与拟合插值与插值函数:已知由(可能未知或⾮常复杂)产⽣的⼀批离散数据,且个互异插值节点,在插值区间内寻找⼀个相对简单的函数,使其满⾜下列插值条件:再利⽤已求得的计算任⼀⾮插值节点的近似值,这就是插值。
其中称为插值函数,称为被插函数。
最⼩⼆乘拟合:已知⼀批离散的数据,互不相同,寻求⼀个拟合函数,使与的误差平⽅和在最⼩⼆乘意义下最⼩。
在最⼩⼆乘意义下确定的称为最⼩⼆乘拟合函数。
1)Lagrange插值法a.待定系数法:假设插值多项式,利⽤待定系数法即可求得满⾜插值条件的插值函数。
关键在于确定待定系数。
b.利⽤基函数的构造⽅法⾸先构造个满⾜条件:的次插值基函数,再将其线性组合即可得如下的Lagrange插值多项式:其中c.Lagrange插值余项注:上述两种构造⽅法所得的Lagrange插值多项式是⼀样的,即满⾜插值条件的Lagrange插值多项式是唯⼀的。
2)分段线性插值作分段线性插值的⽬的在于克服Lagrange插值⽅法可能发⽣的不收敛性缺点。
所谓分段线性插值就是利⽤每两个相邻插值节点作线性插值,即可得如下分段线性插值函数:其中特点:插值函数序列具有⼀致收敛性,克服了⾼次Lagrange插值⽅法的缺点,故可通过增加插值节点的⽅法提⾼其插值精度。
但存在于节点处不光滑、插值精度低的缺点。
3)三次样条插值三次样条插值的⽬的在于克服Lagrange插值的不收敛性和提⾼分段线性插值函数在节点处的光滑性。
所谓三次样条插值⽅法就是在满⾜下列条件:a.b.在每个⼦区间上是三次多项式的三次样条函数中寻找满⾜如下插值条件:以及形如等边界条件的插值函数的⽅法。
特点:三次样条插值函数序列⼀致收敛于被插函数,因此可通过增加节点的⽅法提⾼插值的精度。
4)插值⽅法的Matlab实现⼀维数据插值MATLAB中⽤函数interp1来拟合⼀维数据,语法是YI = INTERP1(X,Y,XI,⽅法)其中(X,Y)是已给的数据点,XI 是插值点,其中⽅法主要有'linear' -线性插值,默认'pchip' -逐段三次Hermite插值'spline' -逐段三次样条函数插值其中最后⼀种插值的曲线⽐较平滑例:x=0:.12:1; x1=0:.02:1;y=(x.^2-3*x+5).*exp(-5*x).*sin(x);plot(x,y,'o'); hold on;y1=interp1(x,y,x1,'spline');plot(x1,y1,':')如果要根据样本点求函数的定积分,⽽函数⼜是⽐较光滑的,则可以⽤样条函数进⾏插值后再积分,在MATLAB 中可以编写如下程序:function y=quadspln(x0,y0,a,b)f=inline(‘interp1(x0,y0,x,’’spline’’)’,’x’,’x0’,’y0’);y=quadl(f,a,b,1e-8,[],x0,y0);现求six(x)在区间[0,pi]上的定积分,只取5点x0=[0,0.4,1,2,pi];y0=sin(x0);I=quadspln(x0,y0,0,pi)结果得到的值为 2.01905,精确值为2⼆元函数插值:MATLAB中⽤函数interp2来拟合⼆维⽹格(X,Y)上的数据Z,语法是YI = INTERP2(X,Y, Z,XI, YI,⽅法)其中(X,Y,Z)是已给的数据点,(XI,YI)是插值点坐标,其中⽅法主要有'linear' -线性插值,默认'pchip' -逐段三次Hermite插值'spline' -逐段三次样条函数插值其中最后⼀种插值的曲⾯⽐较平滑例:[x,y]=meshgrid(-3:.6:3,-2:.4:2);z=(x.^2-2*x).*exp(-x.^2-y.^2-x..*y);[x1,y1]=meshgrid(-3:.2:3,-2:.2:2);%⽣成⽹格,x1和y1均为同样size的矩阵z1=interp2(x,y,z,x1,y1,’spline’); %z1是矩阵,size 和x1,y1相同surf(x1,y1,z1);axis([-3,3,-2,2,-0.7,1.5]);-33如果数据不是在⽹格上取的,则可⽤函数griddata 来解决语法是YI = griddata(X,Y, Z ,XI, YI ,‘v4’)其中(X , Y ,Z )是已给的数据点,(XI ,YI )是插值点坐标,其中除了⽅法‘v4’外还有 'linear' -线性插值,默认 'cublc' -逐段三次Hermite 插值 'nearest' 其中‘v4’⽅法⽐较好例x=-3+6*rand(200,1); %⽣成随机点的x坐标向量xy=-2+4*rand(200,1); %⽣成随机点的y坐标向量yz=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); % 上述点的样本值向量z[x1,y1]=meshgrid(-3:.2:3,-2:.2:2); %⽣成⽹格,x1和y1均为同样size的矩阵z1=griddata(x,y,z,x1,y1,’v4’);surf(x1,y1,z1);axis([-3,3,-2,2,-0.7,1.5]);⽣成的图类似上图。
插值与拟合

且 f(1.5) ≈L1(1.5) = 0.885。
Lagrange插值法的缺点
• 多数情况下,Lagrange插值法效果是不错的, 但随着节点数n的增大,Lagrange多项式的次 (Runge)现象。
• 例:在[-5,5]上用n+1个等距节点作插值多项 式Ln(x),使得它在节点处的值与函数y = 1/(1+25x2)在对应节点的值相等,当n增大时, 插值多项式在区间的中间部分趋于y(x),但 对于满足条件0.728<|x|<1的x, Ln(x)并不趋 于y(x)在对应点的值,而是发生突变,产生 剧烈震荡,即Runge现象。
总结
• 拉格朗日插值:其插值函数在整个区间 上是一个解析表达式;曲线光滑;收敛 性不能保证,用于理论分析,实际意义 不大。
• 分段线性插值和三次样条插值:曲线不 光滑(三次样条已有很大改进);收敛 性有保证;简单实用,应用广泛。
1.2 二维插值
• 二维插值是基于一维插值同样的思想, 但是它是对两个变量的函数Z=f(x,y)进 行插值。
• n=5; • x0=-1:1/(n-1):1;y0=1./(1+25*x0.^2);y1=lagr(x0,y0,x); • subplot(2,2,2), • plot(x,z,'r-',x,y,'m-'),hold on %原曲线 • plot(x,y1,'b'),gtext('L8(x)','FontSize',12),pause %Lagrange曲线
基函数为
l0 (x)
x x1 x0 x1
x2 1 2
2
x
l1(x)
线性插值函数为
数学建模十大经典算法( 数学建模必备资料)

建模十大经典算法1、蒙特卡罗算法。
该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时通过模拟可以来检验自己模型的正确性。
2、数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具。
3、线性规划、整数规划、多元规划、二次规划等规划类问题。
建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo、MATLAB软件实现。
4、图论算法。
这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。
5、动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中。
6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法。
这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。
7、网格算法和穷举法。
网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。
8、一些连续离散化方法。
很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9、数值分析算法。
如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10、图象处理算法。
赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理。
历年全国数学建模试题及解法赛题解法93A非线性交调的频率设计拟合、规划93B足球队排名图论、层次分析、整数规划94A逢山开路图论、插值、动态规划94B锁具装箱问题图论、组合数学95A飞行管理问题非线性规划、线性规划95B天车与冶炼炉的作业调度动态规划、排队论、图论96A最优捕鱼策略微分方程、优化96B节水洗衣机非线性规划97A零件的参数设计非线性规划97B截断切割的最优排列随机模拟、图论98A一类投资组合问题多目标优化、非线性规划98B灾情巡视的最佳路线图论、组合优化99A自动化车床管理随机优化、计算机模拟99B钻井布局0-1规划、图论00A DNA序列分类模式识别、Fisher判别、人工神经网络00B钢管订购和运输组合优化、运输问题01A血管三维重建曲线拟合、曲面重建01B 公交车调度问题多目标规划02A车灯线光源的优化非线性规划02B彩票问题单目标决策03A SARS的传播微分方程、差分方程03B 露天矿生产的车辆安排整数规划、运输问题04A奥运会临时超市网点设计统计分析、数据处理、优化04B电力市场的输电阻塞管理数据拟合、优化05A长江水质的评价和预测预测评价、数据处理05B DVD在线租赁随机规划、整数规划06A 出版资源配置06B 艾滋病疗法的评价及疗效的预测 07A 中国人口增长预测 07B 乘公交,看奥运 多目标规划 数据处理 图论 08A 数码相机定位 08B 高等教育学费标准探讨09A 制动器试验台的控制方法分析 09B 眼科病床的合理安排 动态规划 10A 10B赛题发展的特点:1.对选手的计算机能力提出了更高的要求:赛题的解决依赖计算机,题目的数据较多,手工计算不能完成,如03B ,某些问题需要使用计算机软件,01A 。
数学建模案例分析插值与拟合方法建模1数据插值方法及应用

第十章 插值与拟合方法建模在生产实际中,常常要处理由实验或测量所得到的一批离散数据,插值与拟合方法就是要通过这些数据去确定某一类已经函数的参数,或寻求某个近似函数使之与已知数据有较高的拟合精度.插值与拟合的方法很多,这里主要介绍线性插值方法、多项式插值方法和样条插值方法,以及最小二乘拟合方法在实际问题中的应用。
相应的理论和算法是数值分析的内容,这里不作详细介绍,请参阅有关的书籍.§1 数据插值方法及应用在生产实践和科学研究中,常常有这样的问题:由实验或测量得到变量间的一批离散样点,要求由此建立变量之间的函数关系或得到样点之外的数据。
与此有关的一类问题是当原始数据),(,),,(),,(1100n n y x y x y x 精度较高,要求确定一个初等函数)(x P y =(一般用多项式或分段多项式函数)通过已知各数据点(节点),即n i x P y i i ,,1,0,)( ==,或要求得函数在另外一些点(插值点)处的数值,这便是插值问题。
1、分段线性插值这是最通俗的一种方法,直观上就是将各数据点用折线连接起来.如果b x x x a n =<<<= 10那么分段线性插值公式为n i x x x y x x x x y x x x x x P i i i i i i i i i i ,,2,1,,)(11111 =≤<--+--=----- 可以证明,当分点足够细时,分段线性插值是收敛的。
其缺点是不能形成一条光滑曲线。
例1、已知欧洲一个国家的地图,为了算出它的国土面积,对地图作了如下测量:以由西向东方向为x 轴,由南向北方向为y 轴,选择方便的原点,并将从最西边界点到最东边界点在x 轴上的区间适当的分为若干段,在每个分mm ).根据地图的比例,18 mm 相当于40 km 。
根据测量数据,利用MATLAB 软件对上下边界进行线性多项式插值,分别求出上边界函数)(2x f ,下边界函数)(1x f ,利用求平面图形面积的数值积分方法—将该面积近似分成若干个小长方形,分别求出这些长方形的面积后相加即为该面积的近似解。
数学建模之插值与拟合

matlab中拟合的函数
非线性曲线拟合 Matlab中对于多项式拟合,有现成的函数
c = lsqcurvefit ( ′fun′, x0, xdata, ydata)
matlab中拟合的函数
非线性曲线拟合例题
对下面的x、y进行数据拟合
x=[3.6,7.7,9.3,4.1,8.6,2.8,1.3,7.9,10,5.4]; y=[16.5,150.6,263.1,24.7,208.5,9.9,2.7,163.9,325,54.3];
最小二乘法
线性最小二乘法是解决曲线拟合最常用的方法,基本 思路是,令
f (x) a1r1(x) a2r2 (x) amrm (x) • 其中,rk(x)是事先选定的一组线性无关的函数,ak是待定系
数(k=1,2,...,m,m<n)。拟a合准则是使yi,i=1,2,3...,n,与f (xi )
• 求:利用最小二乘法求得上述拟合函数
求解方法
(1)做散点图,通过散点图判断函数为:y=ax+b
(2)根据最小二乘法原理可知,即使下式中M最小
10
M yi axi b2
i 1
(3)把M看作是自变量为a和b的函数,由多元函数取最值
的条件可知:
M M
a b
a, a,
b b
0 0
M
a
M
b
目录
1
插值法与拟合法
2 matlab中插值的函数
3 matlab中拟合的函数 4 插值与拟合的运用
插值法与拟合法的基本介绍
插值法:求过已知有限个数据点的近似函数。
拟合法:已知有限个数据点,求近似函数,不要求
过已知数据点,只要求在某种意义下它在这些点上 的总偏差最小。
数学建模插值与拟合课件
设函数 y f (x) 在 n 1个相异点 x0 , x1, x2 , , xn 上的值为 y 0 , y1, y2 , , yn ,要求一个次数≤n 的代数多
项式
Pn (x) a0 a1x a2 x 2 an x n
使在节点 xi 上成立 Pn (xi ) yi (i 0,1,2, , n) ,称此为 n 次代数插值问题,Pn (x) 称为插值多项式。可以证明 n
如果不要求近似函数通过所有数据点, 而是要求它能较好地反映数据变化规律的近 似函数的方法称为数据拟合。(必须有函数 表达式)
近似函数不一定(曲线或曲面)通过所 有的数据点。
三、插值与拟合的区别和联系
1、联系 都是根据实际中一组已知数据来构造一个能够 反映数据变化规律的近似函数的方法。 2、区别 插值问题不一定得到近似函数的表达形式,仅 通过插值方法找到未知点对应的值。数据拟合 要求得到一个具体的近似函数的表达式。
图所示,当n 增大时,pn x在两端会发出激烈
的振荡,这就是所谓龙格现象。
龙格现象
2
y=1/(1+x2) y=p4(x) y=p10(x) 1.5
1
0.5
0
-0.5
-5 -4 -3 -2 -1
0
1
2
3
4
5
x
To MATLAB lch(larg1)
分段插值的概念
所谓分段插值,就是将被插值函数逐段 多项式化。一般来说,分段插值方法的处理 过程分两步,先将所考察的区间作一分划
y1
lj(x)
当n =2 时,有三点二次(抛物线)插值多项式:
P2
(x)
(x (x0
x1)(x x2 ) x1)(x0 x2 )
数学建模常见的一些方法【04拟合算法】

数学建模常见的⼀些⽅法【04拟合算法】@⽬录数学建模常见的⼀些⽅法1. 拟合算法与插值问题不同,在拟合问题中不需要曲线⼀定经过给定的点。
拟合问题的⽬标是寻求⼀个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合的最好(最⼩化损失函数)。
1.1 插值和拟合的区别 插值算法中,得到的多项式f(x)要经过所有样本点。
但是如果样本点太多,那么这个多项式次数过⾼,会造成。
尽管我们可以选择分段的⽅法避免这种现象,但是更多时候我们更倾向于得到⼀个确定的曲线,尽管这条曲线不能经过每⼀个样本点,但只要保证误差⾜够⼩即可,这就是拟合的思想。
(拟合的结果是得到⼀个确定的曲线)1.2 求解最⼩⼆乘法1.3 Matlab求解最⼩⼆乘测试数据:x =4.20005.90002.70003.80003.80005.60006.90003.50003.60002.90004.20006.10005.50006.60002.90003.30005.90006.00005.6000>> yy =8.400011.70004.20006.10007.900010.200013.20006.60006.00004.60008.400012.000010.300013.30004.60006.700010.800011.50009.9000计算代码:>> plot(x,y,'o')>> % 给x和y轴加上标签>> xlabel('x的值')>> ylabel('y的值')>> n = size(x,1);>> k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))>> b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))>> hold on % 继续在之前的图形上来画图形>> grid on % 显⽰⽹格线>> f=@(x) k*x+b; % 函数线>> fplot(f,[2.5,7]); % 设置显⽰范围>> legend('样本数据','拟合函数','location','SouthEast')计算过程:>> plot(x,y,'o')>> % 给x和y轴加上标签>> xlabel('x的值')>> ylabel('y的值')>> n = size(x,1);>> n*sum(x.*y)-sum(x)*sum(y)ans = 1.3710e+03>> n*sum(x.*x)-sum(x)*sum(x)ans = 654.4600>> k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))k = 2.0948>> b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))b = -1.0548>> hold on>> grid on>> f=@(x) k*x+b;>> fplot(f,[2.5,7]);>> legend('样本数据','拟合函数','location','SouthEast')1.4 如何评价拟合的好坏线性函数是指对参数为线性(线性于参数)在函数中,参数仅以⼀次⽅出现,且不能乘以或除以其他任何的参数,并不能出现参数的复合函数形式。
数学建模案例与方法教学课件第5章插值法与拟合方法

5.1 城市供水量的预测问题
图5-3 三种插值函数曲线
5.1 城市供水量的预测问题
3. 用2000—2006年每年1月份城市的总用水量预测
由表5-2可得到7个 插值节点(x i,y i), 其中,xi=i,i=1,2,…,7, 其散点图如图5-4所示。 用三次样条插值法求得 的f(8)=4 378.139 0×104 t即为所求的 2007年1月份总用水量 的估计值,表5-3
5.1 城市供水量的预测问题
5.1.2 用插值法预测2007年1月份城市的总用水量
预测2007年1月份城市的用水量有三种 办法:一是用2006年的日用水量进行预测, 二是用2000—2006年每年1月份的日用水量 进行预测,三是用2000—2006年每年1月份
5.1 城市供水量的预测问题
1. 用2006年的日用水量进行预测
图5-4 2000—2006年每年1月份 城市的总用水量散点图
5.1 城市供水量的预测问题
5.1 城市供水量的预测问题
5.1.3 用数据拟合方法预测2007年1月份城市的总用水量 1. 用2006年每天的日用水量进行预测
由图5-1可知,这些点并不是简单地成线性或二次关系, 而是具有很强的聚集性。我们试图用几个多项式进行拟合。 用 MATLAB工具箱得到的拟合结果见表5-4。
5.2.1 曲线拟合
【实例】 气象部门观测到一天中某些时刻t的温度T变化数据见 表5-6。试描绘出温度变化曲线。
5.2 MATLAB与拟合、插值
曲线拟合就是计算出两组数据之间的一 种函数关系,由此可描绘其变化曲线及估计
曲线拟合有多种方式,下面是一元函数 采用最小二乘法对给定数据进行多项式曲线
5.2 MATLAB与拟合、插值
数学建模插值和拟合问题的总结

插值和数据拟合一、 插值方法问题:已知n+1个节点(x j ,y j )(j=0,1,…,n),a=x 0<x 1<…< x n =b ,求任一插值点x*处的插值y*方法:构造一个相对简单的函数y=f(x),使得f 通过所有节点,即f(x j )= y j ,再用y=f(x)计算x*的值。
1. 拉格朗日多项式插值设f(x)是n 次多项式,记作1110()n n n n n L x a x a x a x a --=++++要求对于节点(,)j j x y 有(),0,1,,n j j L x y j n ==将n+1个条件带入多项式,就可以解出多项式的n+1个系数。
实际上,我们有n 次多项式011011()()()()()()()()()i i n i i i i i i i n x x x x x x x x l x x x x x x x x x -+-+----=----满足1,()0,,,0,1,,i j i jl x i j i j n =⎧=⎨≠=⎩则0()()nn i i i L x y l x ==∑就是所要的n 次多项式,称为拉格朗日多项式。
由拉格朗日多项式计算的插值称为拉格朗日插值。
一般来讲,并不是多项式的阶数越高就越精确,一般采用三阶、二阶或一阶(线性)多项式,对相邻点进行分段插值。
2. 样条插值在分段插值时,会造成分段点处不光滑,如果要求在分段点处光滑,即不仅函数值相同,还要一阶导数和二阶导数相同,则构成三阶样条插值。
一般用于曲线绘制,数据估计等。
例 对21,[5,5](1)y x x =∈-+,用n=11个等分节点做插值运算,用m=21个等分插值点作图比较结果。
见inter.m 程序二、 曲线拟合 三、 给药方案 1. 问题一种新药用于临床必须设计给药方案,在快速静脉注射的给药方式下,就是要确定每次注射剂量多大,间隔时间多长.我们考虑最简单的一室模型,即整个机体看作一个房室,称为中心室,室内血液浓度是均匀的.注射后浓度上升,然后逐渐下降,要求有一个最小浓度1c 和一个最大浓度2c .设计给药浓度时,要使血药浓度保持在1c ~2c 之间.2. 假设(1)药物排向体外的速度与中心室的血药浓度成正比,比例系数是k(>0),称为排出速度.(2)中心室血液容积为常数V ,t=0的瞬间注入药物的剂量为d ,血药浓度立即为dV. 3. 建模设中心室血药浓度为c(t),满足微分方程(0)dckc dtd c V=-=用分离变量法解微分方程,有()ktd c te V-=(*) 4. 方案设计每隔一段时间τ,重复注入固定剂量D ,使血药浓度c(t)呈周期变化,并保持在1c ~2c 之间.如图:设初次剂量加大到D 0,易知0221,D Vc D Vc Vc ==-,2121()11ln[],()()ln c Vc t t t c t c k d k c τ=-=-= 那么,当12,c c 确定后,要确定给药方案0{,,}D D τ,就要知道参数V 和k .5. 由实验数据做曲线拟合确定参数值已知1210,25(/)c c g ml μ==,一次注入300mg 药物后,间隔一定ln lndc kt V=- 记12ln ,,lndy c a k a V==-=,则有 12y a t a =+求解过程见medicine_1.m得120.2347, 2.9943a a =-=,由d=300(mg)代入算出k=0.2347,V=15.02(L) 从而有0375.5(),225.3(), 3.9()D mg D mg τ===小时四、 口服给药方案 1. 问题口服给药相当于先有一个将药物从肠胃吸收入血液的过程,可简化为一个吸收室,一个中心室,记t 时刻,中心室和吸收室的血液浓度分别是1()()c t c t 和,容积分别是V ,V1,中心室的排除速度为k ,吸收速度为k1,且k,k1分别是中心室和吸收室血液浓度变化率与浓度的比例系数,t=0口服药物的剂量为d ,则有11111,(0)dc dk c c dt V =-= (1) 111,(0)0V dckc k c c dt V=-+= (2) 解方程(1)有111()k td c te V -=代入方程(2)有111()()k t kt k d c t e e V k k--=--其中三个参数1,,dk k b V=,可由下列数据拟合得到:(非线性拟合)。
数学建模——拟合与插值
即要求 出二次多项式: f(x)a1x2a2xa3
11
中 的 A(a1,a2,a3) 使得:
[f (xi)yi]2 最小
i1
fun是一个事先建立的 定义函数F(x,xdata) 的 M-文件, 自变量为x和 xdata
选项见无 迭代初值 已知数据点 约束优化
18
25.03.2020
2. lsqnonlin
已知数据点: xdata=(xdata1,xdata2,…,xdatan) ydata=(ydata1,ydata2,…,ydatan)
+
+
y=f(x) +
x i 为点(xi,yi) 与曲线 y=f(x) 的距离
6
25.03.2020
线性最小二乘拟合 f(x)=a1r1(x)+ …+amrm(x)中 函数{r1(x), …rm(x)}的选取 1. 通过机理分析建立数学模型来确定 f(x);
2. 将数据 (xi,yi) i=1, …n 作图,通过直观判断确定 f(x):
2)计算结果:A = [-9.8108, 20.1293, -0.0317]
f(x) 9.81x0 2 8 2.1 02x9 0 3 .0317
16
25.03.2020
用MATLAB作非线性最小二乘拟合
两个求非线性最小二乘拟合的函数:
lsqcurvefit、lsqnonlin。
相同点和不同点:两个命令都要先建立M-文件fun.m,定义函 数f(x),但定义f(x)的方式不同。
数学建模精品教材第九章插值与拟合...

数学建模精品教材-第九章插值与拟合第九章插值与拟合插值:求过已知有限个数据点的近似函数。
拟合:已知有限个数据点,求近似函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最小。
插值和拟合都是要根据一组数据构造一个函数作为近似,由于近似的要求不同,二者的数学方法上是完全不同的。
而面对一个实际问题,究竟应该用插值还是拟合,有时容易确定,有时则并不明显。
§1 插值方法下面介绍几种基本的、常用的插值:拉格朗日多项式插值、牛顿插值、分段线性插值、Hermite 插值和三次样条插值。
1.1 拉格朗日多项式插值1.1.1 插值多项式用多项式作为研究插值的工具,称为代数插值。
其基本问题是:已知函数 f x 在区间[a,b]上n +1个不同点x ,x , L,x 处的函数值 y f x i 0,1, L,n,求一个0 1 n i i至多n次多项式nx a +a x + L +a x (1)n 0 1 n使其在给定点处与 f x同值,即满足插值条件 x f x y i 0,1, L,n(2) n i i ix称为插值多项式,x i 0,1, L,n称为插值节点,简称节点,[a,b]称为插值区n i间。
从几何上看,n次多项式插值就是过n +1个点 x , f x i 0,1, L,n,作一条i i多项式曲线 y x近似曲线 y f x。
nn次多项式(1)有n +1个待定系数,由插值条件(2)恰好给出n +1个方程2 na +a x +a x + L +a x y0 1 0 2 0 n 0 02 na +a x +a x + L +a x y0 1 1 2 1 n 1 1(3)L L L L L L L L L L L L2 na +a x +a x + L +a x y0 1 n 2 n n n n 记此方程组的系数矩阵为A,则2 n1 x x L x0 0 02 n1 x x L x1 1 1 detAL L L L L L L2 n1 x x L xn n n是范德蒙特Vandermonde行列式。
(完整版)数学建模 插值和拟合

x
xn
x
4.2 MATLAB实现插值
Matlab 实现:实现插值不需要编制函 数程序,它自身提供了内部的功能函数 interp1(一维分段插值) interp2(二维) interp3(三维) intern(n维)
4.3.1一维插值
用MATLAB作插值计算
一维插值函数: yi=interp1(x,y,xi,'method')
h=1:0.1:12;
t=interp1(hours,temps,h,'spline');
plot(hours,temps,'+',h,t,'r:')
xlabel('Hour'),ylabel('Degrees Celsius’)
例1:从1点12点的11小时内,每隔1小时测量一次温度, 测得的温度的数值依次为:5,8,9,15,25,29, 31,30,22,25,27,24.试估计(1)每隔1/10小时 的温度值;(2)估计1点30分和13的温度值。
例1:从1点到12点的11小时内,每隔1小时测量一次温 度,测得的温度的数值依次为:5,8,9,15,25, 29,31,30,22,25,27,24.试估计(1)每隔 1/10小时的温度值;(2)估计1点30分和13的温度值。
hours=1:12;
temps=[5 8 9 15 25 29 31 30 22 25 27 24];
x x0 y y0
x1 … xn y1 … yn
其中x0,x1, …xn是n+1个互不相同的点,求一个 近似函数 (x) ,使得
( xi ) f ( xi ) i 0,1 …n
数学建模 插值与拟合
%作图
2020/8/19
例 已知飞机下轮廓线上数据如下,Байду номын сангаасx每改变0.1时的y值。
X0 3
5
7
9 11 12 13 14 15
Y 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6
机翼下轮 廓线
y
x
自己思考,10分钟小组讨论!
2020/8/19
二维插值
(1)二维插值的定义
用MATLAB作网格节点数据的插值
z=interp2(x0,y0,z0,x,y,’method’)
被插值点 的函数值
插值 节点
被插值点 插值方法
‘nearest’ 最邻近插值 ‘linear’ 双线性插 值 ‘cubic’ 双三次插 值 要求x0,y0单调;x,y可取为缺矩省阵时,, 或x取双行线向性量插,值y 取为列向量,x,y的值分别不能超出x0,y0的范围。
一、函数插值 二、曲线拟合
一维插值 二维插值
2020/8/19
在工程中,常有这样的问题:给定 一批数据点(它可以是设计师给定,也 可能是从测量与采样中得到),需确定 满足特定要求的曲线(面)通过所给所 有数据点,这就是插值问题。
2020/8/19
一维插值
(1)插值的定义 (2)插值的方法
拉格朗日插值 分段线性插值 三次样条插值
x x2 x0 x2
y0
x x1
x0 x0
x x2 x1 x2
y1
x x2
x0 x0
x x1 x2 x1
y2
直接验证可知,Ln x满足插值条件.
Notice:拉格朗日多项式插值次数越高,越易产生振荡,这 种振荡称为龙格(Runge)现象 。
数学建模讲稿插值拟合方程求根

根据直线的点斜式方程变形得到 q(x)在第 i 段 ?xi?1, xi ?上的表达式
为
q(x) ?
x ? xi xi?1 ? xi
yi ?1
?
x ? xi?1 xi ? xi?1
yi , xi?1
?
x?
xi ,i
? 1,2,?
,n
可以证明,分段线性插值具有良好的收敛性,即 lim q(x) ? f (x), 其 n? ?
[xi,yi]=meshgrid(1:0.1:12,5:85);
zi=interp2(x, y, z, xi, yi,); mesh(xi, yi, zi) xlabel(‘月份' ) ylabel(‘纬度' ) zlabel(‘气旋' )
axis([0 12 0 90 0 50])
title(‘南半球气旋可视化图形' )
j?0
可知
m
mn
? ? ? ?
2 2
? (S ( xi ) ? yi )2? ( a j? j ( xi ) ? yi )2
i? 0
i?0 j?0
为拟合系数 a j ( j ? 0,1, L , n )的函数
因此可假设
mn
? ? ? (a0 , a1 ,L , an ) ? ( a j? j ( xi ) ? yi )2
y=
5 5 5 5 5 5 5 5 5 5 55 15 15 15 15 15 15 15 15 15 15 15 15 25 25 25 25 25 25 25 25 25 25 25 25 35 35 35 35 35 35 35 35 35 35 35 35 45 45 45 45 45 45 45 45 45 45 45 45 55 55 55 55 55 55 55 55 55 55 55 55 65 65 65 65 65 65 65 65 65 65 65 65 75 75 75 75 75 75 75 75 75 75 75 75 85 85 85 85 85 85 85 85 85 85 85 85
Matlab数学建模学习笔记——插值与拟合
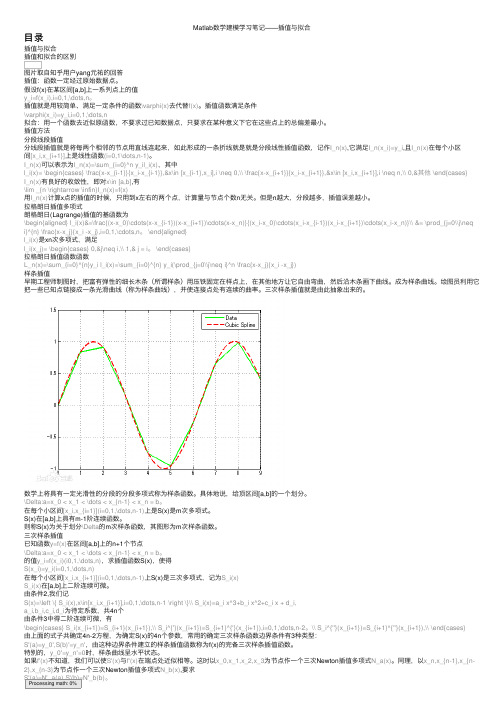
Matlab数学建模学习笔记——插值与拟合⽬录插值与拟合插值和拟合的区别图⽚取⾃知乎⽤户yang元祐的回答插值:函数⼀定经过原始数据点。
假设f(x)在某区间[a,b]上⼀系列点上的值y_i=f(x_i),i=0,1,\dots,n。
插值就是⽤较简单、满⾜⼀定条件的函数\varphi(x)去代替f(x)。
插值函数满⾜条件\varphi(x_i)=y_i,i=0,1,\dots,n拟合:⽤⼀个函数去近似原函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最⼩。
插值⽅法分段线段插值分线段插值就是将每两个相邻的节点⽤直线连起来,如此形成的⼀条折线就是就是分段线性插值函数,记作I_n(x),它满⾜I_n(x_i)=y_i,且I_n(x)在每个⼩区间[x_i,x_{i+1}]上是线性函数(i=0,1\dots,n-1)。
I_n(x)可以表⽰为I_n(x)=\sum_{i=0}^n y_il_i(x),其中l_i(x)= \begin{cases} \frac{x-x_{i-1}}{x_i-x_{i-1}},&x\in [x_{i-1},x_i],i \neq 0,\\ \frac{x-x_{i+1}}{x_i-x_{i+1}},&x\in [x_i,x_{i+1}],i \neq n,\\ 0,&其他 \end{cases}I_n(x)有良好的收敛性,即对x\in [a,b],有\lim _{n \rightarrow \infin}I_n(x)=f(x)⽤I_n(x)计算x点的插值的时候,只⽤到x左右的两个点,计算量与节点个数n⽆关。
但是n越⼤,分段越多,插值误差越⼩。
拉格朗⽇插值多项式朗格朗⽇(Lagrange)插值的基函数为\begin{aligned} l_i(x)&=\frac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)}{(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n)}\\ &= \prod_{j=0\\j\neq i}^{n} \frac{x-x_j}{x_i -x_j},i=0,1,\cdots,n。
(数学建模课件)第八部分插值与拟合
例9 多项式函数拟合 x=[34 36 37 38 39 39 39 40 40 41 42 43 43 45 47 48]; y=[1.30 1.00 0.73 0.90 0.81 0.70 0.60 0.50 0.44 0.56 0.30 0.42 0.35 0.40 0.41 0.60]; close; plot(x,y) p=polyfit(x,y,2) xi=linspace(34,48,1000); %绘图的X轴数据 z=polyval(p,xi); %得到多项式在数据点处 的值 close; plot(x,y,’ko’,xi,z,’r-’)
2020/10/23
2、二维插值
Z1=interp2 (X,Y,Z,X1,Y1,’method’) 其中X和Y为两个向量,分别描述原始数据点的 自变量取值,Z是对应于X和Y的函数值;X1和 Y1是两个向量,描述欲插值的点。Method的含 义同一维插值。Z1是根据相应的插值方法得到 的插值结果。
2020/10/23
2020/10/23
使用MATLAB软件中的三次样条插值命 令得到用水率函数如下图所示。 x0=t;y0=r; [l,n]=size (x0); dl=x0(n)-x0(1); x=x0(1):1/3600:x0(n); %被插值点 ys=interp1 (x0,y0,x,’spline’); %样条插值输出 plot (x,ys); title (‘样条插值下的流速图’); xlabel(’时间(小时)’); ylabel(‘流速(立方米/小时)’)
例8 非线性函数化为线性函数拟合 t=[0 1 2 3 4 5 6 7 8 9 10]; u=[100 75 55 40 30 20 15 10 10 5 5]; close; plot(t,u) T=t; U=log(u); p=polyfit(T, U,1) b=p(1) a=exp(p(2))
插值与数据拟合建模

因此,在时段[t,t+Δt],从B侧渗透至A侧的该物质的质量为:
于是有:
两边除以Δt,并令Δt→0取极限再稍加整理即得:
(1)
2) 注意到整个容器的溶液中含有该物质的质量不变,与初始时刻该物质的含量相同,因此
思考
最小二乘拟合函数 f(x,a1, …am)的选取
1. 通过机理分析建立数学模型来确定 f;
2. 将数据 (xi,yi) i=1, …n 作图,通过直观判断确定 f:
2. 作一般的最小二乘曲线拟合,可利用已有程序curvefit,其调用格式为: a=curvefit(‘f’, a0, x, y)
这本四位数学用表给出sin =0.576,sin =0.5783。小华认为在sin 到sin 这样小的范围内,正弦可以近似为线性函数,于是很容易地得到Sin =0.576+(0.5783-0.5760)×0.6=0.5774
聪明的小华用的这个办法是一种插值方法——分段线性插值。实际上,插值可以理解为,要根据一个用表格表示的函数,计算表中没有的函数值。 表中有的,如(sin ,0.5760)(sin ,0.5783)称为节点;要计算的,如sin ,称为插值点,结果(0.5774)即为插值。小华作的线性函数为插值函数,插值函数所表示的直线当然要通过节点。
1. 作多项式f(x)=a1xm+ …+amx+am+1函数拟合,可利用已有程序polyfit,其调用格式为:
a=polyfit(x,y,m)
用MATLAB作最小二乘拟合
注:f为拟合函数y=f(a,x)的函数M—文件,f(a,x)为拟合函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
20/"geometry.cfg"
20/"natbib.cfg"
20/"bblopts.cfg"
20/"english.cfg"20/"____________.aux"
插值算法February3,2020
需要根据已知的函数点进行数据,模型的处理和分析,有时候现有的数据是极少的,不足以分析支撑的比较,这时候需要数学的方法,模拟产生一些洗呢但又比较靠谱的值来满足需求。
一维插值问题多项式插值分段插值
拉格朗日插值多项式公式
L n(x)=
n
∑
k=0
y k
ωn+1(x)
(x−x k)ω′
n+!
(x k)
其中ωn+1(x)=(x−x0)(x−x1)....(x−x n)
龙格现象(runge phenomenon)高次插值会产生龙格现象,在两端处的波动计大,产生明显的震荡.在不熟悉曲线的运动趋势下,不要轻易使用高次插值.
采用分段低次插值的思路:在随便两个点之间,采用分段二次或者三次插值的方法/又叫分段抛物插值.
牛顿插值法:f(x)=f(x0)+f|x0,x1|(x−x0)+f|x0,x1,x2|(x−x0)(x−x1)+.....差商的定义:称f|x0,x k|=f(x k)−f(x0)
x k−x0
两种插值的区别在于没有体现在导数的一致上
埃尔米特插值法:要求节点处的函数值相同,同时要求对应的导数值也相同分段三次埃尔米特插值法:
matlab里有内存的函数pchip(x,y,new_w)x是已知样本点的横坐标,y是已知样本点的纵坐标,new_x是要插入的对应的横坐标
n维数据的插值了解:p=interpn(x1,x2,...xn,y,new_x1,newx_2,....newx_n,method) x1,x2,x3...是样本点的横坐标
y是样本点的纵坐标
输入的new是要输入点的横坐标
method是要插值的方法拟合算法
拟合和插值的区别:找到一个确定的曲线保证误差足够小,不要求曲线经过每一个样本点,只要足够接近就可以.
最小二乘法的几何解释:
k,b =argmin k,b (
n ∑n =1
(y n −y i )2)
要求这个函数的值是最小的即命令函数的两个之间的距离是最小的,但是一般如果有绝对值都不好求导,所以用第二种方法求平方比较好求极小值.
同时要注意不可以用三次方会出现正负相抵的事情,同时也不能用四次方,四次方会加大异常值的偏差.MLE 极大数量估计.??概率论与数理统计,可以写到论文里.
最小化的式子可以换成:
k,b =argmin k,b (
n ∑n =1
(y −kx 1−b )2)
令L =
∑n
i =1(y i
−kx i −b )2,现找k,b 使L 最小>即残差平方和,求一阶导让其为零,就
是求回归直线公式的推导过程,如果写论文要把整个推导过程写上去.拟合优度:可决系数R 2
用来看拟合的结果怎么样总体平方和SST =∑n
i =1(y i −y )2
误差平方和SSE =∑n i =1(y i −y i )
2
回归平方和SSR =∑n i =1(y i −y i )
2
由于在飞机上不记得这些平均和拟合值的大小怎么用latex 打,所以这一块的符号式子都
是有问题的.
可以证明SST =SSE +SSR 拟合优度:0≤R 2=
SSR
SST
≤1
R 2越接近1,说明误差平方和越接近于0,误差越小拟合程度越好.
注意这个参数只能表达线性拟合的优化程度,不可以表达非线性的.线性函数和其余函数比较拟合程度的好坏,直接比较SSE 大小即可。
误差平方和越小就证明你和的程度越好。
SSE 中有量纲的问题,这个值与有关系.为了消除这个问题,可以用SST =SSE +SSR 这个式子来消除这个情况,因为拟合优度处于01之间
拟合的式子越复杂,得到SSE 越小,权衡取舍的时候既要满足简单同时要满足不能误差太大。
线性函数的介绍:线性函数有两种解释:对于变量为线性或者对于参数为线性。
而我们所指的函数都是指对于参数为线性。
所以举例
y =a +bx 2
这个也是线性函数,因为a,b前面都没有相乘,仅仅有一个参数。
在函数中,参数仅仅以一次方的形式出现,而不能乘以或者除以其余形式的参数,并不能出现参数的复合函数的形式。
