(完整)十年真题_解析几何_全国高考理科数学.doc

十年真题(2010-2019)高考数学(理)分类汇编专题11 平面解析几何选择填空题(新课标Ⅰ卷)(解析版)

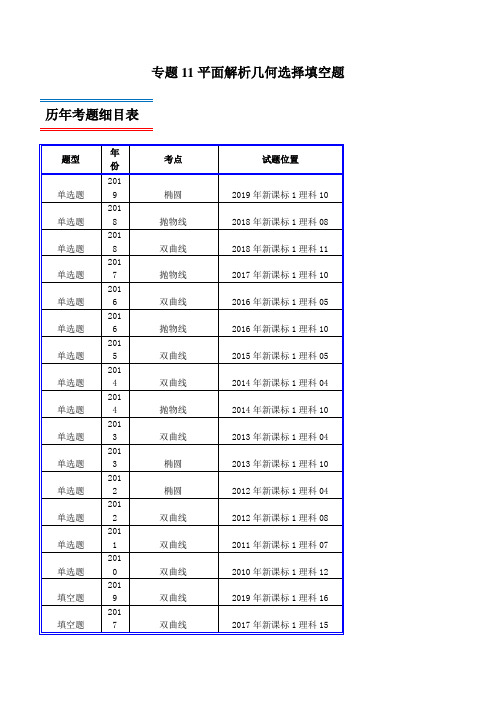
专题11平面解析几何选择填空题历年考题细目表填空题2015 圆的方程2015年新课标1理科14填空题2011 椭圆2011年新课标1理科14填空题2010 圆的方程2010年新课标1理科15历年高考真题汇编1．【2019年新课标1理科10】已知椭圆C的焦点为F1（﹣1，0），F2（1，0），过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为（）A．y2＝1 B． 1C． 1 D． 1【解答】解：∵|AF2|＝2|BF2|，∴|AB|＝3|BF2|，又|AB|＝|BF1|，∴|BF1|＝3|BF2|，又|BF1|+|BF2|＝2a，∴|BF2|，∴|AF2|＝a，|BF1|a，在Rt△AF2O中，cos∠AF2O，在△BF1F2中，由余弦定理可得cos∠BF2F1，根据cos∠AF2O+cos∠BF2F1＝0，可得0，解得a2＝3，∴a．b2＝a2﹣c2＝3﹣1＝2．所以椭圆C的方程为：1．故选：B．2．【2018年新课标1理科08】设抛物线C：y2＝4的焦点为F，过点（﹣2，0）且斜率为的直线与C交于M，N两点，则•（）A．5 B．6 C．7 D．8【解答】解：抛物线C：y2＝4的焦点为F（1，0），过点（﹣2，0）且斜率为的直线为：3y＝2+4，联立直线与抛物线C：y2＝4，消去可得：y2﹣6y+8＝0，解得y1＝2，y2＝4，不妨M（1，2），N（4，4），，．则•（0，2）•（3，4）＝8．故选：D．3．【2018年新课标1理科11】已知双曲线C：y2＝1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M，N．若△OMN为直角三角形，则|MN|＝（）A．B．3 C．2D．4【解答】解：双曲线C：y2＝1的渐近线方程为：y，渐近线的夹角为：60°，不妨设过F（2，0）的直线为：y，则：解得M（，），解得：N（），则|MN|3．故选：B．4．【2017年新课标1理科10】已知F为抛物线C：y2＝4的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为（）A．16 B．14 C．12 D．10【解答】解：如图，l1⊥l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，要使|AB|+|DE|最小，则A与D，B，E关于轴对称，即直线DE的斜率为1，又直线l2过点（1，0），则直线l2的方程为y＝﹣1，联立方程组，则y2﹣4y﹣4＝0，∴y1+y2＝4，y1y2＝﹣4，∴|DE|•|y1﹣y2|8，∴|AB|+|DE|的最小值为2|DE|＝16，方法二：设直线l1的倾斜角为θ，则l2的倾斜角为θ，根据焦点弦长公式可得|AB||DE|∴|AB|+|DE|，∵0＜sin22θ≤1，∴当θ＝45°时，|AB|+|DE|的最小，最小为16，故选：A．5．【2016年新课标1理科05】已知方程1表示双曲线，且该双曲线两焦点间的距离为4，则n的取值范围是（）A．（﹣1，3）B．（﹣1，）C．（0，3）D．（0，）【解答】解：∵双曲线两焦点间的距离为4，∴c＝2，当焦点在轴上时，可得：4＝（m2+n）+（3m2﹣n），解得：m2＝1，∵方程1表示双曲线，∴（m2+n）（3m2﹣n）＞0，可得：（n+1）（3﹣n）＞0，解得：﹣1＜n＜3，即n的取值范围是：（﹣1，3）．当焦点在y轴上时，可得：﹣4＝（m2+n）+（3m2﹣n），解得：m2＝﹣1，无解．故选：A．6．【2016年新课标1理科10】以抛物线C的顶点为圆心的圆交C于A、B两点，交C的准线于D、E两点．已知|AB|＝4，|DE|＝2，则C的焦点到准线的距离为（）A．2 B．4 C．6 D．8【解答】解：设抛物线为y2＝2p，如图：|AB|＝4，|AM|＝2，|DE|＝2，|DN|，|ON|，A，|OD|＝|OA|，5，解得：p＝4．C的焦点到准线的距离为：4．故选：B．7．【2015年新课标1理科05】已知M（0，y0）是双曲线C：1上的一点，F1，F2是C的左、右两个焦点，若0，则y0的取值范围是（）A．B．C．D．【解答】解：由题意，（0，﹣y0）•（0，﹣y0）＝02﹣3+y02＝3y02﹣1＜0，所以y0．故选：A．8．【2014年新课标1理科04】已知F为双曲线C：2﹣my2＝3m（m＞0）的一个焦点，则点F到C的一条渐近线的距离为（）A．B．3 C．m D．3m【解答】解：双曲线C：2﹣my2＝3m（m＞0）可化为，∴一个焦点为（，0），一条渐近线方程为0，∴点F到C的一条渐近线的距离为．故选：A．9．【2014年新课标1理科10】已知抛物线C：y2＝8的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若4，则|QF|＝（）A．B．3 C．D．2【解答】解：设Q到l的距离为d，则|QF|＝d，∵4，∴|PQ|＝3d，∴不妨设直线PF的斜率为2，∵F（2，0），∴直线PF的方程为y＝﹣2（﹣2），与y2＝8联立可得＝1，∴|QF|＝d＝1+2＝3，故选：B．10．【2013年新课标1理科04】已知双曲线C：（a＞0，b＞0）的离心率为，则C的渐近线方程为（）A．y B．y C．y＝±D．y【解答】解：由双曲线C：（a＞0，b＞0），则离心率e，即4b2＝a2，故渐近线方程为y＝±，故选：D．11．【2013年新课标1理科10】已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．【解答】解：设A（1，y1），B（2，y2），代入椭圆方程得，相减得，∴．∵1+2＝2，y1+y2＝﹣2，．∴，化为a2＝2b2，又c＝3，解得a2＝18，b2＝9．∴椭圆E的方程为．故选：D．12．【2012年新课标1理科04】设F1、F2是椭圆E：1（a＞b＞0）的左、右焦点，P为直线上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为（）A．B．C．D．【解答】解：∵△F2PF1是底角为30°的等腰三角形，∴|PF2|＝|F2F1|∵P为直线上一点∴∴故选：C．13．【2012年新课标1理科08】等轴双曲线C的中心在原点，焦点在轴上，C与抛物线y2＝16的准线交于点A和点B，|AB|＝4，则C的实轴长为（）A．B．C．4 D．8【解答】解：设等轴双曲线C：2﹣y2＝a2（a＞0），y2＝16的准线l：＝﹣4，∵C与抛物线y2＝16的准线l：＝﹣4交于A，B两点，∴A（﹣4，2），B（﹣4，﹣2），将A点坐标代入双曲线方程得4，∴a＝2，2a＝4．故选：C．14．【2011年新课标1理科07】设直线l过双曲线C的一个焦点，且与C的一条对称轴垂直，l与C交于A，B两点，|AB|为C的实轴长的2倍，则C的离心率为（）A．B．C．2 D．3【解答】解：不妨设双曲线C：，焦点F（﹣c，0），对称轴y＝0，由题设知，，∴，b2＝2a2，c2﹣a2＝2a2，c2＝3a2，∴e．故选：B．15．【2010年新课标1理科12】已知双曲线E的中心为原点，P（3，0）是E的焦点，过P的直线l与E 相交于A，B两点，且AB的中点为N（﹣12，﹣15），则E的方程式为（）A．B．C．D．【解答】解：由已知条件易得直线l的斜率为＝PN＝1，设双曲线方程为，A（1，y1），B（2，y2），则有，两式相减并结合1+2＝﹣24，y1+y2＝﹣30得，从而 1即4b2＝5a2，又a2+b2＝9，解得a2＝4，b2＝5，故选：B．16．【2019年新课标1理科16】已知双曲线C：1（a＞0，b＞0）的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若，•0，则C的离心率为．【解答】解：如图，∵，且•0，∴OA⊥F1B，则F1B：y，联立，解得B（，），则，，∴4c2，整理得：b2＝3a2，∴c2﹣a2＝3a2，即4a2＝c2，∴，e．故答案为：2．17．【2017年新课标1理科15】已知双曲线C：1（a＞0，b＞0）的右顶点为A，以A为圆心，b 为半径作圆A，圆A与双曲线C的一条渐近线交于M、N两点．若∠MAN＝60°，则C的离心率为．【解答】解：双曲线C：1（a＞0，b＞0）的右顶点为A（a，0），以A为圆心，b为半径做圆A，圆A与双曲线C的一条渐近线交于M、N两点．若∠MAN＝60°，可得A到渐近线b+ay＝0的距离为：b cos30°，可得：，即，可得离心率为：e．故答案为：．18．【2015年新课标1理科14】一个圆经过椭圆1的三个顶点．且圆心在轴的正半轴上．则该圆标准方程为．【解答】解：一个圆经过椭圆1的三个顶点．且圆心在轴的正半轴上．可知椭圆的右顶点坐标（4，0），上下顶点坐标（0，±2），设圆的圆心（a，0），则，解得a，圆的半径为：，所求圆的方程为：（）2+y2．故答案为：（）2+y2．19．【2011年新课标1理科14】在平面直角坐标系Oy，椭圆C的中心为原点，焦点F1F2在轴上，离心率为．过F1的直线交于A，B两点，且△ABF2的周长为16，那么C的方程为．【解答】解：根据题意，△ABF2的周长为16，即BF2+AF2+BF1+AF1＝16；根据椭圆的性质，有4a＝16，即a＝4；椭圆的离心率为，即，则a c，将a c，代入可得，c＝2，则b2＝a2﹣c2＝8；则椭圆的方程为1；故答案为：1．20．【2010年新课标1理科15】过点A（4，1）的圆C与直线﹣y＝1相切于点B（2，1），则圆C的方程为．【解答】解：设圆的方程为（﹣a）2+（y﹣b）2＝r2，则（4﹣a）2+（1﹣b）2＝r2，（2﹣a）2+（1﹣b）2＝r2，1，解得a＝3，b＝0，r，故所求圆的方程为（﹣3）2+y2＝2．故答案为：（﹣3）2+y2＝2．考题分析与复习建议本专题考查的知识点为：直线方程、圆的方程，直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线，曲线与方程等.历年考题主要以选择填空题型出现，重点考查的知识点为：直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线等，预测明年本考点题目会比较稳定，备考方向以知识点直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线等为重点较佳.最新高考模拟试题1．已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，直线l 经过点F 且与双曲线的一条渐近线垂直，直线l 与双曲线的右支交于不同两点A ，B ，若3AF FB =u u u r u u u r ，则该双曲线的离心率为（）ABCD【答案】A【解析】由题意得直线l 的方程为b x y c a=+，不妨取1a =，则x by c =+，且221b c =-. 将x by c =+代入2221y x b -=，得()4234120b y b cy b -++=. 设()11,A x y ，()22,B x y ，则312421b c y y b +=--，41241b y y b =-. 由3AF FB u u u r u u u r =，得123y y =-，所以324422422131bc y b by b ⎧-=-⎪⎪-⎨⎪-=⎪-⎩，得22431b c b =-，解得214b =，所以2c ===c e a ==，故选A 。

十年真题(2010-2019)高考数学(理)分类汇编专题12 平面解析几何解答题(新课标Ⅰ卷)(原卷版)

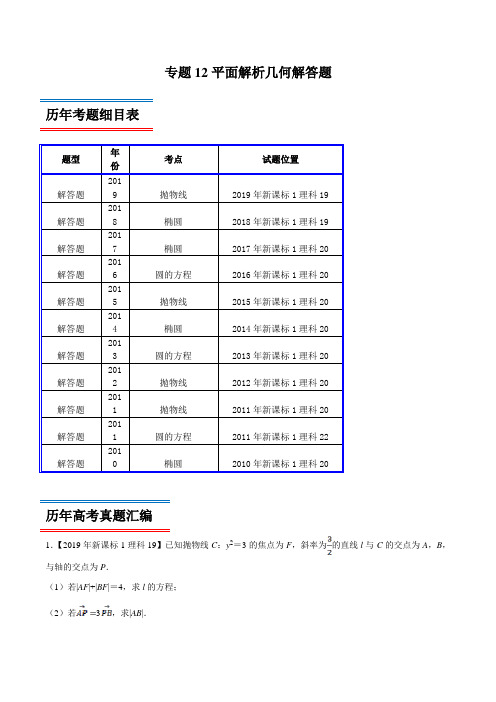
专题12平面解析几何解答题历年考题细目表题型年份考点试题位置解答题2019 抛物线2019年新课标1理科19解答题2018 椭圆2018年新课标1理科19解答题2017 椭圆2017年新课标1理科20解答题2016 圆的方程2016年新课标1理科20解答题2015 抛物线2015年新课标1理科20解答题2014 椭圆2014年新课标1理科20解答题2013 圆的方程2013年新课标1理科20解答题2012 抛物线2012年新课标1理科20解答题2011 抛物线2011年新课标1理科20解答题2011 圆的方程2011年新课标1理科22解答题2010 椭圆2010年新课标1理科20历年高考真题汇编1．【2019年新课标1理科19】已知抛物线C：y2＝3的焦点为F，斜率为的直线l与C的交点为A，B，与轴的交点为P．（1）若|AF|+|BF|＝4，求l的方程；（2）若3，求|AB|．2．【2018年新课标1理科19】设椭圆C：y2＝1的右焦点为F，过F的直线l与C交于A，B两点，点M的坐标为（2，0）．（1）当l与轴垂直时，求直线AM的方程；（2）设O为坐标原点，证明：∠OMA＝∠OMB．3．【2017年新课标1理科20】已知椭圆C：1（a＞b＞0），四点P1（1，1），P2（0，1），P3（﹣1，），P4（1，）中恰有三点在椭圆C上．（1）求C的方程；（2）设直线l不经过P2点且与C相交于A，B两点．若直线P2A与直线P2B的斜率的和为﹣1，证明：l 过定点．4．【2016年新课标1理科20】设圆2+y2+2﹣15＝0的圆心为A，直线l过点B（1，0）且与轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E．（Ⅰ）证明|EA|+|EB|为定值，并写出点E的轨迹方程；（Ⅱ）设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围．5．【2015年新课标1理科20】在直角坐标系Oy中，曲线C：y与直线l：y＝+a（a＞0）交于M，N两点．（Ⅰ）当＝0时，分別求C在点M和N处的切线方程．（Ⅱ）y轴上是否存在点P，使得当变动时，总有∠OPM＝∠OPN？（说明理由）6．【2014年新课标1理科20】已知点A（0，﹣2），椭圆E：1（a＞b＞0）的离心率为，F是椭圆的右焦点，直线AF的斜率为，O为坐标原点．（Ⅰ）求E的方程；（Ⅱ）设过点A的直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程．7．【2013年新课标1理科20】已知圆M：（+1）2+y2＝1，圆N：（﹣1）2+y2＝9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|．8．【2012年新课标1理科20】设抛物线C：2＝2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，F A为半径的圆F交l于B，D两点；（1）若∠BFD＝90°，△ABD的面积为，求p的值及圆F的方程；（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．9．【2011年新课标1理科20】在平面直角坐标系Oy中，已知点A（0，﹣1），B点在直线y＝﹣3上，M 点满足∥，•，M点的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）P为C上的动点，l为C在P点处的切线，求O点到l距离的最小值．10．【2011年新课标1理科22】如图，D，E分别为△ABC的边AB，AC上的点，且不与△ABC的顶点重合．已知AE的长为m，AC的长为n，AD，AB的长是关于的方程2﹣14+mn＝0的两个根．（Ⅰ）证明：C，B，D，E四点共圆；（Ⅱ）若∠A＝90°，且m＝4，n＝6，求C，B，D，E所在圆的半径．11．【2010年新课标1理科20】设F1，F2分别是椭圆的左、右焦点，过F1斜率为1的直线ℓ与E相交于A，B两点，且|AF2|，|AB|，|BF2|成等差数列．（1）求E的离心率；（2）设点P（0，﹣1）满足|P A|＝|PB|，求E的方程．考题分析与复习建议本专题考查的知识点为：直线方程、圆的方程，直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线，曲线与方程等.历年考题主要以解答题题型出现，重点考查的知识点为：直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线等，预测明年本考点题目会比较稳定，备考方向以知识点直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线等为重点较佳.最新高考模拟试题1．已知椭圆22122:1(0)x y C a b a b +=>>的离心率为6，椭圆22222:1(0)33x y C a b a b +=>>经过点33,22⎛⎫ ⎪ ⎪⎝⎭. （1）求椭圆1C 的标准方程；（2）设点M 是椭圆1C 上的任意一点，射线MO 与椭圆2C 交于点N ，过点M 的直线l 与椭圆1C 有且只有一个公共点，直线l 与椭圆2C 交于,A B 两个相异点，证明：NAB △面积为定值.2．如图，在平面直角坐标系Oy 中，椭圆C ：22221x y a b+=(a ＞b ＞0)经过点(0，3-)，点F 是椭圆的右焦点，点F 到左顶点的距离和到右准线的距离相等．过点F 的直线l 交椭圆于M ，N 两点．（1）求椭圆C 的标准方程；（2）当MF ＝2FN 时，求直线l 的方程；（3）若直线l 上存在点P 满足PM·PN＝PF 2，且点P 在椭圆外，证明：点P 在定直线上．3．已知抛物线C ：24y x =的焦点为F ，直线l 与抛物线C 交于A ，B 两点，O 是坐标原点．（1）若直线l 过点F 且8AB =，求直线l 的方程；（2）已知点(2,0)E -，若直线l 不与坐标轴垂直，且AEO BEO ∠=∠，证明：直线l 过定点．4．已知椭圆22221(0)x y a b a b+=>>，()2,0A 是长轴的一个端点，弦BC 过椭圆的中心O ，点C 在第一象限，且0AC BC ⋅=u u u r u u u r ，||2||OC OB AB BC -=+u u u r u u u r u u u r u u u r．（1）求椭圆的标准方程；（2）设P 、Q 为椭圆上不重合的两点且异于A 、B ，若PCQ ∠的平分线总是垂直于x 轴，问是否存在实数λ，使得PQ AB =λu u u r u u u r ？若不存在，请说明理由；若存在，求λ取得最大值时的PQ 的长．5．已知抛物线216y x =，过抛物线焦点F 的直线l 分别交抛物线与圆22(4)16x y -+=于,,,A C D B （自上而下顺次）四点.（1）求证：||||AC BD ⋅为定值；（2）求||||AB AF ⋅的最小值.6．已知O 为坐标原点，点()()2,02,0A B -，，()01AC AD CB CD λλ===<>F 是椭圆C 的一个焦点．点(02)M ,，直线MF 的（1）求椭圆C 的方程；（2）若过点M 的直线l 与椭圆C 交于A B ，两点，线段AB 的中点为N ，且AB MN ＝．求l 的方程．8．已知椭圆2222:1(0)x y C a b a b +=>>过点(，右焦点F 是抛物线28y x =的焦点. （1）求椭圆C 的方程；（2）已知动直线l 过右焦点F ，且与椭圆C 分别交于M ，N 两点.试问x 轴上是否存在定点Q ，使得13516QM QN ⋅=-u u u u r u u u r 恒成立?若存在求出点Q 的坐标若不存在，说明理由.9．关于椭圆的切线由下列结论：若11(,)P x y 是椭圆22221(0)x y a b a b+=>>上的一点，则过点P 的椭圆的切线方程为11221x x y y a b +=.已知椭圆22:143x y C +=. (1)利用上述结论，求过椭圆C 上的点(1,)(0)P n n >的切线方程；(2)若M 是直线4x =上任一点，过点M 作椭圆C 的两条切线MA ，MB （A ，B 为切点），设椭圆的右焦点为F ，求证：MF AB ⊥.10．已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12F F ，，离心率为12，P 为椭圆上一动点（异于左右顶点），若12AF F △（1）求椭圆C 的方程；（2）若直线l 过点1F 交椭圆C 于,A B 两点，问在x 轴上是否存在一点Q ，使得QA QB ⋅u u u r u u u r 为定值？若存在，求点Q 的坐标；若不存在，请说明理由．11．已知点()1,0F ，直线:1l x =-，P 为平面上的动点，过点P 作直线的垂线，垂足为Q ，且QP QF FP FQ ⋅=⋅u u u r u u u r u u u r u u u r .（1）求动点P 的轨迹C 的方程；（2）设直线y kx b =+与轨迹C 交于两点，()11,A x y 、()22,B x y ，且12y y a -= (0a >，且a 为常数)，过弦AB 的中点M 作平行于x 轴的直线交轨迹C 于点D ，连接AD 、BD .试判断ABD ∆的面积是否为定值，若是，求出该定值，若不是，请说明理由12．已知点P 在抛物线()220C x py p =：＞上，且点P 的横坐标为2，以P 为圆心，PO 为半径的圆（O 为原点），与抛物线C 的准线交于M ，N 两点，且2MN =．（1）求抛物线C 的方程；（2）若抛物线的准线与y 轴的交点为H ．过抛物线焦点F 的直线l 与抛物线C 交于A ，B ，且AB HB ⊥，求AF BF -的值．13．已知抛物线方程24y x =，F 为焦点，P 为抛物线准线上一点，Q 为线段PF 与抛物线的交点，定义()PF d P FQ=. （1）当8(1)3P --，时，求()d P ；（2）证明存在常数a ，使得2()d P PF a =+.（3）123,,P P P 为抛物线准线上三点，且1223PP P P =，判断13()()d P d P +与22()d P 的关系. 14．已知抛物线2:2(0)C x py p =>的焦点F 到准线距离为2.（1）若点(1,1)E ，且点P 在抛物线C 上，求||||PE PF +的最小值；（2）若过点(0,)N b 的直线l 与圆22:(2)4M x y +-=相切，且与抛物线C 有两个不同交点,A B ，求AOB ∆的面积.15．已知曲线C 上的任意一点到直线l ：=12的距离与到点F （102，）的距离相等．（1）求曲线C 的方程；（2）若过P （1，0）的直线与曲线C 相交于A ，B 两点，Q （1，0）为定点，设直线AQ 的斜率为1，直线BQ 的斜率为2，直线AB 的斜率为，证明：22212112k k k +-为定值．。

专题12 解析几何-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)

则 C 的焦距为_________．
【答案】4
【分析】由渐近线方程
3x + my = 0 化简得 y = −
3 x ，即 b =
m
a
3 ，同时平方得 b2
m
a2
= 3 ，又双曲线中 m2
a2
=
m, b2
= 1，故
3 m2
=
1 m
，解得 m = 3, m = 0 （舍去）， c2
= a2
+ b2
= 3+1= 4 c
C 上一点， PF 与 x 轴垂直， Q 为 x 轴上一点，且 PQ ⊥ OP ，若 FQ = 6 ，则 C 的准线方程为______.
【答案】 x = − 3 2
【分析】抛物线 C ： y2 = 2 px
(
p
0
)的焦点
F
p 2
,
0
,
∵P 为 C 上一点， PF 与 x 轴垂直，
所以 P 的横坐标为 p ，代入抛物线方程求得 P 的纵坐标为 p , 2
x2 a2
+
y2 b2
= 1(a
b
0) 的上顶点，若 C
上的任
意一点 P 都满足| PB | 2b ，则 C 的离心率的取值范围是（）
A．
2 2
,1
【答案】C
B．
1 2
,1
C． 0,
2
2
D．
0,
1 2
【分析】设 P ( x0 ,
y0
)
，由
B
(
0,
b
)
，因为
x02 a2
+
y02 b2
所以 C 的准线方程为 x = − 3 2

2012-2021十年全国高考数学(理科)真题分类汇编解析立体几何大题

(1)证明：AA1∥MN，且平面A1AMN⊥EB1C1F；
(2)设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN所成Байду номын сангаас的正弦值．
5．(2020年高考数学课标Ⅲ卷理科)如图，在长方体中，点分别在棱上，且，．
(1)证明：点平面内；
(2)若，，，求二面角的正弦值．
7．(2019年高考数学课标全国Ⅱ卷理科)如图，长方体的底面是正方形，点在棱上，．
证明：平面；
若，求二面角的正弦值．
8．(2019年高考数学课标全国Ⅰ卷理科) 如图，直四棱柱的底面是菱形，分别是，，的中点．
(1)证明：平面；
(2)求二面角的正弦值．
9．(2018年高考数学课标Ⅲ卷（理）)(12分)如图，边长为的正方形所在平面与半圆弧所在的平面垂直，是弧上异于的点．
( )证明平面；
( )求二面角的余弦值．
18．(2015高考数学新课标2理科)(本题满分12分)如图，长方体中, ，，，点，分别在，上，．过点，的平面与此长方体的面相交，交线围成一个正方形．
(Ⅰ)在图中画出这个正方形(不必说出画法和理由)；
(Ⅱ)求直线与平面所成角的正弦值．
6．(2019年高考数学课标Ⅲ卷理科)图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2．
(1)证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；
(2)求图2中的二面角B−CG−A的大小．
(1)证明：平面平面；

解析几何历年高考真题试卷--带详细答案

解析几何高考真题一、单选题（共11题；共22分）1.（2020·新课标Ⅲ·理）设双曲线C ：x 2a 2−y 2b 2=1 （a>0，b>0）的左、右焦点分别为F 1 ， F 2 ，离心率为 √5 ．P 是C 上一点，且F 1P ⊥F 2P ．若△PF 1F 2的面积为4，则a=（） A. 1 B. 2 C. 4 D. 82.（2020·新课标Ⅲ·理）设O 为坐标原点，直线x=2与抛物线C ：y 2=2px(p>0)交于D ，E 两点，若OD ⊥OE ，则C 的焦点坐标为（）A. （ 14 ，0）B. （ 12 ，0） C. （1，0） D. （2，0） 3.（2020·新课标Ⅱ·理）设O 为坐标原点，直线 x =a 与双曲线 C:x 2a2−y 2b 2=1(a >0,b >0) 的两条渐近线分别交于 D,E 两点，若 △ODE 的面积为8，则C 的焦距的最小值为（） A. 4 B. 8 C. 16 D. 32 4.（2020·天津）设双曲线 C 的方程为x 2a 2−y 2b 2=1(a >0,b >0) ，过抛物线 y 2=4x 的焦点和点 (0,b) 的直线为l ．若C 的一条渐近线与 l 平行，另一条渐近线与l 垂直，则双曲线C 的方程为（） A.x 24−y 24=1 B. x 2−y 24=1 C.x 24−y 2=1 D. x 2−y 2=15.（2019·天津）已知抛物线的焦点为F ，准线为l.若与双曲线x 2a2−y 2b 2=1(a >0,b >0) 的两条渐近线分别交于点A 和点B ，且 |AB|=4|OF| （O 为原点），则双曲线的离心率为（） A. √2 B. √3 C. 2 D. √56.（2020·北京）设抛物线的顶点为O ，焦点为F ，准线为l ．P 是抛物线上异于O 的一点，过P 作 PQ ⊥l 于Q ，则线段 FQ 的垂直平分线（）．A. 经过点OB. 经过点PC. 平行于直线 OPD. 垂直于直线 OP7.（2019·天津）已知抛物线 y 2=4x 的焦点为 F ，准线为 l ，若 l 与双曲线 x 2a 2−y 2b 2=1 (a >0,b >0) 的两条渐近线分别交于点 A 和点 B ，且 |AB|=4|OF| （ O 为原点），则双曲线的离心率为（）A. √2B. √3C. 2D. √5 8.（2019·全国Ⅲ卷理）双曲线 C:x 24−y 22=1 的右焦点为F,点P 在C 的一条渐近线上,O 为坐标原点,若|PO|=|PF|,则△PFO 的面积为（）A. 3√24B. 3√22C. 2√2D. 3√29.已知椭圆E:x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ．短轴的一个端点为M ，直线l:3x-4y=0交椭圆E 于A,B两点．若|AF+BF|=4，点M 到直线l 的距离不小于45 ，则椭圆E 的离心率的取值范围是（）A. (0,√32] B. (0,34] C. [√32.1) D. [34,1)10.将离心率为e 1的双曲线c 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度，得到离心率为e 2的双曲线c 2 ，则（）A. 对任意的a,b ， e 1>e 2B. 当a >b 时，e 1>e 2；当a b 时，e 1<e 2；当a e 211.将离心率为e 1的双曲线c 1的实半轴长a 和虚半轴长b (a ≠b )同时增加(m >0)个单位长度，得到离心率为e 2的双曲线c 2 ，则（）A. 对任意的a,b,e 1>e 2B. 当a >b 时，e 1>e 2；当a b 时，e 1<e 2；当a e 2二、填空题（共5题；共6分）12.（2020·新课标Ⅰ·理）已知F 为双曲线 C:x 2a2−y 2b 2=1(a >0,b >0) 的右焦点，A 为C 的右顶点，B 为C上的点，且BF 垂直于x 轴.若AB 的斜率为3，则C 的离心率为________.13.（2019·江苏）在平面直角坐标系 xOy 中，P 是曲线 y =x +4x (x >0) 上的一个动点，则点P 到直线x +y =0的距离的最小值是________. 14.（2019·浙江）已知椭圆x 29+y 25=1 的左焦点为F ，点P 在椭圆且在x 轴上方，若线段PF 的中点在以原点O 为圆心，|OF|为半径的圆上，则直线PF 的斜率是________ 15.（2018·北京）已知椭圆 M:x 2a 2+y 2b 2=1(a >b >0) ,双曲线 N:x 2m 2−y 2n 2=1 . 若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为________；双曲线N 的离心率为________16.（2017·江苏）在平面直角坐标系xOy 中，双曲线x 23﹣y 2=1的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是F 1 ， F 2 ，则四边形F 1PF 2Q 的面积是________．三、解答题（共9题；共85分）17.（2020·新课标Ⅲ·理）已知椭圆 C:x 225+y 2m 2=1(0<m <5) 的离心率为√154，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线 x =6 上，且 |BP|=|BQ| ， BP ⊥BQ ，求 △APQ 的面积．18.（2020·新课标Ⅱ·文）已知椭圆C 1：x 2a 2+y 2b 2=1 (a>b>0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴重直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD|= 43 |AB|．（1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．19.（2020·新课标Ⅰ·理）已知A 、B 分别为椭圆E ：x 2a 2+y 2=1 （a>1）的左、右顶点，G 为E 的上顶点，AG ⃗⃗⃗⃗⃗ ⋅GB ⃗⃗⃗⃗⃗ =8 ，P 为直线x=6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.20.（2020·新高考Ⅱ）已知椭圆C ： x 2a 2+y 2b 2=1(a >b >0) 过点M （2，3）,点A 为其左顶点，且AM 的斜率为 12 ，（1）求C 的方程；（2）点N 为椭圆上任意一点，求△AMN 的面积的最大值.21.（2019·天津）设椭圆x2a2+y2b2=1(a>b>0)的左焦点为F，左顶点为A，顶点为B.已知√3|OA|=2|OB|（O为原点）.（Ⅰ）求椭圆的离心率；（Ⅱ）设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为p，圆C同时与x轴和直线l 相切，圆心C在直线x=4上，且OC∥AP，求椭圆的方程.22.（2019·全国Ⅲ卷文）已知曲线C：y= x22，D为直线y= −12上的动点，过D作C的两条切线，切点分别为A，B.（1）证明：直线AB过定点：（2）若以E(0，52)为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程.23.（2019·全国Ⅲ卷理）已知曲线C: y=x22，D为直线y=- 12的动点，过D作C的两条切线，切点分别为A，B.（1）证明：直线AB过定点；（2）若以E（0，52）为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积.24.（2019·全国Ⅱ卷文）已知F1,F2是椭圆C：x2a2+y2b2=1(a>b>0)的两个焦点，P为C上的点，O为坐标原点。

历年高考数学真题(全国卷整理版)完整版完整版.doc

参考公式：如果事件A 、B 互斥，那么球的表面积公式()()()P AB P A P B 24S R如果事件A 、B 相互独立，那么其中R 表示球的半径()()()P A B P A P B 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么334VRn 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(0,1,2,)kkn kn n P k C p p k n …普通高等学校招生全国统一考试一、选择题1、复数131i i=A 2+IB 2-IC 1+2iD 1- 2i2、已知集合A ＝{1.3. m }，B ＝{1，m} ,AB ＝A, 则m=A0或3B 0或3C 1或3D 1或33 椭圆的中心在原点，焦距为4 一条准线为x=-4 ，则该椭圆的方程为A216x+212y=1 B212x+28y=1C28x+24y=1 D212x+24y=14 已知正四棱柱ABCD- A 1B 1C 1D 1中，AB=2，CC 1=22E 为CC 1的中点，则直线AC 1与平面BED 的距离为A 2B3C2D 1（5）已知等差数列{a n }的前n 项和为S n ，a 5=5，S 5=15，则数列的前100项和为(A)100101(B)99101(C)99100(D)101100（6）△ABC 中，AB 边的高为CD ，若a ·b=0，|a|=1，|b|=2，则(A)（B ）(C)(D)（7）已知α为第二象限角，sinα＋sinβ=33，则cos2α=(A)5-3（B）5-9(C)59(D)53（8）已知F1、F2为双曲线C：x2-y2=2的左、右焦点，点P在C上，|PF1|=|2PF2|，则cos ∠F1PF2=(A)14（B）35(C)34(D)45（9）已知x=lnπ，y=log52，12z=e，则(A)x＜y＜z （B）z＜x＜y (C)z＜y＜x (D)y＜z＜x(10) 已知函数y＝x2-3x+c的图像与x恰有两个公共点，则c＝（A）-2或2 （B）-9或3 （C）-1或1 （D）-3或1（11）将字母a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，梅列的字母也互不相同，则不同的排列方法共有（A）12种（B）18种（C）24种（D）36种（12）正方形ABCD的边长为1，点E在边AB上，点F在边BC上，AE＝BF＝73。

十年高考理科数学真题专题九解析几何二十八抛物线及答案

专题九解析几何第二十八讲抛物线2019年1.（2019全国II 理8）若抛物线y 2=2px (p >0)的焦点是椭圆2231x y pp+=的一个焦点，则p =A ．2B ．3C ．4D ．82.（2019北京理18（1））已知抛物线2:2C x py =-经过点(2，-1).求抛物线C 的方程及其准线方程；3．（2019全国I 理19）已知抛物线C ：y 2=3x 的焦点为F ，斜率为32的直线l 与C 的交点为A ，B ，与x 轴的交点为P ．（1）若4AF BF +=，求l 的方程；（2）若3AP PB =uu u r uu r，求AB ．4. （2019全国III 理21）已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B .（1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.2010-2018年一、选择题1．(2018全国卷Ⅰ)设抛物线C ：24=y x 的焦点为F ，过点(2,0)-且斜率为23的直线与C 交于M ，N 两点，则⋅u u u u r u u u r FM FN =A ．5B ．6C ．7D ．82．（2017新课标Ⅰ）已知F 为抛物线C ：24y x =的焦点，过F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D 、E 两点，则||||AB DE +的最小值为A ．16B ．14C ．12D ．103．(2016年四川)设O 为坐标原点，P 是以F 为焦点的抛物线22(0)y px p =>上任意一点，M 是线段PF 上的点，且PM =2MF ,则直线OM 的斜率的最大值为A ．3 B ．23C ．22D ．1 4．(2016年全国I)以抛物线C 的顶点为圆心的圆交C 于A ，B 两点，交C 的准线于D ，E两点．已知||AB =42，||DE =25，则C 的焦点到准线的距离为 A ．2 B ．4 C ．6 D ．85．（2015浙江）如图，设抛物线24y x =的焦点为F ，不经过焦点的直线上有三个不同的点,,A B C ，其中点,A B 在抛物线上，点C 在y 轴上，则BCF ∆与ACF ∆的面积之比是A ．11BF AF -- B ．2211BF AF -- C ．11BF AF ++ D ．2211BF AF ++6．（2015四川）设直线l 与抛物线24y x =相交于,A B 两点，与圆()()22250x y r r -+=>相切于点M ，且M 为线段AB 的中点．若这样的直线l 恰有4条，则r 的取值范围是 A ．()13， B ．()14， C ．()23， D ．()24，7．（2014新课标1）已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个焦点，若4FP FQ =u u u r u u u r，则||QF =A ．72 B ．52C ．3D ．2 8．（2014新课标2）设F 为抛物线C ：23y x =的焦点，过F 且倾斜角为30°的直线交C 于,A B 两点，O 为坐标原点，则△OAB 的面积为（）A ．33 B ．938 C ．6332 D ．949．（2014辽宁）已知点(2,3)A -在抛物线C ：22y px =的准线上，过点A 的直线与C 在第一象限相切于点B ，记C 的焦点为F ，则直线BF 的斜率为（） A ．12 B ．23 C ．34 D ．4310．（2013新课标1）O 为坐标原点，F 为抛物线2:42C y x =的焦点，P 为C 上一点，若||42PF =，则POF ∆的面积为（） A ．2B ．22C ．23D ．411．（2013江西）已知点()2,0A ，抛物线2:4C x y =的焦点为F ，射线FA 与抛物线C 相交于点M ，与其准线相交于点N ，则||:||FM MN = A ．2:5 B ．1:2 C ．1:5 D ．1:312．（2012新课标）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线x y 162=的准线交于A 、B 两点，34||=AB ，则C 的实轴长为 A 、2B 、22C 、4D 、813．（2012山东）已知双曲线1C ：22221(0,0)x y a b a b-=>>的离心率为2．若抛物线22:2(0)C x py p =>的焦点到双曲线1C 的渐近线的距离为2，则抛物线2C 的方程为 A ．283x y =B ．2163x y = C ．28x y = D ．216x y = 14．（2011新课标）已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于A ，B 两点，||12AB =，P 为C 的准线上一点，则ABP ∆的面积为A ．18B ．24C ．36D ．48 二、填空题15．(2018全国卷Ⅲ)已知点(1,1)M -和抛物线C ：24y x =，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若90AMB ∠=o，则k =______．16．（2017新课标Ⅱ）已知F 是抛物线C ：28y x =的焦点，M 是C 上一点，FM 的延长线交y 轴于点N ．若M 为FN 的中点，则||FN = ．17．（2015陕西）若抛物线22(0)y px p =>的准线经过双曲线221x y -=的一个焦点，则p =18．（2014湖南）如图4，正方形ABCD DEFG 和正方形的边长分别为,()a b a b <，原点O 为AD 的中点，抛物线22(0)y px p =>经过,bC F a=两点，则．19．（2013北京）若抛物线22y px =的焦点坐标为(1,0)，则p = ，准线方程为． 20．（2012陕西）右图是抛物线形拱桥，当水面在l 时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽米．21．（2010浙江）设抛物线22(0)y px p =>的焦点为F ，点(0,2)A ．若线段FA 的中点B在抛物线上，则B 到该抛物线准线的距离为_____________．三、解答题22．（2018北京）已知抛物线C ：22y px =经过点(1,2)P ．过点(0,1)Q 的直线l 与抛物线C 有两个不同的交点A ，B ，且直线PA 交y 轴于M ，直线PB 交y 轴于N ．(1)求直线l 的斜率的取值范围；(2)设O 为原点，QM QO λ=u u u u r u u u r ，QN QO μ=u u u r u u u r ，求证：11λμ+为定值．23．（2018全国卷Ⅱ）设抛物线24=：C y x 的焦点为F ，过F 且斜率为(0)>k k 的直线l与C 交于A ，B 两点，||8=AB ．(1)求l 的方程；(2)求过点A ，B 且与C 的准线相切的圆的方程．24．（2018浙江）如图，已知点P 是y 轴左侧(不含y 轴)一点，抛物线C ：24y x =上存在不同的两点A ，B 满足PA ，PB 的中点均在C 上．(1)设AB 中点为M ，证明：PM 垂直于y 轴；(2)若P 是半椭圆2214y x +=(0x <)上的动点，求PAB ∆面积的取值范围． 25．（2017新课标Ⅲ）已知抛物线C ：22y x =，过点(2,0)的直线l 交C 与A ，B 两点，圆M 是以线段AB 为直径的圆． (1)证明：坐标原点O 在圆M 上；(2)设圆M 过点(4,2)P -，求直线l 与圆M 的方程．26．（2017浙江）如图，已知抛物线2x y =．点11(,)24A -，39(,)24B ，抛物线上的点(,)P x y 13()22x -<<，过点B 作直线AP 的垂线，垂足为Q ．x（Ⅰ）求直线AP 斜率的取值范围；（Ⅱ）求||||PA PQ ⋅的最大值．27．（2017北京）已知抛物线C ：22y px =过点(1,1)P ．过点1(0,)2作直线l 与抛物线C 交于不同的两点M ，N ，过点M 作x 轴的垂线分别与直线OP ，ON 交于点A ，B ，其中O 为原点．（Ⅰ）求抛物线C 的方程，并求其焦点坐标和准线方程；（Ⅱ）求证：A 为线段BM 的中点．28．(2016年全国III)已知抛物线C ：22y x =的焦点为F ，平行于x 轴的两条直线1l ，2l 分别交C 于A ，B 两点，交C 的准线于P ，Q 两点.（Ⅰ）若F 在线段AB 上，R 是PQ 的中点，证明AR ∥FQ ；（Ⅱ）若△PQF 的面积是△ABF 的面积的两倍，求AB 中点的轨迹方程．29．（2015新课标1）在直角坐标系xoy 中，曲线C ：24x y =与直线y kx a =+(0)a >交与M ，N 两点，（Ⅰ）当0k =时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有OPM OPN ∠=∠？说明理由． 30．（2014山东）已知抛物线）＞0(2:2p px y C =的焦点为F ，A 为C 上异于原点的任意一点，过点A 的直线l 交C 于另一点B ，交x 轴的正半轴于点D ，且有FA FD =，当点A 的横坐标为3时，ADF ∆为正三角形。

历年高考数学真题(全国卷整理版)完整版完整版

参考公式：如果事件 A、B互斥，那么球的表面积公式P( A B) P( A) P(B)S 4R2如果事件 A、B相互独立，那么其中 R表示球的半径P(A B) P( A) P(B)球的体积公式如果事件 A 在一次试验中发生的概率是p ，那么V3R3n 次独立重复试验中事件 A 恰好发生k次的概率4其中 R 表示球的半径P n (k ) C n k p k (1 p)n k (k 0,1,2, n)普通高等学校招生全国统一考试一、选择题13i 1、复数i =1A 2+I B2-I C 1+2i D 1- 2i2、已知集合 A ＝{1.3.m }，B＝{1，m} ,A B ＝ A, 则 m=A0或3 B 0或3C1或3 D 1或33椭圆的中心在原点，焦距为 4 一条准线为 x=-4 ，则该椭圆的方程为A x2y2=1Bx2y2=1 16++12128C x2y2=1Dx2y28+12+=1 444已知正四棱柱ABCD- A 1B 1C1D1中，AB=2 ，CC1= 2 2 E 为 CC1的中点，则直线 AC 1与平面 BED 的距离为A2B3C2D1（5）已知等差数列{a n} 的前 n 项和为 S n， a5=5， S5=15，则数列的前100项和为10099(C)99101(A)(B)(D)100101101100（6）△ ABC 中， AB 边的高为 CD ，若a· b=0， |a|=1， |b|=2，则(A)（B）(C)(D)3（7）已知α为第二象限角，sinα＋ sinβ =3，则 cos2α = 5555--(C) 9(D)3(A)3（B）9（8）已知 F1、 F2 为双曲线 C： x2-y2=2的左、右焦点，点P 在 C 上， |PF1|=|2PF2|，则 cos ∠F1PF2=1334(A) 4（B）5(C)4(D)51（9）已知 x=ln π， y=log52 ，z=e2，则(A)x ＜ y＜ z（B）z＜x＜y(C)z ＜ y＜ x(D)y ＜ z＜ x(10) 已知函数y＝ x2-3x+c 的图像与 x 恰有两个公共点，则c＝（A ）-2 或 2 （B）-9 或 3 （C）-1 或 1 （D）-3 或 1（11）将字母 a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，梅列的字母也互不相同，则不同的排列方法共有（A）12 种（ B）18 种（ C）24 种（ D）36 种7（12）正方形 ABCD 的边长为1，点 E 在边 AB 上，点 F 在边 BC 上， AE ＝ BF ＝3。

十年真题(2010-2019)高考数学(理)分类汇编专题12 平面解析几何解答题(新课标Ⅰ卷)(解析版)

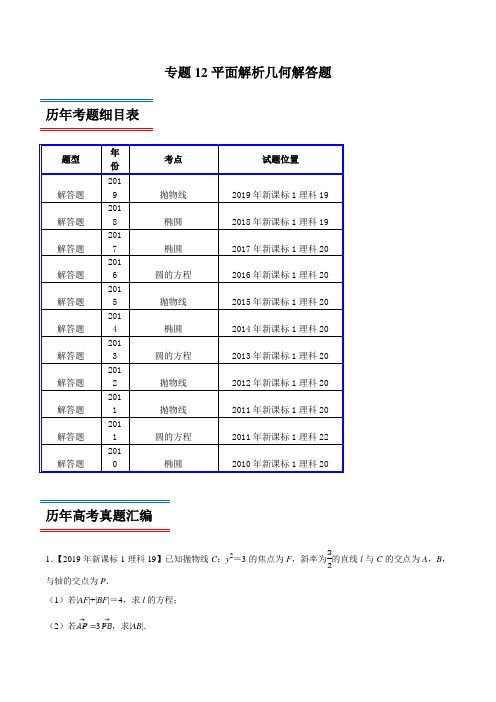
专题12平面解析几何解答题历年考题细目表题型年份考点试题位置解答题2019 抛物线2019年新课标1理科19解答题2018 椭圆2018年新课标1理科19解答题2017 椭圆2017年新课标1理科20解答题2016 圆的方程2016年新课标1理科20解答题2015 抛物线2015年新课标1理科20解答题2014 椭圆2014年新课标1理科20解答题2013 圆的方程2013年新课标1理科20解答题2012 抛物线2012年新课标1理科20解答题2011 抛物线2011年新课标1理科20解答题2011 圆的方程2011年新课标1理科22解答题2010 椭圆2010年新课标1理科20历年高考真题汇编1．【2019年新课标1理科19】已知抛物线C：y2＝3的焦点为F，斜率为的直线l与C的交点为A，B，与轴的交点为P．（1）若|AF|+|BF|＝4，求l的方程；（2）若3，求|AB|．【解答】解：（1）设直线l的方程为y（﹣t），将其代入抛物线y2＝3得：2﹣（t+3）t2＝0，设A（1，y1），B（2，y2），则1+22t，①，12＝t2②，由抛物线的定义可得：|AF|+|BF|＝1+2+p＝2t4，解得t，直线l的方程为y．（2）若3，则y1＝﹣3y2，∴（1﹣t）＝﹣3（2﹣t），化简得1＝﹣32+4t，③由①②③解得t＝1，1＝3，2，∴|AB|．2．【2018年新课标1理科19】设椭圆C：y2＝1的右焦点为F，过F的直线l与C交于A，B两点，点M的坐标为（2，0）．（1）当l与轴垂直时，求直线AM的方程；（2）设O为坐标原点，证明：∠OMA＝∠OMB．【解答】解：（1）c1，∴F（1，0），∵l与轴垂直，∴＝1，由，解得或，∴A（1.），或（1，），∴直线AM的方程为y，y，证明：（2）当l与轴重合时，∠OMA＝∠OMB＝0°，当l与轴垂直时，OM为AB的垂直平分线，∴∠OMA＝∠OMB，当l与轴不重合也不垂直时，设l的方程为y＝（﹣1），≠0，A（1，y1），B（2，y2），则1，2，直线MA，MB的斜率之和为MA，MB之和为MA+MB，由y1＝1﹣，y2＝2﹣得MA+MB，将y＝（﹣1）代入y2＝1可得（22+1）2﹣42+22﹣2＝0，∴1+2，12，∴212﹣3（1+2）+4（43﹣4﹣123+83+4）＝0从而MA+MB＝0，故MA，MB的倾斜角互补，∴∠OMA＝∠OMB，综上∠OMA＝∠OMB．3．【2017年新课标1理科20】已知椭圆C：1（a＞b＞0），四点P1（1，1），P2（0，1），P3（﹣1，），P4（1，）中恰有三点在椭圆C上．（1）求C的方程；（2）设直线l不经过P2点且与C相交于A，B两点．若直线P2A与直线P2B的斜率的和为﹣1，证明：l 过定点．【解答】解：（1）根据椭圆的对称性，P3（﹣1，），P4（1，）两点必在椭圆C上，又P4的横坐标为1，∴椭圆必不过P1（1，1），∴P2（0，1），P3（﹣1，），P4（1，）三点在椭圆C上．把P2（0，1），P3（﹣1，）代入椭圆C，得：，解得a2＝4，b2＝1，∴椭圆C的方程为1．证明：（2）①当斜率不存在时，设l：＝m，A（m，y A），B（m，﹣y A），∵直线P2A与直线P2B的斜率的和为﹣1，∴1，解得m＝2，此时l过椭圆右顶点，不存在两个交点，故不满足．②当斜率存在时，设l：y＝+t，（t≠1），A（1，y1），B（2，y2），联立，整理，得（1+42）2+8t+4t2﹣4＝0，，12，则1，又t≠1，∴t＝﹣2﹣1，此时△＝﹣64，存在，使得△＞0成立，∴直线l的方程为y＝﹣2﹣1，当＝2时，y＝﹣1，∴l过定点（2，﹣1）．4．【2016年新课标1理科20】设圆2+y2+2﹣15＝0的圆心为A，直线l过点B（1，0）且与轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E．（Ⅰ）证明|EA|+|EB|为定值，并写出点E的轨迹方程；（Ⅱ）设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围．【解答】解：（Ⅰ）证明：圆2+y2+2﹣15＝0即为（+1）2+y2＝16，可得圆心A（﹣1，0），半径r＝4，由BE∥AC，可得∠C＝∠EBD，由AC＝AD，可得∠D＝∠C，即为∠D＝∠EBD，即有EB＝ED，则|EA|+|EB|＝|EA|+|ED|＝|AD|＝4，故E的轨迹为以A，B为焦点的椭圆，且有2a＝4，即a＝2，c＝1，b，则点E的轨迹方程为1（y≠0）；（Ⅱ）椭圆C1：1，设直线l：＝my+1，由PQ⊥l，设PQ：y＝﹣m（﹣1），由可得（3m2+4）y2+6my﹣9＝0，设M（1，y1），N（2，y2），可得y1+y2，y1y2，则|MN|•|y1﹣y2|••12•，A到PQ的距离为d，|PQ|＝22，则四边形MPNQ面积为S|PQ|•|MN|••12•＝24•24，当m＝0时，S取得最小值12，又0，可得S＜24•8，即有四边形MPNQ面积的取值范围是[12，8）．5．【2015年新课标1理科20】在直角坐标系Oy中，曲线C：y与直线l：y＝+a（a＞0）交于M，N两点．（Ⅰ）当＝0时，分別求C在点M和N处的切线方程．（Ⅱ）y轴上是否存在点P，使得当变动时，总有∠OPM＝∠OPN？（说明理由）【解答】解：（I）联立，不妨取M，N，由曲线C：y可得：y′，∴曲线C在M点处的切线斜率为，其切线方程为：y﹣a，化为．同理可得曲线C在点N处的切线方程为：．（II）存在符合条件的点（0，﹣a），下面给出证明：设P（0，b）满足∠OPM＝∠OPN．M（1，y1），N（2，y2），直线PM，PN的斜率分别为：1，2．联立，化为2﹣4﹣4a＝0，∴1+2＝4，12＝﹣4a．∴1+2．当b＝﹣a时，1+2＝0，直线PM，PN的倾斜角互补，∴∠OPM＝∠OPN．∴点P（0，﹣a）符合条件．6．【2014年新课标1理科20】已知点A（0，﹣2），椭圆E：1（a＞b＞0）的离心率为，F是椭圆的右焦点，直线AF的斜率为，O为坐标原点．（Ⅰ）求E的方程；（Ⅱ）设过点A的直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程．【解答】解：（Ⅰ）设F（c，0），由条件知，得又，所以a＝2，b2＝a2﹣c2＝1，故E的方程．…．（Ⅱ）依题意当l⊥轴不合题意，故设直线l：y＝﹣2，设P（1，y1），Q（2，y2）将y＝﹣2代入，得（1+42）2﹣16+12＝0，当△＝16（42﹣3）＞0，即时，从而又点O到直线PQ的距离，所以△OPQ的面积，设，则t＞0，，当且仅当t＝2，＝±等号成立，且满足△＞0，所以当△OPQ的面积最大时，l的方程为：y﹣2或y﹣2．…7．【2013年新课标1理科20】已知圆M：（+1）2+y2＝1，圆N：（﹣1）2+y2＝9，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|．【解答】解：（I）由圆M：（+1）2+y2＝1，可知圆心M（﹣1，0）；圆N：（﹣1）2+y2＝9，圆心N（1，0），半径3．设动圆的半径为R，∵动圆P与圆M外切并与圆N内切，∴|PM|+|PN|＝R+1+（3﹣R）＝4，而|NM|＝2，由椭圆的定义可知：动点P的轨迹是以M，N为焦点，4为长轴长的椭圆，∴a＝2，c＝1，b2＝a2﹣c2＝3．∴曲线C的方程为（≠﹣2）．（II）设曲线C上任意一点P（，y），由于|PM|﹣|PN|＝2R﹣2≤3﹣1＝2，所以R≤2，当且仅当⊙P的圆心为（2，0）R＝2时，其半径最大，其方程为（﹣2）2+y2＝4．①l的倾斜角为90°，则l与y轴重合，可得|AB|．②若l的倾斜角不为90°，由于⊙M的半径1≠R，可知l与轴不平行，设l与轴的交点为Q，则，可得Q（﹣4，0），所以可设l：y＝（+4），由l于M相切可得：，解得．当时，联立，得到72+8﹣8＝0．∴，．∴|AB|由于对称性可知：当时，也有|AB|．综上可知：|AB|或．8．【2012年新课标1理科20】设抛物线C：2＝2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，F A为半径的圆F交l于B，D两点；（1）若∠BFD＝90°，△ABD的面积为，求p的值及圆F的方程；（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．【解答】解：（1）由对称性知：△BFD是等腰直角△，斜边|BD|＝2p点A到准线l的距离，∵△ABD的面积S△ABD，∴，解得p＝2，所以F坐标为（0，1），∴圆F的方程为2+（y﹣1）2＝8．（2）由题设，则，∵A，B，F三点在同一直线m上，又AB为圆F的直径，故A，B关于点F对称．由点A，B关于点F对称得：得：，直线，切点直线坐标原点到m，n距离的比值为．9．【2011年新课标1理科20】在平面直角坐标系Oy中，已知点A（0，﹣1），B点在直线y＝﹣3上，M 点满足∥，•，M点的轨迹为曲线C．（Ⅰ）求C的方程；（Ⅱ）P为C上的动点，l为C在P点处的切线，求O点到l距离的最小值．【解答】解：（Ⅰ）设M（，y），由已知得B（，﹣3），A（0，﹣1）．所（﹣，﹣1﹣y），（0，﹣3﹣y），（，﹣2）．再由题意可知（）•0，即（﹣，﹣4﹣2y）•（，﹣2）＝0．所以曲线C的方程式为y2．（Ⅱ）设P（0，y0）为曲线C：y2上一点，因为y′，所以l的斜率为0，因此直线l的方程为y﹣y00（﹣0），即0﹣2y+2y0﹣02＝0．则o点到l的距离d．又y02，所以d2，所以02＝0时取等号，所以O点到l距离的最小值为2．10．【2011年新课标1理科22】如图，D，E分别为△ABC的边AB，AC上的点，且不与△ABC的顶点重合．已知AE的长为m，AC的长为n，AD，AB的长是关于的方程2﹣14+mn＝0的两个根．（Ⅰ）证明：C，B，D，E四点共圆；（Ⅱ）若∠A＝90°，且m＝4，n＝6，求C，B，D，E所在圆的半径．【解答】解：（I）连接DE，根据题意在△ADE和△ACB中，AD×AB＝mn＝AE×AC，即又∠DAE＝∠CAB，从而△ADE∽△ACB因此∠ADE＝∠ACB∴C，B，D，E四点共圆．（Ⅱ）m＝4，n＝6时，方程2﹣14+mn＝0的两根为1＝2，2＝12．故AD＝2，AB＝12．取CE的中点G，DB的中点F，分别过G，F作AC，AB的垂线，两垂线相交于H点，连接DH．∵C，B，D，E四点共圆，∴C，B，D，E四点所在圆的圆心为H，半径为DH．由于∠A＝90°，故GH∥AB，HF∥AC．HF＝AG＝5，DF（12﹣2）＝5．故C，B，D，E四点所在圆的半径为511．【2010年新课标1理科20】设F1，F2分别是椭圆的左、右焦点，过F1斜率为1的直线ℓ与E相交于A，B两点，且|AF2|，|AB|，|BF2|成等差数列．（1）求E的离心率；（2）设点P（0，﹣1）满足|P A|＝|PB|，求E的方程．【解答】解：（I）由椭圆定义知|AF2|+|BF2|+|AB|＝4a，又2|AB|＝|AF2|+|BF2|，得，l的方程为y＝+c，其中．设A（1，y1），B（2，y2），则A、B两点坐标满足方程组化简的（a2+b2）2+2a2c+a2（c2﹣b2）＝0则因为直线AB斜率为1，|AB||1﹣2|，得，故a2＝2b2所以E的离心率（II）设AB的中点为N（0，y0），由（I）知，．由|P A|＝|PB|，得PN＝﹣1，即得c＝3，从而故椭圆E的方程为．考题分析与复习建议本专题考查的知识点为：直线方程、圆的方程，直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线，曲线与方程等.历年考题主要以解答题题型出现，重点考查的知识点为：直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线等，预测明年本考点题目会比较稳定，备考方向以知识点直线与圆、圆与圆的位置关系，椭圆、双曲线、抛物线及其性质，直线与圆锥曲线等为重点较佳.最新高考模拟试题1．已知椭圆22122:1(0)x y C a b a b +=>>，椭圆22222:1(0)33x y C a b a b +=>>经过点22⎛⎫⎪ ⎪⎝⎭. （1）求椭圆1C 的标准方程；（2）设点M 是椭圆1C 上的任意一点，射线MO 与椭圆2C 交于点N ，过点M 的直线l 与椭圆1C 有且只有一个公共点，直线l 与椭圆2C 交于,A B 两个相异点，证明：NAB △面积为定值.【答案】（1）22113y x +=；（2）见解析. 【解析】（1）解：因为1C，所以22619b a=-，解得223a b =.①将点22⎛ ⎝⎭代入2222133x y a b +=，整理得2211144a b +=.② 联立①②，得21a =，213b =，故椭圆1C 的标准方程为22113y x +=. （2）证明：①当直线l 的斜率不存在时，点M 为()1,0或()1,0-，由对称性不妨取()1,0M ，由（1）知椭圆2C 的方程为2213x y +=，所以有()N .将1x =代入椭圆2C的方程得y =所以11122NAB S MN AB ∆=⋅==. ②当直线l 的斜率存在时，设其方程为y kx m =+，将y kx m =+代入椭圆1C 的方程得()222136310kxkmx m +++-=，由题意得()()()2226413310km k m∆=-+-=，整理得22313m k =+.将y kx m =+代入椭圆2C 的方程，得()222136330kxkmx m +++-=.设()11,A x y ，()22,B x y ，则122613km x x k +=-+，21223313m x x k -=+，所以AB =2313k m==+. 设()00,M x y ，()33,N x y ，ON MO λ=u u u v u u u u v，则可得30x x λ=-，30y y λ=-.因为220022333113x y x y ⎧+=⎪⎨+=⎪⎩，所以2200222003113x y x y λ⎧+=⎪⎛⎫⎨+= ⎪⎪⎝⎭⎩，解得λ=λ=，所以ON =u u u vu u u v，从而)1NM OM =. 又因为点O 到直线l的距离为d =所以点N到直线l 的距离为)11m d ⋅=所以()()221126131312231NABmk S d AB m k∆+=+⋅=+⋅⋅+ 62=+，综上，NAB ∆的面积为定值62+. 2．如图，在平面直角坐标系Oy 中，椭圆C ：22221x y a b+=(a ＞b ＞0)经过点(0，3-)，点F 是椭圆的右焦点，点F 到左顶点的距离和到右准线的距离相等．过点F 的直线l 交椭圆于M ，N 两点．（1）求椭圆C 的标准方程；（2）当MF ＝2FN 时，求直线l 的方程；（3）若直线l 上存在点P 满足PM·PN＝PF 2，且点P 在椭圆外，证明：点P 在定直线上．【答案】（1）22143x y +=；（25250x y ±-=；（3）见解析. 【解析】（1）设椭圆的截距为2c ，由题意，b 3由点F 到左顶点的距离和到右准线的距离相等，得a+c ＝2a c c-，又a 2＝b 2+c 2，联立解得a ＝2，c ＝1．∴椭圆C 的标准方程为22143x y +=；（2）当直线l 与轴重合时，M （﹣2，0），N （2，0），此时MF ＝3NF ，不合题意；当直线l 与轴不重合时，设直线l 的方程为＝my+1，M （1，y 1），N （2，y 2），联立22my 1x y 143x =+⎧⎪⎨+=⎪⎩，得（3m 2+4）y 2+6my ﹣9＝0．△＝36m 2+36（m 2+4）＞0．122634m y y m +=-+ ①，1229y y 3m 4=-+②，由MF ＝2FN ，得y 1＝﹣2y 2③，联立①③得，1222126,3434m my y m m =-=++，代入②得，()22227293434m m m-=-++，解得m 5=±20y ±-=；（3）当直线l 的斜率为0时，则M （2，0），N （﹣2，0），设P （0，y 0），则PM•PN＝|（0﹣2）（0+2）|，∵点P 在椭圆外，∴0﹣2，0+2同号，又()()()()2220000PF x 1,x 2x 2x 1=-∴-+=-，解得052x =．当直线l 的斜率不为0时，由（2）知，1212226m 9y y ,y y 3m 43m 4+=-=-++，10200PM y ,PN y ,PF =-=-=．∵点P 在椭圆外，∴y 1﹣y 0，y 2﹣y 0同号，∴PM•PN＝（1+m 2）（y 1﹣y 0）（y 2﹣y 0）＝()()221201201my yy y y y ⎡⎤+-++⎣⎦()()2222002269113434m m y m y m m ⎛⎫=++-=+ ⎪++⎝⎭，整理得032y m =，代入直线方程得052x =．∴点P 在定直线52x =上． 3．已知抛物线C ：24y x =的焦点为F ，直线l 与抛物线C 交于A ，B 两点，O 是坐标原点．（1）若直线l 过点F 且8AB =，求直线l 的方程；（2）已知点(2,0)E -，若直线l 不与坐标轴垂直，且AEO BEO ∠=∠，证明：直线l 过定点．【答案】（1）1y x =-或1y x =-+；（2）(2,0). 【解析】解：（1）法一：焦点(1,0)F ，当直线l 斜率不存在时，方程为1x =，与抛物线的交点坐标分别为(1,2)，(1,2)-，此时4AB =，不符合题意，故直线的斜率存在．设直线l 方程为(1)=-y k x 与24y x =联立得()2222220k x k x k -+-=，当0k =时，方程只有一根，不符合题意，故0k ≠.()212222k x x k++=，抛物线的准线方程为1x =-，由抛物线的定义得()()12||||||11AB AF BF x x =+=+++()222228k k+=+=，解得1k =±，所以l 方程为1y x =-或1y x =-+.法二：焦点(1,0)F ，显然直线l 不垂直于x 轴，设直线l 方程为1x my =+,与24y x =联立得2440y my --=，设11(,)A x y ，22(,)B x y ，124y y m +=，124y y =.||AB ==()241m ==+，由8AB =，解得1m =±，所以l 方程为1y x =-或1y x =-+. （2）设11(,)A x y ，22(,)B x y ，设直线l 方程为(0)x my b m =+≠与24y x =联立得：2440y my b --=，可得124y y m +=，124y y b =-. 由AEO BEO ∠=∠得EA EB k k =，即121222y yx x =-++. 整理得121122220y x y x y y +++=，即121122()2()20y my b y my b y y +++++=，整理得12122(2)()0my y b y y +++=，即84(2)0bm b m -++=，即2b =. 故直线l 方程为2x my =+过定点(2,0).4．已知椭圆22221(0)x y a b a b +=>>，()2,0A 是长轴的一个端点，弦BC 过椭圆的中心O ，点C 在第一象限，且0AC BC ⋅=u u u r u u u r，||2||OC OB AB BC -=+u u u r u u u r u u u r u u u r ．（1）求椭圆的标准方程；（2）设P 、Q 为椭圆上不重合的两点且异于A 、B ，若PCQ ∠的平分线总是垂直于x 轴，问是否存在实数λ，使得PQ AB =λu u u r u u u r？若不存在，请说明理由；若存在，求λ取得最大值时的PQ 的长．【答案】(1) 223144x y += (2)【解析】（1）∵0AC BC ⋅=u u u r u u u r，∴90ACB ∠=︒，∵||2||OC OB AB BC -=+u u u r u u u r u u u r u u u r．即||2||BC AC =u u u r u u u r ，∴AOC △是等腰直角三角形， ∵()2,0A ，∴()1,1C ，而点C 在椭圆上，∴22111a b +=，2a =，∴243b =， ∴所求椭圆方程为223144x y +=．（2）对于椭圆上两点P ，Q ， ∵PCQ ∠的平分线总是垂直于x 轴， ∴PC 与CQ 所在直线关于1x =对称，PC k k =，则CQ k k =-，∵()1,1C ，∴PC 的直线方程为()11y k x =-+，①QC 的直线方程为()11y k x =--+，②将①代入223144x y +=，得()()22213613610k x k k x k k +--+--=，③∵()1,1C 在椭圆上，∴1x =是方程③的一个根，∴2236113P k k x k--=+，以k -替换k ，得到2236131Q k k x k +-=+． ∴()213P Q PQ P Qk x x kk x x +-==-， ∵90ACB ∠=o ，()2,0A ，()1,1C ，弦BC 过椭圆的中心O ，∴()2,0A ，()1,1B --，∴13AB k =， ∴PQ AB k k =，∴PQ AB ∥，∴存在实数λ，使得PQ AB =λu u u r u u u r，||PQ =u u ur =≤ 当2219k k =时，即3k =±时取等号，max ||PQ =u u u r ，又||AB =u u u r，maxλ==，∴λ取得最大值时的PQ5．已知抛物线216y x =，过抛物线焦点F 的直线l 分别交抛物线与圆22(4)16x y -+=于,,,A C D B （自上而下顺次）四点.（1）求证：||||AC BD ⋅为定值；（2）求||||AB AF ⋅的最小值. 【答案】(1)见证明；(2)108 【解析】（1）有题意可知，(4,0)F可设直线l 的方程为4x my =+，1122(,),(,)A x y B x y联立直线和抛物线方程2164y x x my ⎧=⎨=+⎩，消x 可得216640y my --=，所以1216y y m +=，1264y y =-，由抛物线的定义可知，112||4,||42pAF x x BF x =+=+=+，又||||4,||||4AC AF BD BF =-=-，所以2221212264||||(||4)(||4)16161616y y AC BD AF BF x x ⋅=--==⋅==，所以||||AC BD ⋅为定值16.（2）由（1）可知，12||||||8AB AF BF x x =+=++，1||4AF x =+，212111212||||(8)(4)12432AB AF x x x x x x x x ⋅=+++=++++，由1216x x =，可得2116x x =，所以211164||||1248AB AF x x x ⋅=+++（其中1>0x ），令264()1248f x x x x =+++，222642(2)(4)()212x x f x x x x-+'=+-=，当(0,2)x ∈时，()0f x '<，函数单调递减，当(2,)x ∈+∞时，()0f x '>，函数单调递增，所以()(2)108f x f ≥=. 所以||||AB AF ⋅的最小值为108.6．已知O 为坐标原点，点()()2,02,0A B -，，()01AC AD CB CD λλ===<<u u u r u u u r，过点B 作AC的平行线交AD 于点E .设点E 的轨迹为τ. （Ⅰ）求曲线τ的方程；（Ⅱ）已知直线l 与圆22:1O x y +=相切于点M ，且与曲线τ相交于P ，Q 两点，PQ 的中点为N ，求三角形MON 面积的最大值.【答案】（Ⅰ）()22105x y y +=≠；. 【解析】（Ⅰ）因为,AD AC EB AC =∥，故EBD ACD ADC ∠=∠=∠，所以EB ED =，故EA EB EA ED AD +=+==由题设得()()2,02,04A B AB -=，，，由椭圆定义可得点E 的轨迹方程为：()22105x y y +=≠.（Ⅱ）由题意，直线l 的斜率存在且不为0，设直线l 的方程为y kx m =+，因为直线l 与圆O 相切，1=，∴221m k =+，由221,5,x y y kx m ⎧+=⎪⎨⎪=+⎩消去y 得()2221510550k x kmx m +++-=. 设()()1122,,,P x y Q x y ，由韦达定理知：()1212122210221515km mx x y y k x x m k k +=-+=++=++，. 所以PQ 中点N 的坐标为225,1515kmm k k ⎛⎫-⎪++⎝⎭，所以弦PQ 的垂直平分线方程为22151515m km y x k k k ⎛⎫-=-+ ⎪++⎝⎭，即 24015kmx ky k ++=+.所以MN =将m =MN =得2441155||||k MN k k k ====++…（当且仅当k =，即m =取等号）.所以三角形MON的面积为11122S OM MN =⨯⨯⨯≤，综上所述，三角形MON. 7．已知椭圆2222:1(0)x y C a b a b +=>>F 是椭圆C 的一个焦点．点(02)M ,，直线MF 的斜率为3．（1）求椭圆C 的方程；（2）若过点M 的直线l 与椭圆C 交于A B ，两点，线段AB 的中点为N ，且AB MN ＝．求l 的方程．【答案】（1）22182x y +=；（2）22y x =±+【解析】（1）由题意，可得223cac⎧=⎪⎪⎨⎪=⎪⎩，解得a c ⎧=⎪⎨=⎪⎩，则222=2b a c =-，故椭圆C 的方程为22182x y +=．（2）当l 的斜率不存在时，=2AB MN AB MN ≠=，，，不合题意，故l 的斜率存在．设l 的方程为2y kx =+，联立221822x y y kx ⎧+=⎪⎨⎪=+⎩，得22(14)1680k x kx +++＝，设1122(()A x y B x y ，)，，，则12122216k 8,14k 14kx x x x +=-=++， ()222(16)3214128320k k k ∆=-+=->即214k >，设00()N x y ，，则12028214x x kx k+==-+，120||||,0AB MN x =-=-Q则0x =，即28||14k k =+ 整理得21124k =>．故k =，l 的方程为22y x =±+．8．已知椭圆2222:1(0)x y C a b a b+=>>过点(，右焦点F 是抛物线28y x =的焦点.（1）求椭圆C 的方程；（2）已知动直线l 过右焦点F ，且与椭圆C 分别交于M ，N 两点.试问x 轴上是否存在定点Q ，使得13516QM QN ⋅=-u u u u r u u u r 恒成立?若存在求出点Q 的坐标若不存在，说明理由.【答案】(1) 2211612x y += (2)见解析【解析】（1）因为椭圆C 过点，所以221231a b+=，又抛物线的焦点为()2,0，所以2c =. 所以2212314a a +=-，解得23a =（舍去）或216a =. 所以椭圆C 的方程为2211612x y +=.（2）假设在x 轴上存在定点(,0)Q m ，使得13516QM QN ⋅=-u u u u r u u u r. ①当直线l 的斜率不存在时，则(2,3)M ，(2,3)N -，(2,3)QM m =-u u u u r ，(2,3)QN m =--u u u r，由2135(2)916QM QN m ⋅=--=-u u u u r u u u r ，解得54m =或114m =；②当直线l 的斜率为0时，则(4,0)M -，(4,0)N ，(4,0)QM m =--u u u u r，(4,0)QN m =-u u u r，由21351616QM QN m ⋅=-=-u u u u r u u u r ，解得114m =-或114m =.由①②可得114m =，即点Q 的坐标为11,04⎛⎫⎪⎝⎭. 下面证明当114m =时，13516QM QN ⋅=-u u u u r u u u r 恒成立.当直线l 的斜率不存在或斜率为0时，由①②知结论成立.当直线l 的斜率存在且不为0时，设其方程为(2)(0)y k x k =-≠，()11,M x y ，()22,N x y .直线与椭圆联立得()()222234161630kxk x k +-+-=，直线经过椭圆内一点，一定与椭圆有两个交点，且21221643k x x k +=+，()212216343k x x k -=+. ()()()222121212122224y y k x k x k x x k x x k =-•-=-++，所以()1122121212111111121,,44416QM QN x y x y x x x x y y ⎛⎫⎛⎫•=-•-=-+++ ⎪ ⎪⎝⎭⎝⎭u u u u r u u u r ()()()()222222221212221631112111161211241244164344316k k k x x k x x k k k k k k -⎛⎫⎛⎫=+-++++=+-+++= ⎪ ⎪++⎝⎭⎝⎭13516-恒成立综上所述，在x 轴上存在点11,04Q ⎛⎫⎪⎝⎭，使得13516QM QN ⋅=-u u u u r u u u r 恒成立. 9．关于椭圆的切线由下列结论：若11(,)P x y 是椭圆22221(0)x y a b a b+=>>上的一点，则过点P 的椭圆的切线方程为11221x x y y a b +=.已知椭圆22:143x y C +=.(1)利用上述结论，求过椭圆C 上的点(1,)(0)P n n >的切线方程；(2)若M 是直线4x =上任一点，过点M 作椭圆C 的两条切线MA ，MB （A ，B 为切点），设椭圆的右焦点为F ，求证：MF AB ⊥.【答案】（1）240x y +-=（2）见证明【解析】(1)由题意，将1x =代入椭圆方程22:143x y C +=，得32y =，所以3(1,)2P ，所以过椭圆C 上的点3(1,)2P 的切线方程为32143yx +=，即240x y +-=.(2)设(4,)M t ，11(,)A x y ，22(,)B x y ，则过A ，B 两点的椭圆C 的切线MA ，MB 的方程分别为11143x x y y +=，22143x x y y+=，因为(4,)M t 在两条切线上，114143x y t ⨯∴+=，224143x y t⨯+=，所以A ，B 两点均在直线4143x yt +=上，即直线AB 的方程为13tyx +=，当0t ≠时，3AB k t=-，又(1,0)F ，0413MFt t k -==-，313AB MF t k k t ⋅=-⨯=-，所以MF AB ⊥，若0t =，点(4,0)M 在x 轴上，A ，B 两点关于x 轴对称，显然MF AB ⊥.10．已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12F F ，，离心率为12，P 为椭圆上一动点（异于左右顶点），若12AF F △（1）求椭圆C 的方程；（2）若直线l 过点1F 交椭圆C 于,A B 两点，问在x 轴上是否存在一点Q ，使得QA QB ⋅u u u r u u u r为定值？若存在，求点Q 的坐标；若不存在，请说明理由．【答案】（1）22143x y +=（2）见解析【解析】（1）由题意，当P 在上或下顶点时，12PF F ∆的面积取值最大值，即最大值为bc = 又12c a =，且222a c b =+，解得24a =，23b =，故椭圆C 的方程为22143x y +=．（2）易知()11,0F -，设直线l 的方程为1x my =-，()()()11220,,,,,0A x y B x y Q x ，联立方程组221431x y x my ⎧+=⎪⎨⎪=-⎩，整理得22(34)690m y my +--=，则122634my y m +=+，122934y y m =-+， ()()()()10120200212,,y QA QB x x y x x y x x x x y y ⋅=-⋅-=--+u u u r u u u r()212001212x x x x x x y y =+-++，∵111x my =-，221x my =-，∴()()()2212121212215111134m x x my my m y y m y y m =--=+-+=-+，()()()212122226112234m x x my my m y y m +=-+-=+-=-+， ∴222000222156912343434m m QA QB x x x m m m ⋅=-+-+-+++u u u r u u u r 2202281253434m x x m m +=+-++()222000231248534x m x x m -++-=+，要使QA QB ⋅u u u r u u u r 为定值，则2200031248534x x x -+-=，解得0118x =-，所以在x 轴上存在点11,08Q ⎛⎫-⎪⎝⎭，使得QA QB ⋅u u u r u u u r 为定值． 11．已知点()1,0F ，直线:1l x =-，P 为平面上的动点，过点P 作直线的垂线，垂足为Q ，且QP QF FP FQ ⋅=⋅u u u r u u u r u u u r u u u r.（1）求动点P 的轨迹C 的方程；（2）设直线y kx b =+与轨迹C 交于两点，()11,A x y 、()22,B x y ，且12y y a -= (0a >，且a 为常数)，过弦AB 的中点M 作平行于x 轴的直线交轨迹C 于点D ，连接AD 、BD .试判断ABD ∆的面积是否为定值，若是，求出该定值，若不是，请说明理由【答案】(1) 24y x = (2)见解析【解析】（1）设(,)P x y ，则(1,)Q y -，QP QF FP FQ •=•u u u r u u u r u u u r u u u r Q ，(1,0)(2,)(1,)(2,)x y x y y ∴+•-=-•-，即22(1)2(1)x x y +=--+，即24y x =，所以动点P 的轨迹的方程24y x =.（2）联立方程组2,4,y kx b y x =+⎧⎨=⎩消去x ，得2440ky y b -+=，依题意，0k ≠，且124y y k+=，124b y y k =，由12y y a -=得()2212124y y y y a +-=，即221616b a k k-=，整理得：221616kb a k -=，所以2216(1)a k kb =-，① 因为AB 的中点222,bk M k k -⎛⎫⎪⎝⎭，所以点212,D k k ⎛⎫⎪⎝⎭，依题意， 122111||22BD bkS DM y y a k ∆∆-=-=，由方程2440ky y b -+=中的判别式16160kb ∆=->，得10kb ->，所以2112ABD bkS a k∆-=••，由①知22116a k kb -=，所以23121632MBDa a S a ∆=••=，又a 为常数，故ABD S ∆的面积为定值. 12．已知点P 在抛物线()220C x py p =：＞上，且点P 的横坐标为2，以P 为圆心，PO 为半径的圆（O 为原点），与抛物线C 的准线交于M ，N 两点，且2MN =．（1）求抛物线C 的方程；（2）若抛物线的准线与y 轴的交点为H ．过抛物线焦点F 的直线l 与抛物线C 交于A ，B ，且AB HB ⊥，求AF BF -的值．【答案】(1) 24x y = (2)4 【解析】（1）将点P 横坐标2P x =代入22x py =中，求得2P y p=， ∴P （2，2p），2244OP p =+，点P 到准线的距离为22p d p =+，∴222||||2MN OP d ⎛⎫=+ ⎪⎝⎭，∴22222212p p p ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭，解得24p =，∴2p =，∴抛物线C 的方程为：24x y =；（2）抛物线24x y =的焦点为F （0，1），准线方程为1y =-，()01H -，；设()()1122A x y B x y ，，，，直线AB 的方程为1y kx =+，代入抛物线方程可得2440x kx --=，∴121244x x k x x +==-，，…① 由AB HB ⊥，可得1AB HB k k ⋅=-，又111AB AF y k k x -==，221HB y k x +=， ∴1212111y y x x -+⋅=-， ∴()()1212110y y x x -++=，即2212121111044x x x x ⎛⎫⎛⎫-++= ⎪⎪⎝⎭⎝⎭， ∴()22221212121110164x x x x x x +--+=，…② 把①代入②得，221216x x -=，则()22121211||||1116444AF BF y y x x -=+--=-=⨯=． 13．已知抛物线方程24y x =，F 为焦点，P 为抛物线准线上一点，Q 为线段PF 与抛物线的交点，定义()PFd P FQ=. （1）当8(1)3P --，时，求()d P ；（2）证明存在常数a ，使得2()d P PF a =+.（3）123,,P P P 为抛物线准线上三点，且1223PP P P =，判断13()()d P d P +与22()d P 的关系. 【答案】（1）83；（2）证明见解析；（3）()()()1322d P d P d P +>. 【解析】（1）因为8443(1)233PFk y x ==⇒=-. 联立方程24(1)1344Q y x x y x ⎧=-⎪⇒=⎨⎪=⎩，则1083()534PF d P QF ⎧=⎪⎪⇒=⎨⎪=⎪⎩. （2）当()1,0P -，易得2()2a d P PF =-=，不妨设()1,P P y -，0P y >，直线:1PF x my =+，则2P my =-，联立214x my y x=+⎧⎨=⎩，2440y my --=，2Q y m ==+2()||2P P Q y d P PF y m -=-=+2=-=.（3）设()()()1122331,,1,,1,P y P y P y ---，则()()()13224d P d P d P +-⎡⎤⎣⎦1322PF P F P F =+-2221324424y y y =+++222131344242y y y y +⎛⎫=+++ ⎪⎝⎭()22213134416y y y y =++++因为()222213134416y y y y ⎡⎤++-++⎣⎦22131224428y y y y =++-，又因()()()()2222213131313444480yy y y y y y y ++-+=+->，所以()()()1322d P d P d P +>.14．已知抛物线2:2(0)C x py p =>的焦点F 到准线距离为2. （1）若点(1,1)E ，且点P 在抛物线C 上，求||||PE PF +的最小值；（2）若过点(0,)N b 的直线l 与圆22:(2)4M x y +-=相切，且与抛物线C 有两个不同交点,A B ，求AOB ∆的面积.【答案】(1)2(2) 2ABC S b ∆=【解析】解：（1）根据题意可知2p =所以抛物线方程为24x y =则抛物线C 焦点为(0,1)F ，准线为1y =-；记点,P E 到抛物线C 准线的距离分别为12,d d ，故12||||||2PE PF PE d d +=+≥=，等号成立当且仅当PE 垂直于准线，故||||PE PF +的最小值为2 （2）设()11,A x y ，()22,B x y由题意知，直线l 斜率存在，设直线l 的方程为：y kx b =+ 将y kx b =+与24x y =联立得2440x kx b --=，由韦达定理得12124,4x x k x x b +==-，由()0,2M 到直线l的距离为12d ==得：2244b b k -=，又||AB ==点O 到直线l 的距离为2d =所以2|ABC S b b ∆=== 15．已知曲线C 上的任意一点到直线l ：=12的距离与到点F （102，）的距离相等．（1）求曲线C 的方程；（2）若过P （1，0）的直线与曲线C 相交于A ，B 两点，Q （1，0）为定点，设直线AQ 的斜率为1，直线BQ 的斜率为2，直线AB 的斜率为，证明：22212112k k k +-为定值．【答案】（1）y 2=2；（2）见解析【解析】（1）由条件可知，此曲线是焦点为F 的抛物线，p 122=，p=1． ∴抛物线的方程为y 2=2；（2）根据已知，设直线AB 的方程为y=（1）（≠0），由()2y k x 1y 2x ⎧=-⎨=⎩，可得y 22y2=0．设A （211y y 2，），B （222y y 2，），则122y y k +=，y 1y 2=2． ∵1112211y 2y k y y 212==++，2222222y 2y k y y 212==++． ∴22221222221212(y 2)(y 2)11k k 4y 4y +++=+=22222212212212(y 2)y (y 2)y 4y y +++ =()42422222122112122212y y y y 8y y 4y y 4y y ++++=()2221212128y y 32(y y )2y y 4162+++-+= =22482k 42k+=+．∴222121124k k k +-=．。

2010-2020全国高考数学卷1(理)解析几何题(含答案)

10年高考数学卷1(理) 解析几何试题(附答案)1.(2020全国卷1理4) 已知A 为抛物线2:2(0)C ypx p =>上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =A ．2B ．3C ．6D ．92.(2020全国卷1理15)已知F为双曲线2222:1x y C a b-=（0,0a b >>）的右焦点，A 为C 的右顶点，B 为C 上的点，且BF 垂直于x 轴．若AB 斜率为3，则C 的离心率为_______．3.(2020全国卷1理20)已知,A B 分别为椭圆222:1(1)x E y a a+=>的左、右顶点，G 为E的上顶点，8AG GB ⋅=．P 为直线6x =上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点．4.(2019全国卷1理10)已知椭圆C 的焦点为121,01,0F F -()，()，过F2的直线与C 交于A ，B 两点.若222AF F B =││││，1AB BF =││││，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=5.(2019全国卷1理16)已知双曲线C ：)0,0(12222>>=-b a by a x 的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120F B F B ⋅=，则C 的离心率为____________．6.(2019全国卷1理20)已知抛物线C ：y 2=3x 的焦点为F ，斜率为32的直线l 与C 的交点为A ，B ，与x 轴的交点为P ．（1）若|AF |+|BF |=4，求l 的方程；（2）若3AP PB =，求|AB |．7.(2018全国卷1理8)设抛物线C ：y 2=4x 的焦点为F ，过点（–2，0）且斜率为23的直线与C 交于M ，N 两点，则FM →·FN →= A ．5B ．6C ．7D ．88.(2018全国卷1理11)已知双曲线C ：x 23 - y 2=1，O 为坐标原点，F 为C 的右焦点，过F的直线与C 的两条渐近线的交点分别为M 、N.若ΔOMN 为直角三角形，则|MN|= A ．32B ．3C ．2 3D ．49.(2018全国卷1理19)设椭圆C: x 22 + y 2=1的右焦点为F ，过F 的直线l 与C 交于A,B两点，点M 的坐标为(2,0).（1）当l 与x 轴垂直时，求直线AM 的方程；（2）设O 为坐标原点，证明：∠OMA=∠OMB.10.已知F 为抛物线C ：24y x =的交点，过F 作两条互相垂直1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D ，E 两点，AB DE+的最小值为（）A ．16B ．14C ．12D ．1011.(2017全国卷1理15) 已知双曲线2222:x y C a b -，（0a >，0b >）的右顶点为A ，以A为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点，若60MAN ∠=︒，则C 的离心率为_______．12.(2017全国卷1理20)已知椭圆C ：22221x y a b+=()0a b >>，四点()111P ，，()201P ，，31P ⎛- ⎝⎭，41P ⎛ ⎝⎭中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过2P 点且与C 相交于A 、B 两点，若直线2P A 与直线2P B 的斜率的和为1-，证明：l 过定点．13.(2016全国卷1理5)已知方程222213x y m n m n-=+-表示双曲线，且该双曲线两焦点间的距离为4,则n 的取值围是（A ）()1,3- （B ）(- （C ）()0,3 （D ）(14.(2016全国卷1理10)以抛物线C 的顶点为圆心的圆交C 于A 、B 两点，交C 的准线于D 、E 两点.已知|AB |=DE|=则C 的焦点到准线的距离为(A)2 (B)4 (C)6 (D)8 15.(2016全国卷1理20)设圆222150xy x ++-=的圆心为A ,直线l 过点B （1,0）且与x 轴不重合，l 交圆A 于C ,D 两点，过B 作AC 的平行线交AD 于点E .（I ）证明EA EB +为定值，并写出点E 的轨迹方程；（II ）设点E 的轨迹为曲线C 1，直线l 交C 1于M ,N 两点，过B 且与l 垂直的直线与圆A 交于P ,Q 两点，求四边形MPNQ 面积的取值围.16.(2015全国卷1理5)已知M （x 0，y 0）是双曲线C ：2212x y -=上的一点，F 1、F 2是C 上的两个焦点，若1MF •2MF ＜0，则y 0的取值范围是（A ）（）（B ）（，）（C ）（）（D ）（） 17.(2015全国卷1理14)一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 轴上，则该圆的标准方程为。

近十年全国高中数学联赛试题一试(解析几何)

十年全国高中数学联赛试题一试解析几何圆锥曲线部分一、选择题2000、已知点A 为双曲线x 2-y 2=1的左顶点，点B 和点C 在双曲线的右分支上，△ABC 是等边三角形，则△ABC 的面积是【答】（） (A)33 (B) 233 (C) 33 (D) 63 答案：C 。

解析：如图所示，设BD=t ，则OD=3t-1，从而B （3t-1，t ）满足方程122=-y x ，可以得到t=3,所以等边三角形，ΔABC 的面积是33.2002．直线x 4+y 3=1与椭圆x 216+y 29=1相交于A 、B 两点，该椭圆上点P ，使得ΔPAB 面积等于3．这样的点P 共有A ．1个B ．2个C ．3个D ．4个解：直线与椭圆的交线长=5．直线方程3x +4y －12=0．设点P (4cos θ，3sin θ)．点P 与直线的距离d=12|cos θ+sin θ－1|5，当0≤θ≤π2时，d ≤125(2－1)，S ABC ≤6(2－1)<3．即此时没有三角形面积=3；当π2<θ<2π时，d ≤125(2+1)，S ABC ≤6(2+1)．即此时有2个三角形面积=3．选B ． 2003. 2设,,0,a b R ab ∈≠那么直线0ax y b -+=和曲线22bx ay ab +=的图形是【答】（）题设方程可化为b ax y +=和122=+by a x ,观察图形可知； 2003.3 过抛物线()282y x =+的焦点F 作倾斜角为60︒的直线. 若此直线与抛物线交于A ，B两点，弦AB 的中垂线与x 轴交于P 点，则线段PF 的长等于【答】（）（A ）163 (B)83163383易知直线AB 的方程为x y 3=,因此A,B 两点的横坐标满足方程016832=--x x ,从而弦AB中点的横坐标为340=x ,纵坐标340=y ,进而求得中垂线方程之后，令y=0，得点P 的横坐标即PF=316； 2004、已知M={}32|),(22=+y x y x ，N={}b mx y y x +=|),(，若对于所有的R m ∈，均有,φ≠⋂N M 则b 的取值范围是A ．[26,26-] B 。

立体几何十年高考题(带详细解析)

D.若 a⊥M，a∥N，则 M⊥N
3.（2002 北京春，2）已知三条直线 m、n、l，三个平面α、β、γ.下面四个命题中，
正确的是（）
α ⊥γ ⎫
A.
β
⊥γ
⎬ ⎭
⇒ α∥β
m // β ⎫
B.
l
⊥
m
⎬ ⎭
⇒
l⊥β
m //γ ⎫
m ⊥γ⎫
C.
n // γ
⎬ ⇒ m∥n ⎭
D.
n ⊥γ
⎬ ⇒ m∥n ⎭
A.1∶3
B.2∶3
C.1∶2
D.2∶9
20.（2000 全国，3）一个长方体共一顶点的三个面的面积分别是 2 , 3, 6 ，这个长
方体对角线的长是（）
A.2 3
B.3 2
C.6
D. 6
图 9—5
21.（2000 全国文，12）如图 9—5，OA 是圆锥底面中心 O 到母线的垂线，OA 绕轴旋转一周所得曲面将圆锥分成相等的两部分，则母线与轴的夹角的余弦值为（）
2
A.
2π
B. 8 π
4
C.
5π
D. 10 π
81
81
81
81
图 9—7
37.（1995 全国文，10）如图 9—7，ABCD—A1B1C1D1 是正方体，B1E1＝D1F1＝ A1 B1 ， 4
则 BE1 与 DF1 所成角的余弦值是（）15A.17183
B.
C.
D.
2
17
2
38.（1995 全国，4）正方体的全面积是 a2，它的顶点都在球面上，这个球的表面积是（）
A.2×5 B.2×5.5 C.2×6.1 D.3×5 8.（2002 全国文 8，理 7）一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么，这个圆锥轴截面顶角的余弦值是（）

【最新】十年高考理科数学真题专题九解析几何二十六椭圆及答案

专题九解析几何第二十六讲椭圆2019年1．（2019全国I 理10）已知椭圆C 的焦点为121,01,0F F -()，()，过F 2的直线与C 交于A ，B 两点．若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y += B ．22132x y += C ．22143x y += D ．22154x y += 2.（2019全国II 理21（1））已知点A (−2,0)，B (2,0)，动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .（1）求C 的方程，并说明C 是什么曲线；3.（2019北京理4）已知椭圆()222210x y a b a b +=>>的离心率为12，则（A ）22.2a b =（B ）22.34a b=（C ）2a b=（D ）34a b=4.（2019全国III 理15）设12F F ，为椭圆C :22+13620x y =的两个焦点，M 为C 上一点且在第一象限.若12MF F △为等腰三角形，则M 的坐标为___________.2010-2018年一、选择题1．(2018全国卷Ⅱ)已知1F ，2F 是椭圆22221(0)+=>>：x y C a b a b的左，右焦点，A 是C 的左顶点，点P 在过A 12△PF F 为等腰三角形，12120∠=︒F F P ，则C 的离心率为A ．23B ．12C ．13D ．142．(2018上海)设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为（）A ．B ．C ．D ．3．（2017浙江）椭圆22194x y +=的离心率是A ．B C ．23 D ．594．（2017新课标Ⅲ）已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A B C D ．135．(2016年全国III)已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点．P 为C 上一点，且PF ⊥x 轴．过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E ．若直线BM 经过OE 的中点，则C 的离心率为 A ．13B ．12C ．23D ．346．(2016年浙江)已知椭圆1C ：2221x y m +=(1m >)与双曲线2C ：2221x y n-=(0n >)的焦点重合，1e ，2e 分别为1C ，2C 的离心率，则A ．m n >且121e e >B ．m n >且121e e <C ．m n <且121e e >D ．m n <且121e e <7．(2014福建)设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是A ．25B ．246+C ．27+D ．268．（2013新课标1）已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为 A ．x 245＋y 236＝1B ．x 236＋y 227＝1C ．x 227＋y 218＝1D ．x 218＋y 29＝19．(2012新课标)设1F 、2F 是椭圆E ：)0(12222>>=+b a by a x 的左、右焦点，P 为直线23a x =上一点，12PF F ∆ 是底角为o30的等腰三角形，则E 的离心率为 A 、21 B 、32 C 、43 D 、54二、填空题10．(2018浙江)已知点(0,1)P ，椭圆224x y m +=(1m >)上两点A ，B 满足2AP PB =，则当m =___时，点B 横坐标的绝对值最大．11．(2018北京)已知椭圆22221(0)x y M a b a b +=>>：，双曲线22221x y N m n-=：．若双曲线N的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为__________；双曲线N 的离心率为__________．12．(2016江苏省)如图，在平面直角坐标系xOy 中，F 是椭圆()222210x y a b a b+=>>的右焦点，直线2by =与椭圆交于,B C 两点，且90BFC ∠=︒，则该椭圆的离心率是．13．（2015新课标1）一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 的正半轴上，则该圆的标准方程为_________．14．（2014江西）过点(1,1)M 作斜率为12-的直线与椭圆C ：22221(0)x y a b a b+=>>相交于,A B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于．15．（2014辽宁）已知椭圆C ：22194x y +=，点M 与C 的焦点不重合，若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则||||AN BN += ．16．（2014江西）设椭圆()01:2222>>=+b a by a x C 的左右焦点为21F F ，，作2F 作x 轴的垂线与C 交于B A ，两点，B F 1与y 轴相交于点D ，若B F AD 1⊥，则椭圆C 的离心率等于________．17．（2014安徽）设21,F F 分别是椭圆)10(1:222<<=+b by x E 的左、右焦点，过点1F 的直线交椭圆E 于B A ,两点，若x AF BF AF ⊥=211,3轴，则椭圆E 的方程为_____．18．（2013福建）椭圆)0(1:2222>>=+Γb a by a x 的左、右焦点分别为21,F F ，焦距为c 2．若直线)y x c =+与椭圆Γ的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于19．（2012江西）椭圆22221(0)x y a b a b+=>>的左、右顶点分别是,A B ，左、右焦点分别是12,F F ．若1121||,||,||AF F F F B 成等比数列，则此椭圆的离心率为_________．20．（2011浙江）设12,F F 分别为椭圆2213x y +=的左、右焦点，点,A B 在椭圆上，若125F A F B =；则点A 的坐标是．三、解答题21．（2018全国卷Ⅰ）设椭圆:C 2212+=x y 的右焦点为F ，过F 的直线l 与C 交于A ,B 两点，点M 的坐标为(2,0)．(1)当l 与x 轴垂直时，求直线AM 的方程； (2)设O 为坐标原点，证明：OMA OMB ∠=∠．22．（2018全国卷Ⅲ）已知斜率为k 的直线l 与椭圆C ：22143x y +=交于A ，B 两点，线段AB 的中点为(1,)M m (0)m >． (1)证明：12k <-； (2)设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0．证明：||FA ，||FP ，||FB 成等差数列，并求该数列的公差．23．(2018天津)设椭圆22221x x a b+=(0a b >>)的左焦点为F ，上顶点为B ．已知椭圆的离心率为3，点A 的坐标为(,0)b ，且FB AB ⋅=． (1)求椭圆的方程；(2)设直线l ：(0)y kx k =>与椭圆在第一象限的交点为P ，且l 与直线AB 交于点Q ．若4AQ AOQ PQ=∠(O 为原点) ，求k 的值． 24．（2017新课标Ⅰ）已知椭圆C ：22221(0)x y a b a b+=>>，四点1(1,1)P ，2(0,1)P ，3(P =-，4P =中恰有三点在椭圆C 上． (1)求C 的方程；(2)设直线l 不经过2P 点且与C 相交于A ，B 两点．若直线2P A 与直线2P B 的斜率的和为1-，证明：l 过定点．25．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足2NP NM =．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．26．（2017江苏）如图，在平面直角坐标系xOy 中，椭圆E ：22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，离心率为12，两准线之间的距离为8．点P 在椭圆E 上，且位于第一象限，过点1F 作直线1PF 的垂线1l ，过点2F 作直线2PF 的垂线2l ．（1）求椭圆E 的标准方程；（2）若直线1l ，2l 的交点Q 在椭圆E 上，求点P 的坐标．27．（2017天津）设椭圆22221(0)x y a b a b+=>>的左焦点为F ，右顶点为A ，离心率为12．已知A 是抛物线22(0)y px p =>的焦点，F 到抛物线的准线l 的距离为12．（Ⅰ）求椭圆的方程和抛物线的方程；（Ⅱ）设l 上两点P ，Q 关于x 轴对称，直线AP 与椭圆相交于点B （B 异于点A ），直线BQ 与x 轴相交于点D ．若APD △的面积为62AP 的方程． 28．（2017山东）在平面直角坐标系xOy 中，椭圆E ：22221x y a b+=()0a b >>2，焦距为2．（Ⅰ）求椭圆E 的方程；（Ⅱ）如图，动直线l：1y k x =E 于,A B 两点，C 是椭圆E 上一点，直线OC 的斜率为2k，且12k k =，M 是线段OC 延长线上一点，且:2:3MC AB =，M 的半径为MC ，,OS OT 是M 的两条切线，切点分别为,S T ．求SOT ∠的最大值，并求取得最大值时直线l 的斜率．x29．(2016年北京)已知椭圆C ：22221(0)x y a ba b +=>>(,0)A a ，(0,)B b ，(0,0)O ，ΔOAB 的面积为1．（Ⅰ）求椭圆C 的方程；（Ⅱ）设P 是椭圆C 上一点，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ．求证：||||AN BM ⋅为定值．30．(2015新课标2）已知椭圆C ：2229x y m +=(0m >)，直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M ．（Ⅰ）证明：直线OM 的斜率与l 的斜率的乘积为定值；（Ⅱ）若l 过点(,)3mm ，延长线段OM 与C 交于点P ，四边形OAPB 能否为平行四边行？若能，求此时l 的斜率；若不能，说明理由．31．（2015北京）已知椭圆C ：()222210x y a ba b+=>>的离心率为，点()01P ，和点()A m n ，()0m ≠都在椭圆C 上，直线PA 交x 轴于点M ．（Ⅰ）求椭圆C 的方程，并求点M 的坐标（用m ，n 表示）；（Ⅱ）设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N ．问：y 轴上是否存在点Q ，使得OQM ONQ ∠=∠？若存在，求点Q 的坐标；若不存在，说明理由．32．（2015安徽）设椭圆E 的方程为()222210x y a b a b+=>>，点O 为坐标原点，点A 的坐标为()0a ，，点B 的坐标为()0b ，，点M 在线段AB 上，满足2BM MA =，直线OM（Ⅰ）求E 的离心率e ；（Ⅱ）设点C 的坐标为()0b -，，N 为线段AC 的中点，点N 关于直线AB 的对称点的纵坐标为72，求E 的方程． 33．（2015山东）平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率1F 、2F ．以1F 为圆心以3为半径的圆与以2F 为圆心以1为半径的圆相交，且交点在椭圆C 上．（Ⅰ）求椭圆C 的方程；（Ⅱ）设椭圆E ：2222144x y a b+=，P 为椭圆C 上任意一点，过点P 的直线=+y kx m交椭圆E 于,A B 两点，射线PO 交椭圆E 于点Q ．( i )求||||OQ OP 的值；（ii ）求△ABQ 面积的最大值．34． (2014新课标1) 已知点A (0,2)-，椭圆E ：22221(0)x y a b a b +=>>F 是椭圆E 的右焦点，直线AF，O 为坐标原点．（Ⅰ)求E 的方程；（Ⅱ）设过点A 的动直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．35．(2014浙江)如图，设椭圆(),01:2222>>=+b a by a x C 动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限．（Ⅰ）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；（Ⅱ）若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -．36．（2014新课标2）设1F ，2F 分别是椭圆C ：()222210y x a b a b+=>>的左，右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ．（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求,a b ．37．（2014安徽）设1F ,2F 分别是椭圆E ：22221(0)x ya b a b+=>>的左、右焦点，过点1F 的直线交椭圆E 于,A B 两点，11||3||AF BF = （Ⅰ）若2||4,AB ABF =∆的周长为16，求2||AF ；（Ⅱ）若23cos 5AF B ∠=，求椭圆E 的离心率．38．（2014山东）在平面直角坐标系xOy 中，椭圆2222:1(0)x y C a b a b +=>>的离心率为3，直线y x =被椭圆C 截得的线段长为410．（Ｉ）求椭圆C 的方程；（Ⅱ）过原点的直线与椭圆C 交于A ，B 两点（A ，B 不是椭圆C 的顶点）．点D 在椭圆C 上，且AD AB ⊥，直线BD 与x 轴、y 轴分别交于M ，N 两点． (ⅰ)设直线BD ，AM 的斜率分别为12,k k ，证明存在常数λ使得12k k λ=，并求出λ的值；(ⅱ)求OMN ∆面积的最大值．39．（2014湖南）如图5，O 为坐标原点，双曲线221112211:1(0,0)x y C a b a b -=>>和椭圆222222222:1(0)x y C a b a b +=>>均过点23(,1)3P ，且以1C 的两个顶点和2C 的两个焦点为顶点的四边形是面积为2的正方形．（Ｉ）求12,C C 的方程；（Ⅱ）是否存在直线l ，使得l 与1C 交于,A B 两点，与2C 只有一个公共点，且||||OA OB AB +=？证明你的结论．40．（2014四川）已知椭圆C ：22221x y a b+=（0a b >>）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q ．（i ）证明：OT 平分线段PQ （其中O 为坐标原点）；（ii ）当||||TF PQ 最小时，求点T 的坐标． 41．（2013安徽）已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4，且过点P ．（Ⅰ）求椭圆C 的方程；（Ⅱ）设0000(,)(0)Q x y x y ≠为椭圆C 上一点，过点Q 作x 轴的垂线，垂足为E ．取y 轴的对称点，作直线QG ，问这样作出的直线QG 是否与椭圆C 一定有唯一的公共点？并说明理由．42．（2013湖北）如图，已知椭圆1C 与2C 的中心在坐标原点O ，长轴均为MN 且在x 轴上，短轴长分别为2m ，2()n m n >，过原点且不与x 轴重合的直线l 与1C ，2C 的四个交点按纵坐标从大到小依次为A ，B ，C ，D ．记mnλ=，△BDM 和△ABN 的面积分别为1S 和2S ．（Ⅰ）当直线l 与y 轴重合时，若12S S λ=，求λ的值；（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l ，使得12S S λ=？并说明理由． 43． (2013天津)设椭圆22221(0)x y a b a b+=>>的左焦点为F ，，过点F 且与x．(Ⅰ) 求椭圆的方程；第20题图(Ⅱ) 设A ， B 分别为椭圆的左、右顶点，过点F 且斜率为k 的直线与椭圆交于C ，D两点．若··8AC DB AD CB +=，求k 的值．44．（2013山东）椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别是12,F F ，过1F 且垂直于x 轴的直线被椭圆C 截得的线段长为l ．（Ⅰ）求椭圆C 的方程；（Ⅱ）点P 是椭圆C 上除长轴端点外的任一点，连接12,PF PF ．设12F PF ∠的角平分线PM 交C 的长轴于点(),0M m ，求m 的取值范围；（Ⅲ）在（Ⅱ）的条件下，过点P 作斜率为k 的直线l ，使得l 与椭圆C 有且只有一个公共点．设直线12,PF PF 的斜率分别为12,k k ，若0k ≠，试证明1211kk kk +为定值，并求出这个定值．45．（2012北京）已知椭圆C :22221(0)x y a b a b+=>>的一个顶点为(2,0)A，离心率为．直线(1y k x =-）与椭圆C 交于不同的两点M ,N ．（Ⅰ）求椭圆C 的方程；（Ⅱ）当△AMN得面积为3时，求k 的值． 46．（2013安徽）如图，21,F F 分别是椭圆C ：22a x +22by =1（0>>b a ）的左、右焦点，A是椭圆C 的顶点，B 是直线2AF 与椭圆C 的另一个交点，1F ∠A 2F =60°．（Ⅰ）求椭圆C 的离心率；（Ⅱ）已知△A B F 1的面积为403，求a , b 的值．47．（2012广东）在平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率e =C 上的点到(0,2)Q 的距离的最大值为3．（Ⅰ）求椭圆C 的方程；（Ⅱ）在椭圆C 上，是否存在点(,)M m n 使得直线l ：1mx ny +=与圆O ：221x y +=相交于不同的两点,A B ，且OAB ∆的面积最大？若存在，求出点M 的坐标及相对应的OAB ∆的面积；若不存在，请说明理由．48．（2011陕西）设椭圆C: ()222210x y a b a b+=>>过点（0，4），离心率为35（Ⅰ）求C 的方程；（Ⅱ）求过点（3，0）且斜率为45的直线被C 所截线段的中点坐标． 49．（2011山东）在平面直角坐标系xOy 中，已知椭圆22:13x C y +=．如图所示，斜率为(0)k k ＞且不过原点的直线l 交椭圆C 于A ，B 两点，线段AB 的中点为E ，射线OE交椭圆C 于点G ，交直线3x =-于点(3,)D m -．（Ⅰ）求22m k +的最小值；（Ⅱ）若2OG OD =∙OE ，（i ）求证：直线l 过定点；（ii ）试问点B ，G 能否关于x 轴对称？若能，求出此时ABG 的外接圆方程；若不能，请说明理由．50．（2010新课标）设1F ,2F 分别是椭圆E ：2x +22y b=1（01b <<）的左、右焦点，过1F的直线l 与E 相交于A 、B 两点，且2AF ，AB ，2BF 成等差数列．（Ⅰ）求AB ；（Ⅱ）若直线l 的斜率为1，求b 的值．51．（2010辽宁）设椭圆C ：22221(0)x y a b a b+=>>的左焦点为F ，过点F 的直线与椭圆C相交于A ，B 两点，直线l 的倾斜角为60o ，2AF FB =．（Ⅰ）求椭圆C 的离心率；（Ⅱ）如果|AB |=154，求椭圆C 的方程．专题九解析几何第二十六讲椭圆答案部分1. 解析 2x =，则22AF x =，所以23BF AB x ==.由椭圆定义122BF BF a +=，即42x a =.又1224AF AF a x +==，22AF x =，所以12AF x =. 因此点A 为椭圆的上顶点，设其坐标为()0,b .由222AF BF =可得点B 的坐标为3,22b ⎛⎫- ⎪⎝⎭.因为点B 在椭圆()222210x y a b a b+=>>上，所以291144a +=. 解得23a =.又1c =，所以22b =.所以椭圆方程为22132x y +=.故选B. 2．解析（1）由题设得1222y y x x ⋅=-+-，化简得221(||2)42x y x +=≠，所以C 为中心在坐标原点，焦点在x 轴上的椭圆，不含左右顶点．3. 解析由题意，c e a ====所以22244a b a -=，即2234a b =．故选B ．4. 解析设(,)M m n ，,0m n >，椭圆C ：22:13620x yC +=的6a =，b =2c =，23c e a ==，由于M 为C 上一点且在第一象限，可得12||||MF MF >， 12MF F △为等腰三角形，可能1||2MF c =或2||2MF c =，即有2683m +=，即3m =，n = 2683m -=，即30m =-<，舍去．可得M .2010-2018年1．D 【解析】由题意可得椭圆的焦点在x 轴上，如图所示，OyxPF 2F 1A设12||2=F F c ，所以12∆PF F 为等腰三角形，且12=120∠F F P ，∴212||||2PF F F c ==，∵2||OF c =，∴点P 坐标为(2cos60,2sin60)c c c +，即点(2)P c ．∵点P 在过点A=14c a =．∴14e =，故选D ． 2．C 【解析】由题意25=a，=a P 到该椭圆的两个焦点的距离之和为2=a C ．3．B 【解析】由题意可知29a =，24b =，∴2225c a b =-=，∴离心率c e a ==，选B4．A 【解析】以线段12A A 为直径的圆是222x y a +=，直线20bx ay ab -+=与圆相切，所以圆心到直线的距离d a ==，整理为223a b =，即()22222323a a c a c =-⇒=，即2223c a =，3c e a ==，故选A ．5．A 【解析】设(0,)E m ，则直线AE 的方程为1x y a b -+=，由题意可知(,)mcM c m a--，(0,)2m和(,0)B a 三点共线，则22mc m m m a c a--=--，化简得3a c =，则C 的离心率13c e a ==．故选A ． 6．A 【解析】由题意知2211m n -=+，即222m n =+，222221222221111()2m n n n e e m n n n -+++=⋅=⋅+4242422111122n n n n n n ++==+>++，所以121e e >．故选A ．7．D【解析】由题意可设,sin )Q αα，圆的圆心坐标为(0,6)C ，圆心到Q 的距离为||CQ =当且仅当2sin 3α=-时取等号，所以max max ||||PQ CQ r +==≤Q P ,两点间的最大距离是8．D 【解析】设1122(,),(,)A x y B x y ，则12x x +=2，12y y +=－2，2211221x y a b += ① 2222221x y a b+= ② ①－②得1212121222()()()()0x x x x y y y y a b +-+-+=，∴AB k =1212y y x x --=212212()()b x x a y y +-+=22b a，又AB k =0131+-=12，∴22b a =12，又9=2c =22a b -，解得2b =9，2a =18，∴椭圆方程为221189x y +=，故选D. 9．C 【解析】∆21F PF 是底角为30的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔==10．5【解析】设11(,)A x y ，22(,)B x y ，由2AP PB =，得1212212(1)x x y y -=⎧⎨-=-⎩，即122x x =-，1232y y =-．因为点A ，B 在椭圆上，所以222222224(3)44x x m x y m⎧+-=⎪⎪⎨⎪+=⎪⎩，得21344y m =+，所以2222221591(32)(5)444244x m y m m m =--=-+-=--+≤，所以当5m =时，点B 横坐标的绝对值最大，最大值为2．1112；【解析】设椭圆的右焦点为(,0)F c ，双曲线N 的渐近线与椭圆M 在第一象限内的交点为A，由题意可知(2c A ，由点A 在椭圆M 上得，22223144c c a b +=，∴22222234b c a c a b +=，222b ac =-，∴22222222()34()a c c a c a a c -+=-，∴4224480a a c c -+=，∴428+40e e -=椭椭，∴24e =±椭，∴1e =椭（舍去）或1e =椭，∴椭圆M1，∵双曲线的渐近线过点(2cA，渐近线方程为y =，故双曲线的离心率2e ==双．12(),0F c，直线2by =与椭圆方程联立可得2b B ⎛⎫ ⎪⎪⎝⎭，2b C ⎫⎪⎪⎝⎭，由90BFC ∠=︒可得0BF CF ⋅=，2b BF c ⎛⎫=- ⎪⎪⎝⎭，2b CF c ⎛⎫=- ⎪ ⎪⎝⎭，则22231044c a b -+=，由222b a c =-可得223142ca =，则ce a==． 13．22325()24-+=x y 【解析】由题意圆过(4,0),(0,2),(0,2)三个点，设圆心为(,0)a，其中0a ，由4-=a ，解得32a ，所以圆的方程为22325()24-+=x y ．14．2【解析】设11(,)A x y ，22(,)B x y ，分别代入椭圆方程相减得 1212121222()()()()0x x x x y y y y a b-+-++=，根据题意有12122,2x x y y +=+=，且121212y y x x -=--，所以22221()02a b +⨯-=，得222a b =，整理222a c =，所以2e =． 15．12【解析】设MN 交椭圆于点P ，连接1F P 和2F P ，利用中位线定理可得AN BN +=122222412F P F P a a +=⨯==．162(,)b A c a ，2(,)b B c a -，由题意可知点D 为1F B 的中点，所以点D 的坐标为2(0,)2b a-，由B F AD 1⊥，所以11AD F B k k ⋅=-22ac =，解得e = 17．22312x y +=【解析】由题意得通径22AF b =，∴点B 坐标为251(,)33c B b -- 将点B 坐标带入椭圆方程得22221()53()13b c b--+=，又221b c =-，解得222313b c ⎧=⎪⎪⎨⎪=⎪⎩∴椭圆方程为22312x y +=．18．13-【解析】由题意可知，21F MF ∆中，︒=∠︒=∠︒=∠90,30,60211221MF F F MF F MF ，所以有⎪⎩⎪⎨⎧==+==+12212221222132)2(MF MF a MF MF c F F MF MF ，整理得13-==a c e ，故答案为13-．19．5【解析】由椭圆的性质可知：1AF a c =-，122F F c =，1F B a c =+.又已知1AF ，12F F ，1F B 成等比数列，故2()()(2)a c a c c -+=，即2224a c c -=，则225a c =.故5c e a ==.即椭圆的离心率为5．20．(0,1)±【解析】设点A 的坐标为(,)m n ，B 点的坐标为(,)c d．12(F F ，可得1()F A m n =，2()F B c d =，∵125F A F B =，∴5nc d ==，又点,A B 在椭圆上， ∴2213m n +=，22(5()135m n ++=，解得0,1m n ==±， ∴点A 的坐标是(0,1)±．21．【解析】(1)由已知得(1,0)F ，l 的方程为1=x ．由已知可得，点A 的坐标为(1,)2或(1,2-．所以AM的方程为2y x =-2y x =． (2)当l 与x 轴重合时，0OMA OMB ∠=∠=︒．当l 与x 轴垂直时，OM 为AB 的垂直平分线，所以OMA OMB ∠=∠．当l 与x 轴不重合也不垂直时，设l 的方程为(1)(0)y k x k =-≠，1221(,),(,)A y x y x B ，则1<x2x MA ，MB 的斜率之和为212122MA MB x x y yk k +=+--．由11=-y kx k ，22=-y kx k 得121212(23()42)(2)MA MB x x x x k k x x kk k -+++=--．将(1)y k x =-代入2212x y +=得 2222(21)4220k x k x k +-+-=．所以，2122421+=+k k x x ，21222221-=+x k k x ．则3131322244128423()4021k k k k kk k k k x x x x --++-++==+．从而0MA MB k k +=，故MA ，MB 的倾斜角互补，所以OMA OMB ∠=∠．综上，OMA OMB ∠=∠．22．【解析】(1)设11(,)A x y ，22(,)B x y ，则2211143x y +=，2222143x y +=．两式相减，并由1212y y k x x -=-得1212043x x y y k +++⋅=．由题设知1212x x +=，122y y m +=，于是34k m=-．①由题设得302m <<，故12k <-．(2)由题意得(1,0)F ，设33(,)P x y ，则331122(1,)(1,)(1,)(0,0)x y x y x y -+-+-=．由(1)及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1,)2P -，3||2FP =．于是1||(22xFA x ===-．同理2||22x FB =-．所以121||||4()32FA FB x x +=-+=．故2||||||FP FA FB=+，即||FA ，||FP ，||FB 成等差数列．设该数列的公差为d ，则1212||||||||||2d FB FA x x =-=-= 将34m =代入①得1k =-．所以l 的方程为74y x =-+，代入C 的方程，并整理得2171404x x -+=．故122x x +=，12128x x =，代入②解得||28d =．所以该数列的公差为28或28-． 23．【解析】设椭圆的焦距为2c ，由已知知2259c a =，又由222a b c =+，可得23a b =．由已知可得，FB a =，AB ，由FB AB ⋅=，可得6ab =，从而3a =，2b =．所以，椭圆的方程为22194x y +=．(2)设点P 的坐标为11(,)x y ，点Q 的坐标为22(,)x y ．由已知有120y y >>，故12sin PQ AOQ y y ∠=-．又因为2sin y AQ OAB =∠，而4OAB π∠=，故2AQ ．由AQ AOQ PQ∠，可得1259y y =．由方程组22194y kx x y=⎧⎪⎨+=⎪⎩，，消去x，可得1y = 易知直线AB 的方程为20x y +-=，由方程组20y kx x y =⎧⎨+-=⎩，，消去x ，可得221ky k =+．由1259y y =，可得5(1)k += 两边平方，整理得25650110k k -+=，解得12k =，或1128k =．所以，k 的值为111228或．24．【解析】（1）由于3P ，4P 两点关于y 轴对称，故由题设知C 经过3P ，4P 两点．又由222211134a b a b +>+知，C 不经过点1P ，所以点2P 在C 上．因此222111314b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得2241a b ⎧=⎪⎨=⎪⎩．故C 的方程为2214x y +=．（2）设直线2P A 与直线2P B 的斜率分别为1k ，2k ，如果l 与x 轴垂直，设l ：x t =，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t，（t，．则121k k +=-=-，得2t =，不符合题设．从而可设l ：y kx m =+（1m ≠）．将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=由题设可知22=16(41)0k m ∆-+>．设11(,)A x y ，22(,)B x y ，则122841km x x k +=-+，21224441m x x k -=+．而12121211y y k k x x --+=+121211kx m kx m x x +-+-=+1212122(1)()kx x m x x x x +-+=．由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=．即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++．解得12m k +=-．当且仅当1m >-时，0∆>，欲使l ：12m y x m +=-+，即11(2)2m y x ++=--，所以l 过定点（2，1-）25．【解析】（1）设(,)P x y ，00(,)M x y ，则0(,0)N x ，0(,)NP x x y =-，0(0.)NM y =．由2NP NM =得 0x x =，02y y =．因为00(,)M x y 在C 上，所以22122x y +=．因此点P 的轨迹方程为222x y +=．（2）由题意知(1,0)F -．设(3,)Q t -，(,)P m n ，则(3,)OQ t =-，(1,)PF m n =---，33OQ PF m tn ⋅=+-，(,)OP m n =，(3,)PQ m t n =---，由1OP PQ ⋅=得2231m m tn n --+-=，又由（1）知222m n +=，故330m tn +-=．所以0OQ PF ⋅=，即OQ PF ⊥．又过点P 存在唯一直线垂直与OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F ． 26．【解析】（1）设椭圆的半焦距为c .因为椭圆E 的离心率为12，两准线之间的距离为8，所以12c a =，228a c=，解得2,1a c ==，于是b =因此椭圆E 的标准方程是22143x y +=.（2）由（1）知，1(1,0)F -，2(1,0)F .设00(,)P x y ，因为点P 为第一象限的点，故000,0x y >>. 当01x =时，2l 与1l 相交于1F ，与题设不符.当01x ≠时，直线1PF 的斜率为001y x +，直线2PF 的斜率为01y x -. 因为11l PF ⊥，22l PF ⊥，所以直线1l 的斜率为001x y -+，直线2l 的斜率为001x y --，从而直线1l 的方程：001(1)x y x y +=-+， ① 直线2l 的方程：001(1)x y x y -=--. ② 由①②，解得20001,x x x y y -=-=，所以2001(,)x Q x y --. 因为点Q 在椭圆上，由对称性，得20001x y y -=±，即22001x y -=或22001x y +=.又P 在椭圆E 上，故2200143x y +=.由220022001143x y x y ⎧-=⎪⎨+=⎪⎩，解得00,77x y ==；220022001143x y x y ⎧+=⎪⎨+=⎪⎩，无解. 因此点P的坐标为(77. 27．【解析】（Ⅰ）设F 的坐标为(,0)c -.依题意，12c a =，2p a =，12a c -=，解得1a =，12c =，2p =，于是22234b ac =-=. 所以，椭圆的方程为22413y x +=，抛物线的方程为24y x =. （Ⅱ）设直线AP 的方程为1(0)x my m =+≠，与直线l 的方程1x =-联立，可得点2(1,)P m --，故2(1,)Q m -.将1x my =+与22413y x +=联立，消去x ，整理得22(34)60m y my ++=，解得0y =，或2634my m -=+.由点B 异于点A ，可得点222346(,)3434m mB m m -+-++. 由2(1,)Q m-，可得直线BQ 的方程为22262342()(1)(1)()03434m m x y m m m m --+-+-+-=++，令0y =，解得222332m x m -=+，故2223(,0)32m D m -+.所以2222236||13232m m AD m m -=-=++. 又因为APD △22162232||m m m ⨯⨯=+，整理得23|20m m -+=，解得||m =，所以m =. 所以，直线AP的方程为330x -=，或330x -=. 28．【解析】（I）由题意知c e a ==，22c =，所以1a b =，因此椭圆E 的方程为2212x y +=．（Ⅱ）设()()1122,,,A x y B x y ，联立方程2211,2x y y k x ⎧+=⎪⎪⎨⎪=⎪⎩得()22114210k x x +--=，由题意知0∆>，且()12122111221x x x x k +=-+，所以121=-AB x ．由题意可知圆M 的半径r为123r AB ==由题设知12k k =所以21k 因此直线OC的方程为1y =．联立方程2211,2,x y y ⎧+=⎪⎪⎨⎪=⎪⎩得2221221181,1414k x y k k ==++，因此OC =由题意可知1sin21SOT rOC r OCr∠==++，而1OC r=2 令2112t k =+，则()11,0,1t t>∈，因此1OC r===≥，当且仅当112t =，即2t =时等号成立，此时1k =，所以1sin 22SOT ∠≤，因此26SOT π∠≤，所以SOT ∠最大值为3π．综上所述：SOT ∠的最大值为3π，取得最大值时直线l的斜率为1k =．29．【解析】（Ⅰ）由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧+===,,121,23222c b a ab ac 解得1,2==b a .所以椭圆C 的方程为1422=+y x . （Ⅱ）由（Ⅰ）知，)1,0(),0,2(B A ，设),(00y x P ，则442020=+y x .当00≠x 时，直线PA 的方程为)2(200--=x x y y . 令0=x ，得2200--=x y y M .从而221100-+=-=x y y BM M . 直线PB 的方程为110+-=x x y y .令0=y ，得100--=y x x N .从而12200-+=-=y x x AN N . 所以221120000-+⋅-+=⋅x y y x BM AN 228844224844400000000000000002020+--+--=+--+--++=y x y x y x y x y x y x y x y x y x 4=. 当00=x 时，10-=y ，,2,2==AN BM 所以4=⋅BM AN . 综上，BM AN ⋅为定值.30．【解析】(Ⅰ)设直线:l y kx b =+(0,0)k b ≠≠，11(,)A x y ，22(,)B x y ，(,)M M M x y ．将y kx b =+代入2229x y m +=得2222(9)20k x kbx b m +++-=，故12229M x x kb x k +==-+，299M M by kx b k =+=+．于是直线OM 的斜率9M OM M y k x k==-，即9OM k k ⋅=-．所以直线OM 的斜率与l 的斜率的乘积为定值．（Ⅱ）四边形OAPB 能为平行四边形．因为直线l 过点(,)3mm ，所以l 不过原点且与C 有两个交点的充要条件是0k >，3k ≠．由(Ⅰ)得OM 的方程为9y x k=-．设点P 的横坐标为P x ．由2229,9,y x k x y m ⎧=-⎪⎨⎪+=⎩得2222981P k m x k =+，即P x =．将点(,)3m m 的坐标代入直线l 的方程得(3)3m k b -=，因此2(3)3(9)M mk k x k -=+．四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分，即2P M x x =．=2(3)23(9)mk k k -⨯+．解得14k =24k =因为0,3i i k k >≠，1i =，2，所以当l的斜率为44四边形OAPB 为平行四边形．31．【解析】（Ⅰ）由题意得2221,,2.b caa b c =⎧⎪⎪=⎨⎪⎪=+⎩解得2a =2．故椭圆C 的方程为2212x y +=．设M (N x ，0)．因为0m ≠，所以11n -<<．直线PA 的方程为11n y x m--=，所以M x =1m n -，即(,0)1mM n-．（Ⅱ）因为点B 与点A 关于x 轴对称，所以(,)B m n -，设(,0)N N x ，则N x =1mn+． “存在点(0,)Q Q y 使得OQM ∠=ONQ ∠等价”，“存在点(0,)Q Q y 使得OM OQ=OQ ON”即Q y 满足2Q M N y x x =．因为1M m x n =-，1N m x n =+，2212m n +=，所以22221Q MN m y x x n===-．所以Q yQ y =．故在y 轴上存在点Q ，使得OQM ∠=ONQ ∠．点Q的坐标为或(0,．32．【解析】（1）由题设条件知，点M 的坐标为21(,)33a b，又OM k =，从而2b a =，进而得,2a c b ===，故c e a ==．（2）由题设条件和（I）的计算结果可得，直线AB1yb+=，点N的坐标为1,)2b-，设点N关于直线AB的对称点S的坐标为17(,)2x，则线段NS的中点T的坐标为117,)244xb+-+．又点T在直线AB上，且1NS ABk k⋅=-,从而有11744171xbbb+-++=⎨+⎪=⎪⎪⎪⎩，解得3b=，所以b=故椭圆E的方程为221459x y+=．33．【解析】（Ⅰ）由题意知42=a，则2=a，又2ca=，222a c b-=，可得1=b，所以椭圆C的方程为1422=+yx．（Ⅱ）由（I）知椭圆E的方程为141622=+yx．（i）设λ=||||),,(0OPOQyxP，由题意知),(yxQλλ--，因为14220=+yx，又14)(16)(220=-+-yxλλ，即1)4(4220=+yxλ，所以2=λ，即2||||=OPOQ．（ii）设),(),,(2211yxByxA，将mkxy+=代入椭圆E的方程，可得01648)41(222=-+++mkmxxk，由0>∆，可得22164km+<，则有222122141164,418k m x x k km x x +-=+-=+，所以22221414164||k m k x x +-+=-．因为直线m kx y +=与y 轴交点的坐标为),0(m ，所以OAB ∆的面积||||2121x x m S -=22241||4162km m k +-+= 222241)416(2k m m k +-+=222241)414(2k m k m ++-= 令t k m =+2241，将m kx y +=代入椭圆C 的方程，可得 0448)41(222=-+++m kmx x k ，由0∆≥，可得 2241k m +≤，由①②可知 10≤<t ，因此t t t t S 42)4(22+-=-=，故 S ≤，当且仅当1=t 时，即2241k m +=时取得最大值32，由（i ）知，ABQ ∆面积为S 3，所以ABQ ∆面积的最大值为36．34．【解析】2(c,0)F c c （I ）设，由条件知，222=2, 1.c a b a c a ==-=又所以 22 1.4x E y +=故的方程为（Ⅱ）1122:=2,(,),(,).l x l y kx P x y Q x y ⊥-当轴时不合题意，故设22214x y kx y =-+=将代入得22(14)16120.k x kx +-+=221,23=16(43)0,4k k x ∆->>=当即时，12241PQ xk=-=+从而O PQ d OPQ=∆又点到直线的距离所以的面积1=2OPQS d PQ∆⋅=244,0,.44OPQtt t St tt∆=>==++则44,20.2t t kt+≥==±∆>因为当且仅当，即OPQι∆所以，当的面积最大时，的方程为2222y x y x=-=--或．35．【解析】（Ⅰ）设直线l的方程为()0y kx m k=+<，由22221y kx mx ya b=+⎧⎪⎨+=⎪⎩，消去y得，()22222222220b a k x a kmx a m a b+++-=，由于直线l与椭圆C只有一个公共点P，故0∆=，即22220b m a k-+=，解得点P的坐标为22222222,a kmb mb a k b a k⎛⎫- ⎪++⎝⎭，由点P在第一象限，故点P的坐标为22⎛⎫⎝；（Ⅱ）由于直线1l过原点O，且与l垂直，故直线1l的方程为0x ky+=，所以点P到直线1l的距离d=，整理得22d=，因为22222ba k abk+≥，2222a b ≤=-，当且仅当2bk a=时等号成立，所以点P 到直线1l 的距离的最大值为b a -.36．【解析】（Ⅰ）根据c 22(,),23b M c b ac a=将222b a c =-代入223b ac =，解得1,22c ca a==-（舍去）故C 的离心率为12．（Ⅱ）由题意，原点O 为12F F 的中点，2MF ∥y 轴，所以直线1MF 与y 轴的交点(0,2)D是线段1MF 的中点，故24b a=，即24b a = ① 由15MN F N =得112DF F N =。

十年高考理科数学真题专题九解析几何二十七双曲线及答案

专题九解析几何第二十七讲双曲线2019年1.（2019全国III 理10）双曲线C ：2242x y -=1的右焦点为F ，点P 在C 的一条渐进线上，O 为坐标原点，若=PO PF ，则△PFO 的面积为A B C ．D ．2.（2019江苏7）在平面直角坐标系xOy 中，若双曲线2221(0)y x b b-=>经过点（3，4)，则该双曲线的渐近线方程是 .3.（2019全国I 理16）已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =uuu r uu u r ，120F B F B ⋅=uuu r uuu r，则C 的离心率为____________．4.（2019年全国II 理11）设F 为双曲线C ：22221(0,0)x y a b a b-=>>的右焦点，O 为坐标原点，以OF 为直径的圆与圆222x y a +=交于P ，Q 两点.若PQ OF =，则C 的离心率为ABC ．2D 5．（2019浙江2）渐近线方程为x ±y =0的双曲线的离心率是A B ．1CD ．26.（2019天津理5）已知抛物线24y x =的焦点为F ，准线为l ，若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ，且||4||AB OF =（O 为原点），则双曲线的离心率为C.22010-2018年一、选择题1．(2018浙江)双曲线2213x y -=的焦点坐标是A ．(，B ．(2,0)-，(2,0)C ．(0,，D ．(0,2)-，(0,2)2．(2018全国卷Ⅰ)已知双曲线C ：2213-=x y ，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M 、N ．若∆OMN 为直角三角形，则||MN =A ．32B ．3C ．D ．43．(2018全国卷Ⅱ)双曲线22221(0,0)-=>>x y a b a bA ．=yB ．=yC ．2=±y x D ．2=±y x 4．(2018全国卷Ⅲ)设1F ，2F 是双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点，O 是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若1|||PF OP =，则C 的离心率为AB ．2CD5．(2018天津)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于A ，B 两点．设A ，B 到双曲线同一条渐近线的距离分别为1d 和2d ，且126d d +=，则双曲线的方程为A ．221412x y -= B ．221124x y -= C ．22139x y -= D ．22193x y -=6．（2017新课标Ⅱ）若双曲线C ：22221(0,0)x y a b a b-=>>的一条渐近线被圆22(2)4x y -+=所截得的弦长为2，则C 的离心率为A ．2BCD ．37．（2017新课标Ⅲ）已知双曲线C ：22221(0,0)x y a b a b-=>>的一条渐近线方程为2y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为 A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -=8．（2017天津）已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ．若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线，则双曲线的方程为A ．22144x y -=B ．22188x y -=C ．22148x y -=D ．22184x y -= 9．(2016天津)已知双曲线222=1(0)4x y b b->，以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点，四边形的ABCD 的面积为2b ，则双曲线的方程为A ．22443=1y x -B ．22344=1y x -C ．2224=1x y b -D ．2224=11x y - 10．(2016年全国I)已知方程222213x y m n m n-=+-表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是A ．(–1,3)B ．(–1,3)C ．(0,3)D ．(0,3)11．(2016全国II)已知1F ,2F 是双曲线E ：22221x y a b-=的左、右焦点，点M 在E 上，1MF 与x 轴垂直，211sin 3MF F ∠=,则E 的离心率为A B ．32C D ．2 12．（2015四川）过双曲线2213y x -=的右焦点且与x 轴垂直的直线，交该双曲线的两条渐近线于,A B 两点，则AB =A B ． C ．6 D ．13．（2015福建）若双曲线22:1916x y E -= 的左、右焦点分别为12,F F ，点P 在双曲线E 上，且13PF =，则2PF 等于A ．11B ．9C ．5D ．314．（2015湖北）将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度，得到离心率为2e 的双曲线2C ，则A ．对任意的,a b ，12e e >B ．当a b >时，12e e >；当a b <时，12e e <C ．对任意的,a b ，12e e <D ．当a b >时，12e e <；当a b <时，12e e > 15．（2015安徽）下列双曲线中，焦点在y 轴上且渐近线方程为2y x =±的是A ．2214y x -= B ．2214x y -= C ．2214y x -= D ．2214x y -= 16．（2015新课标1）已知00(,)M x y 是双曲线C ：2212x y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅>）的右焦点为F ，右顶点为A ，过F作AF 的垂线与双曲线交于,B C 两点，过,B C 分别作,AC AB 的垂线，两垂线交于点D ．若D 到直线BC 的距离小于a ，则该双曲线的渐近线斜率的取值范围是A ．(1,0)(0,1)-∪B ．(,1)(1,)-∞-+∞∪C ．∪D ．(,1))-∞-∞∪18．（2014新课标1）已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C的一条渐近线的距离为A B ．3 C D ．3m19．（2014广东）若实数k 满足09k <<，则曲线221259x y k-=-与曲线221259x y k -=-的 A ．焦距相等 B ．实半轴长相等 C ．虚半轴长相等 D ．离心率相等20．（2014天津）已知双曲线22221x y a b-=()0,0a b >>的一条渐近线平行于直线l ：210y x =+，双曲线的一个焦点在直线l 上，则双曲线的方程为 A ．221520x y -= B ．221205x y -= C ．2233125100x y -= D ．2233110025x y -= 21．（2014重庆）设21F F ，分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点，双曲线上存在一点P 使得,49||||,3||||2121ab PF PF b PF PF =⋅=+则该双曲线的离心率为 A ．34 B ．35 C ．49D ．322．（2013新课标1）已知双曲线C ：22221x y a b-=（0,0a b >>C的渐近线方程为A ．14y x =± B ．13y x =± C ．12y x =± D ．y x =± 23．(2013湖北)已知04πθ<<，则双曲线1C ：22221cos sin x y θθ-=与2C ：22sin y θ2221sin tan y θθ-=的 A ．实轴长相等 B ．虚轴长相等 C ．焦距相等 D ．离心率相等 24．（2013重庆）设双曲线C 的中心为点O ，若有且只有一对相较于点O 、所成的角为060的直线11A B 和22A B ，使1122A B A B =，其中1A 、1B 和2A 、2B 分别是这对直线与双曲线C 的交点，则该双曲线的离心率的取值范围是A ．(2]3 B ．[,2)3 C ．()3+∞ D ．[)3+∞ 25．（2012福建）已知双曲线22215x y a -=的右焦点为(3,0)，则该双曲线的离心率等于A ．14B ．4 C ．32D ．4326．（2012湖南）已知双曲线C ：22x a -22y b=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C 的方程为A ．220x -25y =1B ．25x -220y =1C ．280x -220y =1 D ．220x -280y =1 27．（2011安徽）双曲线x y 222-=8的实轴长是A ．2B ．C ．4D ．28．（2011山东）已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均和圆22:650C x y x +-+=相切，且双曲线的右焦点为圆C 的圆心，则该双曲线的方程为A ．22154x y -=B ．22145x y -=C ．22136x y -=D ．22163x y -= 29．（2011湖南）设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=，则a 的值为 A ．4 B ．3 C ．2 D ．130．（2011天津）已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为(2,1)--，则双曲线的焦距为A ．B ．C ．D ．31．（2010新课标）已知双曲线E 的中心为原点，(3,0)P 是E 的焦点，过F 的直线l 与E 相交于A ，B 两点，且AB 的中点为(12,15)N --,则E 的方程式为A ．22136x y -= B ．22145x y -= C ．22163x y -= D ．22154x y -= 32．（2010新课标）中心在原点，焦点在x 轴上的双曲线的一条渐近线经过点(4,2)-，则它的离心率为A B C ．2 D ．233．（2010福建）若点O 和点F 分别为椭圆22143x y +=的中心和左焦点，点P 为椭圆上的任意一点，则OP FP ⋅u u u r u u u r的最大值为A ．2B ．3C ．6D ．8 二、填空题34．(2018上海)双曲线2214x y -=的渐近线方程为． 35．(2018江苏)在平面直角坐标系xOy 中，若双曲线22221(0,0)x y a b a b-=>>的右焦点(,0)F c 到一条渐近线的距离为2c ，则其离心率的值是． 36．（2017江苏）在平面直角坐标系xOy 中，双曲线2213x y -=的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是1F ，2F ，则四边形12F PF Q 的面积是．37．（2017新课标Ⅰ）已知双曲线C ：22221(0,0)x y a b a b-=>>的右顶点为A ，以A 为圆心，b 为半径做圆A ，圆A 与双曲线C 的一条渐近线交于M 、N 两点．若MAN ∠=60°，则C 的离心率为________．38．（2017山东）在平面直角坐标系xOy 中，双曲线22221(00)x y a b a b-=>>，的右支与焦点为F 的抛物线22(0)x py p =>交于A ，B 两点，若||||4||AF BF OF +=，则该双曲线的渐近线方程为．39．（2017北京）若双曲线221y x m-=m =_________．40．(2016年北京)双曲线22221(0,0)x y a b a b-=>>的渐近线为正方形OABC 的边,OA OC所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a =______．41．(2016山东)已知双曲线E ：22221x y a b-=(0,0)a b >>，若矩形ABCD 的四个顶点在E上，AB ，CD 的中点为E 的两个焦点，且2||3||AB BC =，则E 的离心率是 .42．（2015北京）已知双曲线()22210x y a a-=>0y +=，则a = ．43．（2015江苏）在平面直角坐标系xOy 中，P 为双曲线122=-y x 右支上的一个动点．若点P 到直线01=+-y x 的距离大于c 恒成立，则是实数c 的最大值为．44．（2015山东）平面直角坐标系xOy 中，双曲线1C ：22221x y a b-=(0,0)a b >>的渐近线与抛物线2C ：22x py =(0p >)交于,,O A B ，若△OAB 的垂心为2C 的焦点，则1C 的离心率为_______．45．（2014山东）已知双曲线22221(0,0)x y a b a b-=>>的焦距为2c ，右顶点为A ，抛物线22(0)x py p =>的焦点为F ，若双曲线截抛物线的准线所得线段长为2c ，且||FA c =，则双曲线的渐近线方程为．46．（2014浙江）设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A ，B ，若点(,0)P m 满足||||PA PB =，则该双曲线的离心率是____．47．（2014北京）设双曲线C 经过点()2,2，且与2214y x -=具有相同渐近线，则C 的方程为________；渐近线方程为________．48．（2013陕西）双曲线221169x y -=的离心率为．49．（2014湖南）设F 1，F 2是双曲线C ：22221(0,0)x y a b a b-=>>的两个焦点．若在C 上存在一点P ，使PF 1⊥PF 2，且∠PF 1F 2=30°，则C 的离心率为_________．50．（2013辽宁）已知F 为双曲线22:1916x y C -=的左焦点，,P Q 为C 上的点，若PQ 的长等于虚轴长的2倍，点(5,0)A 在线段PQ ，则PQF ∆的周长为．51．（2012辽宁）已知双曲线122=-y x ，点21,F F 为其两个焦点，点P 为双曲线上一点，若21PF PF ⊥，则21PF PF +的值为．52．（2012天津）已知双曲线)0,0(1:22221>>=-b a by a x C 与双曲线1164:222=-y x C 有相同的渐近线，且1C 的右焦点为F ,则a = b = ．53．（2012江苏）在平面直角坐标系xOy 中，若双曲线22214x y m m -=+则m 的值为．54．（2011山东）已知双曲线22221(0,0)x y a b a b -=>>和椭圆221169x y +=有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为．55．(2011北京)已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =，则b = ．三、解答题56．（2014江西）如图，已知双曲线C ：2221x y a-=(0a >)的右焦点F ，点B A ,分别在C的两条渐近线上，x AF ⊥轴，BF OB AB ,⊥∥OA (O 为坐标原点）．（1）求双曲线C 的方程；（2）过C 上一点)0)((00,0≠y y x P 的直线1:020=-y y axx l 与直线AF 相交于点M ，与直线23=x 相交于点N ，证明：当点P 在C 上移动时，NFMF 恒为定值，并求此定值．57．（2011广东）设圆C 与两圆2222(5)4,(5)4x y x y ++=+=中的一个内切，另一个外切．（1）求C 的圆心轨迹L 的方程；（2）已知点M 3545(,5,0)55F ，且P 为L 上动点，求MP FP -的最大值及此时点P 的坐标．专题九解析几何第二十七讲双曲线答案部分2019年1. 解析双曲线22:142x y C -=的右焦点为6,0)F ，渐近线方程为：22y x =±，不妨设点P 在第一象限，可得2tan POF ∠=，63(P ，所以PFO △的面积为： 13326224=．故选A ．2. 解析因为双曲线2221(0)y x b b-=>经过点(3,4)，所以221631b-=，解得22b =，即2b =．又1a =，所以该双曲线的渐近线方程是2y x =±．3.解析如图所示，因为1F A AB=uuu r uu u r,所以A 为1F B 的中点. 又O 为12F F 的中点，所以212AO BF P，212AO BF =. 因为120F B F B ⋅=uuu r uuu r ，所以1290F BF ∠=︒，且O 为12F F 的中点，所以12212OB F F OF c ===. 由212AO BF P得2121BOF AOF BF F ∠=∠=∠，所以2OB BF =，因此2OPF △为等边三角形，260BOF ∠=︒，即渐近线的斜率为3，也即3ba=，所以2212b e a=+=.4．A 解析：解法一：由题意，把2c x =代入222x y a +=，得2224c PQ a =-，再由PQ OF =，得2224ca c -=，即222a c =，所以222c a=，解得2c e a ==.故选A ．解法二：如图所示，由PQ OF =可知PQ 为以OF 为直径圆的另一条直径，所以,22c c P ⎛⎫± ⎪⎝⎭，代入222x y a +=得222a c =，所以222c a=，解得2c e a ==.故选A ．解法三：由PQ OF =可知PQ 为以OF 为直径圆的另一条直径，则1222OP a OF ===，2c e a ==故选A ． 5．解析根据渐进线方程为0x y ±=的双曲线，可得a b =，所以2c a =，则该双曲线的离心率为2ce a==C ． 6.解析因为抛物线24y x =的焦点为F ，准线为l ，所以()1,0F ，准线l 的方程为1x =-.因为与双曲线()222210,0x y a b a b=>>的两条渐近线分别交于点A 和点B ，且4AB OF =（为原点），所以2b AB a =，1OF =，所以24b a=，即2b a =，所以225c a b a +=，所以双曲线的离心率为5ca==．故选D ．2010-2018年1．B 【解析】由题可知双曲线的焦点在x 轴上，因为222314c a b =+=+=，所以2c =，故焦点坐标为(2,0)-，(2,0)．故选B ．2．B 【解析】因为双曲线2213-=x y 的渐近线方程为33=±y x ，所以60∠=o MON ．不妨设过点F 的直线与直线3=y x 交于点M ，由∆OMN 为直角三角形，不妨设90∠=o OMN ，则60∠=o MFO ，又直线MN 过点(2,0)F ，所以直线MN 的方程为3(2)=-y x ，由2)⎧=-⎪⎨=⎪⎩y x y x，得32⎧=⎪⎪⎨⎪=⎪⎩x y3(,22M ，所以||==OM所以|||3==MN OM ．故选B ． 3．A 【解析】解法一由题意知，==ce a，所以=c，所以=b ，所以=b a=±=by x a，故选A ．解法二由===c e a，得=ba，所以该双曲线的渐近线方程为=±=by x a．故选A ．4．C 【解析】不妨设一条渐近线的方程为by x a=，则2F 到by x a =的距离d b ==，在2Rt F PO ∆中，2||F O c =，所以||PO a =，所以1||PF =，又1||F O c =，所以在1F PO ∆与2Rt F PO ∆中，根据余弦定理得22212)cos cos 2a c aPOF POF ac c+-∠==-∠=-，即2223)0a c +-=，得223a c =．所以ce a==．故选C ． 5．C 【解析】通解因为直线AB 经过双曲线的右焦点，所以不妨取2(,)b A c a，2(,)b B c a -，取双曲线的一条渐近线为直线0bx ay -=，由点到直线的距离公式可得221bc b d c -==，222bc b d c +==，因为126d d +=，所以226bc b bc b c c-++=，所以26b =，得3b =．因为双曲线22221(0,0)x y a b a b -=>>的离心率为2，所以2ca=，所以2224a b a+=，所以2294a a +=，解得23a =，所以双曲线的方程为22139x y -=，故选C ．优解由126d d +=，得双曲线的右焦点到渐近线的距离为3，所以3b =．因为双曲线22221(0,0)x y a b a b -=>>的离心率为2，所以2ca=，所以2224a b a+=，所以2294a a +=，解得23a =，所以双曲线的方程为22139x y -=，故选C ． 6．A 【解析】双曲线C 的渐近线方程为0bx ay ±=，圆心(2,0)到渐近线的距离为2bd c==，圆心(2,0)到弦的距离也为d ==所以2b c =222c a b =+，所以得2c a =，所以离心率2ce a==，选A ． 7．B【解析】由题意可得：b a =，3c =，又222a b c +=，解得24a =，25b =，则C 的方程为2145x y 2-=．选B ． 8．B 【解析】设(,0)F c -，双曲线的渐近线方程为b y x a =±，由44PF k c c-==-，由题意有4bc a=，又c a =222c a b =+，得b =，a =．选B ．9．D 【解析】不妨设A 在第一象限，(,)A x y ，所以2242x y b y x ⎧+=⎪⎨=⎪⎩，解得x y ⎧=⎪⎪⎨⎪=⎪⎩，故四边形ABCD的面积为2324424bxy b b ===+，解得212b =．故所求的双曲线方程为2224=11x y -，选D ． 10．A 【解析】由题意得22()(3)0m n m n +->，解得223m n m -<<，又由该双曲线两焦点间的距离为4，得M 2234m n m n ++-=，即21m =，所以13n -<<．11．A 【解析】设1(,0)F c -，将x c =-代入双曲线方程，得22221c y a b -=，化简得2by a=±，因为211sin 3MF F ∠=，所以222212112||tan ||222b MF b c a a MF F F F c ac ac -∠=====，12222c a e a c e -=-=210e --=，所以e =A ． 12．D 【解析】由双曲线的标准方程2213y x -=得，右焦点(2,0)F ，两条渐近线方程为y =，直线AB ：2x =，所以不妨设取(2,A，(2,B -，则||AB =，选D ．13．B 【解析】由双曲线定义得1226PF PF a -==，即236PF -=，解得29PF =，故选B ．14．D【解析】由题意1e ==2e ==∵()()b b m m b a a a m a a m +--=++，由于0m >，0a >，0b >，所以当a b >时，01b a <<，01b m a m +<<+，b b m a a m +<+，22()()b b m a a m+<+，所以12e e <；当a b <时，1ba>，1b m a m +>+，而b b m a a m +>+，22()()b b m a a m +>+，所以12e e >．所以当a b >时，12e e <；当a b <时，12e e >．15．C 【解析】由题意，选项,A B 的焦点在x 轴，故排除,A B ，C 项的渐近线方程为2204y x -=，即2y x =±，故选C ． 16．A 【解析】由题意知22a =，21b =，所以23c =，不妨设1(F，2F ，所以100(,)=-u u u u r MF x y，200,)=-u u u u rMF x y ，又∵00(,)M x y 在双曲线上，所以220012x y -=，即220022x y =+，222120003310MF MF x y y u u u r u u u r ⋅=-+=-<，所以033-<<y ，故选A ． 17．A 【解析】由题意22(,0),(,),(,)b b A a B c C c a a-，由双曲线的对称性知D 在x 轴上，设(,0)D x ，由BD AC ⊥得221b b a a c x a c-⋅=---，解得42()b c x a c a -=-，所以42()b c x a a c a c a -=<+=+-，所以42222b c a b a <-=221b a⇒<01b a ⇒<<，而双曲线的渐近性斜率为ba±，所以双曲线的渐近线的斜率取值范围是(1,0)(0,1)-U ，选A ．18．A 【解析】双曲线方程为22133x y m -=，焦点F到一条渐近线的距离为b =A ． 19．A 【解析】∵09k <<，∴90,250k k ->->，本题两条曲线都是双曲线，又25(9)(25)9k k +-=-+，∴两双曲线的焦距相等，选A ．20．A 【解析】依题意得22225b ac c a b ìï=ïïï=íïïï=+ïî，所以25a =，220b =，双曲线的方程为 221520x y -=．21．B 【解析】由双曲线的定义得12||||||2PF PF a -=，又12||||3PF PF b +=，所以22221212(||||)(||||)94PF PF PF PF b a +--=-，即124||||9PF PF ab =，因此22949b a ab -=，即299()40b b aa --=，则（31b a +）（34ba-）=0，解得41(33b b a a ==-舍去），则双曲线的离心率53e ==．22．C 【解析】由题知，2c a =，即54=22c a =222a b a +，∴22b a =14，∴b a =12±，∴C 的渐近线方程为12y x =±，故选C ． 23．D 【解析】双曲线1C 的离心率是11cos e θ=，双曲线2C 的离心率是21cos e θ==，故选D ． 24．A 【解析】设双曲线的焦点在x 轴上，则由作图易知双曲线的渐近线的离心率ba必须满足3b a <，所以21()33b a <≤，241()43b a<+≤，2<，又双曲线的离心率为c e a ==23e <≤． 25．C 【解析】∵双曲线22215x y a -=的右焦点为（3，0），∴2a +5=9，∴2a =4，∴a =2∵c =3，∴32c e a ==，故选C ． 26．A 【解析】设双曲线C ：22x a -22y b=1的半焦距为c ，则210,5c c ==．又Q C 的渐近线为b y x a =±，点P(2,1)在C 的渐近线上，12ba∴=g ，即2a b =．又222c a b =+，a ∴==，∴C 的方程为220x -25y =1．27．C 【解析】x y 222-=8可变形为22148x y -=，则24a =，2a =，24a =.故选C ． 28．A 【解析】圆22:(3)4C x y -+=，3,c =而32bc =，则22,5b a ==，应选A ． 29．C 【解析】由双曲线方程可知渐近线方程为3y x a=±，故可知2a =．30．B 【解析】双曲线22221(0,0)x y a b a b -=>>的渐近线为by x a=±，由双曲线的一条渐近线与抛物线的准线的交点坐标为（－2，－1）得22p-=-，即4p =，又∵42p a +=，∴2a =，将（－2，－1）代入by x a=得1b =，∴c ==2c =31．B 【解析】由双曲线E 的中心为原点，(3,0)P 是E 的焦点可设双曲线的方程为2222221(9)x y a b a b -=+=，设1122(,),(,)A x y B x y ，即 2222112222221,1x y x y a b a b -=-= 则22121222121212015115312y y x x b b x x a y y a -+-+=⋅=⋅==-+-+，则22225,5,44b b a a ===，故E 的方程式为22145x y -=.应选B ． 32．D 【解析】设双曲线的方程为22221(0,0)x y a b a b -=>>，其渐近线为x aby ±=，∵点(4,2)-在渐近线上，所以12b a =，由2e ==． 33．C 【解析】由题意，F （－1，0），设点P 00(,)x y ，则有2200143x y +=, 解得22003(1)4x y =-，因为00(1,)FP x y =+u u u r ，00(,)OP x y =u u u r，所以2000(1)OP FP x x y ⋅=++u u u r u u u r =00(1)OP FP x x ⋅=++u u u r u u u r 203(1)4x -=20034x x ++，此二次函数对应的抛物线的对称轴为02x =-，因为022x -≤≤，所以当02x =时，OP FP ⋅u u u r u u u r 取得最大值222364++=，选C ． 34．12y x =±【解析】由题意2a =，1b =，∴12b y x x a =±=±．35．2【解析】不妨设双曲线的一条渐近线方程为b y x a =2b ==，所以222234b c a c =-=，得2c a =，所以双曲线的离心率2ce a==． 36．232a x c ==，渐近线的方程为3y x =±，设3(,22P，则3(,22Q -，1(2,0)F -，2(2,0)F ，所以四边形12F PF Q的面积为1211||||422F F PQ =⨯=． 37．3【解析】如图所示，AH MN ⊥，AM AN b ==，MAN ∠=60°， x所以30HAN ∠=o，又MN 所在直线的方程为by x a=， (,0)A a 到MN的距离AH =，在Rt HAN ∆中，有cos HA HAN NA=，所以2==因为222c a b =+a c =，所以c e a ==．38．y x =【解析】设11(,)A x y ，22(,)B x y ，由抛物线的定义有1212||||22p p AF BF y y y y p +=+++=++，而||2p OF =，所以1242py y p ++=⨯，即12y y p +=，由2222212x y a b x py⎧-=⎪⎨⎪=⎩得2222220a y pb y a b -+=，所以21222pb y y a +=，所以222pb p a=，即a =，所以渐近性方程为2y x =±． 39．2【解析】221,a b m ==，所以1c a ==，解得2m =． 40．2【解析】不妨令B 为双曲线的右焦点，A 在第一象限，则双曲线图象如图∵OABC 为正方形，2=OA∴==c OB ，π4∠=AOB ∵直线OA 是渐近线，方程为=b y x a ，∴tan 1=∠=bAOB a又∵2228+==a b c ∴2=a41．2【解析】由题意||2BC c =，所以||3AB c =，于是点3(,)2cc 在双曲线E 上，代入方程，得2222914c c a b -=，在由222a b c +=得E 的离心率为2ce a==，应填2. 42．3【解析】因为双曲线()22210x y a a -=>的一条渐近线为y =，所以1a=故3a =． 43．2(,),(1)P x y x ≥，因为直线10x y -+=平行于渐近线0x y -=，所以c 的最大值为直线10x y -+=与渐近线0x y -== 44．32【解析】22122:1(0,0)x y C a b a b -=>>的渐近线为by x a=±，则2222(,)pb pb A a a ，2222(,)pb pb B a a -，22:2(0)C x py p =>的焦点(0,)2p F ，则22222AFpb pa a k pb b a-==，即2254b a =，2222294c a b a a +==，32c e a ==． 45．y x =±【解析】抛物线的准线2p y =-，与双曲线的方程联立得2222(1)4p x a b =+，根据已知得2222(1)4p a c b += ①，由||AF c =得2224p a c += ②，由①②得22a b =，即a b =，所以所求双曲线的渐近线方程为y x =±．46．2【解析】联立直线方程与双曲线渐近线方程by x a=±可解得交点为(,)33am bm A b a b a --，(,)33am bm B b a b a -++，而13AB k =，由||||PA PB =，可得AB 的中点3333(,)22am am bm bmb a b a b a b a -+-+-+与点)0,(m P 连线的斜率为-3，可得224b a =，所以e =47．221312x y -= 2y x =±【解析】设与2214y x -=具有相同渐近线的双曲线C 的方程为224y x k -=，将点()2,2代入C 的方程中，得3k =-．∴双曲线的方程为221312x y -=，渐近线方程为2y x =±．48．45【解析】。

十年高考理科数学真题专题九解析几何二十九曲线与方程及答案(优质)

专题九解析几何第二十九讲曲线与方程2019年1.（2019北京理8）数学中有许多形状优美、寓意美好的曲线，曲线C :x 2+y 2=1+x y 就是其中之一（如图）。

给出下列三个结论：① 曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）； ② 曲线C 上任意一点到原点的距离都不超过2; ③ 曲线C 所围城的“心形”区域的面积小于3. 其中，所有正确结论的序号是（A ）① （B ）② （C ）①② （D ）①②③2．（2019浙江15）已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______.3．（2019江苏17）如图，在平面直角坐标系xOy 中，椭圆C :22221(0)x y a b a b+=>>的焦点为F 1（–1、0），F 2（1，0）．过F 2作x 轴的垂线l ，在x 轴的上方，l 与圆F 2:222(1)4x y a -+=交于点A ，与椭圆C 交于点D .连结AF 1并延长交圆F 2于点B ，连结BF 2交椭圆C 于点E ，连结DF 1．已知DF 1=52．（1）求椭圆C 的标准方程；（2）求点E 的坐标．4.（2019全国III 理21（1））已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C的两条切线，切点分别为A ，B . （1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.5.（2019北京理18）已知抛物线2:2C x py =-经过点(2，-1). (I) 求抛物线C 的方程及其准线方程； (II)设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线y =-1分别交直线OM ，ON 于点A 和点B ，求证：以AB 为直径的圆经过y 轴上的两上定点.6.（2019全国II 理21）已知点A (−2,0)，B (2,0)，动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .（1）求C 的方程，并说明C 是什么曲线；（2）过坐标原点的直线交C 于P ，Q 两点，点P 在第一象限，PE ⊥x 轴，垂足为E ，连结QE 并延长交C 于点G .（i ）证明：PQG △是直角三角形；（ii ）求PQG △面积的最大值.7. （2019浙江21）如图，已知点(10)F ，为抛物线22(0)y px p =>的焦点，过点F 的直线交抛物线于A 、B 两点，点C 在抛物线上，使得ABC △的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S .（1）求p 的值及抛物线的准线方程；（2）求12S S 的最小值及此时点G 的坐标. 8.（2019天津理18）设椭圆22221(0)x y a b a b+=>>的左焦点为F ，上顶点为B .已知椭圆的短轴长为4，离心率为5. （Ⅰ）求椭圆的方程；（Ⅱ）设点P 在椭圆上，且异于椭圆的上、下顶点，点M 为直线PB 与x 轴的交点，点N在y 轴的负半轴上.若||||ON OF =（O 为原点），且OP MN ⊥，求直线PB 的斜率.2010-2018年解答题1．（2018江苏）如图，在平面直角坐标系xOy 中，椭圆C 过点1)2，焦点12(F F ，圆O 的直径为12F F ．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △，求直线l 的方程． 2．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足NP =u u u r u u u r．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=u u u r u u u r．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．3．(2016年山东)平面直角坐标系xOy 中，椭圆C ：()222210x y a b a b+=＞＞的离心率是2，抛物线E ：22x y =的焦点F 是C 的一个顶点. （Ⅰ）求椭圆C 的方程；（Ⅱ）设P 是E 上的动点，且位于第一象限，E 在点P 处的切线l 与C 交与不同的两点A ，B ，线段AB 的中点为D ，直线OD 与过P 且垂直于x 轴的直线交于点M ．（i ）求证：点M 在定直线上；（ii ）直线l 与y 轴交于点G ，记PFG △的面积为1S ，PDM △的面积为2S ，求12S S的最大值及取得最大值时点P 的坐标．4．(2016年天津)设椭圆13222=+y ax (a >的右焦点为F ，右顶点为A ，已知||3||1||1FA eOA OF =+，其中O 为原点，e 为椭圆的离心率．（Ⅰ）求椭圆的方程；（Ⅱ）设过点A 的直线l 与椭圆交于点B （B 不在x 轴上），垂直于l 的直线与l 交于点M ，与y 轴交于点H ，若HF BF ⊥，且MOA MAO ∠∠≤，求直线l 的斜率的取值范围．5．(2016年全国II)已知椭圆:E 2213x y t +=的焦点在x 轴上，A 是E 的左顶点，斜率为(0)k k >的直线交E 于,A M 两点，点N 在E 上，MA NA ⊥．（Ⅰ）当4,||||t AM AN ==时，求AMN ∆的面积；（Ⅱ）当2AM AN =时，求k 的取值范围．6．（2015湖北）一种作图工具如图1所示．O 是滑槽AB 的中点，短杆ON 可绕O 转动，长杆MN 通过N 处铰链与ON 连接，MN 上的栓子D 可沿滑槽AB 滑动，且1DN ON ==，3MN =．当栓子D 在滑槽AB 内作往复运动时，带动．．N 绕O 转动一周（D 不动时，N也不动），M 处的笔尖画出的曲线记为C ．以O 为原点，AB 所在的直线为x 轴建立如图2所示的平面直角坐标系．（Ⅰ）求曲线C 的方程；（Ⅱ）设动直线l 与两定直线1:20l x y -=和2:20l x y +=分别交于,P Q 两点．若直线l总与曲线C 有且只有一个公共点，试探究：△OPQ 的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．7．（2015江苏）如图，在平面直角坐标系xoy 中，已知椭圆()222210x y a b a b+=>>的离心率为22，且右焦点F 到左准线l 的距离为3．（1）求椭圆的标准方程；（2）过F 的直线与椭圆交于,A B 两点，线段AB 的垂直平分线分别交直线l 和AB 于点,P C ，若2PC AB =，求直线AB 的方程．8．（2015四川）如图，椭圆E ：2222+1(0)x y a b a b=>>的离心率是22，过点(0,1)P 的动直线l 与椭圆相交于,A B 两点，当直线l 平行与x 轴时，直线l 被椭圆E 截得的线段长为22（1）求椭圆E 的方程；（2）在平面直角坐标系xOy 中，是否存在与点P 不同的定点Q ，使得QA PAQB PB=恒成立？若存在，求出点Q 的坐标；若不存在，请说明理由．9．（2015北京）已知椭圆C ：()222210x y a b a b+=>>的离心率为22，点()01P ，和点 ()A m n ，()0m ≠都在椭圆C 上，直线PA 交x 轴于点M ．（Ⅰ）求椭圆C 的方程，并求点M 的坐标（用m ，n 表示）；（Ⅱ）设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N ．问：y 轴上是否存在点Q ，使得OQM ONQ ∠=∠？若存在，求点Q 的坐标；若不存在，说明理由．10．（2015浙江）已知椭圆2212x y +=上两个不同的点,A B 关于直线12y mx =+对称．（Ⅰ）求实数m 的取值范围；（Ⅱ）求AOB ∆面积的最大值（O 为坐标原点）．11．（2014广东）已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点为5,0)，5（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若动点00(,)P x y 为椭圆外一点，且点P 到椭圆C 的两条切线相互垂直，求点P的轨迹方程．12．（2014辽宁）圆224x y +=的切线与x 轴正半轴，y 轴正半轴围成一个三角形，当该三角形面积最小时，切点为P （如图），双曲线22122:1x y C a b-=过点P 3．（1）求1C 的方程；（2）椭圆2C 过点P 且与1C 有相同的焦点，直线l 过2C 的右焦点且与2C 交于A ，B 两点，若以线段AB 为直径的圆心过点P ，求l 的方程．13．（2013四川）已知椭圆C ：)0(12222>>=+b a by a x 的两个焦点分别为1(10)F -，，210F （，），且椭圆C 经过点），3134(P ．（Ⅰ）求椭圆C 的离心率（Ⅱ）设过点），（20A 的直线l 与椭圆C 交于M ，N 两点，点Q 是MN 上的点，且 222112ANAMAQ+=，求点Q 的轨迹方程．14．（2012湖南）在直角坐标系xoy 中，曲线1C 的点均在2C ：22(5)9x y -+=外，且对1C 上任意一点M ，M 到直线2x =-的距离等于该点与圆2C 上点的距离的最小值. （Ⅰ）求曲线1C 的方程；（Ⅱ）设00(,)P x y （3y ≠±）为圆2C 外一点，过P 作圆2C 的两条切线，分别与曲线1C 相交于点A ，B 和C ，D.证明：当P 在直线4x =-上运动时，四点A ，B ，C ，D 的纵坐标之积为定值．15．（2011天津）在平面直角坐标系xOy 中，点(,)P a b (0)a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．已知△12F PF 为等腰三角形．（Ⅰ）求椭圆的离心率e ；（Ⅱ）设直线2PF 与椭圆相交于,A B 两点，M 是直线2PF 上的点，满足2AM BM ⋅=-u u u u r u u u u r ，求点M 的轨迹方程．16．（2009广东）已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ，且A B x x <．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（1）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（2）若曲线22251:24025G x ax y y a -+-++=与D 有公共点，试求a 的最小值．专题九解析几何第二十九讲曲线与方程答案部分1. 由221x y x y +=+可得221y x y x -=-.配方得2230241x x y ⎛⎫-≥ ⎪ ⎪⎝⎭-=，解得234x ≤.所以x 可取的整数值为-1，0，1，则曲线经过()()()()()()1,0,1,1,0,1,0,1,1,0,1,1,----这6个整点，结论①正确；当x ＞0时，由221x y xy +=+得222212x y x y xy ++-=≤（当x=y 时取等号），所以222x y +≤，所以222x y +≤，即曲线C 上y 轴右边的点到原点的距离不超过2，结论②正确；根据对称性可得：曲线C 上任意一点到原点的距离都不超过2；故②正确．如图所示，()()()()0,1,1,0,1,1,0,1A B C D -13111122ABCD S =⨯⨯+⨯=，根据对称性可知23ABCD S S >=心形. 即心形区域的面积大于3，故③错误．正确结论为①②. 故选C ．2．解析设椭圆的右焦点为F '，连接PF '，线段PF 的中点A 在以原点O 为圆心，2为半径的圆，连接AO ，可得24PF AO '==，设P 的坐标为（m,n ），可得2343m -=，可得32m =-，15n =，由(2,0)F -，可得直线PF 的斜率为15215322=-+．3.解析（1）设椭圆C 的焦距为2c .因为F 1(-1，0)，F 2(1，0)，所以F 1F 2=2，c =1. 又因为DF 1=52，AF 2⊥x 轴，所以DF 2222211253()222DF F F -=-=，因此2a =DF 1+DF 2=4，从而a =2. 由b 2=a 2-c 2，得b 2=3.因此，椭圆C 的标准方程为22143x y +=.（2）解法一：由（1）知，椭圆C ：22143x y +=，a =2，因为AF 2⊥x 轴，所以点A 的横坐标为1.将x =1代入圆F 2的方程(x -1) 2+y 2=16，解得y =±4. 因为点A 在x 轴上方，所以A (1，4). 又F 1(-1，0)，所以直线AF 1：y =2x +2.由22()22116y x x y =+-+=⎧⎨⎩，得256110x x +-=，解得1x =或115x =-. 将115x =-代入22y x =+，得 125y =-，因此1112(,)55B --.又F 2(1，0)，所以直线BF 2：3(1)4y x =-.由221433(1)4x y x y ⎧⎪⎪⎨⎪+=-⎩=⎪，得276130x x --=，解得1x =-或137x =. 又因为E 是线段BF 2与椭圆的交点，所以1x =-. 将1x =-代入3(1)4y x =-，得32y =-.因此3(1,)2E --. 解法二：由（1）知，椭圆C ：22143x y +=.如图所示，联结EF 1.因为BF 2=2a ，EF 1+EF 2=2a ，所以EF 1=EB ，从而∠BF 1E =∠B .因为F 2A =F 2B ，所以∠A =∠B ，所以∠A =∠BF 1E ，从而EF 1∥F 2A . 因为AF 2⊥x 轴，所以EF 1⊥x 轴.因为F 1(-1，0)，由221431x x y ⎧⎪⎨+==-⎪⎩，得32y =±.又因为E 是线段BF 2与椭圆的交点，所以32y =-. 因此3(1,)2E --. 4. 解析（1）设()111,,,2D t A x y ⎛⎫-⎪⎝⎭，则2112x y =.由于y'x =，所以切线DA 的斜率为1x ，故11112y x x t+=- ，整理得112 2 +1=0. tx y -设()22,B x y ，同理可得222 2 +1=0tx y -.故直线AB 的方程为2210tx y -+=. 所以直线AB 过定点1(0,)2.5.解析（I ）由抛物线2:2C x py =-经过点()2,1-，得2p =.所以抛物线C 的方程为24x y =-，其准线方程为1y =. （II ）抛物线C 的焦点为()0,1-，设直线l 的方程为()10y kx k =-≠.由241x y y kx ⎧=-⎨=-⎩，得2440x kx +-=. 设()()1122,,,,Mx y N x y 则124x x=-.直线OM 的方程为11y y x x =，令1y =-，得点A 的横坐标为11A x x y =- 同理可得点B 的横坐标22B x x y =-.设点()0,Dn ，则()()2212122212121144x x x x DA DB n n y yx x ⋅=++=++⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭uu u r uu u r()()221216141n n x x =++=-++. 令0,DA DB ⋅=uu u r uu u r 即()2410n -++=，得1n =或3n =-.综上，以AB 为直径的圆经过y 轴上的定点()()0,10,-3和．6．解析（1）由题设得1222y y x x ⋅=-+-，化简得221(||2)42x y x +=≠，所以C 为中心在坐标原点，焦点在x 轴上的椭圆，不含左右顶点．（2）（i ）设直线PQ 的斜率为k ，则其方程为(0)y kx k =>．由22142y kxx y =⎧⎪⎨+=⎪⎩得x =．记u =，则(,),(,),(,0)P u uk Q u uk E u --．于是直线QG 的斜率为2k ，方程为()2ky x u =-．由22(),2142k y x u x y ⎧=-⎪⎪⎨⎪+=⎪⎩得 22222(2)280k x uk x k u +-+-=．①设(,)G G G x y ，则u -和G x 是方程①的解，故22(32)2G u k x k +=+，由此得322G uk y k =+．从而直线PG 的斜率为322212(32)2uk uk k u k kuk -+=-+-+．所以PQ PG ⊥，即PQG △是直角三角形．（ii ）由（i）得||2PQ =||PG =，所以△PQG 的面积222218()18(1)||12(12)(2)12()k k k k S PQ PG k k k k++===++++‖．设t =k +1k ，则由k >0得t ≥2，当且仅当k =1时取等号．因为2812t S t =+在[2，+∞）单调递减，所以当t =2，即k =1时，S 取得最大值，最大值为169．因此，△PQG 面积的最大值为169．7．解析（I ）由题意得12p=，即p =2.所以，抛物线的准线方程为x =−1.（Ⅱ）设()()(),,,,,A A B B c c A x y B x y C x y ，重心(),G G G x y .令2,0A y t t =≠，则2A x t =.由于直线AB 过F ，故直线AB 方程为2112t x y t-=+，代入24y x =，得 ()222140t y y t---=，故24B ty =-，即2B y t =-，所以212,B tt ⎛⎫- ⎪⎝⎭.又由于()()11,33G A B c G A B c x x x x y y y y =++=++及重心G 在x 轴上，故220c t y t-+=，得242211222,2,,03t t C t t G t t t ⎛⎫⎛⎫-+⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 所以，直线AC 方程为()222y t t x t-=-，得()21,0Q t-.由于Q 在焦点F 的右侧，故22t >.从而4224221244242222211|2|||322221222211|||1||2|23A c t t t FG y t S t t t t t S t t QG y t t t t-+-⋅⋅--====--+--⋅--⋅-. 令22m t =-，则m >0，1221222134324S m S m m m m =-=-=+++++….当m =12S S取得最小值1+G （2，0）.8.解析（Ⅰ）设椭圆的半焦距为c ，依题意，24,c b a ==，又222a b c =+，可得a =2,b =1c =.所以，椭圆的方程为22154x y +=. （Ⅱ）由题意，设()()()0,,0P P p M P x y x M x ≠，.设直线PB 的斜率为()0k k ≠，又()0,2B ，则直线PB 的方程为2y kx =+，与椭圆方程联立222154y kx x y =+⎧⎪⎨+=⎪⎩，整理得()2245200k x kx ++=，可得22045P kx k =-+，代入2y kx =+得2281045P k y k -=+，进而直线OP 的斜率24510P p y k x k-=-.在2y kx =+中，令0y =，得2M x k =-.由题意得()0,1N -，所以直线MN 的斜率为2k -.由OP MN ⊥，得2451102k k k-⎛⎫⋅-=- ⎪-⎝⎭，化简得2245k =，从而k =所以，直线PB或. 2010-2018年1．【解析】(1)因为椭圆C的焦点为12(),F F -，可设椭圆C 的方程为22221(0)x y a b a b +=>>．又点1)2在椭圆C 上，所以2222311,43,a ba b ⎧+=⎪⎨⎪-=⎩，解得224,1,a b ⎧=⎪⎨=⎪⎩ 因此，椭圆C 的方程为2214x y +=．因为圆O 的直径为12F F ，所以其方程为223x y +=．(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>，则22003x y +=，所以直线l 的方程为0000()x y x x y y =--+，即0003x y x y y =-+．由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩消去y ，得222200004243640()x y x x x y +-+-=．（*）因为直线l 与椭圆C 有且只有一个公共点，所以222222000000()()(24)44364(48)20x x y y y x =--+-=-=∆．因为00,0x y >，所以001x y ==．因此，点P的坐标为． ②因为三角形OAB，所以1 2AB OP ⋅=7AB =．设1122,,()(),A x y B x y ，由（*）得001,2x =，所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+．因为22003x y +=，所以22022016(2)32(1)49x AB x -==+，即42002451000x x -+=，解得22005(202x x ==舍去），则2012y =，因此P的坐标为．综上，直线l的方程为y =+2．【解析】（1）设(,)P x y ，00(,)M x y ，则0(,0)N x ，0(,)NP x x y =-u u u r ，0(0.)NM y =u u u u r．由NP =u u u r u u u r得 0x x =，02y y =．因为00(,)M x y 在C 上，所以22122x y +=．因此点P 的轨迹方程为222x y +=．（2）由题意知(1,0)F -．设(3,)Q t -，(,)P m n ，则(3,)OQ t =-u u u r ，(1,)PF m n =---u u u r ，33OQ PF m tn ⋅=+-u u u r u u u r， (,)OP m n =u u u r ，(3,)PQ m t n =---u u u r，由1OP PQ ⋅=u u u r u u u r 得2231m m tn n --+-=，又由（1）知222m n +=，故330m tn +-=．所以0OQ PF ⋅=u u u r u u u r ，即OQ PF ⊥u u u r u u u r．又过点P 存在唯一直线垂直与OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F ． 3．【解析】(Ⅰ) 由离心率是23，有224=b a ，又抛物线y x 2=2的焦点坐标为)21,0(F ，所以21=b ，于是1=a ，所以椭圆C 的方程为1=4+22y x ．(Ⅱ) （i ）设P 点坐标为2,),(0)2m Pm m >（，由y x 2=2得x y =′，所以E 在点P 处的切线l 的斜率为m ，因此切线l 的方程为2=2m mx －y ，设),(),,(2211y x B y x A ，),(00y x D ，将2=2m mx －y 代入1=4+22y x ，得0=1+4)4+12322－m x m －x m （．于是23214+14=+m m x x ，232104+12=2+=m m x x x ，又2200222(14)m m y mx m -=-=+，于是直线OD 的方程为x m－y 41=．联立方程x m －y 41=与m x =，得M 的坐标为1(,)4M m -．所以点M 在定直线41=y －上．（ii ）在切线l 的方程为2=2m mx －y 中，令0x =，得22m y =－，即点G 的坐标为2(0,)2m G -，又2(,)2m P m ，1(0,)2F ，所以4)1+(=×21=S 21m m GF m ；再由32222(,)412(41)m m D m m -++，得 )1+4(8)1+2(=1+4+2×41+2×21=S 2222322m m m m m m m于是有 222221)1+2()1+)(1+4(2=S S m m m ．令1+2=2m t ，得222111+2=)1+)(21(2=S S t －t t t t －当21=1t时，即2=t 时，21S S 取得最大值49．此时21=2m ，22=m ，所以P 点的坐标为)41,22P(．所以21S S 的最大值为49，取得最大值时点P的坐标为1()24P ． 4．【解析】（Ⅰ）设(,0)F c ，由113||||||c OF OA FA +=，即113()cc a a a c +=-，可得2223a c c -=，又2223a c b -==，所以21c =，因此24a =，所以椭圆的方程为22143x y +=．（Ⅱ）解：设直线l 的斜率为k （0≠k ），则直线l 的方程为)2(-=x k y .设),(B B y x B ，由方程组⎪⎩⎪⎨⎧-==+)2(13422x k y y x ，消去y ，整理得0121616)34(2222=-+-+k x k x k ．解得2=x ，或346822+-=k k x ，由题意得346822+-=k k x B ，从而34122+-=k k y B．由（Ⅰ）知，)0,1(F ，设),0(H y H ，有),1(H y FH -=，)3412,3449(222++-=k kk k BF . 由HF BF ⊥，得0=⋅HF BF ，所以034123449222=+++-k ky k k H，解得k k y H 12492-=.因此直线MH 的方程为kk x k y 124912-+-=．设),(M M y x M ，由方程组⎪⎩⎪⎨⎧-=-+-=)2(124912x k y k k x k y 消去y ，解得)1(1292022++=k k x M . 在MAO ∆中，||||MO MA MAO MOA ≤⇔∠≤∠，即2222)2(M M M M y x y x +≤+-，化简得1≥M x ，即1)1(1292022≥++k k ，解得46-≤k 或46≥k ．所以，直线l 的斜率的取值范围为),46[]46,(+∞--∞Y ． 5．【解析】（I ）设11(,)M x y ，则由题意知10y >．当4t =时，椭圆E 的方程为22143x y +=，A 点坐标为()20-，，由已知及椭圆的对称性知，直线AM 的倾斜角为4π．因此直线AM 的方程为2y x =+．将2x y =-代入22143x y +=得27120y y -=．解得0y =或127y =，所以1127y =．所以AMN △的面积为21112121442227749AMN S AM ∆==⨯⨯⨯=．（Ⅱ）由题意知3,0,(t k A >>，则直线AM的方程为(y k x =，联立()2213x y t y k x t ⎧+=⎪⎨⎪=+⎩并整理得，()222223230tk x t tk x t k t +++-=解得x t =-或23t tk tx -=-，所以2223611t tk t t AM k t k -=+-+=+⋅ 由题意MA NA ⊥，所以AN 的方程为1()y x t k=-+，同理可得26(1)||k t k AN +=由2AM AN =,得22233k tk k t=++，即3(2)3(21)k t k k -=- 当32k =时上式成立，因此23632k kt k -=-．因为3t >，即236332k k k ->-，整理得()()231202k k k +-<- 即3202k k -<-，解得322k <<． 6．【解析】（Ⅰ）设点(,0)D t (||2)t ≤，00(,),(,)N x y M x y ，依题意，2MD DN =u u u u r u u u r，且||||1DN ON ==u u u r u u u r ，所以00(,)2(,)t x y x t y --=-，且2200220()11x t y x y ⎧-+=⎪⎨+=⎪⎩ 即00222t x x ty y -=-⎧⎨=-⎩，且0(2)0t t x -=．由于当点D 不动时，点N 也不动，所以t 不恒等于0，于是02t x =，故00,42x y x y ==-，代入22001x y +=，可得221164x y +=，即所求的曲线C 的方程为221164x y +=．（Ⅱ）（1）当直线l 的斜率不存在时，直线l 为4x =或4x =-，都有14482OPQ S ∆=⨯⨯=．（2）当直线l 的斜率存在时，设直线1:()2l y kx m k =+≠±，由22416y kx m x y =+⎧⎨+=⎩ ，消去y ，可得222(14)84160k x kmx m +++-=．因为直线l 总与椭圆C 有且只有一个公共点，所以2222644(14)(416)0k m k m ∆=-+-=，即22164m k =+． ① 又由,20,y kx m x y =+⎧⎨-=⎩可得2(,)1212m m P k k --；同理可得2(,)1212m m Q k k -++．由原点O 到直线PQ 的距离为d =和|||P Q PQ x x =-，可得22111222||||||||222121214OPQP Q m m m S PQ d m x x m k k k ∆=⋅=-=⋅+=-+-．② 将①代入②得，222241281441OPQk m S k k ∆+==--．当214k >时，2224128()8(1)84141OPQ k S k k ∆+==+>--；当2104k ≤<时，2224128()8(1)1414OPQ k S k k ∆+==-+--．因2104k ≤<，则20141k <-≤，22214k ≥-，所以228(1)814OPQ S k∆=-+≥-，当且仅当0k =时取等号．所以当0k =时，OPQ S ∆的最小值为8．综合（1）（2）可知，当直线l 与椭圆C 在四个顶点处相切时，△OPQ 的面积取得最小值8．7．【解析】（1）由题意，得c a =且23a c c +=，解得a =1c =，则1b =，所以椭圆的标准方程为2212x y +=．（2）当AB ⊥x 轴时，AB =C 3P =，不合题意．当AB 与x 轴不垂直时，设直线AB 的方程为()1y k x =-，()11,x y A ，()22,x y B ，将AB 的方程代入椭圆方程，得()()2222124210k x k x k +-+-=，则1,2x=C 的坐标为2222,1212k k k k ⎛⎫- ⎪++⎝⎭，且)22112k AB k+===+．若0k =，则线段AB 的垂直平分线为y 轴，与左准线平行，不合题意．从而0k ≠，故直线C P 的方程为222121212k k y x k k k ⎛⎫+=-- ⎪++⎝⎭，则P 点的坐标为()22522,12k k k ⎛⎫+ ⎪- ⎪+⎝⎭，从而(()2223112k PC k k +=+．因为2PC AB=，所以(())222223111212k k k k k++=++，解得1k =±．此时直线AB 方程为1y x =-或1y x =-+． 8．【解析】（1）由已知，点在椭圆E 上．因此，22222211,,2a b a b c c a⎧+=⎪⎪⎪-=⎨⎪⎪=⎪⎩解得2a =，b =所以椭圆的方程为22142x y +=．（2）当直线l 与x 轴平行时，设直线l 与椭圆相交于C 、D 两点．如果存在定点Q 满足条件，则||||1||||QC PC QD PD ==，即||||QC QD =．所以Q 点在y 轴上，可设Q 点的坐标为0(0,)y ．当直线l 与x 轴垂直时，设直线l 与椭圆相交于M、N 两点．则M ，(0,N ，由||||||||QMPM QN PN ==，解得01y =或02y =．所以，若存在不同于点P 的定点Q 满足条件，则Q 点的坐标只可能为(0,2)Q ．下面证明：对任意的直线l ，均有||||||||QA PA QB PB =．当直线l 的斜率不存在时，由上可知，结论成立．当直线l 的斜率存在时，可设直线l 的方程为1y kx =+，A 、B 的坐标分别为1122(,),(,)x y x y ．联立221,421x y y kx ⎧+=⎪⎨⎪=+⎩得22(21)420k x kx ++-=．其判别式22168(21)0k k ∆=++>，所以，12122242,2121k x x x x k k +=-=-++．因此121212112x x k x x x x ++==．易知，点B 关于y 轴对称的点的坐标为22(,)B x y '-．又121122122111,QA QB y y k k k k k x x x x x '--==-==-+=--，所以QA QB k k '=，即,,Q A B '三点共线．所以12||||||||||||||||x QA QA PA QB QB x PB ==='．故存在与P 不同的定点(0,2)Q ，使得||||||||QA PA QB PB =恒成立． 9．【解析】（Ⅰ）由题意得2221,,.b caa b c =⎧⎪⎪=⎨⎪⎪=+⎩解得2a =2．故椭圆C 的方程为2212x y +=．设M (N x ，0)．因为0m ≠，所以11n -<<．直线PA 的方程为11n y x m--=，所以M x =1m n -，即(,0)1mM n-．（Ⅱ）因为点B 与点A 关于x 轴对称，所以(,)B m n -，设(,0)N N x ，则N x =1mn+． “存在点(0,)Q Q y 使得OQM ∠=ONQ ∠等价”，“存在点(0,)Q Q y 使得OM OQ=OQ ON”即Q y 满足2Q M N y x x =．因为1M m x n =-，1N mx n=+，2212m n +=，所以22221Q MN m y x x n ===-．所以Q y或Q y =故在y 轴上存在点Q ，使得OQM ∠=ONQ ∠．点Q的坐标为或(0,．10．【解析】（Ⅰ）由题意知0m ≠，可设直线AB 的方程为1y x b m=-+．由22112y x b m x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消去y ，得222112()102b x x b m m +-+-=．因为直线1y x b m=-+与椭圆2212x y +=有两个不同的交点，所以224Δ220b m=-++>，① 设M 为AB 的中点，则2222(,)22mb m bM m m ++，代入直线方程12y mx =+解得2222m b m +=-．②由①②得3m <-或3m >．（Ⅱ）令1((0,)22t m =∈-U ，则2||2AB t =+且O 到直线AB的距离21t d +=．设ΔAOB 的面积为()S t ，所以1()||2S t AB d =⋅= 当且仅当212t =时，等号成立．故ΔAOB． 11．【解析】（Ⅰ）可知c =c a =，3a ∴=，2224b a c =-=，椭圆C 的标准方程为22194x y +=；（Ⅱ）设两切线为12,l l ，①当1l x ⊥轴或1//l x 轴时，对应2//l x 轴或2l x ⊥轴，可知(3,2)P ±±②当1l 与x 轴不垂直且不平行时，03x ≠±，设1l 的斜率为k ，则0k ≠，2l 的斜率为1k-，1l 的方程为00()y y k x x -=-，联立22194x y +=，得2220000(94)18()9()360k x y kx kx y kx ++-+--=，因为直线与椭圆相切，所以0∆=，得222200009()(94)[()4]0y kx k k y kx --+--=，2200364[()4]0k y kx ∴-+--=，2220000(9)240x k x y k y ∴--+-=所以k 是方程2220000(9)240x x x y x y --+-=的一个根，同理1k-是方程2220000(9)240x x x y x y --+-=的另一个根，1()k k ∴⋅-=202049y x --，得220013x y +=，其中03x ≠±，所以点P 的轨迹方程为2213x y +=（3x ≠±），因为(3,2)P ±±满足上式，综上知：点P 的轨迹方程为2213x y +=． 12．【解析】（Ⅰ）设圆的半径为r ，P 点上下两段分别为,m n ，24r =，由射影定理得2r mn =，三角形的面积s ==≥=当2m n ==时，s取得最大，此时P∵222cc b a a==+，P 在双曲线上 ∴222321c b a ===，，，∴双曲线的方程为22-12y x = （Ⅱ）由（Ⅰ）知2C的焦点为，由此设2C 的方程为22221113x y b b +=+，其中10b >，由P 在2C 上，得213b =，∴2C 的方程为22163x y +=，显然，l 不是直线0y =，设l的方程为x my =+1122(,),(,)A x y B x y ，由22163x my x y ⎧=⎪⎨+=⎪⎩得22(2)-30m y ++=，∴12122-32y y y y m +==+①11220(PA PB x y x y =•=u u u r21212(1))m y y m y y =++++由①②得220m +=，解得12m m ==因此直线l的方程02x y -=或02x y -= 13．【解析】（Ⅰ）由椭圆定义知，2a ＝|PF 1|＋|PF 2|=所以a =c ＝1.所以椭圆C的离心率2c e a ===．（Ⅱ）由（Ⅰ）知，椭圆C 的方程为22x ＋y 2＝1．设点Q 的坐标为(x ，y )．(ⅰ)当直线l 与x 轴垂直时，直线l 与椭圆C 交于(0,1)，(0，－1)两点，此时点Q的坐标为0,2⎛ ⎝⎭． (ⅱ)当直线l 与x 轴不垂直时，设直线l 的方程为y ＝kx ＋2．因为M ，N 在直线l 上，可设点M ，N 的坐标分别为(1x ，k 1x ＋2)，(2x ，k 2x ＋2)，则|AM |2＝(1＋k 2)21x ，|AN |2＝(1＋k 2)22x ．又|AQ |2＝x 2＋(y －2)2＝(1＋k 2)2x ．由222211||||||AQ AM AN =+，得22222212211111k x k x k x =+(+)(+)(+)，即212122222212122211x x x x x x x x x (+)-=+=.① 将y ＝kx ＋2代入22x ＋y 2＝1中，得(2k 2＋1)x 2＋8kx ＋6＝0.②由Δ＝(8k )2－4×(2k 2＋1)×6＞0，得k 2＞32.由②可知，12x x +＝2821k k -+，12x x ＝2621k +，代入①中并化简，得2218103x k =-.③因为点Q 在直线y ＝kx ＋2上，所以2y k x-=，代入③中并化简，得10(y －2)2－3x 2＝18.由③及k 2＞32，可知0＜x 2＜32，即x ∈⎛⎫ ⎪ ⎪⎝⎭∪⎛ ⎝⎭.又0,25⎛⎫- ⎪ ⎪⎝⎭满足10(y －2)2－3x 2＝18，故x ∈,22⎛- ⎝⎭. 由题意，Q (x ，y )在椭圆C 内，所以－1≤y ≤1.又由10(y －2)2＝18＋3x 2有(y －2)2∈99,54⎡⎫⎪⎢⎣⎭且－1≤y ≤1，则y ∈1,225⎛- ⎝⎦. 所以，点Q 的轨迹方程为10(y －2)2－3x 2＝18，其中x ∈⎛⎝⎭，y ∈1,22⎛- ⎝⎦. 14．【解析】（Ⅰ）解法1 ：设M 的坐标为(,)x y ，由已知得23x +=，易知圆2C 上的点位于直线2x =-的右侧.于是20x +>，所以5x =+.化简得曲线1C 的方程为220y x =．解法2 ：由题设知，曲线1C 上任意一点M 到圆心2C (5,0)的距离等于它到直线5x =-的距离，因此，曲线1C 是以(5,0)为焦点，直线5x =-为准线的抛物线，故其方程为220y x =．（Ⅱ）当点P 在直线4x =-上运动时，P 的坐标为0(4,)y -，又03y ≠±，则过P 且与圆2C 相切的直线的斜率k 存在且不为0，每条切线都与抛物线有两个交点，切线方程为0(4),y y k x -=+0即kx-y+y +4k=0.于是3.=整理得 2200721890.k y k y ++-= ①设过P 所作的两条切线,PA PC 的斜率分别为12,k k ，则12,k k 是方程①的两个实根，故001218.724y yk k +=-=- ② 由101240,20,k x y y k y x -++=⎧⎨=⎩得21012020(4)0.k y y y k -++= ③ 设四点A,B,C,D 的纵坐标分别为1234,,,y y y y ，则12,y y 是方程③的两个实根，所以0112120(4).y k y y k +⋅=④同理可得0234220(4).y k y y k +⋅=⑤于是由②，④，⑤三式得010*******400(4)(4)y k y k y y y y k k ++=2012012124004()16y k k y k k k k ⎡⎤+++⎣⎦=22001212400[16]6400y y k k k k -+==.所以，当P 在直线4x =-上运动时，四点,,,A B C D 的纵坐标之积为定值6400． 15．【解析】（Ⅰ）解：设12(,0),(,0)(0)F c F c c ->，由题意，可得212||||,PF F F =2.c = 整理得22()10,1cc c aa a +-==-得（舍），或1.2c a =所以1.2e =（Ⅱ）解：由（Ⅰ）知2,,a c b ==可得椭圆方程为2223412,x y c +=直线PF 2方程为).y x c =-A ，B两点的坐标满足方程组2223412,).x y c y x c ⎧+=⎪⎨=-⎪⎩消去y 并整理，得2580.x cx -= 解得1280,.5x x c ==得方程组的解21128,0,5,.x c x y y ⎧=⎪=⎧⎪⎪⎨⎨=⎪⎪⎩=⎪⎩不妨设8(),(0,)5A c B 设点M的坐标为8(,),(,),(,)55x y AM x c y c BM x y =--=+u u u u r u u u ur 则，由),.3y x c c x y =-=-得于是38(,),15555AM y x y x =--u u u u r().BM x =u u u u r 由2,AM BM ⋅=-u u u u r u u u u r即38()()215555y x x y x -⋅+-=-，化简得218150.x --=将22105,0.316x y c x y c x +==-=>得所以0.x >因此，点M的轨迹方程是218150(0).x x --=>16．【解析】（1）联立2x y =与2+=x y 得2,1=-=B A x x ，则AB 中点)25,21(Q ，设线段PQ 的中点M 坐标为),(y x ，则225,221ty s x +=+=，即252,212-=-=y t x s ，又点P 在曲线C 上，∴2)212(252-=-x y 化简可得21128y x x =-+，又点P 是L 上的任一点，且不与点A 和点B 重合，则22121<-<-x ，即4541<<-x ，∴中点M 的轨迹方程为21128y x x =-+（4541<<-x ）．（2）曲线22251:24025G x ax y y a -+-++=，即圆E ：2549)2()(22=-+-y a x ，其圆心坐标为)2,(a E ，半径57=r ，设圆G 与直线l ：20x y -+=相切于点(,)T T T x y ，75=，即5a =±．过点(,2)N a 与直线l 垂直的直线l '的方程是21()y x a -=-⨯-，即20x y +-=．由2020x y x y a -+=⎧⎨+--=⎩，解得2T a x =，22T ay =+．当5a =-时，1210T x -<<-<． ∵1,2-分别是D 上的点的最小和最大横坐标，∴切点T D ∈，故min 5a =-．。

十年高考理科数学真题专题九解析几何二十六椭圆及答案(优质)

专题九解析几何第二十六讲椭圆2019年1．（2019全国I 理10）已知椭圆C 的焦点为121,01,0F F -()，()，过F 2的直线与C 交于A ，B 两点．若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y += B ．22132x y += C ．22143x y += D ．22154x y += 2.（2019全国II 理21（1））已知点A (−2,0)，B (2,0)，动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .（1）求C 的方程，并说明C 是什么曲线；3.（2019北京理4）已知椭圆()222210x y a b a b +=>>的离心率为12，则（A ）22.2a b =（B ）22.34a b=（C ）2a b=（D ）34a b=4.（2019全国III 理15）设12F F ，为椭圆C :22+13620x y =的两个焦点，M 为C 上一点且在第一象限.若12MF F △为等腰三角形，则M 的坐标为___________.2010-2018年一、选择题1．(2018全国卷Ⅱ)已知1F ，2F 是椭圆22221(0)+=>>：x y C a b a b的左，右焦点，A 是C 的左顶点，点P 在过A 12△PF F 为等腰三角形，12120∠=︒F F P ，则C 的离心率为A ．23B ．12C ．13D ．142．(2018上海)设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为（）A ．B ．C ．D ．3．（2017浙江）椭圆22194x y +=的离心率是A ．3 B ．3 C ．23 D ．594．（2017新课标Ⅲ）已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A ．3 B ．3 C ．3 D ．135．(2016年全国III)已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点．P 为C 上一点，且PF ⊥x 轴．过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E ．若直线BM 经过OE 的中点，则C 的离心率为 A ．13B ．12C ．23D ．346．(2016年浙江)已知椭圆1C ：2221x y m +=(1m >)与双曲线2C ：2221x y n-=(0n >)的焦点重合，1e ，2e 分别为1C ，2C 的离心率，则A ．m n >且121e e >B ．m n >且121e e <C ．m n <且121e e >D ．m n <且121e e <7．(2014福建)设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是A ．25B ．246+C ．27+D ．268．（2013新课标1）已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为 A ．x 245＋y 236＝1B ．x 236＋y 227＝1C ．x 227＋y 218＝1D ．x 218＋y 29＝19．(2012新课标)设1F 、2F 是椭圆E ：)0(12222>>=+b a by a x 的左、右焦点，P 为直线23a x =上一点，12PF F ∆ 是底角为o30的等腰三角形，则E 的离心率为 A 、21 B 、32 C 、43 D 、54二、填空题10．(2018浙江)已知点(0,1)P ，椭圆224x y m +=(1m >)上两点A ，B 满足2AP PB =u u u r u u u r ，则当m =___时，点B 横坐标的绝对值最大．11．(2018北京)已知椭圆22221(0)x y M a b a b +=>>：，双曲线22221x y N m n-=：．若双曲线N的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为__________；双曲线N 的离心率为__________．12．(2016江苏省)如图，在平面直角坐标系xOy 中，F 是椭圆()222210x y a b a b+=>>的右焦点，直线2by =与椭圆交于,B C 两点，且90BFC ∠=︒，则该椭圆的离心率是．13．（2015新课标1）一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 的正半轴上，则该圆的标准方程为_________．14．（2014江西）过点(1,1)M 作斜率为12-的直线与椭圆C ：22221(0)x y a b a b +=>>相交于,A B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于．15．（2014辽宁）已知椭圆C ：22194x y +=，点M 与C 的焦点不重合，若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则||||AN BN += ．16．（2014江西）设椭圆()01:2222>>=+b a by a x C 的左右焦点为21F F ，，作2F 作x 轴的垂线与C 交于B A ，两点，B F 1与y 轴相交于点D ，若B F AD 1⊥，则椭圆C 的离心率等于________．17．（2014安徽）设21,F F 分别是椭圆)10(1:222<<=+b by x E 的左、右焦点，过点1F 的直线交椭圆E 于B A ,两点，若x AF BF AF ⊥=211,3轴，则椭圆E 的方程为_____．18．（2013福建）椭圆)0(1:2222>>=+Γb a by a x 的左、右焦点分别为21,F F ，焦距为c 2．若直线)y x c =+与椭圆Γ的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于19．（2012江西）椭圆22221(0)x y a b a b+=>>的左、右顶点分别是,A B ，左、右焦点分别是12,F F ．若1121||,||,||AF F F F B 成等比数列，则此椭圆的离心率为_________．20．（2011浙江）设12,F F 分别为椭圆2213x y +=的左、右焦点，点,A B 在椭圆上，若125F A F B =u u u r u u u u r；则点A 的坐标是．三、解答题21．（2018全国卷Ⅰ）设椭圆:C 2212+=x y 的右焦点为F ，过F 的直线l 与C 交于A ,B 两点，点M 的坐标为(2,0)．(1)当l 与x 轴垂直时，求直线AM 的方程； (2)设O 为坐标原点，证明：OMA OMB ∠=∠．22．（2018全国卷Ⅲ）已知斜率为k 的直线l 与椭圆C ：22143x y +=交于A ，B 两点，线段AB 的中点为(1,)M m (0)m >． (1)证明：12k <-； (2)设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0u u u r u u u r u u u r ．证明：||FA u u u r ，||FP u u u r，||FB u u u r成等差数列，并求该数列的公差．23．(2018天津)设椭圆22221x x a b+=(0a b >>)的左焦点为F ，上顶点为B ．已知椭圆的离A 的坐标为(,0)b ，且FB AB ⋅= (1)求椭圆的方程；(2)设直线l ：(0)y kx k =>与椭圆在第一象限的交点为P ，且l 与直线AB 交于点Q ．若4AQ AOQ PQ=∠(O 为原点) ，求k 的值． 24．（2017新课标Ⅰ）已知椭圆C ：22221(0)x y a b a b+=>>，四点1(1,1)P ，2(0,1)P ，3(2P =-，4(1,2P =中恰有三点在椭圆C 上． (1)求C 的方程；(2)设直线l 不经过2P 点且与C 相交于A ，B 两点．若直线2P A 与直线2P B 的斜率的和为1-，证明：l 过定点．25．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足NP =u u u r u u u r．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=u u u r u u u r．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．26．（2017江苏）如图，在平面直角坐标系xOy 中，椭圆E ：22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，离心率为12，两准线之间的距离为8．点P 在椭圆E 上，且位于第一象限，过点1F 作直线1PF 的垂线1l ，过点2F 作直线2PF 的垂线2l ．（1）求椭圆E 的标准方程；（2）若直线1l ，2l 的交点Q 在椭圆E 上，求点P 的坐标．27．（2017天津）设椭圆22221(0)x y a b a b +=>>的左焦点为F ，右顶点为A ，离心率为12．已知A 是抛物线22(0)y px p =>的焦点，F 到抛物线的准线l 的距离为12．（Ⅰ）求椭圆的方程和抛物线的方程；（Ⅱ）设l 上两点P ，Q 关于x 轴对称，直线AP 与椭圆相交于点B （B 异于点A ），直线BQ 与x 轴相交于点D ．若APD △6AP 的方程． 28．（2017山东）在平面直角坐标系xOy 中，椭圆E ：22221x y a b+=()0a b >>2，焦距为2．（Ⅰ）求椭圆E 的方程；（Ⅱ）如图，动直线l：1y k x =E 于,A B 两点，C 是椭圆E 上一点，直线OC 的斜率为2k，且12k k ，M 是线段OC 延长线上一点，且:2:3MC AB =，M e 的半径为MC ，,OS OT 是M e 的两条切线，切点分别为,S T ．求SOT ∠的最大值，并求取得最大值时直线l 的斜率．x29．(2016年北京)已知椭圆C ：22221(0)x y a b ab+=>>(,0)A a ，(0,)B b ，(0,0)O ，ΔOAB 的面积为1．（Ⅰ）求椭圆C 的方程；（Ⅱ）设P 是椭圆C 上一点，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ．求证：||||AN BM ⋅为定值．30．(2015新课标2）已知椭圆C ：2229x y m +=(0m >)，直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M ．（Ⅰ）证明：直线OM 的斜率与l 的斜率的乘积为定值；（Ⅱ）若l 过点(,)3mm ，延长线段OM 与C 交于点P ，四边形OAPB 能否为平行四边行？若能，求此时l 的斜率；若不能，说明理由．31．（2015北京）已知椭圆C ：()222210x y a ba b+=>>的离心率为，点()01P ，和点()A m n ，()0m ≠都在椭圆C 上，直线PA 交x 轴于点M ．（Ⅰ）求椭圆C 的方程，并求点M 的坐标（用m ，n 表示）；（Ⅱ）设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N ．问：y 轴上是否存在点Q ，使得OQM ONQ ∠=∠？若存在，求点Q 的坐标；若不存在，说明理由．32．（2015安徽）设椭圆E 的方程为()222210x y a b a b+=>>，点O 为坐标原点，点A 的坐标为()0a ，，点B 的坐标为()0b ，，点M 在线段AB 上，满足2BM MA =，直线OM的斜率为10．（Ⅰ）求E 的离心率e ；（Ⅱ）设点C 的坐标为()0b -，，N 为线段AC 的中点，点N 关于直线AB 的对称点的纵坐标为72，求E 的方程． 33．（2015山东）平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率为2，左、右焦点分别是1F 、2F ．以1F 为圆心以3为半径的圆与以2F 为圆心以1为半径的圆相交，且交点在椭圆C 上．（Ⅰ）求椭圆C 的方程；（Ⅱ）设椭圆E ：2222144x y a b+=，P 为椭圆C 上任意一点，过点P 的直线=+y kx m交椭圆E 于,A B 两点，射线PO 交椭圆E 于点Q ．( i )求||||OQ OP 的值；（ii ）求△ABQ 面积的最大值．34． (2014新课标1) 已知点A (0,2)-，椭圆E ：22221(0)x y a b a b+=>>，F 是椭圆E 的右焦点，直线AF的斜率为3，O 为坐标原点．（Ⅰ)求E 的方程；（Ⅱ）设过点A 的动直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．35．(2014浙江)如图，设椭圆(),01:2222>>=+b a by a x C 动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限．（Ⅰ）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；（Ⅱ）若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -．36．（2014新课标2）设1F ，2F 分别是椭圆C ：()222210y x a b a b+=>>的左，右焦点，M是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ．（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求,a b ．37．（2014安徽）设1F ,2F 分别是椭圆E ：22221(0)x y a b a b+=>>的左、右焦点，过点1F的直线交椭圆E 于,A B 两点，11||3||AF BF = （Ⅰ）若2||4,AB ABF =∆的周长为16，求2||AF ；（Ⅱ）若23cos 5AF B ∠=，求椭圆E 的离心率．38．（2014山东）在平面直角坐标系xOy 中，椭圆2222:1(0)x y C a b a b+=>>的离心率为32，直线y x =被椭圆C 截得的线段长为4105．（Ｉ）求椭圆C 的方程；（Ⅱ）过原点的直线与椭圆C 交于A ，B 两点（A ，B 不是椭圆C 的顶点）．点D 在椭圆C 上，且AD AB ⊥，直线BD 与x 轴、y 轴分别交于M ，N 两点． (ⅰ)设直线BD ，AM 的斜率分别为12,k k ，证明存在常数λ使得12k k λ=，并求出λ的值；(ⅱ)求OMN ∆面积的最大值．39．（2014湖南）如图5，O 为坐标原点，双曲线221112211:1(0,0)x y C a b a b -=>>和椭圆222222222:1(0)x y C a b a b +=>>均过点23(,1)3P ，且以1C 的两个顶点和2C 的两个焦点为顶点的四边形是面积为2的正方形．（Ｉ）求12,C C 的方程；（Ⅱ）是否存在直线l ，使得l 与1C 交于,A B 两点，与2C 只有一个公共点，且||||OA OB AB +=u u u r u u u r u u u r？证明你的结论．40．（2014四川）已知椭圆C ：22221x y a b+=（0a b >>）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q ．（i ）证明：OT 平分线段PQ （其中O 为坐标原点）；（ii ）当||||TF PQ 最小时，求点T 的坐标． 41．（2013安徽）已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4，且过点P ．（Ⅰ）求椭圆C 的方程；（Ⅱ）设0000(,)(0)Q x y x y ≠为椭圆C 上一点，过点Q 作x 轴的垂线，垂足为E ．取y 轴的对称点，作直线QG ，问这样作出的直线QG 是否与椭圆C 一定有唯一的公共点？并说明理由．42．（2013湖北）如图，已知椭圆1C 与2C 的中心在坐标原点O ，长轴均为MN 且在x 轴上，短轴长分别为2m ，2()n m n >，过原点且不与x 轴重合的直线l 与1C ，2C 的四个交点按纵坐标从大到小依次为A ，B ，C ，D ．记mnλ=，△BDM 和△ABN 的面积分别为1S 和2S ．（Ⅰ）当直线l 与y 轴重合时，若12S S λ=，求λ的值；（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l ，使得12S S λ=？并说明理由．43． (2013天津)设椭圆22221(0)x y a b a b+=>>的左焦点为F ，，过点F 且与x(Ⅰ) 求椭圆的方程；第20题图(Ⅱ) 设A ， B 分别为椭圆的左、右顶点，过点F 且斜率为k 的直线与椭圆交于C ，D两点．若··8AC DB AD CB +=u u u r u u u r u u u r u u u r，求k 的值．44．（2013山东）椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是12,F F ，离心率为2，过1F 且垂直于x 轴的直线被椭圆C 截得的线段长为l ．（Ⅰ）求椭圆C 的方程；（Ⅱ）点P 是椭圆C 上除长轴端点外的任一点，连接12,PF PF ．设12F PF ∠的角平分线PM 交C 的长轴于点(),0M m ，求m 的取值范围；（Ⅲ）在（Ⅱ）的条件下，过点P 作斜率为k 的直线l ，使得l 与椭圆C 有且只有一个公共点．设直线12,PF PF 的斜率分别为12,k k ，若0k ≠，试证明1211kk kk +为定值，并求出这个定值．45．（2012北京）已知椭圆C :22221(0)x y a b a b+=>>的一个顶点为(2,0)A，离心率为2．直线(1y k x =-）与椭圆C 交于不同的两点M ,N ．（Ⅰ）求椭圆C 的方程；（Ⅱ）当△AMNk 的值． 46．（2013安徽）如图，21,F F 分别是椭圆C ：22a x +22by =1（0>>b a ）的左、右焦点，A是椭圆C 的顶点，B 是直线2AF 与椭圆C 的另一个交点，1F ∠A 2F =60°．（Ⅰ）求椭圆C 的离心率；（Ⅱ）已知△A B F 1的面积为403，求a , b 的值．47．（2012广东）在平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率e =C 上的点到(0,2)Q 的距离的最大值为3．（Ⅰ）求椭圆C 的方程；（Ⅱ）在椭圆C 上，是否存在点(,)M m n 使得直线l ：1mx ny +=与圆O ：221x y +=相交于不同的两点,A B ，且OAB ∆的面积最大？若存在，求出点M 的坐标及相对应的OAB ∆的面积；若不存在，请说明理由．48．（2011陕西）设椭圆C: ()222210x y a b a b +=>>过点（0，4），离心率为35（Ⅰ）求C 的方程；（Ⅱ）求过点（3，0）且斜率为45的直线被C 所截线段的中点坐标． 49．（2011山东）在平面直角坐标系xOy 中，已知椭圆22:13x C y +=．如图所示，斜率为(0)k k ＞且不过原点的直线l 交椭圆C 于A ，B 两点，线段AB 的中点为E ，射线OE交椭圆C 于点G ，交直线3x =-于点(3,)D m -．（Ⅰ）求22m k +的最小值；（Ⅱ）若2OG OD =∙OE ，（i ）求证：直线l 过定点；（ii ）试问点B ，G 能否关于x 轴对称？若能，求出此时ABG V 的外接圆方程；若不能，请说明理由．50．（2010新课标）设1F ,2F 分别是椭圆E ：2x +22y b=1（01b <<）的左、右焦点，过1F的直线l 与E 相交于A 、B 两点，且2AF ，AB ，2BF 成等差数列．（Ⅰ）求AB ；（Ⅱ）若直线l 的斜率为1，求b 的值．51．（2010辽宁）设椭圆C ：22221(0)x y a b a b+=>>的左焦点为F ，过点F 的直线与椭圆C相交于A ，B 两点，直线l 的倾斜角为60o ，2AF FB =u u u r u u u r．（Ⅰ）求椭圆C 的离心率；（Ⅱ）如果|AB |=154，求椭圆C 的方程．专题九解析几何第二十六讲椭圆答案部分1. 解析 2x =，则22AF x =，所以23BF AB x ==.由椭圆定义122BF BF a +=，即42x a =.又1224AF AF a x +==，22AF x =，所以12AF x =. 因此点A 为椭圆的上顶点，设其坐标为()0,b .由222AF BF =可得点B 的坐标为3,22b ⎛⎫-⎪⎝⎭. 因为点B 在椭圆()222210x y a b a b+=>>上，所以291144a +=.解得23a =.又1c =，所以22b =.所以椭圆方程为22132x y +=.故选B. 2．解析（1）由题设得1222y y x x ⋅=-+-，化简得221(||2)42x y x +=≠，所以C 为中心在坐标原点，焦点在x 轴上的椭圆，不含左右顶点．3. 解析由题意，c e a ====所以22244a b a -=，即2234a b =．故选B ．4. 解析设(,)M m n ，,0m n >，椭圆C ：22:13620x y C +=的6a =，b =2c =，23c e a ==，由于M 为C 上一点且在第一象限，可得12||||MF MF >， 12MF F △为等腰三角形，可能1||2MF c =或2||2MF c =，即有2683m +=，即3m =，n = 2683m -=，即30m =-<，舍去．可得M .2010-2018年1．D 【解析】由题意可得椭圆的焦点在x 轴上，如图所示，OyxPF 2F 1A设12||2=F F c ，所以12∆PF F 为等腰三角形，且12=120∠oF F P ，∴212||||2PF F F c ==，∵2||OF c =，∴点P 坐标为(2cos 60,2sin 60)c c c +oo，即点(2)P c ．∵点P 在过点A，且斜率为6的直线上，∴26c a =+，解得14c a =．∴14e =，故选D ．2．C 【解析】由题意25=a，=a P 到该椭圆的两个焦点的距离之和为2=a ，故选C ．3．B 【解析】由题意可知29a =，24b =，∴2225c a b =-=，∴离心率c e a ==，选B4．A 【解析】以线段12A A 为直径的圆是222x y a +=，直线20bx ay ab -+=与圆相切，所以圆心到直线的距离d a ==，整理为223a b =，即()22222323a a c a c =-⇒=，即2223c a =，c e a ==，故选A ．5．A 【解析】设(0,)E m ，则直线AE 的方程为1x y a b -+=，由题意可知(,)mc M c m a--，(0,)2m和(,0)B a 三点共线，则22mc m m m a c a--=--，化简得3a c =，则C 的离心率13c e a ==．故选A ． 6．A 【解析】由题意知2211m n -=+，即222m n =+，222221222221111()2m n n n e e m n n n -+++=⋅=⋅+4242422111122n n n n n n ++==+>++，所以121e e >．故选A ．7．D【解析】由题意可设,sin )Q αα，圆的圆心坐标为(0,6)C ，圆心到Q 的距离为||CQ ===，当且仅当2sin 3α=-时取等号，所以max max ||||PQ CQ r +==≤Q P ,两点间的最大距离是8．D 【解析】设1122(,),(,)A x y B x y ，则12x x +=2，12y y +=－2，2211221x y a b += ① 2222221x y a b+= ② ①－②得1212121222()()()()0x x x x y y y y a b +-+-+=，∴AB k =1212y y x x --=212212()()b x x a y y +-+=22b a，又AB k =0131+-=12，∴22b a =12，又9=2c =22a b -，解得2b =9，2a =18，∴椭圆方程为221189x y +=，故选D. 9．C 【解析】∆21F PF 是底角为30o 的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔==10．5【解析】设11(,)A x y ，22(,)B x y ，由2AP PB =u u u r u u u r ，得1212212(1)x x y y -=⎧⎨-=-⎩，即122x x =-，1232y y =-．因为点A ，B 在椭圆上，所以222222224(3)44x x m x y m⎧+-=⎪⎪⎨⎪+=⎪⎩，得21344y m =+，所以2222221591(32)(5)444244x m y m m m =--=-+-=--+≤，所以当5m =时，点B 横坐标的绝对值最大，最大值为2．1112-；【解析】设椭圆的右焦点为(,0)F c ，双曲线N 的渐近线与椭圆M 在第一象限内的交点为A，由题意可知(,)22c A ，由点A 在椭圆M 上得，22223144c c a b+=，∴22222234b c a c a b +=，222b ac =-，∴22222222()34()a c c a c a a c -+=-，∴4224480a a c c -+=，∴428+40e e -=椭椭，∴24e =±椭，∴1e =椭（舍去）或1e =椭，∴椭圆M1，∵双曲线的渐近线过点(2cA，渐近线方程为y =，故双曲线的离心率2e ==双．12(),0F c ，直线2by =与椭圆方程联立可得2b B ⎛⎫⎪ ⎪⎝⎭，2b C ⎫⎪⎪⎝⎭，由90BFC ∠=︒可得0BF CF ⋅=u u ur u u u r ，2b BF c ⎛⎫=+- ⎪ ⎪⎝⎭u u u r ，2b CF c ⎛⎫=-- ⎪ ⎪⎝⎭u u u r ，则22231044c a b -+=，由222b a c =-可得223142c a=，则c e a ==． 13．22325()24-+=x y 【解析】由题意圆过(4,0),(0,2),(0,2)-三个点，设圆心为(,0)a ，其中0a >，由4-=a ，解得32a =，所以圆的方程为22325()24-+=x y ．14．2【解析】设11(,)A x y ，22(,)B x y ，分别代入椭圆方程相减得 1212121222()()()()0x x x x y y y y a b-+-++=，根据题意有12122,2x x y y +=+=，且121212y y x x -=--，所以22221()02a b +⨯-=，得222a b =，整理222a c =，所以2e =． 15．12【解析】设MN 交椭圆于点P ，连接1F P 和2F P ，利用中位线定理可得AN BN +=122222412F P F P a a +=⨯==．16．3【解析】由题意可得2(,)b A c a，2(,)b B c a -，由题意可知点D 为1F B 的中点，所以点D 的坐标为2(0,)2b a-，由B F AD 1⊥，所以11AD F B k k ⋅=-22ac =，解得3e =． 17．22312x y +=【解析】由题意得通径22AF b =，∴点B 坐标为251(,)33c B b -- 将点B 坐标带入椭圆方程得22221()53()13b c b--+=，又221b c =-，解得222313b c ⎧=⎪⎪⎨⎪=⎪⎩∴椭圆方程为22312x y +=．18．13-【解析】由题意可知，21F MF ∆中，︒=∠︒=∠︒=∠90,30,60211221MF F F MF F MF ，所以有⎪⎩⎪⎨⎧==+==+12212221222132)2(MF MF a MF MF c F F MF MF ，整理得13-==a c e ，故答案为13-．19由椭圆的性质可知：1AF a c =-，122F F c =，1F B a c =+.又已知1AF ，12F F ，1F B 成等比数列，故2()()(2)a c a c c -+=，即2224a c c -=，则225a c =.故c e a ==.20．(0,1)±【解析】设点A 的坐标为(,)m n ，B 点的坐标为(,)c d．12(F F ，可得1()F A m n =u u u r，2()F B c d =u u u u r ，∵125F A F B =u u u r u u u u r，∴,55m nc d +==，又点,A B 在椭圆上， ∴2213m n +=，22(5()135m n ++=，解得0,1m n ==±， ∴点A 的坐标是(0,1)±．21．【解析】(1)由已知得(1,0)F ，l 的方程为1=x ．由已知可得，点A的坐标为(1,2或(1,2-．所以AM的方程为2y x =-2y x =． (2)当l 与x 轴重合时，0OMA OMB ∠=∠=︒．当l 与x 轴垂直时，OM 为AB 的垂直平分线，所以OMA OMB ∠=∠．当l 与x 轴不重合也不垂直时，设l 的方程为(1)(0)y k x k =-≠，1221(,),(,)A y x y x B ，则1<x2x MA ，MB 的斜率之和为212122MA MB x x y yk k +=+--．由11=-y kx k ，22=-y kx k 得121212(23()42)(2)MA MB x x x x k k x x kk k -+++=--．将(1)y k x =-代入2212x y +=得 2222(21)4220k x k x k +-+-=．所以，2122421+=+k k x x ，21222221-=+x k k x ．则3131322244128423()4021k k k k kk k k k x x x x --++-++==+．从而0MA MB k k +=，故MA ，MB 的倾斜角互补，所以OMA OMB ∠=∠．综上，OMA OMB ∠=∠．22．【解析】(1)设11(,)A x y ，22(,)B x y ，则2211143x y +=，2222143x y +=．两式相减，并由1212y y k x x -=-得1212043x x y y k +++⋅=．由题设知1212x x +=，122y y m +=，于是34k m=-．①由题设得302m <<，故12k <-．(2)由题意得(1,0)F ，设33(,)P x y ，则331122(1,)(1,)(1,)(0,0)x y x y x y -+-+-=．由(1)及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1,)2P -，3||2FP =u u u r ．于是1||22x FA ===-u u u r ．同理2||22x FB =-u u u r ．所以121||||4()32FA FB x x +=-+=u u u r u u u r ．故2||||||FP FA FB =+u u u r u u u r u u u r ，即||FA u u u r ，||FP u u u r ，||FB u u u r 成等差数列．设该数列的公差为d ，则1212||||||||||2d FB FA x x =-=-=u u u r u u u r将34m =代入①得1k =-．所以l 的方程为74y x =-+，代入C 的方程，并整理得2171404x x -+=．故122x x +=，12128x x =，代入②解得||28d =．所以该数列的公差为28或28-． 23．【解析】设椭圆的焦距为2c ，由已知知2259c a =，又由222a b c =+，可得23a b =．由已知可得，FB a =，AB =，由FB AB ⋅=，可得6ab =，从而3a =，2b =．所以，椭圆的方程为22194x y +=．(2)设点P 的坐标为11(,)x y ，点Q 的坐标为22(,)x y ．由已知有120y y >>，故12sin PQ AOQ y y ∠=-．又因为2sin y AQ OAB =∠，而4OAB π∠=，故2AQ =．由AQ AOQ PQ=∠，可得1259y y =．由方程组22194y kx x y =⎧⎪⎨+=⎪⎩，，消去x，可得1y = 易知直线AB 的方程为20x y +-=，由方程组20y kx x y =⎧⎨+-=⎩，，消去x ，可得221ky k =+．由1259y y =，可得5(1)k += 两边平方，整理得25650110k k -+=，解得12k =，或1128k =．所以，k 的值为111228或．24．【解析】（1）由于3P ，4P 两点关于y 轴对称，故由题设知C 经过3P ，4P 两点．又由222211134a b a b +>+知，C 不经过点1P ，所以点2P 在C 上．因此222111314b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得2241a b ⎧=⎪⎨=⎪⎩．故C 的方程为2214x y +=．（2）设直线2P A 与直线2P B 的斜率分别为1k ，2k ，如果l 与x 轴垂直，设l ：x t =，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t，（t，）．则121k k +==-，得2t =，不符合题设．从而可设l ：y kx m =+（1m ≠）．将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=由题设可知22=16(41)0k m ∆-+>．设11(,)A x y ，22(,)B x y ，则122841kmx x k +=-+，21224441m x x k -=+．而12121211y y k k x x --+=+121211kx m kx m x x +-+-=+ 1212122(1)()kx x m x x x x +-+=．由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=．即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++．解得12m k +=-．当且仅当1m >-时，0∆>，欲使l ：12m y x m +=-+，即11(2)2m y x ++=--，所以l 过定点（2，1-）25．【解析】（1）设(,)P x y ，00(,)M x y ，则0(,0)N x ，0(,)NP x x y =-u u u r ，0(0.)NM y =u u u u r．由NP =u u u r u u u r得 0x x =，02y y =．因为00(,)M x y 在C 上，所以22122x y +=．因此点P 的轨迹方程为222x y +=．（2）由题意知(1,0)F -．设(3,)Q t -，(,)P m n ，则(3,)OQ t =-u u u r ，(1,)PF m n =---u u u r ，33OQ PF m tn ⋅=+-u u u r u u u r，(,)OP m n =u u u r ，(3,)PQ m t n =---u u u r，由1OP PQ ⋅=u u u r u u u r 得2231m m tn n --+-=，又由（1）知222m n +=，故330m tn +-=．所以0OQ PF ⋅=u u u r u u u r ，即OQ PF ⊥u u u r u u u r．又过点P 存在唯一直线垂直与OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F ． 26．【解析】（1）设椭圆的半焦距为c .因为椭圆E 的离心率为12，两准线之间的距离为8，所以12c a =，228a c=，解得2,1a c ==，于是b =因此椭圆E 的标准方程是22143x y +=.（2）由（1）知，1(1,0)F -，2(1,0)F .设00(,)P x y ，因为点P 为第一象限的点，故000,0x y >>. 当01x =时，2l 与1l 相交于1F ，与题设不符.当01x ≠时，直线1PF 的斜率为001y x +，直线2PF 的斜率为01y x -. 因为11l PF ⊥，22l PF ⊥，所以直线1l 的斜率为001x y -+，直线2l 的斜率为001x y --，从而直线1l 的方程：001(1)x y x y +=-+， ① 直线2l 的方程：001(1)x y x y -=--. ② 由①②，解得20001,x x x y y -=-=，所以2001(,)x Q x y --. 因为点Q 在椭圆上，由对称性，得20001x y y -=±，即22001x y -=或22001x y +=.又P 在椭圆E 上，故2200143x y +=.由220022001143x y x y ⎧-=⎪⎨+=⎪⎩，解得00x y ==220022001143x y x y ⎧+=⎪⎨+=⎪⎩，无解. 因此点P的坐标为. 27．【解析】（Ⅰ）设F 的坐标为(,0)c -.依题意，12c a =，2pa =，12a c -=，解得1a =，12c =，2p =，于是22234b ac =-=. 所以，椭圆的方程为22413y x +=，抛物线的方程为24y x =. （Ⅱ）设直线AP 的方程为1(0)x my m =+≠，与直线l 的方程1x =-联立，可得点2(1,)P m --，故2(1,)Q m-.将1x my =+与22413y x +=联立，消去x ，整理得22(34)60m y my ++=，解得0y =，或2634my m -=+.由点B 异于点A ，可得点222346(,)3434m mB m m -+-++. 由2(1,)Q m-，可得直线BQ 的方程为22262342()(1)(1)()03434m m x y m m m m --+-+-+-=++，令0y =，解得222332m x m -=+，故2223(,0)32m D m -+.所以2222236||13232m m AD m m -=-=++. 又因为APD △的面积为2，故22162232||m m m ⨯⨯=+，整理得23|20m m -+=，解得||3m =，所以3m =±. 所以，直线AP的方程为330x +-=，或330x -=. 28．【解析】（I）由题意知c e a ==，22c =，所以1a b ==，因此椭圆E 的方程为2212x y +=．（Ⅱ）设()()1122,,,A x y B x y ，联立方程2211,2x y y k x ⎧+=⎪⎪⎨⎪=⎪⎩得()22114210k x x +--=，由题意知0∆>，且()12122111221x x x x k +=-+，所以121=-=AB x ．由题意可知圆M 的半径r为1233r AB ==由题设知12k k =，所以214k k =因此直线OC的方程为1y =．联立方程2211,2,x y y ⎧+=⎪⎪⎨⎪=⎪⎩得2221221181,1414k x y k k ==++，因此OC ==由题意可知1sin21SOT rOC r OCr∠==++，而1OC r=2 令2112t k =+，则()11,0,1t t>∈，因此1OC r==≥，当且仅当112t =，即2t =时等号成立，此时1k =，所以1sin 22SOT ∠≤，因此26SOT π∠≤，所以SOT ∠最大值为3π．综上所述：SOT ∠的最大值为3π，取得最大值时直线l的斜率为12k =±．29．【解析】（Ⅰ）由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧+===,,121,23222c b a ab ac 解得1,2==b a . 所以椭圆C 的方程为1422=+y x . （Ⅱ）由（Ⅰ）知，)1,0(),0,2(B A ，设),(00y x P ，则442020=+y x .当00≠x 时，直线PA 的方程为)2(200--=x x y y . 令0=x ，得2200--=x y y M .从而221100-+=-=x y y BM M . 直线PB 的方程为110+-=x x y y .令0=y ，得100--=y x x N .从而12200-+=-=y x x AN N . 所以221120000-+⋅-+=⋅x y y x BM AN 228844224844400000000000000002020+--+--=+--+--++=y x y x y x y x y x y x y x y x y x 4=.当00=x 时，10-=y ，,2,2==AN BM 所以4=⋅BM AN . 综上，BM AN ⋅为定值.30．【解析】(Ⅰ)设直线:l y kx b =+(0,0)k b ≠≠，11(,)A x y ，22(,)B x y ，(,)M M M x y ．将y kx b =+代入2229x y m +=得2222(9)20k x kbx b m +++-=，故12229M x x kb x k +==-+，299M M by kx b k =+=+．于是直线OM 的斜率9M OM M y k x k==-，即9OM k k ⋅=-．所以直线OM 的斜率与l 的斜率的乘积为定值．（Ⅱ）四边形OAPB 能为平行四边形．因为直线l 过点(,)3mm ，所以l 不过原点且与C 有两个交点的充要条件是0k >，3k ≠．由(Ⅰ)得OM 的方程为9y x k=-．设点P 的横坐标为P x ．由2229,9,y x k x y m ⎧=-⎪⎨⎪+=⎩得2222981P k m x k =+，即P x =．将点(,)3m m 的坐标代入直线l 的方程得(3)3m k b -=，因此2(3)3(9)M mk k x k -=+．四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分，即2P M x x =．=2(3)23(9)mk k k -⨯+．解得14k =24k =．因为0,3i i k k >≠，1i =，2，所以当l的斜率为44四边形OAPB 为平行四边形．31．【解析】（Ⅰ）由题意得2221,,2.b caa b c =⎧⎪⎪=⎨⎪⎪=+⎩解得2a =2．故椭圆C 的方程为2212x y +=．设M (N x ，0)．因为0m ≠，所以11n -<<．直线PA 的方程为11n y x m--=，所以M x =1m n -，即(,0)1mM n-．（Ⅱ）因为点B 与点A 关于x 轴对称，所以(,)B m n -，设(,0)N N x ，则N x =1mn+． “存在点(0,)Q Q y 使得OQM ∠=ONQ ∠等价”，“存在点(0,)Q Q y 使得OM OQ=OQ ON”即Q y 满足2Q M N y x x =．因为1M m x n =-，1N mx n=+，2212m n +=，所以22221Q MN m y x x n===-．所以Q y或Q y =故在y 轴上存在点Q ，使得OQM ∠=ONQ ∠．点Q的坐标为或(0,．32．【解析】（1）由题设条件知，点M 的坐标为21(,)33a b，又10OM k =，从而210b a =，进而得,2a c b ===，故5c e a ==．（2）由题设条件和（I）的计算结果可得，直线AB1yb+=，点N的坐标为1,)22b-，设点N关于直线AB的对称点S的坐标为17(,)2x，则线段NS的中点T的坐标为117,)4244xb+-+．又点T在直线AB上，且1NS ABk k⋅=-,从而有11744171xb bbb+-+=⎨+⎪=⎪⎪⎪⎩，解得3b=，所以b=故椭圆E的方程为221459x y+=．33．【解析】（Ⅰ）由题意知42=a，则2=a，又2ca=，222a c b-=，可得1=b，所以椭圆C的方程为1422=+yx．（Ⅱ）由（I）知椭圆E的方程为141622=+yx．（i）设λ=||||),,(0OPOQyxP，由题意知),(yxQλλ--，因为14220=+yx，又14)(16)(220=-+-yxλλ，即1)4(4220=+yxλ，所以2=λ，即2||||=OPOQ．（ii）设),(),,(2211yxByxA，将mkxy+=代入椭圆E的方程，可得01648)41(222=-+++mkmxxk，由0>∆，可得22164km+<，则有222122141164,418k m x x k km x x +-=+-=+，所以22221414164||k m k x x +-+=-．因为直线m kx y +=与y 轴交点的坐标为),0(m ，所以OAB ∆的面积||||2121x x m S -=22241||4162km m k +-+= 222241)416(2k m m k +-+=222241)414(2k m k m ++-= 令t k m =+2241，将m kx y +=代入椭圆C 的方程，可得 0448)41(222=-+++m kmx x k ，由0∆≥，可得 2241k m +≤，由①②可知 10≤<t ，因此t t t t S 42)4(22+-=-=，故 S ≤当且仅当1=t 时，即2241k m +=时取得最大值32，由（i ）知，ABQ ∆面积为S 3，所以ABQ ∆面积的最大值为36．34．【解析】2(c,0)=3F c c （I ）设，由条件知，222=2, 1.c a b a c a ==-=又所以 22 1.4x E y +=故的方程为（Ⅱ）1122:=2,(,),(,).l x l y kx P x y Q x y ⊥-当轴时不合题意，故设22214x y kx y =-+=将代入得22(14)16120.k x kx +-+=221,2238=16(43)0,441k k k x k ±∆->>=+当即时，12PQ x=-=从而O PQ d OPQ=∆又点到直线的距离所以的面积1=2OPQS d PQ∆⋅=244,0,.44OPQtt t St tt∆=>==++则44,20.t t kt+≥==±∆>因为当且仅当，即OPQι∆所以，当的面积最大时，的方程为22y x y x=-=-或．35．【解析】（Ⅰ）设直线l的方程为()0y kx m k=+<，由22221y kx mx ya b=+⎧⎪⎨+=⎪⎩，消去y得，()22222222220b a k x a kmx a m a b+++-=，由于直线l与椭圆C只有一个公共点P，故0∆=，即22220b m a k-+=，解得点P的坐标为22222222,a kmb mb a k b a k⎛⎫-⎪++⎝⎭，由点P在第一象限，故点P的坐标为22⎛⎫⎝；（Ⅱ）由于直线1l过原点O，且与l垂直，故直线1l的方程为0x ky+=，所以点P到直线1l的距离d=，整理得22d=，因为22222ba k abk+≥，2222a b ≤=-，当且仅当2bk a=时等号成立，所以点P 到直线1l 的距离的最大值为b a -.36．【解析】（Ⅰ）根据c =22(,),23b M c b ac a=将222b a c =-代入223b ac =，解得1,22c ca a==-（舍去）故C 的离心率为12．（Ⅱ）由题意，原点O 为12F F 的中点，2MF ∥y 轴，所以直线1MF 与y 轴的交点(0,2)D是线段1MF 的中点，故24b a=，即24b a = ① 由15MN F N =得112DF F N =。

十年高考理科数学真题专题九解析几何二十五直线与圆及答案

专题九解析几何第二十五讲直线与圆2019年1.（2019北京理3）已知直线l 的参数方程为x =1+3t y =2+4tìíî （t 为参数），则点（1，0）到直线l 的距离是（A ）15 （B ）25 （C ）45 （D ）652.（2019江苏10）在平面直角坐标系xOy 中，P 是曲线4(0)y x x x =+>上的一个动点，则点P 到直线x +y =0的距离的最小值是 .3（2019江苏18）如图，一个湖的边界是圆心为O 的圆，湖的一侧有一条直线型公路l ，湖上有桥AB （AB 是圆O 的直径）．规划在公路l 上选两个点P 、Q ，并修建两段直线型道路PB 、QA ．规划要求：线段PB 、QA 上的所有点到点O 的距离均不小于圆．．．．O 的半径．已知点A 、B 到直线l 的距离分别为AC 和BD （C 、D 为垂足），测得AB =10，AC =6，BD =12（单位：百米）．（1）若道路PB 与桥AB 垂直，求道路PB 的长；（2）在规划要求下，P 和Q 中能否有一个点选在D 处？并说明理由；（3）在规划要求下，若道路PB 和QA 的长度均为d （单位：百米）.求当d 最小时，P 、Q 两点间的距离．4．（2019浙江12）已知圆C 的圆心坐标是(0,)m ，半径长是r .若直线230x y -+=与圆C 相切于点(2,1)A --，则m =_____，r =______.2010-2018年2010-2018年一、选择题1．(2018全国卷Ⅲ)直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆22(2)2x y -+=上，则ABP ∆面积的取值范围是A ．[2,6]B ．[4,8] C． D．2．(2018天津)已知圆2220x y x +-=的圆心为C，直线1,232⎧=-+⎪⎪⎨⎪=-⎪⎩x y t (t 为参数)与该圆相交于A ，B 两点，则ABC △的面积为． 3．(2018北京)在平面直角坐标系中，记d 为点(cos ,sin )P θθ到直线20x my --=的距离，当θ，m 变化时，d 的最大值为A ．1B ．2C ．3D ．44．（2017新课标Ⅲ）已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A．3 B．3 C．3 D ．135．（2017新课标Ⅲ）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD相切的圆上．若AP AB AD λμ=+u u u r u u u r u u u r ，则λμ+的最大值为A ．3 B． CD ．26．（2015山东）一条光线从点(2,3)--射出，经y 轴反射后与圆22(3)(2)1x y ++-=相切，则反射光线所在直线的斜率为A ．53-或35- B ．32-或23- C ．54-或45- D ．43-或34-7．（2015广东）平行于直线210x y ++=且与圆225x y +=相切的直线的方程是A ．250x y ++=或250x y +-=B ．20x y +=或20x y +=C ．250x y -+=或250x y --=D ．20x y -+=或20x y -=8．（2015新课标2）过三点(1,3)A ，(4,2)B ，(1,7)C -的圆交于y 轴于M 、N 两点，则MN =A ．26B ．8C ．46D ．109．（2015重庆）已知直线l ：10()x ay a R +-=∈是圆C ：224210x y x y +--+=的对称轴，过点(4,)A a -作圆C 的一条切线，切点为B ，则AB ＝A ．2B ．C ．6D ．10．（2014新课标2）设点0(,1)M x ，若在圆22:=1O x y +上存在点N ，使得°45OMN ∠=，则0x 的取值范围是A ．[]1,1-B ．1122⎡⎤-⎢⎥⎣⎦，C ．⎡⎣D ．22⎡-⎢⎣⎦， 11．（2014福建）已知直线l 过圆()2234x y +-=的圆心，且与直线10x y ++=垂直，则l 的方程是A ．20x y +-=B ．20x y -+=C ．30x y +-=D ．30x y -+=12．（2014北京）已知圆()()22:341C x y -+-=和两点(),0A m -，()(),00B m m >，若圆C 上存在点P ，使得90APB ∠=o，则m 的最大值为A ．7B ．6C ．5D ．413．（2014湖南）若圆221:1C x y +=与圆222:680C x y x y m +--+=外切，则m = A ．21 B ．19 C ．9 D ．11-14．（2014安徽）过点P ）（1,3--的直线l 与圆122=+y x 有公共点，则直线l 的倾斜角的取值范围是A ．]60π，（B ．]30π，（C ．]60[π，D ．]30[π， 15．（2014浙江）已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4，则实数a 的值是A ．－2B ．－4C ．－6D ．－816．（2014四川）设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ，则||||PA PB +的取值范围是A ．B ．C ．D ．17．（2014江西）在平面直角坐标系中，,A B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线240x y +-=相切，则圆C 面积的最小值为A ．45πB ．34πC ．(6π-D ．54π18．（2013山东）过点(3，1)作圆()2211x y -+=的两条切线，切点分别为A ，B ，则直线AB 的方程为A ．230x y +-=B ．230x y --=C ．430x y --=D ．430x y +-=19．（2013重庆）已知圆()()221:231C x y -+-=，圆()()222:349C x y -+-=，,M N分别是圆12,C C 上的动点，P 为x 轴上的动点，则PM PN +的最小值为A ．4B 1C ．6- D20．（2013安徽）直线250x y +-+=被圆22240x y x y +--=截得的弦长为A ．1B ．2C ．4D ．21．（2013新课标2）已知点()1,0A -；()1,0B ；()0,1C ，直线y ax b =+(0)a >将△ABC 分割为面积相等的两部分，则b 的取值范围是A ．(0,1)B ．1122⎛⎫- ⎪ ⎪⎝⎭ C ．1123⎛⎤-⎥ ⎦⎝ D ．11,32⎡⎫⎪⎢⎣⎭22．（2013陕西）已知点(,)M a b 在圆221:O x y +=外, 则直线1ax by +=与圆O 的位置关系是A ．相切B ．相交C ．相离D ．不确定23．（2013天津）已知过点P (2，2) 的直线与圆225(1)x y +=-相切，且与直线10ax y -+=垂直，则a =A ．12-B ．1C ．2D ．1224．（2013广东）垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是A ．0x y +-=B ．10x y ++=C ．10x y +-=D ．0x y +=25．（2013新课标2）设抛物线2:4C y x =的焦点为F ，直线l 过F 且与C 交于A ，B 两点．若||3||AF BF =，则l 的方程为A ．1y x =-或1y x =-+B ．1)y x =-或1)y x =-C ．1)y x =-或1)y x =-D ．(1)2y x =-或(1)2y x =-- 26．（2012浙江）设a R ∈，则“1a =”是“直线1l ：210ax y +-=与直线2l ：(1)40x a y +++=平行”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件27．（2012天津）设m ，n R ∈，若直线(1)+(1)2=0m x n y ++-与圆22(1)+(y 1)=1x --相切，则+m n 的取值范围是A ．[1B ．(,1)-∞-∞UC ．[2-D ．(,2)-∞-∞U28．（2012湖北）过点(1,1)P 的直线，将圆形区域{}22(,)|4x y x y +…分为两部分，使得这两部分的面积之差最大，则该直线的方程为A ．20x y +-=B ．10y -=C ．0x y -=D ．340x y +-=29．（2012天津）在平面直角坐标系xOy 中，直线3450x y +-=与圆224x y +=相交于,A B 两点，则弦AB 的长等于A ．B ．CD ．130．（2011北京）已知点A (0,2)，B (2,0)．若点C 在函数y = x 的图像上，则使得ΔABC 的面积为2的点C 的个数为A ．4B ．3C ．2D ．1 31．（2011江西）若曲线1C ：2220x y x +-=与曲线2C ：()0y y mx m --=有四个不同的交点，则实数m 的取值范围是A ．(3-，3)B ．(3-，0)U (0，3)C ．[D ．(-∞，-U ，+∞) 32．（2010福建）以抛物线24y x =的焦点为圆心,且过坐标原点的圆的方程为A ．22++2=0x y xB ．22++=0x y xC ．22+y =0x x - D ．22+2=0x y x -33．（2010广东）若圆心在x O 位于y 轴左侧，且与直线20x y +=相切，则圆O 的方程是A ．22(5x y +=B ．22(5x y +=C ．22(5)5x y -+=D ．22(5)5x y ++= 二、填空题34．(2018江苏)在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，(5,0)B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=u u u r u u u r ，则点A 的横坐标为．35．（2017江苏）在平面直角坐标系xOy 中，(12,0)A -，(0,6)B ，点P 在圆O ：2250x y +=上，若20PA PB ⋅u u u r u u u r ≤，则点P 的横坐标的取值范围是．36．（2015湖北）如图，圆C 与x 轴相切于点(1,0)T ，与y 轴正半轴交于两点,A B （B 在A的上方），且2AB =．（Ⅰ）圆C 的标准．．方程为；（Ⅱ）过点A 任作一条直线与圆22:1O x y +=相交于,M N 两点，下列三个结论：①NAMANB MB =； ②2NBMANA MB -=； ③22NBMANA MB +=．其中正确结论的序号是 . （写出所有正确结论的序号）37．（2014江苏）在平面直角坐标系xOy 中，直线032=-+y x 被圆4)1()2(22=++-y x 截得的弦长为．38．（2014重庆）已知直线02=-+y ax 与圆心为C 的圆()()4122=-+-a y x 相交于B A ，两点，且ABC ∆为等边三角形，则实数=a _________．39．（2014湖北）直线1l ：y x a =+和2l ：y x b =+将单位圆22:1C x y +=分成长度相等的四段弧，则22a b +=________．40．（2014山东）圆心在直线20x y -=上的圆C 与y 轴的正半轴相切，圆C 截x 轴所得弦的长为3C 的标准方程为．41．（2014陕西）若圆C 的半径为1，其圆心与点)0,1(关于直线x y =对称，则圆C 的标准方程为____．42．（2014重庆）已知直线0=+-a y x 与圆心为C 的圆044222=--++y x y x 相交于B A ，两点，且BC AC ⊥，则实数a 的值为_________．43．（2014湖北）已知圆22:1O x y +=和点(2,0)A -，若定点(,0)B b (2)b ≠-和常数λ满足：对圆O 上任意一点M ，都有||||MB MA λ=，则（Ⅰ）b = ；（Ⅱ）λ= .44．（2013浙江）直线23y x =+被圆22680x y x y +--=所截得的弦长等于__________.45．（2013湖北）已知圆O ：225x y +=，直线l ：cos sin 1x y θθ+=(π02θ<<)．设圆O 上到直线l 的距离等于1的点的个数为k ，则k = .46．（2012北京）直线y x =被圆22(2)4x y +-=截得的弦长为 .47．（2011浙江）若直线250x y -+=与直线260x my +-=互相垂直，则实数m =__．48．(2011辽宁)已知圆C 经过A (5，1)，B (1，3)两点，圆心在x 轴上，则C 的方程为__．49．(2010新课标)圆心在原点上与直线20x y +-=相切的圆的方程为．50．(2010新课标)过点A (4,1)的圆C 与直线0x y -=相切于点(2,1)B ，则圆C 的方程为．三、解答题51．(2016年全国I)设圆222150x y x ++-=的圆心为A ，直线l 过点(1,0)B 且与x 轴不重合，l 交圆A 于C ，D 两点，过B 作AC 的平行线交AD 于点E .（I ）证明EA EB +为定值，并写出点E 的轨迹方程；（II ）设点E 的轨迹为曲线1C ，直线l 交1C 于M ，N 两点，过B 且与l 垂直的直线与圆A 交于P ，Q 两点，求四边形MPNQ 面积的取值范围．52．(2014江苏)如图，为了保护河上古桥OA ，规划建一座新桥BC ，同时设立一个圆形保护区．规划要求：新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上并与BC 相切的圆．且古桥两端O 和A 到该圆上任意一点的距离均不少于80m ．经测量，点A 位于点O 正北方向60m 处，点C 位于点O 正东方向170m 处(OC 为河岸)，34tan =∠BCO ．（I ）求新桥BC 的长；（II ）当OM 多长时，圆形保护区的面积最大？53．（2013江苏）如图，在平面直角坐标系xOy 中，点()03A ,，直线24l y x =-：.设圆C的半径为1，圆心在l 上. ylO A（I ）若圆心C 也在直线1y x =-上，过点A 作圆C 的切线，求切线的方程；（II ）若圆C 上存在点M ，使2MA MO =，求圆心C 的横坐标a 的取值范围．54．(2013新课标2)在平面直角坐标系xOy 中，已知圆P 在x 轴上截得线段长为22在y 轴上截得线段长为23（I ）求圆心P 的轨迹方程；（II ）若P 点到直线y x =2，求圆P 的方程． 55．（2011新课标）在平面直角坐标系xoy 中，曲线261y x x =-+与坐标轴的交点都在圆C 上．（I ）求圆C 的方程；（II ）若圆C 与直线0x y a -+=交于A ，B 两点，且,OA OB ⊥求a 的值．56．（2010北京）已知椭圆C 的左、右焦点坐标分别是(2,0)，(2,0)6直线y t =椭圆C 交与不同的两点M ，N ，以线段MN 为直径作圆P ,圆心为P ．（I ）求椭圆C 的方程；（II ）若圆P 与x 轴相切，求圆心P 的坐标；（Ⅲ）设(,)Q x y 是圆P 上的动点，当t 变化时，求y 的最大值．专题九解析几何第二十五讲直线与圆答案部分2019年1.解析由直线l 的参数方程消去t ，可得其普通方程为4320x y -+=．则点（1，0）到直线l 的距离是d ==2. 解析解法一：由4(0)y x x x =+>，得241y x'=-，设斜率为1-的直线与曲线4(0)y x x x =+>切于0004(,)x x x +，由20411x-=-，解得000)x x =>．所以曲线4(0)y x x x=+>上，点P 到直线0x y +=的距离最小，4=．解法二：由题意可设点P 的坐标为4,x x x ⎛⎫+⎪⎝⎭()0x >，则点P 到直线0x y +=的距离222242x d ⎛⎫+ ⎪==⨯⨯=…，当且仅当x = 所以点P 到直线0x y +=的距离的最小值为4.3.解析解法一：（1）过A作AE BD ⊥，垂足为E .由已知条件得，四边形ACDE 为矩形，6, 8DE BE AC AE CD =====.' 因为PB ⊥AB ，所以84cos sin 105PBD ABE ∠=∠==. 所以12154cos 5BD PB PBD ===∠.因此道路PB 的长为15（百米）.（2）①若P 在D 处，由（1）可得E 在圆上，则线段BE 上的点（除B ，E ）到点O 的距离均小于圆O 的半径，所以P 选在D 处不满足规划要求. ②若Q 在D 处，联结AD ，由（1）知2210AD AE ED =+=，从而2227cos 0225AD AB BD BAD AD AB +-∠==>⋅，所以∠BAD 为锐角. 所以线段AD 上存在点到点O 的距离小于圆O 的半径. 因此，Q 选在D 处也不满足规划要求. 综上，P 和Q 均不能选在D 处. （3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设1P 为l 上一点，且1PB AB ⊥，由（1）知，1P B =15，此时11113sin cos 1595PD PB PBD PB EBA =∠=∠=⨯=；当∠OBP >90°时，在1PPB △中，115PB PB >=. 由上可知，d ≥15.再讨论点Q 的位置.由（2）知，要使得QA ≥15，点Q 只有位于点C 的右侧，才能符合规划要求.当QA =15时，2222156321CQ QA AC =-=-=.此时，线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上，当PB ⊥AB ，点Q 位于点C 右侧，且CQ =321时，d 最小，此时P ，Q 两点间的距离PQ =PD +CD +CQ =17+321.因此，d 最小时，P ，Q 两点间的距离为17+321（百米）. 解法二：（1）如图，过O 作OH ⊥l ，垂足为H. 以O 为坐标原点，直线OH 为y 轴，建立平面直角坐标系.因为BD =12，AC =6，所以OH =9，直线l 的方程为y =9，点A ，B 的纵坐标分别为3，−3. 因为AB 为圆O 的直径，AB =10，所以圆O 的方程为x 2+y 2=25. 从而A （4，3），B （−4，−3），直线AB 的斜率为34. 因为PB ⊥AB ，所以直线PB 的斜率为43-，直线PB 的方程为42533y x =--. 所以P （−13，9），22(134)(93)15PB =-+++=. 因此道路PB 的长为15（百米）.（2）①若P 在D 处，取线段BD 上一点E （−4，0），则EO =4<5，所以P 选在D 处不满足规划要求.②若Q 在D 处，联结AD ，由（1）知D （−4，9），又A （4，3），所以线段AD ：36(44)4y x x =-+-剟.在线段AD 上取点M （3，154），因为22221533454OM ⎛⎫=+<+= ⎪⎝⎭，所以线段AD 上存在点到点O 的距离小于圆O 的半径. 因此Q 选在D 处也不满足规划要求. 综上，P 和Q 均不能选在D 处. （3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设1P 为l 上一点，且1PB AB ⊥，由（1）知，1P B =15，此时1P （−13，9）；当∠OBP >90°时，在1PPB △中，115PB PB >=. 由上可知，d ≥15. 再讨论点Q 的位置.由（2）知，要使得QA≥15，点Q 只有位于点C 的右侧，才能符合规划要求.当QA =15时，设Q （a ，9），由22(4)(93)15(4)AQ a a =-+-=>，得a =4321+，所以Q （4321+，9），此时，线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上，当P （−13，9），Q （4321+，9）时，d 最小，此时P ，Q 两点间的距离4321(13)17321PQ =+--=+.因此，d 最小时，P ，Q 两点间的距离为17321+（百米）. 4.解析：解法一：如图，由圆心与切点的连线与切线垂直，得1122m +=-，解得2m =-．所以圆心为（0，-2），则半径r ==．解法二：由r ==，得2m =-，所以r ==2010-2018年1．A 【解析】圆心(2,0)到直线的距离d == 所以点P到直线的距离1d ∈．根据直线的方程可知A ，B 两点的坐标分别为(2,0)A -，(0,2)B -，所以||AB = 所以ABP ∆的面积111||2S AB d ==．因为1d ∈，所以[2,6]S ∈，即ABP ∆面积的取值范围是[2,6]．故选A ． 2．12【解析】直线的普通方程为20x y +-=，圆的标准方程为22(1)1x y -+=，圆心为(1,0)C ，半径为1，点C 到直线20x y +-=的距离2d ==以||AB ==1122ABC S ∆==． 3．C【解析】由题意可得d ====（其中cos ϕ=，sin ϕ=，∵1sin()1θϕ--≤≤,d ≤1=+∴当0m =时，d 取得最大值3，故选C ．4．A 【解析】以线段12A A 为直径的圆是222x y a +=，直线20bx ay ab -+=与圆相切，所以圆心到直线的距离d a ==，整理为223a b =，即()22222323a a c a c =-⇒=，即2223c a =，3c e a ==，故选A ．5．A 【解析】如图建立直角坐标系，x则(0,1)A ，(0,0)B ，(2,1)D ，(,)P x y 所以圆的方程为224(2)5x y -+=，所以(,1)AP x y =-u u u r ，(0,1)AB =-u u u r ，(2,0)AD =u u u r，由AP AB AD λμ=+u u u r u u u r u u u r ，得21x y μλ=⎧⎨-=-⎩，所以λμ+=12x y -+，设12x z y =-+，即102xy z -+-=，点(,)P x y 在圆上，所以圆心到直线102xy z -+-=的距离小于半径，≤，解得13z ≤≤，所以z 的最大值为3，即λμ+的最大值为3，选A ．6．D 【解析】(2,3)--关于y 轴对称点的坐标为(2,3)-，设反射光线所在直线为3(2)y k x +=-，即230kx y k ---=，则1d ==，|55|k +=43k =-或34-．7．A 【解析】设所求直线的方程为20x y c ++=(1)≠c，则=，所以c =250x y ++=或250x y +-=．8．C 【解析】设过,,A B C 三点的圆的方程为220x y Dx Ey F ++++=，则3100422007500D E F D E F D E F +++=⎧⎪+++=⎨⎪-++=⎩，解得2,4,20D E F =-==-，所求圆的方程为2224200x y x y +-+-=，令0x =，得24200y y +-=，设1(0,)M y ，2(0,)N y ，则124y y +=-，1220y y ⋅=-，所以12||||MN y y =-==9．C 【解析】圆C 标准方程为22(2)(1)4x y -+-=，圆心为(2,1)C ，半径为2r =，因此2110a +⨯-=，1a =-，即(4,1)A --，6AB ===．选C ．10．A 【解析】当点M 的坐标为(1,1)时，圆上存在点(1,0)N ，使得45OMN ∠=o，所以01x =符合题意，排除B 、D ；当点M的坐标为时，OM =M 作圆O 的一条切线MN '，连接ON '，则在Rt OMN '∆中，sin 2OMN '∠=<，则45OMN '∠<o ，故此时在圆O 上不存在点N ，使得°45OMN ∠=，即0x =合题意，排除C ，故选A ．11．D 【解析】直线l 过点(0,3)，斜率为1，所以直线l 的方程为30x y -+=． 12．B 【解析】因为圆C 的圆心为(3,4)，半径为1，||5OC =，所以以原点为圆心、以m为半径与圆C 有公共点的最大圆的半径为6，所以m 的最大值为6，故选B ．13．C 【解析】由题意得12(0,0),(3,4)C C ，121,r r ==1212||15C C r r =+==，所以9m =．14．D 【解析】设直线l 的倾斜角为θ，由题意可知min max 0,263ππθθ==⨯=．15．B 【解析】圆的标准方程为22(1)(1)2x y a ++-=-，则圆心(1,1)C -，半径r 满足22r a =-，则圆心C 到直线20x y ++=的距离d == 所以2422r a =+=-，故4a =-16．B 【解析】易知直线0x my +=过定点(0,0)A ，直线30mx y m --+=过定点(1,3)B ，且两条直线相互垂直，故点P 在以AB 为直径的圆上运动，故||||||cos ||sin PA PB AB PAB AB PAB +=∠+∠)4PAB π=∠+∈．故选B ．17．A 【解析】由题意可知以线段AB 为直径的圆C 过原点O ，要使圆C 的面积最小，只需圆C 的半径或直径最小．又圆C 与直线240x y +-=相切，所以由平面几何知识，知圆的直径的最小值为点O 到直线240x y +-=的距离，此时2r =，得r =，圆C 的面积的最小值为245S r ππ==． 18．A 【解析】根据平面几何知识，直线AB 一定与点(3，1)，(1，0)的连线垂直，这两点连线的斜率为12，故直线AB 的斜率一定是2-，只有选项A 中直线的斜率为2-． 19．A 【解析】圆C 1，C 2的圆心分别为C 1，C 2，由题意知|PM |≥|PC 1|－1，|PN |≥|PC 2|－3，∴|PM |＋|PN |≥|PC 1|＋|PC 2|－4，故所求值为|PC 1|＋|PC 2|－4的最小值．又C 1关于x 轴对称的点为C 3(2，－3)，所以|PC 1|＋|PC 2|－4的最小值为|C 3C 2|－444=，故选A ．20．C 【解析】圆心(1,2)，圆心到直线的距离=1d =，半径r =，所以最后弦长为4=.21．B 【解析】（1）当y ax b =+过()1,0A -与BC 的中点D 时，符合要求，此13b =，（2）当y ax b =+位于②位置时1,0b A a ⎛⎫-⎪⎝⎭,11,11b a b D a a -+⎛⎫⎪++⎝⎭，令1112A BD S ∆=得212b a b =-,∵0a >,∴12b < (3) 当y ax b =+位于③位置时21,11b b a A a a --⎛⎫⎪--⎝⎭,21,11b a b D a a -+⎛⎫⎪++⎝⎭，令2212A CD S ∆=,即()111112112b b b a a --⎛⎫--= ⎪+-⎝⎭，化简得22241a b b -=-+,∵0a >, ∴22410b b -+<，解得1122b -<<+综上：112b -<<，选B 22．B 【解析】点M(a, b )在圆221x y +=外，∴221a b +>．圆(0,0)O 到直线1ax by +=距离1d =<=圆的半径，故直线与圆相交．所以选B ．23．C【解析】设直线斜率为k ，则直线方程为2(2)y k x -=-，即220kx y k -+-=，圆心(1,0)==12k =-．因为直线与直线10ax y -+=垂直，所以112k a =-=-，即2a =，选C ． 24．A 【解析】∵圆心到直线的距离等于1r =，排除B 、C ；相切于第一象限排除D ，选A.直接法可设所求的直线方程为：()0y x k k =-+>，再利用圆心到直线的距离等于1r =，求得k =25．C 【解析】抛物线24y x =的焦点坐标为(1,0)，准线方程为1x =-，设11(,)A x y ，22(,)B x y ，则因为|AF |=3|BF |，所以1213(1)x x +=+，所以1232x x =+，因为1||y =32||y ，1x =92x ，所以1x =3，2x =13，当1x =3时，2112y =，所以此时1y ==±1y =1(3,(,3A B ,此时AB k =此时直线方程为1)y x =-。

十年高考理科数学真题专题九解析几何二十九曲线与方程及答案【推荐】

专题九解析几何第二十九讲曲线与方程2019年1.（2019北京理8）数学中有许多形状优美、寓意美好的曲线，曲线C :x 2+y 2=1+x y 就是其中之一（如图）。

给出下列三个结论：① 曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）； ② 曲线C 上任意一点到原点的距离都不超过2; ③ 曲线C 所围城的“心形”区域的面积小于3. 其中，所有正确结论的序号是（A ）① （B ）② （C ）①② （D ）①②③2．（2019浙江15）已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______.3．（2019江苏17）如图，在平面直角坐标系xOy 中，椭圆C :22221(0)x y a b a b+=>>的焦点为F 1（–1、0），F 2（1，0）．过F 2作x 轴的垂线l ，在x 轴的上方，l 与圆F 2:222(1)4x y a -+=交于点A ，与椭圆C 交于点D .连结AF 1并延长交圆F 2于点B ，连结BF 2交椭圆C 于点E ，连结DF 1．已知DF 1=52．（1）求椭圆C 的标准方程；（2）求点E 的坐标．4.（2019全国III 理21（1））已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C的两条切线，切点分别为A ，B . （1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.5.（2019北京理18）已知抛物线2:2C x py =-经过点(2，-1). (I) 求抛物线C 的方程及其准线方程； (II)设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线y =-1分别交直线OM ，ON 于点A 和点B ，求证：以AB 为直径的圆经过y 轴上的两上定点.6.（2019全国II 理21）已知点A (−2,0)，B (2,0)，动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .（1）求C 的方程，并说明C 是什么曲线；（2）过坐标原点的直线交C 于P ，Q 两点，点P 在第一象限，PE ⊥x 轴，垂足为E ，连结QE 并延长交C 于点G .（i ）证明：PQG △是直角三角形；（ii ）求PQG △面积的最大值.7. （2019浙江21）如图，已知点(10)F ，为抛物线22(0)y px p =>的焦点，过点F 的直线交抛物线于A 、B 两点，点C 在抛物线上，使得ABC △的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S .（1）求p 的值及抛物线的准线方程；（2）求12S S 的最小值及此时点G 的坐标. 8.（2019天津理18）设椭圆22221(0)x y a b a b+=>>的左焦点为F ，上顶点为B .已知椭圆的短轴长为4，离心率为5. （Ⅰ）求椭圆的方程；（Ⅱ）设点P 在椭圆上，且异于椭圆的上、下顶点，点M 为直线PB 与x 轴的交点，点N在y 轴的负半轴上.若||||ON OF =（O 为原点），且OP MN ⊥，求直线PB 的斜率.2010-2018年解答题1．（2018江苏）如图，在平面直角坐标系xOy 中，椭圆C 过点1)2，焦点12(F F ，圆O 的直径为12F F ．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △，求直线l 的方程． 2．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足NP =u u u r u u u r．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=u u u r u u u r．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．3．(2016年山东)平面直角坐标系xOy 中，椭圆C ：()222210x y a b a b+=＞＞的离心率是2，抛物线E ：22x y =的焦点F 是C 的一个顶点. （Ⅰ）求椭圆C 的方程；（Ⅱ）设P 是E 上的动点，且位于第一象限，E 在点P 处的切线l 与C 交与不同的两点A ，B ，线段AB 的中点为D ，直线OD 与过P 且垂直于x 轴的直线交于点M ．（i ）求证：点M 在定直线上；（ii ）直线l 与y 轴交于点G ，记PFG △的面积为1S ，PDM △的面积为2S ，求12S S的最大值及取得最大值时点P 的坐标．4．(2016年天津)设椭圆13222=+y ax (a >的右焦点为F ，右顶点为A ，已知||3||1||1FA eOA OF =+，其中O 为原点，e 为椭圆的离心率．（Ⅰ）求椭圆的方程；（Ⅱ）设过点A 的直线l 与椭圆交于点B （B 不在x 轴上），垂直于l 的直线与l 交于点M ，与y 轴交于点H ，若HF BF ⊥，且MOA MAO ∠∠≤，求直线l 的斜率的取值范围．5．(2016年全国II)已知椭圆:E 2213x y t +=的焦点在x 轴上，A 是E 的左顶点，斜率为(0)k k >的直线交E 于,A M 两点，点N 在E 上，MA NA ⊥．（Ⅰ）当4,||||t AM AN ==时，求AMN ∆的面积；（Ⅱ）当2AM AN =时，求k 的取值范围．6．（2015湖北）一种作图工具如图1所示．O 是滑槽AB 的中点，短杆ON 可绕O 转动，长杆MN 通过N 处铰链与ON 连接，MN 上的栓子D 可沿滑槽AB 滑动，且1DN ON ==，3MN =．当栓子D 在滑槽AB 内作往复运动时，带动．．N 绕O 转动一周（D 不动时，N也不动），M 处的笔尖画出的曲线记为C ．以O 为原点，AB 所在的直线为x 轴建立如图2所示的平面直角坐标系．（Ⅰ）求曲线C 的方程；（Ⅱ）设动直线l 与两定直线1:20l x y -=和2:20l x y +=分别交于,P Q 两点．若直线l总与曲线C 有且只有一个公共点，试探究：△OPQ 的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．7．（2015江苏）如图，在平面直角坐标系xoy 中，已知椭圆()222210x y a b a b+=>>的离心率为22，且右焦点F 到左准线l 的距离为3．（1）求椭圆的标准方程；（2）过F 的直线与椭圆交于,A B 两点，线段AB 的垂直平分线分别交直线l 和AB 于点,P C ，若2PC AB =，求直线AB 的方程．8．（2015四川）如图，椭圆E ：2222+1(0)x y a b a b=>>的离心率是22，过点(0,1)P 的动直线l 与椭圆相交于,A B 两点，当直线l 平行与x 轴时，直线l 被椭圆E 截得的线段长为22（1）求椭圆E 的方程；（2）在平面直角坐标系xOy 中，是否存在与点P 不同的定点Q ，使得QA PAQB PB=恒成立？若存在，求出点Q 的坐标；若不存在，请说明理由．9．（2015北京）已知椭圆C ：()222210x y a b a b+=>>的离心率为22，点()01P ，和点 ()A m n ，()0m ≠都在椭圆C 上，直线PA 交x 轴于点M ．（Ⅰ）求椭圆C 的方程，并求点M 的坐标（用m ，n 表示）；（Ⅱ）设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N ．问：y 轴上是否存在点Q ，使得OQM ONQ ∠=∠？若存在，求点Q 的坐标；若不存在，说明理由．10．（2015浙江）已知椭圆2212x y +=上两个不同的点,A B 关于直线12y mx =+对称．（Ⅰ）求实数m 的取值范围；（Ⅱ）求AOB ∆面积的最大值（O 为坐标原点）．11．（2014广东）已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点为5,0)，5（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若动点00(,)P x y 为椭圆外一点，且点P 到椭圆C 的两条切线相互垂直，求点P的轨迹方程．12．（2014辽宁）圆224x y +=的切线与x 轴正半轴，y 轴正半轴围成一个三角形，当该三角形面积最小时，切点为P （如图），双曲线22122:1x y C a b-=过点P 3．（1）求1C 的方程；（2）椭圆2C 过点P 且与1C 有相同的焦点，直线l 过2C 的右焦点且与2C 交于A ，B 两点，若以线段AB 为直径的圆心过点P ，求l 的方程．13．（2013四川）已知椭圆C ：)0(12222>>=+b a by a x 的两个焦点分别为1(10)F -，，210F （，），且椭圆C 经过点），3134(P ．（Ⅰ）求椭圆C 的离心率（Ⅱ）设过点），（20A 的直线l 与椭圆C 交于M ，N 两点，点Q 是MN 上的点，且 222112ANAMAQ+=，求点Q 的轨迹方程．14．（2012湖南）在直角坐标系xoy 中，曲线1C 的点均在2C ：22(5)9x y -+=外，且对1C 上任意一点M ，M 到直线2x =-的距离等于该点与圆2C 上点的距离的最小值. （Ⅰ）求曲线1C 的方程；（Ⅱ）设00(,)P x y （3y ≠±）为圆2C 外一点，过P 作圆2C 的两条切线，分别与曲线1C 相交于点A ，B 和C ，D.证明：当P 在直线4x =-上运动时，四点A ，B ，C ，D 的纵坐标之积为定值．15．（2011天津）在平面直角坐标系xOy 中，点(,)P a b (0)a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．已知△12F PF 为等腰三角形．（Ⅰ）求椭圆的离心率e ；（Ⅱ）设直线2PF 与椭圆相交于,A B 两点，M 是直线2PF 上的点，满足2AM BM ⋅=-u u u u r u u u u r ，求点M 的轨迹方程．16．（2009广东）已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ，且A B x x <．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（1）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（2）若曲线22251:24025G x ax y y a -+-++=与D 有公共点，试求a 的最小值．专题九解析几何第二十九讲曲线与方程答案部分1. 由221x y x y +=+可得221y x y x -=-.配方得2230241x x y ⎛⎫-≥ ⎪ ⎪⎝⎭-=，解得234x ≤.所以x 可取的整数值为-1，0，1，则曲线经过()()()()()()1,0,1,1,0,1,0,1,1,0,1,1,----这6个整点，结论①正确；当x ＞0时，由221x y xy +=+得222212x y x y xy ++-=≤（当x=y 时取等号），所以222x y +≤，所以222x y +≤，即曲线C 上y 轴右边的点到原点的距离不超过2，结论②正确；根据对称性可得：曲线C 上任意一点到原点的距离都不超过2；故②正确．如图所示，()()()()0,1,1,0,1,1,0,1A B C D -13111122ABCD S =⨯⨯+⨯=，根据对称性可知23ABCD S S >=心形. 即心形区域的面积大于3，故③错误．正确结论为①②. 故选C ．2．解析设椭圆的右焦点为F '，连接PF '，线段PF 的中点A 在以原点O 为圆心，2为半径的圆，连接AO ，可得24PF AO '==，设P 的坐标为（m,n ），可得2343m -=，可得32m =-，15n =，由(2,0)F -，可得直线PF 的斜率为15215322=-+．3.解析（1）设椭圆C 的焦距为2c .因为F 1(-1，0)，F 2(1，0)，所以F 1F 2=2，c =1. 又因为DF 1=52，AF 2⊥x 轴，所以DF 2222211253()222DF F F -=-=，因此2a =DF 1+DF 2=4，从而a =2. 由b 2=a 2-c 2，得b 2=3.因此，椭圆C 的标准方程为22143x y +=.（2）解法一：由（1）知，椭圆C ：22143x y +=，a =2，因为AF 2⊥x 轴，所以点A 的横坐标为1.将x =1代入圆F 2的方程(x -1) 2+y 2=16，解得y =±4. 因为点A 在x 轴上方，所以A (1，4). 又F 1(-1，0)，所以直线AF 1：y =2x +2.由22()22116y x x y =+-+=⎧⎨⎩，得256110x x +-=，解得1x =或115x =-. 将115x =-代入22y x =+，得 125y =-，因此1112(,)55B --.又F 2(1，0)，所以直线BF 2：3(1)4y x =-.由221433(1)4x y x y ⎧⎪⎪⎨⎪+=-⎩=⎪，得276130x x --=，解得1x =-或137x =. 又因为E 是线段BF 2与椭圆的交点，所以1x =-. 将1x =-代入3(1)4y x =-，得32y =-.因此3(1,)2E --. 解法二：由（1）知，椭圆C ：22143x y +=.如图所示，联结EF 1.因为BF 2=2a ，EF 1+EF 2=2a ，所以EF 1=EB ，从而∠BF 1E =∠B .因为F 2A =F 2B ，所以∠A =∠B ，所以∠A =∠BF 1E ，从而EF 1∥F 2A . 因为AF 2⊥x 轴，所以EF 1⊥x 轴.因为F 1(-1，0)，由221431x x y ⎧⎪⎨+==-⎪⎩，得32y =±.又因为E 是线段BF 2与椭圆的交点，所以32y =-. 因此3(1,)2E --. 4. 解析（1）设()111,,,2D t A x y ⎛⎫-⎪⎝⎭，则2112x y =.由于y'x =，所以切线DA 的斜率为1x ，故11112y x x t+=- ，整理得112 2 +1=0. tx y -设()22,B x y ，同理可得222 2 +1=0tx y -.故直线AB 的方程为2210tx y -+=. 所以直线AB 过定点1(0,)2.5.解析（I ）由抛物线2:2C x py =-经过点()2,1-，得2p =.所以抛物线C 的方程为24x y =-，其准线方程为1y =. （II ）抛物线C 的焦点为()0,1-，设直线l 的方程为()10y kx k =-≠.由241x y y kx ⎧=-⎨=-⎩，得2440x kx +-=. 设()()1122,,,,Mx y N x y 则124x x=-.直线OM 的方程为11y y x x =，令1y =-，得点A 的横坐标为11A x x y =- 同理可得点B 的横坐标22B x x y =-.设点()0,Dn ，则()()2212122212121144x x x x DA DB n n y yx x ⋅=++=++⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭uu u r uu u r()()221216141n n x x =++=-++. 令0,DA DB ⋅=uu u r uu u r 即()2410n -++=，得1n =或3n =-.综上，以AB 为直径的圆经过y 轴上的定点()()0,10,-3和．6．解析（1）由题设得1222y y x x ⋅=-+-，化简得221(||2)42x y x +=≠，所以C 为中心在坐标原点，焦点在x 轴上的椭圆，不含左右顶点．（2）（i ）设直线PQ 的斜率为k ，则其方程为(0)y kx k =>．由22142y kxx y =⎧⎪⎨+=⎪⎩得x =．记u =，则(,),(,),(,0)P u uk Q u uk E u --．于是直线QG 的斜率为2k ，方程为()2ky x u =-．由22(),2142k y x u x y ⎧=-⎪⎪⎨⎪+=⎪⎩得 22222(2)280k x uk x k u +-+-=．①设(,)G G G x y ，则u -和G x 是方程①的解，故22(32)2G u k x k +=+，由此得322G uk y k =+．从而直线PG 的斜率为322212(32)2uk uk k u k kuk -+=-+-+．所以PQ PG ⊥，即PQG △是直角三角形．（ii ）由（i）得||2PQ =||PG =，所以△PQG 的面积222218()18(1)||12(12)(2)12()k k k k S PQ PG k k k k++===++++‖．设t =k +1k ，则由k >0得t ≥2，当且仅当k =1时取等号．因为2812t S t =+在[2，+∞）单调递减，所以当t =2，即k =1时，S 取得最大值，最大值为169．因此，△PQG 面积的最大值为169．7．解析（I ）由题意得12p=，即p =2.所以，抛物线的准线方程为x =−1.（Ⅱ）设()()(),,,,,A A B B c c A x y B x y C x y ，重心(),G G G x y .令2,0A y t t =≠，则2A x t =.由于直线AB 过F ，故直线AB 方程为2112t x y t-=+，代入24y x =，得 ()222140t y y t---=，故24B ty =-，即2B y t =-，所以212,B tt ⎛⎫- ⎪⎝⎭.又由于()()11,33G A B c G A B c x x x x y y y y =++=++及重心G 在x 轴上，故220c t y t-+=，得242211222,2,,03t t C t t G t t t ⎛⎫⎛⎫-+⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 所以，直线AC 方程为()222y t t x t-=-，得()21,0Q t-.由于Q 在焦点F 的右侧，故22t >.从而4224221244242222211|2|||322221222211|||1||2|23A c t t t FG y t S t t t t t S t t QG y t t t t-+-⋅⋅--====--+--⋅--⋅-. 令22m t =-，则m >0，1221222134324S m S m m m m =-=-=+++++….当m =12S S取得最小值1+G （2，0）.8.解析（Ⅰ）设椭圆的半焦距为c ，依题意，24,c b a ==，又222a b c =+，可得a =2,b =1c =.所以，椭圆的方程为22154x y +=. （Ⅱ）由题意，设()()()0,,0P P p M P x y x M x ≠，.设直线PB 的斜率为()0k k ≠，又()0,2B ，则直线PB 的方程为2y kx =+，与椭圆方程联立222154y kx x y =+⎧⎪⎨+=⎪⎩，整理得()2245200k x kx ++=，可得22045P kx k =-+，代入2y kx =+得2281045P k y k -=+，进而直线OP 的斜率24510P p y k x k-=-.在2y kx =+中，令0y =，得2M x k =-.由题意得()0,1N -，所以直线MN 的斜率为2k -.由OP MN ⊥，得2451102k k k-⎛⎫⋅-=- ⎪-⎝⎭，化简得2245k =，从而k =所以，直线PB或. 2010-2018年1．【解析】(1)因为椭圆C的焦点为12(),F F -，可设椭圆C 的方程为22221(0)x y a b a b +=>>．又点1)2在椭圆C 上，所以2222311,43,a ba b ⎧+=⎪⎨⎪-=⎩，解得224,1,a b ⎧=⎪⎨=⎪⎩ 因此，椭圆C 的方程为2214x y +=．因为圆O 的直径为12F F ，所以其方程为223x y +=．(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>，则22003x y +=，所以直线l 的方程为0000()x y x x y y =--+，即0003x y x y y =-+．由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩消去y ，得222200004243640()x y x x x y +-+-=．（*）因为直线l 与椭圆C 有且只有一个公共点，所以222222000000()()(24)44364(48)20x x y y y x =--+-=-=∆．因为00,0x y >，所以001x y ==．因此，点P的坐标为． ②因为三角形OAB，所以1 2AB OP ⋅=7AB =．设1122,,()(),A x y B x y ，由（*）得001,2x =，所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+．因为22003x y +=，所以22022016(2)32(1)49x AB x -==+，即42002451000x x -+=，解得22005(202x x ==舍去），则2012y =，因此P的坐标为．综上，直线l的方程为y =+2．【解析】（1）设(,)P x y ，00(,)M x y ，则0(,0)N x ，0(,)NP x x y =-u u u r ，0(0.)NM y =u u u u r．由NP =u u u r u u u r得 0x x =，02y y =．因为00(,)M x y 在C 上，所以22122x y +=．因此点P 的轨迹方程为222x y +=．（2）由题意知(1,0)F -．设(3,)Q t -，(,)P m n ，则(3,)OQ t =-u u u r ，(1,)PF m n =---u u u r ，33OQ PF m tn ⋅=+-u u u r u u u r， (,)OP m n =u u u r ，(3,)PQ m t n =---u u u r，由1OP PQ ⋅=u u u r u u u r 得2231m m tn n --+-=，又由（1）知222m n +=，故330m tn +-=．所以0OQ PF ⋅=u u u r u u u r ，即OQ PF ⊥u u u r u u u r．又过点P 存在唯一直线垂直与OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F ． 3．【解析】(Ⅰ) 由离心率是23，有224=b a ，又抛物线y x 2=2的焦点坐标为)21,0(F ，所以21=b ，于是1=a ，所以椭圆C 的方程为1=4+22y x ．(Ⅱ) （i ）设P 点坐标为2,),(0)2m Pm m >（，由y x 2=2得x y =′，所以E 在点P 处的切线l 的斜率为m ，因此切线l 的方程为2=2m mx －y ，设),(),,(2211y x B y x A ，),(00y x D ，将2=2m mx －y 代入1=4+22y x ，得0=1+4)4+12322－m x m －x m （．于是23214+14=+m m x x ，232104+12=2+=m m x x x ，又2200222(14)m m y mx m -=-=+，于是直线OD 的方程为x m－y 41=．联立方程x m －y 41=与m x =，得M 的坐标为1(,)4M m -．所以点M 在定直线41=y －上．（ii ）在切线l 的方程为2=2m mx －y 中，令0x =，得22m y =－，即点G 的坐标为2(0,)2m G -，又2(,)2m P m ，1(0,)2F ，所以4)1+(=×21=S 21m m GF m ；再由32222(,)412(41)m m D m m -++，得 )1+4(8)1+2(=1+4+2×41+2×21=S 2222322m m m m m m m于是有 222221)1+2()1+)(1+4(2=S S m m m ．令1+2=2m t ，得222111+2=)1+)(21(2=S S t －t t t t －当21=1t时，即2=t 时，21S S 取得最大值49．此时21=2m ，22=m ，所以P 点的坐标为)41,22P(．所以21S S 的最大值为49，取得最大值时点P的坐标为1()24P ． 4．【解析】（Ⅰ）设(,0)F c ，由113||||||c OF OA FA +=，即113()cc a a a c +=-，可得2223a c c -=，又2223a c b -==，所以21c =，因此24a =，所以椭圆的方程为22143x y +=．（Ⅱ）解：设直线l 的斜率为k （0≠k ），则直线l 的方程为)2(-=x k y .设),(B B y x B ，由方程组⎪⎩⎪⎨⎧-==+)2(13422x k y y x ，消去y ，整理得0121616)34(2222=-+-+k x k x k ．解得2=x ，或346822+-=k k x ，由题意得346822+-=k k x B ，从而34122+-=k k y B．由（Ⅰ）知，)0,1(F ，设),0(H y H ，有),1(H y FH -=，)3412,3449(222++-=k kk k BF . 由HF BF ⊥，得0=⋅HF BF ，所以034123449222=+++-k ky k k H，解得k k y H 12492-=.因此直线MH 的方程为kk x k y 124912-+-=．设),(M M y x M ，由方程组⎪⎩⎪⎨⎧-=-+-=)2(124912x k y k k x k y 消去y ，解得)1(1292022++=k k x M . 在MAO ∆中，||||MO MA MAO MOA ≤⇔∠≤∠，即2222)2(M M M M y x y x +≤+-，化简得1≥M x ，即1)1(1292022≥++k k ，解得46-≤k 或46≥k ．所以，直线l 的斜率的取值范围为),46[]46,(+∞--∞Y ． 5．【解析】（I ）设11(,)M x y ，则由题意知10y >．当4t =时，椭圆E 的方程为22143x y +=，A 点坐标为()20-，，由已知及椭圆的对称性知，直线AM 的倾斜角为4π．因此直线AM 的方程为2y x =+．将2x y =-代入22143x y +=得27120y y -=．解得0y =或127y =，所以1127y =．所以AMN △的面积为21112121442227749AMN S AM ∆==⨯⨯⨯=．（Ⅱ）由题意知3,0,(t k A >>，则直线AM的方程为(y k x =，联立()2213x y t y k x t ⎧+=⎪⎨⎪=+⎩并整理得，()222223230tk x t tk x t k t +++-=解得x t =-或23t tk tx -=-，所以2223611t tk t t AM k t k -=+-+=+⋅ 由题意MA NA ⊥，所以AN 的方程为1()y x t k=-+，同理可得26(1)||k t k AN +=由2AM AN =,得22233k tk k t=++，即3(2)3(21)k t k k -=- 当32k =时上式成立，因此23632k kt k -=-．因为3t >，即236332k k k ->-，整理得()()231202k k k +-<- 即3202k k -<-，解得322k <<． 6．【解析】（Ⅰ）设点(,0)D t (||2)t ≤，00(,),(,)N x y M x y ，依题意，2MD DN =u u u u r u u u r，且||||1DN ON ==u u u r u u u r ，所以00(,)2(,)t x y x t y --=-，且2200220()11x t y x y ⎧-+=⎪⎨+=⎪⎩ 即00222t x x ty y -=-⎧⎨=-⎩，且0(2)0t t x -=．由于当点D 不动时，点N 也不动，所以t 不恒等于0，于是02t x =，故00,42x y x y ==-，代入22001x y +=，可得221164x y +=，即所求的曲线C 的方程为221164x y +=．（Ⅱ）（1）当直线l 的斜率不存在时，直线l 为4x =或4x =-，都有14482OPQ S ∆=⨯⨯=．（2）当直线l 的斜率存在时，设直线1:()2l y kx m k =+≠±，由22416y kx m x y =+⎧⎨+=⎩ ，消去y ，可得222(14)84160k x kmx m +++-=．因为直线l 总与椭圆C 有且只有一个公共点，所以2222644(14)(416)0k m k m ∆=-+-=，即22164m k =+． ① 又由,20,y kx m x y =+⎧⎨-=⎩可得2(,)1212m m P k k --；同理可得2(,)1212m m Q k k -++．由原点O 到直线PQ 的距离为d =和|||P Q PQ x x =-，可得22111222||||||||222121214OPQP Q m m m S PQ d m x x m k k k ∆=⋅=-=⋅+=-+-．② 将①代入②得，222241281441OPQk m S k k ∆+==--．当214k >时，2224128()8(1)84141OPQ k S k k ∆+==+>--；当2104k ≤<时，2224128()8(1)1414OPQ k S k k ∆+==-+--．因2104k ≤<，则20141k <-≤，22214k ≥-，所以228(1)814OPQ S k∆=-+≥-，当且仅当0k =时取等号．所以当0k =时，OPQ S ∆的最小值为8．综合（1）（2）可知，当直线l 与椭圆C 在四个顶点处相切时，△OPQ 的面积取得最小值8．7．【解析】（1）由题意，得c a =且23a c c +=，解得a =1c =，则1b =，所以椭圆的标准方程为2212x y +=．（2）当AB ⊥x 轴时，AB =C 3P =，不合题意．当AB 与x 轴不垂直时，设直线AB 的方程为()1y k x =-，()11,x y A ，()22,x y B ，将AB 的方程代入椭圆方程，得()()2222124210k x k x k +-+-=，则1,2x=C 的坐标为2222,1212k k k k ⎛⎫- ⎪++⎝⎭，且)22112k AB k+===+．若0k =，则线段AB 的垂直平分线为y 轴，与左准线平行，不合题意．从而0k ≠，故直线C P 的方程为222121212k k y x k k k ⎛⎫+=-- ⎪++⎝⎭，则P 点的坐标为()22522,12k k k ⎛⎫+ ⎪- ⎪+⎝⎭，从而(()2223112k PC k k +=+．因为2PC AB=，所以(())222223111212k k k k k++=++，解得1k =±．此时直线AB 方程为1y x =-或1y x =-+． 8．【解析】（1）由已知，点在椭圆E 上．因此，22222211,,2a b a b c c a⎧+=⎪⎪⎪-=⎨⎪⎪=⎪⎩解得2a =，b =所以椭圆的方程为22142x y +=．（2）当直线l 与x 轴平行时，设直线l 与椭圆相交于C 、D 两点．如果存在定点Q 满足条件，则||||1||||QC PC QD PD ==，即||||QC QD =．所以Q 点在y 轴上，可设Q 点的坐标为0(0,)y ．当直线l 与x 轴垂直时，设直线l 与椭圆相交于M、N 两点．则M ，(0,N ，由||||||||QMPM QN PN ==，解得01y =或02y =．所以，若存在不同于点P 的定点Q 满足条件，则Q 点的坐标只可能为(0,2)Q ．下面证明：对任意的直线l ，均有||||||||QA PA QB PB =．当直线l 的斜率不存在时，由上可知，结论成立．当直线l 的斜率存在时，可设直线l 的方程为1y kx =+，A 、B 的坐标分别为1122(,),(,)x y x y ．联立221,421x y y kx ⎧+=⎪⎨⎪=+⎩得22(21)420k x kx ++-=．其判别式22168(21)0k k ∆=++>，所以，12122242,2121k x x x x k k +=-=-++．因此121212112x x k x x x x ++==．易知，点B 关于y 轴对称的点的坐标为22(,)B x y '-．又121122122111,QA QB y y k k k k k x x x x x '--==-==-+=--，所以QA QB k k '=，即,,Q A B '三点共线．所以12||||||||||||||||x QA QA PA QB QB x PB ==='．故存在与P 不同的定点(0,2)Q ，使得||||||||QA PA QB PB =恒成立． 9．【解析】（Ⅰ）由题意得2221,,.b caa b c =⎧⎪⎪=⎨⎪⎪=+⎩解得2a =2．故椭圆C 的方程为2212x y +=．设M (N x ，0)．因为0m ≠，所以11n -<<．直线PA 的方程为11n y x m--=，所以M x =1m n -，即(,0)1mM n-．（Ⅱ）因为点B 与点A 关于x 轴对称，所以(,)B m n -，设(,0)N N x ，则N x =1mn+． “存在点(0,)Q Q y 使得OQM ∠=ONQ ∠等价”，“存在点(0,)Q Q y 使得OM OQ=OQ ON”即Q y 满足2Q M N y x x =．因为1M m x n =-，1N mx n=+，2212m n +=，所以22221Q MN m y x x n ===-．所以Q y或Q y =故在y 轴上存在点Q ，使得OQM ∠=ONQ ∠．点Q的坐标为或(0,．10．【解析】（Ⅰ）由题意知0m ≠，可设直线AB 的方程为1y x b m=-+．由22112y x b m x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消去y ，得222112()102b x x b m m +-+-=．因为直线1y x b m=-+与椭圆2212x y +=有两个不同的交点，所以224Δ220b m=-++>，① 设M 为AB 的中点，则2222(,)22mb m bM m m ++，代入直线方程12y mx =+解得2222m b m +=-．②由①②得3m <-或3m >．（Ⅱ）令1((0,)22t m =∈-U ，则2||2AB t =+且O 到直线AB的距离21t d +=．设ΔAOB 的面积为()S t ，所以1()||2S t AB d =⋅= 当且仅当212t =时，等号成立．故ΔAOB． 11．【解析】（Ⅰ）可知c =c a =，3a ∴=，2224b a c =-=，椭圆C 的标准方程为22194x y +=；（Ⅱ）设两切线为12,l l ，①当1l x ⊥轴或1//l x 轴时，对应2//l x 轴或2l x ⊥轴，可知(3,2)P ±±②当1l 与x 轴不垂直且不平行时，03x ≠±，设1l 的斜率为k ，则0k ≠，2l 的斜率为1k-，1l 的方程为00()y y k x x -=-，联立22194x y +=，得2220000(94)18()9()360k x y kx kx y kx ++-+--=，因为直线与椭圆相切，所以0∆=，得222200009()(94)[()4]0y kx k k y kx --+--=，2200364[()4]0k y kx ∴-+--=，2220000(9)240x k x y k y ∴--+-=所以k 是方程2220000(9)240x x x y x y --+-=的一个根，同理1k-是方程2220000(9)240x x x y x y --+-=的另一个根，1()k k ∴⋅-=202049y x --，得220013x y +=，其中03x ≠±，所以点P 的轨迹方程为2213x y +=（3x ≠±），因为(3,2)P ±±满足上式，综上知：点P 的轨迹方程为2213x y +=． 12．【解析】（Ⅰ）设圆的半径为r ，P 点上下两段分别为,m n ，24r =，由射影定理得2r mn =，三角形的面积s ==≥=当2m n ==时，s取得最大，此时P∵222cc b a a==+，P 在双曲线上 ∴222321c b a ===，，，∴双曲线的方程为22-12y x = （Ⅱ）由（Ⅰ）知2C的焦点为，由此设2C 的方程为22221113x y b b +=+，其中10b >，由P 在2C 上，得213b =，∴2C 的方程为22163x y +=，显然，l 不是直线0y =，设l的方程为x my =+1122(,),(,)A x y B x y ，由22163x my x y ⎧=⎪⎨+=⎪⎩得22(2)-30m y ++=，∴12122-32y y y y m +==+①11220(PA PB x y x y =•=u u u r21212(1))m y y m y y =++++由①②得220m +=，解得12m m ==因此直线l的方程02x y -=或02x y -= 13．【解析】（Ⅰ）由椭圆定义知，2a ＝|PF 1|＋|PF 2|=所以a =c ＝1.所以椭圆C的离心率2c e a ===．（Ⅱ）由（Ⅰ）知，椭圆C 的方程为22x ＋y 2＝1．设点Q 的坐标为(x ，y )．(ⅰ)当直线l 与x 轴垂直时，直线l 与椭圆C 交于(0,1)，(0，－1)两点，此时点Q的坐标为0,2⎛ ⎝⎭． (ⅱ)当直线l 与x 轴不垂直时，设直线l 的方程为y ＝kx ＋2．因为M ，N 在直线l 上，可设点M ，N 的坐标分别为(1x ，k 1x ＋2)，(2x ，k 2x ＋2)，则|AM |2＝(1＋k 2)21x ，|AN |2＝(1＋k 2)22x ．又|AQ |2＝x 2＋(y －2)2＝(1＋k 2)2x ．由222211||||||AQ AM AN =+，得22222212211111k x k x k x =+(+)(+)(+)，即212122222212122211x x x x x x x x x (+)-=+=.① 将y ＝kx ＋2代入22x ＋y 2＝1中，得(2k 2＋1)x 2＋8kx ＋6＝0.②由Δ＝(8k )2－4×(2k 2＋1)×6＞0，得k 2＞32.由②可知，12x x +＝2821k k -+，12x x ＝2621k +，代入①中并化简，得2218103x k =-.③因为点Q 在直线y ＝kx ＋2上，所以2y k x-=，代入③中并化简，得10(y －2)2－3x 2＝18.由③及k 2＞32，可知0＜x 2＜32，即x ∈⎛⎫ ⎪ ⎪⎝⎭∪⎛ ⎝⎭.又0,25⎛⎫- ⎪ ⎪⎝⎭满足10(y －2)2－3x 2＝18，故x ∈,22⎛- ⎝⎭. 由题意，Q (x ，y )在椭圆C 内，所以－1≤y ≤1.又由10(y －2)2＝18＋3x 2有(y －2)2∈99,54⎡⎫⎪⎢⎣⎭且－1≤y ≤1，则y ∈1,225⎛- ⎝⎦. 所以，点Q 的轨迹方程为10(y －2)2－3x 2＝18，其中x ∈⎛⎝⎭，y ∈1,22⎛- ⎝⎦. 14．【解析】（Ⅰ）解法1 ：设M 的坐标为(,)x y ，由已知得23x +=，易知圆2C 上的点位于直线2x =-的右侧.于是20x +>，所以5x =+.化简得曲线1C 的方程为220y x =．解法2 ：由题设知，曲线1C 上任意一点M 到圆心2C (5,0)的距离等于它到直线5x =-的距离，因此，曲线1C 是以(5,0)为焦点，直线5x =-为准线的抛物线，故其方程为220y x =．（Ⅱ）当点P 在直线4x =-上运动时，P 的坐标为0(4,)y -，又03y ≠±，则过P 且与圆2C 相切的直线的斜率k 存在且不为0，每条切线都与抛物线有两个交点，切线方程为0(4),y y k x -=+0即kx-y+y +4k=0.于是3.=整理得 2200721890.k y k y ++-= ①设过P 所作的两条切线,PA PC 的斜率分别为12,k k ，则12,k k 是方程①的两个实根，故001218.724y yk k +=-=- ② 由101240,20,k x y y k y x -++=⎧⎨=⎩得21012020(4)0.k y y y k -++= ③ 设四点A,B,C,D 的纵坐标分别为1234,,,y y y y ，则12,y y 是方程③的两个实根，所以0112120(4).y k y y k +⋅=④同理可得0234220(4).y k y y k +⋅=⑤于是由②，④，⑤三式得010*******400(4)(4)y k y k y y y y k k ++=2012012124004()16y k k y k k k k ⎡⎤+++⎣⎦=22001212400[16]6400y y k k k k -+==.所以，当P 在直线4x =-上运动时，四点,,,A B C D 的纵坐标之积为定值6400． 15．【解析】（Ⅰ）解：设12(,0),(,0)(0)F c F c c ->，由题意，可得212||||,PF F F =2.c = 整理得22()10,1cc c aa a +-==-得（舍），或1.2c a =所以1.2e =（Ⅱ）解：由（Ⅰ）知2,,a c b ==可得椭圆方程为2223412,x y c +=直线PF 2方程为).y x c =-A ，B两点的坐标满足方程组2223412,).x y c y x c ⎧+=⎪⎨=-⎪⎩消去y 并整理，得2580.x cx -= 解得1280,.5x x c ==得方程组的解21128,0,5,.x c x y y ⎧=⎪=⎧⎪⎪⎨⎨=⎪⎪⎩=⎪⎩不妨设8(),(0,)5A c B 设点M的坐标为8(,),(,),(,)55x y AM x c y c BM x y =--=+u u u u r u u u ur 则，由),.3y x c c x y =-=-得于是38(,),15555AM y x y x =--u u u u r().BM x =u u u u r 由2,AM BM ⋅=-u u u u r u u u u r即38()()215555y x x y x -⋅+-=-，化简得218150.x --=将22105,0.316x y c x y c x +==-=>得所以0.x >因此，点M的轨迹方程是218150(0).x x --=>16．【解析】（1）联立2x y =与2+=x y 得2,1=-=B A x x ，则AB 中点)25,21(Q ，设线段PQ 的中点M 坐标为),(y x ，则225,221ty s x +=+=，即252,212-=-=y t x s ，又点P 在曲线C 上，∴2)212(252-=-x y 化简可得21128y x x =-+，又点P 是L 上的任一点，且不与点A 和点B 重合，则22121<-<-x ，即4541<<-x ，∴中点M 的轨迹方程为21128y x x =-+（4541<<-x ）．（2）曲线22251:24025G x ax y y a -+-++=，即圆E ：2549)2()(22=-+-y a x ，其圆心坐标为)2,(a E ，半径57=r ，设圆G 与直线l ：20x y -+=相切于点(,)T T T x y ，75=，即5a =±．过点(,2)N a 与直线l 垂直的直线l '的方程是21()y x a -=-⨯-，即20x y +-=．由2020x y x y a -+=⎧⎨+--=⎩，解得2T a x =，22T ay =+．当5a =-时，1210T x -<<-<． ∵1,2-分别是D 上的点的最小和最大横坐标，∴切点T D ∈，故min 5a =-．。

专题12 解析几何-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)

专题12 解析几何【2021年】1．（2021年全国高考乙卷数学（文）试题）设B 是椭圆22:15x C y +=的上顶点，点P 在C 上，则PB 的最大值为（）A ．52B C D ．2【答案】A【分析】设点()00,P x y ，因为()0,1B ，220015x y +=，所以()()()222222200000001251511426444PB x y y y y y y ⎛⎫=+-=-+-=--+=-++ ⎪⎝⎭，而011y -≤≤，所以当014y =-时，PB 的最大值为52．故选：A ．2．（2021年全国高考乙卷数学（理）试题）设B 是椭圆2222:1(0)x y C a b a b+=>>的上顶点，若C 上的任意一点P 都满足||2PB b ≤，则C 的离心率的取值范围是（）A ．⎫⎪⎪⎣⎭B ．1,12⎡⎫⎪⎢⎣⎭C ．⎛ ⎝⎦D ．10,2⎛⎤ ⎥⎝⎦【答案】C【分析】设()00,P x y ，由()0,B b ，因为2200221x y a b+=，222a b c =+，所以()()2223422222220000022221y c b b PB x y b a y b y a b b b c c ⎛⎫⎛⎫=+-=-+-=-++++ ⎪ ⎪⎝⎭⎝⎭，因为0b y b -≤≤，当32bb c-≤-，即22b c ≥时，22max 4PB b =，即max 2PB b =，符合题意，由22b c ≥可得222a c ≥，即0e <≤；当32b b c ->-，即22b c <时，42222max b PB a b c=++，即422224b a b b c ++≤，化简得，()2220c b -≤，显然该不等式不成立．故选：C ．3．（2021年全国高考甲卷数学（文）试题）点()3,0到双曲线221169x y -=的一条渐近线的距离为（） A ．95B ．85C ．65D ．45【答案】A【分析】由题意可知，双曲线的渐近线方程为：220169x y -=，即340±=x y ，结合对称性，不妨考虑点()3,0到直线340x y +=的距离：95d ==.故选：A.4．（2021年全国新高考Ⅰ卷数学试题）已知1F ，2F 是椭圆C ：22194x y +=的两个焦点，点M 在C 上，则12MF MF ⋅的最大值为（）A ．13B ．12C ．9D ．6【答案】C【分析】由题，229,4a b ==，则1226MF MF a +==，所以2121292MF MF MF MF ⎛+⎫⋅≤= ⎪⎝⎭（当且仅当123MF MF ==时，等号成立）．故选：C ．二、多选题5．（2021年全国新高考Ⅰ卷数学试题）已知点P 在圆()()225516x y -+-=上，点()4,0A 、()0,2B ，则（）A ．点P 到直线AB 的距离小于10B ．点P 到直线AB 的距离大于2C ．当PBA ∠最小时，PB =D ．当PBA ∠最大时，PB =【答案】ACD【分析】圆()()225516x y -+-=的圆心为()5,5M ，半径为4，直线AB 的方程为142x y+=，即240x y +-=，圆心M 到直线AB45==>，所以，点P 到直线AB42<410+<，A 选项正确，B 选项错误；如下图所示：当PBA ∠最大或最小时，PB 与圆M 相切，连接MP 、BM ，可知PM PB ⊥，BM ==4MP =，由勾股定理可得BP ==CD 选项正确.故选：ACD.三、填空题6．（2021年全国高考乙卷数学（文）试题）双曲线22145x y -=的右焦点到直线280x y +-=的距离为________．【分析】由已知，3c ===，所以双曲线的右焦点为(3,0)，所以右焦点(3,0)到直线280x y +-===7．（2021年全国高考乙卷数学（理）试题）已知双曲线22:1(0)x C y m m-=>0my +=，则C 的焦距为_________．【答案】40my +=化简得y =，即b a =，同时平方得2223b a m =，又双曲线中22,1a m b ==，故231m m=，解得3,0m m ==（舍去），2223142c a b c =+=+=⇒=，故焦距24c = 故答案为：48．（2021年全国高考甲卷数学（理）试题）已知12,F F 为椭圆C ：221164x y+=的两个焦点，P ，Q 为C 上关于坐标原点对称的两点，且12PQ F F =，则四边形12PFQF 的面积为________．【答案】8【分析】因为,P Q 为C 上关于坐标原点对称的两点，且12||||PQ F F =，所以四边形12PFQF 为矩形，设12||,||PF m PF n ==，则228,48m n m n +=+=，所以22264()2482m n m mn n mn =+=++=+，8mn =，即四边形12PFQF 面积等于8.故答案为：8.9．（2021年全国新高考Ⅰ卷数学试题）已知O 为坐标原点，抛物线C ：22y px =(0p >)的焦点为F ，P为C 上一点，PF 与x 轴垂直，Q 为x 轴上一点，且PQ OP ⊥，若6FQ =，则C 的准线方程为______.【答案】32x =-【分析】抛物线C ：22y px = (0p >)的焦点,02p F ⎛⎫ ⎪⎝⎭, ⅠP 为C 上一点，PF 与x 轴垂直，所以P 的横坐标为2p，代入抛物线方程求得P 的纵坐标为p ±, 不妨设(,)2pP p , 因为Q 为x 轴上一点，且PQ OP ⊥，所以Q 在F 的右侧，又||6FQ =，(6,0),(6,)2pQ PQ p ∴+∴=- 因为PQ OP ⊥，所以PQ OP ⋅=2602pp ⨯-=, 0,3p p >∴=，所以C 的准线方程为32x =- 故答案为：32x =-.四、解答题10．（2021年全国高考乙卷数学（文）试题）已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2．（1）求C 的方程;（2）已知O 为坐标原点，点P 在C 上，点Q 满足9PQ QF =，求直线OQ 斜率的最大值. 【答案】（1）24y x =；（2）最大值为13. 【分析】（1）抛物线2:2(0)C y px p =>的焦点,02p F ⎛⎫⎪⎝⎭，准线方程为2p x =-，由题意，该抛物线焦点到准线的距离为222p p p ⎛⎫--== ⎪⎝⎭，所以该抛物线的方程为24y x =；（2）设()00,Q x y ，则()00999,9PQ QF x y ==--，所以()00109,10P x y -，由P 在抛物线上可得()()200104109y x =-，即20025910y x +=，所以直线OQ 的斜率000220001025925910OQ y y y k y x y ===++，当00y =时，0OQ k =；当00y ≠时，0010925OQ k y y =+，当00y >时，因为0092530y y +≥=，此时103OQk <≤，当且仅当00925y y =，即035y =时，等号成立；当00y <时，0OQ k <；综上，直线OQ 的斜率的最大值为13. 11．（2021年全国高考乙卷数学（理）试题）已知抛物线()2:20C x py p =>的焦点为F ，且F 与圆22:(4)1M x y ++=上点的距离的最小值为4．（1）求p ；（2）若点P 在M 上，,PA PB 是C 的两条切线，,A B 是切点，求PAB △面积的最大值．【答案】（1）2p =；（2）【分析】（1）抛物线C 的焦点为0,2p F ⎛⎫ ⎪⎝⎭，42pFM =+，所以，F 与圆22:(4)1M x y ++=上点的距离的最小值为4142p+-=，解得2p =；（2）抛物线C 的方程为24x y =，即24x y =，对该函数求导得2x y '=，设点()11,A x y 、()22,B x y 、()00,P x y ，直线PA 的方程为()1112x y y x x -=-，即112x x y y =-，即11220x x y y --=，同理可知，直线PB 的方程为22220x x y y --=，由于点P 为这两条直线的公共点，则10102020220220x x y y x x y y --=⎧⎨--=⎩，所以，点A 、B 的坐标满足方程00220x x y y --=，所以，直线AB 的方程为00220x x y y --=，联立0022204x x y y x y --=⎧⎪⎨=⎪⎩，可得200240x x x y -+=，由韦达定理可得1202x x x +=，1204x x y =，所以，AB ===，点P 到直线AB的距离为d =，所以，()3220011422PABS AB d x y =⋅==-△， ()()2222000000041441215621x y y y y y y -=-+-=---=-++，由已知可得053y -≤≤-，所以，当05y =-时，PAB△的面积取最大值321202⨯=12．（2021年全国高考甲卷数学（理）试题）抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ⊥．已知点()2,0M ，且M 与l 相切．（1）求C ，M 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M 相切．判断直线23A A 与M 的位置关系，并说明理由．【答案】（1）抛物线2:C y x =，M 方程为22(2)1x y -+=；（2）相切，理由见解析【分析】（1）依题意设抛物线200:2(0),(1,),(1,)C y px p P y Q y =>-，20,1120,21OP OQ OP OQ y p p ⊥∴⋅=-=-=∴=，所以抛物线C 的方程为2y x =，(0,2),M M 与1x =相切，所以半径为1，所以M 的方程为22(2)1x y -+=；（2）设111222333(),(,),(,)A x y A x y A x y若12A A 斜率不存在，则12A A 方程为1x =或3x =，若12A A 方程为1x =，根据对称性不妨设1(1,1)A ，则过1A 与圆M 相切的另一条直线方程为1y =，此时该直线与抛物线只有一个交点，即不存在3A ，不合题意；若12A A 方程为3x =，根据对称性不妨设12(3,A A 则过1A 与圆M 相切的直线13A A为3)y x -=-，又131********A A y y k y x x y y -====∴=-+，330,(0,0)x A =，此时直线1323,A A A A 关于x 轴对称，所以直线23A A 与圆M 相切；若直线121323,,A A A A A A 斜率均存在，则121323121323111,,A A A A A A k k k y y y y y y ===+++，所以直线12A A 方程为()11121y y x x y y -=-+，整理得1212()0x y y y y y -++=，同理直线13A A 的方程为1313()0x y y y y y -++=，直线23A A 的方程为2323()0x y y y y y -++=，12A A 与圆M相切，1=整理得22212121(1)230y y y y y -++-=，13A A 与圆M 相切，同理22213131(1)230y y y y y -++-=所以23,y y 为方程222111(1)230y y y y y -++-=的两根，2112323221123,11y y y y y y y y -+=-⋅=--，M 到直线23A A 的距离为：2123|2|y -+=22121111y y +===+，所以直线23A A 与圆M 相切；综上若直线1213,A A A A 与圆M 相切，则直线23A A 与圆M 相切.13．（2021年全国新高考Ⅰ卷数学试题）在平面直角坐标系xOy中，已知点()1F、)2122F MF MF -=，，点M 的轨迹为C .（1）求C 的方程；（2）设点T 在直线12x =上，过T 的两条直线分别交C 于A 、B 两点和P ，Q 两点，且TA TB TP TQ ⋅=⋅，求直线AB 的斜率与直线PQ 的斜率之和.【答案】（1）()221116y x x -=≥；（2）0.【分析】因为12122MF MF F F -=<=所以，轨迹C 是以点1F 、2F 为左、右焦点的双曲线的右支，设轨迹C 的方程为()222210,0x y a b a b-=>>，则22a =，可得1a =，4b ==，所以，轨迹C 的方程为()221116y x x -=≥；（2）设点1,2T t ⎛⎫ ⎪⎝⎭，若过点T 的直线的斜率不存在，此时该直线与曲线C 无公共点，不妨直线AB 的方程为112y t k x ⎛⎫-=-⎪⎝⎭，即1112y k x t k =+-，联立1122121616y k x t k x y ⎧=+-⎪⎨⎪-=⎩，消去y 并整理可得()()222111111621602k x k t k x t k ⎛⎫-+-+-+= ⎪⎝⎭，设点()11,A x y 、()22,B x y ，则112x >且212x >. 由韦达定理可得2111221216k k t x x k -+=-，211221116216t k x x k ⎛⎫-+ ⎪⎝⎭=-，所以，()()()()22122121121122112111111222416t k x x TA TB k x x k x x k +++⎛⎫⋅=+⋅-⋅-=+⋅-+=⎪-⎝⎭，设直线PQ 的斜率为2k ，同理可得()()2222212116t k TP TQ k ++⋅=-，因为TA TB TP TQ ⋅=⋅，即()()()()22221222121211211616tk t k k k ++++=--，整理可得2212k k =，即()()12120k k k k -+=，显然120k k -≠，故120k k +=. 因此，直线AB 与直线PQ 的斜率之和为0.【2012年——2020年】1．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））已知圆2260x y x +-=，过点（1，2）的直线被该圆所截得的弦的长度的最小值为（） A ．1 B ．2 C ．3 D ．4【答案】B【分析】圆2260x y x +-=化为22(3)9x y -+=，所以圆心C 坐标为(3,0)C ，半径为3，设(1,2)P ，当过点P 的直线和直线CP 垂直时，圆心到过点P 的直线的距离最大，所求的弦长最短，此时||CP ==根据弦长公式得最小值为2==. 故选：B.2．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））设12,F F 是双曲线22:13y C x -=的两个焦点，O为坐标原点，点P 在C 上且||2OP =，则12PF F △的面积为（） A ．72B ．3C ．52D ．2【答案】B【分析】由已知，不妨设12(2,0),(2,0)F F -，则1,2a c ==，因为12122OP F F ==，所以点P 在以12F F 为直径的圆上，即12F F P 是以P 为直角顶点的直角三角形，故2221212||||||PF PF F F +=，即2212||||16PF PF +=，又12||||22PF PF a -==，所以2124||||PF PF =-=2212||||2PF PF +-12||||162PF PF =-12||||PF PF ，解得12||||6PF PF =，所以12F F P S =△121||||32PF PF = 故选：B3．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））已知A 为抛物线C :y 2=2px （p >0）上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =（）A ．2B ．3C ．6D ．9【答案】C【分析】设抛物线的焦点为F ，由抛物线的定义知||122A p AF x =+=，即1292p=+，解得6p .故选：C.4．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））已知ⅠM ：222220x y x y +---=，直线l ：220x y ++=，P 为l 上的动点，过点P 作ⅠM 的切线,PA PB ，切点为,A B ，当||||PM AB ⋅最小时，直线AB 的方程为（） A ．210x y --= B ．210x y +-= C ．210x y -+= D ．210x y ++=【答案】D【分析】圆的方程可化为()()22114x y -+-=，点 M 到直线l的距离为2d ==>，所以直线 l 与圆相离．依圆的知识可知，四点,,,A P B M 四点共圆，且AB MP ⊥，所以14442PAMPM AB SPA AM PA ⋅==⨯⨯⨯=，而PA =当直线MP l ⊥时，min MP ， min 1PA =，此时PM AB ⋅最小．Ⅰ()1:112MP y x -=-即 1122y x =+，由1122220y x x y ⎧=+⎪⎨⎪++=⎩解得，1x y =-⎧⎨=⎩．所以以MP 为直径的圆的方程为()()()1110x x y y -++-=，即 2210x y y +--=，两圆的方程相减可得：210x y ++=，即为直线AB 的方程．故选：D.5．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））若过点（2，1）的圆与两坐标轴都相切，则圆心到直线230x y --=的距离为（） ABC．5D．5【答案】B【分析】由于圆上的点()2,1在第一象限，若圆心不在第一象限，则圆与至少与一条坐标轴相交，不合乎题意，所以圆心必在第一象限，设圆心的坐标为(),a a ，则圆的半径为a ，圆的标准方程为()()222x a y a a -+-=. 由题意可得()()22221a a a -+-=，可得2650a a -+=，解得1a =或5a =，所以圆心的坐标为()1,1或()5,5，圆心到直线的距离均为121132555d ⨯--==；圆心到直线的距离均为225532555d ⨯--== 圆心到直线230x y --=的距离均为5d ==；所以，圆心到直线230x y --=. 故选：B.6．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线分别交于,D E 两点，若ODE 的面积为8，则C 的焦距的最小值为（） A ．4 B ．8C ．16D ．32【答案】B 【分析】2222:1(0,0)x y C a b a b-=>> ∴双曲线的渐近线方程是by x a=±直线x a =与双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线分别交于D ，E 两点不妨设D 为在第一象限，E 在第四象限联立x ab y x a =⎧⎪⎨=⎪⎩，解得x a y b =⎧⎨=⎩故(,)D a b联立x ab y x a =⎧⎪⎨=-⎪⎩，解得x a y b =⎧⎨=-⎩ 故(,)E a b -∴||2ED b =∴ODE 面积为：1282ODE S a b ab =⨯==△ 双曲线2222:1(0,0)x y C a b a b-=>>∴其焦距为28c =≥==当且仅当a b ==取等号∴C 的焦距的最小值：8故选：B.7．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））在平面内，A ，B 是两个定点，C 是动点，若=1AC BC ⋅，则点C 的轨迹为（） A ．圆 B ．椭圆C ．抛物线D ．直线【答案】A【分析】设()20AB a a =>，以AB 中点为坐标原点建立如图所示的平面直角坐标系，则：()(),0,,0A a B a -，设(),C x y ，可得：()(),,,AC x a y BC x a y →→=+=-，从而：()()2AC BC x a x a y →→⋅=+-+，结合题意可得：()()21x a x a y +-+=，整理可得：2221x y a +=+，即点C 的轨迹是以AB. 故选：A.8．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））设O 为坐标原点，直线2x =与抛物线C ：22(0)y px p =>交于D ，E 两点，若OD OE ⊥，则C 的焦点坐标为（）A ．1,04⎛⎫⎪⎝⎭B ．1,02⎛⎫ ⎪⎝⎭C ．(1,0)D ．(2,0)【答案】B【分析】因为直线2x =与抛物线22(0)y px p =>交于,E D 两点，且OD OE ⊥，根据抛物线的对称性可以确定4DOx EOx π∠=∠=，所以()2,2D ，代入抛物线方程44p =，求得1p =，所以其焦点坐标为1(,0)2，故选：B.9．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））若直线l 与曲线yx 2+y 2=15都相切，则l 的方程为（） A ．y =2x +1 B ．y =2x +12C ．y =12x +1 D ．y =12x +12【答案】D【分析】设直线l在曲线y =(0x ，则00x >，函数y =y '=，则直线l的斜率k =，设直线l的方程为)0y x x =-，即00x x -+=，由于直线l 与圆2215x y +== 两边平方并整理得2005410x x --=，解得01x =，015x =-（舍），则直线l 的方程为210x y -+=，即1122y x =+.故选：D.10．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））设双曲线C ：22221x y a b-=（a >0，b >0）的左、右焦点分别为F 1，F 2P 是C 上一点，且F 1P ⅠF 2P ．若ⅠPF 1F 2的面积为4，则a =（） A ．1 B ．2C ．4D ．8【答案】A【分析】5ca=，c ∴=，根据双曲线的定义可得122PF PF a -=， 12121||42PF F PF F S P =⋅=△，即12||8PF PF ⋅=， 12F P F P ⊥，()22212||2PF PF c ∴+=，()22121224PF PF PF PF c ∴-+⋅=，即22540a a -+=，解得1a =，故选：A.11．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为130°，则C 的离心率为 A ．2sin40° B ．2cos40° C ．1sin50︒D ．1cos50︒【答案】D【分析】由已知可得tan130,tan 50b ba a-=︒∴=︒，1cos50c e a ∴======︒，故选D ． 12．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））已知椭圆C 的焦点为121,01,0F F -()，()，过F 2的直线与C 交于A ，B 两点.若222AF F B =││││，1AB BF =││││，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=【答案】B【分析】法一：如图，由已知可设2F B n =，则212,3AF n BF AB n ===，由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=．在1AF B △中，由余弦定理推论得22214991cos 2233n n n F AB n n +-∠==⋅⋅．在12AF F △中，由余弦定理得2214422243n n n n +-⋅⋅⋅=，解得n =．22224312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=，故选B ．法二：由已知可设2F B n =，则212,3AF n BF AB n ===，由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=．在12AF F △和12BF F △中，由余弦定理得2221222144222cos 4,422cos 9n n AF F n n n BF F n⎧+-⋅⋅⋅∠=⎨+-⋅⋅⋅∠=⎩，又2121,AF F BF F ∠∠互补，2121cos cos 0AF F BF F ∴∠+∠=，两式消去2121cos cos AF F BF F ∠∠,，得223611n n +=，解得n =．22224312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=，故选B ．13．（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））若抛物线y 2=2px （p >0）的焦点是椭圆2231x y pp+=的一个焦点，则p = A ．2 B ．3 C ．4 D ．8【答案】D【分析】因为抛物线22(0)y px p =>的焦点(,0)2p 是椭圆2231x y p p +=的一个焦点，所以23()2p p p -=，解得8p =，故选D ．14．（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））设F 为双曲线C ：22221x y a b-=（a >0，b >0）的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点．若|PQ |=|OF |，则C 的离心率为A BC ．2D 【答案】A【分析】设PQ 与x 轴交于点A ，由对称性可知PQ x ⊥轴，又||PQ OF c ==，||,2cPA PA ∴=∴为以OF 为直径的圆的半径，A ∴为圆心||2cOA =．,22c c P ⎛⎫∴ ⎪⎝⎭，又P 点在圆222x y a +=上，22244c c a ∴+=，即22222,22c c a e a =∴==．e ∴=A ．15．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））已知F 是双曲线22:145x y C 的一个焦点，点P 在C 上，O 为坐标原点，若=OP OF ，则OPF △的面积为A ．32B ．52C ．72D ．92【答案】B【分析】设点()00,P x y ，则2200145x y -=Ⅰ．又3OP OF ===，22009x y ∴+=Ⅰ．由ⅠⅠ得20259y =，即053y =， 0115532232OPFS OF y ∆∴==⨯⨯=，故选B ．16．（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））双曲线C ：2242x y -=1的右焦点为F ，点P 在C的一条渐近线上，O 为坐标原点，若=PO PF ，则ⅠPFO 的面积为A ．4B ．2C ．D ．【答案】A【分析】由2,,,a b c ====．,2P PO PF x =∴=，又P 在C 的一条渐近线上，不妨设为在y x =上，11224PFO P S OF y ∴=⋅==△，故选A ． 17．（2018年全国普通高等学校招生统一考试文科数学（新课标I 卷））已知椭圆C ：2221(0)4x y a a +=>的一个焦点为(20)，，则C 的离心率为A ．13B ．12C ．2D ．3【答案】C【详解】：根据题意，可知2c =，因为24b =，所以2228a b c =+=，即a = 所以椭圆C的离心率为2e ==，故选C. 18．（2018年全国普通高等学校招生统一考试理科数学（新课标I 卷））设抛物线C ：y 2=4x 的焦点为F ，过点（–2，0）且斜率为23的直线与C 交于M ，N 两点，则FM FN ⋅= A ．5 B ．6C ．7D ．8【答案】D【分析】根据题意，过点（–2，0）且斜率为23的直线方程为2(2)3y x =+，与抛物线方程联立22(2)34y x y x⎧=+⎪⎨⎪=⎩，消元整理得：y y -+=2680，解得(1,2),(4,4)M N ，又(1,0)F ，所以(0,2),(3,4)FM FN ==，从而可以求得03248FM FN ⋅=⨯+⨯=，故选D.19．（2018年全国普通高等学校招生统一考试理科数学（新课标I 卷））已知双曲线C ：2213x y -=，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M 、N .若OMN 为直角三角形，则|MN |= A ．32B ．3C．D ．4【答案】B【详解】：根据题意，可知其渐近线的斜率为3±(2,0)F ，从而得到30FON ︒∠=，所以直线MN 的倾斜角为60︒或120︒，根据双曲线的对称性，设其倾斜角为60︒，可以得出直线MN的方程为2)y x =-，分别与两条渐近线y x =和y x =联立，求得3(,2M N ，所以3MN ==，故选B. 20．（2018年全国普通高等学校招生统一考试理数（全国卷II ））双曲线22221(0,0)x y a b a b-=>>的离心率A ．y =B ．y =C ．2y x =±D ．2y x =±【答案】A【详解】：2222221312,c b c a b e e a a a a-==∴==-=-=∴=因为渐近线方程为by x a=±，所以渐近线方程为y =，选A. 点睛：已知双曲线方程22221(,0)x y a b a b-=>求渐近线方程：22220x y by x a b a -=⇒=±.21．（2018年全国普通高等学校招生统一考试文数（全国卷II ））已知1F ，2F 是椭圆C 的两个焦点，P 是C 上的一点，若12PF PF ⊥，且2160PF F ∠=︒，则C 的离心率为A ．1-B ．2C D 1【答案】D【详解】：在12F PF ∆中，122190,60F PF PF F ∠=∠=︒设2||PF m =，则12122,c F F m PF ===，又由椭圆定义可知1221)a PF PF m =+=则离心率212c c e a a ====，故选D.22．（2018年全国普通高等学校招生统一考试理数（全国卷II ））已知1F ，2F 是椭圆22221(0)x y C a b a b+=>>：的左，右焦点，A 是C 的左顶点，点P 在过A且斜率为6的直线上，12PF F △为等腰三角形，12120F F P ∠=︒，则C 的离心率为A ．23B ．12C ．13D ．14【答案】D【详解】：因为12PF F △为等腰三角形，12120F F P ∠=︒，所以PF 2=F 1F 2=2c, 由AP222tan sin cos 6PAF PAF PAF ∠=∴∠=∠=，由正弦定理得2222sin sin PF PAF AF APF ∠=∠,所以22214,54sin()3c a c e a c PAF =∴==+-∠，故选D. 23．（2018年全国卷Ⅰ理数高考试题）直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP △面积的取值范围是A ．[]26，B ．[]48，C．D．⎡⎣【答案】A【详解】：直线x y 20++=分别与x 轴，y 轴交于A ，B 两点()()A 2,0,B 0,2∴--,则AB =点P 在圆22x 22y -+=（）上 ∴圆心为（2，0），则圆心到直线距离1d ==故点P 到直线x y 20++=的距离2d的范围为则[]2212,62ABPSAB d ==∈故答案选A.24．（2018年全国卷Ⅰ文数高考试题）已知双曲线22221(00)x y C a b a b-=>>：，，则点(4,0)到C 的渐近线的距离为 AB ．2C．2D．【答案】D 【详解】：e c a ===1ba∴= 所以双曲线的渐近线方程为x y 0±= 所以点（4，0）到渐近线的距离d ==故选D25．（2018年全国卷Ⅰ理数高考试题）设1F ,2F 是双曲线2222:1x y C a b-=（）的左、右焦点，O是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若16PF OP =，则C 的离心率为 A B C ．2D【答案】B【详解】：由题可知22,PF b OF c ==PO a ∴=在2Rt PO F 中，222cos P O PF bF OF c∠==在12PF F △中,22221212212cos P O 2PF F F PF b F PF F F c+-∠==)222224322b c bc a b cc+-∴=⇒=⋅ e ∴=故选B.26．（2017年全国普通高等学校招生统一考试文科数学（新课标1卷））已知F 是双曲线C ：2213y x -=的右焦点，P 是C 上一点，且PF 与x 轴垂直，点A 的坐标是(1，3)，则APF 的面积为A ．13B ．1 2C ．2 3D ．3 2【答案】D【详解】由2224c a b =+=得2c =，所以(2,0)F ，将2x =代入2213y x -=，得3=±y ，所以||3PF =，又点A 的坐标是(1，3)，故ⅠAPF 的面积为133(21)22⨯⨯-=，选D ．27．（2017年全国普通高等学校招生统一考试文科数学（新课标1卷））（2017新课标全国卷Ⅰ文科）设A ，B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足ⅠAMB =120°，则m 的取值范围是A ．(0,1][9,)+∞B ．[9,)+∞C ．(0,1][4,)+∞D ．[4,)+∞【答案】A【详解】当03m <<时，焦点在x 轴上，要使C 上存在点M 满足120AMB ∠=，则tan 603ab≥=≥，得01m <≤；当3m >时，焦点在y 轴上，要使C 上存在点M 满足120AMB ∠=，则tan 603ab ≥=≥，得9m ≥，故m 的取值范围为(0,1][9,)+∞，选A ． 28．（2017年全国普通高等学校招生统一考试理科数学（新课标1卷））已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为 A ．16 B ．14C ．12D ．10【答案】A【详解】设11223344(,),(,),(,),(,)A x y B x y D x y E x y ，直线1l 的方程为1(1)y k x =-，联立方程214(1)y x y k x ⎧=⎨=-⎩，得2222111240k x k x x k --+=，Ⅰ21122124k x x k --+=-212124k k +=，同理直线2l 与抛物线的交点满足22342224k x x k ++=，由抛物线定义可知12342AB DE x x x x p +=++++=22122222121224244448816k k k k k k ++++=++≥=，当且仅当121k k =-=（或1-）时，取等号.29．（2017年全国普通高等学校招生统一考试文科数学（新课标2卷））若1a >，则双曲线2221x y a-=的离心率的取值范围是 A．)+∞ B．2)C．D ．(1,2)【答案】C【详解】221c a =+，222222111c a e a a a +===+， 1a >，2101a∴<< ，212e <<，则0e << C. 30．（2017年全国普通高等学校招生统一考试）过抛物线C ：y 2＝4x 的焦点FC 于点M (M 在x 轴的上方)，l 为C 的准线，点N 在l 上且MN Ⅰl ，则M 到直线NF 的距离为（） AB．C．D．【答案】C【分析】依题意得F (1,0)，则直线FM 的方程是yx －1)．由214y y x⎧=-⎪⎨=⎪⎩得x ＝13或x ＝3. 由M 在x 轴的上方得M (3，，由MN Ⅰl 得|MN |＝|MF |＝3＋1＝4又ⅠNMF 等于直线FM 的倾斜角，即ⅠNMF ＝60°，因此ⅠMNF 是边长为4的等边三角形点M 到直线NF的距离为4= 故选：C .31．（2017年全国普通高等学校招生统一考试理科数学（新课标2卷））若双曲线C:22221x y a b-=（0a >，0b >）的一条渐近线被圆()2224x y -+=所截得的弦长为2，则C 的离心率为 A ．2 BCD．3【答案】A【详解】由几何关系可得，双曲线()222210,0x y a b a b-=>>的渐近线方程为0bx ay ±=，圆心()2,0到渐近线距离为d =()2,0到直线0bx ay +=的距离为2bd c=== 即2224()3c a c -=，整理可得224c a =，双曲线的离心率2e ===．故选A ． 32．（2017年全国普通高等学校招生统一考试文科数学（新课标3卷）已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为 A．3B．3C．3D ．13【答案】A【详解】以线段12A A 为直径的圆的圆心为坐标原点()0,0，半径为r a =，圆的方程为222x y a +=，直线20bx ay ab -+=与圆相切，所以圆心到直线的距离等于半径，即d a ==，整理可得223a b ，即()2223,a a c =-即2223a c =，从而22223c e a ==，则椭圆的离心率3c e a ===，故选A.33．（2016年全国普通高等学校招生统一考试文科数学新课标Ⅰ卷））已知双曲线2222:1(0,0)x y C a b a b -=>>的一条渐近线方程为y x =，且与椭圆221123x y +=有公共焦点.则C 的方程为（）A ．221810x y -=B ．22145x y -=C ．22154x y -=D ．22143x y -=【答案】B【分析】因为双曲线的一条渐近线方程为2y x =，则2b a =.Ⅰ 又因为椭圆221123x y +=与双曲线有公共焦点，双曲线的焦距26c =，即c ＝3，则a 2＋b 2＝c 2＝9.Ⅰ由ⅠⅠ解得a ＝2，b C 的方程为22145x y -=.故选：B.34．（2016年全国普通高等学校招生统一考试）已知方程222213x y m n m n-=+-表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是A ．(–1,3)B ．C ．(0,3)D ．)【答案】A【详解】：双曲线的焦点在x 轴上，所以2234m n m n ++-=，解得21m =，因为方程22113x yn n-=+-表示双曲线，所以10{30n n +>->，解得1{3n n >-<，所以n 的取值范围是()1,3-，故选A ．35．（2016年全国普通高等学校招生统一考试）以抛物线C 的顶点为圆心的圆交C 于A 、B 两点，交C 的准线于D 、E 两点.已知|AB |=|DE |=C 的焦点到准线的距离为 A ．8B ．6C ．4D ．2【答案】C【详解】：如图，设抛物线方程为22y px =，,AB DE 交x 轴于,C F点，则AC =A点纵坐标为则A 点横坐标为4p ，即4OC p=，由勾股定理知2222DF OF DO r +==，2222AC OC AO r +==，即22224()()2pp+=+，解得4p =，即C 的焦点到准线的距离为4，故选C.36．（）设F 为抛物线2:4C y x =的焦点，曲线()0ky k x=>与C 交于点P ，PF x ⊥轴，则k = A ．12B ．1C ．32D ．2【答案】D【解析】试题分析：由抛物线的性质可得(1,2)221kP y k ⇒==⇒=，故选D.37．（2016年全国普通高等学校招生统一考试）圆2228130+--+=x y x y 的圆心到直线10ax y +-=的距离为1，则a = A ．43-B ．34-CD ．2【答案】A【详解】：由2228130x y x y +--+=配方得22(1)(4)4x y -+-=，所以圆心为(1,4)，因为圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为11=，解得43a =-，故选A.38．（（2016新课标全国Ⅰ理科）已知F 1，F 2是双曲线E ：22221x y a b-=的左，右焦点，点M 在E 上，M F 1与x 轴垂直，sin 2113MF F ∠= ,则E 的离心率为 AB ．32CD ．2【答案】A 【详解】：由已知可得，故选A.39．（2016年全国普通高等学校招生统一考试）已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点.P 为C 上一点，且PF Ⅰx 轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则C 的离心率为 A ．13B ．12C ．23D ．34【答案】A【详解】：如图取P 与M 重合，则由2(,0),(,)bA a M c a--⇒直线22:()(0,)b b a AM y x a E c a a c=+⇒-+-同理由222221(,0),(,)(0,)33b b b b B a Mc G a c e a a c a c a c -⇒⇒=⇒=⇒=+-+,故选A.40．（2015年全国普通高等学校招生统一考试文科数学（新课标Ⅰ））已知椭圆E 的中心为坐标原点，离心率为12，E 的右焦点与抛物线2:8C y x =的焦点重合，,A B 是C 的准线与E 的两个交点，则AB = A ．3 B ．6 C ．9 D ．12【答案】B【详解】：抛物线28y x =的焦点为(2,0),所以椭圆的右焦点为(2,0),即2,c =且1,4,2c a b a ====椭圆的方程为221.1612x y 抛物线准线为2,x =-代入椭圆方程中得(2,3),(2,3), 6.A B AB ---=故选B.41．（2015年全国普通高等学校招生统一考试理科数学（新课标Ⅰ））已知00(,)M x y 是双曲线C ：2212x y -=上的一点，1F ，2F 是C 的两个焦点，若120MF MF ⋅<，则0y 的取值范围是A ．(B ．(66-C ．(D ．( 【答案】A【详解】由题知12(F F ，220012x y -=，所以12MF MF ⋅=0000(,),)x y x y -⋅-=2220003310x y y +-=-<，解得0y <<，故选A.42．（2015年全国普通高等学校招生统一考试理科数学（新课标Ⅰ））已知A ，B 为双曲线E 的左，右顶点，点M 在E 上，∆ABM 为等腰三角形，且顶角为120°，则E 的离心率为A B ．2C D【答案】D【详解】设双曲线方程为22221(0,0)x y a b a b-=>>，如图所示，AB BM =，，过点M 作MN x ⊥轴，垂足为N ，在Rt BMN ∆中，BN a =，3MN a =，故点M 的坐标为(2,3)M a a ，代入双曲线方程得2222a b a c ==-，即222c a =，所以2e =，故选D ．43．（2014年全国普通高等学校招生统一考试文科数学（新课标Ⅰ）已知双曲线的离心率为2，则A ．2B ．C ．D ．1【答案】D【详解】由离心率c e a =可得: 222232a e a+==，解得：1a =．44．（2014年全国普通高等学校招生统一考试文科数学（新课标Ⅰ））已知抛物线C ：的焦点为,是C 上一点，，则A ．1B ．2C ．4D ．8【答案】A【详解】：根据抛物线的定义：到焦点的距离等于到准线的距离，又抛物线的准线方程为：14x =-，则有：014AF x =+，即有001544x x +=，可解得01x =． 45．（2014年全国普通高等学校招生统一考试理科数学（新课标Ⅰ））已知抛物线C ：的焦点为F ，准线为，P 是上一点，Q 是直线PF 与C 得一个交点，若4FP FQ =，则A ．B ．C ．D ．【答案】B【详解】：如图所示，因为4FP FQ =，故34PQ PF =，过点Q 作QM l ⊥，垂足为M ，则//QM x 轴，所以344MQ PQ PF==，所以3MQ =，由抛物线定义知，3QF MQ ==，选B ．46．（2014年全国普通高等学校招生统一考试文科数学（全国Ⅰ卷））设F 为抛物线2:3C y x =的焦点，过F 且倾斜角为30的直线交C 于A ，B 两点，则AB =A ．3B ．6C ．12D ．【答案】C【详解】：由题意，得3(,0)4F ．又因为0k tan 30==，故直线AB 的方程为3)4y x =-，与抛物线2=3y x 联立，得21616890x x -+=，设1122(,),(,)A x y B x y ，由抛物线定义得，12AB x x p =++=168312162+=，选C ．47．（2014年全国普通高等学校招生统一考试文科数学（全国Ⅰ卷））设点()0,1M x ，若在圆22:+1O x y =上存在点N ，使得45OMN ∠=︒，则0x 的取值范围是（）A ．[]1,1- B ．11,22⎡⎤-⎢⎥⎣⎦C ．⎡⎣D ．⎡⎢⎣⎦【答案】A【详解】：依题意，直线MN 与圆O 有公共点即可，即圆心O 到直线MN 的距离小于等于1即可，过O 作OA⊥MN ，垂足为A ，在Rt OMA ∆中，因为OMA ∠045=，故0sin 45OA OM ==1≤，所以OM ≤≤011x -≤≤．48．（2014年全国普通高等学校招生统一考试理科数学（全国Ⅰ卷））设F 为抛物线C:23y x =的焦点，过F且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则 ⅠOAB 的面积为A B C ．6332D ．94【答案】D【详解】：直线AB 的方程为3)34y x =-，代入抛物线的方程可得：2490y --=，设A 11(,)x y 、B 22(,)x y ，则所求三角形的面积为1324⨯94，故选D.49．（2013年全国普通高等学校招生统一考试文科数学（新课标1卷））为坐标原点，为抛物线的焦点，为上一点，若，则的面积为 A ． B ．C ．D ．【答案】C【详解】易知OF =P 点作准线的垂线交于M ，可知PM =F 在线段PM 上的射影记为F '，则F M '=F P '=F F '=1·2S == 50．（2013年全国普通高等学校招生统一考试理科数学（新课标1卷）已知椭圆22x a＋22y b ＝1(a>b>0)的右焦点为F(3,0)，过点F 的直线交椭圆于A 、B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为A ．245x ＋236y ＝1B ．236x ＋227y ＝1C ．227x ＋227x ＝1D ．218y ＋218x ＝1【答案】D 【详解】设11(,)A x y 、22(,)B x y ，所以2211222222221{1x y a b x y a b +=+=，运用点差法，所以直线AB 的斜率为22b k a =，设直线方程为22(3)b y x a=-，联立直线与椭圆的方程222224()690a b x b x b a +-+-=，所以2122262b x x a b +==+；又因为229a b -=，解得229,18b a ==.51．（2012年全国普通高等学校招生统一考试理科数学）设1F 、2F 是椭圆E ：22221(0)x y a b a b+=>>的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30的等腰三角形，则E 的离心率为 A ．12B ．23C ．34D ．45【答案】C【详解】：如下图所示，21F PF ∆是底角为30的等腰三角形，则有1221221,30F F PF PF F F PF =∠=∠= 所以2260,30PF A F PA ∠=∠=，所以22322322PF AF a c a c ⎛⎫==-=- ⎪⎝⎭又因为122F F c =，所以，232c a c =-，所以34c e a == 所以答案选C.二、填空题52．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））已知F 为双曲线2222:1(0,0)x y C a b a b-=>>的右焦点，A 为C 的右顶点，B 为C 上的点，且BF 垂直于x 轴.若AB 的斜率为3，则C 的离心率为______________. 【答案】2【分析】联立22222221x cx y a b a b c =⎧⎪⎪-=⎨⎪⎪=+⎩，解得2x c b y a =⎧⎪⎨=±⎪⎩，所以2b BF a =.依题可得，3BF AF =，AF c a =-，即()2223b c a a c a a c a -==--，变形得3c a a +=，2c a =, 因此，双曲线C 的离心率为2. 故答案为：2．53．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））设双曲线C ：22221x y a b-= (a >0，b >0)的一条渐近线为yx ，则C 的离心率为_________．【分析】由双曲线方程22221x y a b-=可得其焦点在x 轴上，因为其一条渐近线为y =，所以b a =c e a ===54．（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120F B F B ⋅=，则C 的离心率为____________．【答案】2. 【分析】如图，由1,F A AB =得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线，即22//,2.BF OA BF OA =由120F B F B =，得121,,F B F B OA F A ⊥⊥则1OB OF =有1AOB AOF ∠=∠，又OA 与OB 都是渐近线，得21,BOF AOF ∠=∠又21BOF AOB AOF π∠+∠+∠=，得02160,BOF AOF BOA ∠=∠=∠=．又渐近线OB 的斜率为0tan 60ba==2c e a ====． 55．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））设12F F ，为椭圆22:+13620x y C =的两个焦点，M为C 上一点且在第一象限.若12MF F △为等腰三角形，则M 的坐标为___________.【答案】(【分析】由已知可得2222236,20,16,4a b c a b c ==∴=-=∴=，11228MF F F c ∴===．Ⅰ24MF =．设点M 的坐标为()()0000,0,0x y x y >>，则121200142MF F S F F y y =⋅⋅=△，又1201442MF F S y =⨯=∴=△0y ，22013620x ∴+=，解得03x =（03x =-舍去）， M ∴的坐标为(．56．（2018年全国卷Ⅰ理数高考试题）已知点()11M ，-和抛物线24C y x =：，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若90AMB ∠=︒，则k =________．【答案】2【分析】：设()()1122A ,,B ,x y x y 则2112224{4y x y x ==所以22121244y y x x -=-所以1212124k y y x x y y -==-+取AB 中点()00M'x y ，,分别过点A,B 作准线x 1=-的垂线，垂足分别为A ,B'' 因为AMB 90∠︒=,()()'111MM '222AB AF BF AA BB ∴==+=+'，因为M’为AB 中点，所以MM’平行于x 轴因为M(-1,1)所以01y =，则122y y +=即k 2= 故答案为2.57．（2017年全国普通高等学校招生统一考试理科数学（新课标1卷））已知双曲线C ：22221(0,0)x y a b a b-=>>的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线于交M 、N 两点，若60MAN ∠=，则C 的离心率为__________．。

(完整)十年真题_解析几何_全国高考理科数学.doc

十年真题(2010-2019)高考数学(理)分类汇编专题11 平面解析几何选择填空题(新课标Ⅰ卷)(解析版)

十年真题(2010-2019)高考数学(理)分类汇编专题12 平面解析几何解答题(新课标Ⅰ卷)(原卷版)

专题12 解析几何-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)

2012-2021十年全国高考数学(理科)真题分类汇编解析 立体几何大题

解析几何历年高考真题试卷--带详细答案

历年高考数学真题(全国卷整理版)完整版完整版.doc

十年高考理科数学真题 专题九 解析几何 二十八 抛物线及答案

历年高考数学真题(全国卷整理版)完整版完整版

十年真题(2010-2019)高考数学(理)分类汇编专题12 平面解析几何解答题(新课标Ⅰ卷)(解析版)

2010-2020全国高考数学卷1(理)解析几何题(含答案)

近十年全国高中数学联赛试题一试(解析几何)

立体几何十年高考题(带详细解析)

【最新】十年高考理科数学真题 专题九 解析几何 二十六 椭圆及答案

十年高考理科数学真题 专题九 解析几何 二十七 双曲线及答案

十年高考理科数学真题 专题九 解析几何 二十九 曲线与方程及答案(优质)

十年高考理科数学真题 专题九 解析几何 二十六 椭圆及答案(优质)

十年高考理科数学真题 专题九 解析几何 二十五 直线与圆及答案

十年高考理科数学真题 专题九 解析几何 二十九 曲线与方程及答案【推荐】

专题12 解析几何-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)

2012-2021十年全国高考数学(理科)真题分类汇编解析立体几何大题

十年高考理科数学真题专题九解析几何二十八抛物线及答案

【最新】十年高考理科数学真题专题九解析几何二十六椭圆及答案

十年高考理科数学真题专题九解析几何二十七双曲线及答案

十年高考理科数学真题专题九解析几何二十九曲线与方程及答案(优质)

十年高考理科数学真题专题九解析几何二十六椭圆及答案(优质)

十年高考理科数学真题专题九解析几何二十五直线与圆及答案

十年高考理科数学真题专题九解析几何二十九曲线与方程及答案【推荐】