小学五年纪奥数数字谜
高斯小学奥数五年级上册含答案_数字谜综合一

第二十讲数字谜综合一在三四年级,我们学过加减法填空格,破译字母、汉字的竖式谜、横式谜,添算符等数字谜问题,其中既有加减法,也有乘除法.它们各有一些特定的解题方法和思路,像加减法的进位、借位、错位,乘除法里面的末位分析、首位及位数的估算等,这些方法我们当然还要进一步的学习和训练.但在这一讲中,我们将主要运用前一阵刚学过的数论知识来解决相应的数字谜问题.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1.已知“BAD BAD GOOD+=”是一个正确的加法算式,其中相同的字母表示相同的数字,不同的字母表示不同的数字.已知GOOD不是8的倍数,那么四位数ABGD是多少?「分析」解决数字谜的题目,最关键在于找突破口.本题的突破口在哪里?练习1.在算式“+=路亨路亨刘吉吉”中,相同的汉字表示相同的数字,不同的汉字表示不同的数字.已知刘吉吉是8的倍数,那么四位数亨吉刘路是多少?例题2.从1~9中选出8个数字填入下式的各个方框中,使等式成立.⨯=⨯=952「分析」从算式来看,是要找出两个两位数的乘积为952.但是把952写成两个两位数的乘积,方法非常多,要从中选出两种满足题目条件还是挺麻烦的.我们不妨先把952分解质因数,通过分析它的构成来选出满足题目条件的填法.练习2.从1~9中选出8个数字填入下式的各个方框中,使等式成立.1026⨯=⨯=- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3.用0至9这10个数字恰好组成一位数、两位数、三位数、四位数各一个(每个数字只能用一次),且这四个数两两互质.其中的四位数是2940.另外三个数可能是多少?「分析」其中四位数是2940,那么组成另外三个数的6个数字就确定了.这四个数两两互质,那么另外三个数都与2940互质,我们就从2940的质因数构成入手.练习3.用1、2、3、4、5、6、7这7个数字恰好组成一个一位数和两个三位数,每个数字只用一次,使得这三个数两两互质.已知其中一个三位数已填好,它是714,那么其他两个数是多少?在前面的例题中,我们通过分解质因数,分析其质因数的构成,从而解决了问题.那如果没有给出具体的数,而是由数字或字母构成的特殊形式又该如何?是否也能分解质因数呢?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4.数数科学学数学.⨯=在上面的算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.请问:“数学”所代表的两位数是多少?「分析」对于乘法数字谜问题,我们一般先考虑个位数字.“数”ד学”的个位数字是“学”,但符合这一条件的情况有好几种,讨论的过程会很长.我们不妨再来仔细观察算式,能发现题中的“数数”有什么特点吗?练习4.⨯数好学好=棒棒棒.在上面的乘法算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字.那么“好棒”所代表的两位数是多少?例题5.在下面两个算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字.“花相似人不同”代表的六位数是多少?⨯=年年岁岁花相似÷=÷岁岁年年人不同「分析」“年年”、“岁岁”都是11的倍数,那么“花相似”所代表的三位数又是多少的倍数呢?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -在暑期中,我们学习了分数与循环小数的互化与四则运算,其实在数字谜里面也有分数与循环小数形式的问题.要解决这一类问题,需要我们灵活运用学过的循环小数的相关知识. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题6.已知a 是一个自然数,A 、B 是1至9中的数字,最简分数0.33222a A B =&&.请问:a 是多少? 「分析」等式两边一个是分数,一个是循环小数,可以都化成分数来比较.美妙的竖式荣获斯大林奖金的前苏联数学家、教育家柯尔⋅詹姆斯基曾以开发心灵美为题,列举了一些令人叹服的巧妙算法,其中之一如下:⨯=.例:88883333296237048 8 8 8⨯ 3 3 3 32 42 4 2 42 4 2 4 2 42 4 2 4 2 4 2 42 4 2 4 2 42 4 2 42 42 9 6 23 7 0 4这道题如果只是要算出结果,办法有很多,甚至拿计算器一按答案就出来了.但结果并非是重点,趣味性才是它的精髓所在.作业1. 在算式12233221⨯=⨯的两个方框中填入一个相同的数字,使得等式成立且等式关于等号是对称的.作业2. 用0至9这十个数码各1次,组成四位数、三位数、两位数和一位数各1个,并使这四个数两两互质.已知组成的四位数是1860,那么其他的三个数是多少?作业3. 将1~9这九个数字各一个填到下面的横式中,使等式成立(其中1,5,6已经填好).156⨯=⨯=作业4. 在算式“⨯⨯⨯=钓钓钓鱼岛钓鱼岛钓鱼岛钓鱼岛”中,“钓”、“鱼”、“岛”各代表一个不同的数字,要使算式成立,那么钓鱼岛表示的三位数是多少?作业5. 已知a 是一个自然数,b 是一个1至9中的数字,如果0.43555a b =&&,那么a 是多少?第二十讲 数字谜综合一例题1. 答案:3810详解:列竖式,易知D 是0,G 是1,且O 是偶数.那么GOOD 可能是1220、1440、1660和1880,其中1220和1660不是8的倍数,对应的加法算式分别是6106101220+=和8308301660+=,只有第二个满足.那么ABGD 是3810.例题2. 答案:56172834952⨯=⨯=详解:39522717=⨯⨯.考虑最大的质因数17,可知等号两边的两位数中都有17的倍数,可能是17、34、68.那么952可以拆成5617⨯、2834⨯和1468⨯.考虑到8个数字不重复,只能是56172834952⨯=⨯=.例题3. 答案:1、67、583或1、67、853详解:2229402357=⨯⨯⨯,则另外三个数不能有质因数2、3、5、7.其中一位数只能是1.还剩3、5、6、7、8这五个数字.两位数要分情况讨论:(1)个位数字为3,有53、73、83三组符合要求.对应的,三位数的三个数字分别为6、7、8;5、6、8;5、6、7.经检验,均不符合要求.(2)个位数字为7,有37、67两组符合要求.对应的,三位数的三个数字分别为5、6、8;3、5、8.经检验,有583、 853符合要求.综上所述,一共有:1、67、583;1、67、853两组答案.例题4. 答案:16详解:数数是11的倍数,所以学数学也是11的倍数.三位数中满足学数学这种形式,又是11的倍数的数有:121、242、363、484、616、737、858、979.依次验证几种情况,发现:当学数学为616,那么“学”为6,“数”为1,“⨯=数数科学学数学”变为“116616⨯=科”,可知“科”为5,符合题意.其它情况逐一检验,没有符合题目要求的答案.所以“数学”代表的两位数为16.例题5. 答案:968510详解:第一个算式可以变为“121⨯⨯=年岁花相似”,所以“花相似”是121的倍数.121的倍数中,三位数有121、242、363、484、605、726、847、968,共8个.“花相似”中没有重复数字,所以只可能是605、726、847、968之一.依次验证几种情况,发现:当“花相似”是968,那么“⨯年岁”为8,只能分别是1、8或2、4.其中1、8这种情况与“似”等于8矛盾,2、4这种情况满足要求.由第二个算式可以看出,“岁”小于“年”,因此岁2=,年4=.第二个算式为2244÷=÷人不同,已经用过的数字为2、4、6、8、9,所以“人”、“不”、“同”只能在0、1、3、5、7中取,只能分别是5和10.综上所述,“花相似人不同”所代表的六位数是968510.例题6. 答案:83详解:按照混循环小数化分数的方法,3330.339990A B A B-=&&,因此等式变为3332229990a A B -=,即4533399909990a A B -=,可知45333a A B ⨯=-.那么333A B -一定是45的倍数,即为5和9的倍数,因此333A B -计算结果的个位一定是0后者5,那么33A B 的个位一定是3或者8,即3B =或8B =.当3B =时,3333333330A B A A -=-=一定是9的倍数,可知3A =,原数为0.3333L 不符合题意.当8B =时,3333383335A B A A -=-=是9的倍数,可知7A =,原数为0.3738&&,符合题意,可知453735a ⨯=,a 为83.练习1. 答案:2417简答:易知刘是1,且吉是偶数.那么刘吉吉可能是100、122、144、166、188,其中只有144是8的倍数.那么算式应该是7272144+=,要求的四位数是2417.练习2. 答案:1026简答:310262319=⨯⨯.考虑最大的质因数19.等号两边都有19的倍数,可以是19、38、57.1026可以拆成1954⨯、3827⨯或5718⨯.考虑到8个数字互不相同,只能是195438271026⨯=⨯=.练习3. 答案:5和263简答:还有2、3、5和6可以用.71423717=⨯⨯⨯,一位数只能是5.剩下的三位数只能以3结尾,而623是7的倍数,不满足条件,只能是263.练习4. 答案:79简答:棒棒棒是37的倍数,说明等号左边一定有37的倍数,可能是37或74.经验证算式只能是2737=999⨯.作业1. 答案:1223113221⨯=⨯简答:21中有质因数7,所以23应该是7的倍数,只能填1或8,经检验,应填1.作业2. 答案:7,43,529简答:2186023531=⨯⨯⨯,一位数只能是7,另外两个数的末尾只能是3和9.剩下的数字之和除以3余2,只能拆成两个除以3余1的组合,所以4和2、5是分成两组,49是7的倍数,所以两位数只能是43,259是7的倍数,所以三位数只能是529.⨯=⨯=作业3.答案:439278156⨯=⨯=.简答:21562313=⨯⨯,所以是439278156作业4.答案:137=⨯⨯,所以简答:两个重复的三位数组成的六位数一定是1001的倍数,而100171113“钓”、“鱼”、“岛”分别为1、3、7.作业5.答案:235b,b=2,a=235.简答:由分数化循环小数的方法可得,5943a b÷⨯=.所以943。
五年级奥数专题-数字谜

五年级奥数专题-数字谜(一)数字谜小朋友们都玩过字谜吧,就是一种文字游戏,例如“空中码头”(打一城市名)。
谜底你还记得吗?记不得也没关系,想想“空中”指什么?“天”。
这个地名第1个字可能是天。
“码头”指什么呢?码头又称渡口,联系这个地名开头是“天”字,容易想到“天津”这个地名,而“津”正好又是“渡口”的意思。
这样谜底就出来了:天津。
算式谜又被称为“虫食算”,意思是说一道算式中的某些数字被虫子吃掉了无法辨认,需要运用四则运算各部分之间的关系,通过推理判定被吃掉的数字,把算式还原。
“虫食算”主要指横式算式谜和竖式算式谜,其中未知的数字常常用□、△、☆等图形符号或字母表示。
文字算式谜是前两种算式谜的延伸,用文字或字母来代替未知的数字,在同一道算式中不同的文字或字母表示不同的数字,相同的数字或字母表示同一个数字。
文字算式谜也是最难的一种算式谜。
在数学里面,文字也可以组成许许多多的数学游戏,就让我们一起来看看吧。
①横式字谜一、例题与方法指导例1 □,□8,□97在上面的3个方框内分别填入恰当的数字,可以使得这3个数的平均数是150。
那么所填的3个数字之和是多少?思路导航:150*3-8-97-=345所以3个数之和为3+4+5=12。
例2 在下列算式的□中填上适当的数字,使得等式成立:(1)6□□4÷56=□0□,(2)7□□8÷37=□1□,(3)3□□3÷2□=□17,(4)8□□□÷58=□□6。
分析:(1) 6104/56=109(2)7548/37=204(3) 3393/29=117(4)8468/58=146例3 在算式40796÷□□□=□99……98的各个方框内填入适当的数字后,就可以使其成为正确的等式。
求其中的除数。
分析:40796/102=399...98。
例4 我学数学乐×我学数学乐=数数数学数数学学数学在上面的乘法算式中,“我、学、数、乐”分别代表的4个不同的数字。
小学奥数数字谜试题及答案

小学奥数数字谜试题及答案一、数字谜题在小学奥数竞赛中,数字谜题常常是考察学生逻辑思维和数学运算能力的重要题型之一。
下面是几个常见的数字谜题,希望能帮助你培养数学思维和解题能力。
1. 数字排列将数字1、2、3、4、5、6、7、8、9组成一个9位数,使得每个数字出现且仅出现一次,并且每两个相邻的数字之间的差值都是一个质数。
请问有多少种可能的排列方式?2. 数字替换给定一个四位数abcd,满足条件:abcd * 4 = dcba。
请问abcd是多少?3. 数字矩阵在3x3的方格中填写数字1-9,使得每一行、每一列和对角线上的数字之和都相等。
请找出所有满足条件的填法。
二、数字谜题答案1. 数字排列的可能性有5040种。
解析:由于质数只有2、3、5、7,所以9位数中第一个数字只能是2或者5。
然后,考虑到相邻数字之间的差值为质数,我们可以根据2和5的不同情况来排列剩下的数字。
根据计算可知,数字排列的可能性有5040种。
2. abc*d = dcba,其中a、b、c、d是0-9的数字。
解析:由于abc * 4 = dcba,根据乘法的性质可知,a最大为2,且a 只能为1或2。
根据计算可知abcd为21978。
3. 数字矩阵的填法有8种。
解析:考虑到每一行、每一列和对角线上的数字之和都相等,由此可得数字矩阵的可能解。
2 9 47 5 36 1 84 3 89 5 12 7 66 7 21 5 98 3 48 1 63 5 74 9 24 9 23 5 78 1 62 7 69 5 14 3 86 1 87 5 32 9 48 3 41 5 96 7 2通过以上数学谜题的解析,我们可以锻炼和提升自己的逻辑思维和数学运算能力。
希望能够对大家的数学学习起到一定的帮助作用。
小五奥数:数字谜 经典练习

小五奥数:数字谜经典练习思维热身有三个筐,一个筐装着橘子和苹果,一个只装了桔子,另一个只装了苹果。
全部封装完毕,然后分别做了“混装”,“桔子”,“苹果”三个标签。
分别往三个筐子上贴,但发现全部贴错了,请你想一个办法,只从一个筐里拿出一个水果,并且不能往筐里看,就能纠正这个错误。
1.在下面算式等号左边合适的地方添上括号,使等式成立:5 + 7 × 8 + 12 ÷ 4 - 2 =202.在下列各式中填入符号+,—,×,÷,(),【】,使等式成立。
1 2 3=11 2 3 4=11 2 3 4 5=11 2 3 4 5 6=13.下面的算式是由1~9九个数字组成的,其中“7”已填好,请将其余各数填入口,使得等式成立:口口口÷口口=口-口=口-74.在下面的算式里填上括号,使等式成立(1)4 × 6 + 24 ÷ 6 - 5 =15(2)4 × 6 + 24 ÷ 6 - 5 =48(3)4 × 6 + 24 ÷ 6 - 5 =05.将2~7这六个数分别填入下列的口中,使等式成立:口+口-口=口×口÷口6.在口里填上合适的数,是算式成立。
口9 口9— 1 口9 口1 1 1 17.把1~9分别填入下面四个算式的九个口中,使得等式都成立口+口=6 口×口=8口-口=6 口口÷口=88. 在下列算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字,求出这个等式:(1)我学数学(2)努学数学努力数学努力学+ 学+ 努力学习4 4 8 85 4 3 2的数字,求出这个等式:学数学用数学学好数学+ 用好数学数学学为用10. 在下面残缺的算式中,只写了3个数字1,其余的数都不是1,那么这个算式的乘积是()11.下面乘法算式中,A+B+C+D+E=( )1 A B C D E× 3A B C D E 1同的数字,那么“学+奥+数”等于()学+奥×奥=学奥,(学+数)×(学+数)=学数。
五年级奥数数字谜的例题解答

五年级奥数数字谜的例题解答
五年级奥数数字谜的例题解答
(数字迷)下面算式中,每一汉字代表一个数字,不同的汉子代表不同的'数字,数数×科学=学数学,那么,“数学”两字代表的两位数是。
答案与解析:思路分析,“数数”所代表的数字一定是11的倍数,那么可能的两位数是11,22,33,…,99,先从11着手试吧,“学数学”代表的数字一定也是11的倍数,2×学-数也是11的倍数,经试算答案是11×56=616,所以“数学”两字代表的两位数是16。
五年级奥数数字谜

数字谜涉及质数与合数等概念,以及需要利用数的整除特征、分解质因数等数论手段解的数字谜问题.1.试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次: 口口口(这是一个三位数).口口口(这是一个三位数),口(这是一个一位数),使得这三个数中任意两个都互质.已知其中一个三位数已填好,它是714,求其他两个数.【分析与解】714=2×3×7×17.由此可以看出,要使最下面方框中的数与714互质,在剩下未填的数字2,3,5,6中只能选5,也就是说,第三个数只能是5.现在来讨论第二个数的三个方框中应该怎样填2,3,6这3个数字.因为任意两个偶数都有公约数2,而714是偶数,所以第二个的三位数不能是偶数,因此个位数字只能是3.这样一来,第二个三位数只能是263或623.但是623能被7整除,所以623与714不互质.最后来看263这个数.通过检验可知:714的质因数2,3,7和17都不是263的因数,所以714与263这两个数互质.显然,263与5也互质.因此,其他两个数为263和5.2.如图19-1,4个小三角形的顶点处有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形3个顶点上的数之和相等.问这6个质数的积是多少?【分析与解】设每个小三角形三个顶点上的数的和都是S.4个小三角形的和S相加时,中间三角形每个顶点上的数被算了3次,所以 4S=2S+20,即S=10.这样,每个小三角形顶点上出现的三个质数只能是2,3,5,从而六个质数是2,2,3,3,5,5,它们的积是:2×2×3×3×5×5=9003.在图19-2.所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立.【分析与解】记两个乘数为7a b 和cd 其中a 、b 、c 、d 的值只能取自2、3、5或7.由已知条件,b 与c 相乘的个位数字仍为质数,这只可能是b 与c 中有一个是5另一个是3、5或7,如果b 不是5,那么c 必然是5,但73×5=365、77×5=385的十位数字都不是质数.因此b 是5,c 是3、5、7中的一个,同样道理,d 也是3、5、7中的一个.再由已知条件,75a 的乘积的各位数字全是质数,所以乘积肯定大于2000,满足积大于2000且a 、c 取质数,只有以下六种情况:775×3=2325,575×5=2875,775×5=3875,375×7=2625,575×7=4025,775×7=5425.其中只有第一组的结果各位数字是质数,因此a=7,c=3,同理,d 也是3.最终算式即为775×33=255754.把一个两位数的个位数字与其十位数字交换后得到一个新数,它与原来的数加起来恰好是某个自然数的平方.那么这个和数是多少?【分析与解】 设原来的两位数为xy ,则交换十位数字与个位数字后的两位数为,两个数的和为yx ,两个数和为 xy +yx =1010x y x y +++()11x y =+是ll 的倍数,因为它是完全平方数,所以也是11 ×11=121的倍数.但是这个和小于100+100=200 <121×2,所以这个和数只能是121.5. 迎杯×春杯=好好好在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.那么“迎+春+杯+好”之和等于多少?【分析与解】 好好好=好×111=好×3×37.那么37必定是“迎杯”或“春杯”的约数,不妨设为“迎杯”的约数,那么“迎杯”为37或74. 当“迎杯”为37时,“春杯”为“好”×3,且“杯”为7,此时“春杯”为27,“好”为9,“迎+春+杯+好”之和为3+2+7+9=21;当“迎杯”为74时,“春杯”为“好”×3÷2,且“杯”为4,此时“春杯”为24,“好”为16,显然不满足.所以“迎+春+杯+好”之和为3+2+7+9=21.6.数数×科学=学数学在上面的算式中,每一汉字代表一个数字,不同的汉字代表不同的数字.那么“数学”所代表的两位数是多少?【分析与解】“学数学”是“数数”的倍数,因而是“数”与1l的倍数.学数学=学×101+数×10是“数”的倍数,而101是质数,所以“学”一定是“数”的倍数.又“学数学”是11的倍数,因而:“学+学-数”为11的倍数.因为“学”是“数”的倍数,从上式推出“数”是11的约数,所以“数”=1,“学”=(11+1)÷2=6.“数学”所代表的两位数是16.7.将1,2,3,4,5,6,7,8,9这9个数字分别填人下式的各个方框中,可使此等式成立:口口×口口=口口×口口口=3634.填好后得到三个两位数和一个三位数,这三个两位数中最大的一个是多少?【分析与解】3634=2×23×79,表达为两个两位数的乘积只能是(2×23)×79,即46×79;表达为一个两位数与一个三位数的乘积,只能是23×(2×79)=23×158.满足题意,所以这三个两位数中最大的一个是79.8.六年级的学生总人数是三位数,其中男生占35,男生人数也是三位数,而组成以上两个三位数的6个数字,恰好是l,2,3,4,5,6.那么六年级共有学生多少人?【分析与解】设六年级总人数为xyz,其中男生有abc人.有xyz×35=abc,即5abc=3xyz,其中xyz为5的倍数,所以z为5.而abc为3的倍数,所以其数字和a+b+c应为3的倍数,则在剩下的5个数中,a、b、c(不计顺序)只能为1,2,6或l,2,3或4,2,6或4,2,3.而c不能是偶数(不然z应为0),所以只能是l,2,6或1,2,3或4,2,3可能满足;又因为xyz最大为645,对应abc为387,即c不超过3.于是abc有可能为261,123,321,213,231,243这6种可能,验证只有当abc=261时,对应xyz为261÷3×5=435.所以六年级共有学毕435人.9.图19-3是三位数与一位数相乘的算式,在每个方格填入一个数字,使算式成立.那么共有多少种不同的填法?【分析与解】设1992=abc×d(a,b,c,d可以相同),有1992=2×2×2×3×83,其中d可以取2,3,4,6,8这5种,对应的算式填法有5种.10.在图19-4残缺的算式中,只写出3个数字l,其余的数字都不是1.那么这个算式的乘积是多少?【分析与解】如下图所示,为了方便说明,将某些数用字母标出.第4行口口1对应为AB×C,其个位为1,那么B×C的个位数字也是1,而B、C又均不能为1,所以只有3×7,9×9对应为1,那么B为9、7或3.第3行10口对应为AB×D,可能为100、102、103、104、105、106、107、108、109.103、107、109均为质数,没有两位数的约数,不满足;100、105没有个位数字为3、7、9的约数,不满足;102=17×6、104=13×8、106=53×2、108=27×4,但102、104对应的AB中4均为1,不满足.所以AB为53或27.当AB为27时,第4行为27×C,且个位数字为1,所以只能为27×3=8l,但不是三位数,不满足.当AB为53时,第4行为53×C,且个位数字为1,所以只能为53×7=371,因此被乘数必须为53,乘数为72,积为3816.11.图19-5是一个残缺的乘法竖式,在每个方框中填入一个不是2的数字,可使其成为正确的算式.那么所得的乘积是多少?【分析与解】 方法一:由已知条件,最后结果的首位数字不能是2,因此只能是3.这说明千位上作加法时有进位.百位数上相加时最多向千位进2,所以要使千位数有进位,其中的未知数字至少是10-2-2=6,即三个三位数加数中的第二个至少是600.因为它是第一个乘数与一个一位数字的乘积,因此该乘数肯定大于60.第二个乘数的百位数字与第一个乘数的乘积在220~229之间,所以它只能是3(否则4×60>229).而220~229之间个位数字不是2且是3的倍数的只有225=3×75和228=3×76.如果第一乘数是75,又第二个乘数的百位数字是3,那么它们的乘积小于75×400=30000,它的首位数字也就不可能是3,不满足.乘数是76,另一个乘数就要大于30000÷76>394,那么只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求.算式中所得的乘积为30096.方法二:为了方便说明,将某些位置标上字母,如下图所示,因为干位最多进1,而最终的乘积万位又不能是2,所以只能是3:而第5行对应为22口=AB×C ,其中C 不可能为1,又不能为2,那么最小为3.当C 为3时,22口=AB×3,那么A 只能为7,B 只能为4,5或6,(1)当B 为4时,74×3=222,第5行个位为2,不满足题意;(2)当B 为5时,AB×CDE 对应为75×3DE ,小于30000,不满足;(3)当B 为6时,AB×CDE 对应为76×3DE ,D 只能为9,此时第4行对应为AB ×D 即76×9=684.因为30000÷76>394,所以39E 只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求.验证C 取其他值时没有满足题意的解.所以算式中所得的乘积为30096.12.请补全图19-6这个残缺的除法竖式.问这个除法算式的商数是多少?【分析与解】 易知除号下第二行的首位为9.除号下第一行开头两位为1、0,商的十位为0.第二行9口对应为CD ×A,(1)9口不可能为90,不然第一行前三位10口与第二行90的差不可能为一位数,不满足第三行特征;(2)9口对应为91时,第三行的首位对应为10口-91,最小为9,所以只能为9,那么有91=CD×A ,928=CD×B ,不可能;(3)9口对应为92时,第三行的首位对应为10口-92,最小为8,所以可能为8、9,①如果为9,那么对应有92=CD×A ,928=CD×B ,不可能;②如果为8,那么对应有92=CD×A ,828=CD×B ,不难得知A=l,B=9,CD=92时满足,那么被除数为92×109=10028.验证没有其他的情况满足,所以这个除法算式的商数为109.13.若用相同汉字表示相同数字,不同汉字表示不同数字,则在等式学习好勤动脑×5=勤动脑学习好×8中,“学习好勤动脑”所表示的六位数最小是多少?【分析与解】 设“学习好”为x,“勤动脑”为Y,则“学习好勤动脑”为1000X+Y,“勤动脑学习好”为1000y+x ,有(1000x+Y)×5=(1000y +x )×8,化简有4992x=7995y,4992=128×3×13,7995=3×41×5×13,即128x=205y,有205,128x y =⎧⎨=⎩410,256x y =⎧⎨=⎩615,384x y =⎧⎨=⎩820512x y =⎧⎨=⎩所以,“学习好勤动脑”所表示的六位数可能为205128,410256,615384,820512,但是不能有重复数字,所以只有410256,615384满足,其中最小的是41025614.互为反序的两个自然数的积是92565,求这两个互为反序的自然数.(例如102和201,35和53,11和11,…,称为互为反序的数,但120和2l 不是互为反序的数.)【分析与解】 首先可以确定这两个自然数均为三位数,不然得到的乘积不可能为五位数. 设ABC ×CBA =92565,那么C 、A 中必定有一个为5,一个为奇数.不妨设C 为5.5AB ×5BA =92565,那么A 只能为1,1551B B =92565.又注意到92565=3×3×5×11×1l×17.验证只有15B 为165时满足,所以这两个自然数为165、561.15.开放的中国盼奥运×口=盼盼盼盼盼盼盼盼盼上面的横式中不同的汉字代表不同的数字,口代表某个一位数.那么,“盼”字所代表的数字是多少?【分析与解】 我们从“口”中所应填入的一位自然数开始分析,设A=“开放的中国盼奥运”,B=“盼盼盼盼盼盼盼盼盼”.于是B=A×口.显然口内不会是1.由于口是B 的约数,因此口不会是“盼”所代表的数字,要不然A 就等于111111111,这说明口内不会是5,而111111111不是7的倍数,说明口内也不会是7.如果口内填3,则“盼”只能是1或2,当“盼”是1时,B÷3=37037037,不符合要求;当“盼”时2时,B ÷3=74074074,也不符合要求;说明口内不能填入3.口内也不会是偶数数字2、4、6和8.因为口内是偶数数字时,“盼”也是偶数数字,口内显然不会是2,如果口内是4,根据被4整除的特征,“盼”只能是8,这时A就成了一个九位数,说明口内不能是4;类似的,可以说明口内不能是6和8.综上所需,口的数字只能是9,这时利用91111...1个=12345679×9,可以得到9个盼盼盼盼...盼=12345679×9×盼.于是“盼”代表的数字必须同时满足下面两个条件:经验证知◇=盼=7,即86419753×9=777777777.。
五年级奥数数字谜综合一——分数小数数字迷

答案
【例1】 1981 【例2】最后只有1.5×2.4=3.6和1.5.×4.2=6.3两个答案。 【例3】 5 【例4】 83 【例5】6.8
2
A 7
是最简分数且
A 7
7 10
,A最小是____。
【例4】(★★★) 已知a是一个自然数,A、B是1至9中的数字, 最简分数 a 0.3A3B 。请问:a是多少? 222
1
【例5】(★★★) 在下图的竖式中,填上数字,使竖式成立,那么 商最大是多少?
本讲总结:
基础:整数数字谜 新增:小数四则运算
小数数字谜
有一个四位整数,在它的某位数字前面加上一个
小数点,再与这个四位数相加,得数是 2000.81,
求这个四位数是多少?
【例2】(★★★) 把1至6填入下面的方框中,每个数字恰好使用一 次,使得等式成立。请写出乘积的所有答案。
【例3】(★★★)2012走美杯五年级
第一讲:数字谜

五年级奥数课程部分第一讲:数字谜数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
(5○13○7)○(17○9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
使等式成立:□□□×□□=□□×□□=5568。
例3 在443后面添上一个三位数,使得到的六位数能被573整除。
例4 已知六位数33□□44是89的倍数,求这个六位数。
例5 在左下方的加法竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字,请你用适当的数字代替字母,使加法竖式成立。
例6 在左下方的减法算式中,每个字母代表一个数字,不同的字母代表不同的数字。
请你填上适当的数字,使竖式成立。
练习11.在一个四位数的末尾添零后,把所得的数减去原有的四位数,差是621819,求原来的四位数。
2.在下列竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字。
请你用适当的数字代替字母,使竖式成立:3.在下面的算式中填上括号,使得计算结果最大:1÷2÷3÷4÷5÷6÷7÷8÷9。
4.在下面的算式中填上若干个(),使得等式成立:1÷2÷3÷4÷5÷6÷7÷8÷9=2.8。
5.将1~9分别填入下式的□中,使等式成立:□□×□□=□□×□□□=3634。
五年级奥数专题算式谜

五年级奥数专题算式谜【一】下面算式中“我”、“爱”、“数”、“学”四个汉字各代表一个数字,请问:“我”=?“爱”=?“数”=?“学”=?练习在下面算式的括号里填上合适的数。
1、()6 ()()2、()0 ()()+ 2 ()1 5 - 3 ()1 68 0 9 1 4 8 5 7【二】下面算式中的“数”、“学”、“俱”、“乐”、“部”这五个汉字各代表什么数字?练习下面题中的字母都表一个数字,不同的字母代表不同的数字,相同的字母代表相同的数字,这些字母各表示那些数字?1、2、【三】有一个六位数,它的个位数字是6,如果将6移至第一位前面,所得的新六位数是原数的4倍。
求原来的六位数。
练习1、已知六位数1ABCDE,这个六位数的3倍正好是ABCDE1。
求这个六位数。
2、下面竖式中每个汉字表示一个数字,不同的汉字表示不同的数字,请说出各个汉字分别表示什么数字?【四】下面竖式中每个小方格都代表一个数字,请把这个算式写完整。
练习1、把下面算式写完整。
2、在算式的“□”里填上合适的数。
【五】右图的五个方格中已经填写入84和72两个两位数,请你在其余三格中也分别填入一个两位数,使得横行的三个数与竖行的三个数的和相等,并且这五个两位数正好由0~9十个数字组成。
练习1、把0~9这十个数字填到圆圈内,每个数字只能用一次,使三个算式成立。
○+○=○○-○=○○×○=○○2、把0、1、2、3、4、7、9填到下面方格里,使等式成立。
□□□×□+□+□=□【六】把0、1、2、3、4、5、6、7、8、9这十个数字填入下面的小方格中,使三个等式都成立。
□+□=□□-□=□□×□=□□练习1、把1、2、3、4、5、6、7、8、这九个不同的数字分别填在○中,使下面的三个等式都成立。
○+○=○○-○=○○×○=○2、将0、1、2、3、4、5、6填到下列只有一、两位数的算式中,使等式成列。
○×○=○=○÷○【七】把2、3、4、5、7、9这六个数字分别填在六个“□”里,使乘积最大,应该怎样填?□□□×□□□练习1、用9、8、2、1四个数字组成两个两位数,并且使它们的积最大。
五年级奥数算式谜题

五年级奥数算式谜题一、加法算式谜题。
1. 在下面的加法算式中,每个字母代表一个数字,相同的字母代表相同的数字,不同的字母代表不同的数字。
求A、B、C的值。
ABC + CBA = 1232.解析:根据加法的竖式计算规则,个位上C + A = 2或者C + A = 12。
十位上B + B的结果个位是3,这是不可能的,因为B + B是偶数,所以个位上C+A = 12,向十位进1。
十位上B + B+1 = 13,则2B = 12,B = 6。
因为C + A = 12,假设A = 5,C = 7(答案不唯一)。
2. 求下面算式中□里的数字。
begin{array}{r}2□3 +□5□ hline 891end{array}解析:个位上3 + □=1,这是不可能的,所以个位上是3+□ = 11,□ = 8,向十位进1。
十位上□+5 + 1=9,□+6 = 9,□ = 3。
百位上2+□ = 8,□ = 6。
二、减法算式谜题。
3. 在下面的减法算式中,相同的字母代表相同的数字,不同的字母代表不同的数字。
求A、B、C的值。
ABC CBA = 198.解析:根据减法的竖式计算规则,个位上C A = 8或者C A=-2(因为不够减借位)。
假设C> A,C A = 8,那么C = 9,A = 1。
百位上A C不够减,向十位借1,10 + A C = 1,把A = 1,C = 9代入验证成立。
十位上B B = 0(因为被借位后相减为0)。
4. 求下面算式中□里的数字。
begin{array}{r}□2□ -□□1 hline 318end{array}解析:个位上□-1 = 8,□ = 9。
百位上□-□ = 3,因为十位上相减没有借位给百位,所以只能是4 1 = 3或者5 2=·s等情况,假设被减数的百位是4,减数的百位是1。
十位上2 □ = 1,□ = 1(因为个位相减没有向十位借位)。
三、乘法算式谜题。
五年级奥数专题 数字谜综合(学生版)

学科培优数学数字谜学生姓名授课日期教师姓名授课时长知识定位什么是数字迷?数字谜,一般是指那些含有未知数字或未知运算符号的算式。
这种不完整的算式,就像“谜”一样,要解开这样的谜,就得根据有关的运算法则、数的性质(和差积商的位数,数的整除性、奇偶性、尾数规律等)来进行正确的推理、判断。
重难点:1.横式迷问题2.竖式迷题中的除法式迷3.试验法在解决数字迷问题的应用考点: 1.复杂的横式迷题2.复杂的竖式谜题3.枚举和筛选相结合的方法(试验法)解决数字谜题知识梳理如何解决数字谜题?解数字谜,一般是从某个数的首位或末位数字上寻找突破口。
推理时应注意:(1)数字谜中的文字、字母或其它符号,只取0~9中的某个数字;(2)要认真分析算式中所包含的数量关系,找出尽可能多的隐蔽条件;(3)必要时应采用枚举和筛选相结合的方法(试验法),逐步淘汰掉那些不符合题意的数字;(4)数字谜解出之后,最好验算一遍。
横式的补填空格和破译字母问题中,解题的基本方法有尾数分析,分情况试算,数值估算,以及因数分解等。
同学们在解题时要灵活应用。
例题精讲【试题来源】【题目】在下面的3个方框内分别填入恰当的数字,可以使得这3个数的平均数是150。
那么所填的3个数字之和是多少?□,□8,□97【试题来源】【题目】在下列各等式的方框中填入恰当的数字,使等式成立,并且算式中的数字关于等号左右对称:(1)12×23□=□32×21, (2)12×46□=□64×21,(3)□8×891=198×8□, (4)24×2□1=1□2×42, (5)□3×6528=8256×3□。
【试题来源】【题目】在下列算式的□中填上适当的数字,使得等式成立:(1)6□□4÷56=□0□, (2)7□□8÷37=□1□,(3)3□□3÷2□=□17, (4)8□□□÷58=□□6。
五年级数学解密数学中的谜题

五年级数学解密数学中的谜题一、引言数学是一门神秘而又有趣的学科,它蕴藏着许多谜题等待探索。
本文将介绍五年级数学中的一些有趣的谜题,并尝试解密其中的奥秘。
二、第一道谜题:数字方块在数字方块谜题中,给出一些数字作为提示,通过观察数字之间的规律,找出正确的数字并填入方块中。
这需要我们运用数学思维和逻辑推理的能力。
例如,给出的数字串为2, 4, 6,则下一个数字很可能是8,因为这是一个等差数列,公差为2。
三、第二道谜题:数独数独是一种经典的数学谜题,由9x9的方格组成,每个方格内需要填入1至9的数字,要求每一行、每一列以及每一个3x3的方块中的数字不能重复。
这个游戏考验我们的逻辑思维、空间想象力和数字推理能力。
四、第三道谜题:拼图在数学课上,我们经常会遇到一些拼图谜题,需要将拼图的碎片重新组合成完整的图形。
这个过程需要我们观察图形的形状、尺寸和角度,并进行计算和推理,以找到正确的解法。
五、第四道谜题:趣味等式趣味等式是通过将数字和数学符号组合起来,使等式成立的谜题。
例如,给定一组数字和运算符号:1, 3, 4, +, -,我们需要通过合理地排列这些数字和符号,使得等式成立。
这需要我们运用加减法的基本原理和运算顺序的规则。
六、第五道谜题:数的推理数的推理谜题是通过观察一系列数字或图形的规律,找出隐藏在其中的规律并推断下一个数字或图形。
例如,给出的数字串为2, 4, 8,则下一个数字可能是16,因为每个数字都是前一个数字的两倍。
七、结论数学中的谜题涉及许多方面的数学知识和思维能力,通过解密这些谜题,我们不仅可以提高自己的数学水平,还可以培养逻辑思维和创造力。
希望这篇文章能给五年级的小朋友们带来启发,让他们对数学产生更大的兴趣和热爱。
八、参考文献无。
五年级奥数数字谜

数字谜涉及质数与合数等概念,以及需要利用数的整除特征、分解质因数等数论手段解的数字谜问题.1.试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次: 口口口(这是一个三位数).口口口(这是一个三位数),口(这是一个一位数),使得这三个数中任意两个都互质.已知其中一个三位数已填好,它是714,求其他两个数.【分析与解】714=2×3×7×17.由此可以看出,要使最下面方框中的数与714互质,在剩下未填的数字2,3,5,6中只能选5,也就是说,第三个数只能是5.现在来讨论第二个数的三个方框中应该怎样填2,3,6这3个数字.因为任意两个偶数都有公约数2,而714是偶数,所以第二个的三位数不能是偶数,因此个位数字只能是3.这样一来,第二个三位数只能是263或623.但是623能被7整除,所以623与714不互质.最后来看263这个数.通过检验可知:714的质因数2,3,7和17都不是263的因数,所以714与263这两个数互质.显然,263与5也互质.因此,其他两个数为263和5.2.如图19-1,4个小三角形的顶点处有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形3个顶点上的数之和相等.问这6个质数的积是多少?【分析与解】设每个小三角形三个顶点上的数的和都是S.4个小三角形的和S相加时,中间三角形每个顶点上的数被算了3次,所以4S=2S+20,即S=10.这样,每个小三角形顶点上出现的三个质数只能是2,3,5,从而六个质数是2,2,3,3,5,5,它们的积是:2×2×3×3×5×5=9003.在图19-2.所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立.【分析与解】记两个乘数为7a b 和cd 其中a 、b 、c 、d 的值只能取自2、3、5或7.由已知条件,b 与c 相乘的个位数字仍为质数,这只可能是b 与c 中有一个是5另一个是3、5或7,如果b 不是5,那么c 必然是5,但73×5=365、77×5=385的十位数字都不是质数.因此b 是5,c 是3、5、7中的一个,同样道理,d 也是3、5、7中的一个.再由已知条件,75a 的乘积的各位数字全是质数,所以乘积肯定大于2000,满足积大于2000且a 、c 取质数,只有以下六种情况:775×3=2325,575×5=2875,775×5=3875,375×7=2625,575×7=4025,775×7=5425.其中只有第一组的结果各位数字是质数,因此a=7,c=3,同理,d 也是3.最终算式即为775×33=255754.把一个两位数的个位数字与其十位数字交换后得到一个新数,它与原来的数加起来恰好是某个自然数的平方.那么这个和数是多少?【分析与解】 设原来的两位数为xy ,则交换十位数字与个位数字后的两位数为,两个数的和为yx ,两个数和为 xy +yx =1010x y x y +++()11x y =+是ll 的倍数,因为它是完全平方数,所以也是11 ×11=121的倍数.但是这个和小于100+100=200 <121×2,所以这个和数只能是121.5. 迎杯×春杯=好好好在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.那么“迎+春+杯+好”之和等于多少?【分析与解】 好好好=好×111=好×3×37.那么37必定是“迎杯”或“春杯”的约数,不妨设为“迎杯”的约数,那么“迎杯”为37或74. 当“迎杯”为37时,“春杯”为“好”×3,且“杯”为7,此时“春杯”为27,“好”为9,“迎+春+杯+好”之和为3+2+7+9=21;当“迎杯”为74时,“春杯”为“好”×3÷2,且“杯”为4,此时“春杯”为24,“好”为16,显然不满足.所以“迎+春+杯+好”之和为3+2+7+9=21.6. 数数×科学=学数学在上面的算式中,每一汉字代表一个数字,不同的汉字代表不同的数字.那么“数学”所代表的两位数是多少?【分析与解】“学数学”是“数数”的倍数,因而是“数”与1l的倍数.学数学=学×101+数×10是“数”的倍数,而101是质数,所以“学”一定是“数”的倍数.又“学数学”是11的倍数,因而:“学+学-数”为11的倍数.因为“学”是“数”的倍数,从上式推出“数”是11的约数,所以“数”=1,“学”=(11+1)÷2=6.“数学”所代表的两位数是16.7.将1,2,3,4,5,6,7,8,9这9个数字分别填人下式的各个方框中,可使此等式成立:口口×口口=口口×口口口=3634.填好后得到三个两位数和一个三位数,这三个两位数中最大的一个是多少? 【分析与解】3634=2×23×79,表达为两个两位数的乘积只能是(2×23)×79,即46×79;表达为一个两位数与一个三位数的乘积,只能是23×(2×79)=23×158.满足题意,所以这三个两位数中最大的一个是79.8.六年级的学生总人数是三位数,其中男生占35,男生人数也是三位数,而组成以上两个三位数的6个数字,恰好是l,2,3,4,5,6.那么六年级共有学生多少人?【分析与解】设六年级总人数为xyz,其中男生有abc人.有xyz×35=abc,即5abc=3xyz,其中xyz为5的倍数,所以z为5.而abc为3的倍数,所以其数字和a+b+c应为3的倍数,则在剩下的5个数中,a、b、c(不计顺序)只能为1,2,6或l,2,3或4,2,6或4,2,3.而c不能是偶数(不然z应为0),所以只能是l,2,6或1,2,3或4,2,3可能满足;又因为xyz最大为645,对应abc为387,即c不超过3.于是abc有可能为261,123,321,213,231,243这6种可能,验证只有当abc=261时,对应xyz为261÷3×5=435.所以六年级共有学毕435人.9.图19-3是三位数与一位数相乘的算式,在每个方格填入一个数字,使算式成立.那么共有多少种不同的填法?【分析与解】设1992=abc×d(a,b,c,d可以相同),有1992=2×2×2×3×83,其中d可以取2,3,4,6,8这5种,对应的算式填法有5种.10.在图19-4残缺的算式中,只写出3个数字l,其余的数字都不是1.那么这个算式的乘积是多少?【分析与解】如下图所示,为了方便说明,将某些数用字母标出.第4行口口1对应为AB×C,其个位为1,那么B×C的个位数字也是1,而B、C又均不能为1,所以只有3×7,9×9对应为1,那么B为9、7或3.第3行10口对应为AB×D,可能为100、102、103、104、105、106、107、108、109.103、107、109均为质数,没有两位数的约数,不满足;100、105没有个位数字为3、7、9的约数,不满足;102=17×6、104=13×8、106=53×2、108=27×4,但102、104对应的AB中4均为1,不满足.所以AB为53或27.当AB为27时,第4行为27×C,且个位数字为1,所以只能为27×3=8l,但不是三位数,不满足.当AB为53时,第4行为53×C,且个位数字为1,所以只能为53×7=371,因此被乘数必须为53,乘数为72,积为3816.11.图19-5是一个残缺的乘法竖式,在每个方框中填入一个不是2的数字,可使其成为正确的算式.那么所得的乘积是多少?【分析与解】方法一:由已知条件,最后结果的首位数字不能是2,因此只能是3.这说明千位上作加法时有进位.百位数上相加时最多向千位进2,所以要使千位数有进位,其中的未知数字至少是10-2-2=6,即三个三位数加数中的第二个至少是600.因为它是第一个乘数与一个一位数字的乘积,因此该乘数肯定大于60.第二个乘数的百位数字与第一个乘数的乘积在220~229之间,所以它只能是3(否则4×60>229).而220~229之间个位数字不是2且是3的倍数的只有225=3×75和228=3×76.如果第一乘数是75,又第二个乘数的百位数字是3,那么它们的乘积小于75×400=30000,它的首位数字也就不可能是3,不满足.乘数是76,另一个乘数就要大于30000÷76>394,那么只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求.算式中所得的乘积为30096.方法二:为了方便说明,将某些位置标上字母,如下图所示,因为干位最多进1,而最终的乘积万位又不能是2,所以只能是3:而第5行对应为22口=AB×C,其中C不可能为1,又不能为2,那么最小为3.当C为3时,22口=AB×3,那么A只能为7,B只能为4,5或6,(1)当B为4时,74×3=222,第5行个位为2,不满足题意;(2)当B为5时,AB×CDE对应为75×3DE,小于30000,不满足;(3)当B为6时,AB×CDE对应为76×3DE,D只能为9,此时第4行对应为AB×D即76×9=684.因为30000÷76>394,所以39E只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求.验证C取其他值时没有满足题意的解.所以算式中所得的乘积为30096.12.请补全图19-6这个残缺的除法竖式.问这个除法算式的商数是多少?【分析与解】 易知除号下第二行的首位为9.除号下第一行开头两位为1、0,商的十位为0.第二行9口对应为CD ×A,(1)9口不可能为90,不然第一行前三位10口与第二行90的差不可能为一位数,不满足第三行特征;(2)9口对应为91时,第三行的首位对应为10口-91,最小为9,所以只能为9,那么有91=CD×A ,928=CD×B ,不可能;(3)9口对应为92时,第三行的首位对应为10口-92,最小为8,所以可能为8、9,①如果为9,那么对应有92=CD×A ,928=CD×B ,不可能;②如果为8,那么对应有92=CD×A ,828=CD×B ,不难得知A=l,B=9,CD=92时满足,那么被除数为92×109=10028.验证没有其他的情况满足,所以这个除法算式的商数为109.13.若用相同汉字表示相同数字,不同汉字表示不同数字,则在等式学习好勤动脑×5=勤动脑学习好×8中,“学习好勤动脑”所表示的六位数最小是多少?【分析与解】 设“学习好”为x,“勤动脑”为Y,则“学习好勤动脑”为1000X+Y,“勤动脑学习好”为1000y+x ,有(1000x+Y)×5=(1000y +x )×8,化简有4992x=7995y,4992=128×3×13,7995=3×41×5×13,即128x=205y,有205,128x y =⎧⎨=⎩410,256x y =⎧⎨=⎩615,384x y =⎧⎨=⎩820512x y =⎧⎨=⎩所以,“学习好勤动脑”所表示的六位数可能为205128,410256,615384,820512,但是不能有重复数字,所以只有410256,615384满足,其中最小的是41025614.互为反序的两个自然数的积是92565,求这两个互为反序的自然数.(例如102和201,35和53,11和11,…,称为互为反序的数,但120和2l 不是互为反序的数.)【分析与解】 首先可以确定这两个自然数均为三位数,不然得到的乘积不可能为五位数. 设ABC ×CBA =92565,那么C 、A 中必定有一个为5,一个为奇数.不妨设C 为5.5AB ×5BA =92565,那么A 只能为1,1551B B =92565.又注意到92565=3×3×5×11×1l×17. 验证只有15B 为165时满足,所以这两个自然数为165、561.15.开放的中国盼奥运×口=盼盼盼盼盼盼盼盼盼上面的横式中不同的汉字代表不同的数字,口代表某个一位数.那么,“盼”字所代表的数字是多少?【分析与解】 我们从“口”中所应填入的一位自然数开始分析,设A=“开放的中国盼奥运”,B=“盼盼盼盼盼盼盼盼盼”.于是B=A×口.显然口内不会是1.由于口是B 的约数,因此口不会是“盼”所代表的数字,要不然A 就等于111111111,这说明口内不会是5,而111111111不是7的倍数,说明口内也不会是7.如果口内填3,则“盼”只能是1或2,当“盼”是1时,B÷3=37037037,不符合要求;当“盼”时2时,B ÷3=74074074,也不符合要求;说明口内不能填入3.口内也不会是偶数数字2、4、6和8.因为口内是偶数数字时,“盼”也是偶数数字,口内显然不会是2,如果口内是4,根据被4整除的特征,“盼”只能是8,这时A 就成了一个九位数,说明口内不能是4;类似的,可以说明口内不能是6和8.综上所需,口的数字只能是9,这时利用91111...1个=12345679×9,可以得到9个盼盼盼盼...盼=12345679×9×盼.于是“盼”代表的数字必须同时满足下面两个条件:经验证知◇=盼=7,即86419753×9=777777777.。
五年级奥数-数阵图与数字谜(含解析)
数阵图与数字谜教学目标1. 熟悉数阵图与数字谜的题目特点;2. 掌握数阵图与数字谜的解题思路。
精讲讲练数阵图数阵图是把一些数按照一定规则填在某一特定图形的规定位置上而来的图形,有时简称数阵。
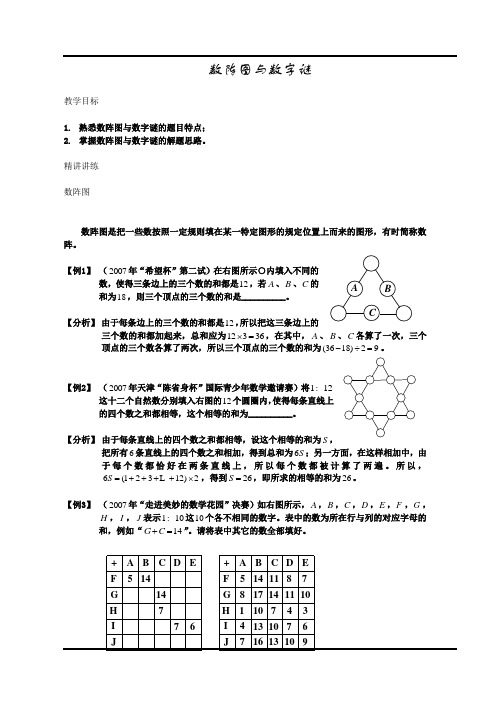
【例1】 (2007年“希望杯”第二试)在右图所示○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点的三个数的和是__________。
【分析】 由于每条边上的三个数的和都是12,所以把这三条边上的三个数的和都加起来,总和应为12336⨯=,在其中,A 、B 、C 各算了一次,三个顶点的三个数各算了两次,所以三个顶点的三个数的和为(3618)29-÷=。
【例2】 (2007年天津“陈省身杯”国际青少年数学邀请赛)将112:这十二个自然数分别填入右图的12个圆圈内,使得每条直线上的四个数之和都相等,这个相等的和为__________。
【分析】 由于每条直线上的四个数之和都相等,设这个相等的和为S ,把所有6条直线上的四个数之和相加,得到总和为6S ;另一方面,在这样相加中,由于每个数都恰好在两条直线上,所以每个数都被计算了两遍。
所以,6(12312)2S =++++⨯L ,得到26S =,即所求的相等的和为26。
【例3】 (2007年“走进美妙的数学花园”决赛)如右图所示,A ,B ,C ,D ,E ,F ,G ,H ,I ,J 表示110:这10个各不相同的数字。
表中的数为所在行与列的对应字母的和,例如“14G C +=”。
请将表中其它的数全部填好。
C BA【分析】 由于5A F +=,14B F +=,所以1459B A -=-=,所以A 和B 只能是0和9。
因此可以推出:0A =,9B =,6C =,3D =,2E =,5F =,8G =,1H =,4I =,7J =。
可得右下图。
【例4】 (2007年“走进美妙的数学花园”初赛)从1、2、3…20这20个数中选出9个不同的数放入33⨯的方格表中,使得每行、每列、每条对角线上的三个数的和都相等。
小学五年纪奥数数字谜

数字谜综合(ii)概述涉及质数与合数等概念,以及需要利用数的整除特征、分解质因数等数论手段解的数字谜问题.典型问题1. 试将1,2,3,4,5,6,7 分别填入下面的方框中,每个数字只用一次:口口口(这是一个三位数).口口口(这是一个三位数),口(这是一个一位数),使得这三个数中任意两个都互质•已知其中一个三位数已填好,它是714,求其他两个数.【分析与解】714=2X 3X 7X 17.由此可以看出,要使最下面方框中的数与714互质,在剩下未填的数字2,3,5 , 6中只能选5,也就是说,第三个数只能是5.现在来讨论第二个数的三个方框中应该怎样填2,3,6这3个数字.因为任意两个偶数都有公约数2,而714是偶数,所以第二个的三位数不能是偶数,因此个位数字只能是3.这样一来,第二个三位数只能是263或623.但是623能被7整除,所以623与714不互质.最后来看263这个数.通过检验可知:714的质因数2,3,7和17都不是263的因数,所以714与263 这两个数互质.显然,263与5也互质.因此,其他两个数为263和5.2. 如图19-1,4个小三角形的顶点处有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20, 而且每个小三角形3个顶点上的数之和相等.问这6个质数的积是多少?【分析与解】设每个小三角形三个顶点上的数的和都是S.4个小三角形的和S相加时,中间三角形每个顶点上的数被算了3次,所以4S=2S+20,即S=10.这样,每个小三角形顶点上出现的三个质数只能是2,3,5,从而六个质数是2,2,3,3,5,5, 它们的积是:2X 2X 3X 3X 5X 5=9003. 在图19-2.所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立.【分析与解】记两个乘数为a7b和cd其中a、b、c、d的值只能取自2、3、5或7.由已知条件,b与c相乘的个位数字仍为质数,这只可能是b与c中有一个是5另一个是3、5或7, 如果b不是5,那么c必然是5,但73X 5 =365、77X5 =385的十位数字都不是质数.因此b是5,c是3、5、7中的一个,同样道理,d也是3、5、7中的一个.再由已知条件,更的乘积的各位数字全是质数,所以乘积肯定大于2000,满足积大于2000且a、c 取质数,只有以下六种情况:775 X 3=2325, 575X 5=2875, 775X 5=3875,375X 7=2625 ,575 X 7=4025, 775X 7=5425.其中只有第一组的结果各位数字是质数,因此a=7,c=3,同理,d也是3.最终算式即为775X 33=255754. 把一个两位数的个位数字与其十位数字交换后得到一个新数,它与原来的数加起来恰好是某个自然数的平方.那么这个和数是多少?【分析与解】设原来的两位数为xy,则交换十位数字与个位数字后的两位数为,两个数的和为yx,两个数和为xy + yx = 10x y x 10y 11 x y是II的倍数,因为它是完全平方数,所以也是11 X 11=121的倍数.但是这个和小于100+100=200 <121X2 ,所以这个和数只能是121.5. 迎杯X春杯=好好好在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.那么“迎+春+杯+好”之和等于多少?【分析与解】好好好=好乂11仁好X 3 X 37.那么37必定是“迎杯”或“春杯”的约数,不妨设为“迎杯”的约数,那么“迎杯”为37或74. 当“迎杯”为37时,“春杯”为“好” X 3,且“杯”为7,此时“春杯”为27, “好”为9, “迎+春+杯+好”之和为3+2+7+9=21;当“迎杯”为74时,“春杯”为“好” X 3 + 2 ,且“杯”为4,此时“春杯”为24, “好”为16,显然不满足.所以“迎+春+杯+ 好”之和为3+2+7+9=21.6. 数数X科学=学数学在上面的算式中,每一汉字代表一个数字,不同的汉字代表不同的数字•那么“数学”所代表的两位数是多少?【分析与解】“学数学”是“数数”的倍数,因而是“数”与11的倍数.学数学=学乂101+数X10是“数”的倍数,而101是质数,所以“学”一定是“数”的倍数.又“学数学”是11的倍数,因而:“学+学-数”为11的倍数.因为“学”是“数”的倍数,从上式推出“数”是11的约数,所以“数” =1 , “学” =(11+1) + 2=6.“数学”所代表的两位数是16.7. 将1,2,3,4,5,6,7,8,9 这9个数字分别填人下式的各个方框中,可使此等式成立:口口X口口=口口X 口口口=3634.填好后得到三个两位数和一个三位数,这三个两位数中最大的一个是多少?【分析与解】3634=2X 23X 79 ,表达为两个两位数的乘积只能是(2 X 23) X 79,即46X 79;表达为一个两位数与一个三位数的乘积,只能是23X (2 X 79) =23X 158.满足题意,所以这三个两位数中最大的一个是79.38. 六年级的学生总人数是三位数,其中男生占3,男生人数也是三位数,而组成以上两个三位数的6个数5字,恰好是1,2,3,4,5,6. 那么六年级共有学生多少人?【分析与解】设六年级总人数为xyz,其中男生有abc人.3有xyz X =abc,即5 abc =3 xyz,其中xyz为5的倍数,所以z为5.而abc为3的倍数,所以其数5字和a+b+c应为3的倍数,则在剩下的5个数中,a、b、c(不计顺序)只能为1,2,6或l,2,3 或4,2,6或4,2,3 .而c不能是偶数(不然z应为0),所以只能是l,2,6 或1,2,3或4,2,3可能满足;又因为xyz最大为645,对应abc为387,即c不超过3.于是abc有可能为261,123,321,213,231,243 这6种可能,验证只有当abc =261时,对应xyz为261 + 3X 5=435.所以六年级共有学毕435人.9. 图19-3是三位数与一位数相乘的算式,在每个方格填入一个数字,使算式成立•那么共有多少种不同的填法?【分析与解】设1992= abc X d(a,b,c,d 可以相同),有1992=2X 2X 2X 3X 83 ,其中d可以取2,3 ,4, 6,8这5种,对应的算式填法有5种.10. 在图19-4残缺的算式中,只写出3个数字I,其余的数字都不是1.那么这个算式的乘积是多少?【分析与解】如下图所示,为了方便说明,将某些数用字母标出.第4行口口1对应为ABX C,其个位为1,那么B X C的个位数字也是1,而BC又均不能为1,所以只有3X 7,9X9对应为1,那么B为9、7或3.第 3 行10 口对应为ABX D,可能为100、102、103、104、105、106、107、108、109.103、107、109均为质数,没有两位数的约数,不满足;100 、105没有个位数字为3、7、9的约数,不满足;102=17X 6、104=13X 8、106=53X 2、108=27X4 ,但102、104 对应的AB中4 均为1,不满足. 所以AB 为53或27.当AB为27时,第4行为27XC ,且个位数字为1,所以只能为27X 3=81 ,但不是三位数,不满足.当AB为53时,第4行为53X C,且个位数字为1,所以只能为53X 7=371 ,因此被乘数必须为53,乘数为72,积为3816.11. 图19-5是一个残缺的乘法竖式,在每个方框中填入一个不是2的数字,可使其成为正确的算式•那么所得的乘积是多少?【分析与解】方法一:由已知条件,最后结果的首位数字不能是2,因此只能是3.这说明千位上作加法时有进位.百位数上相加时最多向千位进2,所以要使千位数有进位,其中的未知数字至少是10-2-2=6,即三个三位数加数中的第二个至少是600.因为它是第一个乘数与一个一位数字的乘积,因此该乘数肯定大于60.第二个乘数的百位数字与第一个乘数的乘积在220〜229之间,所以它只能是3(否则4X 60>229).而220〜229之间个位数字不是2且是3的倍数的只有225=3X 75和228=3X 76.如果第一乘数是75,又第二个乘数的百位数字是3,那么它们的乘积小于75X 400 =30000,它的首位数字也就不可能是3,不满足.乘数是76,另一个乘数就要大于30000- 76>394 ,那么只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76 X396=30096满足题目的要求.算式中所得的乘积为30096.方法二:为了方便说明,将某些位置标上字母,如下图所示,因为干位最多进1,而最终的乘积万位又不能是2,所以只能是3:而第5行对应为22 口=ABX C ,其中C不可能为1,又不能为2,那么最小为3.当C为3时,22 口=ABX3 ,那么A只能为7,B只能为4,5或6,(1) 当B为4时,74X 3=222,第5行个位为2,不满足题意;(2) 当B为5时,ABX CDE对应为75X 3DE,小于30000,不满足;(3) 当B为6时,ABX CDE对应为76X 3DE.D只能为9,此时第4行对应为ABX D 即76X 9=684.因为30000- 76>394 ,所以39E 只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324. 由于各个数字都不能是2,所以只有76X 396=30096满足题目的要求.验证C取其他值时没有满足题意的解.所以算式中所得的乘积为30096.12.请补全图19-6这个残缺的除法竖式•问这个除法算式的商数是多少第二行9 口对应为CD X A,(1) 9 口不可能为90,不然第一行前三位10 口与第二行90的差不可能为一位数,不满足第三行特征;(2) 9 口对应为91时,第三行的首位对应为10 口-91,最小为9,所以只能为9,那么有9仁CD<A , 928=CD<B ,不可能;(3) 9 口对应为92时,第三行的首位对应为10 口-92,最小为8,所以可能为& 9,①如果为9,那么对应有92=CD XA , 928=CD<B ,不可能;Ex E E回—□ □ EE®2 2 g]□③□口□口【分析与解】易知除号下第二行的首位为9.除号下第一行开头两位为1、0,商的十位为0.TEE1 罔0 ) □ 0 3 27~ 回②⑧②国S S E验证没有其他的情况满足,所以这个除法算式的商数为109.②如果为8,那么对应有92=CDX A , 828=CD<B ,不难得知A=l,B=9,CD=92时满足,那么被除数为92 X 109=10028.13. 若用相同汉字表示相同数字,不同汉字表示不同数字,则在等式学习好勤动脑X 5=勤动脑学习好X8 中,“学习好勤动脑”所表示的六位数最小是多少?【分析与解】设“学习好”为x, “勤动脑”为Y,则“学习好勤动脑”为1000X+Y, “勤动脑学习好”为1000y+x,有(lOOOx+Y) X 5=(1000y +x) X8 ,化简有4992x=7995y, 4992=128X 3X 13,7995=3X41 X 5X 13,即x 205 x 410 x 615 x 820128x=205y,有,,,y 128 y 256 y 384 y 512所以,“学习好勤动脑”所表示的六位数可能为205128,410256,615384,820512,但是不能有重复数字,所以只有410256,615384满足,其中最小的是41025614. 互为反序的两个自然数的积是92565,求这两个互为反序的自然数.(例如102和201,35和53,11和11,…,称为互为反序的数,但120和21不是互为反序的数.)【分析与解】首先可以确定这两个自然数均为三位数,不然得到的乘积不可能为五位数.设ABC X CBA=92565,那么C、A中必定有一个为5, 一个为奇数•不妨设C为5.AB5 X 5BA =92565,那么A只能为1, 1B5 5B1 =92565.又注意到92565=3X 3X 5X 11X 11 X 17.验证只有1B5为165时满足,所以这两个自然数为165、561 .15. 开放的中国盼奥运X 口=盼盼盼盼盼盼盼盼盼上面的横式中不同的汉字代表不同的数字,口代表某个一位数.那么,“盼”字所代表的数字是多少?【分析与解】我们从“口”中所应填入的一位自然数开始分析,设A= “开放的中国盼奥运”,B= “盼盼盼盼盼盼盼盼盼”.于是B=A X 口.显然口内不会是 1 .由于口是B的约数,因此口不会是“盼”所代表的数字”这说明口内不会是5,,说明口内也不会是7.如果口内填3,则“盼”只能是1或2,当“盼”是1时,B+3=,不符合要求;当“盼”时2时,B, 也不符合要求;说明口内不能填入3.口内也不会是偶数数字2、4、6和8.因为口内是偶数数字时,“盼”也是偶数数字,口内显然不会是2,如果口内是4,根据被4整除的特征,“盼”只能是8,这时A就成了一个九位数,说明口内不能是4; 类似的,可以说明口内不能是6和8.综上所需,口的数字只能是9,这时利用1113.1,可以得到盼盼盼.4 4盼=9个1 9个盼X盼.于是“盼”代表的数字必须同时满足下面两个条件:经验证知^。
五年级奥数 第2讲 数字谜

第2讲数字谜(二)这一讲主要讲数字谜的代数解法及小数的除法竖式问题。
例1 在下面的算式中,不同的字母代表不同的数字,相同的字母代表相分析与解:这道题可以从个位开始,比较等式两边的数,逐个确定各个(100000+x)×3=10x+1,300000+3x=10x+1,7x=299999,x=42857。
这种代数方法干净利落,比用传统方法解简洁。
我们再看几个例子。
例2 在□内填入适当的数字,使左下方的乘法竖式成立。
求竖式。
例3 左下方的除法竖式中只有一个8,请在□内填入适当的数字,使除法竖式成立。
解:竖式中除数与8的积是三位数,而与商的百位和个位的积都是四位数,所以x=112,被除数为989×112=110768。
右上式为所求竖式。
代数解法虽然简洁,但只适用于一些特殊情况,大多数情况还要用传统的方法。
例4 在□内填入适当数字,使下页左上方的小数除法竖式成立。
分析与解:先将小数除法竖式化为我们较熟悉的整数除法竖式(见下页右上方竖式)。
可以看出,除数与商的后三位数的乘积是1000=23×53的倍数,即除数和商的后三位数一个是23=8的倍数,另一个是53=125的奇数倍,因为除数是两位数,所以除数是8的倍数。
又由竖式特点知a=9,从而除数应是96的两位数的约数,可能的取值有96,48,32,24和16。
因为,c=5,5与除数的乘积仍是两位数,所以除数只能是16,进而推知b=6。
因为商的后三位数是125的奇数倍,只能是125,375,625和875之一,经试验只能取375。
至此,已求出除数为16,商为6.375,故被除数为6.375×16=102。
右式即为所求竖式。
求解此类小数除法竖式题,应先将其化为整数除法竖式,如果被除数的末尾出现n个0,则在除数和商中,一个含有因子2n(不含因子5),另一个含有因子5n(不含因子2),以此为突破口即可求解。
例5 一个五位数被一个一位数除得到下页的竖式(1),这个五位数被另一个一位数除得到下页的竖式(2),求这个五位数。
小学五年纪奥数(数字谜)

数字谜综合(ii )概述涉及质数与合数等概念,以及需要利用数的整除特征、分解质因数等数论手段解的数字谜问题.典型问题1.试将1,2,3,4,5,6,7分别填入下面的方框中,每个数字只用一次:口口口(这是一个三位数).口口口(这是一个三位数),口(这是一个一位数),使得这三个数中任意两个都互质.已知其中一个三位数已填好,它是714,求其他两个数.【分析与解】714=2×3×7×17.由此可以看出,要使最下面方框中的数与714互质,在剩下未填的数字2,3,5,6中只能选5,也就是说,第三个数只能是5.现在来讨论第二个数的三个方框中应该怎样填2,3,6这3个数字.因为任意两个偶数都有公约数2,而714是偶数,所以第二个的三位数不能是偶数,因此个位数字只能是3.这样一来,第二个三位数只能是263或623.但是623能被7整除,所以623与714不互质.最后来看263这个数.通过检验可知:714的质因数2,3,7和17都不是263的因数,所以714与263这两个数互质. 显然,263与5也互质.因此,其他两个数为263和5.2.如图19-1,4个小三角形的顶点处有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形3个顶点上的数之和相等.问这6个质数的积是多少【分析与解】设每个小三角形三个顶点上的数的和都是S.4个小三角形的和S 相加时,中间三角形每个顶点上的数被算了3次,所以4S=2S+20,即S=10.这样,每个小三角形顶点上出现的三个质数只能是2,3,5,从而六个质数是2,2,3,3,5,5,它们的积是: 2×2×3×3×5×5=9003.在图19-2.所示算式的每个方框内填人一个数字,要求所填的数字都是质数,并使竖式成立.【分析与解】记两个乘数为7a b 和cd 其中a 、b 、c 、d 的值只能取自2、3、5或7.由已知条件,b 与c 相乘的个位数字仍为质数,这只可能是b 与c 中有一个是5另一个是3、5或7,如果b 不是5,那么c 必然是5,但73×5=365、77×5=385的十位数字都不是质数.因此b 是5,c 是3、5、7中的一个,同样道理,d 也是3、5、7中的一个.再由已知条件,75a 的乘积的各位数字全是质数,所以乘积肯定大于2000,满足积大于2000且a 、c 取质数,只有以下六种情况:775×3=2325,575×5=2875,775×5=3875,375×7=2625,575×7=4025,775×7=5425.其中只有第一组的结果各位数字是质数,因此a=7,c=3,同理,d 也是3.最终算式即为775×33=255754.把一个两位数的个位数字与其十位数字交换后得到一个新数,它与原来的数加起来恰好是某个自然数的平方.那么这个和数是多少【分析与解】设原来的两位数为xy ,则交换十位数字与个位数字后的两位数为,两个数的和为yx ,两个数和为xy +yx =1010x y x y +++()11x y =+是ll 的倍数,因为它是完全平方数,所以也是11×11=121的倍数.但是这个和小于100+100=200<121×2,所以这个和数只能是121.5.迎杯×春杯=好好好在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字.那么“迎+春+杯+好”之和等于多少【分析与解】好好好=好×111=好×3×37.那么37必定是“迎杯”或“春杯”的约数,不妨设为“迎杯”的约数,那么“迎杯”为37或74.当“迎杯”为37时,“春杯”为“好”×3,且“杯”为7,此时“春杯”为27,“好”为9,“迎+春+杯+好”之和为3+2+7+9=21;当“迎杯”为74时,“春杯”为“好”×3÷2,且“杯”为4,此时“春杯”为24,“好”为16,显然不满足.所以“迎+春+杯+好”之和为3+2+7+9=21.6.数数×科学=学数学在上面的算式中,每一汉字代表一个数字,不同的汉字代表不同的数字.那么“数学”所代表的两位数是多少【分析与解】“学数学”是“数数”的倍数,因而是“数”与1l的倍数.学数学=学×101+数×10是“数”的倍数,而101是质数,所以“学”一定是“数”的倍数.又“学数学”是11的倍数,因而:“学+学-数”为11的倍数.因为“学”是“数”的倍数,从上式推出“数”是11的约数,所以“数”=1,“学”=(11+1)÷2=6.“数学”所代表的两位数是16.7.将1,2,3,4,5,6,7,8,9这9个数字分别填人下式的各个方框中,可使此等式成立:口口×口口=口口×口口口=3634.填好后得到三个两位数和一个三位数,这三个两位数中最大的一个是多少【分析与解】3634=2×23×79,表达为两个两位数的乘积只能是(2×23)×79,即46×79;表达为一个两位数与一个三位数的乘积,只能是23×(2×79)=23×158.满足题意,所以这三个两位数中最大的一个是79.8.六年级的学生总人数是三位数,其中男生占35,男生人数也是三位数,而组成以上两个三位数的6个数字,恰好是l,2,3,4,5,6.那么六年级共有学生多少人【分析与解】设六年级总人数为xyz,其中男生有abc人.有xyz×35=abc,即5abc=3xyz,其中xyz为5的倍数,所以z为5.而abc为3的倍数,所以其数字和a+b+c应为3的倍数,则在剩下的5个数中,a、b、c(不计顺序)只能为1,2,6或l,2,3或4,2,6或4,2,3.而c不能是偶数(不然z应为0),所以只能是l,2,6或1,2,3或4,2,3可能满足;又因为xyz最大为645,对应abc为387,即c不超过3.于是abc有可能为261,123,321,213,231,243这6种可能,验证只有当abc=261时,对应xyz为261÷3×5=435.所以六年级共有学毕435人.9.图19-3是三位数与一位数相乘的算式,在每个方格填入一个数字,使算式成立.那么共有多少种不同的填法【分析与解】设1992=abc×d(a,b,c,d可以相同),有1992=2×2×2×3×83,其中d可以取2,3,4,6,8这5种,对应的算式填法有5种.10.在图19-4残缺的算式中,只写出3个数字l,其余的数字都不是1.那么这个算式的乘积是多少【分析与解】如下图所示,为了方便说明,将某些数用字母标出.第4行口口1对应为AB×C,其个位为1,那么B×C的个位数字也是1,而B、C又均不能为1,所以只有3×7,9×9对应为1,那么B为9、7或3.第3行10口对应为AB×D,可能为100、102、103、104、105、106、107、108、109.103、107、109均为质数,没有两位数的约数,不满足;100、105没有个位数字为3、7、9的约数,不满足;102=17×6、104=13×8、106=53×2、108=27×4,但102、104对应的AB中4均为1,不满足.所以AB为53或27.当AB为27时,第4行为27×C,且个位数字为1,所以只能为27×3=8l,但不是三位数,不满足.当AB为53时,第4行为53×C,且个位数字为1,所以只能为53×7=371,因此被乘数必须为53,乘数为72,积为3816.11.图19-5是一个残缺的乘法竖式,在每个方框中填入一个不是2的数字,可使其成为正确的算式.那么所得的乘积是多少【分析与解】方法一:由已知条件,最后结果的首位数字不能是2,因此只能是3.这说明千位上作加法时有进位.百位数上相加时最多向千位进2,所以要使千位数有进位,其中的未知数字至少是10-2-2=6,即三个三位数加数中的第二个至少是600.因为它是第一个乘数与一个一位数字的乘积,因此该乘数肯定大于60.第二个乘数的百位数字与第一个乘数的乘积在220~229之间,所以它只能是3(否则4×60>229).而220~229之间个位数字不是2且是3的倍数的只有225=3×75和228=3×76.如果第一乘数是75,又第二个乘数的百位数字是3,那么它们的乘积小于75×400=30000,它的首位数字也就不可能是3,不满足.乘数是76,另一个乘数就要大于30000÷76>394,那么只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求. 算式中所得的乘积为30096.方法二:为了方便说明,将某些位置标上字母,如下图所示,因为干位最多进1,而最终的乘积万位又不能是2,所以只能是3:而第5行对应为22口=AB×C ,其中C 不可能为1,又不能为2,那么最小为3.当C 为3时,22口=AB×3,那么A 只能为7,B 只能为4,5或6,(1)当B 为4时,74×3=222,第5行个位为2,不满足题意;(2)当B 为5时,AB×CDE 对应为75×3DE ,小于30000,不满足;(3)当B 为6时,AB×CDE 对应为76×3DE ,D 只能为9,此时第4行对应为AB ×D 即76×9=684.因为30000÷76>394,所以39E 只有395、396、397、398、399这五种可能,它们与76的乘积依次为30020、30096、30172、30248、30324.由于各个数字都不能是2,所以只有76×396=30096满足题目的要求. 验证C 取其他值时没有满足题意的解.所以算式中所得的乘积为30096.12.请补全图19-6这个残缺的除法竖式.问这个除法算式的商数是多少【分析与解】易知除号下第二行的首位为9.除号下第一行开头两位为1、0,商的十位为0.第二行9口对应为CD ×A,(1)9口不可能为90,不然第一行前三位10口与第二行90的差不可能为一位数,不满足第三行特征;(2)9口对应为91时,第三行的首位对应为10口-91,最小为9,所以只能为9,那么有91=CD×A ,928=CD×B ,不可能;(3)9口对应为92时,第三行的首位对应为10口-92,最小为8,所以可能为8、9,①如果为9,那么对应有92=CD×A ,928=CD×B ,不可能;②如果为8,那么对应有92=CD×A ,828=CD×B ,不难得知A=l,B=9,CD=92时满足,那么被除数为92×109=10028.验证没有其他的情况满足,所以这个除法算式的商数为109.13.若用相同汉字表示相同数字,不同汉字表示不同数字,则在等式学习好勤动脑×5=勤动脑学习好×8中,“学习好勤动脑”所表示的六位数最小是多少【分析与解】设“学习好”为x,“勤动脑”为Y,则“学习好勤动脑”为1000X+Y,“勤动脑学习好”为1000y+x , 有(1000x+Y)×5=(1000y +x )×8,化简有4992x=7995y,4992=128×3×13,7995=3×41×5×13,即128x=205y,有205,128x y =⎧⎨=⎩410,256x y =⎧⎨=⎩615,384x y =⎧⎨=⎩820512x y =⎧⎨=⎩ 所以,“学习好勤动脑”所表示的六位数可能为205128,410256,615384,820512,但是不能有重复数字,所以只有410256,615384满足,其中最小的是41025614.互为反序的两个自然数的积是92565,求这两个互为反序的自然数.(例如102和201,35和53,11和11,…,称为互为反序的数,但120和2l 不是互为反序的数.)【分析与解】首先可以确定这两个自然数均为三位数,不然得到的乘积不可能为五位数. 设ABC ×CBA =92565,那么C 、A 中必定有一个为5,一个为奇数.不妨设C 为5.5AB ×5BA =92565,那么A 只能为1,1551B B ⨯=92565.又注意到92565=3×3×5×11×1l×17. 验证只有15B 为165时满足,所以这两个自然数为165、561.15.开放的中国盼奥运×口=盼盼盼盼盼盼盼盼盼上面的横式中不同的汉字代表不同的数字,口代表某个一位数.那么,“盼”字所代表的数字是多少【分析与解】我们从“口”中所应填入的一位自然数开始分析,设A=“开放的中国盼奥运”,B=“盼盼盼盼盼盼盼盼盼”.于是B=A×口.显然口内不会是1.由于口是B 的约数,因此口不会是“盼”所代表的数字,,这说明口内不会是5,,说明口内也不会是7.如果口内填3,则“盼”只能是1或2,当“盼”是1时,B÷3=,不符合要求;当“盼”时2时,B,也不符合要求;说明口内不能填入3.口内也不会是偶数数字2、4、6和8.因为口内是偶数数字时,“盼”也是偶数数字,口内显然不会是2,如果口内是4,根据被4整除的特征,“盼”只能是8,这时A 就成了一个九位数,说明口内不能是4;类似的,可以说明口内不能是6和8.综上所需,口的数字只能是9,这时利用91111...1个,可以得到9个盼盼盼盼...盼=×盼.于是“盼”代表的数字必须同时满足下面两个条件:经验证知◇。
五年级奥数基础教程-数字谜小学

数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
解:将5568质因数分解为5568=26×3×29。
由此容易知道,将 5568分解为两个两位数的乘积有两种:58×96和64×87,分解为一个两位数与一个三位数的乘积有六种:12×464, 16×348, 24×232,29×192, 32×174, 48×116。
显然,符合题意的只有下面一种填法:174×32=58×96=5568。
例3 在443后面添上一个三位数,使得到的六位数能被573整除。
分析与解:先用443000除以573,通过所得的余数,可以求出应添的三位数。
由443000÷573=773 (71)推知, 443000+(573-71)=443502一定能被573整除,所以应添502。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
399 这五种可能 , 它们与 76 的乘积依次为 30020、 30096、 30172、 30248、 30324.
由于各个数字都不能是 2, 所以只有 76×396=30096 满足题目的要求.
验证 C取其他值时没有满足题意的解.
所以算式中所得的乘积为 30096.
12. 请补全图 19-6 这个残缺的除法竖式 . 问这个除法算式的商数是多少 ?
“数学”所代表的两位数是 16.
7. 将 1,2,3,4,5,6,7,8,9
这 9 个数字分别填人下式的各个方框中 , 可使此等式成立 : 口口×口口 =口
口×口口口 =3634.填好后得到三个两位数和一个三位数 , 这三个两位数中最大的一个是多少 ?
【分析与解】 3634=2×23×79 , 表达为两个两位数的乘积只能是 (2 ×23) × 79, 即 46×79;
4, 6,8 这 5 种 , 对应的算式填法有 5 种. 10. 在图 19-4 残缺的算式中 , 只写出 3 个数字 l, 其余的数字都不是 1. 那么这个算式的乘积是多少 ?
【分析与解】 如下图所示 , 为了方便说明 , 将某些数用字母标出. 第 4 行口口 1 对应为 AB× C, 其个位为 1, 那么 B× C 的个位数字也是 1, 而 B、C 又均不能为 1, 所以只 有 3× 7, 9×9对应为 1, 那么 B 为 9、 7 或 3. 第 3 行 10 口对应为 AB×D, 可能为 100、102、103、104、105、106、107、108、109.103 、107、109
表达为一个两位数与一个三位数的乘积 , 只能是 23×(2 ×79) =23×158.
满足题意 , 所以这三个两位数中最大的一个是 79.
8. 六年级的学生总人数是三位数
, 其中男生占 3 , 男生人数也是三位数 , 而组成以上两个三位数的 5
6 个数
字, 恰好是 l,2,3,4,5,6. 那么六年级共有学生多少人 ?
所以只能为 9, 那么有 91=CD×A, 928=CD×B, 不可能; (3)9 口对应为 92 时 , 第三行的首位对应为 10 口 -92, 最小为 8,
数字也就不可能是 3, 不满足.
乘数是 76, 另一个乘数就要大于 30000÷76>394 , 那么只有 395、 396、397、 398、 399 这五种可能 ,
它们与 76 的乘积依次为 30020、 30096、 30172、 30248、 30324. 由于各个数字都不能是 2, 所以只有
其中只有第一组的结果各位数字是质数 , 因此 a=7,c=3 ,同理 ,d 也是 3.
最终算式即为 775×33 =25575
4. 把一个两位数的个位数字与其十位数字交换后得到一个新数
, 它与原来的数加起来恰好是某个自然数
的平方 . 那么这个和数是多少 ?
【分析与解】 设原来的两位数为 xy , 则交换十位数字与个位数字后的两位数为 , 两个数的和为 yx ,
它是 714, 求其他两个数. 【分析与解】 714=2×3×7×17.
由此可以看出 , 要使最下面方框中的数与 714 互质 , 在剩下未填的数字 2,3,5 , 6 中只能选 5,也就
是说,第三个数只能是 5. 现在来讨论第二个数的三个方框中应该怎样填
2,3,6 这 3 个数字.
因为任意两个偶数都有公约数 2, 而 714 是偶数 , 所以第二个的三位数不能是偶数 , 因此个位数字只
【分析与解】 好好好 =好× 111=好× 3× 37.
那么 37 必定是“迎杯”或“春杯”的约数 , 不妨设为“迎杯”的约数 , 那么“迎杯”为 37 或 74.
当“迎杯”为 37 时 , “春杯”为“好”× 3, 且“杯”为 7, 此时“春杯”为 27, “好”为 9, “迎 +春
+杯 +好”之和为 3+2+7+9=21;
(1) 当 B 为 4 时 , 74×3=222 , 第 5 行个位为 2, 不满足题意;
(2) 当 B 为 5 时 , AB×CDE对应为 75×3DE, 小于 30000, 不满足;
(3) 当 B 为 6 时 , AB×CDE对应为 76×3DE,D 只能为 9, 此时第 4 行对应为
AB×D即 76×9=684 . 因为 30000÷76>394 , 所以 39E 只有 395、396、397、398、
数是多少 ?
【分析与解】 “学数学”是“数数”的倍数,因而是“数”与
1l 的倍数 . 学数学 =学× 101+数×
10 是“数”的倍数 , 而 101 是质数 , 所以“学”一定是“数”的倍数.
又“学数学”是 11 的倍数 , 因而 : “学 +学 - 数”为 11 的倍数.
因为“学”是“数”的倍数 , 从上式推出“数”是 11 的约数 , 所以“数” =1 , “学” =(11+1) ÷2=6.
数字谜综合( ii )
概述
涉及质数与合数等概念 , 以及需要利用数的整除特征、分解质因数等数论手段解的数字谜问题.
典型问题
1 . 试将 1,2,3,4,5,6,7 分别填入下面的方框中 , 每个数字只用一次 : 口口口 ( 这是一个三位数 ). 口口口
( 这是一个三位数 ), 口 ( 这是一个一位数 ), 使得这三个数中任意两个都互质 . 已知其中一个三位数已填好 ,
再由已知条件 , a 75 的乘积的各位数字全是质数 , 所以乘积肯定大于 2000, 满足积大于 2000 且 a、 c
取质数 , 只有以下六种情况:
775 × 3=2325, 575×5=2875 , 775×5=3875 , 375×7=2625 ,575 × 7=4025, 775×7=5425.
76×396=30096 满足题目的要求.
算式中所得的乘积为 30096.
方法二 :为了方便说明,将某些位置标上字母,如下图所示,因为干位最多进
1,而最终的乘积万位又不能是 2,所以只能是 3:
而第 5 行对应为 22 口=AB×C, 其中 C不可能为 1, 又不能为 2, 那么最小为 3.
当 C 为 3 时 ,22 口=AB×3, 那么 A 只能为 7,B 只能为 4,5 或 6,
均为质数 , 没有两位数的约数 , 不满足;
100 、 105 没有个位数字为 3、 7、9 的约数 , 不满足;
102=17×6、 104=13× 8、106=53×2、108=27×4, 但 102、 104 对应的 AB中 4 均为 1, 不满足.
所以 AB为 53 或 27.
当 AB为 27 时 , 第 4 行为 27×C, 且个位数字为 1, 所以只能为 27×3=8l , 但不是三位数 , 不满足.
当 AB为 53 时 , 第 4 行为 53× C, 且个位数字为 1, 所以只能为 53×7=371 , 因此被乘数必须为 53, 乘数
为 72, 积为 3816.
11. 图 19-5 是一个残缺的乘法竖式 , 在每个方框中填入一个不是 所得的乘积是多少 ?
2 的数字 , 可使其成为正确的算式 . 那么
因此 , 其他两个数为 263 和 5.
2. 如图 19-1,4 个小三角形的顶点处有 6 个圆圈 . 如果在这些圆圈中分别填上 6 个质数, 它们的和是 20,
而且每个小三角形 3 个顶点上的数之和相等 . 问这 6 个质数的积是多少 ?
【分析与解】 设每个小三角形三个顶点上的数的和都是
S.4 个小三角形的和 S 相加时 , 中间三角
【分析与解】 设六年级总人数为 xyz , 其中男生有 abc 人.
有 xyz × 3 = abc , 即 5 abc =3 xyz, 其中 xyz 为 5 的倍数 , 所以 z 为 5. 而 abc 为 3 的倍数, 所以其数 5
字和 a+b+c 应为 3 的倍数 , 则在剩下的 5 个数中 ,a 、 b、 c( 不计顺序 ) 只能为 1,2,6 或 l,2,3 或 4,2,6 或
能是 3. 这样一来 , 第二个三位数只能是 263 或 623. 但是 623 能被 7 整除 , 所以 623 与 714 不互质. 最后来看 263 这个数 . 通过检验可知 :714 的质因数 2,3,7 和 17 都不是 263 的因数 , 所以 714 与 263
这两个数互质.
显然 ,263 与 5 也互质.
【分析与解 】记两个乘数为 a 7b 和 cd 其中 a、 b、 c、 d 的值只能取自 2、 3、 5 或 7.
由已知条件 ,b 与 c 相乘的个位数字仍为质数 , 这只可能是 b 与 c 中有一个是 5 另一个是 3、5 或 7, 如果 b 不是 5, 那么 c 必然是 5, 但 73×5=365、77×5=385 的十位数字都不是质数 . 因此 b 是 5,c 是 3、5、 7 中的一个 , 同样道理 ,d 也是 3、 5、 7 中的一个.
261÷3×5=435. 所以六年级共有学法 ?
, 在每个方格填入一个数字 , 使算式成立 . 那么共有多少种不同
【分析与解】 设 1992= abc ×d( a,b,c,d 可以相同 ), 有 1992=2×2×2×3×83 , 其中 d 可以取 2,3 ,
【分析与解】 易知除号下第二行的首位为 9. 除号下第一行开头两位为 1、 0, 商的十位为 0.
第二行 9 口对应为 CD×A,
(1)9 口不可能为 90, 不然第一行前三位 10 口与第二行 90 的差不 可能为一位数 , 不满足第三行特征;
(2)9 口对应为 91 时 , 第三行的首位对应为 10 口 -91, 最小为 9,
【分析与解】 方法一 : 由已知条件 , 最后结果的首位数字不能是 2, 因此只能是 3. 这说明千位上作
