2017年成都市一诊测验考试数学试题及答案word理科
2017成都一诊

2017成都一诊篇一:成都七中2017届一诊模拟考试数学试卷(理科)成都七中2017届一诊模拟考试数学试卷(理科)考试时间:120分钟总分:150分命题人:刘在廷审题人:张世永一.选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求.把答案凃在答题卷上.) 1.设全集为R,集合A?{x|x2?9?0},B?{x|?1?x?5},则A?CRB?()A(?3,0)B(?3,?1]C(?3,?1)D(?3,3) 2.设i为虚数单位,复数i(1?i)的虚部为() A?1 B1 C?i Di????????????3.已知点O、A、B不在同一条直线上,点P为该平面上一点,且2OP?2OA+BA,则()A.点P不在直线AB上B.点P在线段AB上C.点P在线段AB的延长线上D.点P在线段AB的反向延长线上 4.我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是()A 44,45,56B 44,43,57C 44,43,56D 45,43,57 5.在三角形ABC中,sinA?A45,cosB?,则cosC?() 51333636333或 B C D 以上都不对 656565656.如图所示的程序框图输出的S是126,则条件①可以为()A n≤5Bn≤6Cn≤7 Dn≤87.住在狗熊岭的7只动物,它们分别是熊大,熊二,吉吉,毛毛,蹦蹦,萝卜头,图图。
为了更好的保护森林,它们要选出2只动物作为组长,则熊大,熊二至少一个被选为组长的概率为() A 1111110B C D24221218.某三棱锥的三视图如图所示,则该三棱锥的表面积是()A2?42??x?y?1?0?x?y?2?0?,又 9. 如果实数x,y满足关系?x?0???y?02x?y?7?c恒成立,则c的取值范围为()x?3AB???,3?C?3,???D?2,3?gx)?(fx)?ax与x轴有三个不同的交10.已知函数f(x)?|lnx|,若在区间[,3]内,曲线(13点,则实数a的取值范围是 ( ) A[ln31ln3111,) B[,) C(0,) D(0,) 3e32ee2etanx的最小正周期为n,则m?n的2?2tan2x11.函数y?cosx?sin2x的最小值为m,函数y?值为()??A???C??? 22x2y2c12.已知椭圆2?2?1(a?b?0,c?e?),其左、右焦点分别为F1,F2,关abaa2a2于椭圆有以下四种说法:(1)设A为椭圆上任一点,其到直线l1:x??的距,l2:x?cc|AF1||AF2|离分别为d2,d1,则;(2)设A为椭圆上任一点,AF1,AF2分别与椭圆交于?d1d2|AF1||AF2|2(1?e2)(当且仅当点A在椭圆的顶点取等);(3)设A为??B,C两点,则2|F1B||F2C|1?e椭圆上且不在坐标轴上的任一点,过A的椭圆切线为l,M为线段F1F2上一点,且|AF1||F1M|,则直线AM?l;(4)面积为2ab的椭圆内接四边形仅有1个。
四川省成都市2017级高中毕业班第一次诊断性检测理数试题

成都市2017级高中毕业班第一次诊断性检测(数学理科)本试卷分选择题和非选择题两部分,第1卷(选择题)1至2页,第11卷(非选择题)3至4页,共4页,满分150分,考试时间120分钟. 注意事项:1,答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2,答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3,答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4,所有题目必须在答题卡上作答,在试题卷上答题无效。
5,考试结束后,只将答题卡交回。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的1.若复数1z 与23z i =--(i 为虚数单位)在复平面内对应的点关于实轴对称,则1z = (A )i --3 (B )i +-3 (C )i +3 (D )i -32.已知集合{}m A ,0,1-=,{}2,1=B ,若{}2,1,0,1-=B A Y ,则实数m 的值为 (A )1-或0 (B )0或1 (C )1-或2 (D )1或23.若)2cos(5sin θπθ-=,则=θ2tan(A )35-(B )35 (C )25- (D )254.某校随机抽取100名同学进行“垃圾分类"的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70), [70,80),[80,90),[90,100],得到如图所示的频率分布直方 图,则这100名同学的得分的中位数为 (A )5.72 (B )75 (C )5.77(D )805.设等差数列{}n a 的前n 项和为n S ,且353a a =,则=59S S (A )59 (B )95 (C )35 (D )5276.已知βα,是空间中两个不同的平面,n m ,是空间中两条不同的直线,则下列说法正确的是 (A )若α//m ,β//n ,且βα//,则n m // (B )若α//m ,β//n ,且βα⊥,则n m // (C )若α⊥m ,β//n ,且βα//,则n m ⊥ (D )若α⊥m ,β//n ,且βα⊥,则n m ⊥ 7.62)1)(2(xx x -+的展开式的常数项为 (A )25(B )25- (C )5 (D )5- 8.将函数)64sin(π-=x y 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得图象向左平移6π个单位长度,得到函数)(x f 的图象,则函数)(x f 的解析式为 (A ))62sin()(π+=x x f (B ))32sin()(π-=x x f(C ))68sin()(π+=x x f (D) )38sin()(π-=x x f9.已知抛物线x y 42=的焦点为F ,N M ,是抛物线上两个不同的点若5||||=+NF MF ,则线段MN 的中点到y 轴的距离为(A )3 (B )23 (C )5 (D )2510.已知212=a ,313=b ,23ln=c ,则 (A )c b a >> (B )b c a >> (C )c a b >>(D )a c b >>11.已知定义在R 上的数)(x f 满足)2()2(x f x f +=-,当2≤x 时()(1)1xf x x e =--.若关于x 的方程012)(=+-+-e k kx x f 有三个不相等的实数根,则实数k 的取值范围是(A )),2()0,2(+∞-Y (B )(2,0)(0,2)-U (C )),()0,(+∞-e e Y (D )),0()0,(e e Y -12.如图,在边长为2的正方形321P P AP 中,线段BC 的端点C B ,分别在边21P P 、32P P 上滑动,且x C P B P ==22,现将B AP 1∆,C AP 3∆分别沿AB ,AC 折起使点31,P P 重合,重合后记为点P ,得到三被锥ABC P -.现有以下结论: ①⊥AP 平面PBC ;②当C B ,分别为21P P 、32P P 的中点时,三棱锥ABC P -的外接球的表面积为π6; ③x 的取值范围为)224,0(-; ④三棱锥ABC P -体积的最大值为31. 则正确的结论的个数为(A )1 (B )2 (C )3 (D )4二、填空题(本大题共4小题,每小题5分,共20分)13.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≥≥+-≤-+002204y y x y x ,则y x z 2+=的最大值为_______.14.设正项等比数列{}n a 满足814=a ,3632=+a a ,则=n a _______.15.已知平面向量a ,b 满足2||=a ,3||=b ,且)(b a b -⊥,则向量a 与b 的夹角的大小为_______.16.已知直线kx y =与双曲线)0,0(1:2222>>=-b a by a x C 相交于不同的两点B A ,,F 为双曲线C 的左焦点,且满足||3||BF AF =,||OA b =(O 为坐标原点),则双曲线C 的离心率为_______.三、解答题(共70分。
2017年四川省高考数学一诊试卷

2017年四川省高考数学一诊试卷(理科)一、选择题(本题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A={x|x2﹣3x<0},B={x|x2>4},则A∩B=()A.(﹣2,0)B.(﹣2,3)C.(0,2)D.(2,3)2.复数z满足:(3﹣4i)z=1+2i,则z=()A.B.C.D.3.设命题p:∀x>0,x﹣lnx>0,则¬p为()A.∀x>0,x﹣lnx≤0B.∀x>0,x﹣lnx<0C.∃x0>0,x0﹣lnx0>0D.∃x0>0,x0﹣lnx0≤04.已知2sin2α=1+cos2α,则tan(α+)的值为()A.﹣3B.3C.﹣3或3D.﹣1或35.函数f(x+1)是偶函数,则函数y=f(x)的图象关于()A.直线x=1对称B.直线x=﹣1对称C.点(1,0)对称D.点(﹣1,0)对称6.函数f(x)=3sin(2x﹣)的图象可以由y=3sin2x的图象()A.向右平移个单位长度得到B.向左平移个单位长度得到C.向右平移个单位长度得到D.向左平移个单位长度得到7.已知长方体ABCD﹣A1B1C1D1中,AB=BC,AA1=2AB,E为AA1中点,则异面直线BE与CD1所形成角的余弦值为()A.B.C.D.8.设数列{a n}的前n项和为S n,若S n,S n,S n+2成等差数列,且a2=﹣2,则a7=+1()A.16B.32C.64D.1289.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(百分比)为“衰分比”.如:甲、乙、丙、丁衰分得100,60,36,21.6个单位,递减的比例为40%,今共有粮m(m>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙衰分得80石,乙、丁衰分所得的和为164石,则“衰分比”与m的值分别为()A.20% 369B.80% 369C.40% 360D.60% 36510.定义[x]表示不超过x的最大整数,例如[2.11]=2,[﹣1.39]=﹣2,执行如下图所示的程序框图,则输出m的值为()A.B.C.D.11.如图所示是一个几何体的三视图,则这个几何体外接球的体积为()A.36πB.πC.8πD.π12.已知△ABC的三个顶点均在抛物线x2=y上,边AC的中线BM∥y轴,|BM|=2,则△ABC的面积为()A.2B.2C.4D.8二、填空题:本大题共4小题,每小题5分,共20分.13.二项式的展开式中常数项为.14.学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是C或D作品获得一等奖”;乙说:“B作品获得一等奖”;丙说:“A,D两项作品未获得一等奖”;丁说:“是C作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是.15.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的表面积为.16.若直线与圆x2+y2﹣2x﹣4y+a=0和函数的图象相切于同一点,则a的值为.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a+b)cosC+ccosB=0.(Ⅰ)求角C的大小;(Ⅰ)求sinAcosB的取值范围.18.张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:年龄(岁)78910111213135141148154160身高(cm)121128(Ⅰ)求身高y关于年龄x的线性回归方程;(Ⅰ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.附:回归直线的斜率和截距的最小二乘法估计公式分别为:=,=﹣.19.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=x3+ax(a∈R),且曲线f(x)在x=处的切线与直线y=﹣x﹣1平行.(Ⅰ)求a的值及函数f(x)的解析式;(Ⅰ)若函数y=f(x)﹣m在区间[﹣3,]上有三个零点,求实数m的取值范围.20.设各项均为正数的数列{a n}的前n项和为S n,且满足2=a n+1(n∈N*).(Ⅰ)求数列{a n}的通项公式;(Ⅰ)若b n=(a n+1)•2,求数列{b n}的前n项和T n.21.已知函数f(x)=ae x﹣x(a∈R),其中e为自然对数的底数,e=2.71828…(Ⅰ)判断函数f(x)的单调性,并说明理由(Ⅰ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范围.请考生在第22、23题中任选一题作答,如果多做则按所做第一题计分,作答时用2B铅笔在答题卡上把所选题目题号涂黑.[选修4-4:坐标系与参数方程] 22.在平面直角坐标系中,曲线C1:(a为参数)经过伸缩变换后的曲线为C2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(Ⅰ)求C2的极坐标方程;(Ⅰ)设曲线C3的极坐标方程为ρsin(﹣θ)=1,且曲线C3与曲线C2相交于P,Q两点,求|PQ|的值.[选修4-5:不等式选讲]23.已知函数f(x)=|x+b2|﹣|﹣x+1|,g(x)=|x+a2+c2|+|x﹣2b2|,其中a,b,c均为正实数,且ab+bc+ac=1.(Ⅰ)当b=1时,求不等式f(x)≥1的解集;(Ⅰ)当x∈R时,求证f(x)≤g(x).2017年四川省高考数学一诊试卷(理科)参考答案与试题解析一、选择题(本题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A={x|x2﹣3x<0},B={x|x2>4},则A∩B=()A.(﹣2,0)B.(﹣2,3)C.(0,2)D.(2,3)【考点】交集及其运算.【分析】分别求出关于A、B的不等式,求出A、B的交集即可.【解答】解:A={x|x2﹣3x<0}={x|0<x<3},B={x|x2>4}={x|x>2或x<﹣2},则A∩B={x|2<x<3},故选:D.2.复数z满足:(3﹣4i)z=1+2i,则z=()A.B.C.D.【考点】复数代数形式的乘除运算.【分析】利用复数的运算法则、共轭复数的定义即可得出.【解答】解:∵(3﹣4i)z=1+2i,∴(3+4i)(3﹣4i)z=(3+4i)(1+2i),∴25z=﹣5+10i,则z=﹣+i.故选:A.3.设命题p:∀x>0,x﹣lnx>0,则¬p为()A.∀x>0,x﹣lnx≤0B.∀x>0,x﹣lnx<0C.∃x0>0,x0﹣lnx0>0D.∃x0>0,x0﹣lnx0≤0【考点】命题的否定.【分析】直接利用全称命题的否定是特称命题写出结果即可.【解答】解:因为全称命题的否定是特称命题,所以命题“∀x>0,x﹣lnx>0”的否定是∃x>0,x﹣lnx≤0.故选:D.4.已知2sin2α=1+cos2α,则tan(α+)的值为()A.﹣3B.3C.﹣3或3D.﹣1或3【考点】两角和与差的正切函数.【分析】由倍角公式求得sinα与cosα的数量关系,结合正弦、余弦以及正切函数的转化关系进行解答即可.【解答】解:∵2sin2α=1+cos2α,∴4sinαcosα=1+2cos2α﹣1,即2sinαcosα=cos2α,①当cosα=0时,,此时,②当cosα≠0时,,此时,综上所述,tan(α+)的值为﹣1或3.故选:D.5.函数f(x+1)是偶函数,则函数y=f(x)的图象关于()A.直线x=1对称B.直线x=﹣1对称C.点(1,0)对称D.点(﹣1,0)对称【考点】函数奇偶性的性质.【分析】由偶函数的性质可知y=f(x+1)的图象关于y轴对称,根据平移变换可得y=f(x+1)与y=f(x)的图象关系,从而可得答案.【解答】解:因为y=f(x+1)是偶函数,所以y=f(x+1)的图象关于y轴对称,而把y=f(x+1)右移1个单位可得y=f(x)的图象,故y=f(x)的图象关于x=1对称,故选A.6.函数f(x)=3sin(2x﹣)的图象可以由y=3sin2x的图象()A.向右平移个单位长度得到B.向左平移个单位长度得到C.向右平移个单位长度得到D.向左平移个单位长度得到【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用y=Asin(ωx+φ)的图象变换规律,得出结论.【解答】解:把y=3sin2x的图象向右平移个单位长度,可得f(x)═3sin2(x ﹣)=3sin(2x﹣)的图象,故选:C.7.已知长方体ABCD﹣A1B1C1D1中,AB=BC,AA1=2AB,E为AA1中点,则异面直线BE与CD1所形成角的余弦值为()A.B.C.D.【考点】异面直线及其所成的角.【分析】以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线BE与CD1所形成角的余弦值.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设AA1=2AB=2,则B(1,1,0),E(1,0,1),C(0,1,0),D1(0,0,2),=(0,﹣1,1),=(0,1,﹣2),设异面直线BE与CD1所形成角为θ,则cosθ===.异面直线BE与CD1所形成角的余弦值为.故选:C.8.设数列{a n}的前n项和为S n,若S n,S n,S n+2成等差数列,且a2=﹣2,则a7=+1()A.16B.32C.64D.128【考点】等差数列的前n项和.【分析】由题意得S n+S n+1=2S n,得a n+2=﹣2a n+1,从而得到{a n}从第二项起是公+2比为﹣2的等比数列,由此能求出结果.【解答】解:∵数列{a n}的前n项和为S n,若S n+1,S n,S n+2成等差数列,且a2=﹣2,∴由题意得S n+S n+1=2S n,得a n+2+a n+1+a n+1=0,即a n+2=﹣2a n+1,+2∴{a n}从第二项起是公比为﹣2的等比数列,∴.故选:C.9.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(百分比)为“衰分比”.如:甲、乙、丙、丁衰分得100,60,36,21.6个单位,递减的比例为40%,今共有粮m(m>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙衰分得80石,乙、丁衰分所得的和为164石,则“衰分比”与m的值分别为()A.20% 369B.80% 369C.40% 360D.60% 365【考点】等比数列的通项公式.【分析】设“衰分比”为a,甲衰分得b石,由题意列出方程组,由此能求出结果.【解答】解:设“衰分比”为a,甲衰分得b石,由题意得,解得b=125,a=20%,m=369.故选:A.10.定义[x]表示不超过x的最大整数,例如[2.11]=2,[﹣1.39]=﹣2,执行如下图所示的程序框图,则输出m的值为()A.B.C.D.【考点】程序框图.【分析】模拟程序的运行,依据程序逐级运算,并通过判断条件n<7?调整运算的继续与结束,即可计算得解.【解答】解:模拟程序的运行,可得m=3,n=1[3]=3为奇数,m=,n=3满足条件n<7,执行循环体,[]=6不为奇数,m=,n=5满足条件n<7,执行循环体,[]=6不为奇数,m=,n=7不满足条件n<7,退出循环,输出m的值为.故选:B.11.如图所示是一个几何体的三视图,则这个几何体外接球的体积为()A.36πB.πC.8πD.π【考点】由三视图求面积、体积.【分析】如图所示,该几何体为四棱锥P﹣ABCD,侧面PAB⊥底面ABCD,底面ABCD是正方形,其对角线AC∩BD=O,取AB的中点E,OE⊥AB,OE⊥侧面PAB,PE=2,AB=4.则点O为其外接球的球心,半径R=2.即可得出.【解答】解:如图所示,该几何体为四棱锥P﹣ABCD,侧面PAB⊥底面ABCD,底面ABCD是正方形,其对角线AC∩BD=O,取AB的中点E,OE⊥AB,OE⊥侧面PAB,PE=2,AB=4.则点O为其外接球的球心,半径R=2.∴这个几何体外接球的体积V==π.故选:B.12.已知△ABC的三个顶点均在抛物线x2=y上,边AC的中线BM∥y轴,|BM|=2,则△ABC的面积为()A.2B.2C.4D.8【考点】抛物线的简单性质.【分析】作AH⊥BM交BM的延长线于H,求出|BM|,|AH|,即可求得△ABC 的面积.【解答】解:根据题意设A(a,a2),B(b,b2),C(c,c2),不妨设a>c,∵M为边AC的中点,∴M(,),又BM∥y轴,则b=,故|BM|=|﹣b2|==2,∴(a﹣c)2=8,即a﹣c=2,作AH⊥BM交BM的延长线于H.==2|a﹣b|=a﹣c=2.故△ABC的面积为2S△ABM故选B.二、填空题:本大题共4小题,每小题5分,共20分.13.二项式的展开式中常数项为24.【考点】二项式系数的性质.【分析】根据二项式展开式的通项公式,令x的指数为0求出r的值,从而求出展开式中常数项.【解答】解:二项式展开式的通项公式为:T r=••x r=24﹣r••x2r﹣4,+1令2r﹣4=0,解得r=2,∴展开式中常数项为T3=22•=24.故答案为:24.14.学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是C或D作品获得一等奖”;乙说:“B作品获得一等奖”;丙说:“A,D两项作品未获得一等奖”;丁说:“是C作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是B.【考点】进行简单的合情推理.【分析】根据学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,故假设A,B,C,D分别为一等奖,判断甲、乙、丙、丁的说法的正确性,即可判断.【解答】解:若A为一等奖,则甲,丙,丁的说法均错误,故不满足题意,若B为一等奖,则乙,丙说法正确,甲,丁的说法错误,故满足题意,若C为一等奖,则甲,丙,丁的说法均正确,故不满足题意,若D为一等奖,则只有甲的说法正确,故不合题意,故若这四位同学中只有两位说的话是对的,则获得一等奖的作品是B故答案为:B15.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的表面积为48π.【考点】球内接多面体;简单空间图形的三视图.【分析】判断几何体的特征,正方体中的三棱锥,利用正方体的体对角线得出外接球的半径求解即可.【解答】解:三棱锥补成正方体,棱长为4,三棱锥与正方体的外接球是同一球,半径为R==2,∴该球的表面积为4π×12=48π,故答案为:48π.16.若直线与圆x2+y2﹣2x﹣4y+a=0和函数的图象相切于同一点,则a的值为3.【考点】直线与圆的位置关系.【分析】设切点为(t,),求出切线方程,利用直线与圆x2+y2﹣2x﹣4y+a=0和函数y=的图象相切于同一点,建立方程,求出t,即可得出结论.【解答】解:设切点为(t,),y′=,x=t时,y′=t,∴切线方程为y﹣=(x﹣t),即y=tx﹣,∵一直线与圆x2+y2﹣2x﹣4y+a=0和函数y=的图象相切于同一点,∴=,∴t=2,∴切点为(2,1),代入圆x2+y2﹣2x﹣4y+a=0,可得a=3,故答案为3.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a+b)cosC+ccosB=0.(Ⅰ)求角C的大小;(Ⅰ)求sinAcosB的取值范围.【考点】余弦定理;正弦定理.【分析】(Ⅰ)由正弦定理、两角和的正弦公式、诱导公式化简已知的式子,由内角的范围和特殊角的三角函数值求出角C的大小;(Ⅰ)由(I)和内角和定理表示出B,并求出A的范围,代入sinAcosB后,由两角差的余弦公式、正弦公式化简后,由A的范围和正弦函数的性质求出答案.【解答】解:(Ⅰ)由题意知,(2a+b)cosC+ccosB=0,∴由正弦定理得,(2sinA+sinB)cosC+sinCcosB=0,则2sinAcosC+sinBcosC+sinCcosB=0,即sin(B+C)=﹣2sinAcosC,∵△ABC中,sin(B+C)=sin(π﹣A)=sinA>0,∴1=﹣2cosC,得cosC=,又0<C<π,∴C=;(Ⅰ)由(I)得C=,则A+B=π﹣C=,即B=﹣A,所以,∴sinAcosB=sinAcos(﹣A)=sinA(cos cosA+sin sinA)=sinA(cosA+sinA)=sin2A+=()=∵,∴,则,即,∴sinAcosB的取值范围是.18.张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:年龄(岁)78910111213135141148154160身高(cm)121128(Ⅰ)求身高y关于年龄x的线性回归方程;(Ⅰ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.附:回归直线的斜率和截距的最小二乘法估计公式分别为:=,=﹣.【考点】线性回归方程.【分析】(Ⅰ)首先根据表格与公式求得相关数据,然后代入线性回归方程求得,由此求得线性回归方程;(Ⅰ)将先15代入(Ⅰ)中的回归方程即可求得张三同学15岁时的身高.【解答】解:(Ⅰ)由题意得=(7+8+9+10+11+12+13)=10,==141,(=9+4+1+0+1+4+9=28,(x i﹣)(y i﹣)=(﹣3)×(﹣20)+(﹣2)×(﹣13)+(﹣1)×(﹣6)+0×0+1×7+2×13+3×19=182,所以==,=﹣=141﹣×10=76,所求回归方程为=x+76.(Ⅰ)由(Ⅰ)知,=>0,故张三同学7岁至13岁的身高每年都在增高,平均每年增高6.5cm.将x=15代入(Ⅰ)中的回归方程,得=×15+76=173.5,故预测张三同学15岁的身高为173.5cm.19.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=x3+ax(a∈R),且曲线f(x)在x=处的切线与直线y=﹣x﹣1平行.(Ⅰ)求a的值及函数f(x)的解析式;(Ⅰ)若函数y=f(x)﹣m在区间[﹣3,]上有三个零点,求实数m的取值范围.【考点】利用导数研究曲线上某点切线方程;导数的运算.【分析】(Ⅰ)首先求得导函数,然后利用导数的几何意义结合两直线平行的关系求得a的值,由此求得函数f(x)的解析式;(Ⅰ)将问题转化为函数f(x)的图象与y=m有三个公共点,由此结合图象求得m的取值范围.【解答】解:(Ⅰ)当x>0时,f′(x)=x2+a,因为曲线f(x)在x=处的切线与直线y=﹣x﹣1平行,所以f′()=+a=﹣,解得a=﹣1,所以f(x)=x3﹣x,设x<0则f(x)=﹣f(﹣x)=x3﹣x,又f(0)=0,所以f(x)=x3﹣x.(Ⅰ)由(Ⅰ)知f(﹣3)=﹣6,f(﹣1)=,f(1)=﹣,f()=0,所以函数y=f(x)﹣m在区间[﹣3,]上有三个零点,等价于函数f(x)在[﹣3,]上的图象与y=m有三个公共点.结合函数f(x)在区间[﹣3,]上大致图象可知,实数m的取值范围是(﹣,0).20.设各项均为正数的数列{a n}的前n项和为S n,且满足2=a n+1(n∈N*).(Ⅰ)求数列{a n}的通项公式;(Ⅰ)若b n=(a n+1)•2,求数列{b n}的前n项和T n.【考点】数列的求和;数列递推式.【分析】(Ⅰ)首先利用S n与a n的关系:当n=1时,a1=S1,当n≥2时,a n=S n﹣S n;结合已知条件等式推出数列{a n}是等差数列,由此求得数列{a n}的通项公﹣1式;(Ⅰ)首先结合(Ⅰ)求得b n的表达式,然后利用错位相减法,结合等比数列的求和公式求解即可.【解答】解:(Ⅰ)当n=1时,a1=S1,有2=a1+1,解得a1=1;当n≥2时,由2=a n+1得4S n=a n2+2a n+1,4S n﹣1=a n﹣12+2a n﹣1+1,两式相减得4a n=a n2﹣a n﹣12+2(a n﹣a n﹣1),所以(a n+a n﹣1)(a n﹣a n﹣1﹣2)=0,因为数列{a n}的各项为正,所以a n﹣a n﹣1﹣2=0,所以数列{a n}是以1为首项,2为公差的等差数列,所以数列{a n}的通项公式为a n=2n﹣1.(Ⅰ)由(Ⅰ)知b n=(a n+1)•2=2n•22n﹣1=n•4n.所以前n项和T n=1•4+2•42+3•43+…+n•4n,4T n=1•42+2•43+3•44+…+n•4n+1,两式相减得﹣3T n=4+42+43+…+4n﹣n•4n+1=﹣n•4n+1,化简可得T n=+•4n+1.21.已知函数f(x)=ae x﹣x(a∈R),其中e为自然对数的底数,e=2.71828…(Ⅰ)判断函数f(x)的单调性,并说明理由(Ⅰ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范围.【考点】函数恒成立问题;函数单调性的判断与证明.【分析】(Ⅰ)求出原函数的导函数,然后对a分类,当a≤0时,f′(x)<0,f (x)=ae x﹣x为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各区间段内的符号得到原函数的单调性;(Ⅰ)x∈[1,2],不等式f(x)≥e﹣x恒成立,等价于ae x﹣x≥e﹣x恒成立,分离参数a,可得恒成立.令g(x)=,则问题等价于a不小于函数g(x)在[1,2]上的最大值,然后利用导数求得函数g(x)在[1,2]上的最大值得答案.【解答】解:(Ⅰ)由f(x)=ae x﹣x,得f′(x)=ae x﹣1,当a≤0时,f′(x)<0,f(x)=ae x﹣x为R上的减函数;当a>0时,令ae x﹣1=0,得x=lna,若x∈(﹣∞,﹣lna),则f′(x)<0,此时f(x)为的单调减函数;若x∈(﹣lna,+∞),则f′(x)>0,此时f(x)为的单调增函数.综上所述,当a≤0时,f(x)=ae x﹣x为R上的减函数;当a>0时,若x∈(﹣∞,﹣lna),f(x)为的单调减函数;若x∈(﹣lna,+∞),f(x)为的单调增函数.(Ⅰ)由题意,x∈[1,2],不等式f(x)≥e﹣x恒成立,等价于ae x﹣x≥e﹣x恒成立,即x∈[1,2],恒成立.令g(x)=,则问题等价于a不小于函数g(x)在[1,2]上的最大值.由g(x)==,函数y=在[1,2]上单调递减,令h(x)=,x∈[1,2],h′(x)=.∴h(x)=在x∈[1,2]上也是减函数,∴g(x)在x∈[1,2]上也是减函数,∴g(x)在[1,2]上的最大值为g(1)=.故x∈[1,2],不等式f(x)≥e﹣x恒成立的实数a的取值范围是[,+∞).请考生在第22、23题中任选一题作答,如果多做则按所做第一题计分,作答时用2B铅笔在答题卡上把所选题目题号涂黑.[选修4-4:坐标系与参数方程] 22.在平面直角坐标系中,曲线C1:(a为参数)经过伸缩变换后的曲线为C2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(Ⅰ)求C2的极坐标方程;(Ⅰ)设曲线C3的极坐标方程为ρsin(﹣θ)=1,且曲线C3与曲线C2相交于P,Q两点,求|PQ|的值.【考点】参数方程化成普通方程.【分析】(Ⅰ)求出C2的参数方程,即可求C2的极坐标方程;(Ⅰ)C2是以(1,0)为圆心,2为半径的圆,曲线C3的极坐标方程为ρsin(﹣θ)=1,直角坐标方程为x﹣y﹣2=0,求出圆心到直线的距离,即可求|PQ|的值.【解答】解:(Ⅰ)C2的参数方程为(α为参数),普通方程为(x′﹣1)2+y′2=1,∴C2的极坐标方程为ρ=2cosθ;(Ⅰ)C2是以(1,0)为圆心,2为半径的圆,曲线C3的极坐标方程为ρsin(﹣θ)=1,直角坐标方程为x﹣y﹣2=0,∴圆心到直线的距离d==,∴|PQ|=2=.[选修4-5:不等式选讲]23.已知函数f(x)=|x+b2|﹣|﹣x+1|,g(x)=|x+a2+c2|+|x﹣2b2|,其中a,b,c均为正实数,且ab+bc+ac=1.(Ⅰ)当b=1时,求不等式f(x)≥1的解集;(Ⅰ)当x∈R时,求证f(x)≤g(x).【考点】绝对值三角不等式;绝对值不等式的解法.【分析】(Ⅰ)当b=1时,把f(x)用分段函数来表示,分类讨论,求得f(x)≥1的解集.(Ⅰ)当x∈R时,先求得f(x)的最大值为b2+1,再求得g(x)的最小值,根据g(x)的最小值减去f(x)的最大值大于或等于零,可得f(x)≤g(x)成立.【解答】解:(Ⅰ)由题意,当b=1时,f(x)=|x+b2|﹣|﹣x+1|=,当x≤﹣1时,f(x)=﹣2<1,不等式f(x)≥1无解,不等式f(x)≥1的解集为∅;当﹣1<x<1时,f(x)=2x,由不等式f(x)≥1,解得x≥,所以≤x<1;当x≥1时,f(x)=2≥1恒成立,所以不等式f(x)≥1的解集为[,+∞).(Ⅰ)(Ⅰ)当x∈R时,f(x)=|x+b2|﹣|﹣x+1|≤|x+b2 +(﹣x+1)|=|b2+1|=b2+1;g(x)=|x+a2+c2|+|x﹣2b2|=≥|x+a2+c2﹣(x﹣2b2)|=|a2+c2+2b2|=a2+c2+2b2.而a2+c2+2b2﹣(b2+1)=a2+c2+b2﹣1=(a2+c2+b2+a2+c2+b2)﹣1≥ab+bc+ac ﹣1=0,当且仅当a=b=c=时,等号成立,即a2+c2+2b2≥b2+1,即f(x)≤g(x).2017年4月2日。
17届高三理科数学一诊模拟考试试卷答案

则面 DMF 的法向量: m ( x
4 3 , 3,
3x )
3
同理可知:面 CDM 的法向量 n (3, 0 , 4 )
由 | c o s m , n | 2 ,则 x 1 3 9 3 或 x 3
5
43
经检验, x 不合题意
3 时二面角 F D M C 的余弦值为 2
1 a
1
3
1 q
3
即数列 a n 是首项为 1 公比为 1 的等比数列
3
3
a
1 (
)n
n
3
(2)由已知可得: f ( a ) n n
则: b
n (n 1) 1 2 3 … … -n
n
2
故: 1
1 2(
1
)
bn
n n 1
Tn
2
(1
成都七中 2017 届一诊模拟考试数学试卷(理科)(参考答案)
一.选择题 1-5:BADBC 6-10:BCDCA 11-12:BA
二、填空题
13. 1120 ; 三.解答题
14. 3 3 ;
28
15. 4
16. 0 或-2
17. 解:(1)∵{ a } 为等比数列,设公比为 q n
1
又a4
81
∴a 1
(2)由(1)知,当 a 1 时, G ( x ) s in (1 x ) ln x 在 ( 0 , 1) 单调增
∴ s in (1 x ) ln x G (1) 0
∴ s in (1 x ) ln 1 ( 0 x 1)
x
∴ sin
成都市2 0 1 7级高中毕业班第一次诊断性检测2017级高三一诊理数答案

的
斜
率k
y1 -y2 = 2-x2
.
������ ������5 分 ������ ������6 分
数学(理科)“一诊”考试题参考答案 第 3 页(共4页)
∴直线 BD
的
方
程
为y
-y1
y1 -y2 = 2-x2
(x
-2).
令y =0,得x
x2y1 -2y2 = y1 -y2
my1y2 +y1 -2y2
������ ������4 分
∴原不等式的解集为
{x|x
2 ≤-3
或x
≥ 0}
.
������ ������5 分
(Ⅱ)∵f(x)=|x -3|,
∴ |x
+
3 2 |-f(x )=|x
+
3 2 |-|x
-3| ≤ | (x
+
3 2)-
(x
-3)|=
9 2
,
当且仅当
(x
+
3 2)(x
-3)≥ 0 且 |x
22.解:(Ⅰ)由题,知点 Q 的轨迹是以(2,0)为圆心,2为半径的圆.
∴曲线 C2 的方程为(x-2)2+y2=4. ∵ρ2 =x2 +y2,x =ρcosθ ,y =ρsinθ , ∴曲线 C1 的极坐标方程为ρ =4sinθ , 曲线 C2 的极坐标方程为ρ =4cosθ . (Ⅱ)在极坐标系中,设点 A,B 的极径分别为ρ1,ρ2.
������ ������2 分
又∵AP ⊥ 平面PBC ,BC ⊂ 平面PBC ,
∴ BC ⊥ AP������
������ ������4 分
∵ AP ∩AE= A ,AP,AE ⊂ 平面PAE ,
高2017届理科数学成都一诊考试试卷和答案

ʑ λ2 +1 8 λ -7=0. ㊀ 解得λ =
1 7 或λ =- ( 不合题意 , 舍去 ) 3 3
������������������������ 1 1分
������������������������6 分 ������������������������8 分
X
������������������������1 1分 ������������������������1 2分
高三数学 ( 理科 ) 一诊测试参考答案第 ㊀ 共 4页) 1 页(
( ) ������������������������1 分 解: 由题意 , 可知 P 1 9. I E, P F, PD 三条直线两两垂直 . ������������������������3 分 ʑPD ʅ 平面 P E F. 在图 1 中 ,ȵE , F 分别是 A B, B C 的中点 , ʑE F ʊA C .ʑG B =2 GH . 又 ȵG 为 B D 的中点 ,ʑD G =2 GH . P R B R D G 在图 2 中 ,ȵ 且 = =2, =2, RH RH GH ������������������������5 分 ʑ 在 әPDH 中 , G R ʊ PD . ������������������������6 分 ʑG R ʅ 平面 P E F. ( ) 由题意 , 分别以 P I I F, P E, PD 所在直线为x 轴 , z 轴建立如图 所 示 的 空 间 直 y 轴, 角坐标系 P x z. y ) , ) , ) , ).ʑH ( ). 设 PD =4, 则 P( 0, 0, 0 F( 2, 0, 0 E( 0, 2, 0 D( 0, 0, 4 1, 1, 0 ������������������������7 分 P R λ λ λ ң ң , , ). ȵ λ, ʑP R= PH . ㊀ ʑR ( 0 = RH 1+λ 1+λ 1+λ λ λ 2+λ λ ң , , ) , , ). ʑR F =( 2- 0 0 - =( - 1+λ 1+λ 1+λ 1+λ ������������������������8 分 ң ң ) , ), 又ȵ E F =( 2, 0 D E =( 0, 2, -2, -4 设平面 D E F 的一个法向量为 m = ( x, z). y, ң F������m = 0 2 x -2 y= 0 取 , , , ) 由 E 则m = ( ⇒ . z= 1 2 2 1 . ң z= 0 y -4 D E������m = 0 2 ������������������9 分
四川省成都市2017届高中毕业班第一次诊断性检测理科数学试题(word))

成都市2014级高中毕业班第一次诊断性检测数学(理科)本试卷分选择题和非选择题两部分。
第1卷(选择题)1至2页,第Ⅱ卷(非选择题)2至4页,共4页,满分150分,考试时间120分钟。
第I 卷(选择题,共60分)一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合U=R ,A={x|x2-x-2>0).则(A)(-∞,-1) ⋃(2,+∞) (B)[-1,2](C)(-∞,-1] ⋃[2,+∞) (D)(-1,2)(2)命题“若a>b ,则a+c>b+c"的否命题是(A)若a ≤6,则a+c ≤b+c(B)若a+c ≤b+c ,则a ≤6(C)若a+c>b+c ,则a>b(D)若a>b ,则a+c ≤b+c(3)执行如图所示的程序框图,如果输出的结果为0,那么输(B) -1或1 (C)l (D)一1 (4)已知双曲线2222-1(0x y a b a b=>>)的左,右焦点分别为F 1,F 2,双曲线上一点P 满足PF 2⊥x 轴,若 |F 1F 2|=12,|PF 2|=5,则该双曲线的离心率为(A)1312 (B) 125 (C) 32 (D)3 (5)已知α为第二象限角,且sin2α=2425,则cos α -sin α的值为 (A) 75 (B) 一75 (C) 15 (D) 一15 (6)(x+1)5(x-2)的展开式中x 2的系数为(A) 25 (B)5 (C) - 15 (D) - 20(7)如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为(A) 136π (B) 34π (C) 25π(D) 18π(8)将函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移6π个单位长度,得到函数g (x)的图象,则g(x)图象的一条对称轴方程是 (A)x=一6π (B)x=6π (C)x=2425π (D)x= 3π (9)在直三棱柱ABC-A1BlC1中,平面口与棱AB ,AC ,A 1C 1,A 1B 1分别交于点E ,F ,G ,H ,且直线AA 1∥平面d .有下列三个命题:①四边形EFGH 是平行四边形;②平面α∥平面BCC 1B 1;③平面α上平面BCFE .其中正确的命题有(A)①② (B)②③ (C)①③ (D)①②③(10)已知A,B 是圆O:x 2+y 2=4上的两个动点,若M 是线段AB 的中点,则的值为(A)3 (D) -3(11)已知函数f(x)是定义在R 上的偶函数,且f (-x-1)=f (x-1),当x ∈[-1,0]时,f(x)= 一x 3.则关于x 的方程f(x ) =|cos πx|在[一52,12]上的所有实数解之和为 (A) -7 (B) -6 (C) -3 (D) -1(12)已知曲线C 1:y 2=tx (y>0,t>0)在点M(4t ,2)处的切线与曲线C 2:y=e x+l —1也相切,则tln 24e t 的值为 (A) 4e 2 (B) 8e (C)2 (D)8第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.(13)若复数z=1ai i+(其中a ∈R ,i 为虚数单位)的虚部为-1,则a= .(14)我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l 的梯形,且当实数t 取[0,3]上的任意值时,直线y=t 被图l和图2所截得的两线段长始终相等,则图l 的面积为 .(15)若实数x ,y 满足约束条件,则的最小值为(16)已知△ABC 中,ABC BA 的延长线上存在点D ,使∠CD = .三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.(17)(本小题满分12分)已知数列{a n }满足a l = -2,a n+1 =2a n +4.(I)证明数列{a n +4)是等比数列;(Ⅱ)求数列{|a n |}的前n 项和S n .(18)(本小题满分12分)某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A 等;分数在[70,85)内,记为B 等;分数在[60,70)内,记为C 等;60分以下,记为D 等.同时认定A ,B ,C 为合格,D 为不合格,已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照[50,60), [60,70), [70,80), [80,90),[90 ,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C ,D 的所有数据的茎叶图如图2所示.(I)求图中x 的值,并根据样本数据比较甲乙两校的合格率;(II)在选取的样本中,从甲,乙两校C 等级的学生中随机抽取3名学生进行调研,用X 表示所抽取的3名学生中甲校的学生人数,求随机变量X 的分布列和数学期望.(19)(本小题满分12分)如图1,在正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,BD 与EF 交于点H ,G 为BD 中点,点R 在线段BH 上,且BR RH=λ(λ>0).现将 △AED ,△CFD ,△DEF 分别沿DE ,DF ,EF 折起,使点A ,C 重合于点B (该点记为P ),如图2所示.(I)若λ=2,求证:GR ⊥平面PEF ;(Ⅱ)是否存在正实数λ,使得直线FR 与平面DEF 求出λ的值;若不存在,请说明理由.(20)(本小题满分12分) 已知椭圆22:154x y E +=的右焦点为F ,设直线l :x=5与x 轴的交点为E ,过点F 且斜率为k 的直线l 1与椭圆交于A ,B 两点,M 为线段EF 的中点.(I)若直线l 1的倾斜角为4π,求△ABM 的面积S 的值; (Ⅱ)过点B 作直线BN ⊥l 于点N ,证明:A ,M ,N 三点共线(21)(本小题满分12分)已知函数f(x)=xln(x+1)+(12一a )x+2一a ,a ∈R . (I)当x>0时,求函数g(x)=f(x)+ln(x+1)+ 12x 的单调区间;(Ⅱ)当a ∈Z 时,若存在x ≥0,使不等式f(x)<0成立,求a 的最小值.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分.(22)(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,倾斜角为α(α≠2π)的直线l 的参数方程为1cos ,sin ,x t y t αα=+⎧⎨=⎩ (t 为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程是ρcosx θ - 4sin θ=0.(I)写出直线l 的普通方程和曲线C 的直角坐标方程;(Ⅱ)已知点P(1,0).若点M 的极坐标为(1,2π),直线l 经过点M 且与曲线C 相交于A ,B 两点,设线段AB 的中点为Q ,求|PQ|的值.(23)(本小题满分10分)选修4-5:不等式选讲已知函数f(x )=x +1+ |3 -x|,x ≥-1.(I)求不等式f(x )≤6的解集;(Ⅱ)若f(x )的最小值为n ,正数a ,b 满足2nab =a+2b ,求2a+b 的最小值.。
2017级成都市高三第一次诊断性检测数学试题(理科)

成都市2017级高中毕业班第一次诊断性检测数学(理科)本试卷分选择题和非选择题两部分。
第1卷(选择题)1至2页,第lI卷(非选择题)3至4页,共4页,满分150分,考试时间120分钟。
注意事项:1. 答题前,务必将自己的姓名考籍号填写在答题卡规定的位置上。
2. 答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦千净后,再选涂其它答案标号。
答非选择题时,必须使用05毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上答题无效。
5. 考试结束后,只将答题卡交回。
第1卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1若复数Z 1与Zz =-— (i 为虚数单位)在复平面内对应的点关于实轴对称,则Z1=CA)-—i (B)-3+ (C)+i (D)—!2.已知集合A={—1,0,m},B={l ,2}. 若A U B = {-1,0,1,2}, 则实数m的值为(A)-1或0(B)O或1CC)—1或23.若si n e =乔cos(2穴-0),则tan20=石乔瓦CA)——CB) -CC)—一 2 4.某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60), [60, 70), [70, 80),[80,90),[90,100], 得到如图所示的频率分布直方图则这100名同学的得分的中位数为CA )72. 50.040 0.030 数学(理科)”一诊“考试题第1页(共4页)CD)l或2CD)-污2 彗0.015 (B )75 0.0100.005 (C)77. 5(D)80。
工丑扫已。
100得分5设等差数列{a ,}的前n项和为S,,,且a ,,-::/:-0.若as =a 3, 则—=s 9 S s 9 5 5 (A)了(B)了(C)了6已知a,/3是空间中两个不同的平面,m,n是空间中两条不同的直线,则下列说法正确的是(A)若m II a ,n II /3, 且a II /3,则m II n (B)若m II a ,n II /3, 且a_l/3,则m II n (C)若m_la ,n II /3, 且a II /3, 则m _l n (D)若m _la,n ll /3,且a_l/3,则m _l n7.(x 2+2)(x ——)6的展开式的常数项为(A)25(B)-25 (C)5(D )—5 8.将函数y =si n (4x -王)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所6 得图象向左平移王个单位长度,得到函数f(x)的图象,则函数f(x)的解析式为6 (A) f(x) =si n (2x +互)6 CA) C —2,0) LJ (2, 十=)穴CB) f(x) =si n (2x —一) 亢(C) f(x) =si n (8x +岊)(D) f(x) =si n (8x —一)9已知抛物线沪=4x 的焦点为F,M,N是抛物线上两个不同的点.若I M Fl+INFl =5,则线段MN的中点到y轴的距离为CA)3 3_2) B ( CC)5 10.巳知a =沪,b=3了,c =l n -2 ,则(A) a> b > c (B) a> c > b (C) b >a> c (D) b > c > a 11已知定义在R上的函数f(x)满足f(2-x)= f(Z +x), 当x冬2时,f(x)= (x —l)e< :--1 若关于x的方程f(x)-kx +zk —e +l=O 有三个不相等的实数根,则实数K的取值范围是(B)(—2,0) LJ (0,2)CC)C —e,O) U (e, 十oo)CD)C —e ,O) U (0, e ) 12.如图,在边长为2的正方形AP 1贮凡中,线段BC的端点B,C分别在边P1P 2,P 2P 3 _t 滑动,且P 2B =P心=x.现将丛AP 1B ,6AP 3C分别沿AB,A C折起使点P1,凡重合,重合后记为点P ,得到三棱锥P-ABC 现有以下结论:(DAP上平面PBC;@当B,C分别为P1P2,P 2凡的中点时,三棱锥P —ABC的外接球的表面积为67(;®x 的取值范圉为(0,4—2迈); 1 @三棱锥P —ABC体积的最大值为—.则正确的结论的个数为P 1 5_2、丿D ( A 27CD)一5 (A)l (B)2CC )3(D )4数学(理科)”一诊“考试题第2页(共4页)。
四川省成都市龙泉驿区第一中学校2017届高三数学一诊模拟考试试题理

四川省成都市龙泉驿区第一中学校2017届高三数学一诊模拟考试试题 理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。
满分150分,考试时刻120分钟。
第Ⅰ卷(选择题,共60分)注意事项:1.必需利用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 2.考试终止后,将本试题卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{|(1)(5)0}M x x x =--<,集合{|4}N x y x ==-,则M N 等于( )A .(1,4]B .(1,4)C .[4,5)D .(4,5) 2.已知2sin 3α=,则sin(2)2πα-=( ) A.53-B.19-C.19D.533.过点)3,1(且垂直于直线032=+-y x 的直线方程为( ) A.052=-+y x B. 012=+-y x C. 052=-+y x D. 052=+-y x4. 某班文艺晚会,预备从A,B 等8个节目当选出4个节目,要求:A,B 两个节目至少有一个选中,且A,B 同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的种数为( ) .1320 C D. 10205.已知点P 在曲线41xy e =+上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( ) A.[0,4π) B.[,)42ππ C. 3(,]24ππ D. 3[,)4ππ 6.设函数)(x f 在R 上存在导数)(x f ',R x ∈∀,有2)()(x x f x f =+-,在),0(+∞上x x f <')(,若(6)()1860f m f m m ---+≥,则实数m 的取值范围为( )A . [3,3]-B . [3,)+∞C . [2,)+∞D .(,2][2,)-∞-+∞ 7.将函数()3cos sin y x x x R =+∈的图像向左平移()0m m >个长度单位后,所取得的图像关于y 轴对称,则m的最小值是( )A.12πB.6πC.3πD.56π8.已知三棱锥SABC的三视图如图所示.在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC. 其中所有正确命题的代号是( )A.① B.② C.①③ D.①②9.函数xexf x ln)(=在点))1(,1(f处的切线方程是()A.)1(2-=xey B.1-=exy C.)1(-=xey D.exy-=10.已知132a-=,21211log,log33b c==,则()A.a b c>> B. a c b>> C.c a b>> D.c b a>>11.已知以4=T为周期的函数⎪⎩⎪⎨⎧∈---∈-=]3,1(|),2|1(]1,1(,1)(2xxmxxxf,其中0>m,若函数xxfxg-=)(3)(恰有5个不同零点,则实数m的取值范围为()A.)38,2( B. )2,32( C. )310,2( D. )38,34(12.已知a为常数,函数f(x)=x(ln x-ax)有两个极值点x1,x2(x1<x2),则( )(x1)>0,f(x2)>-12 (x1)<0,f(x2)<-12(x1)>0,f(x2)<-12 (x1)<0,f(x2)>-12二、填空题(每小题5分,共20分)13. 已知数列}{na是等差数列,其前n项和为nS,若9,100510==aS,则_______100994321=-++-+-SSSSSS .14.已知1052==ba,则=+ba11________。
成都市2017级高中毕业班第一次诊断性检测数学理科试卷及答案

成都市2017级高中毕业班第一次诊断性检测数 学(理科)第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z 1与z 2=-3- i (i 为虚数单位)在复平面内对应的点关于实轴对称,则z 1=(A)-3-i (B)-3+i (C)3+i (D)3-i2已知集合A={-l ,0,m ),B={l ,2}若A B={-l ,0,1,2},则实数m 的值为(A)-l 或0 (B)0或1 (C) -l 或2 (D)l 或23.若θθcos 5sin =,则tan2θ = (A) -35 (B) 35 (C) -25 (D) 25 4.某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这l00名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70),[70,80), [80,90),[90,100],得到如图所示的频率分布直方图则这100名同学的得分的中位数为(A)72. 5 (B)75 (C)77. 5 (D)805.设等差数列{a n }的前n 项和为S n ,且a n ≠0,若a 5=3a 3,则 =59S S ( A) 59 (B) 95 (C) 35 (D) 527 6. 已知α,β是空间中两个不同的平面,m ,n 是空间中两条不同的直线,则下列说法正确的是(A 若m ∥α,n ∥β,且α∥β,则m ∥n(B)若m ∥α,n ∥β,且α⊥β,则m ∥n(C)若m ⊥α,n ∥β,且α∥β,则m ⊥n(D)若m ⊥α,n ∥β且α⊥β,则m ⊥n7.62)1)(2(x x x -+的展开式的常数项为(A )25 (B)-25 (C)5 (D)-58.将函数y= sin(4x-6π)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得图象向左平移6π个单位长度,得到函数f(x)的图象,则函数f(x)的解析式为 (A) )62sin()(π+=x x f (B) )32sin()(π-=x x f (C) )68sin()(π+=x x f (D) )38sin()(π-=x x f 9已知抛物线y 2=4x 的焦点为F ,M ,N 是抛物线上两个不同的点若|MF|+|NF|=5,则线段MN 的中点到y 轴的距离为(A)3 (B) 23 (C)5 (D) 25 10.已知23ln ,3,23121===c b a ,则 (A)a>b>c (B)a>c>b (C)b>a>c (D)b>c>a11.已知定义在R 上的函数f(x)满足f(2-x)=f(2+x),当x ≤2时,f(x)=(x-1)e x -1.若关于x 的方程f(x)-kx+2k-e+1=0有三个不相等的实数根,则实数k 的取值范围是(A)(-2,0) (0,2) (B)(-2,0) (2,+∞) (C)(-e, 0) (0, +∞) (D)(-e ,0) (0,e) 12. 如图,在边长为2的正方形AP 1 P 2P 3中,边 P 1P 2,P 2P 3的中点分别为B ,C 现将△AP 1B ,△BP 2C ,△CP 3A 分别沿AB ,BC ,CA 折起使点P 1,P 2,P 3重合,重合后记为点P ,得到三棱锥P-ABC .现有以下结论:①AP ⊥平面PBC;②当B ,C 分别为P 1P 2,P 2P 3的中点时,三棱锥P-ABC 的外接球的表面积为π6;③x 的取值范围为(0,4-22);④三棱锥P-ABC 体积的最大值为31 .则正确的结论的个数为 (A)1 (B)2 (C)3 (D)4第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上. 13已知实数x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥+-≤-+002204y y x y x ,则z=x+2y 的最大值为____14设正项等比数列{a n }满足a 4= 81,a 1+a 3 =36,则a n = .15已知平面向量a ,b 满足|a |=2,b =3,且b ⊥(a -b ),则向量a 与b 的夹角的大小为 .16.已知直线y=kx 与双曲线C : 12222=-by a x (a>0,b>0)相交于不同的两点A ,B ,F 为双曲线C 的左焦点,且满足|AF|=3|BF|,|OA|=b (O 为坐标原点),则双曲线C 的离心率为 三、解答题:本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且bc a c b 324222=-+. (I)求sinA 的值;(Ⅱ)若△ABC 的面积为2 ,且2sinB=3sinC ,求△ABC 的周长18.(本小题满分12分)某公司有l000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G 手机购买意向的调查,将计划在今年购买5G 手机的员工称为“追光族”,计划在明年及明年以后才购买5G 手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.(I)完成下列2×2列联表,并判断是否有95%的把握认为该公司员工属于“追光族”与 “性别”有关;(Ⅱ)已知被抽取的这l00名员工中有10名是人事部的员工,这10名中有3名属于“追光族”现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X ,求X 的分布列及数学期望.19.(本小题满分12分)如图,在四棱锥P -ABCD 中,AP ⊥平面PBC ,底面ABCD 为菱形,且∠ABC = 60°,E 分别为BC 的中点.(I)证明:BC ⊥平面PAE ;(Ⅱ)若AB=2.PA=1,求平面ABP 与平面CDP 所成锐二面角的余弦值.20.(本小题满分1 2分)已知函数f (x )=(a-1)lnx+x+xa ,a ∈R. (I)讨论函数f (x )的单调性;(Ⅱ)当a<-1时,证明.)(),,1(2a a x f x -->+∞∈∀21.(本小题满分12分)已知椭圆C :22x +y 2=1的右焦点为F ,过点F 的直线(不与x 轴重合)与椭圆C 相交于A ,B 两点,直线l :x=2与x 轴相交于点H ,过点A 作AD ⊥l ,垂足为D.(1)求四边形OAHB(O 为坐标原点)面积的取值范围;(Ⅱ)证明直线BD 过定点E .并求出点E 的坐标请考生在第22,23题中任选择一题作答,如果多做,则按所做的第一题记分,作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22(本小题满分l0分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知P 是曲线C 1:x 2+(y-2)2 =4上的动点,将OP 绕点O 顺时针旋转90°得到OQ ,设点Q 的轨迹为曲线C 2以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.(I)求曲线C 1,C 2的极坐标方程;(Ⅱ)在极坐标系中,点M (3,2π ),射线ρπθ(6=≥0)与曲线C 1,C 2分别相交于异于极点O 的A ,B 两点,求△MAB 的面积23.(本小题满分l0分)选修4 5:不等式选讲已知函数f(x)=|x-3|(I)解不等式f (x )≥4-|2x+l|;(Ⅱ)若n m 41+ =2(m>0, n>0),求证:m+n ≥|x+ 23|-f(x).。
2017成都一诊理科数学试题及答案
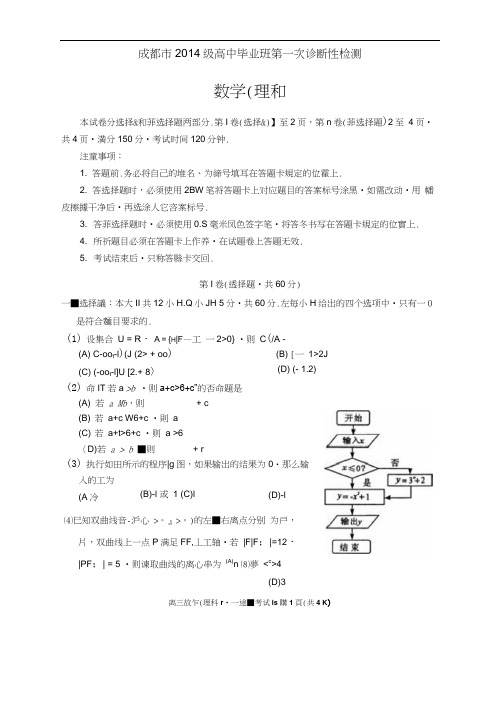
成都市2014级高中毕业班第一次诊断性检测数学(理和本试卷分选择&和菲选择题两部分.第I 卷(选择&)】至2页,第n 卷(菲选择題)2至 4页•共4页•満分150分•考试时间120分钟.注童事项:1. 答題前.务必将自己的堆名、为締号填耳在答題卡規定的位霍上.2. 答选择题时,必须使用2BW 笔将答題卡上对应題目的答案标号涂黑•如需改动•用 幡皮擦據干净后•再选涂人它咨案标号.3. 答菲选择题时•必须使用0.S 毫米凤色签字笔•将答冬书写在答題卡規定的位實上.4. 所祈題目必须在答題卡上作养•在试題卷上答題无效.5. 考试结束后•只称答縣卡交回.第I 卷(透择題•共60分)离三故乍(理科r •一途■考试is 購1頁(共4 K )一■选择議:本大II 共12小H.Q 小JH 5分•共60分.左毎小H 给出的四个选项中•只有一0是符合麵目要求的.(1) 设集合 U = R ・ A = {H |F —工 一2>0} •则 C (/A - (A) C-oo t -l )(J (2> + oo ) (B) [一 1>2J(C) (-oo t -l]U [2.+ 8〉(2) 命IT 若a >b •则a+c>6+c”的否命題是(A) 若 a Mb ,则 + c(B) 若 a+c W6+c •則 a (C) 若 a+t>6+c •则 a >6 〈D)若 a > b ■则 + r (3) 执行如田所示的程序|g 图,如果输出的结果为0・那么输入的工为 (A 冷(B)-l 或 1 (C)l(D) (- 1.2)(D)-l⑷巳知双曲线音-沪心 >。
』>。
)的左■右离点分别 为戸,片,双曲线上一点P 满足FF,丄工轴•若 |F|F ;|=12・|PF ;| = 5 •则谏取曲线的离心串为 (A)n ⑻夢 <c >4(D)3(5)巳知a为第二◎限角sin2a 芫•则cosa — sina的(ft为7 7 1(A) 5 ⑻ 一丁<C) 5(6) (x4-l),(x-2)的展开式中F的累數为CA)25 (B)5 (0-15 <D)-20(7) 如阳,网格址上小正方形的边长为1,91实线逊出的丑某四綾惟的三视图,则该四棱锥的外接球的表面积为(A) 136K(B) 34K(C) 25n (D) 18x⑻将Sft/(x)=sin2x +V3cos2x图象上所有点的横坐标伸长刊廉*的2ffi(纵坐标不变》,再将图欽上所有点向右平移y个小位长度•初到函敷^(x)的用◎,則&(工)图农的一条对称轴方程是(AI MQ —*CBI H** (C) x(D) x ■* y(9)在玄三棱柱ABC-A|B|Ci中•平面a与校AB .AC.AG ・4B|分别交于点E.F.G, H•且直线Mi JI平面a.布下列三个金題:①四边形EFGH超平行四边形;② 平面a 〃平而BCC.B.'③平面a丄平面BCFE•其中正确的命題有(A)Q②⑻②③(C》①③(D)(D②③仆0)巳知A,B是BSOd+b・4上的曲个动点,|AB|-2,(X:-jOA-yOB .若M超线段AB的中点■则0C・0M的值为(A)3 (B) 273 (02 <D)-3“1〉巳知函数/(r)是定义在R上的個函数•且/(-x-1) - /(x-l> •当X C [— 1,0]时JT*.则关于X的方I COSJTX在[―y 上的所有实数堺之和为(A>-7 (B)-6 (0-3 (D)-l(12)巳知曲线G2・“0>0">0)在点M(\2)处的切线与曲线Ci^-c^ - 1也相切•则t\ny~的值为(A) 4e»(B)8e (02 (D)8第II卷《菲选择题.共90分》二、填空題:本大18共4小18•毎小題5分,共20分.(13)若其中a € R,i为虚数单位)的曲部为一1 •则a- _________________________ •1 +1(14)K^m北朝时代的数学家祖丽提岀体枳的计算顶理(祖期原理)厂耳好既同•则枳不容异”•■势”即是舄广矿是曲枳•怠思是;如果曲等髙的几何体在同高处飲得两几何体的住而积恒彎•那么这两个几何体的体积相靠•类比祖阳原理•如图所示•在平面点角坐标禹三敗学(理科》•一诊••考试題訥2 4 JT)系中•图1泉一个形状不观則的对闭图形•图2是一个上底为1的梯形•且当实数f敢[0.3]上的任住值时• 直线y-f被图1和图2所皱得的两线段长始终相尊• 则图1的面积为______________________ ・2 JT + y — 4 < 0y «1(15)若实ttx.y tM足约束条件^r-2y-2<0 •则 =-x - 1 > 0 ”的最小值为__________ •(⑹已知AABC中.ACM'BCY・AABC的面积为睜.若线段/M的延长线上存在点 D •使ZBDC-7•-则CD = ___________•4三■解笞题:本大题共6小JH ■共70分.解苦R巧出文字说明■证明过程或演尊步*L (17〉(本小聽摘分12分〉已知效列(aj 満足at =-2.a.fI =2a.+4.(1>证阴数列S.+4}是等比数列$(□>求数列{\a.\}的前力項和S…“8)(本小題満分12分〉某知2016年离中数学学业水平测试的原始成绩采用百分朋•发布底塡便用零级制.各等级划分标准为*5 分及以上•记为A等,分数在[70.85〉内•记为B等『分數在:60.70)内•记为C^,6 0分以下•记为D尊•同时认定A .B.C为合格•£>为不合格•已知甲•乙対所学校学生的顶始成绩均分布在〔50. 100]内•为了比较两校学生的成绩•分别抽肢50名学生的原始成绩作为样本进行统比按照[50.60〉■ [60.70)■[70.80〉■ [80.90). [90 JOO] 的分组作出甲较的样本檢率分布直方图如图1所示•乙牧的样本中寺级为C.U的所冇数据的茎叶WJUffl 2所示.(I)求阳中龙的值•并根扳样本救据比较甲乙两校的合〈0)在选取的样本中•从甲•乙两牧C等级的学生中圈机抽取3名学生进行调研•用X农示所抽取的3名学生中甲校的学生人数•求随机变■ X的分布列和数学期垫.CWX*小題港分12分〉iflffl】•在正方形ABCD中•点E.F分别足AB.BC的中点・BD与EF交于点H.G为BD中UD点•点R在线段BH上•且—=AQ >0).«将ffl2ffll 阳2岛三科)•一诊■考试聽第3页(箕4△AED心CFSEF分别沿DE.DF.EF折起•使点A.C 1K合于点该点记为P). 如图2所示.(I)若A-2^i£,GR 丄平面PEF i< n)是否存在正实数A •使御克线FR与平面DEF所成角的正戎值为够?若存在. 求出入的tfb若不存在•请说明理由.(20〉(本小越體分12分)已知柄圆£ + ・■】的右焦点为F•设£(线/:x・5与工轴的交点为E •过点F且斜睾为A的直线人与楠関交于A.P阿点・M为线段£F的中点.(I)若直线/>的倾斜角为于•求AABM的而枳S的值;(0)过点B作直线BN丄/于点N •证明:A.M.N三点共线.(21〉(本小題肚分12分》巳知函数/Ct) ■工ln(T + 1)+(*—门工+2-a・a € R・(I )当x >OH4.求函ttg(-r)-/U)4-ln(jr + 1)+-jx 的瞅调区间:(D)当a W Z时•若存在工—0•使不等式/(zXO 立•求a的尺小(ft.请考生在M(22) J23)H中任选一越作答•如果多做•则按所借的计分.(22)(本小题満分10分)选修4一4,坐标系与豔效方程在平面直角坐标系MOy中•傾斜角为aS工芳)的直级/的蛊数方程为Z ly・fsin<r(e为<«>.以型标风点为做点•以工紬的正半紬为桜軸•漣立极坐标糜•曲线C的谡坚标方程是pcos2G — "in。
2017年四川省成都市高考数学一诊试卷(理科)

2017年四川省成都市高考数学一诊试卷(理科)一、选择题(共12小题;共60分)1. 若全集,集合,则A. B. C. D.2. 命题“若,则”的否命题是A. 若,则B. 若,则C. 若,则D. 若,则3. 执行如图所示的程序框图,如果输出的结果为,那么输入的为A. B. 或 C. D.4. 已知双曲线的左,右焦点分别为,,双曲线上一点满足轴,若,,则该双曲线的离心率为A. B. C. D.5. 已知为第二象限角,且,则的值为A. B. C. D.6. 的展开式中的系数为A. B. C. D.7. 如图,网格纸上小正方形的边长为,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为A. B. C. D.8. 将函数图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将图象上所有点向右平移个单位长度,得到函数的图象,则图象的一条对称轴方程是A. B. C. D.9. 在直三棱柱中,平面与棱,,,分别交于点,,,,且直线 平面.有下列三个命题:①四边形是平行四边形;②平面 平面;③平面平面.其中正确的命题有A. ①②B. ②③C. ①③D. ①②③10. 已知,是圆上的两个动点,,.若是线段的中点,则的值为A. B. C. D.11. 已知函数是定义在上的偶函数,且,当时,,则关于的方程在上的所有实数解之和为A. B. C. D.12. 已知曲线:(,)在点处的切线与曲线:也相切,则的值为A. B. C. D.二、填空题(共4小题;共20分)13. 若复数(其中,为虚数单位)的虚部为,则 ______.14. 我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为的梯形,且当实数取上的任意值时,直线被图1和图2所截得的两线段长始终相等,则图1的面积为______.15. 若实数,满足约束条件则的最小值为______.16. 已知中,,,的面积为.若线段的延长线上存在点,使,则 ______.三、解答题(共7小题;共91分)17. 已知数列满足,(1)证明数列是等比数列;(2)求数列的前项和.18. 云南省2016年高中数学学业水平考试的原始成绩采用百分制,发布成绩使用等级制,各登记划分标准为:分及以上,记为A等,分数在内,记为B等,分数在内,记为C 等,分以下,记为D等,同时认定等级分别为A,B,C 都为合格,等级为D为不合格,已知甲、乙两所学校学生的原始成绩均分布在内,为了比较两校学生的成绩,分别抽取名学生的原始成绩作为样本进行统计,按照,,,,分别作出甲校如图1 所示样本频率分布直方图,乙校如图2所示样本中等级为C,D的所有数据茎叶图.(1)求图中的值,并根据样本数据比较甲乙两校的合格率;(2)在选取的样本中,从甲、乙两校C等级的学生中随机抽取名学生进行调研,用表示所抽取的名学生中甲校的学生人数,求随机变量的分布列和数学期望.19. 如图1,在正方形中,点,分别是,的中点,与交于点,为中点,点在线段上,且.现将,,分别沿,,折起,使点,重合于点(该点记为)如图2所示.(1)若,求证:平面;(2)是否存在正实数,使得直线与平面所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.20. 已知椭圆:的右焦点为,设直线:与轴的交点为,过点且斜率为的直线与椭圆交于,两点,为线段的中点.(1)若直线的倾斜角为,求的面积的值;(2)过点作直线于点,证明:,,三点共线.21. 已知函数.(1)当时,求函数的单调区间;(2)当时,若存在,使不等式成立,求的最小值.22. 在平面直角坐标中,倾斜角为的直线的参数方程为(为参数).以坐标原点为极点,以轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程是.(1)写出直线的普通方程和曲线的直角坐标方程;(2)已知点.若点的极坐标为,直线经过点且与曲线相交于,两点,设线段的中点为,求的值.23. 已知函数,.(1)求不等式的解集;(2)若的最小值为,正数,满足,求的最小值.答案第一部分1. C2. A3. C4. C5. B6. C7. B8. D9. C 10. A11. A 12. D第二部分13.14.15.16.第三部分17. (1)因为数列满足,,所以,所以数列是等比数列,公比与首项为.(2)由(1)可得:,所以,所以当时,;时,,所以时,时也成立.所以.18. (1)由频率分布直方图可得:,解得.甲校的合格率,乙校的合格率.可得:甲乙两校的合格率相同,都为.(2)甲乙两校的C等级的学生数分别为:人,人..则,,,,.所以的分布列为:.19. (1)由题意,,,三条直线两两垂直,所以平面,图1中,,所以,因为为中点,所以.图2中,因为,所以中,,所以平面;(2)由题意,建立如图所示的坐标系,,则,,,,所以,因为,所以,所以,因为,,设平面的一个法向量为,则取,因为直线与平面所成角的正弦值为,,所以,所以存在正实数,使得直线与平面所成角的正弦值为.20. (1)由题意可知:右焦点,,,设,,由直线的倾斜角为,则,直线的方程,即,则整理得:.则,,的面积,所以的面积的值.(2)设直线的方程为,则整理得:.则,.直线于点,则,由,,而所以.所以,,三点共线.21. (1)因为,所以,当即时,对恒成立,此时,在递增,无递减区间,当即时,由,得,由,得,此时,在递减,在递增,综上,时,在递增,无递减区间;时,在递减,在递增.(2)由,得,当时,上式等价于,令,,由题意,存在,使得成立,则只需,因为,令,显然在递增,而,,故存在,使得,即,又当时,,递减,当时,,递增,故时,有极小值(也是最小值),故,故,,而,故的最小整数值是.22. (1)因为直线的参数方程为(为参数).所以直线的普通方程为,由曲线的极坐标方程是,得,所以,所以曲线的直角坐标方程为.(2)因为点的极坐标为,所以点的直角坐标为,所以,直线的倾斜角为,所以直线的参数方程为(为参数),代入,得,设,两点对应的参数为,,因为为线段的中点,所以点对应的参数值为,又,则.23. (1)当时,;当时,.所以不等式等价于或所以,或.所以所以原不等式的解集为.(2)由(1),得.可知的最小值为.所以.所以,变形得.因为,,所以当且仅当,即时,取等号.所以的最小值为.。
2017年四川省成都市双流中学高考一模数学试卷(理科)【解析版】

2017年四川省成都市双流中学高考数学一模试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x2﹣2x﹣3<0},B={﹣1,0,1,2,3},则A∩B=()A.{0,1}B.{0,1,2}C.{﹣1,0,1}D.{﹣1,3} 2.(5分)设复数z满足(1﹣i)z=2i,则z=()A.﹣1+i B.﹣1﹣i C.1+i D.1﹣i3.(5分)已知向量=(1,m),=(3,﹣2),且(+)⊥,则m=()A.﹣8B.﹣6C.6D.84.(5分)已知倾斜角为θ的直线l与直线x﹣3y+1=0垂直,则=()A.B.C.D.5.(5分)如图是求样本x1,x2,…,x10平均数的程序框图,图中空白框中应填入的内容为()A.S=S+x n B.S=S+C.S=S+n D.S=S+ 6.(5分)已知p:∃x0∈(﹣1,0),<2;q:∀a∈(0,+∞),函数y=|tan ax|最小正周期为,则下列命题中为真命题的是()A.p∧q B.p∧(¬q)C.p∨q D.p∨(¬q)7.(5分)一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为()A.36B.48C.64D.728.(5分)如图所示,在一个边长为1的正方形AOBC内,曲y=x2和曲线y=围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是()A.B.C.D.9.(5分)如图所示为函数的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(θx+w)图象的对称轴为()A.x=12k﹣8,(k∈Z)B.x=6k﹣2,(k∈Z)C.x=6k﹣4(k∈Z)D.x=12k﹣2,(k∈Z)10.(5分)已知函数y=2|x|﹣4的图象与曲线C:x2+λy2=4恰有两个不同的公共点,则实数λ的取值范围是()A.[﹣,)B.[﹣,]C.(﹣∞,﹣]∪(0,)D.(﹣∞,﹣]∪[,+∞)11.(5分)已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g (x)>f(x)g′(x),且f(x)=a x•g(x)(a>0,且a≠1),,若数列的前n项和大于62,则n的最小值为()A.6B.7C.8D.912.(5分)已知A,B,C是球O球面上的三点,且,D为该球面上的动点,球心O到平面ABC的距离为球半径的一半,则三棱锥D﹣ABC 体积的最大值为()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)若x,y满足约束条件.则的最大值为.14.(5分)在的展开式中,含的项的系数为15.(5分)已知双曲线的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的一条渐近线交于P,Q两点.若∠P AQ=60°且,则双曲线的离心率.16.(5分)我国南宋时期著名的数学家秦九韶在其著作《数学九章》中独立提出了一种求三角形面积的方法﹣“三斜求积术”,即△ABC的面积S=.其中a,b,c分别为△ABC内角A、B、C的对边.若b=2,且tan C=,则△ABC的面积S的最大值为.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知数列{a n}的前n项和S n满足.(1)求证:数列{a n}为等比数列;(2)设函数,求T100.18.(12分)随着移动互联网的快速发展,基于互联网的共享单车应用而生,某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系,求y关于x的线性回归方程,并预测M公司2017年4月份(即x=7时)的市场占有率;(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?(参考公式:回归直线方程=x +,其中=,=﹣)19.(12分)如图•所示,E 为矩形ABCD 的边AD 上一点,,现将△BCE 以BC 为旋转轴旋转到△BCF ,使平面BCF ⊥平面ABCD ,设G 、H 分别为AD 、CF 的中点,如图‚所示.(1)求证:平面BGF ⊥平面CDF ;(2)求平面BFG 与平面DEH 所成锐二面角的余弦值.20.(12分)平面直角坐标系中,动圆C 与圆(x ﹣1)2+y 2=外切,且与直线x=﹣相切,记圆心C的轨迹为曲线T(Ⅰ)求曲线T的方程;(Ⅱ)设过定点Q(m,0)(m为非零常数)的动直线l与曲线T交于A、B两点,问:在曲线T上是否存在点P(与A、B两点相异),当直线P A、PB的斜率存在时,直线P A、PB的斜率之和为定值,若存在,求出点P的坐标;若不存在,请说明理由.21.(12分)已知函数,其中a∈R,e为自然对数的底数.(1)求函数f(x)的极值;(2)若函数y=f(x)+h(x)在R上单调递增,求实数a能取到的最大整数值.选考部分请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.选修4-4:坐标系与参数方程22.(10分)在直角坐标系xOy中,曲线C1的参数方程为(其中α为参数),曲线C2:(x﹣1)2+y2=1,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;(Ⅱ)若射线θ=(ρ>0)与曲线C1,C2分别交于A,B两点,求|AB|.选修4-5:不等式选讲23.设函数f(x)=|﹣2x+4|﹣|x+6|.(1)求不等式f(x)≥0的解集;(2)若f(x)>a+|x﹣2|存在实数解,求实数a的取值范围.2017年四川省成都市双流中学高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x2﹣2x﹣3<0},B={﹣1,0,1,2,3},则A∩B=()A.{0,1}B.{0,1,2}C.{﹣1,0,1}D.{﹣1,3}【解答】解:集合A={x|x2﹣2x﹣3<0}={x|﹣1<x<3},B={﹣1,0,1,2,3},则A∩B={0,1,2},故选:B.2.(5分)设复数z满足(1﹣i)z=2i,则z=()A.﹣1+i B.﹣1﹣i C.1+i D.1﹣i【解答】解:∵复数z满足z(1﹣i)=2i,∴z==﹣1+i故选:A.3.(5分)已知向量=(1,m),=(3,﹣2),且(+)⊥,则m=()A.﹣8B.﹣6C.6D.8【解答】解:∵向量=(1,m),=(3,﹣2),∴+=(4,m﹣2),又∵(+)⊥,∴12﹣2(m﹣2)=0,解得:m=8,故选:D.4.(5分)已知倾斜角为θ的直线l与直线x﹣3y+1=0垂直,则=()A.B.C.D.【解答】解:∵倾斜角为θ的直线,与直线x﹣3y+1=0垂直,∴﹣×tanθ=﹣1,解得tanθ=﹣3.∴===﹣.故选:C.5.(5分)如图是求样本x1,x2,…,x10平均数的程序框图,图中空白框中应填入的内容为()A.S=S+x n B.S=S+C.S=S+n D.S=S+【解答】解:由题目要求可知:该程序的作用是求样本x1,x2,…,x10平均数,由于“输出”的前一步是“”,故循环体的功能是累加各样本的值,故应为:S=S+x n故选:A.6.(5分)已知p:∃x0∈(﹣1,0),<2;q:∀a∈(0,+∞),函数y=|tan ax|最小正周期为,则下列命题中为真命题的是()A.p∧q B.p∧(¬q)C.p∨q D.p∨(¬q)【解答】解:p:∀x∈(﹣1,0),x﹣2∈(1,+∞),2x∈(,1),因此:不存在x0∈(﹣1,0),使得<2;是假命题.q:∀a∈(0,∞),函数y=|tan ax|最小正周期为,是真命题.则下列命题中为真命题的只有C.故选:C.7.(5分)一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为()A.36B.48C.64D.72【解答】解:根据几何体的三视图得该几何体的体积为长宽高分别为4,4,6的长方体体积的一半,即=48,故选:B.8.(5分)如图所示,在一个边长为1的正方形AOBC内,曲y=x2和曲线y=围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是()A.B.C.D.【解答】解:可知此题求解的概率类型为关于面积的几何概型,由图可知基本事件空间所对应的几何度量S(Ω)=1,满足所投的点落在叶形图内部所对应的几何度量:S(A)==.所以P(A)=.故选:C.9.(5分)如图所示为函数的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(θx+w)图象的对称轴为()A.x=12k﹣8,(k∈Z)B.x=6k﹣2,(k∈Z)C.x=6k﹣4(k∈Z)D.x=12k﹣2,(k∈Z)【解答】解:由函数的部分图象知,AB=5,∴==3,∴T =6,w ==,f (0)=2sin θ=1,∴θ=,∴函数g (x )=2cos (x +),x +=k π,x =6k ﹣2,k ∈Z ;∴g (x )图象的对称轴为x =6k ﹣2,k ∈Z . 故选:B .10.(5分)已知函数y =2|x |﹣4的图象与曲线C :x 2+λy 2=4恰有两个不同的公共点,则实数λ的取值范围是( ) A .[﹣,)B .[﹣,]C .(﹣∞,﹣]∪(0,)D .(﹣∞,﹣]∪[,+∞)【解答】解:由y =2x ﹣4可得,x ≥0时,y =2x ﹣4;x <0时,y =﹣2x ﹣4, ∴函数y =2x ﹣4的图象与方程x 2+λy 2=4的曲线必相交于(±2,0),如图.所以为了使函数y =2x ﹣4的图象与方程x 2+λy 2=4的曲线恰好有两个不同的公共点,则将y =2x ﹣4代入方程x 2+λy 2=4, 整理可得(1+4λ)x 2﹣16λx +16λ﹣4=0, 当λ=﹣时,x =2满足题意,∵函数y =2x ﹣4的图象与曲线C :x 2+λy 2=4恰好有两个不同的公共点, ∴△>0,2是方程的根, ∴<0,即﹣<λ<时,方程两根异号,满足题意;综上知,实数λ的取值范围是[﹣,). 故选:A .11.(5分)已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g (x)>f(x)g′(x),且f(x)=a x•g(x)(a>0,且a≠1),,若数列的前n项和大于62,则n的最小值为()A.6B.7C.8D.9【解答】解:∵f′(x)g(x)>f(x)g′(x),∴f′(x)g(x)﹣f(x)g′(x)>0,∴,从而可得单调递增,从而可得a>1,∵,∴a=2.故=2+22+…+2n=.∴2n+1>64,即n+1>6,n>5,n∈N*.∴n=6.故选:A.12.(5分)已知A,B,C是球O球面上的三点,且,D为该球面上的动点,球心O到平面ABC的距离为球半径的一半,则三棱锥D﹣ABC 体积的最大值为()A.B.C.D.【解答】解:如图,在△ABC中,∵AB=AC=3,BC=3,∴由余弦定理可得cos A==﹣,则A=120°,∴sin A=.设△ABC外接圆的半径为r,则,得r=3.设球的半径为R,则,解得R=2.∵×3×3×=,∴三棱锥D﹣ABC体积的最大值为=,故选:D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)若x,y满足约束条件.则的最大值为3.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).设k=,则k的几何意义为区域内的点到原点的斜率,由图象知OA的斜率最大,由,解得,即A(1,3),k OA==3,即的最大值为3.故答案为:3.14.(5分)在的展开式中,含的项的系数为15【解答】解:的展开式中,是由3种情况得到:①(1+x)3的常数项与的含的项的乘积;②(1+x)3的含x的项与的含项的乘积;③(1+x)3的含x2的项与的含项的乘积故C31+C31•C32+C32=15故答案为1515.(5分)已知双曲线的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的一条渐近线交于P,Q两点.若∠P AQ=60°且,则双曲线的离心率.【解答】解:因为∠P AQ=60°且,所以△QAP为等边三角形,设AQ=R,则PQ=R,OP=R,三角形OAQ是直角三角形,∠QOA=30°,渐近线方程为y=x,,可得e====.故答案为:.16.(5分)我国南宋时期著名的数学家秦九韶在其著作《数学九章》中独立提出了一种求三角形面积的方法﹣“三斜求积术”,即△ABC的面积S=.其中a,b,c分别为△ABC内角A、B、C的对边.若b=2,且tan C=,则△ABC的面积S的最大值为.【解答】解:∵tan C=,∴sin C=sin(B+C)=sin A,∴c=a,∵b=2,∴S===,∴a=2时,△ABC的面积S的最大值为,故答案为.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知数列{a n}的前n项和S n满足.(1)求证:数列{a n}为等比数列;(2)设函数,求T100.【解答】(1)证明:因为a n=1﹣2s n,所以a n﹣1=1﹣2s n﹣1(n≥2),…………(1分)所以a n﹣a n﹣1=2s n﹣1﹣2s n=﹣2a n(n≥2),所以…………(3分)又a1=1﹣2s1,所以.…………(4分)所以数列为首项为,公比为的等比数列.…………(5分)(2)解:因为,所以==因为所以…(12分)18.(12分)随着移动互联网的快速发展,基于互联网的共享单车应用而生,某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系,求y关于x的线性回归方程,并预测M公司2017年4月份(即x=7时)的市场占有率;(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A 、B 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?(参考公式:回归直线方程=x +,其中=,=﹣)【解答】解:(Ⅰ)由题意,=3.5,=16,===2,=﹣=16﹣2×3.5=9,∴=2x +9,x =7时,=2×7+9=23,即预测M 公司2017年4月份(即x =7时)的市场占有率为23%;(Ⅱ)由频率估计概率,每辆A 款车可使用1年,2年,3年、4年的概率分别为0.2,0.35,0.35,0.1,∴每辆A 款车的利润数学期望为(500﹣1000)×0.2+(1000﹣1000)×0.35+(1500﹣1000)×0.35+(2000﹣1000)×0.1=175元;每辆B款车可使用1年,2年,3年、4年的概率分别为0.1,0.3,0.4,0.2,∴每辆B款车的利润数学期望为(500﹣1200)×0.1+(1000﹣1200)×0.3+(1500﹣1200)×0.4+(2000﹣1200)×0.2=150元;∵175>150,∴应该采购A款车.19.(12分)如图•所示,E为矩形ABCD的边AD上一点,,现将△BCE以BC为旋转轴旋转到△BCF,使平面BCF⊥平面ABCD,设G、H分别为AD、CF的中点,如图‚所示.(1)求证:平面BGF⊥平面CDF;(2)求平面BFG与平面DEH所成锐二面角的余弦值.【解答】解:(1)在图①中,∵E为矩形ABCD的边AD上一点,,∴,∴BE2+CE2=BC2,∴BE⊥CB…………(2分)∵平面BCF⊥平面ABCD,且平面BCF∩平面ABCD=BC,DC⊥BC,∴DC⊥平面BCF,∴DC⊥BF……………………(4分)而DC,CF是平面DCF内两条相交直线,∴EF⊥平面DCF……………………(5分)又BF⊂平面BGF,∴平面BGF⊥平面CDF.…………(6分)解:(2)以F为坐标原点,FC,FB所在直线为轴建立空间直角坐标系,则F(0,0,0),B,G,H(1,0,0),D………………(7分)设平面BFG的法向量为,则,即,取z=﹣1得平面BFG的一个法向量为;…………………………(9分)同理可得平面DEH的一个法向量为………………………………(10分)∴===.故平面BFG与平面DEH所成锐二面角的余弦值为.……………………………………………………(11分)20.(12分)平面直角坐标系中,动圆C与圆(x﹣1)2+y2=外切,且与直线x =﹣相切,记圆心C的轨迹为曲线T(Ⅰ)求曲线T的方程;(Ⅱ)设过定点Q(m,0)(m为非零常数)的动直线l与曲线T交于A、B两点,问:在曲线T上是否存在点P(与A、B两点相异),当直线P A、PB的斜率存在时,直线P A、PB的斜率之和为定值,若存在,求出点P的坐标;若不存在,请说明理由.【解答】解:(1)设动圆圆心为C(x,y),动圆圆心C到点(1,0)的距离与到直线x=﹣距离差为定圆半径,即动点C到顶点(1,0)的距离等于到定直线x=﹣1的距离,根据圆锥曲线的定义,动点C的轨迹是以定点(1.0)为焦点,直线x=﹣1为准线的抛物线.圆心C的轨迹为曲线T的方程为:y2=4x(2)假设在曲线T上存在点P满足题设条件,不妨设P(x0,y0),A(x1,y1),B(x2,y2);,;=…(1).显然动直线l的斜率非零,故可设其方程为x=ty+m,(t∈R),联立y2=4x,整理得y2﹣4ty﹣4m=0,∴y1+y2=4t,y1y2=﹣4m,且y1≠y2,代入(1)式得显然y0≠0,于是[4y0(k P A+k PB)﹣16]+(k PB+k P A)(y02﹣4m)﹣8y0=0 (2)欲使(2)式对任意t∈R成立,必有∵y0≠0,m≠0,∴,∴,即于是,当m>0时,不存在满足条件的y0,即不存在满足题设条件的点P;当m<0时,,将此代入抛物线T的方程可求得满足条件的P点坐标为(﹣m,2),(﹣m,﹣2)综上所述,存在点P(与A,B两点相异),其坐标为(﹣m,2),(﹣m,﹣2)直线P A、PB的斜率之和为定值.21.(12分)已知函数,其中a∈R,e为自然对数的底数.(1)求函数f(x)的极值;(2)若函数y=f(x)+h(x)在R上单调递增,求实数a能取到的最大整数值.选考部分【解答】解:(1)f(x)=(x﹣2)e x,f'(x)=e x+(x﹣2)e x=(x﹣1)e x,令f'(x)=0,得x=1,当x>1时,f'(x)>0;当x<1时,f′(x)<0,∴x=1是f(x)的唯一的极小值点,无极大值点,故f(x)的极小值为﹣e,无极大值,(2)方法一:记,由题意知g'(x)=(x﹣1)e x﹣ax+2≥0在R上恒成立,由g'(1)=﹣a+2≥0,可得g'(x)≥0的必要条件是a≤2,若a=2,则g'(x)=(x﹣1)e x﹣2x+2=(x﹣1)(e x﹣2),当In2<x<1时,g'(x)<0,故a<2,下面证明:当a=1时,不等式(x﹣1)e x﹣x+2≥0恒成立,令h(x)=(x﹣1)e x﹣x+2,则h'(x)=xe x﹣1,记H(x)=xe x﹣1,则H(x)=(x+1)e x,从而(x﹣1)e x﹣x+2≥0恒成立,故a能取得的最大整数为1,方法二:记由题意知g'(x)=(x﹣1)e x﹣ax+2≥0在R上恒成立,∵g'(1)=﹣a0,+2≥0∴g'(x)≥0的必要条件是a≤2,若a=2,则g'(x)=(x﹣1)e x﹣2x+2=(x﹣1)(e x﹣2),当In2<x<1时,g'(x)<0,故a<2,下面证明:当a=1时,不等式(x﹣1)e x﹣x+2≥0恒成立,即(x﹣1)e x≥x﹣2,先证明∀x∈R,e x≥x+1,令k(x)=e x﹣x﹣1,则k'(x)=e x﹣1,当x>0时,k'(x)>0,k(x)单调递增;当x<0时k'(x)<0,k(x)单调递减.∴k(x)min=k(0)=0,∴e x≥x+1恒成立,当x≥1时,(x﹣1)e x≥(x﹣1)(x+1)=x2﹣1>x﹣2,当x<1时,由e x≥x+1得e﹣x≥﹣x+1>0,即,∴,综上所述,(x﹣1)e x﹣x+2≥0恒成立,故a能取得的最大整数为1.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.选修4-4:坐标系与参数方程22.(10分)在直角坐标系xOy中,曲线C1的参数方程为(其中α为参数),曲线C2:(x﹣1)2+y2=1,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;(Ⅱ)若射线θ=(ρ>0)与曲线C1,C2分别交于A,B两点,求|AB|.【解答】解:(Ⅰ)∵曲线C1的参数方程为(其中α为参数),∴曲线C1的普通方程为x2+(y﹣2)2=7.∵曲线C2:(x﹣1)2+y2=1,∴把x=ρcosθ,y=ρsinθ代入(x﹣1)2+y2=1,得到曲线C2的极坐标方程(ρcosθ﹣1)2+(ρsinθ)2=1,化简,得ρ=2cosθ.(Ⅱ)依题意设A(),B(),∵曲线C1的极坐标方程为ρ2﹣4ρsinθ﹣3=0,将(ρ>0)代入曲线C1的极坐标方程,得ρ2﹣2ρ﹣3=0,解得ρ1=3,同理,将(ρ>0)代入曲线C 2的极坐标方程,得,∴|AB|=|ρ1﹣ρ2|=3﹣.选修4-5:不等式选讲23.设函数f(x)=|﹣2x+4|﹣|x+6|.(1)求不等式f(x)≥0的解集;(2)若f(x)>a+|x﹣2|存在实数解,求实数a的取值范围.【解答】解:(1)f(x)≥0即|2x﹣4|﹣|x+6|≥0,可化为①或②,或③,解得x<﹣6或﹣6≤x≤﹣或x≥10,综上,不等式的解集是(﹣∞,﹣]∪[10,+∞);(2)f(x)>a+|x﹣2|等价于2|x﹣2|﹣|x+6|>a+|x﹣2|,等价于|x﹣2|﹣|x+6|>a,而|x﹣2|﹣|x+6|≤|x﹣2﹣x﹣6|=8,若f(x)>a+|x﹣2|存在实数解,则a<8,即实数a的范围是(﹣∞,8).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理科第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合U =R ,{}220A x x x =-->,则UA =(A )()()12,,-∞-+∞(B )[]12,-(C )(][)12,,-∞-+∞(D )()12,-(2)命题“若a b >,则a c b c +>+”的否命题是 (A )若a b >,则a c +≤b c + (B )若a c +≤b c +,则a ≤b (C )若a c b c +>+,则a b > (D )若a ≤b ,则a c +≤b c +(3)执行如图所示的程序框图,如果输出的结果为0,那么输入的x 为(A )19(B ) -1或1(C ) 1 (D ) -1(4)已知双曲线2222100x y a >b >a b-=(,)的左,右焦点分别为12F ,F ,曲线上一点P 满足2PF x ⊥轴,若122125F F PF ==,,则该双曲线的离心率为 (A )1312(B )32(C )125(D )3(5)已知α为第二象限角,且24sin225α=-,则cos sin αα-的值为 (A )75(B )75-(C )15(D )15- (6)()()512x x +-的展开式中2x 的系数为(A )25 (B )5(C )15-(D )20-(7)如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为 (A )136π(B )34π(C )25π(D )18π(8)将函数()sin 23cos2f x x x =+图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移6π个单位长度,得到函数()g x 的图象,则该图象的一条对称轴方程是(A )6x π=-(B )6x π=(C )524x π=(D )3x π=(9)在直三棱柱111ABC A B C -中,平面α与棱1111,,,AB AC A C A B 分别交于点,,,E F G H ,且直线1//AA 平面α,有下列三个命题:①四边形EFGH 是平行四边形;②平面α∥平面11BCC B ;③平面α⊥平面BCFE .其中正确的命题有(A ) ①②(B ) ②③(C )①③(D )①②③(10)已知,A B 是圆22:4O x y +=上的两个动点,=2AB ,5233=-OC OA OB .若M 是线段AB 的中点,则OC OM ⋅的值为 (A )3 (B )3C )2 (D )3- (11)已知函数()f x 是定义在R 上的偶函数,且()()11f x f x --=-,当[]1,0∈-x 时,()3=-f x x ,则关于x 的方程()|cos |f x x =π在51[,]22-上的所有实数解之和为(A )-7(B )-6(C )-3(D )-1(12)已知曲线()210C y tx t =>:在点42M ,t ⎛⎫⎪⎝⎭处的切线与曲线12e 1x C y +=-:也相切,则24e ln t t的值为(A )24e (B )8e (C )2(D )8第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.(13)若复数i1ia z =+(其中a ∈R ,i 为虚数单位)的虚部为1-,则a = .(14)我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是,如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为1的梯形,且当实数t 取[]03,上的任意值时,直线y t =被图1和图2所截得的两线段长始终相等,则图1的面积为 .(15)若实数x,y 满足约束条件24022010x y x y x +-≤⎧⎪--≤⎨⎪-≥⎩,则1-y x 的最小值为 .(16)已知ABC ∆中,26AC ,BC ==,ABC ∆的面积为32,若线段BA 的延长线上存在点D ,使4BDC π∠=,则CD = . 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分)已知数列{}n a 满足11224n n a,a a +=-=+.(I )证明数列{}4n a +是等比数列;(II )求数列{}n a 的前n 项和n S .(18)(本小题满分12分)某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A 等;分数在[70,85)内,记为B 等;分数在[60,70)内,记为C 等;60分以下,记为D 等.同时认定A,B,C 为合格,D 为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的情况,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,作出乙校的样本中等级为C,D 的所有数据的茎叶图如图2所示. (I )求图中x 的值,并根据样本数据比较甲乙两校的合格率; (II )在选取的样本中,从甲,乙两校C 等级的学生中随机抽取3名学生进行调研,用X 表示所抽取的3名学生中甲校的学生 人数,求随机变量X 的分布列和数学期望.(19)(本小题满分12分)如图1,正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,BD 与EF 交于点H ,G 为BD 中点,点R 在线段BH 上,且0BRRHλλ=>(),现将AED,CFD,DEF ∆∆∆分别沿DE,DF,EF 折起,使点A ,C 重合于点B (该点记为P ),如图2所示. (I )若2=λ,求证:GR ⊥平面PEF ;(II )是否存在正实数λ,使得直线FR 与平面DEF?若存在,求出λ的值;若不存在,请说明理由.(20)(本小题满分12分)已知椭圆22154x y +=的右焦点为F ,记直线5l x =:与x 轴的交点为E ,过点F 且斜率为k 的直线1l 与椭圆交于A,B 两点,点M 为线段EF 的中点.(I )若直线1l 的倾斜角为4π,求ABM ∆的面积S 的值; (II )过点B 作直线BN l ⊥于点N ,证明:A ,M ,N 三点共线.(21)(本小题满分12分)已知函数()()1ln 1()22f x x x a x a,a =++-+-∈R .(I )当0x >时,求函数()()()1ln 12g x f x x x =+++的单调区间; (II )当a ∈Z 时,若存在x ≥0,使()0f x <成立,求a 的最小值.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分.(22)(本小题满分10分)选修4-4 :坐标系与参数方程在平面直角坐标系xOy 中,倾斜角为2ααπ≠()的直线l 的参数方程为1cos sin x t y t αα=+⎧⎨=⎩(t 为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程是2cos 4sin 0ρθθ-=.(Ⅰ)写出直线l 的普通方程和曲线C 的直角坐标方程;(Ⅱ)已知点P (1,0),点M 直线l 经过点M 且与曲线C 相交于,A B两点,设线段AB 的中点为Q ,求PQ 的值. (23)(本小题满分10分)选修4-5 :不等式选讲1-.(Ⅰ)求不等式()f x ≤6的解集;(Ⅱ)若()f x 的最小值为n ,正数,a b 满足22nab a b =+,求2a b +的最小值.文科第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合U =R ,()(){}120A x |x x =+-<,则UA =(A )()()12,,-∞-+∞(B )[]12,-(C )(][)12,,-∞-+∞ (D )()12,-(2) 命题“若a b >,则a c b c +>+”的逆命题是(A )若a b >,则a c +≤b c +(B )若a c +≤b c +,则a ≤b (C )若a c b c +>+,则a b >(D )若a ≤b ,则a c +≤b c +(3)双曲线22145x y -=的离心率为(A )4(B )355(C 5(D )32(4)已知α为锐角,且4sin 5α=,则()cos απ+= (A )35-(B )35(C )45-(D )45(5)执行如图所示的程序框图,如果输出的结果为0,那么输入的x 为(A )19(B ) -1或1(C )-1(D )1(6)已知x x 1 2 3 4 y m 3.2 4.8 7.5若y 关于x 的线性回归方程为21125ˆy .x .=-,则m 的值为 (A )1 (B )0.85 (C ) 0.7 (D ) 0.5(7)定义在R 上的奇函数()f x 满足()()3f x f x +=,当302,⎡⎫⎪⎢⎣⎭时,()3f x x =-,则112f =⎛⎫⎪⎝⎭(A )18-(B )18(C )1258-(D )1258(8)如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的所有棱中,最长的棱的长度为(A 41B 34C )5(D )32(9)将函数()sin 23cos2f x x x =+的图象上的所有点向右平移6π个单位长度,得到函数()g x 的图象,则该图象的一个对称中心是(A ),03π()(B ),04π()(C )(,0)12π-(D ),02π⎛⎫ ⎪⎝⎭(10)在直三棱柱111ABC A B C -中,平面α与棱1111,,,AB AC A C A B 分别交于点,,,E F G H ,且1//AA 平面α,有下列三个命题:①四边形EFGH 是平行四边形;②平面α∥平面11BCC B ;③平面α⊥平面BCFE .其中正确的命题有(A ) ①②(B ) ②③(C )①③(D )①②③(11)已知,A B 是圆22:4O x y +=上的两个动点,=2AB ,5233=-OC OA OB ,若点M 是AB 的中点,则OC OM ⋅的值为 (A )3(B )23C )2(D )3-(12)已知曲线()2100C y tx y ,t =>>:在点42M ,t ⎛⎫⎪⎝⎭处的切线与曲线12e 1x C y +=+:也相切,则t 的值为(A )24e (B )4e (C )2e 4(D )e 4第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.(13)复数2i1iz =+(i 为虚数单位)的虚部为 .(14)我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是,如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t 取[]04,上的任意值时,直线y t =被图1和图2所截得的线段长始终相等,则图1的面积为 .(15)若实数x,y 满足约束条件2402010x y x y x +-≤⎧⎪--≤⎨⎪-≥⎩,则3x y -的最大值为 .(16)已知ABC ∆中,26AC ,BC ==,ABC ∆的面积为32,若线段BA 的延长线上存在点D ,使4BDC π∠=,则CD = . 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分)某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A 等;分数在[70,85)内,记为B 等;分数在[60,70)内,记为C 等;60分以下,记为D 等.同时认定A,B,C 为合格,D 为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的情况,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,作出乙校的样本中等级为C,D 的所有数据的茎叶图如图2所示.(I )求图中x 的值,并根据样本数据比较甲乙两校的合格率;(II )在乙校的样本中,从成绩等级为C,D 的学生中随机抽取2名学生进行调研,求抽出的2名学生中至少有一名学生成绩等级为D 的概率.(18)(本小题满分12分)在等比数列{}n a 中,418aa =,且1231a a a +,,成等差数列.(I )求数列{}n a 的通项公式;(II )求数列{}4n a -的前n 项和n S . (19)(本小题满分12分)如图1,正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,BD 与EF 交于点H ,点G ,R 分别在线段DH ,HB 上,且DG BRGH RH=,将AED,CFD,BEF ∆∆∆分别沿DE,DF,EF 折起,使点A ,B ,C 重合于点P ,如图2所示.(I )求证:GR ⊥平面PEF ;(II )若正方形ABCD 的边长为4,求三棱锥P DEF -的内切球的半径.(20)(本小题满分12分)已知椭圆22154x y +=的右焦点为F ,记直线5l x =:与x 轴的交点为E ,过点F 且斜率为k 的直线1l 与椭圆交于A,B 两点,点M 为线段EF 的中点.(I )若直线1l 的倾斜角为4π,求AB 的值; (II )设直线AM 交直线l 于点N ,证明:直线BN l ⊥.(21)(本小题满分12分) 已知函数()ln (1)f x x x k x k =+-+,k ∈R .(I )若1k =,求()f x 的单调区间;(II )当1x >时,求使不等式()0f x >恒成立的最大整数k 的值.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分.(22)(本小题满分10分)选修4-4 :坐标系与参数方程在平面直角坐标系xOy 中,倾斜角为2ααπ≠()的直线l 的参数方程为1cos sin x t y t αα=+⎧⎨=⎩(t 为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程是2cos 4sin 0ρθθ-=.(Ⅰ)写出直线l 的普通方程和曲线C 的直角坐标方程; (Ⅱ)已知点P (1,0),点M 的极坐标为(1,)2π,直线l 经过点M 且与曲线C 相交于,A B两点,设线段AB 的中点为Q ,求PQ 的值. (23)(本小题满分10分)选修4-5 :不等式选讲1-.(Ⅰ)求不等式()f x ≤6的解集;(Ⅱ)若()f x 的最小值为n ,正数,a b 满足22nab a b =+,求2a b +的最小值.参考答案 理科一、选择题1.B ; 2.D ;3.D ;4.B ;5.B ;6.C ;7.B ;8.D ;9.C ;10.A ;11.A ;12.D . 二、填空题13. 2- 14. 92 15. 32-16. 三、解答题 17. (I )12a =-,142a ∴+= ·1分124n n a a +=+,14282(4)n n n a a a +∴+=+=+·3分 1424n n a a ++∴=+·4分∴{4}n a +是以2为首项,2为公比的等比数列.·5分(II )由(I )可知 42nn a +=,24nn a ∴=-·7分 当1n =时,120a =-<,11||2S a ∴==;·8分 当2n ≥时,0n a ≥,12n n S a a a ∴=-+++·9分22(24)(24)n =+-++-22(22)4(1)n n =+++--14(12)24(1)12n n --=+---1242n n +=-+·11分又1n =时,上式也满足,n N *∴∈,1242n n S n +=-+·………………………………………··12分18.(I )由题意可知,100.012100.056100.018100.010101x +⨯+⨯+⨯+⨯=, 0.004x ∴=·2分∴甲学校的合格率为1100.96x -=·3分而乙学校的合格率为210.9650-=·4分 ∴甲、乙两校的合格率均为96%·5分(II )样本中甲校C 等级的学生人数为0.01210506⨯⨯=人··6分 而乙校C 等级的学生人数为4人,∴随机抽取3人中,甲校学生人数X 的可能取值为0,1,2,3·7分343101(0)30C P X C ∴===,12643103(1)10C C P X C ===,21643101(2)2C C P X C ===,363101(3)6C P X C ===∴X 的分布列为X1 2 3 P130 310 12 16分数学期望311912310265EX =⨯+⨯+⨯=·………………··12分 19.(I )由题意可知,,,PE PF PD 三条直线两两垂直··1分 PD ∴⊥平面PEF ,·2分 在图1中,//EF AC ,H 为EF 的中点,又G 为BD 的中点,2DG GH ∴=·4分所以在图2中,2BRRHλ==,且2=GH DG , ∴在PDH ∆中,//GR DP ·5分GR ∴⊥平面PEF ·6分(II )由题意,分别以,,PF PE PD 为,,x y z 轴建立空间直角坐标系Pxyz , 设4PD =,则(0,0,0),(2,0,0),(0,2,0),(0,0,4)P F E D ,(1,1,0)H ∴·7分PR RH λ=,1PR PH λλ∴=+,(,,0)11R λλλλ∴++ 2=(2,,0)(,,0)1111RF λλλλλλλλ+∴--=-++++·8分又因为(2,2,0)(0,2,4)EF DE =-=-,, 设平面DEF 的一个法向量为(,,)x y z =m ,·9分。
