扬声器非线性指南
声学漫谈之七:扬声器等效电路与参数

声学漫谈之七:扬声器等效电路与参数弱非线性在非线性系统中又分强非线性和弱非线性,两者只是一个定性的概念。
在非线性物理系统中,其微分方程中包含了常系数线性项,以及非线性项。
当非线性部分与线性部分相比是比较微小的时候,这种系统可以称为弱非线性系统。
扬声器正是这种弱非线性的系统。
时不变性系统的参数不会随时间而变化,同一个输入信号,不论输入时间先还是后,输出的响应信号都是一样的。
需要注意的是,扬声器只能基本上算是时不变系统,因为其某些参数在长时间工作以后,特性可能会有些变化,比如线圈。
因果性即输出只取决于输入,和此前的信号无关,也不会影响以后的输出信号。
稳定系统只要输入是有界的,可收敛的,输出必定是有界的,可以收敛的。
扬声器系统实现了电声的转换,系统中其实包括了电-->力-->声之间的转化。
扬声器的等效电路有多种的表达方式,有声学、力学、电学等。
对于音频功放的设计或者应用者来说,关注的是其电学的等效电路,如下图所示。
其中,eg是输入信号源(比如正弦波,PWM波等);Rg是输入信号源的内阻(一般比较小,mΩ级别);Re是音圈电阻(Ω级别,常见的是8Ω);Le是音圈电感(几十uH级别,常见的是33uH);Res是扬声器等效声阻折算到电路端的电阻(Ω级别)Les是扬声器等效声顺折算到电路端的电感(mH级别)Ces是扬声器等效声质量折算到电路端的电容(百uF级别)根据上图中的等效电路,可以得到扬声器的电学等效阻抗可以表示为:等效阻抗随着频率变化的曲线如下图所示,横轴为信号频率,纵轴为扬声器阻抗。
从图中可以看出,阻抗的模值会随着频率变化,当频率从低频逐渐增大时,阻抗曲线慢慢上升。
当在某个频率点,阻抗曲线会出现一个峰值,该频点就是扬声器的谐振频点,经过谐振点以后,阻抗快速下降到最低点。
此最低点对应的阻抗就是扬声器的额定阻抗(又称为标称阻抗,扬声器手册中给出的额定阻抗,一般和此点阻抗的偏差小于20%)。
扬声器的阻抗实际上由3部分组成,a表示扬声器音圈的直流阻抗,不随频率变化(严格讲会随着温度变化);b表示电感部分,根据电感特性其感抗随频率上升而增加,和音圈的绕法、匝数有关;c表示反电动势部分,当音圈振动时,会产生一个反电动势,反电动势的电流与音圈输入电流的方向相反,事实上相当于减小输入电流,输入电流减小,则说明阻抗增高。
扬声器低频非线性参数建模与仿真研究

Z U C unu H N Mi" I O Y e HO h ajn,C E n,X A u (. ntueo s oa t sad A rnui ; a Istt fA t nui n eo at s i r c c b c olo Eetc E g er g nvri fEet ncS i c n eh ooy o hn ,C eg u 6 1 3 ,C ia .Sho f lc n i e n ,U iesyo l r i c ne ad T c nlg fC ia h nd 17 1 hn ) i r n i t co e
s o t o e w t g e t r o c f co a d id ca c i mo e a a t e f r h h g f q e c wi s l h r n i h r a e f r e a tr n n u t n e s r d p i o t e ih r u n y v e t h mal
( 电子科技 大学 a .空天科 学技 术研 究院;b .电子工程 学院, 四川 成都 6 13 ) 17 1
【 】在小信号条件下对具有相同匝数的扬声器长、 摘 短音圈进行了仿真, 重点讨论 了扬声器电一 力变换因数与
音 圈位移 的非线性关系 , 现在 位移交化 时, 发 长线 圈的电一 力变换 因数 的变化 率较 小, 但在 小位移 时短线 圈能够提 供 较大的电一 力变换 因数; 同时研 究 了音圈电感 与频率、 位移 的联 系, 发现长音圈 电感的变化率较小 , 随着频 率升高
e p ai d n h hn n ai o h og v i oc at s l e hn ta o h h r oes he m h s e ,a d te ca g g rt fte ln o eS f e f o i o rta ht fte sot n ,t z i o c r cr w
扬声器热传递非线性模型

没有 加短 路环 或没 有在 导磁 极柱 上设 置铜 帽 的单元
童0. \{ 0} 薹一i . 2 3} 4\ _ i 一一  ̄ l ~ ÷ I _
性模 型所 预 测 的结 果 是一 致 的 , 热态 时 的 功率 压 缩 P C达到 29d 。在更 高频段 , . B 因为 电感 较之于 电阻有 更 为 明显的贡献 , 因此 功率压缩 开始减小 。在谐振频
率之 下 , 由于扬声 器单 元 的非线 性特 性 的影 响 , 线 非
性热学模 型预示 出将 有 8 B的声输 出减 少。然而 , d 此 时若 用线 性热 学模 型来 预 测音 圈发 热仅仅 只 产生 了
。 。苦 苔; ‘“ ~ { 髓 古 “ 齿 } 蕊 ; 击
笔 者是用 ~ 个正 弦激 励信 号来 研究 非线 性 系纷
设计 的典 型特征 。非线性元件 : ) () ( , 表征的
是 较 高 频 段 的 寄 生 电感 , 和 () 曲线 形 状 相 它 的
扬 声 器 与 传 声 器
⑥ 圈 @囿 囿响 咖 6 响⑨响@ @ @⑥
文章编号 :0 2 8 8 (0 10 — 0 6 0 10 - 64 2 1 )9 0 1— 5
扬声器热传递非线性模型
W o fa g Kl p l l n i e g p
・
译 文
( l plG b K i e m H,M neson l e3 ,D edn 0 3 9 emay p e dlsh a e 0 rse 10 。G r n ) l
功 率转 换 成热 的量 。 图 5中的等 效 电路 考虑 到 了 电
如何用COMSOL软件对扬声器驱动器执行非线性失真分析
如何用COMSOL软件对扬声器驱动器执行非线性失真分析扬声器驱动器的全面分析不仅限于频域研究。
一些我们需要或不需要(但仍令人着迷)的效应只能通过非线性时域研究来捕获。
在本文中,我们将讨论系统非线性如何影响声音的生成,以及如何使用COMSOL Multiphysics® 软件对扬声器驱动器执行非线性失真分析。
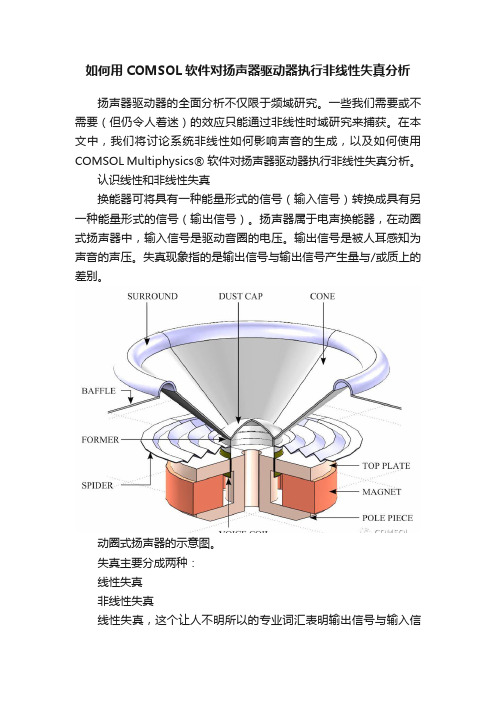
认识线性和非线性失真换能器可将具有一种能量形式的信号(输入信号)转换成具有另一种能量形式的信号(输出信号)。
扬声器属于电声换能器,在动圈式扬声器中,输入信号是驱动音圈的电压。
输出信号是被人耳感知为声音的声压。
失真现象指的是输出信号与输出信号产生量与/或质上的差别。
动圈式扬声器的示意图。
失真主要分成两种:线性失真非线性失真线性失真,这个让人不明所以的专业词汇表明输出信号与输入信号具有相同的频率组成。
在线性失真中,失真对象是输出信号的幅度和/或相位。
非线性失真则暗示输出信号包含输入信号中不存在的频率组成。
这意味着输入端为单一频率的能量到达输出端时产生了多个频率。
线性和非线性换能器的输入和输出信号。
将正弦信号应用于采用非线性传递函数的换能器后,输出信号将由多频组成。
除了与频率对应的信号基本部分之外,还存在着失真部分。
它的频谱通常(但不总是)由频率组成,这些频率均为基频的倍数,即,其中。
这些频率存在于声音之中,被称为泛音。
泛音赋予了乐器与众不同的音色:小提琴弹奏的乐声听起来与吉他迥然不同。
扬声器发出的声音亦是如此。
失真是一个相对量,可以通过总谐波失真(total harmonic distortion,简称THD)的值来描述,该值为信号失真部分与基本部分的大小比:具有较高 THD 值的信号的轮廓明显不同于纯正弦波信号。
不幸的是,输出信号本身的 THD 值可能不足以作为判断扬声器质量的依据。
THD 值较小的信号可能听起来比THD 较大的信号差,原因是人耳能够以不同的方式感知各种泛音。
失真可以被表征为一组单独的偶数阶分量和奇数阶分量。
扬声器的非线性特性指南

扬声器的非线性特性指南产生的原因、相关的参数及表现的征兆原作:Wolfgang Klippel翻译:王刚平(Danny Wang)ABSTRACTThe relationship between nonlinear distortion measurements and nonlinearities is addressed-the physical causes for signal distortion in loudspeakers, headphones, microspeakers and other transducers. Using simulation techniques characteristic symptoms are identified for each nonlinearity and presented systematically in a guide for loudspeaker diagnostics. This information is important for understanding the implications of nonlinear parameters and for performing measurements that describe the loudspeaker more comprehensively. Practical applications of the new technique are demonstrated on three different loudspeakers.摘要该篇论文指出了在扬声器、耳机、微型喇叭及其它换能器中,非线性失真测量结果与非线性特性之间的关系,即信号失真的实质因素。
使用模拟仿真技术,在对扬声器的诊断指导中,每一个非线性特性的特征征兆都可以加以辨识并将系统地呈现出来。
对于理解非线性参数的深层含义和完成对扬声器全面分析的测量来说,这些信息都是很重要的。
扬声器非线性失真的分析与改进
・
论文 ・
( A 南京 电声技 术研 发 中心 , 江 苏 南 京 20 0 ) A C 10 9
【 摘 要】扬声器单元非线性失真是 影响扬声器单元重放 品质的最重要 的因素之 一。介 绍 了扬声器单元非线性失
真 产 生 的原 因 , 针 对 扬 声 器 单 元 的磁 路 及 其 零 部 件 设 计 提 出 了 改进 方 法 。 并
【 关键词 】扬声器 ;非 线性 失真 ;有 限元分析 【 中图分 类号 】T 4 N6 【 文献标识码】A
An lss a mp o e n f No l a so t n o u s e k r a y i nd I r v me t o n i r Dit ri f Lo d p a e s ne o Y AN u d n X -og
3 士 . 5
3+ . o
2.
主 2} . 0
1 圭 . O
1 \ .\ 一 }
- 5 - 4
/ /
_ 2 一l O l X/ m a r 2 3 4 5
O5 .七
n n ,
— 3
图 4 关 于 平 衡 位 置 为 对称 并且 平 坦 分 布 的劲 度 分 布 曲线
21 磁 路 设 计 中的 问 题 及 改 进【 .
扬声器单元低频时磁场 因素对非线性失真影 响较 大, 到达 中高频 后 , 由于单 元振 幅变 小 , 磁场 因素对非 线性失真 的影响也逐渐减小 。在磁路设计 中以往 的电
声 工 程 师 经 常 把 磁 隙 中磁 场 强 度 随 位 移 的 分 布 看
( A cut &D C ne,N ni 10 9 h a A C A o sc R e t i r aj g 2 00 ,C i ) n n
扬声器热传递非线性模型

s
第 二 个功 率测 试 中 , 音 信号 的频 率 . 应 尽可 能设 单 厂 B
定 得 较高 些 , 以测 量 涡流 的最 大影 响 ; 在第 三个 功率 测试中, 单音信 号 的频 率 . 被设 定在谐 振频率 附近 , 厂 c
衡 状态 。
点 测 量 , 2 显示 的是进 行第 一 个 功率 测 试 时 的测 图 7
量 曲线 。音圈 的时间 常数 较短 将会 引起在 阶段 的初始 就会 出现温度 快速 下降 。磁铁/ 盆架组 件 的时
间常 数 r 大 , 引起 在 稍后 时 间里 出现 一 个额 外 较 将
⑨凹
扬 声 器 与 传 声 器 @囿 @ 囿响圈 购 6 , 啼⑨响 @0 ⑥
of f阶段 时 , 找 当温 度 △ 查
fa v tu
—
等 于 下 式 时 的 时 间
:
Ar o
— —
 ̄
f A ) (, AT ( i )
-
o .
() 3 5
—
AT ,
一
的最大值△ ,)m n tf 5m n 。激励 源 的幅值大 小是根 t 2 i, f i ) 。= 据特 定单 元来 调整 的 , 以获得 足够 的发 热 , 时也要 同 避 免 热或 机械 损 坏 。功率 测试 的持 续 时 间应 当足够 长( ) >4r 以便使 得 导磁 极板 、 体 及盆 架 处 于热平 磁
( l p lG b K i e m H,Me d l o n l e 3 ,D e d n 0 3 9 p n e sh al 0 s e rs e 1 0 ,G r n ) e ma y
扬声器单元非线性Bl值和驱动力的研究

【 A b s t r a c t 】T h e r e l a t i o n s h i p b e t w e e n t h e i m p e d a n c e o f t h e l o u d s p e a k e r d i r v e r a n d t h e i n p u t v o l t a g e i s a n a l y z e d . he T c a l c u —
●一 技一
aKi o g a#tat tri n g
@凹 s @囿 @旷囿响 呦6 @ 0 , ⑥ 响⑥响
塑! ! ! 堡 焦! ! ! 壁
扬 声 器 单 元 非 线 性 Z 值 和 驱 动 力 的研 究 ・ 论 文 ・
卢 国潮 . - , 沈 勇。 , 刘 殷
e a r i t y o f B 1 .
【 Ke y wo r s 】l d o u d s p e a k e r d i r v e r ; B l ; i mp e d a n c e c u r v e
1 引言
非线性 值 已经成为扬声器 单元测量 与研发 的
M
对 应 的 电容 , C =
; L e s 为扬声器 单 元悬 置 系统 的等 效力 顺 c 对应
的电感 , LLeabharlann 。 =C B Z 。 2 扬声器单元 T— S参数 的计算
扬声 器单元 的电阻抗 曲线 如图 1 所示 。
电阻抗 Z 为
+
可将式 ( 1 ) 转换 为
究重 点 均 着 眼 于 某 一 频 率 点 的 值 与 位 移 的 关 系 。本 文着眼于扬 声器单元非 线性 值和驱 动力 频 响曲线 , 通过研究 其与扬声 器单元 阻抗 曲线 与输 入
扬声器热传递非线性模型

【 摘
要】传统的扬声器热流建模是用一个等效电路来表示的, 它是 由两个不同时间常数的R C电路 串联, 并假定
集总元件 的参数 与信 号幅值无关。对于 强迫 空气对流冷却方 式, 这一简单 的模 型却不适用 , 当音 圈速度( 而 或磁 间
隙中的空气速度) 很高时, 强迫对流冷却却是行之有效的的散热机理。考虑到电一 力与热学机理之间的非线性相互
wi d f r n t c n t n s T e a a tr o h l mp d l me t a e s u d o e n e e d n o h t h ie e t i me o sa t . h p r me e s f t e u e e e ns r a s me t b i d p n e t f t e
( l plG b K i e m H,Med l o n l 0 rse 10 ,G r a y p n e sh a e 3 ,D edn 0 3 9 e n ) s l e m
WAN ag ig,Z ua Tas td b ) G G npn HU M ln( rnl e y a
a l u e f te in 1 T e i l mo e fi i d srbn te fre ar c n e t n o l g mpi d o h sg a. h smpe t d l al n ec ig h oc d i o v ci c oi whc b c me s i o n ih e o s
(.C mp pl( ru )C roa o ,J xn hj n 1 13 hn ; 1 o u a G op op rt n i ig Z ea g 34 ,C ia i a i 1
2 L v e t o oa o ,J xn h j n 1 1 2 hn ) . a o e L d C r rt n i ig Z ei g 3 4 1 ,C ia p i a a
扬声器热传递非线性模型-Klippel

Wolfgang Klippel Klippel GmbH,Dresden,01277, Germany 译者:王刚平 [浙江恒科实业有限公司
Compupal (Group) Corporation]
朱木兰
[浙江意莱声电子有限公司 Lavoce Ltdeling describes the heat flow in loudspeakers by an equivalent circuit using integrators with different time constants. The parameters of the lumped elements are assumed to be independent of the amplitude of the signal. The simple model fails in describing the forced air convection cooling which becomes an effective cooling mechanism if the velocity of the coil and/or the air velocity in the gap becomes high. This paper presents a large-signal model considering the nonlinear interactions between the electro-mechanical and thermal mechanisms. The model and parameters are verified by practical measurements on the drivers. The dominant paths for the heat flow are identified and means for increasing the power handling capacity are discussed. 传统的扬声器热流建模是用一个等效电路来表示的,它是由两个不同时间常数的RC电路串 联,并假定集总元件的参数与信号幅值无关。对于强迫空气对流冷却方式,这一简单的模型 却不适用,而当音圈速度(或磁间隙中的空气速度)很高时,强迫对流冷却却是行之有效的 的散热机理。本文考虑到电-力与热学机理之间的非线性相互作用,提出了一个大信号热学 模型。 该模型及其参数可以在实例单元上进行实际测量加以验证, 还对热流的主要路径加以 确定,并讨论了提高扬声器单元功率承受能力的方法。
系统中扬声器位移非线性的控制

系统中扬声器位移非线性的控制摘要:本文第一部分将分析影响扬声器位移非线性大小的主要因素,把搜索范围扩大到包括扬声器、箱体、电路的整个音响系统中。
所总结出来的因素将成为稍后LEAP仿真实例中的主要调整项。
第二部分指出扬声器位移非线性在极端状态下对音响产品音质及扬声器可靠性的危害。
第三部分利用LEAP软件,举一个简单的仿真例子,演示音响系统中各环节的参数对扬声器位移、系统声频响应曲线的影响,为综合音响系统声频响应、效率、扬声器位移非线性等性能提供量化数据。
关键词:扬声器;位移;非线性;一、影响扬声器位移非线性大小的主要因素扬声器位移非线性出现的主要原因是驱动力的非线性及悬置系统的非线性,由于篇幅原因扬声器自身性能问题,这里不做讨论。
俗话讲,单巴掌拍不响,如果扬声器不工作,音圈静止,就没有任何非线性。
系统中扬声器位移非线性显著增大的原因是由于扬声器工作位移大于其线性工作范围。
在设计中要注意,要使扬声器位移在未受限制的情况下,小于等于线性工作范围,才能将扬声器位移的非线性控制在一定范围内。
所以,本文主要讨论影响系统中扬声器位移大小的主要因素:系统的工作功率大小;电路中高通滤波器的低频截止频率点,衰减的阶数及Q值;音箱箱体的声学结构,形状尺寸大小;扬声器悬置系统的顺性及扬声器的BL值;二、扬声器位移非线性对音响产品音质及扬声器可靠性的危害2.1、扬声器位移非线性对音响产品音质的危害:音响产品音质、音色的好坏,主要取决于其音乐信号波形重放的保真度。
功放输出的音乐信号波形,在示波器上可以看出,是波长较短的中高频信号骑在波长较长的低频信号上这样波形的信号馈给扬声器,反应到扬声器振幅:由于扬声器低频时振幅大,中高频时振幅小,这样就转变成中高音的小幅度运动“骑”在低音的大幅度运动上(见图1-1b)。
如果扬声器振幅处于非线性状态下,低音连同中高音一起被削顶(见图1-1c):此时,即使音响产品功率余量足够,声音也会吵、闹、躁、不清晰,严重的会出现破音现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 引言
扬声器和其它发声的或是振动的激励器一样,它们在较小的振幅和在较大振幅情况下的表现是不同的。依赖于振幅的大 小就意味着在系统中存在着固有的非线性特性。第二个非线性影响就是,产生了激励信号中并不存在的额外频谱分量。这些 分量通常为输入信号基波的整数倍,因此定义它为谐波失真或互调失真。这些失真测量的结果较大程度地依赖于激励信号的 属性,比如:所选择的信号的频率、幅度、以及激励音的相位等等。这些结果并不能完全地描述大信号下的表现,但可以作为 征兆来理解。
_____
图2:悬挂系统的力学劲度特征曲线。(….)代表有渐变劲度的定心支片;(- - -)代表受限制的折环; (
)代表总的悬挂系统
的劲度
大多数的悬挂系统都是由含浸的织物、橡胶或是注塑成形的特殊形状的塑胶材质做成。悬挂系统的运动就像一个普通弹 簧,它的特点可以由图1的力-偏移曲线表征。在小位移段,它有着几乎线性的关系,但是在较大位移情况下,悬挂系统的回 复力就比一个线性弹簧所预期的要大。对于缓慢的交变力的响应,由于材质存在内部损失,位移的变化通常还会有一个滞后 现象。
1. 术语表
AMD Bl(x) C E EHDn ETHD fs fp FT Fm (x,i) HDn H(jω) ICHD IHD IMDn IMDtotal i(t) Kms(x)
幅度调制失真(%) 有效的瞬时力电耦合系数(磁路系统的力因数),定义为永久磁场产生的磁感应强度 B 对音圈长度 l 的积分 基波的幅值压缩(dB) 时间信号的包络线 换能器输入端的等效的 n 次谐波失真(%) 换能器输入端的等效的总的谐波失真(%) 谐振频率 开口箱风管的亥姆霍兹谐振频率 付里叶变换 电磁驱动力(磁阻力),缘于电感随位移 x 的变化 n 次谐波失真(%) 线性传输函数 瞬时谐波失真峰值因子(dB) 瞬时谐波失真分量大小(%) n 次互调失真(%) 总的互调失真(%) 输入电流 扬声器单元的悬挂系统的力学劲度,是顺性 Cms(x)的倒数
Bl(x) 曲线的形状与气隙和音圈的的几何结构有关,与磁体所产生的磁场有关。图4用例子说明一个音圈的卷幅(hcoil) 大于气隙深度(hgap)的长音圈的磁路结构的特点。与之对应的Bl(x) 曲线在图5中用实线表示。小位移情况下,力因数几乎 为常数,因为磁间隙中的音圈匝数是相等的。图5中的点划线是指音圈卷幅的高度与气隙深度相等的情况下Bl 的变化曲线, 它表明此时,即使在小振幅时,力因数也会下降,它没有恒值的平坦区。
2.1.3. 音圈电感
电气性能的输入阻抗值与线圈的位置有关。比如,图6显示的是线圈在三种位置情况下(x=0;音圈被箝定在x=+7mm处; 音圈被箝定在x=-7mm处),电气输入阻抗与频率的关系。在谐振频率70Hz以上(被箝定的音圈是不会有此谐振的),电阻抗在 负位移(音圈位置往内)时明显比在正位移(音圈位置往外)时要高。
回复力是位移和非线性劲度Kms(x)的乘积,即F=Kms(x)x,劲度Kms(x)就是力-偏移曲线上的任意一点至原点间的正切值。由 于劲度并不是一个常数,而它本身是位移x 的函数,回复力则包含了音圈位移间的乘积项。这些结果项产生了与时间信号有 关的非线性失真,在悬挂系统中,这种现象很典型。由于悬挂系统本身材质所具有的粘滞效应,劲度系数也会随着频率而变 化。然而,这种影响是可以通过线性系统来模拟的[1]。
扬声器的非线性特性指南
产生的原因王刚平
ABSTRACT
The relationship between nonlinear distortion measurements and nonlinearities is addressed-the physical causes for signal distortion in loudspeakers, headphones, microspeakers and other transducers. Using simulation techniques characteristic symptoms are identified for each nonlinearity and presented systematically in a guide for loudspeaker diagnostics. This information is important for understanding the implications of nonlinear parameters and for performing measurements that describe the loudspeaker more comprehensively. Practical applications of the new technique are demonstrated on three different loudspeakers. 摘要 该篇论文指出了在扬声器、耳机、微型喇叭及其它换能器中,非线性失真测量结果与非线性特性之间的关系,即信号失 真的实质因素。使用模拟仿真技术,在对扬声器的诊断指导中,每一个非线性特性的特征征兆都可以加以辨识并将系统地呈 现出来。对于理解非线性参数的深层含义和完成对扬声器全面分析的测量来说,这些信息都是很重要的。在本文中我们将用 三款不同的扬声器单元实例来示范这项新技术的的实际应用。
u’(t) v(t) x(t) Zm (s)
总的等效输入电压 u’ = u + uD 音圈速度 音圈位移 代表力学和声学负载的阻抗
2. 扬声器建模
在较大振幅情况下,所有的扬声器都或多或少地会表现出非线性特性,并会有在输入信号中并不存在的信号分量产生。 扬声器系统的非线性机理是各种各样的,我们的研究大体上是集中在以下“主要”的非线性特性上:
图4:长音圈的磁路结构
图5:长音圈的Bl(x) 曲线以及音圈卷幅与磁气隙等长的Bl(x)曲线. 力因数Bl(x)有两个非线性影响,在表1中已有列出: • Bl(x)作为电力间的耦合系数,它的任何变化都会影响到驱动力 F [F = Bl(x)i ]。 这个机理也就是谐振系统的参量激励。 大的音圈位移 x 和电流 i 势必将产生明显的失真。 • Bl(x) 的第二个影响就是,音圈的位移与在永磁场中音圈运动所产生的反向电动势有关。这时力因数 Bl(x)与速度的乘积将 改变电气阻尼的特性。
图2显示的是一个由有渐变特性的定心支片和可以限制其正向位移的折环所组成的悬挂系统的Kms(x)的特征曲线.
图3:包含磁路和悬挂系统的扬声器的等效电路
2.1.2. 力因数
力因数Bl(x)描述的是电动式换能器集中参数模式下的力与电间的耦合,如图3示。这个参数是磁束密度B 对音圈长度l 的 积分值。力因数Bl(x)不是一个常数,而是与音圈的位移x有关。很显然,如果音圈离开磁气隙,力因数就会降低。此非线性 函数是静态函数(与频率无关),我们可以用非线性图表或者幂级数展开的方式来表示。
Le(x,i) L2(x,i) R2(x,i)
与位移 x 和电流 i 有关的集总参数,用于音圈的电感模型的建立
LAMD LHD,n LTHD LEHD,n LETHD LIMD,n LIMD,total Mms p(t) P(jω) Pn Pt Pr(f1,Ui) n Rms Re(TV) THD u(t) uD(t)
• 限制声输出 • 产生了可闻的失真 • 预示过载情况的出现 • 引起振动不稳定 • 涉及到成本、重量及体积 • 降低了换能器的效率 • 影响扬声器系统的配置
2.1. 固有的非线性特性
大多数主要的非线性特性的产生都可以从换能器的原理得到,与磁路系统、悬挂系统、振动盆和箱体的几何结构和材质 属性有着直接关系。物理上的限制使得扬声器的设计不得不折衷处理,但是为了得到所需的大信号的表现,一些非线性特性 却是有意而为之的(如:渐变的悬挂系统的劲度)。因此,我们按设计制程生产的扬声器,即使在生产线上通过测试并被判定 为合格的产品,也会发现存在着固有的非线性特性。
这与在小信号范围内的测量结果主要的不同点在于:在小信号测量中,线性传输函数或是脉冲响应特性可以完全地描述输 入与输出间的关系。
依赖于征兆的这种测量方式可行吗?它给人们提出了如下的问题: • 测量技术能触发和侦测到扬声器非线性特性重要的征兆吗? • 那些征兆确有意义吗? • 它们与实质因素有着怎样的关系? • 如何能在短时高效的情况下,获得一套全面的测量数据?
在低音、高音、微型扬声器、号角压缩驱动器以及扬声器系统中,最主要的固有的非线性特性在表一中作了总结,接下 来我们将加以讨论。
表1:电动式扬声器中重要的固有非线性特性总览
非线性特性
影响
悬挂系统的劲度 Kms(x) 力因数 Bl(x)
非线性回复力 Fs = Kms(x)x 驱动力 F = Bl(x)i 引起参量激励
图6:音圈在不同位置点时的电气特性阻抗曲线
我们观察到许多扬声器都有这一特性,而且可以用随位移变化的电感来解释它。音圈中的电流会产生一个变化的磁场, 扩散于磁铁、导磁体及空气中(如图 7)。磁通量的大小与音圈的位置以及电流的强度有关。如果音圈跳出气隙,它的电感量 要比音圈在气隙之下要低得多,这是因为音圈在气隙之下时,它的周围都是可以减小磁阻的铁磁物质.
与时间信号有关的量 位移 x 位移 x、电流 i 位移 x、速度 v 位移 x、电流 i 电流 i
