2019-2020学年黑龙江省佳木斯市第一中学高一下学期第一学段考试文科数学试题
2019-2020年高一下学期学段检测数学试题 含答案

2019-2020年高一下学期学段检测数学试题含答案高一数学试题第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.有20位同学,编号从1至20,现从中抽取4人作问卷调查,用系统抽样方法确定的编号有可能是A. B. C. D.2.圆与圆的位置关系是A. 相交B. 内切C. 相离D.外切3.样本中共有五个个体,其值分别为,若该样本的平均值为1,则样本的标准差为A. B. C. D.4.某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示,规定不低于90分为优秀等级,则该校学生优秀等级的人数是A. B. C. D.5.若一口袋中装有4个白球和3个红球,现从中任取两球,则取出的两球中至少有一个白球的概率为A. B. C. D.6.过点作圆的两条切线,切点分别为,为原点,则的外接圆方程是A. B.C. D.7.分别写上数字1,2,3,…,9的9张卡片中,任取2张,观察上面的数字,则两数之积为完全平方数的概率是A. B. C. D.8.阅读下边的程序框图,若输出S的值为-7,则判断框内可填写A. B. C. D.9.已知蚂蚁在三边长分别为3,4,5的三角形内爬行,某时刻此蚂蚁距离三角形三个顶点距离均超过1的概率为A. B. C. D.10.已知直线过点,P是上的一动点,是圆的两条切线,A,B为切点,若四边形PACB的最小面积为2,则直线的斜率为A. B. C. D.第Ⅱ卷(非选择题共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.一幅混合后的扑克牌(无大小王)共52张,从中随机抽取1张,事件A为“抽得红桃K”,事件B为“抽得黑桃”,则概率(结果用分数表示).12.已知圆与圆相交,则交点连成的直线方程为 .13.一束光线从点出发,经轴反射到圆上的最短距离是 .14.两艘轮船都要停靠在同一泊位,它们可能在一昼夜的任意时刻到达.设两船停靠泊位的时间分布为1h和2h,则有一艘船停靠泊位时必须等待一段时间的概率是 .15.对任意非零实数,若的运算规则如右图的程序框图所示,则的值是 .三、解答题:解答应写出文字说明、证明过程或演算步骤.16. (本小题满分12分)求经过点,圆心在直线上的圆的方程.17.(本小题满分12分)某市风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高编成如右图所示的茎叶图(单位:).若身高在以上(包括)定义为“高精灵”,身高在以下(不包括)定义为“帅精灵”.已知A大学志愿者的身高的平均数为,B大学志愿者身高的中位数为.(1)求的值;(2)如果用分层抽样的方法从“高精灵”和“帅精灵”中抽取5人,再从这5人中选2人.求至少有一人为“高精灵”的概率.18.(本小题满分12分)月份12345甲的纯收入 2.9 3.3 3.6 4.4 4.8乙的纯收入 2.8 3.4 3.8 4.5 5.5(1)由表中数据直观分析甲、乙二人中谁的纯收入比较稳定?(2)求关于的线性回归方程,并推测甲在6月份的纯收入;(3)现从这5个月的纯收入中随机抽取两个月,求恰好有1月的纯收入在区间中的概率.19.(本小题满分12分)已知圆与直线交于M,N两点,O为坐标原点,问是否存在实数,使,若存在,求出的值,若不存在,请说明理由.20.(本小题满分12分)在某高校自主招生考试中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级,某考场的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.(1)求该考场考生中,“阅读与表达”科目中成绩为A的人数;(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1,分,求该考场考生“数学与逻辑”科目的平均分;(3)已知参加考场测试的考生中,恰有两人的两科成绩均为A,在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.21.(本小题满分12分)已知圆O的方程为,直线过点且与圆O相切.(1)求直线的方程;(2)设圆O与轴交于P,Q两点,M是圆O上异于P,Q的任意一点,过点A且与轴垂直的直线为,直线交直线于点,直线交直线于点,求证:以为直径的圆总过定点,并求出定点的坐标.xx 学年度第二学期学段检测高一数学答案一、选择题: ABDCC AADBD二、填空题:11.726 12. 13. 4 14. 139115215. 三、解答题:16解:设所求圆的方程为 ………2分则 ………6分解得 ………11分所求圆的方程为 ………12分17.解:(1)由题意得: 1768191187182176170170168159=++++++++x ………2分 ………4分解得 ………5分(2)由题意得“高精灵”有8人,“帅精灵”有12人,如果用分层抽样的方法从“高精灵”和“帅精灵”中抽取5人,则抽取的“高精灵”和“帅精灵”人数分别为和 ………6分记抽取“高精灵”为,抽取“帅精灵”为.从已抽取的5人中任选两人的所有可能(,) ,( ,) ,( ,),(,),(,),(,),(,),(,),(,),(,),共10种, ………8分设选取的两人中至少有一人为“高精灵”为事件A,则事件A 包括(,) ,( ,) ,( ,),(,),(,),(,),(,),共7种 ………10分所以 为所求. ………12分18. 解(1) 甲的纯收入稳定 ……2分(2), ∴=0.49……5分 , =2.33 ……6分=0.49+2.33 ……………………………………………………………………………7分令,得=5.27,即推测甲在6月份的纯收入为5.27千元 ……8分.(3) 现从乙这5个月的纯收入中,随机抽取两个月的基本事件有:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5) 共10种 ……10分. 记:恰有一个月的纯收入在区间(3,3.5)为事件A,其中,有:(1,2),(2,3),(2,4),(2,5)共4种.∴恰有一个月的纯收入在区间(3,3.5)的概率为 ……12分.19. 设点,当时,有,(1) ……………………2分又直线与圆相交于M 、N ,联立 ,消可得:,则有:,,· (2) ……4分又M 、N 在直线上, 故1212121264(9)(32)(32)96()4955m y y x x x x x x -=--=-++=-+ (3) ……6分 由 (1)(2)(3)得: ………………………………………………………………………10分且检验成立 ………………………………………………11分故存在,使OM ⊥ON ………………………………………………………………12分20. 解:(1)因为“数学与逻辑”科目中成绩等级为B 的考生有10人,所以该考场有人 ……………………2分所以该考场考生中“阅读与表达”科目中成绩等级为A 的人数为……………………4分(2)该考场考生“数学与逻辑”科目的平均分为……………………8分(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,所以还有2人只有一个科目得分为A,设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁},有6个基本事件设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则. ……………………13分21.解:(1)∵直线过点,且与圆:相切,设直线的方程为,即,…………………………2分则圆心到直线的距离为,解得,∴直线的方程为,即.………………………4分(2)对于圆方程,令,得,即.又直线过点且与轴垂直,∴直线方程为,设,则直线方程为解方程组,得同理可得, ………………10分∴以为直径的圆的方程为,又,∴整理得,………………………12分若圆经过定点,只需令,从而有,解得,∴圆总经过定点坐标为.……………………………………………14分.。
黑龙江省佳木斯市2019-2020年度高一下学期数学期中考试试卷(I)卷(模拟)

黑龙江省佳木斯市2019-2020年度高一下学期数学期中考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2019·定远模拟) 若集合,,则()A .B .C .D .2. (2分) (2016高二上·会宁期中) 若a,b,c∈R,且a>b,则下列不等式中恒成立的是()A .B . ac>bcC . a2>b2D . a+c>b+c3. (2分)(2019高一下·雅安月考) 已知中,内角所对的边分别为,,,则()A .B .C .D .4. (2分)(2018·恩施模拟) 某几何体的三视图如图所示,则该几何体的体积为()A . 4B . 3C . 2D . 15. (2分)设且,则x+y的最小值为()A . 12B . 15C . 16D . -166. (2分) (2019高一下·广州期中) 如图,圆锥的主视图是等边三角形,圆锥的底面半径为 ,假若点有一只蚂蚁只能沿圆锥的表面爬行,它要想吃到母线的中点处的食物,那么它爬行的最短路程是()A . 6B .C . 4D .7. (2分)等差数列-3,-7,-11,...,的一个通项公式为()A . 4n-7B . -4n-7C . 4n+1D . -4n+18. (2分)已知函数(ω>0)的图象的两相邻对称轴间的距离为,则f(x)的单调递增区间是()A .B .C .D .9. (2分) (2017高三上·蕉岭开学考) 在等比数列{an}中,首项a1=1,且4a3 , 2a4 , a5成等差数列,若数列{an}的前n项之积为Tn ,则T10的值为()A . 29﹣1B . 236C . 210﹣1D . 24510. (2分)(2017·郴州模拟) 在△ABC中,A1 , B1分别是边BA,CB的中点,A2 , B2分别是线段A1A,B1B的中点,…,An , Bn分别是线段的中点,设数列{an},{bn}满足:向量,有下列四个命题,其中假命题是()A . 数列{an}是单调递增数列,数列{bn}是单调递减数列B . 数列{an+bn}是等比数列C . 数列有最小值,无最大值D . 若△ABC中,C=90°,CA=CB,则最小时,11. (2分) (2016高三上·武邑期中) 已知正项数列{an}中,a1=1,a2=2,2an2=an﹣12+an+12(n≥2),bn=,记数列{bn}的前n项和为Sn ,则S33的值是()A .B .C .D . 312. (2分)(2018·淮南模拟) 已知,集合,集合的所有非空子集的最小元素之和为,则使得的最小正整数的值为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)(2017·吴江模拟) 已知平面向量,的夹角为,且| |=1,| |= ,则与的夹角大小是________.14. (1分)(2017·深圳模拟) 若数列{an},{bn}满足a1=b1=1,bn+1=﹣an , an+1=3an+2bn ,n∈N* .则a2017﹣a2016=________.15. (1分) (2016高一下·苏州期中) 在等差数列{an}中,当a2+a9=2时,它的前10项和S10=________.16. (1分) (2017高一下·正定期末) 已知数列的首项为,且,若,则数列的前项和 ________.三、解答题 (共6题;共57分)17. (10分) (2018高二上·淮北月考) 已知在中,角的对边分别是,且.(1)求角的大小;(2)若,求面积的最大值.18. (10分)(2018·茂名模拟) 已知等差数列的公差不为零,,且 .(1)求与的关系式;(2)当时,设 ,求数列的前项和 .19. (2分) (2017高一下·黄冈期末) 某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A 产品的利润y1与投资金额x的函数关系为y1=18﹣,B产品的利润y2与投资金额x的函数关系为y2= (注:利润与投资金额单位:万元).(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?20. (10分) (2017高一上·正定期末) 已知f(x)=4sinωxsin(ωx+ )﹣1(ω>0),f(x)的最小正周期为π.(Ⅰ)当x∈[0, ]时,求f(x)的最大值;(Ⅱ)请用“五点作图法”画出f(x)在[0,π]上的图象.21. (10分) (2016高二上·郑州期中) 在等比数列{an}中,公比q≠1,等差数列{bn}满足a1=b1=3,a2=b4 ,a3=b13 .(1)求数列{an}的{bn}通项公式;(2)记cn=an•bn,求数列{cn}的前n项和Sn.22. (15分) (2016高一上·台州期末) 已知a>0,b∈R,函数f(x)=4ax2﹣2bx﹣a+b,x∈[0,1].(1)当a=b=2时,求函数f(x)的最大值;(2)证明:函数f(x)的最大值|2a﹣b|+a;(3)证明:f(x)+|2a﹣b|+a≥0.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共57分)17-1、17-2、18-1、18-2、19-1、19-2、20-1、21-1、21-2、22-1、22-2、22-3、第11 页共11 页。
2019-2020年高一下学期第一次考试数学含答案

2019-2020年高一下学期第一次考试数学含答案注意事项:1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再改涂在其它答案标号.第Ⅰ卷(共50分)一:选择题(每小题5分,共5分)1: 圆x 2+y 2+4x-2y+4=0的点到直线y=x-1上的最近距离为( ) (A) 2 2 (B) 2 –1 (C) 2 2 –1 (D) 12: 过点(1,3)P 且在x 轴上的截距和在y 轴上的截距相等的直线方程为( )A.40x y +-=B.30x y -=C.40x y +-=或30x y +=D.40x y +-=或30x y -=3:若过点P(-2,1)作圆(x-3)2+(y+1)2=r 2的切线有且仅有一条,则圆的半径r 为( ) (A) 29 (B) 29 (C)小于 29 (D) 大于294:直线 y=33 x 绕原点按逆时针方向旋转π6后所得直线与圆(x-2)2+y 2=3的位置关系是( )(A )直线过圆心 (B ) 直线与圆相交,但不过圆心 (C )直线与圆相切 (D ) 直线与圆没有公共点 5:若A(1,2),B(-2,3),C(4,y)在同一条直线上,则y 的值是( )(A) 12 (B) 32(C) 1 (D) -16:已知直线3x+2y-3=0和6x+my+1=0互相平行,则它们之间的距离是( ) (A) 4 (B) 2 1313 (C) 5 1326 (D) 7 13267:设点A(2,-3),B(-3,-2),直线l 过点P(1,1)且与线段AB 相交,则l 的斜率k 的取值范围是( )(A) k ≥34 或k ≤-4 (B) k ≥34 或k ≤ - 14 (C) -4≤k ≤34 (D) 34 ≤k ≤48:圆x 2+y 2+2x+4y-3=0上到直线x+y+1=0的距离为 2 的点共有( ) (A )1个 (B ) 2个 (C ) 3个 (D )4个9:把直线x-2y+m=0向左平移1个单位后,再向下平移2个单位,与圆C:x 2+y 2+2x-4y=0相切,则实数m 的值是( ) (A) –13或3 (B )13或-3 (C )13或3 (D )-13或-310:若P (2,-1)为圆(x-1)2+y 2=25的弦AB 的中点,则直线AB 方程是( ) (A )x-y-3=0 (B) 2x+y-3=0 (C) x+y-1=0 (D) 2x+y-5=0第Ⅱ卷(共100分)二:填空题(每小题5分,共25分)11、以点(1,2)为圆心,与直线4x+3y-35=0相切的圆的方程是__________________12、设直线L 过点A (2,4),它被平行线x-y+1=0与x-y-1=0所截是线段的中点在直线x+2y-3=0上,则L 的方程是_____________________13、三条直线x+y+1=0,2x-y+8=0和ax+3y-5=0只有两个不同的交点,则a=______________14、过点M (0,4)、被圆(x-1)2+y 2=4截得的线段为2 3 的直线方程为___________________15:设有一组圆224*:(1)(3)2()k C x k y k k k -++-=∈N . A.存在一条定直线与所有的圆均相切 B.存在一条定直线与所有的圆均相交 C.存在一条定直线与所有的圆均不.相交 D.所有的圆均不.经过原点 以上说法正确的是 .三、解答题(共6小题,计75分。
黑龙江省佳木斯市2019-2020年度高一下学期数学期中考试试卷(I)卷

黑龙江省佳木斯市2019-2020年度高一下学期数学期中考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)某初级中学采用系统抽样方法,从该校全体800名学生中抽50名做健康检查.现将800名学生从1到800进行编号,求得间隔数,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33 ~ 48这16个数中应取的数是A . 40B . 39C . 38D . 372. (2分) (2019高二上·安徽月考) 某公司在甲、乙、丙、丁四个地区分别有150,120,180,150个销售点.公司为了调查产品销售情况,需从这600个销售点中抽取一个容量为100的样本.按照分层抽样的方法抽取样本,则丙地区抽取的销售点比乙地区抽取的销售点多()A . 5个B . 8个C . 10个D . 12个3. (2分) (2019高二上·会宁期中) 设是等差数列的前项和,若,则()A .B .C . 2D .4. (2分)重庆市2013年各月的平均气温(℃)数据的茎叶图如下:则这组数据的中位数是()A . 19B . 20C . 21.5D . 235. (2分)(2018·成都模拟) 甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为、,标准差分别为,则()A . ,B . ,C . ,D . ,6. (2分)某考察团对中国10个城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)调查,y与x具有相关关系,回归方程y=0.66x+1.562,若A城市居民人均消费水平为7.765(千元),估计该城市人均消费额占人均工资收入的百分比约为()A . 83%B . 72%C . 67%D . 66%7. (2分)执行如右图的程序框图,如果输入a=5,那么输出的n值为A . 1B . 2C . 3D . 48. (2分)(2020·乌鲁木齐模拟) 若正整数除以正整数的余数为,则记为,例如.如图程序框图的算法源于我国古化著名的《中国剩余定理》,执行该程序框图,则输出的等于()A . 2B . 4C . 8D . 169. (2分)(2018·中原模拟) 执行如图所示的程序框图,若输出的的值为5,则判断框内填入的条件可以是()A .B .C .D .10. (2分)口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是()A . 0.42B . 0.28C . 0.7D . 0.311. (2分)甲、乙两人下棋,甲获胜的概率为40%,甲不输的概率为90%,则甲、乙两人下成和棋的概率为()A . 60%B . 30%C . 10%D . 50%12. (2分)已知圆C:x2+y2=1,在线段AB:x﹣y+2=0(﹣2≤x≤3)上任取一点M,过点M作圆C切线,求“点M与切点的距离不大于3”的概率P为()A .B .C .D .二、填空题 (共4题;共5分)13. (1分)某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间内,其频率分布直方图如图所示.(Ⅰ)直方图中的________ ;(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为________ .14. (2分) (2016高二上·宝应期中) 五个数1,2,3,4,a的平均数是3,这五个数的方差是________.15. (1分) (2016高二下·福建期末) 投篮测试中,某同学投3次,每次投篮投中的概率相同,且各次投篮是否投中相互独立.已知他至少投中一次的概率为,则该同学每次投篮投中的概率为________.16. (1分)从甲,乙,丙,丁4个人中随机选取两人,甲乙两人中有且只一个被选取的概率为________.三、解答题 (共6题;共70分)17. (15分) (2018高二上·齐齐哈尔期中) 某地统计局就该地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)).(1)求居民月收入在[3000,3500)的频率;(2)根据频率分布直方图算出样本数据的中位数;(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,则月收入在[2500,3000)的这段应抽多少人?18. (10分)(2013·广东理) 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本均值;(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.19. (10分)某居民区的物业管理部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费只需画出程序框图即可.20. (10分)某区工商局、消费者协会在3月15号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.(Ⅰ)若电视台记者要从抽取的群众中选1人进行采访,求被采访人恰好在第2组或第4组的概率;(Ⅱ)已知第1组群众中男性有2人,组织方要从第1组中随机抽取3名群众组成维权志愿者服务队,求至少有两名女性的概率.21. (10分)(2020·西安模拟) 某险种的基本保费为(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险次数01234保费随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:出险次数01234频数605030302010(I)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;(Ⅲ)求续保人本年度的平均保费估计值.22. (15分)产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:x24568y3040605070(1)画出散点图.(2)求回归方程.(3)试预测广告费支出为10百万元时,销售额多大?参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共70分) 17-1、17-2、17-3、18-1、18-2、18-3、19-1、20-1、21-1、22-1、22-2、22-3、。
黑龙江省佳木斯市2019-2020学年中考数学一模考试卷含解析
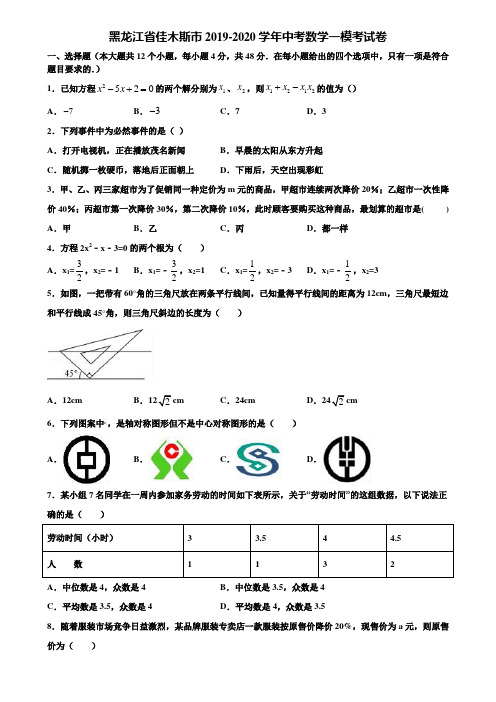
黑龙江省佳木斯市2019-2020学年中考数学一模考试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知方程2520x x -+=的两个解分别为1x 、2x ,则1212x x x x +-的值为() A .7-B .3-C .7D .32.下列事件中为必然事件的是( ) A .打开电视机,正在播放茂名新闻 B .早晨的太阳从东方升起 C .随机掷一枚硬币,落地后正面朝上D .下雨后,天空出现彩虹3.甲、乙、丙三家超市为了促销同一种定价为m 元的商品,甲超市连续两次降价20%;乙超市一次性降价40%;丙超市第一次降价30%,第二次降价10%,此时顾客要购买这种商品,最划算的超市是( ) A .甲B .乙C .丙D .都一样4.方程2x 2﹣x ﹣3=0的两个根为( ) A .x 1=32,x 2=﹣1 B .x 1=﹣32,x 2=1 C .x 1=12,x 2=﹣3 D .x 1=﹣12,x 2=3 5.如图,一把带有60°角的三角尺放在两条平行线间,已知量得平行线间的距离为12cm ,三角尺最短边和平行线成45°角,则三角尺斜边的长度为( )A .12cmB .122cmC .24cmD .242cm6.下列图案中,是轴对称图形但不是中心对称图形的是( )A .B .C .D .7.某小组7名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( ) 劳动时间(小时) 3 3.5 4 4.5 人 数1132A .中位数是4,众数是4B .中位数是3.5,众数是4C .平均数是3.5,众数是4D .平均数是4,众数是3.58.随着服装市场竞争日益激烈,某品牌服装专卖店一款服装按原售价降价20%,现售价为a 元,则原售价为( )A .(a ﹣20%)元B .(a+20%)元C .a 元D . a 元9.下列计算正确的是( ) A .a 3﹣a 2=a B .a 2•a 3=a 6 C .(a ﹣b )2=a 2﹣b 2D .(﹣a 2)3=﹣a 610.如图,△ABC 中,∠C=90°,D 、E 是AB 、BC 上两点,将△ABC 沿DE 折叠,使点B 落在AC 边上点F 处,并且DF ∥BC ,若CF=3,BC=9,则AB 的长是( )A .254B .15C .454D .911.如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,垂足为D ,AB=c ,∠A=α,则CD 长为( )A .c•sin 2αB .c•cos 2αC .c•sinα•tanαD .c•sinα•cosα12.如图,在半径为5的⊙O 中,弦AB=6,点C 是优弧»AB 上一点(不与A ,B 重合),则cosC 的值为( )A .43B .34C .35D .45二、填空题:(本大题共6个小题,每小题4分,共24分.) 13.函数1x y x =-的自变量x 的取值范围是_____. 14.2018年5月18日,益阳新建西流湾大桥竣工通车,如图,从沅江A 地到资阳B 地有两条路线可走,从资阳B 地到益阳火车站可经会龙山大桥或西流湾大桥或龙洲大桥到达,现让你随机选择一条从沅江A 地出发经过资阳B 地到达益阳火车站的行走路线,那么恰好选到经过西流湾大桥的路线的概率是_____.15.如图,菱形ABCD 的边AD ⊥y 轴,垂足为点E ,顶点A 在第二象限,顶点B 在y 轴的正半轴上,反比例函数y =kx(k≠0,x >0)的图象经过顶点C 、D ,若点C 的横坐标为5,BE =3DE ,则k 的值为______.16.如图,为了解全校300名男生的身高情况,随机抽取若干男生进行身高测量,将所得数据(精确到1cm )整理画出频数分布直方图(每组数据含最低值,不含最高值),估计该校男生的身高在170cm ﹣175cm 之间的人数约有_____人.17.已知a ,b ,c ,d 是成比例的线段,其中3cm a =,2cm b =,6cm c =,则d =_______cm . 18.将直线y =x +b 沿y 轴向下平移3个单位长度,点A(-1,2)关于y 轴的对称点落在平移后的直线上,则b 的值为____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)先化简,再求值:(1﹣11x x -+)÷22691x x x ++-,其中x =1. 20.(6分)如图,AB 为⊙O 的直径,直线BM ⊥AB 于点B ,点C 在⊙O 上,分别连接BC ,AC ,且AC 的延长线交BM 于点D ,CF 为⊙O 的切线交BM 于点F . (1)求证:CF =DF ;(2)连接OF ,若AB =10,BC =6,求线段OF 的长.21.(6分)从2017年1月1日起,我国驾驶证考试正式实施新的驾考培训模式,新规定C 2驾驶证的培训学时为40学时,驾校的学费标准分不同时段,普通时段a 元/学时,高峰时段和节假日时段都为b 元/学时. (1)小明和小华都在此驾校参加C 2驾驶证的培训,下表是小明和小华的培训结算表(培训学时均为40),请你根据提供的信息,计算出a ,b 的值. 学员培训时段 培训学时 培训总费用小明普通时段 20 6000元 高峰时段 5节假日时段 15小华普通时段 30 5400元高峰时段 2节假日时段8(2)小陈报名参加了C 2驾驶证的培训,并且计划学够全部基本学时,但为了不耽误工作,普通时段的培训学时不会超过其他两个时段总学时的12,若小陈普通时段培训了x 学时,培训总费用为y 元 ①求y 与x 之间的函数关系式,并确定自变量x 的取值范围; ②小陈如何选择培训时段,才能使得本次培训的总费用最低? 22.(8分)关于x 的一元二次方程mx 2+(3m ﹣2)x ﹣6=1. (1)当m 为何值时,方程有两个不相等的实数根; (2)当m 为何整数时,此方程的两个根都为负整数.23.(8分)已知:如图,AB AD =,AC AE =,BAD CAE ∠=∠.求证:BC DE =.24.(10分)为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:车型目的地A村(元/辆)B村(元/辆)大货车800 900小货车400 600(1)求这15辆车中大小货车各多少辆?(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.25.(10分)如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数kyx 的图象上,过点A的直线y=x+b交x轴于点B.求k和b的值;求△OAB的面积.26.(12分)如图,四边形ABCD的四个顶点分别在反比例函数y=与y=(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为1.(1)当m=1,n=20时.①若点P的纵坐标为2,求直线AB的函数表达式.②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.27.(12分)如图,在△ABC中,∠C=90°.作∠BAC的平分线AD,交BC于D;若AB=10cm,CD=4cm,求△ABD的面积.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.D【解析】【分析】由根与系数的关系得出x1+x2=5,x1•x2=2,将其代入x1+x2−x1•x2中即可得出结论.【详解】解:∵方程x2−5x+2=0的两个解分别为x1,x2,∴x1+x2=5,x1•x2=2,∴x1+x2−x1•x2=5−2=1.故选D.【点睛】本题考查了根与系数的关系,解题的关键是根据根与系数的关系得出x1+x2=5,x1•x2=2.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系得出两根之和与两根之积是关键.2.B【解析】分析:根据必然事件、不可能事件、随机事件的概念可区别各类事件:A、打开电视机,正在播放茂名新闻,可能发生,也可能不发生,是随机事件,故本选项错误;B、早晨的太阳从东方升起,是必然事件,故本选项正确;C、随机掷一枚硬币,落地后可能正面朝上,也可能背面朝上,故本选项错误;D、下雨后,天空出现彩虹,可能发生,也可能不发生,故本选项错误.故选B.3.B【解析】【分析】根据各超市降价的百分比分别计算出此商品降价后的价格,再进行比较即可得出结论.【详解】解:降价后三家超市的售价是:甲为(1-20%)2m=0.64m,乙为(1-40%)m=0.6m,丙为(1-30%)(1-10%)m=0.63m,∵0.6m<0.63m<0.64m,∴此时顾客要购买这种商品最划算应到的超市是乙.故选:B.【点睛】此题考查了列代数式,解题的关键是根据题目中的数量关系列出代数式,并对代数式比较大小.4.A【解析】【分析】利用因式分解法解方程即可.【详解】解:(2x-3)(x+1)=0,2x-3=0或x+1=0,所以x1=32,x2=-1.故选A.【点睛】本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想). 5.D 【解析】 【分析】过A 作AD ⊥BF 于D,根据45°角的三角函数值可求出AB 的长度,根据含30°角的直角三角形的性质求出斜边AC 的长即可. 【详解】如图,过A 作AD ⊥BF 于D , ∵∠ABD=45°,AD=12, ∴sin 45ADAB ︒==122, 又∵Rt △ABC 中,∠C=30°, ∴AC=2AB=242, 故选:D .【点睛】本题考查解直角三角形,在直角三角形中,30°角所对的直角边等于斜边的一半,熟记特殊角三角函数值是解题关键. 6.D 【解析】分析:根据轴对称图形与中心对称图形的概念分别分析得出答案.详解:A .是轴对称图形,也是中心对称图形,故此选项错误; B .不是轴对称图形,也不是中心对称图形,故此选项错误; C .不是轴对称图形,是中心对称图形,故此选项错误; D .是轴对称图形,不是中心对称图形,故此选项正确. 故选D .点睛:本题考查了轴对称图形和中心对称图形的概念.轴对称图形的关键是寻找对称轴,图形沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,图形旋转180°后与原图形重合. 7.A【分析】根据众数和中位数的概念求解.【详解】这组数据中4出现的次数最多,众数为4,∵共有7个人,∴第4个人的劳动时间为中位数,所以中位数为4,故选A.【点睛】本题考查众数与中位数的意义,一组数据中出现次数最多的数据叫做众数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.8.C【解析】【分析】根据题意列出代数式,化简即可得到结果.【详解】根据题意得:a÷(1−20%)=a÷= a(元),故答案选:C.【点睛】本题考查的知识点是列代数式,解题的关键是熟练的掌握列代数式.9.D【解析】各项计算得到结果,即可作出判断.解:A、原式不能合并,不符合题意;B、原式=a5,不符合题意;C、原式=a2﹣2ab+b2,不符合题意;D、原式=﹣a6,符合题意,故选D10.C【解析】由折叠得到EB=EF,∠B=∠DFE,根据CE+EB=9,得到CE+EF=9,设EF=x,得到CE=9-x,在直角三角形CEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出EF与CE的长,由FD与BC平行,得到一对内错角相等,等量代换得到一对同位角相等,进而确定出EF与AB平行,由平行得比例,即可求出AB的长.【详解】由折叠得到EB=EF,∠B=∠DFE,在Rt△ECF中,设EF=EB=x,得到CE=BC-EB=9-x,根据勾股定理得:EF2=FC2+EC2,即x2=32+(9-x)2,解得:x=5,∴EF=EB=5,CE=4,∵FD∥BC,∴∠DFE=∠FEC,∴∠FEC=∠B,∴EF∥AB,∴EF CE AB BC=,则AB=•EF BCCE=549⨯=454,故选C.【点睛】此题考查了翻折变换(折叠问题),涉及的知识有:勾股定理,平行线的判定与性质,平行线分线段成比例,熟练掌握折叠的性质是解本题的关键.11.D【解析】【分析】根据锐角三角函数的定义可得结论.【详解】在Rt△ABC中,∠ACB=90°,AB=c,∠A=a,根据锐角三角函数的定义可得sinα=BC AB,∴BC=c•sinα,∵∠A+∠B=90°,∠DCB+∠B=90°,∴∠DCB=∠A=α在Rt△DCB中,∠CDB=90°,∴cos∠DCB= CD BC,∴CD=BC•cosα=c•sinα•cosα,故选D.12.D【解析】解:作直径AD,连结BD,如图.∵AD为直径,∴∠ABD=90°.在Rt△ABD中,∵AD=10,AB=6,∴BD=22106=8,∴cosD=BDAD=810=45.∵∠C=∠D,∴cosC=45.故选D.点睛:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.x≠1【解析】【分析】根据分母不等于2列式计算即可得解.【详解】由题意得,x-1≠2,解得x≠1.故答案为x≠1.【点睛】本题考查的知识点为:分式有意义,分母不为2.14.13.【解析】【分析】由题意可知一共有6种可能,经过西流湾大桥的路线有2种可能,根据概率公式计算即可.【详解】解:由题意可知一共有6种可能,经过西流湾大桥的路线有2种可能,所以恰好选到经过西流湾大桥的路线的概率=21=63.故答案为13.【点睛】本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.15.15 4【解析】【分析】过点D作DF⊥BC于点F,由菱形的性质可得BC=CD,AD∥BC,可证四边形DEBF是矩形,可得DF =BE,DE=BF,在Rt△DFC中,由勾股定理可求DE=1,DF=3,由反比例函数的性质可求k的值.【详解】如图,过点D作DF⊥BC于点F,∵四边形ABCD是菱形,∴BC=CD,AD∥BC,∵∠DEB=90°,AD∥BC,∴∠EBC=90°,且∠DEB=90°,DF⊥BC,∴四边形DEBF是矩形,∴DF=BE,DE=BF,∵点C的横坐标为5,BE=3DE,∴BC=CD=5,DF=3DE,CF=5﹣DE,∵CD2=DF2+CF2,∴25=9DE2+(5﹣DE)2,∴DE=1,∴DF=BE=3,设点C(5,m),点D(1,m+3),∵反比例函数y=kx图象过点C,D,∴5m=1×(m+3),∴m=34,∴点C(5,34 ),∴k=5×34=154,故答案为:15 4【点睛】本题考查了反比例函数图象点的坐标特征,菱形的性质,勾股定理,求出DE的长度是本题的关键.16.1【解析】【分析】用总人数300乘以样本中身高在170cm-175cm之间的人数占被调查人数的比例.【详解】估计该校男生的身高在170cm-175cm之间的人数约为300×1261016126++++=1(人),故答案为1.【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.17.4【解析】【分析】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.根据定义ad=cb,将a,b及c的值代入即可求得d.【详解】已知a,b,c,d是成比例线段,根据比例线段的定义得:ad=cb,代入a=3,b=2,c=6,解得:d=4,则d=4cm.故答案为:4【点睛】本题主要考查比例线段的定义.要注意考虑问题要全面.18.1【解析】试题分析:先根据一次函数平移规律得出直线y=x+b沿y轴向下平移3个单位长度后的直线解析式y=x+b ﹣3,再把点A (﹣1,2)关于y 轴的对称点(1,2)代入y=x+b ﹣3,得1+b ﹣3=2,解得b=1.故答案为1.考点:一次函数图象与几何变换三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.15. 【解析】 【分析】 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x 的值代入计算即可求出值.【详解】原式=2221(1)(1)1(3)x x x x x x +-++-⋅++=2(1)(1)(3)3113x x x x x x x +-=-++⋅++ 当x=1时,原式2123-=+=15. 【点睛】 本题考查了分式的化简求值,熟练掌握运算法则是解答本题的关键.20.(1)详见解析;(2)OF =254. 【解析】【分析】(1)连接OC ,如图,根据切线的性质得∠1+∠3=90°,则可证明∠3=∠4,再根据圆周角定理得到∠ACB=90°,然后根据等角的余角相等得到∠BDC=∠5,从而根据等腰三角形的判定定理得到结论; (2)根据勾股定理计算出AC=8,再证明△ABC ∽△ABD ,利用相似比得到AD=252,然后证明OF 为△ABD 的中位线,从而根据三角形中位线性质求出OF 的长.【详解】(1)证明:连接OC ,如图,∵CF 为切线,∴OC ⊥CF ,∴∠1+∠3=90°,∵BM⊥AB,∴∠2+∠4=90°,∵OC=OB,∴∠1=∠2,∴∠3=∠4,∵AB为直径,∴∠ACB=90°,∴∠3+∠5=90°,∠4+∠BDC=90°,∴∠BDC=∠5,∴CF=DF;(2)在Rt△ABC中,AC=8,∵∠BAC=∠DAB,∴△ABC∽△ABD,∴AB ACAD AB=,即10810AD=,∴AD=25 2,∵∠3=∠4,∴FC=FB,而FC=FD,∴FD=FB,而BO=AO,∴OF为△ABD的中位线,∴OF=12AD=254.【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理和垂径定理.21.(1)120,180;(2)①y=-60x+7200,0≤x≤403;②x=403时,y有最小值,此时y最小=-60×403+7200=6400(元).【解析】【分析】(1)根据小明和小华的培训结算表列出关于a、b的二元一次方程组,解方程即可求解;(2)①根据培训总费用=普通时段培训费用+高峰时段和节假日时段培训费用列出y与x之间的函数关系式,进而确定自变量x 的取值范围;②根据一次函数的性质结合自变量的取值范围即可求解.【详解】(1)由题意,得{20a 20b 600030a 10b 5400+=+=, 解得{a 120b 180==,故a ,b 的值分别是120,180;(2)①由题意,得y=120x+180(40-x ),化简得y=-60x+7200, ∵普通时段的培训学时不会超过其他两个时段总学时的12, ∴x≤12(40-x ), 解得x≤403, 又x≥0,∴0≤x≤403; ②∵y=-60x+7200,k=-60<0,∴y 随x 的增大而减小,∴x 取最大值时,y 有最小值,∵0≤x≤403; ∴x=403时,y 有最小值,此时y 最小=-60×403+7200=6400(元). 【点睛】本题考查了一次函数的应用,二元一次方程组的应用,理解题意得出数量关系是解题的关键. 22. (1) m≠1且m≠2-3;(2) m=-1或m=-2. 【解析】【分析】(1)由方程有两个不相等的实数根,可得△>1,列出关于m 的不等式解之可得答案;(2) 解方程,得:12x =m,2x =-3,由m 为整数,且方程的两个根均为负整数可得m 的值. 【详解】解:(1) Q △=2b -4ac=(3m-2)2+24m=(3m+2)2≥1∴当m≠1且m≠2-3时,方程有两个不相等实数根. (2)解方程,得:12x =m,2x =-3, Q m 为整数,且方程的两个根均为负整数, ∴m=-1或m=-2.∴m=-1或m=-2时,此方程的两个根都为负整数【点睛】本题主要考查利用一元二次方程根的情况求参数.23.见解析【解析】【分析】先通过∠BAD=∠CAE 得出∠BAC=∠DAE ,从而证明△ABC ≌△ADE ,得到BC=DE .【详解】证明:∵∠BAD=∠CAE ,∴∠BAD+∠DAC=∠CAE+∠DAC .即∠BAC=∠DAE ,在△ABC 和△ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△ADE (SAS ).∴BC=DE .【点睛】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:AAS 、SSS 、SAS 、SSA 、HL .24.(1)大货车用8辆,小货车用7辆;(2)y=100x+1.(3)见解析.【解析】【分析】(1)设大货车用x 辆,小货车用y 辆,根据大、小两种货车共15辆,运输152箱鱼苗,列方程组求解;(2)设前往A 村的大货车为x 辆,则前往B 村的大货车为(8-x )辆,前往A 村的小货车为(10-x )辆,前往B 村的小货车为[7-(10-x )]辆,根据表格所给运费,求出y 与x 的函数关系式;(3)结合已知条件,求x 的取值范围,由(2)的函数关系式求使总运费最少的货车调配方案.【详解】(1)设大货车用x辆,小货车用y辆,根据题意得:15{128152 x yx y+=+=解得:8{7xy==.∴大货车用8辆,小货车用7辆.(2)y=800x+900(8-x)+400(10-x)+600[7-(10-x)]=100x+1.(3≤x≤8,且x为整数).(3)由题意得:12x+8(10-x)≥100,解得:x≥5,又∵3≤x≤8,∴5≤x≤8且为整数,∵y=100x+1,k=100>0,y随x的增大而增大,∴当x=5时,y最小,最小值为y=100×5+1=9900(元).答:使总运费最少的调配方案是:5辆大货车、5辆小货车前往A村;3辆大货车、2辆小货车前往B村.最少运费为9900元.25.(1)k=10,b=3;(2)15 2.【解析】试题分析:(1)、将A点坐标代入反比例函数解析式和一次函数解析式分别求出k和b的值;(2)、首先根据一次函数求出点B的坐标,然后计算面积.试题解析:(1)、把x=2,y=5代入y=kx,得k==2×5=10把x=2,y=5代入y=x+b,得b=3(2)、∵y=x+3 ∴当y=0时,x=-3,∴OB=3 ∴S=12×3×5=7.5考点:一次函数与反比例函数的综合问题.26.(1)①直线AB的解析式为y=﹣x+3;理由见解析;②四边形ABCD是菱形,(2)四边形ABCD能是正方形,理由见解析.【解析】分析:(1)①先确定出点A,B坐标,再利用待定系数法即可得出结论;②先确定出点D坐标,进而确定出点P坐标,进而求出PA,PC,即可得出结论;(2)先确定出B(1,),进而得出A(1-t,+t),即:(1-t)(+t)=m,即可得出点D(1,8-),即可得出结论.详解:(1)①如图1,∵m=1,∴反比例函数为y=,当x=1时,y=1,∴B(1,1),当y=2时,∴2=,∴x=2,∴A(2,2),设直线AB的解析式为y=kx+b,∴,∴,∴直线AB的解析式为y=-x+3;②四边形ABCD是菱形,理由如下:如图2,由①知,B(1,1),∵BD∥y轴,∴D(1,5),∵点P是线段BD的中点,∴P(1,3),当y=3时,由y=得,x=,由y=得,x=,∴PA=1-=,PC=-1=,∴PA=PC,∵PB=PD,∴四边形ABCD为平行四边形,∵BD⊥AC,∴四边形ABCD是菱形;(2)四边形ABCD能是正方形,理由:当四边形ABCD是正方形,∴PA=PB=PC=PD,(设为t,t≠0),当x=1时,y==,∴B(1,),∴A(1-t,+t),∴(1-t)(+t)=m,∴t=1-,∴点D的纵坐标为+2t=+2(1-)=8-,∴D(1,8-),∴1(8-)=n,∴m+n=2.点睛:此题是反比例函数综合题,主要考查了待定系数法,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD是平行四边形是解本题的关键.27.(1)答案见解析;(2)220cm【解析】【分析】(1)根据三角形角平分线的定义,即可得到AD;(2)过D作于DE⊥ABE,根据角平分线的性质得到DE=CD=4,由三角形的面积公式即可得到结论.【详解】解:(1)如图所示,AD即为所求;(2)如图,过D作DE⊥AB于E,∵AD平分∠BAC,∴DE=CD=4,∴S△ABD=12AB·DE=20cm2.【点睛】掌握画角平分线的方法和角平分线的相关定义知识是解答本题的关键.。
2019-2020学年黑龙江省佳木斯市第一中学高一下学期第一次月考数学试题Word版含解析

2019-2020学年黑龙江省佳木斯市第一中学下学期第一次月考高一数学试题一、选择题1.若A 为ABC ∆的内角,则下列函数中一定取正值的是( ) A. cos A B. sin A C. tan A D. sin2A 【答案】B【解析】因为()0,πA ∈ ,所以sin 0A > ,选B. 2.在ABC ∆中,45,105AB A C ===o o ,则BC =( )A. 2C. 3D. 3【答案】C【解析】由正弦定理得()3sin sin sin105sin452sin 4560AB BC BC BC C A =⇒=⇒===+o o o o,选C.3.已知ABC ∆中,45a b A ===o ,则三角形的解的个数( )A. 0个B. 1个C. 2个D. 0个或1个 【答案】C【解析】由正弦定理得πsin sin sin sin453a b B B A B =⇒=⇒=⇒=o 或2π3B = ,所以三角形的解的个数为两个,选C.点睛:(1)判断三角形解的个数的两种方法①代数法:根据大边对大角的性质、三角形内角和公式、正弦函数的值域等判断. ②几何图形法:根据条件画出图形,通过图形直观判断解的个数.(2)已知三角形的两边和其中一边的对角解三角形.可用正弦定理,也可用余弦定理.用正弦定理时,需判断其解的个数,用余弦定理时,可根据一元二次方程根的情况判断解的个数. 4.化简11sin15cos15-=o o的结果是( )2C.- 【答案】C【解析】()1154511cos15sin15211sin15cos15sin15cos15sin3024+--====o oooo o o o o ,选C.5.在ABC ∆ 中,角,,A B C 所对的边分别为,,a b c,若222a cb +-=,则角B 的值为 ( )A.6π B. 3π C. 6π或56π D. 3π或23π【答案】A【解析】由余弦定理得2223cos 22a c b B ac +-== ,因为()0,πB ∈ ,所以π6B = ,选A.6.设函数()22cos sin ,R 44f x x x x ππ⎛⎫⎛⎫=+-+∈ ⎪ ⎪⎝⎭⎝⎭,则函数()f x 是 ( )A. 最小正周期为π的奇函数B. 最小正周期为π的偶函数C. 最小正周期为2π的奇函数D. 最小正周期为2π的偶函数 【答案】A【解析】()πcos2sin24f x x x ⎛⎫=+=- ⎪⎝⎭,为最小正周期为π的奇函数选A. 7.设向量2cos ,2a α⎛⎫= ⎪⎪⎝⎭r的模为3,则cos2α=( ) A. 14-B. 12-C. 12D. 3【答案】B【解析】由题意得2221311cos cos cos22cos 12242αααα+=⇒=⇒=-=- 选B. 8.在ABC ∆中,若cos cos cos a b c A B C==,则ABC ∆形状是( ) A .直角三角形 B .等腰直角三角形 C .钝角三角形 D .等边三角形 【答案】D 【解析】略9.如图, ,,D C B 三点在地面同一直线上, ,DC a =从,C D 两点测得A 点的仰角分别是,()βααβ<,则A 点离地面的高度等于( )A.()sin sin sin a αββα- B. ()sin sin cos a αβαβ-C.()sin cos sin a αββα- D. ()cos sin cos a αβαβ-【答案】A【解析】试题分析:在ACD ∆中, CAD βα∠=-,由正弦定理可得()()sin ,sin sin sin CD AC a AC αβααβα=∴=--,在直角三角形ABC 中, ()sin sin sin sin a AB AC αβββα==-,故选A.【考点】正弦定理在实际问题中的应用.10.,的一个通项公式是n a =; ②已知数列{}n a ,123,6a a ==,且21n n n a a a ++=-,则数列的第五项为6-; ③在等差数列{}n a 中,若34567450a a a a a ++++=,则28180a a +=; ④在等差数列{}n a 中, 241,5a a ==,则{}n a 的前5项和515S =,其中正确的个数是( )A. 2B. 3C. 4D. 1 【答案】C【解析】, n a =②123,6a a ==, 33a =, 43a =-, 56a =-,③由34567450a a a a a ++++=,得552855450902180a a a a a ==+==,,;④()()()152455551515.222a a a a S +++==== 因此正确的个数是4,选C.11.下列结论:①函数sin22x x y = 的图象的一条对称轴方程是3x π=; ②ABC ∆中,若2sin b a B =,则A 等于30o ;③在ABC ∆中,若120,5,7A AB BC ∠===o ,则ABC ∆的面积4S =;④1sin70cos40cos60cos808=o o o o ,其中正确的是( ) A. ① ② B. ① ③ C. ③ ④ D. ② ④ 【答案】B【解析】①π2sin 23x y ⎛⎫=+⎪⎝⎭,当3x π=时, 2y = ,所以①对;②由正弦定理得1sin 2sin sin ,sin 302B A B A A ==⇒=o 或150A =o , ②不对; ③由余弦定理得22227525cos120,5240,3b b b b b =+-⨯⨯+-==o (舍负),所以ABC ∆的面积153sin1202S =⨯⨯⨯=o ,③对; ④11sin20cos20cos40cos80sin1601sin70cos40cos60cos80cos20cos40cos8022sin2016sin2016====o o o o o ooooo o o o o ,④不对;正确的是① ③,选B.12.ABC ∆中, ,,a b c 分别为,,A B C ∠∠∠的对边,如果,,a b c 成等差数列, 30,B ABC ∠=∆o的面积为32,那么b =( )2 D. 1+ 【答案】D【解析】由三角形面积公式得13sin30,622ac ac ==o ;由余弦定理得()2222222cos3024241b a c ac a c ac b ac b b =+-=+-=-⇒=+=o 选D.点睛:(1)运用余弦定理时,要注意整体思想的运用.(2)在已知三角形两边及其中一边的对角,求该三角形的其它边角的问题时,首先必须判断是否有解,如果有解,是一解还是两解,注意“大边对大角”在判定中的应用.二、填空题13.在ABC ∆ 中, ,,a b c 分别为角,,A B C 所对的边,若()()3a b c a b c ac -+++=,则B =__________.【答案】60o【解析】由题意得()222223,a c b ac a c b ac +-=+-= ,所以由余弦定理得2221πcos ,.223a cb B B ac +-===14.已知1sin 3α=,则sin cos 22αα+=__________.【答案】3±【解析】24sin cos 1223sin ααα⎛⎫+=+= ⎪⎝⎭,所以sin cos 223αα+=±15.下列结论:正确的序号是__________.①ABC ∆中,若A B >则一定有sin sin A B >成立;②数列{}n a 的前n 项和221n S n n =-+,则数列{}n a 是等差数列;③锐角三角形的三边长分别为3,4,a ,则a的取值范围是5a <<;④等差数列数列{}n a 的前n 项和为n S ,已知7891024a a a a +++=,则1696S =.【答案】① ③ ④【解析】①ABC ∆中, sin sin A B a b A B >⇒>⇒> ;②221n S n n =-+得12213320,1,3a a S S a S S ==-==-= ,故数列{}n a 不是等差数列;③由余弦定理得222222340,3405a a a +->+->⇒<< ; ④由7891024a a a a +++=得8912a a +=,所以()()116168916881296.2a a S a a +==+=⨯=16.在ABC ∆中, D 为AB 的一个三等分点,且3,,3AB AD AC AD CB CD ===,则cos B =__________.【答案】18【解析】设,AD m CD n == ,则22222222299cos 32223m n m m n A n m m m m-+-==⇒=⨯⨯ ,所以22229914cos 2331818m n m m B m n mn +-====⨯⨯三、解答题17.根据下列各题中的条件,求相应的等差数列{}n a 的有关未知数:(1)151,,566n a d S ==-=-,求n 及n a ; (2)2,15,10n d n a ===-,求1a 及n S .【答案】(1)116n a n =-+(2)-360 【解析】试题分析:(1)由等差数列前项和公式()11-12n S na n n d =+解得15n = ,再利用等差数列通项公式()11n a a n d =+-求n a ;(2)先由等差数列通项公式()11n a a n d =+-求1a ,再利用等差数列前项和公式()11-12n S na n n d =+求n S .试题解析: (1) ()1515626n n n S n -⎛⎫=+⨯-=- ⎪⎝⎭Q ,211600n n ∴--=,解得15n =或4n =-(舍去), 则()51111666n a n n ⎛⎫=+-⨯-=-+ ⎪⎝⎭. (2) ()11151414210,38,153823602n n a a a S ⨯=+⨯=-∴=-=⨯-+⨯=-Q . 点睛:在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.18.已知函数()2cos cos 1f x x x x =+.(1)若R x ∈,求()f x 的最小正周期和最值; (2)若0x π<<,求这个函数的单调区间.【答案】(1)3y sin 262x π⎛⎫=++ ⎪⎝⎭(2)单调递增区间为0,6π⎛⎤ ⎥⎝⎦和2,3ππ⎡⎫⎪⎢⎣⎭;单调递减区间为2,63ππ⎡⎤⎢⎥⎣⎦.【解析】试题分析:(1)先利用二倍角公式及配角公式将()2cos cos 1f x x x x =+化为基本三角函数 3y sin 262x π⎛⎫=++ ⎪⎝⎭.再根据正弦函数性质求最小正周期和最值; (2)先根据正弦函数单调增区间列不等式()222Z 262k x k k πππππ-+≤+≤+∈,结合0x π<<,解不等式组可得函数的单调增区间0,6π⎛⎤ ⎥⎝⎦和2,3ππ⎡⎫⎪⎢⎣⎭;剩下的就为单调减区间2,63ππ⎡⎤⎢⎥⎣⎦..试题解析:(1) 2cos2111cos cos 11cos21222x y x x x x x +=++=++=+++ 33sincos2cossin2sin 266262x x x πππ⎛⎫=++=++ ⎪⎝⎭.(2)因为函数sin y x =的单调递增区间为()2,2Z 22k k k ππππ⎡⎤-++∈⎢⎥⎣⎦,由(1)知3sin 262y x π⎛⎫=++ ⎪⎝⎭,故()222Z 262k x k k πππππ-+≤+≤+∈, ()Z 36k x k k ππππ∴-+≤≤+∈,故函数3sin 2,062y x x ππ⎛⎫=++<< ⎪⎝⎭的单调递增区间为0,6π⎛⎤ ⎥⎝⎦和2,3ππ⎡⎫⎪⎢⎣⎭;单调递减区间为2,63ππ⎡⎤⎢⎥⎣⎦. 点睛:三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合,通过变换把函数化为()sin y A x B ωϕ=++的形式再借助三角函数图象研究性质,解题时注意观察角、函数名、结构等特征.19.在ABC ∆ 中,角,,A B C 所对的边分别为,,a b c ,且满足()2cos cos a c B b C -=.(1)求角B 的大小;(2)设()()sin ,cos2,4,1(1)m A A n k k ==>r r ,且·m n r r的最大值是5,求k 的值.【答案】(1)3B π=(2)32k =【解析】试题分析:(1)先利用正弦定理将边角关系转化为角的关系:()2sin sin cos sin cos A C B B C -= ,再根据两角和正弦公式及诱导公式化简得2sin cos sin A B A = ,即1cos 2B =,解得3B π= ,(2)先根据向量数量积化简·4sin cos2m n k A A =+r r ,再利用二倍角公式及换元转化为一元二次函数2y 241t kt =-++,其中(]sin 0,1A t =∈,最后根据对称轴与定义区间位置关系求最大值41k -,利用最大值是5,求出k 的值.试题解析:(1) ()()2cos cos ,2sin sin cos sin cos a c B b C A C B B C -=∴-=Q ,即()2sin cos sin cos sin cos sin A B B C C B B C =+=+,,2sin cos sin A B C A B A π++=∴=Q , 10,sin 0,cos ,0,23A AB B B πππ<<∴≠∴=<<∴=Q Q . (2) 22·4sin cos22cos 4sin 1,0,3m n k A A A k A A π⎛⎫=+=-++∈ ⎪⎝⎭r r ,设sin A t =,则(]0,1t ∈,则 ()(]222·241212,0,1m n t kt t k k t =-++=--++∈r r , 1,1k t >∴=Q 时, ·m n r r 取最大值,依题意得, 32415,2k k -++=∴=. 20.如图所示,在梯形ABCD 中, ,5,9,30,45AD BC AB AC BCA ADB ==∠=∠=ooP ,求BD 的长.【答案】922【解析】试题分析:先在ABC ∆中,根据正弦定理解出9sin 10ABC ∠=,再根据平行性质得9sin sin 10BAD ABC ∠=∠=.最后在ABD ∆中,利用正弦定理解出.BD 试题解析:在ABC ∆中, 5,9,30AB AC BCA ==∠=o ,由正弦定理,得,sin sin AB ACACB ABC=∠∠·sin 9sin309sin 510AC BCA ABC AB ∠∠===o . ,180AD BC BAD ABC ∴∠=-∠o Q P ,于是9sin sin 10BAD ABC ∠=∠=.同理,则ABD ∆中, 95,sin ,4510AB BAD ADB =∠=∠=o ,由正弦定理:sin sin AB BDBDA BAD=∠∠,解得922BD =,故BD 的长为922.点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果.21.在ABC ∆ 中,角,,A B C 所对的边分别为,,a b c ,且23ACB π∠=. (1)若,,a b c 依次成等差数列,且公差为2,求c 的值;(2)若3,c ABC θ=∠=,试用θ表示ABC ∆的周长,并求周长的最大值.【答案】(1)7c =(2)23【解析】试题分析:(1)由等差数列定义可得 4,2a c b c =-=- ,再根据余弦定理得方程()()()()2224212422c c c c c -+--=--- ,解方程可得c 的值;(2)先根据正弦定理用θ表示表示边2sin ,2sin 3AC BC πθθ⎛⎫==- ⎪⎝⎭,再利用两角差正弦公式及配角公式将周长函数转化为基本三角函数2sin 3πθ⎛⎫+ ⎪⎝⎭,最后根据θ范围及正弦函数性质求最大值.试题解析:(1) ,,a b c Q 成等差数列,且公差为2,4,2a c b c ∴=-=-,又()()()()222222422111,cos ,,32222422c c c a b c BCA C ab c c π-+--+-∠=∴=-∴=-∴=---Q ,恒等变形得29140c c -+=,解得7c =或2c =,又4,7c c >∴=Q . (2)在ABC ∆中,,2sin sin sin sin sinsin 33AC BC AB ACBC ABC BAC ACB πθθ==∴===∠∠∠⎛⎫- ⎪⎝⎭,2sin ,2sin 3AC BC πθθ⎛⎫==- ⎪⎝⎭. ABC∴∆的周长()2sin 2sin 3f AC BC AB πθθθ⎛⎫=++=+-+ ⎪⎝⎭12sin 2sin 23πθθθ⎡⎤⎛⎫=+=++⎢⎥ ⎪⎝⎭⎣⎦20,,3333ππππθθ⎛⎫∈∴<+<⎪⎝⎭Q , ∴当32ππθ+=即6πθ=时, ()f θ取得最大值2+.22.在ABC ∆ 中, ,,a b c 分别为角,,A B C 所对的边, 且三个内角,,A B C 满足2A C B +=.(1)若2b =,求ABC ∆的面积的最大值,并判断取最大值时三角形的形状; (2)若11cos cos cos A C B +=-,求cos 2A C-的值. 【答案】(1)等边三角形.(2)cos22A C -= 【解析】试题分析:(1)由2A CB +=及三角形内角和为180o得60B =o ,根据余弦定理及基本不等式得224a c ac ac =+-≥,再结合三角形面积公式得1sin602S ac =≤o ,当且仅当,a c ABC =V 为正三角形时取等号, (2) 设2A Cα-=,因为120A C +=o ,所以60,60A C αα=+=-o o ,代入条件,通分,利用两角和与差余弦公式化简得2cos 3cos 4αα=--cos a方程得cos a =,即为cos2A C-的值. 试题解析:(1) 由题设条件知60,120,26ABC B A C S A π∆⎛⎫=+==-+⎪⎝⎭o o , ()max ABC S ∆=,此时3A π=,又3B π=,所以ABC ∆是等边三角形.(2) 由题设条件知60,120B A C =+=o o ,设2A Cα-=,则2A C α-=,可得60,60A C αα=+=-o o ,()()1111cos cos cos 60cos 60A C αα∴+=++-o o222cos cos 133cos sin cos 4442222ααααα===--,依题设条件有22cos 1cos cos ,332cos cos 44B αααα==∴=---Q()22cos 0,2cos 30,30a a a a a +-=+=+≠Q ,2cos 0a ∴=.从而得cos2A C -= 点睛:判断三角形形状的方法①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.②化角:通过三角恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用πA B C ++=这个结论.。
黑龙江省佳木斯市一中2019~2020学年高一下学期第一学段检测语文试题

黑龙江省佳木斯市一中2019-2020学年高一下学期第一学段检测语文试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)请点击修改第I卷的文字说明一、选择题1.下列加点词的意义不同的一组是()A.涂有饿莩而不知发.春心莫共花争发.B.弃甲曳兵.而走斩木为兵.C.或.五十步而后止人固有一死,或重于泰山,或.轻于鸿D.是.亦走也是.使民养生丧死无憾也2.下列加点词意义相同的一项是()A.学不可以已.且壮士不死即已.,死即举大名耳B.非能水也,而绝.江河率妻子邑人来此绝.境C.虽有槁暴,不复挺者.,輮使之然也非蛇鳝之穴无可寄托者.,用心躁也D.尝学琵琶于.穆、曹二善才转徙于.江湖间3.下列句中加点词语的用法归类正确的一项是( )①南.取汉中,西.举巴蜀②且夫天下非小弱..也③吞二周而亡.诸侯④却.匈奴七百余里⑤于是废先王之道,以愚.黔首⑥子孙帝王..万世之业也⑦五十者可以衣帛..矣⑧履.至尊而制六合⑨不耻相师.A.①/②/③④⑤/⑥⑦⑧⑨B.①/②③/④⑤⑥/⑦⑧⑨C.①/②⑤/③④⑥/⑦⑧⑨D.①⑥/②⑦/⑧⑨/③④⑤4.下列哪一项中的“以为”与其他三项不相同()A.南取百越之地,以为桂林、象郡B.收天下之兵,聚之咸阳,销锋镝,铸以为金人十二C.据亿丈之城,临不测之渊,以为固D.天下已定,始皇之心,自以为关中之固5.下列句,没有通假字的一项是()A.颁白者不负戴于道路矣B.则知明而行无过矣C.蒙故业因遗策D.或师焉或不焉6.下列句子中与“蚓无爪牙之利,筋骨之强”句式相同的一项是()A.句读之不知,惑之不解B.马之千里者,一食或尽粟一石C.申之以孝悌之义D.然而不王者,未之有也7.下列各句内容解说不正确的一项是()A.古代兄弟行辈中长幼排行的次序:伯(孟)是老大,仲是老二,叔是老三,季是老四。
古代贵族男子的字前常加伯(孟)、仲、叔、季表示排行。
B.前人有所谓“六书”说,即认为汉字的构成有“象形”“指事”“会意”“形声”“转注”“假借”六种方法。
黑龙江省佳木斯市2019-2020学年中考一诊数学试题含解析

黑龙江省佳木斯市2019-2020学年中考一诊数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.△ABC的三条边长分别是5,13,12,则其外接圆半径和内切圆半径分别是()A.13,5 B.6.5,3 C.5,2 D.6.5,22.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于12MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为()A.a=b B.2a+b=﹣1 C.2a﹣b=1 D.2a+b=13.如图,二次函数y=ax1+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=1,且OA=OC.则下列结论:①abc>0;②9a+3b+c>0;③c>﹣1;④关于x的方程ax1+bx+c=0(a≠0)有一个根为﹣1a;⑤抛物线上有两点P(x1,y1)和Q(x1,y1),若x1<1<x1,且x1+x1>4,则y1>y1.其中正确的结论有()A.1个B.3个C.4个D.5个4.太原市出租车的收费标准是:白天起步价8元(即行驶距离不超过3km都需付8元车费),超过3km 以后,每增加1km,加收1.6元(不足1km按1km计),某人从甲地到乙地经过的路程是xkm,出租车费为16元,那么x的最大值是()A.11 B.8 C.7 D.55.在函数x x+-x的取值范围是()A.x≥0B.x≤0C.x=0 D.任意实数6.如图,Rt△ABC中,∠C=90°,AC=4,3,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为()A .2πB .4πC .6πD .8π7.某校九年级共有1、2、3、4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是( ) A .B .C .D .8.已知A (,1y ),B (2,2y )两点在双曲线32my x +=上,且12y y >,则m 的取 值范围是( ) A .m 0>B .m 0<C .3m 2>-D .3m 2<-9.已知圆锥的底面半径为2cm ,母线长为5cm ,则圆锥的侧面积是( ) A .20cm2B .20πcm2C .10πcm2D .5πcm210.在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )A .27B .51C .69D .7211.如图,在△ABC 中,DE ∥BC 交AB 于D ,交AC 于E ,错误的结论是( ).A .AD AEDB EC= B .AB ACAD AE= C .AC ECAB DB= D .AD DEDB BC= 12.一元二次方程x 2﹣3x+1=0的根的情况( ) A .有两个相等的实数根 B .有两个不相等的实数根 C .没有实数根D .以上答案都不对二、填空题:(本大题共6个小题,每小题4分,共24分.)13.在反比例函数2yx=图象的每一支上,y随x的增大而______(用“增大”或“减小”填空).14.某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制了如图1和图2所示的统计图,则B品牌粽子在图2中所对应的扇形的心角的度数是_____.15.将161000用科学记数法表示为1.61×10n,则n的值为________.16.已知一纸箱中,装有5个只有颜色不同的球,其中2个白球,3个红球,若往原纸箱中再放入x个白球,然后从箱中随机取出一个白球的概率是,则x的值为_____17.如果将“概率”的英文单词probability中的11个字母分别写在11张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b的概率是________.18.函数y=22xx-+x的取值范围是_________.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.20.(6分)反比例函数kyx=在第一象限的图象如图所示,过点A(2,0)作x轴的垂线,交反比例函数kyx=的图象于点M,△AOM的面积为2.求反比例函数的解析式;设点B 的坐标为(t ,0),其中t >2.若以AB 为一边的正方形有一个顶点在反比例函数ky x=的图象上,求t 的值. 21.(6分)计算:(π﹣3.14)0+|2﹣1|﹣2sin45°+(﹣1)1. 22.(8分)如图,在三个小桶中装有数量相同的小球(每个小桶中至少有三个小球), 第一次变化:从左边小桶中拿出两个小球放入中间小桶中; 第二次变化:从右边小桶中拿出一个小球放入中间小桶中;第三次变化:从中间小桶中拿出一些小球放入右边小桶中,使右边小桶中小球个数是最初的两倍. (1)若每个小桶中原有3个小球,则第一次变化后,中间小桶中小球个数是左边小桶中小球个数的____倍; (2)若每个小桶中原有a 个小球,则第二次变化后中间小桶中有_____个小球(用a 表示); (3)求第三次变化后中间小桶中有多少个小球?23.(8分)解不等式组:10241x x x +>⎧⎨+≥-⎩,并把解集在数轴上表示出来。
黑龙江省佳木斯市第一中学2019_2020学年高一化学下学期第一学段考试试题

黑龙江省佳木斯市第一中学2019-2020学年高一化学下学期第一学段考试试题(时间:90分钟总分:100分)可能用到的相对原子质量:H∶1C∶12N∶14O∶16Na∶23S∶32Fe∶56Cu∶64Zn∶65Cl∶35.5 Ba∶137第Ⅰ卷(56分)一、选择题(本题包括16小题,每小题2分,共32分。
每小题只有一个选项符合题意。
)1.据我国古代第一部药物学专著《神农本草经》记载:“石硫黄(即硫磺)能化金银钢铁,奇物”。
硫与某些金属单质化合所得的产物可能是()A.AlS B.AgSC.CuS D.FeS2.硝酸被称为“国防工业之母”是因为它是制取炸药的重要原料。
下列实验事实与硝酸性质不相对应的一组是()A.浓硝酸使紫色石蕊试液先变红后褪色——酸性和强氧化性B.不能用稀硝酸与锌反应制氢气——强氧化性C.要用棕色瓶盛装浓硝酸——不稳定性D.稀硝酸能使滴有酚酞的氢氧化钠溶液红色褪去——强氧化性3.高纯度单晶硅是典型的无机非金属材料,又称“半导体”材料.它的发现和使用曾引起计算机的一场“革命”。
它可以按下列方法制备:下列说法正确的是()A.步骤①的化学方程式为:SiO2+C Si+CO2↑B.SiO2既能与HF反应,又能与NaOH反应,所以SiO2属于两性氧化物C.高纯硅是制造太阳能电池的常用材料,二氧化硅是制造光导纤维的基本原料D.含硅化合物硅酸钠属于盐类,不属于碱,可以保存在磨口玻璃塞试剂瓶中4.下列有关物质的性质与用途具有对应关系的是()A.Al2O3熔点高,可用作耐高温材料B.NH4HCO3受热易分解,可用作氮肥C.Fe2(SO4)3易溶于水,可用作净水剂D.SO2具有氧化性,可用于漂白纸浆5.同温、同压下,等体积的NH3和CH4两种气体,下列有关说法错误的是()A.所含分子数目相同B.质量之比为16:17C.所含氢原子物质的量之比为3:4D.密度之比为17:166.设N A代表阿伏加德罗常数,下列说法正确的是()A.1 mol硫单质在过量氧气中完全燃烧产生N A个SO3分子B.5.4 g铝单质与足量NaOH溶液反应,转移电子数为0.6N AC.标准状况下,36 g H2O中含有氧原子数为1 molD.标准状况下,22.4 L SO3中含有氧原子数为3N A7.下列各组物质中,不满足组内任意两种物质在一定条件下均能发生反应的是()8A.因为SO2具有漂白性,所以它能使溴水、石蕊试液褪色B.湿润的氯气具有漂白作用,它能使石蕊试液先变红色再褪色C.SO2和Cl2都能使品红溶液褪色,两者等体积混合可以增强漂白能力D.在蔗糖中加入浓硫酸后出现发黑现象,说明浓硫酸具有吸水性,能使蔗糖炭化9.按照氟、氯、溴、碘的顺序,下列递变规律中正确的是()A.F-、Cl-、Br-、I-的还原性逐渐增强B.与H2反应越来越容易C.单质的熔、沸点逐渐降低D.单质的氧化性逐渐增强10.检验溶液中是否含有某种离子,下列操作方法正确的是()A.向某溶液中加稀BaCl2,产生白色沉淀,再加入HCl溶液,沉淀不溶解,证明有SO42-B.向某溶液中加入稀 HCl,放出能使澄清的石灰水变浑浊的气体,证明有CO32-C.向某溶液中先加入Ba(NO3)2溶液无明显现象,再加入硝酸酸化的AgNO3溶液产生白色沉淀,证明有Cl-D.向某溶液中加入浓氢氧化钠溶液后加热,产生使湿润蓝色石蕊试纸变红的气体,证明含有NH4+11.火柴头上通常含有氯酸钾、二氧化锰、硫等物质。
【精准解析】黑龙江省佳木斯市第一中学2019-2020学年高一下学期第一学段考试数学(文)试题

佳一中2019-2020学年度第二学期第一学段考试高一数学试题(文)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.数列1,-3,5,-7,9,…的一个通项公式为( ) A. 21n a n =- B. (1)(21)nn a n =--C. (1)(12)nn a n =-- D. (1)(21)nn a n =-+【答案】C 【解析】 【分析】观察,奇偶相间排列,偶数位置为负,所以为1(1)n +-,数字是奇数,满足2n-1,所以可求得通项公式.【详解】由符号来看,奇数项为正,偶数项为负,所以符号满足1(1)n +-,由数值1,3,5,7,9…显然满足奇数,所以满足2n-1,所以通项公式 为1(1)(21)n n a n +=--,选C.【点睛】本题考查观察法求数列的通项公式,解题的关键是培养对数字的敏锐性,属于基础题.2.已知集合2{|430}A x x x =-+<,{|24}B x x =<<,则A B =( )A. (1,3)B. (1,4)C. (2,3)D. (2,4)【答案】C 【解析】 【分析】根据一元二次不等式的解法,可得集合A ,然后根据交集的概念,可得结果. 【详解】由()()2430130x x x x -+<⇒--<所以13x <<,所以()1,3A = 又(){|24}2,4B x x =<<=,所以(2,3)A B =故选:C【点睛】本题考查一元二次不等式的解法,记住口诀“大于取两边,小于取中间”,还考查集合之间的运算,属基础题.3.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cosC 等于 ( ) A.23B. 23-C. 13-D. 14-【答案】D 【解析】【详解】解:由正弦定理可得;sinA :sinB :sinC=a :b :c=2:3:4 可设a=2k ,b=3k ,c=4k (k >0)由余弦定理可得,cosC=1-4,选D 4.在等差数列{}n a 中,若45615a a a ++=,则28a a +=( ) A. 6 B. 10C. 7D. 5【答案】B 【解析】 【分析】根据等差数列的性质,可得5a ,然后由2852a a a +=,简单计算结果. 【详解】由题可知:456553155++==⇒=a a a a a 又2852a a a +=,所以2810a a += 故选:B【点睛】本题主要考查等差数列的性质,若m n p q +=+,则m n p q a a a a +=+,考验计算,属基础题. 5.《九章算术》教会了人们用等差数列的知识来解决问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织( )尺布.A.12B.2429C.1631D.1629【答案】B 【解析】此数列为等差数列,设公差为d ,那么()112n n n S na d -=+,3030293065402S d ⨯=⨯+= ,解得:2429d = ,故选B. 6.设等比数列{}n a 的前n 项和为n S ,且639S S =,764a =,则1(a = ) A. 1 B. 2C. 3D. 4【答案】A 【解析】 【分析】利用等比数列前n 项和公式和通项公式列出方程组,能求出1a . 【详解】等比数列{}n a 的前n 项和为n S ,且639S S =,764a =,∴631161(1)9(1)1164a q a q q q a q ⎧--=⎪--⎨⎪=⎩, 解得11a =,2q .故选:A .【点睛】本题考查等比数列的首项的求法,考查等比数列的性质等基础知识,考查运算求解能力,是基础题.7.已知等差数列{}n a 的公差d >0,则下列四个命题: ①数列{}n a 是递增数列; ②数列{}n S 是递增数列; ③数列n a n ⎧⎫⎨⎬⎩⎭是递增数列; ④数列n S n ⎧⎫⎨⎬⎩⎭是递增数列. 其中正确命题的个数为( ) A. 1 B. 2C. 3D. 4【答案】B 【解析】 【分析】根据等差数列的通项公式和前n 项和公式,结合数列的通项公式的函数性质进行求解即可.【详解】①:因为数列{}n a 是等差数列, 所以11(1)n a a n d nd a d =+-=+-, 因此可以把n a 看成关于n 的一次函数,而0d >,所以数列{}n a 是递增数列,因此本命题是真命题; ②:因为数列{}n a 是等差数列, 所以211111(1)(2)222n S na n n d n d n a d =+-=+-, 因此可以把n S 看成关于n 的二次函数,而二次函数的单调性与开口和对称轴有关, 虽然0d >能确定开口方向,但是不能确定对称轴的位置,故不能判断数列{}n S 的单调性,故本命题是假命题;③:因为数列{}n a 是等差数列, 所以11(1)n a a n d nd a d =+-=+-,设n na b n =,因此数列n a n ⎧⎫⎨⎬⎩⎭的通项公式为:1n n a a d b d n n -==+, 显然当1a d =时,数列n a n ⎧⎫⎨⎬⎩⎭是常数列,故本命题是假命题; ④:因为数列{}n a 是等差数列, 所以211111(1)(2)222n S na n n d n d n a d =+-=+-, 设n n S c n =,因此数列n S n ⎧⎫⎨⎬⎩⎭的通项公式为111(2)22n n S c nd a d n ==+-, 所以可以把n c 看成关于n 的一次函数,而102d >,所以数列n S n ⎧⎫⎨⎬⎩⎭是递增数列,因此本命题是真命题. 故选:B【点睛】本题考查了等差数列的通项公式和前n 项和公式的应用,考查了利用数列的函数性质判断数列的单调性,考查了推理论证能力和数学运算能力.8.对于任意实数a b c d ,,,,下列正确的结论为( ) A. 若,0a b c >≠,则ac bc >; B. 若a b >,则22ac bc >; C. 若a b >,则11a b<. D. 若22ac bc >,则a b >;【答案】D 【解析】 【分析】对字母a ,b ,c 的正负进行分类讨论即可排除ABC 三个选项,得出D 选项. 【详解】A 选项若c <0则不满足ac bc >; B 选项若c =0,不满足22ac bc >; C 选项若a >0,b <0,不满足11a b<; D 选项22ac bc >必有20c >,所以a b >. 故选:D【点睛】此题考查不等关系的判别,关键在于熟练掌握不等式性质,也可根据选项结合排除法求解.9.下列命题中,不正确的是( )A. 在ABC 中,若A B >,则sin sin A B >B. 在锐角ABC 中,不等式sin cos A B >恒成立C. 在ABC 中,若2,60b ac B ==,则ABC 必是等边三角形 D. 在ABC 中,若cos cos a A b B =,则ABC 必是等腰三角形 【答案】D 【解析】 【分析】根据正余弦定理以及有关知识,对各选项逐个判断即可求解. 【详解】对A ,因为A B >,所以a b >,又sin sin a b A B=,所以sin 1sin A aB b =>,即sin sin A B >,所以A 正确;对B ,因为ABC 为锐角三角形,所以2A B π+>,即有022A B ππ>>->,所以sin sin cos 2A B B π⎛⎫>-= ⎪⎝⎭,B 正确;对C ,因为2221cos 22a cb B ac +-==,所以()20a c -=,即a c =,而60B =,所以ABC是等边三角形,C 正确;对D ,由cos cos a A b B =可得,sin cos sin cos A A B B =,即sin 2sin 2A B =,所以22A B =或22A B π+=,亦即A B =或2A B π+=,所以ABC 是等腰三角形或者直角三角形,D 不正确. 故选:D【点睛】本题主要考查正余弦定理在解三角形中的应用,属于基础题.10.在ABC 中,4c =,30B ∠=︒,若给出一个b 的值,使得此三角形有两解,则b 的一个可能值是( ) A. 5 B. 3C. 2D. 1【答案】B 【解析】 【分析】根据三角形解的个数和三角形中两边与其中一边对角的关系即可求出b 的范围,从而解出. 【详解】因为三角形有两解,所以sin c B b c <<,即24b <<. 故选:B .【点睛】本题主要考查已知三角形的解的个数求边所在的范围,属于基础题.11.已知数列{}n a 是等差数列,若91130a a +<,10110a a ⋅<,且数列{}n a 的前n 项和n S 有最大值,那么n S 取得最小正值时n 等于( ) A. 20 B. 17C. 19D. 21【答案】C 【解析】试题分析:由等差数列的性质和求和公式可得10110,0a a ><又可得:而20101110()0S a a =+<,进而可得n S 取得最小正值时19n =.考点:等差数列的性质12.如图,AD 是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔BD ,若某科研小组在坝底A 点测得15BAD ∠=,沿着坡面前进40米到达E 点,测得45BED ∠=,则大坝的坡角(DAC ∠)的余弦值为( )31 31- 2121- 【答案】A 【解析】 【分析】由15BAD ∠=,45BED ∠=,可得30ABE ∠=,在ABE ∆中,由正弦定理得2062BE =,在BED ∆中,由正弦定理得sin 31BDE ∠=,进而由()sin sin 90BDE DAC ∠=∠+可得结果.【详解】因15BAD ∠=,45BED ∠=,所以30ABE ∠=.在ABE ∆中,由正弦定理得sin 30sin15AE BE=,解得2062BE =.在BED ∆中,由正弦定理得sin sin 45BE BDBDE =∠,所以220622sin 3120BDE ⨯∠==.又90ACD ∠=,所以()sin sin 90BDE DAC ∠=∠+,所以cos 31DAC ∠=. 故选A.【点睛】本题考查正弦定理解三角形,考查诱导公式,考查学生合理进行边角转化的能力,属于中档题.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填写在题中的横线上) 13.已知数列{}n a 为等比数列,n S 是它的前n 项和,若2312a a a ⋅=,且4a 与72a 的等差中项为54,则4S =________. 【答案】30 【解析】 【分析】设等比数列的公比为q ,运用等比数列的通项公式和等差中项的性质,解方程可得首项和公比,运用等比数列的求和公式,即可得到所求和. 【详解】设等比数列{}n a 的公比为q ,2312a a a ⋅=,且4a 与72a 的等差中项为54可得23611471115,22224a q q a a a a a q a q ⨯=+=+⋅=解得:1116,2a q ==则4414116(1)(1)2301112a q S q ⨯--===-- 故答案为:30【点睛】本题考查了等差和等比数列的综合应用,考查了等差中项,等比数列的通项公式,求和公式等知识点,考查了学生概念理解,数学运算的能力,属于中档题.14.已知数列{}n a ,n S 是它的前n 项和,2321n S n n =++,则=_________.【答案】6,161,2,n n n n N=⎧⎨-≥∈⎩【解析】 【分析】根据11,1,2n n n S n a S S n -=⎧=⎨-≥⎩,直接求n a .【详解】当1n =时,116a S ==;当2n ≥时,1n n n a S S -=-=22(321)3(1)2(1)1n n n n ⎡⎤++--+-+⎣⎦61n =-,综上可得6,161,2,n n a n n n N =⎧=⎨-≥∈⎩.故答案为:6,161,2,n n n n N =⎧⎨-≥∈⎩【点睛】本题考查了n a 与n S 的关系,由n S 求n a ,特别注意要分段,属于容易题. 15.在锐角三角形ABC 中,A B =,则ABAC的取值范围是_________.【答案】 【解析】 【分析】锐角三角形ABC 中,角,,A B C 都是锐角,求出角B 的取值范围.由正弦定理可得sin sin 2sin sin AB C B AC B B==,化简,即求求得ABAC 的取值范围.【详解】锐角ABC 中,020202A B C πππ⎧<<⎪⎪⎪<<⎨⎪⎪<<⎪⎩,即0202022A B B ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩,42B ππ∴<<.ABC 中,由正弦定理sin sin AB ACC B=, 可得()sin 2sin sin 22sin cos 2cos sin sin sin sin B AB C B B BB AC B B B B π-=====,0cos 42B Bππ<<∴<<(2cos B ∴∈,即AB AC ∈. 故答案为:.【点睛】本题考查正弦定理、二倍角公式、余弦函数的性质,属于中档题.16.已知实数,x y 满足14,23x y x y -<+<<-<,则32x y +的取值范围是________.【答案】323,22⎛⎫- ⎪⎝⎭【解析】 【分析】令32=()()x y m x y n x y +++-,构造方程组求出m ,n 的值,进而根据不等式的基本性质可得32x y +的范围.【详解】令32=()()x y m x y n x y +++-,则32m n m n +=⎧⎨-=⎩,解得:5212m n ⎧=⎪⎪⎨⎪=⎪⎩,即5132=()()22x y x y x y +++-,14x y -<+<,23x y <-<∴55()1022x y -<+<,131()22x y <-<, ∴35123()()2222x y x y -<++-<,即3233222x y -<+<,故答案为323,22⎛⎫-⎪⎝⎭ 【点睛】本题考查不等式的性质,利用待定系数法,结合不等式的基本性质是解决本题的关键,属于基础题.三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤) 17.已知{}2680A x x x =-+≤,103x B x x ⎧⎫-=>⎨⎬-⎩⎭,{}4C x a x a =≤≤+.(1)求AB ;(2)若A C ⊆,求实数a 的取值范围. 【答案】(1)(]3,4;(2)[]0,2. 【解析】 【分析】(1)解出集合A 、B ,然后利用交集的定义可求出集合A B ;(2)根据A C ⊆得出关于a 的不等式组,解出即可.【详解】(1)解不等式2680x x -+≤,得24x ≤≤,[]2,4A ∴=. 解不等式103x x ->-,解得1x <或3x >,()(),13,B ∴=-∞+∞.因此,(]3,4AB =;(2){}4C x a x a =≤≤+,A C ⊆,244a a ≤⎧∴⎨+≥⎩,解得02a ≤≤.因此,实数a 的取值范围是[]0,2.【点睛】本题考查集合交集的计算、利用集合的包含关系求参数,同时也考查了一元二次不等式与分式不等式的求解,考查运算求解能力,属于基础题.18.在ABC 角中,角A ,B ,C 所对的边分别是a,b ,c ,若sin cos a B A =. (1)求角A ; (2)若ABC面积为5a =,求b c +.【答案】(1)60A =︒(2)7b c += 【解析】 【分析】(1)先由正弦定理,得到tan A =A ;(2)根据三角形面积公式,以及余弦定理,分别得到8bc =,()223a b c bc +-=,即可求出结果.【详解】(1)由正弦定理得:sin sin cos A B B A =, ∵sin 0B ≠, ∴tan A =∵A 是ABC 的内角, ∴60A =︒.(2)∵ABC 的面积为 ∴1sin 2bc A = 由(1)知60A =︒, ∴8bc =,由余弦定理得:()2222222cos 3a b c bc A b c bc b c bc =+-=+-=+-. ∴()22425b c +-=, 得:7b c +=,【点睛】本题主要考查解三角形,熟记正弦定理,余弦定理,以及三角形面积公式即可,属于常考题型.19.已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,若22(sin sin )sin sin sin B C A B C -=-.(1)求A ;(2)求sin sin B C +的取值范围.【答案】(1)3π;(2). 【解析】 【分析】(1)利用正弦定理和余弦定理进行求解即可;(2)利用两角差的正弦公式和辅助角公式,结合正弦函数的性质进行求解即可.【详解】(1)22222(sin sin )sin sin sin sin sin sin sin sin B C A B C B C B C A -=-⇒+-=, 根据正弦定理可化简为:222b c bc a +-=,由余弦定理可知:2222cos a b c bc A =+-⋅,因此有1cos 2A =, ()0,,3A A ππ∈∴=;(2)由(1)可知:3A π=,由三角形内角和定理可知:23C B π=-,23sin sin sin sin()sin )326B C B B B B B ππ+=+-=+,25(0,),()(,)3666B B ππππ∈∴+∈,因此有1sin()(,1])626B B ππ+∈+∈,因此sin sin B C +的取值范围为.【点睛】本题考查了正弦定理和余弦定理的应用,考查了三角式的取值范围问题,考查了正弦函数的值域问题,考查了辅助角公式的应用,考查了数学运算能力.20.已知数列{}n a 满足111,21n n a a a +==+,数列{}n b 的前n 项的和为2n S n =.(1)证明数列{}1n a +是等比数列.(2)设n n n c b a =⋅,求数列{}n c 的前n 项的和n T . 【答案】(1)详见解析;(2)12(23)26n n T n n +=-⨯-+.【解析】 【分析】(1)直接运用等比数列的定义证明,即证明111n n a a ++=+常数; (2)由(1)求出n a ,根据n b 与n S 的关系求出n b ,根据n n n c b a =⋅,观察特点分析,可采用分组求和法和错位相减法求出数列{}n c 的前n 项的和n T .【详解】(1)由121n n a a +=+, 11a =,可推出10n a +>,则12111211n n n n a a a a +++++==+, ∴数列{}1n a +是首项为11a +=2,公比为2的等比数列.(2)由(1)11222n n n a -+=⋅=,∴21nn a =-.即数列{}n a 的通项公式为()*21,nn a n N=-∈.由数列{}n b 的前n 项的和为2n S n =,可得111b S ==,当2n ≥时,221(1)21n n n b S S n n n -=-=--=-,当1n =时,也符合.故数列{}n b 的通项公式为()*21,n b n n N=-∈.则()(21)21nn n n c b a n =⋅=-⋅-(21)2(21)nn n =-⨯--设23123252(21)2n n A n =⨯+⨯+⨯++-⋅,23121232(23)2(21)2n n n A n n +=⨯+⨯++-⋅+-⋅,两式相减可得()23122222(21)2n n n A n +-=++++--⋅,化简可得,16(23)2n n A n +=+-⋅.而数列{21}n -的前n 项的和为2(121)2n n nB n +-⨯==,所以12(23)26n n T n n +--=+⋅.【点睛】本题主要考查利用定义证明数列是等比数列,数列通项公式的求法,n a 与n S 的关系的应用,以及利用分组求和法,错位相减法求数列的和,意在考查学生的数学运算能力,属于中档题.21.在公差为d 的等差数列{}n a 中,已知110a =,且123,22,5a a a +成等比数列. (1)求n a ;(2)若0d <,设2nn n b a =+,数列{}n b 的前n 项和为n S ,求5S .【答案】(1)46n a n =+或=+11n a n -;(2)102. 【解析】 【分析】(1)先根据已知求出1d =-或4d =,即得n a ; (2)由题得=+11n a n -,再利用分组求和求解即可. 【详解】(1)因为123,22,5a a a +成等比数列,所以22213,(222)50(102),4(22)5d d d a a a ⨯∴+=⨯+∴==+或1d =-. 所以=10+(1)4=4+6n a n n -⨯或=10+(1)(1)=+11n a n n -⨯--. 所以46n a n =+或=+11n a n -; (2)因为0d <,所以=+11n a n -, 所以112nn b n =-++,所以5552(12)=(106)102212S -++=-.【点睛】本题主要考查等差数列通项的求法,考查等比中项的应用,考查等差数列和等比数列求和,考查数列分组求和,意在考查学生对这些知识的理解掌握水平. 22.已知函数2()(1)1f x m x mx m =+-+-(m R ∈). (1)若不等式()0f x <的解集为∅,求m 的取值范围; (2)当2m >-时,解不等式()f x m ≥;(3)若不等式()0f x ≥的解集为D ,若[11]D -⊆,,求m 的取值范围. 【答案】(1)m ≥;(2)1|11x x m ⎧⎫≤≤-⎨⎬+⎩⎭.;(3)m ≥. 【解析】试题分析:(1)对二项式系数进行讨论,可得10{m +>∆≤求出解集即可;(2)分为10m +=,10m +>,10m +<分别解出3种情形对应的不等式即可;(3)将问题转化为对任意的[]1,1x ∈-,不等式()2110m x mx m +-+-≥恒成立,利用分离参数的思想得2211xm x x -≥-+-+恒成立,求出其最大值即可.试题解析:(1)①当10m +=即1m =-时,()2f x x =-,不合题意; ②当10m +≠即1m ≠-时,()()210{4110m m m m +>∆=-+-≤,即21{340m m >--≥,∴1{33m m m >-≤-≥,∴m ≥ (2)()f x m ≥即()2110m x mx +--≥ 即()()1110m x x ⎡⎤++-≥⎣⎦①当10m +=即1m =-时,解集为{|1}x x ≥ ②当10m +>即1m >-时,()1101x x m ⎛⎫+-≥ ⎪+⎝⎭∵1011m -<<+,∴解集为1{|1}1x x x m ≤-≥+或 ③当10m +<即21m -<<-时,()1101x x m ⎛⎫+-≤ ⎪+⎝⎭∵21m -<<-,所以110m -<+<,所以111m ->+ ∴解集为1{|1}1x x m ≤≤-+ (3)不等式()0f x ≥的解集为D ,[]1,1D -⊆,即对任意的[]1,1x ∈-,不等式()2110m x mx m +-+-≥恒成立,即()2211m x x x -+≥-+恒成立,因为210x x -+>恒成立,所以22212111x xm x x x x -+-≥=-+-+-+恒成立, 设2,x t -=则[]1,3t ∈,2x t =-,所以()()2222131332213x t t x x t t t t t t-===-+-+---++-,因为3t t+≥,当且仅当t =时取等号,所以221x x x -≤=-+,当且仅当2x =所以当2x =22max113x x x ⎛⎫-+= ⎪-+⎝⎭,所以3m ≥点睛:本题主要考查了含有参数的一元二次不等式的解法,考查了分类讨论的思想以及转化与化归的能力,难度一般;对于含有参数的一元二次不等式常见的讨论形式有如下几种情形:1、对二次项系数进行讨论;2、对应方程的根进行讨论;3、对应根的大小进行讨论等;考查恒成立问题,正确分离参数是关键,也是常用的一种手段.通过分离参数可转化为()a h x >或()a h x <恒成立,即()max a h x >或()min a h x <即可,利用导数知识结合单调性求出()max h x 或()min h x 即得解.。
黑龙江省数学普高2019-2020学年文数第一次诊断性考试试卷

黑龙江省数学普高2019-2020学年文数第一次诊断性考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共12分)1. (1分)已知集合,则()A .B .C .D .2. (1分)复数(是虚数单位)在复平面内对应的点是位于()A . 第一象限B . 第二象限C . 第三象限D . 第四象限3. (1分) (文科)若为等差数列,是其前n项的和,且,则()A .B .C .D .4. (1分) (2017高二下·营口会考) sin300°等于()A . ﹣B .C . ﹣D .5. (1分) (2018高一下·新乡期末) 向边长为1的正方形内随机投入粒芝麻,假定这些芝麻全部均匀地落入该正方形中,发现有粒芝麻离点的距离不大于1,则用随机模拟的方法得到的圆周率的近似值为()A .B .C .D .6. (1分)某程序框图如图所示,该程序运行后输出的结果为()A . 7B . 6C . 5D . 47. (1分) (2019高二上·滦县月考) 已知命题,则的()A . 充分不必要条件B . 既不充分也不必要条件C . 充要条件D . 必要不充分条件8. (1分) (2020高一下·驻马店期末) 有以下变换方式:①先向右平移个单位长度,再将每个点的横坐标缩短为原来的倍;②先向左平移个单位长度,再将每个点的横坐标伸长为原来的2倍;③先将每个点的横坐标伸长为原来的2倍,再向左平移个单位长度;④先将每个点的横坐标缩短为原来的倍,再向右平移个单位长度.其中能将函数的图像变为函数的图像的是()A . ①和④B . ①和③C . ②和④D . ②和③9. (1分)已知A、B、C是单位圆上三个互不相同的点.若,则的最小值是()A . 0B .C .D .10. (1分)已知f(x)是实数集上的偶函数,且在区间上是增函数,则,,的大小关系是()A .B .C .D .11. (1分)已知正三棱锥P-ABC的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为()A . 4πB . 12πC .D .12. (1分) (2020高一上·利辛期中) 如图,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分种上草坪,使草坪的面积不小于300m2.设道路宽为xm,根据题意可列出的不等式为()A .B .C .D .二、填空题 (共3题;共3分)13. (1分) (2017高一下·上饶期中) 已知cos(﹣α)= ,则sin(﹣α)=________.14. (1分)已知一个容量为80的样本,把它分为6组,第三组到第六组的频数分别为10,12,14,20,第一组的频率为0.2,那么第一组的频数是________;第二组的频率是________.15. (1分) (2019高一上·石家庄月考) 如图是某公共汽车线路收支差额元与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图上点、点以及射线上的点的实际意义,用文字说明图方案是________,图方案是________.三、解答题 (共7题;共14分)16. (2分)(2019·深圳模拟) 如图,在平面四边形中,与为其对角线,已知,且.(1)若平分,且,求的长;(2)若,求的长.17. (2分)(2019·乌鲁木齐模拟) 某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知100人中同意父母生“二孩”占60%,统计情况如下表:同意不同意合计男生a5女生40d合计100(1)求 a , d 的值,根据以上数据,能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;(2)将上述调查所得的频率视为概率,现在从所有学生中,采用随机抽样的方法抽取4 位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为 X ,求 X 的分布列及数学期望.附:0.150.1000.0500.0250.0102.072 2.7063.841 5.024 6.63518. (2分)(2020·广东模拟) 在公差为2的等差数列中,,,成等比数列.(1)求的通项公式;(2)求数列的前项和 .19. (2分)(2017·成安模拟) 如图所示,在四棱锥P﹣ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.(1)证明:直线MN∥平面PCD;(2)若点Q为PC中点,∠BAD=120°,PA= ,AB=1,求三棱锥A﹣QCD的体积.20. (2分)(2020·广州模拟) 已知函数.(1)求函数在上的单调区间;(2)用表示中的最大值,为的导函数,设函数,若在上恒成立,求实数的取值范围;(3)证明:.21. (2分)(2019·山西模拟) 在平面直角坐标系中,曲线的参数方程为(为参数).以为极点,轴的正半轴为极轴,建立极坐标系 .(1)求曲线的极坐标方程;(2)已知是曲线上任意两点,且,求面积的最大值.22. (2分) (2016高三上·湖北期中) 已知f(x)=|x﹣1|﹣|2x+3|.(1)解不等式f(x)>2;(2)关于x的不等式f(x)≤ a2﹣a的解集为R,求a的取值范围.参考答案一、单选题 (共12题;共12分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共3题;共3分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:三、解答题 (共7题;共14分)答案:16-1、答案:16-2、考点:解析:答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、答案:20-3、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、考点:解析:。
【精准解析】黑龙江省佳木斯市一中2019-2020学年高一下学期第一学段检测语文试题

佳木斯一中2019—2020学年度第二学期第一学段考试高一语文试题(时间:150分钟总分:150分)命题人:审题人:Ⅰ卷阅读题(共81分)一.论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成小题文艺是一种表现而不是一种卖弄。
表现的理想是文情并茂,“充实而有光辉”,虽经苦心雕琢,却是天衣无缝,自然熨贴,不现勉强作为痕迹。
一件完美的艺术品像一个大家闺秀,引人注目而却不招邀人注目,举止大方之中仍有她的贞静幽闲,有她的高贵的身份。
艺术和人一样,有它的品格,我们常说某种艺术品高,某种艺术品低,品的高低固然可以在多方面见出,最重要的仍在作者的态度。
品高的是诚于中,形于外,表里如一的高华完美。
品低的是内不充实而外求光辉,存心卖弄,像小家娼妇涂脂抹粉,招摇过市,眉挑目送的样子。
文艺的卖弄有种种方式。
最普遍的是卖弄词藻,只顾堆砌漂亮的字眼,显得花枝招展,绚烂夺目,不管它对于思想情感是否有绝对的必要。
从前骈俪文犯这毛病的最多,现在新进作家也有时不免。
其次是卖弄学识。
文艺作者不能没有学识,但是他的学识须如盐溶解在水里,尝得出味,指不出形状。
有时饱学的作者无心中在作品中流露学识,我们尚不免有“学问汩没性灵”之感,至于有意要卖弄学识,如暴发户对人夸数家珍,在寻常人如此已足见趣味低劣,在文艺作品中如此更不免令人作呕了。
过去中国文人犯这病的最多,在诗中用僻典,谈哲理,写古字,都是最显著的例。
新文学作家常爱把自己知道比较清楚的材料不分皂白地和盘托出,不管它是否对于表现情调、描写人物或是点明故事为绝对必需,写农村就把农村所有的东西都摆进去,写官场也就把官场所有的奇形怪状都摆进去,有如杂货店,七零八落的货物乱堆在一起,没有一点整一性,连比较著名的作品如赛珍珠的《大地》,吴趼人的《二十年来目睹之怪现状》之类均不免此病,这也还是卖弄学识。
第三是卖弄才气。
文艺作者固不能没有才气,但是逞才使气,存心炫耀,仍是趣味低劣。
像英国哲学家休谟和法国诗人魏尔兰所一再指示的,文学不应只有“雄辩”(eloquence),而且带不得雄辩的色彩。
2019-2020学年黑龙江省佳木斯市第一中学高一下学期第一学段考试数学(理)试题(解析版)

2019-2020学年黑龙江省佳木斯市第一中学高一下学期第一学段考试数学(理)试题一、单选题1.数列1,-3,5,-7,9,…的一个通项公式为( ) A .21n a n =- B .(1)(21)nn a n =--C .(1)(12)nn a n =-- D .(1)(21)nn a n =-+【答案】C【解析】观察,奇偶相间排列,偶数位置为负,所以为1(1)n +-,数字是奇数,满足2n-1,所以可求得通项公式. 【详解】由符号来看,奇数项为正,偶数项为负,所以符号满足1(1)n +-,由数值1,3,5,7,9…显然满足奇数,所以满足2n-1,所以通项公式 为1(1)(21)n n a n +=--,选C.【点睛】本题考查观察法求数列的通项公式,解题的关键是培养对数字的敏锐性,属于基础题. 2.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cosC 等于 ( ) A .23B .23-C .13-D .14-【答案】D 【解析】【详解】解:由正弦定理可得;sinA :sinB :sinC=a :b :c=2:3:4 可设a=2k ,b=3k ,c=4k (k >0)由余弦定理可得,cosC=1-4,选D 3.已知集合2{|430}A x x x =-+<,{|24}B x x =<<,则A B =( )A .(1,3)B .(1,4)C .(2,3)D .(2,4)【答案】C【解析】根据一元二次不等式的解法,可得集合A ,然后根据交集的概念,可得结果. 【详解】由()()2430130x x x x -+<⇒--<所以13x <<,所以()1,3A =又(){|24}2,4B x x =<<=,所以(2,3)A B ⋂= 故选:C 【点睛】本题考查一元二次不等式的解法,记住口诀“大于取两边,小于取中间”,还考查集合之间的运算,属基础题.4.在等差数列{}n a 中,若45615a a a ++=,则28a a +=( ) A .6 B .10C .7D .5【答案】B【解析】根据等差数列的性质,可得5a ,然后由2852a a a +=,简单计算结果. 【详解】由题可知:456553155++==⇒=a a a a a 又2852a a a +=,所以2810a a += 故选:B 【点睛】本题主要考查等差数列的性质,若m n p q +=+,则m n p q a a a a +=+,考验计算,属基础题.5.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思是“有一个人走378里,第一天健步行走,从第二天起脚痛每天走的路程是前一天的一半,走了6天后到达目的地.”请问第三天走了( ) A .60里 B .48里C .36里D .24里【答案】B【解析】根据题意得出等比数列的项数、公比和前n 项和,由此列方程,解方程求得首项,进而求得3a 的值. 【详解】依题意步行路程是等比数列,且12q =,6n =,6378S =,故16112378112a ⎛⎫- ⎪⎝⎭=-,解得1192a =,故2311192484a a q ==⨯=里.故选B. 【点睛】本小题主要考查中国古典数学文化,考查等比数列前n 项和的基本量计算,属于基础题. 6.已知数列{}n a 满足11a =,11nn n a a a +=+,则数列{}1n n a a +的前10项和10S =( ) A .1011B .910 C .1112D .1213【答案】A【解析】变换得到1111n na a +=+,设1n nb a =得到{}n b 是首项为1,公差为1的等差数列,故1n a n=,再利用裂项相消法求和. 【详解】11n n n a a a +=+,易知0n a ≠,故11111n n n n a a a a ++==+, 设1n nb a =,则11n n b b +-=,1111b a ==,故{}n b 是首项为1,公差为1的等差数列,故n b n =,1n a n=,()111111n n a a n n n n +==-++,故1011111101 (223101111)S =-+-++-=. 故选:A. 【点睛】本题考查了构造法求通项公式,裂项相消法求和,意在考查学生对于数列公式方法的综合应用.7.已知等差数列{}n a 的公差d >0,则下列四个命题: ①数列{}n a 是递增数列; ②数列{}n S 是递增数列; ③数列n a n ⎧⎫⎨⎬⎩⎭是递增数列; ④数列n S n ⎧⎫⎨⎬⎩⎭是递增数列.其中正确命题的个数为( ) A .1B .2C .3D .4【答案】B【解析】根据等差数列的通项公式和前n 项和公式,结合数列的通项公式的函数性质进行求解即可. 【详解】①:因为数列{}n a 是等差数列, 所以11(1)n a a n d nd a d =+-=+-, 因此可以把n a 看成关于n 的一次函数,而0d >,所以数列{}n a 是递增数列,因此本命题是真命题; ②:因为数列{}n a 是等差数列, 所以211111(1)(2)222n S na n n d n d n a d =+-=+-, 因此可以把n S 看成关于n 的二次函数,而二次函数的单调性与开口和对称轴有关, 虽然0d >能确定开口方向,但是不能确定对称轴的位置,故不能判断数列{}n S 的单调性,故本命题是假命题; ③:因为数列{}n a 是等差数列, 所以11(1)n a a n d nd a d =+-=+-,设n n a b n =,因此数列n a n ⎧⎫⎨⎬⎩⎭的通项公式为:1n n a a d b d n n -==+,显然当1a d =时,数列n a n ⎧⎫⎨⎬⎩⎭是常数列,故本命题是假命题; ④:因为数列{}n a 是等差数列, 所以211111(1)(2)222n S na n n d n d n a d =+-=+-, 设n n S c n =,因此数列n S n ⎧⎫⎨⎬⎩⎭的通项公式为111(2)22n n S c nd a d n ==+-, 所以可以把n c 看成关于n 的一次函数,而102d >,所以数列n S n ⎧⎫⎨⎬⎩⎭是递增数列,因此本命题是真命题. 故选:B 【点睛】本题考查了等差数列的通项公式和前n 项和公式的应用,考查了利用数列的函数性质判断数列的单调性,考查了推理论证能力和数学运算能力.8.对于任意实数a b c d ,,,,下列正确的结论为( ) A .若,0a b c >≠,则ac bc >; B .若a b >,则22ac bc >; C .若a b >,则11a b <; D .若0a b <<,则b a a b<. 【答案】D【解析】根据不等式的基本性质,结合举特例、作差比较法进行求解即可. 【详解】A :根据不等式的基本性质可知:只有当0c >时,才能由a b >推出ac bc >,故本选项结论不正确;B :若0c时,由a b >推出22ac bc =,故本选项结论不正确;C :若3,0a b ==时,显然满足a b >,但是1b没有意义,故本选项结论不正确; D :22()()b a b a b a b a a b ab ab-+--==,因为0a b <<,所以0,0,0b a ab a b ->>+<, 因此0b a b aa b a b-<⇒<,所以本选项结论正确. 故选:D 【点睛】本题考查了不等式的基本性质的应用,考查了作差比较法的应用,属于基础题. 9.下列命题中,不正确的是( ) A .在ABC ∆中,若A B >,则sin sin A B > B .在锐角ABC ∆中,不等式sin cos A B >恒成立C .在ABC ∆中,若60B =︒,2b ac =,则ABC ∆必是等边三角形D .在ABC ∆中,若cos cos a A b B =,则ABC ∆必是等腰三角形 【答案】D【解析】A :根据三角形大角对大边的性质,结合正弦定理进行判断即可; B :根据锐角三角形的性质,结合正弦函数的单调性进行判断即可; C :利用余弦定理,结合等边三角形的判定方法进行判断即可;D :根据正弦定理,结合二倍角的正弦公式、正弦函数的性质进行求解即可. 【详解】A :在ABC ∆中,因为AB >,所以a b >,由正弦定理可知:sin sin A B >,故本命题是正确的;B :因为ABC ∆是锐角三角形,所以02C <<π,由三角形内角和定理可知;02A B ππ<--<,即有22A B A B ππ+>⇒>-,因为ABC ∆是锐角三角形,所以,A B 为锐角,因此可得:sin sin()cos 2A B B π>-=,故本命题是正确的;C :由余弦定理可知;2222cos b a c ac B =+-⋅,又因为60B =︒,2b ac =, 所以有:2222220()0ac a c ac a c ac a c a c =+-⇒+-=⇒-=⇒=,因此ABC ∆是等腰三角形,而60B =︒,所以ABC ∆是等边三角形,故本命题是正确的; D :由正弦定理可知;sin sin a bA B=,而cos cos a A b B =, 所以有11sin cos sin cos sin 2sin 2sin 2sin 222A AB B A B A B =⇒=⇒=, ,(0,)2,2(0,2)A B A B ππ∈∴∈,于是有22A B =或22A B π+=,即A B =或2A B π+=,所以ABC ∆是等腰三角形或直角三角形,因此本命题不正确. 故选:D 【点睛】本题考查了正弦定理和余弦定理的应用,考查了二倍角正弦公式的应用,考查了正弦函数的性质,考查了数学运算能力.10.在ABC 中,已知a x =cm ,2b =cm ,45B =︒,如果利用正弦定理解三角形有两解,则x 的取值范围是( ) A.2<x B.2<x ≤C .2x >D .<2x【答案】A【解析】先由正弦定理,根据题意,得到sin A x =,再由三角形有两解,得到45135A <<︒,90A ≠︒,进而可求出结果.【详解】因为在ABC 中,a x =cm ,2b =cm ,45B =︒,所以,由正弦定理得sin sin a b A B=得:sin 2sin 24x a B A x b ⋅===,因为45B =︒, 所以0135A <<︒,要使三角形有两解,得到45135A <<︒,因此2sin 12A <≤; 又若90A =︒,此时只有一个解,不满足题意,所以2sin 12A <<, 即22124x <<,解得:2<<22x . 故选:A. 【点睛】本题主要考查由三角形解的个数求参数的问题,熟记正弦定理即可,属于常考题型. 11.已知数列{}n a 是等差数列,若91130a a +<,10110a a ⋅<,且数列{}n a 的前n 项和n S 有最大值,那么n S 取得最小正值时n 等于( ) A .20 B .17C .19D .21【答案】C【解析】试题分析:由等差数列的性质和求和公式可得10110,0a a ><又可得:而20101110()0S a a =+<,进而可得n S 取得最小正值时19n =.【考点】等差数列的性质12.如图,AD 是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔BD ,若某科研小组在坝底A 点测得15BAD ∠=,沿着坡面前进40米到达E 点,测得45BED ∠=,则大坝的坡角(DAC ∠)的余弦值为( )A .31B 31- C 21D .212【答案】A【解析】由15BAD ∠=,45BED ∠=,可得30ABE ∠=,在ABE ∆中,由正弦定理得20BE =,在BED ∆中,由正弦定理得sin 1BDE ∠=,进而由()sin sin 90BDE DAC ∠=∠+可得结果.【详解】因为15BAD ∠=,45BED ∠=,所以30ABE ∠=.在ABE ∆中,由正弦定理得sin 30sin15AE BE=,解得20BE =.在BED ∆中,由正弦定理得sin sin 45BE BDBDE =∠,所以202sin 120BDE ⨯∠==.又90ACD ∠=,所以()sin sin 90BDE DAC ∠=∠+,所以cos 1DAC ∠=. 故选A . 【点睛】本题考查正弦定理解三角形,考查诱导公式,考查学生合理进行边角转化的能力,属于中档题.二、填空题13.设n S 为等比数列{}n a 的前n 项和,4727a a =,则63S S =_________. 【答案】2827【解析】根据已知求出等比数列的公比,再由等比数列的前n 项和公式,即可求解. 【详解】设等比数列{}n a 的公比为q , 根据题意,有3127q =,解得13q =, 则()()6136331128112711a q S q q S a q q--==+=--.故答案为:2827. 【点睛】本题考查等比数列的前n 项和,考查计算求解能力,属于基础题.14.在数列{}n a 中,13a =,12nn n a a +=+,则n a =__________.【答案】21n +.【解析】根据题意分析,递推公式满足累加法形式,运用累加法计算,即可求解通项公式. 【详解】由12n n n a a +=+,得12nn n a a +-=,由累加法可得211222n n a a --=++⋯+=()12122212n n --=--,21n n a ∴=+.故答案为:21n + 【点睛】本题考查由递推关系求通项公式,考查累加法,属于基础题. 15.在锐角三角形ABC 中,2A B =,则ABAC的取值范围是______. 【答案】()1,2【解析】锐角三角形ABC 中,角,,A B C 都是锐角,求出角B 的取值范围.由正弦定理可得sin sin 3sin sin AB C B AC B B==,把sin3B 展开,即求ABAC 的取值范围.【详解】锐角ABC 中,020202A B C πππ⎧<<⎪⎪⎪<<⎨⎪⎪<<⎪⎩,即02202032B B B ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩,64B ππ∴<<.在ABC 中,由正弦定理sin sin AB ACC B=, 可得()()sin 3sin 2sin sin 3sin cos 2cos sin 2sin sin sin sin sin B B B AB C B B B B BAC B B B B Bπ-++=====()2234sin sin 34sinsin B B B B-==-,2111,sin sin ,642242B B B ππ⎛⎫<<∴<<∴∈ ⎪⎝⎭, ()234sin 1,2B ∴-∈,即()1,2ABAC∈. 故答案为:()1,2. 【点睛】本题考查正弦定理、两角和的正弦公式、二倍角公式,属于较难的题目.16.设实数,x y 满足2238,49x xy y ≤≤≤≤,则34xy的最大值是_______. 【答案】27【解析】根据不等式的性质用配凑法可求34x y的最大值.【详解】由题设可知,x y 为正数,设()2324ba x xy y x y ⎛⎫ ⎪⎝⎭=,则3242ab b a =+⎧⎨=-⎩,故12a b =-⎧⎨=⎩.故()232421x xy y x y -⎛⎫ ⎪⎝⎭= ∵238xy ≤≤,249x y≤≤, ∴221681x y ⎛⎫≤≤ ⎪⎝⎭,211183xy ≤≤, ∴[]2212,27x y xy⎛⎫⋅∈ ⎪⎝⎭,∵()232124x x xy y y -⎛⎫=⋅ ⎪⎝⎭,∴[]342,27x y∈即最大值为27.【点睛】本题考查不等式性质的应用,当已知代数式和目标代数式之间的关系难以寻觅时,可以用待定系数法(配凑法)来整合,本题属于中档题.三、解答题17.已知等比数列{}n a 各项都是正数,其中3a ,23a a +,4a 成等差数列,532a =. (1)求数列{}n a 的通项公式;(2)设2n n b a n =+, 数列{}n b 的前n 项和为n S ,求5S .【答案】(1)2nn a =;(2)92.【解析】(1)根据等比数列的通项公式,结合等差数列的性质进行求解即可; (2)结合(1)求出数列{}n b 的通项公式,根据等差数列和等比数列的前n 项和公式进行求解即可. 【详解】(1)设等比数列{}n a 的公比为q ,因为等比数列{}n a 各项都是正数,所以有10,0a q >>,因为3a ,23a a +,4a 成等差数列,所以有34232432(0)2a a a a a a a =⇒--++=,于是有3211120a q a q a q --=,而10,0a q >>,解得2q,又因为532a =,所以4132a q =,而2q ,所以12a =,因此数列{}n a 的通项公式为:2nn a =;(2)由(1)可知;2nn a =,所以22n n b n =+,25255221222225(222)2(125)S =+⨯++⨯+++⨯=+++++++根据等差数列和等比数列的前n 项和公式可得;552(12)(15)5292122S -+⨯=+⨯=-.【点睛】本题考查了等差数列和等比数列的前n 项和公式的应用,考查了等比数列通项公式的应用,考查了等差数列的性质,考查了数学运算能力.18.ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知2cos (cos cos )C a B b A c +=.(1)求角C ;(2)若c =ABC S ∆=,求ABC ∆的周长.【答案】(1)3C π=(2)5【解析】【详解】试题分析:(1)根据正弦定理把2cos (cos cos )C a B b A c +=化成2cos (sin cos sin cos )sin C A B B A C +=,利用和角公式可得1cos ,2C =从而求得角C ;(2)根据三角形的面积和角C 的值求得6ab =,由余弦定理求得边a 得到ABC ∆的周长.试题解析:(1)由已知可得2cos (sin cos sin cos )sin C A B B A C +=12cos sin()sin cos 23C A B C C C π∴+=⇒=⇒=(2)11sin 622ABC S ab C ab ab ∆=⇒=⇒= 又2222cos a b ab C c +-=2213a b ∴+=,2()255a b a b ∴+=⇒+=ABC ∆∴的周长为5+【考点】正余弦定理解三角形.19.已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,若22(sin sin )sin sin sin B C A B C -=-.(1)求A ;(2)求sin sin B C +的取值范围.【答案】(1)3π;(2). 【解析】(1)利用正弦定理和余弦定理进行求解即可;(2)利用两角差的正弦公式和辅助角公式,结合正弦函数的性质进行求解即可. 【详解】(1)22222(sin sin )sin sin sin sin sin sin sin sin B C A B C B C B C A -=-⇒+-=,根据正弦定理可化简为:222b c bc a +-=,由余弦定理可知:2222cos a b c bc A =+-⋅,因此有1cos 2A =, ()0,,3A A ππ∈∴=;(2)由(1)可知:3A π=,由三角形内角和定理可知:23C B π=-,23sin sin sin sin()sin )326B C B B B B B ππ+=+-==+,25(0,),()(,)3666B B ππππ∈∴+∈, 因此有1sin()(,1])626B B ππ+∈+∈,因此sin sin B C +的取值范围为. 【点睛】本题考查了正弦定理和余弦定理的应用,考查了三角式的取值范围问题,考查了正弦函数的值域问题,考查了辅助角公式的应用,考查了数学运算能力.20.已知数列{}n a 中,12a =且*122(2,)n n a a n n n N -=-+≥∈.(1)证明{}n a n -是等比数列;(2)设12nn n a b -=,求数列{}n b 的前n 项和n S . 【答案】(1)详见解析;(2)1242n n nS n -+=+-.【解析】(1)根据所求数列的形式,对已知的递推公式进行恒等变形,结合等比数列的定义进行证明即可;(2)结合(1)求出数列{}n b 的通项公式,利用分组求数列和的方法,结合错位相减法进行求解即可. 【详解】(1)由已知()*1222,n n a a n n n N-=-+≥∈可得:24a =,37a =,1222n n a n a n --=-+,即()121n n a n a n -⎡⎤-=--⎣⎦,因为()()*122,1n n a nn n N a n --=≥∈--,又因为111a -=,所以{}n a n -是以1为首项,2为公比的等比数列.(2)由(1)得()1112n n a n a --=-⋅,即12n n a n -=+,所以11122n n n n a nb --==+, 设12n n nC -=,且前n 项和为n T ,所以01231123422222n n nT -=+++++,①123112322222n nnT =++++, ② ①-②得:12311111111122112122222222212n n n n n n n n n T ---+⎛⎫=+++++-=+⋅-=-⎪⎝⎭-所以1242n n nT -+=-, 因此1242n n nS n -+=+-.【点睛】本题考查了由递推公式证明数列是等比数列,考查了利用分组求和法求数列和问题,考查了错位相减法的应用,考查了数学运算能力. 21.已知数列{}n a 满足:()()123141236n n n n a a a na +-++++=,n *∈N .(1)求数列{}n a 的通项公式; (2)设11n n n b a a +=⋅,数列{}n b 的前n 项和n T ,求证:12n T <.【答案】(1)21n a n =-(n *∈N ).(2)证明见解析 【解析】(1)根据题意,可得()()()123114112316n n n n a a a n a ----⎡⎤⎣⎦+++⋅⋅⋅+-=,两者相减,即可得到数列{}n a 的通项公式, (2)由(1)得()()1112121n n n b a a n n +==⋅-+,利用裂项相消求出n T ,从而可证12n T <【详解】(1)由已知得112316a ⨯⨯== 由()()123141236n n n n a a a na +-+++⋅⋅⋅+=,①得2n ≥时,()()()123114112316n n n n a a a n a ----⎡⎤⎣⎦+++⋅⋅⋅+-=,②①-②得()()()()()1411452166n n n n n n n na n n +---=-=-∴21n a n =-,11a =也适合此式,∴21n a n =-(n *∈N ). (2)由(1)得21n a n =-,∴()()111111212122121n n n b a a n n n n +⎛⎫===- ⎪⋅-+-+⎝⎭∴111111111123352121221n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+-=- ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ∵*n N ∈,∴1021n >+ ∴12n T <【点睛】本题考查数列的递推,考查数列的通项与求和,考查数列求和方法中的裂项相消,属于中档题。
2019-2020学年黑龙江省佳木斯市新高考高一数学下学期期末检测试题

一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.过点A(3,3)且垂直于直线4270x y +-=的直线方程为 A .122y x =+ B .27y x =-+ C .1522y x =+ D .1322y x =+ 2.已知角α的终边经过点(4,3)-,则cos α=( ) A .45B .35C .35-D .45-3.已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是02,接下来的两项是012,2,再接下来的三项是0122,2,2,依此类推,记此数列为{}n a ,则2019a =( )A .1B .2C .4D .84.赵爽是三国时期吴国的数学家,他创制了一幅“勾股圆方图”,也称“赵爽弦图”,如图,若在大正方形内随机取-点,这一点落在小正方形内的概率为15,则勾与股的比为( )A .13B .12C .33D .225.在一次随机试验中,彼此互斥的事件A,B,C,D 的概率分别是0.1,0.2,0.3,0.4,则下列说法正确的是 A .A+B 与C 是互斥事件,也是对立事件B .B+C 与D 不是互斥事件,但是对立事件C .A+C 与B+D 是互斥事件,但不是对立事件 D .B+C+D 与A 是互斥事件,也是对立事件6.若各项为正数的等差数列{}n a 的前n 项和为n S ,且22640a a a +-=,则7S =( )A .9B .14C .7D .187.已知{}n a 是公差d 不为零的等差数列,其前n 项和为n S ,若348,,a a a 成等比数列,则 A .140,0a d dS >> B .140,0a d dS << C .140,0a d dS >< D .140,0a d dS <>8.已知,x y 都是正数,且211x y+=,则x y +的最小值等于 A .6 B .2 C .322+D .422+9.已知等比数列{a n }中,a 3•a 13=20,a 6=4,则a 10的值是( ) A .16B .14C .6D .510.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,60A =︒,43a =,4b =,则B =( )A .30B =︒或150B =︒ B .150B =︒C .30B =︒D .60B =︒11.设R a ∈,若不等式221148x x ax x x x++-+≥-恒成立,则实数a 的取值范围是( ) A .[2,12]-B .[2,10]-C .[4,4]-D .[4,12]-12.若函数()()12,1,1,1,x x f x f x x -⎧≤⎪=⎨->⎪⎩则20192f ⎛⎫= ⎪⎝⎭( )A .12B .2 C .2D .2-二、填空题:本题共4小题13.若无穷等比数列{}n a 的各项和等于21a ,则1a 的取值范围是_____.14.方程组210320x y x y +-=⎧⎨-=⎩对应的增广矩阵为__________.15.如图,在三棱锥A BCD -中,它的每个面都是全等的正三角形,P 是棱CD 上的动点,设()01CP tCD t =<<,分别记AP 与BC ,BD 所成角为α,β,则cos cos αβ+的取值范围为__________.16.不等式23710x x -≤的解集为______.三、解答题:解答应写出文字说明、证明过程或演算步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年黑龙江省佳木斯市第一中学高一下学期第一学段考试
文科数学试题
(时间:120分钟 总分:150分)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.数列1,-3,5,-7,9,…的一个通项公式为( ) A .21n a n =-
B .(1)(21)n
n a n =--
C .(1)(12)n n a n =--
D .(1)(21)n
n a n =-+
2.已知集合2{|430}A x x x =-+<,{|24}B x x =<<,则A B I =( ) A .(1,3) B .(1,4)
C .(2,3)
D .(2,4)
3.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cosC 等于 ( ) A .
2
3
B .23-
C .13
-
D .14
-
4.在等差数列{}n a 中,若45615a a a ++=,则28a a +=( ) A .6
B .10
C .7
D .5
5.《九章算术》教会了人们用等差数列的知识来解决问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织( )尺布.
A .12
B .
2429
C .
1631
D .
1629
6.设等比数列{}n a 的前n 项和为n S ,且639S S =,764a =,则1(a = ) A .1
B .2
C .3
D .4
7.已知等差数列{}n a 的公差d >0,则下列四个命题: ①数列{}n a 是递增数列; ②数列{}n S 是递增数列;
③数列n a n ⎧⎫
⎨⎬⎩⎭是递增数列; ④数列n S n ⎧⎫⎨⎬⎩⎭
是递增数列。
其中正确命题的个数为( )
A .1
B .2
C .3
D .4
8.对于任意实数a b c d ,,,,下列正确的结论为( ) A.若,0a b c >≠,则ac bc >; B.若a b >,则22ac bc >; C.若a b >,则
11
a b
<. D.若22ac bc >,则a b >; 9.下列命题中,不正确的是( ) A .在ABC ∆中,A B >,sin sin A B ∴> B .在锐角ABC ∆中,不等式sin cos A B >恒成立
C .在ABC ∆中,若060B =,2b ac =,则ABC ∆必是等边三角形
D .在ABC ∆中,若cos cos a A b B =,则ABC ∆必是等腰三角形
10.在△ABC 中,c =4,∠B =30°,若给出一个b 的值,使得此三角形有两解,则b 的一个可能值是( ) A .5
B.3
C .2
D .1
11.已知数列{}n a 是等差数列,若91130a a +<,10110a a ⋅<,且数列{}n a 的前n 项和n S 有最大值,那么n S 取得最小正值时n 等于( ) A 17
B .20
C .19
D .21
12.如图,AD 是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔BD ,若某科研小组在坝底A 点测得15BAD ∠=o ,沿着坡面前进40米到达E 点,测得45BED ∠=o ,则大坝的坡角(DAC ∠)的余弦值为( )
A .31
B 31
- C 21
D 21
-
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填写在题中的横线上) 13.已知数列{}n a 为等比数列,n S 是它的前n 项和,若2312a a a ⋅=,且4a 与72a 的等差中项为
5
4
,则4S =________. 14.已知数列{}n a 为等差数列,n S
是它的前n 项和 ,S n n n =++3212,则a n =_________.
15.在锐角三角形ABC 中,A=B ,则
AB
AC
的取值范围是_________. 16.已知R y x ∈,,-1 <x+y < 4, 2< x - y < 3, 则3x +2y 的取值范围是________.
三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤) 17.(本小题满分10分)
已知{}
2
680A x x x =-+≤,103x B x
x ⎧⎫-=>⎨⎬-⎩⎭
,{}4C x a x a =≤≤+. (1)求A B I ;
(2)若A C ⊆,求实数a 的取值范围. 18.(本小题满分12分)
ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .若sin cos a B A =. (1)求角A ;
(2)若ABC V 的面积为5a =,求b+c 的值 19. (本小题满分12分)
已知ABC ∆的内角C B A ,,的对边分别为c b a ,,,若C B A C B sin sin sin )sin (sin 22-=-. (1)求A ;
(2)求sin sin B C +的取值范围. 20.(本小题满分12分)
已知数列{}n a 满足111,21n n a a a +==+,数列{}n b 的前n 项的和为2
n S n =.
(1)证明数列
{}1+n a 是等比数列.
(2)设n n n c b a =⋅,求数列{}n c 的前n 项的和n T .
21. (本小题满分12分)
在公差为d 的等差数列{}n a 中,已知110a =,且123,22,5a a a +成等比数列. (Ⅰ)求n a ;
(2)若0d <,设2n n n
b a =+, 数列{}n b 的前n 项和为n S ,求5S .
22.(本小题满分12分)
已知函数2()(1)1f x m x mx m =+-+-(m R ∈)
(1)若不等式()0f x <的解集为∅,求m 的取值范围; (2)当2m >-时,解不等式()f x m ≥;
(3)若不等式()0f x ≥的解集为D ,若[11]
D -⊆,,求m 的取值范围. 佳一中2019-2020学年度第二学期第一学段考试
高一数学(文)答案
一CCDBB ABDDB CA 二13. 30; 14. {
N
n n n n a n ∈≥-==,2.161
.6
15. 15.(0.2)
16. 16.( 2
23
23,-) 三17.
18
19
(2)
)
6
sin(
3
sin
sin
π
+
=
+B
C
B⎥
⎦
⎤
⎝
⎛
∈1
2
3
,
20(1)略.
21(1)n a=4n+6或11-n (2)102
22。
