8个硬币怎么分横竖5个
人教版一年级数学上册《8和9的组成》课件 (3)
动手摆一摆 你分我数，并做好记录
9 ∧ 18 81
9可以分成1和8 还可以分成8和1
1和8组成9
9 ∧ 27 72
9可以分成2和7 还可以分成7和2
2和7组成9
9 ∧ 36 63
9可以分成3和6 还可以分成6和3
3和6组成9
9 ∧ 45
54
9可以分成4和5 还可以分成5和4
4和5组成9
我来说，你来做
人教版一年级上册第5单元
把8个苹果分给大头儿子和小头爸爸，你有几种分法？
两人一组，用你手里的学具摆 一摆吧！
8 ∧
17
71
8可以分成1和7
我还能想 到什么？
8还可以分成7和1
8
17
1和7组成8
8 ∧ 26 62
8可以分成2和6 还可以分成6和2
8
26
2和6组成8
8 ∧ 35
53
8可以分成3和5 还可以分成5和3
9 8
8
8
9
9
44
5
3
7
25 4
8
3
5
4
5
9
打地鼠
9
1
8
2
7
9
8
1762 Nhomakorabea8
5和4组成我
我去掉1是7
9
5
8
8是“3”和几 的好朋友
我是6和3的 好朋友
9
7
9可以分成2 和几
我要飞得更高
3
8
9
2
5
小朋友，今天你们有什么 收获和大家一起分享？
8
35
3和5组成8
8 ∧
44
8可以分成4和4
算法笔记_004：8枚硬币问题【减治法】
算法笔记_004：8枚硬币问题【减治法】⽬录1 问题描述（1）实验题⽬在8枚外观相同的硬币中，有⼀枚是假币，并且已知假币与真币的重量不同，但不知道假币与真币相⽐较轻还是较重。
可以通过⼀架天平来任意⽐较两组硬币，设计⼀个⾼效的算法来检测这枚假币。
（2）实验⽬的1）深刻理解并掌握减治法的设计思想并理解它与分治法的区别；2）提⾼应⽤减治法设计算法的技能。
3）理解这样⼀个观点：建⽴正确的模型对于问题的求解是⾮常重要的。
（3）实验要求1）设计减治算法实现8枚硬币问题；2）设计实验程序，考察⽤减治技术设计的算法是否⾼效；3）扩展算法，使之能处理n枚硬币中有⼀枚假币的问题。
（4）实现提⽰假设⽤⼀个数组B[n]表⽰硬币，元素B[i]中存放第i枚硬币的重量，其中n-1个元素的值都是相同的，只有⼀个元素与其他元素值不同，则当n=8时即代表8枚硬币问题。
由于8枚硬币问题限制只允许使⽤天平⽐较轻重，所以，算法中只能出现元素相加和⽐较的语句。
2 解决⽅案2.1 减治法原理叙述在说减法法原理之前，我们先来简单看看分治法原理：分治法是把⼀个⼤问题划分为若⼲⼦问题，分别求解⼦问题，然后再把⼦问题的解进⾏合并得到原问题的解。
⽽减治法同样是把⼤问题分解成为若⼲个⼦问题，但是这些⼦问题不需要分别求解，只需求解其中的⼀个⼦问题，也⽆需对⼦问题进⾏合并。
换种说法，可以说减治法是退化的分治法。
减治法原理正式描述：减治法（reduce and conquer method）将原问题的解分解为若⼲个⼦问题，并且原问题的解与⼦问题的解之间存在某种确定关系，如果原问题的规模为n，则⼦问题的规模通常是n/2 或n-1。
2.2 8枚硬币规模解法求解思路：（1）⾸先输⼊8枚硬币重量，存放在⼀个长度为8的⼀维数组中。
（2）定义a,b,c,d,e,f,g,h⼋个变量，分别对应⼀枚硬币的重量。
然后把这8枚硬币分成三组，分别为abc(abc = a+b+c)、def(def =d+e+f)、gh。
发明创造作业
练习1班级：姓名：学号：1.某君买了一盒每盘可燃1小时的蚊香，他想用这种蚊香计算45分钟，怎么计算呢7.有一个正方形的水池，水池四角靠近水面处各有一座小房子。
水池需要扩大，但仍要保持正方形。
房子不拆迁，水池扩大后四座房子要在原地，而且不能浸在水里，仍在水池岸边。
你能做到吗12. 有四副手套，大小、质量都完全相同，每副叠放在一起。
其中，两副是黑色的，两副是红色的。
这四副手套不规则地放在桌子上的不同位置，如果蒙住眼睛，你能准确地拿出一副黑色的和一副红色的手套吗写出方法。
74. 尽可能地列举出雨衣的缺点；95. 尽可能多地写出用“敲”的方法可以办成哪些事情或解决哪些问题；练习 2班级：姓名：学号：3.在8个同样大小的杯子中，有7杯盛的是凉开水，1杯盛的是白糖水。
你能否只品尝3次，就能找出盛有白糖水的杯子来吗13、横竖每排5个圆点，一共25个圆点。
如图所示连线，成十字型。
十字的外侧有4点，内侧留下5点。
如果要连成相同的十字形状，并且使外侧留有8点，内侧留有5点，该怎么连23．两女孩一同来到一所学校报名，她俩长得一模一样，出生年月日与父母的名字也完全相同。
当教师问她们：“你们是双胞胎吗”，她们却异口同声地回答说：“不是！”，她俩到底是什么关系67. 尽可能地列举出保暖瓶的缺点；102. 尽可能多地写出老王下班未回家的各种可能的原因；练习 3班级：姓名：学号：2.一个等腰三角形，其底边为10厘米，腰长为13厘米。
现在请你再画一个等腰三角形，腰长也为13厘米，底边变了，其面积仍与这个三角形相等。
你知道怎么画吗14、请你将图中这不规范的图形，分为形状、大小完全相同的5块，并使每块图形中都各有一个圆圈。
25．一辆满载货物的汽车要通过一座铁桥，通过时发现货物高于桥洞一厘米，现在问你，在不准卸货重装的情况下，能让车通过吗71. 尽可能多地写出玻璃瓶的各种用途；86. 尽可能多地设想利用味道可以做什么或办什么事；练习 4班级：姓名：学号：4.一位公安局长在茶馆里与一位老头下棋。
称硬币问题公式
称硬币问题公式几个常见的称硬币问题1．假设有4枚硬币，其中3枚是相同的，另外一枚看起来相同，但稍微轻一些。
现有一架天平，请试着找出假币，要求称量次数不超过2次。
【方案一】首先把四枚硬币进行编号1、2、3、4。
然后第一步：称量1——2，若二者不等，则较轻者为假币；若二者相等，则说明假币在3——4之中。
此时进行第二步：称量3——4，较轻者为假币。
【方案二】首先把四枚硬币进行编号1、2、3、4。
然后第一步：称量1、2——3、4，选出较轻的一边的两个硬币，接下来进行第二步：称量选出的两个硬币，较轻者为假币。
2．假设有4枚硬币，其中3枚是相同的，另外一枚看起来相同，但稍重或稍轻一些。
现有一架天平，请试着找出假币，要求称量次数不超过3次。
【解答】首先把四枚硬币进行编号1、2、3、4。
然后第一步：称量1、2——3、4，此时有两种结果，①1、2重量小于3、4②1、2重量大于3、4。
第二步：选择第一次称出的较轻的两枚硬币进行称量，若第二次称量结果不等，则说明假币在这两枚硬币之中且假币较轻，即第二次称量较轻者为假币，此时只需称量两次；若第二次称量结果相等，则假币在较重的两枚硬币之中，且假币较重。
这时需进行第三次称量，称量剩下的两枚硬币，选出较重者即为假币。
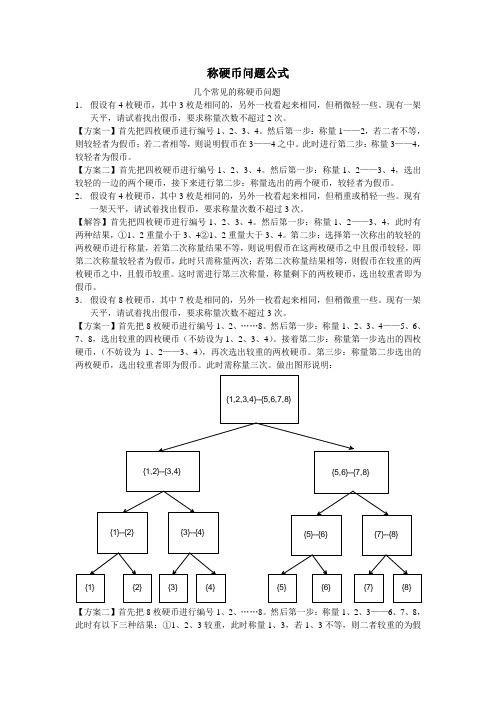
3．假设有8枚硬币，其中7枚是相同的，另外一枚看起来相同，但稍微重一些。
现有一架天平，请试着找出假币，要求称量次数不超过3次。
【方案一】首先把8枚硬币进行编号1、2、……8。
然后第一步：称量1、2、3、4——5、6、7、8，选出较重的四枚硬币（不妨设为1、2、3、4）。
接着第二步：称量第一步选出的四枚硬币，（不妨设为1、2——3、4），再次选出较重的两枚硬币。
第三步：称量第二步选出的两枚硬币，选出较重者即为假币。
此时需称量三次。
做出图形说明：【方案二】首先把8枚硬币进行编号1、2、……8。
然后第一步：称量1、2、3——6、7、8，此时有以下三种结果：①1、2、3较重，此时称量1、3，若1、3不等，则二者较重的为假币，否则若1,3相等，则2为假币②6、7、8较重，此时称量6、8，若6、8不等，则二者较重的为假币，否则若6,8相等，则7为假币③1、2、3等于6、7、8，则假币在4,5之中，此时称量4、5，选出较重者即为假币。
八枚硬币的判定树
树的应用举例——八枚硬币问题设有八枚硬币，分别表示为a，b，c，d，e，f，g，h，其中有且仅有一枚硬币是假币，并且假币的重量与真币的重量不同，可能轻，也可能重。
现要求以天平为工具，用最少的比较次数挑选出假币，并同时确定这枚假币的重量比其它真币是轻还是重。
问题的解决是经过一系列的判断，这些判断构成了树结构，可以用判定树来描述这个判定过程。
解决这个问题的最自然的想法就是把硬币分成两组，也就是一分为二。
但是，如果一分为三的话，会获得更少的比较次数。
从八枚硬币中任取六枚a，b，c，d，e，f，在天平两端各放三枚进行比较。
假设a，b，c三枚放在天平的一端，d，e，f三枚放在天平的另一端，可能出现三种比较结果：⑴a＋b＋c > d＋e＋f⑵a＋b＋c＝d＋e＋f⑶a＋b＋c < d＋e＋f若a＋b＋c >d＋e＋f，可以肯定这六枚硬币中必有一枚为假币，同时也说明，为真币。
这时可将天平两端各去掉一枚硬币，假设去掉和，同时将天平两端的硬币各换一枚，假设硬币，作了互换，然后进行第二次比较，比较的结果同样可能有三种：①a＋e>d＋b：这种情况表明天平两端去掉硬币c，f且硬币b，e互换后，天平两端的轻重关系保持不变，从而说明了假币必然是a，d中的一个，这时我们只要用一枚真币（例如h）和a进行比较，就能找出假币。
若a>h，则a是较重的假币；若a＝h，则d为较轻的假币；不可能出现a②a＋e＝d＋b：此时天平两端由不平衡变为平衡，表明假币一定在去掉的两枚硬币c，f中，同样用一枚真币（例如h）和c进行比较，若c>h，则c是较重的假币；若c＝h，则f为较轻的假币；不可能出现c③a＋e：此时表明由于两枚硬币b，e的对换，引起了两端轻重关系的改变，那么可以肯定b或e中有一枚是假币，同样用一枚真币（例如h）和b进行比较，若b>h，则b是较重的假币；若b＝h，则e为较轻的假币；不可能出现b 对于结果⑵和⑶的情况，可按照上述方法作类似的分析。
小学奥数整数拆分的要点及解题技巧
【导语】数学给予⼈们的不仅是知识，更重要的是能⼒，这种能⼒包括观察实验、收集信息、归纳类⽐、直觉判断、逻辑推理、建⽴模型和精确计算。
这些能⼒和培养，将使⼈终⾝受益。
以下是整理的相关资料，希望对您有所帮助。
【篇⼀】 ⼀、概念：把⼀个⾃然数(0除外)拆成⼏个⼤于0的⾃然数相加的形式。
⼆、类型----⽅法 1、基本型 2、造数型 3、求加数最多 ⽅法：1+2+3+……接近结果但是不超过已知数为⽌，再补差 4、两数型 (1)和不变：差⼩积⼤，差⼤积⼩ (2)积不变：差⼤和⼤，差⼩和⼩ 5、拆数型 积(1)允许相同：多3少2没有1 (2)不允许相同：从2连续拆分2+3+4+……刚好超过⽬标数为⽌ 1)超⼏就去⼏ 2)多1去2，差1补尾【篇⼆】 例题 例1、若⼲只同样的盒⼦排成⼀列，⼩明把42个同样的⼩球放在这些盒⼦⾥然后外出，⼩聪从每只盒⼦⾥取出⼀个⼩球，然后把这些⼩球放到⼩球最少的盒⼦⾥去，在把盒⼦从新排列了⼀下。
⼩明回来，仔细查看，没有发现友⼈动过⼩球和盒⼦。
问：⼀共有多少只盒⼦? 分析：设原来⼩球数最少的盒⼦⾥装有a只⼩球，现在增加到了b只，但⼩明发现没有⼈动过⼩球和盒⼦，这说明现在⼜有了⼀只装有a个球的盒⼦，这只盒⼦原来装有a+1个⼩球， 同理，现在另有⼀个盒⼦⾥装有a+1个⼩球，这只盒⼦⾥原来装有a+2个⼩球。
依此类推可知：原来还有⼀个盒⼦⾥装有a+3个⼩球，a+4个⼩球等等，故原来那些盒⼦⾥装有的⼩球数是⼀些连续⾃然数。
现在这个问题就变成了：将42分拆成若⼲个连续整数的和，⼀共有多少种分法，每⼀种分法有多少个加数? 因为42=6×7，故可将42看成7个6的和，⼜： (7+5)+(8+4)+(9+3) 是六个6，从⽽： 42=3+4+5+6+7+8+9 ⼀共有7个加数;⼜因为42=14×3，可将42写成13+14+15，⼀共有3个加数; ⼜因为42=21×2，故可将42写成9+10+11+12，⼀共有4个加数。
小学一年级奥数题及答案
小学一年级奥数题及答案1.图形的变化规律在下图的一组图形中，“？”处应填什么样的图形？答案：解析：仔细视察可发觉，第一行和第二行中的最右边的完全图形是这样变来的：将最左边的半个图形，往右平移到中间图形位置，然后再去掉两个图形的重合部分。
按这个规律可知“？”处就填：2.图形的等份划分在下图中画一条直线，把图形分成形状相同、大小相等的两部分。
答案：解析：图中共有18个正方形小格，若分成大小相等的两部分时，每一部分应包含有9个正方形小格。
还可以看出，此图中有一条"斜线"边沿酒囊饭袋。
经尝试可做出如虚线所示的划分。
3.找数字规律按规律填数：15、11、13、13、11、15、9、17、7、（）、（）、21、3 。
答案：两个空里面应当填19、5 。
解析：这一排数的规律应当一个数隔一个数来看，分成两组顺次为：15、13、11、9、7、……11、13、15、17、……所以两个空里面应当填19、5 。
4.猜猜他几岁？小亮今年7岁，爸爸比他大30岁，三年前爸爸是多少岁？答案：37－3=34（岁）答：三年前爸爸是34岁。
解析：由于爸爸比小亮大30岁，所以爸爸今年有30＋7=37（岁），因此三年前爸爸的年龄：37－3=34（岁）。
5.填数字运算在下面的○中填上数字，使得每一条线上的三个○中的数字加起来都等于15答案：6、9、5 。
解析：由于每条线上的三个○里的数之和都等于15，所以要求第三个数，就必须用15减去已知的两个数的和。
因此，第一个○中应当填15－8－1=6 ；第二个○中应当填15－2－4=9 ；第三个○中应当填15－3－7=5 。
6.找规律画图试一试，把图中的形状连续画下去○△□□□○△□□□。
答案：○△□□□○△□□□……解析：通过视察可以发觉，图中的图形由○△□□□五个一组循环的不停显现，因此在后面应当连续是这五个图形交替显现的。
7.数线段答案：有三条线段。
解析：①我们先数单独线段，图中一共有两条。
实用的数学日记范文集锦10篇
实用的数学日记范文集锦10篇数学日记篇120某某年11月14日星期日天气：晴斀裉彀晚，我和表姐在操场上玩，我们在操场边发现一张面积大约是一平方米的正方形废纸板，表姐看了看，说：”小婧，如果把这个纸板分割成一个个面积为一平方毫米的小正方形，再把这些小正方形一个紧挨一个的接成一条直线，这条直线会有多长呢？”我不假思索地脱口而出：”这能有多长，顶多不过四米吧！”表姐笑了笑说：”你先别急着下结论，让我们一起来算算吧。
”开始了片刻的思考：1平方米等于100平方分米，……平方毫米的正方形的边长就是毫米，那毫米不就是100米吗？哇！这条由一些一平方毫米的小正方形拼成的直线竟长达100米。
我明白学习数学不能只是简单地把题目看一看，就轻易的下结论，应该认真想、仔细算，才能做得对，并探究到其中的奥妙。
数学日记篇2今天上午，我们进行了一场惊悚的数学考试，几何学渣的我根本就是手忙脚乱，连该做的都忘了。
早晨，刚进教室，就很惊悚，教室里的空气是凝固的。
因为这次数学考试大家都没有底气，作业一般做得都很慢，有的还要想很长时间才会做,而这次20几道题要在一个小时完成，这就意味着一道题最多只能花3分钟，我们都心慌了.不知道这次考试的难易程度，更不知道自己这次会考的怎么样，怎么办？早自修铃声一大，孙老师就拿着考试卷走了进来---考试了。
开始考试了，我的心就像十五个吊桶打水七上八下的，有的题目就怕花的时间长还做得不对。
这是孟老师又进来说了一句‘‘最后一道附加题是当考试题目的，请控制好时间”这下子我们更慌了，怎么办？离考试快结束的时候，我还有3道题目没有写，还有三分钟了……“好，所有同学停笔，考试借宿了最后一个同学起来收一下试卷”听见这句话我可变成了敢死队的一员了，拼了命的写，但没有证明过程，写和不写也是一样的了。
刘煜轩无情地把试卷收走了，把我的分给收走了，我想哭但已经上课了，而且这次心理课还是我讲课，我只能强忍着哭，一步一步迈上了心理课的楼梯。