全等三角形的经典模型(一)
全等三角形基本模型综合训练(一)(解析版)
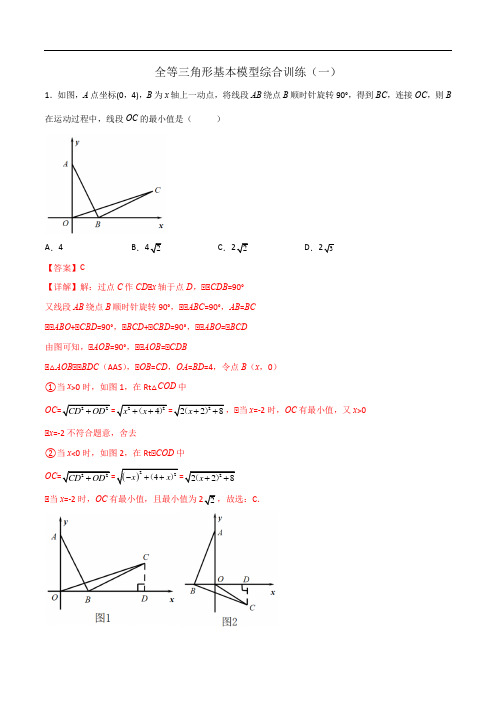
全等三角形基本模型综合训练(一)1.如图,A 点坐标(0,4),B 为x 轴上一动点,将线段AB 绕点B 顺时针旋转90°,得到BC ,连接OC ,则B 在运动过程中,线段OC 的最小值是( )A .4B .2C .2D .3【答案】C 【详解】解:过点C 作CD ⊥x 轴于点D ,⊥⊥CDB =90°又线段AB 绕点B 顺时针旋转90°,⊥⊥ABC =90°,AB =BC⊥⊥ABO +⊥CBD =90°,⊥BCD +⊥CBD =90°,⊥⊥ABO =⊥BCD由图可知,⊥AOB =90°,⊥⊥AOB =⊥CDB⊥△AOB ⊥⊥BDC (AAS ),⊥OB =CD ,OA =BD =4,令点B (x ,0)①当x >0时,如图1,在Rt △COD 中OC 22CD OD +224x x ++()2228x ++()⊥当x =-2时,OC 有最小值,又x >0⊥x =-2不符合题意,舍去②当x <0时,如图2,在Rt⊥COD 中OC 22CD OD +()224x x -++()2228x ++()⊥当x =-2时,OC 有最小值,且最小值为2,故选:C .2.如图,在ABC ∆中,40A ∠=︒,60C ∠=°,D 为AC 边上一点,DE BC ⊥于点E .若AD BD =,2BE =,则AB 的长为( )A 3B .2C .3D .4【答案】D【详解】解:如图,作DF ⊥AB 于点F ,⊥ AD =BD⊥△ADB 是等腰三角形,⊥ABD =⊥A =40°⊥AB =2AF =2BF⊥40A ∠=︒,60C ∠=°,⊥⊥ABC =180°-⊥A -⊥C =80°,⊥ ⊥DBE =⊥ABC -⊥ABD =40°⊥⊥DBE =⊥ABD⊥DE BC ⊥⊥ ⊥DE =DF⊥BD =BD⊥Rt △BDF ⊥Rt △BDE (HL )⊥BF =BE =2⊥AB =2BF =4,故选:D3.如图,Rt ABC ∆中,90C ∠=︒,AD 平分BAC ∠,交BC 于点D ,10AB =,15ABD S ∆=,则CD 的长为( )A .3B .4C .5D .6【答案】A 【详解】解:过点D 作DF ⊥AB 于点F ,⊥10AB =,15ABD S ∆=,⊥1152AB DF ⋅=,⊥110152DF ⨯=,得DF =3, ⊥90C ∠=︒,AD 平分BAC ∠,DF ⊥AB ,⊥CD =DF =3,故选:A .4.正方形ABCD 的边长为4,点E 是射线AD 上的一个动点,连结CE ,以CE 为边往右侧作正方形CEFG ,连结DF 、DG .(1)当点E在AD延长线上,且DE=AD时,DG=________.(2)当点E在线段AD上,且△DGF为等腰三角形时,DG=________.【答案】454或542【详解】解:(1)过点F作FH⊥AD交AD延长线于点H,⊥四边形ABCD是正方形,且DE=AD,⊥DE=AD=CD,⊥ADC=⊥CDE=90°,⊥△EDC是等腰直角三角形,⊥⊥DCE=⊥DEC=45°,⊥四边形CEFG是正方形,⊥CG=CE=EF,⊥GCE=⊥CEF=90°,⊥⊥DCG=⊥DEF=135°,⊥△DCG⊥△DEF,⊥DG=DF,⊥⊥DEC=45°,⊥CEF=90°,⊥⊥HEF=45°,⊥△EHF是等腰直角三角形,⊥CE=EF,⊥DE=CD=EH=FH=4,在Rt△DFH中,FH=4,DH=8,⊥DG=DF22+=4845(2)当点E与点A重合时,DG=DF,⊥DG=DE=DC=4;当DG=GF时,过点G作GI⊥CD于点I,⊥四边形CEFG是正方形,⊥CG=GF=CE,⊥GCE=90°,⊥DG=GC,CD=2,⊥CI=DI=12⊥DCE+⊥ICG=90°,⊥IGC+⊥ICG=90°,⊥⊥DCE=⊥IGC,⊥△DCE⊥△IGC,⊥IG=DC=4,⊥DG=GC22+=2425点E与点D重合时,DF=GF,此时,FG=FD=DC=4,⊥DG224442;综上,△DGF为等腰三角形时,DG=4或542故答案为:4或5425.如图,在边长为3的正方形ABCD中,点E是AB的中点,点F在BC上,且BF=2CF,DE,AF相交于点G,则DG的长为___________.958【详解】如图,延长DG、CB,二线交于点H,⊥四边形ABCD是正方形,E是AB的中点,⊥⊥DAE=⊥HBE=90°,AE=BE,⊥⊥AED =⊥BEH⊥△DAE ⊥△HBE ,⊥BH =AD =3,⊥BF =2CF ,BC =3,⊥BF =2,CF =1,⊥FH =FB +BH =3+2=5,CH =FH +CF =1+5=6,⊥四边形ABCD 是正方形,⊥⊥DCH =90°,AD ∥BC ,⊥△DAG ⊥△HFG ,DH 22223635CD CH ++=⊥35DG AD GH FH ==,⊥38DG DH =, ⊥333588DG DH ==⨯958958 6.如图,△ABC 中,AB =AC ,点 D 在 AC 上,连接 BD ,△ABD 的中线 AE 的延长线交 BC 于点 F ,⊥F AC =60°,若 AD =5,AB =7,则 EF 的长为__________.【答案】23【详解】解:延长AE 至点G ,使得AE =EG ,⊥E 是BD 的中点,⊥BE =DE ,在△ADE 和△GBE 中,DE BE AED GEB AE GE =⎧⎪∠=∠⎨⎪=⎩⊥⊥ADE ⊥⊥GBE (SAS ), ⊥AD =GB =5,⊥G=⊥F AC =60°,过点B 作BH ⊥GE 于点H ,在Rt ⊥BGH 中,⊥GBH =180°﹣90°﹣60°=30°,⊥GH =12BG =52,BH 22555()322-=, 在Rt ⊥ABH 中,AH 225117(3)22-,⊥AG =AH +GH =8,⊥AE =GE =4, 过点D 作DM AB 2AC =EF ,交BC 于点M .⊥12BE EF BD DM == , 设EF =x ,则DM =2x ,⊥DM AB 2AC =EF ,⊥225DM CD AF CA ==+,⊥AF =7x ,⊥AE =7x ﹣x =6x =4,⊥x =23,⊥EF =23, 故答案为:23. 7.如图,将矩形ABCD 绕着点B 逆时针旋转得到矩形GBEF ,使点C 恰好落到线段AD 上的E 点处,连接CE ,连接CG 交BE 于点H .(1)求证:CE 平分⊥BED ;(2)取BC 的中点M ,连接MH ,求证:MH ∥BG ;(3)若BC =2AB =4,求CG 的长.【答案】(1)见解析;(2)见解析;(3)7【解析】(1)⊥四边形ABCD 是矩形,⊥BC =BE ,DE ∥BC ,⊥⊥BEC =⊥BCE ,⊥BCE =⊥DEC ,⊥⊥BEC =⊥DEC ,⊥CE 平分⊥BED .(2)过点C 作CN ⊥BE ,垂足为N ,⊥四边形ABCD 是矩形,⊥CD ⊥DE ,⊥CE 平分⊥BED ,⊥CD =CN ,⊥矩形ABCD 绕着点B 逆时针旋转得到矩形GBEF ,⊥CD =BG ,⊥GBH =⊥CNH =90°,⊥CN =BG ,⊥BHG =⊥NHC ,⊥△BHG ⊥△CHN ,⊥HG =HC ,⊥H 是GC 的中点,⊥BC 的中点是M ,⊥MH 是△BGC 中位线,⊥MH ∥BG .(3)过点C 作CN ⊥BE ,垂足为N ,⊥四边形ABCD 是矩形,BC =2AB =4,矩形ABCD 绕着点B 逆时针旋转得到矩形GBEF ,⊥GB ⊥BH ,GB =BM =2,⊥MH 是△BGC 中位线,⊥MH =1,⊥⊥HBM =⊥QGB ,⊥GB =BM =2,⊥BHM =⊥GQB ,⊥△QBG ⊥△HMB ,⊥QB =MH =1,GQ =BH 3QC =5,⊥CG 22(3)52827+=.8.如图,在正方形ABCD 中,点E 是CD 中点,连接AE .过点C 作CF AE ⊥,交AE 的延长线于点F ,连接DF .过点D 作DG DF ⊥交AF 于点G .若2DF =,则正方形ABCD 的边长为________.10【详解】解:⊥四边形ABCD 是正方形,⊥AD =CD ,⊥ADC =90°,⊥⊥DAE +⊥AED =90°,⊥CF ⊥AE ,⊥⊥ECF +⊥CEF =90°,⊥⊥DAE =⊥ECF ,同理,⊥⊥ADG +⊥GDE =90°,⊥GDE +⊥CDF =90°,在⊥AGD 与⊥CFD 中,DAE ECF AD CD ADG CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩,⊥⊥AGD ⊥⊥CFD (ASA ),⊥DG =DF ,AG =CF ,⊥DG ⊥DF ,⊥⊥DGF 是等腰直角三角形,⊥2222GF DG DF +=过点D 作DK ⊥AE 于点K ,则122DK GK GF === , 在⊥DKE 与⊥CFE 中,DEK CEF DKE CFE DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DKE ⊥⊥CFE (AAS ),⊥DK =CF ,⊥2AG CF DK GK ====⊥22AK =⊥2210AD AK DK +10.9.已知:如图,AC ⊥BD ,AE 、BE 分别平分⊥CAB 和⊥ABD ,点E 在CD上.用等式表示线段AB 、AC 、BD 三者之间的数量关系,并证明.【答案】AC +BD =AB ,理由见见解析【详解】解:AC +BD =AB ,证明如下:在BA 上截取BF =BD ,连接EF ,如图所示:⊥AE 、BE 分别平分⊥CAB 和⊥ABD ,⊥⊥EAF =⊥EAC ,⊥EBF =⊥EBD ,在⊥BEF 和⊥BED 中,BF BD EBF EBD BE BE =⎧⎪∠=∠⎨⎪=⎩,⊥BEF BED ≌(SAS ),⊥⊥BFE =⊥D ,⊥AC ⊥BD ,⊥⊥C +⊥D =180°,⊥⊥AFE +⊥BFE =180°,⊥⊥AFE +⊥D =180°,⊥⊥AFE =⊥C ,在⊥AEF 和⊥AEC 中,EAF EAC AFE C AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥AEF AEC ≌(AAS ),⊥AF =AC ,⊥AF +BF =AB ,⊥AC +BD =AB .10.如图1,ΔΔRt ABF Rt CBE ≌,90ABC ∠=︒,点E ,F 分别在边AB,BC 上,点M 为AF 中点.(1)请直接写出线段CE 与BM 的关系;(2)连接EF ,将EBF ∆绕点B 逆时针旋转至如图2位置,请写出CE 与BM 的关系,并说明理由;(3)在EBF ∆绕点B 旋转的过程中,当B ,C ,E 三点共线时,若3BC =,2EF =CM 的长.【答案】(1)2CE BM = ,CE BM ⊥;(2)2CE BM = ,CE BM ⊥,理由见解析;(3)13CM =10【解析】(1)2CE BM =,CE BM ⊥,理由如下,设BM 与CE 相交于点N ,如图,⊥Rt ABF Rt CBE ≅△△,⊥ABC =90°,⊥AF =CE ,⊥A =⊥C ,⊥⊥A +⊥AFB =90°,⊥M 为AF 的中点,⊥BM =AM =FM =12AF ,⊥BM =12CE ,即2BM =CE ,⊥AFB =⊥CBM ,⊥⊥C +⊥CBM =90°,⊥⊥CNB =90°,⊥BM ⊥CE ,故BM 与CE 的关系为:2CE BM =,CE BM ⊥,(2)2CE BM =,CE BM ⊥,理由如下:证明:延长AB 至点N ,使NB AB =,连接NF⊥M 为AF 的中点,B 为AN 中点⊥BM 为ANF 的中位线⊥2NF BM =⊥90ABC ∠=︒,90EBF ∠=︒,⊥ABE ABF CBF ABF ∠+∠=∠+∠,⊥ABE CBF ∠=∠,⊥90ABC ∠=︒,AB BC BN ==,⊥CBA ABE CBN CBF ∠+∠=∠+∠,⊥CBE NBF ∠=∠,又⊥BE BF =,⊥()CBE NBF SAS ≅△△,⊥NF CE =,⊥2CE BM =,⊥BM 为ANF 的中位线,⊥BM FN ∥,⊥MBA N ∠=∠,⊥CBE NBF ≅△△,⊥ECB N ∠=∠,⊥MBA ECB ∠=∠,⊥90MBA CBM ∠+∠=︒,⊥90ECB CBM ∠+∠=︒,⊥CE BM ⊥,综上2CE BM =且CE BM ⊥;(3)当点E 在CB 的延长线上时,如图,⊥⊥ABC =⊥ABE =90°,AB =BC =3,BE =BF ,⊥在等腰Rt ⊥BEF 中,有EF 22,又⊥EF 2⊥BE =BF =1,⊥AF =AB -EF =3-1=2,⊥M 为AF 的中点,⊥FM =12AF =1,⊥22223213CM BC BM ++=当点E 在CB 上时,如图,同理可求得BF =BE =1,⊥AF =AB +BF =3+1=4,⊥M 为AF 的中点,⊥FM =12AF =2,⊥BM =FM -BF =2-1=1, ⊥22223110CM BC BM ++ 即CM 1310.11.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分⊥BAD .(1)推理证明:如图1,若120DAB ∠=︒,且90D ∠=︒,求证:AD AB AC +=;(2)问题探究:如图2,若120DAB ∠=︒,试探究AD 、AB 、AC 之间的数量关系;(3)迁移应用:如图3,若90DAB ∠=︒,AD =2,AB =4,求线段AC 的长度.【答案】(1)见解析;(2)AD AB AC +=;(3)32AC =【解析】(1)证明:⊥AC 平分BAD ∠,⊥12DAC BAC DAB ∠=∠=∠, 又⊥120DAB ∠=,⊥60DAC BAC ∠=∠=,又⊥180B D ∠+∠=,90D ∠=,⊥90B D ∠=∠=,⊥30ACD ACB ∠=∠=︒,⊥12AD AC =,12AB AC =, ⊥AD AB AC +=.(2)解:AD AB AC +=;过点C 作CE AD ⊥于点E ,过点C 作CF AE ⊥的延长线于点F ,⊥AC 平分BAD ∠,⊥CE CF =,90DEC CFB ∠=∠=,⊥180D ABC ∠+∠=,而180ABC FBC ∠+∠=,⊥D FBC ∠=∠,在BFC △与DEC 中D FBC DEC BFC CE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥()AAS BFC DEC ≌,⊥DF BF =,⊥AD AB AE DE AF BF AE AF +=++-=+,由(1)知AE AF AC +=,⊥AD AB AC +=.(3)过点C 作CM AB ⊥于点M ,过点C 作CN AD ⊥的延长线于点N ,由(2)知:CDN CBM ∆∆≌,⊥DN BM =,⊥AD AB AN DN AM BM AN AM +=-++=+,而90DAB ∠=︒,AC 平分BAD ∠,⊥45NAC MAC ACN ∠=∠=∠=︒,⊥2AN AM NC AC ===,⊥2AD AB AN AM +=+=, 又2AD =,4AB =,⊥32AC =12.如图,点F 在四边形ABCD 的边AB 上.(1)如图1,当四边形ABCD 是正方形时,过点B 作BE CF ⊥,垂足为O ,交AD 于点.E 求证:BE CF =;(2)当四边形ABCD 是矩形,6AD =,8AB =时,①如图2,点P 是BC 上的一点,过点P 作PE CF ⊥,垂足为O ,点O 恰好落在对角线BD 上,求OC OE 的值; ②如图3,点P 是BC 上的一点,过点P 作PE CF ⊥,垂足为O ,点O 恰好落在对角线BD 上,延长EP 、AB 交于点G,当2BG =时,请直接写出DE 的值.【答案】(1)证明见解析;(2)①34;②83. 【解析】(1)证明:四边形ABCD 是正方形,AB BC ∴=,90A FBC ∠=∠=︒,BE CF ⊥于点O ,90BOC ∴∠=︒,90ABE OBC BCF ∴∠=︒-∠=∠,ABE ∴⊥()BCF ASA , BE CF ∴=.(2)解:①如图2,过O 作OM AD ⊥于点M ,ON CD ⊥于点N ,则90OMD OND ∠=∠=︒,四边形ABCD 是矩形,6BC AD ∴==,8AB CD ==,90MDN A BCD ∠=∠=∠=︒,∴四边形OMDN 是矩形,90MON ∴∠=︒,PE CF ⊥于点O ,90COE ∴∠=︒,90CON EOM EON ∴∠=∠=︒-∠,90ONC OME ∠=∠=︒,ONC ∴⊥OME ,OC ON OE OM ∴=, OND BCD ∠=∠,//ON BC ∴, DON ∴⊥DBC △,ON OD BC BD ∴=,同理OM OD AB BD =, ON OM BC AB ∴=,ON BC OM AB ∴=,6384OC BC OE AB ∴===; ②如图3,连接CE 、CG ,90ABC ∠=︒,18090PBG ABC ∴∠=︒-∠=︒,90PBG POC ∴∠=∠=︒,BPG OPC ∠=∠,BPG ∴⊥OPC ,PB PG PO PC ∴=,PB PO PG PC ∴=,OPB CPG ∠=∠,OPB ∴⊥CPG △,CBD OGC ∴∠=∠, 34OC OE =,6384CB CD ==;OC CB OE CD ∴=, 90COE BOD ∠=∠=︒,COE ∴⊥BOD ,CDB OEC ∴∠=∠,90OGC OEC CBD CDB ∴∠+∠=∠+∠=︒,90ECG ∴∠=︒,90BCG DCE BCE ∴∠=∠=︒-∠,90CBG CDE ∠=∠=︒,CBG ∴△⊥CDE △,34BG CB DE CD ∴==,4482333DE BG ∴==⨯=. 13.将一块足够大的直角三角板的直角顶点P 放在边长为1的正方形ABCD 的对角线AC 上滑动,一条直角边始终经过点B ,另一条直角边与射线DC 交于点E .(1)当点E 在边DC 上时(如图1),求证:①⊥PBC ⊥⊥PDC ;②PB =PE .(2)当点E 在边DC 的延长线上时(如图2),(1)中的结论②还成立吗?如果不成立,请说明理由;如果成立,请给予证明.【答案】(1)①见解析;②见解析(2)(1)中的结论②仍然成立,证明见解析【解析】(1)①⊥四边形ABCD 是正方形,⊥BC =CD ,⊥BCP =⊥DCP=45°,又⊥CP =CP ,⊥⊥PBC ⊥⊥PDC ,②过点P 分别作PF ⊥BC 于点F ,PG ⊥CD 于点G ,易证四边形PFCG 为正方形,⊥⊥BFP =⊥EGP=90°,PF =PG ,⊥⊥EPG+⊥EPF=90°=⊥BPF+⊥EPF ,⊥⊥BFP =⊥EGP ⊥⊥PGE ⊥⊥PFB (ASA),⊥PB =PE .(2)PB =PE 成立,证明:设PE 交BC 于点O ,⊥⊥BPE =⊥BCE=90°,⊥BOP =⊥COE ,⊥⊥PBC =⊥PEC ,由(1)得:⊥PBC =⊥PDC ,⊥⊥PDC =⊥PEC ,PB =PD ,⊥PE =PD=PB ,故(1)中的结论②仍然成.14.在ABC 中,22BAC ABC ACB ∠=∠=∠,D 是BC 所在直线上的一个动点(点D 不与点B 、点C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF .(1)观察发现:如图1,当点D 在线段BC 上时,①BC 、CF 的位置关系为___________;②BC 、CD 、CF 之间的数量关系为___________.(2)探究证明:如图2,当点D 在线段CB 的延长线上时,(1)中的两个结论是否仍然成立?请说明理由.(3)问题解决:如图3,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE .若62AB =4BC CD =时,直接写出GE 的长.【答案】(1)①BC CF ⊥,②BC CF CD =+;(2)(1)中结论①成立,②不成立,理由见解析; (3)310【解析】(1)①在正方形ADEF 中,AD =AF ,⊥DAF =90°,⊥⊥BAC =90°,⊥⊥BAC =⊥DAF =90°⊥⊥BAD =⊥CAF ,在△DAB 与△F AC 中,AD AF BAD CAF AB AC =⎧⎪∠=∠⎨⎪=⎩,⊥⊥DAB ⊥⊥F AC (SAS ),⊥⊥ABD =⊥ACF ,⊥⊥ACB +⊥ACF =⊥ACB +⊥ABD =180°-⊥BAC =90°,⊥BC ⊥CF ;故答案为:BC ⊥CF ;②由①知,△DAB ⊥⊥F AC ,⊥BD =CF ,⊥BC =BD +CD ,⊥BC =CF +CD ;故答案为:BC =CF +CD ;(2)(1)中结论①成立.②不成立.理由如下:⊥四边形ADEF 是正方形:⊥AD AF =,90DAF ∠=︒.⊥22BAC ABC ACB ∠=∠=∠,180BAC ABC ACB ∠+∠+∠=︒,⊥90BAC ∠=︒,45ABC ACB ∠=∠=︒,⊥AB AC =,BAC DAF ∠=∠,⊥BAD CAF ∠=∠,⊥()SAS DAB FAC △△≌,⊥135ABD ACF ∠=∠=︒,=CF BD . ⊥45ACB ∠=︒,⊥1354590DCF ACF ACB ∠=∠-∠=︒-︒=︒,⊥CF BD ⊥. ⊥BC CD BD =-,⊥BC CD CF =-.⊥(1)中结论①成立.②不成立.(3)如图,作AH BC ⊥于点H ,EM BD ⊥于点M ,EN CF 于点N .易证90BAC ∠=︒,45ABC ACB ∠=∠=︒,⊥AB AC =,⊥BH CH =,⊥6212sin 452AB BC ==︒,⊥6AH BH CH ===. ⊥4BC CD =,3CD =,⊥9DH =.由(2)得BC CF ⊥,15CF BD ==.⊥BC CF ⊥,EM BD ⊥,EN CF ,⊥四边形CMEN 是矩形,⊥NE CM =,EM CN =. ⊥90AHD ADE EMD ∠=∠=∠=︒,⊥90ADH EDM ∠+∠=︒,90EDM DEM ∠+∠=︒,⊥ADH DEM =∠∠. ⊥AD DE =,⊥()ADH DEM AAS △△≌,⊥9EM DH ==,6DM AH ==, ⊥9CN EM ==,9669EN CM DH DM CH ==+-=+-=.⊥45ABC ∠=︒,⊥45BGC ∠=︒,⊥12CG BC ==,⊥1293GN CG CN =-=-=. ⊥2239310EG +=15.【探究建模】已知正方形ABCD ,E ,F 为平面内两点.(1)如图1,当点E 在边AB 上时,DE ⊥DF ,且B ,C ,F 三点共线.求证:AE =CF ;(2)【类比应用】如图2,当点E 在正方形ABCD 外部时,DE ⊥DF ,AE ⊥EF ,且E ,C ,F 三点共线.①(1)中的结论AE=CF还成立吗?请说明理由;②猜想并证明线段AE,CE,DE之间的数量关系.【答案】(1)见解析;(2)①成立,理由见解析;②EA+EC2,证明见解析【解析】(1)证明:⊥四边形ABCD是正方形,⊥DA=DC,⊥A=⊥ADC=⊥DCB=90°,⊥DE⊥DF,⊥⊥EDF=⊥ADC=90°,⊥⊥ADE=⊥CDF,在⊥DAE和⊥DCF中,ADE CDF AD CDA DCF∠=∠⎧⎪=⎨⎪∠=∠⎩,⊥⊥DAE⊥⊥DCF(ASA),⊥AE=CF.(2)解:①(1)中的结论AE=CF还成立.证明:⊥四边形ABCD是正方形,⊥DA=DC,⊥DAB=⊥ADC=⊥DCB=⊥DCF=90°,⊥DE⊥DF,⊥⊥EDF=⊥ADC=90°,⊥⊥ADE=⊥CDF,⊥AE⊥EF,⊥⊥AEF=90°,⊥⊥DAE+⊥DCE=180°,⊥⊥DCF+⊥DCE=180°,⊥⊥DAE=⊥DCF,在⊥DAE和⊥DCF中,ADE CDFAD CDDAE DCF∠=∠⎧⎪=⎨⎪∠=∠⎩,⊥⊥DAE⊥⊥DCF(ASA),⊥AE=CF.②解:结论:EA+EC2.理由:由①知,⊥DAE⊥⊥DCF(ASA),⊥AE=CF,DE=DF,∥ADE=∥CDF,⊥∥EDF=90°,⊥⊥DEF为等腰直角三角形,⊥EF2⊥FC+EC2.⊥AE+EC2.。
全等三角形的10个模型(一)

全等三角形的10个模型(一)引言概述:全等三角形是指两个或多个三角形的对应边和对应角完全相等的情况。
全等三角形在几何学中有广泛的应用,不仅在证明和推导定理时起到重要的作用,还在实际问题的解决中提供了有力的工具。
本文将介绍十个关于全等三角形的模型。
这些模型旨在帮助读者更好地理解和运用全等三角形的性质和应用。
正文:1. 模型一:完全相等的三边- 全等三角形的基本条件就是三边相等。
- 通过边的对应关系确定两个三角形是否全等。
- 证明时可利用边长相等的性质进行推导。
2. 模型二:完全相等的两边和夹角- 如果已知两个三角形的两边和夹角都相等,则这两个三角形全等。
- 通过边角边(SAS)或角边角(ASA)的条件可以判定两个三角形相等。
3. 模型三:完全相等的两角和夹边- 如果已知两个三角形的两角和夹边都相等,则这两个三角形全等。
- 边角边(SAS)或角边角(ASA)的条件可以判定两个三角形相等。
4. 模型四:等腰三角形和全等条件- 等腰三角形是指两边相等或两角相等的三角形。
- 如果两个三角形中有一个是等腰三角形,且两个等腰三角形的两边或两角都相等,则这两个三角形全等。
5. 模型五:直角三角形和全等条件- 直角三角形是指其中一个角为90度的三角形。
- 如果两个三角形中有一个是直角三角形,且两个直角三角形的两边或两个锐角均相等,则这两个三角形全等。
总结:通过十个模型的介绍,我们可以看到全等三角形是几何学中一个重要而广泛应用的概念。
理解全等三角形的性质和应用对于解决几何问题具有重要意义。
在实际问题中,我们常常可以利用全等三角形的模型来推导和证明定理,从而得出更深入的结论。
中考数学总复习全等三角形的五种模型

全等三角形的五种模型一、手拉手模型已知:△ABE和△ACD为两个的等腰三角形,∠BAE=∠CAD=∠α,连接EC,BD交于点O结论:①△ABD ≌△AEC;②∠α+∠BOC=180°;③OA平分∠BOC已知:△ABD和△ACE均为等腰直角三角形,连接CD,BE交于点O结论:①△ACD ≌△ABE;②∠BOC=90°;③OA平分∠BOC已知:直线AB的同一侧作△ABD和△BCE都为等边三角形,连接AE,CD,二者交点为H结论:①△ABE≌△DBC;②AE=DC;③∠DHA=60°;④△AGB≌△DFB;⑤△EGB≌△CFB;⑥连接GF,GF∥AC;⑦连接HB,HB平分∠AHC模型应用1. (2010·深圳改编)如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D 在AB上.(1)求证:△AOC≌△BOD;(2)判断△CAD是什么形状的三角形,说明理由.2.如图,△ABC与△ADE都是等腰直角三角形,连接CD,BE,CD,BE相交于点O,判断CD 与BE的位置关系,并说明理由半角模型已知:正方形ABCD中,E,F分别是BC,CD边上的点,且∠EAF=45°结论:将△ADF绕点A旋转90°到△ABG,则:①EF=DF+BE;②△CEF的周长为正方形ABCD周长的一半已知:正方形ABCD中,E,F分别是BC,CD边上的点,且∠EAF=45°结论:将△AEB绕点A为旋转90°到△ADE′,则:EF=DF-BE已知:在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF,AE,AF,过A 作AH⊥EF于点H,BE=EH结论:①△ABE≌△AHE;②△AHF≌△ADF;③∠EAF=45°;④EF=BE+DF模型应用3. (2015·深圳改编)如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE 折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③∠GDE=45°;④DG=DE.在以上4个结论中,正确的共有()A. 1个B. 2 个C. 3 个D. 4个4. 如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF,AE,AF,过A作AH⊥EF于点H.若EF=BE+DF,那么下列结论:①AE平分∠BEF;②FH=FD;③∠EAF =45°;④S△EAF=S△ABE+S△ADF;⑤△CEF的周长为2.其中正确结论的个数是() A. 2 B. 3C. 4D. 5第三题第四题倍长中线模型已知:在△ABC 中,AD 是BC 边中线结论:延长AD 到E ,使DE =AD ,连接BE ,则:①△ADC ≌△EDB ;②AD< 21(AB +AC)已知:在△ABC 中,AD 是BC 边中线结论:作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E ,连接BE ,则:①△BDE ≌△CDF ;②BE ∥FC模型应用6. 已知:在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF.一直线三垂直模型已知:AE=DE,AE⊥DE,∠B=∠C=90结论:①△ABE≌△ECD;②BC=AB+CD已知:在正方形ABCD中,∠ABF=∠C=90°,AF⊥BE,交于点H结论:①△ABF≌△BCE;②EC=AB-FC模型应用7. (2016·深圳改编)如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF 为正方形,过点F作FG∠CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S∠FAB∠S四边形CBFG=1∠2;③∠ABC=∠ABF.其中正确的结论的个数是()A.1B. 2C. 3D. 08. 如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM.其中正确的结论有()A. 0个B. 1个C. 2个D. 3个9. 如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE∠AG于点E,BF∠DE,交AG 于点F.给出以下结论:①∠AED∠∠BFA;②DE-BF=EF;③∠BGF∠∠DAE;④DE-BG=FG.其中正确的有()A. 1个B. 2个C. 3个D. 4个10. (2018·深圳)如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是________.对角互补模型已知:已知∠AOB=∠DCE=90°,OC平分∠AOB结论模型应用11.(2012·深圳)如图,Rt∠ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形6,则另一直角边BC的长为________.对角线交于点O,连接OC,已知AC=5,OC=212. (2017·深圳)如图,在Rt∠ABC中,∠ABC=90°,AB=3,BC=4,Rt∠MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.。
全等三角形判定经典

11.2三角形全等的判定ABC DEF(1)三边对应相等的两个三角形全等,简写为“边边边”或“SSS ”。
表示方法:如图所示,在△ABC 和△DEF 中,AB DEAC DF BC EF=⎧⎪=⎨⎪=⎩,∴△ABC ≌△DEF (SSS )。
例1. 如图所示,AB =CD ,AC =DB 。
求证:△ABC ≌△DCB 。
A BCD分析:由已知可得AB =CD ,AC =DB ,又因为BC 是两个三角形的公共边,所以根据SSS 可得出△ABC ≌△DCB 。
证明:在△ABC 和△DCB 中,∵⎩⎨⎧AB =CD AC =DB BC =CB,∴△ABC ≌△DCB (SSS )评析:证明格式:①点明要证明的两个三角形;②列举两个三角形全等的条件(注意写在前面的三角形,条件也放在前面),用大括号括起来;③条件按照“SSS ”顺序排序;④得出结论,并把判断的依据注在后面。
“ASA ”。
表示方法:如图所示,在△ABC 和△DEF 中,B E BC EF C F∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC ≌△DEF (ASA )。
例2. 如图所示,AB ∥CD ,AF ∥DE ,BE =CF ,求证:AB =CD 。
ABEFCD分析:要证明AB =CD ,由于AB 、CD 分别是△ABF 和△DCE 的边,可尝试证明△ABF ≌△DCE ,由已知易证:∠B =∠C ,∠AFB =∠DEC ,下面只需证明有一边对应相等即可。
事实上,由BE =CF 可证得BF =CE ,由ASA 即可证明两三角形全等。
证明:∵AB ∥CD ,∴∠B =∠C (两直线平行,内错角相等) 又∵AF ∥DE ,∴∠AFC =∠DEB (同上) ∴∠AFB =∠CED (等角的补角相等)又∵BE =CF ,∴BE -EF =CF -EF ,即BF =CE 在△ABF 和△DCE 中,()()()B C BF CE AFB CED ∠=∠⎧⎪=⎨⎪∠=∠⎩已证已证已证∴△ABF ≌△DCE (ASA )∴AB =CD (全等三角形对应边相等)角边”或“AAS ”。
(完整版)全等三角形经典模型总结

全等三角形相关模型总结一、角平分线模型(一)角平分线的性质模型辅助线:过点G作GE⊥射线ACA、例题1、如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那么点D到直线AB 的距离是cm.2、如图,已知,∠1=∠2,∠3=∠4,求证:AP平分∠BAC.B、模型巩固1、如图,在四边形ABCD中,BC>AB,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.(二)角平分线+垂线,等腰三角形必呈现A、例题辅助线:延长ED交射线OB于F 辅助线:过点E作EF∥射线OB 例1、如图,在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于F .求证:1()2BE AC AB=-.例2、如图,在△ABC中,∠BAC的角平分线AD交BC于点D,且AB=AD,作CM⊥AD交AD的延长线于M. 求证:1()2AM AB AC=+.(三)角分线,分两边,对称全等要记全两个图形飞辅助线都是在射线ON上取点B,使OB=OA,从而使△OAC≌△OBC .A、例题1、如图,在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,BQ平分∠ABC 交AC于Q,求证:AB+BP=BQ+AQ .2、如图,在△ABC中,AD是∠BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.B、模型巩固1、在△ABC中,AB>AC,AD是∠BAC的平分线,P是线段AD上任意一点(不与A重合).求证:AB-AC>PB-PC .2、如图,△ABC中,AB=AC,∠A=100°,∠B的平分线交AC于D,求证:AD+BD=BC .3、如图,△ABC中,BC=AC,∠C=90°,∠A的平分线交BC于D,求证:AC+CD=AB .二、等腰直角三角形模型(一)旋转中心为直角顶点,在斜边上任取一点的旋转全等:操作过程:(1)将△ABD逆时针旋转90°,得△ACM ≌△ABD,从而推出△ADM为等腰直角三角形.(2)辅助线作法:过点C作MC⊥BC,使CM=BD,连结AM.(二)旋转中心为斜边中点,动点在两直角边上滚动的旋转全等:操作过程:连结AD.(1)使BF=AE(或AF=CE),导出△BDF ≌△ADE.(2)使∠EDF+∠BAC=180°,导出△BDF ≌△ADE.A、例题1、如图,在等腰直角△ABC中,∠BAC=90°,点M、N在斜边BC上滑动,且∠MAN=45°,试探究BM、MN、CN之间的数量关系.2、两个全等的含有30°,60°角的直角三角板ADE和ABC,按如图所示放置,E、A、C三点在一条直线上,连接BD,取BD的中点M,连接ME、MC.试判断△EMC的形状,并证明你的结论.B、模型巩固1、已知,如图所示,Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点,若M、N分别在线段AC、AB上移动,且在移动中保持AN=CM.(1)试判断△OMN的形状,并证明你的结论.(2)当M、N分别在线段AC、AB上移动时,四边形AMON的面积如何变化?2、在正方形ABCD中,BE=3,EF=5,DF=4,求∠BAE+∠DCF为多少度.(三)构造等腰直角三角形(1)利用以上(一)和(二)都可以构造等腰直角三角形(略);(2)利用平移、对称和弦图也可以构造等腰直角三角形.(四)将等腰直角三角形补全为正方形,如下图:A、例题应用1、如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,P为三角形ABC内部一点,满足PB=PC,AP=AC,求证:∠BCP=15°.三、三垂直模型(弦图模型)A、例题已知:如图所示,在△ABC中,AB=AC,∠BAC=90°,D为AC中点,AF⊥BD于点E,交BC于F,连接DF .求证:∠ADB=∠CDF .变式1、已知:如图所示,在△ABC中,AB=AC,AM=CN,AF⊥BM于E,交BC于F,连接NF .求证:(1)∠AMB=∠CNF;(2)BM=AF+FN .变式2、在变式1的基础上,其他条件不变,只是将BM和FN分别延长交于点P,求证:(1)PM=PN;(2)PB=PF+AF .四、手拉手模型1、△ABE和△ACF均为等边三角形结论:(1)△ABF≌△AEC .(2)∠BOE=∠BAE=60°.(3)OA平分∠EOF .(四点共圆证)拓展:△ABC和△CDE均为等边三角形结论:(1)AD=BE;(2)∠ACB=∠AOB;(3)△PCQ为等边三角形;(4)PQ∥AE;(5)AP=BQ;(6)CO平分∠AOE;(四点共圆证)(7)OA=OB+OC;(8)OE=OC+OD .((7),(8)需构造等边三角形证明)例、如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.(1)求证:△AMB≌△ENB;(2)若AM+BM+CM的值最小,则称点M为△ABC的费尔马点.若点M为△ABC的费尔马点,试求此时∠AMB、∠BMC、∠CMA的度数;(3)小翔受以上启发,得到一个作锐角三角形费尔马点的简便方法:如图②,分别以△ABC 的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M 即为△ABC的费尔马点.试说明这种作法的依据.2、△ABD 和△ACE 均为等腰直角三角形结论:(1)BE =CD ;(2)BE ⊥CD .3、四边形ABEF 和四边形ACHD 均为正方形结论:(1)BD =CF ;(2)BD ⊥CF .变式1、四边形ABEF 和四边形ACHD 均为正方形,AS ⊥BC 交FD 于T ,求证:(1)T 为FD 中点;(2)ABC ADF SS .变式2、四边形ABEF和四边形ACHD均为正方形,T为FD中点,TA交BC于S,求证:AS⊥BC .4、如图,以△ABC的边AB、AC为边构造正多边形时,总有:360 12180n︒∠=∠=︒-五、半角模型条件:1,+=1802αββθβ=︒且,两边相等.思路:1、旋转辅助线:①延长CD到E,使ED=BM,连AE或延长CB到F,使FB=DN,连AF②将△ADN绕点A顺时针旋转90°得△ABF,注意:旋转需证F、B、M三点共线结论:(1)MN=BM+DN;(2)=2CMNC AB;(3)AM、AN分别平分∠BMN、∠MND .2、翻折(对称)辅助线:①作AP⊥MN交MN于点P②将△ADN、△ABM分别沿AN、AM翻折,但一定要证明M、P、N三点共线 .A、例题例1、在正方形ABCD中,若M、N分别在边BC、CD上移动,且满足MN=BM+DN,求证:(1)∠MAN=45°;C AB;(2)=2CMN(3)AM、AN分别平分∠BMN和∠DNM .变式:在正方形ABCD中,已知∠MAN=45°,若M、N分别在边CB、DC的延长线上移动,AH⊥MN,垂足为H,(1)试探究线段MN、BM、DN之间的数量关系;(2)求证:AB=AH例2、在四边形ABCD中,∠B+∠D=180°,AB=AD,若E、F分别为边BC、CD上的点,且满足EF=BE+DF,求证:12EAF BAD ∠=∠.变式:在四边形ABCD中,∠B=90°,∠D=90°,AB=AD,若E、F分别为边BC、CD上的点,且12EAF BAD∠=∠,求证:EF=BE+DF .。
第4讲专题一全等三角形常见几何模型(原卷版)

专题一全等三角形的模型(原卷版)专题解读:全等三角形指能够完全重合的两个三角形,它们的三条边三个角都对应相等,全等三角形是几何类型中研究的全等之一,当题目中出现角平分线,重点或中线,三条线段之间的关系,垂直平分线等条件时,可以考虑作辅助线构造全等三角形。
类型一角平分线模型模型描述:OF是∠AOB的平分线,如图(1)若PC⊥OA,PD⊥OB,则△PCO≌△PDO;如图(2)若OC =OD,则△PCO≌△PDO(1)(2)典例1如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.针对训练1.(2022秋•临西县期末)已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC 于点N.求证:AP平分∠MAN.2.(2023春•禅城区校级月考)如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.(1)求∠EDA的度数;(2)若AB=20,AC=16,DE=6,求S△ABC.类型二三垂直模型模型描述:有下面三种情况典例2如图(1),已知AB⊥BD,ED⊥BD,AB=CD,BC=DE,(1)试判断AC与CE的位置关系,并说明理由.(2)若将CD沿CB方向平移得到图(2)(3)(4)(5)的情形,其余条件不变,此时第(1)问中AC 与CE的位置关系还成立吗?结论还成立吗?请任选一个说明理由.针对训练1.(2021秋•海丰县期末)如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.(1)求证:△ACD≌△CBE;(2)试探究线段AD,DE,BE之间有什么样的数量关系,请说明理由.2.(2021秋•柘城县期中)已知△ABC在平面直角坐标系中,在△ABC中,AB=BC,∠ABC=90°.(1)如图①,已知点A(0,﹣4),B(1,0),求点C的坐标;(2)如图②,已知点A(0,0),B(3,1),求点C的坐标.类型三半角模型模型描述:半角模型常见的图形有正方形,正三角形等。
全等三角形的经典模型
i作弊?三角形9级 全等三角形的经典模型(二) 3三角形7级 倍长中线与截长补短Q 三角形8级 全等三角形的经典模型(一) 满分晋级漫画释义 订全等三角形的经典模型(一)秋季班第二讲秋季班第三讲秋季班第四讲/考试尺砸件阳.目才卜宙曲学邺三曲帮三垂直模型等腰直角三角形数学模型思路:⑴利用特殊边特殊角证题( AC=BC或90° ,45 ,45 ).如图1;⑵常见辅助线为作高,禾U用三线合一的性质解决问题•如图2;⑶补全为正方形.如图3, 4.的经典模型等IB宜角三箱形模型图3 图4已知:如图所示, Rt △ ABC 中,AB=AC , BAC 90° O 为BC 的中点,⑴写出点O 到厶ABC 的三个顶点A 、B 、C 的距离的关系(不要 求证明) ⑵如果点M 、N 分别在线段AC 、AB 上移动,且在移动中保持 AN=CM.试判断△ OMN 的形状,并证明你的结论 .⑶如果点 M 、N 分别在线段 CA 、AB 的延长线上移动,且在移动中 保持AN=CM ,试判断⑵中结论是否依然成立,如果是请给出证明.证明:•••/ BAC=90° , AB=AC , O 为 BC 中点 •••/ BAO= / OAC = ZABC = Z ACB=45° , ••• AO=BO=OC , •••在△ ANO 和厶CMO 中, AN CM BAO C AO CO• △ ANO 也厶 CMO ( SAS )• ON=OM , / AON = Z COM , 又•••/ COM / AOM =90° ,, • △ OMN 为等腰直角三角形.两个全等的含30° , 60°角的三角板 ADE 和三角板ABC ,女口 图所示放置,E,A,C 三点在一条直线上,连接 BD ,取BD 的 中点M ,连接ME , MC •试判断△ EMC 的形状,并说明理由.【解析】△ EMC 是等腰直角三角形典题精练_________ i t ■【解析】 ⑴OA=OB=OC⑵连接OA,•/OA=OC BAO C 45° AN=CM• △ ANO CMO •ON=OM• NOA MOC• NOA BONMOC BON 90• NOM 90• △ OMN是等腰直角三角形 ⑶厶ONM 依然为等腰直角三角形,【例1】【例2】 MA证明:连接AM •由题意,得 DE AC, DAE BAC 90°, DAB 900 :.△ DAB 为等腰直角三角形•••• DM MB ,••• MA MB DM , MDA MAB 45° . ••• MDE MAC 105° , • △ EDM △ CAM . • EM MC, DME AMC .又 EMC EMA AMC EMA DME 90° . • CM EM ,• △ EMC 是等腰直角三角形.【例3】 已知:如图, △ ABC 中,AB AC , BAC 点,AFBD 于E ,交BC 于F ,连接DF . 求证: ADB CDF . 1 2 AB AC 3 C• △ ABM ◎△ CAF . • AM CF . 在△ ADM 和△ CDF 中, AD CD DAM C AM CF• △ ADM ◎△ CDF . • ADB CDF .证法二:如图,作 CM AC 交AF 的延长线于 M .T AF BD , •32 90° ,BAC 90° , • 1 2 90° , • 13.在△ ACM 和△ BAD 中,【解析】证法一: 如图,过点 A 作AN BC 于N ,交 •/ ABAC , BAC 90° ,• 3DAM 45° .••• C45° , • 3 C .••• AF BD , 1 BAE 90°BAC 90° , • 2 BAE 90° .• 1 2 .在△ ABM 和△ CAF 中,C1 3AC ABACM BAD 90°••• △ ACM ◎△ BAD .二M ADB, AD CM•/ AD DC , • CM CD .在△ CMF和△ CDF中,CF CFMCF DCF 45°CM CD• △ CMF ◎△ CDF . • M CDF•- ADB CDF .【例4】如图,等腰直角△ ABC中,AC BC , ACB 90°, P为△ ABC内部一点,满足【解析】补全正方形ACBD,连接DP,易证△ ADP是等边三角形,DAP 60 ,BAP 15 , PAC 30 , • ACP 75 ,BCP 15【探究对象】等腰直角三角形添补成正方形的几种常见题型在解有关等腰直角三角形中的一些问题,若遇到不易解决或解法比较复杂时,可将等腰直角三角形引辅助线转化成正方形,再利用正方形的一些性质来解,常常可以起到化难为易的效果,从而顺利地求解。
七年级下册数学全等三角形的模型及应用(知识点串讲)(解析版)

专题12 全等三角形的模型及应用知识网络重难突破知识点一全等三角形常见模型(1)一线三等角常见图形如下:(含特殊的一线三垂直)(2)手拉手模型常见图形如下:(等腰三角形、等边三角形、等腰直角三角形)(2)半角模型常见图形如下:(正方形、一般四边形)(1)一线三等角典例1(2019春•莲湖区期末)如图1,在ABC⊥∆中,90∠=︒,AB ACBAC=,过点A作直线DE,且满足BD DE 于点D,CE DE⊥于点E,当B,C在直线DE的同侧时,(1)求证:DE BD CE=+.(2)如果上面条件不变,当B,C在直线DE的异侧时,如图2,问BD、DE、CE之间的数量关系如何?写出结论并证明.(3)如果上面条件不变,当B,C在直线DE的异侧时,如图3,问BD、DE、CE之间的数量关系如何?写出结论并证明.【解答】(1)证明:如图1,BD DE⊥,CE DE⊥,90D E ∴∠=∠=︒,90BAC ∠=︒,90BAD CAE ∴∠+∠=︒.90BAD ABD ∠+∠=︒,CAE ABD ∴∠=∠.在ADB ∆和CEA ∆中,D E ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADB CEA AAS ∴∆≅∆,BD AE ∴=,AD CE =,DE AD AE =+,DE CE BD ∴=+;(2)解:BD DE CE =+,理由:如图2,BD DE ⊥,CE DE ⊥,90ADB CEA ∴∠=∠=︒.90BAD ABD ∴∠+∠=︒.90BAD EAC ∠+∠=︒ABD EAC ∴∠=∠.在ADB ∆和CEA ∆中,ADB CEA ABD EAC AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADB CEA AAS ∴∆≅∆,BD AE ∴=,AD CE =.AE AD ED =+,BD DE CE ∴=+.(3)解:DE CE BD =-,理由是:如图3,同理易证得:()ABD CAE AAS ∆≅∆,BD AE ∴=,AD CE =,DE AD AE =-,DE CE BD ∴=-.典例2(2019春•长清区期末)CD 是经过BCA ∠顶点C 的一条直线,CA CB =,E 、F 分别是直线CD 上两点,且BEC CFA α∠=∠=∠.(1)如图(1),若直线CD 经过BCA ∠的内部,且E 、F 在射线CD 上,当90BCA α∠=∠=︒时,线段BE与CF有怎样的大小关系?并说明理由.(2)如图(2),若直线CD经过BCA∠的外部,当90∠=∠>︒时,则EF、BE、AF三条线段之间BCAα有怎样的数量关系?并说明理由.【解答】解:(1)BE CF=,理由:FCA FAC∠+∠=︒,90∠+∠=︒,90BCE ACF∴∠=∠,(同角的余角相等)BCE FCA=,∠=∠,CA CBBEC CFA∴∆≅∆,Rt BCE Rt CAF(AAS)∴=;BE CF(2)EF AF BE=+,理由:CAF ACFα∠+∠=︒-∠,BCE ACFα∠+∠=︒-∠,180180∴∠=∠,(同角的补角相等)BCE CAF=,∠=∠,CA CBBEC CFA∴∆≅∆,BCE CAF AAS()=,∴=,BE CFCE AF∴=+=+.EF CE CF AF BE(2)手拉手全等典例1如图,等边ABC∆中,D是AB边上的一动点,以CD为一边,向上作等边EDC∆,连接AE.(1)求证:ACE BCD∆≅∆;(2)判断AE与BC的位置关系,并说明理由.【解答】证明:(1)ABC ∆和DCE ∆都是等边三角形,BC AC ∴=,DC CE =,60ACB DCE ∠=∠=︒,ACB DCA DCE DCA ∴∠-∠=∠-∠,即BCD ACE ∠=∠,在ACE ∆和BCD ∆中,BC AC BCD ACE DC CE =⎧⎪∠=∠⎨⎪=⎩,()ACE BCD SAS ∴∆≅∆;(2)//AE BC ,理由是:ACE BCD ∆≅∆,CAE ABC ∴∠=∠,ABC ∆是等边三角形,ABC ACB ∴∠=∠,CAE ACB ∴∠=∠,//AE BC ∴.典例2(2019春•金牛区期末)如图.已知∠BAD =∠CAE =90°,AB =AD ,AE =AC ,AF ⊥CB ,垂足为F .(1)求证:△ABC ≌△ADE ;(2)求∠F AB +∠DAE 的度数;(3)请问线段CE 、BF 、DE 之间有什么数量关系?请说明理由.【解答】(1)证明:∵∠BAD =∠CAE =90°,∴∠BAC +∠CAD =90°,∠CAD +∠DAE =90°,∴∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(SAS);(2)解:∵∠CAE=90°,AC=AE,∴∠E=45°,由(1)知△BAC≌△DAE,∴∠CAB=∠DAE,∠BCA=∠E=45°,∠F AB+∠DAE=∠F AB+∠CAB=∠F AC,∵∠AFC=90°,∠BCA=45°,∴∠F AC=45°,∴∠F AB+∠DAE=45°;(3)解:CE=2BF+2DE;理由如下:延长BF到G,使得FG=FB,连接AG,如图所示:∵AF⊥BG,∴AB=AG,∴∠ABF=∠G,∵△BAC≌△DAE,∴AB=AD,∠CBA=∠EDA,CB=ED,∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,∵∠GCA=∠DCA=45°,在△CGA和△CDA中,,∴△CGA≌△CDA(AAS),∴CG=CD,∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE,∴CE=2BF+2DE.典例3(2019春•天桥区期末)如图1,在ABC ∆中,AB AC =,点D 是BC 边上一点(不与点B 、C 重合),以AD 为边在AD 的右侧作ADE ∆,使AD AE =,DAE BAC ∠=∠,连接CE ,设BAC α∠=,BCE β∠=.(1)线段BD 、CE 的数量关系是 ;并说明理由;(2)探究:当点D 在BC 边上移动时,α,β之间有怎样的数量关系?请说明理由;(3)如图2,若90BAC ∠=︒,CE 与BA 的延长线交于点F .求证:EF DC =.【解答】解:(1)结论:BD CE =.理由:如图1中,AB AC =,AD AE =,BAC DAE ∠=∠,BAD CAE ∴∠=∠,()BAD CAE SAS ∴∆≅∆,BD CE ∴=.(2)结论:180αβ+=︒.理由:如图1中,BAD CAE ∆≅∆(已证),ABD ACE ∴∠=∠,BCE ACB ABC ABC ACE β∴∠=∠+∠=∠+∠=,180BAC ABC ACB ∠+∠+∠=︒,BAC α∠=,180αβ∴+=︒.(3)如图2中,由(1)可知BAD CAE ∆≅∆,BD EC ∴=,B ACE ∠=∠,AB DC =,90BAC ∠=︒,45B ACB ACF ∴∠=∠=∠=︒,90BCF ∴∠=︒,45F ∠=︒,B F ∴∠=∠,CB CF ∴=,BD EC =,EF CD ∴=.(3)半角模型典例1(2019春•罗湖区期末)四边形ABCD 是正方形(四条边相等,四个角都是直角).(1)如图1,将一个直角顶点与A 点重合,角的两边分别交BC 于E ,交CD 的延长线于F ,试说明BE=DF;(2)如图2,若将(1)中的直角改为45°角,即∠EAF=45°,E、F分别在边BC、CD上,试说明EF=BE+DF;(3)如图3,改变(2)中的∠EAF的位置(大小不变),使E、F分别在BC、CD的延长线上,若BE =15,DF=2,试求线段EF的长.【解答】证明:(1)∵正方形ABCD是正方形,∴AD=AB,∠BAD=∠B=∠ADC=90°,∵∠EAF=90°,∴∠BAE+∠EAD=∠EAD+∠DAF=90°,∴∠BAE=∠DAF,在△BAE和△DAF中,∵,∴△ABE≌△ADF(ASA),∴BE=DF;(2)如图2,∵AD=AB,将△ABE绕点A逆时针旋转90°得到△ADE',此时AB与AD重合.由旋转可得∠BAE=∠DAE',BE=DE',∠B=∠ADE'=90°.∴∠ADF+∠ADE'=90°+90°=180°,∴点F、D、E'在同一条直线上,∵∠EAF=45°,∴∠BAE+∠DAF=∠DAF+∠DAE'=45°=∠EAF,在△EAF和△E'AF中,∵,∴△EAF≌△E'AF(SAS),∴EF=E'F,∵E'F=DF+DE'=DF+BE,∴EF=BE+DF;(3)将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,如图3所示,由四边形ABCD为正方形可知点B、C、F′在一条直线上,∵∠BAF′=∠DAF,∠EAF=∠EAD+∠DAF=45°,∴∠EAF′+∠EAD+∠DAF=90°,∴∠EAF′=∠EAF=45°.在△EAF和△EAF′中,,∴△EAF≌△EAF′(SAS),∴EF=EF′,∴EF=EF'=BE﹣BF'=BE﹣DF=15﹣2=13.知识点二全等三角形的应用典例1(2019春•皇姑区期末)要测量河岸相对两点A、B的距离,已知AB垂直于河岸BF,先在BF上取两点C、D,使CD CB=,再过点D作BF的垂线段DE,使点A、C、E在一条直线上,如图,测出10BD=,5ED=,则AB的长是()A.2.5B.10C.5D.以上都不对【解答】解:AB BD⊥,ED AB⊥,90ABC EDC∴∠=∠=︒,在ABC∆和EDC∆中,90ABC EDCBC DCACB ECD∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,()ABC EDC ASA∴∆≅∆,5AB ED∴==.故选:C.典例2(2019春•灵石县期末)某大学计划为新生配备如图1所示的折叠凳图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,由以上信息能求出CB的长度吗?如果能,请求出BC的长度,如果不能,请你说明理由.【解答】解:O是AB、CD的中点,OA OB∴=,OC OD=,在AOD∆和BOC∆中,OA OBAOD BOC OC OD=⎧⎪∠=∠⎨⎪=⎩,()AOD BOC SAS∴∆≅∆,CB AD∴=,30AD cm=,30CB cm∴=.巩固训练一、单选题(共6小题)1.(2019春•罗湖区期末)如图,为估计罗湖公园小池塘岸边A、B两点之间的距离,思雅学校小组在小池塘的一侧选取一点O,测得OA=28m,OB=20m,则A,B间的距离可能是()A.8m B.25m C.50m D.60m【解答】解:连接AB,根据三角形的三边关系定理得:28﹣20<AB<28+20,即:8<AB<48,则AB的值在8和48之间.2.(2019春•市中区期末)如图,有一池塘,要测池塘两端A ,B 间的距离,可先在平地上取一个不经过池塘可以直接到达点A 和B 的点C ,连接AC 并延长至D ,使CD CA =,连接BC 并延长至E ,使CE CB =,连接ED .若量出58DE =米,则A ,B 间的距离即可求.依据是( )A .SASB .SSSC .AASD .ASA【解答】解:在ABC ∆和DEC ∆中,AC CD ACB DCE BC CE =⎧⎪∠=∠⎨⎪=⎩,()ABC DEC SAS ∆≅∆,58AB DE ∴==米,故选:A .3.(2018春•槐荫区期末)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD 是一个筝形,其中AD CD =,AB CB =,詹姆斯在探究筝形的性质时,得到如下结论:①AC BD ⊥;②12AO CO AC ==;③ABD CBD ∆≅∆;④四边形ABCD 的面积12AC BD =⨯其中正确的结论有( )A .1个B .2个C .3个D .4个【解答】解:在ABD ∆与CBD ∆中,AD CD AB BC DB DB =⎧⎪=⎨⎪=⎩,()ABD CBD SSS ∴∆≅∆,ADB CDB ∴∠=∠,在AOD ∆与COD ∆中,AD CD ADB CDB OD OD =⎧⎪∠=∠⎨⎪=⎩,()AOD COD SAS ∴∆≅∆,90AOD COD ∴∠=∠=︒,AO OC =,AC DB ∴⊥,故①②正确;四边形ABCD 的面积111222S ADB S BDC DB OA DB OC AC BD =∆+∆=⨯+⨯=, 故④正确;故选:D .4.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )A .①B .②C .③D .①和②【解答】解:带③去可以利用“角边角”得到全等的三角形.故选:C .5.(2019春•青羊区期末)如图,∠ACB =90°,AC =BC ,AE ⊥CE 于点E ,BD ⊥CE 于点D ,AE =5cm ,BD =2cm ,则DE 的长是( )A .8cmB .5cmC .3cmD .2cm【解答】解:∵AE ⊥CE 于点E ,BD ⊥CE 于点D ,∴∠AEC =∠D =∠ACB =90°,∴∠A+∠ACE=90°,∠ACE+∠BCD=90°,∴∠A=∠BCD,∵AC=BC,∴△ACE≌△CBD(AAS),∴AE=CD=5cm,CE=BD=2cm,∴DE=CD﹣CE=5﹣2=3cm.故选:C.6.(2019春•罗湖区期末)如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中,正确的个数是(),①BE=CD;②∠BOD=60°;③∠BDO=∠CEO;④若∠BAC=90°,且DA∥BC,则BC⊥CE.A.1 B.2 C.3 D.4【解答】解:∵△ABD与△AEC都是等边三角形,∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,∴∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE(SAS),∴BE=DC,∠ADC=∠ABE,∵∠BOD=180°﹣∠ODB﹣∠DBA﹣∠ABE=180°﹣∠ODB﹣60°﹣∠ADC=120°﹣(∠ODB+∠ADC)=120°﹣60°=60°,∴∠BOD=60°,∴①正确;②正确;∵△ABD与△AEC都是等边三角形,∴∠ADB=∠AEC=60°,但根据已知不能推出∠ADC=∠AEB,∴∠BDO=∠CEO错误,∴③错误;∵DA ∥BC ,∴∠DAB =∠ABC =60°,∵∠BAC =90°,∴∠ACB =30°,∵∠ACE =60°,∴∠ECB =90°,∴BC ⊥CE ,④正确,综上所述,①②④正确,故选:C .二、填空题(共5小题)7.(2018春•历下区期中)如图,两棵大树间相距13m ,小华从点B 沿BC 走向点C ,行走一段时间后他到达点E ,此时他仰望两棵大树的顶点A 和D ,两条视线的夹角正好为90︒,且EA ED =.已知大树AB 的高为5m ,小华行走的速度为1/m s,小华走的时间是 .【解答】解:90AED ∠=︒,90AEB DEC ∴∠+∠=︒,90ABE =︒,90A AEB ∴∠+∠=︒,A DEC ∴∠=∠,在ABE ∆和DCE ∆中B C A DEC AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABE ECD AAS ∴∆≅∆,5EC AB m ∴==,13BC m =,8BE m ∴=,∴小华走的时间是818()s ÷=,故答案为:8s .8.(2018春•槐荫区期末)如图,要测量河两岸相对两点A 、B 间的距离,先在过点B 的AB 的垂线上取两点C 、D ,使CD BC =,再在过点D 的垂线上取点E ,使A 、C 、E 三点在一条直线上,可证明EDC ABC ∆≅∆,所以测得ED 的长就是A 、B 两点间的距离,这里判定EDC ABC ∆≅∆的理由是.【解答】解:AB BD ⊥,ED BD ⊥,90ABD EDC ∴∠=∠=︒,在EDC ∆和ABC ∆中,ABC EDC BC DCACB ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()EDC ABC ASA ∴∆≅∆.故答案为:ASA .9.(2019春•商河县期末)如图,要在湖两岸A ,B 两点之间修建一座观赏桥,由于条件限制,无法直接测量A 、B 两点间的距离,于是小明想出来这样一种做法:在AB 的垂线BF 上取两点C 、D ,使BC CD =,再定出BF 的垂线DE ,使A ,C ,E 三点在一条直线上,这时测得50DE =米,则AB = 米.【解答】解:根据题意可知90B D ∠=∠=︒,BC CD =,ACB ECD ∠=∠()ABC EDC ASA ∴∆≅∆50AB DE ∴==米.故答案为:5010.(2019春•平阴县期末)如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边ABC ∆和等边CDE ∆,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ .以下五个结论:①AD BE =;②//PQ AE ;③AP BQ =;④DE DP =;⑤120AOE ∠=︒,其中正确结论有 (填序号).【解答】解:等边ABC ∆和等边CDE ∆,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,ACB BCD DCE BCD ∴∠+∠=∠+∠,即ACD BCE ∠=∠,在ACD ∆与BCE ∆中,AC BC ACD BCECD CE =⎧⎪∠=∠⎨⎪=⎩,()ACD BCE SAS ∴∆≅∆, AD BE ∴=,①正确,ACD BCE ∆≅∆,CBE DAC ∴∠=∠, 又60ACB DCE ∠=∠=︒,60BCD ∴∠=︒,ACP BCQ ∴∠=∠,在CQB ∆和CPA ∆中,CBE DAC AC BCBCQ ACP ∠=∠⎧⎪=⎨⎪∠=∠⎩,()CQB CPA ASA ∴∆≅∆,CP CQ ∴=, 又60PCQ ∠=︒,PCQ ∴∆为等边三角形,60PQC DCE ∴∠=∠=︒,//PQ AE ∴,②正确,CQB CPA ∆≅∆,AP BQ ∴=③正确,AD BE =,AP BQ =,AD AP BE BQ ∴-=-,即DP QE =,60DQE ECQ CEQ CEQ ∠=∠+∠=︒+∠,60CDE ∠=︒,DQE CDE ∴∠≠∠,故④错误;//BC DE ,CBE BED ∴∠=∠,CBE DAE ∠=∠,60AOB OAE AEO ∴∠=∠+∠=︒,同理可得出120AOE ∠=︒,60DOE ∴∠=︒,故⑤正确;∴正确结论有:①②③⑤;故答案为:①②③⑤.11.(2019春•金牛区期末)如图,已知四边形ABCD 中,AB =12厘米,BC =8厘米,CD =14厘米,∠B =∠C ,点E 为线段AB 的中点.如果点P 在线段BC 上以3厘米秒的速度由B 点向C 点运动,同时,点Q 在线段CD 上由C 点向D 点运动.当点Q 的运动速度为 厘米/秒时,能够使△BPE 与以C 、P 、Q 三点所构成的三角形全等.【解答】解:设点P 运动的时间为t 秒,则BP =3t ,CP =8﹣3t ,∵∠B =∠C ,∴①当BE =CP =6,BP =CQ 时,△BPE 与△CQP 全等,此时,6=8﹣3t ,解得t,∴BP=CQ=2,此时,点Q的运动速度为23厘米/秒;②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,此时,3t=8﹣3t,解得t,∴点Q的运动速度为6厘米/秒;故答案为:3或.三、解答题(共2小题)12.如图,Rt ABC⊥于D,CE AE∠=︒,直线l为经过点A的任一直线,BD l⊥,∆中,AB AC=,90BAC若BD CE>,试问:(1)AD与CE的大小关系如何?请说明理由;(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.【解答】解:(1)AD与CE的大小关系为AD CE=,理由是:90∠+∠=∠=︒,BAD EAC BAC又CE l⊥于E,90∴∠+∠=︒,ACE EAC∴∠=∠;BAD ACEBD l ⊥于D ,CE l ⊥于E ,90BDA AEC ∴∠=∠=︒;又AB AC =;()ABD CAE AAS ∴∆≅∆,AD CE ∴=.(2)线段BD ,DE ,CE 之间的数量之间关系为:BD DE CE =+,理由如下: ABD CAE ∆≅∆,BD AE ∴=,AD CE =,又AE DE AD =+,BD DE CE ∴=+.13.(2018秋•宿松县期末)(1)问题背景:如图1:在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒,E 、F 分别是BC ,CD 上的点且EAF ∠=60︒,探究图中线段BE 、EF 、FD 之间的数量关系.小王同学探究此问题的方法是,延长FD 到点G .使DG BE =.连结AG ,先证明ABE ADG ∆≅∆,再证明AEF AGF ∆≅∆,可得出结论,他的结论应是 ;(2)探索延伸:如图2,若在四边形ABCD 中,AB AD =,180B D ∠+∠=︒.E ,F 分别是BC ,CD 上的点,且12EAF BAD ∠=∠,上述结论是否仍然成立,并说明理由; (3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30︒的A 处,舰艇乙在指挥中心南偏东70︒的B 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50︒的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E 、F 处,且两舰艇之间的夹角为70︒,试求此时两舰艇之间的距离.【解答】解:(1)EF BE DF =+,证明如下:DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,()ABE ADG SAS ∴∆≅∆,AE AG ∴=,BAE DAG ∠=∠,12EAF BAD ∠=∠, GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠, EAF GAF ∴∠=∠,在AEF ∆和GAF ∆中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,()AEF AGF SAS ∴∆≅∆,EF FG ∴=,FG DG DF BE DF =+=+,EF BE DF ∴=+;故答案为EF BE DF =+.(2)结论EF BE DF =+仍然成立;理由:延长FD 到点G .使DG BE =.连结AG ,如图2,在ABE ∆和ADG ∆中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,AE AG∴=,BAE DAG∠=∠,12EAF BAD∠=∠,GAF DAG DAF BAE DAF BAD EAF EAF∴∠=∠+∠=∠+∠=∠-∠=∠,EAF GAF∴∠=∠,在AEF∆和GAF∆中,AE AGEAF GAFAF AF=⎧⎪∠=∠⎨⎪=⎩,()AEF AGF SAS∴∆≅∆,EF FG∴=,FG DG DF BE DF=+=+,EF BE DF∴=+;(3)如图3,连接EF,延长AE、BF相交于点C,3090(9070)140AOB∠=︒+︒+︒-︒=︒,70EOF∠=︒,12EOF AOB∴∠=∠,又OA OB=,(9030)(7050)180OAC OBC∠+∠=︒-︒+︒+︒=︒,∴符合探索延伸中的条件,∴结论EF AE BF=+成立,即2(4560)210EF=⨯+=(海里).答:此时两舰艇之间的距离是210海里.。
全等三角形经典模型总结
全等三角形相关模型总结一、角平分线模型(一〕角平分线的性质模型辅助线:过点G作⊥射线A、例题1、如图,在△中,∠90°,平分∠,6,4,那么点D到直线的距离是 .2、如图,,∠1=∠2,∠3=∠4,求证:平分∠.B、模型稳固1、如图,在四边形中,>,=,平分∠,求证:∠A+∠C=180°.〔二〕角平分线+垂线,等腰三角形必呈现A、例题辅助线:延长交射线于F 辅助线:过点E作∥射线例1、如图,在△中,∠=3∠C,是∠的平分线,⊥于F .求证:.例2、如图,在△中,∠的角平分线交于点D,且=,作⊥交的延长线于M. 求证:.〔三〕角分线,分两边,对称全等要记全两个图形飞辅助线都是在射线上取点B,使=,从而使△≌△ .A、例题1、如图,在△中,∠60°,∠40°,平分∠交于P,平分∠交于Q,求证:+=+ .2、如图,在△中,是∠的外角平分线,P是上异于点A的任意一点,试比拟+与+的大小,并说明理由 .B、模型稳固1、在△中,>,是∠的平分线,P是线段上任意一点〔不与A 重合〕.求证:->- .2、如图,△中,=,∠A=100°,∠B的平分线交于D,求证:+= .3、如图,△中,=,∠C=90°,∠A的平分线交于D,求证:+= .二、等腰直角三角形模型〔一〕旋转中心为直角顶点,在斜边上任取一点的旋转全等:操作过程:〔1〕将△逆时针旋转90°,得△≌△,从而推出△为等腰直角三角形.〔2〕辅助线作法:过点C作⊥,使=,连结.〔二〕旋转中心为斜边中点,动点在两直角边上滚动的旋转全等:操作过程:连结.〔1〕使=〔或=〕,导出△≌△.〔2〕使∠+∠=180°,导出△≌△.A、例题1、如图,在等腰直角△中,∠=90°,点M、N在斜边上滑动,且∠=45°,试探究、、之间的数量关系.2、两个全等的含有30°,60°角的直角三角板和,按如下图放置,E、A、C三点在一条直线上,连接,取的中点M,连接、. 试判断△的形状,并证明你的结论.B、模型稳固1、,如下图,△中,=,∠=90°,O为中点,假设M、N分别在线段、上移动,且在移动中保持=.〔1〕试判断△的形状,并证明你的结论.〔2〕当M、N分别在线段、上移动时,四边形的面积如何变化?2、在正方形中,=3,=5,=4,求∠+∠为多少度.〔三〕构造等腰直角三角形〔1〕利用以上〔一〕和〔二〕都可以构造等腰直角三角形〔略〕;〔2〕利用平移、对称和弦图也可以构造等腰直角三角形.〔四〕将等腰直角三角形补全为正方形,如下列图:A、例题应用1、如图,在等腰直角△中,=,∠=90°,P为三角形内部一点,满足=,=,求证:∠=15° .三、三垂直模型〔弦图模型〕A、例题:如下图,在△中,=,∠=90°,D为中点,⊥于点E,交于F,连接 .求证:∠=∠ .变式1、:如下图,在△中,=,=,⊥于E,交于F,连接 .求证:〔1〕∠=∠;〔2〕=+ .变式2、在变式1的根底上,其他条件不变,只是将和分别延长交于点P,求证:〔1〕=;〔2〕=+ .四、手拉手模型1、△和△均为等边三角形结论:〔1〕△≌△ .〔2〕∠=∠=60° .〔3〕平分∠ .〔四点共圆证〕拓展:△和△均为等边三角形结论:〔1〕=;〔2〕∠=∠;〔3〕△为等边三角形;〔4〕∥;〔5〕=;〔6〕平分∠;〔四点共圆证〕〔7〕=+;〔8〕=+ .〔〔7〕,〔8〕需构造等边三角形证明〕例、如图①,点M为锐角三角形内任意一点,连接、、.以为一边向外作等边三角形△,将绕点B逆时针旋转60°得到,连接.〔1〕求证:△≌△;〔2〕假设的值最小,那么称点M为△的费尔马点.假设点M为△的费尔马点,试求此时∠、∠、∠的度数;〔3〕小翔受以上启发,得到一个作锐角三角形费尔马点的简便方法:如图②,分别以△的、为一边向外作等边△和等边△,连接、,设交点为M,那么点M即为△的费尔马点.试说明这种作法的依据.2、△和△均为等腰直角三角形结论:〔1〕=;〔2〕⊥ .3、四边形和四边形均为正方形结论:〔1〕=;〔2〕⊥ .变式1、四边形和四边形均为正方形,⊥交于T,求证:〔1〕T 为中点;〔2〕ABC ADF SS .变式2、四边形和四边形均为正方形,T为中点,交于S,求证:⊥ .4、如图,以△的边、为边构造正多边形时,总有:五、半角模型 条件:1,+=1802αββθβ=︒且,两边相等 .思路:1、旋转辅助线:①延长到E ,使,连或延长到F ,使,连②将△绕点A 顺时针旋转90°得△,注意:旋转需证F 、B 、M 三点共线结论:〔1〕=+;〔2〕=2CMN C AB ;〔3〕、分别平分∠、∠ .2、翻折〔对称〕辅助线:①作⊥交于点P②将△、△分别沿、翻折,但一定要证明M、P、N三点共线 .A、例题例1、在正方形中,假设M、N分别在边、上移动,且满足=+,求证:〔1〕∠=45°;〔2〕=2C AB;CMN〔3〕、分别平分∠和∠ .变式:在正方形中,∠=45°,假设M、N分别在边、的延长线上移动,⊥,垂足为H,〔1〕试探究线段、、之间的数量关系;〔2〕求证:=例2、在四边形中,∠B+∠D=180°,=,假设E、F分别为边、上的点,且满足=+,求证:.变式:在四边形中,∠B=90°,∠D=90°,=,假设E、F分别为边、上的点,且,求证:=+ .。
专题-全等三角形的基本模型

∴△ABC≌△DEF(ASA),∴AB=DE
模型二 翻折型 模型解读:将原图形沿着某一条直线折叠后,直线两边的部分能够完全重 合,这两个三角形称之为翻折型全等三角形.此类图形中要注意其隐含条 件,即公共边或公共角相等.
八年级上册人教版数学 第十二章 全等三角形
专题(二) 全等三角形的基本模型(选用)
模型一 平移型 模型解读:把△ABC沿着某一条直线l平行移动,所得到△DEF与△ABC称为 平移型全等三角形.图①,图②是常见的平移型全等三角形.
1.如图,AB∥DE,AC∥DF,BE=CF,求证:AB=DE.
解:∵BE=CF,∴BE+EC=CF+EC,即 BC=EF,∵AB∥DE,AC∥
2.如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE,CD交于点O.求证: OB=OC.
解:∵BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=∠BDO=∠CEO=90°, 在△ABE与△ACD中,∠BEA=∠CDA,∠A=∠A,AB=AC, ∴△ABE≌△ACD(AAS),∴AD=AE,∴BD=EC,∠B=∠C,在△BDO与 △CEO中,∠BDO=∠CEO,DB=EC,∠B=∠C, ∴△BDO≌△CEO(ASA),∴OB=OC
与△BEC 中,∠∠AD==∠∠BEC,B,∴△ACD≌△BEC(AAS),∴AC=BE,CB= DC=CE,
AD,∴AB=AC+CB=AD+BE
模型四 一线三等角型 模型解读:基本图形如下:此类图形 CE⊥DE,那么一定有∠B=∠CAB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD= CE.求证:AB=AD+BE.
(完整版)全等三角形的经典模型(一)
.3全等三角形的经典模型(一)满分晋级三角形 7级倍长中线与截长补短三角形 8级秋天班第二讲全等三角形的经典模型(一)三角形 9级全等三角形的经典模型(二)秋天班第三讲秋天班第四讲漫画释义舞弊?知识互联网题型一:等腰直角三角形模型思路导航等腰直角三角形数学模型思路:⑴利用特别边特别角证题( AC=BC 或 90°,45 ,45 ) . 如图 1; ⑵常有协助线为作高,利用三线合一的性质解决问题 .如图 2;⑶补全为正方形 . 如图 3, 4.CC45° 45°BAABD图 1 图 2图3 图4典题精练【例 1】已知:以下图, Rt△ABC 中, AB=AC, BAC 90°, O 为 BC 的中点,⑴写出点 O 到△ ABC 的三个极点 A、 B、 C 的距离的关系(不要 B求证明)⑵假如点 M、 N 分别在线段 AC、 AB 上挪动,且在挪动中保持OAN=CM .试判断△ OMN 的形状,并证明你的结论 . N⑶假如点 M、 N 分别在线段 CA、 AB 的延伸线上挪动,且在挪动中保持 AN=CM,试判断⑵中结论能否依旧建立,假如是请给出证明.A CM【分析】⑴ OA=OB=OCB⑵连结 OA,∵OA=OCBAOC 45° AN=CMO ∴△ ANO ≌△ CMO∴ON=OM N∴NOA MOC∴NOA BONMOCBON 90 ∴NOM 90 A CM∴△ OMN 是等腰直角三角形⑶△ ONM 依旧为等腰直角三角形,证明:∵∠ BAC=90°, AB=AC,O 为 BC 中点∴∠ BAO=∠ OAC =∠ABC =∠ ACB=45°,∴AO=BO=OC,∵在△ANO 和△CMO 中,AN CMBAO C NBOAO COM AC ∴△ ANO≌△ CMO ( SAS)∴ON=OM,∠AON=∠COM ,又∵∠ COM∠ AOM =90°,∴△ OMN 为等腰直角三角形.M B 【例 2】两个全等的含 30o, 60o角的三角板ADE和三角板 ABC ,如 D图所示搁置, E, A,C 三点在一条直线上,连结BD ,取 BD的中点 M ,连结 ME ,MC.试判断△EMC的形状,并说明原因. ECA【分析】△ EMC 是等腰直角三角形..证明:连结AM .由题意,得DE AC , DAE BAC 90o , DAB90.oD ∴△DAB 为等腰直角三角形.∵DM MB,∴MA MB DM , MDA MAB 45o. E∴MDE MAC 105o,∴△EDM ≌ △CAM.∴EM MC, DME AMC .又EMC EMA AMC EMA DME 90o.∴CM EM,∴△ EMC 是等腰直角三角形.【例 3】已知:如图,△ ABC 中,AB AC ,BAC ,D 是AC 的中90°点, AF BD于E,交BC于F,连结 DF.求证:ADB CDF .【分析】证法一:如图,过点A作AN BC于 N,交BD于M.B ∵ AB AC ,BAC 90°,∴ 3 DAM 45°.∵ C ,∴ 3 C .45°∵ AF BD,∴ 1 BAE 90°∵BAC ,∴.90°2BAE 90°∴ 1 2 .在△ ABM 和△CAF 中,1B1 2AB AC3 C∴ △ ABM ≌△CAF .∴ AM CF .在△ ADM 和△CDF 中,AD CDDAM CAM CF∴△ADM ≌△CDF .∴ADB CDF .证法二:如图,作CM AC 交AF的延伸线于M.∵AF BD ,∴32 ,90°∵BAC ,90°∴ 1 2 90°,∴ 1 3 .3 在△ ACM 和△BAD 中,BM BA CADEFCA3 2DMEN FCA21DEC.1 3AC ABACM BAD90°∴△ACM ≌△BAD .∴ M ADB ,AD CM∵ AD DC ,∴ CM CD .在△CMF 和△CDF 中,CF CFMCF DCF 45°CM CD∴ △CMF ≌△ CDF .∴M CDF∴ADB CDF .【例 4】如图,等腰直角△ ABC中,AC BC , ACB 90°,P为△ ABC 内部一点,知足PB PC ,AP AC ,求证:BCP 15 .AD AP PB CB C【分析】补全正方形ACBD ,连结 DP,易证△ ADP 是等边三角形,DAP 60 ,BAD 45 ,∴BAP 15 ,PAC 30 ,∴ACP 75 ,∴BCP 15 .【研究对象】等腰直角三角形添加成正方形的几种常有题型在解相关等腰直角三角形中的一些问题,若碰到不易解决或解法比较复杂时,可将等腰直角三角形引协助线转变成正方形,再利用正方形的一些性质来解,经常能够起到化难为易的成效,进而顺利地求解。
专题07 全等三角形经典模型一线三等角模型(四大类型)(原卷版)

专题07 全等三角形经典模型一线三等角模型(四大类型)【题型一:标准“K”型图】【题型二:做辅助线构造“K”型图】【题型三:“K”型图与平面直角坐标综合】【题型四:特殊“K”型图】【方法技巧】模型一一线三垂直全等模型如图一,∠D=∠BCA=∠E=90°,BC=AC。
结论:Rt△BDC≌Rt△CEA模型二一线三等角全等模型如图二,∠D=∠BCA=∠E,BC=AC。
结论:△BEC≌△CDA图一图二应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解【类型一:标准“K”型图】【典例1】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图(1)的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;CD EBA(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE 之间的等量关系.【变式1-1】如图,∠BAC=90°,AD是∠BAC内部一条射线,若AB=AC,BE ⊥AD于点E,CF⊥AD于点F.求证:△ABE≌△CAF.【变式1-2】在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E.(1)特例体验:如图①,若直线l∥BC,AB=AC=,分别求出线段BD、CE和DE的长;(2)规律探究:(Ⅰ)如图②,若直线l从图①状态开始绕点A旋转α(0<α<45°),请探究线段BD、CE和DE的数量关系并说明理由;(Ⅱ)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探线段BD、CE和DE的数量关系并说明理由;(3)尝试应用:在图③中,延长线段BD交线段AC于点F,若CE=3,DE .=1,求S△BFC【类型二:做辅助线构造“K”型图】【典例2】如图,△ABC为等腰直角三角形,∠ABC=90°,△ABD为等腰三角形,AD=AB=BC,E为DB延长线上一点,∠BAD=2∠CAE.(1)若∠CAE=20°,求∠CBE的度数;(2)求证:∠BEC=135°;(3)若AE=a,BE=b,CE=c.则△ABC的面积为.(用含a,b,c的式子表示)【变式2-1】已知Rt△ABC和Rt△ADE,AB=AC,AD=AE.连接BD、CE,过点A作AH⊥CE于点H,反向延长线段AH交BD于点F.(1)如图1,当AB=AD时①请直接写出BF与DF的数量关系:BF=DF(填“>”、“<”、“=”)②求证:CE=2AF(2)如图2,当AB≠AD时,上述①②结论是否仍然成立?若成立,请证明;若不成立,请说明理由.【变式2-2】直线l经过点A,△ABC在直线l上方,AB=AC.(1)如图1,∠BAC=90°,过点B,C作直线l的垂线,垂足分别为D、E.求证:△ABD≌△CAE;(2)如图2,D,A,E三点在直线l上,若∠BAC=∠BDA=∠AEC=α(α为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明;(3)如图3,∠BAC=90°过点B作直线l上的垂线,垂足为F,点D是BF 延长线上的一个动点,连结AD,作∠DAE=90°,使得AE=AD,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.【类型三:“K”型图与平面直角坐标综合】【典例3】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).(1)当a=2时,则C点的坐标为;(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.【变式3-1】如图,在平面直角坐标系中,点A的坐标是(4,0),点B的坐标是(0,3),把线段BA绕点B逆时针旋转90°后得到线段BC,则点C的坐标是()A.(3,4)B.(4,3)C.(4,7)D.(3,7)【变式3-4】问题背景:(1)如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,请直接写出BD、CE、DE的数量关系.拓展延伸:(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC请写出DE、BD、CE三条线段的数量关系,并说明理由.实际应用:(3)如图③,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求B点的坐标.【变式3-5】(1)如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线DE,AD⊥DE于点D,BE⊥DE于点E,求证:△ADC≌△CEB;(2)如图2,在等腰直角△ABC中,∠ACB=90°,AC=BC,过点C作直线CE,AD⊥CE于点D,BE⊥CE于点E,AD=2.5cm,DE=1.7cm,求BE 的长;(3)如图3,在平面直角坐标系中,A(﹣1,0),C(1,3),△ABC为等腰直角三角形,∠ACB=90°,AC=BC,求点B坐标.【变式3-6】在直角坐标平面内,点A(3,0),点B是第二象限内任意一点(如图所示).线段AB绕点A旋转90°后的图形为AC,连接BC.(1)当线段AB绕点A顺时针旋转时,①如果点B的坐标为(﹣1,2),过点B作BH⊥OA,垂足为点H,直接写出线段AH的长;②如果点B的横坐标为a,且BC∥OA,求点B的纵坐标;(用含a的代数式表示)(2)设点B的坐标为(m,n),直接写出点C的坐标.(用含m、n的代数式表示)【变式3-7】如图,已知A(3,0),B(0,﹣1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC.(1)如图1,求C点坐标;(2)如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,P A与CQ有何位置和数量关系,猜想并证明;(3)在(2)的条件下若C、P,Q三点共线,求此时∠APB的度数及P点坐标.【变式3-8】点A的坐标为(4,0),点B为y轴负半轴上的一个动点,分别以OB、AB为直角边在第三象限和第四象限作等腰Rt△OBC和等腰Rt△ABD.(1)如图一,若点B坐标为(0,﹣3),连接AC、OD.①求证:AC=OD;②求D点坐标.(2)如图二,连接CD,与y轴交于点E,试求BE长度.【类型四:特殊“K”型图】【典例4】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.【变式4-1】如图,△ABC为等边三角形,点D为BC边上一点,先将三角板60°角的顶点与D点重合,平放三角板,再绕点D转动三角板,三角板60°角的两边分别与边AB、AC交于点E、点F,当DE=DF时,如图(2)所示.求证:△BDE≌△CFD.【变式4-2】如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD,DE.已知∠1=∠2,AD=DE.(1)求证:△ABD≌△DCE;(2)若BD=3,CD=5,求AE的长.【变式4-3】已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE=9cm,∠BDA=∠AEC=∠BAC(1)如图①,若AB⊥AC,则BD与AE的数量关系为,CE与AD 的数量关系为;(2)如图②,判断并说明线段BD,CE与DE的数量关系;(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.。
全等三角形的经典模型(一)

全等三角形的经典模型(一)全等三角形的经典模型(一)在研究三角形的时候,全等三角形是一个非常重要的概念。
这里介绍一些经典的模型,帮助大家更好地理解和应用全等三角形。
三角形7级:倍长中线与截长补短倍长中线与截长补短是一个非常经典的全等三角形模型。
当三角形的中线等于另一条边的一半时,可以证明三角形全等。
此外,如果一条边被截成两段,其中一段的长度等于另一条边的长度减去另一段的长度,那么这两个三角形也是全等的。
三角形8级:全等三角形的经典模型(一)这是一个非常基础的全等三角形模型,利用的是三边对应相等的原理。
如果两个三角形的三条边分别相等,那么这两个三角形是全等的。
三角形9级:全等三角形的经典模型(二)这个模型利用的是两边一角相等的原理。
如果两个三角形的两条边和夹角分别相等,那么这两个三角形是全等的。
题型一:等腰直角三角形模型等腰直角三角形是一个非常特殊的三角形,可以利用其特殊的性质来解决问题。
常见的辅助线包括作高和补全为正方形等。
思路导航如果要解决一个等腰直角三角形的问题,可以尝试以下思路:1.利用特殊边特殊角证题,如AC=BC或90°,45,45。
2.常见辅助线为作高,利用三线合一的性质解决问题。
3.补全为正方形。
等腰直角三角形数学模型思路:⑴利用特殊边特殊角证题(AC=BC或90°,45,45).如图1;⑵常见辅助线为作高,利用三线合一的性质解决问题.如图2;⑶补全为正方形.如图3,4.典题精练例1】已知:如图所示,Rt△ABC中,AB=AC,BAC90°,O为BC的中点。
B⑴写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)⑵如果点M、N分别在线段AC、AB上移动,且在移动中保持AN=CM.试判断△XXX的形状,并证明你的结论.⑶如果点M、N分别在线段CA、AB的延长线上移动,且在移动中保持AN=CM,试判断⑵中结论是否依然成立,如果是请给出证明.解析】⑴OA=OB=OC⑴连接OA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作弊?漫画释义三角形9级全等三角形的经典模型(二)三角形8级全等三角形的经典模型(一)三角形7级 倍长中线与截长补短 满分晋级3全等三角形的经典模型(一)DC B A等腰直角三角形数学模型思路:⑴利用特殊边特殊角证题(AC=BC 或904545︒︒°,,).如图1; ⑵常见辅助线为作高,利用三线合一的性质解决问题.如图2; ⑶补全为正方形.如图3,4.图1 图2图3 图4思路导航知识互联网题型一:等腰直角三角形模型ABCOMN A B COMN【例1】 已知:如图所示,Rt △ABC 中,AB =AC ,90BAC ∠=°,O 为BC 的中点,⑴写出点O 到△ABC 的三个顶点A 、B 、C 的距离的关系(不要求证明)⑵如果点M 、N 分别在线段AC 、AB 上移动,且在移动中保持 AN =CM .试判断△OMN 的形状,并证明你的结论. ⑶如果点M 、N 分别在线段CA 、AB 的延长线上移动,且在移动中保持AN =CM ,试判断⑵中结论是否依然成立,如果是请给出证明. 【解析】 ⑴OA =OB =OC ⑵连接OA ,∵OA =OC 45∠=∠=BAO C ° AN =CM ∴△ANO ≌△CMO∴ON =OM∴∠=∠NOA MOC∴90∠+∠=∠+∠=︒NOA BON MOC BON ∴90∠=︒NOM∴△OMN 是等腰直角三角形⑶△ONM 依然为等腰直角三角形, 证明:∵∠BAC =90°,AB =AC ,O 为BC 中点 ∴∠BAO =∠OAC =∠ABC =∠ACB =45°, ∴AO =BO =OC ,∵在△ANO 和△CMO 中, AN CM BAO C AO CO =⎧⎪∠=∠⎨⎪=⎩∴△ANO ≌△CMO (SAS )∴ON =OM ,∠AON =∠COM , 又∵∠COM -∠AOM =90°, ∴△OMN 为等腰直角三角形.【例2】 两个全等的含30,60角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连接BD ,取BD 的中点M ,连接ME ,MC .试判断EMC △的形状,并说明理由.典题精练ABCOM NMEDCBAFE DCBANM 12A B CDE F312A BCDEF 3【解析】EMC △是等腰直角三角形.证明:连接AM .由题意,得,90,90.DE AC DAE BAC DAB =∠+∠=∠= ∴DAB △为等腰直角三角形. ∵DM MB =,∴,45MA MB DM MDA MAB ==∠=∠=.∴105MDE MAC ∠=∠=, ∴EDM △≌CAM △.∴,EM MC DME AMC =∠=∠.又90EMC EMA AMC EMA DME ∠=∠+∠=∠+∠=. ∴CM EM ⊥,∴EMC △是等腰直角三角形.【例3】 已知:如图,ABC △中,AB AC =,90BAC ∠=°,D 是AC 的中点,AF BD ⊥于E ,交BC 于F ,连接DF . 求证:ADB CDF ∠=∠. 【解析】 证法一:如图,过点A 作AN BC ⊥于N ,交BD 于M .∵AB AC =,90BAC ∠=°, ∴345DAM ∠=∠=°.∵45C ∠=°,∴3C ∠=∠.∵AF BD ⊥,∴190BAE ∠+∠=°∵90BAC ∠=°,∴290BAE ∠+∠=°. ∴12∠=∠.在ABM △和CAF △中,123AB AC C ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABM CAF △≌△.∴AM CF =. 在ADM △和CDF △中, AD CD DAM C AM CF =⎧⎪∠=∠⎨⎪=⎩∴ADM CDF △≌△. ∴ADB CDF ∠=∠.证法二:如图,作CM AC ⊥交AF 的延长线于M . ∵AF BD ⊥,∴3290∠+∠=°, ∵90BAC ∠=°, ∴1290∠+∠=°, ∴13∠=∠.在ACM △和BAD △中,MEDCBAPCBA PCBAD1390AC ABACM BAD ∠=∠⎧⎪=⎨⎪∠=∠=⎩° ∴ACM BAD △≌△.∴M ADB ∠=∠,AD CM = ∵AD DC =,∴CM CD =. 在CMF △和CDF △中, 45=⎧⎪∠=∠=⎨⎪=⎩CF CF MCF DCF CM CD ° ∴CMF CDF △≌△.∴M CDF ∠=∠ ∴ADB CDF ∠=∠.【例4】 如图,等腰直角ABC △中,90AC BC ACB =∠=,°,P 为ABC △内部一点,满足求证:15BCP ∠=︒. PB PC AP AC ==,,【解析】 补全正方形ACBD ,连接DP ,易证ADP △是等边三角形,60DAP ∠=︒,45BAD ∠=︒, ∴15BAP ∠=︒,30PAC ∠=︒,∴75∠=︒ACP , ∴15BCP ∠=︒.【探究对象】等腰直角三角形添补成正方形的几种常见题型 在解有关等腰直角三角形中的一些问题,若遇到不易解决或解法比较复杂时,可将等腰直角三角形引辅助线转化成正方形,再利用正方形的一些性质来解,常常可以起到化难为易的效果,从而顺利地求解。
例4为求角度的应用,其他应用探究如下:【探究一】证角等【备选1】如图,Rt △ABC 中,∠BAC =90°,AB =AC ,M 为AC 中点,连结BM ,作AD ⊥BM交BC 于点D ,连结DM ,求证:∠AMB =∠CMD .21NFA BCDM E EMDCBA【解析】 作等腰Rt △ABC 关于BC 对称的等腰Rt △BFC ,延长AD 交CF 于点N ,∵AN ⊥BM ,由正方形的性质,可得AN =BM ,易证Rt △ABM ≌Rt △CAN ,∴∠AMB =∠CND ,CN =AM , ∵M 为AC 中点,∴CM =CN ,∵∠1=∠2,可证得△CMD ≌△CND , ∴∠CND =∠CMD , ∴∠AMB =∠CMD .【探究二】判定三角形形状【备选2】如图,Rt △ABC 中,∠BAC = 90°,AB =AC ,AD =CE ,AN ⊥BD 于点M ,延长BD交NE 的延长线于点F ,试判定△DEF 的形状.ABCD E FNMKHM NFE D C BA【解析】 作等腰Rt △ABC 关于BC 对称的等腰Rt △BHC ,可知四边形ABHC 为正方形,延长AN 交HC 于点K , ∵AK ⊥BD ,可知AK =BD ,易证:Rt △ABD ≌Rt △CAK , ∴∠ADB =∠CKN ,CK =AD , ∵AD =EC ,∴CK =CE ,易证△CKN ≌△CEN ,∴∠CKN =∠CEN ,易证∠EDF =∠DEF ,∴△DEF 为等腰三角形.【探究三】利用等积变形求面积【备选3】如图,Rt △ABC 中,∠A =90°,AB =AC ,D 为BC 上一点,DE ∥AC ,DF ∥AB ,且BE =4,CF =3,求S 矩形DF AE .GMNFED C BAF EDCB A【解析】 作等腰Rt △ABC 关于BC 的对称的等腰Rt △GCB ,可知四边形ABGC 为正方形,分别延长FD 、ED 交BG 、CG 于点N 、M ,可知DN =EB =4,DM =FC =3, 由正方形对称性质,可知S 矩形DF AE =S 矩形DMGN =DM ·DN =3⨯4=12.【探究四】求线段长【备选4】如图,△ABC 中,AD ⊥BC 于点D ,∠BAC =45°,BD =3,CD =2,求AD 的长.GFED CBADCBA【分析】此题若用面积公式结合勾股定理再列方程组求解是可以的,但解法太繁琐,本题尽管已知条件不是等腰直角三角形,但∵∠BAC =45°,若分别以AB 、AC 为对称轴作Rt △ADB 的对称直角三角形和Rt △ADC 的对称直角三角形,这样就出现两边相等且夹角为90°的图形,满足等腰直角三角形的条件,然后再引辅助线使之转化为正方形.【解析】 以AB 为轴作Rt △ADB 的对称的Rt △AEB ,再以AC 为轴作Rt △ADC 的对称的Rt △AFC .可知BE =BD =3,FC =CD =2,延长EB 、FC 交点G ,∵∠BAC =45°, 由对称性,可得∠EAF =90°,且AE =AD =AF , 易证四边形AFGE 为正方形,且边长等于AD , 设AD =x ,则BG =x -3,CG =x -2,在Rt △BCG 中,由勾股定理,得()()222235x x -+-=, 解得x =6,即AD =6.【探究五】求最小值EA 21【备选5】如图,Rt △ABC 中,∠ACB =90°,AC =BC =4,M 为AC 的中点,P 为斜边AB 上的动点,求PM +PC 的最小值.M PDBCAMPB C A【解析】 将原图形通过引辅助线化归为正方形,即作Rt △ACB 关于AB 对称的Rt △ADB ,可知四边形ACBD 为正方形,连接CD ,可知点C 关于AB 的对称点D ,连接MD 交AB 于点P ,连接CP ,则PM +PC 的值为最小,最小值为:PM +PC =DM =224225+=.常见三垂直模型【引例】已知AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE ,⑴求证:AC ⊥CE ;⑵若将△CDE 沿CB 方向平移得到①②③④等不同情形,1AB C D =, 其余条件不变,试判断AC ⊥C 1E 这一结论是否成立?若成立,给予证例题精讲思路导航题型二:三垂直模型C 1ABC ED D E(C )B AC 1C 1AB C ED C 1AB CED2yDCAyDCA明;若不成立,请说明理由.① ② ③ ④【解析】 ⑴∵AB ⊥BD ,ED ⊥BD∴90∠=∠=︒B D 在ABC △与CDE△中 =⎧⎪∠=∠⎨⎪=⎩AB CDB D BC DE ∴ABC CDE △≌△(SAS )∴1∠=∠E ∵290∠+∠=︒E∴90∠=︒ACE ,即AC ⊥CE⑵ 图①②③④四种情形中,结论永远成立,证明方法与⑴完全类似,只要证明1ABC C DE △≌△∴1∠=∠ACB C ED∵1190∠+∠=︒C ED DC E ∴190∠+∠=︒DC E ACB∴AC ⊥C 1E【例5】 正方形ABCD 中,点A 、B 的坐标分别为()010,,()84,,点C 在第一象限.求正方形边长及顶点C 的坐标.(计算应用:在直角三角形中,两条直角边的平方和等于斜边的平方.)典题精练【解析】 过点C 作CG ⊥x 轴于G ,过B 作BE ⊥y 轴于E ,并反向延长交CG 于F点A 、B 的坐标分别为()010,,()84,∴BE =8, AE =6,∴AB =10∵四边形ABCD 是正方形,∴AB =BC ∵1390∠+∠=︒ 2390∠+∠=︒∴12∠=∠∵90AEB BFC ∠=∠=︒∴△AEB ≌△BFC∴CF =BE =8,BF =AE =6 ∴CG =12 EF =14∴C (14,12),正方形的边长为10【点评】 此题中三垂直模型:【例6】 如图所示,在直角梯形ABCD 中,90ABC ∠=︒,AD BC ∥,AB BC =,E 是AB 的中点,CE BD ⊥. ⑴ 求证:BE AD =;⑵ 求证:AC 是线段ED 的垂直平分线; ⑶ DBC △是等腰三角形吗?请说明理由.【解析】⑴∵90ABC ∠=︒,BD EC ⊥,∴9090ECB DBC ABD DBC ∠+∠=︒∠+∠=︒,,∴ECB ABD ∠=∠, ∵90ABC DAB ∠=∠=︒,AB BC =, ∴BAD CBE △≌△,∴AD BE =. ⑵∵E 是AB 中点,∴EB EA =由⑴得:AD BE =,∴AE AD =∵AD BC ∥,∴45CAD ACB ∠=∠=︒, ∵45BAC ∠=︒,∴BAC DAC ∠=∠由等腰三角形的性质,得:EM MD AM DE =⊥, 即AC 是线段ED 的垂直平分线. ⑶DBC △是等腰三角形,CD BD =由⑵得:CD CE =,由⑴得:CE BD = ∴CD BD =,∴DBC △是等腰三角形.A B CDEM【例7】 ⑴如图1,△ABC 是等边三角形,D 、E 分别是AB 、BC 上的点,且BD =CE ,连接AE 、CD 相交于点P .请你补全图形,并直接写出∠APD 的度数= ; ⑵如图2,Rt △ABC 中,∠B =90°,M 、N 分别是AB 、BC 上的点,且AM =BC 、BM =CN ,连接AN 、CM 相交于点P .请你猜想∠APM = °,并写出你的推理过程.(2013平谷一模)【解析】 ⑴图略,60°⑵45°证明:作AE ⊥AB 且AE CN BM ==. 可证EAM △≌MBC △∴ME MC =,.AME BCM ∠=∠∵90,CMB MCB ∠+∠=︒∴ 90.CMB AME ∠+∠=︒∴ 90.EMC ∠=︒∴ EMC △是等腰直角三角形,45.MCE ∠=︒ 又△AEC ≌△CAN (SAS ) ∴ .ECA NAC ∠=∠ ∴ EC ∥AN.∴ 45.APM ECM ∠=∠=︒EA B CMN P 图2图1P N M CB A CB AA B C D E F E D CB A训练1. 已知:如图,ABC △中,AC =BC ,90∠=︒ACB ,D 是AC 上一点,AE ⊥BD 的延长线于E ,并且12=AE BD ,求证:BD 平分∠ABC .【解析】 延长AE 交BC 的延长线于F∵BE ⊥AF ,90∠=︒ACB ∴ ∠=∠FAC DBC∴ 在△AFC 和△BDC 中, ∠=∠⎧⎪=⎨⎪∠=∠⎩FAC DBC AC BCACF BCD∴△AFC ≌△BDC (ASA )∴AF =BD 又∵12=AE BD 思维拓展训练(选讲)GO FE DCBAE FDA G HF E D CBA∴12==AE AF EF ∴BE 是AF 的中垂线∴BA =BF ∴BD 平分∠ABC训练2. 已知,在正方形ABCD 中,E 在BD 上,DG ⊥CE 于G ,DG 交AC 于F .求证:OE =OF 【解析】 ∵ABCD 是正方形∴OD =OC 90∠=︒DOC ∵DG ⊥CE ∴90∠=︒DGC∴∠=∠DOC DGC ∵ ∠=∠OFD GFC∴ ∠=∠ODF ECO∴ 在△DOF 和△COE 中,∠=∠⎧⎪=⎨⎪∠=∠⎩DOF COE OD OCODF OCE∴△DOF ≌△COE (ASA ) ∴OE=OF训练3. 已知:如图,ABC △中,AB AC =,90BAC ∠=°,D 是BC 的中点,⊥AF BE 于G .求证:DH DF = 【解析】 ∵AB AC =,90BAC ∠=°,D 是BC 的中点∴AD=BD=CD , AD ⊥BC∴90∠=︒ADB∵⊥AF BE∴90∠=︒AGH∴∠=∠DBE DAF∴在△BDH 和△ADF 中, ∠=∠⎧⎪=⎨⎪∠=∠⎩DBH DAF BD ADADB ADF ∴△BDH ≌△ADF (ASA ) ∴DH =DF训练4. 如图,已知矩形ABCD 中,E 是AD 上的一点,F 是AB 上的一点,EF ⊥EC ,且EF =EC ,DE =4cm ,矩形ABCD 的周长为32cm ,求AE 的长.【解析】 在Rt △AEF 和Rt △DEC 中, ∵EF ⊥CE , ∴∠FEC =90°,∴∠AEF +∠DEC =90°,而∠ECD +∠DEC =90°,∴∠AEF =∠ECD . 又∠F AE =∠EDC =90°.EF =EC∴Rt△AEF≌Rt△DCE.∴AE=CD.∴AD=AE+4.∵矩形ABCD的周长为32 cm,∴2(AE+AE+4)=32.解得AE=6 cm.E DCBAABC DEF题型一 等腰直角三角形模型 巩固练习 【练习1】 如图,△ACB 、△ECD 均为等腰直角三角形,则图中与△BDC 全等的三角形为_________.【解析】 △AEC【练习2】 如图,已知Rt ABC △中90ACB ∠=°,AC BC =,D 是BC 的中点,CE AD ⊥,垂足为E .BF AC ∥,交CE 的延长线于点F .求证:2AC BF =.【解析】 ∵90ACB ∠=°,BF AC ∥,∴90ACD CBF ∠=∠=°, 90ADC CAD ∠+∠=°. ∵CE AD ⊥,∴90FCB ADC ∠+∠=°, ∴CAD FCB ∠=∠. 又∵AC CB =,∴ADC CFB △≌△. ∴DC FB =.∵D 是BC 的中点, ∴2BC BF =, 即2AC BF =.题型二 三垂直模型 巩固练习【练习3】 已知:如图,四边形ABCD 是矩形(AD >AB ),点E 在BC 上,且AE =AD ,DF ⊥AE ,垂足为F .请探求DF 与AB 有何数量关系?写出你所得到的结论并给予证明.【解析】 经探求,结论是:DF = AB .证明如下:∵四边形ABCD 是矩形, ∴ ∠B = 90 , AD ∥BC ,∴ ∠DAF = ∠AEB .∵ DF ⊥AE , ∴ ∠AFD = 90,复习巩固F A DC E B图2图1G GA B C DE F F E D C B A ∵ AE = AD ,∴ABE DFA △≌△. ∴ AB = DF .【练习4】 如图,ABC △中,AC BC =,90BCA ∠=°,D 是AB 上任意一点,AE CD ⊥交CD 延长线于E ,BF CD ⊥于F .求证:EF BF AE =-.【解析】 根据条件,ACE ∠、CBF ∠都与BCF ∠互余,∴ACE CBF ∠=∠. 在ACE △和CBF △中,AC CB =,90AEC CFB ∠=∠=°, ∴ACE CBF △≌△. 则CE BF =,AE CF =, ∴EF CE CF BF AE =-=-.【练习5】 四边形ABCD 是正方形.⑴如图1,点G 是BC 边上任意一点(不与B 、C 两点重合),连接AG ,作BF ⊥AG 于点F ,DE ⊥AG 于点E .求证:△ABF ≌△DAE ; ⑵在⑴中,线段EF 与AF 、BF 的等量关系是 (直接写出结论即可,不需要证明);⑶如图2,点G 是CD 边上任意一点(不与C 、D 两点重合),连接AG ,作BF ⊥AG 于点F ,DE ⊥AG 于点E .那么图中全等三角形是 ,线段EF 与AF 、BF 的等量关系是 (直接写出结论即可,不需要证明).【解析】 ⑴在正方形ABCD 中,AB=AD ,90∠=BAD °∴90BAF DAE ∠+∠=° 90∠+∠=︒BAF ABF∴ABF DAE ∠=∠ 在△ABF 和△DAE 中 ,,,∠=∠⎧⎪∠=∠⎨⎪=⎩ABF DAE AFB DEA AB DA ∴ABF DAE △≌△(AAS ) ⑵EF AF BF=-F E D CBA⑶△ABF ≌△DAEEF BF AF=-测试1. 问题:已知ABC △中,2BAC ACB ∠=∠,点D 是ABC △内的一点,且AD CD =,BD BA =.探究DBC ∠与ABC ∠度数的比值.请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明. 当90BAC ∠=︒时,依问题中的条件补全右图. 观察图形,AB 与AC 的数量关系为________; 当推出15DAC ∠=︒时,可进一步推出DBC ∠的度数为_______; 可得到DBC ∠与ABC ∠度数的比值为_________.(2010北京中考)课后测BC B AE CD BAFPQMCBA【解析】 相等;15° ;1:3测试2. 已知:如图,在△ABC 中,90ACB CD AB ∠=︒⊥,于点D ,点E 在AC 上,CE =BC ,过E 点作AC 的垂线,交CD 的延长线于点F . 求证:AB =FC . 【解析】 ∵FE AC ⊥于点E ,90ACB ∠=°,∴90FEC ACB ∠=∠=°. ∴90F ECF ∠+∠=°. 又∵CD AB ⊥于点D , ∴90A ECF ∠+∠=°. ∴A F ∠=∠.在ABC △和FCE △中,,,,A F ACB FEC BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC FCE △≌△. ∴AB FC =.测试3. 如图, Rt △ABC 中,∠C =90°,10cm AC =,5cm BC =,一条线段PQ =AB ,P ,Q 两点分别在AC 上和过A 点且垂直于AC 的射线AM 上运动. 当△ABC 和△APQ 全等时,点Q 到点A 的距离为___________ .5cm 或10cm.(注:文档可能无法思考全面,请浏览后下载,供参考。
