动态规划 销售人员分配问题(matlab编程)
matlab安排生产计划例题及代码

一、概述Matlab是一种理想的工具,可用于制定生产计划。
它具有强大的计算能力和灵活的编程语言,可以帮助企业有效地预测和安排生产计划。
本文将介绍一个生产计划的例题,并提供Matlab代码来解决这个问题。
二、生产计划问题描述假设某工厂需要在未来12个月内生产不同种类的产品。
每个产品有自己的生产时间和成本,也受到市场需求的限制。
现在需要制定一个生产计划,以最大化利润。
具体来说,有以下几个问题需要解决:1. 每个产品的生产时间和成本是多少?2. 每个产品的市场需求是多少?3. 如何制定生产计划,使得利润最大化?三、Matlab代码实现1. 定义产品参数为了方便计算,首先定义每个产品的生产时间、成本和市场需求。
假设有三种产品A、B和C,它们的参数如下:```matlabproduct_time = [4, 5, 6];product_cost = [100, 120, 150];product_demand = [500, 600, 400];```2. 制定生产计划接下来,可以使用Matlab的优化工具箱来制定生产计划。
假设生产计划为x,可以使用线性规划来解决这个问题:```matlabf = -product_cost * x;A = product_time * x;b = product_demand;Aeq = [];beq = [];lb = zeros(1, 3);ub = [];x = linprog(f, A, b, Aeq, beq, lb, ub);```3. 计算最大利润根据得到的生产计划,可以计算出最大利润:```matlabmax_profit = -f * x;disp(['最大利润为:' num2str(max_profit)]);```四、结论通过以上的Matlab代码,可以方便地解决生产计划问题,并得到最大利润。
Matlab的强大计算能力和优化工具箱使得这个问题的解决变得简单而高效。
matlab解决用人分配问题

2010/2011学年第一学期"MATLAB程序设计"大作业一、题目matlab解决用人分配问题二、问题描述和分析(一)问题描述某厂每日8小时的产量不低于1800件。
为了进行质量控制,计划聘请两种不同水平的检验员。
一级检验员的标准为:速度25件/小时,正确率98%,计时工资4元/小时;二级检验员的标准为:速度15件/小时,正确率95%,计时工资3元/小时。
检验员每错检一次,工厂要损失2元。
为使总检验费用最省,该工厂应聘一级、二级检验员各几名?(二)问题分析本题意在考察用MATLAB解决线性规划的问题。
线性规划是合理利用、调配资源的一种应用数学的方法它的基本思路就是在满足一定的约束条件下,使预定的目标达到最优。
即如何合理筹划,精细安排,用最少的资源去实现这个任务,或以最少的投入产生最大的利润。
线性规划问题的标准形式:Min f=c1x1+c2x2+…..+c n x ns.t. a11x1+a12x2+….+a1n x n=b1a21x1+a22x2+….+a2n x n=b2………………….a m1x1+a m2x2+….+a mn x n=b mx1,x2….x n ≥ 0其中:c j, a ij,b i ≥ 0(i=1,2,….m;j=1,2,…n)均为已知数三、建立数学模型设需要一级和二级检验员的人数分别为X1、X2人,总检验费用为fval。
由题意可知每日8小时的检验费用为:fval=(4X1+3X2)*8+(25X1*2%+15X2*5%)*8*2;化简得:fval=40X1+36X2 ;(2)又由“每日8小时的产量不低于1800件”可知:(25X1+15X2)*8≥1800化简得:-5X1-3X2≤-45;(3)若每日检验工作都由一级检验员来做,则:25X1*8≤1800化简得:X1≤9,若每日检验工作都由二级检验员来做,则:15X2*8≤1800化简得:X2≤15;(4)X1、X2自身必须满足条件:X1≥0,X2≥0。
任务分配matlab

在MATLAB中,任务分配通常涉及将任务分配给一组处理器或线程以并行执行。
这可以通过使用MATLAB 的并行计算工具箱(Parallel Computing Toolbox)来实现。
以下是一个简单的任务分配的示例,展示了如何使用这个工具箱。
首先,确保你已经安装了并行计算工具箱。
然后,你可以按照以下步骤进行:1.初始化并行环境:使用parpool函数初始化一个并行工作池。
这个函数将启动一组工作进程,你可以指定进程的数量。
2.matlabparpool('local', 4); % 使用4个工作进程在本地机器上启动并行池1.定义任务:定义一个可以并行执行的任务。
这个任务通常是一个函数或者一个可以独立执行的代码块。
例如,假设我们有一个函数myFunction,它接受一个输入参数并返回一个结果。
matlabfunction result = myFunction(input)% 这里是函数的代码result = input * 2; % 只是一个简单的示例end1.创建任务数组:创建一个包含所有任务的数据数组。
每个元素代表一个单独的任务。
2.matlabtasks = 1:10; % 创建一个包含10个任务的数组,每个任务是将一个数字乘以21.分配和执行任务:使用parfor(并行for循环)来分配和执行任务。
parfor循环将自动将任务分配给可用的工作进程。
2.matlabresults = zeros(size(tasks)); % 初始化结果数组parfor i = 1:numel(tasks)results(i) = myFunction(tasks(i)); % 执行任务并将结果存储在结果数组中end1.关闭并行池:完成任务后,使用delete函数关闭并行池。
2.matlabdelete(gcp); % 关闭当前并行池1.查看结果:最后,你可以查看results数组来检查任务的结果。
动态规划投资分配问题

投资分配问题
按顺序解法计算。 第一阶段:求 f1(x)。显然有 f1(x) = g1(x),得到下表
投资 0 10 20 30 40 50 60
利润
f1(x) = g1(x) 0 20 50 65 80 85 85 最优策略 0 10 20 30 40 50 60
第二阶段:求 f2(x)。此时需考虑第一、第二个工厂如何进行投资分配,以取得 最大的总利润。
y 0,10,L ,50
g2 ( y) f1(50 y)
g2 (0) f1(50)
g
2
(10)
f1
(40)
g g
2 2
(20) (30)
f1 f1
(30) (20)
105
g
2
(40)
f1
(10)
g2 (50) f1(0)
最优策略为(30,20),此时最大利润为105万元。
投资分配问题
现有数量为a(万元)的资金,计划分配给n 个工厂,用于 扩大再生产。
假设:xi 为分配给第i 个工厂的资金数量(万元);gi(xi) 为第i 个工厂得到资金后提供的利润值(万元)。
问题:如何确定各工厂的资金数,使得总的利润为最大。
据此,有下式:
n
max z gi ( xi ) i 1
f2 (20)
max
y 0,10,20
g2 ( y)
f1(20
y)
50
最优策略为(20,0),此时最大利润为50万元。
f2 (10)
max
y 0,10,
g2 ( y)
f1(10
y) 20
最优策略为(10,0)或( 0 , 10 ) ,此时最大利润为20万元。
数学建模解决基本人力资源分配问题

数学建模解决基本人力资源分配问题091001000摘要中国是一个典型的多人口国家,人口基数大是我国的一个显著特点,但与此同时也给我国带来了一个很大并且很难解决的问题,那就是就业问题。
说到就业问题就不能不谈到人力资源分配问题,多人口也就意味着多劳动力,但劳动力分配不均反而给社会带来了负担。
因此不仅仅是知识型人才的分配,就算是社会基层的工作人员的分配也是很重要的问题。
与此对应的是企业公司的收益问题,收益最大化是每个企业的最终目标这是不可否认的,这样的话,人员分配与收益最大的平衡将成为一个很值得考虑的问题。
本文就针对某中型百货商场如何对售货员的分配使得商场需要的人数最少,支付工资最少这一问题进行建模。
本文建模主要从售货员的人数,售货员的交接及岗位需要的人数与时间来着手分析问题,以配备售货员人数最少为目标来解决问题。
1.问题的重述一家中型的百货商场对售货员的需求经过统计分析如下表所示:为了保证售货员充分休息,要求售货员每周工作五天,休息两天,并要求休息的两天是连续的,应如何安排售货员的休息日期,既满足工作需要,又要使配备的售货员的人数最少?2.问题的分析在本模型中,要解决售货员分配人数最少的问题,最先要明白的是售货员的人员分配方式及每天所需的售货员人数,其次要注意的是对售货员连续两天休息时间的安排。
从题中可看出,售货员的时间安排都应该是5天工作2天休息接着再是5天工作2天休息,为使配备人员最少就要使得各售货员之间的工作与休息时间衔接好。
因为每个售货员都工作5天,休息2天,所以只要计算出连续休息2天的售货员人数,也就计算出了售货员的总数。
把连续休息2天的售货员按照开始休息的时间分成7类,再按照每天所需的售货员的人数写出约束条件,即可建立模型,求出最优方案。
3.假设与符号X1,X2,...,X7分别表示从星期一,二,…,日开始休息的人数Min=X1+X2+X3+X4+X5+X6+X7为所要求的目标函数4.模型的建立与求解目标函数为:X1+X2+X3+X4+X5+X6+X7.再按照每天所需售货员的人数写出约束条件。
【精品】线性规划模型与销售计划问题

线性规划模型与销售计划问题摘要:这篇文章主要讨论了线性规划模型与销售计划问题。
这是在生产和销售中经常提到的问题。
通过合理的销售方案以达到更大的经济效益。
为解决这样的问题,主要是通过分析建立线性规划模型,然后利用Matlab软件工具箱中求解线性规划模型的函数linprog,编写Matlab程序,最后就可以求出满足题意的解。
关键词:销售;线性;实际1问题的提出某商店拟制定某种商品7—12月的进货、售货计划,已知商店仓库最大容量为1500件,6月底已存货300件,年底的库存以不少于300件为宜,以后每月初进货一次,假设各月份该商品买进、售出单价如下表。
表1月 7 8 9 10 11 12买进(元/件) 28 26 25 27 24 23.5 售出(元/件) 29 27 26 28 25 25假设每件每月的库存费用为0.5元,为使净收益最多,各月进货、售货计划该如何安排。
2问题的分析在中国战国时期,曾经有过一次流传后世的赛马比赛,相信大家都知道,这就是田忌赛马。
田忌赛马的故事说明在已有的条件下,经过筹划、安排,选择一个最好的方案,就会取得最好的效果。
解决该问题的核心是要确定一组决策变量,使得在确定的约束条件下,目标函数取得最大值。
其中,约束条件是决策变量的线性方程或线性不等式,目标函数是决策变量的线性函数。
由此可知,这种计划的安排归属于线性规划问题,可以建立线性规划模型求解。
该问题中决策变量、目标函数较多,无法利用图解法,而如果利用单纯性法求解过程很复杂,所以使用Matlab 软件编程求解。
3模型假设(1)该种商品的价值不随时间变化而发生增值或减值,每月实际售出商品可以是库存商品或是当月买进商品;(2)每月月初进货,需要计算库存费用的商品量为当月月底库存商品量;(3)只有销售商品收入、买进商品费用、库存费用计入净收益计算公式,而运输费,摊位费等管理费用不计;(4)每月进货、售货计划商品量相互独立,互不影响。
售货员问题的分支限界算法设计

售货员问题的分支限界算法设计售货员问题(Traveling Salesman Problem,TSP)是一个经典的组合优化问题,其目标是找到一条最短的路径,让售货员访问每个城市一次并回到起始城市。
分支限界算法是一种常用于解决组合优化问题的方法之一,可以用于 TSP。
以下是一个简单的分支限界算法设计框架:问题定义:将售货员问题明确定义为一个具体的数学模型,包括城市之间的距离矩阵等。
状态空间树的构建:将问题表示为状态空间树,其中每个节点代表问题的一个可能状态,每个边代表状态之间的转移。
起始节点对应于售货员的起始城市。
界的计算:在每个节点上计算一个上界(可行解的上界)和一个下界(最优解的下界)。
这些界用于指导搜索。
搜索过程:使用深度优先搜索或广度优先搜索策略,通过分支和界的计算逐步构建状态空间树,直到找到最优解或搜索完整个状态空间。
分支操作:在每个节点上,生成所有可能的分支(城市的排列顺序),并计算每个分支的成本。
剪枝操作:对于某些分支,如果它们的成本已经超过已知的最优解,可以剪枝,减少搜索空间。
更新最优解:在搜索过程中,不断更新已知的最优解。
终止条件:当搜索到达树的叶子节点时,或者当已知的最优解不再被更新时,算法终止。
下面是一个简单的伪代码示例,演示了 TSP 的分支限界算法:function traveling_salesman(node, cost):if is_leaf(node):update_best_solution(cost)else:for each branch in generate_branches(node):if cost_of(branch) < current_best_solution_cost:traveling_salesman(branch, cost + cost_of(branch))在这个伪代码中,generate_branches 生成当前节点的所有可能分支,is_leaf 判断节点是否是叶子节点,cost_of(branch) 计算分支的成本。
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划算法是一种解决多阶段决策问题的优化方法,它可以在每个阶段选择最优决策,并且在各个阶段间保持最优子结构,从而达到整体最优的目的。
在实际应用中,动态规划算法被广泛用于求解优化问题、路径规划、资源分配等方面。
本文将介绍基于Matlab 的动态规划算法的实现及应用,并深入探讨其在实际问题中的应用。
一、动态规划算法的基本原理动态规划算法的基本原理是通过将问题分解为子问题,并计算每个子问题的最优解,然后存储下来以供后续使用。
最终得到整体最优解。
动态规划算法通常包括以下几个步骤:1. 确定状态和状态转移方程:首先需要确定问题的状态,然后建立状态之间的转移关系,也就是状态转移方程。
状态转移方程描述了问题的子问题之间的关系,是动态规划算法的核心。
2. 初始化:初始化动态规划数组,将初始状态下的值填入数组中。
3. 状态转移:利用状态转移方程计算出各个阶段的最优解,并将其存储在动态规划数组中。
4. 求解最优解:根据动态规划数组中存储的各个阶段的最优解,可以得到整体最优解。
Matlab是一种强大的计算软件,具有丰富的数值计算函数和可视化工具,非常适合实现动态规划算法。
下面以一个简单的背包问题为例,介绍如何在Matlab中实现动态规划算法。
假设有n件物品,每件物品的重量为w[i],价值为v[i]。
现在有一个容量为C的背包,问如何选择物品放入背包,使得背包中物品的总价值最大。
我们需要确定问题的状态和状态转移方程。
在这个问题中,我们可以定义状态dp[i][j]表示在前i件物品中选择若干个放入容量为j的背包中所能获得的最大价值。
状态转移方程可以表示为:dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])然后,我们可以利用Matlab实现这个动态规划算法,代码如下:```matlabfunction max_value = knapsack(w, v, C)n = length(w);dp = zeros(n+1, C+1);for i = 1:nfor j = 1:Cif j >= w(i)dp(i+1,j+1) = max(dp(i,j+1), dp(i,j-w(i)+1)+v(i));elsedp(i+1,j+1) = dp(i,j+1);endendendmax_value = dp(n+1,C+1);end```三、动态规划算法在实际问题中的应用动态规划算法在实际问题中有着广泛的应用,下面以路径规划问题为例,介绍动态规划算法的应用。
matlab求动态规划最优解

matlab求动态规划最优解求解步骤:(1)将过程划分为恰当的阶段。
(2)选择状态变量Xk,使它既能描述过程的状态,又满足无后效性,同时确定允许状态集合Xk。
(3)选择决策变量Uk,确定允许决策集合Uk(Xk)。
(4)写出状态转移方程。
(5)确定阶段指标Vk(xk,Wx)及指标函数Vkn的形式。
(6)写出基本方程即最优值函数满足的递归方程,以及端点条件。
例题:最短路线问题阶段按过程的演变划分,状态由各段的初始位置确定,决策为从各个状态出发的走向,即有Xk+1=Uk(Xk),阶段指标为相邻两段状态间的距离dk(Xk,Uk(Xk)),指标函数为阶段指标之和,最优值函数fk(Xk)是由出发Xk到终点的最短距离(或最小费用),基本方程为:fk(Xk)=min[dk(Xk,Uk(Xk))+fk+1(Xk+1)],k=n,n-1...,2,1,fn+1(Xn+1)=0利用这个模型可以算出例1的最短路线为AB1C2D1E2F2G,相应的最短距离为18。
动态规划的最优性原理:无论过去的状态跟决策如何,对前面的决策所形成的状态而言,后续决策必须构成最优策略。
对于动态规划而言,重要的并不是所谓的模板,比较重要的是在动态规划中,推导的思维方式。
在个人看来动态规划实际就是编程解决大量数据的决策问题的一种重要编程理念和编程思路。
在动态规划的思路即是反向确立后三次状态改变的两次决策量的最优决策,确定了该最优决策之后每次反向推导一步,穷举倒数第三次的不同决策所带来的状态变化量,与之前所得到的的最优决策量进行加成处理(可能加和也可能相减或相乘相除,具体视情况而定),将所得后三次决策的总决策量对比选取最优值,作为后四步的最优状态变化值。
先前重复推导,最终得到该问题的最优策略。
基于MATLAB的动态规划常用算法的实现

第 4期
太 原 师 范 学 院 学 报 ( 自然 科 学 版 )
J OURNAL OF TAI YUAN NORM AL UNI VERS TY ( t rlS in eEdto ) I Nau a ce c iin
Vo. No 4 17 .
De . 2 0 c 08
了 MAT I AB优 化 工 具 箱 .
1 动 态 规 划 的 基 本 模 型
实际 中 , 要构 造一个标 准 的动 态规划模 型 , 常需 要采用 以下几 个步骤 l : 通 2 1 划 分 阶段 : 照问题 的 时间或 空间特 征 , 问题 分为若 干个 阶段. ) 按 把 这些 阶段 必须 是有 序 的或 者是 可排
不 同于 以上单 向递 推算法 的双 向混合 算法 的基本方 程为 :
( ¨1一ma / n V女 ¨l“ ) L一 ( ) ,一1 2 … ) x mi[ ( , +f 1 女]k , ,
解 几 类 典 型 问 题 , 证 了 该 方 法 的 有 效 性 , 时 表 明 该 程 序 对 求 解 动 态 规 划 多 类 典 型 问 题 是 通 用 验 同
的 , 富 了 M ATIAB 优 化 工 具 箱 , 有 一 定 的 应 用 价 值 . 丰 具 [ 键 词 ] 动 态 规 划 ; 序 算 法 ; 序 算 法 ; 合 双 向 算 法 ; ATIAB 关 逆 顺 混 M [ 章 编 号 ] 1 7 - 0 ( 0 8) 4 0 26 05 [ 图 分 类 号 ] 文 6 2 2 27 2 0 0 — 0 - 中 02 . [ 献 标 识 码 ] A 21 3 文
当求 解 时 , 由边 界条件 从 k z 始 , 一,开 由后 向前逆推 , 阶段求 出最 优决 策 和过程 的最 优值 , 到最 后求 逐 直 出 厂 ( 即得到 问题 的最优 解. z ) 类似地 , 动态 规划基本 方程 的顺 序形 式为 :
MATLAB 编程题总结

1.输出x,y 两个中值较大的一个值。
x=input('x='); y=input('y='); if x>y x else y end2.输入x ,计算y 的值。
计算函数的值⎩⎨⎧≥-<+=01201x x x x y ,, x=input('x='); if x<0 y=x+1 elsey=2*x-1 End3.输入一学生成绩,评定其等级。
方法是:90~100分为“优秀”,80~89分为“良好”,70~79分为“中等”,60~69分为“及格”,60分以为“不合格”x=input('x='); if x>100 | x<0 y='输入错误' elseif x>=90 y='优秀' elseif x>=80 y='良好' elseif x>=70 y='中等'elseif x>=60 y='及格' elsey='不合格' end4.某购物超市节日期间举办购物打折扣的促销活动,优惠办法是:每位顾客当天一次性购物在100元以上者,按九五折优惠;在200元以上者,按九折优惠;在300元以上者,按八五折优惠;在500元以上者,按八折优惠。
则可以根据顾客购物款数计算出优惠价。
x=input('x='); if x>=500y=x*0.8 elseif x>=300 y=x*0.85 elseif x>=200 y=x*0.9 elsey=x*0.95 end5.编程计算:S=1+2+3+…+100sum=0;for i=1:100 sum=sum+i; end sum6.计算1~100的奇数和.sum=0;for i=1:2:100 sum=sum+i; end Sum 或sum=0;for i=1:100if mod(i,2)==1 sum=sum+i; endend sum7.百元买百鸡问题。
MATLAB解决数学模型中规划问题

数学模型数学规划1. 某厂生产甲乙两种口味的饮料,每百箱甲饮料需用原料6千克,工人10名,可获利10万元;每百箱乙饮料需用原料5千克,工人20名,可获利9万元.今工厂共有原料60千克,工人150名,又由于其他条件所限甲饮料产量不超过8百箱.问如何安排生产计划,即两种饮料各生产多少使获利最大.进一步讨论:1)若投资0.8万元可增加原料1千克,问应否作这项投资.2)若每百箱甲饮料获利可增加1万元,问应否改变生产计划.解:基本模型决策变量:设生产x1百箱甲饮料,x2百箱乙饮料目标函数:设获利为z=10x+9y万元约束条件:原料和工人的数量均有限,6x1+5x2≤60,10x1+20x2≤150,又有其他条件所限x1≤8非负约束:x1,x2均不能为负值,即x1≥0,x2≥0综上可得:Max z=10x1+9x2s.t. 6x1+5x2≤6010x1+20x2≤1500≤x1≤80≤x2编写Matlab程序如下:C=[-10 -9];A=[6 5;10 20;1 0];B=[60 150 8];Aeq=[];beq=[];vlb=[0;0];vub=[];[x,fval]=linprog(C,A,B,Aeq,beq,vlb,vub)运行结果如下:x =6.42864.2857fval =-102.8571结果分析:若取整数箱饮料,则应该生产6百箱甲饮料,4百箱乙饮料,可最大获利96万元。
进一步讨论:1)若投资0.8万元可增加原料1千克,设增加原料x3千克,则目标函数变为:z=10x1+9x2-0.8x3约束条件变为:s.t 6x1+5x2-x3≤6010x1+20x2≤1500≤x1≤80≤x20≤x3Matlab程序如下:C=[-10 -9 0.8];A=[6 5 -1;10 20 0;1 0 0];B=[60 150 8];Aeq=[];beq=[];vlb=[0;0;0];vub=[];[x,fval]=linprog(C,A,B,Aeq,beq,vlb,vub)运行结果如下:x =8.00003.50005.5000fval =-107.1000结果分析:因为107.1000 >102.8571,所以投资增加原料可以使得最大获利增加,商家应该考虑进行这项投资。
运筹学课设-商场售货员分配问题

目录一、问题提出 ........................................................................ - 1 -二、问题分析 ........................................................................ - 1 -三、模型建立 ........................................................................ - 2 -3.1建立目标函数 (2)3.2建立约束方程 (2)3.3建立数学模型 (3)四、问题求解 ........................................................................ - 3 -五、结果分析 ........................................................................ - 7 - 总结.................................................................................... - 11 - 参考文献............................................................................... - 12 -一、问题提出某商场对售货员的需求分析经过统计分析如下表所示,为了保证售货人员充分休息,售货人员每周工作5天,休息2天,并且要求休息的两天是连续的,那么应该如何安排售货员的作息,就能满足工作需求,又使配备的售货人员的数目最少呢?二、问题分析如何在保证售货员充分休息,售货员每周工作五天,连续休息两天的前提下,排售货员分配问题,既满足工作需求,又能使配备的收货人员的数目最少,这是一个线性规划的问题,以你我们可以建立模型,然后用lindo软件求得最优解。
(完整word版)TSP问题的动态规划解法

TSP问题的动态规划解法第十七组:3103038028 郑少斌3103038029 王瑞锋3103038035 江飞鸿3103038043 韩鑫3103055004 唐万强1.TSP问题简介旅行商问题(Traveling Salesman Problem,简称TSP, 亦称为货单郎问题)可以描述为:对于N 个城市,它们之间的距离已知,有一旅行商要从某一城市走遍所有的城市,且每一城市只能经过一次,最后回到出发的城市,问如何选择路线可使他走过的路径最短。
这是一个典型的组合优化问题。
它有很强的现实意义,可以应用于交通运输,物资调配,旅游线路设置。
对于了解某个国家地理分布也有一定的现实意义。
这个问题的解法有很多种,在这里我们尝试使用最优控制中的动态规划的相关知识来进行求解。
2.TSP问题分析对于这个问题,我们首先想到的是应用穷举法进行解答,但是这个方法时间和空间的复杂度很高。
从表面上看,TSP 问题很简单,其实则不然。
对于N 个城市的TSP,存在的可能路径为(N-1)!/2条,当N较大时,其数量是惊人的。
计算每条路经都需求出N 个距离之和,这样各种路径及其距离之和的计算量正比与N!/2.用搜索法要求就规模大的TSP是不现实的。
例如使用1GFLOPs 次的计算机搜索TSP 所需的时间如下表所示 城市数7152050100200加法量 3105.2⨯ 11105.6⨯ 18102.1⨯ 64105.1⨯ 157105⨯ 37410搜索时间s 5105.2-⨯1.8h350yy 48105⨯ y 14210y 35810由上可知,对于这个问题采用穷举法进行解答是不现实的,这就要求我们采用其他的方法进行解答。
3. 其他求解TSP 问题的方法*贪心法a. 所谓贪心法,就是在组合算法中,将每一步都取局部最优的求解方法。
b. 下表表示用贪心法求解TSP 的过程。
先将各城市间的距离用行列式形式表示,主对角线上用∞表示。
matlab遗传算法求解指派问题

matlab遗传算法求解指派问题
遗传算法(Genetic Algorithm)是一种模拟自然界遗传和进化过程的优化算法,在解决指派问题(Assignment Problem)中具有较好的效果。
指派问题是在给定的
N个任务和N个工人之间,如何分配任务,使得总成本或总效益达到最优化的问题。
使用MATLAB编程语言,我们可以实现遗传算法来求解指派问题。
首先,我
们需要定义一个适应度函数来衡量每个个体的优劣程度。
对于指派问题,适应度函数可以是总成本的负数,或者总效益的正数。
接下来,我们需要定义遗传算法的基本操作,包括选择、交叉和变异。
选择操
作根据个体的适应度进行概率选择,选择适应度较高的个体作为父代。
交叉操作通过交换父代个体的基因片段来产生新的子代个体。
变异操作随机改变个体的某个基因值,增加种群的多样性。
在编写遗传算法代码之前,我们首先需要构建指派问题的数学模型,并使用MATLAB提供的优化函数(如linprog)求解这个模型。
然后,我们可以使用遗传
算法对结果进行进一步优化,以获得更好的解。
在编写遗传算法代码时,我们需要定义种群大小、迭代次数、交叉概率和变异
概率等参数。
通过多次迭代,遗传算法能够搜索到较优的解,并逐渐收敛到最优解。
最后,我们可以将遗传算法求解的指派问题结果与其他方法进行比较,评估遗
传算法在解决指派问题中的效果。
综上所述,遗传算法是一种有效求解指派问题的方法,在MATLAB中实现遗
传算法可以帮助我们得到更好的解。
使用合适的适应度函数和遗传算法操作,我们可以提高算法的性能,并得到最优的任务分配方案。
matlab平均分配问题

matlab平均分配问题在MATLAB中,平均分配问题通常涉及到将一组数据分成若干个相等的部分。
下面是一个简单的例子,说明如何在MATLAB中实现平均分配。
假设我们有一组数据x,长度为n,我们想要将其平均分成m个部分。
在MATLAB 中,我们可以使用以下步骤来实现:确定每部分的长度:每部分的长度是n/m。
确定第一个元素的位置:第一个元素的位置是1。
确定最后一个元素的位置:最后一个元素的位置是n。
计算每个部分中的元素:使用线性索引来访问每个部分中的元素。
下面是一个示例代码,演示如何在MATLAB中实现平均分配:matlab% 定义数据x = [1 2 3 4 5 6 7 8 9 10];% 确定每部分的长度m = 3;length_per_part = length(x) / m;% 计算每个部分中的元素for i = 1:mstart_index = (i-1) * length_per_part + 1; end_index = i * length_per_part;part(i) = x(start_index:end_index);end% 输出结果disp('第一部分:');disp(part(1));disp('第二部分:');disp(part(2));disp('第三部分:');disp(part(3));在这个例子中,我们将数据x平均分成3个部分。
代码中的for循环用于计算每个部分中的元素,并存储在变量part中。
最后,我们输出每个部分的内容。
请注意,如果数据的长度不是m的整数倍,则最后一个部分可能包含较少的元素。
在上面的代码中,我们使用线性索引来访问每个部分中的元素,确保了结果的正确性。
数学建模“教你如何进行人员分配”的问题
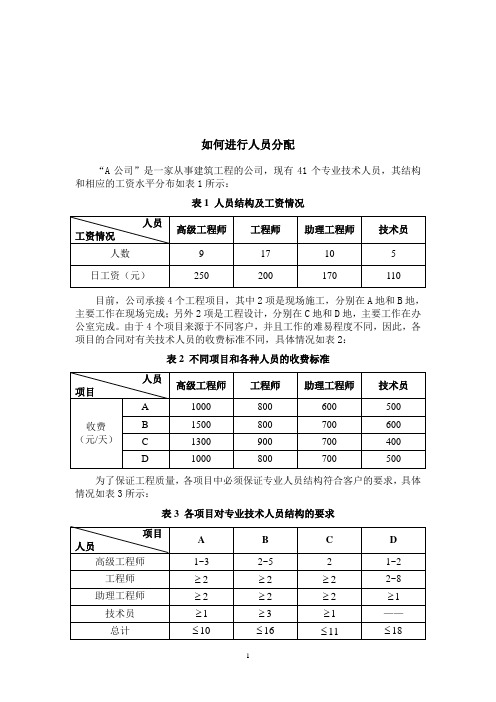
如何进行人员分配“A公司”是一家从事建筑工程的公司,现有41个专业技术人员,其结构和相应的工资水平分布如表1所示:表1 人员结构及工资情况目前,公司承接4个工程项目,其中2项是现场施工,分别在A地和B地,主要工作在现场完成;另外2项是工程设计,分别在C地和D地,主要工作在办公室完成。
由于4个项目来源于不同客户,并且工作的难易程度不同,因此,各项目的合同对有关技术人员的收费标准不同,具体情况如表2:表2 不同项目和各种人员的收费标准为了保证工程质量,各项目中必须保证专业人员结构符合客户的要求,具体情况如表3所示:表3 各项目对专业技术人员结构的要求说明:(1)项目D,由于技术要求较高,人员配备必须是助理工程师以上,技术员不能参加;(2)高级工程师相对稀少,而且是保证质量的关键,因此,各项目客户对高级工程师的配备要求不能少于一定数目的限制。
各项目对其他专业人员也有不同的限制或要求;(3)各项目客户对总人数都有限制;(4)由于C,D两项目是在办公室完成,所以每人每天有50元的管理费开支;由于收费是按人工计算的,而且4个项目总共同时最多需要的人数是10+16+11+18=55,多于公司现有人数41,应如何合理地分配现有的人员力量,使公司每天的直接受益最大?2011年高教社杯全国大学生数学建模竞赛选拔赛题目如何进行人员分配摘要人力资源管理是一个公司进行人力资源分配的重要工作,合理地安排人力资源,能够为企业带来最大的经济效益。
公司不只要对现有的人员进行任务分配,还要使公司的人力资源结构保持一个科学的比例。
本模型旨在为A建筑公司提供一个良好的人员分配方案,达到公司获利最大的目的,以及怎样在以后的人员招聘中使人力资源结构保持一个良好的比例。
在公司现有的情况下,通过分析各种影响因素,排除掉一些不必要的干扰因素,运用整数线性规划和分支定界法的知识建立数学模型,并使用LINGO软件进行编程求解,得出公司人员分配的最佳方案。
算法设计与分析——任务分配问题

算法设计与分析——任务分配问题【问题描述】假设有n个任务需要分配给n个⼈执⾏,每个⼈只执⾏⼀个任务,每个任务只由⼀个⼈执⾏。
第i个⼈执⾏第j个任务的成本是Cij(1<=i,j<=n),求解初最⼩成本的分配⽅案。
【基本算法思想】暴⼒法:⽤矩阵表⽰任务分配问题,矩阵元素Cij(1<=i,j<=n)表⽰⼈员i执⾏任务j的成本。
任务分配问题转化为,在矩阵中的每⼀⾏选取⼀个元素,这些元素分别属于不同的列。
⽤⼀个n元组(j1,j2,...,jn)表⽰⼀个可能解,其中ji表⽰第i⾏中选择的列号。
⽤暴⼒法解决此问题则可表⽰成,⽣成⼀个n元组的全排列,遍历输出最⼩的成本代价即可。
复杂度分析: ⼀个n元组的全排列的个数为n!个。
暴⼒法慎⽤【源代码】#include<stdio.h>#include<iostream>#include<stdlib.h>#include<math.h>#include<algorithm>#define MAX 99999using namespace std;int main(){int num,c[10][10],i,j,temp[10],minCost=MAX,cost=0;cout<<"输⼊任务个数:\n";cin>>num;cout<<"输⼊成本矩阵\n";for(i=1;i<=num;i++){ //输⼊成本的矩阵值for(j=1;j<=num;j++)cin>>c[i][j];temp[i]=i; //设置全排列辅助数组,默认升序}do{ //利⽤next_permutation函数依次求出数组的全排列cost=0;for(i=1;i<=num;i++)cost+=c[i][temp[i]];if(cost<minCost)minCost=cost; //记录最⼩代价}while(next_permutation(temp+1,temp+1+num));cout<<"最⼩成本:\n"<<minCost;return0;}。
matlab求解 产销平衡,求解运输价最优

问题:产销平衡,求解运输价最优:完成者:解:设:从第i 个产地运输到第j 个产地的产品量为x ij , c ij 为第i 个产地运输到第j 个产地的产品的单位运价。
∑∑===n j m i i 1min x c ij ijs.t,1a x i n j ij =∑=i =1,2,3, ,1,1==∑=j b x j mi ij 2,3,40≥xij , i=1,2,3 j=1,2,3,4解决次模型的lingo 程序为:Model :sets :Warehouse /1..3/: a;Customer /1..4/: b;Routes( Warehouse, Customer) : c, x;endsetsdata :a = 3, 6, 6;b = 4, 3, 4, 4;c = 2, 2,2,1,10,8,5,4,7,6,6,8;enddata[OBJ] min = @sum ( Routes: c * x);@for ( Warehouse(i): [SUP]@sum ( Customer(j): x(i,j)) = a(i));@for( Customer(j): [DEM]@sum( Warehouse(i): x(i,j)) = b(j));End下面是此程序运行的结果:Global optimal solution found.Objective value: 69.00000Total solver iterations: 2Variable Value Reduced Cost A( 1) 3.000000 0.000000 A( 2) 6.000000 0.000000 A( 3) 6.000000 0.000000 B( 1) 4.000000 0.000000 B( 2) 3.000000 0.000000 B( 3) 4.000000 0.000000 B( 4) 4.000000 0.000000 C( 1, 1) 2.000000 0.000000 C( 1, 2) 2.000000 0.000000 C( 1, 3) 2.000000 0.000000 C( 1, 4) 1.000000 0.000000 C( 2, 1) 10.00000 0.000000 C( 2, 2) 8.000000 0.000000 C( 2, 3) 5.000000 0.000000 C( 2, 4) 4.000000 0.000000 C( 3, 1) 7.000000 0.000000 C( 3, 2) 6.000000 0.000000 C( 3, 3) 6.000000 0.000000 C( 3, 4) 8.000000 0.000000 X( 1, 1) 3.000000 0.000000 X( 1, 2) 0.000000 1.000000 X( 1, 3) 0.000000 1.000000 X( 1, 4) 0.000000 1.000000 X( 2, 1) 0.000000 4.000000 X( 2, 2) 0.000000 3.000000 X( 2, 3) 2.000000 0.000000 X( 2, 4) 4.000000 0.000000 X( 3, 1) 1.000000 0.000000 X( 3, 2) 3.000000 0.000000 X( 3, 3) 2.000000 0.000000 X( 3, 4) 0.000000 3.000000Row Slack or Surplus Dual Price OBJ 69.00000 -1.000000SUP( 1) 0.000000 0.000000 SUP( 2) 0.000000 -4.000000 SUP( 3) 0.000000 -5.000000 DEM( 1) 0.000000 -2.000000 DEM( 2) 0.000000 -1.000000 DEM( 3) 0.000000 -1.000000 DEM( 4) 0.000000 0.000000由lingo运行的结果可知:由1产地向1销地运送3个单位物品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学规划课程设计
题目:销售人员费配问题
姓名:
学号:
成绩:
2011年6月
销售人员费配问题
摘要:动态规划程序设计是对解最优化问题的一种途径、一种方法,而不是一种特殊算法,本论文通过对动态规划的基本概念和基本思路,并利用Matlab对动态规划中的销售人员分配问题进行了分析,然后利用Matlab语言进行了程序设计和计算,是复杂问题简单化,避免了繁琐的计算,从而使问题能跟方便地得到解决。
关键词:动态规划销售人员分配问题Matlab语言
一、问题重述
某企业甲、乙、丙三个销售市场,其市场的利润与销售人员的分配有关,现有6个销售人员,
二、问题分析
首先我们对设备的分配规定一个顺序,即先考虑分配给甲市场,其次乙市场,最后丙市场,但分配时必须保证企业的总收益最大。
将问题按分配过程分为三个阶段,根据动态规划逆序算法,可设: 1、阶段数k=1,2,3(即甲、乙、丙三个市场的编号分别为1,2,3);
2、状态变量x k 表示分配给第k 个市场至第3个市场的人员数(即第k 阶段初尚未分配的人员数);
3、决策变量u k 表示分配给第k 市场的人员数;
4、状态转移方程:x k+1=x k -u k ;
5、g k (u k )表示u k 个销售人员分配到第k 个市场所得的收益值,它由下表可查得;
6、f k (x k )表示将x k 个销售人员分配到第k 个市场所得到的最大收益值,因而可得出递推方程:
f k (x k )=
6
,...,1,0max =k u [ g k (u k )+ f k+1(x k -u k )],k=1,2,3
f 4(x 4)=0
三、问题求解
1)k=3时,市场丙的分配方案和总收益.
最大收益:f 3(x 3)=6
,...,1,0max
3=u [g 3(x 3)]
最大收益:f 2(x 2)=2max u [g 2(u 2)+ f 3(x 3)]= 2
max
u [g 2(u 2)+ f 3(x 2- u 2
)]
最大收益:f 1(x 1)=1
max
u [g 1(u 1)+ f 2(x 1- u 1)]= max[g 1(u 1)+ f 2(4- u 1)] 为此,我们可以用Matlab 语言编程使问题能跟方便地得到解决,其算法设计如下图:
运用Matlab语言编程,程序如下:m=1;
A=[0 60 80 105 115 130 150];
B=[0 65 85 110 140 160 175];
C=[0 75 100 120 135 150 180];
for i=1:7
for j=1:7
for k=1:7
if i+j+k==9
d(m)=A(i)+B(j)+C(k);
E(m,1)=i;
E(m,2)=j;
E(m,3)=k;
m=m+1;
else
continue;
end
end
end
end
MAXNum=d(1);
for l=1:size(d,2)
if d(l)>MAXNum
MAXNum=d(l);
p=l;
else
continue;
end
end
for l=1:size(d,2)
if d(l)==MAXNum
E(l,:)
else
continue;
end
end
MAXNum
按回车键后可得到以下结果:
ans =
2 5 2
MAXNum =
275
然后可以容易得到最大利润为275,最优分配方案有一个:(1,4,1)。
这样通过计算机的运行可以方便简洁的得到结果,避免了繁琐的计算,大大降低了工作量。
四、参考文献
附录
[1]范玉妹,徐尔.数学规划及其应用[M].北京:冶金工业出版社,2009.9.
[2]百度文库,/view/8be10bc76137ee06eff918ea.html.
[3]楼顺天,MATLAB程序设计语言[M]西安:电子科技大学出版社,1997.8.。
