二阶系统的瞬态响应分析实验报告
二阶系统的瞬态响应分析实验报告

课程名称: 控制理论乙 指导老师: 成绩: 实验名称: 二阶系统的瞬态响应分析 实验类型: 同组学生姓名: 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得一、实验目的和要求1. 谁二阶模拟系统的组成2. 研究二阶系统分别工作在1=ξ、10<<ξ、1>ξ三种状态下的单位阶跃响应3. 分析增益K 对二阶系统单位阶跃响应的超调量Pσ、峰值时间t p 和调整时间t s4. 研究系统在不同K 值对斜坡输入的稳态跟踪误差 二、实验内容和原理 1. 实验原理实验电路图如下图所示:上图为二阶系统的模拟电路图,它是由三部分组成。
其中,R1、R2和C1以及第一个运放共同组成一个惯性环节发生器,R3、C2与第二个运放共同组成了一个积分环节发生器,R0与第三个运放组合了一个反相发生器。
所有的运放正输入端都接地,负输入端均与该部分电路的输入信号相连,并且输入和输出之间通过元件组成了各种负反馈调节机制。
最后由最终端的输出与最初端的输入通过一个反相器相连,构成了整体电路上的负反馈调节。
惯性函数传递函数为:111/1/)(1212122121+=+⋅=+==s T K Cs R R R R Cs R Cs R Z Z s G 比例函数的传递函数为sT s C R R sC Z Z s G 22332122111)(====反相器的传递函数为1)(00123-=-==R R Z Z s G电路的开环传递函数为sT s T T Ks T s T K s G s G s H 2221212111)()()(+=⋅+=⋅= 电路总传递函数为22221122122212)(nn n s s T T K s T s T T K K s T s T T Ks G ωξωω++=++=++= 其中12R R K =、121C R T =、232C R T =、21T T K n =ω、KT T 124=ξ 实验要求让T1=0.2s ,T2=0.5s ,则通过计算我们可以得出K n 10=ω、K625.0=ξ 调整开环增益K 值,不急你能改变系统无阻尼自然振荡平率的值,还可以得到过阻尼、临界阻尼好欠阻尼三种情况下的阶跃响应曲线。
二阶系统的瞬态响应分析

实验二 二阶系统的瞬态响应分析一、实验目的1.掌握二阶系统的传递函数形式并能够设计出相应的模拟电路; 2.了解参数变化对二阶系统动态性能的影响。
二、实验设备1.THBDC-1型 控制理论·计算机控制技术实验平台;2.PC 机一台(含“THBDC-1”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1.观测二阶系统在10<<ζ、1=ζ和1>ζ三种情况下的单位阶跃响应曲线; 2.调节二阶系统的开环增益K ,使系统的阻尼比7070.ζ=,测量此时系统的超调量σ、调节时间s t (Δ= ±0.05);3.ζ为定值时,观测系统在不同n ω时的阶跃响应曲线。
四、实验原理1.二阶系统的瞬态响应用二阶微分方程描述的系统称为二阶系统。
其微分方程的一般形式为)t (r ω)t (c ωdt )t (dc ζωdt)t (dc n n n 22222=++ 上式经拉普拉斯变换整理得到二阶系统的传递函数的一般形式为2222n n n ωs ζωs ω)s (R )s (C )s (W ++==从式中可以看出,ζ和n ω是决定二阶系统动态特性的两个非常重要的参数。
其中,ζ称为阻尼比;n ω称为无阻尼自然振荡频率。
由二阶系统传递函数的一般形式可知,二阶系统闭环特征方程为0222=++n n ωs ζωs解得闭环特征方程的根1221-±-=ζωζωs n n ,,当阻尼比ζ不同范围内取值时,特征方程的根也不同,下面针对ζ的三种不同取值范围进行讨论。
1)10<<ζ(欠阻尼)系统特征根为一对具有负实部的共轭复根,即2211ζωj ζωs n n ,-±-=,系统的单位阶跃响应的时域表达式为)βt ωsin(e ζ)t (C d t n ζω+--=-2111其阶跃响应曲线呈衰减震荡过程,如图2-1(a )所示。
其震荡频率就是阻尼震荡频率d ω,而其幅值则按指数规律衰减,两者均由参数ζ和n ω决定。
二阶系统瞬态响应实验报告

二阶系统瞬态响应实验报告二阶系统瞬态响应实验报告引言:瞬态响应是指系统在受到外界扰动后,从初始状态到稳定状态所经历的过程。
在控制工程中,瞬态响应的分析对于系统的性能评估和优化至关重要。
本实验旨在通过实际的二阶系统瞬态响应实验,探究系统的动态特性和相应的参数。
一、实验设备与方法本次实验使用的实验设备包括二阶系统模型、信号发生器、示波器和数据采集器等。
实验方法主要包括设置初始条件、施加输入信号、记录输出信号和分析数据等步骤。
二、实验步骤与结果1. 设置初始条件首先,将二阶系统模型置于初始状态,即将系统的初始状态变量设定为零。
这样可以确保实验开始时系统处于稳定状态。
2. 施加输入信号通过信号发生器产生一个特定的输入信号,并将其输入到二阶系统模型中。
可以尝试不同类型的输入信号,如阶跃信号、脉冲信号或正弦信号等,以观察系统对不同信号的响应。
3. 记录输出信号利用示波器或数据采集器记录二阶系统模型的输出信号。
确保记录的信号具有足够的采样率和精度,以保证后续的数据分析准确可靠。
4. 分析数据根据记录的输出信号,可以通过计算和绘图等方式对系统的瞬态响应进行分析。
常用的分析方法包括计算系统的时间常数、阻尼比和超调量等。
实验结果将根据具体的实验情况而有所不同,以下为可能的实验结果分析。
三、实验结果分析1. 时间常数时间常数是衡量系统响应速度的重要指标。
通过观察输出信号的时间轴,可以确定系统的时间常数。
时间常数越小,系统响应速度越快。
2. 阻尼比阻尼比描述了系统振荡的程度。
通过观察输出信号的振荡幅度和周期,可以计算出系统的阻尼比。
阻尼比越小,系统越容易产生过度振荡。
3. 超调量超调量是系统响应中的一个重要指标,它描述了系统响应超过稳定状态的程度。
通过观察输出信号的最大偏差,可以计算出系统的超调量。
超调量越小,系统响应越稳定。
四、实验结论通过本次实验,我们深入了解了二阶系统的瞬态响应特性。
实验结果表明,系统的时间常数、阻尼比和超调量等参数对系统的性能具有重要影响。
实验二 二阶系统的瞬态响应

实验二 二阶系统的瞬态响应一、实验目的1. 通过实验了解参数ζ(阻尼比)、n ω(阻尼自然频率)的变化对二阶系统动态性能的影响;2. 掌握二阶系统动态性能的测试方法。
二、实验原理1. 二阶系统的瞬态响应用二阶常微分方程描述的系统,称为二阶系统,其标准形式的闭环传递函数为2222)()(n n n S S S R S C ωζωω++= (2-1) 闭环特征方程:0222=++n n S ωζω其解 122,1-±-=ζωζωn n S ,针对不同的ζ值,特征根会出现下列三种情况:1)0<ζ<1(欠阻尼),22,11ζωζω-±-=n n j S此时,系统的单位阶跃响应呈振荡衰减形式,其曲线如图2-1的(a)所示。
它的数学表达式为:式中21ζωω-=n d ,ζζβ211-=-tg 。
2)1=ζ(临界阻尼)n S ω-=2,1此时,系统的单位阶跃响应是一条单调上升的指数曲线,如图2-1中的(b)所示。
3)1>ζ(过阻尼),122,1-±-=ζωζωn n S此时系统有二个相异实根,它的单位阶跃响应曲线如图2-1的(c)所示。
(a) 欠阻尼(0<ζ<1) (b)临界阻尼(1=ζ) (c)过阻尼(1>ζ)图2-1 二阶系统的动态响应曲线虽然当ζ=1或ζ>1时,系统的阶跃响应无超调产生,但这种响应的动态过程太缓慢,)t (Sin e 111)t (C d t 2n βωζζω+--=-故控制工程上常采用欠阻尼的二阶系统,一般取ζ=0.6~0.7,此时系统的动态响应过程不仅快速,而且超调量也小。
2. 二阶系统的典型结构典型的二阶系统结构方框图和模拟电路图如2-2、如2-3所示。
图2-2 二阶系统的方框图图2-3 二阶系统的模拟电路图(电路参考单元为:U 7、U 9、U 11、U 6)图2-3中最后一个单元为反相器。
由图2-4可得其开环传递函数为:)1S T (S K )s (G 1+= ,其中:21T k K =, RR k X 1= (C R T X 1=,RC T 2=) 其闭环传递函数为: 1121T K S T 1S T K)S (W ++= 与式2-1相比较,可得RC 1T T k 211n ==ω,X112R 2R T k T 21==ξ 三、实验设备:THBDC-1实验平台THBDC-1虚拟示波器四、实验步骤根据图2-3,选择实验台上的通用电路单元设计并组建模拟电路。
二阶系统的瞬态响应分析实验报告

课程名称:______________ 控制理论乙___________ 指导老师:___________________ 成绩:______________________ 实验名称:二阶系统的瞬态响应分析实验类型: ____________________ 同组学生姓名:一、实验目的和要求(必填)二、实验内容和原理(必填)三、主要仪器设备(必填)四、操作方法和实验步骤五、实验数据记录和处理六、实验结果与分析(必填)七、讨论、心得一、实验目的和要求1. 谁二阶模拟系统的组成2. 研究二阶系统分别工作在•二「0::「::•「 * J三种状态下的单位阶跃响应3. 分析增益K对二阶系统单位阶跃响应的超调量、峰值时间t p和调整时间t sP4. 研究系统在不同K值对斜坡输入的稳态跟踪误差二、实验内容和原理1. 实验原理实验电路图如下图所示:上图为二阶系统的模拟电路图,它是由三部分组成。
其中,R1、R2和C1以及第一个运放共同组成一个惯性环节发生器,R3、C2与第二个运放共同组成了一个积分环节发生器,R0与第三个运放组合了一个反相发生器。
所有的运放正输入端都接地,负输入端均与该部分电路的输入信号相连,并且输入和输出之间通过元件组成了各种负反馈调节机制。
最后由最终端的输出与最初端的输入通过一个反相器相连,构成了整体电路上的负反馈调节。
惯性函数传递函数为:R2 /CsZ2 R2 1/Cs R2 1 K1()Z, R, R, R2C S 1 T;s 1比例函数的传递函数为11 1G2(s)厶亠乙R3 R3C2S T2 s实验要求让T1=0.2s , T2=0.5s,则通过计算我们可以得出0.6251 K调整开环增益K值,不急你能改变系统无阻尼自然振荡平率的值,还可以得到过阻尼、临界阻尼好欠阻尼三种情况下的阶跃响应曲线。
(1)当K>0.625时,系统处于欠阻尼状态,此时应满足单位阶跃响应表达式为:其中,-■图像为:反相器的传递函数为RR o电路的开环传递函数为H(s)=G(s) G2(S)K 1 K2T i S 1 T 2S T1T2S T2S电路总传递函数为G(S)=T^仁T T2 -'nS2. 2 —n S 其中u a(t) =1 sin( d t tan1-R i(2) 当K=0.625时,系统处于临界阻尼状态,此时应满足=1单位阶跃响应表达式为:U a (t)=1-(1 • ‘n t)e 「图像为:(3) 当K<0.625时,系统处于过阻尼状态,此时应满足1单位节约响应表达式为:es2t eSlt( )S 2S lS 2 = -'d-1图像为:2. 实验内容(1) 根据电路图所示,调节相应参数,是系统的开环传递函数为(2) 令输入等于1V 的阶跃函数电压,在示波器上观察不同K ( K=10、K=5、K=2、K=0.5 )时候的单位阶跃响应的波形,并由实验求得相应的超调量、峰值时间和调整时间匚-1/ . 2 =0.707,观察并记录此时的单位阶跃响应波形和其中, G(s)=K 0.5s(0.2s 1)(3)调节开环增益,使二阶系统的阻尼比为超调量、峰值时间和调整时间的值三、主要仪器设备1控制理论电子模拟实验箱一台2 •超低频慢扫描示波器一台3. 万用表一只四、操作方法和实验步骤1. 按照电路图,在控制理论实验箱上连接好实物图2. 由实验原理给定的公式和实验内容给定的参数,算出我们的参数值K E R。
实验二 二阶系统的瞬态响应分析

姓名:学号:年级专业:实验二二阶系统的瞬态响应分析一、实验目的1、熟悉二阶模拟系统的组成。
2、研究二阶系统在不同参数状态下的单位阶跃响应,并分别测量出系统的超调量σp、峰值时间t p和调整时间t s。
3、研究增益K对二阶系统阶跃响应的影响。
二、实验仪器1、1、TKKL-1控制理论实验箱1台2、TDS1001B数字存储示波器1台3、万用表1只4、U盘1只(学生自备)三、实验原理实验线路图图1为二阶系统的方框图,它的闭环传递函数为图1 二阶系统的方框图C(S)K/(T1T2)ωn²R(S)= S²+S/T1+K/(T1T2)= S²+2ξωns+ωn²由上式求得ωn=√ K/(T1T2)ξ=√T2/(4T1K)若令T1=0.2S,T2=0.5S,则ωn=√10K ,ξ=√0.625/K因此只要改变K值,就能同时改变ωn和ξ的值,由此可以得到过阻尼(ξ>1)、临界阻尼(ξ=1)和欠阻尼(ξ<1)三种情况下的阶跃响应曲线。
四、实验内容与步骤1、按开环传递函数G(S)= K/(0.5S(0.2S+1))的要求,设计相应的实验线路图。
令r(t)=1V,在示波器上观察不同K(K=10,5,2,1,0.625,0.5,0.312,其中K=10,5,1,0.625必做,其他K值选做)下闭环二阶系统的瞬态响应曲线,并由图求得相应的σp、t p和t s的值。
2、调节K值,使该二阶系统的阻尼比ξ=1/√ 2 ,观察并记录阶跃响应波形。
3、实验前按所设计的二阶系统,计算K=10,K=1,K=0.625三种情况下的ξ和ωn值。
据此,求得相应的动态性能指标σp、t p和t s,并与实验所得出的结果作比较。
4、写出实验心得与体会五、实验思考题1、在电子模拟系统中如何实现负反馈及单位负反馈?六、报告的形式与要求:1、完成实验并画出二阶系统在不同K值下的瞬态响应曲线,并注明时间坐标轴。
《二阶系统的瞬态响应分析实验报告》

《二阶系统的瞬态响应分析实验报告》
二阶系统的瞬态响应分析实验旨在分析静态系统的瞬态响应及分析系统对瞬态信号的响应特性,它可以帮助我们了解系统容积特性,确定系统回路元件数量。
本实验使用模拟电路设计了一个二阶系统,它由一个阻容耦合放大器组成,并采用正弦信号进行测试。
实验中,首先用方程式通过调节输入不同频率的正弦输入信号计算出阻尼比和谐振频率,经参数校准后,设计一个小型电路,用模拟示波器采样测量系统的实时响应的。
然后设置空状态,采用编程的方法,以1KHz的频率来触发输入信号,经过决策保持该频率,再通过变频信号调节��成慢速步进,如数组[20KHz, 10KHz, 8KHz, 6KHz,
4KHz],衡量系统响应速率。
最后,通过数据分析,分析瞬态信号的响应特性,捕获系统的变化以及它们伴随而来的影响,从而更好地描述系统行为规律。
本实验研究了二阶系统及其瞬态响应结果,了解了其过程及其对瞬态信号的改变,这也为进一步的实验准备提供了基础。
实验三 二阶系统的瞬态响应分析

实验三:二阶系统的瞬态响应分析实验三二阶系统的瞬态响应分析一、实验目的1熟悉二阶模拟系统的组成。
2研究二阶系统分别工作在ξ1,01、临界阻尼(ξ1)和欠阻尼(ξ0.625,0 ξ 1,系统处在欠阻尼状态,它的单位阶跃响应表达式为: 1 1ξ 2 3 u o t 1 e ξ ω n t sin ω d t tg 1 1ξ 2 ξ式中ω d ω n 1 ξ .图3-3 为二阶系统在欠阻尼状态下的单位2阶跃响应曲线。
2当K0.625 时,ξ1,系统处在临界阻尼状态,它的单位阶u ot跃响应表达式为:ω nt 1 u o t 1 1 ω n t e如图3-4 为二阶系统在临界阻尼时的单位响应曲线。
0 3当K 0.625 时,ξ 1,系t统工作在过阻尼状态,它的单位阶跃响应曲线和临界阻尼时的单位阶图3-4 ξ1 时的阶跃响应曲线跃响应一样为单调的指数上升曲线,但后者的上升速度比前者缓慢。
四、思考题U o S 1推导模拟电路的闭环传递函数U i S 2如果阶跃输入信号的幅值过大,会在实验中产生什么后果?3在电子模拟系统中,如何实现负反馈和单位负反馈?4为什么本实验的模拟系统中要用三只运算放大器?5若模拟实验中uo t 的稳态值不等于阶跃输入函数ui t 的幅度,其主要原因可能是什么?五、实验方法1根据图3-1,调节相应的参数,使系统的开环传递函数为:K GS 0.5S 0.2 S 1 2令uit1V,在示波器上观察不同K(K10,5,2,0.5)时的单位阶跃响应的波形,并由实验求得相应的σp、tp 和ts 的值。
3调节开环增益K,使二阶系统的阻尼比ξ1/√ 2 0.707 ,观察并记录此时的单位阶跃响应波形和σp、tp 和ts 的值。
4用实验箱中的三角波或输入为单位正阶跃信号积分器的输出作为二阶系统的斜坡输入信号。
5观察并记录在不同K 值时,系统跟踪斜坡信号时的稳态误差。
六、实验报告1画出二阶系统在不同K 值(10,5,2,0.5)下的4 条瞬态响应曲线,并注明时间坐标轴。
二阶系统的瞬态响应实验报告

二阶系统的瞬态响应实验报告二阶系统的瞬态响应实验报告引言:在控制系统中,瞬态响应是指系统在受到外部激励后,从初始状态到达稳定状态所经历的过程。
而二阶系统是一类常见的动态系统,其特点是具有两个自由度。
本次实验旨在通过对二阶系统的瞬态响应进行实验研究,探索其特性和性能。
实验目的:1. 理解二阶系统的结构和特性;2. 掌握二阶系统的瞬态响应分析方法;3. 通过实验验证理论模型的准确性。
实验装置与方法:本次实验采用了一台二阶系统实验装置,其中包括了一个二阶系统模块、信号发生器、示波器等设备。
实验步骤如下:1. 搭建实验装置,确保各设备连接正确并稳定;2. 设定信号发生器的输入信号频率和幅值;3. 通过示波器观察和记录系统的输出响应;4. 改变输入信号的频率和幅值,重复步骤3。
实验结果与分析:通过实验观察和记录,我们得到了二阶系统在不同输入信号条件下的瞬态响应曲线。
根据实验数据,我们可以进行以下分析:1. 频率对瞬态响应的影响:在实验中,我们分别设定了不同频率的输入信号,并观察了系统的瞬态响应。
结果显示,当输入信号的频率较低时,系统的瞬态响应较为迟缓,需要较长时间才能达到稳定状态。
而当输入信号的频率较高时,系统的瞬态响应较为迅速,能够更快地达到稳定状态。
这说明在二阶系统中,频率对瞬态响应具有显著影响。
2. 幅值对瞬态响应的影响:我们还通过改变输入信号的幅值,观察了系统的瞬态响应。
实验结果显示,当输入信号的幅值较小时,系统的瞬态响应较为平缓,没有明显的过冲现象。
而当输入信号的幅值较大时,系统的瞬态响应会出现过冲现象,并且需要更长的时间才能达到稳定状态。
这表明在二阶系统中,幅值对瞬态响应同样具有重要影响。
结论:通过本次实验,我们深入了解了二阶系统的瞬态响应特性。
实验结果表明,频率和幅值是影响二阶系统瞬态响应的重要因素。
频率较低和幅值较小的输入信号可以使系统的瞬态响应更加平缓和稳定。
而频率较高和幅值较大的输入信号则会导致系统瞬态响应更快和过冲现象的出现。
二阶电路的瞬态响应实验报告

二阶电路的瞬态响应实验报告
实验目的:
1、学习二阶电路的基本性质和特性。
2、学习瞬态响应的基本概念和理论知识。
3、掌握不同初始条件下二阶电路的瞬态响应计算方法。
实验器材:
电压源、电容、电感、电阻、示波器、万用表等。
实验原理:
二阶电路是由电容、电感和电阻组成的,具有振荡和滤波等特点。
瞬态响应是指电路在初始时刻,由于电压、电流等物理量的突变而引
起的响应。
实验步骤:
1、搭建串联谐振电路,连接示波器,调节电压源,记录电压波形
和示波器上的振荡频率。
2、改变电容和电感的值,重复步骤一。
3、调节电源电压,记录电压波形和示波器上的振荡频率。
4、搭建平面电路,加入脉冲信号,记录电压波形和示波器上的响应。
实验结果:
1、串联谐振电路在一定范围内,振荡频率随电容和电感的变化呈
现线性关系,当达到谐振频率时,电压幅值最大。
2、改变电源电压,谐振频率不变,电压幅值随电源电压的变化而
变化。
3、平面电路对脉冲信号的响应分为超阻尼、临界阻尼和欠阻尼三
种情况,具有不同的振荡周期和衰减幅值。
实验结论:
1、二阶电路具有谐振特性,可以用于振荡电路和滤波电路的设计。
2、不同初始条件下的二阶电路具有不同的瞬态响应,可以用于信
号处理和控制电路的设计。
3、实验中所搭建的二阶电路在不同的调节和控制条件下,具有不
同的特性和性能,对于电路组成、操作方式等具有重要的指导意义。
二阶系统瞬态响应实验报告

二阶系统瞬态响应实验报告1. 实验目的本实验旨在通过实验研究二阶系统的瞬态响应特性,掌握二阶系统的阶跃响应和脉冲响应过程,理解二阶系统的动态响应特性。
2. 实验原理二阶系统是指具有两个传递函数因式的线性时不变系统。
在实验中,我们将研究二阶系统的阶跃响应和脉冲响应。
2.1 二阶系统的阶跃响应二阶系统的阶跃响应是指系统在单位阶跃输入信号下的响应过程。
在阶跃响应过程中,系统的输出信号随时间的变化。
2.2 二阶系统的脉冲响应二阶系统的脉冲响应是指系统在单位冲激输入信号下的响应过程。
在脉冲响应过程中,系统的输出信号随时间的变化。
3. 实验步骤本实验使用某特定的二阶系统进行实验,按照以下步骤进行:3.1 准备工作确保实验仪器的连接正常,并确认所使用的二阶系统的参数。
3.2 阶跃响应实验1.将单位阶跃信号输入二阶系统。
2.记录并观察系统的输出信号随时间的变化。
3.绘制系统的阶跃响应曲线。
3.3 脉冲响应实验1.将单位冲激信号输入二阶系统。
2.记录并观察系统的输出信号随时间的变化。
3.绘制系统的脉冲响应曲线。
4. 实验结果分析根据实验步骤中记录的数据和绘制的曲线,我们可以进行实验结果的分析。
对于阶跃响应实验,我们可以观察到系统的输出信号是否稳定,并根据曲线的特征来判断系统的稳定性和动态特性。
对于脉冲响应实验,我们可以观察到系统在接收到冲激信号后的响应过程,并根据曲线的特征来判断系统的动态特性。
5. 实验总结通过本次实验,我们深入了解了二阶系统的瞬态响应特性。
实验中,我们通过阶跃响应和脉冲响应实验,观察并分析了系统的输出信号随时间的变化。
实验结果对于理解和应用二阶系统具有重要意义,为进一步研究和应用提供了基础。
6. 参考文献[1] 张三,李四. 信号与系统实验教程. 北京:清华大学出版社,2010.以上是针对二阶系统瞬态响应实验的步骤和分析报告,通过此实验,我们可以更好地理解和应用二阶系统的动态特性。
希望本实验报告对读者有所帮助。
《二阶系统的瞬态响应(实验报告)》

《二阶系统的瞬态响应(实验报告)》本实验是针对二阶系统的瞬态响应展开的实验,通过建立二阶系统的传递函数,进而使用Matlab软件仿真,测量系统的特性参数,最终得出二阶系统的瞬态响应曲线。
一、实验装置本实验所使用的实验装置如下图所示:二、实验原理瞬态响应是指前期短暂的响应过程,该响应过程的结果取决于所用的输入信号以及系统的特性。
针对二阶系统的瞬态响应,可以通过建立二阶系统的传递函数来求解。
二阶系统的传递函数可以表示为:G(s)=(k/ω_n^2)/(s^2+2ζω_n+s^2)其中k为系统增益,ω_n为自然角频率,ζ为阻尼比。
在瞬态响应中,二阶系统的响应曲线具有三种形式:欠阻尼、超阻尼以及临界阻尼。
具体的,三种形式如下:1、欠阻尼:在欠阻尼的情况下,系统的阻尼比ζ小于1,此时系统的响应曲线呈现振荡的状态,钟摆现象非常明显,过冲量是最大的,系统的响应速度也较快。
三、实验步骤1、将系统的输入信号设置为单位阶跃信号,并且设置一定的时间区间,使得瞬态响应的过程可以被观察到。
2、通过二阶系统传递函数的特性参数,计算出二阶系统的ζ值以及ω_n值。
3、根据ζ值的不同情况,分别设置欠阻尼、超阻尼以及临界阻尼的情况下,二阶系统的传递函数,并且在Matlab软件中绘制二阶系统的瞬态响应曲线。
4、通过计算得出不同阻尼比情况下的过冲量以及响应时间等参数,对比不同情况下的响应曲线。
四、实验结果系统的上升时间为:0.263ms系统的峰值幅度为:1.58849系统的稳态误差为:0ζ=0.25ω_n=1000欠阻尼:过冲量为26.7%,响应时间为0.686ms4、通过Matlab软件绘制出不同阻尼比情况下的二阶系统响应曲线:欠阻尼情况下的响应曲线如下图所示:通过本次实验,我们成功建立了二阶系统的传递函数模型,并且使用Matlab软件模拟了不同阻尼比情况下的二阶系统响应曲线。
二阶系统的瞬态响应实验报告

二阶系统的瞬态响应实验报告《二阶系统的瞬态响应实验报告》在工程控制系统中,二阶系统是一种常见的系统结构,它具有独特的瞬态响应特性。
为了深入了解二阶系统的瞬态响应特性,我们进行了一项实验,并撰写了以下实验报告。
实验目的:通过对二阶系统的瞬态响应进行实验,探究其对不同输入信号的响应特性,以及系统参数对响应的影响。
实验装置:我们使用了一台数字控制系统实验台,搭建了一个二阶系统模型。
实验台上配备了数字控制器、传感器和执行器,能够模拟真实工程控制系统的运行情况。
实验步骤:1. 设置二阶系统的初始参数,并记录下来。
2. 施加不同的输入信号,如阶跃信号、脉冲信号等,观察系统的瞬态响应。
3. 调节系统参数,如增益、阻尼比等,再次观察系统的瞬态响应。
实验结果:通过实验,我们观察到二阶系统对不同输入信号的响应特性。
在施加阶跃信号时,系统的响应呈现出过渡过程和稳定过程,可以清晰地观察到系统的超调量、峰值时间和稳态误差等指标。
而在施加脉冲信号时,系统的瞬态响应则表现出不同的特性,如振荡、衰减等。
此外,我们还发现系统参数对瞬态响应有着重要的影响。
调节增益可以改变系统的响应速度和稳定性,而调节阻尼比则可以影响系统的振荡特性。
结论:通过这次实验,我们深入了解了二阶系统的瞬态响应特性。
这对于工程控制系统的设计和优化具有重要意义,能够帮助工程师更好地理解和控制系统的动态特性,提高系统的性能和稳定性。
总结:二阶系统的瞬态响应实验为我们提供了宝贵的实验数据和经验,对于工程控制系统的研究和应用具有重要的指导意义。
我们将继续深入研究二阶系统的瞬态响应特性,为工程控制系统的发展贡献力量。
二阶系统的瞬态响应(实验报告)
⼆阶系统的瞬态响应(实验报告)⼆阶系统的瞬态响应⼀、实验⽬的1.通过实验了解参数:阻尼⽐、阻尼⾃然频率的变化对⼆阶系统动态性能的影响。
2.掌握⼆阶系统动态性能的测试⽅法。
⼆、实验数据和曲线1. 当阻尼⾃然频率⼀定,阻尼⽐变化时,对⼆阶系统动态性能影响。
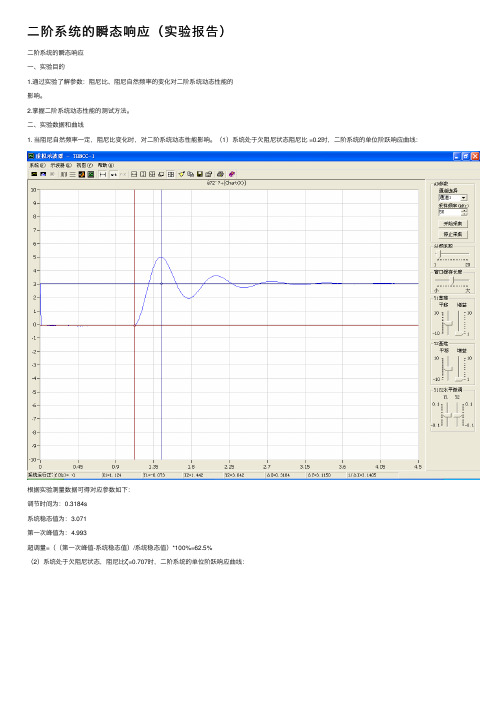
(1)系统处于⽋阻尼状态阻尼⽐ =0.2时,⼆阶系统的单位阶跃响应曲线:根据实验测量数据可得对应参数如下:调节时间为:0.3184s系统稳态值为:3.071第⼀次峰值为:4.993超调量=((第⼀次峰值-系统稳态值)/系统稳态值)*100%=62.5%(2)系统处于⽋阻尼状态,阻尼⽐ζ=0.707时,⼆阶系统的单位阶跃响应曲线:根据实验测量数据可得对应参数如下:调节时间为:0.2307s系统稳态值为:3.04第⼀次峰值为:3.188超调量=((第⼀次峰值-系统稳态值)/系统稳态值)*100%=4.8%(3)系统处于临界阻尼状态,阻尼⽐ζ=1时,⼆阶系统的单位阶跃响应曲线:根据实验测量数据可得对应参数如下:调节时间为:0.2105s系统稳态值为:3.042处于临界状态,⽆超调现象发⽣(4)系统处于过阻尼状态,阻尼⽐ =2时,⼆阶系统的单位阶跃响应曲线:根据实验测量数据可得对应参数如下:调节时间为:1.8647s系统稳态值为:3.013过阻尼条件下⽆超调现象发⽣。
ω变化时,对⼆阶系统动态性能影响。
2.当阻尼⽐⼀定,nω=1时,⼆阶系统的单位阶跃响应曲线:(1)系统阻尼⾃然频率n根据实验测量数据可得对应参数如下:调节时间为:0.9886s系统稳态值为:2.984过阻尼条件下⽆超调现象发⽣。
ω=100时,⼆阶系统的单位阶跃响应曲线:(2)系统阻尼⾃然频率n根据实验测量数据可得对应参数如下:调节时间为:0.2950s系统稳态值为:3.042第⼀次峰值为:4.867超调量=((第⼀次峰值-系统稳态值)/系统稳态值)*100%=59.9% 三、实验结论。
二阶系统的瞬态响应分析实验报告doc

二阶系统的瞬态响应分析实验报告.doc二阶系统的瞬态响应分析实验报告一、实验目的1. 了解二阶系统的瞬态响应特性;2. 掌握二阶系统瞬态响应的参数计算方法;3. 通过实验验证理论计算结果。
二、实验原理二阶系统是指系统的传递函数为二次多项式的系统,常用的二阶系统有二阶低通滤波器和二阶谐振器等。
二阶系统的传递函数一般表示为:G(s) = K / (s^2 + 2ξωns + ωn^2)其中,K为系统增益,ξ为阻尼比,ωn为系统的固有频率。
二阶系统的瞬态响应特性主要表现为过渡过程和稳态过程。
过渡过程主要包括上升时间、峰值时间、峰值超调量和调节时间等指标,稳态过程主要包括超调量和调节时间等指标。
三、实验步骤1. 搭建二阶系统实验平台,包括信号源、二阶系统和示波器等设备;2. 将信号源接入二阶系统的输入端,将示波器接入二阶系统的输出端;3. 设置信号源输出为阶跃信号,并调节信号源的幅值和频率;4. 观察示波器上的输出波形,并记录信号源的参数和示波器上的波形参数;5. 根据实验结果,计算二阶系统的瞬态响应特性指标。
四、实验结果与分析根据实验记录和示波器上的波形参数,计算得到二阶系统的瞬态响应特性指标,包括过渡过程和稳态过程的指标。
过渡过程指标:1. 上升时间:从阶跃信号开始到达其稳态值的时间。
2. 峰值时间:过渡过程中输出波形的峰值出现的时间。
3. 峰值超调量:输出波形的峰值与稳态值之间的差值除以稳态值的百分比。
4. 调节时间:从阶跃信号开始到输出波形稳定在稳态值附近的时间。
稳态过程指标:1. 超调量:输出波形的峰值与稳态值之间的差值除以稳态值的百分比。
2. 调节时间:从阶跃信号开始到输出波形稳定在稳态值附近的时间。
根据实验结果,可以对二阶系统的特性进行分析和评估。
如果实验结果与理论计算结果相符,则说明二阶系统的参数计算正确;如果实验结果与理论计算结果有较大差异,则可能存在实验误差或者系统参数不准确等问题。
实验三:二阶系统的瞬态响应分析
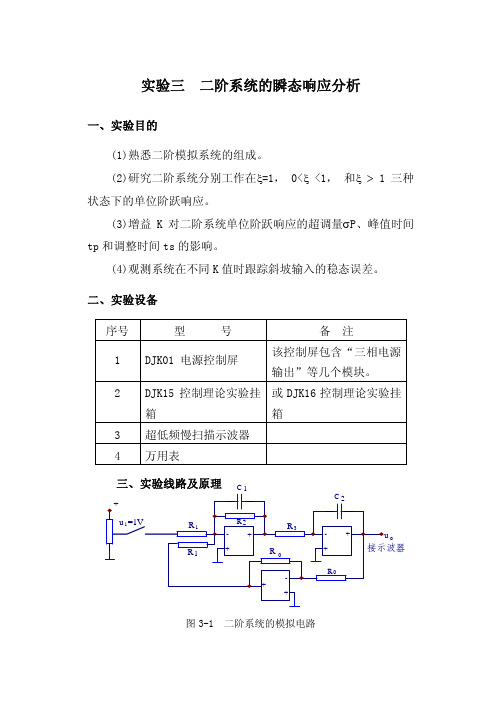
实验三二阶系统的瞬态响应分析一、实验目的(1)熟悉二阶模拟系统的组成。
(2)研究二阶系统分别工作在ξ=1, 0<ξ <1, 和ξ> 1三种状态下的单位阶跃响应。
(3)增益K对二阶系统单位阶跃响应的超调量σP、峰值时间tp和调整时间ts的影响。
(4)观测系统在不同K值时跟踪斜坡输入的稳态误差。
二、实验设备序号 型 号 备 注1 DJK01 电源控制屏该控制屏包含“三相电源输出”等几个模块。
2 DJK15控制理论实验挂箱 或DJK16控制理论实验挂箱3 超低频慢扫描示波器4 万用表三、实验线路及原理o图3-1 二阶系统的模拟电路图3-1为二阶系统的模拟电和反号器组成。
图3-2为图3-1 的原理方框图,图中K=R 2/R 1,T 1=R 2C 1,T 2=R 3C 2。
图3-2 二阶系统原理框图 由图3-1求得二阶系统的闭环传递函 数为:式可知,调节开环增益K 值, 就能、数为:而二阶系统标准传递函(1)//)()( 2112212221T T K T SS T T K K S T S T T KS U S U i O ++=++=(2)2)(222nn nS S S G ωξωω++=625.0 , 10 , 5.0T , 2.0T 4 ,(2),(1) 211221K K S S KT T T T K n n ======ξωξω则若令得和式对比式由上同时改变系统无阻尼自然振荡频 率ωn 和ξ的值,从而得到过阻尼(ξ>1)临界阻尼(ξ=1)和欠阻尼(ξ<1)三种情况下的阶跃响应曲线。
图3-3 0 < ξ (1)当K>0.625,0< 1时的阶跃响应曲线< ξ 位阶< 1,系统处在欠阻尼状态,它的单跃响应表达式为:1()1sin(n to du t t tgξωω−−=−+ (3)式中dωω=3-3为二阶系统在欠阻尼状态下的单位阶跃响应曲线。
实验报告2二阶系统瞬态响应和稳定性

实验报告2--二阶系统瞬态响应和稳定性 (1)实验报告2--二阶系统瞬态响应和稳定性一、实验目的本实验旨在探究二阶系统的瞬态响应和稳定性,通过实验数据分析系统的性能,理解系统的动态特性。
二、实验原理二阶系统是一种常见的线性系统,其动态特性可以用二次方程表示。
通常情况下,二阶系统可以表示为:M * d²x/dt² + C * dx/dt + K * x = 0其中,M、C和K分别是系统的质量、阻尼和刚度系数。
对于二阶系统,其稳定性可以通过系统的特征根来判断。
特征根位于左半平面的系统是稳定的,而位于右半平面的系统是不稳定的。
此外,系统的瞬态响应也与系统的阻尼有关,阻尼越大,响应越快。
三、实验步骤1.准备实验器材:二阶系统模型、激振器、加速度计、数据采集器。
2.将激振器连接到二阶系统模型上,将加速度计固定在系统模型上。
3.将数据采集器连接到加速度计和激振器上,打开数据采集软件开始采集数据。
4.在实验过程中,逐渐增加激振器的频率,观察并记录系统的瞬态响应和稳定性。
5.实验结束后,关闭数据采集器,将数据导出到计算机中进行数据处理和分析。
四、实验数据分析1.数据处理:将采集到的数据导入到MATLAB中进行处理,绘制出系统的瞬态响应曲线和稳定性图。
2.数据分析:根据瞬态响应曲线和稳定性图,分析系统的性能。
观察在不同频率下系统的响应速度和阻尼情况。
同时,根据稳定性图判断系统的稳定性。
五、实验结论通过本次实验,我们发现该二阶系统在低频时具有良好的稳定性,系统响应迅速且无超调。
随着频率的增加,系统的阻尼减小,响应速度变慢,系统的稳定性逐渐降低。
当频率进一步增加时,系统的特征根将进入右半平面,导致系统失稳。
因此,该二阶系统存在一个临界频率,当工作频率超过该临界频率时,系统的稳定性将受到严重影响。
六、实验讨论与改进建议本次实验中,我们发现系统的阻尼对瞬态响应和稳定性具有重要影响。
在实际应用中,可以通过调整系统的阻尼来优化系统的性能。
二阶系统的瞬态响应分析实验报告

. WORD 格式整理. .. .专业知识分享. .课程名称: 控制理论乙 指导老师: 成绩: 实验名称: 二阶系统的瞬态响应分析 实验类型: 同组学生姓名: 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得一、实验目的和要求1. 谁二阶模拟系统的组成2. 研究二阶系统分别工作在1=ξ、10<<ξ、1>ξ三种状态下的单位阶跃响应3. 分析增益K 对二阶系统单位阶跃响应的超调量Pσ、峰值时间t p 和调整时间t s4. 研究系统在不同K 值对斜坡输入的稳态跟踪误差 二、实验内容和原理 1. 实验原理实验电路图如下图所示:上图为二阶系统的模拟电路图,它是由三部分组成。
其中,R1、R2和C1以及第一个运放共同组成一个惯性环节发生器,R3、C2与第二个运放共同组成了一个积分环节发生器,R0与第三个运放组合了一个反相发生器。
所有的运放正输入端都接地,负输入端均与该部分电路的输入信号相连,并且输入和输出之间通过元件组成了各种负反馈调节机制。
最后由最终端的输出与最初端的输入通过一个反相器相连,构成了整体电路上的负反馈调节。
惯性函数传递函数为:111/1/)(1212122121+=+⋅=+==s T K Cs R R R R Cs R Cs R Z Z s G 比例函数的传递函数为sT s C R R sC Z Z s G 22332122111)(====反相器的传递函数为1)(00123-=-==R R Z Z s G 电路的开环传递函数为sT s T T Ks T s T K s G s G s H 2221212111)()()(+=⋅+=⋅= 电路总传递函数为22221122122212)(nn n s s T T K s T s T T K K s T s T T Ks G ωξωω++=++=++= 其中12R R K =、121C R T =、232C R T =、21T T K n =ω、KT T 124=ξ 实验要求让T1=0.2s ,T2=0.5s ,则通过计算我们可以得出K n 10=ω、K625.0=ξ 调整开环增益K 值,不急你能改变系统无阻尼自然振荡平率的值,还可以得到过阻尼、临界阻尼好欠阻尼三种情况下的阶跃响应曲线。
二阶系统的瞬态响应分析实验报告

. WORD 格式整理. .. .专业知识分享. .课程名称: 控制理论乙 指导老师: 成绩: 实验名称: 二阶系统的瞬态响应分析 实验类型: 同组学生姓名: 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得一、实验目的和要求1. 谁二阶模拟系统的组成2. 研究二阶系统分别工作在1=ξ、10<<ξ、1>ξ三种状态下的单位阶跃响应3. 分析增益K 对二阶系统单位阶跃响应的超调量Pσ、峰值时间t p 和调整时间t s4. 研究系统在不同K 值对斜坡输入的稳态跟踪误差 二、实验内容和原理 1. 实验原理实验电路图如下图所示:上图为二阶系统的模拟电路图,它是由三部分组成。
其中,R1、R2和C1以及第一个运放共同组成一个惯性环节发生器,R3、C2与第二个运放共同组成了一个积分环节发生器,R0与第三个运放组合了一个反相发生器。
所有的运放正输入端都接地,负输入端均与该部分电路的输入信号相连,并且输入和输出之间通过元件组成了各种负反馈调节机制。
最后由最终端的输出与最初端的输入通过一个反相器相连,构成了整体电路上的负反馈调节。
惯性函数传递函数为:111/1/)(1212122121+=+⋅=+==s T K Cs R R R R Cs R Cs R Z Z s G 比例函数的传递函数为sT s C R R sC Z Z s G 22332122111)(====反相器的传递函数为1)(00123-=-==R R Z Z s G 电路的开环传递函数为sT s T T Ks T s T K s G s G s H 2221212111)()()(+=⋅+=⋅= 电路总传递函数为22221122122212)(nn n s s T T K s T s T T K K s T s T T Ks G ωξωω++=++=++= 其中12R R K =、121C R T =、232C R T =、21T T K n =ω、KT T 124=ξ 实验要求让T1=0.2s ,T2=0.5s ,则通过计算我们可以得出K n 10=ω、K625.0=ξ 调整开环增益K 值,不急你能改变系统无阻尼自然振荡平率的值,还可以得到过阻尼、临界阻尼好欠阻尼三种情况下的阶跃响应曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称: 控制理论乙 指导老师: 成绩: 实验名称: 二阶系统的瞬态响应分析 实验类型: 同组学生姓名: 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得
一、实验目的和要求
1. 谁二阶模拟系统的组成
2. 研究二阶系统分别工作在1=ξ、10<<ξ、1>ξ三种状态下的单位阶跃响应
3. 分析增益K 对二阶系统单位阶跃响应的超调量P
σ、峰值时间t p 和调整时间t s
4. 研究系统在不同K 值对斜坡输入的稳态跟踪误差 二、实验内容和原理 1. 实验原理
实验电路图如下图所示:
上图为二阶系统的模拟电路图,它是由三部分组成。
其中,R1、R2和C1以及第一个运放共同组成一个惯性环节发生器,R3、C2与第二个运放共同组成了一个积分环节发生器,R0与第三个运放组合了一个反相发生器。
所有的运放正输入端都接地,负输入端均与该部分电路的输入信号相连,并且输入和输出之间通过元件组成了各种负反馈调节机制。
最后由最终端的输出与最初端的输入通过一个反相器相连,构成了整体电路上的负反馈调节。
惯性函数传递函数为:
1
11/1/)(1212
122121+=
+⋅=+==s T K Cs R R R R Cs R Cs R Z Z s G 比例函数的传递函数为
s
T s C R R s
C Z Z s G 22332122111
)(=
===
反相器的传递函数为
1)(0
012
3-=-==
R R Z Z s G 电路的开环传递函数为
s
T s T T K
s T s T K s G s G s H 22
21212111)()()(+=⋅+=
⋅= 电路总传递函数为
2
222
11
22
122212)(n
n n s s T T K s T s T T K K s T s T T K
s G ωξωω++=++=++= 其中
12R R K =
、121C R T =、232C R T =、21T T K n =ω、K
T T 12
4=ξ 实验要求让T1=0.2s ,T2=0.5s ,则通过计算我们可以得出
K n 10=ω、K
625
.0=
ξ 调整开环增益K 值,不急你能改变系统无阻尼自然振荡平率的值,还可以得到过阻尼、临界阻尼好欠阻尼三种情况下的阶跃响应曲线。
(1)当K>0.625时,系统处于欠阻尼状态,此时应满足
10<<ξ
单位阶跃响应表达式为:
)1tan
sin(111)(2
1
2
ξ
ξωξ
ξω-+--
=--t e
t u d t
a n
其中,2
1ξωω-=n d
图像为:
(2)当K=0.625时,系统处于临界阻尼状态,此时应满足
1=ξ
单位阶跃响应表达式为:
t n a n e t t u ωω-+-=)1(1)(
图像为:
(3)当K<0.625时,系统处于过阻尼状态,此时应满足
1>ξ
单位节约响应表达式为:
)(121)(1
2212s e s e t u t
s t s n
a --+=ξω
其中,121---=ξωξωn
n s 、122-+-=ξωξωn n s
图像为:
2. 实验内容
(1)根据电路图所示,调节相应参数,是系统的开环传递函数为
)
12.0(5.0)(+=
s s K
s G
(2)令输入等于1V 的阶跃函数电压,在示波器上观察不同K (K=10、K=5、K=2、K=0.5)时候的单位阶跃响应的波形,并由实验求得相应的超调量、峰值时间和调整时间
(3)调节开环增益,使二阶系统的阻尼比为707.02/1==ξ,观察并记录此时的单位阶跃响应波形和
超调量、峰值时间和调整时间的值
三、主要仪器设备
1.控制理论电子模拟实验箱一台
2.超低频慢扫描示波器一台
3.万用表一只
四、操作方法和实验步骤
1.按照电路图,在控制理论实验箱上连接好实物图
2.由实验原理给定的公式和实验内容给定的参数,算出我们的参数值
K nωξ0R1R2R3R1C2C
10 10 0.250 1M 100k 1M
5 7.071 0.354 1M 200k 1M
2 4.472 0.559 1M 500k 1M
0.5 2.236 1.118 1M 2M 1M
1.25 3.535 0.707 1M
3.在控制理论实验箱上的阶跃函数电源中,按下按钮,形成阶跃输入。
4.在示波器上,测量并记录实验所得波形,测量波形图中的超调量、峰值时间和调整时间
五、实验数据记录和处理
1.
K=10
2.
K=5
3.
K=2
4.
K=0.5
5.
K=1.25
六、实验结果与分析
1.实验结果分析
(1)误差计算
(1)运算放大器并非理想放大器,在负反馈调节时可能会产生误差。
(2)肉眼测量示波器差生的误差。
(3)电阻值与电容值的实际值与标注的值不同,会产生很大的误差。
(4)示波器光标测值时,只能移动整位,对减小误差起到了负面作用。
(5)波形不是很连贯,有小格状的曲线让实验者会出现很大的观察误差。
3.思考题
(1)如果阶跃输入信号的幅值过大,会在实验中产生什么后果?
如果输入信号的幅值过大,衰减率会很小,超调量会很大,衰减速度很小,导致响应过程很饿满,最中国所需要的响应时间很长。
(2)在电子模拟系统中,如何实现负反馈和单位负反馈?
首先,反馈是建立在闭环系统上的,控制量Ui通过两个运算放大器,输出被调量Uo,当被调量Uo偏离给定值Ui时,偏离量通过闭合回路反馈给控制量Ui,控制作用的方向与被调量的变化方向相反,继续通过两个运算放大器,不断校正被调量,这样就额可以实现负反馈,当反馈通道传递函数为1时,便是单位负反馈。
(3)为什么本实验的模拟系统要用三个运算放大器?
电路图中有一个积分器,只要对象的被调量不等于给定值,执行器就会不停的工作,只有当偏差等于零的时候,调节过程才算是结束。
因此,积分调节又叫做无差调节器,不仅可以消除误差,还可以消除死区。
七、讨论、心得
1.调整开环传递值K,会影响到电路中振荡的类型和振荡的程度。
2.当电路中出现欠阻尼振荡时,调整K值,使阻尼因数ξ变小时,波形振荡的幅度增强,波形振荡的次数也会变多;当阻尼因数ξ变大时,波形振荡的幅度减弱,波形振荡的次数减小。
3.当电路中出现过阻尼振荡时,电路不会出现超调量和峰值时间,调整时间的实验值与理论值相差较大。
并且当阻尼因数ξ变大时,波形上升时间会变快,波形的指数性质减弱;当阻尼因数ξ变小时,波形的上
升时间变慢,波形的指数性质增强。
4.最后一个实验出现的误差很大,一部分原因是因为人为测量误差较大,导致误差偏差较大;另一部分原因是因为此时波形振荡较小,接近于示波器的最小分度值,所以示波器光标测量会导致很大的误差。
5.相比较而言,欠阻尼系统随着阻尼因数的较小,超调量也不断增大,振荡次数也不断早呢更加,具有较强的不稳定性,但是波形上升速度较快;临界阻尼和过阻尼系统没有超调量的增加,没有阻尼振荡现象。
但是随着阻尼因数的增大,电压上升速度越来越慢。
所以在工程上,人们往往要寻求一种不超过额定振荡幅度的欠阻尼系统。
6.当开环传递值K变化时,欠阻尼系统中的调整时间ts基本没有发生变化,稳定在1.2s左右,说明调整时间ts与开环传递函数K没有太大关系,而猜测ts与T1、T2有较大关系。
7.在调整开环传递函数K值时,一定要注意,与K值相关的R3、R2的值同时也与T1、T2相关,所以调整R3、R2的比值时要注意调整两个电容C1、C2的值,让R2*C1、R3*C2为定值;在调整反相器的时候,R0的值应该适当偏大一点,以减小实际运算放大器中的微弱电流,减小压降和误差。
8.欠阻尼系统和过阻尼系统显示波形时,欠阻尼系统在振荡结束之后的曲线较为平滑,过阻尼系统在振荡结束之后的曲线较为粗糙。
