数量积向量积混合积
高等数学高数课件 8.3数量积、向量积、混合积

的单位向量.
解
i j k i j c a b ax a y az 3 2
k
4 10 j 5k,
bx by bz 1 1 2
| c | 102 52 5 5,
c
|
c c
|
2
j
5
1 5
k
.
例7 在顶点为 A(1,1,2)、B(5,6,2) 和 C(1,3,1)
的三角形中, 求 AC 边上的高 BD.
解 AC 0,4,3, AB 4,5,0,
三角形 ABC 的面积为
S
Hale Waihona Puke 1 2|AC
AB
|
1 2
152
122
162
25 2
,
又
S
1 2
|
AC
|
|
BD
|,
|
AC |
42 (3)2 5,
所以
25 2
1 2
5
|
BD
|,
从而 | BD | 5.
例8
设向量
m
,
n,
p
两两垂直,
符合右手规则,
且
| m | 4,
2
3 .
(3) a b | b | Pr jba,
4 Pr
jba
a b |b |
3.
例2
证明向量
c
与向量
(a
c
)b
(b
c )a
垂直.
证 [(a c )b (b c )a] c
[(a c )b c (b c )a c]
(b c )[a c a c]
ax j ax
bx
bx
数量积向量积混合积

数量积向量积混合积数量积、向量积和混合积是向量分析中的重要概念,它们是描述向量之间关系的数学工具。
在物理学、工程学、数学等领域,这些概念都有广泛的应用。
本文将介绍数量积、向量积和混合积的定义、性质和应用。
一、数量积数量积又称点积,是两个向量的数量乘积与它们夹角的余弦值的乘积。
设有两个向量a和b,它们的数量积表示为a·b,计算公式为:a·b = |a| |b| cosθ其中,|a|和|b|分别表示向量a和b的模长,θ表示它们之间的夹角。
数量积有以下性质:1. 交换律:a·b = b·a2. 分配律:(a+b)·c = a·c + b·c3. 数量积为零的条件:a·b = 0,当且仅当a和b垂直数量积有广泛的应用,例如,可以用来计算向量的模长、夹角、投影等。
在物理学中,数量积也可以用来计算功、能量等。
二、向量积向量积又称叉积,是两个向量的向量乘积。
设有两个向量a和b,它们的向量积表示为a×b,计算公式为:a×b = |a| |b| sinθ n其中,|a|和|b|分别表示向量a和b的模长,θ表示它们之间的夹角,n表示垂直于a和b所在平面的单位向量,其方向由右手定则确定。
向量积有以下性质:1. 反交换律:a×b = -b×a2. 分配律:a×(b+c) = a×b + a×c3. 向量积为零的条件:a×b = 0,当且仅当a和b平行或其中一个向量为零向量向量积可以用来计算向量之间的夹角、面积、体积等。
在物理学中,向量积也可以用来计算力矩、角动量等。
三、混合积混合积是三个向量的数量积与它们所在平面的法向量的向量积的乘积。
设有三个向量a、b和c,它们的混合积表示为(a×b)·c,计算公式为:(a×b)·c = a·(b×c) = b·(c×a) = c·(a×b)混合积有以下性质:1. 反交换律:a×(b×c) ≠ (a×b)×c2. 分配律:a×(b×c) = b(a·c) - c(a·b)3. 混合积为零的条件:a、b和c共面,或其中一个向量为零向量混合积可以用来计算三角形和四面体的面积和体积。
数量积向量积混合积(IV)

线性代数
03
混合积是线性代数中的一个重要概念,用于描述三个向量的关
系。
向量积和混合积在其他领域的应用
工程学
向量积和混合积在工程学中有广 泛应用,如机械工程、航空航天 工程等。
计算机图形学
向量积和混合积在计算机图形学 中用于描述三维空间中的方向和 旋转,实现三维物体的渲染和动 画效果。
物理学
除了上述的物理应用外,向量积 和混合积在物理学其他分支也有 广泛应用,如光学、量子力学等 。
03
CATALOGUE
混合积
定义与性质
定义
混合积是一个三重积,表示三个向量的乘积,记作((mathbf{A} cdot mathbf{B} cdot mathbf{C}))。
性质
混合积具有分配律,即((mathbf{A} + mathbf{B}) cdot mathbf{C} = mathbf{A} cdot mathbf{C} + mathbf{B} cdot mathbf{C})。
关领域的发展。
THANKS
感谢观看
几何意义
混合积也可以用来计算三个向量构成的平行六面体的体积。
计算方法
计算方法
计算方法
计算方法
混合积的计算公式为((mathbf{A} cdot mathbf{B} cdot mathbf{C}) = |mathbf{A}||mathbf{B}||mathbf{C}|cost heta),其中(theta)是向量(mathbf{A})、 (mathbf{B})和(mathbf{C})之间的夹角。
数量积、向量积和 混合积(iv)
contents
目录
• 数量积 • 向量积 • 混合积 • 向量积、混合积的应用 • 总结与展望
(6)两向量的 数量积 向量积 混合积

a b 0 a x bx a y by a z bz
当 a , b 0 cos
a b a b
2 y
ax bx a y by az bz a a a
2 x 2 y 2 z
b b b
2 x
2 z
二、两向量的向量积 定义2 若由向量 a与 b 所确定的一个向量 c 满足下列条件: c的 b c 的方向既垂直于 a又垂直于 (1) , b 来确定(如图) a 指向 按右手规则从 转向 c 的模为| c || a || b | sin (2) (其中 为 a 与 b 的夹角 ), 则称向量 c 为向量 a与 b 的向量积(或称外 积、叉积),记为 c a b
(2)
3.数量积满足下列运算规律:
(1)交换律 (2)分配律
(3)结合律
a b b a; (a b ) c a c b c ; (a b ) (a) b a (b )
1 V [ AB 6 AC AD] ,
x2 x1 AB x2 x1 , y 2 y1, z 2 z1 1 AC x x , y y , z z . V x3 x1 3 1 3 1 3 1 6 AD x x , y y , z z x4 x1 4 1 4 1 4 1
证略(右手,左手系)
证明:以空间任一点为始点作三个不共面的向量
a, b , c ,令 (a b ) r 则 r
表示以 a, b
为邻边的平行四边形OADB的面积S,而
[abc] r c r c cos S h V(这里h表示以
数量积 向量积 混合积

关于这一类运算,在实际问题中很多,为此,给出向量数量积 的定义.
一、向量的数量积
定义1
设有两个非零向量a与b,它们正向间的夹角为 θ(0≤θ≤π),则称|a|·|b|·cosθ为两向量a与b的数量积(又称 点积),记为a·b,即
【例1】
已知M1(0,2,-1),M2(1,0,1),M3(1,3,2),求 解 因为
所以
一、向量的数量积
【例2】
设力F={1,3,5}作用在一物体上,物体的位移是 s={2,-1,3},求力F对物体做的功W.
解 W=F·s=1×2+3×(-1)+5×3=14.
一、向量的数量积
【例3】
已知三角形的三个顶点为 A(1,2,2),B(1,1,1),C(1,2,0),求证:△ABC为直角三角形, 并求∠A.
而M的方向(按右手系法则确定)垂直于OA和F所确定的平面. 根据此类实际问题研究的需要,我们引入向量积的定义.
二、向量的向量积
图 7-19
二、向量的向量积
定义2
设a,b为两个非零向量,我们定义向量a与b的向量积(又称叉 积).向量积是满足下面条件的一个向量,记为a×b,它的模和方向分别为
(1)|a×b|=|a|·|b| ·sinθ(θ为a与b夹角). (2) a×b垂直于a与b所确定的平面,且a,b,a×b符合右手规则(见 图7-20),从几何上看|a×b|等于以a,b为邻边的平行四边形的面积.
三、向量的混合积
事实上,由图7-21可知 [abc]=a·(b×c)=|a|·|b×c|cosθ=±|b×c|h,其中θ为a与b×c 的夹角,h为两平行底面间的距离.显然a在b×c方向的投影为 ±h,θ为锐角时取正,θ为钝角时取负.注意到|b×c|等于以b, c为邻边的平行四边形的面积,所以|b×c|h 为以a,b,c为棱的 平行六面体的体积的值.如果a,b,c符合右手系法则,θ为锐 角,[abc]>0;否则,θ为钝角,[abc]<0.
向量的数量积向量积混合积课件

b 0 (c b , c o b o , c s b s ) o , s
co a ,sb a b a 0b 0 |a | |||b | ||
ca c o b o c sa c s o b o c sa c s o b 。 o ss
二. 向量的向量积 • 向量的向量积的概念. • 向量的向量积的性质. • 向量的向量积的坐标形式.
1. 向量的向量积的概念 向量积的物理模型
力矩的大小=力 力的 臂大 的小 长度 方向: 由力臂到力符合右则 手法
设力 F作用于杠杆 P处 上 , 点O
( a b ) ( c d ) a ( c d ) b ( c d )
a c a d b c b d
( a b ) ( a b ) ( a b ) ( a ( b )) a a a ( b ) b a b ( b ) a ( b ) | a a | ||a |b p ||p |a ( a r b b r )jj a a 2 2 b a 2 。 b b a b 2
b c 0 ( 5 ) 3 1 1 ( 3 ) 0 。 (bc) pb r a j|a b | b | | 0 2 3 1 2 1 2 1 1。 0 pa r b j|a a | b | | 4 2 ( 1 1 )2 2 2 1 2。 1
问
位于坐标面上的量非的零特向征是什么?
2. 向量的数量积的性质
性质 1
a b b a (交换 ) 律
证 由数量积的定,义得
a b |a ||b ||c | a o , b ,s b a |b ||a ||c | b o , a ,s 因 c a o , b 为 s c b o , a ,所 s 以
数量积 、向量积、混合积

1 ,所以 3π .
ax2
a
2 y
பைடு நூலகம்az2
bx2 by2 bz2
2
4
(3) Prjb a |a|cos
12
12
(4)2
1 2
3
.
1.2 两向量的向量积
在力学上,研究物体转动问题时,不但要考虑这物体所受的力,还要分析这些力
所产生的力矩.下面举一个简单的例子来说明力矩的表达方法.
如图所示,设 O 为一根杠杆 L 的支点,力 F 作用于这杠杆上点 P 处,且 F 与 OP
的夹角为 .由力学中的规定可知,力 F 对支点 O 的力矩是一向量 M ,它的模为
| M || OQ || F || OP || F | sin .
1.2 两向量的向量积
M 的方向垂直于 OP 与 F 所决定的平面; M 的指向符合右手规则,即当右手的四 个手指从 OP 以不超过 π 的角转向 F 来握拳时,大拇指的指向就是 M 的指向,如图所示.
高等数学
1.1 两向量的数量积
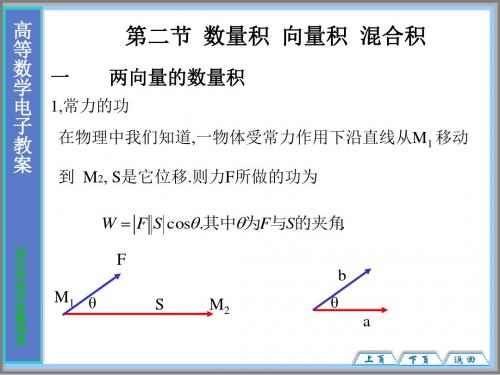
如图所示,设一物体在恒力 F 作用下沿某一直线移动,其位移为 s ,由物理学知,
力 F 所做的功为
W | F | | s | cos ,
其中 为 F 与 s 的夹角.
像这样由两向量的模与其夹角余弦的乘积构成的算式,也会出现在其他问题中.为 此,我们引入两向量数量积的概念.
高等数学 第八章 第二节 数量积 向量积 混合积

5
第八章 第二节
16
例6 已知三点 A(1, 2 , 3 ) , B(3 , 4 , 5 ) , C( 2 , 4 , 7) ,求三
角形 ABC 的面积。
解: 如图
B
S ABC
=
1 2
AB
AC
sin
= 1 AB AC
A
C
2
i jk
= 1 2 2 2 = 1 (4 , − 6 , 2)
2
2
124
且 | m |= 4 , | n |= 2 , | p |= 3 ,计算 (m n) p 。
第八章 第二节
19
内容小结
1 向量的数量积 (结果是一个数量) ; 2 向量的向量积 (结果是一个向量) ; 3 数量积的坐标表示(对应坐标乘积之和) ; 4 向量积的坐标表示(行列式) ;
5 向量垂直的充要条件 (数量积为零) ;
= axbx + a yby + azbz
数量积的 坐标表达式 a b = (ax , a y , az ) (bx , by , bz )
= axbx + a yby + azbz
第八章 第二节
6
a
b
=
a x bx
+
a yby
+
azbz
a ⊥ b axbx + a yby + azbz
b
证: 如图, 设
CB = a , CA = b , AB = c
c B
C
aห้องสมุดไป่ตู้
则
c
2
=
cc
= (a − b)(a − b)
=
高等数学@2.数量积向量积混合积

4 5 0
S 1 | AC AB | 1 152 122 162 25 ,
2
2
2
16
| AC | 42 (3)2 5, S 1| AC | | BD | 2
25 1 5 | BD | | BD | 5. 22
17
练习题 1.已知 | a | 3 | b | 26 | a b | 72 则a b ___3_0_ 2.已知 (a,b) 2 ,且 | a | 1 | b | 2 则(a b)2 __3___
(其中θ是 a与 b的夹角) a×b 的方向既垂直于 a,又垂直于 b 且按 a , b , a×b 的顺序 符合右手法则. 向量积也称“叉积”、“外积”.
注:(1) a a 0. (2) a//b a b 0.
10
(3) | a×b | 等于以 a,b
a×b
为邻边的平行四边形的面积.
| i || j || k | 1, i j k j k i k i j a b (axi ay j azk) (bxi by j bzk),
axbxi i aybx j i azbxk i axbyi j ayby j j
prpr2已知为单位向量且满足计算二两向量的向量积二两向量的向量积实例设o为杠杆l的支点有一力f作用于杠杆对支点o的力矩是一向量mop所决定的平面符合右手法则
第二节 数量积 向量积 混合积
1
一、两向量的数量积
一物体在常力F 作用下沿直线运动,以 s 表示位移,
则力F 所作的功为 W | F || s | cos
所求向量为: 1 (0,10,5) (0, 2 , 1 )
《高等数学》第七章-数量积-向量积-混合积

首页
上页
返回
下页
结束
3. 运算律
(1) 交换律 (2) 结合律
b a
a ( b)
( a ) ( b) a ( b)
(ab)
(3) 分配律
(a b) c
Pr jc a Pr jc b Pr jc ( a b)
事实上, 当 c 0 时, 显然成立 ; 当c 0时
a b c c Pr jc a b c Prjc a Prjc b
c Pr jc a c Pr jc b a c b c
首页
上页
返回
下页
结束
例1. 证明三角形余弦定理
c2 a2 b2 2abcos
证: 如图 . 设
i j jk ki 0
a b axbx ayby azbz
两向量的夹角公式 当 为非零向量时, 由于
a b cos , 得
cos
axbx ayby azbz
ab
a
2 x
a
2 y
az2
bx2 by2 bz2
首页
上页Biblioteka 返回下页结束
例2. 已知三点 M (1,1,1), A( 2, 2,1), B( 2,1, 2), 求
叉积:
i jk ab ax ay az
bx by bz
首页
上页
返回
下页
结束
ax ay az
混合积: a b c ( a b ) c bx by bz
2. 向量关系:
cx cy cz
ab 0
bx by bz ax ay az
数量积向量积混合积

cx cy cz
混合积的坐标表达式
关于混合积的说明: 关于混合积的说明: (1)向量混合积的几何意义: )向量混合积的几何意义:
r r向量的混合积 r r r r [ab c ] = (a × b ) c 是这样
的一个数, r 的一个数,它的绝对值表 r r 示以向量a 、b 、c 为棱的 平行六面体的体积. 平行六面体的体积
r r r 证 ( ) Q a × b = 0,
r | b |≠ 0, r r ∴ sinθ = 0, θ = 0, a // b r r ( ) Q a // b ∴θ = 0或 π ∴ sinθ = 0 r r r r | a × b |=| a || b | sinθ = 0.
r | a |≠ 0,
r i r j ay by r k
r i r j r k
r r 4 = 10 j + 5k ,
垂直的单位向量. 垂直的单位向量
解
r r r c = a × b = ax bx
az = 3 2 bz 1 1 2
r 2 2 Q | c |= 10 + 5 = 5 5 ,
r c 2 r 1 r 0 ∴ c = ± r = ± j+ k . 5 |c | 5
结论 两向量的数量积等于其中一个向量的 模和另一个向量在这向量的方向上的投影的 乘积. 乘积. 数量积也称为“点积” 内积” 数量积也称 a || b | cosθ
关于数量积的说明: 关于数量积的说明:
r r r 2 (1) a a =| a | . r r r r r 2 证 Qθ = 0, ∴ a a =| a || a | cosθ =| a | . r r r r ( 2) a b = 0 a⊥b . r r r r 证 () Q a b = 0, | a |≠ 0, | b |≠ 0, r r π ∴ a ⊥b . ∴ cosθ = 0, θ = , 2 π r r () Q a⊥b , ∴θ = , ∴ cosθ = 0, 2 r r r r a b =| a || b | cosθ = 0.
向量的数量积、向量积、混合积

混合积
混合积在解析几何中可以用于表示向量的旋 转和缩放。例如,在三维空间中,混合积可 以用来计算三个向量的旋转角度和缩放因子。
在物理学中的应用
向量积
在物理学中,向量积可以用于描述矢量场中的矢量线。 例如,在电磁学中,向量积可以用来计算磁场中的矢量 线。
混合积
在物理学中,混合积可以用于描述物体的转动惯量。例 如,在刚体动力学中,混合积可以用来计算刚体的转动 惯量。
性质
混合积为标量,其值与三个向量的顺序有关,但与向量的排列顺序无关。
几何意义
几何意义
向量$mathbf{a}$、$mathbf{b}$、 $mathbf{c}$的混合积等于以这三个向量 为邻边的平行六面体的体积。
VS
特殊情况
当其中一个向量是零向量时,混合积为零 ;当两个向量共线时,混合积为零。
运算性质
交换律
$(mathbf{a}, mathbf{b}, mathbf{c}) = (mathbf{c}, mathbf{b}, mathbf{a})$
分配律
$(mathbf{a} + mathbf{b}, mathbf{c}, mathbf{d}) = (mathbf{a}, mathbf{c}, mathbf{d}) + (mathbf{b}, mathbf{c}, mathbf{d})$
运算性质
要点一
分配律
$mathbf{A} times (mathbf{B} + mathbf{C}) = mathbf{A} times mathbf{B} + mathbf{A} times mathbf{C}$。
要点二
结合律
$(mathbf{A} + mathbf{B}) times mathbf{C} = mathbf{A} times mathbf{C} + mathbf{B} times mathbf{C}$。
第二节数量积向量积混合积
数
学
axbx ayby azbz 0
电
子 教
例1 求向量a={5,2,5}在向量b={2,-1,2}上的投影.
案
M3
θ
M1
M2
武 汉
解:因为 a·b=|b|Prjba, 所以
科
技
学 院 数 理
Pr
jba
ab |b|
52 22
21 5 2 (1)2 22
18 3
等 数 (3)向量积还符合如下的结合律:设λ是个数,则(λa) ×b=a
学 电
×(λb) =λ(a ×b)
子 5. 向量积的坐标表示式 教
案 设 a=axi+ayj+azk, b=bxi+byj+bzk. 根据向量积的运算规则,有
a b (axi ay j azk) (bxi by j bzk) axi (bxi by j bzk)
0
例4 设a=3i-j-2k, b=i+2j-k. 求a×b.
解: a {3, 1, 2},b {1, 2, 1}
武 汉 科 技 学 院 数 理 系
高 等
例5 已知三角形ABC的顶点是
B
数 A(1,2,3),B(3,4,5),C(2,4,7).求该
学 电 三角形的面积.
A
C
子
教 以AB,AC为邻边作平行四边形,它的面积是|AC×AB|,
汉
科 技
(1) |a×b|=|a||b|sin(a,b).
学 院
(2) a×b垂直于a和b,其指向使三个向量a,b和a×b符合右手
数
理 系
法则.
向量的乘法运算公式

向量的乘法运算公式向量有很多种乘法运算,包括数量积、向量积和混合积等。
在本文中,我将详细介绍这些向量乘法运算的公式及其应用。
一、数量积1.1定义数量积是两个向量的乘积,结果是一个数。
它的定义如下:设有两个向量A和B,它们的数量积定义为:A·B = ,A,·,B,·cosθ其中,A·B表示A和B的数量积,A,和,B,分别表示向量A和B的模长,θ表示A和B之间的夹角。
1.2公式(1)两向量平行时,数量积为:A·B=,A,·,B(2)简化公式:对于i、j、k三个单位向量,有:i·i=j·j=k·k=1i·j=j·k=k·i=0(3)余弦定理:对于非零向量A和B,有:A - B,^2 = ,A,^2 + ,B,^2 - 2,A,B,cosθ1.3应用数量积在几何学和物理学中都有广泛的应用。
(1)求向量的模长:,A,=√(A·A)(2)求两个向量之间的夹角:cosθ = A·B / (,A,·,B,)θ = arccos(A·B / (,A,·,B,))(3)求向量的投影:设A为向量,B为单位向量。
则A在B上的投影为:A_B = ,A,·cosθ其中,θ为A和B的夹角。
二、向量积2.1定义向量积(叉乘)是两个向量的乘积,结果是一个向量。
它的定义如下:设有两个向量A和B,它们的向量积定义为:A ×B = ,A,·,B,·sinθ·n其中,A×B表示A和B的向量积,A,和,B,分别表示向量A和B的模长,θ表示A和B之间的夹角,n为垂直于A和B所在平面的单位向量。
2.2公式(1)A和B的向量积为:A ×B = ,A,·,B,·sinθ·n(2)A和B的向量积的模长为:A × B, = ,A,·,B,·sinθ(3)A和B的向量积的方向由右手定则确定:握住右手,让四指从A旋转到B所经过的角度为θ,则大拇指的方向就是A×B的方向。
数量积向量积混合积

第三节 数量积 向量积 混合积内容分布图示★ 两向量的数量积 ★ 数量积的运算★ 例1 ★ 例2 ★ 例3★ 例4 ★ 例5★ 引例 ★ 向量积的定义★ 向量积的运算★ 例6 ★ 例7 ★ 例8★ 例9 ★ 例10★ 向量的混合积 ★ 混合积的几何意义★ 例11 ★ 例12 ★ 例13★ 内容小结 ★ 课堂练习★ 习题7-3 ★ 返回内容要点:一、 两向量的数量积:定义1设有向量a 、b ,它们的夹角为θ,乘积θcos ||||b a 称为向量a 与b 的数量积(或称为内积、点积),记为b a ⋅,即θcos ||||b a b a =⋅.根据数量积的定义,可以推得: (1) b j a a j b b a a b Pr ||Pr ||==⋅;(2) 2||a a a =⋅; (3) 设a 、b 为两非零向量,则 b a ⊥的充分必要条件是 0=⋅b a .数量积满足下列运算规律:(1) 交换律 ;a b b a ⋅=⋅(2)分配律 ;)(c b c a c b a ⋅+⋅=⋅+(3)结合律 )()()(b a b a b a λλλ⋅=⋅=⋅,(λ为实数).二、两向量的向量积定义2 若由向量a 与b 所确定的一个向量c 满足下列条件:(1)c 的方向既垂直于a 又垂直于b , c 的指向按右手规则从a 转向b 来确定(图7-3-5);(2)c 的模 θsin ||||||b a c =,(其中θ为a 与b 的夹角),则称向量c 为向量a 与b 的向量积(或称外积、叉积),记为b ac ⨯=.根据向量积的定义,即可推得(1)0 =⨯a a ;(2)设a 、b 为两非零向量,则 b a //的充分必要条件是 0=⨯b a .向量积满足下列运算规律:(1);a b b a ⨯-=⨯(2)分配律 ;)(c b c a c b a ⨯+⨯=⨯+(3)结合律 )()()(b a b a b a λλλ⨯=⨯=⨯,(λ为实数).三、向量的混合积例题选讲:两向量的数量积例1 (讲义例1) 已知},2,2,1{},4,1,1{-=-=b a 求(1) ;b a ⋅ (2) a 与b 的夹角θ; (3) a 与b 上的投影.例2 证明向量c 与向量a c b b c a )()(⋅-⋅垂直.例3 (讲义例2) 试用向量方法证明三角形的余弦定理.例4 (讲义例3) 设b a 3+与b a 57-垂直, b a 4-与b a 27-垂直, 求a 与b 之间的夹角θ.例5 (讲义例4) 设液体流过平面S 上面积为A 的一个区域, 液体在这区域上各点处的流速均为(常向量) v . 设n 为垂直于S 的单位向量(图7-3-3a), 计算单位时间内经过这区域流向n 所指一方的液体的质量P (液体的密度为ρ).两向量的向量积例6 (讲义例5) 求与k j i b k j i a 2,423-+=+-=都垂直的单位向量.例7 (讲义例6) 在顶点为)2,6,5(),2,1,1(--B A 和)1,3,1(-C 的三角形中, 求AC 边上的高BD . 例8 设向量p n m ,,两两垂直, 伏隔右手规则, 且,4=m ,2=n ,3=p 计算.)(p n m ⋅⨯例9 (讲义例7) 设刚体以等角速度ω绕l 轴旋转, 计算刚体上一点M 的线速度. 例10 利用向量积证明三角形正弦定理.向量的混合积 例11 (讲义例8) 已知2)(=⋅⨯c b a , 计算).()]()[(a c c b b a +⋅+⨯+例12 (讲义例9) 已知空间内不在同一平面上的四点),,(),,,(),,,(),,,(444333222111z y x D z y x C z y x B z y x A求四面体的体积.例13 已知k j i c k j b i a +-=-==22,2,, 求一单位向量,γ 使c ⊥γ, 且γ 与b a ,此同时共面.课堂练习1.已知向量,0,0 ≠≠b a 证明.)(||||||2222b a b a b a ⋅-⋅=⨯2.已知c b a ,,两两垂直, 且,3||,2||,1||===c b a 求c b a s ++=的长度与它和c b a ,,的夹角.。
数量积 向量积 混合积

AMB .
解: MA (1, 1, 0 ), MB ( 1, 0, 1)
则 cos AMB MA MB MA MB
100 22
A
B M
故
AMB
例3. 设均匀流速为 的流体流过一个面积为 A 的平 面域 , 且 与该平面域的单位垂直向量 的夹角为 求单位时间内流过该平面域的流体的质量P (流体密度
F
oP
F
O
P L
Q
OQ OP sin
M
1. 定义
设 a , b的夹角为 ,定义
向量 c
方向 : c a , c b 且符合右手规则
模 : c a b sin
称 c 为向量 a 与b 的向量积 , 记作
b
c a b (叉积)
a
引例中的力矩 思考: 右图三角形面积
S=
a
b
c ab
2. 性质
bx by bz
a ax i ay j az k b bx i by j bz k
ax az , bx bz
例4. 已知三点 A(1, 2,3), B(3, 4,5),C( 2, 4 ,7 ), 求三
角形 ABC 的面积 .
解: 如图所示,
S ABC
1 2
AB
AC sin
1 2
AB AC
为) .
解: P v
为单位向量
A vn
A
单位时间内流过的体积:
v
二、两向量的向量积
引例. 设O 为杠杆L 的支点 , 有一个与杠杆夹角为
的力 F 作用在杠杆的 P点上 , 则力 F 作用在杠杆上的力
矩是一个向量 M :
M OQ F OP F sin
数量积 向量积 混合积

例 3 (a b ) ( a b ) aa b a ab b b 2a b .
例4 设向量 α β 不共线,若向量 3α + kβ 与 kα + 27 β 共线, 求k的值. 解: (3α + kβ kα + 27 β 0 , 即
| c | 10 2 52 5 5 ,
c 2 1 0 c j k . |c | 5 5
例7 在顶点为 A(1,1,2) 、 B(5,6,2) 和C (1,3,1)
的三角形中,求 AC 边上的高BD .
解
AC (0,4,3)
2 2 2
bx b y bz
2
2
2
由此可知两向量垂直的充要条件为
a b a x bx a y b y a z bz 0
例2 已知 a (1, 1, 4) , b (1, 2 , 2) , 求 (1) a b ;(2)a 与 b 的夹角.
3α α +81α β + k 2 β α + 27kβ β 0
由于 α α β β 0,α β β α , 所以
(81 k 2 )α β 0
由于 α β 0, 故
k 9
例5 证明:
(α β )2 + | α β |2 | α |2 | β |
第二节
数量积
向量积
混合积
一、两向量的数量积 (Scalar Product)
例如: 设力 F 作用于某物体上, 物体有一段位移 S , 求功的表示式.
F
解: 由物理知, 与位移平行的 分力作功, 与位移垂直的 分力不作功. 于是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a b sin 0 sin 0,即 0 或
a∥ b
(1) a b b a
(2) 分配律 ( a b ) c a c b c
(证明略)
(3) 结合律 ( a ) b a ( b ) ( a b )
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
4. 向量积的坐标表示式
设 a ax i ay j az k , b bx i by j bz k ,
则
( ax i ay j az k ) (bx i by j bz k )
axbx ( i i )
ayby ( j j )
azbz ( k k )
(aybz azby ) i (azbx axbz ) j
解: P v
为单位向量
A vn
A
单位时间内流过的体积
v
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
二、两向量的向量积
引例. 设O 为杠杆L 的支点 , 有一个与杠杆 夹角为 的力 F 作用在杠杆的 P点上 , 则力 F
作用在杠杆上的力矩是一个向量 M :
F
M OQ F OP F sin O
[ a b c ] [ b c a ][c a b]
(可用三阶行列式推出)
a
b
c
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
例6. 已知一四面体的顶点 4 ) , 求该四面体体积 .
解: 已知四面体的体积等于以向量 A1A2 , A1A3 , A1A4
为棱的平行六面体体积的 故
第七章
第二节 数量积 向量积 *混合积
一、两向量的数量积 二、两向量的向量积 *三、向量的混合积
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
一、两向量的数量积
引例. 设一物体在常力 F 作用下, 沿与力夹角为
的直线移动, 位移为 s , 则力F 所做的功为
W F s cos
1. 定义
设向量 a , b 的夹角为 , 称
记作
ab
M1 s
M2
W F s
为a与b的数量积 (点积) .
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
b在 a上的投影为
记作
b
Pr ja b
故
同理
,当
ab a
b
0
时,
Pr
ja
b
2. 性质
(1) a a
(2) a ,b为两个非零向量, 则有
( a b ) c 记作 a b c
ab
为a , b , c 的混合积 .
几何意义
以 a , b , c 为棱作平行六面体, 则其
c
b a
底面积 A a b , 高 h c
故平行六面体体积为
V Ah
( ab)c
a b c
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
事实上, 当 c 0 时, 显然成立 ; 当c 0时
a b c c Pr jc a b c Prjc a Prjc b
c Pr jc a c Pr jc b a c b c
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
例1. 证明三角形余弦定理
ab 0
YANGZHOU UNIVERSITY
a 0, b 0 则 ab 0
机动 目录 上页 下页 返回 结束
3. 运算律
(1) 交换律 (2) 结合律
ab
a ( b)
(a b)
( a ) ( b) a ( b)
c
(3) 分配律
(ab)
Pr jc a Pr jc b Pr jc( a b)
1 AB AC 2
A
C
i jk
1 2 2 21 2
2 4
1 2
( 4,6,
2)
1 42 (6)2 22 2
YANGZHOU UNIVERSITY
14
机动 目录 上页 下页 返回 结束
例5. 设刚体以等角速度 绕 l 轴旋转, 导出
刚体上一点 M 的线速度 的表示式 .
解: 在轴 l 上引进一个角速度向量 , 使 , 其
k
(axby aybx ) k
YANGZHOU UNIVERSITY
ij
机动 目录 上页 下页 返回 结束
向量积的行列式计算法
(aybz azby ) i (azbx axbz ) j (axby aybx ) k
i jk ax ay az
bx by bz
a ax i ay j az k b bx i by j bz k
D(10,15,17)共面 .
解: 因
[ AB AC AD ]
B C
3 45
D
1 2 2 0
A
9 14 16
故 A , B , C , D 四点共面 .
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
内容小结
设 a (ax , ay , az ) , b (bx ,by ,bz ), c (cx , cy , cz )MA MB
10 0 22
故
AMB
B M
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
例3. 设均匀流速为 的流体流过一个面积为 A 的平面域 , 且 与该平面域的单位垂直向量
的夹角为 求单位时间内流过该平面域的流
体的质量P (流体密度为 ) .
b
c a b (叉积)
a
引例中的力矩 思考: 右图三角形面积
S=
YANGZHOU UNIVERSITY
c ab
a b
机动 目录 上页 下页 返回 结束
2. 性质
(1) a a 0
(2) a , b为非零向量, 则 a b 0
a∥ b
证明: 当a 0, b 0 时,
ab 0
3. 运算律
ax ay az
混合积: a b c ( a b ) c bx by bz
2. 向量关系:
cx cy cz
ab 0
bx by bz ax ay az
axbx ayby azbz 0
a ,b,c 共面
( ab )c 0
ax ay az bx by bz 0 cx cy cz
YANGZHOU UNIVERSITY
4. 数量积的坐标表示
设 a ax i ay j az k , b bx i by j bz k ,
则
( ax i ay j az k ) (bx i by j bz k )
i j jk ki 0
a b axbx ayby azbz
两向量的夹角公式 当 为非零向量时, 由于
c2 a2 b2 2abcos
证: 如图 . 设
CB a, C A b, AB c
则
Ab
c
C
Ba
c 2 (a b)(a b) aa bb2ab
a 2 b 2 2 a b cos
a a ,b b ,c c
c2 a2 b2 2abcos
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
1. 向量运算
加减: 数乘: 点积:
a b (ax bx , ay by , az bz )
a (ax ,ay ,az )
a b axbx ayby azbz
叉积:
i jk ab ax ay az
bx by bz
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
的三角形中, 求 AC 边上的高 BD .
解: AC ( 0, 4, 3)
B
AB ( 0, 2, 2 )
三角形 ABC 的面积为
A
DC
S 1 | AC AB | 1 (2)2 02 02 1
2
2
而
| AC | 42 (3)2 5, S 1 | AC | | BD |
2
故有 1 1 5 | BD | | BD | 2
机动 目录 上页 下页 返回 结束
思考与练习
1. 设 a i 2 j k , b i j , 计算 a b 及 a b,并求 a , b 夹角 的正弦与余弦 .
答案: a b 1 ,
a b (1, 1, 3)
cos 1 ,
23
sin
11 12
2. 用向量方法证明正弦定理:
a b cos , 得
cos
axbx ayby azbz
ab
a
2 x
a
2 y
az2
bx2 by2 bz2
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
例2. 已知三点 M (1,1,1), A( 2, 2,1), B( 2,1, 2),
求 AMB .
解: MA (1, 1, 0 ), MB ( 1, 0, 1 )
B
abc sin A sin B sin C
ca
A
bC
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
证: 由三角形面积公式
SABC
1 2
AC AB
1 BA BC 1 CB CA
2
2
因 AC AB b c sin A
B
c a sin B CB CA a b sin C
