matlab第四章课后答案
电机与拖动基础及MATLAB仿真习题答案(第四章)

电机与拖动基础及MATLAB仿真习题答案(第四章)4-14 ⼀台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=87.5%,求电动机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-15 ⼀台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-16 已知⼀台直流电机极对数p=2,槽数Z 和换向⽚数K 均等于22,采⽤单叠绕组。
试求:(1)绕组各节距;(2)并联⽀路数。
解:(1)第⼀节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第⼆节距415y 12=-=-=y y(2)并联⽀路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,⽓隙每极磁通Φ=2.1×10-2Wb ,试求:(1)采⽤单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持⽀路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联⽀路对数a=p=3,电磁转矩 m N I a pN T a ?==Φ=38.1310021.0314.3240032π如果把电枢绕组改为单波绕组, 保持⽀路电流a i 的数值不变,则电磁转矩也不变,仍为 13.369m N ?,因为⽆论是叠绕组还是波绕组,所有导体产⽣的电磁转矩的⽅向是⼀致的, 保持⽀路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
也可以⽤计算的⽅法: 单叠绕组时并联⽀路数为6,⽀路电流 A I i a a 6106==改为单波绕组, 保持⽀路电流a i 的数值不变,仍为A 610,⽽并联⽀路数为2 (a=1), 电枢电流A i I a a 3102== 电磁转矩 m N T ?==38.13310021.0114.324003。
MATLAB课后习题集附标准答案

第2章MATLAB概论1、与其他计算机语言相比较,MA TLAB语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MA TLAB系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可.4、MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?答:在MATLAB操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的view菜单中选择Dock,菜单项就可以将独立的窗口重新防止的桌面上.5、如何启动M文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.8、如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?答:当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的Set Path菜单项来完成.在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被MATLAB运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上.9、在MA TLAB中有几种获得帮助的途径?答:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器.(2)help命令:在命令窗口键入“help”命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息.(3)lookfor命令:在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数.(4)模糊查询:输入命令的前几个字母,然后按Tab键,就可以列出所有以这几个字母开始的命令和函数.注意:lookfor和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用help命令显示详细信息.第3章 MATLAB 数值运算3.1在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375,并将其赋予变量a ? 答:在Command Window 窗口输入操作:>> a=[5 7 3;4 9 1]3.2有几种建立矩阵的方法?各有什么优点? 答:(1)直接输入法,如a=[1 2 3 4],优点是输入方法方便简捷;(2)通过M 文件建立矩阵,该方法适用于建立尺寸较大的矩阵,并且易于修改; (3)由函数建立,如y=sin(x),可以由MATLAB 的内部函数建立一些特殊矩阵; (4)通过数据文件建立,该方法可以调用由其他软件产生数据.3.3在进行算术运算时,数组运算和矩阵运算各有什么要求?答:进行数组运算的两个数组必须有相同的尺寸.进行矩阵运算的两个矩阵必须满足矩阵运算规则,如矩阵a 与b 相乘(a*b )时必须满足a 的列数等于b 的行数.渗釤呛俨匀谔鱉调硯錦。
matlab课后习题答案第四章
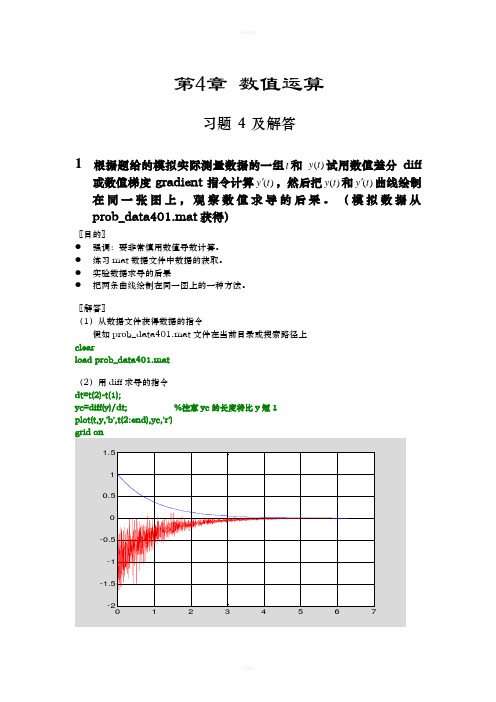
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
(完整版)汽车理论课后作业答案MATLAB
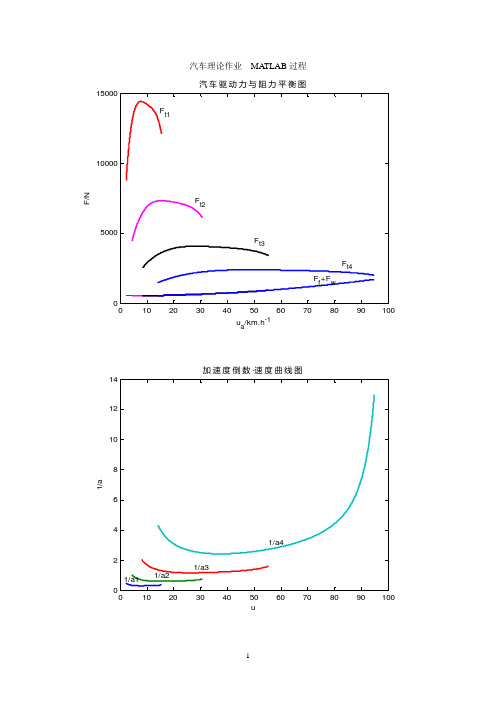
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序:《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知,他们无交点,u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档,较高转速(n取3401 ),最经济负荷(即90%负荷大约 46.9366Kw)行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间:(这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间)因与题1.3第三问求法相同,这里不在累述,可直接有计算机求得:figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31)前轴利用附着系数为:gf zh b zL +=βϕ后轴利用附着系数为: ()gr zh a zL --=βϕ1空载时:g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。
电机与拖动基础及MATLAB仿真习题答案(第四章)

4-14 一台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=%,求电动机的额定电流和额定负载时的输入功率 解:(1)额定电流(2)输入功率4-15 一台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输入功率 解:(1)额定电流(2)输入功率4-16 已知一台直流电机极对数p=2,槽数Z 和换向片数K 均等于22,采用单叠绕组。
试求:(1)绕组各节距;(2)并联支路数。
解:(1)第一节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第二节距415y 12=-=-=y y(2)并联支路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,气隙每极磁通Φ=×10-2Wb ,试求:(1)采用单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持支路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联支路对数a=p=3,电磁转矩 m N I a pN T a ⋅=⨯⨯⨯⨯⨯=Φ=38.1310021.0314.3240032π 如果把电枢绕组改为单波绕组, 保持支路电流a i 的数值不变,则电磁转矩也不变,仍A U P I N N N N 79.207875.022010403=⨯⨯==ηkWI U P N N 71.4579.2072201=⨯=⨯=A U P I N N N 5.35623010823=⨯==KW P P N 11.911==η为m N ⋅,因为无论是叠绕组还是波绕组,所有导体产生的电磁转矩的方向是一致的,保持支路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
matlab第四章课后作业解答

matlab第四章课后作业解答第四章习题解答1、求下列多项式的所有根,并进行验算。
(3)267235865x x x x-+-(4)4)32(3-+x 解:>> p=zeros(1,24); >> p(1)=5;p(17)=-6;p(18)=8;p(22)=-5; >> root=roots(p)root =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927>> polyval(p,root)ans =1.0e-012 *-0.07120.0459 - 0.0081i0.0459 + 0.0081i-0.0419 + 0.0444i-0.0419 - 0.0444i0.0509 + 0.0929i0.0509 - 0.0929i-0.2059 + 0.0009i-0.2059 - 0.0009i-0.0340 + 0.0145i-0.0340 - 0.0145i0.1342 + 0.0910i0.1342 - 0.0910i0.0025 + 0.0027i0.0025 - 0.0027i-0.0077 + 0.4643i-0.0077 - 0.4643i-0.3548 - 0.1466i-0.3548 + 0.1466i-0.0251-0.0073(4) >> p1=[2 3];>> p=conv(conv(p1,p1),p1)-[0 0 0 4]; >> root=roots(p)root =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.7063>> polyval(p,root)ans =1.0e-014 *-0.7105 - 0.6217i-0.7105 + 0.6217i6、求解下列方程组在区域1,0<<βα内的解-=+=.sin 2.0cos 7.0,cos 2.0sin 7.0βαββαα 解:以初值)5.0,5.0(),(00=βα进行求解>> fun=inline('[0.7*sin(x(1))+0.2*cos(x(2))-x(1),0.7*cos(x(1))-0.2*sin(x(2))-x(2)]');>> [x,f,h]=fsolve(fun,[0.5 0.5])Optimization terminated: first-order optimality is less than options.TolFun.x =0.5265 0.5079f =1.0e-007 *-0.1680 -0.2712h =1因而,该方程组的近似根为5079.0,5265.0==βα。
数学实验第四章函数和方程习题MATLAB编码(胡良剑版)

%p0,p1是初始值
%delta是给定允许误差
%m是p1-p0的误差估计?
%k是所需
%要的迭代次数?%y=f(p1)
% K=0,p0,p1,feval('f',p0),feval('f',p1)
% for k=1:max1
% if(f1==0)
% root=a;
% end
% if(f2==0)
% root=b;
% end
% if(f1*f2>0)
% disp('两端点函数值乘积大于0!');
% return;
% else
% tol=1;
% fun=diff(sym(f));
% fa=subs(sym(f),findsym(sym(f)),a);
% x=fminsearch(fun,[0 0]) %求极小值
% fun2=inline('-(x(2)^3/9+3*x(1)^2*x(2)+9*x(1)^2+x(2)^2+x(1)*x(2)+9)');
% x=fminsearch(fun2,[0 -5]) %求极大值
%第10题
% t=0:24;
% c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...
% x(2)=fminsearch(fun2,-2.5);
% x(4)=3;
% feval(fun,x)
%第8题(3)
% fun=inline('abs(x^3-x^2-x-2)');
% fplot(fun,[0 3]);grid on; %作图观察
MATLAB基础及其应用教程-周开利-邓春晖课后标准答案
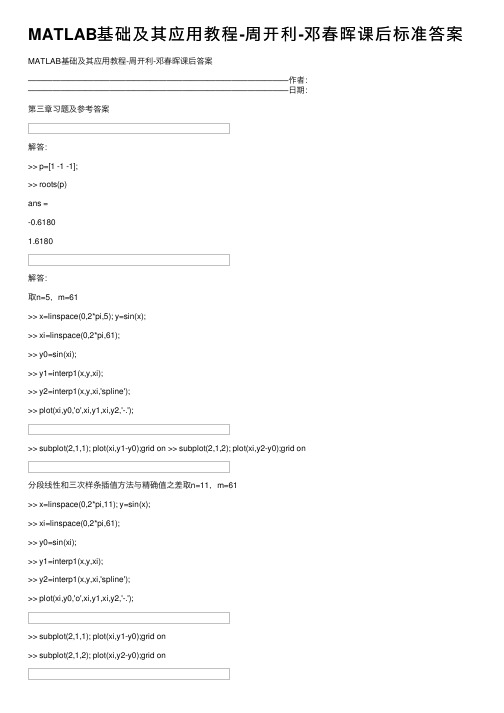
MATLAB基础及其应⽤教程-周开利-邓春晖课后标准答案MATLAB基础及其应⽤教程-周开利-邓春晖课后答案————————————————————————————————作者:————————————————————————————————⽇期:第三章习题及参考答案解答:>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答:取n=5,m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on >> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值⽅法与精确值之差取n=11,m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on分段线性和三次样条插值⽅法与精确值之差解答:>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.'); >> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合⽅法相⽐较,都合理,误差也相近。
第4章 MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
matlab第四章课后答案

%Exerc ise 1(1)r oots([1 11])%Exer cise1(2)roots([3 0 -4 0 2 -1])%Exerc ise 1(3)p=zero s(1,24);p([1 17 1822])=[5 -6 8 -5];ro ots(p)%E xerci se 1(4)p1=[2 3];p2=conv(p1,p1);p3=co nv(p1, p2);p3(end)=p3(en d)-4; %原p3最后一个分量-4r oots(p3)%Exer cise2fun=inli ne('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzer o(fun,2)%Exer cise3fun=inli ne('x^4-2^x');fplot(fun,[-2 2]);gr id on;fze ro(fu n,-1),fzer o(fun,1),f minbn d(fun,0.5,1.5)%Exe rcise 4fu n=inl ine('x*sin(1/x)','x');fp lot(f un, [-0.10.1]);x=z eros(1,10);fori=1:10, x(i)=fz ero(f un,(i-0.5)*0.01);end;x=[x,-x]%Ex ercis e 5f un=in line('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fso lve(f un,[0 0 0])%E xerci se 6fun=@(x)[x(1)-0.7*si n(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolv e(fun,[0.5 0.5])%E xerci se 7clear; clo se; t=0:p i/100:2*pi;x1=2+sqr t(5)*cos(t); y1=3-2*x1+sq rt(5)*sin(t);x2=3+s qrt(2)*cos(t);y2=6*sin(t);pl ot(x1,y1,x2,y2); gri d on; %作图发现4个解的大致位置,然后分别求解y1=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsol ve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fso lve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exerc ise 8(1)c lear;fun=inlin e('x.^2.*(x.^2-x-2)');fp lot(f un,[-2 2]);grid on;%作图观察x(1)=-2;x(2)=fminb nd(fu n,-1,-0.5);x(4)=fmi nbnd(fun,1,2);fun2=inlin e('-x.^2.*(x.^2-x-2)');x(3)=f minbn d(fun2,-0.5,0.5);x(5)=2feval(fun,x)%答案: 以上x(2)(4)是局部极小,x(1)(3)(5)是局部极大,从最后一句知道x(1)全局最大, x(4)最小。
MATLAB原理及应用实验报告第四章答案

《MATLAB 原理及应用》实验报告三.课后练习题答案1.为 ⎪⎩⎪⎨⎧<-=>+=01001x x x xx x y 编写赋值程序。
程序如下:①建立如下的M 文件:x=input('x=');%让用户通过键盘输入数值、字符串或表达式if x>0y=x+1;elseif x==0y=x;else x<0y=x-1;e nd程序执行结果如下>> kh1 %在当前工作目录下,文件名为“kh.1.m ” x=1>> yy =22.使用for ... end循环的array向量编程求出1+3+5...+100 的值程序如下:sum=0;>> for k=1:2:100sum=sum+k;end>> sumsum =25003.计算1+3+5...+100 的值,当和大于1000时终止计算。
程序如下:sum=0;for m=1:2:100; %建立1 3 5….100的向量if sum<=1000 %如果sum小于1000则可以继续加sum=sum+m; %累加elsebreak; %若sum的结果不符合条件就跳出整个循环endend结果为:sum =1024k =653.1计算从1开始多少个自然数之和超过100。
程序如下:>> sum=0;n=0;>> while sum<=100n=n+1;sum=sum+n;end结果为:n =14sum =1054.求1!+2!+3!+……+8!的值程序如下:n=1;sum=1;for m=2:8; %循环7次使得得到各次阶乘n=n*m;sum=sum+n; %累加end结果为:sum =462335.写程序,判断一年是否为闰年,符合下面两条件之一:(1990~2014)A、能被4整除,不能被100整除B、能被400整除程序如下count=0;for y=1990:2014;if((rem(y,4)==0&rem(y,100)~=0)|(rem(y,4)==0&rem(y,400)~=0));count=count+1;endend结果为:count =5。
MATLAB程序设计知到章节答案智慧树2023年广西科技大学

MATLAB程序设计知到章节测试答案智慧树2023年最新广西科技大学第一章测试1.当在命令行窗口执行命令时,如果不想立即在命令行窗口中输出结果,可以在命令后加上()。
参考答案:分号(;)2.MATLAB命令行窗口中提示用户输入命令的符号是()。
参考答案:>> ;3.fix(264/100)+mod(264,10)*10的值是()。
参考答案:424.下列可作为MATLAB合法变量名的是()。
参考答案:xyz_2a。
5.在命令行窗口输入下列命令后,x的值是()。
>> clear>> x=i*j参考答案:-1;6.建立矩阵时,不同行的元素之间用()分隔。
参考答案:分号;7.输入字符串时,要用()将字符序列括起来。
参考答案:' ';8.最初的MATLAB核心程序是采用()语言编写的。
参考答案:FORTRAN;9.下列选项中能反应MATLAB特点的是()。
参考答案:编程效率高。
10.如果要重新执行以前输入的命令,可以使用()。
参考答案:上移光标键(↑)。
11.plot(x,y)是一条()命令。
参考答案:绘图;12.以下两个命令行的区别是()。
>> x=5,y=x+10>> x=5,y=x+10;参考答案:第一个命令行同时显示x和y的值,第二个命令行只显示x的值;13.下列选项中,不是MATLAB帮助命令的是()。
参考答案:search;14.下列数值数据表示中错误的是()。
参考答案:2e;15.下列语句中错误的是()。
参考答案:x=y=3;16.已知s='显示"hello"',则s的元素个数是()。
参考答案:9;17.建立矩阵时,同一行的元素之间用()分隔。
参考答案:空格;;逗号;18.在当前文件夹和搜索路径中都有fpp.m文件,那么在命令行窗口输入fpp时,下列说法错误的是()。
参考答案:先执行当前文件夹的fpp.m文件,再执行搜索路径中的fpp.m文件;;先执行搜索路径中的fpp.m文件,再执行当前文件夹的fpp.m文件;;执行搜索路径中的fpp.m文件;19.内存变量文件是二进制格式文件,扩展名为.mat。
(完整版)第4章MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
MATLAB编程与应用知到章节答案智慧树2023年山东科技大学

MATLAB编程与应用知到章节测试答案智慧树2023年最新山东科技大学第一章测试1.MATLAB、FORTRAN、MAPLE并称为三大数学软件,以研究和解决各种具体的数学问题和工程问题。
参考答案:错2.下列属于MATLAB独特优势的是()。
参考答案:强大的科学计算及数据处理能力;简单易用的程序语言;友好的工作平台和编程环境;出色的图形处理功能3.MATLAB界面有()个窗口。
参考答案:64.MATLAB、FORTRAN、Mathematica并称为三大数学软件,以研究和解决各种具体的数学问题和工程问题。
参考答案:错5.在MATLAB中,可以在命令行窗口中通过帮助命令来查询帮助信息,最常用的帮助命令是()。
参考答案:help第二章测试1.下列可作为MATLAB合法变量名的是()。
参考答案:xyz_2a2.设A=[1,2;3,4],B=[5,6;7,8],则A*B=()。
参考答案:[19,22;43,50]3.输⼊字符串时,要⼊()将字符括起来。
参考答案:' '4.使⼊语句t=0:7⼊成的是7个元素的向量。
()参考答案:错5.下列语句中正确的是()。
参考答案:x==y==3;y=3,x=y;x=y==3第三章测试1.sym函数可以建立一个符号量。
()参考答案:对2.下列指令可用于对符号运算表达式进行化简的是()。
参考答案:expand(S);factor(S);collect(S);horner(S)3.MATLAB用于符号常微分方程求解的函数是()。
参考答案:dsolve4.ezplot函数可用于绘制符号函数的三维曲线。
()参考答案:错5.MATLAB将函数展开为幂级数,所使用的函数是()。
参考答案:taylor第四章测试1.File菜单的命令形式和windows系统中File菜单的命令形式类似,包括New、Open、Save、Close和SaveAs等命令。
()参考答案:对2.关于控制坐标性质的axis函数的多种调用格式,下列解释错误的是()。
MATALB第四章部分课后答案

习题4.1绘制图形)y t--=8t)(tsin(21e≤t并在横轴标注Time纵0≤轴标注“amplitude”,图形的标题为Decaying-oscillating Exponential t=0:0.1:8;y=1-2*exp(-t).*sin(t);plot(t,y,'k')grid ontitle('Decaying-oscillating Exponential')xlabel('Time');ylabel('amplitude')4.2绘制如下函数图形并加上适当的修饰3008.0)309.0cos(5)(22.0≤≤+︒-=--t e t e t y ttt=0:0.1:30;y=5*exp(-0.2*t).*cos(0.9*t-pi/6); plot(t,y,'r:')4.3在同一张图中绘制下列函数曲线100625.0)24083.2cos(23.1)(625.0)(≤≤+︒+==t t t z t yt=0:0.1:10;y=0.625;z=1.23*cos(2.83*t+4*pi/3)+0.625;plot(t,y,'r:')hold onplot(t,z,'b:')text(0,(0.625-1.23*0.5),'这是z(t=0)的位置')text(10,4*pi/3,'这是z(t=10)的位置')4.4对应于250≤≤t 区间内,在同一图中绘制下列函数曲线tt t te t e t y e t y et y ----+︒-===25.1)128554.0cos(02.2)(02.2)(25.1)(3.033.021t=0:0.1:25;y1=1.25*exp(-t);y2=2.02*exp(-0.3*t);y3=2.02*exp(-0.3*t).*cos(0.554*t-128)+1.25*exp(-t);plot(t,y1,'k')hold onplot(t,y2,'b')hold on plot(t,y3,'r')4.5已知椭圆的长、短轴分别为a=4,b=2,用“小红点线”画椭圆 {)cos()sin(t a x t b y ==t=0:pi/100:2*pi;a=4;b=2;x=a.*cos(t);y=b.*sin(t);plot(x,y,'r.')4.6在同一图形框中绘制两个子图,分别显示下列曲线x=0:0.01:10;y1=sin(2*x).*sin(3*x);y2=0.4*x;subplot(1,2,1),plot(x,y1,'r'),title('y1')subplot(1,2,2),plot(x,y2,'b'),title('y2')4.7试将图形分割成3个子图,并分别绘制lgx在100≤区间内对数坐0≤t标、x半对数坐标和y半对数坐标的函数曲线,并加上适当的图形修饰。
matlab课后习题及答案

第一章5题已知a=4.96,b=8.11,计算)ln(b a e b a +-的值。
解:clearclca=4.96;b=8.11;exp(a-b)/log(a+b)ans =0.01676题已知三角形的三边a=9.6,b=13.7,c=19.4,求三角形的面积。
提示:利用海伦公式area =))()((c s b s a s s ---计算,其中S=(A+B+C)/2.解:clearclca=9.6;b=13.7;c=19.4;s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c))s =21.3500第二章8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解:clearclcS=0;for i=0:1:63S=S+2^i;endSS =1.8447e+0199题分别用for 和while 循环结构编写程序,计算∑=-1001n 1n 2)(的值。
解:clearclcs=0;for n=1:100s=s+(2*n-1);endss =10000clearclcn=1;s=0;while n<=100s=s+(2*n-1);n=n+1;endss =10000第三章2题在同一坐标下绘制函数x ,,2x -,2x xsin(x)在()∏∈,0x 的曲线。
解:clearclcx=0:0.2:pi;y1=x;y2=x.^2;y3=-(x.^2);y4=x.*sin(x);plot(x,y1,'-',x,y2,'-',x,y3,'-',x,y4,'-')00.51 1.52 2.53-10-8-6-4-22468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2e x 5.0 、y2=sin(2∏x )的图形。
解:clearclcx=0:0.01:pi;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'b:',x,y2,'r--')00.51 1.52 2.53 3.5-1-0.50.511.52第四章1题对表达式f=3238641+++x x x 进行化简。
MATLAB习题参考答案(胡良剑

第一章 MATLAB 入门4、求近似解解:>> x=-2:0.05:2;y=x.^4-2.^x两个近似解:y1=f(-0.85)= -0.0328; y2=f(1.250)= 0.0630第二章 MATLAB 编程与作图1、 设x 是数组,求均值和方差解:函数文件如下:function [xx,s]=func1(x)n=length(x);xx=sum(x)/n;s=sqrt((sum(x.^2)-n*xx^2)/(n-1));命令窗口:>> x=[1 2 3 4 5];[xx,s]=func1(x)2、求满足的最小m 值 100)1ln(0>+∑=m n n s=0;n=0;while(s<=100)s=s+log(1+n);n=n+1;endn,s3、用循环语句形成Fibonacci 数列,....4,3,,12121=+===−−k F F F F F k k k 。
并验证极限2511+→−k k F F (提示:计算至两边误差小于精度1e-8为止) 解: 求Fibonacci 数列的函数文件:function f=fun(n)if n<=2f=1;elsef=fun(n-1)+fun(n-2);end验证极限的函数文件:function [k,a]=funTest(e)a=abs(1-(1+sqrt(5))/2);k=2;while(a>e)k=k+1;a=abs(fun(k)/fun(k-1)-(1+sqrt(5))/2);end命令行:>> [k,a]=funTest(10^-8)k =21a =9.7719e-009或者M 文件如下:clear; F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1; F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k4、分别用for 和while 循环结构编写程序,求出∑==610123i i K ,并考虑一种避免循环语句的程序设计,比较各种算法的运行时间。
matlab课后习题答案第四章
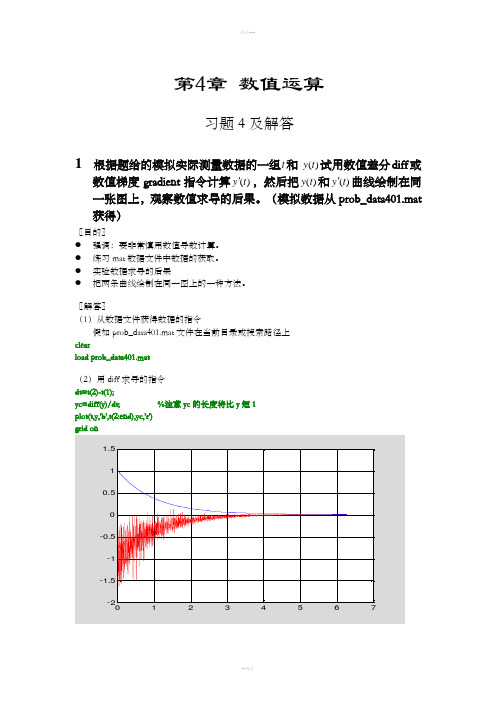
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
MATLAB程序设计与应用(第二版)第4章课后题答案

a=input('请输入一个4位数:');while (a<1000|a>9999)a=input('输入错误,请重新输入一个4位数:'); endb=fix(a/1000);c=rem(fix(a/100),10);d=rem(fix(a/10),10);e=rem(a,10);b=b+7;c=c+7;d=d+7;e=e+7;b=rem(b,10);c=rem(c,10);d=rem(d,10);e=rem(e,10);g=b;b=d;d=g;g=c;c=e;e=g;a=1000*b+100*c+10*d+e;disp(['加密后:',num2str(a)])逻辑表达式法:a=input('请输入a: ');b=input('请输入b: ');c=input('请输入c: ');x=0.5:1:5.5;x1=(x>=0.5&x<1.5);x2=(x>=1.5&x<3.5);x3=(x>=3.5&x<=5.5);y1=a.*(x.^2)+b.*x+c;y2=a*(sin(b)^c)+x;y3=log(abs(b+c./x));y=y1.*x1+y1.*x2+y3.*x3; disp(y)if语句法:a=input('请输入a: ');b=input('请输入b: ');c=input('请输入c: ');for x=0.5:1:5.5if x>=0.5 & x<1.5y=a.*(x.^2)+b.*x+c elseif x>=1.5 & x<3.5西安建筑科技大学陈y=a*(sin(b)^c)+xelseif x>=3.5 & x<5.5y=log(abs(b+c./x))endendswitch语句法:a=input('请输入a: ');b=input('请输入b: ');c=input('请输入c: ');for x=0.5:1:5.5switch floor(x/0.5)case {1,2}y=a.*(x.^2)+b.*x+c;case {3,4,5,6}y=a*(sin(b)^c)+x;case {7,8,9,10}y=log(abs(b+c./x));enddisp(y)end3.x=fix(rand(1,20)*89)+10;x1=mean(x);n=find(rem(x,2)==0 & x<x1);disp(['小于平均数的偶数是:',num2str(x(n))]);4.(1)A=input('请输入20个数的一个行向量:');a=A(1);b=A(1);for m=Aif a>=ma=m;elseif b<=mb=m;endenddisp(['最小数是:',num2str(a)])disp(['最大数是:',num2str(b)])(2)A=input('请输入20个数的一个行向量:');西安建筑科技大学陈maxval=max(A)minval=min(A)5.s=0;for a=0:63c=2^a;s=s+c;enddisp(['2的0次方到63次方的和是:',num2str(s)])k=0:63n=2.^ks=sum(n)6.(1)sum1=0;for n=1:100x=(-1)^(n+1)*(1/n);sum1=sum1+x;enddisp(['当n取100时: sum=',num2str(sum1)])sum2=0;for n=1:1000x=(-1)^(n+1)*(1/n);sum2=sum2+x;enddisp(['当n取1000时: sum=',num2str(sum2)])sum3=0;for n=1:10000x=(-1)^(n+1)*(1/n);sum3=sum3+x;enddisp(['当n取10000时:sum=',num2str(sum3)])(2)sum1=0;n1=0;for n=1:2:100x=(-1)^n1*(1/n);sum1=sum1+x;西安建筑科技大学陈n1=n1+1;enddisp(['当n取100时: sum=',num2str(sum1)])sum2=0;n2=0;for n=1:2:1000x=(-1)^n2*(1/n);sum2=sum2+x;n2=n2+1;enddisp(['当n取1000时: sum=',num2str(sum2)])sum3=0;n3=0;for n=1:2:10000x=(-1)^n3*(1/n);sum3=sum3+x;n3=n3+1;enddisp(['当n取10000时:sum=',num2str(sum3)])(3)sum1=0;for n=1:100x=1/(4^n);sum1=sum1+x;enddisp(['当n取100时: sum=',num2str(sum1)])sum2=0;for n=1:1000x=1/(4^n);sum2=sum2+x;enddisp(['当n取1000时: sum=',num2str(sum2)])sum3=0;for n=1:10000x=1/(4^n);sum3=sum3+x;enddisp(['当n取10000时:sum=',num2str(sum3)])西安建筑科技大学陈(4)sum1=1;for n=1:100x=4*n*n/(2*n-1)/(2*n+1);sum1=sum1*x;enddisp(['当n取100时: sum=',num2str(sum1)])sum2=1;for n=1:1000x=4*n*n/(2*n-1)/(2*n+1);sum2=sum2*x;enddisp(['当n取1000时: sum=',num2str(sum2)])sum3=1;for n=1:10000x=4*n*n/(2*n-1)/(2*n+1);sum3=sum3*x;enddisp(['当n取10000时:sum=',num2str(sum3)])7.函数文件function f=fibnacci(n)if n==1 | n==2f=1;elsef=fibnacci(n-1)+fibnacci(n-2); end命令文件:shulie=[];for k=1:nshulie=[shulie fibnacci(k)]; endshulie8.function [f1,f2]=juzhenji(x1,x2)f1=x1*x2;f2=x1.*x2;命令文件:西安建筑科技大学陈clear alla=input('请输入一个矩阵:');b=input('请再输入一个矩阵:(注意:两矩阵要可以相乘)'); [f1,f2]=juzhenji(a,b);disp(f1)disp(f2)9.function sum=qiuhe(n,m)if n<=1sum=0;elsesum=n^m+qiuhe(n-1,m);end命令文件:clear ally=qiuhe(100,1)+qiuhe(50,2)+qiuhe(10,-1);disp(y)10.s=0;a=[12,13,14;15,16,17;18,19,20;21,22,23];for k=afor j=1:4if rem(k(j),2)~=0 s=s+k(j);endendendss =108(2)global xx=1:2:5;y=2:2:6;sub(y);xyfunction fun=sub(z) global xz=3*x;x=x+z;西安建筑科技大学陈x =4 12 20y =2 4 6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%|f'(x)|<1则稳定
%Exercise 18
%先写M文件
function f=ex4_18(a,x0,n)
x=zeros(1,n);y=x;
x(1)=x0;
y(1)=a*x(1)+1;
x(2)=y(1);
plot([x(1),x(1),x(2)],[0,y(1),y(1)],'r');
%以下Matlab计算
clear;fun= inline('sin(2*th)-2*th*cos(2*th)-pi/2','th')
th=fsolve(fun,pi/4)
R=20*cos(th)
%Exercise 14
%先在Editor窗口写M函数保存
function x=secant(fname,x0,x1,e)
plot(x(1000:1500),y(1000:1500),'+g');hold on
plot(x(1501:2000),y(1501:2000),'.b');
plot(x(2001:2500),y(2001:2500),'*y');
plot(x(2501:3001),y(2501:3001),'.r');
x=fminsearch(fun,[0 0])%求极小值
fun2=inline('-(x(2)^3/9+3*x(1)^2*x(2)+9*x(1)^2+x(2)^2+x(1)*x(2)+9)');
x=fminsearch(fun2,[0 -5])%求极大值
%Exercise 10
clear;t=0:24;
%取初始值pi/4, 计算如下
fun=@(t)5/sin(t)+10/cos(t);
[t,f]=fminsearch(fun, pi/4)
t =
0.6709
f =
20.8097
%Exercise 17
%提示:x(k+2)=f(x(k))=a^2*x(k)*(1-x(k))*(1-a*x(k)*(1-x(k)))
%Exercise 9
close;
x=-2:0.1:1;y=-7:0.1:1;
[x,y]=meshgrid(x,y);
z=y.^3/9+3*x.^2.*y+9*x.^2+y.^2+x.*y+9;
mesh(x,y,z);grid on;%作图观察
fun=inline('x(2)^3/9+3*x(1)^2*x(2)+9*x(1)^2+x(2)^2+x(1)*x(2)+9');
fplot(fun,[-3 3]);grid on;%作图观察
x(1)=-3;
x(3)=fminsearch(fun,2.5);
fun2=inline('-(3*x.^5-20*x.^3+10)');
x(2)=fminsearch(fun2,-2.5);
x(4)=3;
feval(fun,x)
subplot(2,2,2);ex4_15fun(-0.9,1,1,20);
subplot(2,2,3);ex4_15fun(1.1,1,1,20);
subplot(2,2,4);ex4_15fun(-1.1,1,1,20);
%Exercise 16
%设夹角t, 问题转化为 min f=5/sin(t)+10/cos(t)
y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])
y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])
a=lsqcurvefit(fun,[0 0],t,c)%初值可以试探
f=feval(fun, a,t)
norm(f-c)%拟合效果
plot(t,c,t,f) %作图检验
fun2=inline('b(1)*sin(pi/12*t+b(2))+20','b','t');%原题修改f(x)+20
%Exercise 8(1)
clear;
fun=inline('x.^2.*(x.^2-x-2)');
fplot(fun,[-2 2]);grid on; %作图观察
x(1)=-2;
x(2)=fminbnd(fun,-1,-0.5);
x(4)=fminbnd(fun,1,2);
fun2=inline('-x.^2.*(x.^2-x-2)');
x=fzero(fun, 0, 1)
%Exerciseห้องสมุดไป่ตู้12
r=5.04/12/100;N=20*12;
x=7500*180 %房屋总价格
y=x*0.3 %首付款额
x0=x-y%贷款总额
a=(1+r)^N*r*x0/((1+r)^N-1)%月付还款额
r1=4.05/12/100;x1=10*10000;%公积金贷款
a1=(1+r1)^N*r1*x1/((1+r1)^N-1)
x2=x0-x1%商业贷款
a2=(1+r)^N*r*x2/((1+r)^N-1)
a=a1+a2
%Exercise 13
%列方程th*R^2+(pi-2*th)*r^2-R*r*sin(th)=pi*r^2/2
%化简得sin(2*th)-2*th*cos(2*th)=pi/2
while abs(x0-x1)>e,
x=x1-(x1-x0)*feval(fname,x1)/(feval(fname,x1)-feval(fname,x0));
x0=x1;x1=x;
end
%再在指令窗口
fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');
c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...
31 32 31 29 27 25 24 22 20 18 17 16];
p2=polyfit(t,c,2)
p3=polyfit(t,c,3)
fun=inline('a(1)*exp(a(2)*(t-14).^2)','a','t');
hold on;
for i=2:n
y(i)=a*x(i)+1;
x(i+1)=y(i);
plot([x(i),x(i),x(i+1)],[y(i-1),y(i),y(i)])
end
hold off;
%再执行指令
>> ex4_18(0.9,1,20)
>> ex4_18(-0.9,1,20)
>> ex4_18(1.1,1,20)
>> ex4_18(-1.1,1,20)
%Exercise 19
clear; close; x(1)=0; y(1)=0;
for k=1:3000
x(k+1)=1+y(k)-1.4*x(k)^2; y(k+1)=0.3*x(k);
end
y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])
y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])
fzero(fun,2)
%Exercise 3
fun=inline('x^4-2^x');
fplot(fun,[-2 2]);grid on;
fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)
%Exercise 4
fun=inline('x*sin(1/x)','x');
fplot(fun, [-0.1 0.1]);
x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;
x=[x,-x]
%Exercise 5
fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');
for i=2:n
y(i)=a*x(i)+1; x(i+1)=y(i);
if i>m, plot([x(i),x(i),x(i+1)],[y(i-1),y(i),y(i)]); end
