第四章 热力学第一定律
第四章 热力学第一定律 4

1 V4 T1 T2 V1
Q2 Q1
V3 V2
V2 V1 V2 V1
V4 V1
V3 V4
V2 V1
Q 2 R T 2 ln
V2 V1
R T 2 ln
T2 T1
R T1 ln
Q2 Q1
V R T 2 ln 2 V1
Q 2 Q1 j
j1
n
§4.6.2 卡诺热机
为了对热机的最大可能效率进行理论研究,1824年法国工 程师卡诺设想了一种理想的热机,称为卡诺热机;这种热机的 循环过程称为卡诺循环。 卡诺循环在温度为T1、T2的两个热源间工作,由两个等温 过程和两个绝热过程构成。一般所说的卡诺循环是准静态的, 且无摩擦等耗散现象。 P 当工质是气体时,卡诺循 环可以用P-V图表示。 可见:在卡诺循环中,工质从T1 热源吸热Q1,向T2热源放热 Q 2 , 向外输出功W′ 。
T
⑵ 转换点、转换曲线:
同一工质在不同的温度段对应的焦汤系 数的趋势是可以不同的。 从T-P 图上看,这种现象是由等焓线的斜率决定的。
P
⑵ 转换点、转换曲线: 同一工质在不同的温度段对应的焦汤系数的趋势是可以不同的。 从T-P 图上看,这种现象是由等焓线的斜率
T P H
则有:
W' Q1
Q1 Q2 Q1 1 Q2 Q1
——热机效率
说明
若循环存在m个高温热源,n个低温热源,热机的吸放热为:
Q 1 i ( i 1, 2 , m ) 及 Q 2 j ( j 1, 2 , n )
则热机效率公式中的吸放热为:
化工热力学__第四章___热力学第一定律及其应用

孤立体系:体系与环境之间没有物质和能量交换。
体系
封闭体系:体系与环境之间没有物质,有能量交换。
敞开体系:体系与环境之间有物质和能量交换。
体系吸热为正值,放热为负值; 体系对环境作功为正值,得功为负值。
化工热力学 第四章 热力学第一定律及其应用 第一节
§4-1、闭系非流动过程的能量平衡
体系能量的变化=体系与环境交换的净能量。
Ws ——机械设备交换的功,也叫轴功。
化工热力学 第四章 热力学第一定律及其应用
E Q Ws i
(e t2
t1
i
Pivi )midt
i
t2 t1
(e j
Pjv j )m jdt
e U gz 1 u2
h U pv
2
再将 e pv U pv gz 1 u代2 入,得:
2、绝热稳定流动方程式
流体:可压缩,与外界无热、无轴功交换.
h 1 u2 0 ——绝热稳定流动方程式 2
⑴、喷管与扩压管 喷管:流体通过时压力沿着流动方向降低,而流速加快的部 件称为喷管。 当出口流速﹤音速时,可用渐缩喷管:
当入口流速﹤音速,当出口流速﹥音速时,用拉法尔喷管 :
亚音速
超音速
扩压管:在流动方向上流速降低、压力增大的装置称为扩压管。
化工热力学 第四章 热力学第一定律及其应用
喷嘴与扩压管
h
u 2 2
gz
q ws
是否存在轴功?
否
是否和环境交换热量? 通常可以忽略
位能是否变化?
否
h 1 u2 0
2
化工热力学 第四章 热力学第一定律及其应用
热学第二版-秦允豪-第四章答案

第四章热力学第一定律(题号有所不同)5-1.0.020Kg的氦气温度由升为,若在升温过程中:(1)体积保持不变;(2)压强保持不变;(3)不与外界交换热量,试分别求出气体内能的改变,吸收的热量,外界对气体所作的功,设氦气可看作理想气体,且,解:理想气体内能是温度的单值函数,一过程中气体温度的改变相同,所以内能的改变也相同,为:热量和功因过程而异,分别求之如下:(1)等容过程:V=常量A=0由热力学第一定律,(2)等压过程:由热力学第一定律,负号表示气体对外作功,(3)绝热过程Q=0由热力学第一定律5-2.分别通过下列过程把标准状态下的0.014Kg氮气压缩为原体积的一半;(1)等温过程;(2)绝热过程;(3)等压过程,试分别求出在这些过程中气体内能的改变,传递的热量和外界对气体所作的功,设氮气可看作理想气体,且,解:把上述三过程分别表示在P-V图上,(1)等温过程理想气体内能是温度的单值函数,过程中温度不变,故由热一、负号表示系统向外界放热(2)绝热过程由或得由热力学第一定律另外,也可以由及先求得A(3)等压过程,有或而所以===由热力学第一定律,也可以由求之另外,由计算结果可见,等压压缩过程,外界作功,系统放热,内能减少,数量关系为,系统放的热等于其内能的减少和外界作的功。
5-3 在标准状态下的0.016Kg的氧气,分别经过下列过程从外界吸收了80cal的热量。
(1)若为等温过程,求终态体积。
(2)若为等容过程,求终态压强。
(3)若为等压过程,求气体内能的变化。
设氧气可看作理想气体,且解:(1)等温过程则故(2)等容过程(3)等压过程5-4 为确定多方过程方程中的指数n,通常取为纵坐标,为横坐标作图。
试讨论在这种图中多方过程曲线的形状,并说明如何确定n。
解:将两边取对数或比较知在本题图中多方过程曲线的形状为一直线,如图所示。
直线的斜率为可由直线的斜率求n。
或即n可由两截距之比求出。
5-5 室温下一定量理想气体氧的体积为,压强为。
新版热学(秦允豪编)习题解答第四章热力学第一定律-新版.pdf

CV T0 2
CV (
R 2R
1
1
27 3 2
T2 T0
T0
(2)由( 1)式:
8
3
1.5 )
(3)左侧初态亦为 P0 T 0 V 0 ,终态为 P1V1T1
27
P1 P2
P0
∵ 活塞可移动,
8 ,由 PV
RT
RT 2
P0 V 0 T 2
V2
P2
T0
P2
14
V 1 2V 0 V 2
V0
9
P0V 0
3 T0
19
23
q 2 1 .60 10
6 .02 10 C
( q 2N Ae )
两极间电压为 , A q
19
A 1 .229 2 1 .60 10
6 .02
Q'
5
2. 858 10
23
10
82 . 84 %
4.4.7 设 1mol 固 体状 态 方程 为: v v 0 aT bP , 内 能 表示 为: u CT
Py L y S
P0 LS
其中 P0
gh 0
Py P0 可改写为
L Ly
1 P0
对微小振动 y L
Py P0
y 1
L
y
1 P0
1
1 P0
L
y P0
L
h0 gy
L
由功能关系:
m gy
1 mv 2 2
m max gy max
AP
式中 A P 是由于右端空气压强 P y 与左端空气压强 P0 对水银柱作功之和,且
2
T0
27 P0
8
热学学 第四章 热力学第一定律.
植物,通过氧化把化学能转化为热和机械能。
16
亥姆霍兹 德国 物理学家(1821~1894) 《力之守恒》 化学、力学、电磁学、热学
17
• 2 内能
内能:在热学参考系下,所有分子的无规则运动的能量之和。
热学参考系:使系统宏观静止的参考系
用的能量,在过程中保持为常数,因此可以省略。
• 内能具体包含哪些能量---普遍
分子的动能(包括平动、转动、振动)
+分子内部的振动势能
+分子间的势能
18
---原子核内的能量,不能被运用,省略。 ---系统整体运动的能量,不是内能,排除。 (系统的整体平动、转动的动能) ---对于理想气体,分子间势能在任何过程中始终保持为常数, 可以省略。 • 例子:单原子分子理想气体的内能。 每个分子的动能之和。---热学坐标系。 • 例子:刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和,每个分子的转动动能之和。 • 例子:非刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和,每个分子的转动动能之和。每个分 子的振动动能之和,每个分子的振动势能之和。 • 例子:前面的例子都为非理想气体时。 都要包含分子间的势能之和。
系统和外界在非功过程交换的能量,称为热量
注意:1)热量过程量。
2)系统和外界必须有温度差,才能交换热量。
3)系统和外界交换能量的方式只有两种:功,热量。
§4.3 热力学第一定律
本质:能量转化和守恒定律在热学系统的表现。
1 历史
14
焦耳(1818-1889),英国。 热功当量
w电=I 2Rt=JQ w重力=JQ Q cmT
《热学》第四章和第五章复习

第四章 热力学第一定律 基本要求一、 可逆和不可逆过程 (1)准静态过程(2)理解什么是可逆过程,什么是不可逆过程.知道只有无耗散的准静态过程才是可逆过程。
二、 功和热量 (1)明确功是在力学相互作用过程中能量转移,热量是在热学相互作用过程中的能量的转移,它们都是过程量,它们都是过程量。
知道“作功”是通过物体宏观位移来完成;而“热传递”是通过分子之间的相互作用来完成。
(2)知道功有正负,熟练掌握从体积膨胀功微分表达式pdV W d -=出发计算体积膨胀功。
从几何上理解功的大小等于p-V 图上热力学过程曲线下面的面积。
三、热力学第一定律(1)知道能量守恒与转化定律应用到热学中就是热力学第一定律。
明确热力学第一定律是把内能、功和热量这三个具有能量量纲的物理量结合在一个方程中:即 W Q U +=∆; (2)一微小过程中热力学第一定律表示为:W d Q d dU +=;对于准静态过程热力学第一定律表示为:pdV Q d dU -=(3)内能是态函数,内能一般应是温度和体积的函数。
内能应当包含分子的热运动动能和分子之间的相互作用势能,也应包括分子内部的能量;在热学中的内能一般不包括系统做整体运动的机械能。
四、热容和焓(1)知道热容的定义、热容是过程量、热容与物体的量有关。
(2)知道焓的定义pV U H +=;知道焓的物理意义。
五、热力学第一定律对理想气体的应用(1)知道焦耳定律;即理想气体的内能仅是温度的函数;知道理想气体的焓也只是温度的函数。
内能和焓的微分可分别表示为:dT C dU m V ,ν=;dT C dH m p ,ν=;这两个公式适用于理想气体任何过程。
(2)理想气体的准静态过程的热力学第一定律可表示为pdV dT C dQ m V +=,ν;利用上式可得迈耶公式:R C C m V m p =-,,ν;(3)会熟练利用热力学第一定律处理一些常见热力学过程。
(4)会推导准静态绝热过程方程,熟记并会熟练利用绝热过程方程,同时应知道绝热过程方程的适用条件。
大学物理-热力学

存在温差而发生的能量传递 .
功与热量的异同 1)过程量:与过程有关;
T1 T2
T1 Q T2
2)等效性:改变系统热运动状态作用相同;
1卡 = 4.18 J , 1 J = 0.24 卡
3)功与热量的物理本质不同 .
功
宏观运动
分子热运动
热量
分子热运动
分子热运动
五、 内 能 (状态量)
物体内分子做无规运动的动能和势能的总和叫做 物体的内能。内能由系统的状态唯一地决定。内能的 改变量只由初末状态决定,和变化的具体过程无关。
p
A*
1
p
A*
1
2 *B
o
V
2 *B
o
V
理想气体内能 : 表征系统状态的单值函数 ,
理想气体 的内能仅是温度的函数 U U (T )
永 动 机 的 设 想 图
第一类永动机试图在不获 取能源的前提下使体系持续 地向外界输出能量。历史上 最著名的第一类永动机是法 国人亨内考在十三世纪提出 的“魔轮”,十五世纪,著 名学者达芬奇也曾经设计了 一个相同原理的类似装置, 1667年曾有人将达芬奇的设 计付诸实践,制造了一部直 径5米的庞大机械,但是这些 装置经过试验均以失败告终。
Cp,m CV ,m R
CV ,m
CV ,m
CV ,m
R 1
R
1
W 1 (T1 T2 ) 1 ( p1V1 p2V2 )
绝热过程方程的推导
dQ 0, dW dU pdV vCV ,mdT
pV vRT
pdV Vdp R pdV CV ,m
整理得
dp dV 0
pV
p
p2
2 T2
热学_热力学第一定律

3、理想气体在几种等值过程中功的计算 前提:理想气体的无摩擦准静态过程。 等温过程:
W =∫
V2
V1
V2 dV = νRT ln pdV = νRT ∫ V1 V V1
V2
气体膨胀时, d V > 0
d W > 0 系统对外界作功。
p p2 C
等 温
Q P1V1 = P2V2
A
P1 W = νRT ln P2
1)对过程 adb
0 a d V
Qadb = ΔU &#
2)对过程 ba
Qba = ( U a − U b ) + W2 = −105 − 42 = −147 J
放热
§4.4 一、定体热容与内能
热容量与焓
p b d c a T 0 V e T+dT
等体过程a—b, ΔV=0,W=0
宏观位移 转 换 分子间作用 传 递
1卡 = 4.18 焦耳 系统内能 系统内能
外界机械能 外界内能
§4.3 内能 热力学第一定律 一、内能 1. 定义: 微观上:热力学系统内部的能量。 包括所有分子热运动动能EK与分子间的势能EP
U = Uk + U p
U = U ( T ,V )
宏观上:系统内能的增量等于绝热过程中外界对 系统作的功。——内能定理
△U > 0 ,系统内能增加。△U < 0,系统内能减少。
2)热力学第一定律的另一种表述: 第一类永动机是不可能制成的。 第一类永动机:不需要任何动力 和燃料,却能对外作功的机器。
3) Q = Δ U + W , dQ = dU + dA 适用于任何系统的任何过程
对微小准静态过程: d Q = d U + p d V 对有限准静态过程: Q = Δ U + pdV V1 i 而 Δ U = ν R Δ T 只适用于理想气体。 2 4)热力学第一定律是大量实验的结果,具有普遍性。 5)实质是包含热能在内的能量转化与守恒定律。
第四章热力学第一定律
转化为热量Q向外释放; 若:dV 0, 等温膨胀,气体对外所做功 PdV > 0,
来源于自外界吸收的热量Q。
V2
W PdV
V1
V2
因而准静态过程的吸热情况为: Q W PdV
V1
理气等温过程内能不变: dU=0
Q
W
V2
PdV
V1
T2
RT
T1
dV V
RT lnV2
V1
RT ln P1
T1
T1
T1
T1
T2
T2
T2
( C p,m R)dT (CP,m R)dT CV ,mdT
T1
T1
T1
三、等温过程:
P
T=常量,dT=0 的过程
理气等温过程内能不变: dU=0 o
U2 U1 0 Q W
T1 T2 V
若:dV 0, 等温压缩,外界对气体所做功 -PdV > 0,
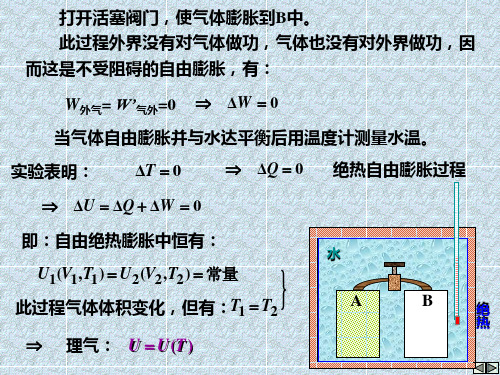
打开活塞阀门,使气体膨胀到B中。 此过程外界没有对气体做功,气体也没有对外界做功,因 而这是不受阻碍的自由膨胀,有:
W外气= W’气外=0 ΔW 0 当气体自由膨胀并与水达平衡后用温度计测量水温。
实验表明: ΔT 0
ΔQ 0 绝热自由膨胀过程
ΔU ΔQ ΔW 0
即:自由绝热膨胀中恒有:
CP,m
CV ,m
dQP ,m dT
dQV ,m dT
R
dQP,m dQV ,m RdT
例:如图,同种单原子理想气体放在同 一容器的两个部分,抽去中间隔板 使之均匀混合。求:混合后的温度 和压强。
解:绝热: ΔQ 0
混合前后: ΔV 0 ΔW 0
绝热壁
P1 V1 T1
热力学第一定律

热力学系统中的力学作用形式多样, 如:压强、表面张力、弹性力、 电磁力、等等。
2. 作用效果
使热力学系统的力学平衡条件被破坏,在系统状态 变化过程中伴随有能量转移,其形式即:作功。
3. 一些常见过程中元功的计算
作用力为广义力, 状态变化量为广义位移,
记 Y 为广义力,X 为广义位移,
则其元功为: W YX .
3.车载的能量有限。
冷却外壳
离合器部分
驱动电机系统概述
二、驱动电机的分类
按照结构和工作原理不同,目前的驱动电动机有直流电动机、交流异步电动 机、永磁同步电动机、开关磁阻电动机等几种。
1.直流电动机 直流电动机通过定子绕组产生磁场,向转子绕组通入直流电,并用换向装置对 绕组内电流在适当时候进行换向,使转子绕组始终受到固定方向的电磁转矩。
驱动电机系统概述
一、驱动电机简介
用于驱动车辆的电动机称为驱动电动机。其任务是在驾驶人的控制下,高效
率地将蓄电池的电量转化为车轮的动能,或者将车轮的动能反馈到蓄电池中。
驱动电动机的工作条件与一般工业电动机有明显不同,体现在以下方面。
1.驱动电动机的转速、转矩变化范围大;
发动机
电动机
就业变速箱
2.驱动电动机所处的使用环境恶劣;
三、驱动电机的额定指标 驱动电动机的额定指标是指根据国家标准及电动机的设计、试验数据而确定的额
定运行数据,是电动机运行的基本依据。电动机的额定指标主要包括以下各项。 1.额定功率。额定功率是指额定运行情况下轴端输出的机械功率(W或kW)。 2.额定电压。额定电压是指外加于线端的电源线电压(V)。 3.额定电流。额定电流是指电动机额定运行(额定电压、额定输出功率)情况下
热力学第一定律知识点总结

热力学第一定律知识点总结热力学第一定律,也被称为能量守恒定律,是热力学中最基本也最重要的定律之一。
它描述了能量的守恒原理,即能量既不能被创造也不能被消灭,只能从一种形式转化为另一种形式。
本文将对热力学第一定律的几个核心知识点进行总结,帮助读者理解和应用这一重要定律。
1. 能量守恒定律热力学第一定律是基于能量守恒定律的原理,它表明能量在系统中的总量守恒。
能量可以以多种形式存在,包括热能、机械能、化学能等。
根据第一定律,能量从一个系统转移到另一个系统时,总能量保持不变。
2. 内能和热量内能是物质系统所具有的能量总量,包括分子间势能和分子内能量。
内能可以通过热量的传递进行改变。
热量是指能量由高温物体传递到低温物体的过程,它可以增加或减少系统的内能。
3. 等内能过程等内能过程是指系统的内能保持不变的过程。
在等内能过程中,系统可能发生其他形式的能量转化,比如从热能到机械能的转化。
根据热力学第一定律,等内能过程中输入和输出的能量必须相等。
4. 功和能量转化功是指力对物体施加的作用导致物体发生移动的过程中所做的能量转化。
功可以改变系统的内能,从而遵循热力学第一定律的原则。
例如,当气体在容器中膨胀时,外界对气体所做的功会增加气体的内能。
5. 热容和热容量热容是指物体吸收单位热量时温度的变化量。
热容量是指物体吸收或释放的热量与温度变化之间的关系。
热容和热容量可以用来量化系统对热量的响应以及系统内能的变化。
6. 等压和等体过程等压过程是指物体在恒定压力下发生的过程,例如,蒸汽锅炉中水的加热过程。
在等压过程中,系统的内能改变等于输入或输出的热量减去所做的功。
同样地,等体过程是指物体的体积保持不变的过程。
总结:热力学第一定律是热力学中的核心原理,它描述了能量的守恒以及能量在系统中的转化。
通过理解和应用热力学第一定律,我们能够分析和解释能量的转移过程,进而更好地理解和掌握热力学的基本概念和定律。
在实际应用中,热力学第一定律也为工程领域提供了重要的理论基础,例如在能源利用和转化、热机工作原理等方面发挥着关键作用。
热力学第一定律

P2V2
ln
V2 V1
7
又 ∵ 等温过程有
V2 P1 V1 P2
有
AT
P1V1 M
ln P1 P2 RT
ln
P2V2 P1
ln
P1 P2
M mol
P2
(3)强调QT=AT
即在等温过程中,系统的热交换不能直接计算,但可用等 温过程中的功值AT来间接计算。
8
※三种过程中气体做的功
等体过程
(1)特征:dT=0, ∴dE=0 热一律为 QT=AT
在等温过程中,理想气体所吸收 的热量全部转化为对外界做功,系 统内能保持不变。
(2)等温过程的功
PI
P1
P2
o
V1
II
V2 V
∵T=C(常数),
P RT 1
V
dAT PdV
AT
V2 RTdV RT ln V2
V V1
V1
P1V1
ln
V2 V1
T1)
M M mol R(T2 T1)
5
C p
C V
R i2R 2
──此即迈耶公式
(3)比热容比:
定义
Cp
Cv
i 2
RR iR
i2 i
2
对理想气体刚性分子有:
单原子分子:
双原子分子:
5 3 7 5
1.67 1.4
*: 经典理论的缺陷
多原子分子:
8 6
1.33
6
3、等温过程
1
符号规定
Q
吸热为正, 放热为负.
系统对外做功为正, A 外界对系统做功为负.
各物理量的单位统一用国际单位制。
04 不可逆过程的热力学

deS为体系与环境所交换的熵,其符号可正,可负,可为零。
过程的耦合:
熵是一个广度性质,若将一个体系划分为几个部分,则体系的 总熵应为各部分熵变的总和: diS=(diS)j (6) 若把每个小部分视为一个小的体系,其内部的熵变均不会小于 零: (diS)j 0 故对于任何体系,不论将体系如何划分,均不可能出现下列情 况: (diS)1 0 (diS)2 0 [di(S1+S2)] 0 即体系的任一局部,其熵的内部变化(diS)均遵守熵增定律。
( A A1i A2 j A3k )
流密度是一个矢量场;散度是一个标量场。
比较(3)式和(4)式,dQ/dt应该是相等的,故有:
( Q t, r ) t
jQ (t , r )
(5)
(5)式即为守恒量所遵守的一般连续性方程。
2、质量守恒方程:
体系中各组分的质量的变化途径一般有两种:
第四章 非平衡态热力学
(不可逆过程的热力学)
平衡态热力学回顾
一、热力学第一定律
dE = Q- W (1) 式中:E:体系的内能;Q:热量;W:功。 对于孤立体系,有: dE=0 (E为恒量) 对于一般体系,因为体系与环境间存在能量的交换,故内能E 的值是不断变动的,体系内能的变化可以分为两项: diE:体系内部过程所引起的内能变化; deE:与环境的交换引起的内能变化。 而diE相当于孤立体系的内能的变化,由热力学第一定律,孤 立体系的内能是恒定的: diE 0 (2)
一、非平衡态体系状态的描述:
在经典热力学中,相图中的相点描述的是热力学平衡态,非平 衡态在相图中无法表示。究其原因: 平衡态只需要极少数变量就可完全确定其状态,如理想气体: 用(T,V,N)或(T,p,V) 就可完全决定确定其平衡态的性质,而 不可能确定其非平衡态的性质。
第四章热力学第一定律及其应用

t2 1 2 1 E Q W s (hi gzi ui )midt (hj gzj u 2 j )mjdt t1 t 1 2 2 i j
(4-7)
3.2开系流动过程的能量平衡
对于时间为dt的微量变化过程,上式可 改写成
dE Q W s 1 1 ( ) (hi gzi u i2 )mi (hi gzi u 2 j )mj dt dt dt 2 2 i i (4-8)
4.3.1开系流动过程的能量平衡
0=Q-Ws-△H-△Ep-△Ex
H hjmj himi
j i
(4-9) (4-10)
(4-11) (4-12)
Ep mjgzj migzi
j i
1 1 2 EK mju j miui2 j 2 i 2
4.3.1开系流动过程的能量平衡 若进入和离开开系的物料都只有一种,在 此情况下 m = mi = mj 式(4-10)至式(4-12)可简化成 Δ H=m(hj - hi) = mΔ h (4-13) Δ EP=mg(zj-zi)=mgΔ z (4-14) Δ EK=(1/2)m(u2j-u2i)=(1/2)mΔ u2 (4-15)
4.1闭系非流动过程的能量平衡
研究化工过程能量变化,对于降低 能量消耗,合理地利用能量是十分 重要的。 体系和外界 热力学体系分为孤立体系、封闭体 系(简称闭系)和敞开体系(简称 开系)。
U = q – w (4-1)
4.2开系流动过程的能量平衡
根据能量守恒原理 体系的能量变化=与外界交换的净能量 在开系的边界上,不仅有以热和功形式 的能量通过,而且还允许有物质通过。 因此,在式(3-1)的右边除了热和功外, 还应考虑由于物质进入和离开体系引起 的能量交换。如果通过边界的物质所携 带的能量只限于内能、位能和动能,则 单位质量流体携带的能量e为:
化工热力学4-6章小结

K 1 K 1 K K p2 K K p 2 RT1 1 P V1 1 1 p1 K 1 K 1 m m m p m p 变化不大) 2 1 (4)真实气体( Z 2 wS ( R ) p1V 1 RT 1 1 p1 m 1 m 1 p1
选择物流量
5
气体压缩
1、恒温压缩过程: pV=常数,Q=W(s) 2、绝热压缩过程: pVK=常数 3、多变压缩过程: pVm=常数 1<m<K
6
气体压缩——单级压缩功计算
(1)等温压缩
wS ( R ) p Vdp p
1
p2
p2
1
RT1 p dp RT1 ln 2 p p1
(2)绝热压缩
(1)可逆轴功Ws(R): ws ( R )
vdp
p1
p2
绝热可逆: WS R H
(2)实际轴功Ws的计算:
WS 1 产功设备:可逆轴功为最大功 m WS ( R ) WS ( R ) 耗功设备:可逆轴功为最小功 m 1 WS
4
5. 热量衡算
稳流过程的热量衡算的基本关系式: △H=Q 四种热效应:显热、潜热、混合热、反应热 选择控制体 热量衡算方法: 选择基准状态 (四选择) 选择初始态
化工热力学4-6章
小结
1
第四章 热力学第一定律
1. 闭系非流动过程的能量平衡
ΔU Q W
2. 开系稳流过程的能量平衡
2 u12 u2 h1 gZ1 ws q h2 gZ2 2 2
1 2 h gZ u ws q 2
第4章 热力学基础

绝热过程方程:
pV C1
TV
1
C2
C3
T p
1绝热过程
V T降低 p降低更多
p
A
C
V T不变 p降低
等温线、绝热线的斜率分别为:
B
O V
dp p V d V T dp p V dV Q
又因混合后的氮气与压强仍分别满足理想气 体状态方程,
由此得:
1 M1 p1 RT V1 +V2 M mol 1 1 M2 p RT 2 V1 +V2 M mol 2
两者相加即得混合气体的压强:
1 p V1 +V2
M1 M2 + M mol 1 M mol 2
RT
解:打开活塞后,原在第一个容器中的氮气向第二个容器中 扩散,氩气则向第一个容器中扩散,直到两种气体都在两容 器中均匀分布为止。达到平衡后,氮气的压强变为p1',氩气 的压强变为p2' ,混合气体的压强为p= p1' + p2' ;温度均为T 。在这个过程中,两种气体相互有能量交换,但由于容器是 绝热的,总体积未变,两种气体组成的系统与外界无能量交 换,总内能不变,所以
利用多方方程和状态方程:
dA PdV Rdt /(n 1)
已知
E1 +E2 =E1 +E2 0 M E1 Cv1 T T1 M mol1 M E2 Cv 2 T T2 M mol 2
代入式得:
M M Cv1 T T1 + Cv 2 T T2 = 0 M mol1 M mol 2
M1 M2 Cv1T1 + Cv2 T2 M mol1 M mol 2 T M1 M2 Cv1 + Cv2 M mol1 M mol 2
大学物理热学 第四章 (热力学第一定律)

理学院 物理系 陈强
第四章 热力学第一定律
四. 理想气体的内能和CV、Cp
对理想气体, 内能仅是温度T的函数, 是状态函数.
U U (T )
所以, 不论对等体或等压过程均有:
dU dU dU dT dT V dT p
理想气体的定容摩尔热容为
Q L 4 . 06 10 J
4
外界对系统作功为
W p ( V g V l ) ... 3 . 05 10 J
3
Q
由热力学第一定律, 水的内能增量为
U Q W 3 . 75 10 J
4
16
理学院 物理系 陈强
第四章 热力学第一定律
绝热
• 微观本质不同:作功 有序; 传热 无序
8
理学院 物理系 陈强
第四章 热力学第一定律
准静态过程中功的计算 如图,dW pSdx pdV
dW:外界对系统作的元功
dV 0 膨胀 , dW 0
S p dx
dV 0 压缩 ,
dW 0
从状态I(p1,V1,T1)变化到状态II (p2,V2,T2)
T1+dT
系统T1 T2
T1+2dT
T1+3dT
5
例1:气体被压缩的过程
例2:系统的加热过程
理学院 物理系 陈强
第四章 热力学第一定律
对一定量气体,任何一个平衡态都对应于状态图(如 P-V图,P-T图或V-T图)中的一点。反之亦然;
一定量气体的任何一个准静态过程都可用系统的 状态图(如P-V图,P-T图或V-T图)中一条光滑连 续曲线表示,反之亦如此。
化工热力学 第四章 热力学第一定律及其应用

根据此式可计算流体终温、质量流速、出口截面积等, 因此它是喷管和扩压管的设计依据。
质量流率
u1 A1 u2 A2 m V1 V2
⑵、节流
使流体通过阀门或孔板,截面突然缩小,摩擦损失较大。 即流体通过阀门或孔板的节流过程为等焓流动。 节流膨胀后往往会使流体的温度下降。理想气体通过节流阀温度
h 0, h1 h2
第一节
§4-2 开系流动过程的能量平衡
开系的特点: ① ② 体系与环境有物质的交换。 除有热功交换外,还包括物流输入和 输出携带能量。 开系的划分: 可以是化工生产中的一台或几台设备。
可以是一个过程或几个过程。
可以是一个化工厂。
把划定的开放体系那部分称为控制体,用σ表示。
化工热力学 第四章
化工热力学 第四章 2、绝热稳定流动方程式
热力学第一定律及其应用
流体:可压缩,与外界无热、无轴功交换.
1 2 h u 0 ——绝热稳定流动方程式 2
⑴、喷管与扩压管 喷管:流体通过时压力沿着流动方向降低,而流速加快的部 件称为喷管。 当出口流速﹤音速时,可用渐缩喷管: 当入口流速﹤音速,当出口流速﹥音速时,用拉法尔喷管 :
1 2 m j h j gz j u j 2 j
此式是开系通用的能量平衡方程
化工热力学
第四章 热力学第一定律及其应用
第一节
§4-3 稳流过程的能量平衡
状态是稳定的 稳流过程 流动是稳定的
一、开系稳流过程的能量平衡式
所有质量和能量的流速均为常量。开系内没有质量
和能量积累的现象。
亚音速 超音速
扩压管:在流动方向上流速降低、压力增大的装置称为扩压管。
高中物理 第四章热力学第一定律

V1
V V1
V1
若膨胀时, V2 V1,则W 0,说明外界对气体作负功 。
p1V1 p2V2
W RT ln p2
p1
7
等压过程: 等体过程:
W
V2 V1
pdV
p(V2
V1 ),
利用状态方程可得:W R(T2 T1)
dV 0,W 0
三、其它形式的功
内能是系统内部所有微观粒子(如分子、原子等) 的微观的无序运动能以及相互作用势能两者之和。内能 是状态函数,处于平衡态系统的内能是确定的。内能与 系统状态间有一一对应关系。
2、内能定理
从能量守恒定理知道:系统吸热,内能应增加;外界 对系统作功,内能也增加。若系统既吸热,外界又对系统 作功,则内能增量应等于这两者之和。
13
W绝热=U2-U1
1、内能是一种宏观热力学的观点,不考虑微观的本质。
注意
2、内能是一个相对量。
3、热学中的内能不包括物体整体运动的统。 5、有些书上提到的热能实质上是指物体的内能。
14
三、热力学第一定律的数学表达式:
U2 U1 Q W
Q是系统所吸收的能量, W是外界对系统所作的功
•对外界也不产生任 何影响
★ 只有无耗散的准静态过程才是可逆过程。 4
§4.2 功和热量
一、功是力学相互作用下的能量转移
力学相互作用:将力学平衡条件被破坏时所产生的对系统 状态的影响。
在力学相互作用过程中系统和外界之间转移的能量就是功。
热力学认为力是一种广义力,所以功也是广义功。
注意:
1)、只有在系统状态变化过程中才有能量转移。
D、了解循环过程,能计算卡诺循环等简单 循环的效率;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华北科技学院化工热力学Chemical Engineering Thermodynamics第四章 热力学第一定律4.1 闭系非流动过程的能量平衡能量平衡式 体系能量的变化=体系与环境交换的净能量。
即:(能量)入 − (能量)出 = (能量)存封闭体系非流动过程的热力学第一定律:ΔU = Q + W4.2 开系通用的能量平衡方程4.3 稳流过程的能量平衡1. 开系稳流过程的能量平衡状态是稳定的 稳流过程 流动是稳定的 1)外部环境对流体提供的能量(对于1kg流体): ①外功(ws)—净功或有效功,J/kg; 规定:外界提供给流体功, ws为正; 流体传递给外界功,ws为负。
②热量(q)—获得的热量,J/kg;4.3 稳流过程的能量平衡2) 流体在流动过程中本身所具有的能量(对于1kg流体): ① 内能 U: J/kg; ② 位能: ③ 动能: ④ 静压能(压强能) m kg: 动能 = mu2/2, J 1 kg: 动能 = u2/2 , J/kg m kg: 位能 = mgZ, J 1 kg: 位能 = gZ, J/kgm kg-V m3 : 静压能 = pV , J 1V kg- m3 m:静压能=pV p = m ρ, J/kg4.3 稳流过程的能量平衡衡算范围:1-1′至2-2′截面 衡算基准:1kg不可压缩流体 基准水平面:0-0′平面流动系统依据: 输入总能量=输出总能量1 2 p1 1 2 p2 U 1 + gz1 + u1 + + we + q = U 2 + gz2 + u2 + 2 ρ 2 ρ总能量衡算式4.3 稳流过程的能量平衡1 ρ= v1 2 p1 1 2 p2 U 1 + gz1 + u1 + + ws + q = U 2 + gz2 + u2 + 2 ρ 2 ρ 1 2 1 2 U 1 + gz1 + u1 + p1v + ws + q = U 2 + gz2 + u 2 + p2 v 2 2h = U + Pv2 u12 u2 h1 + gZ1 + + ws + q = h2 + gZ 2 + 2 2P97,例4-11 2 Δh + gΔZ + Δu = ws + q 2mkg1 ΔH + mgΔZ + mΔu 2 = Ws + Q 21kg流体稳流能量衡算式mkg流体稳流能量衡算式4.3 稳流过程的能量平衡2. 稳流过程能量平衡的简化形式(1)机械能平衡方程式(柏努利方程): 流体不可压缩→ρ=常数=1/v,v△p=△p/ρ 无热、无轴功交换→q=0,ws=0 理想流体,无粘性→摩擦损耗hf=0,△U=0Δh + gΔZ + 1 2 Δu = ws + q 2条件△h=△U+v△pΔpρ+ gΔZ +1 Δu 2 = 0 24.3 稳流过程的能量平衡(2)绝热稳定流动方程式 条件:可压缩,与外界无热、无轴功交换。
1 2 Δu = 0 2 z根据此式可计算流体终温、质量流速、出口截面积 Δh +等,因此它是喷管和扩压管的设计依据。
dh = Tds + vdp = δq + vdp z另外,δq = 0,T ≠ 0,ds = 0 ∴为等熵过程 dh = vdpz节流:△H≈0,等焓过程 孔板、阀门、多孔塞 P↓,∆u≈04.3 稳流过程的能量平衡(3)与外界有大量热、轴功交换的稳流过程 (动能≈0,势能≈0)ΔH = Q + WS 或 Δh = q + wsa. 有大量热、无轴功交换,Ws=0泵、压缩机、透平ΔH = Q,Δh = q换热器、反应器体系状态变化,如发生化学反应,相变化,温度变化, 与环境交换的热量(反应热,相变热,显热) 等于体系的焓差b. 无热交换(绝热) Q = 0ΔH = W S或Δh = wsP99,例4-2,34.3 稳流过程的能量平衡3. 轴功(1)可逆轴功Ws(R)的计算: 无任何摩擦损失的轴功 ①对于静止的或流动的封闭体系 单位质量流体:Δh = q + ∫ vdpp1 p2dh = tds + vdp = δqR + vdpws ( R ) = ∫液体p2 p1可逆1 Δh + gΔZ + Δu 2 = ws + q 21 2 vdp + gΔZ + Δu 2p2ws(R)=v△pws ( R ) = ∫ vdpp1②绝热可逆过程(等熵):dh = vdpWS ( R ) = ΔH4.3 稳流过程的能量平衡3. 轴功(2)实际轴功Ws的计算: 产功设备(透平):WS实 < WS ( R ) 可逆轴功为最大功ηm :机械效率其大小与机器 制作水平有关WS ηm = <1 WS ( R )耗功设备:WS实 > WS ( R )ηm =WS ( R ) WS<1可逆轴功为最小功P105,例4-4,54.3 稳流过程的能量平衡4. 热量衡算热量衡算:无轴功交换,只有热交换过程的能量衡算 稳流过程的热量衡算的基本关系式: △H=Q 四种热效应: ① 显热――物流的温度变化 ② 潜热――物流的相变化 ③ 混合热效应――多股物流混合 ④ 反应热效应――化学反应产生 热量衡算方法:(四选择) ¾ 选择控制体 ¾ 选择物流量¾选择基准状态¾ 选择初始态4.3 稳流过程的能量平衡物流A:温度TA1→TA2,放热QA,流量mA,平均等压热容CpmhA 物流B:温度TB1→TB2,吸热QB ,流量mB,平均等压热容CpmhB 换热器:热损失QL 对于换热器,△H=Q △H= △HA+△HB,Q=QL=QA +QB △HA=mACpmhA(TA2-TA1) △HB=mBCpmhB(TB2-TB1) 换热器的热量平衡式: QL=mACpmhA(TA2-TA1)+mBCpmhB(TB2-TB1)TA2 A物流 TA1 QB QL QA TB1 B物流 TB2换热器热平衡4.3 稳流过程的能量平衡循环气:冷凝氨量mL ,温度TG1→TG2,流量mG,CpmhG 液氨:汽化液氨量mA ,温度TA1→TA2,流量mA,CpmhA 氨冷器:热泄入QL 对于氨冷器,△H= △HG+△HA=QL △HG=mGCpmhG(TG2-TG1)+ mL△hL循环气入TG1 气氨TA2△HA=mACpmhA(TA2-TA1)+ mA△hA 氨冷器的热量平衡式: QL=mACpmhA(TA2-TA1)+mA△hA循环气出TG2QL液氨TA1 氨冷器热平衡+mGCpmhG(TG2-TG1)+mL△hL4.4 气体压缩过程概述常用于压缩气体的机械有: ¾ 压缩机(终压>0.3MPa,压缩比>4)¾ 鼓风机(终压0.015~0.3MPa,压缩比<4) ¾ 通风机(终压<0.015MPa(表压) 往复式 按运动机构,压缩机 叶轮式外界输入功4.4 气体压缩过程1. 压缩过程热力学分析理想压缩过程: 整个过程均为可逆,不存在任何摩擦 损耗,输入的功完全用于压缩气体。
往复式压缩机压缩过程示意图: 活塞 冲程排气活门 吸气活门冲程:活塞从一端到另一端的行程距离称为冲程或行程4.4 气体压缩过程绝热(Ws,T2,V2)>多变(Ws,T2,V2)>等温(Ws,T2,V2)P2P 3 2a 2b 2c 1、恒温压缩过程: PV=常数,-Q=W(s) 2、绝热压缩过程: PVK=常数 3、多变压缩过程: PVm=常数 1<m<KP 1V 往复式压缩机压缩过程示意图14.4 气体压缩过程2. 单级压缩机可逆轴功的计算(1)等温压缩 理想气体:PV=RT △H=Q+Ws等温△H=0,Ws(R)= -Q2Ws(R)由T1 和压缩比 P2/P1决定P P WS ( R ) = ∫P VdP = ∫ RT1 dP = RT1 ln 2 PP211PP1(2)绝热过程 Q=0 PVK=常数 Ws=△H= VdP ∫ PP214.4 气体压缩过程气体压缩过程所耗的理论轴功决定于 始温下绝热指数K和压缩比。
WS ( R ) ⎡ ⎛ P2 K ⎢ RT1 ⎜ = ⎢⎜ K −1 ⎝ P1 ⎢ ⎣ ⎞ ⎟ ⎟ ⎠K −1 KK −1 ⎤ ⎡ ⎤ K ⎛ ⎞ P K 2 ⎥ − 1⎥ = ⎟ P1V1 ⎢⎜ 1 − ⎥ K −1 ⎢⎜ ⎥ P1 ⎟ ⎝ ⎠ ⎢ ⎥ ⎥ ⎣ ⎦ ⎦式中,K为绝热指数,与气体性质有关。
理想气体K的取值: 单原子气体:K=5/3 双原子气体:K=7/5 三原子气体:K=4/3 混合气体的绝热指数Km:yi 1 =∑ K m − 1 i Ki − 1Ki:某组分的绝热指数 yi:某组分的摩尔数4.4 气体压缩过程(3)多变压缩WS ( R )PVm=常数⎡ ⎛ P2 m P1V1 ⎢⎜ = ⎢⎜ m −1 ⎝ P1 ⎢ ⎣ ⎞ ⎟ ⎟ ⎠m −1 mP114,例4-8m −1 ⎤ ⎡ ⎤ m ⎛ ⎞ P m 2 ⎥ ⎟ − 1⎥ = − RT1 ⎢⎜ 1 ⎥ m −1 ⎢⎜ ⎥ P1 ⎟ ⎝ ⎠ ⎢ ⎥ ⎥ ⎣ ⎦ ⎦式中,m为多变指数。
(4)真实气体压缩功 a. Z变化不大: 取平均值:Zm=(Z进 +Z出)/2,将Zm看成常数 真实气体压缩功=Zm×理想气体压缩功 b. Z变化大: 绝热过程: 多变过程: △H=Ws(R) Ws(R)=△H-Q4.4 气体压缩过程3. 多级压缩功的计算气体的压缩,通常都是采用多级压缩。
多级压缩可用适当的压缩比,并且各级都设有中 间冷凝器,使之更趋近于等温压缩。
多级压缩所消耗的总功,应为各级压缩所消耗功 的代数和,因此可减少总的功耗。
4.4 气体压缩过程单级等温压缩: 功为ABFHA所包围的面积P2PF HED单级绝热压缩: 功为ABDHA所包围的面积 C 二级绝热压缩: 功为ABCGEHA所包围的面积 阴影部分面积: BP2′ P 1IGA V二级绝热压缩节省的功二级压缩P-V 图4.4 气体压缩过程设,某理想气体由P1压缩至PS+1(S级压缩),总功耗为各 级压缩功之和:WS ( R ) ⎡ ⎛ P2 m = P1V1 ⎢⎜ ⎢⎜ m −1 ⎝ P1 ⎢ ⎣ ⎞ ⎟ ⎟ ⎠m −1 m⎤ ⎡ ⎛ P3 m − 1⎥ + P2V2 ⎢⎜ ⎥ m −1 ⎢⎜ ⎝ P2 ⎥ ⎢ ⎦ ⎣⎞ ⎟ ⎟ ⎠m −1 mm −1 ⎤ ⎡ ⎤ m ⎛ ⎞ P m s +1 ⎥ ⎟ − 1⎥ + LL + PS VS ⎢⎜ 1 − ⎥ ⎢⎜ ⎥ m −1 Ps ⎟ ⎝ ⎠ ⎥ ⎢ ⎥ ⎦ ⎣ ⎦各级进气温度相同,且为理想气体。
故:P 1V1 = P 2V2 = LL = P SVS = RT1因此上式写成:WS ( R )m−1 m−1 ⎡ ⎛ P2 ⎞ m ⎛ P3 ⎞ m m ⎢ ⎟ ⎟ = RT1 ⎜ +⎜ ⎜ ⎟ ⎜ ⎢⎝ P m −1 P2 ⎟ 1 ⎠ ⎝ ⎠ ⎢ ⎣⎛ PS +1 ⎞ + LL + ⎜ ⎟ ⎜ P ⎟ S ⎠ ⎝m−1 m⎤ − S⎥ ⎥ ⎥ ⎦Ws(R)绝对值最小的条件:它对中间各压力的一阶偏导数=04.4 气体压缩过程⎡ ∂W S ( R ) ⎤ =0 ⎢ ⎥ ⎣ ∂P2 ⎦ P1 P3 LL⎡ ∂WS ( R ) ⎤ =0 ⎥ ⎢ ⎣ ∂P3 ⎦ P1P2 LL……PS +1 P2 P3 = = LL = =r 于是得: P1 P2 PS(压缩比)r相同,各级功耗也相同,Ws(R),1= Ws(R),2=…… W s(R),sQ P2 = P1rP3 = P2 r = P1r 2SPs +1 = Ps r = P1r s所以最适宜的压缩比 r =sPS +1 代入表示总功的式子,则: P1m =S RT1 (r m −1m −1 mWS ( R ) = ∑ WS ( R ),ii=s− 1)4.4 气体压缩过程4. 气体压缩的实际功耗实际压缩过程,有摩擦,所以耗功>可逆功 损失功:流动过程的损耗,机械传动部分的损耗 设,ηm为考虑各种摩擦损耗因素的机械效率,则压 缩过程的实际功耗为:WS =WS ( R )ηmηm由压缩机类型及实际而异,由实验测定。
