二次函数与圆综合题
二次函数与圆的综合题(中考数学必考压轴题)
二次函数与圆的综合题(中考数学压轴题必考)例1.如图,已知抛物线与x轴交于A,B两点(A在左边),抛物线经过点D以AB为直径画⊙P,试判定点D与⊙P的位置关系,并证明.练习1.如图,二次函数y=ax2﹣(a+1)x(a为常数,且0<a<1)的图象过原点O并与x轴交于点P;过点A(1,﹣1)的直线l垂直y轴于点B,并与二次函数的图象交于点Q,以OA为直径的⊙C交x轴于点D,连接DQ.(1)点B与⊙C的位置关系是;(2)点A是否在二次函数的图象上;(填“是”或“否”)(3)若DQ恰好为⊙C的切线,①猜想:四边形OAQD的形状是,证明你的猜想;②求二次函数的表达式.例2.如图示已知点M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于A、B,抛物线过A、B两点且与y轴交于点C.过C点作⊙M 的切线CE,求直线OE的解析式.练习2.平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴,设平行于x轴的直线交抛物线y=﹣x2﹣x+2于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.练习3.如图,抛物线y=﹣x2﹣x+2与x轴交于A(﹣4,0),B(2,0),与y 轴交于点C(0,2).以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.练习4.如图,抛物线y=﹣x2+x+2.经过A、B、C三点,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C,M为抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论.练习5.如图,抛物线与x轴交于A、B两点,与y轴交于C点.以AB为直径作⊙M.(1)求出M的坐标并证明点C在⊙M上;(2)若P为抛物线上一动点,求出当CP与⊙M相切时P的坐标;练习6.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D.(1)求点C的坐标和过A,B,C三点的抛物线的析式;(2)求点D的坐标:(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.练习7.如图,在平面直角坐标系中,已知OA=n,OC=m,⊙M与y轴相切于点C,与x轴交于A,B两点,∠ACD=90°,抛物线y=ax2+bx+c经过A,B,C三点.(1)求证:∠OCA=∠OBC;(2)若A(x1,0),B(x2,0),且x1,x2满足x1+x2=5,x1•x2=4,求点C 的坐标和抛物线的解析式;(3)若△ACD≌△ABD,在四边形ABDC内有一点P,且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小,求此时距离之和的最小值及P点的坐标(用含n的式子表示).练习8.已知二次函数y=mx2+(m﹣3)x﹣3(m>0)(1)求证:它的图象与x轴必有两个交点;(2)这条抛物线与x轴交于两点A、B(A在B左),与y轴交于点C,顶点为D,sin∠ABD=,⊙M过A、B、C三点,求⊙M的面积;(3)在(2)的条件下,抛物线上是否存在点P,使P A是⊙M的切线?若存在,求出P点的坐标,若不存在,说明理由.例3.如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN 为等腰三角形时,求圆心P的纵坐标.练习9.已知:如图,抛物线y=ax2+bx+1的图象关于y轴对称,且抛物线过点(2,2),点P为抛物线上的动点,以点P为圆心的⊙P与x轴相切,当点P运动对,⊙P始终经过y轴上的一个定点E.(1)求抛物线的解析式;(2)当⊙P的半径为时,⊙P与y轴交于M、N两点,求MN的长;(3)求定点E到直线y=kx﹣8k的距离的最大值.练习10.已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx (a>0)经过A、O两点,且顶点B的纵坐标为﹣2(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连接AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.练习11.已知A是x轴正半轴上一个动点,以线段OA为直径作⊙B,圆心为点B,直径OA=m,线段EF是⊙B的一条弦,EF∥x轴,点C为劣弧EF的中点,过点E作DE垂直于EF,交抛物线C1:y=ax2+bx(a>0)于点G,抛物线经过点O和点A.(1)求证:DG=m;(2)拖动点A,如果抛物线C1与⊙B除点O和点A外有且只有一个交点,求b的值;(3)拖动点A,抛物线C1交⊙B于点O、E、F、A,①求证:DE=m﹣;②直接写出FC2的值(用a,m的代数式表示)练习13.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A.B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.(1)求∠ACB的大小;(2)写出A,B两点的坐标;(3)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),求出抛物线的解析式;(4)在该抛物线上是否存在一点D点,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.例4.如图1,抛物线y=ax2+3ax(a为常数,a<0)与x轴交于O,A两点,点B 为抛物线的顶点,点D是线段OA上的一个动点,连接BD并延长与过O,A,B三点的⊙P相交于点C,过点C作⊙P的切线交x轴于点E.(1)①求点A的坐标;②求证:CE=DE;(2)如图2,连接AB,AC,BE,BO,当,∠CAE=∠OBE时,①求证:AB2=AC•BE;②求的值.练习14.如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E 四点,B为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.练习15.如图,二次函数与x轴的一个交点A的坐标为(﹣3,0),以点A为圆心作圆A,与该二次函数的图象相交于点B,C,点B,C的横坐标分别为﹣2,﹣5,连接AB,AC,并且满足AB⊥AC.过点B作BM⊥x轴于点M,过点C作CN⊥x轴于点N.(1)求该二次函数的关系式;(2)经过点B作直线BD,在A点右侧与x轴交于点D,与二次函数的图象交于点E,使得∠ADB=∠ABM,连接AE,求证:AE=AD;(3)若直线y=kx+1与圆A相切,请求出k的值.例5.已知抛物线y=ax2+bx+5(a≠0)经过A(5,0),B(6,1)两点,且与y 轴交于点C.(1)求抛物线y=ax2+bx+5(a≠0)的函数关系式;(2)如图1,连接AC,E为线段AC上一点且横坐标为1,⊙P是△OAE外接圆,求圆心P点的坐标;(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F;①点E在运动过程中四边形OEAF的面积是否为定值?如果是,请求出这个定值;如果不是,请说明理由;②求出当△AEF的面积取得最大值时,点E的坐标.练习16.如图1,已知抛物线y=﹣x2+bx+c经过点A(1,0),B(﹣5,0)两点,且与y轴交于点C.(1)求b,c的值.(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值.若不存在,请说明理由.(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.练习17.如图1,抛物线y=+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,顶点为D.(1)求抛物线的解析式;(2)如图2,以AB为直径在x轴上方画半圆交y轴于点E,圆心为G,P为半圆上一动点,连接DP,点Q为PD的中点.①判断点C、D与⊙G的位置关系,并说明原因;②当点P沿半圆从点B运动到点A时,求线段AQ的最小值.练习18.如图1,二次函数y=ax2﹣3ax+b(a、b为参数,其中a<0)的图象与x 轴交于A、B两点,与y轴交于点C,顶点为D.(1)若b=﹣10a,求tan∠CBA的值(结果用含a的式子表示);(2)若△ABC是等腰三角形,直线AD与y轴交于点P,且AP:DP=2:3.求抛物线的解析式;(3)如图2,已知b=﹣4a,E、F分别是CA和CB上的动点,且EF=AB,若以EF为直径的圆经过点C,并交x轴于M、N两点,求MN的最大值.课后练习1.抛物线y=ax2+bx﹣4交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是介于B、C之间的抛物线上的动点(包括B、C两点),点E是△ABP 的外接圆圆心.(1)求抛物线的解析式;(2)如图1,当P为抛物线的顶点时,求圆心E的坐标;(3)如图2,作PH⊥x轴于点H,延长PH交⊙E于点Q,当P从C点出发,沿该抛物线运动到B点,求点Q在这个运动过程中的路径长.2.如图,在正方形OABC中,AB=4,点E是线段OA(不含端点)边上一动点,作△ABE的外接圆交AC于点D.抛物线y=ax2﹣x+c过点O,E.(1)求证:∠BDE=90°;(2)如图1,若抛物线恰好经过点B,求此时点D的坐标;(3)如图2,AC与BE交于点F.①请问点E在运动的过程中,CF•AD是定值吗?如果是,请求出这个值,如果不是,请说明理由;②若,求点E坐标及a的值.。
二次函数和圆综合(压轴题+例题+巩固+答案解析)

【例1】.如图,点()40M ,,以点M 为圆心、2为半径的圆与x 轴交于点A B ,.已知抛物216y x bx c =++过点A 和B ,与y 轴交于点C .⑴ 求点C 的坐标,并画出抛物线的大致图象.⑵ 点()8Q m ,在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ PB + 最小值. ⑶ CE 是过点C 的M ⊙的切线,点E 是切点,求OE 所在直线的解析式.【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式2y x =-+并且线段CM 的长为(1)求抛物线的解析式。
(2)设抛物线与x 轴有两个交点A (X 1 ,0)、B (X 2 ,0),且点A 在B 的左侧,求线段AB 的长。
(3)若以AB 为直径作⊙N ,请你判断直线CM 与⊙N 的位置关系,并说明理由。
【例2】如图,在平面直角坐标系中,以点(04)C ,为圆心,半径为4的圆交y 轴正半轴于点A ,AB 是C ⊙的切线.动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动,点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动,且动点P 、Q 从点A 和点O 同时出发,设运动时间为t (秒).⑴当1t =时,得到1P 、1Q 两点,求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ;⑵当t 为何值时,直线PQ 与C ⊙相切?并写出此时点P 和点Q 的坐标;⑶在⑵的条件下,抛物线对称轴l 上存在一点N ,使NP NQ +最小,求出点N 的坐标并说明理由.提示:(1)先求出t=1时,AP 和OQ 的长,即可求得P 1,Q 1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l 的解析式.(2)当直线PQ 与圆C 相切时,连接CP ,CQ 则有Rt △CMP ∽Rt △QMC (M 为PG 与圆的切点),因此可设当t=a 秒时,PQ 与圆相切,然后用a 表示出AP ,OQ 的长即PM ,QM 的长(切线长定理).由此可求出a 的值.(3)本题的关键是确定N 的位置,先找出与P 点关于直线l 对称的点P ′的坐标,连接P ′Q ,那么P ′Q 与直线l 的交点即为所求的N 点,可先求出直线P ′Q 的解析式,进而可求出N 点的坐标.【巩固】已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与 二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线l 过()01-,点.⑴ 求一次函数与二次函数的解析式;⑵ 判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明;⑶ 把二次函数的图象向右平移2个单位,再向下平移t 个单位()0t >,二次函数的图象与x轴交于M N,,三点的圆的,两点,一次函数图象交y轴于F点.当t为何值时,过F M N面积最小?最小面积是多少?【例3】如图1,⊙O的半径为1,正方形ABCD顶点B坐标为(),,顶点D在⊙O上运动.50⑴当点D运动到与点A、O在同一条直线上时,试证明直线CD与⊙O相切;⑵当直线CD与⊙O相切时,求OD所在直线对应的函数关系式;⑶设点D的横坐标为x,正方形ABCD的面积为S,求S与x之间的函数关系式,并求出S 的最大值与最小值.【巩固】如图,已知点A 从()10,出发,以1个单位长度/秒的速度沿x 轴向正方向运动,以O A ,为顶点作菱形OABC ,使点B C ,在第一象限,且60AOC ∠=︒;以()03P ,为圆心,PC 为半径作圆.设点A 运动了t 秒,求: ⑴ 点C 的坐标(用含t 的代数式表示);⑵ 当点A 在运动过程中,所有使P 与菱形OABC 的边所在直线相切的t 的值.【例4】已知:如图,抛物线213y x m =+与x 轴交于A B ,两点,与y 轴交于C 点,90ACB ∠=︒⑴ 求m 的值及抛物线顶点坐标;⑵ 过A B C ,,的三点的M ⊙交y 轴于另一点D ,连结DM 并延长交M ⊙于点E ,过E 点的M ⊙的切线分别交x 轴、y 轴于点F G ,,求直线FG 的解析式;⑶ 在条件⑵下,设P 为CBD 上的动点(P 不与C D ,重合),连结PA 交y 轴于点H ,问是否存在一个常数k ,始终满足AH AP k ⋅=,如果存在,请写出求解过程;如果不存在,请说明理由.【巩固】如图,已知点A的坐标是(),,以AB为直径作O',90-,,点B的坐标是()10交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.⑴求抛物线的解析式;⑵点E是AC延长线上一点,BCE∠的平分线CD交O'于点D,连结BD,求直线BD的解析式;⑶在⑵的条件下,抛物线上是否存在点P,使得PDB CBD∠=∠?如果存在,请求出点P的坐标;如果不存在,请说明理由.DCEA yxBO O'课后作业:1.如图,直角坐标系中,已知两点()A,,点B在第一象限且OAB2000O,,()∆为正三角形,OAB∆的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.⑴求B C,两点的坐标;⑵求直线CD的函数解析式;⑶设E F,分别是线段AB AD,上的两个动点,且EF平分四边形ABCD的周长.试探究:AEF∆的最大面积?参考答案例1【巩固】例2分析:(1)先求出t=1时,AP和OQ的长,即可求得P1,Q1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l的解析式.(2)当直线PQ与圆C相切时,连接CP,CQ则有Rt△CMP∽Rt△QMC(M为PG与圆的切点),因此可设当t=a秒时,PQ与圆相切,然后用a表示出AP,OQ的长即PM,QM的长(切线长定理).由此可求出a的值.(3)本题的关键是确定N的位置,先找出与P点关于直线l对称的点P′的坐标,连接P′Q,那么P′Q与直线l的交点即为所求的N点,可先求出直线P′Q的解析式,进而可求出N点的坐标.【巩固】例3【巩固】例4【巩固】作业。
最新中考数学复习中考专题:圆与二次函数结合题

2017年中考数学复习中考专题: 圆与函数综合题1、如图,平面直角坐标系中,以点C (22为半径的圆与轴交于A 、B 两点.(1)求A 、B 两点的坐标;(2)若二次函数2y x bx c =++的图象经过点A 、B ,试确定此二次函数的解析式.1、解:(1)过点C 作CM ⊥轴于点M ,则点M 为AB 的中点.∵CA =2,CM =, ∴AM ==1.于是,点A 的坐标为(1,0),点B 的坐标为(3,0)(2)将(1,0),(3,0)代入得,解得 所以,此二次函数的解析式为.2、如图,半径为2的⊙C 与x 轴的正半轴交于点A ,与y 轴的正半轴交于点B ,点C 的坐标为(1,0).若抛物线2y x bx c =++过A 、B 两点. (1)求抛物线的解析式;(2)在抛物线上是否存在点P ,使得∠PBO=∠POB ?若存在,求出点P 的坐标;若不存在说明理由;(3)若点M 是抛物线(在第一象限内的部分)上一点,△MAB 的面积为S ,求S 的最大(小)值.3、如图,抛物线2y ax bx c =++的对称轴为轴,且经过(0,0116)两点,点P 在抛物线上运动,以P 为圆心的⊙P 经过定点A (0,2),(1)求a,b,c 的值;(2)求证:点P 在运动过程中,⊙P 始终与轴相交;(3)设⊙P 与轴相交于M ()1x ,0,N ()()212x ,0x x 两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标。
4、如图,二次函数y =x 2+bx -3b +3的图象与x 轴交于A 、B 两点(点A 在点B 的左边),交y 轴于点C ,且经过点(b -2,2b 2-5b -1).(1)求这条抛物线的解析式;(2)⊙M 过A 、B 、C 三点,交y 轴于另一点D ,求点M 的坐标;(3)连接AM 、DM ,将∠AMD 绕点M 顺时针旋转,两边MA 、MD 与x 轴、y 轴分别交于点E 、F ,若△DMF 为等腰三角形,求点E 的坐标.5、类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到,如下是一个案例,请补充完整。
初三数学 圆与二次函数综合训练题

圆为背景的二次函数综合训练卷1.如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC,BC,过A,B,C三点作抛物线.(1)求抛物线的解析式;(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连接BD,求直线BD的解析式;(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.第三问改成,在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.2.在平面直角坐标系xOy中,当图形W上的点P的横坐标和纵坐标相等时,则称点P为图形W的“梦之点”.(1)已知⊙O的半径为1.①在点E(1,1),,M(-2,-2)中,⊙O的“梦之点”为;②若点P位于⊙O内部,且为双曲线(k≠0)的“梦之点”,求k的取值范围.(2)已知点C的坐标为(1,t),⊙C的半径为,若在⊙C上存在“梦之点”P,直接写出t的取值范围.(3)若二次函数的图象上存在两个“梦之点”,求二次函数图象的顶点坐标.3.如图,在平面直角坐标系中,圆D与轴相切于点C(0,4),与轴相交于A、B两点,且AB=6(1)D点的坐标是,圆的半径为;(2)求经过C、A、B三点的抛物线所对应的函数关系式;(3)设抛物线的顶点为F,试证明直线AF与圆D相切;(4)在轴下方的抛物线上,是否存在一点N,使面积最大,最大面积是多少?并求出点坐标.4.(2018年山东省济宁市中考数学模拟)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.(1)求抛物线对应的函数表达式;(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).5.已知,如图,点M在x轴上,以点M为圆心,2.5长为半径的圆交y轴于A、B两点,交x轴于C(x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.(1)求点C、D及点M的坐标;(2)若直线y=kx+b切⊙M于点A,交x轴于P,求PA的长;(3)⊙M上是否存在这样的点Q,使点Q、A、C三点构成的三角形与△AOC相似?若存在,请求出点的坐标,并求出过A、C、Q三点的抛物线的解析式;若不存在,请说明理由.6.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).(1)求抛物线的解析式;(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.7.如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.8.如图,O是平面直角坐标系的原点.在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,1),B(3,1),动点P 从O点出发,沿x轴正方向以2个单位/秒的速度运动.设P点运动的时间为t秒(0<t<2).(1)求经过O、A、B三点的抛物线的解析式;(2)过P作PD⊥OA于D,以点P为圆心,PD为半径作⊙P,⊙P在点P的右侧与x轴交于点Q.①则P点的坐标为_____,Q点的坐标为_____;(用含t的代数式表示)②试求t为何值时,⊙P与四边形OABC的两边同时相切;③设△OPD与四边形OABC重叠的面积为S,请直接写出S与t的函数解析式.9.已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO=,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.(1)求B点坐标;(2)用含m的式子表示抛物线的对称轴;(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.(4)是否存在点C(m,0),使得BD=AB?若存在,求出此时m的值;若不存在,说明理由.10.在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A、B两点,点A在点B的左侧.(1)如图1,当k=1时,直接写出A,B两点的坐标;(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,请说明理由.[来源:]11.如图,抛物线与x轴交于A、B两点,与y轴交于点C.直线经过抛物线与坐标轴的两个交点B和C。
专题:二次函数与圆

专题:二次函数与圆1、如图,抛物线m :21y (x h)k 4=-++与x 轴的交点为A 、B ,与y 轴的交点为C ,顶点为(3,)M 254,将抛物线m 绕点B 旋转!180,得到新的抛物线n,它的顶点为D.(1)求抛物线n 的解析式;(2)设抛物线n 与x 轴的另一个交点为E ,点P 是线段ED 上一个动点(P 不与E 、D 重合),过点P 作y 轴的垂线,垂足为F ,连接EF.如果P 点的坐标为(x,y) ,△PEF 的面积为S ,求S 与x 的函数关系式,写出自变量x 的取值范围,并求出S 的最大值;(3)设抛物线m 的对称轴与x 轴的交点为G ,以G 为圆心,A 、B 两点间的距离为直径作⊙G ,试判断直线CM 与⊙G 的位置关系,并说明理由.2、抛物线与轴相交于,两点,与轴相交于,为抛物线的顶点,直线轴,垂足为,. (1)求这个抛物线的解析式;(2)为直线上的一动点,以为斜边构造直角三角形,使直角顶点落在轴上.若在轴上的直角顶点只有一个时,求点的坐标;3、如图,已知二次函数y=ax2+bx+3的图象与x轴相交于点A.C,与y轴相交于点B,A(−94,0),且△AOB∽△BOC.(1)求C点坐标、∠ABC的度数及二次函数y=ax2+bx+3的关系式;(2)在线段AC上是否存在点M(m,0).使得以线段BM为直径的圆与边BC交于P 点(与点B不同) ,且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由。
4、如图,在平面直角坐标系中,四边形ABCD是以AB为直径的M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交M于点E,垂足为点M,且点D平分AC.(1)求过A,B,E三点的抛物线的解析式;(2)求证:四边形AMCD是菱形;(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由。
(最新整理)一元二次方程二次函数圆综合测试题

(完整)一元二次方程二次函数圆综合测试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)一元二次方程二次函数圆综合测试题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)一元二次方程二次函数圆综合测试题的全部内容。
一元二次方程 二次函数 圆综合测试题(海淀西城期末)1.二次函数()257y x =-+的最小值是 A .7- B .7 C .5- D .5 2.抛物线2(2)1y x =-+的顶点坐标是 A .(21)--,B .(21)-,C .(21)-,D .(21),3.如图,△ABC 内接于⊙O ,若o100AOB ∠=,则∠ACB 的度数是 A .40° B .50° C .60° D4.如图,⊙C 与∠AOB 的两边分别相切,其中OA 相切于点P .若∠AOB =90°,OP =6,则OC 的长为A.12 B ...5.将二次函数265y x x =-+用配方法化成2()y x h k =-+的形式,下列结果中正确的是 A .2(6)5y x =-+ B .2(3)5y x =-+ C .2(3)4y x =-- D .2(3)9y x =+-6.若一个扇形的半径是18cm,且它的弧长是12π cm ,则此扇形的圆心角等于 A .30° B .60° C .90° D .120° 7.如图,在平面直角坐标系xOy 中,点A 的坐标为(1-,2),AB ⊥x 轴于点B .以原点O 为位似中心,将△OAB 放大为原来的2倍,得到△OA 1B 1,且点A 1在第二象限,则点A 1 的坐标为 A .(2-,4)B .(12-,1)C .(2,4-)D .(2,4)8.如图,A ,B ,C 三点在已知的圆上,在△ABC ∠ABC =70°,∠ACB =30°,D 是 的中点, 连接DB ,DC ,则∠DBC 的度数为A .30°B .45°C .50°D .70°9.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x 元后,每星期售出BAC商品的总销售额为y 元,则y 与x 的关系式为A .60(30020)y x =+B .(60)(30020)y x x =-+C .300(6020)y x =-D .(60)(30020)y x x =--10.二次函数228y x x m =-+满足以下条件:当21x -<<-时,它的图象位于x 轴的下方;当67x <<时,它的图象位于x 轴的上方,则m 的值为 A .8B .10-C .42-D .24-12.抛物线22y x =向左平移1个单位,再向下平移3个单位,则平移后的抛物线的解析式为A .()2213y x =++ B .()2213y x =+- C .()2213y x =-- D .()2213y x =-+ 二、填空题(本题共18分,每小题3分)13.点A (3-,1y ),B (2,2y )在抛物线25y x x =-上,则1y 2y .(填“>”,“<"或“=”) 14.已知关于x 的方程260x x m -+=范围是 .15.如图,线段AB 和射线AC 交于点A ,∠A =30°,AB 点D 在射线AC 上,且∠ADB 是钝角,写出一个满足条件的AD 的长度值:AD = .16.古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x 尺,则可列方程为 . 17.程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?” 【注释】1步=5尺.译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?"如图,假设秋千的绳索长始终保持直线状态,OA 是秋千的静止状态,A 是踏板,CD是地面,点B 是推动两步后踏板的位置,弧AB 是踏板移动的轨迹.已知AC =1尺,CD =EB =10尺,人的身高BD =5尺.设绳索长OA =OB =x 尺,则可列方程为 .18.阅读下面材料:在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:小敏的作法如下如图,(1)连接OP ,作线段OP 的垂直平分线MN交OP 于点C ;(2)以点C 为圆心,CO 的长为半径作圆,交⊙O 于A ,B 两点;(3)作直线PA ,PB .所以直线PA ,PB 就是所求作的切线.老师认为小敏的作法正确.请回答:连接OA ,OB 后,可证∠OAP =∠OBP =90°,其依据是 由此可证明直线PA ,PB 都是⊙O 的切线,其依据是 . 19.解方程:2250x x +-=。
圆、相似三角形、二次函数经典综合题

中考数学《圆》综合复习【1】已知:如图,△ABC 内接于⊙O ,∠BAC 的平分线交BC 于D ,交⊙O 于E ,EF ∥BC 且交AC 延长线于F ,连结CE.求证:(1)∠BAE=∠CEF ;(2)CE 2=BD ·EF.【2】如图,△ABC 内接于圆,D 为BA 延长线上一点,AE 平分∠BAC 的外角,交BC 延长线于E ,交圆于F.若AB=8,AC=5,EF=14.求AE 、AF 的长.【3】如图,已知AB 是⊙O 的弦,OB =2,∠B =30°,C 是弦AB 上的任意一点(不与点A 、B 重合),连接 CO 并延长CO 交于⊙O 于点D ,连接AD . (1)弦长AB 等于 ▲ (结果保留根号); (2)当∠D =20°时,求∠BOD 的度数;(3)当AC 的长度为多少时,以A 、C 、D 为顶点的三角形与以B 、C 、O 为顶点的三角形相似?请写出解答过程.【4】如图,在ABC △中90ACB ∠=,D 是AB 的中点,以DC 为直径的O 交ABC △的三边,交点分别是G F E ,,点.GECD ,的交点为M ,且ME = :2:5MD CO =.(1)求证:GEF A ∠=∠. (2)求O 的直径CD 的长.B CF E A D O .A B D C EF 第9题图【5】如图右,已知直线PA 交⊙0于A 、B 两点,AE 是⊙0的直径.点C 为⊙0上一点,且AC 平分∠PAE ,过C 作CD ⊥PA ,垂足为D 。
(1)求证:CD 为⊙0的切线;(2)若DC+DA=6,⊙0的直径为l0,求AB 的长度. 【6】【7】如图,已知⊙O 1与⊙O 2都过点A ,AO 1是⊙O 2的切线,⊙O 1交O 1O 2于点B ,连结AB 并延长交⊙O 2于点C ,连结O 2C. (1)求证:O 2C ⊥O 1O 2; (2)证明:AB ·BC=2O 2B ·BO 1;(3)如果AB ·BC=12,O 2C=4,求AO 1的长.O 1O 2A B【8】如图,在平面直角坐标系中,点A (10,0),以OA 为 直径在第一象限内作半圆C ,点B 是该半圆周上一动点,连 结OB 、AB ,并延长AB 至点D ,使DB=AB ,过点D 作x 轴垂线,分别交x 轴、直线OB 于点E 、F ,点E 为垂足,连结CF (1)当∠AOB =30°时,求弧AB 的长度; (2)当DE =8时,求线段EF 的长;(3)在点B 运动过程中,是否存在以点E 、C 、F 为顶点的三角形与△AOB 相似,若存在,请求出此 时点E 的坐标;若不存在,请说明理由.【9】 如图(18),在平面直角坐标系中,ABC △的边AB 在x 轴上,且OA OB >,以AB 为直径的圆过点C .若点C 的坐标为(02),,5AB =,A 、B 两点的横坐标A x ,B x 是关于x 的方程2(2)10x m x n -++-=的两根. (1)求m 、n 的值;(2)若ACB ∠平分线所在的直线l 交x 轴于点D ,试求直线l 对应的一次函数解析式; (3)过点D 任作一直线l '分别交射线CA 、CB (点C 除外)于点M 、N .则11CM CN+第24题图图(3)l '【10】如图l0.在平面直角坐标系xoy中,AB在x轴上,AB=10.以AB为直径的⊙O’与y轴正半轴交于点C.连接BC,AC。
专题63 构造圆与隐形圆在二次函数中的综合问题(解析版)

由已知,点 D 坐标为(﹣1,0),点 B 坐标为(0,﹣1),
设点 P 的坐标为(a,﹣ a﹣1),
①当△AOB∽△ADP 时,
AD AO
=
DP,即2
OB
=
a+
,
解得:a=﹣1;
点 P 坐标为(﹣1,− 2);
②当△AOB∽△APD 时, 过点 P 作 PE⊥x 轴于点 E, 则△APE∽△PED, ∴PE2=AE•ED,
【答案】(1)点 B 的坐标为 (2, 1 ) ;(2)对称轴为直线 x 1 ;(3)当 a 1 时,抛物线与线段 PQ 恰有
a
2
一个公共点.
【解析】
解:(1)∵抛物线与 y 轴交于点 A,∴令 x 0 ,得 y 1 , a
∴点 A 的坐标为 (0, 1 ) ,∵点 A 向右平移两个单位长度,得到点 B, a
∴(﹣ a﹣1)2=(a+3)(﹣a﹣1),
解得 a1=﹣3(舍去),a2=﹣65,
∴点 P 坐标为(﹣6,﹣ );
5
5
(3)存在,CQ 最小值为
7− 5;
2
如图,取点 F(﹣1,﹣1),过点 ADF 作圆,则点 E(﹣2,﹣2)为圆心,
2
∵tan∠AFD=2,
∴弧 AFD(A、D 除外)上的点都是满足条件的 Q 点,
则∠ODC=2∠CMO=∠OMN、MC=MO=MD, ∴sin∠ODC=sin∠OMN= = , 又 MO=MD, ∴当 MD 取最小值时,sin∠ODC 最大, 此时⊙M 与直线 x=1 相切,MD=2, MN= 2 − 2= , ∴点 M(﹣1,﹣ ), 根据对称性,另一点(﹣1, )也符合题意; 综上所述,点 M 的坐标为(﹣1, )或(﹣1,﹣ ).
专题62 二次函数与圆综合性问题(解析版)
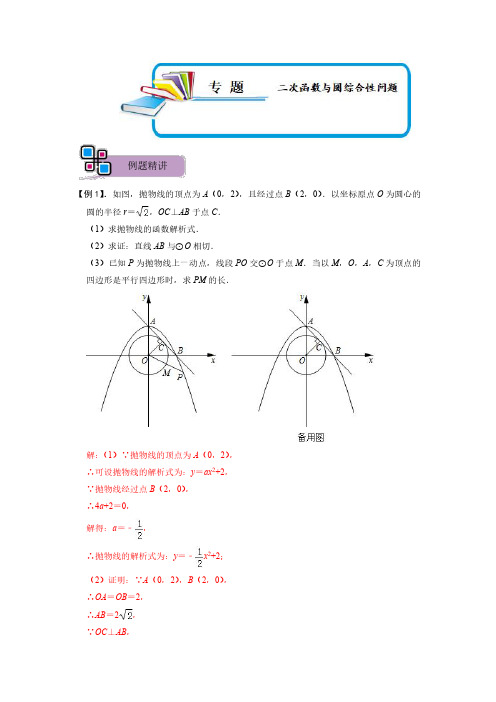
例题精讲【例1】.如图,抛物线的顶点为A(0,2),且经过点B(2,0).以坐标原点O为圆心的圆的半径r=,OC⊥AB于点C.(1)求抛物线的函数解析式.(2)求证:直线AB与⊙O相切.(3)已知P为抛物线上一动点,线段PO交⊙O于点M.当以M,O,A,C为顶点的四边形是平行四边形时,求PM的长.解:(1)∵抛物线的顶点为A(0,2),∴可设抛物线的解析式为:y=ax2+2,∵抛物线经过点B(2,0),∴4a+2=0,解得:a=﹣,∴抛物线的解析式为:y=﹣x2+2;(2)证明:∵A(0,2),B(2,0),∴OA=OB=2,∴AB=2,∵OC⊥AB,∴•OA•OB=•AB•OC,∴×2×2=×2•OC,解得:OC=,∵⊙O的半径r=,∴OC是⊙O的半径,∴直线AB与⊙O相切;(3)∵点P在抛物线y=﹣x2+2上,∴可设P(x,﹣x2+2),以M,O,A,C为顶点的四边形是平行四边形时,可得:AC=OM=,CM=OA=2,∵点C是AB的中点,∴C(1,1),M(1,﹣1),设直线OM的解析式为y=kx,将点M(1,﹣1)代入,得:k=﹣1,∴直线OM的解析式为y=﹣x,∵点P在OM上,∴﹣x2+2=﹣x,解得:x1=1+,x2=1﹣,∴y1=﹣1﹣,y2=﹣1+,∴P1(1+,﹣1﹣),P2(1﹣,﹣1+),如图,当点P位于P1位置时,OP1===(1+)=+,∴P1M=OP1﹣OM=+﹣=,当点P位于P2位置时,同理可得:OP2=﹣,∴P2M=OP2﹣OM=﹣﹣=﹣2;综上所述,PM的长是或﹣2.变式训练【变1-1】.如图,抛物线y=ax2+bx+2与直线AB相交于A(﹣1,0),B(3,2),与x轴交于另一点C.(1)求抛物线的解析式;(2)在y上是否存在一点E,使四边形ABCE为矩形,若存在,请求出点E的坐标;若不存在,请说明理由;(3)以C为圆心,1为半径作⊙O,D为⊙O上一动点,求DA+DB的最小值解:(1)把A(﹣1,0)、B(3,2)代入y=ax2+bx+2,得,解得,∴抛物线的解析式为y=x2+x+2.(2)存在.如图1,作AE⊥AB交y轴于点E,连结CE;作BF⊥x轴于点F,则F(3,0).当y=0时,由x2+x+2=0,得x1=1,x2=4,∴C(4,0),∴CF=AO=1,AF=3﹣(﹣1)=4;又∵BF=2,∴,∵∠BFC=∠AFB=90°,∴△BFC∽△AFB,∴∠CBF=∠BAF,∴∠ABC=∠CBF+∠ABF=∠BAF+∠ABF=90°,∴BC∥AE,∵∠BCF=90°﹣∠BAC=∠EAO,∠BFC=∠EOA=90°,∴△BCF≌△EAO(ASA),∴BC=EA,∴四边形ABCE是矩形;∵OE=FB=2,∴E(0,﹣2).(3)如图2,作FL⊥BC于点L,连结AL、CD.由(2)得∠BFC=90°,BF=2,CF=1,∴CF=CD,CB==.∵∠FLC=∠BFC=90°,∠FCL=∠BCF(公共角),∴△FCL∽△BCF,∴=,∴=,∵∠DCL=∠BCD(公共角),∴△DCL∽△BCD,∴=,∴LD=DB;∵DA+LD≥AL,∴当DA+LD=AL,即点D落在线段AL上时,DA+DB=DA+LD=AL最小.∵CL=CF=,∴BL==,∴BL2=()2=,又∵AB2=22+42=20,∴AL===,DA+DB的最小值为.【例2】.如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.(1)求抛物线的表达式;(2)判断△BCE的形状,并说明理由;(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP 的值最小,若存在,请求出最小值;若不存在,请说明理由.解:(1)∵抛物线的顶点坐标为E(2,8),∴设该抛物线的表达式为y=a(x﹣2)2+8,∵与y轴交于点C(0,6),∴把点C(0,6)代入得:a=﹣,∴该抛物线的表达式为y=x2+2x+6;(2)△BCE是直角三角形.理由如下:∵抛物线与x轴分别交于A、B两点,∴令y=0,则﹣(x﹣2)2+8=0,解得:x1=﹣2,x2=6,∴A(﹣2,0),B(6,0),∴BC2=62+62=72,CE2=(8﹣6)2+22=8,BE2=(6﹣2)2+82=80,∴BE2=BC2+CE2,∴∠BCE=90°,∴△BCE是直角三角形;(3)⊙C上存在点P,使得BP+EP的值最小且这个最小值为.理由如下:如图,在CE上截取CF=(即CF等于半径的一半),连结BF交⊙C于点P,连结EP,则BF的长即为所求.理由如下:连结CP,∵CP为半径,∴==,又∵∠FCP=∠PCE,∴△FCP∽△PCE,∴==,即FP=EP,∴BF=BP+EP,由“两点之间,线段最短”可得:BF的长即BP+EP为最小值.∵CF=CE,E(2,8),∴由比例性质,易得F(,),∴BF==.变式训练【变2-1】.在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.(1)求二次函数的解析式;(2)如图甲,当△ACP是以AC为直角边的直角三角形时,求点P的坐标;(3)如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D.交OM于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.解:(1)把A(﹣2,0),B(4,0)代入y=x2+bx+c得:,解得,∴二次函数的解析式为y=x2﹣x﹣4;(2)如图:由y=x2﹣x﹣4可得C(0,﹣4),设P(x,x2﹣x﹣4),∴AC2=(﹣2﹣0)2+(0+4)2=20,CP2=x2+(x2﹣x)2,AP2=(x+2)2+(x2﹣x ﹣4)2,∵△ACP是以AC为直角边的直角三角形,∴AC2+CP2=AP2,即20+x2+(x2﹣x)2=(x+2)2+(x2﹣x﹣4)2,∴20+x2+(x2﹣x)2=x2+4x+4+(x2﹣x)2﹣8(x2﹣x)+16,解得x=0(与C重合,舍去)或x=3,∴P(3,﹣);(3)点P在运动过程中线段DE的长不变,理由如下:连接AP、BE,如图:∵=,=,∴∠APD=∠DBE,∠DAP=∠DEB,∴△ADP∽△EDB,∴=,∴DE=,设P(m,m2﹣m﹣4),则D(m,0),∵A(﹣2,0),B(4,0),C(0,﹣4),∴AD=m+2,BD=4﹣m,PD=﹣(m2﹣m﹣4)=﹣m2+m+4,∴DE===2,∴DE是定值2,∴点P在运动过程中线段DE的长不变,是定值2.1.如图,已知⊙P的半径为2,圆心P在抛物线y=x2﹣1上运动,当⊙P与坐标轴相切时,圆心P的坐标可以是(,2)或(﹣,2)或(2,1)或(﹣2,1).解:分两种情况:(1)当⊙P与x轴相切时,依题意,可设P(x,2)或P(x,﹣2).①当P的坐标是(x,2)时,将其代入y=x2﹣1,得2=x2﹣1,解得x=±,此时P(,2)或(﹣,2);②当P的坐标是(x,﹣2)时,将其代入y=x2﹣1,得﹣2=x2﹣1,无解.(2)当⊙P与y轴相切时,∵⊙P的半径为2,∴当⊙P与y轴相切时,点P到y轴的距离为2,∴P点的横坐标为2或﹣2,当x=2时,代入y=x2﹣1可得y=1,当x=﹣2时,代入y=x2﹣1可得y=1,∴点P的坐标为(2,1)或(﹣2,1),综上所述,符合条件的点P的坐标是(,2)或(﹣,2)或(2,1)或(﹣2,1);故答案为:(,2)或(﹣,2)或(2,1)或(﹣2,1).2.如图1,抛物线与x轴交于O、A两点,点B为抛物线的顶点,连接OB.(1)求∠AOB的度数;(2)如图2,以点A为圆心,4为半径作⊙A,点M在⊙A上.连接OM、BM,①当△OBM是以OB为底的等腰三角形时,求点M的坐标;②如图3,取OM的中点N,连接BN,当点M在⊙A上运动时,求线段BN长度的取值范围.解:(1)令y=0,则﹣2x=0,解得:x=0或8.∴A(8,0).∴OA=8.∵y=﹣2x=﹣4,∴B(4,﹣4).过点B作BD⊥OA于点D,如图,则OD=4,BD=4,∴OD=BD,∴∠AOB=∠OBD=45°;(2)①设⊙A与x轴交于点C,则C(4,0).连接BC,如图,∵B(4,﹣4),∴BC⊥OA.∵CO=CB=4,∴△CBO是以OB为底的等腰三角形.∴点M与点C重合时,△MBO是以OB为底的等腰三角形.此时点M(4,0);过点A作AM⊥x轴,交⊙A于点M,延长MA交⊙A于点E,连接BE,过点M作MF⊥y轴于点F,如图,则M(8,4),E(8,﹣4),F(,4).∴MF=ME=8.∵B(4,﹣4),∴BE∥x轴.∴BE⊥ME,BE=4.∴∠BEM=∠MFO=90°,BE=OF=4.在△MOF和△MBE中,,∴△MOF≌△MBE(SAS).∴MO=MB.∴△MBO是以OB为底的等腰三角形.此时点M(8,4);综上,当△OBM是以OB为底的等腰三角形时,点M的坐标为(4,0)或(8,4);②设⊙A与x轴交于点C,则C(4,0).连接BC,CN,AM,如图,∵A(8,0),∴点C是OA的中点.∵N为OM的中点,∴CN是△OMA的中位线.∴CN=AM=2.当点M在⊙A上运动时,由三角形的三边的关系定理可知:BC﹣CN≤BN≤BC+CN.∵BC=4,∴4﹣2≤BN≤4+2.∴线段BN长度的取值范围为:2≤BN≤6.3.如图,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且OB=OC.(1)求抛物线的解析式;(2)如图1,若点P是线段BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,将△PCM沿CM对折,如果点P的对应点N恰好落在y轴上,求此时点P的坐标;(3)如图2,若第四象限有一动点E,满足BE=OB,过E作EF⊥x轴于点F,设F坐标为(t,0),0<t<3,△BEF的内心为I,连接CI,直接写出CI的最小值.解:(1)在y=ax2﹣2ax﹣3a(a>0)中,令y=0,得:ax2﹣2ax﹣3a=0,解得:x1=3,x2=﹣1,∴A(﹣1,0),B(3,0),∴OB=3,∵OB=OC,∴OC=3,∴C(0,﹣3),∴﹣3a=﹣3,∴a=1,∴抛物线解析式为:y=x2﹣2x﹣3.(2)设直线BC解析式为y=kx+b,∵B(3,0),C(0,﹣3),∴,解得:,∴直线BC解析式为:y=x﹣3,设M点坐标为(m,m2﹣2m﹣3),∵PM⊥x轴,∴P(m,m﹣3),∴PM=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,∵OB=OC,∠BOC=90°,∴CB=OB,∴CP=m,∵△PCM沿CM对折,点P的对应点N恰好落在y轴上,∴∠PCM=∠NCM,∵PM∥y轴,∴∠NCM=∠PMC,∴∠PCM=∠PMC,∴PC=PM,∴m=﹣m2+3m,整理得:m2+(﹣3)m=0,解得:m1=0(舍去),m2=3﹣,∴当m=3﹣时,m﹣3=﹣,∴P(3﹣,﹣).(3)如图2,连接BI,OI,EI,作△OBI的外接圆⊙M,连接OM,BM,MI,CM,过M作MH⊥y轴于H,∵EF⊥x轴,∴∠BFE=90°,∴∠FBE+∠FEB=90°,∵△BEF的内心为I,∴BI,EI分别平分∠FBE,∠FEB,∴∠IBE=∠FBE,∠IEB=∠FEB,∴∠IBE+∠IEB=(∠FBE+∠FEB)=45°,∴∠BIE=135°,在△BIO和△BIE中,,∴△BIO≌△BIE(SAS),∴∠BIO=∠BIE=135°,∵⊙M是△OBI的外接圆,∴∠OMB=2×(180°﹣∠BIO)=90°,∴OM=BM=OB=,∴MI=OM=,∴∠MOB=∠MOH=45°,∵MH⊥y轴,∴∠HOM=∠HMO=45°,∴OH=HM=OM=,∴CH=OH+OC=+3=,∴CM==,∵CI≥CM﹣MI,当且仅当C、M、I三点共线时,CI取得最小值,∴CI的最小值为﹣.4.已知抛物线y=x2﹣(2m﹣1)x+4m﹣6.(1)试说明对于每一个实数m,抛物线都经过x轴上的一个定点;(2)设抛物线与x轴的两个交点A(x1,0)和B(x2,0)(x1<x2)分别在原点的两侧,且A、B两点间的距离小于6,求m的取值范围;(3)抛物线的对称轴与x轴交于点C,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.解:(1)由题意可知:y=(x﹣2)(x﹣2m+3),因此抛物线与x轴的两个交点坐标为:(2,0)(2m﹣3,0),因此无论m取何值,抛物线总与x轴交于(2,0)点;(2)令y=0,有:x2﹣(2m﹣1)x+4m﹣6=0,则:x1+x2=2m﹣1,x1x2=4m﹣6;∵AB<6∴x2﹣x1<6,即(x2﹣x1)2<36,(x1+x2)2﹣4x1x2<36,即(2m﹣1)2﹣4(4m﹣6)<36,解得﹣<x<.①根据A、B分别在原点两侧可知:x1x2<0,即4m﹣6<0,m<.②综合①②可得﹣<m<;(3)假设存在这样的m,设圆M与y轴的切点为D,过M作x轴的垂线设垂足为E.①当C点在x轴正半轴时,x=>0,因此<m<,∵弧BC=弧CD,因此BC=CD.OC=,CD=BC=OB﹣OC=2﹣=,EC=BC=,OE=MD=OC+CE=+=.易知:OD=ME,即OD2=ME2∴CD2﹣OC2=CM2﹣CE2,()2﹣()2=()2﹣()2;解得m=,符合m的取值范围.②当C点在x轴负半轴时,x=<0,因此﹣<m<,同①可求得OC=,CD=AC=,CE=,MD=OE=.同理有:CD2﹣OC2=MC2﹣CE2()2﹣()2=()2﹣()2化简得:m2=,∴m=±,均不符合m的取值范围,因此这种情况不成立.综上所述,存在符合条件的m,且m=.5.已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与x轴总有两个不同的交点;(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;②若点C关于直线x=﹣的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求的值.解:(1)令y=0,∴x2+mx﹣2m﹣4=0,∴△=m2﹣4[﹣2m﹣4]=m2+8m+16,∵m>0,∴Δ>0,∴该抛物线与x轴总有两个不同的交点;(2)令y=0,∴x2+mx﹣2m﹣4=0,∴(x﹣2)[x+(m+2)]=0,∴x=2或x=﹣(m+2),∴A(2,0),B(﹣(m+2),0),∴OA=2,OB=m+2,令x=0,∴y=﹣2(m+2),∴C(0,﹣2(m+2)),∴OC=2(m+2),①通过定点(0,1)理由:如图,∵点A,B,C在⊙P上,∴∠OCB=∠OAF,在Rt△BOC中,tan∠OCB===,在Rt△AOF中,tan∠OAF===,∴OF=1,∴点F的坐标为(0,1);②如图1,由①知,点F(0,1),∵D(0,1),∴点D在⊙P上,∵点E是点C关于抛物线的对称轴的对称点,∴∠DCE=90°,∵⊙P是△ABC的外接圆,∴点P在抛物线的对称轴上,∴点E在⊙P上,∴DE是⊙P的直径,∴∠DBE=90°,∵∠BED=∠OCB,∴tan∠BED=,设BD=n,在Rt△BDE中,tan∠BED===,∴BE=2n,根据勾股定理得,DE==n,∴l=BD+BE+DE=(3+)n,r=DE=n,∴==.6.如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M (4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.(1)求线段CD的长及顶点P的坐标;(2)求抛物线的函数表达式;=8S△QAB,(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN 且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.解:(1)如图,连接OC,∵M(4,0),N(0,3),∴OM=4,ON=3,∴MN=5,∴OC=MN=,∵CD为抛物线对称轴,∴OD=MD=2,在Rt△OCD中,由勾股定理可得CD===,∴PD=PC﹣CD=﹣=1,∴P(2,﹣1);(2)∵抛物线的顶点为P(2,﹣1),∴设抛物线的函数表达式为y=a(x﹣2)2﹣1,∵抛物线过N(0,3),∴3=a(0﹣2)2﹣1,解得a=1,∴抛物线的函数表达式为y=(x﹣2)2﹣1,即y=x2﹣4x+3;(3)在y=x2﹣4x+3中,令y=0可得0=x2﹣4x+3,解得x=1或x=3,∴A(1,0),B(3,0),∴AB=3﹣1=2,∵ON=3,OM=4,PD=1,=S△OMP+S△OMN=OM•PD+OM•ON=×4×1+×4×3=8=8S△QAB,∴S四边形OPMN=1,∴S△QAB设Q点纵坐标为y,则×2×|y|=1,解得y=1或y=﹣1,当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,当y=﹣1时,可知P点即为所求的Q点,∵D为AB的中点,∴AD=BD=QD,∴△QAB为等腰直角三角形,∵ON=OB=3,∴△OBN为等腰直角三角形,∴△QAB∽△OBN,综上可知存在满足条件的点Q,其坐标为(2,﹣1).7.如图,已知二次函数的图象顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M、N两点.(1)求二次函数的表达式;(2)P为平面内一点,当△PMN是等边三角形时,求点P的坐标;(3)在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和点N,且与直线y=﹣1相切.若存在,求出点E的坐标,并求⊙E的半径;若不存在,说明理由.解:(1)∵二次函数的图象顶点在原点,故设二次函数表达式为:y=ax2,将(2,1)代入上式并解得:a=,故二次函数表达式为:y=x2;(2)将y=1代入y=x2并解得:x=±2,故点M、N的坐标分别为(﹣2,1)、(2,1),则MN=4,∵△PMN是等边三角形,∴点P在y轴上且PM=4,∴PF=2;∵点F(0,1),∴点P的坐标为(0,1+2)或(0,1﹣2);(3)假设二次函数的图象上存在一点E满足条件,设点Q是FN的中点,则点Q(1,1),故点E在FN的中垂线上.∴点E是FN的中垂线与y=x2图象的交点,∴y=×12=,则点E(1,),EN==,同理EF==,点E到直线y=﹣1的距离为|﹣(﹣1)|=,故存在点E,使得以点E为圆心半径为的圆过点F,N且与直线y=﹣1相切.8.已知二次函数y=﹣x2+bx+c+1,①当b=1时,求这个二次函数的对称轴的方程;②若c=﹣b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?③若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足=,求二次函数的表达式.解:①二次函数y=﹣x2+bx+c+1的对称轴为x=,当b=1时,=,∴当b=1时,求这个二次函数的对称轴的方程为x=.②二次函数y=﹣x2+bx+c+1的顶点坐标为(,),∵二次函数的图象与x轴相切且c=﹣b2﹣2b,∴,解得:b=,∴b为,二次函数的图象与x轴相切.③∵AB是半圆的直径,∴∠AMB=90°,∴∠OAM+∠OBM=90°,∵∠AOM=∠MOB=90°,∴∠OAM+∠OMA=90°,∴∠OMA=∠OBM,∴△OAM∽△OMB,∴,∴OM2=OA•OB,∵二次函数的图象与x轴交于点A(x1,0),B(x2,0),∴OA=﹣x1,OB=x2,x1+x2,=b,x1•x2=﹣(c+1),∵OM=c+1,∴(c+1)2=c+1,解得:c=0或c=﹣1(舍去),∴c=0,OM=1,∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足=,∴AD=BD,DF=4DE,DF∥OM,∴△BDE∽△BOM,△AOM∽△ADF,∴,,∴DE=,DF=,∴×4,∴OB=4OA,即x2=﹣4x1,∵x1•x2=﹣(c+1)=﹣1,∴,解得:,∴b=﹣+2=,∴二次函数的表达式为y=﹣x2+x+1.9.已知抛物线y=ax2+bx+c过点A(0,2).若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足;当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且△ABC 有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.解:①当x1<x2<0时,x1﹣x2<0,∵(x1﹣x2)(y1﹣y2)>0,∴y1﹣y2<0,∴当x<0时,y随x的增大而增大,当0<x1<x2时,x1﹣x2<0,∵(x1﹣x2)(y1﹣y2)<0,∴y1﹣y2>0,∴当x>0时,y随x的增大而减小.∴抛物线关于y轴对称,∴b=0,∵抛物线y=ax2+bx+c过点A(0,2),∴c=2,如图,连接OB、OC,设BC y轴于点D.由对称性可知,△ABC为等腰三角形,又∵△ABC有一个内角为60°,∴△ABC是等边三角形,∴OD=OA=1,CD=OD=,∴B(﹣,﹣1),C(,﹣1),将C点坐标代入y=ax2+2可求得a=﹣1,∴抛物线的解析式为y=﹣x2+2.②设直线OM的解析式为y=k1x,∵O、M、N三点共线,∴x1≠0,x2≠0,且=,化为x1﹣x2=,∵x1≠x2,∴x1x2=﹣2,∴,∴,设点N关于y轴的对称点为N',则N'的坐标为,∵点P是点O关于点A的对称点,∴OP﹣2OA=4,即点P的坐标为(0,4),设直线PM的解析式为y=k2x+4,∵点M的坐标为,∴,∴,∴直线PM的解析式为x+4.∵,即N'在直线PM上,∴PA平分∠MPN.10.如图,在平面直角坐标系xOy中,O为坐标原点,点A(4,0),点B(0,4),△ABO 的中线AC与y轴交于点C,且⊙M经过O,A,C三点.(1)求圆心M的坐标;(2)若直线AD与⊙M相切于点A,交y轴于点D,求直线AD的函数表达式;(3)在(2)的条件下,在过点B且以圆心M为顶点的抛物线上有一动点P,过点P作PE∥y轴,交直线AD于点E.若以PE为半径的⊙P与直线AD相交于另一点F.当EF =4时,求点P的坐标.解:(1)点B(0,4),则点C(0,2),∵点A(4,0),则点M(2,1);(2)应该是圆M与直线AD相切,则∠CAD=90°,设:∠CAO=α,则∠CAO=∠ODA=∠PEH=α,tan∠CAO===tanα,则sinα=,cosα=,AC=,则CD==10,则点D(0,﹣8),将点A、D的坐标代入一次函数表达式:y=mx+n并解得:直线AD的表达式为:y=2x﹣8;(3)抛物线的表达式为:y=a(x﹣2)2+1,将点B坐标代入上式并解得:a=,故抛物线的表达式为:y=x2﹣3x+4,过点P作PH⊥EF,则EH=EF=2,cos∠PEH=,解得:PE=5,设点P(x,x2﹣3x+4),则点E(x,2x﹣8),则PE=x2﹣3x+4﹣2x+8=5,解得x=或2,则点P(,)或(2,1).11.如图,抛物线y=ax2+6ax(a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.(1)求点A的坐标;(2)过点C作⊙P的切线CE交x轴于点E.①如图1,求证:CE=DE;②如图2,连接AC,BE,BO,当a=,∠CAE=∠OBE时,求﹣的值.解:(1)令ax2+6ax=0,ax(x+6)=0,∴A(﹣6,0);(2)①证明:如图,连接PC,连接PB,延长交x轴于点M,∵⊙P过O、A、B三点,B为顶点,∴PM⊥OA,∠PBC+∠BDM=90°,又∵PC=PB,∴∠PCB=∠PBC,∵CE为切线,∴∠PCB+∠ECD=90°,又∵∠BDM=∠CDE,∴∠ECD=∠CDE,∴CE=DE.②解:设OE=m,点D的坐标为(t,0),∵∠CAE=∠CBO,∠CAE=∠OBE,∴∠CBO=∠EBO,由角平分线成比例定理可得:,即:,∴,∴,∴,=,=.12.抛物线y=﹣x2+x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.(1)点B,D的坐标分别为(3,0),(,);(2)如图①,抛物线翻折后,点D落在点E处,当点E在△ABC内(含边界)时,求t的取值范围;(3)如图②,当t=0时,点Q是“M”形新图象上一动点.①直接写出“M”形图象AB段的函数关系式;②是否存在以CQ为直径的圆与x轴相切于点P?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)令y=0,则﹣x2+x﹣1=0,解得x=3或x=,∴B(3,0),A(,0),令x=0,则y=﹣1,∴C(0,﹣1),∵y=﹣x2+x﹣1=﹣(x﹣)2+,∴顶点D(,),故答案为:(3,0),(,);(2)∵E与D关于直线y=t对称,∴E(,2t﹣),设直线BC的解析式为y=kx+b,将B(3,0),C(0,﹣1)代入,得,∴,∴y=x﹣1,当x=时,y=﹣,∵E点在△ABC内(含边界),∴2t﹣≥﹣,∴t≥,∵2t﹣≤0,∴t≤,∵t<,∴t的取值范围是≤t≤;(3)①当t=0时,y=﹣x2+x﹣1关于x轴对称的函数为y=x2﹣x+1,∴“M”形图象AB段的函数关系式为y=x2﹣x+1(≤x≤3);②存在点P,理由如下:设Q点的横坐标为m,∵以CQ为直径的圆与x轴相切于点P,∴P点的横坐标为m,当m>3或m<时,Q(m,﹣m2+m﹣1),∵△CPQ为直角三角形,∴CQ2=CP2+PQ2,即m2+(﹣m2+m)2=m2+1+m2+(﹣m2+m﹣1)2,解得m=或m=,∴P(,0)或P(,0);当≤m≤3时,Q(m,m2﹣m+1),∵△CPQ为直角三角形,∴CQ2=CP2+PQ2,即m2+(m2﹣m+2)2=m2+1+m2+(m2﹣m+1)2,解得m=2或m=,∴P(,0)或P(1,0);综上所述:存在以CQ为直径的圆与x轴相切于点P,P点坐标为(,0)或(,0)或(,0)或P(1,0).13.已知抛物线y=ax2+bx+c过点A(0,2).(1)若点(﹣,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与抛物线的另两个交点为B,C,且△ABC有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.解:(1)∵抛物线y=ax2+bx+c过点A(0,2),∴c=2.又∵点(﹣,0)也在该抛物线上,∴a(﹣)2+b(﹣)+c=0,∴2a﹣b+2=0(a≠0).(2)①∵当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0,∴x1﹣x2<0,y1﹣y2<0,∴当x<0时,y随x的增大而增大;同理:当x>0时,y随x的增大而减小,∴抛物线的对称轴为y轴,开口向下,∴b=0.∵OA为半径的圆与抛物线的另两个交点为B、C,∴△ABC为等腰三角形,又∵△ABC有一个内角为60°,∴△ABC为等边三角形.设线段BC与y轴交于点D,则BD=CD,且∠OCD=30°,又∵OB=OC=OA=2,∴CD=OC•cos30°=,OD=OC•sin30°=1.不妨设点C在y轴右侧,则点C的坐标为(,﹣1).∵点C在抛物线上,且c=2,b=0,∴3a+2=﹣1,∴a=﹣1,∴抛物线的解析式为y=﹣x2+2.②证明:由①可知,点M的坐标为(x1,﹣+2),点N的坐标为(x2,﹣+2).直线OM的解析式为y=k1x(k1≠0).∵O、M、N三点共线,∴x1≠0,x2≠0,且=,∴﹣x1+=﹣x2+,∴x1﹣x2=﹣,∴x1x2=﹣2,即x2=﹣,∴点N的坐标为(﹣,﹣+2).设点N关于y轴的对称点为点N′,则点N′的坐标为(,﹣+2).∵点P是点O关于点A的对称点,∴OP=2OA=4,∴点P的坐标为(0,4).设直线PM的解析式为y=k2x+4,∵点M的坐标为(x1,﹣+2),∴﹣+2=k2x1+4,∴k2=﹣,∴直线PM的解析式为y=﹣x+4.∵﹣•+4==﹣+2,∴点N′在直线PM上,∴PA平分∠MPN.14.如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y 轴交于点C,连接AB、AC、BC.(1)求此二次函数的关系式;(2)判断△ABC的形状;若△ABC的外接圆记为⊙M,请直接写出圆心M的坐标;(3)若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点A1、B1、C1,△A1B1C1的外接圆记为⊙M1,是否存在某个位置,使⊙M1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.解:(1)把点A(3,0),B(4,1)代入y=ax2+bx+3中,,解得:,所以所求函数关系式为:y=x2﹣x+3;(2)△ABC是直角三角形,过点B作BD⊥x轴于点D,易知点C坐标为:(0,3),所以OA=OC,所以∠OAC=45°,又∵点B坐标为:(4,1),∴AD=BD,∴∠DAB=45°,∴∠BAC=180°﹣45°﹣45°=90°,∴△ABC是直角三角形,圆心M的坐标为:(2,2);(3)存在取BC的中点M,过点M作ME⊥y轴于点E,∵M的坐标为:(2,2),∴MC==,OM=2,∴∠MOA=45°,又∵∠BAD=45°,∴OM∥AB,∴要使抛物线沿射线BA方向平移,且使⊙M1经过原点,则平移的长度为:2﹣或2+;∵∠BAD=45°,∴抛物线的顶点向左、向下均分别平移=个单位长度或=个单位长度,∵y=x2﹣x+3=(x﹣)2﹣,∴平移后抛物线的关系式为:y=(x﹣+)2﹣﹣,即y=(x﹣)2﹣,或y=(x﹣+)2﹣﹣,即y=(x﹣)2﹣.综上所述,存在一个位置,使⊙M1经过原点,此时抛物线的关系式为:y=(x﹣)2﹣或y=(x﹣)2﹣.15.已知抛物线C1:y=ax2过点(2,2)(1)直接写出抛物线的解析式y=x2;(2)如图,△ABC的三个顶点都在抛物线C1上,且边AC所在的直线解析式为y=x+b,若AC边上的中线BD平行于y轴,求的值;(3)如图,点P的坐标为(0,2),点Q为抛物线上C1上一动点,以PQ为直径作⊙M,直线y=t与⊙M相交于H、K两点是否存在实数t,使得HK的长度为定值?若存在,求出HK的长度;若不存在,请说明理由.解:(1)把点(2,2)坐标代入y=ax2,解得:a=,∴抛物线的解析式为y=x2;(2)把y=x+b和y=x2得:x2﹣2x﹣2b=0,设A、C两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1•x2=﹣2b,点D坐标为(,),即;D(1,1+b),B坐标为(1,),AC2=[(x2﹣x1)]2=16b+8BD=+b,∴=16;(3)设点Q坐标为(a,a2),点P的坐标为(0,2),由P、Q坐标得点M的坐标为(,a2+1),设圆的半径为r,由P(0,2)、M两点坐标可以求出r2=+(a2﹣1)2=a4﹣a2+1,设点M到直线y=t的距离为d,则d2=(a2+1﹣t)2=a4+a2+1+t2﹣2t﹣a2t,则HK=2=2,当t﹣=0时,HK为常数,t=,HK=.16.定义:平面直角坐标系xOy中,过二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.(1)已知点P(2,2),以P为圆心,为半径作圆.请判断⊙P是不是二次函数y=x2﹣4x+3的坐标圆,并说明理由;(2)如图1,已知二次函数y=x2﹣4x+4图象的顶点为A,坐标圆的圆心为P,求△POA 周长的最小值;(3)如图2,已知二次函数y=ax2﹣4x+4(0<a<1)图象交x轴于点A,B,交y轴于点C,与坐标圆的第四个交点为D,连结PC,PD.若∠CPD=120°,求a的值.解:(1)对于二次函数y=x2﹣4x+3,当x=0时,y=3;当y=0时,解得x=1或x=3,∴二次函数图象与x轴交点为A(1,0),B(3,0),与y轴交点为C(0,3),∵点P(2,2),∴PA=PB=PC=,∴⊙P是二次函数y=x2﹣4x+3的坐标圆.(2)如图1,连接PH,∵二次函数y=x2﹣4x+4图象的顶点为A,坐标圆的圆心为P,∴A(2,0),与y轴的交点H(0,4),∴△POA周长=PO+PA+OA=PO+PH+2≥OH+2=6,∴△POA周长的最小值为6.(3)如图2,连接CD,PA,设二次函数y=ax2﹣4x+4图象的对称轴l与CD交于点E,与x轴交于点F,由对称性知,对称轴l经过点P,且l⊥CD,∵AB=,∴AF=BF=,∵∠CPD=120°,PC=PD,C(0,4),∴∠PCD=∠PDC=30°,设PE=m,则PA=PC=2m,CE=m,PF=4﹣m,∵二次函数y=ax2﹣4x+4图象的对称轴l为,∴,即,在Rt△PAF中,PA2=PF2+AF2,∴,即,化简,得,解得,∴.17.如图,在平面直角坐标系中,抛物线y=x2﹣bx﹣c交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).(1)求此抛物线的解析式;(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;(3)在(2)的条件下,设抛物线对称轴l交x轴于点H,△ABD的外接圆圆心为M(如图1),过点B作⊙M的切线交于点P(如图2),设Q为⊙M上一动点,则在点运动过程中的值是否变化?若不变,求出其值;若变化,请说明理由.解:(1)将点B、C的坐标代入抛物线表达式得:,解得:,∴抛物线的解析式为y=x2﹣x﹣2;(2)当x=5时,y=x2﹣x﹣2=3,故D的坐标为(5,3),令y=0,则x=4(舍去)或﹣1,故点A(﹣1,0),如图,连接BD,作BN⊥AD于N,∵A(﹣1,0),B(4,0),C(0,﹣2),∴AD=3,BD=,AB=5,==,∵S△ABD∴BN=,∴sin∠BDN===,∴∠BDN=45°,∴∠ADB=∠BDN=45°;(3)不变.如图,连接MQ,MB,∵过点B作⊙M的切线交1于点P,∴∠MBP=90°,∵∠MBO=45°,∴∠PBH=45°,∴PH=HB=2.5,∵==,==,∵∠HMQ=∠QMP,∴△HMQ∽△QMP,∴==,∴在点Q运动过程中的值不变,其值为.18.如图,抛物线y=ax2+bx+c(a≠0),与x轴交于A(4,0)、O两点,点D(2,﹣2)为抛物线的顶点.(1)求该抛物线的解析式;(2)点E为AO的中点,以点E为圆心、以1为半径作⊙E,交x轴于B、C两点,点M为⊙E上一点.①射线BM交抛物线于点P,设点P的横坐标为m,当tan∠MBC=2时,求m的值;②如图2,连接OM,取OM的中点N,连接DN,则线段DN的长度是否存在最大值或最小值?若存在,请求出DN的最值;若不存在,请说明理由.解:(1)由抛物线顶点式表达式得:y=a(x﹣2)2﹣2,将点A的坐标代入上式并解得:a=,故抛物线的表达式为:y=(x﹣2)2﹣2=x2﹣2x①;(2)①点E是OA的中点,则点E(2,0),圆的半径为1,则点B(1,0),当点P在x轴下方时,如图1,∵tan∠MBC=2,故设直线BP的表达式为:y=﹣2x+s,将点B(1,0)的坐标代入上式并解得:s=2,故直线BP的表达式为:y=﹣2x+2②,联立①②并解得:x=±2(舍去﹣2),故m=2;当点P在x轴上方时,同理可得:m=4±2(舍去4﹣2);故m=2或4+2;②存在,理由:连接BN、BD、EM,则BN是△OEM的中位线,故BN=EM=,而BD==,在△BND中,BD﹣BN≤ND≤BD+BN,即﹣0.5≤ND≤+0.5,故线段DN的长度最小值和最大值分别为﹣0.5和+0.5.19.如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B(3,0)、C(0,3)三点,连接BC并延长.(1)求抛物线的解析式;(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.1°求线段MN的最大值;2°当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.解:(1)把A、B、C三点的坐标代入抛物线y=ax2+bx+c(a≠0)中,得,解得,,∴抛物线的解析式为:y =x 2﹣4x +3;(2)1°设直线BC 的解析式为y =mx +n (m ≠0),则,解得,,∴直线BC 的解析式为:y =﹣x +3,设M (t ,﹣t +3)(0<t <3),则N (t ,t 2﹣4t +3),∴MN =﹣t 2+3t =﹣,∴当t =时,MN 的值最大,其最大值为;2°∵△PMN 的外接圆圆心Q 在△PMN 的边上,∴△PMN 为直角三角形,由1°知,当MN 取最大值时,M (),N (),①当∠PMN =90°时,PM ∥x 轴,则P 点与M 点的纵坐标相等,∴P 点的纵坐标为,当y =时,y =x 2﹣4x +3=,解得,x =,或x =(舍去),∴P ();②当∠PNM =90°时,PN ∥x 轴,则P 点与N 点的纵坐标相等,∴P 点的纵坐标为﹣,当y =﹣时,y =x 2﹣4x +3=﹣,解得,x =,或x =(舍去),∴P (,);③当∠MPN =90°时,则MN 为△PMN 的外接圆的直径,∴△PMN的外接圆的圆心Q为MN的中点,∴Q(),半径为,过Q作QK∥x轴,与在MN右边的抛物线图象交于点K,如图②,令y=,得y=x2﹣4x+3=,解得,x=<(舍),或x=,∴K(,),∴QK=>,即K点在以MN为直径的⊙Q外,设抛物线y=x2﹣4x+3的顶点为点L,则l(2,﹣1),连接LK,如图②,则L到QK的距离为,LK=,设Q点到LK的距离为h,则,∴=,∴直线LK下方的抛物线与⊙Q没有公共点,∵抛物线中NL部分(除N点外)在过N点与x轴平行的直线下方,∴抛物线中NL部分(除N点外)与⊙Q没有公共点,∵抛物线K点右边部分,在过K点与y轴平行的直线的右边,∴抛物线K点右边部分与⊙Q没有公共点,综上,⊙Q与MN右边的抛物线没有交点,∴在线段MN右侧的抛物线上不存在点P,使△PMN的外接圆圆心Q在MN边上;综上,点P的坐标为()或().20.如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:x…﹣10123…y…03430…(1)求出这条抛物线的解析式;(2)如图1,直线y=kx+1(k<0)与抛物线交于P,Q两点,交抛物线的对称轴于点T,若△QMT的面积是△PMT面积的两倍,求k的值;(3)如图2,点D是第四象限内抛物线上一动点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.解:(1)根据表格可得出A(﹣1,0),B(3,0),C(0,3),设抛物线解析式为y=a(x+1)(x﹣3),将C(0,3)代入,得:3=a(0+1)(0﹣3),解得:a=﹣1,∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3,∴该抛物线解析式为y=﹣x2+2x+3;(2)设P(x1,y1),Q(x2,y2),令y=kx+1=﹣x2+2x+3,整理得:x2+(k﹣2)x﹣2=0,∴x1+x2=2﹣k,x1x2=﹣2①,∵△QMT的面积是△PMT面积的两倍,∴MT•(x2﹣1)=2×MT•(1﹣x1),∴2x1+x2=3,即x2=3﹣2x1②,将②代入①得:2x12﹣3x1﹣2=0,解得:x1=2或,∴或,∴k=1或,∵k<0,∴k=﹣;(3)线段EF的长为定值1,如图,连接BE,设D(t,﹣t2+2t+3),且t>3,∵EF⊥x轴,∴DF=﹣(﹣t2+2t+3)=t2﹣2t﹣3,∵F(t,0),∴BF=OF﹣OB=t﹣3,AF=t﹣(﹣1)=t+1,∵四边形ABED是圆内接四边形,∴∠DAF+∠BED=180°,∵∠BEF+∠BED=180°,∴∠DAF=∠BEF,∵∠AFD=∠EFB=90°,∴△AFD∽△EFB,∴,∴,∴EF===1,∴线段EF的长为定值1.21.如图,抛物线y=﹣x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴.(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②△BCF的面积为S,求S与m的函数关系式,并求出S的最大值.(3)现有一个以原点O为圆心,长为半径的圆沿y轴正半轴方向向上以每秒1个单位的速度运动,问几秒后⊙O与直线AC相切?解:(1)设0=﹣x2+2x+3,解得:x=﹣1或3,∵抛物线y=﹣x2+2x+3与x相交于AB(点A点B左侧),∴A(﹣1,0),B(3,0),∵抛物线与y轴相交于点C,∴C(0,3),∴抛物线的对称轴是:直线x=1.(2)①设直线BC的函数关系式为y=kx+b,把B(3,0),C(0,3)分别代入,得,解得:k=﹣1,b=3∴直线BC的函数关系式为y=﹣x+3.当x=1时,y=﹣1+3=2,∴E(1.2).当x=m时,y=﹣m+3,∴P(m,﹣m+3)在y=﹣x2+2x+3中,当x=1时,y=4,∴D(1,4).当x=m时,y=﹣m2+2m+3,∴F(m,﹣m2+2m+3),∴线段DE=4﹣2=2,线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∵PF∥DE∴当PF=DE时,四边形PEDF为平行四边形.由﹣m2+3m=2,解得m=2或m=1(不合题意,舍去).因此,当m=2时,四边形PEDF为平行四边形.②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得OB=OM+MB=3.+S△CPF,∵S=S△EPF即S=PF•BM+PF•OM=PF(BM+OM)=PF•OB,∴S=×3(﹣m2+3m)=﹣m2+m(0≤m≤3)∴当m=﹣=时S最大值=;。
二次函数与圆综合题

圆与二次函数综合题1. 抛物线交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3).(1)求二次函数的关系式;(2)在抛物线对称轴上是否存在一点P,使P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;(3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.3. 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B 两点(A点在B点左侧),与y轴交于点C.(1)求抛物线的解析式及A、B、C三点的坐标(2)若直线y=kx+b经过C、M两点,且与x轴交于点D,证明四边形CDAN是平行四边形.(3)点P在抛物线的对称轴x=1上运动,请探索,在x轴上方是否存在这样的点P,使以P为圆心的圆经过A、B两点,且与直线CD相切,若存在,请求出点P的坐标,若不存在,请说明理由.4.已知:如图,抛物线的图象与x轴分别交于A(-3,0),B(1,0)两点,与y轴交于点(1)求抛物线的顶点E的坐标;(2)求⊙M的面积;(3)连CD交AO于点F,延长CD至G,使FG=2,试探究,当点D运动到何处时,直线GA与⊙M相切,并请说明理由.5.在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、E(3,)三点(1)求此抛物线的解析式(2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l ,且l与x轴的夹角为30°,若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号)6. 已知二次函数的图象如图.(1)求它的对称轴与x轴交点D的坐标;(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.参考答案1、(1)将C(0,-3)代入,得c=-3.将c=-3、B(3,0)代入,得9a+3b-3=0.①因为x=1是抛物线的对称轴,所以.②将②变形后代入①得a=1,b=-2.所以二次函数的关系式是.(2)AC与对称轴的交点P即为到B、C的距离之差最大的点. 因为PA=PB,所以点P到B、C两点距离之差就等于|PA-PC|.由于三角形的两边之差小于第三边,所以只有当点P、C、A在一直线上时,|PA-PC|=AC最大. 因为C点的坐标为(0,-3),A点的坐标为(-1,0),所以直线AC的关系式是y=-3x-3.又对称轴为x=1,所以点P的坐标(1,-6).(3)设M(,y)、N(,y),所求圆的半径为r,则,③因为对称轴为x=1,所以.④由③、④得:.⑤将N(r+1,y)代入关系式,得,整理,得.由于r=±y,当y=r>0时,,解得,(舍去);当y=r<0时,,解得,(舍去).所以此圆的半径是或.2. 解:(1)作AH⊥OB于H,设AD与OC的交点为G∵BC是⊙A的直径∴点A为BC的中点∴AG、AH分别是△BOC的中位线∴AH=12×OC=3√AG=12×OB=1 (三角形的中位线等于第三边的一半)故A点的坐标为(1,3√)(2)∵抛物线过O、B两点∴根据抛物线的对称性,可知抛物线的顶点横坐标为1∵抛物线的顶点在直线y=−(3√3)×x上∴x=1时y=−3√3∴抛物线的顶点坐标为(1,−3√3)设所求抛物线为y=a×x2+bx+c(a≠0)将三点坐标代入抛物线解析式y=a×x2+bx+c中得a=3√3,b=−2×3√3,c=0故抛物线解析式为y=(3√3)×x2−(2×3√3)×x(3)BC=22+(2×3√)2−−−−−−−−−−−√=4∵DE∥x轴A(1,3√) DE=BC=4∴D(-1,3√) E(3,3√)将x=-1代入抛物线解析式中得y=(3√3)+(2×3√3)=3√,故点D在抛物线y=(3√3)×x2−(2×3√3)×x上将x=3代入抛物线解析式得y=3×3√−2×3√=3√,点E在抛物线y=(3√3)×x2−(2×3√3)×x上(4)当点P在抛物线的OD或BE上时,∠BPC为钝角∴X0的取值范围是−1<X0<0或2<X0<33.(1) 已知顶点M(1,4),抛物线的开口向下则,y-4=k(x-1)2经过N点,则有,3-4=k(2-1)2=k=-1所以,y=-(x-1)2+4.此即抛物线的解析式令y=0,易得:x1-1=2,即x1=3x2-1=-2,即,x2=-1据题意,A(-1,0),B(3,0)令x=0,则,y=-1+4=3,故,C(0,3)(2) 由(1)的解可知,Yc=Yn,则,CN//AB,|CN|=2将C、M的坐标代入直线方程:y=kx+bb=3,4=k×1+3,k=1y=x+3与x轴的交点D(-3,0),则,|AD|=2线段CN=线段AD,CN//AD.亦即四边形ADCN是平行四边形(3) 设⊙P与CD的切点为G,有PG=PA=PB设P(1,m).由以上计算知道:BD=6,∠CDB=45°PG所在直线方程的斜率k=-1,P在直线PG上,则有y=-x+m+1与y=x+3的交点即Gx=(m-2)/2,y=(m+4)/2.即G[(m-2)/2,(m+4)/2]据PG=PA,有PG2=m2+4=(4-m)2/4+(m-4)2/42m2+8=m2-8m+16m=2√6-4,m=-4-2√6(1,2√6-4),和(1,-4-2√6)即为所求⊙P的圆心坐标4. 1)抛物线y=−3√3x2−23√3x+3√=−3√3(x2+2x+1)+3√+3√3=−3√3(x+1)2+43√3∴E的坐标为(−1,43√3);(2)连AC;∵M过A,O,C,∠AOC=90∘,∴AC为O的直径。
【新】中考数学人教版 二次函数,旋转,圆综合测试题【精编版】
二次函数,旋转,圆综合题1、在同一平面直角坐标系内,一次函数b ax y +=与二次函数b x ax y ++=82的图象可能是( )2、已知二次函数()02≠++=a c bx ax y 的图象如图所示,有下列5个结论:①0>abc ;②c a b +<;③024>c b a ++;④b c 32<;⑤()()的实数>1≠++m b am m b a ,其中正确的是( ) A 、2个 B 、3个 C 、4个 D 、5个第2题第4题 第5题3、已知实数a 、b 分别满足0462=+-a a ,0462=+-b b ,且b a ≠,则baa b +的值是。
4、如图所示,直线1+=x y 与y 轴相交于点1A ,以1OA 为边作正方形111C B OA ,记作第一个正方形;然后延长11B C 与直线1+=x y 相交于点2A ,再以21A C 为边作正方形2221C B A C ,记作第二个正方形;同样延长22B C 与直线1+=x y 相交于点3A ,再以32A C 为边作正方形3332C B A C ,记作第三个正方形;…以此类推,则第n 个正方形的边长为。
5、二次函数232x y =的图象如图,点0A 位于原点,点、、、321A A A ……、n A 在y 轴正半轴上,点、、、321B B B ……、n B 在二次函数位于第一象限的图象上,点、、、321C C C ……、n C 在二次函数位于第二象限的图象上,四边形1110C A B A ,四边形2221C A B A ,四边形3332C A B A ……四边形n n n n C A B A 1-都是菱形,︒-=∠=⋯=∠=∠=∠601332221110n n n A B A A B A A B A A B A ,菱形n n n n C A B A 1-的周长为。
第5题5、如图,已知点),(q p M 在抛物线12-=x y 上,以M 为圆心的圆与x 轴交于B A 、两点,且B A 、两点的横坐标是关于x 的方程022=+-q px x 的两根,则弦AB 的长等于_________。
专题30 圆与二次函数结合(解析版)
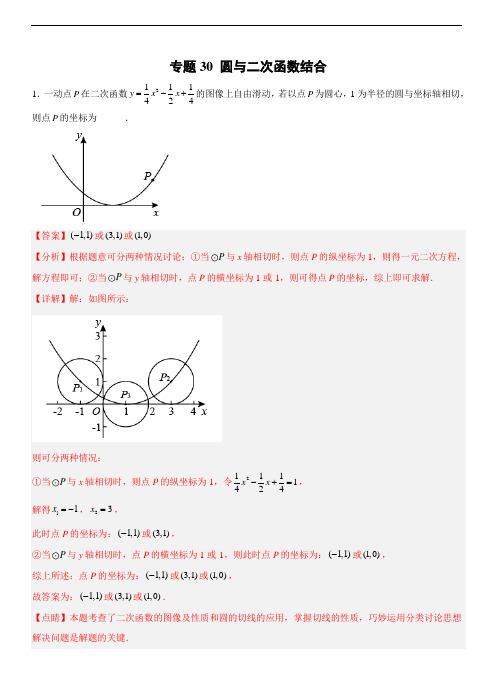
专题30 圆与二次函数结合1.一动点P 在二次函数2111424y x x =-+的图像上自由滑动,若以点P 为圆心,1为半径的圆与坐标轴相切,则点P 的坐标为______.【答案】(1,1)-或(3,1)或(1,0)【分析】根据题意可分两种情况讨论:①当P 与x 轴相切时,则点P 的纵坐标为1,则得一元二次方程,解方程即可;②当P 与y 轴相切时,点P 的横坐标为1或-1,则可得点P 的坐标,综上即可求解. 【详解】解:如图所示:则可分两种情况:①当P 与x 轴相切时,则点P 的纵坐标为1,令21111424x x -+=,解得11x =-,23x =,此时点P 的坐标为:(1,1)-或(3,1),②当P 与y 轴相切时,点P 的横坐标为1或-1,则此时点P 的坐标为:(1,1)-或(1,0), 综上所述:点P 的坐标为:(1,1)-或(3,1)或(1,0), 故答案为:(1,1)-或(3,1)或(1,0).【点睛】本题考查了二次函数的图像及性质和圆的切线的应用,掌握切线的性质,巧妙运用分类讨论思想解决问题是解题的关键.2.如图,平面直角坐标系中,以点C (2,3)为圆心,以2为半径的圆与x 轴交于A ,B 两点.若二次函数y =x 2+bx +c 的图象经过点A ,B ,试确定此二次函数的解析式为 ____________.【答案】y=x 2-4x +3【分析】过点C 作CH ⊥AB 于点H ,然后利用垂径定理求出CH 、AH 和BH 的长度,进而得到点A 和点B 的坐标,再将A 、B 的坐标代入函数解析式求得b 与c ,最后求得二次函数的解析式. 【详解】解:过点C 作CH ⊥AB 于点H ,则AH=BH ,∵C (2,3), ∴CH=3, ∵半径为2, ∴AH=BH=()2223-=1,∵A (1,0),B (3,0),∴二次函数的解析式为y=(x ﹣1)(x ﹣3)=x 2﹣4x +3, 故答案为:y=x 2-4x +3.【点睛】本题考查了圆的垂径定理、二次函数的解析式,解题的关键是过点C 作CH ⊥AB 于点H ,利用垂径定理求出点A 和点B 的坐标. 3.如图,抛物线2143115y x =-与x 轴交于A 、B 两点,与y 轴交于C 点,⊙B 的圆心为B ,半径是1,点P 是直线AC 上的动点,过点P 作⊙B 的切线,切点是Q ,则切线长PQ 的最小值是__.【答案】26【分析】先根据解析式求出点A 、B 、C 的坐标,求出直线AC 的解析式,设点P 的坐标,根据过点P 作⊙B 的切线,切点是Q 得到PQ 的函数关系式,求出最小值即可. 【详解】令214311515y x x =--中y=0,得x 1=-3,x 2=53, ∴直线AC 的解析式为313y x =--, 设P (x ,313x ), ∵过点P 作⊙B 的切线,切点是Q ,BQ=1 ∴PQ 2=PB 2-BQ 2, =(x-53)2+(313x )2-1, =242837533x x , ∵43a =0<, ∴PQ 2有最小值24283475()3326443,∴PQ 的最小值是26, 故答案为:26,【点睛】此题考查二次函数最小值的实际应用,求动线段的最小值,需构建关于此线段的函数解析式,利用二次函数顶点坐标公式求最值,此题找到线段PQ 、BQ 、PB 之间的关系式是解题的关键.二、解答题4.如图,在平面直角坐标系中,以()5,4D 为圆心的圆与y 轴相切于点C ,与x 轴相交于A 、B 两点,且6AB =.(1)求经过C 、A 、B 三点的抛物线的解析式; (2)设抛物线的顶点为F ,证明直线FA 与D 相切;(3)在x 轴下方的抛物线上,是否存在一点N ,使CBN 面积最大,最大值是多少,并求出N 点坐标. 【答案】(1)215442y x x =-+ (2)证明见解析 (3)存在.当4n =时,BCNS 最大,最大值为16,此时()4,2N -.【分析】(1)连接CD ,由y 轴是D 的切线,可得DC y ⊥轴,过点D 作DE AB ⊥于点E ,根据垂径定理可得3AE BE ==,连接AD ,在Rt ADE △中可求出AD ,即圆的半径,然后利用矩形的判定证明四边形OCDE 是矩形,得到4CO =,2OA =,8OB =,从而得到C 、A 、B 三点的坐标,再利用待定系数法即可确定经过点C 、A 、B 三点的抛物线的解析式;(2)因为点D 为圆心,点A 在圆周上,5r AD ==,利用勾股定理的逆定理证明90DAF ∠=︒即可; (3)设存在点N ,过点N 作NPy 轴,交BC 于点P ,求出直线BC 的解析式,设点N 的坐标215,442n n n ⎛⎫-+ ⎪⎝⎭,则可得点P 的坐标为1,42n n ⎛⎫-+⎪⎝⎭,从而根据BCN PNC PNB S S S =+△△△,表示出BCN △的面积,利用配方法可确定最大值,继而可得出点N 的坐标. (1)解:如图,连接CD ,AD ,过点D 作DE AB ⊥于点E , ∴90DEO ∠=︒,∵以()5,4D 为圆心的圆与y 轴相切于点C ,且6AB =,90COB ∠=︒,∴DC y ⊥轴,1AE BE AB 32===,4DE =,∴90DCO ∠=︒,2222435DA DE AE A =+=+=, ∴四边形OCDE 是矩形, ∴4CO DE ==,5==OE CD ,∴2OA OE AE =-=,8OB OA AB =+=, ∴()0,4C ,()2,0A ,()8,0B ,设经过点C 、A 、B 三点的抛物线解析式为:2y ax bx c =++, 将点C 、A 、B 三点的坐标代入可得:42064804a b c a b c c ++=⎧⎪++=⎨⎪=⎩, 解得:14524a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,∴经过C 、A 、B 三点的抛物线的解析式为:215442y x x =-+.(2)证明:∵点D 为圆心,点A 在圆周上, 由(1)知,5r DA ==, 抛物线解析式为:215442y x x =-+,且顶点F 的坐标为95,4⎛⎫- ⎪⎝⎭, 又∵()5,4D ,与D 相切.N ,使CBN 面积最大,N 作NP y 轴,交()8,0B ,的解析式为:y kx =NPy 轴,交的坐标为142n =-+BCN PNC S =△当4n =时,BCNS最大,最大值为16,此时()4,2N -.【点睛】本题考查了二次函数及圆的综合应用,涉及垂径定理,矩形的判定和性质,切线的判定与性质,勾股定理及勾股定理逆定理,待定系数法求二次函数解析式,二次函数的性质等知识.由BCN PNC PNB S S S =+△△△得到BCNS与n 的函数关系是解题的关键.5.定义:平面直角坐标系xOy 中,过二次函数图像与坐标轴交点的圆,称为该二次函数的坐标圆.(1)已知点P (2,2),以P 5P 是不是二次函数y =x 2﹣4x +3的坐标圆,并说明理由;(2)已知二次函数y =x 2﹣4x +4图像的顶点为A ,坐标圆的圆心为P ,如图1,求△POA 周长的最小值; (3)已知二次函数y =ax 2﹣4x +4(0<a <1)图像交x 轴于点A ,B ,交y 轴于点C ,与坐标圆的第四个交点为D ,连接PC ,PD ,如图2.若∠CPD =120°,求a 的值. 【答案】(1)⊙P 是二次函数y =x 2﹣4x +3的坐标圆,理由见解析 (2)△POA 周长的最小值为6 (3)43312a +=【分析】(1)先求出二次函数y=x2-4x+3图像与x轴、y轴的交点,再计算这三个交点是否在以P(2,2)为圆心,5为半径的圆上,即可作出判断.(2)由题意可得,二次函数y=x2-4x+4图像的顶点A(2,0),与y轴的交点H(0,4),所以△POA周长=PO+P A+OA=PO+PH+2≥OH+2,即可得出最小值.(3)连接CD,P A,设二次函数y=ax2-4x+4图像的对称轴l与CD交于点E,与x轴交于点F,由对称性知,对称轴l经过点P,且l⊥CD,设PE=m,由∠CPD=120°,可得P A=PC=2m,CE=3m,PF=4-m,表示出AB、AF=BF,在Rt△P AF中,利用勾股定理建立方程,求得m的值,进而得出a的值.(1)对于二次函数y=x2﹣4x+3,当x=0时,y=3;当y=0时,解得x=1或x=3,∴二次函数图像与x轴交点为A(1,0),B(3,0),与y轴交点为C(0,3),∵点P(2,2),∴P A=PB=PC=5,∴⊙P是二次函数y=x2﹣4x+3的坐标圆.(2)如图1,连接PH,∵二次函数y=x2﹣4x+4图像的顶点为A,坐标圆的圆心为P,∴A(2,0),与y轴的交点H(0,4),∴△POA周长=PO+P A+OA=PO+PH+2≥OH+2=6,∴△POA周长的最小值为6.(3)如图2,连接CD ,P A ,设二次函数y =ax 2﹣4x +4图像的对称轴l 与CD 交于点E ,与x 轴交于点F ,由对称性知,对称轴l 经过点P ,且l ⊥CD , ∵AB =161641a aa a--=, ∴AF =BF =21aa-, ∵∠CPD =120°,PC =PD ,C (0,4), ∴∠PCD =∠PDC =30°,设PE =m ,则P A =PC =2m ,CE =3m ,PF =4﹣m , ∵二次函数y =ax 2﹣4x +4图像的对称轴l 为2x a=, ∴23m a=,即23a m =,在Rt △P AF 中,P A 2=PF 2+AF 2, ∴222214(4)()a m m a-=-+, 即22224(1)34(4)43mm m m -=-+,化简,得(823)16m +=,解得843m =+, ∴2433123a m+==.【点睛】此题是二次函数与圆的综合题,主要考查了二次函数的性质、圆的基本性质、解直角三角形、勾股定理等知识以及方程的思想,添加辅助线构造直角三角形是解答本题的关键.6.已知抛物线y =ax 2+bx +3(a ≠0)经过A (3,0)、B (4,1)两点,且与y 轴交于点C . (1)求抛物线的解析式;(2)如图,设抛物线与x 轴的另一个交点为D ,在抛物线上是否存在点P ,使△P AB 的面积是△BDA 面积的2倍?若存在,求出点P 的坐标;若不存在,请说明理由.(3)如图(2),连接AC ,E 为线段AC 上任意一点(不与A 、C 重合),经过A 、E 、O 三点的圆交直线AB 于点F ,当△OEF 的面积取得最小值时,求面积的最小值及E 点坐标.【答案】(1)215322y x x =-+;(2)存在,点P 坐标(7172-,5172-)或(7172+,5172+);(3)面积的最小值为94,E 点坐标(32,32) 【分析】(1)根据待定系数法求解即可;(2)根据抛物线的解析式求出点D 的坐标,取点E (1,0),作EP ∥AB 交抛物线于点P ,得到直线EP 为y =x ﹣1,联立方程组求解即可;(3)作BD ⊥OA 于D ,得到OA =OC =3,AD =BD =1,证明EF 是△AEO 的外接圆的直径,得到△EOF 是等腰直角三角形,当OE 最小时,△EOF 的面积最小,计算即可; 【详解】(1)将点A (3,0),B (4,1)代入可得: 933014431a b a b ++⎧⎨++⎩==,解得:1252a b ⎧=⎪⎪⎨⎪=-⎪⎩, 故函数解析式为215322y x x =-+; (2)∵抛物线与x 轴的交点的纵坐标为0, ∴2153022x x -+=,解得:x 1=3,x 2=2, ∴点D 的坐标为(2,0),取点E (1,0),作EP ∥AB 交抛物线于点P ,∵ED =AD =1,∴此时△P AB 的面积是△DAB 的面积的两倍, ∵直线AB 解析式为y =x ﹣3, ∴直线EP 为y =x ﹣1,由2115322y x y x x =-⎧⎪⎨=-+⎪⎩解得71725172x y ⎧-=⎪⎪⎨-⎪=⎪⎩或71725172x y ⎧+=⎪⎪⎨+⎪=⎪⎩, ∴点P 坐标(7172-,5172-)或(7172+,5172+). (3)如图2中,作BD ⊥OA 于D .∵A (3,0),C (0,3),B (4,1), ∴OA =OC =3,AD =BD =1, ∴∠OAC =∠BAD =45°, ∵∠OAF =∠BAD =45°, ∴∠EAF =90°,∴EF 是△AEO 的外接圆的直径, ∴∠EOF =90°,∴∠EFO =∠EAO =45°, ∴△EOF 是等腰直角三角形, ∴当OE 最小时,△EOF 的面积最小, ∵OE ⊥AC 时,OE 最小,OC =OA ,∴CE =AE ,OE =12AC =322, ∴E (32,32),S △EOF =1323292224⨯⨯=.∴当△OEF 的面积取得最小值时,面积的最小值为94,E 点坐标(32,32). 【点睛】本题主要考查了二次函数综合、一次函数的性质、圆的综合应用,准确计算是解题的关键. 7.如图,在直角坐标系中,抛物线y =ax 2+bx -2与x 轴交于点A (-3,0)、B (1,0),与y 轴交于点C .(1)求抛物线的函数表达式.(2)在抛物线上是否存在点D ,使得△ABD 的面积等于△ABC 的面积的53倍?若存在,求出点D 的坐标;若不存在,请说明理由.(3)若点E 是以点C 为圆心且1为半径的圆上的动点,点F 是AE 的中点,请直接写出线段OF 的最大值和最小值.【答案】(1)224x 233y x =+-;(2)存在,理由见解析;D (-4, 103)或(2,103);(3)最大值13122+;最小值13122- 【分析】(1)将点A 、B 的坐标代入函数解析式计算即可得到;(2)点D 应在x 轴的上方或下方,在下方时通过计算得∴△ABD 的面积是△ABC 面积的43倍,判断点D 应在x 轴的上方,设设D (m ,n ),根据面积关系求出m 、n 的值即可得到点D 的坐标;(3)设E(x,y),由点E 是以点C 为圆心且1为半径的圆上的动点,用两点间的距离公式得到点E 的坐标为E 2(,12)x x,再根据点F 是AE 中点表示出点F 的坐标2312(,)22x x ,再设设F(m,n),再利用m 、n 、与x 的关系得到n=21(23)22m ,通过计算整理得出22231(1)()()22n m ,由此得出F 点的轨)时,02C (,-)4533<,所以设D (m ,n ), △∴n =103∴223m +y=212x ,2,12)x x ,是AE 的中点, 的坐标2312(,)22x x ,,n=2122x ,n=21(23)22m ,∴2n+2=21(23)m ,∴(2n+2)2=1-(2m+3)2, ∴4(n+1)2+4(32m)2=1, ∴22231(1)()()22n m, ∴F 点的轨迹是以3(,1)2--为圆心,以12为半径的圆,∴最大值:2231131(0)12222, 最小值:2231131(0)12222最大值13122+;最小值13122- 【点睛】此题是二次函数的综合题,考察待定系数法解函数关系式,图像中利用三角形面积求点的坐标,注意应分x 轴上下两种情况,(3)还考查了两点间的中点坐标的求法,两点间的距离的确定方法:两点间的距离的平方=横坐标差的平方+纵坐标差的平方.8.如图,点M (4,0),以点M 为圆心、2为半径的圆与x 轴交于点A 、B .已知抛物线y =16x 2+bx+c 过点A 和B ,与y 轴交于点C .(1)求点C 的坐标,并画出抛物线的大致图象(要求过点A 、B 、C ,开口方向、顶点和对称轴相对准确)(2)点Q (8,m )在抛物线y =16x 2+bx+c 上,点P 为此抛物线对称轴上一个动点,求PQ+PB 的最小值;(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.【答案】(1)C (0,2),图象见解析;(2)PQ+PB 的最小值210;(3)OE 的解析式为y=12x -. 【详解】试题分析:(1)根据题意可知点A ,B 的坐标分别为(2,0),(6,0),代入函数解析式即可求得抛物线的解析式,即可得点C 的坐标;(2)根据图象可得PQ+PB 的最小值即是AQ 的长,所以抛物线对称轴l 是x=4.所以Q (8,m )抛物线上,∴m=2.过点Q 作QK ⊥x 轴于点K ,则K (8,0),QK=2,AK=6,求的AQ 的值即可;(3)此题首先要证得OE ∥CM ,利用待定系数法求得CM 的解析式,即可求得OE 的解析式. 试题解析:(1)由已知,得A (2,0),B (6,0),∵抛物线y=16x 2+bx+c 过点A 和B ,则2212206{16606b c b c ⨯++⨯++== 解得4{32b c -== 则抛物线的解析式为y=16x 2-43x+2.故C (0,2).(说明:抛物线的大致图象要过点A 、B 、C ,其开口方向、顶点和对称轴相对准确) (2)如图①,抛物线对称轴l 是x=4. ∵Q (8,m )在抛物线上,∴m=2.过点Q 作QK ⊥x 轴于点K ,则K (8,0),QK=2,AK=6, ∴AQ=22=210AK QK +.又∵B (6,0)与A (2,0)关于对称轴l 对称, ∴PQ+PB 的最小值=AQ=210. (3)如图②,连接EM 和CM .由已知,得EM=OC=2.∵CE是⊙M的切线,∴∠DEM=90°,则∠DEM=∠DOC.又∵∠ODC=∠EDM.故△DEM≌△DOC.∴OD=DE,CD=MD.又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC.则OE∥CM.设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0),∴40 {2k bb+==解得1 {22 kb-==直线CM的解析式为y=−12x+2.又∵直线OE过原点O,且OE∥CM,∴OE的解析式为y=−12x或y=0.5x.9.如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).(1)求抛物线的函数表达式;(2)当0<x<3时,求线段CD的最大值;(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;(4)过点B,C,P的外接圆恰好经过点A时,x的值为.(直接写出答案)【答案】(1)y=﹣x 2+2x+3;(2)当x=32时,CD 最大=94;(3)x=±12或x=±2;(4)1.【详解】分析:(1)用待定系数法求出抛物线解析式即可;(2)先确定出直线AB 解析式,进而得出点D ,C 的坐标,即可得出CD 的函数关系式,即可得出结论;(3)先确定出CD=|-x2+3x|,DP=|-x+3|,再分两种情况解绝对值方程即可;(4)利用四个点在同一个圆上,得出过点B ,C ,P 的外接圆的圆心既是线段AB 的垂直平分线上,也在线段PC 的垂直平分线上,建立方程即可. 本题解析:(1)∵抛物线y=﹣x 2+bx+c 与x 轴正半轴交于点A (3,0),与y 轴交于点B (0,3),∴﹣9+3b+c=0,c=3,∴b=2,∴抛物线解析式为y=﹣x 2+2x+3;(2)∵A (3,0),B (0,3),∴直线AB 解析式为y=﹣x+3, ∵P (x ,0).∴D (x ,﹣x+3),C (x ,﹣x 2+2x+3), ∵0<x <3,∴CD=﹣x 2+2x+3﹣(﹣x+3)=﹣x 2+3x=﹣(x ﹣32)2+94,当x=32时,CD 最大=94; (3)由(2)知,CD=|﹣x 2+3x|,DP=|﹣x+3|①当S △PDB =2S △CDB 时,∴PD=2CD ,即:2|﹣x 2+3x|=|﹣x+3|,∴x=±12或x=3(舍),②当2S △PDB =S △CDB 时,∴2PD=CD ,即:|﹣x 2+3x|=2|﹣x+3|,∴x=±2或x=3(舍), 即:综上所述,x=±12或x=±2; (4)直线AB 解析式为y=﹣x+3,∴线段AB 的垂直平分线l 的解析式为y=x , ∵过点B ,C ,P 的外接圆恰好经过点A ,∴过点B ,C ,P 的外接圆的圆心既是线段AB 的垂直平分线上,也在线段PC 的垂直平分线上, ∴2232x x x -++=,∴x=±3,故答案为3± 10.如图,已知抛物线的对称轴为直线l :4,x =且与x 轴交于点(2,0),A 与y 轴交于点C (0,2).(1)求抛物线的解析式;(2)试探究在此抛物线的对称轴l 上是否存在一点P ,使AP CP +的值最小?若存在,求AP CP +的最小值,若不存在,请说明理由;(3)以AB 为直径作⊙M ,过点C 作直线CE 与⊙M 相切于点E ,CE 交x 轴于点D ,求直线CE 的解析式. 【答案】解:(1)如图,由题意,设抛物线的解析式为:2y a x 4a 0k =-+≠()()∵抛物线经过(2,0)A 、C (0,2).∴24)204)2(0{(2a k a k --+=∴+= 解得:a=16,23k =-.∴212(4)63y x =--,即:214263y x x =-+. (2)存在.令0y =,得28120,x x -+=即(2)(6)0x x --=,122, 6.x x ∴== ∴抛物线与x 轴的另-交点(6,0)B .如本题图2,连接CB 交l 于点P ,则点P 即是使AP CP +的值最小的点.因为A B 、关于l 对称,则AP BP =,AP CP CB ∴+=,即AP CP +的最小值为BC . ∵6,2OB OC ==,226240210.BC ∴=+==AP CP ∴+的最小值为210;(3)如图3,连接ME ,∵CE 是⊙M 的切线,∴90ME CE CEM ,⊥∠=︒,由题意,得2.OC ME ODC MDE ==∠=∠, ∵在COD MED ∆∆与中,{COD MED ODC EDM OC EM∠=∠∠=∠=, ∴AAS COD MED ∆∆≌(), OD DE DC DM ∴==,,设OD x =,则4CD DM OM OD x ==-=-, 则在Rt △COD 中,又222OD OC CD +=,∴2224(4)x x +=-,解得32x =,∴D (32,0) 设直线CE 的解析式为y mx b =+,∵直线CE 过C (0,2)、D (32,0)两点, ∴3{22m b b +==,解方程组得:4{32m b =-=. ∴直线CE 的解析式为y 423x =-+.【详解】试题分析:(1)根据题意设抛物线的解析式为2y a x 4a 0k =-+≠()(),将(2,0)A 、C (0,2)代入解析式,即可求出a ,k 的值,得出抛物线的解析式,令0y =,即可求出抛物线与x 轴另-交点(6,0)B ;(2)连接CB 交l 于点P ,则点P 即是使AP CP +的值最小的点. 则AP CP +的最小值为BC ,在Rt △OBC 中,根据勾股定理即可求出BC 的值;(3)连接ME ,根据已知条件可得COD MED ∆∆≌,根据全等三角形的对应边相等可得OD DE DC DM ==,,在Rt △COD 中,根据勾股定理求出OD ,即可得出D 点坐标,设直线CE 的解析式为y mx b =+,代入C ,D 两点坐标,即可解得直线CE 的解析式. 考点:二次函数的综合题.点评:本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,一次函数的解析式,也考查了二次函数与圆的综合,本题综合性强,有一定难度.11.如图,已知二次函数23y ax bx =++的图象与x 轴交于点A (1,0)、B (3-,0),与y 轴的正半轴交于点C .(1)求二次函数23y ax bx =++的表达式;(2)点D 是线段OB 上一动点,过点D 作y 轴的平行线,与BC 交于点E ,与抛物线交于点F ,连接CF ,探究是否存在点D 使得△CEF 为直角三角形?若存在,求点D 的坐标;若不存在,说明理由;(3)若点P在二次函数图象上,是否存在以P BC相切,若存在,求点P的坐标;若不存在,说明理由.y x.3∥OB关于抛物线对称轴直线x=)②当∠ECF =90°时,作FG ⊥y 轴于G , 由OB =OC ,∠BOC =90°,可知∠BCO =45° ∵CF ⊥CB , ∴∠FCG =45°,∴△CFG 是等腰直角三角形, 设CG =a ,则点F 坐标为(-a ,a +3),代入223y x x =--+得:23()2()3a a a +=----+ 解得11a =,20a =(舍去) 点F (-1,4),此时点D 坐标为(-1,0).综上所述:存在这样的点D ,点D 坐标为(-2,0)或(-1,0) (3)解:①当点P 在BC 上方时,过点P 作PG ⊥BC 于点G ,作PM ⊥x 轴,交BC 于点N ,过点P 作直线PH ∥BC .则PNG 是等腰直角三角形,∵PG =2, ∴PN =2, ∵PM ⊥x 轴,∴直线PH 由直线BC 向上平移两个单位长度得到, ∴直线PH 的解析式为5y x =+. 联立直线PH 和抛物线的解析式,得:2235y x x y x ⎧=--+⎨=+⎩, 解得:14x y =-⎧⎨=⎩或23x y =-⎧⎨=⎩.∴点P 坐标为(-1,4)或(-2,3) .②当点P 在BC 下方时,同理可得直线PH 由直线BC 向下平移两个单位长度得到, ∴直线PH 的解析式为1y x =+.2231y x x y x ⎧=--+⎨=+⎩, 解得:31721172x y ⎧-+=⎪⎪⎨-+⎪=⎪⎩或31721172x y ⎧--=⎪⎪⎨--⎪=⎪⎩.∴点P 坐标为(31711722,-+-+)或(31711722----,). 综上所述:点P 坐标为(-1,4)或(-2,3)或(31711722,-+-+)或(31711722----,). 【点睛】此题考查了二次函数的综合应用,涉及了待定系数法求解析式,二次函数的性质,圆的切线的性质,解题的关键是熟练掌握并灵活应用相关性质进行求解,难度适中.12.已知二次函数的图象交x 轴于点A (3,0),B (-1,0),交y 轴于点C (0,-3),P 这抛物线上一动点,设点P 的横坐标为m .(1)求抛物线的解析式:(2)当△P AC 是以AC 为直角边的直角三角形时,求点P 的坐标:(3)抛物线上是否存在点P ,使得以点P 为圆心,2为半径的圆既与x 轴相切,又与抛物线的对称轴相交?若存在,求出点P 的坐标,并求出抛物线的对称轴所截的弦MN 的长度;若不存在,请说明理由.(写出过程) 【答案】(1)223y x x =--(2)点P 的坐标为(-2,5)或(1,-4);(3)点P 的坐标为()122--,或()122+-,,抛物线的对称轴所截的弦MN 的长度为22【分析】(1)利用待定系数法求解即可;(2)分当∠P AC =90°时,当∠PCA =90°时,两种情况讨论求解即可;(3)由圆P 的半径为2,且圆P 与抛物线对称轴有交点,且与x 轴相切,可得点P 的纵坐标为-2,由此求出点P 的坐标即可;过点P 作PE ⊥MN 于E ,由垂径定理可得MN =2ME ,利用勾股定理求出ME 即可得到答案.(1)解:设抛物线解析式为()()13y a x x =+-,把点C (0,-3)代入得,()()01033a +-=-,∴1a =,∴抛物线解析式为()()21323y x x x x =+-=--;(2)解:如图所示,当∠P AC =90°时,设P A 与y 轴交点为D , ∵点A 坐标为(3,0),点C 坐标为(0,-3), ∴OA =OC =3, ∵∠AOC =90°, ∴∠CAO =45°, ∴∠DAO =45°, ∴OA =OD =3,∴点D 的坐标为(0,3), 设直线AD 的解析式为y kx b =+,∴303k b b +=⎧⎨=⎩,∴13k b =-⎧⎨=⎩,∴直线AD 的解析式为3y x =-+,联立2323y x y x x =-+⎧⎨=--⎩, 解得25x y =-⎧⎨=⎩或30x y =⎧⎨=⎩(舍去),∴点P 的坐标为(-2,5);当∠PCA =90°,设直线PC 与x 轴的交点为E , 同理可证∠ECO =45°,即OE =OC , ∴点E 的坐标为(-3,0),同理可以求出直线PC 的解析式为3y x =--,联立2323y x y x x =--⎧⎨=--⎩, 解得14x y =⎧⎨=-⎩或03x y =⎧⎨=-⎩(舍去),∴点P 的坐标为(1,-4),综上所述,点P 的坐标为(-2,5)或(1,-4);(3)解:∵抛物线解析式为()222314y x x x =--=--, ∴抛物线对称轴为直线1x =,∴点A 和点B 到抛物线的对称轴的距离都为2,∵圆P 的半径为2,且圆P 与抛物线对称轴有交点,且与x 轴相切, ∴点P 的纵坐标为-2, 当2y =-时,2232x x --=-, 解得121212x x =-=+,,∴点P 的坐标为()122--,或()122+-,, 过点P 作PE ⊥ME 交抛物线对称轴于E ,∴1212PE =+-=或()112=2--,2MN ME =, ∴222ME MP PE =-=, ∴22MN =,∴点P 的坐标为()122--,或()122+-,,抛物线的对称轴所截的弦MN 的长度为22【点睛】本题主要考查了二次函数综合,一次函数与几何综合,圆与函数综合,待定系数法求函数解析式等等,正确理解题意,利用分类讨论和数学结合的思想求解是解题的关键.13.如图,二次函数24y ax =+的图象与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C ,且OA=OC(1)求二次函数的解析式;(2)若以点O 为圆心的圆与直线AC 相切于点D ,求点D 的坐标;(3)在(2)的条件下,抛物线上是否存在点P 使得以P 、A 、D 、O 为顶点的四边形是直角梯形?若存在,直接写出点P 坐标;若不存在,请说明理由.【答案】(1)2144y x =-+(2)点D 的坐标为()2,2-(3)存在,点1P 的坐标为()8,12-,点2P 的坐标为()225,225----【分析】(1)由题意可知C 坐标,根据题意得到三角形AOC 为等腰直角三角形,确定出A 坐标,代入二次函数解析式求出a 的值,即可确定出解析式;(2)由题意连接OD ,作DE ∥y 轴,交x 轴于点E ,DF ∥x 轴,交y 轴于点F ,如图1所示,由圆O 与直线AC 相切于点D ,得到OD 垂直于AC ,由OA =OC ,利用三线合一得到D 为AC 中点,进而求出DE 与DF 的长,确定出D 坐标即可;(3)根据题意分两种情况考虑:经过点A 且与直线OD 平行的直线的解析式为y =-x -4,与抛物线解析式联立求出P 坐标;经过点O 且与直线AC 平行的直线的解析式为y =x ,与抛物线解析式联立求出P 坐标即可. (1)解:∵二次函数24y ax =+的图象与y 轴交于点C , ∴点C 的坐标为()0,4,∵二次函数24y ax =+的图象与x 轴交于点A ,tan ∠OAC =1, ∴∠CAO =45°, ∴OA =OC =4, ∴点A 的坐标为()4,0-, ∴()2044a =-+,∴14a =-,∴二次函数的解析式为2144y x =-+;(2)连接OD ,作DE 轴,交x 轴于点E ,DF 轴,交y 轴于点F ,如图1所示,∵⊙O 与直线AC 相切于点D ,∴OD ⊥AC , ∵OA =OC =4, ∴点D 是AC 的中点,∴122DE OC ==,122DF OA ==,∴点D 的坐标为()2,2-; (3)直线OD 的解析式为y =-x ,如图2所示,则经过点A 且与直线OD 平行的直线的解析式为y =-x -4,解方程组24144y x y x =--⎧⎪⎨=-+⎪⎩,消去y ,得24320x x --=,即()()840x x -+=, ∴18x =,24x =-(舍去), ∴y =-12,∴点1P 的坐标为()8,12-;直线AC 的解析式为y =x +4, 则经过点O 且与直线AC 平行的直线的解析式为y =x ,解方程组2144y x y x =⎧⎪⎨=-+⎪⎩, 消去y ,得24160x x +-=,即225x =-+, ∴1225x =--,2225x =-+(舍去), ∴225y =--,∴点2P 的坐标为()225,225----.【点睛】本题属于二次函数综合题,涉及的知识有:待定系数法确定二次函数解析式,坐标与图形性质,直线与抛物线的交点,直线与圆相切的性质,锐角三角函数定义,以及等腰直角三角形的性质,熟练掌握二次函数的性质是解答本题的关键.14.如图,已知二次函数213442y x x =-++的图像与x 轴交于点A ,B ,与y 轴交于点C ,顶点为D ,连接BC ;(1)求顶点D 的坐标; (2)求直线BC 的解析式;(3)点E 是第一象限内抛物线上的动点,连接BE ,CE ,求△BCE 面积的最大值; (4)以AB 为直径,M 为圆心作圆M ,试判断直线CD 与圆M 的位置关系,并说明理由 【答案】(1)25(3,)4(2)142y x =-+(3)16(4)直线与圆M 相交,理由见解析【分析】(1)利用配方法将一般式解析式转化为顶点式解析式;(2)先解得(2,0),(8,0)A B -,(0,4)C ,再利用待定系数法,代入点B 、C 的坐标即可解答; (3)根据中点公式解得点M 的坐标,再利用两点间的距离公式解得CM ,MD 的长,比较MD <CM ,得到直线与圆M 有两个交点,据此解答. (1)解:222213114612264=()4()445949(3)44y x x x x x x x --=-++-+=-+--+=+-即顶点D 的坐标25(3,)4; (2)由(1)知(0,4)C 令0y =得201(3)254=4x -+- 解得128,2x x ==-(2,0),(8,0)A B ∴-设直线BC 的解析式:y kx b =+,代入点B 、C480b k b =⎧⎨+=⎩124k b ⎧=-⎪∴⎨⎪=⎩ 142y x ∴=-+ (3)如图,设21(,)3442E x x x ++-(0<x <8),过点E 作EH x ⊥于H , BCE BOC COBE S S S=-四边形 BHE BOC COHE SS S =+-梯形 1()1222EH CO OH BH EH BO CO +⋅=⋅+-⋅223432421(4)1114(8)()842422x x x x x x -+⋅=-⋅-+-++⨯+⨯+ 2=8x x -+2(4)16=x --+即当x =4时,△BCE 面积的最大值为16;(4)直线与圆M 的位置是相交,理由如下,如图,M 为BC 的中点,0804(,)22M ++∴ 即(4,2)M222225305(04)(42)25,(34)(2)44CM MD ∴=-+-==-+-= 32030532025,444=< MD MC ∴<∴直线CD 与圆M 有两个交点,即直线与圆M 的位置是相交.【点睛】本题考查二次函数与一次函数的综合,涉及配方法、待定系数法求一次函数的解析式、直线与圆的位置关系、勾股定理、中点公式、两点距离公式等知识,是重要考点,掌握相关知识是解题关键. 15.如图,已知二次函数y =ax 2+bx +3的图象与x 轴交于点A (﹣1,0)、B (4,0),与y 轴交于点C . (1)二次函数的表达式为 ;(2)点M 在直线BC 上,当△ABM 为等腰三角形时,求点M 的坐标;(3)若点E 在二次函数的图象上,以E 为圆心的圆与直线BC 相切于点F ,且EF =65,请直接写出点E 的坐标. 【答案】(1)239344y x x =-++;(2)点M 为(0,3)或(8,﹣3)或(32,158);(3)点E 的坐标为3626,4⎛⎫- ⎪ ⎪⎝⎭或3626,4⎛⎫+- ⎪ ⎪⎝⎭或3222,34⎛⎫-+ ⎪ ⎪⎝⎭或3222,34⎛⎫+- ⎪ ⎪⎝⎭. 【分析】(1)根据A 、B 两点的坐标,应用待定系数法即可求出二次函数的表达式;(2)首先通过BC 两点坐标,求出直线BC 的解析式,再根据三角形△ABM 是等腰三角形,分3种情况考虑,得到关于M 点横坐标x 的方程,解之即可得到x 的值,进而得到M 点坐标;(3)利用面积法求出O 到直线BC 的距离,结合EF 的长度可知P 1为线段OC 中点,可得P 1的坐标,进而可得P 2坐标,结合直线BC 的表达式,可求出直线EP 的表达式,联立直线EP 和抛物线的函数表达式,组成方程组,即可解得点E 的坐标.【详解】解:(1)将A (﹣1,0),B (4,0)代入y =ax 2+bx +3得:3016430a b a b -+=⎧⎨++=⎩, ∴a =34-,b =94, ∴239344y x x =-++, 故二次函数表达式为:239344y x x =-++; (2)当x =0时,y =3,∴点C 的坐标是(0,3),设直线BC 的表达式为:y =kx +c (k ≠0),将B (4,0),C (0,3)代入y =kx +c 得:4303k c +=⎧⎨=⎩, ∴343k c ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为:334y x =-+,使得△ABM 为等腰三角形,存在如图所示的三种情况:过点M 1作M 1D ⊥AB ,∵A (﹣1,0),B (4,0),∴AD =12AB =52, ∴OD =32, 设M 1(x ,﹣34x +3), ∴M 1(32,158), ∵△ABM 为等腰三角形,∴AB =BM 2=5或AB =BM 3=5,设M 2(x 1,﹣34x 1+3), ∴BM 2=()22113434x x ⎛⎫-+-+ ⎪⎝⎭=5, 解得x 1=8或0,当x 1=0时,y =3,当x 1=8时,y =﹣3,∴点M 为(0,3)或(8,﹣3)或(32,158); (3)过点E 作EP ∥BC ,交y 轴于点P ,这样的点有两个,分别记为P 1,P 2,如图所示:∵OB =4,OC =3,∴BC =22OB OC +=5,∴点O 到直线BC 的距离为:125OB OC BC ⋅=, ∵以E 为圆心的圆与直线BC 相切于点F ,且EF =65, ∴点E 到直线BC 的距离是65, ∴点P 1为线段OC 的中点,∴CP 1=CP 2,∴P 2(0,92), ∵直线BC 的函数表达式为y =﹣34x +3, ∴直线EP 的函数表达式为y =﹣34x +32或y =﹣34x +92, 联立直线EP 和抛物线的表达式方程组,得:2334239344y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩或2394239344y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩, 得1126364x y ⎧=-⎪⎨=⎪⎩或2226364x y ⎧=+⎪⎨=-⎪⎩或33223234x y ⎧=-⎪⎨=+⎪⎩或44223234x y ⎧=+⎪⎨=-⎪⎩, ∴点E 的坐标为36264⎛⎫- ⎪ ⎪⎝⎭,或36264⎛⎫+- ⎪ ⎪⎝⎭,或322234⎛⎫-+ ⎪ ⎪⎝⎭,或322234⎛⎫+- ⎪ ⎪⎝⎭,.【点睛】本题主要考查了二次函数与几何的综合应用.解题的关键要熟练掌握代入法求二次函数的解析式和一次函数的解析式、两点间的距离公式及勾股定理等.。
初中数学二次函数与圆相结合的压轴题专题,中考数学二次函数与圆相结合的经典题型讲解及答案解析
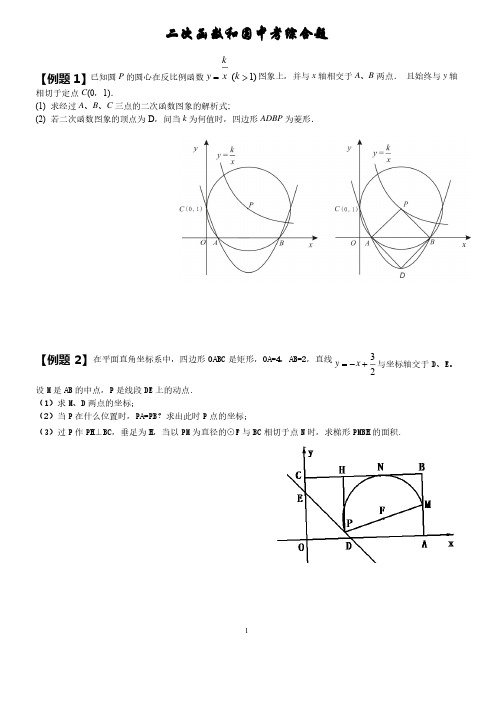
【仲烦1】(我市)已知圆P的圆心在反比例函数y=-(A:>1)上,并与工轴相交于X、3两点.且x始终与]轴相切于定点C(0,1).⑴求经过三点的二次匣1数图象的解析式;(2)若二次函教图象的顶点为D,问当上为何值时'四边形也站尹为菱形.【耕音】解:(1)连接PC、PAx PB,谊P点ffPHXx轴.垂足为H・(1分)与y轴相切于点C(0, 1),.-.PC±y^.•.•P点在反比例函数》二占的囹象上,X•.•P点坐标为(k,1).(2分)•.•PAU.在RtAAPH中,AH=厨2_尸於后一1,•'•A(k-90 ).(3分)•.•由。
P交x轴于A、B两点,且PHJLAB,由垂径击理可知,PH垂直平分AB.AOB=OA+2AH=k•••B3小2_1,0).《4分〉故过A、B两点的抛物线的对称轴为PH所在的直钱斛析式为x=k.可设该抛物线解析式为y=a<x-k)2+h.(5分)又二.抛物线过C(。
,1),B(k-^2_r0),[ak^-^h=1•3|—?昭得a=l,h=1-k^.(7分)•.•抛物线解析式为y=心)2+1上2.(B分)(2)由<1)知抛物线顶点D坐标为(k,l-k2>•・•DH-k2-l.若四边形ADBP为装形.则必有PH=DH.(10分)VPH=1,.•-k2-l=l.又">1,(11分)•・•当k取以时,PD与AB互相垂直平分,则四边形ADBP为菱形•(12分)3【百麒2]翎南省韶关市)25.如图6,在平面直角坐标系中旭边形OABC是矩形,。
虹4应=2,直线),=-":与坐标轴交于D、E。
设M是加的中点,P是线段DE上的动点.(1)求M、D两点的坐标;<2)当P在什么位置时,PA=PB?求出此时P点的坐标j<3)过P作PH1BC,垂足为H,当以PM为直径的OF与BC相切于点N时,求梯形PHBH的面积.图6【分析】(1)因为四边形OABC是逅形,0A=4,AB=2»直线>=r-?与坐标轴交于D、E,M是AB的中点2.所以令y=0,即司术出D的坐标,而AM-1.印以M(4,1);(2)因为PA=PB.断以P是AB的香直平分线和直线ED的交点,而AE的中垂线是y=l,断以P的纵坐标为1,令直线ED的解析式中的y=l,求出的x的值即为相应的P的横坐标;(3〉可设P(x,y>,连将PN、MN、NF,因为点P在y・x-:上,所以P《x,粮据蹦意可2得PNlMNi FN±BCi F是圈心,又因N是钱段HB的中点,HN-NB-—»PH-2-(-x*-)t2 2 2BM=1,利用直径对的圆周角是直甬可得到ZHPX-ZHNP=ZHNP-ZBNM=90°•所以ZHPN=ZB取ph ir£x+| NM,又因ZPHN-ZB-900-所以可得到R tAPNH<^RtANMB•所以—•A2=—^,这BM BN—4-x1—样牧可得到关于X的方程,解之即可求出X的值,而饬求面招的四边形是一个直角梯形,南以Spg=也皿滋或"医号)("6+应)=.21_色叵.2 2 24满答】俄;《1)M", 1),D《9,0);(2分)2(2)V PA=PB>•七点P在线段AB的中毒线上,•.•点P的纵坐标是I,3又•:点P在尸-X-—上,2・.•点P的坐标为(【,1)?(4分)(3)设P(x,y),连接PN、MN、NF,3点P lSy=・x+-上,匕3・'・P(x ,-w+—),2依题意知:PN«LMN>FN^BC,F是圆心,・'・N是线段HB的中点,HN=NB=±M,PH=2.2口,BM=1,<6分)22HPN-ZHNP=NHNP-ZBNM=90°,NHPN=ZBNN1,又ZPHN=ZB=90°5RtAPNH^RtANMBs:HN_PH•'两南,4-x x*.."F=二,-等」22,(8分)x?-12x+14=0»朋得;x-6-j22(^-*>^舍去),k=6-皿=些罕=空也艾竺=一*孕屈,(9分)2【例题31(||-4省白银等7市新课程)28.在直角坐标系中>0A的丰径为4,圆心A曜标为(2, 0),S与X轴交于E、尸两点,与),轴交于(7、D两点,过点(7作0X的切线时,交x轴于点3.(1)求直线C5的解析式:(2)若抛物线.件履7)日€的顶点在直线3C上,与x轴的交点恰为点E、已求该抛物线的解析式J(3)试判断点C是否在抛物线上?(4)在抛物线上是否存在三个点,由它构成的三角形与A4OC相似?直接与出两组这样的点•4[分析】(1>SHAC.根撮区]的李径求出AC. W1B点人的坐麻求出0A,燃后利用勾腹定理列式求出0C・从而得到点C的坐标,再求出ZCAO=60=.然后粮掘直有三甬形两锐角互余米出NB=30。
2024年中考数学综合与实践:圆、二次函数有关重难点题型

综合与实践、圆、二次函数有关重难点题型题型一综合与实践1.综合与实践问题情境:综合与实践课上,老师让同学们以“等腰直角三角形”为主题开展数学活动,并提出如下问题:如题2-1图,将等腰Rt△ABC的直角边AC与等腰Rt△ADC的斜边AC 重合,∠BAC=∠ADC=90°,试判断线段BC 与CD之间的数量关系,并加以证明.(1)数学思考:请你解答老师提出的问题;(2)猜想证明:如题2-2图,点 E 是线段AD上的一个动点(不与A,D重合),连接CE,过点 E作EF⊥CE,分别交AB,AC于F,G两点,连接FC,试判断△CEF的形状,并说明理由.2.综合与实践【阅读理解】如题1-1图,在△ABC中,AM是BC边上的高线,由勾股定理得AM²=AB²−BM²,AM²= AC²−CM²,故AB²−BM²=AC²−CM².【知识迁移】如题1-2 图,在矩形ABCD中,当点P在矩形ABCD内任意位置时,连接AP,BP,CP,DP.求证: AP²+ CP²=BP²+DP².【探索发现】如题1-3 图,若点 P在矩形ABCD 的外部时,上述结论是否仍然成立?请加以判断,并说明理由.【尝试应用】如题1-4图,在△ABC中, AB=3,AC=4,Q为平面内一点,且AQ=1,∠BQC=90°,求 BC 的最大值.3.如题1-1图,正方形ABCD的边AB上有一点E,连接DE.(1)若AD=3AE,则sin∠ADE= ;(2)如题1-2图,将边 CB绕点 C顺时针旋转,旋转角为α,使得点 B 的对应点 F 落在DE上(点F不与点D 重合),连接BF,求∠BFE的度数;(3)如题1-3图,在(2)的条件下,若E为AB的中点,DF=n,正方形ABCD的面积为S,求S关于n的函数关系式.4.小颖在学习了摩擦力的相关知识后,准备在水平面上探究滑动摩擦力与压力之间的关系,探究步骤如下:第一步:如题3-1图,在一水平放置的木板上放置一个质量为1kg的木块(压力大小=重力大小),用弹簧测力计沿水平方向拉动木块,使木块做匀速直线运动(滑动摩擦力的大小可以由弹簧测力计读出);第二步:在木块上增加质量不同的砝码,使木块做匀速直线运动;当在木块上增加质量不同的砝码后,设弹簧测力计所拉物体的质量为m(kg),弹簧测力计的示数为F(N),通过多次测量,得到如下数据:(1)把表中的图的坐标系中,描点,连线,画出弹簧测力计拉力F关于物体质量m的图象;(2)观察所画的图象,猜测F和m之间的函数关系,求出函数表达式;(3)小颖将水平拉动木块实验变成在斜面拉动木块实验,如题3-3图,用弹簧测力计拉着木块分别沿倾斜程度不同的斜面向上做匀速直线运动.经测算,在弹性范围内,沿斜面的拉力 F(N)是高度h(m)的一次函数.当斜面水平放置在地面上时,弹簧测力计的读数为2N,高度h每增加0.1m,弹簧测力计的读数增加0.8N,若弹簧测力计的最大量程是8N,求装置高度h的取值范围.5.综合与实践某数学实验小组在学习了电阻的知识后,计划通过实验探究铂电阻在0∼100°C范围内的温度特性,具体过程如下:【知识背景】电阻温度计是根据导体电阻随温度而变化的规律来测量温度的温度计,铂电阻温度计是最精确的温度计.【实验过程】如题2-1图,将电阻温度计接入电路,开始使导体温度升温,控制温度在( 0°C−100°C范围内,每升温20°C记录一次指示仪表输出的电阻值(单位:Ω),实验完毕后,关闭所有电源.【收集数据】记录的数据如下表:(1)如题2-2图,建立平面直角坐标系,横轴表示温度( (°C),纵轴表示电阻值(Ω),描出以上表中的数据为坐标的各点,并进行连线;(2)观察上述各点的分布规律,判断它们是否在同一条直线上,若在同一条直线上,请你建立适当的函数模型,并求出解析式,若不在同一条直线上,请说明理由;(3)当温度为50°C时,求铂电阻的电阻值.题型二圆的综合题1. 如题1图, △ABC内接于⊙O,AB是⊙O 的直径,分别过点 C 作⊙O 的切线,过点 O作AB的垂线,两线相交于点 D.(1)求证: ∠D=2∠A;(2)请用无刻度的直尺和圆规过点O 作AC 的垂线交AC 于点 E(保留作图痕迹,不写作法);(3)在(2)的条件下,若AB=8,CD=3,求OE的长.2. 如题2图, △ABC内接于⊙O,延长BA至点D,连接DC,使DB=DC,过点A作AE⊥AB交DC于点E,连接B E,BE 与AC相交于点F,且满足∠ADE=2∠EAC.(1)求证:CA=CB;(2)若AD:AB=1:4,求tan∠ABC的值;的值.(3)在(2)的条件下,求AFFC3.如题1-1图, △ABC内接于⊙O,BC是⊙O的直径,CD是∠ACB的平分线,交⊙O 于点D,连接OD,交AB于点E.(1)求证:OD∥AC;,求直线AF与⊙O的位关系.(2)如题1-2图,延长OD至点 F,连接AF,使得AF=BC,且tanB=12在△ABC中,AB=AC,点O是AB边上一动点,以点O为圆心,OB长为半径作圆,交BC于点 D.过点 D作DE⊥AC,垂足为E.(1)如题2-1图,若点O为AB的中点,求证:BD=CD;(2)如题2-2图,当点O为AB 上任意一点时,求证:DE 与⊙O 相切;(3)如题2-3图,若⊙O与AC相切于点F,且⊙O的半径为3,CE=1,求AF的长.如题4图,四边形ABCE内接于⊙O, AB=AC,CE⊥BC,,过点A作BC的平行线交CE的延长线于点 D.(1)求证:AD是⊙O的切线;(2)若DE=2,AE平分∠CAD,求⊙O的半径;(3)新考法探究线段数量关系若( CE=m,DE=n,⊙O的直径为d,探究m,n与d的数量关系,并说明理由.题型三二次函数综合题1. 已知抛物线y₁=ax²−4ax+c经过点(3,−2),与x轴交于点A(x₁,0),B两点.(1)若抛物线过点(−1,2),求抛物线的解析式;(2)若−1<x₁<0,点P(5,n)(n⟩0))在该抛物线上,求a的取值范围;(3)若抛物线y₁向上平移两个单位长度后得到抛物线y₂,抛物y₁与直线y₁=kx+b(k≠0)交于点(x₁,0)(x₁<2),且函数y=y₁+y₁的图象与x轴仅有一个交点.求证:k=2a.2.如题2图,在平面直角坐标系中,抛物线y=−x²+bx+c交x轴于A,B(1,0)两点,交y轴于点C(0,3),连接AC,BC.(1)求抛物线的解析式;(2)N是线段AC上一点,过点N作NN′⊥x轴于点N′,若△ABC的面积被 NN'分为1∶2的两部分,求点N 的坐标;(3)将抛物线向左平移m(m⟩0))个单位长度,与原抛物线的交点为点 D,连接 AD,BD,AC 与 BD 相交于点 E,若△ADE与△BCE的面积差为1,求m的值.3.已知抛物线y=25x2+bx+c的顶点坐标为(−2,185),与x轴交于点A,B(点A在点 B左侧),与y轴交于点C.(1)求b,c的值;(2)点M(-4,2),N是抛物线上两点,若点N到对称轴的距离等于点M到对称轴距离的2倍,求点 N的坐标;(3)若点 P是第二象限内抛物线上一点,连接PB交AC于点D,求PDBD的最大值.x−3与x轴,y轴交于A,B两点,抛物线y=x²+bx+c经过A,B两点,M是射线4.如题2图,直线y=34BA上一动点,过点 M作MN∥y轴交抛物线于点 N.(1)求抛物线的解析式;(2)当M在线段BA上时,连接AN,BN,若S∆ABN=S∆ABO,求此时点M的坐标;(3)新考法与点的运动结合点M从点 B 出发,沿射线BA方向以每秒5个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,MB=MN?请直接写出所有符合条件的t值.5.如题3图,在平面直角坐标系中,已知抛物线y=ax²+bx−2(a≠0)与x轴交于点A(−1,0),B(0),与y 轴交于点 C,点P为直线BC下方抛物线上一动点.(1)求抛物线的解析式;(2)过点P作PE⊥x轴于点 E,连接OP,是否存在点 P 使得. ∠OPE=∠ABC?若存在,求出点的横坐标;若不存在,请说明理由;(3) 将抛物线沿着x轴翻折,点P 的对应点为P′,连接P'B,求△P′CB面积的最大值及此时点 P的坐标.。
二次函数压轴题(与圆综合问题)

二次函数压轴题(与圆综合问题)【典例分析】例1 如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C 三点的圆与y轴的另一个交点为D.(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);①求此抛物线的函数解析式;②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;(2)如图2,若a=1,c=-4,求证:无论b取何值,点D的坐标均不改变.思路点拨(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,可得C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,根据根与系数的关系可得OA•OB=4.由A、D、B、C四点共圆可得∠ADC=∠ABC,∠DAB=∠DCB,从而可得△ADO∽∽△CBO,根据相似三角形的性质可得OC•OD=OA•OB=4,从而可得OD=1,即可得到D(0,1),因而无论b 取何值,点D的坐标均不改变.满分解答(1)①∵抛物线y=ax2+bx+c过点A(-2,0),B(8,0),C(0,-4),∴42064804a b ca b cc-+=⎧⎪++=⎨⎪=-⎩,解得14324abc⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩.学#科网∴抛物线的解析式为y=14x2-32x-4;②过点M作ME∥y轴,交BD于点E,连接BC,如图1.∴D(0,4).设直线BD的解析式为y=mx+n.∵B(8,0),D(0,4),∴804m nn+=⎧⎨=⎩,学&科网解得124mn⎧=-⎪⎨⎪=⎩,(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,则C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,∴OA•OB=-x1•x2=-(-4)=4.考点:圆的综合题例2已知抛物线经过A(3,0), B(4,1)两点,且与y轴交于点C.(1)求抛物线的函数关系式及点C的坐标;(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB 于点F,当△OEF的面积取得最小值时,求点E的坐标.思路点拨(1)用待定系数法求解;(2) 假设存在,分两种情况讨论(3)根据面积公式,列出二次函数,求函数的最值.满分解答(1)将A(3,0),B(4,1)代人得∴∴∴C(0,3) 学科@网②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P. ∵A(3,0),C(0,3)∴直线AC的函数关系式为将直线AC向上平移2个单位与直线BP重合.则直线BP的函数关系式为由,得又B(4,1),∴P2(-1,6).综上所述,存在两点P1(0,3), P2(-1,6).(3)∵∠OAE=∠OAF=45O,而∠OEF=∠OAF=45O, ∠OFE=∠OAE=45O,∴∠OEF=∠OFE=45O,∴OE=OF,∠EOF=90O∵点E在线段AC上,∴设E∴=∴===∴当时,取最小值,此时,∴例3如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.(1)求D点的坐标和圆D的半径;(2)求sin∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;(3)设抛物线的顶点为F,证明直线AF与圆D相切.思路点拨(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.依据垂径定理可知AE=3,然后依据切线的性质可知CD⊥y轴,然后可证明四边形OCDE为矩形,则DE=4,然后依据勾股定理可求得AD的长,故此可求得⊙D的半径和点D的坐标;学科.网(2)先求得A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入可求得a 的值.根据三角形面积公式得:S△ABC=BC×AC sin∠ACB=AB×CO,代入计算即可;(3)求得抛物线的顶点F的坐标,然后求得DF和AF的长,依据勾股定理的逆定理可证明△DAF为直角三角形,则∠DAF=90°,故此AF是⊙D的切线.满分解答(2)如图1所示:∵D(5,4),∴E(5,0),∴A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a,∴抛物线的解析式为y x 2x +4.∵S △ABC =BC ×AC sin ∠ACB =AB ×CO ,∴sin ∠ACB ==.例4如图,已知二次函数()22y x m 4m =--(m >0)的图象与x 轴交于A 、B 两点.(1)写出A 、B 两点的坐标(坐标用m 表示);(2)若二次函数图象的顶点P 在以AB 为直径的圆上,求二次函数的解析式; (3)设以AB 为直径的⊙M 与y 轴交于C 、D 两点,求CD 的长. 思路点拨(1)解关于x 的一元二次方程()22x m 4m 0--=,求出x 的值,即可得到A 、B 两点的坐标。
中考数学复习:二次函数和圆的综合题(含答案)
1 二次函数和圆中考综合题【例题1】已知圆P 的圆心在反比例函数ky x =(1)k >图象上,并与x 轴相交于A 、B 两点.且始终与y 轴相切于定点C (0,1).(1)求经过A 、B 、C 三点的二次函数图象的解析式; (2)若二次函数图象的顶点为D ,问当k 为何值时,四边形ADBP 为菱形.【例题2】在平面直角坐标系中,四边形OABC 是矩形,是矩形,OA=4OA=4OA=4,,AB=2AB=2,直线,直线32y x =-+与坐标轴交于D 、E 。
设M 是AB 的中点,的中点,P P 是线段DE 上的动点上的动点. .(1)求M 、D 两点的坐标;(2)当P 在什么位置时,在什么位置时,PA=PB PA=PB PA=PB?求出此时?求出此时P 点的坐标;(3)过P 作PH PH⊥⊥BC BC,垂足为,垂足为H ,当以PM 为直径的⊙为直径的⊙F F 与BC 相切于点N 时,求梯形PMBH 的面积的面积. .【例题3】在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y 轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B.的解析式;(1)求直线CB的解析式;(2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x轴的交点恰为点E、F,求该抛物线的解析式;,求该抛物线的解析式;(3)试判断点C是否在抛物线上?是否在抛物线上?相似?直接写出两组这样的点. (4)在抛物线上是否存在三个点,由它构成的三角形与△AOC相似?直接写出两组这样的点.【例题4】如图,已知抛物线y= ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E.的值及抛物线的解析式;(1)求m的值及抛物线的解析式;(a-b)的值;)的值;sin((2)设∠DBC = a,∠CBE = b,求sin(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指的坐标;若不存在,请说明理由.出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.【例题5】如图,点M (4,0),以点M 为圆心、为圆心、22为半径的圆与x 轴交于点A 、B .已知抛物线216y x bx c =++过点A 和B ,与y 轴交于点C .(1)求点C 的坐标,并画出抛物线的大致图象.的坐标,并画出抛物线的大致图象.(2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.最小值.(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.所在直线的解析式.【例题6】如图所示,如图所示,在平面直角坐标系中,在平面直角坐标系中,M 经过原点O ,且与x 轴、y 轴分别相交于A (-8,0),B (0,-6)两点.)两点.(1)请求出直线AB 的函数表达式;的函数表达式;(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,且经过点B ,求此抛物线的函数表达式;函数表达式;(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上是否存在点P ,使得115PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.(4)点H 是抛物线对称轴上的一个动点,且在点M 的下方,请问抛物线上是否存在另一点Q ,使得△ABH 与△ABQ 全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
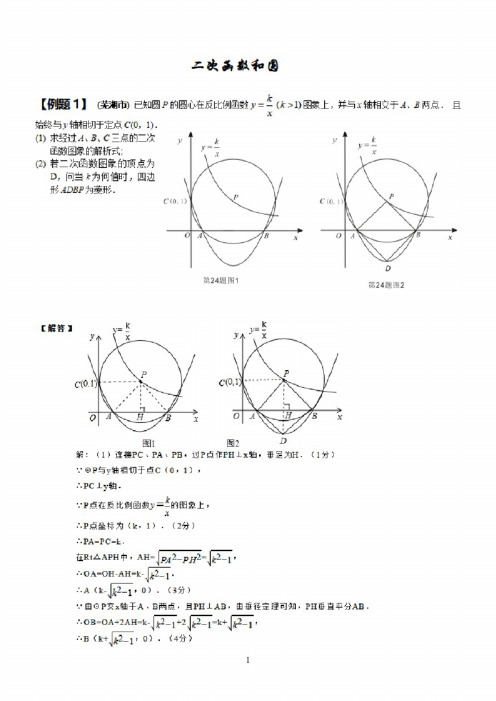
过点A 和 B,则
解得
4 b , 3 c 2.
y
(2,0)(6,0)
则抛物线的解析式为:
故 C(0,2).
C
l P
(2)如图①,抛物线对称轴l是x=4. ∵ Q(8,m)抛物线上,∴ m=2. O 过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
Q
A
E
D
M
x B K
初中数学九年级上册
二次函数与圆综合题
展示讨论
1.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点 1 y x bx c 过点A和B,与y轴交于点C. A,B.已知抛物线 6 ⑴ 求点C的坐标,并画出抛物线的大致图象.
2
⑵ 点Q(8,m)在抛物线 动点,求PQ+PB 最小值.
C D A E 图② M x B
O
展示讨论
Байду номын сангаас
展示讨论
2.如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4 的圆交y轴正半轴于点A, AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度 的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的 速度运动,且动点P、Q从点A和点O同时出发,设运动时间为 t(秒). ⑴当t=1时,得到P1、Q1两点,求经过A、 P1、Q1三点的抛物线解析式及对称轴l; ⑵当t为何值时,直线PQ与⊙C相切?并 写出此时点P和点Q的坐标; ⑶在⑵的条件下,抛物线对称轴l上存在 一点N,使NP+NQ最小,求出点N 的坐标 并说明理由.
1 y x2 bx c 上,点P为此抛物线对称轴上一个 6
⑶ CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.
解:(1)由已知,得 A(2,0),B(6,0),
∵ 抛物线
1 2 6 2 2b c 0, 1 62 6b c 0, 6
展示讨论
y
O
x l
展示讨论
C y D O B 5 x A 图1
1
展示讨论
展示讨论
y P C O 1 A B x
展示讨论
y D M A C G O E B F x
展示讨论
y
O A C
O'
B x
D E
图①
展示讨论
y
(3)如图②,连结EM和CM. 由已知,得 EM=OC=2. CE是⊙M的切线,∴ ∠DEM=90º ,则 ∠DEM=∠DOC. 又∵ ∠ODC=∠EDM. 故 △DEM≌△DOC. ∴ OD=DE,CD=MD. 又在△ODE和△MDC中,∠ODE=∠MDC, ∠DOE=∠DEO=∠DCM=∠DMC. 则 OE∥CM.
