Maple变量管理的简单操作介绍
怎样用Maple给数学式赋值

怎样用Maple给数学式赋值怎样用Maple给数学式赋值利用Maple解决数学问题时,中间会涉及到很多计算过程。
对于比较简单的计算过程时可以直接用Maple计算,但多数情况下问题会比较复杂,需要对变量进行赋值计算。
在Maple 使用的过程中,如何进行赋值计算呢?更多Maple入门操作及使用技巧请访问Maple 2015中文版官网。
赋值当输入表达式或完成计算后,用户可以将结果赋值(分配)给一个变量名。
示例:1.输入表达式(x+2y)3,输完后鼠标右击,从右键菜单中选择“Expand”。
2.鼠标右击输出x3+6x2y+12xy2+8y3从右键菜单中选择“Assign to a Name”,输入“Answer1”。
在接下来的操作中,用户可以使用这个命名引用结果,使用它完成进一步的计算。
先输入要赋值的语句,再输入“:”、“=”(冒号,等于号),再输入数值就将右边部分赋值给左边的变量名了。
示例:赋值给“value1”和“value2”,然后相加它们。
显示和隐藏结果某些情况下,我们不希望显示赋值语句的结果。
为了隐藏Maple 操作的结果,在输入语句的后面加上一个冒号(:)。
示例:赋值给a1,不显示结果。
按照上面操作进行输入,最后记得要输入“:”,然后计算a12。
清除变量赋值,使用unassign命令。
注意必须使用单引号('')封装变量名。
以上内容向大家介绍了Maple计算数学赋值时的一些常见用法,Maple初级用法是比较简单的,只有掌握了这些简单的用法才能一步步地熟练掌握。
如果需要了解更多Maple使用教程,可以参考Maple 中文官网教程:强大的数学计算——Maple内置函数包简介。
Maple入门手册(1)

绘制多图 我们经常喜欢同时显示多个图。其中一种方法是,给绘图函数一列要绘制的表达式组或函数 。 先将表达式或函数列出来,然后列出范围。如果你想用不同颜色来表示不同的表达式,你可 以使用关键词“color”来按对应顺序定义图形颜色。
要想得到函数值,输入函数名和变量值。用 f(x)的形式计算,f 是函数名,x 是设置的变量 值。
定义多变量函数: 多变量函数的定义和单变量函数定义非常相似。唯一的不同是,多变量函数有更多独立变量 。 在下面的例子中,函数名士 f,有两个独立变量 x 和 y。假如,我们要定义这样一个多变量 函数 f(x,y)=x^2+y^2
展开表达式 expand 函数可以展开含有相乘项的表达式。展开并不是总会使得原表达式更复杂。相反, 在很多情况下,它可以的到简化解。
分解因式 这个函数是展开函数的逆运算,它可以将多项式因式分解。
6
本稿由 哈尔滨工程大学船舶工程学院 张崇伟 制作,免费学术共享,禁止用于商业目的。
通分约分 如果表达式包含分数,那么有必要通分约分重新构造一个分数。normal 函数可以实现这一 过程。
12
3、数值计算
Maple 可以做浮点型、整型和复数型的计算。 浮点型数值计算 Maple 的一个重要的性质就是做准确数学计算的能力:在浮点近似中有效数字不会减少。这 样舍入误差就可被避免。 例子:五舍入误差计算
如果需要得到近似值,可使用 evalf 函数将准确的结果转化为近似浮点数解。 例子:把准确结果转化成近似浮点数解
第二讲_Maple初步和应用续

第二部分 Maple 的简单应用
单种群模型的解析求解和稳定性分析
dN (t ) dt
= rN ( t )[1 −
N (t ) k
]
dN (t ) dt
= N(t)[r − ln(N(t)/ k)]
单种群模型的解析求解和稳定性分析
> dsolve({diff(x(t),t)=r*x(t)*(1-x(t)/K),x(0)=x0});
Holling prey-predator model with limit cycles
> with(DEtools): Example of a system of two autonomous first order differential equations: > dfieldplot([diff(x(t),t)=x(t)*(0.1+1.2*x(t)-0.5*x(t)^2)-x(t)*y(t), diff(y(t),t)=y(t)+x(t)*y(t)], [x(t),y(t)],t=-2..2, x=0..3, y=0..2, arrows=LARGE, title=`Lotka-Volterra model`, color=[x(t)*(0.1+1.2*x(t)-0.5*x(t)^2)-x(t)*y(t),y(t)+x(t)*y(t),.1]);
{ x = 0 }, { x = K }
程序 Logisticequ.mws
强调求解功能强大
第二功能性反应函数与捕食被捕食系统
dx α xy = x ( a − b x ) − 1+ ω x dt dy eα x y = y ( − d + 1+ ω x ) dt
数学软件Maple使用教程

数学软件Maple使⽤教程数学实验数学软件Maple使⽤教程序⾔⼀.什么是数学实验?我们都熟悉物理实验和化学实验,就是利⽤仪器设备,通过实验来了解物理现象、化学物质等的特性。
同样,数学实验也是要通过实验来了解数学问题的特性并解决对应的数学问题。
过去,因为实验设备和实验⼿段的问题,⽆法解决数学上的实验问题,所以,⼀直没有听说过数学实验这个词。
随着计算机的飞速发展,计算速度越来越快,软件功能也越来越强,许多数学问题都可以由计算机代替完成,也为我们⽤实验解决数学问题提供了可能。
数学实验就是以计算机为仪器,以软件为载体,通过实验解决实际中的数学问题。
⼆.常⽤的数学软件⽬前较流⾏的数学软件主要有四种:1.MathACD其优点是许多数学符号键盘化,通过键盘可以直接输⼊数学符号,在教学⽅⾯使⽤起来⾮常⽅便。
缺点是⽬前仅能作数值运算,符号运算功能较弱,输出界⾯不好。
2.Matlab优点是⼤型矩阵运算功能⾮常强,构造个⼈适⽤函数⽅便很⽅便,因此,⾮常适合⼤型⼯程技术中使⽤。
缺点是输出界⾯稍差,符号运算功能也显得弱⼀些。
不过,在这个公司购买了Maple公司的内核以后,符号运算功能已经得到了⼤⼤的加强。
再⼀个缺点就是这个软件太⼤,按现在流⾏的版本5.2,⾃⾝有400多兆,占硬盘空间近1个G,⼀般稍早些的计算机都安装部下。
我们这次没⽤它主要就是这个原因。
3.Mathematica其优点是结构严谨,输出界⾯好,计算功能强,是专业科学技术⼈员所喜爱的数学软件。
缺点是软件本⾝较⼤,⽬前流⾏的3.0版本有200兆;另⼀个缺点就是命令太长,每⼀个命令都要输⼊英⽂全名,因此,需要英语⽔平较⾼。
4.Maple优点是输出界⾯很好,与我们平常书写⼏乎⼀致;还有⼀个最⼤的优点就是它的符号运算功能特别强,这对于既要作数值运算,⼜要作符号运算时就显得⾮常⽅便了。
除此之外,其软件只有30兆,安装也很⽅便(直接拷贝就可以⽤)。
所以,我们把它放到学校⽹上直接调⽤。
利用Maple计算数学的常见命令

Maple工作表左侧的20个面板含有1,000多个符号。用户也可以使用Maple面
板输入数据,面板含有用于常规操作的填充模版。
示例:使用微积分面板求表达式4t6+sin(t)的积分。
操作过程:
打开“微积分”面板,然后点击不定积分的模板。一个不定积分模版将出当前工作表中。在占位符处输入被积表达式,完成后,按下回车键计算。
区分大小写
Maple区分大小写,X,x表示不同的变量名。
示例:输入“x+x”。输入“y+Y”。对比一下输出结果。
隐式乘号
Maple能够理解隐式乘号,项之间的空格理解为乘号。
示例:</strong>键入“3x”隐含的意思为“化表达式,在不同的项之间加入了空格。
示例:使用表达式面板用于求解函数的极限。
操作过程:将光标移到要工作的位置,点击极限表达式,在占位符中填入表达式,完成后按回车键计算。
提示:可以将经常要用的面板项移到收藏夹中。操作方式是鼠标右击面板按钮,然后选
择添加到收藏夹面板中。
符号和命令补全
符号和命令补全机制帮助用户完成符号和命令的输入。键入符号名称开始的几个字符,按下“Esc”键,从弹出的下拉菜单中选择需要的符号。
示例:对表达式y=ex绘图,使用符号补全方式创建指数e。
操作过程:
1.利用面板输入ab模板,在a处输入“e”,再按下“[Esc]”键,然后从列表中选择“exponential‘e’”,在b处输入x,按下回车键。
2.使用右键菜单对表达式绘图,选择“Plots—2-D Plot”。
一些命令补全模板提供Maple命令的调用格式,方便我们快速输入正确的语法命令。
利用maple计算数学的常见命令在进行数学论文撰写时会根据具体的问题来对数学问题进行求解计算
Maple简介

Maple简介一、Maple操作界面介绍1、编辑功能:编辑功能中查找模块,可以帮助查找你所需要的关键字节.具体操作如图所示:按上述操作完成后,出现下图所示的对话框:在文本框中输入你要查找的字符或者符号,可以通过findprevious上下翻看,也可以通过replacewith操作替代你所查找的字符或者符号.cancle表示取消操作.其他编辑操作包括分割或连接(splitorjoin)分为一个执行过程(快截键为f3、f4)和选定块(shift+f3、shift+f4)过程四个操作块运行操作(Execute):运行选定或者当前的maple中的语句;删除运行结果操作(Removeoutput):将选定或者当前的maple中运行结果从工作爷中删除或者不显示;2、示图操作( VIEW)文档在屏幕上的显示模式称为“示图”,maple示图菜单主要设置工作爷文档的一些视图属性,所包括菜单如上图所示。
工具条(toolbar)的功能和其他系统一样,主要包括打开文件、创建新文档、存盘、打印当前页面、复制、剪切、粘贴、撤消操作等。
内容工具条:“枫叶”表示设置工作页和标准公式和maple语言之间的转换“X”表示设置工作页和标准公式在活动和非活动方式之间的转换“(对号)”表示标准公式有效时自动检查输入表达式的正确性“!”表示运行当前表达式3、插入操作(INSERT)插入操作比较简单这里就不做详细介绍,主要功能分为:文本插入(textinput);标准maple数学表达式插入;运行单元executegroup插入其中包括在光标前插入和光标后插入图形插入plot,其中包括两维和三维图象的插入电子表格插入spreadsheet段落插入parigraph,其中包括光标前插入和光标后插入数学输入对象(image)插入插入超级连接hyperlink4、其他操作窗口的功能和其他软件基本相同,这里就不做详细介绍了。
二、基本语法规则MaPle的科学计算功能主要是以命令输入的方式来实现的。
Maple用法

Maple函数用法一、基本命令重新开始:restart 命名:名字:= 引用前值:% 字符连接:|| 保护命名:protect 解除保护命名:unprotrct 变量类型:whattype 检验命名:assigned 别名:alias 宏:macro 帮助:?函数名map把命令作用到每一个元素,seq生成序列,add生成和,mul生成积二、基本运算1. 近似计算:evalf(表达式,小数位数),用Digits命令提前设定小数位数2. 取整运算:round四舍五入,trunc向0取整, ceil向-∝取整, floor向∝取整3. 范围限定:assume(限定变量范围)frac小数部分4. 绝对值(模):abs(表达式),复数求其模5. 同余:mod(数1,数2),或者:数1 mod 数26. 平方根:sqrt(表达式),平方根最接近整数:isqrt(表达式)7. 阶乘:factorial(数),双阶乘:doublefactorial(数)8. 分解质因数:ifactor(数),分解质因数成组ifactors(数)9. 商与余数:商iquo(除数,被除数),余数irem(除数,被除数)10.最大公约数:igcd(数1,数2),最小公倍数:ilcm(数1,数2)11.形如as+bt=(a,b)分解:igcdex(a,b,’s’,’t’)12.数组最大最小值:max(数1,数2,…),min(数1,数2,…)13.实部、虚部与幅角:实部Re(复数),虚部Im(复数),幅角argument14.共轭复数:conjugate(复数)15.形如a+bi整理:evalc(表达式)16.并集:集合1 union 集合2,交集:intersect,差集:minus17.元素个数:nops(集合),用op可把集合转化成表达式三、多项式1. 降幂排列:sort(多项式),字典排序plex(第三个参数)2. 次数:degree(多项式),系数:coeff(多项式,项),首项系数:lcoeff尾项系数:tcoeff,所有系数:coeffs(多项式,变量,‘power‘)3. 合并同类项:collect(多项式,合并参数)4. 商式:quo(除式,被除式,变量),余式:rem,整除检验:divide5. 最大公因式:gcd(多项式1,多项式2),最小公倍式lcm6. 因式分解:factor(多项式),可用第二个参数限定数域缺省代表有理数域7. 分母有理化:rationalize(多项式),有理分式化简:normal或者factor8. 化简表达式:simplify,带假设化简:simplify(表达式,assume=范围)附加关系化简:simplify(表达式,{条件})代换:subs(条件,表达式)9. 展开与合并:展开expand(表达式),合并combine(表达式)10.等价转换:convert(函数,转化成的函数)四、解方程1. 方程(组):solve({方程(组)},{未知量(缺省对所有变量求解})2. 数值解:fsolve(方程,变量范围(可缺省),数域(可缺省))3. 三角方程:添加_EnvAllSolutions:=ture以求得所有解4. 多项式方程解的区间:realroot(多项式)5. 不等式(组):solve({不等式(组)},{变量})6. 整数解:isolve(方程,变量)7. 模m的解:msolve(方程,模m)8. 递推关系的通项:rsolve({递推关系,初值},{通项})9. 函数方程:solve(函数方程,函数)10.系数匹配:match(式子1=式子2,变量,’s’)11.Grobner基原理:先调用with(grobner),此命令将方程的解等价化简Gsolve({式子1,式子2,…},[变量1,变量2,…]12.微分方程:dsolve({方程,初值(可缺)},函数,’explicit’(可缺))13.微分方程组:dsolve({方程1、2,…,初值},{函数1,函数2,…})14.拉普拉斯变换法:dsolve({微分方程},函数,method=laplace)15.微分方程级数解:dsolve({微分方程},函数,type=series)16.微分方程数值解:dsolve({微分方程},函数,type=numeric)17.微分方程图形解:DEplot图形表示微分方程,dfielplot箭头表示向量场,phaseportrait向量场及积分曲线,DEplot3d三维空间图形表示微分方程18.偏微分方程:pdsolve(偏微分方程,求解函数)19.分离变量解偏微分方程:pdsolve(方程,函数,HINT=’*’,’build’)20.偏微分方程图形解:PDEplot(方程,函数,ini边界s,s范围)五、数据处理1. 统计软件包:先调用程序包with(stats) ,有7个子包:anova方差分析,describe描述数据分析,fit拟合回归分析,transform数据形式变换,random分布产生随机数,statevalf分布的数值计算,statplots统计绘图2. 基本命令:平均值mean,方差variance,标准差standarddeviation,中位数median,众数mode,数据求和sumdata,协方差covariance,相对标准差(标准差/平均值)coefficientofvariation,计数(非缺失)count,计缺失数countmissing,范围range,几何平均值geometricmean,线性相关数linearcorrelation3. 统计图形:直方图histogram,散点图scatter2d、quantile2(先从小到大排序再作图),箱式图boxplot4. 统计分布函数值:正态分布随机分布命令normald[期望,方差]先调用程序包with(statevalf)用法statevalf(分布函数,求解函数)连续分布:cdf累积密度函数,icdf逆累积密度函数,pdf概率密度函数离散分布:dcdf离散累积概率函数,idcdf逆离散累积函数,pf概率函数5. 插值:整体插值命令f:=interp(数据1,数据2,变量)分段插值命令f:=spline(数据1,数据2,变量,次数)6. 回归:leastsquare[[x,y],y=多项式,{多项式系数}]([数据1,数据2]) f:=fit(数据1,数据2,拟合函数,变量)六、微积分1. 函数定义:函数名:=->表达式,复合函数:f(g(x)):=f@g2. 表达式转换成函数:unapply(表达式,函数变量)3. 极值:极大值maximize(函数,变量,范围,location=true(极值点))极小值 minimize(函数,变量,范围,location=true(极值点))条件极值:extreme(函数,约束条件,{变量},’s’(极值点))4. 极限:limit(函数,x=趋值,方向(省缺,left,right,complex))5. 连续性:判断iscont(函数,x=范围)第三个参数closed表示闭区间求解discont(函数,变量)6. 微分:显函数diff(函数,变量)对x多次求导用x$n 微分算子D隐函数implicitdiff(函数,依赖关系y(x),对象y,变量x)7. 切线作图:showtangent(函数,x=点,view=[x范围,y范围])8. 不定积分:int(函数,积分变量),定积分:int(函数,x=下限..上限)9. 复函数积分:先求奇点solve(denom(函数)),再用留数规则求解2*Pi*I(residue(f,z=奇点1)+ residue(f,z=奇点2)+…)10.定积分矩形:下矩形:作图leftbox(f,x=范围,块数)面积leftsum(f,x=范围,块数)。
《Maple》使用手册

O O O O (1.7)(1.3)(1.2)O (1.13)(1.9)(1.14)(1.15)(1.1)O O O (1.8)(1.5)(1.12)(1.10)O O O O O O (1.6)(1.11)(1.4)O 第1章 Maple的基本量1.1数值类型whattype 0integerwhattype12fractionwhattype 0.floatconstants;false ,γ,N ,true ,Catalan ,FAIL ,πwhattype falsesymbolwhattype infinityextended_numericwhattype πsymbolwhattype undefinedextended_numericwhattype arcsin 1`*`whattype sqrt 2`^`whattype ln 2functionwhattype Icomplex extended_numericwhattype "ustc"stringwhattype 'ustc 'symbolwhattype ustcsymbolO (2.1)O (1.16)O (2.3)O (1.19)O O (2.2)O O O (1.21)O (1.20)O O (1.18)O O O (1.22)(1.17)类型转化convert 65535,hexFFFFconvert FFFF ,decimal ,1665535convert FFFF ,decimal ,88775Why?evalf π3.141592654evalf 20π3.1415926535897932385floor π,round π,ceil π3,3,4convert evalf π,string"3.141592654"1.2赋值x d 1x :=1y ,z d 2,3y ,z :=2,3z3y ,z d 2,3Error, illegal use of an object as a namey ,z d 2,3清除unassign xError, (in unassign) cannot unassign `1' (argument must be assignable)unassign "x"Error, (in unassign) cannot unassign `x' (argument must be assignable)unassign 'x 'x d 1; x d 'x ';x(2.8)(2.11)O O(2.9)(2.12)O O O (2.13)O (2.4)(2.7)(2.6)O O (2.10)O O (2.5)x :=1x :=x x替换x ,y d sqrt 2,sqrt 3x ,y :=2,3subs x =a ,y =b ,x y13a b Why?subs x =y ,y =x ,x y1Why?unassign 'x ','y 'subs x =a ,y =b ,x ya bsubs x =y 2,y =x 2,x yx 2subs y =x 2,x =y 2,x y1y2algsubs x C x 2=y ,1C x4x C 14algsubs x C x 2=y ,1C 2 x C x 221C 2 x C x 22algsubs x C x 2=y ,1C 4 x C 6 x 2C 4 x 3C x 41C 3 y C y 2C 1C 2 y x1.3定义O OO O O (3.5)(4.2)O O (4.3)(3.2)O O (3.1)(3.4)(4.4)O (3.7)(4.1)(3.3)O O (4.5)(3.6)O (3.8)a ,b ,cd 1,2,3a ,b ,c :=1,2,3f d x /a x 2C b x C c f :=x /a x 2C b x C cg d x ,y /x yg :=x ,y /x y注意:此处(x,y)的括号不可省。
Maple软件的介绍 使用方法

二、用Maple绘图(8)
其他一些命令
序列:x:=1,2,3;or x:=seq(sin(t),t=1..5); 列表:x:=[1,2,3];or x:=[seq(sin(t),t=1..5)]; 集合: x:={1,2,3};or x:={seq(sin(t),t=1..5)}; 求和:sum(k^2,k=1..100); 求项数:nops(expr); 提取表达式中的操作数:op(i,expr);or op(i..j,expr); 拟合: With(CurveFitting); LeastSquares([[],…,[]],t);
一、基本概念和操作(2)
• Maple“内核”在进行运算的同时,也会将当前 的运行环境变量保存起来。 • 当同时处理多个工作表时,有两种运行模式可 供用户选择:共享“内核” 、独占“内核” 。 • 共享“内核”模式:在一个工作表中定义的变 量可同样在其它已经打开的工作表调用。这样, 百分号“ %”就代表刚刚计算得到的结果,而 与当前激活的工作表是哪一个无关。 • 独占“内核”模式:在一个工作表中定义的变 量仅仅在本工作表中有效,而不影响其它已经 打开的工作表。这样,百分号“ %”就代表当 前激活的工作表中刚刚计算得到的结果。
一、基本概念和操作(8)
命令: evalf:用来把非浮点数的计算结果或者表达式转 化为浮点数形式的近似结果。其基本的命令格 式为evalf(expr,n) expr:任意的算术表达式 n:计算结果的精度,当n缺省时采用环境变量 Digits的值
一、基本概念和操作(9)
simplify(expr):对计算的结果进行化简 combine(f):对数的乘积的合并 coeff(p,x,n)或coeff(p,x^n)以x为变量的 多项式p中x^n项的系数 degree(p,x):计算多项式p中变量x的最高次 数 sort(p,[x,y]):对多项式p按字典序排列 subs(x=a,expr):用表达式a替换表达式expr 中出现的所有子表达式x。 eval(expr,x=a) eval(name)完全求值命令
介绍Maple入门的一些常见操作

介绍Maple⼊门的⼀些常见操作介绍Maple⼊门的⼀些常见操作在学习使⽤Maple的过程中,对于刚刚接触Maple的⼈们来说,了解Maple计算数学的基本操作是很必要,这也是Maple⼊门基本操作之⼀。
下⾯就介绍Maple的⼀些常见的操作。
更多Maple使⽤教程请访问Maple中⽂版官⽹。
进⼊Maple窗⼝后,可以通过“帮助”菜单了解Maple的操作和使⽤⽅法。
输⼊数学表达式后,如果要进⾏数学运算,需要将光标放在要运算的数学表达式上,按回车键,或单击⼯具栏上的“执⾏所有选中的组”按钮,也可以单击⿏标右键,使⽤弹出的右键菜单求解数学问题。
Maple将每次输⼊纪录在案,输出将另起⼀⾏居中显⽰,后⾯⾃动附加⼀个标签。
提⽰:[>是Maple⾃动显⽰的命令⾏提⽰符,⽆需我们⼿⼯输⼊。
如要输出结果,可在运算表达式后“;”;如不要显⽰输出结果,则在运算表达式后加“:”。
Maple中的运算命令必须在英⽂模式下输⼊,不然Maple不能运算。
如果要删除单个⽂字,可以使⽤“Del”键,如果要删除整⾏,可以使⽤“Ctrl+Del”组合键,Maple的这⼀“超级删除”功能键可⽤于对复杂对象的整⾏删除操作。
当输⼊的数学表达式较长时,为了在窗⼝中看到整个数学表达式,可将光标停在任⼀运算符后⾯并按“Shift+Enter”组合键,便可使数学表达式换⾏。
如要同时计算⼏个数学表达式,实现⽅法有两种。
⼀种是在每个数学表达式后⾯加“;”,然后按回车键或者单击⼯具栏上的执⾏按钮。
例如:第⼆种是分别输⼊数学表达式并单击⼯具栏上的“执⾏整个⼯作表”按钮" alt="执⾏整个⼯,Maple将执⾏⽂件中的所有运算。
例如:Maple中许多操作和菜单与Word是⼀样的。
在以后操作中使⽤较多的打开、关闭、复制、存盘等与Word操作完全⼀致,⼤家⼀样操作就可以了。
以上内容向⼤家介绍了Maple⼊门时的基本操作,在Maple中编辑公式后怎样进⾏计算。
maple 教程

maple 教程
Maple是一种数学建模和计算软件,用于进行高级数学运算和数据分析。
它被广泛应用于科学研究、工程设计和教育教学等领域。
在使用Maple进行数学建模时,我们首先需要了解变量的定义和使用。
可以使用等号将数值或表达式赋值给变量。
例如,我们可以使用以下语句定义一个变量x,并将其赋值为3:
x := 3;
接下来,我们可以使用已定义的变量进行数学计算。
Maple支持各种基本数学操作,如加减乘除和幂运算。
例如,我们可以使用以下语句计算x的平方:
x^2;
除了基本的数学运算,Maple还支持各种复杂的数学函数和操作。
例如,我们可以使用以下语句计算x的正弦值:
sin(x);
此外,Maple还提供了丰富的数学函数库,包括三角函数、对数函数、指数函数等等。
可以使用这些函数来进行更复杂的数学计算。
在进行数据分析时,Maple提供了强大的数据处理和可视化功能。
可以使用Maple的数据结构和函数来处理和分析数据,
并使用图表来可视化数据结果。
总之,Maple是一种功能强大的数学建模和计算软件,具有广泛的应用领域。
通过学习Maple的基本语法和功能,我们可以进行高级数学运算和数据分析,从而更好地理解和应用数学知识。
Maple 入门教程
是一
例子:输入上面的方程(使用单引号作为 微分符号),为了验证它是一个微分方 程,从关联菜单中选择 Solve DE 求解。
标签 无论你何时使用【回车键】获得一个计算 结果,工作表将自动给出一个公式标签。 如果想引用前面的计算结果,使用 C t r l + L 并输入标签数字。
例子:将上面的结果 标签。
操作步骤
结果
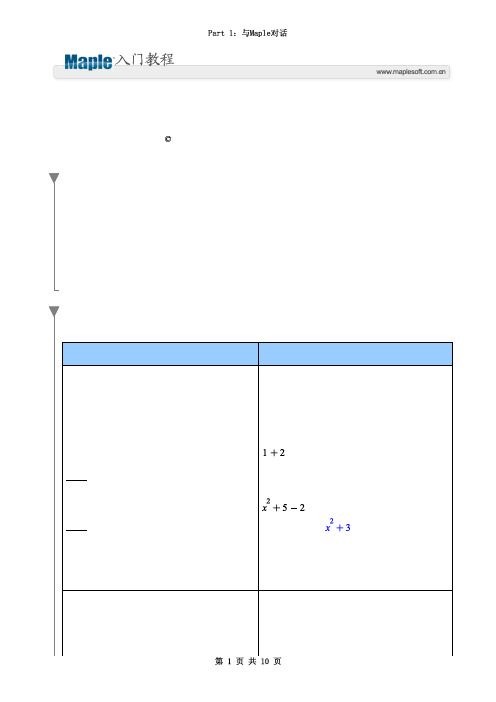
求精确解和数值近似 Maple 计算精确结果,也就是说,分数计算 时保持分数形式,e 和 在整个计算过程中 保留为符号形式。这些将减少在多步计算 中由于近似产生的误差。
例子:在新的一行,输入 1/2 + 1/3。 我们注意到光标 / 自动移到分母的位置。按 回车键得到计算结果。
Maple也可以计算数值近似解。 例子:鼠标右击上面的结果表达式,选择 关联菜单的Approximate,精度位选择 5。
例如," " 意思为 "x 乘以 y",但是 " " 表示一个名为" x y "的变量。
= =
=
= =
(3.4)
例子: 键入 " [ 空格]
".
如果你从右键菜单中选择Differentiate,你
将看到 x, y, 和 xy 被当作三个独立的变量。
如果你使用关联菜单选择 Differentiate,你 可以看到 x, y, 和 xy 被作为三个不同的变量 区别对待。
(3.15)
注意:在Maple中,任何想要获得求值结果 的表达式都必须为数学格式,任何文本格 式的表达式都是非执行语句。
(3.16) (3.17)
(3.18)
提示: 如何找到计算机系统下的快捷键,点击菜单 帮助 > 快速帮助,并选择 切换文本/数 学。
《Maple》使用手册

O O O O (1.7)(1.3)(1.2)O (1.13)(1.9)(1.14)(1.15)(1.1)O O O (1.8)(1.5)(1.12)(1.10)O O O O O O (1.6)(1.11)(1.4)O 第1章 Maple的基本量1.1数值类型whattype 0integerwhattype12fractionwhattype 0.floatconstants;false ,γ,N ,true ,Catalan ,FAIL ,πwhattype falsesymbolwhattype infinityextended_numericwhattype πsymbolwhattype undefinedextended_numericwhattype arcsin 1`*`whattype sqrt 2`^`whattype ln 2functionwhattype Icomplex extended_numericwhattype "ustc"stringwhattype 'ustc 'symbolwhattype ustcsymbolO (2.1)O (1.16)O (2.3)O (1.19)O O (2.2)O O O (1.21)O (1.20)O O (1.18)O O O (1.22)(1.17)类型转化convert 65535,hexFFFFconvert FFFF ,decimal ,1665535convert FFFF ,decimal ,88775Why?evalf π3.141592654evalf 20π3.1415926535897932385floor π,round π,ceil π3,3,4convert evalf π,string"3.141592654"1.2赋值x d 1x :=1y ,z d 2,3y ,z :=2,3z3y ,z d 2,3Error, illegal use of an object as a namey ,z d 2,3清除unassign xError, (in unassign) cannot unassign `1' (argument must be assignable)unassign "x"Error, (in unassign) cannot unassign `x' (argument must be assignable)unassign 'x 'x d 1; x d 'x ';x(2.8)(2.11)O O(2.9)(2.12)O O O (2.13)O (2.4)(2.7)(2.6)O O (2.10)O O (2.5)x :=1x :=x x替换x ,y d sqrt 2,sqrt 3x ,y :=2,3subs x =a ,y =b ,x y13a b Why?subs x =y ,y =x ,x y1Why?unassign 'x ','y 'subs x =a ,y =b ,x ya bsubs x =y 2,y =x 2,x yx 2subs y =x 2,x =y 2,x y1y2algsubs x C x 2=y ,1C x4x C 14algsubs x C x 2=y ,1C 2 x C x 221C 2 x C x 22algsubs x C x 2=y ,1C 4 x C 6 x 2C 4 x 3C x 41C 3 y C y 2C 1C 2 y x1.3定义O OO O O (3.5)(4.2)O O (4.3)(3.2)O O (3.1)(3.4)(4.4)O (3.7)(4.1)(3.3)O O (4.5)(3.6)O (3.8)a ,b ,cd 1,2,3a ,b ,c :=1,2,3f d x /a x 2C b x C c f :=x /a x 2C b x C cg d x ,y /x yg :=x ,y /x y注意:此处(x,y)的括号不可省。
学习如何使用Maple进行数学建模和计算

学习如何使用Maple进行数学建模和计算Maple是一款强大的数学软件,广泛应用于数学建模和计算上。
本文将介绍如何使用Maple进行数学建模和计算,并按照类别将其分为以下章节进行讲解。
第一章:Maple的基本操作在开始学习Maple之前,我们首先需要了解Maple的基本操作。
我们可以通过打开Maple软件,新建一个工作表开始操作。
在Maple中,我们可以进行基本的计算,如加法、减法、乘法和除法。
此外,Maple还支持各种数学函数和运算符的使用,如三角函数、指数函数和积分等。
第二章:使用Maple进行代数运算代数运算是数学建模的重要一环。
Maple可以进行代数表达式的简化,如合并同类项、展开式子和因式分解等。
此外,Maple还支持方程的求解和变量的替换,可以帮助我们轻松地解决代数问题。
第三章:使用Maple进行微积分计算微积分是数学建模和计算中的关键内容。
Maple可以进行函数的微分和积分计算。
我们可以通过使用Maple的微分函数对函数进行微分,并得到导数的表达式。
同样地,Maple也提供了积分函数,可以帮助我们求解各种类型的不定积分和定积分。
第四章:使用Maple进行数值计算在实际的数学建模和计算中,很多问题无法通过解析方法求解,而需要采用数值计算的方法。
Maple提供了丰富的数值计算函数,如求解方程组、数值积分和数值微分等。
我们可以使用这些函数快速解决实际问题,并得到数值结果。
第五章:使用Maple进行图形绘制数据的可视化对于数学建模和计算来说至关重要。
Maple可以绘制各种类型的函数图像和数据图表。
我们可以通过调用绘图函数,设置绘图参数和数据,得到漂亮的图形结果。
此外,Maple还支持图像的导出和保存,方便我们将图形结果用于报告和展示。
第六章:使用Maple进行数据分析数据分析是数学建模和计算的重要一环。
Maple提供了丰富的数据处理和分析函数,如数据拟合、统计分析和回归分析等。
我们可以通过调用这些函数,输入原始数据,得到数据的分析结果和统计性质。
maple教程

Maple教程Maple是一款强大的数学软件,它被广泛用于科学研究、工程设计、教育等领域。
本教程将为你介绍Maple的基本使用方法和一些常用功能,帮助你快速上手和利用Maple解决数学问题。
一、Maple的安装与启动1. 安装MapleMaple的安装非常简单,你只需要从官方网站下载Maple 的安装程序,然后按照提示进行安装即可。
2. 启动Maple安装完成后,你可以在桌面或开始菜单中找到Maple的启动图标,双击它即可启动Maple。
二、Maple的基本功能1. Maple的界面Maple的界面非常直观和友好,主要包括以下几个部分:•菜单栏:包含了各种功能和工具的菜单选项;•工具栏:提供了常用功能的快捷操作按钮;•输入框:可以输入和编辑Maple代码;•输出区:显示Maple执行代码的结果。
2. Maple的基本操作在Maple中,你可以通过输入和执行代码来完成各种数学运算和数据处理。
下面是一些常用的基本操作方法:•输入代码:在输入框中输入Maple代码,然后按下回车键执行;•注释代码:使用#符号可以在代码中添加注释,注释的内容将被忽略;•查看帮助:通过菜单栏的帮助选项或使用?键,可以查看Maple的帮助文档和函数说明。
3. Maple的数学计算Maple支持各种数学计算,包括基本运算、符号计算、数值计算等。
下面是一些常用的数学计算方法:•基本运算:Maple可以进行各种基本运算,如加减乘除、幂运算、取余等;•符号计算:Maple可以处理符号表达式,进行符号计算、方程求解、微分积分等;•数值计算:Maple可以进行数值计算,如数值积分、方程数值求解、函数拟合等。
三、Maple的扩展功能除了基本功能外,Maple还提供了许多强大的扩展功能,帮助用户进行更复杂的数学运算和数据处理。
1. 绘图功能Maple具有强大的绘图功能,可以绘制各种类型的图形,如曲线图、散点图、三维图等。
你可以使用Maple提供的绘图函数来创建自定义的图形,并对图形进行样式设置。
Maple软件的介绍使用方法

Maple软件可以绘制各种类型的 函数图像,包括曲线图、散点图、 极坐标图等。
Maple软件支持绘制三维图像, 可以展示函数的立体形状和表面 等。
绘制等值线图
Maple软件可以绘制等值线图, 用于表示函数在二维平面上的等 高线。
Maple软件的数据分析功能
数据导入
Maple软件可以导入各种数据格 式,包括文本文件、Excel文件 等。
Maple软件的功能特点
1 强大的计算能力
Maple软件具有高精度的计算能力,可以进 行符号计和数值计算,并能处理复杂的数 学运算。
2 丰富的数学函数
Maple软件内置了丰富的数学函数,可以用 于求解方程、绘制函数图像、进行数学推理 等。
3 友好的用户界面
Maple软件采用直观的界面设计,使用户能 够轻松使用各种功能,同时提供了丰富的学 习资源和帮助文档。
编辑结果
在输出区域对计算结果进行编 辑、调整格式和导出。
Maple软件的数学运算功能
1
代数运算
Maple软件可以进行代数运算,包括多项
微积分运算
2
式运算、方程求解、矩阵运算等。
Maple软件支持微积分运算,可以进行导
数计算、积分计算、微分方程求解等。
3
概率统计运算
Maple软件具有强大的概率统计功能,可 以进行随机数生成、概率分布计算、统计 分析等。
Maple软件的介绍使用方 法
Maple软件是一款功能强大的数学软件,被广泛应用于科学研究、工程领域、 教育教学以及金融等领域。本文将介绍Maple软件的各种功能和应用,帮助您 更好地理解和使用Maple软件。
Maple软件简介
Maple软件是一种先进的数学软件,通过其强大的计算和分析功能,可以解决各种数学问题,包括代数、微积 分、差分方程等。
Maple基础教程(修订稿).

Maple 基础一Maple 的基本运算1 数值计算问题在应用Maple 做算术运算时, 只需将Maple 当作一个“计算器”使用, 所不同的是命令结束时需加“;”或“:”.在Maple 中, 主要的算术运算符有“+”(加)、“–”(减)、“*”(乘)、“/”(除)以及“^”(乘方或幂,或记为**),值得注意的是, “^”的表达式只能有两个操作数, 换言之, c b a ^^是错误的, 而“+”或“*”的任意表达式可以有两个或者两个以上的操作数.2.1.1 有理数运算作为一个符号代数系统, Maple 可以绝对避免算术运算的舍入误差.如果要求出两个整数运算的近似值时, 只需在任意一个整数后加“.”(或“.0”), 或者利用“evalf ”命令把表达式转换成浮点形式, 默认浮点数位是10 (即: Digits:=10, 据此可任意改变浮点数位, 如Digits:=20).> 123456789/987654321;13717421109739369> evalf(%); .1249999989> big_number:=3^(3^3);:= big_number 7625597484987> length(%);13函数“length ”作用在整数上时是整数的十进制位数即数字的长度. “%”是一个非常有用的简写形式, 表示最后一次执行结果1)整数的余(irem)/商(iquo)命令格式:irem(m,n); #求m 除以n 的余数irem(m,n,'q'); #求m 除以n 的余数, 并将商赋给qiquo(m,n); #求m 除以n 的商数iquo(m,n,'r'); #求m 除以n 的商数, 并将余数赋给r其中, m, n 是整数或整数函数, 也可以是代数值, 此时, irem 保留为未求值.2)素数判别(isprime)命令格式: isprime(n);如果判定n 可分解, 则返回false, 如果返回true, 则n “很可能”是素数. > isprime(2^(2^4)+1);true3) 确定第i 个素数(ithprime)若记第1个素数为2,判断第i 个素数的命令格式: ithprime(i);4) 一组数的最大值(max)/最小值(min)命令格式: max(x1,x2,…,xn); #求x 1,x 2,…,x n 中的最大值min(x1,x2,…,xn); #求x 1,x 2,…,x n 中的最小值5)随机数生成器(rand)命令格式:rand( ); #随机返回一个12位数字的非负整数rand(a..b); #调用rand(a..b)返回一个程序, 它在调用时生成一个在范围[a, b]内的随机数> rand();427419669081> myproc:=rand(1..2002):> myproc();1916> myproc();1204注意, rand(n)是rand(0..n-1)的简写形式.2.1.2 复数运算复数是Maple中的基本数据类型. 虚数单位i在Maple中用I表示可以用Re( )、Im( )、conjugate( )和argument( )等函数分别计算实数的实部、虚部、共轭复数和幅角主值等运算. 试作如下实验:> complex_number:=(1+2*I)*(3+4*I);-510Icomplex_number +:=> Re(%);Im(%%);conjugate(%%%);argument(complex_number);-510-510I-- +arctan2π()1) 绝对值函数命令格式: abs(expr);当expr为实数时,返回其绝对值,当expr为复数时,返回复数的模.2)复数的幅角函数命令格式: argument(x); #返回复数x的幅角的主值3)共轭复数命令格式: conjugate(x); #返回x的共轭复数2.2 初等数学2.2.1 常用函数1) 确定乘积和不确定乘积命令格式: product(f,k);product(f,k=m..n);product(f,k=alpha);product(f,k=expr);其中, f—任意表达式, k—乘积指数名称, m,n—整数或任意表达式, alpha—代数数RootOf, expr—包含k的任意表达式.> product(k^2,k=1..10); #计算2k关于1..10的连乘13168189440000> product(k^2,k); #计算2k的不确定乘积()Γk 2> product(a[k],k=0..5); #计算a i (i=0..5)的连乘a 0a 1a 2a 3a 4a 5> Product(n+k,k=0..m)=product(n+k,k=0..m); #计算(n+k)的连乘, 并写出其惰性表达式= ∏ = k 0m() + n k ()Γ + + n m 1()Γn> product(k,k=RootOf(x^3-2)); #计算23-x 的三个根的乘积22)指数函数计算指数函数exp 关于x 的表达式的命令格式为: exp(x);3)确定求和与不确定求和sum命令格式: sum(f,k);sum(f,k=m..n);sum(f,k=alpha);sum(f,k=expr);其中, f —任意表达式, k —乘积指数名称, m,n —整数或任意表达式, alpha —代数数RootOf,expr —不含k 的表达式.> Sum(k^2,k=1..n)=sum(k^2,k=1..n);= ∑ = k 1nk 2 - + + 13() + n 1312() + n 1216n 16> Sum(1/k!,k=0..infinity)=sum(1/k!,k=0..infinity);= ∑ = k 0∞1!k e> sum(a[k]*x[k],k=0..n);∑ = k 0n a k xk> sum(k/(k+1),k=RootOf(x^2-3));33)三角函数/双曲函数命令格式: sin(x); cos(x); tan(x); cot(x); sec(x); csc(x);sinh(x); cosh(x); tanh(x); coth(x); sech(x); csch(x);其中, x 为任意表达式.> Sin(Pi)=sin(Pi);= ()Sin π04)反三角函数/反双曲函数命令格式: arcsin(x); arccos(x); arctan(x); arccot(x); arcsec(x); arccsc(x);arcsinh(x); arccosh(x); arctanh(x); arccoth(x); arcsech(x); arccsch(x);arctan(y,x);其中, x, y 为表达式. 反三角函数/反双曲函数的参数必须按弧度计算.> arcsinh(1);()ln + 12> cos(arcsin(x));- 1x 25)对数函数命令格式: ln(x); #自然对数log[a](x); #一般对数log10(x); #常用对数一般地, 在ln(x)中要求x>0. 但对于复数型表达式x, 有:)(argument *))(abs ln()ln(x I x x += (其中, ππ≤<-)(argument x )> log10(1000000);()ln 1000000()ln 10 > simplify(%); #化简上式62.2.2 函数的定义试看下面一个例子:> f(x):=a*x^2+b*x+c;---并不是函数,而是一个表达式:= ()f x + + a x 2b x c> f(x),f(0),f(1/a);,, + + a x 2b x c ()f 0⎛⎝ ⎫⎭⎪⎪f 1a 由上述结果可以看出, 用赋值方法定义的f(x)是一个表达式而不是一个函数在Maple 中, 要真正完成一个函数的定义, 需要用算子(也称箭头操作符):> f:=x->a*x^2+b*x+c;:= f → x + + a x 2b x c> f(x),f(0),f(1/a);,,+ + a x 2b x c c + + 1a b ac > f:=(x,y)->x^2+y^2; := f → (),x y + x 2y 2> f(1,2);5> f:=(x,y)->a*x*y*exp(x^2+y^2);:= f → (),x y a x y e() + x 2y 2另一个定义函数的命令是unapply,其作用是从一个表达式建立一个算子或函数.命令格式为: f:=unapply(expr, x);命令格式为: f:=unapply(expr, x, y, …);> f:=unapply(x^4+x^3+x^2+x+1,x);:= f → x + + + + x 4x 3x 2x 1借助函数piecewise 可以生成简单分段函数:> abs(x)=piecewise(x>0,x,x=0,0,x<0,-x); = x ⎧⎩⎪⎪⎪⎪⎪⎨x < 0x 0 = x 0-x < x 0清除函数的定义用命令unassign.> unassign(f);> f(1,1); ()f ,11定义了一个函数后, 就可以使用op 或nops 指令查看有关函数中操作数的信息. nops(expr), 函数op 的主要功能是,其命令格式为:op(expr); #获取表达式的操作数op(i, expr); #取出expr 里第i 个操作数,op(i .. j, expr); #expr 的第i 到第j 个操作数nops(expr); #返回操作数的个数> expr:=6+cos(x)+sin(x)*cos(x)^2;:= expr + + 6()cos x ()sin x ()cos x 2> op(expr);,,6()cos x ()sin x ()cos x 2> nops(expr);32.2.3 Maple 中的常量与变量名为了解决数学问题, 一些常用的数学常数是必要的. Maple 系统中已经存储了一些数学常数在表达式序列constants 中:> constants;,,,,,,false γ∞true Catalan FAIL π为了方便使用, 现将上述常数的具体含义列示如下:2.2.4 函数类型转换实现函数类型转换的命令是convert . 命令格式:convert(expr, form); #把数学式expr 转换成form 的形式convert(expr, form, x); #指定变量x, 此时form 只适于exp 、sin 、cosconvert 指令所提供的三角函数、指数与函数的转换共有exp 等7种:(1) exp : 将三角函数转换成指数(2) expln : 把数学式转换成指数与对数(3) expsincos : 分别把三角函数与双曲函数转换成sin 、cos 与指数的形式(4) ln : 将反三角函数转换成对数(5) sincos : 将三角函数转换成sin 与cos 的形式, 而把双曲函数转换成sinh 与cosh 的形式(6) tan : 将三角函数转换成tan 的形式(7) trig : 将指数函数转换成三角函数与对数函数> convert(sinh(x),exp); #将sinh(x)转换成exp 类型 - 12e x 121ex 2.2.5 函数的映射—map 指令在符号运算的世界里, 映射指令map 可以说是相当重要的一个指令, 它可以把函数或指令映射到这些结构里的元素, 而不破坏整个结构的完整性. 命令格式为:map(f, expr); #将函数f 映射到expr 的每个操作数map(f, expr, a); #将函数f 映射到expr 的每个操作数, 并取出a 为f 的第2个自变量map(f, expr, a1, a2,…, an); #将函数f 映射到expr 的每个操作数, 并取a1~an 为f 的第2~n+1个自变量map2(f, a1, expr, a2, …, an); #以a1为第1个自变量, expr 的操作数为第2个自变量, a2为第3个自变量…, an 为第n+1个自变量来映射函数f> f:=x->sqrt(x)+x^2;:= f → x + x x 2> map(f,[a,b,c]); [],, + a a 2 + b b 2 + c c 2> map(h, [a,b,c],x,y);[],,()h ,,a x y ()h ,,b x y ()h ,,c x y3 求 值3.1 赋值在Maple 中, 不需要申明变量的类型, 甚至在使用变量前不需要将它赋值, 这是Maple 与其它高级程序设计语言不同的一点, 也正是Maple 符号演算的魅力所在, 这个特性是由Maple 与众不同的赋值方法决定的. 为了理解其赋值机制, 先看下面的例子.> p:=9*x^3-37*x^2+47*x-19;:= p - + - 9x 337x 247x 19> roots(p);⎡⎣⎢⎢⎤⎦⎥⎥,[],12⎡⎣⎢⎢⎤⎦⎥⎥,1991> subs(x=19/9,p);3.2 变量代换subs ( var = repacedment , expression );调用的结果是将表达式expression 中所有变量var 出现的地方替换成 replacement.> f:=x^2+exp(x^3)-8;:= f + - x 2e()x 38> subs(x=1,f); - + 7e如果需要计算, 必须调用求值函数evalf . 如:> evalf(%);5.> subs(x=y,y=z,x^2*y); (顺序替换)z 3> subs({x=y,y=z},x^2*y); (同步替换)y 2z> subs((a=b,b=c,c=a),a+2*b+3*c); (顺序替换)6a> subs({a=b,b=c,c=a},a+2*b+3*c); (轮 换)+ + b 2c 3a> subs({p=q,q=p},f(p,q)); (互 换)()f ,q p3.3 求值规则1) 对表达式求值命令格式: eval(e, x=a); #求表达式e 在x=a 处的值eval(e, eqns); #对方程或方程组eqns 求值eval(e); #表达式e 求值到上面两层eval(x,n); #给出求值名称的第n 层求值> p:=x^5+x^4+x^3+x^2+x+73;:= p + + + + + x 5x 4x 3x 2x 73> eval(p,x=7);19680当表达式在异常点处求值时, eval 会给一个错误消息. 如下:> eval(sin(x)/x,x=0);Error, numeric exception: division by zero2) 在代数数(或者函数)域求值命令格式: evala(expr); # 对表达式或者未求值函数求值evala(expr,opts); #求值时可加选项(opts)在Maple 中, 代数数用函数RootOf ()来表示. 如3作为一个代数数, 可以表示为:> alpha:=RootOf(x^2-3,x);:= α()RootOf - _Z 23> simplify(alpha^2);3在Maple 内部, 代数数α不再表示为根式, 而在化简时, 仅仅利用到32=α这样的事实. 这里, Maple 用到一个内部变量_Z. 再看下面一个例子,其中alias 是缩写的定义函数,而参数lenstra 指lenstra 椭圆曲线方法:> alias(alpha=RootOf(x^2-2)):> evala(factor(x^2-2,alpha),lenstra); () + x α() - x α> evala(quo(x^2-x+3,x-alpha,x,'r'));- + + 1αx> r;- + 3αα2> simplify(%);- 5α3) 在复数域上符号求值操纵复数型表达式并将其分离给出expr 的实部和虚部的函数为evalc, 命令格式为:evalc(expr);evalc 假定所有变量表示数值, 且实数变量的函数是实数类型. 其输出规范形式为: expr1+I*expr2. > evalc(sin(6+8*I));+ ()sin 6()cosh 8I ()cos 6()sinh 8> evalc(f(exp(alpha+x*I)));()f + e α()cos x I e α()sin x4) 使用浮点算法求值命令格式为: evalf(expr, n);> evalf(Pi,50);3.1415926535897932384626433832795028841971693993751> evalf(sin(3+4*I)); - 3.853********.01681326I5) 对惰性函数求值把只用表达式表示而暂不求值的函数称为惰性函数,对任意代数表达式f 求值的命令格式为: value(f); > F:=Int(exp(x),x);:= F d ⎛⎠⎜e x x > value(%);e x> f:=Limit(sin(x)/x,x=0);:= f lim→ x 0()sin x x> value(%); 1另外, 将惰性函数的大写字母改为小写字母亦即可求值. 如下例:> Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0);= lim → x 0()sin x x1 4 数据结构Maple 中有许多内建的与FORTRAN 、C 或Pascal 不同的数据结构. 主要的数据结构有序列(sequence)、列表(list)、集合(set)、代数数( algebraic number)、未求值或惰性函数调用、表(table)、级数(series)、串(string)、索引名(index)、关系(relation)、过程体(process)以及整数(integer)、分数(fraction)、浮点数(float)、复数(complex number)等数据结构, 而矩阵(matrix)在Maple 中表示为阵列, 是一种特殊的表.4.1 数据类型查询在Maple 中, 用whattype 指令来查询某个变量的数据类型或特定类型, 命令格式为:whattype(expr) # 查询expr 的数据类型type(expr, t) # 查询expr 是否为t 类型, 若是则返回true, 否则返回false4.2 序列, 列表和集合4.2.1 序列所谓序列(Sequence), 就是一组用逗号隔开的表达式列. 如:> s:=1,4,9,16,25;:= s ,,,,1491625> t:=sin,com,tan,cot;:= t ,,,sin com tan cot一个序列也可以由若干个序列复合而成, 如:> s:=1,(4,9,16),25;:= s ,,,,1491625> s,s;,,,,,,,,,14916251491625而符号NULL 表示一个空序列. 序列有很多用途, 如构成列表、集合等. 事实上, 有些函数命令也是由序列构成. 例如:> max(s);25> min(s,0,s);函数seq 是最有用的生成序列的命令, 通常用于写出具有一定规律的序列的通项, 命令格式为: seq(f(i), i=m..n); # 生成序列f(m), f(m+1), …, f(n) (m,n 为任意有理数)seq(f(i), i=expr); # 生成一个f 映射expr 操作数的序列seq(f(op(i,expr)), i=1..nops(expr)); # 生成nops(expr)个元素组成的序列> seq(i^2,i=1..10);149162536496481100,,,,,,,,,> seq(i^3,i=x+y+z);x3y3z3,,获得一个序列中的特定元素选用操作符[ ], 如:> seq(ithprime(i),i=1..20);235711131719232931374143475359616771,,,,,,,,,,,,,,,,,,,> %[6],%[17];1359,4.2.2 列表列表(list), 就是把对象(元素)放在一起的一种数据结构, 一般地, 用方括号[ ]表示列表. 如下例: > l:=[x,1,1-z,x];x1 -1z x,,,:=l[]> whattype(%);list4.2.3 集合集合(set)也是把对象(元素)放在一起的数据结构,一般地, 用花括号表示集合.> s:={x,1,1-z,x};1z1x -,,s{}:=> whattype(%);set空集定义为{ }.Maple中集合的基本运算有交(intersect)、并(union)、差(minus):> A:={seq(i^3,i=1..10)};B:={seq(i^2,i=1..10)};,,,,,,,,,1827641252163435127291000A{}:=149162536496481100,,,,,,,,,B{}:=> A intersect B;,164{}4.3 数组和表在Maple中, 数组(array)由命令array产生, 其下标变量(index)可以自由指定. 下标由1开始的一维数组称为向量(vector), 二维以上的数组称为矩阵(matrix). 数组的元素按顺序排列, 任意存取一数组的元素要比列表或序列快的多. 区分一个数据结构是数组还是列表要用“type”命令.表(table)在建立时使用圆括号, 变量能对一个表赋值, 但一个在存取在算子中的未赋值变量会被自动地假定是表, 表的索引可以成为任意Maple表达式. 表中元素的次序不是固定的.5 Maple 高级输入与输出操作生成LATEXMaple 可以把它的表达式转换成LATEX, 使用latex 命令即可: > latex(x^2+y^2=z^2);{x}^{2}+{y}^{2}={z}^{2}还可以将转换结果存为一个文件(LatexFile):> latex(x^2 + y^2 = z^2, LatexFile);再如下例:> latex(Int(1/(x^2+1),x)=int(1/(x^2+1),x));\int \! \left( {x}^{2}+1 \right) ^{-1}{dx}=\arctan\left( x \right)二 微积分运算1 函数的极限和连续1.1 函数和表达式的极限)(lim x f ax →命令格式为: limit(f,x=a);求)(lim x f a x +→时的命令格式为limit(f, x=a, right); 求)(lim x f ax -→时的命令格式为limit(f, x=a, left); 请看下述例子:> Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity);= lim → x ∞⎛⎝ ⎫⎭⎪⎪ + 11x xe > Limit((x^n-1)/(x-1),x=1)=limit((x^n-1)/(x-1),x=1);= lim → x 1 - x n 1 - x 1n > Limit(x^x,x=0,right)=limit(x^x,x=0,right);= lim → +x 0x x 1> limit(a*x*y-b/(x*y),{x=1,y=1});- a b> limit(x^2*(1+x)-y^2*((1-y))/(x^2+y^2),{x=0,y=0});undefined下例就是化二重极限为二次极限而得正确结果:> limit((sin(x+y)/(sin(x)*sin(y)),{x=Pi/4,y=Pi/4}));⎛⎝ ⎫⎭⎪⎪limit ,()sin + x y ()sin x ()sin y {}, = x 14π = y 14π > limit(limit(sin(x+y)/(sin(x)*sin(y)),x=Pi/4),y=Pi/4);21.2 函数的连续性1.2.1 连续在Maple 中可以用函数iscont 来判断一个函数或者表达式在区间上的连续性. 命令格式为: iscont(expr, x=a..b, 'colsed '/'opened');其中, closed 表示闭区间, 而opened 表示开区间(此为系统默认状态).如果表达式在区间上连续, iscont 返回true, 否则返回false, 当iscont 无法确定连续性时返回FAIL. 另外, iscont 函数假定表达式中的所有符号都是实数型. 颇为有趣的是, 当给定区间[a,b ] (a >b )时, iscont 会自动按[b,a ]处理.> iscont(1/x,x=1..2);true> iscont(1/x,x=-1..1,closed);false> iscont(1/(x+a),x=0..1);FAIL> iscont(ln(x),x=10..1);true1.2.2 间断函数discont 可以寻找函数或表达式在实数域的间断点, 当间断点周期或成对出现时, Maple 会利用一些辅助变量予以表达, 比如, _Zn ~(任意整数)、_NZn ~(任意自然数)和Bn ~(一个二进制数, 0或者1), 其中n 是序号. 判定f(x)间断点的命令为:discont(f, x);> discont(ln(x^2-4),x);{},-22> discont(arctan(1/2*tan(2*x))/(x^2-1),x);{},,-11 + 12π_Z1~14π> discont(round(3*x-1/2),x);{} + 1313_Z1 函数round 为“四舍五入”函数,上例并非一目了然,对其进一步理解可借助于函数plot 或下面给出的fdiscont 例子。
maple assuming的用法

在Maple中,assuming命令用于定义或修改某些变量的属性。
这可以让你更方便地执行某些特定的操作,例如积分、微分等。
使用assuming命令的一般语法如下:
其中,symbol(s)是你想要定义或修改属性的符号或符号列表,而property(s)是你想要赋予这些符号的属性或属性列表。
例如,如果你想要将变量x定义为实数,你可以使用以下命令:
然后,你可以使用这个假设来执行某些操作,例如积分或微分。
例如,你可以执行以下命令:
这会计算x^2在x为实数时的积分。
注意,这个假设仅在当前Maple会话中有效。
如果你想要在以后会话中仍然保持这个假设,你需要使用with命令:。
Maple变量管理的简单操作介绍

Maple变量管理的简单操作介绍Maple既然是一款强大的计算软件,那么在计算方面必不可少会处理变量的问题,那么大Maple计算的过程中,对变量怎样管理呢?本教程来对此稍作介绍。
更多Maple基本功能与常用操作命令介绍请访问Maple中文版网站。
在Maple 中,一个变量名可以有值,也可以没有值。
例如:其中,变量x、a、b就没有任何值。
另一方面,Maple的任一变量名都可以指给另一个Maple对象,如:我们说“数100已经赋值给名称a”。
从此以后,Maple每当遇到a时都把它作为100看待。
我们说“变量名a就指的是数100”。
例如:现在我们可以说Maple已经求出了a^2*t-2*a-1的值,术语求值(evaluation)在计算机语言中有不同的含意。
严格地讲,Maple里的求值是求变量的值(即通过对名称所指向的内存的搜寻过程),并不包含任何计算的意义。
在Maple的术语里,计算(calculation)叫做化简(simplication)。
一般地,化简必须由用户提出要求,但某些基本的化简是可以自动执行的,例如像计算100的平方,合并-200与-1。
实际上Maple在上例中是通过以下几步计算求出结果的:将a的值计为100:自动化简(autosimplication)所得的表达式。
根据Maple内存的内部序对结果表达式的子式进行分类。
以上内容对Maple计算过程中对变量处理原理作了一些简单的介绍,在明白了这些的基础上自如地计算一些简单变量是没有问题的,如果需要了解更多Maple使用方面的技巧,或者想要下载Maple申请试用等,请访问Maple中文版网站进行查看下载。
第四章Maple简介.ppt

精选
16
3. 定义函数
• 定义函数的根本方式是:
• “函数名 := 变量 - > 变量的表达式〞
1. 极限运算
• Limit(f(x), x = a ) 求表达式f(x)当x趋于a时的极限
• Limit(f(x), x=a, dir ) 求表达式f(x)当x沿方向dir趋于a时的极限
• Limit(f(x,y,…),{x=a,y=b}) 求表达式f(x, y,…)
当x,y,…分别趋于a、b,…时的极限
• Maple承受中文输入,这为我们编写中文课 件或做中文注释提供了方便.
精选
3
二、安装、启动与退出
• 1. 软件的安装 • 2. 软件的启动与退出
精选
4
三、界面简介
精选
5
四、根本操作
• 1. 根本运算符
• 加、减、乘、除和乘方的符号+、-、*、/ 和 ^
• 在运算过程中加注释, 用符号“#〞起始就 行了
• 加载程序包LinearAlgebra • 1. 向量和矩阵的输入和运算 • 2. 向量的其他运算 • 3. 矩阵的其他运算 • 4. 求解线性方程组 • 5. 矩阵的特征值和特征向量
精选
31
1. 向量和矩阵的输入和运算
• v := <a1, a2, …, ak> 定义k维列向量 • vv := <a1 | a2 | … | ak> 定义k维行向量v • M:=<<a11, …, ak1>|…|<a1n, …, akn>> 定义kΧn
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Maple变量管理的简单操作介绍
Maple既然是一款强大的计算软件,那么在计算方面必不可少会处理变量的问题,那么大Maple计算的过程中,对变量怎样管理呢?本教程来对此稍作介绍。
更多Maple基本功能与常用操作命令介绍请访问Maple中文版网站。
在Maple 中,一个变量名可以有值,也可以没有值。
例如:
其中,变量x、a、b就没有任何值。
另一方面,Maple的任一变量名都可以指给另一个Maple对象,如:
我们说“数100已经赋值给名称a”。
从此以后,Maple每当遇到a时都把它作为100看待。
我们说“变量名a就指的是数100”。
例如:
现在我们可以说Maple已经求出了a^2*t-2*a-1的值,术语求值(evaluation)在计算机语言中有不同的含意。
严格地讲,Maple里的求值是求变量的值(即通过对名称所指向的内存的搜寻过程),并不包含任何计算的意义。
在Maple的术语里,计算(calculation)叫做化简(simplication)。
一般地,化简必须由用户提出要求,但某些基本的化简是可以自动执行的,例如像计算100的平方,合并-200与-1。
实际上Maple在上例中是通过以下几步计算求出结果的:
将a的值计为100:
自动化简(autosimplication)所得的表达式。
根据Maple内存的内部序对结果表达式的子式进行分类。
以上内容对Maple计算过程中对变量处理原理作了一些简单的介绍,在明白了这些的基础上自如地计算一些简单变量是没有问题的,如果需要了解更多Maple使用方面的技巧,或者想要下载Maple申请试用等,请访问Maple中文版网站进行查看下载。
