南京邮电大学数学实验练习题参考的答案
南邮离散数学课后习题答案

南邮离散数学课后习题答案南京邮电大学离散数学课程是一门重要的数学基础课程,它涵盖了许多重要的离散数学概念和方法。
在学习这门课程时,我们经常会遇到一些难题,需要通过课后习题来巩固和加深对所学知识的理解。
然而,由于离散数学的题目类型繁多,解题方法各异,很多同学在课后习题中遇到了困惑。
为了帮助同学们更好地学习离散数学,我整理了一些常见课后习题的答案,供大家参考。
一、集合论1. 设A={1,2,3,4,5},B={3,4,5,6,7},C={2,4,6,8},求(A∩B)∪C的元素个数。
答:首先求A∩B,即A和B的交集,得到{3,4,5}。
然后求(A∩B)∪C,即交集{3,4,5}与C的并集,得到{2,3,4,5,6,8}。
所以(A∩B)∪C的元素个数为6。
2. 设集合A={1,2,3,4,5},B={3,4,5,6,7},C={2,4,6,8},求(A-B)∪C的元素个数。
答:首先求A-B,即A与B的差集,得到{1,2}。
然后求(A-B)∪C,即差集{1,2}与C的并集,得到{1,2,4,6,8}。
所以(A-B)∪C的元素个数为5。
二、关系与函数1. 设集合A={1,2,3,4,5},B={3,4,5,6,7},C={2,4,6,8},定义关系R为A到B的映射,若R={(1,4),(2,5),(3,6),(4,7)},求R的逆关系R^-1。
答:逆关系R^-1是由R中的有序对的元素颠倒位置得到的。
所以R^-1={(4,1),(5,2),(6,3),(7,4)}。
2. 设集合A={1,2,3,4,5},B={3,4,5,6,7},C={2,4,6,8},定义函数f为A到B的映射,若f(1)=4,f(2)=5,f(3)=6,f(4)=7,求f的逆函数f^-1。
答:逆函数f^-1是由f中的元素的自变量和因变量颠倒位置得到的。
所以f^-1(4)=1,f^-1(5)=2,f^-1(6)=3,f^-1(7)=4。
三、图论1. 设G=(V,E)为一个无向图,V={A,B,C,D,E,F},E={{A,B},{A,C},{B,C},{C,D},{D,E}},求G的邻接矩阵。
数学实验(南邮)答案2

第二次练习题1、 设⎪⎩⎪⎨⎧=+=+32/)7(11x x x x n n n ,数列}{n x 是否收敛?若收敛,其值为多少?精确到6位有效数字。
>> f=inline('(x+7/x)/2'); syms x; x0=3; for i=1:1:20 x0=f(x0);fprintf('%g,%g\n',i,x0); end 1,2.66667 2,2.64583 3,2.64575 4,2.64575 5,2.64575 6,2.64575 7,2.64575 8,2.64575 9,2.64575 10,2.64575 11,2.64575 12,2.64575 13,2.64575 14,2.64575 15,2.64575 16,2.64575 17,2.64575 18,2.64575 19,2.64575 20,2.64575本次计算运行到第三次结果稳定,可得: 数列}{n x 收敛,收敛到2.645752、 设 ,131211pp p n n x ++++= }{n x 是否收敛?若收敛,其值为多少?精确到17位有效数字。
学号为单号,取7=p >> s=0; for i=1:1:200 s=s+1/i^7;fprintf('%g,%20.17f\n',i,s); end1, 1.00000000000000000 2, 1.00781250000000000 3, 1.00826974737082750 4, 1.00833078252707750 5, 1.00834358252707750 6, 1.00834715477216210 7, 1.00834836903784100 8, 1.00834884587499920 9, 1.00834905495015730 10, 1.00834915495015730 …………………………… 181, 1.00834927738191870 182, 1.00834927738191890 183, 1.00834927738191920 184, 1.00834927738191940 185, 1.00834927738191960 186, 1.00834927738191980 187, 1.00834927738192000 188, 1.00834927738192030 189, 1.00834927738192050190, 1.00834927738192070 191, 1.00834927738192070 192, 1.00834927738192070 193, 1.00834927738192070 194, 1.00834927738192070 195, 1.00834927738192070 196, 1.00834927738192070 197, 1.00834927738192070 198, 1.00834927738192070 199, 1.00834927738192070 200, 1.00834927738192070运行至第190次后稳定,值为1.00834927738192070书上习题:(实验四) 1,2,4,7(1),8,12(改为:对例2,取 120,55,25,5.4=a 观察图形有什么变化.),13,14 。
南邮-《高数B》练习册(下)答案(第10章)备课讲稿

南邮-《高数B》练习册(下)答案(第10章)参考答案与提示第10章 微分方程与差分方程§10.1 微分方程的基本概念2. 0)()(='+p x p p x§10.2 一阶微分方程1、(1)))1(212+=x y e e (2)xCxy -=44(3)Cx xe y = (4) 322y x y =- (5) )(C x e y x +=- (6)21x x y -+=(7) 3221Cy y x +=2、xe xf cos 1)(--=§10.3 一阶微分方程在经济学中的综合应用1、(1)P P Q -= (2)0lim =+∞→Q P ,即需求趋于稳定2、N t x t =+∞→)(lim ,表明,在题目给出的条件下,最终每个人都要染上传染病. 3. 33911000)(t t y -⋅+=,500,6==y t 时.§10.4 可降阶的二阶微分方程1. (1) 213sin 61C x C x x y ++-=(2) 21)(C e x C y x +-=- 2.(1)x y 11+= (2))1ln(1+-=ax ay §10.5 二阶常系数线性微分方程1、(1) B (2) C2、2)(21x e x C C y += 3.(1) x x e C e C y 3231-+= (2) x e x C C y 221)(+= (3) )23sin 23cos(2121x C x C ey x +=- 4. (1)=*y x e b ax 2)(+(2) =*y )(2c bx ax x ++(3)=*y x axe(4)=*y x e b ax x )(2+(5) =*y ]2sin )(2cos )[(4x d cx x b ax xe x +++ (6)=*y x e dx x c bx ae x sin )(cos )(++++5.(1) xx e e C C y 2421121-++= (2) )sin (x x e y x-=-§10.6 差分与差分方程的概念、常系数线性差分方程解的结构1.(1)1462++=∆x x y x , 10122+=∆x y x(2)1)21(2+-=∆x x x y , 22)21(2++=∆x x x y(3)x x x y 3)32(⋅+=∆, x x x y 3)124(2⋅+=∆ 2.(1)6阶 (2)1阶§10.7 一阶常系数线性差分方程1.(1) C (2) x C )1(-2 (1) x x y )23(-= (2) x y x 32+=(3) 435-=x x y(4) t t t C y 2)2(⋅-+=(5) )8181()4()4(+--+-=x x C y x x x§10.8 二阶常系数线性差分方程1.(1) x x x C C y )5)((21-+= (2) x x x y 2)3(2--=(3) )3sin 3(cos 4x x y x x ππ+=* (4) 8)21)((21++=x x x C C y* (5) )507101()4(21-+-+=x x C C y x x总习题十1.(1) x Ce y tan = (2)C y x =++)21)(1(2 (3)y x y '=(4)02=+'-''y y y(5))3sin 3cos (21x C x C e y x +=-(6)=*y x e c bx ax x )(2++2.(1)B (2)C (3)C3.(1)ee y x+++=11ln 21 (2))sin(x yCe x =(3)221121xx y +-=(4) x y arcsin =(5) xy -=11(6) 21)cos(C x C y +-=(7) x e x C C y λλ-+==)(,1212时当xxe C e C y )1(2)1(1222,1----+-+=>λλλλλ时当)1sin 1cos (,122212x C x C e y x λλλλ-+-=<-时当(8) x x e e x x y -+++=41)212343(2 (9) x xe y xsin 2=(10) x x C x C ey x 2cos 263)23sin 23cos(2121++=- 212sin 131+-x 4.(1) x x y 41+=(2)27591035)2(2--+-=x x C y x x(3) x x x x C y 3)2(+-+= 5. x e x f 2)(-= 6. x x x y --=ln 41 7. (1)3ba P e = (2) 31333])1([)(bkt eee P P t P --+=(3) e t P t P =+∞→)(lim8. 31323123+-=x x y9. x x xe e y --+=210. x x x x f cos 21sin 21)(+=11. rr f 12)(-=。
南京邮电大学《线性代数与解析几何》期末试卷4

0
−1 1 0 1 −1 0
1
0
当 = 2 时, A − E = 1 − 1 0 → 0 0 0 2 = 1 , 3 = 0 ,
0 0 0 0 0 0
=
25
,故所求平面方程为: 24x + 18 y + 25z − 7 = 0 .
8
五、证明: r ( B) min{ m, n} = n , 又 n = r ( I ) = r ( AB) r ( B) , 故有 r ( B) = n , 即矩阵 B 的
列向量组线性无关.
第 2 页 共 2 页
0 0 0 1
(3)当 = 1 时,同解方程组为 1 + 2 + 3 = 1 , 通解为:
X = (1, 0 , 0 )T + k1 (1, − 1, 0 )T + k2 (1, 0 , − 1)T , k1 , k2 R
1 − a 1 + a 0
4. 解:
(1)二次型的矩阵 A = 1 + a 1 − a 0 , r ( A) = 2 A = 0 a = 0 .
4 = −31 + 2 + 3 .
第 1 页 共 2 页
《线性代数与解析几何》练习册参考解答——期末试卷四
a 1 1
3. 解: A = 1 a 1 = (a + 2)(a − 1) 2 ,
1 1 a
(1)当 ≠ −2且 ≠ 1 时,方程组有唯一解;
1 1 −2 4
南京邮电大学2013-2014第二学期高等数学A下期末自测试题及答案详解

南京邮电大学2013-2014学年第二学期《高等数学》(A 下)自测模拟试题及详细答案1.极限2221lim 1x x yx y x +→∞→⎛⎫+= ⎪⎝⎭2e .2.设()2y z x y x ϕ=++,其中ϕ具有连续二阶偏导数,则2z x y∂∂∂=2x ()''21()ln 1y x y x y x ϕ-+++. 3.曲面arctan()z xy =在点(1,1,)4P π处的法线方程为41122111z x y π---==-.4.函数2(,,)21f x y z z e xy =-++在点(2,1,0)处的方向导数的最大值为5.设2x u v z y u vz ⎧=-++⎨=+⎩确定u=u(x,y,z),v=(x,y,z),则u x ∂=∂12z zu -+. 6.幂函数21(1)9nnn x ∞=-∑的收敛区域是 (2,4)- . 7.设2,10()1,01x x f x x x --<≤⎧=⎨-<≤⎩,是周期为2的周期函数,则其傅里叶级数 在点x=4处收敛于12. 8.设2222y z R ++=∑:x 外侧,则2223/2()xdydz ydzdx zdxdyx y z ++=++∑⎰⎰4π. 9.已知22A=y +2z +xy ,=x +y +z ,i j k B i j k u r r r r u r r r r ,则div (A )B ⨯u r u r =3224x y z x z ---.10.设L 为取正向的圆周x 2+y 2=9,则曲线积分2(22)(4)Lxy y dx xx dy -+-⎰= 18π- .(用格林公式易) 二(8分).将函数f(x)= 212565xx x ---在点x 0=2处展开成泰勒级数,并指出其收敛域.解:若用泰勒级数2()0000000''()()()()()()'()()2!!n nf x x x f x x x f x f x f x x x n --=+-++++L L =2()1''(2)(2)(2)(2)'(2)(2)42!!n nf x f x f x n ---+-++++L L ,不易。
南京邮电大学 数字电路 第九章 习题

2013年7月21日星期日
第九章 习题
节目录
3
m0
m7
A 1 B 1 C 1
A B
C
(D0) F 1 (D1) F (D2) 2
或
F1 ( A, B, C ) m(2,3,4,5,7) F2 ( A, B, C ) m(3,4,5,7) F3 ( A, B, C ) m(0,1,3,6,7)
2013年7月21日星期日 第九章 习题
节目录
2
采用有3位地址、3位数据输出的8字节×3位
F3
题 9.1 ROM 阵列
2013年7月21日星期日 第九章 习题
节目录
4
9.7 试用位扩展方法,将2片256×4位的RAM组成一 个256×8位的RAM,画出电路图。
CS R/W A0 A7 A 7 L A 0 R/W CS A 7 I)
D3 D7 D2 D6 D1 D5 D0 D4 数据输出
第九章 习题
节目录
1
解: 首先应将以上三个逻辑函数化成由最小项
组成的标准“与-或”式,即
F1 ( A, B, C ) ABC ABC ABC ABC ABC F2 ( A, B, C ) m(3,4,5,7) F3 ( A, B, C ) ABC ABC ABC ABC ABC
256×4(Ⅱ)
D3 D3 D2 D2 D1 D1 D0 D0
题9.7 256×4芯片位扩展
2013年7月21日星期日 第九章 习题
南邮数学实验答案

第一次练习题1、求032=-x e x 的所有根。
>>x=-5:0.01:5;y=exp(x)-3*x.^2;plot(x,y);grid on>> fsolve('exp(x)-3*x.^2',-1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =-0.4590>> fsolve('exp(x)-3*x.^2',1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =0.9100>> fsolve('exp(x)-3*x.^2',4)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =3.73312、求下列方程的根。
南邮数电-习题答案

10.1 PLD器件有哪几种分类方法?按不同的方法划分PLD器件分别有哪几种类型?PLD器件通常有两种分类方法:按集成度分类和按编程方法分类。
按集成度分类,PLD 器件可分为低密度可编程逻辑器件(LDPLD)和高密度可编程逻辑器件(HDPLD)两种。
具体分类如下:PLD LDPLDHDPLDPROMPLAPALGALCPLDFPGA按编程方法分类,PLD器件可分为一次性编程的可编程逻辑器件、紫外线可擦除的可编程逻辑器件、电可擦除的可编程逻辑器件和采用SRAM结构的可编程逻辑器件四种。
10.2 PLA、PAL、GAL和FPGA等主要PLD器件的基本结构是什么?PLA的与阵列、或阵列都可编程;PAL的与阵列可编程、或阵列固定、输出结构固定;GAL的与阵列可编程、或阵列固定、输出结构可由用户编程定义;FPGA由CLB、IR、IOB 和SRAM构成。
逻辑功能块(CLB)排列成阵列结构,通过可编程的内部互连资源(IR)连接这些逻辑功能块,从而实现一定的逻辑功能,分布在芯片四周的可编程I/O模块(IOB)提供内部逻辑电路与芯片外部引出脚之间的编程接口,呈阵列分布的静态存储器(SRAM)存放所有编程数据。
10.3 PAL器件的输出与反馈结构有哪几种?各有什么特点?PAL器件的输出与反馈结构有以下几种:(1)专用输出结构:输出端为一个或门或者或非门或者互补输出结构。
(2)可编程输入/输出结构:输出端具有输出三态缓冲器和输出反馈的特点。
(3)寄存器输出结构:输出端具有输出三态缓冲器和D触发器,且D触发器的Q端又反馈至与阵列。
(4)异或输出结构:与寄存器输出结构类似,只是在或阵列的输出端又增加了异或门。
10.4 试分析图P10.4给出的用PAL16R4构成的时序逻辑电路的逻辑功能。
要求写出电路的激励方程、状态方程、输出方程,并画出电路的状态转移图。
工作时,11脚接低电平。
图中画“×”的与门表示编程时没有利用,由于未编程时这些与门的所有输入端均有熔丝与列线相连,所以它们的输出恒为0。
南邮 数学实验参考答案(选题版)

syms x y;>> a=int(int(exp(x^2+y^2),x,0,1),y,0,1) a =(pi*erfi(1)^2)/41.7、n=20;for i=1:(n-2)a(1)=1;a(2)=1;a(i+2)=a(i+1)+a(i);enda'ans =112358132134558914423337761098715972584418167651.8、>> A=[-2,1,1;0,2,0;-4,1,303/1000]; >> inv(A)0.0893 0.1027 -0.29460 0.5000 01.1786 -0.2946 -0.5893>> eig(A)ans =-0.8485 + 1.6353i-0.8485 - 1.6353i2.0000>> [p,D]=eig(A)p =0.2575 - 0.3657i 0.2575 + 0.3657i 0.24250 0 0.97010.8944 0.8944 0.0000D =-0.8485 + 1.6353i 0 00 -0.8485 - 1.6353i 00 0 2.0000 >> det(A)ans =6.7880>> A^6ans =45.0194 4.7452 -6.37180 64.0000 025.4870 -6.3718 30.3452>> A.^6ans =1.0e+003 *0.0640 0.0010 0.00100 0.0640 04.0960 0.0010 0.0000 1.9、M文件定义如下:function y=f(x)if x>=0&&x<=1/2y=2*x;else if x>1/2&&x<=1y=2-2*x;endend命令窗口执行:fplot(@f,[0,1])1.10、t=-8:0.1:8;x=cos(t);y=sin(t);z=t;plot3(x,y,z,'r');hold onx1=2*cos(t);y1=2*sin(t);z1=t;plot3(x1,y1,z1)grid on1.11、>> A=[4 -2 2;-3 0 5;1 5*303 3];>> B=[1 3 4;-2 0 -3;2 -1 -1];>> det(A)ans =-39418>> 2*A-Bans =7 -7 0-4 0 130 3031 7>> A*Bans =12 10 207 -14 -17-3023 0 -4544>> A.*Bans =4 -6 86 0 -152 -1515 -3>> A*B^-1ans =-0.4211 -1.4737 0.7368-1.0000 -2.0000 -3.0000637.7368 716.5789 398.2105>> A^-1*Bans =0.3467 0.5763 0.99950.0015 -0.0017 -0.0013-0.1920 0.3458 -0.0003>> A^2ans =24 3022 4-7 7581 9 -4538 4543 7586>> A'ans =4 -3 1-2 0 15152 5 31.12、syms x;fplot('(1/(sqrt(2*pi)*514/600))*exp(-((x)^2)/2)',[-3,3],'r') hold onfplot('(1/(sqrt(2*pi)*514/600))*exp(-((x-1)^2)/2)',[-3,3],'b') hold onfplot('(1/(sqrt(2*pi)*514/600))*exp(-((x+1)^2)/2)',[-3,3],'g') hold offlegend('u为0','u为-1','u为1')syms x;fplot('(1/(sqrt(2*pi)*1))*exp(-((x)^2)/2)',[-3,3],'r')hold onfplot('(1/(sqrt(2*pi)*2))*exp(-((x)^2)/2)',[-3,3],'b')hold onfplot('(1/(sqrt(2*pi)*4))*exp(-((x)^2)/2)',[-3,3],'--')hold onfplot('(1/(sqrt(2*pi)*5.14))*exp(-((x)^2)/2)',[-3,3],'g')hold off1.15、ezplot('exp(x)-3*303*x.^2',[-10,10]);grid onfsolve('exp(x)-3*303*x.^2',0)ans =-0.0326第二次练习:2.1、f=inline('(x+7/x)/2');syms x;x0=3;for i=1:1:15x0=f(x0);fprintf('%g,%g\n',i,x0);end结果如下:1,2.666672,2.645833,2.645754,2.645755,2.645756,2.645757,2.645758,2.645759,2.6457510,2.6457511,2.6457512,2.6457513,2.6457514,2.6457515,2.645752.2、同2.1的方法,把f=inline('(x+7/x)/2');把未知表达式改一下就可以了;2.3、f=inline('1-2*abs(x-1/2)');x=[];y=[];x(1)=rand;y(1)=0;x(2)=x(1);y(2)=f(x(1));for i=1:10000x(1+2*i)=y(2*i);x(2+2*i)=x(1+2*i);y(1+2*i)=x(1+2*i);y(2+2*i)=f(x(2+2*i));endplot(x,y,'r');hold on;syms x;ezplot(x,[0,1]);ezplot(f(x),[0,10]);axis([0,1,0,1]);hold off答案如下:2.4、以α=3.5为例;其他的把α改变就可以了;f=inline('3.5(是α的取值)*x*(1-x)');x=[];y=[];x(1)=0.5;y(1)=0;x(2)=x(1);y(2)=f(x(1));for i=1:10000x(1+2*i)=y(2*i);x(2+2*i)=x(1+2*i);y(1+2*i)=x(1+2*i);y(2+2*i)=f(x(2+2*i));endplot(x,y,'r');hold on;syms x;ezplot(x,[0,1]);ezplot(f(x),[0,1]);axis([0,1,0,1]);hold off结果如下:整体结果如下:3.3 3.5 3.56 3.568 3.6 3.84序列收敛情况不收敛循环周期为2不收敛循环周期为4不收敛循环周期为8混沌混沌不收敛循环周期为32.5、对着书上的代码先输入到M文件里,然后再在命令窗口输入执行命令如:Martin(303,303,303,5000);即可。
高等数学2019-2020-2A(Ⅰ)

南京邮电大学2019 /2020 学年第 二 学期《 高等数学A (I)下》测验试卷答案及评分标准院(系) 班级 学号 姓名一、选择题(本大题分5小题,每小题3分,共15分)1、考虑二元函数),(y x f z =的下列四条性质: (1) (,)f x y 在点(,)00x y 连续; (2) (,)x f x y 、(,)y f x y 在点(,)00x y 连续;(3) (,)f x y 在点(,)00x y 可微分; (4) (,)00x f x y 、(,)00y f x y 存在。
则下列选项中正确的是 ( A )(A ) (2) ⇒(3) ⇒(1) (B ) (3)⇒ (2) ⇒(1) (C ) (3) ⇒(4) ⇒(1) (D ) (3)⇒ (1) ⇒(4) 2、设函数),(y x f z =在),(00y x 处取得极大值,则函数),()(0y x f x =ϕ在0x 处与函数),()(0y x f y =ψ在0y 处 (A )(A ) 一定都取得极大值 (B ) 恰有一个取得极大值 (C ) 至多有一个极大值 (D ) 都不能取得极大值 3、二次积分=⎰⎰−dx y x f dy Ry Ry 20202),( (D)(A )ρθρθρθπθd f d R ⎰⎰sin 0)sin ,cos ( (B )ρρθρθρθπθd f d R ⎰⎰sin 0)sin ,cos ((C )ρθρθρθπθd f d R ⎰⎰20sin 20)sin ,cos ( (D )ρρθρθρθπθd f d R ⎰⎰20sin 20)sin ,cos (4、函数223y y x z −=在点)2,1(A 处沿点A 指向点)4,2(B 方向的方向导数为 (C ) (A ) 25 (B ) 25−(C ) 52 (D ) 52− 装订 线 内 不 要 答 题自觉遵 守 考 试 规 则,诚 信 考 试,绝 不 作 弊5、设),(y x f 是连续函数,交换二次积分⎰⎰x e dy y x f dx ln 01),(的积分次序为 ( B )(A ) ⎰⎰x e dx y x f dy ln 01),( (B ) ⎰⎰e e y dx y x f dy ),(10(C )⎰⎰e x dx y xf dy 1ln 0),( (D )⎰⎰1),(dx y x f dy e ey二、填空题(本大题分5小题,每小题4分,共20分)1、化三重积分(,,)d d d Ωf x y z x y z ⎰⎰⎰为三次积分为110(,,)xxydx dy f x y z dz −⎰⎰⎰,其中Ω是由双曲抛物面xy z =及平面10x y +−=,0z =所围成的闭区域.2、曲线⎩⎨⎧==22xz y x 在点)1,1,1(处的切线方程为411121−==−z y x - 3、设,arctanx y z = 则=)1,1(dz dy dx 2121+- 4、函数),(y x z z =由方程0),(2222=−−y z x z F 所确定,其中函数F 可微,则=∂∂x z )(211F F z F x '+''5、函数)ln(222z y x u ++=在)2,2,1(-M 处的梯度=M u grad )2,2,1(92− 三、(本题9分) 设),,()2(xyxy g y x f z +−=其中函数)(t f 二阶可导,),(v u g 具有二阶连续偏导数,求,x z ∂∂yx z∂∂∂2.解:),(),()2()(221221xyxy g x y y x y xy g y x f x y g y g f x z '−'+−'=−'+⋅'+'=∂∂ ··············4分)1(1)1(22221222112112xg x g x y g x g y x g x g f y x z ⋅''+⋅''−'−'+⋅''+⋅''+''−=∂∂∂ ··············3分2232211112g xyg x g xy g f ''−'−'+⋅''+''−= ··············2分 四、(本题9分) 求函数)(),(22y y x e y x f x ++=的极值。
南京邮电大学高数书上的习题答案下册

南京邮电大学高数书上的习题答案下册南京邮电大学 《高等数学》(下册) 习题参考答案第七章 习题7.12.(1);)()(32⎰⎰⎰⎰+≥+DDd y x d y x σσ (2);)()(23⎰⎰⎰⎰+≥+DDd y x d y x σσ (3);1⎰⎰⎰⎰⎰⎰ΩΩ>xyzdv xyzdv (4);)()(2222222⎰⎰⎰⎰⎰⎰ΩΩ++≤++dv z y x dv z y x3. (1);02π≤≤I (2);10036ππ≤≤I(3);33323323ππ≤≤-I习题7.2 1.(1) ;),(),(4420402⎰⎰⎰⎰-yy x dx y x f dy dy y x f dx 或(2);),(),(2222220⎰⎰⎰⎰-----y r y r rx r r rdx y x f dy dy y x f dx 或(3) ;),(),(),(22121121121⎰⎰⎰⎰⎰⎰+yyxxdx y x f dy dx y x f dy dyy x f dx 或(4)222222221411142411142414(,)(,)(,)(,)x x x x x x x x dx f x y dy dx f x y dy dx f x y dy dx f x y dy----------------+++⎰⎰⎰⎰⎰⎰⎰⎰或.),(),(),(),(2222222241.11141144124421⎰⎰⎰⎰⎰⎰⎰⎰----------------+++y y y y y y y y dx y x f dy dx y x f dy dx y x f dy dx y x f dy 2.(1) ;),(110⎰⎰xdy y x f dx (2) ;),(240⎰⎰xx dy y x f dx (3) ;),(21011⎰⎰--x dy y x f dx (4);),(212111⎰⎰+--y y dx y x f dy(5);),(1⎰⎰ee ydx y x f dy (6).),(),(arcsin arcsin 1arcsin 201⎰⎰⎰⎰---+yyydx y x f dy dx y x f dy ππ3.(1);320 (2);23π-(3);556 (4);1--e e (5);49(6).12-π 4..3π 5..27 6..6179.(1);)sin ,cos (20⎰⎰bad f d ρρθρθρθπ(2);)sin ,cos (cos 2022⎰⎰-θππρρθρθρθd f d(3) .)sin ,cos (1)sin (cos 021⎰⎰-+θθπρρθρθρθd f d10.(1);)sin ,cos ()sin ,cos (csc 024sec 040⎰⎰⎰⎰+θππθπρρθρθρθρρθρθρθd f d d f d (2);)(sec 2034⎰⎰θππρρρθd f d(3);)sin ,cos (1)sin (cos 201⎰⎰-+θθπρρθρθρθd f d(4) .)sin ,cos (sec tan sec 4⎰⎰θθθπρρθρθρθd f d11.(1) ;434a π(2) ;12- (3);)1(4-e π (4).6432π12.(1) ;222π+(2);)2(8-ππ(3) ;144a (4)).(3233a b -π13..42a π14.(1);6π (2) .32π15. (1);2ln 37 (2);21-e (3).21ab π16.(1)提示:作变换;⎩⎨⎧-=+=xy v yx u (2)提示:作变换.⎩⎨⎧+==yx v x u 习题7.3 1.(1) ;),,(111112222⎰⎰⎰+----y x x xdz z y x f dy dx (2);),,(22222221111⎰⎰⎰-+----x y x x x dz z y x f dy dx(3);),,(222111⎰⎰⎰+-y x x dz z y x f dy dx (4).),,(01010⎰⎰⎰-xy xdz z y x f dy dx2. (1);3641(2));852(ln 21- (3);0 (4);422R h π (5).2π-4. (1) ;81 (2) ;127π (3).316π5. (1);54π (2);674a π (3)).(15455a A -π6.直角坐标系 ;),,(22222221111⎰⎰⎰--+----y x y x x x dz z y x f dy dx柱面坐标系 ;),sin ,cos (22120⎰⎰⎰-ρρπρθρθρρθdz z f d d 球面坐标系.sin )cos ,sin sin ,cos sin (2024020⎰⎰⎰dr r r r r f d d ϕϕθϕθϕϕθππ7.(1) ;332π(2) ;233a π (3);6π (4)).455(32-π8. .)(422t f t π 9..4R k π习题7.41..)612655(2a π-+ 2..2π 3..162R5.(1);34,0πb y x ==(2);0,)(222=+++=y b a a ab b x(3);)(8)(3,0,03344⎪⎪⎭⎫ ⎝⎛--a A a A (4).43,0,0⎪⎭⎫ ⎝⎛6..796,572==y xI I7. (1) ;384a (2);157,0,02a z y x ===(3) .451126ρa8..])([2,02222h R a R a h G F F F z y x ++-+--===ρπ总习题71.(1) (C); (2) (A); (3) (B); (4) (D); (5) (B),(D).2. (1) ;32π(2) ;0 (3);2π (4);4μ(5) .344R π3.(1);94124R R ππ+ (2).π4. (1) ;3250π (2).328163a π-5..)]0(3[3hf h +π第八章 习题8.11.(1);),(,),(22⎰⎰==Ly Lxds y x x I ds y x y I μμ(2).),(),(,),(),(⎰⎰⎰⎰==LL L L dsy x ds y x y y dsy x ds y x x x μμμμ。
(南京邮电大学)DSP习题答案汇总~~

(南京邮电⼤学)DSP习题答案汇总~~第⼀章习题1.1 在⼀间暗室⾥通过⼀个闪光频率为8Hz 的闪光灯观察⼀个以6Hz 为频率旋转的转轮。
求转轮表现出的转速并判断观察者对转轮旋转⽅向的判断正误。
若闪光灯频率变为12Hz ,16Hz 或24Hz ,重复上述问题。
本题涉及了转轮的问题,⽤到了公式)mod(s a f f f =,当a f 和f 符号相同时,观察者能观察到正确的转动⽅向;当a f 和f 符号相反时,观察者观察到的是错误的转动⽅向;否则,观察者不能辨别转轮的⽅向。
参考课本28页例题1.4.10。
1.2 对模拟信号x(t)=10sin(2πt)+10sin(8πt)+5sin(12πt) (其中t 以秒为单位)进⾏采样,采样频率s f =5Hz ,求x(t)的重建信号)(t x a 的表达式;证明两个信号具有相同的采样值,即)()(nT x nT x a =。
若采样率s f =10Hz ,重复上述问题。
本题通过证明说明了当a f1.3 以3Hz 的频率对信号x(t)=cos(5πt)+4sin(2πt)sin(3πt)进⾏抽样(其中t 以毫秒为单位)。
求(1)x(t)的重建信号)(t x a ;(2)写出重建信号是)(t x a ,但⼜不同于x(t)的另外两个信号x 1(t)和x 2(t)。
⽤到了公式)mod(s a f f f =,参见课本19页例1.4.7。
1.9 Consider the following sound wave, where t is in millisecond: x(t )=sin(10πt )+sin(20πt )+sin(60πt )+sin(90πt )This signal is prefiltered by an analog antialiasing prefilter H (f ) and then sampled at audio rate of 40kHz.The resulting samples are immediately reconstructed using an ideal reconstructor. Determine the output ya(t ) of the reconstructor in the following cases and compare it with the audible part of x(t ):a. When there is no prefilter ,that is, H(f )≡1.b. When H(f ) is an ideal prefilter with cutoff of 20kHz.c. When H(f ) is a practical prefilter that has a flat passband up to 20kHz and attenuates at arate of 48db?ocate beyond 20kHz.(You may ignore the effects of the phase response of the filter.)1.11 Give Eq.(1.5.4), prove the inverse DTFT property (1.5.5),that is,)(f X ∧=∞-∞=∑n x(nT)ejfTnπ-2 => x(nT)=-221fs fs sf )(f X ∧ejfTnπ2df1.12 Consider a pure sinusoid of frequency f 0 , x (t )=cos(2πf 0t ). Show that the spectrum of the sampled sinusoid x (n T) is : )(f X ∧=)]()([2100s s m mf f f mf f f T ++δ+--δ∑∞-∞=第⼆章习题2.1考虑⼀个3⽐特长的双极性⼆进制补码的逐次逼近A/D 转换器,其中满量程幅度为R =16V 。
南京邮电大学-高数书上的习题答案(下册)

南京邮电大学 《高等数学》(下册) 习题参考答案第七章 习题7.1 2.(1);)()(32⎰⎰⎰⎰+≥+DD d y x d y x σσ (2);)()(23⎰⎰⎰⎰+≥+DDd y x d y x σσ(3);1⎰⎰⎰⎰⎰⎰ΩΩ>xyzdv xyzdv (4);)()(2222222⎰⎰⎰⎰⎰⎰ΩΩ++≤++dv z y x dv z y x3. (1);02π≤≤I (2);10036ππ≤≤I (3);33323323ππ≤≤-I习题7.21.(1);),(),(442042⎰⎰⎰⎰-yy xdx y x f dy dy y x f dx 或(2);),(),(22222200⎰⎰⎰⎰-----y r y r rx r r rdx y x f dy dyy x f dx 或(3);),(),(),(22121121121⎰⎰⎰⎰⎰⎰+yyxxdx y x f dy dx y x f dy dyy x f dx 或(4)11121121(,)(,)(,)(,)dx f x y dy dx f x y dy dx f x y dy dx f x y dy ----+++⎰⎰⎰⎰⎰或.),(),(),(),(2222222241.11141144124421⎰⎰⎰⎰⎰⎰⎰⎰----------------+++y y y y y y y y dx y x f dy dx y x f dy dx y x f dy dx y x f dy2.(1);),(11⎰⎰xdy y x f dx (2);),(24⎰⎰xx dy y x f dx(3);),(21011⎰⎰--x dy y x f dx (4);),(212111⎰⎰+--y y dx y x f dy(5) ;),(1⎰⎰ee y dx y xf dy (6).),(),(arcsin arcsin 1arcsin 201⎰⎰⎰⎰---+yyydx y x f dy dx y x f dy ππ3.(1);320 (2);23π- (3);556 (4);1--e e (5);49 (6).12-π 4. .3π 5. .27 6. .617 9.(1);)sin ,cos (20⎰⎰bad f d ρρθρθρθπ(2);)sin ,cos (cos 2022⎰⎰-θππρρθρθρθd f d(3) .)sin ,cos (1)sin (cos 021⎰⎰-+θθπρρθρθρθd f d10.(1);)sin ,cos ()sin ,cos (csc 024sec 040⎰⎰⎰⎰+θππθπρρθρθρθρρθρθρθd f d d f d(2);)(sec 2034⎰⎰θππρρρθd f d (3);)sin ,cos (1)sin (cos 201⎰⎰-+θθπρρθρθρθd f d(4).)sin ,cos (sec tan sec 40⎰⎰θθθπρρθρθρθd f d11.(1) ;434a π (2);12- (3) ;)1(4-e π (4) .6432π12.(1) ;222π+ (2);)2(8-ππ(3) ;144a (4)).(3233a b -π 13..42a π14.(1);6π (2) .32π 15. (1) ;2ln 37 (2) ;21-e (3) .21ab π16.(1)提示:作变换;⎩⎨⎧-=+=x y v y x u (2)提示:作变换.⎩⎨⎧+==y x v xu习题7.3 1.(1) ;),,(111112222⎰⎰⎰+----y x x x dz z y x f dy dx (2);),,(22222221111⎰⎰⎰-+----x y x x x dz z y x f dy dx(3);),,(222111⎰⎰⎰+-y x x dz z y x f dy dx (4).),,(01010⎰⎰⎰-xy xdz z y x f dy dx2. (1);3641 (2) );852(ln 21- (3) ;0 (4) ;422R h π(5) .2π- 4. (1) ;81 (2) ;127π (3) .316π5. (1) ;54π (2) ;674a π (3) ).(15455a A -π6.直角坐标系 ;),,(22222221111⎰⎰⎰--+----y x y x x x dz z y x f dy dx柱面坐标系 ;),sin ,cos (22120⎰⎰⎰-ρρπρθρθρρθdz z f d d球面坐标系 .sin )cos ,sin sin ,cos sin (224020⎰⎰⎰dr r r r r f d d ϕϕθϕθϕϕθππ7.(1);332π (2) ;233a π (3) ;6π (4) ).455(32-π 8. .)(422t f t π 9..4R k π 习题7.4 1. .)612655(2a π-+ 2. .2π 3. .162R5.(1);34,0πby x == (2);0,)(222=+++=y b a a ab b x (3);)(8)(3,0,03344⎪⎪⎭⎫ ⎝⎛--a A a A (4) .43,0,0⎪⎭⎫⎝⎛6..796,572==y x I I 7. (1) ;384a (2) ;157,0,02a z y x === (3) .451126ρa8. .])([2,02222h R a R a h G F F F z y x ++-+--===ρπ 总习题71.(1) (C); (2) (A); (3) (B); (4) (D); (5) (B),(D).2. (1) ;32π (2) ;0 (3) ;2π (4) ;4μ (5) .344R π 3.(1) ;94124R R ππ+ (2).π4. (1);3250π (2).328163a π- 5..)]0(3[3hf h +π 第八章 习题8.1 1.(1);),(,),(22⎰⎰==Ly Lx ds y x x I ds y x y I μμ(2).),(),(,),(),(⎰⎰⎰⎰==LL LL dsy x ds y x y y dsy x ds y x x x μμμμ 2. (1) ;212+n aπ (2);)12655(121-+ (3) ;2)42(-+a e a π(4);)1(232--e (5) ;9 (6) .152563a 3.质心在扇形的对称轴上且与圆心的距离为ϕϕsin a 处. 4..6πk6. (1) ;23a π- (2) ;2π- (3) ;1514-(4) ;3233ππa k - (5) ;13 (6) .217. (1);334 (2) ;11 (3) ;14 (4) .3328. ;)(12z z mg - 9. .23a π10. (1) ;2),(),(ds y x Q y x P L⎰+ (2);41),(2),(2ds xy x xQ y x P L⎰++(3).)],()1(),(2[2ds y x Q x y x P x x L⎰-+-11..941),,(3),,(2),,(22ds yx z y x yR z y x xQ z y x P L⎰++++习题8.21. (1) ;8 (2).301 2. (1) ;12 (2) ;0 (3) ;24a π(4) ;42π (2) .6742sin - 3. (1) ;25 (2) ;236 (3) ;5 (4) .23- 4. (1) ;2122122y xy x ++ (2) ;cos cos 22y x x y + (3) .12124223yy ye e y x y x +-+习题8.3 1. ⎰⎰∑+=.),,()(22dS z y x z y I x μ 3. (1);313π (2) ;30149π (3) .10111π 4. (1) ;614 (2) ;427- (3) ;)(22h a a -π (4) .215644a5. ).136(152+π6. (1) ;10527R π (2) ;23π (3) ;21 (4) .817.(1)⎰⎰∑++;)5325253(dS R Q P (2) .4412222⎰⎰∑++++dS yx R yQ xP8. .8π习题8.4 1. (1);23(2) ;5125a π (3) ;81π (4) ;525a π (5) .4π2. (1) ;0 (2) ;)62(23a a - (3) .108π 3. (1) ;222z y x ++ (2) ;)sin(2)sin(2xz xz xy x ye xy-- (3) .2x习题8.51. (1) ;32a π- (2) );(2b a a +-π (3) ;20π- (4) .29-2. (1) ;642k j i ++ (2) ;j i +(3) )]cos()sin(cos [2xz xy z x -i )sin(cos z y -j ]cos )cos([22y x xz z y -+k 3. (1) ;0 (2) .4- 4. (1) ;2π (2) ;12π 6. .0 总习题81. (1) ;12a (2) ;4a π (3) ;4 (4) ;6π-(5) ;)(22223γβαπ++R (6) ;23R π (7) );(C (8) ).(B2.(1);2arctan 222222ln )41(3ln 2+--+++ππ(2) ;18π (3) ;0 (4) ;2a π (5).162π 3. (1) ;arctan 2RHπ (2) ;414h π- (3) ;2π4. .85. .216. .27..93,3,3,3max abc W c b a ====ςηξ 8..23 习题9. 11. (1) 2(1)ln(1)=++n n u n n ; (2) 11(1)-+=-n n n u n ;(3)1(1)!-=-n n x u n ; (4) 1sin (1)-=-n n nx u n .2. (1) 收敛; (2) 发散; (3) 收敛; (4) 发散.3. (1) 发散; (2) 发散; (3) 发散; (4) 收敛; (5) 收敛; (6) 发散.4. 提示:利用数列收敛与其子列收敛之间的关系.5. 提示:21221++=+n n n s s u .习题9. 21. (1) 发散; (2) 收敛; (3) 发散; (4) 收敛; (5) 收敛; (6) 收敛.2. (1) 发散; (2) 收敛; (3) 发散; (4) 收敛; (5) 收敛; (6) 收敛;(7) 收敛; (8)<b a 时收敛,>b a 时发散,=b a 不能确定.3. (1) 收敛; (2) 收敛; (3) 收敛; (4) 发散; (5) 收敛; (6) 收敛.4. (1) 绝对收敛; (2) 条件收敛; (3) 条件收敛; (4) 发散; (5) 条件收敛; (6) 条件收敛. 6. 提示:11≤n n a b a b . 7.211()2≤+n u n.8. 提示:0≤-≤-n n n n c a b a . 9. 提示:≤⋅n n n n a b a b .10. 当1<a 时绝对收敛,当1>a 时发散,1=a 时条件收敛,1=-a 时发散. 习题 9. 31. (1) 1,[1,1]=-R ; (2) 111,[,]222=-R ; (3) 1,[1,1]=-R ;(4) ,(,)=+∞-∞+∞R ; (5) 3,[0,6)=R ; (6) 1,[1,0)2=-R .2. (1) 11ln (11)21+-<<-xx x; (2)3424(11)(1)-<<-x x x ; (3)32(11)(1)-<<-x x ; (4) ln(1)(11)1---<<-xx x x.3. ()arctan ,[1,1];=-s x x .4. (1) 4π; (2) 4; (3) ln 22π-; (4) 2(1)ππ-+. 习题9. 41. 20cos (1),(,)(2)!∞==-∈-∞+∞∑nnn x x x n . 2. (1) 210,(,)(21)!+∞=∈-∞+∞+∑n n x x n ; (2) 11ln 2(1),(2,2]∞-=+-∈-∑n n n n x x na ;(3) 0(ln ),(,)!∞=∈-∞+∞∑n nn a x x n ; (4) 2121(1)21,(,)(2)!-∞=-+∈-∞+∞∑n n n n x x n ; (5) 111(1),(1,1](1)+∞+=-+∈-+∑n n n x x x n n ; (6) 21211(1)211arctan 2,[,]2122-∞-=-+∈--∑n n n n x x n .3. (1) 11011()(1),(3,1)23∞++=-+∈-∑nn n n x x ; (2) 111(1)(1),(0,2]ln10∞-=--∈∑nn n x x n ; (3)(1),(,)!∞=-∈-∞+∞∑nn ex x n ;(4) 221111(1)[())],(,)2(2)!33ππ∞+=-++∈-∞+∞∑n n n n x x x n .4. (1) 1110(1)[1],(1,1)2+∞++=--+∈-∑n n n n x x ; (2)211(1)(1)(2),(1,3)2∞+=-+-∈∑n n n n x x .5. 21212(2)!(),[1,1]2(21)(!)∞+=+∈-+∑n n n x x x n n ,()2220,2,(0)[(2)!],2 1.2(!)=⎧⎪=⎨=+⎪⎩n k n k f k n k k6. 11(),(,)(1)!-∞==∈-∞+∞+∑n n nx f x x n .7. (1) 0.9848; (2) 0.9461.习题9. 52. (1) 11cos(43)cos(41)()[],(21),0,1,2,4341ππ∞=--=-≠+=±±--∑n n x n xf x x k k n n ;(2)121[1(1)]()(1)()(){cos sin },(21),0,1,4πππ-∞=-----+=++≠+=±∑n n n b a a b a b f x nx nx x k k n n2,±;(3) 21212(1)()4cos ,3π+∞=-=+-∞<<+∞∑n n f x nx x n ; (4) 33211(1)()[(3cos sin )],(21),0,1,2,69ππππ-∞=--=+-≠+=±±+∑nn e e f x nx n nx x k k n .3. (1) 12124(1)()cos ,[,]41ππππ-∞=-=+∈--∑n n f x nx x n ;(2) 221111(1)(1)1(1)(){cos []sin },211ππππππ--∞=+----+---=+++++∑n n nn e e n ne f x nx nx n n n(,)ππ∈-x .4. 123121(1)6(){(31)[1(1)]}sin ,ππ-∞=-=++---∑n n n f x nx n n n(0,)π∈x .5. 211(1)()cos ,[0,]4πππ∞=--=+∈∑nn f x nx x n .6. 121cos ()sin ,(0,)(,)ππ∞=-=∈⋃∑n nhf x nx x h h n ; 12sin ()cos ,[0,)(,)πππ∞==+∈⋃∑n hnhf x nx x h h n. 习题9. 61. (1) 221(1)12()cos ,(,)4ππ∞=--=+∈-∞+∞∑n n l ln xf x x l n ; (2)112()sin ,,0,1,2,2ππ∞==-≠=±±∑n E E n xf x x kT k n T ;(3) 1221111(1)()cos 2,(,)12ππ+∞=-=+∈-∞+∞∑n n f x n x x n . 2. (1) 2212(1)()sin sin sin ,[0,)(,]22221ππππ∞=-=+∈⋃-∑n x n n n x l lf x x l l l n ;2211211()cos(cos 1)cos ,[0,)(,]2221ππππππ∞=-=++-∈⋃-∑n x n n x l lf x n x l ll n;(2) 33141(1)()sin ,[0,1]ππ∞=--=∈∑nn f x n x x n ;221121(1)()cos ,[0,1]6ππ∞=+-=-∈∑nn f x n x x n . 3. 2222015411()cos(21),[1,1],26(21)πππ∞∞===-+∈-=+∑∑n n f x n x x n n .4. (1) 1sin ()12,(0,2)ππ∞==--∈∑n nxf x x n ; (2) 12(1)(1)1()sin ,(0,)πππ∞=---=∈∑n n f x nx x n;(3) 12sin 2(),(0,)2ππ∞=-=-∈∑n nxf x x n ; (4) 112(1)()1sin ,(1,1)ππ+∞=-=-+∈-∑n n f x n x x n.5. 112(1)51sin ,(3,5)ππ+∞=--=-+∈∑n n x n x x n.6. 0(1)51,(3,5)ππ+∞=-∞≠--=-+∈∑n in xn n i x e x n ;7. 121()sin cos ,2,0,1,2,τπτπτπ∞==+≠±+=±±∑n E E n n t f t t kl k l n l l.总习题 91. (1) C ; (2) C ; (3) B ; (4) A ; (5) A .2. (1) 8; (2) 1,01,0><≤≤p p p ; (3)2=R ;(4) 2ln(1),[2,0)(0,2),[2,2),()210;⎧--∈-⋃⎪-=⎨⎪=⎩x x s x x x (5)14-. 3. (1) 收敛; (2) 发散; (3) 发散; (4) 发散; (5) 1>a 时收敛, 01<≤a 时发散;(6) 01<<a 时收敛, 1>a 时发散, 1=a 且1>k 时收敛, 1=a 且01<≤k 时发散. 4. (1) 绝对收敛; (2) 绝对收敛; (3) 条件收敛; (4) 条件收敛. 5. 12>k 时收敛, 12≤k 时发散. 6. (1) 11[,)33-; (2) 11(,)-e e; (3) (2,0)-; (4) (1,1)-.7. (1)111ln arctan (11)412++--<<-x x x x x ; (2)11(1)ln(1),(1,0)(0,1],()0,0,1,1;⎧-++∈-⋃⎪⎪==⎨⎪=-⎪⎩x x x s x x x (3)21(02)(2)-<<-x x x ;(4)2222((2)+<-x x x . 8. (1)1ln 34; (2)2227. 9. (1)881()(11)∞+=--<<∑nn n xxx ; (2) 210(1)(11)421π∞+=-+-≤<+∑n n n x x n . 10. 3318sin(21)()(0);32(21)πππ∞=-=≤≤-∑n n x f x x n .习题10.11.(1) 1 ; (2)2 ; (3)1 ; (4) 2 ,2.(1)不是; (2)不是; (3)不是; (4)是,4.(1)22(1)4y y '+= ; (2)2220x y xy y '''-+=, 5.(1)222x y y += ; (2)2xy xe =, 6.20x yy '+= , 习题10.21.(1)22(1)x y C -+= ; (2)222(1)(1)x y Cx ++= (3)sin cos y x C = ; (4)1010xyC -+=(5)()(1)y C x a ay =+- ;(6)(y x C =2.(1)212ln(1)2ln(1)xy e e -=+-+; (2)arctan 4xy e π-= ;(3)(1)1x y += ;(4)ln tan2xy =, 3.()ln 1f x x =+ 4.(1)cxy xe =;(2)3()x yy Ce=;(3)tan()y x x C +=+(4)2sin()y x C x=5.(1)33x y Ce-=;(2)()xy x C e -=+;(3)(ln ln )y x x C =+(4)2sin 1x C y x +=-; (5)12(1)yx y Ce =+; (6)()x x C y e +=6.(1)x ae ab e y x+-=;(2)1cos xy xπ--=;(3)y x = (4)sin 2sin 1xy ex -=+-7.(1)535(5)2y x Cx +=;(2)82291(1)x C x =-+-; (3)22212xy Cex x =---;(4)3243(12ln )xyx x C -=-+8.(1)21xy e =-;(2)2xy e =-9.(1)是,323x xy y C +-=;(2)是,cos cos y x x y C +=(3)是,2(1)e C θρ+=10.(1)4242x xy y C +-=;(2)arctan()xx C y=+(3arctan xC y=; (4)2x y C y x =+ 11.约3.4秒,13.(1)2321234ln 2x y x C x C x C x C =++++; (2)12()xy C x e C -=-+;(3)1211y C x C =-+;(4)221124(1)()C y C x C -=-习题10.3 1.(1) 相关;(2)无关;(3)无关; (4)相关,2.212()x y C C x e =+, 3.(1)212xy C x C e-=+ ; (2)212(21)xy C e C x =++5.2212()(1)1y C x x C x =-+-+,6.(1)2211210(21)!!(2)!!(1(1))((1))(2)!!(21)!!kk k k k k k k y C x C x k k +∞+∞+==-=+-+-+∑∑; (2)211(21)!!kk x y k +∞==+-∑ ,7.(1)2312x x y C e C e -=+; (2)412xy C C e =+(2)(1(112xxy C e C e =+;(4)212(cossin )22x y eC x C x -=+ (5)当0a <时,12y C C e =+;当0a =时,12y C C x =+;当0a >时,12y C C =+;(6)当1λ>时,((12xxy C e C e λλ--=+;当1λ=时,12x x y C e C xe λλ--=+;当1λ<时,12()x y e C C λ-=+;(7)1234cos sin x xy C e C e C x C x -=+++;(8)123cos sin y C x C x C =++; (9)1234()cos ()sin y C C x x C C x x =+++;(10)y =21234()()x xC C x e C C x e -+++; (11)2123()ax y e C C x C x =++;(12)1234()cos sin xy C C x e C x C x =+++;8.(1)342x xy e e =+;(2)2(2)x y x e-=+;(3)2(42)x y x e-=-;(4)(cos3sin 3)xy e x x -=+; (5)1cos sin 2x t t t =+ 9.1cos3sin 33y x x =- ,10.(1)3122x xy C e C e =++;(2)2121()(1)4xy C C x ex =+++; (3)3212123x y C C e x x x =+---; (4)121cos sin cos 2y C x C x x x =+-;(5)61275cos sin 7474x xy C e C e x x =+++;(6)212231(cossin )sin 2cos 22226262x y eC x C x x x -=+-++, 11.(1)()cos ()sin xy Ae B Cx x D Ex x =++++; (2)4[()cos 2()sin 2]xy xe B Cx x D Ex x =+++; (3)2[()(cos 2sin 2)]xy e x B Cx D x E x =+++; (4)32[()(cos 2sin 2)]xy e x Ax Bx C D x E x =++++; (5)[()cos ()sin ]y x B Cx x D Ex x =+++; (6)2x y A =, 12.(1)21122xx y e e x -=---; (2)11cos3cos 248y x x =+; (3)(sin )x y e x x -=-; (4)2sin xy xe x =,13.(1)121(ln )y C x C x=+;(2)12ln y C C x ax =++;(3)212(ln )ln y x C x C x x =++; (4)2123(ln )y x C x C C x -=++,14.x a = ; 15.约1.9秒 ,总习题101.(3)23222(ln )33x x x C y =-++; (4)2212x y C y-= ;(5)1y C C =; (6)11y x=- ,2.()1f x =- 3.()cos sin x x x ϕ=+4.nx Cy = 或ny Cx = 5.22x y Cx += , 6.(1)21213()164xx y C C x ee -=+++; (2)12cos3cos sin sin 416x xy C x C x x =+--; (3)1211cos 2210x x y C e C e x -=+-+; (4)12))sin(ln )2x y C x C x x =++ , 7.()x ϕ=22121(1)22xxx xC e C e x e ++-, 8.1sin 2xx y e e x -=-- 9. 约2.8秒. 习题11. 1 1. (1) 32322Re ,Im ,,arctan 2()131313133π==-=+==-+∈z z z i z Argz k k Z ;(2) 31311Re ,Im ,,arctan 2()22223π==-=+==-+∈z z z i z Argz k k Z ; ;(3) 7726Re ,Im 13,13,arctan 2()227ππ=-=-=-+==-+∈z z z i z Argz k k Z ;(4) Re 1,Im 3,13,arctan 32()π==-=+==-+∈z z z i z Argz k k Z . 2. 1,11==x y . 3. (1)2cos sin22πππ=+=ii i e ; (2) 1cos sin πππ-=+=i i e ;(3) 6sincoscos()sin()3366πππππ--=-+-=ii i e; (4) 42sin )144πππ---=+-+i i i i .6. (1)8-i ; (2)16-i ; 7512124,πππ-ii i ee ; 11,22±i i i . 7. 1.9. (1) 以1为中心,半径为2的圆周; (2)直线3=-x ;(4) 中心在2-i ,半径为1的圆周及其外部区域;(4)不包含实轴的上半平面. 10. (1) 直线=y x ;(2)双曲线1=xy ;(3)双曲线1=xy 在第一象限中的一支; (4)抛物线21=+y x .习题11. 21. (1)123,22,8=-=-+=w i w i w i ; (2)0arg π<<w .2. (1)圆周2211()24-+=u v ; (2) 圆周2214+=u v ; (3)直线=-v u ; (4) 直线12=u . 3. (1)不存在; (2)0; (3)不存在.4. (1)处处连续; (2)除=±z i 外处处连续. 习题11. 32. (1) 在直线12=y 上可导,在复平面上处处不解析;(2) 0=上可导,在复平面上处处不解析; (3) 在0=z 点可导,在复平面上处处不解析; (4) 在复平面上处处可导、处处解析.3. (1) 除=±z i 外在复平面上处处解析, 222()(1)'=-+zf z z ;(2) 当0≠c 时除=-dz c外在复平面上处处解析, 2()()-'=+ad bc f z cz d .4. 3,1,==-=l n m 3()=f z iz , 2()3'=f z iz . 习题11. 41. (1) -ei ; )i +; (3)1ch ; (4)sin12cos12ch i sh +.2. (1)1ln 2(2),24i k k Z ππ++∈; (2) 4ln 5arctan (21),3i k i k Z π-++∈; (3) 2,k e k Z π-∈; (4) 1(2)4ln 2ln 2(cossin ),22k ei k Z π-+∈. 3. (1) k π; (2) 2k ππ+; (3) (21)k i π+; (4) 4k ππ-, 这里0,1,2,k =±±.4. (1) k i π; (2)212k i π+; (3) 1(2)2k i π+, 这里0,1,2,k =±±.5. ln z 与Lnz 在除原点与负实轴外处处解析,且1()()Lnz lnz z''==. 6. Lnz w z e αα==对每个单值分支在除原点与负实轴外处处解析,且1()z z ααα-'=. 总习题 111. (1) 33333Re ,Im ,,22422z z z argz z i π=-====--; (2)充分,必要; (3)C ; (4)2,3,2a b c ==-=; (4) sin 1i ish =, 22()k ii e k Z ππ+-=∈, 1ln(1)ln 224i i π-=-.2. (1)2(1); (2)2222cossin,0,1,2,344k k i k ππππ-+-++=.3. (1)(22)i ; (2)2468tan,0,,,,45555i i e ααππππα-=. 6. ()f z 处处不可导、处处不解析.8. (1) ln 2(2),3i k k Z ππ++∈; (2) 2e -.习题12. 12. (1)31(3)3i +;(2)31(3)3i +;(3)31(3)3i +.3. (1)1566i -+;(2) 1566i -+. 4. (1)i ; (2) 2i .5. (1)4i π; (2) 8i π.6. (1)0; (2) 0.习题12. 21. (1) 0; (2) 0; (3) 0; (4) 0.2. 相等;不能利用闭路变形原理.3. 0.4. (1) 0; (2) π.5. i π.6. (1) 0; (2) 1(2)2sh i ππ-; (3) sin1cos1-; (4) 2211(tan1tan 11)122th ith -+++. 习题12. 32. (1)22e i π;(2)i a π;(3) eπ;(4)0;(5) 0;(6) 0;(7) 0;(8) 12i π.3. (1) 0;(2) 0,当1α>时;i ie απ-,当1α<时.4. 当α与α-都不在C 的内部时,积分值为0;当α与α-中有一个在C 的内部时,积分值为i π;当α与α-都在C 的内部时,积分值为2i π.习题12. 44. 2222,()(1)v x xy y C f z i z iC =+-+=++(C 为实数).5. (1)2(1)i z --;(2)2(1)i z iC -+ (C 为实数);(3)21iz +;(4)ln z C +.6. 当1p =±时,v 为调和函数;当1p =时, ()()z f z e C C R =+∈;当1p =-时,()()z f z e C C R -=-+∈.总习题 121. (1)D ; (2)D ; (3)C ; (4)D ;(5)B .2. (1)0; (2)π; (3)i π; (4)2i π;(5)12i π;(6)64i π.3. (1)0; (2)2i π; (3)ei π-; (4)(2)e i π-. 5. 2i π. 9. 12()u C ax by C =++.习题13. 14. (1) 收敛,极限为1-;(2) 收敛,极限为0;;(3) 收敛,极限为0;(4)发散.5. (1) 发散;(2) 发散; (3)绝对收敛; (4)条件收敛.6. (1)2;; (3)1; (4)1.习题13. 21. (1) i ; (2) 11(1)n n n z ∞-=+∑.2. (1)30(1),1nnn z R ∞=-=∑; (2)11,1n n nzR ∞-==∑; (3) 40(1),(2)!nnn z R n ∞=-=∞∑; (4) 212121(1),(2)!n nnn z R n -∞=+-=∞∑;(5)210,(21)!n n z R n +∞==∞+∑;(6) 20,!nn z R n ∞==∞∑. 3. (1) 11(1)(1),22n n n n z R -∞=--=∑; (2)211011(1)()(2),323n n n n n z R ∞++=---=∑;(3) 103[(1)],(13)n n n n z i R i ∞+=-+=-∑; (4) 11(1)(1),1n n n z R n -∞=--=∑. 习题13. 32. (1) 1(1)nn z ∞=---∑, 201(1)(2)nn n z ∞+=--∑;(2) 1(2)nn n z∞=-+∑,2(1)(1)nnn z ∞=---∑;(3) 23432121211()524816z z z z z z z++-------;(4) 112()(2),(2)()n nn n n n z i i i z i -∞∞++==+-+∑∑; (5) 2111()(1),01n n n n n z i z i i -∞-+=--<-<∑; 30(1)(1),1()n nn n n i z i z i ∞+=+-<-<+∞-∑; (6) 234111112!3!4!z z z z ---++.习题13. 41. (1)0z =,一级极点;z i =±,二级极点; (2)1z =-,一级极点;1z =,二级极点; (3)0z =,可去奇点; (4)0z =,三级极点;2(1,2,)k z k i k π==±±,一级极点; (5)z i =±,二级极点;(21)(1,2,)k z k i k =+=±,一级极点;(6)0z =,二级极点;1,2,)k ±=均为一级极点.2. (1)z a =, m n +级极点;(2) z a =,当m n >时为m n -级极点,当m n <时为n m -级 极点,当m n =时为可去奇点; (3) z a =为极点,级数为m 、n 中较大者;当m n =时z a =为极点, 级数小于或等于m , 也可能是可去奇点.7. (1)1Re [(),0]2s f z =-,3Re [(),2]2s f z =;(2)4Re [(),0]3s f z =-;(3)1Re [(),0]6s f z =-;(4)Re [(),0]0s f z =,1Re [(),](1),1,2,ks f z k k k ππ=-=±±.8. (1) 0;(2) 24e i π;(3) 2i π-;(4) 2i π.总习题 131. (1)D ; (2)C ; (3)A ; (4)D ;(5)B .2. (1)0; (2)1,1R z i =-≤;(3)31a -=-;(4)Re [()(),0](0)s f z g z f =;(5)一级极点, 4sin 1Re [,0]6z z s z -=.3. (1)1e ; (2)1; (3)2; (4)2;; 4. (1)1111,()lnarctan 412z R s z z z z +==+--; (2) 231,()(4)z R s z z -==-.5. (1) 101(1),33n n n z R ∞+=-+=∑; (2)11(1),1n n n z R ∞-=+=∑;(3) 210(1)(),(21)!nn n z R n π∞+=---=+∞+∑; (4)21(1),121n n n z R n ∞+=-=+∑. 6. (1) 在014z <-<内,101(1)54nn n z z ∞+=-=--∑; 在41z <-<+∞内,10145(1)n n n z z ∞+==--∑; (2) 在12z <<内,1221001()2(1)2nn n n n n z f z z ∞∞+++===--∑∑;在02z <-<11101(2)(2)()(1)(2)25n n n n n n i i f z i z z ++∞+=+--=+---∑; (3) 2101(1)sin (1),011(21)!nn n z z z n ∞--=-=--<-<+∞-+∑;(4) 1(1),011!z n n e z e z z n -∞=-=-<-<+∞-∑.8. (1)0z =为一级极点,z i =±为二级极点; (2)0z =为三级极点;(3)0z =为可去奇点,1z =为三级极点; (4)1z =为本性奇点,2()k z k i k Z π=∈ 为一级极点.9. (1)1Re [,](1)(),cos 22k z s k k k Z z ππππ++=-+∈; (2)42313Re [,]8(1)z s i i z +=-+, 42313Re [,]8(1)z s i iz +-=+; (3) 1Re [cos ,1]01s z =-; (4) 1Re [,0]0s zshz=, 11(1)Re [,],1,2,k s k i i k zshz k ππ--==±±.10. m -.11. (1)2i π-; (2)当3m ≥且为奇数时,原式12(1)(2)!n i n π-=-;当3m <或为偶数时,原式0=; (3)12i -; (4)26i π-. 12.. (1)2π; .。
南邮高等数学上练习册_最全答案

1.1 函数1、(1) x -- (2) ]3,0()0,( -∞ (3) 奇函数(4) )(101log 2<<-x xx(5)22+x (6)xe 1sin 2-2、⎪⎪⎪⎩⎪⎪⎪⎨⎧><<-==<<=e x e x e x e x e x e x g f 或或1011011)]([ 3、⎪⎩⎪⎨⎧>+-≤<--≤+=262616152)(2x x x xx x x f 4)(ma x =x f 1.2 数列的极限1、(1) D (2) C (3) D1.3 函数的极限1、(1) 充分 (2) 充要1.4 无穷小与无穷大1、(1) D (2) D (3) C (4) C1.5 极限运算法则1、 (1) 21-(2) 21(3) ∞ (4) 1- (5) 06(4) 1 (5) 4 (6) 1 4、a = 1 b = -11.6 极限存在准则 两个重要极限1、(1) 充分 (2) ω 0 (3) 3-e 2e2、(1)32(2) 2 (3) 1-e 1.7 无穷小的比较1、(1) D (2) A (3) C2、(1) 23- (2) 23 (3) 32-3、e1.8 函数的连续性与间断点1、(1) 2 (2) 跳跃 无穷 可去2、(1) B (2) B (3) B3、12e- 4、1,2a b ==5、(1))(2,0Z k k x x ∈+==ππ是可去间断点,)0(≠=k k x π是无穷间断点;(2) 0=x 是跳跃间断点,1=x 是无穷间断点 6、e b a ==,01.9 闭区间上连续函数的性质1、2、略1.10 总 习 题1、(1) 2 (2) },,,max{d c b a (3) 21(4) 2 (5) 2 8- (6) 2 (7)23(8) 0 1- (9) 跳跃 可去 (10) 2 2、(1) D (2) D (3) D (4) C (5) D (6) B (7) D (8) D (9) B (10) B3、(1)⎪⎩⎪⎨⎧≥<<-≤≤=11575115100190100090)(x x x x x p(2)⎪⎩⎪⎨⎧≥<<-≤≤=-=11515115100130100030)60(2x x x x x x xx p P (3)15000=P (元)。
南京邮电大学2013-2014第二学期高等数学A下期末自测试题及答案详解

南京邮电大学2013-2014学年第二学期《高等数学》(A 下)自测模拟试题及详细答案1.极限2221lim 1x x yx y x +→∞→⎛⎫+= ⎪⎝⎭2e .2.设()2y z x y x ϕ=++,其中ϕ具有连续二阶偏导数,则2z x y∂∂∂=2x ()''21()ln 1y x y x y x ϕ-+++. 3.曲面arctan()z xy =在点(1,1,)4P π处的法线方程为41122111z x y π---==-.4.函数2(,,)21f x y z z e xy =-++在点(2,1,0)处的方向导数的最大值为5.设2x u v z y u vz ⎧=-++⎨=+⎩确定u=u(x,y,z),v=(x,y,z),则u x ∂=∂12z zu -+. 6.幂函数21(1)9nnn x ∞=-∑的收敛区域是 (2,4)- . 7.设2,10()1,01x x f x x x --<≤⎧=⎨-<≤⎩,是周期为2的周期函数,则其傅里叶级数 在点x=4处收敛于12. 8.设2222y z R ++=∑:x 外侧,则2223/2()xdydz ydzdx zdxdyx y z ++=++∑⎰⎰4π. 9.已知22A=y +2z +xy ,=x +y +z ,i j k B i j k u r r r r u r r r r ,则div (A )B ⨯u r u r =3224x y z x z ---.10.设L 为取正向的圆周x 2+y 2=9,则曲线积分2(22)(4)Lxy y dx xx dy -+-⎰= 18π- .(用格林公式易) 二(8分).将函数f(x)= 212565xx x ---在点x 0=2处展开成泰勒级数,并指出其收敛域.解:若用泰勒级数2()0000000''()()()()()()'()()2!!n nf x x x f x x x f x f x f x x x n --=+-++++L L =2()1''(2)(2)(2)(2)'(2)(2)42!!n nf x f x f x n ---+-++++L L ,不易。
南京邮电大学数学实验练习题参考答案

南京邮电⼤学数学实验练习题参考答案第⼀次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作⼆维、三维⼏何图形,能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。
补充命令vpa(x,n) 显⽰x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx→∞- 程序:syms xlimit((1001*x-sin(1001*x))/x^3,x,0) 结果:1003003001/6程序: syms xlimit((1001*x-sin(1001*x))/x^3,x,inf) 结果: 01.2 cos1000xmxy e =,求''y 程序: syms xdiff(exp(x)*cos(1001*x/1000),2) 结果:-2001/1000000*exp(x)*cos(1001/1000*x)-1001/500*exp(x)*sin(1001/1000*x)1.3 计算221100xy e dxdy +??程序:dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1) 结果:2.139350195142281.4 计算44x dx m x+? 程序: syms xint(x^4/(1000^2+4*x^2)) 结果:1/12*x^3-1002001/16*x+1003003001/32*atan(2/1001*x)1.5 (10)cos ,x y e mx y =求程序: syms xdiff(exp(x)*cos(1000*x),10) 结果:-1009999759158992000960720160000*exp(x)*cos(1001*x)-10090239998990319040000160032*exp(x)*sin(1001*x) 1.6 0x =的泰勒展式(最⾼次幂为4).程序: syms xtaylor(sqrt(1001/1000+x),5) 结果:1/100*10010^(1/2)+5/1001*10010^(1/2)*x-1250/1002001*10010^(1/2)*x ^2+625000/1003003001*10010^(1/2)*x^3-390625000/1004006004001*10010^(1/2)*x^41.7 Fibonacci 数列{}n x 的定义是121,1x x ==,12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项(要求将结果⽤向量的形式给出)。
南邮概率答案(含解答过程)

(2,1)和(4,4)
P( A) 2 1 36 18
10
练习三
1. (1)已知 P( A) 0.3, P(B) 0.4, P( AB) 0.5,求 P(B | A B)。
解: P(B | A B) P(B ( A B))
P(A B)
P( AB) P( A) P(B) P( AB)
P( A) P( AB)
1 P( A) P( AB)
P( A) P(B) P( AB) 1 P( A) 1 P(B) P( AB)
1 0.3 0.5 0.2 1 1 0.3 1 0.4 0.5 0.8 4
(2)已知P( A) 1 , P(B | A) 1 , P( A | B) 1 ,求 P( A B) 。
解:以A表示事件“白漆10桶,黑漆3桶,红漆2桶”
P( A)
C1100C43C32 C 15
17
1 4 3 17 8
3 34
8
4.已知在10只晶体管中有2只是次品,在其中取两次, 每次任取一只,作不放回抽样,求下列事件的概率。
(1)两只都是正品 解:以A表示事件“两只都是正品”
P( A) 8 7 28 10 7 45
1
S {v | v 0}
A {v | 60 v 80}
2.设A、B、C 为三个事件试用A、B、C 表示下列事件
(1)A与B 不发生,而C 发生
ABC
(2)A,B,C 都不发生
ABC
(3)A、B、C 至少有一个发生
A B C
(4)A、B、C中恰有一个发生 ABC ABC ABC
(5)A、B、C 中恰有两个发生 ABC ABC ABC (6) A、B、C 中至多有两个发生
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
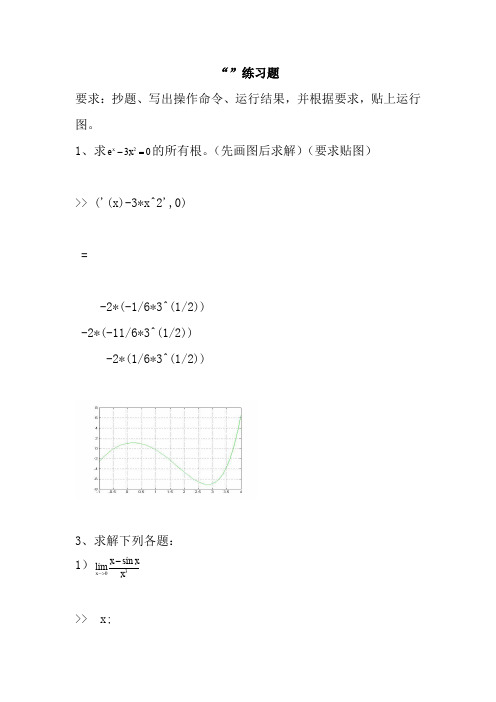
“”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根。
(先画图后求解)(要求贴图)>> ('(x)-3*x^2',0)=-2*(-1/6*3^(1/2))-2*(-11/6*3^(1/2))-2*(1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x->->> x;>> (((x))^3)=1/62) (10)cos ,x y e x y =求 >> x;>> ((x)*(x),10)=(-32)*(x)*(x)3)21/20(17x e dx ⎰精确到位有效数字)>> x;>> ((((x^2),0,1/2)),17)=0.544987104183622224)42254x dx x+⎰>> x;>> (x^4/(25^2))=125*(5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
>> t;>> ((1^2))(t);>> ()()=16)设函数(x)由方程e所确定,求y′(x)。
>> x y;*(y)(1);>> ()()=(x + (y))7)sin2xe xdx+∞-⎰>> x;>> ()*(2*x); >> (y,0)=2/58)08x =展开(最高次幂为)>> x(1);taylor(f,0,9)=- (429*x^8)/32768 + (33*x^7)/2048 - (21*x^6)/1024 + (7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + 2 + 19) 1sin (3)(2)x y e y =求>> x y;>> ((1));>> ((y,3),2)=-0.582610)求变上限函数x⎰对变量x的导数。
