QPSK系统的误码率和星座图仿真
BPSK QPSK 8PSK 16QAM等调制方式的性能仿真及频率利用率的对比及分析

引言 (2)1 BPSK QPSK 8PSK 16QAM 调制方式的性能仿真和频率利用率的对比分析 (2)1.1 BPSK QPSK 8PSK 的性能仿真 (2)1.2 16QAM 的性能仿真 (6)2 四种调制方式各自的使用场景 (9)3 能量利用率 (10)3.2 QPSK的能量效率 (10)3.3 8PSK的能量效率 (10)3.4 16QAM的能量效率 (11)结论 (11)参考文献 (11)引言随着信息事业的迅猛发展,对数字信号调制性能上的要求越来越高本文对BPSK QPSK 8PSK 16QAM等调制方式的性能进行仿真及频率利用率的对比及分析,主要对QPSK和16QAM的相关性能进行了阐述。
并对上述四种调制方式各自的使用场景进行总结。
同时分析以上四种方式的能量效率,即每比特能量消耗的对比分析。
1 BPSK QPSK 8PSK 16QAM 调制方式的性能仿真和频率利用率的对比分析1.1 BPSK QPSK 8PSK 的性能仿真BPS K调制方式:所谓BPSK就是根据数字基带信号的两个电平,使载波相位在两个不同的数值之间切换的一种相位调制方法。
在恒参信道条件下,相移键控(BPSK) 与幅移键控( AS K) 和频移键控( F S K) 相比,具有较高的抗噪声干扰性能,且能有效地利用所给定的信道频带,即使在有多径衰落的信道中也有较好的结果,所以BPSK是一种较好的调制方式。
四相相移键控( Q P S K ) 是一种性能优良,应用十分广泛的数字调制方式,它的频带利用率高,是二相相移键控( B P S K) 的2倍。
且Q P S K调制技术的抗干扰性能强,采用相干检测时其误码率性能与B P S K相同。
8PSK,即8 Phase Shift Keying,也就是八相相移键控的意思。
QPSK调制方式中,每个相位包含了2位二进制信息,而8PSK调制方式中,每个相位包含了3位二进制信息,因而编码效率提高了50%,但同时,8PSK的抗扰性比QPSK要低很多。
QPSK的系统仿真

QPSK的系统仿真作者:白根炜(陕西理工学院物电学院通信工程1104班,陕西汉中,723000)指导老师:井敏英[摘要]在数字信号的调制方式中4PSK是目前最常用的一种数字信号调制方式,它具有较高的频谱利用率、较强的抗干扰性、在电路上实现也较为简单。
调制技术是通信领域里非常重要的环节,一种好的调制技术不仅可以节约频谱资源而且可以提供良好的通信性能。
[关键词]4PSK; MATLAB ;调制QPSK system simulationAuth or:Bai GenWei(Garde11 class4 Major communication engineering,School of Physics and Telecommunication Engineering,Shaanxi University of Telechnology,shaanxi hanzhong 723000)Tutor:Jing Mingying[Abstract]4PSK modulation in the digital signal is the most common kind of digital signal modulation mode, it has high spectrum efficiency,Strong anti-interference, realized in the circuit is relatively simple. Modulation technology is a very important role in the field of communication, a kind of modulation technology can not only save the spectrum resources with good communication and can provide good performance.[Keywords] QPSK ,A TLAB, modulation目录引言 (1)1.QPSK通信系统的性能指标 (2)1.1 有效性指标 (2)1.2可靠性指标 (2)2. 基带信号处理 (3)3 调制/解调 (3)3.1. QPSK调制 (3)3.2 QPSK解调原理 (5)4.QPSK通信系统的仿真图和结果分析 (6)致谢 (8)参考文献 (9)引言QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
(完整word版)QPSK通信系统的设计与仿真

摘要介绍了数字通信中的QPSK调制解调的原理,通过用Matlab编写脚本程序对QPSK通信系统的发射和接收过程的具体实现进行模拟仿真,绘出信号在理想信道和加噪信道中模拟传输时的时域图,并对各模块进行了频谱分析,所得到的结果与理论基本相符,对于理解QPSK系统的性能并在系统的实际应用上作进一步的设计,提供了有效的参考依据。
通过利用MATLAB软件SUMLINK实现了QPSK通信系统的仿真,完成了QPSK通信系统的调制解调过程的仿真实现,使接收端能够准确地接收到来自发放的信息。
QPSK调制方式在通信工程中的应用十分广泛,其误码率随信噪比的增加而减少并最终可能为零。
在QPSK调制方式以后,还会出现进制更多的调制方式。
而我们着重要解决的问题也从如何提高相位谱利用率转变为如何减少误差以及提高传送速率。
阐述QPSK 调制解调的实现过程,并运用软件实现手段对信号变换过程加以分析,希望有所收获。
关键词:数字通信四相相位键控(Quadrature Phase Shift Keying,QPSK) MATLAB目录前言 0一、QPSK简介 (1)2.1 QPSK调制原理 (2)2.2 QPSK解调原理 (3)三、MATLAB仿真结果 (5)3.1 QPSK的产生及加噪仿真 (5)3.2 QPSK解调前后信号仿真 (5)3.3 QPSK码元恢复 (6)3.4误码率分析 (8)四、程序清单 (9)五、总结............................................................................................................................ 错误!未定义书签。
六、参考文献 (17)七、致谢.............................................................................................................................. 错误!未定义书签。
数字通信原理课程设计 误码性能仿真报告

SER 的一半,这与理论结果契合。此外,BER、SER 的 仿真值都与其理论值基本一致。
(a)
(b)
图 3.(a)QPSK 星座图,(b)SNR=14dB 时的星座图
图 2.BPSK 的误码率仿真值与理论值,仿真 100 次取平均值
尽管 BPSK 两星座点的正交分量均为 0,星座点 相似于 2ASK,但 BPSK 的误码性能优于 2ASK。BPSK 是二维调制,而 ASK 是一维,对于同一 SNR,在平均 信号功率、平均噪声功率均相同的情况下,BPSK 的 噪声被分散在两个维度中,因而 BPSK 的抗噪声性能 比 2ASK 更强。 (2)QPSK 在 AWGN 信道下的误码性能 QPSK 的误码率可由 BPSK 推导得到, QPSK 可以视 为两个正交的 BPSK,且两者相互独立。于是有如下 推导过程:
s(t ) Bk e j 2π f k t k
k 0
N 1
式中:Bk 为之前 16QAM 调制所得的第 k 路子信 道中的复输入数据。 由于 OFDM 信号表达形式如同逆离散傅里叶变换 (IDFT),所以可以用计算 IDFT 和 DFT 的方法进行 OFDM 调制和解调。OFDM 信号的实现基于快速傅里叶 变换(FFT),其调制原理[1]如图 11 所示:
图 5.Gray-16QAM 星座图
图 6.Gray-16QAM 与普通 16QAM 的 BER 对比
图 7.SNR=[5dB,10dB,15dB,20dB]时的 16QAM 星座图
判决时比较 r1 和 r2,如果 r1>r2,则判决为 1, 接收正确,反之则误码。此算法与 2FSK 比较判决的 调制解调原理相契合。仿真程序据此设计。 2FSK 误码性能的仿真 2000 次的仿真结果如图 8 所示。从图 8 中可以看出,SNR 达到 13dB 时,基本 可实现无差错数据传输。
基于matlab的QPSK与BPSK信号性能比较仿真

┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (1)第二章QPSK通信系统原理与仿真 (1)2.1 QPSK系统框图介绍 (1)2.2QPSK信号的调制原理 (2)2.2.1QPSK信号产生方法 (2)2.2.2QPSK星座图 (2)2.3QPSK解调原理及误码率分析 (3)2.3.1QPSK解调方法 (3)2.3.2QPSK系统误码率 (3)2.4QPSK信号在AWGN信道下仿真 (4)第三章BPSK通信系统原理与仿真 (4)3.1BPSK信号的调制原理 (4)3.2BPSK解调原理及误码率分析 (4)第四章QPSK与BPSK性能比较 (5)4.1QPSK与BPSK在多信道下比较仿真 (5)4.1.1纵向比较分析 (5)4.1.2横向比较分析 (7)4.2仿真结果分析 (7)4.2.1误码率分析 (7)4.2.2频带利用率比较 (7)附录 (8)代码1 (8)代码2 (8)代码3 (10)代码4 (12)┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
2.在相同信息速率条件下,四进制数字调制系统的传码率是二进制系统的1/4倍,这一特点使得四进制码元宽度是二进制码元宽度的2倍,码元宽度的加大,可增加每个码元的能量,也可减小码间串扰的影响。
(完整)QPSK系统的误码率和星座图仿真

(完整)QPSK系统的误码率和星座图仿真编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)QPSK系统的误码率和星座图仿真)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)QPSK系统的误码率和星座图仿真的全部内容。
目录一、课题内容………………………………………..…。
……。
..1二、设计目的……………………………………….。
…。
…。
…。
1三、设计要求…………………………………………………。
.1四、实验条件................................................。
....。
(1)五、系统设计....................................................。
.。
.. (2)六、详细设计与编码……………………………。
……………。
.41. 设计方案………………………………。
…….…..……。
42。
编程工具的选择……………………………………。
…。
43。
程序代码…………………………………….。
.………。
54. 运行结果及分析 (8)七、设计心得………………………………………。
……….。
9八、参考文献……………………………….………。
………。
10一、课题内容基于MATLAB或C语言模拟仿真OFDM通信系统。
主要功能:1、搭建基带OFDM系统仿真平台,实现OFDM信号体制与解调;2、能够画出输入数据与输出数据的星座图;3、能在不同信噪比信道的情况下,对信号进行误码分析。
3、能够和理论误码率公式比较二、设计目的1、综合应用《Matlab原理及应用》、《信号与系统》、《通信原理》等多门课程知识,使学生建立通信系统的整体概念;2、培养学生系统设计与系统开发的思想;3、培养学生利用软件进行通信仿真的能力。
QPSK调制解调实验

实验一QPSK 调制实验一、实验目的1、掌握QPSK 的调制解调原理。
2、掌握QPSK 的软件仿真方法。
3、掌握QPSK 的硬件设计方法。
二、预习要求1、掌握QPSK 的编解码原理和方法。
2、熟悉matlab 的应用和仿真方法。
3、熟悉DSP 和FPGA 的开发方法。
三、实验原理1、QPSK 调制的工作原理多相相移键控(MPSK ),特别是四相相移键控(QPSK )是目前移动通信、微波通信和卫星通信中最常用的载波传输方式。
四相相移键控(QPSK )信号的正弦载波有4个可能的离散相位状态,每个载波相位携带2个二进制符号,其信号表达式为:)cos()(i c i t A t S θω+= i =1,2,3,4 0≤t ≤TsTs 为四进制符号间隔,{i θ:i=1,2,3,4}为正弦波载波的相位,有四种可能状态。
如以下矢量图所示:如图为QPSK 的相位图,QPSK 的相位为(-3π/4,-π/4,π/4,3π/4)。
对于QPSK :)sin cos cos (sin )sin()(i c i c i c i t t A t A t S θωθωθω+=+= 0≤t ≤Ts由于21cos ±=i θ 21s i n ±=i θ所以:)cos )(sin )((2)(t t Q t t I A t S c c i ωω+=21cos )(±==i t I θ21s i n )(±==i t Q θQPSK 正交调制器方框图如图所示:I图QPSK 正交调制器方框图在kTs ≤t ≤(k+1) Ts(Ts=2Tb)的区间,QPSK 产生器的输出为:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=-+-=--+=+++=+=----11),43cos(11),4cos(11),43cos(11),4cos()(1111n n c n n c n n c n n c a a t A a a t A a a t A a a t A t s πωπωπωπω2、QPSK 的相干解调的基本工作原理 QPSK 的相干解调方框图如图所示:图QPSK 的相干解调方框图当调制信号为I =1,Q =1时,由调制原理,调制输出信号为t t t S c c i ωωcos sin )(+=,在没有噪声和延时的理想状态时,解调器的输入t t t S t r c c i ωωcos sin )()(+==,则I 检测器的输出为:t t t t t t r c c c c c ωωωωωsin cos sin sin sin )(+=t t t t c c c c ωωωω2sin 212cos 21212sin 21)2cos 1(21+-=+-=则Q 检测器的输出为:t t t t t t r c c c c c ωωωωωcos cos cos sin cos )(+=t t t t c c c c ωωωω2sin 212cos 21212sin 21)2cos 1(21++=++=用截止频率小于2c ω的低通滤波器对I 检测器的输出滤波后得到1/2,即为逻辑1;对Q 检测器的输出滤波后得到1/2,即为逻辑1。
QPSK误码率仿真分析

[键入文字]通信工程专业《通信原理》课程设计题目 QPSK的误码率仿真分析学生姓名谭夕林学号 **********所在院(系)陕西理工学院物理与电信工程学院专业班级通信工程专业 1102 班指导教师魏瑞完成地点陕西理工学院物理与电信工程学院实验室2014年 3 月 12 日通信工程专业课程设计任务书院(系) 物理与电信工程学院专业班级通信工程专业1102班学生姓名谭夕林一、课程设计题目 QPSK的误码率仿真分析二、课程设计工作自 2014 年 2 月 24 日起至 2014 年 3 月 16 日止三、课程设计进行地点: 物理与电信工程学院实验室四、课程设计的内容要求:利用仿真软件等工具,结合所学知识和各渠道资料,对QPSK在高斯通道下的误码率进行研究分析指导教师魏瑞系(教研室)通信工程系接受任务开始执行日期2014年2月24日学生签名谭夕林QPSK的误码率仿真分析谭夕林陕西理工学院物理与电信工程学院通信1102班,陕西汉中723003)指导教师:魏瑞【摘要】为实现QPSK应用到无线通信中,该文对QPSK系统性能进行了理论研究。
介绍了QPSK调制解调原理,对高斯白噪声信道的系统性能进行了研究,分析对比了在高斯白噪声信道下的系统误码性能。
为基于副载波QPSK无线激光通信系统的研究奠定了理论基础。
使用MATLAB中M语言完成QPSK的蒙特卡罗仿真,得出在加性高斯白噪声的信道下,传输比特错误率以及符号错误率。
并将比特错误率与理论值相比较,并得出关系曲线。
使用simulink搭建在加性高斯白噪声信道下的QPSK调制解调系统,其中解调器使用相关器接收机。
并计算传输序列的比特错误率。
通过多次运行仿真得到比特错误率与信噪比之间的关系。
【关键词】: QPSK,误码率,仿真,星座图【中图分类号】 TN702 [文献标志码] AQPSK BER simulation analysisTan Xilin(Grade11,Class2,Major of Communication Engineering,School of Physics and telecommunication Engineering of Shaanxi University of Technology, Hanzhong 723003,China)Tutor:Wei Rui[Abstract]For the application of the QPSK (Phase-Shift-Keying) to the wireless laser communication, this paper emphasizes the system of QPSK's performance, theoretically. In the paper, the principle of the QPSK's modulation and demodulation were introduced in brief and the performance of the system at white Gaussian noise (AWGN) channel was also analyzed carefully. The above results provide the theoretical foundation for the wireless laser communication system based on the QPSK with e the MATLAB language to complete Monte Carlo simulation of QPSK, and to obtain the transmission sequence bit error rate and symbol error rate in the additive white Gaussian noise channel, comparing it with the theoretical value, then get curve. The second aspect is to learn how to use Simulink and the functions and principles of various modules. Then we use Simulink to create the model of QPSK through additive white Gaussian noise channel. And take the advantage of the Correlator receiver to complete the operation of demodulation. Then calculate the transmission sequence bit error rate. By running the simulation repeatedly, we can get the relationship between the bit error rate and SNR.Keywords: QPSK, BER, simulation, constellation目录摘要 (3)Abstract (4)一绪论 (6)1.1 课题背景及仿真 (6)1.1.1QPSK系统的应用背景简介 (6)1.1.2QPSK实验仿真的意义 (6)1.1.3仿真平台和仿真内容 (6)二系统实现框图和分析 (7)2.1QPSK调制部分 (7)2.2QPSK解调部分 (8)三QPSK特点及应用领域 (9)3.1QPSK特点 (9)3.2误码率 (10)3.3QPSK时域信号 (10)3.4扩充认知QPSK-OQPSK (10)3.5QPSK的应用领域 (11)四使用simulink搭建QPSK调制解调系统 (12)4.1信源产生 (12)4.2QPSK系统理论搭建 (13)五仿真模型参数设置及结果 (15)5.1仿真附图及参数设置 (15)5.2仿真结果 (16)5.3误码率曲线程序及其仿真结果 (17)六仿真结果分析 (19)七总结与展望 (20)致谢 (21)参考文献 (21)一.绪论1.1课题背景及仿真:1.1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
QPSK系统设计与仿真实验指导书

QPSK系统设计与仿真实验指导书QPSK系统仿真实验一、实验目的1、了解QPSK工作原理。
2、了解不同信道条件下对QPSK信号带来的影响,分析QPSK的信号特点,找出恰当的解调方法。
3、研究Simulink的仿真原理与过程。
4、通过仿真实现QPSK,并能通过数据及图形来分析不同信道条件下的系统性能。
5、掌握Matlab软件的基本使用方法,学会Simulink环境的基本操作与应用。
二、实验原理正交相移键控(QPSK)是一种恒包络调制技术,广泛用于无线传感器网络、短距无线通信、移动通信以及卫星通信领域。
人们常常用数学建模或使用基于数学模块的硬件或软件来实现其仿真设计,比如用Matlab编程或直接调用Simulink的工具箱中的QPSK基带调制器模块等,但这种仿真过程或者要编写一套复杂的程序代码,或者只能调用工具库中的封装模块,不便于读者具体地了解、修改和增强QPSK调制解调器的设计功能,也无法修复任何因系统不完善而导致的错误。
为此进行具有功能清晰、性能良好和实现过程简单等优点的QPSK调制解调器仿真设计具有重要教学和科研意义。
QPSK的调制过程可以描述为:串行输入的二进制数据流被分成I路和Q路2个不同的路径传输,其中“I”是用来与数据波形“同步”的成分,“Q”是与数据波形“正交”的部分,即原始输入数据的偶数位被分配到I路,奇数位被分配到Q路。
之后,分别用I路和Q路数据对载波进行调制,即用4种离散相位变化中的1种来代表要传输的每对比特位。
QPSK的解调过程是在接收端对接收信号作2个混频运算,I路的混频使用一个和载波频率相同的余弦波来乘已调信号,Q路的混频使用一个和载波频率相同的正弦波乘已调信号。
它们分别经过低通滤波和基带处理后,将被合并为一路数据,在正确的排序下,重现原始数据。
其中,为信号一个符号(symbol)的时间,为信号一个符号(symbol)的能量,传输的信息:,){(1,1),(1,-1),(-1,-1),(-1,1)}。
PAM、PSK、QAM数字调制解调系统误码性能仿真

数字通信系统传输误码性能仿真(一)摘要:脉冲幅度调制(PAM)、频移键控(PSK)、正交振幅调制(QAM)等数字信号调制解调模式在经典和现代通信中得到广泛应用。
不同调制方式在不同的条件下传输可靠性能不尽相同。
Matlab/Simulink包含多种仿真模块库,可以对各种通信调制方式的调制解调进行仿真,并验证其传输可靠性能。
关键字:通信系统、仿真、PAM、PSK、QAMAbstract:Digital signal modulation and demodulation modes such as pulse amplitude modulation (PAM), frequency shift keying (PSK), quadrature amplitude modulation (QAM)are widely used in classical and modern communication. The transmission reliability of different modulation are different under different conditions. Matlab/Simulink contains a variety of library of simulation modules for various communications modem modulation to simulate and verify its transmission reliability.Keywords: communication systems, simulation, PAM,PSK,QAM0 引言系统仿真是进行协议标准制定、算法分析优化和产品总体设计的重要步骤,对验证算法和理论的设计性能、缩减设计开发时间、降低总体成本具有重要意义。
传统的系统仿真方法主要使用基于C语言等计算机编程语言的方法,工作量大,效率低,仿真程序的可读性、可靠性、可移植性无法达到现代大中型系统的要求。
bpskqpsk8psk16qam等调制方式的性能仿真及频率利用率的对比及分析

引言 (2)1 BPSK QPSK 8PSK 16QAM 调制方式的性能仿真和频率利用率的对比分析 (2)1.1 BPSK QPSK 8PSK 的性能仿真 (2)1.2 16QAM 的性能仿真 (6)2 四种调制方式各自的使用场景 (9)3 能量利用率 (10)3.1 BPSK的能量效率 (10)3.2 QPSK的能量效率 (10)3.3 8PSK的能量效率 (10)3.4 16QAM的能量效率 (11)结论 (11)参考文献 (11)引言随着信息事业的迅猛发展,对数字信号调制性能上的要求越来越高本文对BPSK QPSK 8PSK 16QAM等调制方式的性能进行仿真及频率利用率的对比及分析,主要对QPSK和16QAM的相关性能进行了阐述。
并对上述四种调制方式各自的使用场景进行总结。
同时分析以上四种方式的能量效率,即每比特能量消耗的对比分析。
1 BPSK QPSK 8PSK 16QAM 调制方式的性能仿真和频率利用率的对比分析1.1 BPSK QPSK 8PSK 的性能仿真BPS K调制方式:所谓BPSK就是根据数字基带信号的两个电平,使载波相位在两个不同的数值之间切换的一种相位调制方法。
在恒参信道条件下,相移键控(BPSK) 与幅移键控( AS K) 和频移键控( F S K) 相比,具有较高的抗噪声干扰性能,且能有效地利用所给定的信道频带,即使在有多径衰落的信道中也有较好的结果,所以BPSK是一种较好的调制方式。
四相相移键控( Q P S K ) 是一种性能优良,应用十分广泛的数字调制方式,它的频带利用率高,是二相相移键控( B P S K) 的2倍。
且Q P S K调制技术的抗干扰性能强,采用相干检测时其误码率性能与B P S K相同。
8PSK,即8 Phase Shift Keying,也就是八相相移键控的意思。
QPSK调制方式中,每个相位包含了2位二进制信息,而8PSK调制方式中,每个相位包含了3位二进制信息,因而编码效率提高了50%,但同时,8PSK的抗扰性比QPSK要低很多。
QPSK误码率仿真分析要点

QPSK误码率仿真分析要点QPSK(Quadrature Phase Shift Keying)是一种常用的调制技术,用于在传输过程中将数字信号调制成模拟信号。
在QPSK中,两个正交的相位信号被组合在一起,每个符号传输两个比特,因此它具有较高的传输效率。
误码率(BER)是衡量数字通信系统性能的一个重要指标,误码率仿真分析是评估QPSK系统性能的一种常用方法。
以下是QPSK误码率仿真分析的要点:1.系统建模:在进行误码率仿真分析之前,需要对QPSK系统进行建模。
这包括确定符号周期、传输速率、信道模型等参数,并根据这些参数生成QPSK调制信号。
2.先验码字分布:QPSK系统中使用的码字通常是先验分布的,即每个码字发生的概率是已知的。
在进行误码率仿真分析时,需要根据这些先验概率来模拟发送端生成码字的过程。
3.加性高斯白噪声:在传输过程中,信号会受到各种干扰,其中最主要的是加性高斯白噪声(AWGN)。
在进行误码率仿真分析时,需要将AWGN添加到信号中,以模拟实际信道中的噪声情况。
4.解调器设计:在接收端,需要设计一个解调器来将接收到的信号转换回数字信号。
这需要使用相干解调技术来提取信号的相位信息。
常用的相干解调算法包括差分解调和相干解调。
5.误码率测量:在进行误码率仿真分析时,需要定义用于测量误码率的指标。
常用的指标包括误码率(BER)、误比特率(BER)等。
这些指标可以帮助评估系统在不同信噪比下的性能。
6.仿真参数选择:误码率仿真分析中的仿真参数选择对结果影响很大。
需要选择适当的信噪比范围、仿真次数等参数来获得准确的误码率结果。
7.结果分析:最后,需要对得到的误码率仿真结果进行分析。
可以绘制误码率曲线,比较不同信噪比下的性能差异。
还可以进行误码率与比特率的关系分析,以评估系统的传输容量。
总之,QPSK误码率仿真分析是评估QPSK系统性能的一种重要方法。
通过对系统建模、先验码字分布、加性高斯白噪声、解调器设计、误码率测量、仿真参数选择和结果分析等方面的探索,可以更好地理解QPSK系统的性能,并为系统设计和优化提供指导。
数字信号频带传输的仿真设计
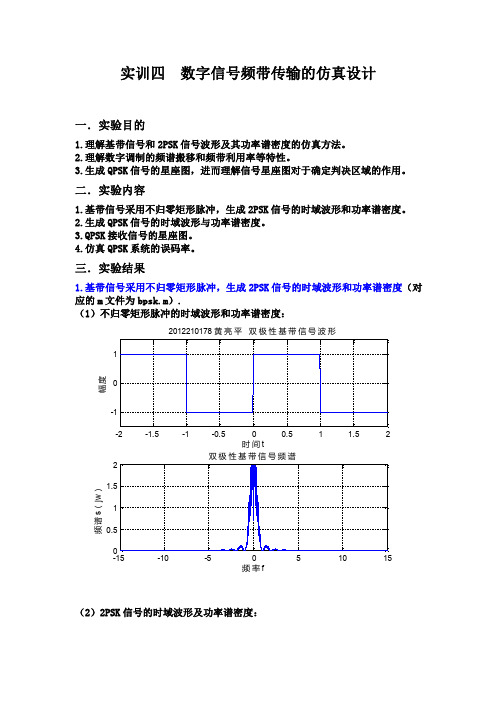
实训四数字信号频带传输的仿真设计一.实验目的1.理解基带信号和2PSK 信号波形及其功率谱密度的仿真方法。
2.理解数字调制的频谱搬移和频带利用率等特性。
3.生成QPSK 信号的星座图,进而理解信号星座图对于确定判决区域的作用。
二.实验内容1.基带信号采用不归零矩形脉冲,生成2PSK 信号的时域波形和功率谱密度。
2.生成QPSK 信号的时域波形与功率谱密度。
3.QPSK 接收信号的星座图。
4.仿真QPSK 系统的误码率。
三.实验结果1.基带信号采用不归零矩形脉冲,生成2PSK 信号的时域波形和功率谱密度(对应的m 文件为bpsk.m).(1)不归零矩形脉冲的时域波形和功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 双极性基带信号波形-15-10-505101500.511.52频率f 频谱s (j w )双极性基带信号频谱(2)2PSK 信号的时域波形及功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 BPSK 已调信号波形-15-10-505101500.51频率f 频谱s (j w )BPSK 已调信号频谱2.基带信号采用不归零矩形脉冲或滚降系数为1的升余弦谱,生成4PSK 信号的时域波形和功率谱密度(不归零矩形脉冲对应的m 文件为rectqpsk.m,升余弦脉冲对应的m 文件为rcosqpsk.m).(1)不归零矩形脉冲的时域波形和功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 双极性基带信号波形-15-10-505101500.511.522.5频率f 频谱s (j w )双极性基带信号频谱(2)QPSK 信号的时域波形与功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 QPSK 已调信号波形-15-10-505101500.511.5频率f 频谱s (j w )QPSK 已调信号频谱(3)基带信号为滚降系数为1的升余弦脉冲信号经QPSK 调制得到的已调信号与功率谱密度:02468101214161820-11时间t幅度QPSK 已调信号波形2 2.2 2.4 2.6 2.83 3.2 3.4 3.6 3.8402468频率幅度QPSK 信号频谱3、QPSK 系统的调制和解调原理随机产生10^5个二进制信息数据,串并变换后进行4PSK 调制。
(完整word版)QPSK调制解调的simulink仿真

摘要QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
四相相移键控信号简称“QPSK”.在现代通信系统中,调制与解调是必不可少的重要手段。
所谓调制,就是把信号转换成适合在信道中传输的形式的一种过程。
解调则是调制的相反过程,而从已调制信号中恢复出原信号。
本课程设计主要介绍通过进行QPSK调制解调的基带仿真,对实现中影响该系统性能的几个重要问题进行了研究。
针对QPSK的特点,调制前后发生的变化,加上噪声后波形出现的各种变化,通过星座图、眼图、波形图等来观察。
程序设计与仿真均采用MATLAB集成环境下的Simulink仿真平台,最后仿真详单与理论分析一致。
关键词:QPSK调制解调; Simulink仿真平台;MATLAB7.0 ;噪声。
目录一、实验目的 (1)二、实验内容 (1)三、设计原理 (1)1. Simulink简介 (1)2。
QPSK星座图 (2)3。
QPSK的调制 (2)4。
QPSK的解调 (4)四、设计步骤 (4)五、设计结果及分析 (8)1。
信号调制解调后的时域波形图 (9)2.数据源的频谱图 (9)3.QPSK调制后的频谱 (8)4.QPSK解调后的频谱 (8)5。
误码曲线图 (9)六、体会 (12)七、参考文献 (12)一、实验目的1、理解电子信号通信原理.2、熟悉系统建模方法。
3、配置电子信号,设计相关应用方法。
二、实验内容1、利用Matlab—Simulink建立系统模型.2、信号参数:信息速率80Hz,载波中心频率15MHz,采样频率120MHz。
3、依据相关参数,产生QPSK调制信号.4、设计一种方法完成QPSK信号的数据解调。
三、设计原理1. Simulink简介Simulink是MATLAB最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。
QPSK通信系统MC仿真

实验二 QPSK通信系统的 MonteCarlo 仿真目录一.实验目的 (2)二.实验原理 (2)1. 未加信道纠错码的QPSK调制通信系统框图: (2)2.加信道编码的QPSK的调制通信系统 (2)三.实验内容 (3)(一)未加信道纠错编码的QPSK调制通信系统 (3)1)最大投影点准则进行判决 (6)2)最小欧氏距离准则进行判决 (10)(二)信道纠错编码(7,4)汉明码+QPSK调制的通信系统 (11)四.实验结果分析及结论 (13)五.实验问题及解决 (14)六.实验心得 (14)一.实验目的1.掌握QPSK通信系统的组成原理以及Monte Carlo仿真方法2.比较编码信号和未编码信号在随机信道中的传输,加深对纠错编码的理解二.实验原理1. 未加信道纠错码的QPSK调制通信系统框图:1). 生成二进制信源序列d(i)(i=0,1)。
首先产生0~1均匀分布的随机序列,并规定:当随机数<0.25时,规定为d=00;当0.25<随机数<0.5时,规定为d=01;当0.5<随机数<0.75时,规定为d=10;当0.75<随机数<1时,规定为d=11。
2). 将二进制序列映射为四进制m。
规定:当d=00时,m=0;当d=01时,m=1;当d=11时,m=2;当d=10时,m=3。
3). 对m映射为QPSK两路正交信号s。
规定:m=0时,s=(1,0);m=1时,s=(0,1);m=2时,s=(-1,0);m=3时,s=(0,-1)。
4). 产生两路正交噪声信号n。
5). 利用最小欧氏距离准则或最大投影点准则对信道输出信号r=s+n进行判决,对判决输出信号进行信号重构。
6). 计算误码率和误信率。
r .注:最大投影点准则:向量r在向量s上的投影为:s2.加信道编码的QPSK的调制通信系统在QPSK调制之前加信道纠错编码(7,4),在解调之后进行信道译码,其他操作和上述1原理相同。
qpsk

基于MATLAB的QPSK传输系统仿真默认分类2008-12-04 10:50:13 阅读900 评论2 字号:大中小订阅/blog/#m=0一.基本原理PSK是利用载波振荡相位的变化来传送数字信息。
最早出现的是二相相移键控BPSK,BPSK是利用载波的相位偏移直接表示数字信号,假若规定:已调载波与未调载波同相表示数字信号“0”,与未调载波反相表示数字信号“1”,则已调信号的表达式为,其中:d(t)为双极性数字基带信号,为载波频率。
为了提高信道频带利用率,提出了多进制数字相移键控(MPSK),它用多个相位状态的正弦振荡分别代表不同的数字信息,最典型的是四相相移键控(QPSK)。
BPSK和QPSK在码元转换点上都可能产生相位突变,使得频谱高频滚降缓慢,带外辐射大。
为了消除相位跳变,在QPSK基础上提出了偏移四相相移键控(OQPSK)。
它将同相和正交两支路的码流在时间上错开了半个码元周期,信号相位只跳变0、。
二.程序及结果分析程序如下:if nargin > 2error('Too many input arguments');elseif nargin==1f=1;endif f〉1;error('Frequency must be bigger than 1');end%*-*-*-*-*-*l=length(g);r=l/2;re=ceil(r);val=re-r;if val~=0;error('Please insert a vector divisible for 2'); end%*-*-*-*-*-*t=0:2*pi/99:2*pi;cp=[];sp=[];mod=[];mod1=[];bit=[];for n=1:2:length(g);if g(n)==0 && g(n+1)==1;die=sqrt(2)/2*ones(1,100);die1=-sqrt(2)/2*ones(1,100);se=[zeros(1,50) ones(1,50)];elseif g(n)==0 && g(n+1)==0;die=-sqrt(2)/2*ones(1,100);die1=-sqrt(2)/2*ones(1,100);se=[zeros(1,50) zeros(1,50)];elseif g(n)==1 && g(n+1)==0;die=-sqrt(2)/2*ones(1,100);die1=sqrt(2)/2*ones(1,100);se=[ones(1,50) zeros(1,50)];elseif g(n)==1 && g(n+1)==1;die=sqrt(2)/2*ones(1,100);die1=sqrt(2)/2*ones(1,100);se=[ones(1,50) ones(1,50)];endc=cos(f*t);s=sin(f*t);cp=[cp die]; %Amplitude cosinosp=[sp die1]; %Amplitude sinomod=[mod c]; %cosino carrier (Q)mod1=[mod1 s]; %sino carrier (I)bit=[bit se];endbpsk=cp.*mod+sp.*mod1;subplot(2,1,1);plot(bit,'LineWidth',1.5);grid on;title('Binary Signal')axis([0 50*length(g) -1.5 1.5]);subplot(2,1,2);plot(bpsk,'LineWidth',1.5);grid on;title('QPSK modulation')axis([0 50*length(g) -1.5 1.5]);结果分析:运行得到理想信道和加噪信道中调制解调信号的波形如下:图一理想信道和加噪信道中调制解调信号的波形图二正交支路中的数据和调制信号通过编程模拟QPSK过程,得到信号传输过程中的时域图.从图一可以知道:在理想情形下,信号的解调和调制过程中,信号只出现了很小的波动,在加噪信道中信号的波动范围虽然变大,但不会影响到解调后信号的识别.即在Matlab编程模拟的过程中,QPSK调制解调即使在加有白噪声干扰时,也能进行有效的解码.根据相位调制的特点,我们可以从图二中看到调制信号(正交支路)在二进制信号每发生一次电平的跃变时发生相位跳变.在信噪比低于7dB 的情形下,理论误码率和实际误码相差很小.从这些图形中我们可以发现Matlab软件很好地模拟出了数字通信系统的QPSK过程.即使在噪声干扰下,解调输出信号与输入信号的波形也保持着基本的一致,对信号的恢复不会有大的影响.三.模块及结果分析图三QPSK传输系统结果分析:QPSK(正交移相键控)基带调制信号的频谱图和星座图如下:图四QPSK(正交移相键控)基带调制信号的频谱图和星座图仿真结果说明在相同传输条件下,QPSK、OQPSK调制以比BPSK调制高1倍的速率传输信息,QPSK误码率高于BPSK约30倍,OQPSK误码率高于BPSK约1.4倍。
基于matlab的QPSK与BPSK信号性能比较仿真

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (2)第二章QPSK通信系统原理与仿真 (2)2.1 QPSK系统框图介绍 (2)2.2 QPSK信号的调制原理 (3)2.2.1 QPSK信号产生方法 (3)2.2.2 QPSK星座图 (4)2.3 QPSK解调原理及误码率分析 (4)2.3.1 QPSK解调方法 (4)2.3.2 QPSK系统误码率 (5)2.4 QPSK信号在AWGN信道下仿真 (5)第三章BPSK通信系统原理与仿真 (6)3.1 BPSK信号的调制原理 (6)3.2 BPSK解调原理及误码率分析 (7)第四章QPSK与BPSK性能比较 (8)4.1 QPSK与BPSK在多信道下比较仿真 (8)4.1.1 纵向比较分析 (8)4.1.2 横向比较分析 (10)4.2 仿真结果分析 (10)4.2.1 误码率分析 (10)4.2.2 频带利用率比较 (10)附录 (11)代码1 (11)代码2 (11)代码3 (14)代码4 (16)┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
QPSK系统的误码率和星座图仿真

QPSK系统的误码率和星座图仿真《MATLAB实践》报告一、引言数字调制就是把数字基带信号的频谱搬移到高频处,形成适合在信道中传输的带通信号。
基本的数字调制方式有振幅键控(ASK)、频移键控(FSK)、绝对相移键控(PSK)、相对(差分)相移键控(DPSK)。
在接收端可以采用想干解调或非相干解调还原数字基带信号。
数字信号的传输方式分为基带传输和带通传输。
然而,实际中的大多数信道(如)无线信道具有丰富的低频分量。
为了使数字信号在带通信道中传输,必须用数字基带信号对载波进行调制,以使信号与信道的特性相匹配。
通信系统的抗噪声性能是指系统克服加性噪声影响的能力。
在数字通信系统中,信道噪声有可能使传输码元产生错误,错误程度通常用误码率来衡量。
因此,与分析数字基带系统的抗噪声性能一样,分析数字调制系统的抗噪声性能,也就是求系统在信道噪声干扰下的总误码率。
误码率(BER:biterrorratio)是衡量数据在规定时间内数据传输精确性的指标。
误码率是指错误接收的码元数在传输总码元数中所占的比例,更确切地说,误码率是码元在传输系统中被传错的概率,即误码率=错误码元数/传输总码元数。
如果有误码就有误码率。
误码的产生是由于在信号传输中,衰变改变了信号的电压,致使信号在传输中遭到破坏,产生误码。
噪音、交流电或闪电造成的脉冲、传输设备故障及其他因素都会导致误码(比如传送的信号是1,而接收到的是0;反之亦然)。
误码率是最常用的数据通信传输质量指标。
它表示数字系统传输质量的式是“在多少位数据中出现一位差错”。
误信率,又称误比特率,是指错误接收的比特数在传输总比特数中所占的比例,即误比特率=错误比特数/传输总比特数。
在数字通信系统中,可靠性用误码率和误比特率表示。
数字调制用“星座图”来描述,星座图中定义了一种调制技术的两个基本参数:(1)信号分布;(2)与调制数字比特之间的映射关系。
星座图中规定了星座点与传输比特间的对应关系,这种关系称为“映射”,一种调制技术的特性可由信号分布和映射完全定义,即可由星座图来完全定义。
QPSK调制解调系统的systemview仿真设计

正文一、课程设计目的1.加深对所学的通信原理知识的理解。
2.熟练应用systemview 仿真软件进行通信系统进行仿真设计。
3.增强分析问题和解决问题的能力,了解通信系统的新技术、新发展。
二、课程设计题目及要求题目:QPSK 调制解调系统的systemview 仿真设计设计任务:1.理解QPSK 数字调制解调基本原理。
2设计V.26标准的QPSK 调制解调系统,其调制信号的码元速率为2.4kb/s ,经串并变换后I 、Q 通道的码元速率为1.2kb/s ;调制载波为1.8khz 的正弦波,数据采样频率为9.6kb/s 。
3.合理设置各模块参数,在systemview 平台进行系统仿真。
4.观察QPSK 调制信号波形及功率谱密度,观察低通滤波器输出波形的眼图。
三、QPSK 调制器的原理及原理框图对于该系统的仿真,关键是构建QPSK 调制与解调系统,具体的QPSK 调制与解调仿真系统如下。
在QPSK 中,数字序列相继两个码元的4种组合对应4个不同相位的正弦载波,即00、01、10、11分别对应)4cos(0πω+t A ,)4cos(0πω-t A ,)43cos(0πω+t A ,)43cos(0πω-t A ,其中0≤t <2T ,T 为比特周期。
图6(a)是QPSK 相位矢量图,图中I 表示同相信号,Q 表示正交信号。
图6(b)是QPSK 星座图,星座图中星座间的距离越大,信号的抗干扰能力就越强,接收端判决再生时就越不容易出现误码。
星座间的最小距离表示调制方式的欧几里德距离,欧几里德距离d 可表示为信号平均功率S 的函数。
QPSK 信号的欧几里德距离与平均功率的关系为S d 2=。
QPSK 的矢量图和星座图QPSK调制器的原理框图四、电路图1.QPSK系统原理仿真总电路图2.子系统--串并变换子系统电路图(50)3.波形恢复子系统电路图(51)4.并串变换子系统电路图.(52)①参数设置Token34:伪随机PN序列发生器(Amp=1V,Rate=2400Hz,Levels=2)。
QPSK下的误码率分析

通信系统原理讨论题(数字频带部分)1.MQAM 的频带利用率和误比特率分析多元正交振幅调制是两个相互正交的同频载波调制后调制信号的双边带调制,利用这种已调信号在同一带宽内频谱正交的性质来实现两路并行的数字信息传输。
MQAM 信号调制框图如下图所示经过MQAM 调制系统后MQAM 信号表示式可表示为000012()cos sin ()()MQAM i i i i S t A a w t A b w t t t ϕϕ=+= (1)i a 、i b 是了已调MQAM 信号在信号空间中的坐标点,200/2E A T =为MQAM 信号最小幅度的信号能量。
若已调信号的最大幅度为1,则MQAM 信号星座图上信号点间的最小距离为1MQAMd L ==- (4)MQAM 信号采用正交相干解调方法时, 其解调器原理图如下图所示。
对于MQAM 其相干解调输出,其同相与正交支路“相关器”输出的信号加噪声混合值为由计算得:符号错误概率为:MQAM 平均能量为:以平均能量表示平均误符号概率为了传输和检测方便,同相和正交支路的L 进制码元一般为双极性码元,其间隔相同。
当L 为偶数时,L 个信号电平取为±1、±3、…±(L -1)。
如果M=L 2为2的偶数次方,则方型星座的MQAM 信号可等效为同相和正交支路的L 进制抑制载波的ASK 信号之和。
所以MQAM 信号是可看作由同相和正交支路的进制的ASK 信号叠加而成,故它的功率谱是两支路信号功率谱的叠加。
故由计算得频带利用率为2.4QAM,4PSK 和2PSK 的有效性和可靠性比较 MQAM 信号表示式可表示为b s 22b 2log log log 2R R M ML B B η====[]bit/(s Hz)⋅其中(ai ,bi)为QAM 同相项和正交项系数,E0 是QAM 最小幅度载波信号能量,T 为符号间隔。
M=4的QAM 信号系数:4QAM: 在信号表示式中,若k θ值仅可以取4π和-4π,k A 值仅可以取+A 和-A ,其星座图如下图所示QAM (M=4)的具体表示式为:由上两种调制方式表达式可知只有已调信号包络有根号2系数之差,4个相位也完全对应相等分别表示一个双比特符号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q P S K系统的误码率和星座图仿真-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN《MATLAB实践》报告——QPSK系统的误码率和星座图仿真一、引言数字调制就是把数字基带信号的频谱搬移到高频处,形成适合在信道中传输的带通信号。
基本的数字调制方式有振幅键控(ASK)、频移键控(FSK)、绝对相移键控(PSK)、相对(差分)相移键控(DPSK)。
在接收端可以采用想干解调或非相干解调还原数字基带信号。
数字信号的传输方式分为基带传输和带通传输。
然而,实际中的大多数信道(如)无线信道具有丰富的低频分量。
为了使数字信号在带通信道中传输,必须用数字基带信号对载波进行调制,以使信号与信道的特性相匹配。
通信系统的抗噪声性能是指系统克服加性噪声影响的能力。
在数字通信系统中,信道噪声有可能使传输码元产生错误,错误程度通常用误码率来衡量。
因此,与分析数字基带系统的抗噪声性能一样,分析数字调制系统的抗噪声性能,也就是求系统在信道噪声干扰下的总误码率。
误码率(BER:bit error ratio)是衡量数据在规定时间内数据传输精确性的指标。
误码率是指错误接收的码元数在传输总码元数中所占的比例,更确切地说,误码率是码元在传输系统中被传错的概率,即误码率=错误码元数/传输总码元数。
如果有误码就有误码率。
误码的产生是由于在信号传输中,衰变改变了信号的电压,致使信号在传输中遭到破坏,产生误码。
噪音、交流电或闪电造成的脉冲、传输设备故障及其他因素都会导致误码(比如传送的信号是1,而接收到的是0;反之亦然)。
误码率是最常用的数据通信传输质量指标。
它表示数字系统传输质量的式是“在多少位数据中出现一位差错”。
误信率,又称误比特率,是指错误接收的比特数在传输总比特数中所占的比例,即误比特率=错误比特数/传输总比特数。
在数字通信系统中,可靠性用误码率和误比特率表示。
数字调制用“星座图”来描述,星座图中定义了一种调制技术的两个基本参数:(1)信号分布;(2)与调制数字比特之间的映射关系。
星座图中规定了星座点与传输比特间的对应关系,这种关系称为“映射”,一种调制技术的特性可由信号分布和映射完全定义,即可由星座图来完全定义。
二、QPSK系统的原理四相相移调制是利用载波的四种不同相位差来表征输入的数字信息,是四进制移相键控。
QPSK是在M=4时的调相技术,它规定了四种载波相位,分别为45°,135°,225°,275°,调制器输入的数据是二进制数字序列,为了能和四进制的载波相位配合起来,则需要把二进制数据变换为四进制数据,这就是说需要把二进制数字序列中每两个比特分成一组,共有四种组合,即00,01,10,11,其中每一组称为双比特码元。
每一个双比特码元是由两位二进制信息比特组成,它们分别代表四进制四个符号中的一个符号。
QPSK中每次调制可传输2个信息比特,这些信息比特是通过载波的四种相位来传递的。
解调器根据星座图及接收到的载波信号的相位来判断发送端发送的信息比特。
在QPSK体制中,由其矢量图(图1)可以看出,错误判决是由于信号矢量的相位因噪声而发生偏离造成的。
例如,设发送矢量的相位为45°,它代表基带信号码元“11”,若因噪声的影响使接收矢量的相位变成135°,则将错判为“01”。
当不同发送矢量以等概率出现时,合理的判决门限应该设定在和相邻矢量等距离的位置。
在图中对于矢量“11”来说,判决门限应该设在0°和90°。
当发送“11”时,接收信号矢量的相位若超出这一范围(图中阴影区),则将发生错判。
图1QPSK 的噪声容限QPSK 信号的误码率:QPSK 信号的误比特率:0111001090??22/2111⎥⎦⎤⎢⎣⎡--=r erfc P e 2/21r erfc P e =图2 QPSK系统原理方框图三、仿真实验图3 仿真实验框图实验结果(即误码率曲线和星座图)图4 B点信号的星座图图5 C点信号的星座图图6 误码率和误比特率的理论和仿真曲线对实验结果的简单分析和说明图4是B点信号的星座图映射,00、01、10、11组合分别映射成-1-j,-1+j,1-j,1+j。
图5是C点信号的星座图映射,它是加入噪声后的映射结果,由图中可以看出加入噪声后大致以-1-j,-1+j,1-j,1+j为中心形成了近似圆的图像,少部分点偏离比较严重,产生了误差。
由图6,可见QPSK仿真误码率曲线和理论误码率曲线重合在一起,QPSK仿真误比特率曲线和理论误比特率曲线也重合在一起,误码率约是误比特率的两倍,说明实验方法是正确可行的。
四、结论本次实验研究了数字调制方式QPSK ,对其误码率进行了考察。
通过理论误码率和仿真误码的比较,了解了误码率的性能。
本次实验还通过运用星座图来对实验结果进行仿真。
本次实验得出结论如下:QPSK 信号的误码率:QPSK 信号的误比特率:误码率是误比特率的两倍。
附录:1、心得体会:本次实验我收获很多,学会了应用MATLAB 来处理问题,加深了对通信原 理中部分公式和概念的理解。
实验过程中也遇到了不少问题,在星座图映射上,一开始将00,01,10,11看成一个整体,这样对整体编程存在很大困难,因此后来尝试将其分开看,并成功映射;在计算噪声的过程中,由于通信原理的知识未能牢固掌握,在分析和计算的过程中花了很多时间;实验过程中,学会了使用find 函数来代替for 循环的功能,从而使程序运行更加快,大大加快了实验的进度。
通过本次MATLAB 的实践,应该加强MATLAB 在各个学科的应用,学会用MATLAB 来处理实际问题。
2、程序:close all clcclear allSNR_DB=[0:1:12]; sum=1000000;data= randsrc(sum,2,[0 1]);22/2111⎥⎦⎤⎢⎣⎡--=r erfc P e 2/21r erfc P e =[a1,b1]=find(data(:,1)==0&data(:,2)==0);message(a1)=-1-j;[a2,b2]=find(data(:,1)==0&data(:,2)==1);message(a2)=-1+j;[a3,b3]=find(data(:,1)==1&data(:,2)==0);message(a3)=1-j;[a4,b4]=find(data(:,1)==1&data(:,2)==1);message(a4)=1+j;scatterplot(message)title('B点信号的星座图')A=1;Tb=1;Eb=A*A*Tb;P_signal=Eb/Tb;NO=Eb./(10.^(SNR_DB/10));P_noise=P_signal*NO;sigma=sqrt(P_noise);for Eb_NO_id=1:length(sigma)noise1=sigma(Eb_NO_id)*randn(1,sum);noise2=sigma(Eb_NO_id)*randn(1,sum);receive=message+noise1+noise2*j;resum=0;total=0;m1=find(angle(receive)<=pi/2&angle(receive)>0); remessage(1,m1)=1+j;redata(m1,1)=1;redata(m1,2)=1;m2= find( angle(receive)>pi/2&angle(receive)<=pi); remessage(1,m2)=-1+j;redata(m2,1)=0;redata(m2,2)=1;m3=find( angle(receive)>-pi&angle(receive)<=-pi/2); remessage(1,m3)=-1-j;redata(m3,1)=0;redata(m3,2)=0;m4=find( angle(receive)>-pi/2&angle(receive)<=0); remessage(1,m4)=1-j;redata(m4,1)=1;redata(m4,2)=0;[resum,ratio1]=symerr(data,redata);pbit(Eb_NO_id)=resum/(sum*2);[total,ratio2]=symerr(message,remessage);pe(Eb_NO_id)=total/sum;endscatterplot(receive)title('C点信号的星座图')Pe=1-(1-1/2*erfc(sqrt(10.^(SNR_DB/10)/2))).^2;Pbit=1/2*erfc(sqrt(10.^(SNR_DB/10)/2));figure(3)semilogy(SNR_DB,pe,':s',SNR_DB,Pe,'-*',SNR_DB,pbit,'-o',SNR_DB,Pbit,':+') legend('QPSK仿真误码率','QPSK理论误码率','QPSK仿真误比特率','QPSK理论误比特率',1)xlabel('信噪比/dB')ylabel('概率P')gird on。
