MeanShift-图像分割方法
sift和meanshift原理和算法

SIFT算法由D.G.Lowe 1999年提出,2004年完善总结,论文发表在2004年的IJCV上:David G. Lowe, "Distinctive image features from scale-invariant keypoints,"International Journal of Computer Vision, 60, 2 (2004), pp. 91-110后来Y.Ke将其描述子部分用PCA代替直方图的方式,对其进行改进。
SIFT方法一经推出就在图像处理界引起巨大反响,其方法效果良好、实现便捷,很快风靡世界。
很多图像检测、识别的应用里都能找到sift方法的身影SIFT算法是一种提取局部特征的算法,在尺度空间寻找极值点,提取位置,尺度,旋转不变量。
算法的主要特点为:a) SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性。
b) 独特性(Distinctiveness)好,信息量丰富,适用于在海量特征数据库中进行快速、准确的匹配[23]。
c) 多量性,即使少数的几个物体也可以产生大量SIFT特征向量。
d) 高速性,经优化的SIFT匹配算法甚至可以达到实时的要求。
e) 可扩展性,可以很方便的与其他形式的特征向量进行联合。
SIFT算法主要步骤:1)检测尺度空间极值点2)精确定位极值点3)为每个关键点指定方向参数4)关键点描述子的生成SIFT算法详细尺度空间理论目的是模拟图像数据的多尺度特征。
高斯卷积核是实现尺度变换的唯一线性核,于是一副二维图像的尺度空间定义为:L(x,y,e) = G(x,y,e)*I(x,y)其中G(x,y,e)是尺度可变高斯函数,G(x,y,e) = [1/2*pi*e2] * exp[ -(x2 + y2)/2e2](x,y)是空间坐标, e是尺度坐标。
为了有效的在尺度空间检测到稳定的关键点,提出了高斯差分尺度空间(DOG scale-space)。
mean-shift图像分割

由式 (4) 获得 :
������ = . ������+1
∑������������=1 ������������������������������(||������������������ℎ−������������������������||2)������(||������������������ℎ−������������������������||2) ∑������������=1 ������������������(||������������������ℎ−������������������������||2)������(||������������������ℎ−������������������������||2)
图4 3. 图像分割的细节图片如图 5 所示:
图5
实验小结
根据 mean-shift 算法原理,通过对聚类中心的不断迭代,从而找到相近的类,达到分割 的目的。通过这次实验,进一步理解了图像分割的含义,也充分体现了 mean-shift 算法在图 像分割中的应用。
参考文献
【1】 【2】 【3】
Mean-shift 跟踪算法中核函数窗宽的自动选取——彭宁嵩 杨杰 刘志 张凤超——软 件学报——2005,16(9) Mean-shift 算法的收敛性分析——刘志强 蔡自兴——《《软件学报》》——2007,18 (2) 基于分级 mean-shift 的图像分割算法——汤杨 潘志庚 汤敏 王平安 夏德深
计算机视觉实验三
——利用 mean-shift 进行图像分割
算法简介
mean-shift 是一种非参数概率密度估计的方法。通过有限次的迭代过程,Parzen 窗定义 的概率密度函数能够快速找到数据分布的模式。由于具有原理简单、无需预处理、参数少等 诸多优点,mean-shift 方法在滤波、目标跟踪、图像分割等领域得到了广泛的应用。
meanshift算法简介

怎样找到数据集合中数据最密集的地方呢?
数据最密集的地方,对应于概率密度最大的地方。我们可 以对概率密度求梯度,梯度的方向就是概率密度增加最大 的方向,从而也就是数据最密集的方向。
令
,假设除了有限个点,轮廓函数 的梯度对所
有
均存在 。将 作为轮廓函数,核函数 为:
fh,K
x
2ck ,d n nhd 2 i1
Meanshift算法的概述及其应用
Meanshift的背景
Mean Shift 这个概念最早是由Fukunaga等人于 1975年在一篇关于概率密度梯度函数的估计中提出 来的,其最初含义正如其名,就是偏移的均值向量。
直到20年以后,也就是1995年,,Yizong Cheng发 表了一篇对均值漂移算法里程碑意义的文章。对基 本的Mean Shift算法在以下两个方面做了改进,首先 Yizong Cheng定义了一族核函数,使得随着样本与 被偏移点的距离不同,其偏移量对均值偏移向量的贡 献也不同,其次Yizong Cheng还设定了一个权重系 数,使得不同的样本点重要性不一样,这大大扩大了 Mean Shift的适用范围.另外Yizong Cheng指出了 Mean Shift可能应用的领域,并给出了具体的例子。
• 一维下的无参数估计 设X1,X2, …Xn是从总体中抽出的独立同分布
的样本,X具有未知的密度函数f(x),则f (x)的核估计为:
h为核函数的带宽。常用的核函数如下:
分别是单位均匀核函数 和单位高斯核函数
多维空间下的无参密度估计:
在d维欧式空间X中,x表示该空间中的一个点, 表示该空间中的
核函数,
(5)若
,则停止;否则y0←y1转步骤②。
限制条件:新目标中心需位于原目标中 心附近。
mean-shift算法公式

mean-shift算法公式Mean-shift算法是一种无参聚类算法,常用于图像分割、目标跟踪和模式识别等领域。
本文将详细介绍mean-shift算法的原理、公式和实际应用场景。
一、原理Mean-shift算法的核心思想是密度估计和质心漂移。
它基于高斯核函数,通过不断更新质心,最终将数据点分为不同的簇。
具体而言,我们要对每个数据点x_i进行密度估计,将其周围的点加权后求和得到密度估计值f(x_i)。
给定一个初始质心x_c,我们通过以下公式计算新质心x_c’:x_c' = \frac{\sum_{x_i \in B(x_c,r)} w(x_i) \times x_i}{\sum_{x_i \in B(x_c,r)} w(x_i)}B(x_c,r)表示以x_c为圆心,半径为r的区域,w(x_i)为高斯权重系数,可以写作w(x_i) = e ^ {-\frac{(x_i - x_c)^2}{2 \times \sigma^2}}\sigma是高斯核函数的标准差,控制窗口大小和权重降低的速度。
在计算新质心后,我们将其移动到新位置,即x_c = x_c’,然后重复以上步骤,直到质心不再改变或者达到预定的迭代次数为止。
最终,所有距离相近的数据点被归为同一簇。
算法的时间复杂度为O(nr^2),其中n为数据点数量,r为窗口半径。
可以通过调整r和\sigma来平衡速度和准确率。
二、公式1. 高斯核函数w(x_i) = e ^ {-\frac{(x_i - x_c)^2}{2 \times \sigma^2}}其中x_i和x_c是数据点和质心的位置向量,\sigma是高斯核函数的标准差。
该函数表示距离越大的数据点的权重越小,与质心距离越近的数据点的权重越大,因此可以有效估计密度。
2. 新质心计算公式x_c' = \frac{\sum_{x_i \in B(x_c,r)} w(x_i) \times x_i}{\sum_{x_i \in B(x_c,r)} w(x_i)}B(x_c,r)表示以x_c为圆心,半径为r的区域,w(x_i)为高斯权重系数。
meanshift 算法matlab代码

一、Meanshift算法简介Meanshift算法是一种基于密度估计的聚类算法,它通过不断调整数据点的位置来找到数据集中的局部最大值。
该算法最初由Fukunaga 和Hostetler在上世纪70年代提出,后来由Dorin Comaniciu和Peter Meer在2002年进行了改进,成为了在计算机视觉和模式识别领域被广泛应用的算法之一。
Meanshift算法在图像分割、目标跟踪和特征提取等领域有着广泛的应用,其优点是不需要预先指定聚类的个数,能够自适应地发现数据中的聚类结构。
本文将介绍Meanshift算法的基本原理,并给出在Matlab中的实现代码。
二、Meanshift算法的基本原理1. 数据点的内核密度估计Meanshift算法基于密度估计的原理,它首先对数据点进行内核密度估计。
对于每一个数据点x,其内核密度估计可以表示为:\[ f(x)=\frac{1}{nh^d}\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)\]其中,n为数据点的数量,h为内核函数的带宽,K为内核函数,d为数据点的维度。
2. Meanshift向量的计算在得到数据点的密度估计之后,Meanshift算法通过不断调整数据点的位置来找到局部最大值。
对于数据点x,其Meanshift向量可以表示为:\[ m(x)=\frac{\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)x_i}{\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)}-x\]Meanshift向量的计算可以理解为将数据点向其密度估计的最大值方向移动,直至收敛于密度估计的局部最大值位置。
3. 聚类的形成Meanshift算法通过不断迭代调整数据点的位置,当数据点的移动趋于收敛之后,将在同一局部最大值处的数据点归为同一类,从而形成聚类。
三、Meanshift算法的Matlab代码实现在Matlab中,可以通过以下代码实现Meanshift算法的聚类:```matlabfunction [labels, centroids] = meanshift(data, bandwidth)[n, d] = size(data);labels = zeros(n, 1);stopThresh = 1e-3 * bandwidth;numClusters = 0;计算内核密度估计f = (x) exp(-sum((x - data).^2, 2) / (2 * bandwidth^2));迭代计算Meanshift向量for i = 1:nif labels(i) == 0x = data(i, :);diff = inf;while truex_old = x;weights = f(x);x = sum(repmat(weights, 1, d) .* data) / sum(weights); diff = norm(x - x_old);if diff < stopThreshbreak;endend将收敛的数据点归为同一类numClusters = numClusters + 1;idx = find(weights > 0.5);labels(idx) = numClusters;endend计算聚类中心centroids = zeros(numClusters, d);for i = 1:numClustersidx = find(labels == i);centroids(i, :) = mean(data(idx, :));endend```以上代码实现了对输入数据data进行Meanshift聚类,其中bandwidth为内核函数的带宽。
meanshift计算方法

meanshift计算方法Meanshift是一种经典的非参数密度估计和聚类算法,常用于图像处理、目标跟踪和图像分割等任务。
Meanshift算法的核心思想是通过迭代寻找样本空间中的密度极大值点,从而找到数据的聚类中心。
该方法的基本原理如下:1.密度估计:首先,对于给定的数据集,通过核密度估计方法来估计数据集中每个样本点的密度。
核密度估计是一种非参数的密度估计方法,通过计算每个样本点周围的核密度来估计该样本点的密度。
常用的核函数有高斯核函数和均匀核函数等。
2.中心寻找:从样本空间中任意选择一个点作为初始中心点。
然后,计算该点与样本空间中其他点之间的距离,并根据距离来调整中心点的位置。
具体而言,可以使用欧氏距离或其他距离度量来计算中心点与样本点之间的距离。
调整中心点的位置是通过计算样本点对中心点的贡献度来实现的,贡献度是根据距离的远近来确定的。
距离越近的样本点对中心点的贡献度越大,距离越远的样本点对中心点的贡献度越小。
3.密度更新:根据样本空间中当前的中心点,计算每个样本点与中心点之间的距离,并根据距离的远近来更新样本点的密度。
即,距离越近的样本点密度越高,距离越远的样本点密度越低。
通过迭代更新样本点的密度,可以逐渐得到数据集在样本空间中的密度分布。
4.收敛判断:判断中心点的位置是否稳定(即中心点是否收敛)。
当中心点的移动距离小于设定的阈值时,算法停止迭代,并输出最终的聚类中心。
Meanshift算法的优点是可以适应任意形状和密度的数据集,并且不需要事先指定聚类的数量。
它能够自动发现数据集中的聚类中心,并将数据点聚集在它们周围。
同时,Meanshift算法对初始中心点的选择不敏感,因此较为稳定。
然而,Meanshift算法也存在一些缺点。
首先,该算法的时间复杂度较高,其计算复杂度为O(N^2),其中N为数据集的大小。
其次,Meanshift算法在处理高维数据时容易受到维数灾难的影响,数据点之间的距离随着维数的增加而呈指数增长,导致聚类结果不准确。
meanshift算法简介

基于核函数G(x)的 概率密度估计
•
用核函数G在 x点计算得到的Mean Shift 向量 正比于归一化的用核函数K估计的概率 密度的函数 的梯度,归一化因子为用核函数 G估计的x点的概率密度.因此Mean Shift向量 总是指向概率密度增加最大的方向.
Mean shift向量的物理意义的什么呢?
2ck ,d
n
2
2ck ,d cg ,d 2 d h cg ,d nh
g i 1
n
n x xi 2 xi g 2 h x xi i 1 x n x x 2 h i g h i 1
为了更好地理解这个式子的物理意义,假设上式中g(x)=1
平均的偏移量会指向样本点最密的方向,也 就是概率密度函数梯度方向
下面我们看一下mean shift算法的步骤
mh x
给定一个初始点x,核函数G(x), 容许误差 ,Mean Shift算法 循环的执行下面三步,直至结束条件满足, •计算mh ( x) •把 mh ( x)赋给 x. •如果 mh ( x) x ,结束循环;若不然,继续执行(1)
0 =1,2…..m i=1,2…..m
(5)若
,则停止;否则y ←y1转步骤②。
0
限制条件:新目标中心需位于原目标中 心附近。
Meanshift跟踪结果
• 转word文档。
• Meanshift优缺点: 优点 ①算法复杂度小; ②是无参数算法,易于与其它算法集 成; ③采用加权直方图建模,对目标小角 度旋转、轻微变形和部分遮挡不敏感等。
MeanShift算法
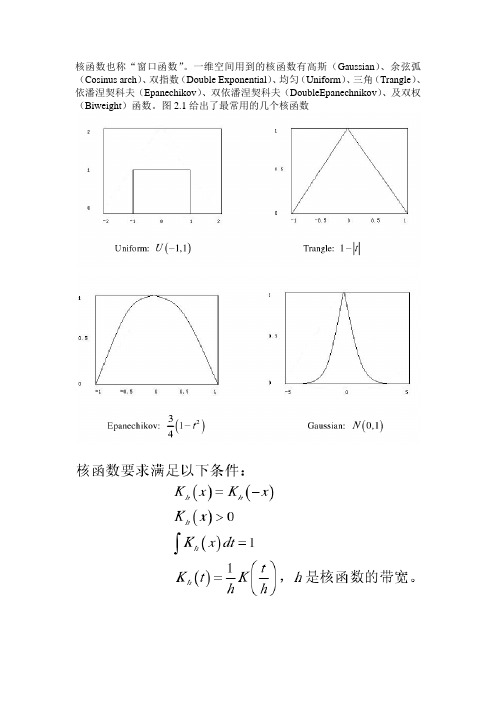
核函数也称“窗口函数”。
一维空间用到的核函数有高斯(Gaussian)、余弦弧(Cosinus arch)、双指数(Double Exponential)、均匀(Uniform)、三角(Trangle)、依潘涅契科夫(Epanechikov)、双依潘涅契科夫(DoubleEpanechnikov)、及双权(Biweight)函数。
图2.1给出了最常用的几个核函数给定一组一维空间的n个数据点集合令该数据集合的概率密度函数假设为f (x),核函数取值为,那么在数据点x处的密度估计可以按下式计算:上式就是核密度估计的定义。
其中,x为核函数要处理的数据的中心点,即数据集合相对于点x几何图形对称。
核密度估计的含义可以理解为:核估计器在被估计点为中心的窗口内计算数据点加权的局部平均。
或者:将在每个采样点为中心的局部函数的平均效果作为该采样点概率密度函数的估计值。
MeanShift实现:1.选择窗的大小和初始位置.2.计算此时窗口内的Mass Center.3.调整窗口的中心到Mass Center.4.重复2和3,直到窗口中心"会聚",即每次窗口移动的距离小于一定的阈值,或者迭代次数达到设定值。
meanshift算法思想其实很简单:利用概率密度的梯度爬升来寻找局部最优。
它要做的就是输入一个在图像的范围,然后一直迭代(朝着重心迭代)直到满足你的要求为止。
但是他是怎么用于做图像跟踪的呢?这是我自从学习meanshift以来,一直的困惑。
而且网上也没有合理的解释。
经过这几天的思考,和对反向投影的理解使得我对它的原理有了大致的认识。
在opencv中,进行meanshift其实很简单,输入一张图像(imgProb),再输入一个开始迭代的方框(windowIn)和一个迭代条件(criteria),输出的是迭代完成的位置(comp )。
这是函数原型:int cvMeanShift( const void* imgProb, CvRect windowIn,CvTermCriteria criteria, CvConnectedComp* comp )但是当它用于跟踪时,这张输入的图像就必须是反向投影图了。
协作机器人技术的识别与感知方法介绍

协作机器人技术的识别与感知方法介绍随着科技的不断发展,机器人在各个领域中扮演着越来越重要的角色。
其中,协作机器人技术的识别与感知方法是实现机器人与人类协调合作的关键。
本文将介绍协作机器人技术的识别与感知方法,从计算机视觉、机器学习以及传感器技术三个方面进行阐述。
一、计算机视觉计算机视觉是协作机器人识别与感知的重要技术之一。
通过摄像头和图像处理算法,机器人能够获取环境中的图像信息,进而识别和感知目标物体或人类行为。
常用的计算机视觉方法包括目标检测、目标跟踪、图像分割等。
目标检测是指在图像或视频序列中检测出特定目标的位置和边界框。
常用的目标检测算法包括基于神经网络的目标检测方法(如YOLO、Faster R-CNN)和传统的特征提取与分类方法(如Haar特征与级联分类器)。
目标检测能够使机器人在复杂环境中识别出各种物体,并做出相应的响应。
目标跟踪是指在视频序列中追踪目标随时间的变化。
机器人利用目标跟踪技术可以实时追踪物体的位置、运动轨迹等信息,从而做出适时的行为。
常见的目标跟踪算法包括基于相关滤波器的方法(如DCF、SAMF)和基于深度学习的方法(如Siamese网络)。
图像分割是指将图像划分为多个不同的区域,从而更好地理解图像中的对象。
图像分割可以分割出目标物体的边界,提取出局部特征,进一步帮助机器人实现更精确的感知。
常用的图像分割算法包括基于像素的方法(如k-means、MeanShift)和基于边缘的方法(如Canny边缘检测)。
二、机器学习机器学习是协作机器人感知方法中的重要技术支撑。
通过对大量数据的学习和归纳,机器能够从中抽取特征,并基于这些特征做出判断和决策。
常用的机器学习方法包括监督学习、无监督学习和强化学习。
监督学习是指通过输入样本和对应输出的标签,训练机器进行正确的分类和回归。
在协作机器人中,监督学习可以用来识别和感知人类行为,例如动作识别、姿态估计等。
常见的监督学习算法包括支持向量机(SVM)、决策树、神经网络等。
医学影像处理中的图像分割技术

医学影像处理中的图像分割技术随着数字化和信息化的发展,各行各业都在积极应用计算机技术进行信息处理和分析,医学领域也不例外。
其中医学影像处理就是医学领域应用计算机技术进行信息处理和分析的重要方向之一。
医学影像处理旨在提高医疗领域的诊断效率、减少诊断误差、改善医疗保健质量。
其中影像分割技术是医学影像处理的重要组成部分。
本文将介绍医学影像处理中的图像分割技术。
一、图像分割技术的概述图像分割是指将数字图像分割成若干个互不重叠的子区域,并使得每个子区域内的像素具有相似的特征,以达到对图像信息的提取、分析或处理等目的。
在医学影像处理中,图像分割技术可以将数字影像中的组织、器官、病变等部位分离开来,从而对医学影像进行定量化分析和诊断。
目前,医学影像分割技术已成为医学领域中应用最广泛的技术之一。
二、图像分割的方法和分类图像分割方法可以分为基于阈值分割、基于聚类分割、基于边缘分割和基于区域分割等四类。
1.基于阈值分割基于阈值分割的方法是最简单、最快速的图像分割方法之一。
它将图像中每个像素的像素值与一个预设的阈值进行比较,将像素值大于或小于阈值的像素划分到不同的子区域中。
基于阈值分割的方法通常适用于图像中只包含两种物体的情况。
2.基于聚类分割基于聚类分割的方法是通过将图像中的像素聚为类别,以区分出不同的物体或背景。
该方法首先将图像中的像素按照其像素值进行聚类,然后根据像素值相似度,判断像素是否属于同一类别。
基于聚类分割的算法通常适用于多物体和多层次的图像分割。
3.基于边缘分割基于边缘分割的方法是通过检测图像中的边缘,将像素划分到边缘不同侧的子区域中。
该方法通常使用边缘检测算法,如Sobel、Canny等进行边缘检测。
4.基于区域分割基于区域分割的方法是通过对区域进行最小化或最大化,以得到对图像的有效划分。
该方法通常使用一些叫做分割匹配算法的方法,如meanshift、K-means等进行区域划分。
三、医学影像分割的应用医学影像分割技术的应用非常广泛,可以用于各种医学检查和诊断,如疾病诊断、手术指导、药物研究等。
mean-shift算法python代码

文章内容:一、Mean-Shift算法介绍Mean-Shift算法是一种基于密度的聚类算法,它通过不断地调整数据点的位置来寻找数据点密度最大的位置,从而实现对数据点的聚类。
该算法的核心思想是将数据点从初始位置向密度最大的方向移动,直到达到局部最大值。
该算法没有对数据点的数量做出假设,因此在处理各种形状和大小的簇时具有很好的效果。
二、Mean-Shift算法步骤1.初始化数据点的位置和带宽大小。
2.计算每个数据点的梯度向量。
3.根据梯度向量对每个数据点的位置进行更新。
4.重复步骤2和步骤3,直到达到收敛条件为止。
三、Mean-Shift算法Python代码实现import numpy as npclass MeanShift:def __init__(self, bandwidth=2):self.bandwidth = bandwidthdef fit(self, data):centroids = {}for i in range(len(data)):centroids[i] = data[i]while True:new_centroids = []for i in centroids:in_bandwidth = []centroid = centroids[i]for featureset in data:if np.linalg.norm(featureset - centroid) < self.bandwidth:in_bandwidth.append(featureset)new_centroid = np.average(in_bandwidth, axis=0) new_centroids.append(tuple(new_centroid))uniques = sorted(list(set(new_centroids)))prev_centroids = dict(centroids)centroids = {}for i in range(len(uniques)):centroids[i] = np.array(uniques[i])optimized = Truefor i in centroids:if not np.array_equal(centroids[i], prev_centroids[i]): optimized = Falseif not optimized:breakif optimized:breakself.centroids = centroidsdef predict(self, data):pass四、Mean-Shift算法代码解析1.在初始化方法中,我们设置了带宽大小,并且定义了fit方法来执行Mean-Shift算法。
基于meanshift算法图像处理

基于meanshift算法图象处理基于meanshift算法的图象处理概述:图象处理是对图象进行数字化处理的过程,通过对图象进行分析、增强、恢复、压缩等操作,提取图象中的信息并改善图象质量。
本文将介绍基于meanshift算法的图象处理方法。
一、背景介绍1.1 图象处理的意义和应用图象处理在多个领域中具有广泛的应用,包括计算机视觉、医学影像处理、图象识别等。
通过图象处理技术,可以实现图象的增强、分割、特征提取等操作,为后续的图象分析和应用提供基础。
1.2 Meanshift算法的原理Meanshift算法是一种基于密度估计的聚类算法,通过迭代寻觅数据点的局部密度最大值,实现数据点聚类的效果。
在图象处理中,Meanshift算法可以用于图象的分割和目标跟踪。
二、基于Meanshift算法的图象分割2.1 图象分割的概念和意义图象分割是将图象划分为不同的区域或者对象的过程,通过将图象分割为不同的区域,可以实现对图象中不同对象的提取和分析。
2.2 基于Meanshift算法的图象分割步骤(1)初始化:选择一个种子点作为初始中心点。
(2)计算密度估计:对于每一个像素点,计算其与中心点的距离,并根据距离计算相应的权重。
(3)更新中心点:根据权重,更新中心点的位置。
(4)迭代:重复步骤(2)和(3),直到中心点再也不变化或者达到预设的迭代次数。
(5)生成份割结果:根据最终的中心点位置,将图象分割为不同的区域。
2.3 示例数据和结果展示以一张室内场景的图象为例,进行Meanshift算法的图象分割。
首先选择种子点作为初始中心点,然后计算每一个像素点与中心点的距离,并根据距离计算相应的权重。
通过迭代更新中心点的位置,最终得到图象的分割结果,将图象分割为不同的区域。
三、基于Meanshift算法的目标跟踪3.1 目标跟踪的概念和意义目标跟踪是指在连续的图象序列中,通过对目标的位置和状态进行估计和预测,实现对目标的跟踪和定位。
基于MeanShift图像分割和支持向量机判决的候梯人数视觉检测系统

Ab s t r a c t :Ac c o r d i n g t o t h e r e q u i r e me n t s o f e l e v a t o r - g r o u p - c o n t r o l s y s t e ms ,a n e w me t h o d b a s e d o n c o mp u t e r
第 2 1卷
第 4期
光 学 精 密 工 程
O pt i c s a n d Pr e c i s i o n Eng i n e e r i ng
Vo l _ 2 1 No . 4
Ap r . 20 13
2 0 1 3年 4月
文章编号
1 0 0 4 — 9 2 4 X( 2 0 1 3 ) 0 4 — 1 0 7 9 — 0 7
Me a n S h i f t s e g me n t a t i o n a nd ቤተ መጻሕፍቲ ባይዱS VM c l a s s i f i c a t i o n
ZHANG Yu — y a n g,LI U Ma n — hu a,H AN Ta o
( I n s t i t u t e o f E l e c t r o n I n f o r ma t i o n a n d El e c t r i c a l En g i n e e r i n g,
文献 标 识 码 : A d o i : l 0 . 3 7 8 8 / O P E . 2 O 1 3 2 1 O 4 . 1 0 7 9
中 图分 类 号 : T P 3 9 1 . 4
El e v a t o r - wa i t i ng pe o p l e c o u nt i n g s y s t e m b a s e d o n
均值平移算法

均值平移算法均值平移算法(Mean Shift Algorithm)是一种用于数据聚类和图像分割的非参数方法。
它的基本思想是通过迭代计算数据点的均值平移向量,将数据点移动到局部密度最大的区域,从而实现聚类的目的。
在介绍均值平移算法之前,先来了解一下聚类的概念。
聚类是指将具有相似特征的数据点分组到一起的过程。
在实际应用中,聚类可以用于图像分割、目标跟踪、无监督学习等领域。
而均值平移算法作为一种常用的聚类算法,具有以下特点:1. 非参数化:均值平移算法不需要事先指定聚类的个数,而是通过迭代计算数据点的均值平移向量,从而确定聚类的个数和位置。
2. 局部搜索:均值平移算法是一种局部搜索算法,它通过计算数据点的均值平移向量,将数据点移动到局部密度最大的区域。
这样可以保证聚类的准确性,并且能够处理非凸形状的聚类。
下面我们来详细介绍均值平移算法的原理和步骤:1. 初始化:首先选择一个合适的窗口大小和数据点的初始位置。
窗口大小决定了局部搜索的范围,而初始位置可以是随机选择的或者根据先验知识进行选择。
2. 计算均值平移向量:对于窗口内的每个数据点,计算它与其他数据点的距离,并将距离加权后的向量相加。
这个加权和即为均值平移向量。
3. 移动数据点:根据计算得到的均值平移向量,将数据点移动到局部密度最大的区域。
具体做法是将数据点沿着均值平移向量的方向移动一定的距离。
4. 更新窗口:更新窗口的位置,使其包含移动后的数据点。
然后回到第2步,继续计算均值平移向量,并移动数据点,直到满足停止条件。
均值平移算法的停止条件可以是迭代次数达到一定的阈值,或者数据点的移动距离小于一定的阈值。
在实际应用中,可以根据具体的情况选择合适的停止条件。
均值平移算法的优点是可以自动发现数据中的聚类,并且对于非凸形状的聚类效果好。
然而,它也有一些缺点,比如对于大规模数据的处理速度较慢,并且对于窗口大小的选择比较敏感。
总结一下,均值平移算法是一种常用的聚类算法,它通过迭代计算数据点的均值平移向量,将数据点移动到局部密度最大的区域,从而实现聚类的目的。
带宽自适应MeanShift图像分割算法

摘
要: Me a n S h i t f 是 目前 为止特征 空间分析 的最好 方 法之一 , 但 其分 割结 果受 带宽 参数 的影响 。 图像 粗糙度 是 与视 觉感
受相 关的 图像 纹 理特 征 , 对 图像 纹理 的描 述 能力很 强。 图像像 素 的平 均偏移 量也 体现 了图像像 素 的总体 离散 情 况。通 过 对 高斯核 函数 的创建 以及 图像 粗糙度 的描述 , 创 新 性地 给 出 了Me a n S h i t的窗 口尺 寸 选择 方法 以及 图像像 素 平均 偏移 的 f 计算, 仿真 结果表 明 , 该 算法对 不 同类型 的 图像 , 均能得 到令人 满 意的效 果。
C o m p u t e r E n g i n e e r i n ga n d A p p l i c a t i o n s 计算 机 工程 与应 用
பைடு நூலகம்
带 宽 自适 应 Me a n S h i f t 图像 分 割 算 法
熊 平 , 白云 鹏
XI ONG Pi ng, BAI Yu np e ng
中南 大学 地球 科 学与信 息物理 学 院 , 长沙 4 1 0 0 8 3
S c h o o l o fGe o s c i e n c e s a n d I n f o — P h y s i c s , Ce n t r a l S o u t h Un i v e r s i t y , Ch a n g s h a 41 0 0 8 3 , Ch i n a
XI ONG Pi n g , BAI Yu n p e n g . Me a n S h i t f i ma g e s e g me n t a t i o n a l g o r i t h m wi t h a d a p t i v e ba nd wi d t h . Co mp u t e r En g i n e e r i ng
meanshift方法

meanshift方法
meanshift方法是一种非参数密度估计和跟踪算法,主要用于图像处理和机器视觉领域。
该方法通过迭代的方式,将每个点的位置向其周围点的均值移动,从而实现密度估计和目标跟踪。
meanshift算法的基本流程如下:
1. 随机选择一个点作为初始点。
2. 以该点为中心,选择一个窗口大小(通常为固定值),计算窗口内的所有点的均值。
3. 将该点的位置更新为均值所对应的位置。
4. 重复步骤2和步骤3,直到所有点的位置不再发生明显的变化。
meanshift算法具有以下优点:
1. 非参数性:不需要预先设定任何参数,能够自动适应数据的分布。
2. 简单易行:算法实现简单,计算速度快,适合处理大规模数据。
3. 鲁棒性:对噪声和异常值具有较强的鲁棒性。
在图像处理中,meanshift算法可以用于图像分割、目标跟踪、特征提取等任务。
在机器视觉中,该算法可以用于行为识别、人脸识别、手势识别等领域。
meanShift算法介绍

meanShift算法介绍(2012-03-26 12:09:35)转载▼分类:其他标签:转载原文地址:[ZZ]meanShift算法介绍作者:千里8848meanShift,均值漂移,在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。
meanShift这个概念最早是由Fukunage在1975年提出的,其最初的含义正如其名:偏移的均值向量;但随着理论的发展,meanShift的含义已经发生了很多变化。
如今,我们说的meanShift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,然后以此为新的起始点,继续移动,直到满足一定的结束条件。
在很长一段时间内,meanShift算法都没有得到足够的重视,直到1995年另一篇重要论文的发表。
该论文的作者Yizong Cheng定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。
其次,他还设定了一个权重系数,使得不同样本点的重要性不一样,这大大扩展了meanShift的应用范围。
此外,还有研究人员将非刚体的跟踪问题近似为一个meanShift的最优化问题,使得跟踪可以实时进行。
目前,利用meanShift进行跟踪已经相当成熟。
meanShift算法其实是一种核密度估计算法,它将每个点移动到密度函数的局部极大值点处,即,密度梯度为0的点,也叫做模式点。
在非参数估计部分(请参考/carson2005/article/details/7243425),我们提到,多维核密度估计可以表示为:估计为0。
meanShift向量也总是指向密度增加最大的方向,这可以由上式中的分子项来保证,而分母项则体现每次迭代核函数移动的步长,在不包含感兴趣特征的区域内,步长较长,而在感兴趣区域内,步长较短。
也就是说,meanShift算法是一个变步长的梯度上升算法,或称之为自适应梯度上升算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要
在图像处理和计算机视觉里,图像分割是一个十分基础而且很重要的部分,决定了最终分析结果的好坏。
图像分割问题的典型定义就是如何在图像处理过程中将图像中的一致性区域和感兴趣对象提取出来。
MeanShift 图像分割方法是一种统计迭代的核密度估计方法。
MeanShift算法以其简单有效而被广泛应用,但该方法在多特征组合方面和数据量较大的图像处理上仍存在不足之处,本文针对这些问题对该算法的结构进行了优化。
本文利用图像上下文信息对图像进行了区域合并以此来对输入数据进行了压缩;并实现特征空间中所有特征量的优化组合。
最后,总结了本文的研究成果。
下一步需要深入的研究工作有:(1)考虑分割的多尺度性,实现基于Mean Shift算法的多尺度遥感图像分割;(2)考虑利用Gabor滤波器来提取纹理特征,或将更多的特征如形状等特征用于MeanShift遥感图像分割中。
关键词: Mean Shift, 图像分割, 遥感图像, 带宽
ABSTRACT
mage segmentation is very essential and critical to image processing and computer vision, which is one of the most difficult tasks in image processing, and determines the quality of the final result of analysis. In image segmentation problem, the typical goal is to extract continuous regions and interest objects in the case of image processing.
The Mean Shift algorithm for segmentation is a statistical iterative algorithm based on kernel density estimation. Mean Shift algorithm has been widely applied for its simplicity and efficiency. But the algorithm has some deficiencies in feature combination and image processing for large data. According to the deficiencies of the Mean Shift algorithm, this paper optimizes the structure of the algorithm for segmentation. Firstly, this paper introduces a method of data compressing by merging the nearest points with similar properties into consistency regions. Secondly, We optimize the combination of features.
At last, after concluding all research work in this paper, further work need to be in-depth studied: (1) Consider multi-scale factors of remote sensing, and realize multi-scale remote sensing image segmentation based on Mean Shift algorithm. (2) Consider extracting textures features by using Gabor filter, or use more features such as shape features to segment remote sensing images based on Mean Shift algorithm.
KEY WORDS: Mean Shift, image segmentation, remote sensing images, bandwidth,
目录
第一章绪论 (1)
1.1选题背景 (1)
1.2国内外研究现状及进展 (2)
1.2.1 Mean Shift算法的国内外研究现状 (2)
1.2现有研究存在的问题 (3)
第二章Mean Shift算法理论基础 (4)
2.1 Mean Shift算法原理 (4)
2.1.1特征空间无参核密度估计 (5)
2.2常用的核函数 (6)
2.2.1多维核Mean Shift算法 (7)
2.3.空间-色度域Mean Shift图像分割 (11)
第三章Mean Shift 图像分割方法研究与改进 (14)
3.1 典型的Mean Shift 图像分割算法 (14)
3.2 基于图像数据的核密度估计 (14)
3.2.1 典型的Mean Shift 图像分割算法 (15)
3.3 一种改进的Mean Shift 图像分割算法 (16)
3.3.1 基于D-S 理论的核密度估计 (16)
3.3.2 基于区域的Mean Shift 过程 (19)
第四章固定带宽Mean Shift分割与区域合并 (22)
4.1区域合并概述 (22)
4.1.1区域合并定义 (22)
4.1.2区域邻接图与区域标记 (22)
4.2区域表示 (24)
4.3固定带宽Mean Shift分割 (26)
4.3.1确定空间带宽固定值 (27)
4.3.2固定灰度带宽的计算 (28)
4.3.3固定带宽高斯核Mean Shift分割算法 (29)
4.4分割后区域合并 (30)
4.4.1合并前的预处理 (31)
4.4.2区域合并过程 (32)
4.5实验结果与分析 (32)
4.5.1定性分析 (32)
总结 (35)
致谢 (36)
参考文献 (37)
第一章绪论
本章阐述了论文的研究背景以及意义、国内外相关研究进展及存在的众多问题,并介绍论文的主要研究内容。
目前,采用Mean Shift分割的高分辨率遥感图像已逐步得到应用Mean Shift分割方法己成为研究的热点,它将推进遥感信息提取技术向高精度、自动化等方向发展。
因此本文将按照“Mean Shift分割-分割评价-分割应用”的主线展开论述。
1.1选题背景
随着航空航天遥感技术的发展,很多用途的对地观测系统相继升空,已获取了大量的各种类型的遥感数据。
研究表明,获取的遥感数据,被使用的是相当少的一部分。
图像分割是将数据转化为信息的一项关键技术,是实现自动化高精度图像分析和图像理解的难题之一。
图像分割是将图像分隔成目标区域,以更抽象更紧凑的形式表示原始图像,使得高层次图像的表达成为可能。
再则,分割质量直接决定了后续的区域描述、特征提取、目标识别等精度问题。
因此,图像分割一直被认为是图像处理、分析、理解的重要技术,分割结果的重要性使得图像分割方法研究仍然是计算机视觉、图像处理与应用领域的研究热点,且仍将是研究者的主要关注点之一。
Mean Shift算法被称为均值漂移算法,是一种基于核密度梯度估计的无参快速统计迭代算法。
Mean Shift算法具有简单的形式,在实际应用中表现出较好的稳定。
