信息论完整公式
信息论总结与复习

(3)稳态符号概率: (4)稳态信息熵:
结论:N阶马氏信源稳态信息熵(即极限熵)等于N+1阶条件熵。
第一部分、信息论基础
1.1 信源的信息理论
[例1] 已知二阶马尔可夫信源的条件概率:
p(0|00)=p(1|11)=0.8;p(0|01)=p(1|10)=0.6;
(2)联合熵:
H(XY)= -0.21log0.21 –0.14log0.14 –0.35log0.35 –0.12log0.12 –0.09log0.09–0.09log0.09 =2.3924 bit/符号
第一部分、信息论基础
1.2 信道的信息理论
(3)噪声熵:
由 和
H(Y | X)= – 0.21log0.3 –0.14log0.2 –0.35log0.5
(4)无噪有损信道:分组多对一(归并),其传输矩阵应具 有多行一列的分块对角化形式。
(5)对称信道:传输矩阵的各行都是一些相同元素的重排, 各列也是一些相同元素的重排。
第一部分、信息论基础
1.2 信道的信息理论
3、信道有关的信息熵:
(1)信源熵 (先验熵):
(2)噪声熵 (散布度):
(3)联合熵: (4)接收符号熵:
–0.12log0.4 –0.09log0.3–0.09log0.3
==(0.21+0.12,0.14+0.09,0.35+0.09) = (0.33, 0.23, 0.44)
H(Y)= -0.33log0.33 -0.23log0.23 -0.44log0.44
[例3]求对称信道 解:C =log4-H(0.2,0.3,0.2,0.3) =2+(0.2log0.2+0.3log0.3)×2 = 0.03 bit/符号; 的信道容量。
信息论

自信息、互信息、信息熵、平均互信息,定义、公式(1)自信息:一个事件(消息)本身所包含的信息量,它是由事件的不确定性决定的。
比如抛掷一枚硬币的结果是正面这个消息所包含的信息量。
随机事件的自信息量定义为该事件发生概率的对数的负值。
设事件 的概率为 ,则它的自信息定义为 (2)互信息:一个事件所给出关于另一个事件的信息量,比如今天下雨所给出关于明天下雨的信息量。
一个事件 所给出关于另一个事件 的信息定义为互信息,用 表示。
(3)平均自信息(信息熵):事件集(用随机变量表示)所包含的平均信息量,它表示信源的平均不确定性。
比如抛掷一枚硬币的试验所包含的信息量。
随机变量X 的每一个可能取值的自信息 的统计平均值定义为随机变量X 的平均自信息量: (4)平均互信息:一个事件集所给出关于另一个事件集的平均信息量,比如今天的天气所给出关于明天的天气的信息量。
为了从整体上表示从一个随机变量Y 所给出关于另一个随机变量 X 的信息量,我们定义互信息 在的XY 联合概率空间中的统计平均值为随机变量X 和Y 间的平均互信息画出各种熵关系图。
并作简要说明I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(XY)当X,Y 统计独立时,I(X;Y)=0实际信源往往是有记忆信源。
对于相互间有依赖关系的N 维随机变量的联合熵存在以下关系(熵函数的链规则) :定理3.1 对于离散平稳信源,有以下几个结论: (1)条件熵 随N 的增加是递减的;(2)N 给定时平均符号熵大于等于条件熵 (3)平均符号熵 随N 的增加是递减的;(4)如果 ,则 存在,并且分组与非分组码,奇异与非奇异码,唯一可译码与非唯一可译码。
即时码与非即时码1. 分组码和非分组码将信源符号集中的每个信源符号固定地映射成一个码字 Si ,这样的码称为分组码W i 。
用分组码对信源符号进行编码时,为了使接收端能够迅速准确地将码译出,分组码必须具有一些直观属性。
信息论里的自熵公式

信息论里的自熵公式
自熵公式是信息论中的一个重要概念,它描述了一个随机变量的不确定性或信息量。
根据自熵公式,自熵是一个概率分布在信息论中所携带的信息量的期望值的负数。
具体而言,自熵公式可以表示为:H(X) = -∑[p(x)log2p(x)]
其中,H(X)表示随机变量X的自熵,p(x)表示随机变量X取值为x 的概率。
自熵公式的应用范围非常广泛。
它可以用于衡量一个信源的信息量,用于评估数据的压缩效率,还可以用于量化密码学中的安全性。
在通信领域,自熵公式可以用于计算信道容量,帮助我们设计更高效的通信系统。
自熵公式的推导基于信息论的基本原理,其中最重要的是香农的噪声信道编码定理。
根据这个定理,我们可以通过合理地编码和解码来克服信道的噪声干扰,从而实现可靠的通信。
自熵公式在这个过程中起到了关键的作用,它帮助我们理解了信息的本质和传输的限制。
除了在通信领域,自熵公式还可以应用于机器学习和数据挖掘等领域。
在机器学习中,我们可以使用自熵公式来评估模型的复杂性和泛化能力,从而帮助我们选择最佳的模型。
在数据挖掘中,自熵公式可以用于特征选择和聚类分析,帮助我们发现数据中的隐藏信息
和模式。
自熵公式是信息论中的一个重要工具,它在各个领域都有着广泛的应用。
通过计算随机变量的自熵,我们可以量化信息的不确定性,并利用这些信息来优化通信、学习和分析等过程。
自熵公式的应用不仅扩展了我们对信息的理解,也推动了科技的发展。
希望通过深入研究和应用自熵公式,我们能够更好地理解和利用信息,为人类的进步和发展做出更大的贡献。
信息论与概率的联系

信息论与概率的联系信息论是一门研究信息传输和处理的学科,而概率论是一门研究随机现象的学科。
尽管两者看似不同,但实际上它们之间存在着密切的联系。
本文将探讨信息论与概率的联系,并阐述它们在现实生活中的应用。
一、信息论的基本概念信息论是由克劳德·香农于1948年提出的,它主要研究信息的度量和传输。
信息的度量通常使用信息熵来衡量,信息熵越大,信息的不确定性就越高。
信息熵的计算公式为:H(X) = -ΣP(x)log2P(x)其中,H(X)表示随机变量X的信息熵,P(x)表示随机变量X取值为x的概率。
二、概率论的基本概念概率论是研究随机现象的规律性的数学理论。
它通过概率的定义和性质,研究随机事件的发生规律和概率分布。
概率的计算通常使用频率概率和古典概率等方法。
三、信息论与概率的联系信息论与概率论之间存在着紧密的联系。
首先,信息熵可以看作是概率分布的度量,它反映了随机变量的不确定性。
信息熵越大,表示随机变量的不确定性越高,即信息量越大。
而概率分布越均匀,信息熵越大。
其次,信息论中的条件熵和互信息等概念与概率论中的条件概率和联合概率有着密切的关系。
条件熵表示在已知某一事件发生的条件下,另一事件的不确定性。
互信息表示两个事件之间的相关性,它可以通过条件熵和边际熵的差值来计算。
这些概念在概率论中有着重要的应用,可以用来描述随机事件之间的关联程度。
最后,信息论中的编码理论和信道容量等概念也与概率论有着密切的联系。
编码理论研究如何将信息进行编码和解码,以便在传输过程中减少误差和提高传输效率。
而信道容量则表示在给定信道条件下,能够传输的最大信息量。
这些概念都涉及到概率分布和概率计算,因此与概率论有着紧密的联系。
四、信息论与概率的应用信息论与概率论的联系在现实生活中有着广泛的应用。
首先,在通信领域中,信息论的概念和方法被广泛应用于数据压缩、信道编码和纠错编码等方面。
通过对信息的压缩和编码,可以提高数据传输的效率和可靠性。
用香农公式计算一下

用香农公式计算一下引言信息论是研究信息的定量处理和传输的数学理论。
而香农公式,也被称为香农熵公式,是信息论中最重要的公式之一。
本文将介绍香农公式的概念和计算方法,并通过一个具体的例子来演示如何使用香农公式进行信息的计算。
香农公式的概述香农公式是由克劳德·香农于1948年提出的,用来计算信息的平均量。
该公式可以用于衡量信息的不确定性或随机性。
香农公式的数学表述如下:Shannon’s FormulaShannon’s Formula其中,H(X)代表随机变量X的熵或信息量,p(x)是X取值为x的概率。
香农公式的基本思想是,如果某个事件发生的概率越高,那么这个事件所提供的信息量就越少;相反,如果某个事件发生的概率越低,那么这个事件所提供的信息量就越大。
一个具体的例子假设有一个硬币,我们已知这个硬币是公平的,即正面和反面出现的概率都是50%。
现在我们想计算抛掷这个硬币时获得的信息量。
根据香农公式,我们可以计算出这个硬币抛掷的熵为:H(硬币) = - (0.5 * log2(0.5) + 0.5 * log2(0.5))根据对数的性质,log2(0.5) = -1,所以上述公式可以简化为:H(硬币) = - (0.5 * -1 + 0.5 * -1) = 1所以,抛掷这个硬币时获得的信息量为1比特。
香农公式的应用香农公式在信息论和通信领域有着广泛的应用。
它可以用于衡量数据的压缩效率、信道的容量以及密码学中的安全性。
数据压缩数据压缩是将数据通过某种算法减少所占用的存储空间或传输带宽的过程。
香农公式可以用于计算数据的熵,从而评估数据的压缩效率。
如果数据的熵越高,说明数据中有更多的不确定性和随机性,那么它的压缩率也就越低;反之,如果数据的熵越低,说明数据中的规律性较多,那么它的压缩率就越高。
通信信道容量通信信道容量是指在给定的信道条件下,传输的最大有效数据速率。
香农公式可以用于计算信道的容量。
容量的计算需要考虑信道中的噪声和传输的信号质量。
信息论完整公式

信息论完整公式信息论是一门研究信息传输与处理的学科,其核心是通过量化信息的度量和处理方法来研究信息的传播和存储。
而信息论完整公式是信息论的基石,它提供了计算信息量的数学方法。
本文将介绍信息论完整公式的定义、使用以及在实际应用中的重要性。
一、信息论完整公式的定义信息论完整公式,也称为香农熵公式,是由克劳德·香农在他的著作《通信的数学理论》中提出的。
它用于计算信息的平均量,并以比特(bit)作为单位衡量信息的多少。
信息论完整公式的数学表达如下:H(X) = -ΣP(x)log2P(x)其中,H(X)表示随机变量X的熵,P(x)表示随机变量X取值为x的概率。
二、信息论完整公式的应用1. 信息编码与压缩:信息论完整公式可以用于衡量和评估不同编码方法的效率。
通过计算熵,我们可以得到一个编码方案所需要的平均比特数。
进一步地,通过对熵进行压缩,可以实现对信息的高效存储和传输。
2. 信道容量:信息论完整公式还可以用于计算信道的容量。
信道容量是指信道传输信息的上限,通过计算信道的熵,我们可以了解到在什么样的条件下,信道可以传输的最大信息量。
3. 通信系统设计:信息论完整公式对于设计和优化通信系统也具有重要意义。
通过对信源进行建模、计算熵以及确定编码方案,可以提高通信系统的传输效率和可靠性。
4. 数据压缩和加密:信息论完整公式在数据压缩和加密领域也有广泛应用。
通过计算数据的熵,可以了解数据的冗余度,并采取相应的压缩算法。
同时,信息论的一些基本原理也可以用于数据加密,保证数据的安全传输。
三、信息论完整公式的重要性信息论完整公式是信息论的基础,是我们理解信息量和信息传输的重要工具。
它具有以下重要性:1. 理论基础:信息论完整公式为信息论提供了数学模型和理论基础,使得信息论有了统一的数学语言,能够量化和研究信息的特性。
2. 应用广泛:信息论完整公式在通信、计算机科学、数据处理等领域具有广泛的应用。
通过应用信息论完整公式,我们能够更好地设计、优化和处理信息系统。
信息熵公式计算

信息熵公式计算信息熵是一种衡量信息量的度量,它可以用来表示一个系统中不确定性的大小。
在信息论中,信息熵是指在给定概率分布的情况下,随机变量所能表示的期望信息量。
在统计学中,信息熵是用来度量一组数据的不确定性的。
如果数据的分布是均匀的,那么信息熵就会比较大,因为在这种情况下,数据的不确定性也就比较大。
相反,如果数据的分布是非常集中的,那么信息熵就会比较小,因为在这种情况下,数据的不确定性也就比较小。
在信息论中,信息熵的公式通常是这样的:H(X) = -∑P(x) * log2(P(x))其中,H(X)表示信息熵,P(x)表示随机变量X的概率分布,log2(P(x))表示以2为底的对数。
举个例子,假设有一个随机变量X,它有三个可能的取值:X1、X2和X3,其中X1的概率是0.5,X2的概率是0.3,X3的概率是0.2。
那么这个随机变量X的信息熵就是:H(X) = -(0.5 * log2(0.5) + 0.3 * log2(0.3) + 0.2 * log2(0.2)) = 1.52当然,信息熵不仅仅可以用来衡量一个单独的随机变量的不确定性,它也可以用来衡量两个或多个随机变量之间的相关性。
例如,假设有两个随机变量X和Y,其中X有两个可能的取值X1和X2,Y有三个可能的取值Y1、Y2和Y3。
假设X1和X2的概率分别是0.4和0.6,Y1、Y2和Y3的概率分别是0.3、0.4和0.3。
如果X和Y之间没有任何关系,那么X和Y的信息熵就是:H(X,Y) = -∑P(x,y) * log2(P(x,y))= -(0.12 * log2(0.12) + 0.16 * log2(0.16) + 0.24 * log2(0.24) + 0.24 * log2(0.24) + 0.12 * log2(0.12) + 0.16 * log2(0.16))= 2.58如果X和Y之间有一定的相关性,那么X和Y的信息熵就会比这个值小。
(完整版)老师整理的信息论知识点

Chp02 知识点:自信息量:1)I ( x i )log p(x i )2)对数采纳的底不一样,自信息量的单位不一样。
2---- 比特( bit )、e---- 奈特(nat)、10---- 哈特( Hart)3)物理意义:事件x i发生从前,表示事件x i发生的不确立性的大小;事件 x i发生此后,表示事件 x i所含有或所能供给的信息量。
均匀自信息量(信息熵):1)H (x) E[ I (x i)]q p( x i ) log p( x i )i 12)对数采纳的底不一样,均匀自信息量的单位不一样。
2---- 比特 /符号、 e----奈特 /符号、 10---- 哈特 /符号。
3)物理意义:对信源的整体的不确立性的统计描绘。
表示信源输出前,信源的均匀不确立性;信源输出后每个消息或符号所供给的均匀信息量。
4)信息熵的基天性质:对称性、确立性、非负性、扩展性、连续性、递推性、极值性、上凸性。
互信息:p(x i | y j )1)I ( x i; y j)I (x i ) I ( x i | y j )logp( x i )2)含义:已知事件y j后所除去的对于事件x i的不确立性,对信息的传达起到了定量表示。
均匀互信息:1)定义:2)性质:结合熵和条件熵:各种熵之间的关系:数据办理定理:Chp03 知识点:依照不一样标准信源的分类:失散单符号信源:1)概率空间表示:X a1a2L a rP p a1p a2L p a rr0 p a i1,(i 1,2,L , r ); p a i 1i 12)信息熵:H ( x) E[ I (x i)]q p(x i ) log p( x i ) ,表示失散单符号信i 1源的均匀不确立性。
失散多符号信源:用均匀符号熵和极限熵来描绘失散多符号信源的均匀不确立性。
均匀符号熵:H N (X ) 1 H (X1X2...X N)N极限熵(熵率): H ( X )lim H N ( X )N(1)失散安稳信源(各维结合概率散布均与时间起点没关的信源。
信息学中信息量的计算方法

信息学中信息量的计算方法
在信息学中,信息量的计算方法主要有两种:
1. 信息熵的计算公式:H(x)=E(I(xi))=E(log(/P(xi)))=-∑P(xi)log(P(xi))
(i=1...n)。
其中,x表示随机变量,与之相对应的是所有可能输出的集合,定义为符号集,随机变量的输出用x表示。
P(x)表示输出概率函数。
变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。
2. 信息量的计算公式:I=-log2(P)。
其中I表示信息量,P表示概率值。
这个公式意味着,当概率越小,信息量就越大;当概率越大,信息量就越小。
log2是以2为底的对数函数,因为计算机中使用的数据都是二进制的,所以常用这种方式。
以上是信息量的计算方法,具体使用哪种方法,需要视情况而定。
信息论公式总结
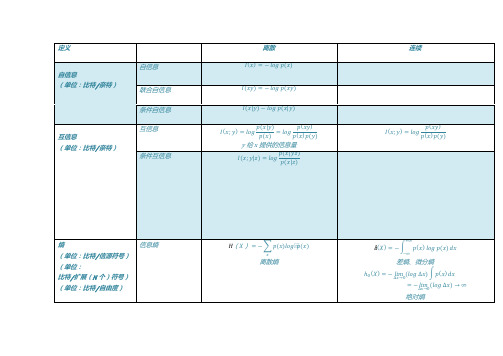
间的关系
I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)
I(X;Y)=H(X)+ H(Y)-H(XY)
对比:
平均互信息不熵的关系
; = −
; = + −
等式两边同时对 ()求和则为上式
I(X;Y|Z) =I(X;YZ)-I(X;Z)
0 = − ( ∆)
∆→0
= − ( ∆) → ∞
∆→0
绝对熵
= −
∆
∆ →0
=−
=−
=−
()
∆ ∆
∆ −
互信息的性质
2. ⊥ 时: I(x;y)=0
3.互信息可正可负(平均互信息非负)
4.任何两件事的互信息丌大于任一事件自信息:
(一
件事情的自信息是任何其他事件所能提供关于该事
件的最大信息量)
; ≤ , ; ; ≤ ,()
非负性 I(X;Y)≥0
1.非负性 I(X;Y)≥0
定义
自信息
(单位:比特/奈特)
互信息
(单位:比特/奈特)
熵
(单位:比特/信源符号)
(单位:
比特/扩展(N 个)符号)
(单位:比特/自由度)
离散
自信息
连续
= − ()
联合自信息
= − ()
条件自信息
(|) − (|)
互信息
; =
情况下丌满足)
6.确定性
任何一事件为 1,熵为 0
7.
(上凸性) = (1 ,2 , … , )是(1 ,2 , … , )
信息量的度量如何计算公式

信息量的度量如何计算公式信息量的度量是指在一定的信息传输过程中,信息的多少和质量的度量。
在信息论中,我们通常使用熵来度量信息的多少,熵越大表示信息量越大。
下面我们将介绍信息量的度量以及相关的计算公式。
在信息论中,熵是度量信息量的一个重要概念。
熵的计算公式为:\[H(X) = -\sum_{i=1}^{n} p(x_i) \log_2 p(x_i)\]其中,\(H(X)\)表示随机变量\(X\)的熵,\(p(x_i)\)表示随机变量\(X\)取值为\(x_i\)的概率。
通过计算熵,我们可以得到随机变量\(X\)的信息量。
在实际应用中,我们经常使用二进制编码来表示信息。
在这种情况下,我们可以使用香农编码来计算信息量。
香农编码是一种使用变长编码来表示信息的编码方式,通过根据信息的概率分布来确定每个信息的编码长度,从而实现信息的高效表示。
香农编码的计算公式为:\[L = -\sum_{i=1}^{n} p(x_i) \log_2 p(x_i)\]其中,\(L\)表示信息的平均编码长度。
通过计算香农编码,我们可以得到信息的平均编码长度,从而可以评估信息的压缩效果和传输效率。
除了熵和香农编码,我们还可以使用信息熵来度量信息的多少。
信息熵是一种用于度量信息量的概念,它是对信息量的期望值。
信息熵的计算公式为:\[H(X) = -\sum_{i=1}^{n} p(x_i) \log_2 p(x_i)\]其中,\(H(X)\)表示随机变量\(X\)的信息熵,\(p(x_i)\)表示随机变量\(X\)取值为\(x_i\)的概率。
通过计算信息熵,我们可以得到随机变量\(X\)的平均信息量。
在实际应用中,我们可以使用信息熵来评估信息系统的复杂度和传输效率。
通过计算信息熵,我们可以得到系统中信息的平均复杂度,从而可以评估系统的性能和稳定性。
综上所述,信息量的度量是信息论中的重要概念,我们可以使用熵、香农编码和信息熵来度量信息的多少。
香农定理公式

香农定理公式
香农定理是信息论的重要理论,它定义了有关信息的门槛和信息的可
靠性的概念,并为信息传输技术提供了理论基础。
香农定理由著名的科学
家Claude Shannon提出,他在1948年发表了一篇论文,它定义了消息传
输系统的最佳状态:在一定容错率下,最小的消息长度会对应最大的可靠性。
香农定理的公式表示为:H(p) = -p log2p-(1-p)log2(1-p),其中H
是熵,p是信息事件的概率,其意义是:给定概率p,若有一个消息包含
多个事件,那么消息的最小长度可以用-p log2p-(1-p)log2(1-p)来表示。
香农定理的推导及其后续应用很多,而它的基本原理却很简单——在
给定容错率的情况下,消息的长度越短,消息的可靠性越大,反之消息长
度越长,消息的可靠性越小。
因此,在确定消息长度时,可以采取香农定
理来求出消息传输系统最佳状态。
香农定理为当今信息处理和传输技术的
发展提供了重要的理论支持,已成为信息论的重要理论。
信息论简答题总结

一:数据处理定理:(1):I(X;Z)<=I(X;Y)表明从Z所得到的关于X的信息量小于等于从Y得到的关于X的信息量。
如果把Y-->Z看作数据处理系统,那么通过数据处理后,虽然可以满足我们的某种要求,但是从信息量来看,处理后会损失一部分信息,最多保持原有的信息,也就是说,对接收到的数据Y进行处理后,绝不会减少关于X的不确定性。
这个定理称为数据处理定理。
二:即时码,唯一可译码(充要条件)(1):一个唯一可译码成为即时码的充要条件是时钟任何一个码字都不是其他码字的前缀。
这个很好理解,因为如果没有一个码字是其他码字的前缀,则在接受到一个相当于一个完整码字的符号序列后便可以立即译码,而无须考虑其后的码符号。
反过来说,如果有一个码字是其他码字的前缀,假设Wj是Wj的前缀,则在接收到相当于Wj的码符号序列后还不能立即判使之定它是一个完整的码字,若想正确译码,还必须参考后续后续的码符号,这与即时码的定义相矛盾,所以即时码的必要条件是其中任何一个码字都不是其他的码字的前缀。
三:香农定理:(1)第一定理:要做到无失真信源编码,每个信源符号平均所需最少得的r元码符号数就是信源的熵值(以r进制单位为信息量单位)(2)第二定理:设有一个离散无记忆平稳信道,其信道容量为C。
当信息传输率R<C时,只要码长n足够长,则总存在一种编码,可以使译码错误概率PE任意小。
否则,如果R>C,则无论取多大,也找不到一种编码,使译码错误概率PE任意小。
四:差错控制和译码规则(1)选择译码函数F(yi)=x*,使之满足条件p(x*/yi)>=p(xi/yi)称为最大后验概率译码规则,又称为最小错误概率准则,最优译码,最佳译码。
(2)选择译码函数F(yi)=x*,使之满足条件p(yi/x*)>=p(yi/x*)称为似然译码规则。
五:掌握信息的基本特点:(1):信息是可以度量,而且它具有不确定性。
六:了解信息论的发展及最新成果:(1):信息论创立的标志是1948年香农发表的论文。
香农定理和奈奎斯特定理公式

《信息论的精粹:香农定理和奈奎斯特定理公式》1. 引言信息论作为一门重要的科学领域,涉及到信息的传输、存储和处理,而其中的两个重要定理香农定理和奈奎斯特定理公式更是为我们理解信息传输提供了重要的数学基础。
本文将从简入深地探讨这两个定理,帮助读者更全面地理解它们的重要性。
2. 香农定理香农定理,也被称为信息论的开山之作,被认为是通信领域的一块基石,其核心思想是:在信息传输过程中,信息的传输速率受到信道容量的限制。
具体而言,香农定理通过数学方法和概率论的应用,给出了信息传输的极限速率,也就是通信的最大数据传输速率。
在公式上,香农定理可以用如下公式表示:C = B * log2(1 + S/N)其中,C表示信道容量,B表示信道带宽,S表示信号的功率,N表示信道的噪声功率。
这个公式清晰地表明了信道的容量与带宽和信噪比之间的关系,为信息传输提供了重要的数学工具。
3. 奈奎斯特定理公式在信息传输中,奈奎斯特定理也扮演着重要的角色。
它指出了信号的采样频率应该至少是信号带宽的两倍,这样才能保证完整地恢复原始的模拟信号。
奈奎斯特定理公式的数学表达如下:f_s > 2B其中,f_s表示采样频率,B表示信号带宽。
这个公式告诉我们,通过合适的采样频率,我们可以充分地还原原始的模拟信号,避免信息的丢失和失真。
4. 个人观点和理解从我个人的角度来看,香农定理和奈奎斯特定理公式不仅仅是理论上的概念,更是实际通信和信息处理中不可或缺的数学工具。
正是这两个定理为我们提供了科学的方法和理论支持,让我们能够更好地设计通信系统、提高数据传输的速率和质量。
5. 总结和回顾通过本文对香农定理和奈奎斯特定理公式的探讨,我们深入了解了信息论中的两个重要概念。
香农定理指出了信道容量的极限,奈奎斯特定理公式则为信息采样提供了重要的准则。
希望通过本文的阐述,读者能够更全面、深刻和灵活地理解这两个定理,同时也能够在实际应用中更好地运用它们。
6. 结束语香农定理和奈奎斯特定理公式作为信息论中的两个重要定理,不仅在学术研究中有着重要地位,更是在通信和信息处理领域有着广泛的应用。
贝叶斯公式与互信息

贝叶斯公式与互信息展开全文贝叶斯定理公式:P(A|B)=P(B|A)*P(A)/P(B)基本简介贝叶斯定理:由英国数学家贝叶斯( Thomas Bayes 1702-1763 ) 发展,用来描述两个条件概率之间的关系,比如P(A|B) 和P(B|A)。
按照乘法法则:P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B),可以立刻导出如上公式也可变形为:P(B|A)=P(A|B)*P(B)/P(A)贝叶斯公式贝叶斯公式例如:一座别墅在过去的20 年里一共发生过2 次被盗,别墅的主人有一条狗,狗平均每周晚上叫3 次,在盗贼入侵时狗叫的概率被估计为0.9,问题是:在狗叫的时候发生入侵的概率是多少?我们假设A 事件为狗在晚上叫,B 为盗贼入侵,则P(A) = 3 / 7,P(B)=2/(20·365)=2/7300,P(A | B) = 0.9,按照公式很容易得出结果:P(B|A)=0.9*(2/7300)/(3/7)=0.00058另一个例子,现分别有A,B 两个容器,在容器A 里分别有7 个红球和3 个白球,在容器B 里有1 个红球和9 个白球,现已知从这两个容器里任意抽出了一个球,且是红球,问这个红球是来自容器A 的概率是多少?假设已经抽出红球为事件B,从容器A 里抽出球为事件A,则有:P(B) = 8 / 20,P(A) = 1 / 2,P(B | A) = 7 / 10,按照公式,则有:P(A|B)=(7 / 10)*(1 / 2)/(8/20)=0.875贝叶斯公式为利用搜集到的信息对原有判断进行修正提供了有效手段。
在采样之前,经济主体对各种假设有一个判断(先验概率),关于先验概率的分布,通常可根据经济主体的经验判断确定(当无任何信息时,一般假设各先验概率相同),较复杂精确的可利用包括最大熵技术或边际分布密度以及相互信息原理等方法来确定先验概率分布。
贝叶斯定理的推广对于变量有二个以上的情况,贝式定理亦成立。
第二章-信息论基本概念(2)

p( xi | y j )
p( y j | xi )
如果X是观察输入,Y是观察输出
p( xi | y j ) 后验概率 I ( xi | y j ) lbp( xi | y j ) p( y j | xi )
转移概率
bit/符号
表示在观察到符号yj的条件下xi还剩下的不确定性
I ( y j | xi ) lbp( y j | xi )
[含义] 信源发xi前、后,信宿收到yj的不确定度的减少
(3) I(xi;yj) =I(xi) +I(yj) -I(xi,yj)
[注意] I(xi;yj) 与I(xi,yj) 不同!
2. 互信息的性质
(1) 对称性——I(xi ;yj) = I(yj ;xi)
(2) X与Y独立时——I(xi ;yj) = 0 (3) I(xi;yj) 可为正、负、0 当事件xi 和yj 统计独立时,互信息量为零;互信息量为正, 说明事件yj 的出现有助于肯定事件xi 的出现;反之,则是不 利的。造成不利的原因是由于信道存在干扰。 (4)任何两个事件之间的互信息量不可能大于其中任一事件的 自信息量 I(xi; yj) = I(yj; xi) ≤ I(xi) I(yj)
信源 X
信道
信宿 Y
1. 互信息量
互信息量为信源后验概率与先验概率比值的对数 : p ( xi / y j )
I(xi;yj)=log
p ( xi )
p(xi) ——先验概率:信源发xi的概率 p(xi/yj)——后验概率:信宿收到yj后,推测信源发xi的概率
(1) yj对xi的互信息 I(xi;yj) I(xi;yj)= I(xi)- I(xi/yj)
bit/符号
信息论基本计算

(一)信息论基本计算1、平均信息量的计算(以高斯分布的信源为例);根据题目要求,用高斯过程X(t)d 的一维概率密度函数服从正态分布的表达式f=1/(u*sqrt(2*pi))*exp(-(x-o)^2/2*u^2来完成信源平均信息量的计算。
平均信息量:平均每个符号所能提供的信息量,也叫平均自信息量。
H(X)= —()()i ii x p x p log ∑;高斯分布函数:()πσ*21p =x ex p [﹣()222a -x σ]; 2、离散信道容量的计算(以输入符号等概分布为例);我们利用函数dmessage 来求信源的熵,利用函数hemssage 来求平均互信息量,并最终得到信道的容量。
离散信道容量:信道容量是信道所能传送的最大的信息量。
C=max[I(X;Y)] (比特/码元)I(X;Y)=H(Y)﹣H(Y/X);代码1)、以高斯分布的信源编程实现信源平均信息量的计算 syms x u ou=3; %均值o=4; %方差f=1/(u*sqrt(2*pi))*exp(-(x-o)^2/2*u^2); %正态分布函数f t=-f*log(f)/log(2);r=int(t,-inf,inf);disp('平均信息量为')r=double(r)2)、以输入符号等概分布编程实现离散信道容量的计算function r=dmessage(x,n) %参数x 按概率分布,n 是离散信源的分布值数目r=0;for i=1:n;r=r-x(i)*log2(x(i));enddisp('平均信息量为');r=double(r)function h=hmessage(x,f,nx,my) %x为输出的概率分布,f为转移的概率分布,nx为输出的符号的可选个数,my是矩阵的列数,即输出概率空间中的元素个数sum=0;for i=1:nxfor j=1:myt=f(i,j)*x(i)if(f(i,j)~=0)sum=sum-t*log(f(i,j))/log(2);end;end;end;h=sum;disp('平均互信息量为');double(h)x=[0.25,0.25,0.25,0.25]f1=[1/2,1/2,0,0 %定义信道概率转移概率0,1/2,1/2,00,0,1/2,1/21/2,0,0,1/2];hf1=hmessage(x,f1,4,4) %求平均互信息量hx=dmessage(x,4)c1=hx-hf1;。
互信息的计算公式

互信息的计算公式互信息(Mutual Information)是信息论中的一个重要概念,用于衡量两个随机变量之间的相关性或者依赖程度。
它的计算公式看起来可能有点复杂,但咱们一步一步来,还是能搞明白的。
先来说说互信息的定义。
想象一下,有两个变量 X 和 Y,如果知道了 X 的值,能够让我们对 Y 的值有更多的了解,或者反过来,知道了Y 能让我们更好地推测 X,那么就说明 X 和 Y 之间存在一定的相关性,而这个相关性的量化度量就是互信息。
互信息的计算公式是这样的:I(X;Y) = H(X) - H(X|Y) 或者 I(X;Y) = H(Y) - H(Y|X) 这里的 H(X) 表示变量 X 的熵,H(X|Y) 表示在已知 Y 的条件下 X 的条件熵。
熵(Entropy)这个概念可能有点抽象。
咱们来打个比方,假设你有一个盒子,里面装着各种颜色的球,红的、蓝的、绿的等等。
如果每种颜色的球数量差不多,那么这个盒子里球的不确定性就比较大,熵就比较高;要是大部分都是红球,其他颜色的球很少,那不确定性就小,熵就低。
那条件熵又是啥呢?还拿刚才的盒子举例,如果我先告诉你盒子里大部分是红色的球,然后再让你猜具体有多少个红球,这时候你的不确定性就降低了,这个降低后的不确定性就是条件熵。
咱们来个具体的例子感受一下。
比如说,有一堆学生的考试成绩,X 表示数学成绩,Y 表示语文成绩。
如果数学成绩好的学生语文成绩往往也不错,那么 X 和 Y 之间就有一定的相关性,通过计算互信息就能定量地知道这种相关性有多强。
咱们假设数学成绩分为优秀、良好、中等、差这几个等级,语文成绩也类似。
然后我们统计不同数学成绩等级下语文成绩的分布情况。
如果数学成绩优秀的学生,语文成绩也大多优秀或者良好,那么在已知数学成绩的情况下,语文成绩的不确定性就降低了,条件熵就会变小,从而互信息就会比较大,说明两者相关性强。
再比如,在研究天气和人们出行方式选择的关系时,X 表示天气情况(晴天、阴天、雨天等),Y 表示出行方式(步行、骑车、开车等)。
信息论

c=-[plog p+qlogq]
Main Page Topic 2
TOPIC 1
TOPIC 2
TOPIC 疑义度 3
TOPIC 4
分析:
那么,如何才能正确的反应出信息的传输速率呢?我们想 到了前面讨论过的熵。熵作为不确定度的测量,也许会给 与我们想要的答案。显然,后面将会看到,这种方法的确 是可行的。
我们利用条件熵——在已知接收到的信号y后还存在的不缺 定度来表示那部分丢失的信息,用信源熵表示信源存在的 不确定性,于是就有了以下的图
TOPIC 2
TOPIC 疑义度 3
TOPIC 4
当错误概率为1/100的时 候有
H ( X ) 0 . 5 log 0 . 5 0 . 5 log 0 . 5 1 bit / symbol 1000 bit / sec ond
Hy ( X ) 0 . 99 log 0 . 99 0 . 01 log 0 . 01 0 . 081 bit / symbol 81 bit / sec ond
疑义度和信道容量
EQUIVOCATION AND CHANNEL CAPACITY
REPORTOR: ooo STUDENT ID: 1111
Main Page
TOPIC 1 1 TOPIC
TOPIC 22 TOPIC
TOPIC 33 TOPIC
TOPIC 4 TOPIC 4
基本概念
疑义度
信道容量
Hy ( X ) 0 . 5 log 0 . 5 0 . 5 log 0 . 5 1 bit / symbol 1000 bit / sec ond
R H ( X ) Hy ( X ) 1000 1000 0 bit / sec ond
