砼梁配筋计算

梁、柱最小配筋面积(㎜2)fy

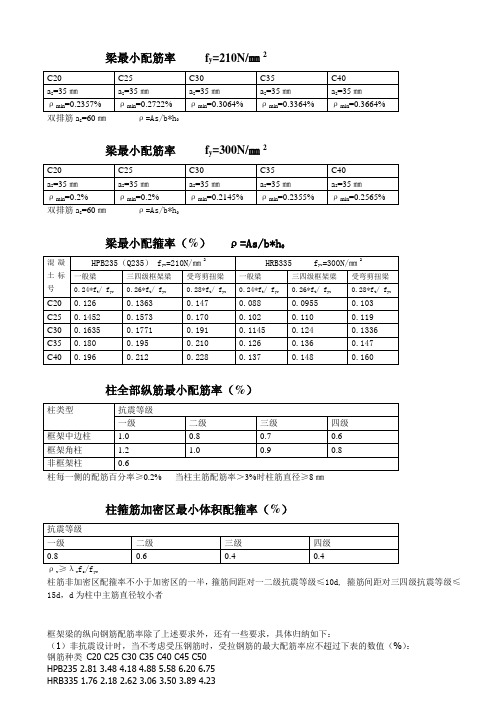
梁最小配筋率f y=210N/㎜2C20 C25 C30 C35 C40a s=35㎜a s=35㎜a s=35㎜a s=35㎜a s=35㎜ρmin=0.2357% ρmin=0.2722% ρmin=0.3064% ρmin=0.3364% ρmin=0.3664% 双排筋a s=60㎜ρ=As/b*h0梁最小配筋率f y=300N/㎜2C20 C25 C30 C35 C40a s=35㎜a s=35㎜a s=35㎜a s=35㎜a s=35㎜ρmin=0.2% ρmin=0.2% ρmin=0.2145% ρmin=0.2355% ρmin=0.2565% 双排筋a s=60㎜ρ=As/b*h0梁最小配箍率（%）ρ=As/b*h0混凝土标号HPB235（Q235） f yv=210N/㎜2 HRB335 f yv=300N/㎜2一般梁三四级框架梁受弯剪扭梁一般梁三四级框架梁受弯剪扭梁0.24*f t/ f yv 0.26*f t/ f yv0.28*f t/ f yv0.24*f t/ f yv 0.26*f t/ f yv0.28*f t/ f yvC200.126 0.1363 0.147 0.088 0.0955 0.103C250.1452 0.1573 0.170 0.102 0.110 0.119C300.1635 0.1771 0.191 0.1145 0.124 0.1336C350.180 0.195 0.210 0.126 0.136 0.147C400.196 0.212 0.228 0.137 0.148 0.160柱全部纵筋最小配筋率（%）柱类型抗震等级一级二级三级四级框架中边柱 1.0 0.8 0.7 0.6框架角柱 1.2 1.0 0.9 0.8非框架柱0.6柱每一侧的配筋百分率≥0.2% 当柱主筋配筋率＞3%时柱筋直径≥8㎜柱箍筋加密区最小体积配箍率（%）抗震等级一级二级三级四级0.8 0.6 0.4 0.4ρv≥λv f c/f yv柱筋非加密区配箍率不小于加密区的一半，箍筋间距对一二级抗震等级≤10d, 箍筋间距对三四级抗震等级≤15d，d为柱中主筋直径较小者框架梁的纵向钢筋配筋率除了上述要求外，还有一些要求，具体归纳如下：（1）非抗震设计时，当不考虑受压钢筋时，受拉钢筋的最大配筋率应不超过下表的数值（%）：钢筋种类C20 C25 C30 C35 C40 C45 C50HPB235 2.81 3.48 4.18 4.88 5.58 6.20 6.75HRB335 1.76 2.18 2.62 3.06 3.50 3.89 4.23HRB400 1.38 1.71 2.06 2.40 2.75 3.05 3.32（2）有地震组合时，当不考虑受压钢筋时，受拉钢筋的最大配筋率应不超过下表的数值（%）：a)抗震等级为一级时钢筋种类C20 C25 C30 C35 C40 C45 C50HPB235 1.14 1.42 1.70 1.99 2.27 2.50 2.50HRB335 0.80 0.99 1.19 1.39 1.59 1.77 1.92HRB400 0.67 0.83 0.99 1.16 1.33 1.47 1.60b)抗震等级为二、三级时钢筋种类C20 C25 C30 C35 C40 C45 C50HPB235 1.60 1.98 2.38 2.50 2.50 2.50 2.50HRB335 1.12 1.39 1.67 1.95 2.23 2.47 2.50HRB400 0.93 1.16 1.39 1.62 1.86 2.06 2.25（3）非地震设计时，纵向受拉钢筋的最小配筋率(%)如下表：钢筋种类C20 C25 C30 C35 C40 C45 C50HPB235 0.24 0.27 0.31 0.34 0.37 0.39 0.41HRB335 0.20 0.20 0.21 0.24 0.26 0.27 0.28HRB400 0.20 0.20 0.20 0.20 0.21 0.23 0.24（4）抗震设计时，纵向受拉钢筋的最小配筋率(%)如下表：a)抗震等级为一级时支座处钢筋种类C20 C25 C30 C35 C40 C45 C50HRB335 0.40 0.40 0.40 0.42 0.46 0.48 0.50HRB400 0.40 0.40 0.40 0.40 0.40 0.40 0.42b)抗震等级为一级时跨中处钢筋种类C20 C25 C30 C35 C40 C45 C50HRB335 0.30 0.30 0.31 0.34 0.37 0.39 0.41HRB400 0.30 0.30 0.30 0.30 0.31 0.33 0.34c)抗震等级为二级时支座处钢筋种类C20 C25 C30 C35 C40 C45 C50HRB335 0.30 0.30 0.31 0.34 0.37 0.39 0.41HRB400 0.30 0.30 0.30 0.30 0.31 0.33 0.34d)抗震等级为二级时跨中处钢筋种类C20 C25 C30 C35 C40 C45 C50HRB335 0.25 0.25 0.26 0.29 0.31 0.33 0.35HRB400 0.25 0.25 0.25 0.25 0.26 0.28 0.29e)抗震等级为三、四级时支座处钢筋种类C20 C25 C30 C35 C40 C45 C50HPB235 0.29 0.33 0.37 0.41 0.45 0.47 0.50HRB335 0.25 0.25 0.26 0.29 0.31 0.33 0.35HRB400 0.25 0.25 0.25 0.25 0.26 0.28 0.29f)抗震等级为三、四级时跨中处钢筋种类C20 C25 C30 C35 C40 C45 C50HPB235 0.24 0.27 0.31 0.34 0.37 0.39 0.41HRB335 0.20 0.20 0.21 0.24 0.26 0.27 0.28HRB400 0.20 0.20 0.20 0.20 0.21 0.23 0.24我觉得这样算欠妥当。

8个钢筋混凝土板梁配筋计算例题[详细]

1、某宿舍的内廊为现浇简支在砖墙上的钢混凝土平板(例图4-1a),板上作用的均布活荷载标准值为q k=2kN/米.水磨石地面及细石混凝土垫层共30米米厚(重力密度为22kN/米3),板底粉刷白灰砂浆12米米厚(重力密度为17kN/米3).混凝土强度等级选用C15,纵向受拉钢筋采用HPB235热轧钢筋.试确定板厚度和受拉钢筋截面面积.例图4-1(a)、(b)、(c)[解]1．截面尺寸内廊虽然很长,但板的厚度和板上的荷载都相等,因此只需计算单位宽度板带的配筋,其余板带均按此板带配筋.取出1米宽板带计算,取板厚h=80米米(例图4-1b),一般板的保护层厚15米米,取a s=20米米,则h0=h-a s=80-20=60米米.2．计算跨度单跨板的计算跨度等于板的净跨加板的厚度.因此有l0=l n+h=2260+80=2340米米3．荷载设计值恒载标准值: 水磨石地面0.03×22=0.66kN/米钢筋混凝土板自重(重力密度为25kN/米3)0.08×25=2.0kN/米白灰砂浆粉刷0.012×17=0.204kN/米g k=0.66+2.0+0.204=2.864kN/米活荷载标准值: q k=2.0kN/米恒载设计值:活荷载设计值:4．弯矩设计值米(例图4-1c)5．钢筋、混凝土强度设计值由附表和表4-2查得:C15砼:HPB235钢筋:6．求x及A s值由式(4-9a)和式(4-8)得:7．验算适用条件8．选用钢筋及绘配筋图选用φ8@130米米(A s=387米米2),配筋见例图4-1d.例图4-1d冷轧带肋钢筋是采用普通低碳钢筋或普通低合金钢筋为原材料加工而成的一种新型高效钢筋.由于它强度高,可以节约许多钢材,加之其直径细、表面带肋、与混凝土的粘结锚固效果特别好,因此在国外得到广泛的应用.我国自80年代中期将其引入后,经过近十年的努力,已经编制了国家标准《冷轧带肋钢筋》GB13788-92和行业标准《冷轧带肋钢筋混凝土结构技术规程》JGJ95-95.国家科委和建设部曾相继下文,要求大力推广采用冷轧带肋钢筋.本例如果改用经调直的550级冷轧带肋钢筋配筋时:选用φ6@125米米(A s=226米米2)即是说,将采用HPB235钢筋配筋改为采用550级的冷轧带肋钢筋配筋以后,可以节省41.6%的受力钢筋用钢量,这个数字是十分可观的.2、某教学楼中的一矩形截面钢筋混凝土简支梁,计算跨度l0=6.0米米,板传来的永久荷载及梁的自重标准值为g k=15.6kN/米米,板传来的楼面活荷载标准值q k=10.7kN/米,梁的截面尺寸为200米米×500米米(例图4-2),混凝土的强度等级为C20,钢筋为HRB335钢筋.试求纵向受力钢筋所需面积.[解]1．内力计算永久荷载的分项系数为1.2,楼面活荷载的分项系数为1.4,结构的重要性系数为1.0,因此,梁的跨中截面的最大弯矩设计值为:2．配筋计算由附表和表4-2查得当混凝土的强度等级为C20时,f c=9.6N/米米2,,由附表3查得HRB335钢筋的f y=300N/米米2.先假定受力钢筋按一排布置,则联立求解上述二式,得x=223.65米米, A s=1431米米23．适用条件验算(1)验算条件式(4-10)本例中的配筋率为(2)验算条件式(4-11)由表4-4查得,而本题实际的相对受压区高度为:因此,两项适用条件均能满足,可以根据计算结果选用钢筋的直径和根数.选择钢筋的直径和根数时,希望选用的钢筋截面面积尽可能接近计算截面面积,力争使误差保持在±5%以内,所选的钢筋直径和根数还应满足构造上的有关规定.本例选用三根直径为25米米的HRB335钢筋,记作3 25,一排配置,实际的配筋截面面积A s=1473米米2,满足计算时钢筋设计强度取值和截面有效高度的假定,配筋面积符合计算要求.例图4-23、某宿舍一预制钢筋混凝土走道板,计算跨长l0=1820米米,板宽500米米,板厚60米米,混凝土的强度等级为C15,受拉区配有4根直径为6米米的HPB235钢筋,当使用荷载及板自重在跨中产生的弯矩最大设计值为米=910000N·米米时,试验算该截面的承载力是否足够？[解]1．求x由附表和表4-2查得由式(4-8)求得受压区计算高度为2．求米u3．判别截面承载力是否满足(满足)某实验室一楼面梁的尺寸为250米米×500米米,跨中最大弯矩设计值为米=180000N·米,采用强度等级C30的混凝土和HRB400级钢筋配筋,求所需纵向受力钢筋的面积.[解]1．利用参考资料中的计算用表1求A s先假定受力钢筋按一排布置,则h0=h-35=500-35=465米米查附表4-1和表4-2得由式(4-22)得由计算用表1查得相应的值为所需纵向受拉钢筋面积为选用4 20(A s=1256米米2),一排可以布置得下,因此不必修改h0重新计算A s值.2．利用参考资料中的计算用表2求A s根据上面求得查计算用表2得由式(4-25)可求出所需纵向受力钢筋的截面面积为:计算结果与利用计算用表1的完全相同,因此以后只需要选用其中的一个表格进行计算便可以.由本例可看出,利用表格进行计算,比利用静力平衡公式计算要简便得多.某处于一般环境下的中型桥桥面梁,截面尺寸b×h=250米米×500米米,跨中最大弯矩设计值米d=1.8×108N·米米,采用强度等级C30的混凝土和HRB400钢筋配筋,求所需纵向受力钢筋的面积.[解]假定受力钢筋按一排布置,混凝土保护层厚30米米,则h0=h-40=500-40=460米米由表查得f cd=13.8N/米米2,f sd=330N/米米2,,=1.0,则所需纵向受力钢筋面积为:选用2 20+2 22(A s=1388米米2).(例图4-8)例图4-8某库房一楼面大梁截面尺寸b×h=250米米×600米米,混凝土的强度等级为C20,用HPB235钢筋配筋,截面承受的弯矩设计值米=4.0×108N·米米,当上述基本条件不能改变时,求截面所需受力钢筋截面面积.[解]1．判别是否需要设计成双筋截面查附表和表4-2得;f y=f y=210N/米米2;查表4-4和表4-6得b=250米米,h0=600-70=530米米(两排布置).单筋矩形截面能够承受的最大弯矩为:因此应将截面设计成双筋矩形截面.2．计算所需受拉和受压纵向受力钢筋截面面积设受压钢筋按一排布置,则a’s=40米米.由式(4-34)得:由式(4-35)得:钢筋的选用情况为:受拉钢筋8受压钢筋4截面的配筋情况如例图4-3所示.例图4-3一基本情况与例4-4相同的梁,但米=2.0×108N·米受压区预先已经配好HRB335级受压钢筋2 20(A's=628米米2),求截面所需配置的受拉钢筋截面面积A s.[解]1．求受压区高度x假定受拉钢筋和受压钢筋按一排布置,则a s=a's=35米米,h0=h-a s=500-35=465米米..由式(4-36)求得受压区的高度x为:且2．计算截面需配置的受拉钢筋截面面积由式(4-37)求得受拉钢筋的截面面积A s为:选用3 25(A s=1473米米2),截面配筋情况如例图4-4所示.例图4-4已知一T形截面梁截面尺寸b'f=600米米、h'f=120米米、b=250米米、h=650米米,混凝土强度等级C20,采用HRB335钢筋,梁所承受的弯矩设计值米=426 kN·米.试求所需受拉钢筋截面面积A s.[解]1．已知条件混凝土强度等级C20,;HRB335级钢筋,.考虑布置两排钢筋,a s=70米米,h0=h-a s=650-70=580米米.2．判别截面类型属第二类T形截面.3．计算x取式(4-52)中米=米u,由式(4-52)得4．计算A s将x代入式(4-51)得5．选用钢筋及绘配筋图选用2 22+4 25(A s=2724米米2),配筋见例图4-5.例图4-5已知一T形截面梁(例图4-6)的截面尺寸h=700米米、b=250米米、h'f=100米米、b'f=600米米,截面配有受拉钢筋822(A s=3041米米2),混凝土强度等级C30,采用HRB400钢筋.梁截面的最大弯矩设计值米=500kN·米.试校核该梁是否安全？[解]1．已知条件混凝土强度等级C30,;HRB400钢筋,,,2．判别截面类型,属第二类T形截面.3．计算x4．计算极限弯矩米u(安全)例图4-6。

WPJ结果文件含义

1、砼梁和劲性梁其中：As1、As2、As3为梁上部(负弯矩)左支座、跨中、右支座的配筋面积(cm2)；Asm1、Asm2、Asm3表示梁下部(负弯矩)左支座、跨中、右支座的配筋面积(cm2)；Asv表示梁在Sb范围内的箍筋面积(cm2)，取抗剪箍筋Asv与剪扭箍筋Astv 的大值；Ast表示梁受扭所需要的纵筋面积(cm2)；Ast1表示梁受扭所需要周边箍筋的单根钢筋的面积(cm2)。

G，TV分别为箍筋和剪扭配筋标志。

梁配筋计算说明：对于配筋率大于1%的截面，程序自动按双排筋计算；此时，保护层取60mm；当按双排筋计算还超限时，程序自动考虑压筋作用，按双筋方式配筋；各截面的箍筋都是按用户输入的箍筋间距计算的，并按沿梁全长箍筋的面积配箍率要求控制。

若输入的箍筋间距为加密区间距，则加密区的箍筋计算结果可直接参考使用，如果非加密区与加密区的箍筋间距不同，则应按非加密区箍筋间距对计算结果进行换算；若输入的箍筋间距为非加密区间距，则非加密区的箍筋计算结果可直接参考使用，如果加密区与非加密区的箍筋间距不同，则应按加密区箍筋间距对计算结果进行换算。

2、钢梁其中：R1表示钢梁正应力与强度设计值的比值F1/f；R2表示钢梁整体稳定应力与强度设计值的比值F2/f；R3表示钢梁剪应力与强度设计值的比值F3/fv。

其中 F1，F2，F3 的具体含义：F1 = M/（Gb Wnb）F2 = M/（Fb Wb）F3（跨中）= V S/(I tw)， F3（支座）= V/Awn3、矩形混凝土柱或劲性混凝土柱在左上角标注：(Uc)、在柱中心标柱：Asv、在下边标注：Asx、在右边标注：Asy、引出线标注：As_corner其中：As_corner为柱一根角筋的面积，采用双偏压计算时，角筋面积不应小于此值，采用单偏压计算时，角筋面积可不受此值控制(cm2)。

Asx，Asy分别为该柱B边和H边的单边配筋，包括角筋(cm2)。

Asv表示柱在Sc范围内的箍筋，它是取柱斜截面抗剪箍筋和节点抗剪箍筋的大值(cm2)。

简单的配筋计算【路桥常用计算公式】

受压区砼和相应的一部分受力钢筋As1的拉力所承担的受弯承载力 Mu1
Mu1=Mu,max =
415.68 kNm
As1
=
x b bh0
a1 fc fy
=
由受压钢筋及相应的受拉钢筋承受的弯矩设计值为
因此所需的受压钢筋为
Mu2=MMu1=
3539.25 ㎜2 -172.68 kNm
As'
=
Mu2
f
' y
(h0
-
a
' s
)
=
-1139.83 ㎜2
与其对应的那部分受拉钢筋截面面积为
纵向受拉钢筋总截面面积
As2=A's= -1139.83 ㎜2
As＝As1＋ As2= 2399.42 ㎜2
受拉钢筋取钢筋直径
￠＝
20
实取 9
实配钢筋面积AS= 2827.43 mm2
受压钢筋取钢筋直径
￠＝
12
实取 2
As＝As1＋ As2= 565.93 ㎜2
受拉钢筋取钢筋直径
￠＝
20
实取 8
实配钢筋面积AS= 2513.27 mm2
验算受压区高度x＝
fyAs1/(α1fcb)=
-31.60 mm
2α's＝ 70 mm
＞
根 OK!
x NO!!!
Mu2=f'yA's( h0-a's)=
由弯矩Mu1按单筋矩形截面求As1
因此所需的受压钢筋为
Mu1=MMu2=
942.48
3 ￠ 20 942.48 mm2
142.79 kNm
-62.79 kNm

承重梁梁长10米,承重45吨钢筋砼梁配筋方案

承重梁梁长10米,承重45吨钢筋砼梁配筋方案方案大纲：混凝土梁的计算与构造设计混凝土柱的计算与构造设计梁柱节点的构造设计一、混凝土梁的计算与构造设计1、梁的最小截面梁正截面受弯承载力计算应满足极限承载弯矩M<Mu。

（抗震6.3.1）梁的截面尺寸，宜符合下列要求：（1）截面宽度不宜小于200mm（2）截面高宽比不宜大于4（3）净跨与截面高度比不宜小于4。

2、梁配筋设计流程抗扭配筋：抗扭腰筋计算、顶筋底筋计算，面积叠加抗扭面积抗弯配筋：底部钢筋、支座负筋、支座，筋截断长度计算抗剪配筋：箍筋、弯起筋构造配筋：架立筋、拉筋、挑耳通同筋二、混凝土柱的计算与构造设计1、构造腰筋设计当梁的腹板高度h>450mm时，在梁的两个侧面应沿高度配置纵向构造钢筋，每侧纵向构造钢筋（不包括梁上、下部受力钢筋及架立钢筋）的截面面积不应小于腹板截面面积的0.1%，且间距不宜大于200mm。

2、纵筋抗扭设计沿截面周边布置的受扭纵向钢筋的间距不应大于200mm和梁截面短边长度；除应在梁截面四角设置受扭纵向钢筋外，其余受扭纵向钢筋宜沿截面周边均匀对称布置。

受扭纵向钢筋应按受拉钢筋锚固在支座内。

在弯剪扭构件中，配置在截面弯曲受拉边的纵向受力钢筋，其截面面积不应小于规定的受弯构件。

受拉钢筋最小配筋率计算出的钢筋截面面积与按本条受扭纵向钢筋配筋率计算并分配到弯曲受拉边的钢筋截面面积之和。

三、梁柱节点的构造设计1、抗弯钢筋设计确定设计配筋面积，根数和直径的选取，上筋截断长度的确定，锚固方式的确定，正常使用极限状态的验算。

2、抗弯钢筋面积的确定由计算软件（SATWE、TAT或PK）根据弯矩包络确定梁各截面的抗弯钢筋面积。

按双筋截面计算，分别用截面的最大正弯矩和最大负弯矩计算配筋面积，然后取二者之间的较大值。

验算配筋面积是否满足最小配筋率和最大配筋要求。

经过归并放大，并叠加抗扭纵筋面积，得到最后用来设计纵筋的钢筋面积。

首层砼悬挑梁配筋计算

首层砼悬挑梁配筋计算书一、依据规范:《建筑施工扣件式钢管脚手架安全技术规范》JGJ130-2011《建筑结构荷载规范》GB50009-2012《钢结构设计规范》GB50017-2003《混凝土结构设计规范》GB50010-2010二、计算参数:梁高h=500mm，梁宽a=200mm，C35混凝土fc=16.7N/m m2，s max=0.4，混凝土容重为25KN/m³，L、L1、L2根据外架平面布置图取值。

首层局部悬挑架搭设从首层至4层梁板底，搭设高度15.3m，步距1800mm，纵距1500mm，横距900mm，钢管直径、壁厚取Φ48.3×3.6，施工活荷载为2.5kN/m2，同时考虑2层施工。

脚手板采用钢筋网片，荷载为0.15kN/m2，按照铺设8层计算。

栏杆采用冲压钢板，荷载为0.16kN/m，安全网荷载取0.0100kN/m2。

三、荷载计算作用于脚手架的荷载包括静荷载、活荷载和风荷载。

静荷载标准值包括以下内容：(1)每米立杆承受的结构自重标准值(kN/m)；本例为0.1072N G1= 0.107×15.3=1.64kN(2)脚手板的自重标准值(kN/m 2)；本例采用钢筋网片脚手板，标准值为0.15 N G2 = 0.150×8×1.500×(0.900+0.300)/2=1.08kN(3)栏杆与挡脚手板自重标准值(kN/m)；本例采用栏杆、冲压钢脚手板挡板，标准值为0.16N G3 = 0.160×1.500×8/2=0.96kN(4)吊挂的安全设施荷载，包括安全网(kN/m 2)；0.010N G4 = 0.010×1.500×15.300=0.23kN经计算得到，静荷载标准值 N G = N G1+N G2+N G3+N G4 = 3.91kN 。

活荷载为施工荷载标准值产生的轴向力总和，内、外立杆按一纵距内施工荷载总和的1/2取值。

矩形梁配筋、T梁型配筋、最大最小配筋率计算

其中，1; HPB235级钢 2; HRB335级钢 3; HRB400级钢
A）单筋矩形截面在纵向受拉钢筋达到充分发挥作用或不出现超筋破坏所能承受的最大弯矩设计值Mu,max
2 M u ,max = a1 f c bh0 x b (1 - 0.5x b )
=
55.66 kNm
B）单筋矩形截面已知弯矩求配筋 M实际= 85 #NUM! kNm ㎜2
3078.76 mm2 验算受压区高度x＝fyAs1/(α1fcb)= 70.46 2α 's＝ 60 mm
OK! OK!
mm
钢 3; HRB400级钢
2045.16
Mu2M (h0 - h02 )= fy a1 fcb
￠＝
取钢筋直径
22 1900.66 mm 258
2
实取＜
5 As
根＜ Asmax=
实配钢筋面积AS= Asmin=
判断: #NUM! C）双筋矩形截面已知弯矩求配筋 M实际= 85.00 kNm ＞ Mu,max 受压区砼和相应的一部分受力钢筋As1的拉力所承担的受弯承载力Mu1 Mu1=Mu,max= 55.66 kNm
As1 = x b bh0
a1 f c fy
=
1604.94 ㎜2
由受压钢筋及相应的受拉钢筋承受的弯矩设计值为 Mu2=M-Mu1= 29.34 kNm 因此所需的受压钢筋为
As' =
M u2 = f ( h0 - a s' )
' y
815.08 ㎜2
与其对应的那部分受拉钢筋截面面积为 As2=A's= 纵向受拉钢筋总截面面积 As＝As1＋As2= 受拉钢筋取钢筋直径实配钢筋面积AS= 受压钢筋取钢筋直径实配钢筋面积AS= 28 ￠＝ 3078.76 mm 22 ￠＝

配筋计算表

弯矩
M=160.00kN·m
砼强度等级
C25
砼抗压强度
fc=12.50N/m2
环境类别
2
保护层最小厚度
c=35mm
纵向受拉钢筋至受拉边距离
a=45mm
截面宽度
b=200mm
截面高度
h=430mm
计算截面高度
h0=385mm
钢筋级别
Ⅱ
临界相对受压区高度
ξb=0.544
钢筋强度
fy=f'y=310N/m2
8mm
箍筋截面面积
Asv=50.3mm
箍筋沿梁轴向的间距
s=100mm
判断计算情况
情况1
Vs=0.07fcbh0+1.25fyvAsvh0/s或
Vs=0.2fcbh0/（λ+1.5）
Vs=227.45kN
+1.25fyvAsvh0/s
判断截面是否满足要求
箍筋不满足抗剪要求
抗剪弯起钢筋的计算
弯起钢筋与纵向轴线的夹角αs αs=60° 同一弯起平面内弯钢筋的截面积 494mm
钢筋砼受扭构件承载力计算(矩形)
弯矩设计值
M=365.00kN·m
剪力设计值
V=300.00kN
扭矩设计值
T=164.00kN·m
砼等级
C25
砼抗压强度fc
fc=12.50N/m2
砼抗压强度ft
ft=1.30N/m2
主筋钢筋级别
Ⅱ
主筋钢筋强度
fy=f'y=310N/m2
保护层厚度
a=20mm
截面宽度
弯矩
M=2784.97kN·m
砼强度等级
C25

配筋计算公式

配筋计算公式配筋（计算规则）率是钢筋混凝土构件中纵向受力（拉或压）钢筋的面积与构件的有效面积之比（轴心受压构件为全截面的面积）。

柱子为轴心受压构件受拉钢筋配筋率、受压钢筋配筋率分别计算。

计算公式：ρA（s）/bh（0）。

此处括号内实为角标，下同。

式中：As为受拉或受压区纵向钢筋的截面面积；b 为矩形截面的宽度；h（0）为截面的有效高度。

配筋率是反映配筋数量的一个参数。

最小配筋率是指，当梁的配筋率ρ 很小，梁拉区开裂后，钢筋应力趋近于屈服强度，这时的配筋率称为最小配筋率ρ（min）。

最小配筋率是根据构件截面的极限抗弯承载力M（u）与使混凝土构件受拉区正好开裂的弯矩M（cr）相等的原则确定。

最小配筋率取0.2和0.45ft/fy二者中的较大值！最大配筋率ρ （max）ξbfc/fy结构设计的时候要满足最大配筋率的要求，当构件配筋超过最大配筋率时塑性变小，不利于抗震。

配筋率是影响构件受力特征的一个参数，控制配筋率可以控制结构构件的破坏形态，不发生超筋破坏和少筋破坏，配筋率又是反映经济效果的主要指标。

控制最小配筋率是防止构件发生少筋破坏，少筋破坏是脆性破坏，设计时应当避免。

钢筋的截面积与所设计的砼结构面的有效面积的比值，称之为配筋率。

在钢筋砼结构中，钢筋的总截面积与所设计的砼结构面的有效高度与宽度的积的比值，称之为配筋率，根据配筋率的大小，其结构分为超筋、适筋、少筋截面。

钢筋面积/构件截面面积（全面积or 全面积-受压翼缘面积）梁的配筋率是梁的受压和受拉钢筋的总截面积除以梁的有效截面?行Ы孛媸歉纸詈狭Φ愕巾派厦娴木嗬搿?合力点：是梁宽乘有效高度，有效高度指梁下部筋为一排筋时用高减35，下部筋为两排筋时减60 1、“柱外侧纵筋配筋率”为：柱外侧纵筋（包括两根角筋）的截面积，除以整个柱的截面积所得到的比率。

2、屋面框架梁（WKL）“上部纵筋配筋率”为：梁上部纵筋的总的截面积，除以梁的有效截面积所得到的比率。

(整理)配筋计算公式及配筋原则

钢筋工程量计算规则(一）钢筋工程量计算规则1、钢筋工程，应区别现浇、预制构件、不同钢种和规格，分别按设计长度乘以单位重量，以吨计算。

2、计算钢筋工程量时，设计已规定钢筋塔接长度的，按规定塔接长度计算；设计未规定塔接长度的，已包括在钢筋的损耗率之内，不另计算塔接长度。

钢筋电渣压力焊接、套筒挤压等接头，以个计算。

3、先张法预应力钢筋，按构件外形尺寸计算长度，后张法预应力钢筋按设计图规定的预应力钢筋预留孔道长度，并区别不同的锚具类型，分别按下列规定计算：（1)低合金钢筋两端采用螺杆锚具时，预应力的钢筋按预留孔道长度减0.35m，螺杆另行计算。

（2）低合金钢筋一端采用徽头插片，另一端螺杆锚具时，预应力钢筋长度按预留孔道长度计算，螺杆另行计算。

（3）低合金钢筋一端采用徽头插片，另一端采用帮条锚具时，预应力钢筋增加0. 15m，两端采用帮条锚具时预应力钢筋共增加0.3m计算。

（4）低合金钢筋采用后张硅自锚时，预应力钢筋长度增加0. 35m计算。

（5）低合金钢筋或钢绞线采用JM， XM， QM型锚具孔道长度在20m以内时，预应力钢筋长度增加lm；孔道长度20m以上时预应力钢筋长度增加1.8m计算。

（6）碳素钢丝采用锥形锚具，孔道长在20m以内时，预应力钢筋长度增加lm；孔道长在2 0m以上时，预应力钢筋长度增加1．8m.（7）碳素钢丝两端采用镦粗头时，预应力钢丝长度增加0. 35m计算。

（二）各类钢筋计算长度的确定钢筋长度=构件图示尺寸－保护层总厚度+两端弯钩长度+（图纸注明的搭接长度、弯起钢筋斜长的增加值）式中保护层厚度、钢筋弯钩长度、钢筋搭接长度、弯起钢筋斜长的增加值以及各种类型钢筋设计长度的计算公式见以下：1、钢筋的砼保护层厚度受力钢筋的砼保护层厚度，应符合设计要求，当设计无具体要求时，不应小于受力钢筋直径，并应符合下表的要求。

（2）处于室内正常环境由工厂生产的预制构件，当砼强度等级不低于C20且施工质量有可靠保证时，其保护层厚度可按表中规定减少5mm，但预制构件中的预应力钢筋的保护层厚度不应小于15mm；处于露天或室内高湿度环境的预制构件，当表面另作水泥砂浆抹面且有质量可靠保证措施时其保护层厚度可按表中室内正常环境中的构件的保护层厚度数值采用。

砼梁配筋计算表 2

2 2
θ x(CD)=-qc(12b2+c2-4(x-d)3/c)/24EI θ x(DB)=-qc(b -(x-a) )/2EI
2 3 2 2 3 2 2 2 4 2 2
fx(AC)=qc(12b L-4b +ac -(12b +c )x)/24EI fx(CD)=qc(12b L-4b +ac -(12b +c )x+(x-d) /c)/24EI fx(DB)=qc(3b2பைடு நூலகம்-b3-3b2x+(x-a)3)/6EI fA=qc(12b2L-4b3+ac2)/24EI q=2.00kN/m L=1.20m Qx=-qx2/2L=-1.20kN x=1.20m ξ =1.00 梁的截面尺寸：砼强度等级 I=1066666667mm4 θ x=-qL3(1-ξ 4)/24EI θ A=-qL3/24EI fx=qL4(4-5ξ +ξ 5)/120EI fA=qL4/30EI q=10.25kN/m L=1.20m 梁的截面尺寸：砼强度等级 I=1066666667mm4 qx=q(1-ξ )=5.13kN Qx=-qx(2-ξ )/2 MB=-qL2/3 MX=-qx (3-ξ )/6 θ x=-qL3(3-4ξ 3+ξ 4)/24EI θ A=-qL /8EI fx=qL (11-15ξ +5ξ -ξ )/120EI fA=11qL4/120EI q=10.00kN/m L=1.50m 梁的截面尺寸：砼强度等级 I=1066666667mm4 α =0.67 β =0.33 ξ =0.53 Qx(AC)=-qx2/2a=-3.20kN a=1.00m b=200mm
C20 E=25500N/m2 ξ =0.40 x=0.60m d=0.50m RB=qc=6.00kN Qx(CD) MB=-qcb=-4.20kN·m Mx(CD)=-0.05kN·m Mx(CD) θ x(AC)=θ A=-0.00006 θ x(CD)=-0.0000540 θx(DB)=-0.0000496

混凝土梁最大配筋率

λ
1.2%,且应沿柱全长
ρ
为竖向、水平分布钢筋
0.20%; 2）框架－剪力
0.4%
1）钢筋砼梁中箍筋配筋率
1) V>0.7f t bh 0ρsv ＝A sv /bs ≥0.24f t /f yv
2) 在弯剪扭构件中，剪扭箍筋的配筋率ρsv ＝Asv/bs ≥0.28ft/fyv ，其中Asv 为配置在同一截面内具体见上表。

2) 梁内受扭纵向钢筋的配筋率
bh
A stl tl
=r
A stl ：沿截面周边布置的受扭纵向钢筋的总截面面积。

受拉纵向钢筋的配筋率不应小于其中，b 为矩形截面的宽度，或T 形截面的腹板宽
受扭纵向受力钢筋的最小配筋百分率
bh
A stl tl
=r y
c f f Vb T 6
.0
sv/(bSh);Sh 、0.25%；，其中Asv 为配置在同一截面内箍筋各肢的全部截面面积。

截面的宽度，或T形截面的腹板宽度，当T/(Vb)>2时，取T/(Vb)=2。

SATWE 计算结果算配筋

砼梁和劲性梁其中：As1、As2、As3为梁上部(负弯矩)左支座、跨中、右支座的配筋面积(cm2)；Asm1、Asm2、Asm3表示梁下部(负弯矩)左支座、跨中、右支座的配筋面积(cm2)；Asv表示梁在Sb范围内的箍筋面积(cm2)，取抗剪箍筋Asv与剪扭箍筋Astv的大值；Ast表示梁受扭所需要的纵筋面积(cm2)；Ast1表示梁受扭所需要周边箍筋的单根钢筋的面积(cm2)。

G，TV分别为箍筋和剪扭配筋标志。

梁配筋计算说明：对于配筋率大于1%的截面，程序自动按双排筋计算；此时，保护层取60mm；当按双排筋计算还超限时，程序自动考虑压筋作用，按双筋方式配筋；各截面的箍筋都是按用户输入的箍筋间距计算的，并按沿梁全长箍筋的面积配箍率要求控制。

若输入的箍筋间距为加密区间距，则加密区的箍筋计算结果可直接参考使用，如果非加密区与加密区的箍筋间距不同，则应按非加密区箍筋间距对计算结果进行换算；若输入的箍筋间距为非加密区间距，则非加密区的箍筋计算结果可直接参考使用，如果加密区与非加密区的箍筋间距不同，则应按加密区箍筋间距对计算结果进行换算。

钢梁其中：R1表示钢梁正应力与强度设计值的比值F1/f；R2表示钢梁整体稳定应力与强度设计值的比值F2/f；R3表示钢梁剪应力与强度设计值的比值F3/fv。

其中F1，F2，F3 的具体含义：F1 = M/（Gb Wnb）F2 = M/（Fb Wb）F3（跨中）= V S/(I tw)，F3（支座）= V/Awn矩形混凝土柱或劲性混凝土柱在左上角标注：(Uc)、在柱中心标柱：Asv、在下边标注：Asx、在右边标注：Asy、引出线标注：As_corner其中：As_corner为柱一根角筋的面积，采用双偏压计算时，角筋面积不应小于此值，采用单偏压计算时，角筋面积可不受此值控制(cm2)。

Asx，Asy分别为该柱B边和H边的单边配筋，包括角筋(cm2)。

Asv表示柱在Sc范围内的箍筋，它是取柱斜截面抗剪箍筋和节点抗剪箍筋的大值(cm2)。

200x500梁配筋计算过程

(1)截面验算，按《混凝土规范》公式(6.3.1)
V=0.25βcfcbh0=0.25×1.000×14.30×200×465=332475N=332.48kN > V=0kN
截面尺寸满足要求。 (2)配筋计算，按混凝土规范公式(6.3.4-2)
V < αcvftbh0+fyv(Asv/s)h0
Asv/s = (V-αcvftbh0)/(fyvh0) = (0.00×103-0.70×1.43×200×465)/(270×465) = -0.74148mm2/mm=-741.48mm2/m
1.1
1.1
0.6041
te s
0.0100 263.4633
受拉区纵向钢筋的等效直径deq:
2
nidi
d eq
16 mm
ni idi
根据《混凝土规范》表7.1.2-1 构件受力特征系数 αcr = 1.9:
(5)最大裂缝宽度计算, 根据《混凝土规范》式7.1.2-1:
σs = σsq max cr
配箍率 ρsv=Asv/s/b=-0.74148/200=-0.37% < ρsvmin=0.13% 不满足最小配箍率抗剪箍筋按构造配筋: Asv/s = ρsvmin×b=0.13%×200=0.25422mm2/mm=254.22mm2/m
4 配置钢筋： (1)上部纵筋：计算As=200mm2，实配2E16(402mm2 ρ=0.40%)，配筋满足 (2)腰筋：计算构造As=b*hw*0.2%=186mm2，实配2d12(226mm2 ρ=0.23%)，配筋满足 (3)下部纵筋：计算As=200mm2，实配2E16(402mm2 ρ=0.40%)，配筋满足 (4)箍筋：计算Av/s=254mm2/m，实配d8@300双肢(335mm2/m ρsv=0.17%)，配筋满足

各种梁配筋计算表格

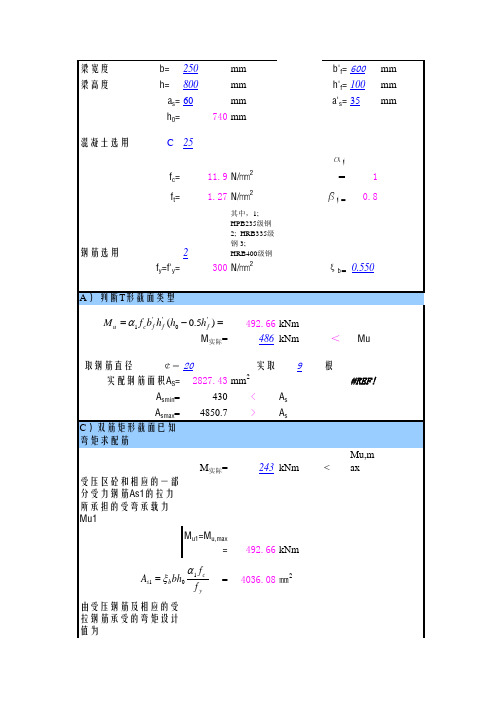
钢筋选用
其中，1; HPB235级钢 2; HRB335级钢 3; HRB400级钢
A）判断T形截面类型
M u = a1 f c b 'f h 'f (h0 - 0.5h 'f ) =
M实际= 取钢筋直径
￠＝
492.66 kNm 486 kNm 实取
2
＜根
Mu
20
2827.43 mm 430
9
As As
20
￠＝
实取
9
根
2827.43 mm2
NO!!!
受压钢筋取钢筋直径实配钢筋面积AS= 2α 's＝
12
￠＝
实取
2
2
mm ≤
根
226.19 mm 70.00 mm
OK!
x
验算受压区高度x＝fyAs1/(α1fcb)=
407.00
OK!
D）双筋矩形截面已知弯矩和受压钢筋求受拉配筋已知： M实际= A's＝ Mu2=f'yA's(h0-a's)= 由弯矩Mu1按单筋矩形截面求As1 Mu1=M-Mu2= 因此所需的受压钢筋为 43.67 kNm 243 kNm 942.48 199.33 kNm > Mu,max ￠ 20
a1 f c fy
=
由受压钢筋及相应的受拉钢筋承受的弯矩设计值为 Mu2=M-Mu1= 因此所需的受压钢筋为 -249.66 kNm
As' =
M u2 = f ( h0 - a s' )
' y
-1180.43 ㎜
2
与其对应的那部分受拉钢筋截面面积为 As2=A's= -1180.43 ㎜2 纵向受拉钢筋总截面面积 As＝As1＋As2= 2855.66 ㎜2 受拉钢筋取钢筋直径实配钢筋面积AS=

梁配筋计算

AS =
a1 fcb 2M (h0 - h02 )= fy a1 fcb
￠＝
3985.52 ㎜2
取钢筋直径
25
2
实取
8 As
根＜ Asmax= 9963.6
实配钢筋面积AS= Asmin=
3926.99 mm 860 ＜
判断: NO!!! C）双筋矩形截面已知弯矩求配筋 M实际= 1183.10 kNm ＜ Mu,max 受压区砼和相应的一部分受力钢筋As1的拉力所承担的受弯承载力Mu1 Mu1=Mu,max= 1981.49 kNm
OK! OK!
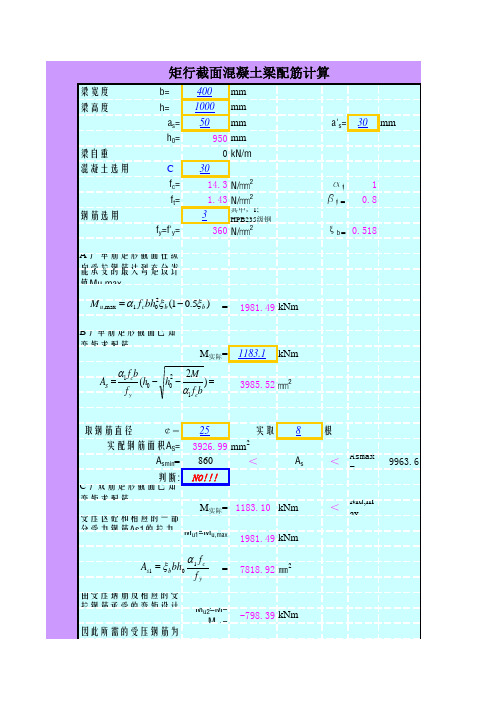
矩行截面混凝土梁配筋计算
梁宽度梁高度 b= h= as= h0= 梁自重混凝土选用 C fc = ft = 钢筋选用 fy=f'y= 3 30 14.3 N/㎜2 1.43 N/㎜2 360 N/㎜2 a1= b1= ξ
b=
400 1000 50
mm mm mm 950 mm 0 kN/m 1 0.8 0.518 a's= 30 mm
2
实取
6 3 mm ≤
根
6107.26 mm 16 ￠＝实取
OK!
根
603.19 mm2 验算受压区高度x＝fyAs1/(α1fcb)= 492.10 2α 's＝ 60.00 mm
OK!
x
OK!
D）双筋矩形截面已知弯矩和受压钢筋求受拉配筋已知：为充分发挥受压钢筋A's的作用，取As2=A's= Mu2=f'yA's(h0-a's)= 由弯矩Mu1按单筋矩形截面求As1 Mu1=M-Mu2= 因此所需的受压钢筋为 983.32 kNm M实际= 1183.10 kNm 3 A's＝ 603.19 199.78 < ￠ Mu,max 16

钢筋混凝土构件的配筋手算方法总结

钢筋混凝土构件的手算方法总结一、单筋梁：已知弯矩求配筋数；②然后求内力矩的力臂系数系①先求截面抵抗矩④在求得截面抵抗矩系数；；后，③得，由由公式可判可得到相对受压区高度断是否超筋，若为超筋，按双筋重新设计，此时，。

二、单筋梁：复核构件弯矩及，，则计若算，。

三、双筋梁：配筋计算时，为最小值，对于HRB335，HRB400当级时，可直接取值，对钢筋及常用的HPB235，当级钢计算，此时筋，砼可C50时，取等级小于，。

1，求四、双筋梁：已知；，①，可按时，若，计算②未知重新，若较大，若出，，现配筋，按单筋计算的值小于时，按双筋计算的，此时应按单筋梁确定。

五、偏心受压：对称配筋计算，已知，N，M，砼标号，钢筋级别，求。

，求，得e求后用M注意此时不能用M代入力矩平衡公式计算，须由Ne代入力矩平衡方程。

应按以下步骤进行。

，按大偏心，与值比较，若①由公式求出x 计算配筋，反之按小偏心计算配筋。

，取心②按大偏计算时，由求得，再判断是否符合最小配筋率要求并验算短边方向轴心受压的稳定。

③按小偏心计算时，，由此求得，此处是砼结构设计基本假定及以下C50时，C80中的矩形受压区高度与中和轴高度的比值，2C50~C80内插。

，是轴向力作用点至受拉钢筋合力点之间的距e④以上求时公式中的离，需考虑初始偏心距和二阶弯矩偏心距增大系数，可由下列公式求出：中的较大值；和20mm是附加偏心距，其值取偏心方向截面尺寸的是柱的计算长度；，取1，时系件截面曲率修正数构偏是心受压形、；中的A对T形截面均取，当是偏心受压构件长细比对截面曲率的影响系数，时，时，当。

六、偏心受压：不对称配筋截面设计①按上小节偏心受压构件对称配筋计算步骤中的公式计算二阶弯矩偏心距时按大偏心计算，反之按小偏心计算。

，当增大系数，心，偏为②若大。

3式和公公式求，可若已由知，，应加联立求出；若求得若，可直；接计算寸或未按知重新配筋大截面尺和按单筋梁计算的实际配筋取由此求得的中的较小值。

混凝土梁配筋计算

混凝土梁配筋计算
1.确定梁的几何尺寸和荷载：根据建筑设计需求和构筑物的使用条件，确定梁的几何尺寸和作用力，包括梁的长度、宽度、高度、跨度和受力点等。

2.确定梁的截面尺寸：根据梁的几何尺寸和受力情况，确定梁的截面
尺寸，包括翼缘宽度、翼缘高度、腹板宽度和腹板高度等。

3.设计配筋方案：根据梁受力情况和设计要求，设计配筋方案，包括
主筋的布置、直径、间距和受力钢筋等。

4.计算荷载：根据设计要求，计算梁的荷载，包括自重、楼面荷载、
悬挑荷载和动荷载等。

5.计算弯矩：根据荷载计算梁的弯矩，包括正弯矩和负弯矩。

6.确定截面抵抗力：根据弯矩和截面尺寸，使用受剪承载力与受弯承
载力的原理，计算截面的抵抗力。

7.确定配筋数量和位置：根据截面抵抗力和配筋的特性，确定配筋的
数量和位置。

8.确定配筋直径和间距：根据配筋数量和位置，确定配筋的直径和间距，满足强度和承载力的要求。

9.进行校核计算：根据设计要求，对计算结果进行校核，包括受剪承
载力、受弯承载力和侧向位移等。

10.编制配筋图：根据配筋方案和计算结果，编制配筋图纸，包括主筋、箍筋和锚筋等的布置和细节。

以上是混凝土梁配筋计算的基本步骤，其中包括了几何尺寸确定、荷载计算、弯矩计算、截面抵抗力计算和配筋设计等内容。

根据实际情况，计算过程会有所调整和细化。

混凝土梁配筋计算是结构设计的重要组成部分，需要严格按照相关规范和标准进行操作，确保梁的安全和稳定性。