分段正交匹配追踪算法StOMP
几种压缩感知算法
.1 压缩感知部分压缩感知算法主要可分为三类:贪婪迭代算法、凸凸优化(或最优化逼近方法)和基于贝叶斯框架提出的重构算法。
由于第三类方法注重信号的时间相关性,不适合图像处理问题,故目前的研究成果主要集中在前两类中。
目前已实现6中算法,分别为正交匹配追踪法(OMP)、迭代硬阈值法(IHT)、分段正交匹配追踪法(StOMP)、分段弱正交匹配追踪法(SwOMP)、广义正交匹配追踪(GOMP)、基追踪法(BP)。
1.1 正交匹配追踪法(OMP)在正交匹配追踪OMP中,残差是总与已经选择过的原子正交的。
这意味着一个原子不会被选择两次,结果会在有限的几步收敛。
OMP的算法如下(1)用x表示你的信号,初始化残差e0=x;(2)选择与e0内积绝对值最大的原子,表示为φ1;(3)将选择的原子作为列组成矩阵Φt,定义Φt列空间的正交投影算子为通过从e0减去其在Φt所张成空间上的正交投影得到残差e1;(4)对残差迭代执行(2)、(3)步;其中I为单位阵。
需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵,因此每次都是不同的,所以由它生成的正交投影算子矩阵P每次都是不同的。
(5)直到达到某个指定的停止准则后停止算法。
OMP减去的Pem是em在所有被选择过的原子组成的矩阵Φt所张成空间上的正交投影,而MP减去的Pem是em在本次被选择的原子φm所张成空间上的正交投影。
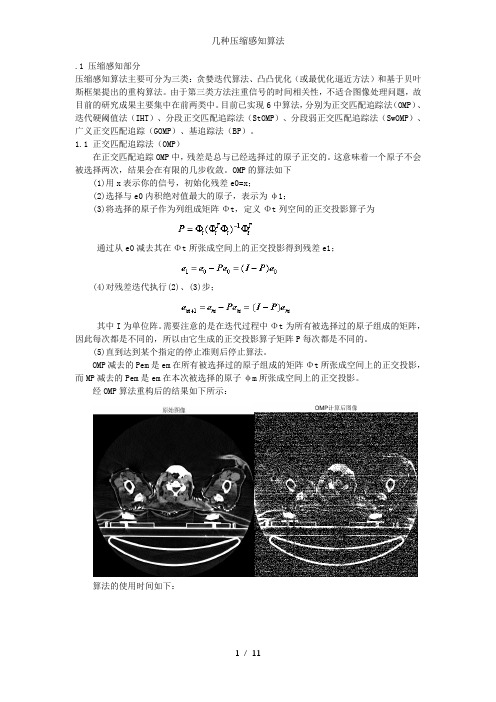
经OMP算法重构后的结果如下所示:算法的使用时间如下:1.2 迭代硬阈值法(IHT)目标函数为这里中的M应该指的是M-sparse,S应该指的是Surrogate。
这里要求:之后我们利用式对目标函数进行变形。
接着便是获得极值点:利用该式进行迭代可以得到极值点,我们需要的是最小值。
此时目标函数的最小值就得到了。
此时便得到我们需要的公式:我们要保证向量y的稀疏度不大于M,即,为了达到这一目标,要保留最大的M项(因为是平方,所以要取绝对值absolute value),剩余的置零(注意这里有个负号,所以要保留最大的M项)。
稀疏优化问题算法研究

稀疏优化问题算法研究作者:李蒙来源:《当代人(下半月)》2018年第03期摘要:稀疏优化问题发展至今,已经广泛应用于压缩感知、图像处理、复杂网络、指数追踪、变量选择等领域,并取得了令人瞩目的成就。
稀疏优化问题的求解算法种类繁多,根据算法设计原理的不同,可将其大致分为三类:贪婪算法、凸松弛方法和阈值类算法。
本文主要介绍稀疏优化问题算法研究进展及各类算法的优缺点。
关键词:稀疏优化问题;压缩感知;信号重构;优化算法随着当代社会信息技术的飞速发展,所获取和需要处理的数据量大幅增多,而基于传统的香农奈奎斯特采样定理中要求采样频率不得低于信号最高频率的两倍才可以精确重构信号。
2006年,Donoho、Candes等人针对稀疏信号或可稀疏表示的信号提出了新的采集和编解码理论,即压缩感知理论。
该理论使得通过少量采样即可准确或近似重构原始信号。
信号重构问题是一个非凸稀疏优化问题(问题)。
该问题是一个NP-hard问题,所以出现了多种不同的处理模型近似地或在一定条件下等价地求解问题。
以下就从压缩感知的信号重构理论出发,分析研究稀疏优化问题的模型和求解算法。
一、压缩感知重构问题在压缩感知理论中,若信号本身是稀疏的,则原始信号和观测信号之间的表达式为:;若信号本身不是稀疏的,但在基底下具有稀疏表示,即,其中是一个稀疏向量,则原始信号和观测信号之间的表达式为:,此时,重构原始信号只需要得到满足该等式约束的稀疏解,便可通过得到原始信号,其中为测量矩阵,为变换矩阵,为感知矩阵。
在压缩感知理论中,感知矩阵是一个很重要的组成部分,感知矩阵的好坏会直接影响原始信号的重构质量。
压缩感知理论中的稀疏信号重构问题旨在通过低维观测数据最大程度恢复出原始的高维信号,其本质为求一个欠定方程组的稀疏解,即(1)压缩感知的重构问题也可通过下述模型来求解:(2)Donoho和Chen证明了当观测矩阵和变换矩阵不相关时,(1)和(2)的解等价,并将(2)称为基追踪(Basis Pursuit,BP)问题。
压缩感知重构算法

4.2.1 高斯白噪声影响
高斯白噪声均值为0,方差为0.01
图A 受高斯白噪声影响OMP算法重构
图B 受高斯白噪声影响信号CoSAMP算法重构
4.2.2 椒盐噪声影响
椒盐噪声噪声密度为0.05
图A 受椒盐噪声影响信号OMP算法重构
图B 受椒盐噪声影响信号IRLS算法重构
4.2.3 受噪声影响结果比较
4
2
0
SAMP
-2 -4
-6
0
50
100
150
200
250
300
2.7.2 各算法仿真实验分析
重构算法时间都较短,误差也都较小
2.7.2 各算法性能分析
随着稀疏度K的增加,到达一定的临界值以后,信号重构的概率逐步降低
3.1 改进算法
基于变步长的正则化回溯自适应追踪算法 2018年,王欣等人针对压缩感知重构过程中稀疏度 未知以及步长大小固定的情况,基于SAMP 算法 存在的而不足,提出一种基于变步长的正则化回
每次迭代时选择多列
2.4 压缩采样匹配追踪CoSaMP
每次迭代选择多个原子, 选择的原子在下次迭代中可能会被抛弃
2.5 压缩采样匹配追踪SP
后向追踪的方式,在每次迭代中将找出的错 误的原子剔出,再把新找的原子放入支撑集 中,最后进行逼近
2.6 压缩采样匹配追踪SAMP
稀疏度自适应匹配追踪算法(SAMP)解决了需己知稀疏度才能准确重 构信号的要求。该算法沿用SP算法的回溯思想,加入步长和分阶段选 择的思想,通过迭代次数的增加,支撑集增加,从而达到每次选择更 多的原子,更快的重构信号。但是,如何选择初始步长及固定步长对 该算法有一定影响。
3.3 迭代硬阈值算法IHT
一种改进StOMP的Massive MIMO下行信道估计方法

一种改进StOMP的Massive MIMO下行信道估计方法沈涛;刘紫燕【摘要】针对传统的压缩感知算法在大规模多输入多输出(Massive MIMO)系统下行信道估计中估计性能较差的问题,提出一种基于粒子群分段正交匹配追踪(PSO-StOMP)压缩感知算法.该算法在分段正交匹配追踪(StOMP)算法求解不同阈值的估计信道矩阵参数和归一化最小均方误差的基础上,利用粒子群(PSO)算法动态地搜索出Massive MIMO系统下行虚拟角域信道中最小均方误差对应的阈值,达到参数自适应的目的.仿真结果表明,当虚拟角域扩展角度发生变化时,PSO-StOMP算法能够自适应信道估计,提升信道估计精度.【期刊名称】《通信技术》【年(卷),期】2019(052)002【总页数】6页(P361-366)【关键词】大规模多输入多输出;信道估计;压缩感知;粒子群分段正交匹配追踪算法【作者】沈涛;刘紫燕【作者单位】贵州大学大数据与信息工程学院,贵州贵阳 550025;贵州大学大数据与信息工程学院,贵州贵阳 550025【正文语种】中文【中图分类】TN929.50 引言作为5G移动通信系统的关键技术之一,大规模多输入多输出(Massive Multi-Input Multi-Output, Massive MIMO)系统通过在基站端部署大量天线,可以有效提升数据传输速率和链路可靠性[1]。
在Massive MIMO系统中,上行链路的信号检测和下行链路的预编码均依赖准确的信道状态信息(Channel State Information,CSI)。
基于导频的信道估计原理简单、易于实现,因此得到了广泛研究[2]。
传统信道估计方案中,正交导频的开销正比于发射端的天线数目,Massive MIMO系统基站端部署数十至上百根天线,因此下行链路中导频会占用大量的系统资源用于信道估计。
在时分双工(Time Division Duplexing,TDD)模式下,可以利用TDD系统的信道互易性,通过对上行信道的CSI转置获得下行链路中的CSI。
正交匹配追踪算法omp原理

正交匹配追踪算法omp原理
正交匹配追踪算法(Orthogonal Matching Pursuit,简称OMP)是一种用于稀疏重构的迭代算法,主要用于解决压缩感知问题。
其原理如下:
1. 稀疏表示假设:假设信号可以通过少量的原子(基底)的线性组合来表示,即稀疏表示。
2. 初始状态:设置初始残差为输入信号,初始解集为空集。
3. 原子选择:在目前残差中选择一个最适合代表残差的原子(基底)。
4. 矩阵变换:将原子调整为正交的形式,即正交化。
5. 正交投影:计算残差与正交基底的投影,得到投影系数。
6. 更新残差:使用投影系数更新残差。
7. 判断结束:如果残差的能量减少到一定程度,则认为重构已经足够准确,结束算法;否则,返回第3步进行下一个迭代。
8. 输出结果:返回最终的解集,其中每个元素对应一个原子。
OMP算法没有要求输入信号满足特定的分布条件,因此适用
于多种应用场景。
算法通过选择最适合的原子来逐步逼近信号,并且通过迭代追踪算法的方式,能够保证逐步收敛到最优解。
该算法的时间复杂度较低,且能在较短的时间内达到令人满意的重构质量。
无线通信信道估计的正交匹配追踪

无线通信信道估计的正交匹配追踪无线通信信道估计的正交匹配追踪无线通信信道估计的正交匹配追踪(Orthogonal Matching Pursuit for Wireless Channel Estimation)无线通信是现代社会中不可或缺的一部分,为人们的生活带来了极大的便利。
然而,无线信道的不稳定性和多路径传播等问题给通信质量带来了挑战。
为了解决这些问题,信道估计技术变得至关重要。
其中,正交匹配追踪(Orthogonal Matching Pursuit,简称OMP)作为一种有效的信道估计算法,备受研究者关注。
正交匹配追踪是一种基于压缩感知理论的信道估计方法,通过利用信道的稀疏性,从少量测量中恢复出信道信息。
该方法可以在保证一定准确度的前提下,大大减少了信道估计所需的资源消耗。
在正交匹配追踪算法中,首先需要构建一个字典矩阵,该矩阵由基向量组成,基向量是通过无线通信信道的特性进行构造的。
然后,通过一系列迭代过程,根据测量信号与字典矩阵的内积,选择与测量信号最匹配的基向量。
通过迭代过程,不断更新估计信道,直到满足一定的收敛准则。
正交匹配追踪算法相比于传统的LS(Least Square)方法具有更好的性能。
首先,正交匹配追踪算法可以减少测量的次数,从而降低了信道估计的时间复杂度。
其次,正交匹配追踪算法能够在信号较弱的情况下,依然保持较高的估计准确度。
再次,正交匹配追踪算法对于信道的稀疏性有很好的适应性,能够更好地应对多路径传播等问题。
然而,正交匹配追踪算法也存在一些问题。
首先,构建字典矩阵需要大量的计算资源,尤其是在大规模MIMO系统中。
其次,正交匹配追踪算法对于信道稀疏性的假设在实际情况中不一定成立,这可能会导致估计结果的偏差。
最后,正交匹配追踪算法对于噪声的敏感度较高,当信噪比较低时,估计结果可能会出现较大的误差。
综上所述,正交匹配追踪作为一种有效的信道估计算法,在无线通信领域具有广泛的应用前景。
贝叶斯追踪算法的稀疏表示

i≠ j i≠ j ∧ ∧
∆
i≠ j
(8)
ˆ 是第i y i 是第i个系数的估计。我们可以定义
ˆ ˆ m j = ∑ y i bij , γ j = ∑ ( y i − y i )bij + v j
i≠ j i≠ j ∆ ∆
我们令模型2中的P=0.9,来产生稀疏系数, 我们令模型2中的P=0.9,来产生稀疏系数, 在信号的稀疏表示中有51个原子是有效的, 在信号的稀疏表示中有51个原子是有效的, 噪声水平或误差可以看成方差不同的高斯 分布。 对于未知统计参数的初始化 ( p, δ r , δ e )我们可 以令:
j
有效( yi ) = z j − m j > Th j
∆
(12)
其中 Th j 定义如下:
Thj =
∆
δγ
j
δr
δ r2 + δγ2j p 2 2 2 δ r + δγ j ln 1 − p δγ j ()来自 (13)
(13) 虽然式(13)确定了最佳阈值,但是他必须依 虽然式(13)确定了最佳阈值,但是他必须依 靠未知参数 p, δ r ,δ γ ,而这些未知参数是通过对原 始信号x的估计获得的,我们可以通过式(7 始信号x的估计获得的,我们可以通过式(7)来 获得这些未知参数的无偏估计:
在贝叶斯框架下,一种新的期望最大化(EM) 在贝叶斯框架下,一种新的期望最大化(EM) 算法和贝叶斯压缩传感(BCS)的算法被提出来 算法和贝叶斯压缩传感(BCS)的算法被提出来 解决这个问题。第二类方法是通过迭代算法得到 有效的系数(也就是指非零)。通常该方法是利 用信号与冗余字典的原子的相关性确定哪个系数 是有效的。这些迭代算法可以是匹配追踪 (MP),正交匹配追踪(OMP),Stage-wise MP) 正交匹配追踪(OMP),StageOMP (StOMP),梯度追踪(GP)。我们所提出 (StOMP),梯度追踪(GP)。我们所提出 的方法可以被认为是迭代检测估计(IDE)中的 的方法可以被认为是迭代检测估计(IDE)中的 改进,在使用简单的贪婪算法的同时使用贝叶斯 工具来得到有效原子的最佳选择。
压缩感知的重构算法

压缩感知的重构算法算法的重构是压缩感知中重要的一步,是压缩感知的关键之处。
因为重构算法关系着信号能否精确重建,国内外的研究学者致力于压缩感知的信号重建,并且取得了很大的进展,提出了很多的重构算法,每种算法都各有自己的优缺点,使用者可以根据自己的情况,选择适合自己的重构算法,大大增加了使用的灵活性,也为我们以后的研究提供了很大的方便。
压缩感知的重构算法主要分为三大类:1.组合算法2.贪婪算法3.凸松弛算法每种算法之中又包含几种算法,下面就把三类重构算法列举出来。
组合算法:先是对信号进行结构采样,然后再通过对采样的数据进行分组测试,最后完成信号的重构。
(1) 傅里叶采样(Fourier Representaion)(2) 链式追踪算法(Chaining Pursuit)(3) HHS追踪算法(Heavy Hitters On Steroids)贪婪算法:通过贪婪迭代的方式逐步逼近信号。
(1) 匹配追踪算法(Matching Pursuit MP)(2) 正交匹配追踪算法(Orthogonal Matching Pursuit OMP)(3) 分段正交匹配追踪算法(Stagewise Orthogonal Matching Pursuit StOMP)(4) 正则化正交匹配追踪算法(Regularized Orthogonal Matching Pursuit ROMP)(5) 稀疏自适应匹配追踪算法(Sparisty Adaptive Matching Pursuit SAMP)凸松弛算法:(1) 基追踪算法(Basis Pursuit BP)(2) 最小全变差算法(Total Variation TV)(3) 内点法(Interior-point Method)(4) 梯度投影算法(Gradient Projection)(5) 凸集交替投影算法(Projections Onto Convex Sets POCS)算法较多,但是并不是每一种算法都能够得到很好的应用,三类算法各有优缺点,组合算法需要观测的样本数目比较多但运算的效率最高,凸松弛算法计算量大但是需要观测的数量少重构的时候精度高,贪婪迭代算法对计算量和精度的要求居中,也是三种重构算法中应用最大的一种。
基于块剪枝多路径匹配追踪的多信号联合重构

基于块剪枝多路径匹配追踪的多信号联合重构司菁菁;候肖兰;程银波【摘要】Considering the disadvantages of ignoring signal’s structured sparsity and the high complexity in high iterative layers in multipath matching pursuit (MMP),the block pruning multipath matching pursuit (BPMMP)is proposed to reconstruct the block-sparse signal.In this algorithm,an atomic block serves as a node in the path expansion,and branch pruning operation is introduced after a certain number of iterations. Thus,BPMMP reduces the data processing cost greatly.Moreover,for multiple measurement vector (MMV) problem,BPMMP for MMV (BPMMPMMV)is proposed.It can achieve joint signal reconstruction for multi-ple sensors within a small range in the wireless sensornetwork.Experimental results show that BPMMP out-performs MMP on the reconstruction performance,and BPMMPMMV achieves higher joint reconstruction per-formance than block A* orthogonal matching pursuitfor MMV,subspace matching pursuit for MMV and or-thogonal matching pursuit for MMV.%针对多路径匹配追踪(multipath matching pursuit,MMP)无法利用稀疏信号的结构信息、迭代层数较高时计算复杂度较大等问题,提出了一种适用于重构块稀疏信号的块剪枝多路径匹配追踪算法。
分段正交匹配追踪(StOMP)算法改进研究

分段正交匹配追踪(StOMP)算法改进研究汪浩然;夏克文;牛文佳【摘要】信号重构是压缩感知的核心技术之一,而其重构精度和所耗时长直接影响其应用效果.现今分段正交匹配追踪算法(StOMP)因耗时短而得到广泛应用,但也存在着重构精度差、稳定性低的缺点.提出一种基于粒子群优化(PSO)算法且同时具有回溯特性的StOMP改进算法(ba-IWPSO-StOMP),即首先在StOMP算法的一次原子选择上,引入回溯策略,实现原子的二次筛选;在每次迭代计算中,使用具有惯性权重指数递减的PSO(IWPSO)算法对传感矩阵中部分原子进行优化,从而实现更高精度,更少迭代次数的信号重构.对一维信号和二维图像的重构结果表明,在稀疏条件相同的情况下,算法在收敛时间较短的情况下,其重构精度明显优于StOMP等同类算法.%Signal reconstruction is one of the core technologies of compressed sensing, and the reconstruction accuracy and time-consuming directly affects its application effect. Nowadays, Stagewise Orthogonal Matching Pursuit(StOMP) algorithm has been widely used for short running time, but its reconstruction accuracy is unsatisfactory. To make up for the defects of the StOMP algorithm, this paper presents a variant of StOMP, called backtracking-based adaptive and iner-tia weight index decreasing particle swarm optimization-based StOMP(ba-IWPSO-StOMP)algorithm. As an extension of the StOMP algorithm, in each iteration, the proposed ba-IWPSO-StOMP algorithm incorporates a backtracking tech-nique to select atoms by the second screening, then uses the IWPSO algorithm to optimize atoms in the measurement matrix. Through these modifications, the ba-IWPSO-StOMP algorithm achieves superior reconstruction accuracyand less times of iteration compared with other OMP-type algorithms. Moreover, unlike its predecessors, the ba-IWPSO-StOMP algorithm does not require to know the sparsity level in advance. The experiments demonstrate the performance of ba-IWPSO-StOMP algorithm is superior to several other OMP-type algorithms.【期刊名称】《计算机工程与应用》【年(卷),期】2017(053)016【总页数】7页(P55-61)【关键词】压缩感知;分段正交匹配追踪;粒子群优化【作者】汪浩然;夏克文;牛文佳【作者单位】河北工业大学电子与信息工程学院,天津 300401;河北工业大学电子与信息工程学院,天津 300401;河北工业大学电子与信息工程学院,天津 300401【正文语种】中文【中图分类】TP391压缩感知(CS)理论是由Donoho和Candes等在2005年提出的一种从信号稀疏分解和逼近理论发展而来的新的信号处理理论[1-3]。
欠定线性方程

欠定线性方程组的稀疏解Sparse Solution of Underdetermined Linear Equations摘要找出欠定线性方程组的稀疏解,y = Φx NP-hard in general. 此处‘典型’或‘随机’的Φ是稀疏解的近似值,通过使用线性代数的标准操作的定值得出。
我们的建议是,和逐步正交匹配追踪(StOMP),陆续将信号转化为忽略不计的残差。
从初始残差r0 = y开始,在s-th阶段形成‘匹配滤波器’ΦT r s−1,指出所有振幅超过特定临界值的坐标,用已选坐标解决最小平方的问题,并减去最小二乘法拟合,得出一个新的残差。
在经过固定的几个阶段后(例如到10后)停止。
与正交匹配追踪算法(OMP)不同,和逐步正交匹配追踪(StOMP)每个阶段,都有多个系数可以进入的其模型,但在正交匹配追踪算法(OMP)的每个阶段,只有一个系数能够进入;此外,和逐步正交匹配追踪(StOMP)有固定的阶段数(例如,10个阶段),而正交匹配追踪算法(OMP)可以有n个不同的阶段。
就稀疏解而言,StOMP的运行速度要快的多,例如期中的ℓ1最小值以及OMP和其他大规模的问题。
利用相图来比较算法性能分析。
恢复K-稀疏向量(y,Φ)中的x0就是随机的n×N且y = Φx0用图中的一点(n/N, k/n)来表示;值得一提的是,此处的范围为k < n < N。
对于n,相比范围是ℓ1时得到的最小值,StOMP(近似的)正确恢复了y = Φx 中稀疏/不确定的平面的稀疏解。
事实上,比起ℓ1最小化和OMP,StOMP能更好地解决极限欠定问题。
我们严格推导出匹配滤波系数中每个步骤,每个阶段的条件高斯分布,并严谨地为StOMP性能变量建立了大型系统极限。
准确计算出大量样本相位;这些都为StOMP稀疏矢量的近似恢复提供了渐进准确极限所需的样本数量。
通过指出StOMP 在压缩传感,纠错码编码以及超完备表征中能快速有效地找出稀疏解,从而给出数值例。
压缩感知原理

压缩感知原理(附程序)1压缩感知引论传统方式下的信号处理,是按照奈奎斯特采样定理对信号进行采样,得到大量的采样数据,需要先获取整个信号再进行压缩,其压缩过程如图。
图传统的信号压缩过程在此过程中,大部分采样数据将会被抛弃,即高速采样后再压缩的过程浪费了大量的采样资源,这就极大地增加了存储和传输的代价。
由于带宽的限制,许多信号只包含少量的重要频率的信息。
所以大部分信号是稀疏的或是可压缩的,对于这种类型的信号,既然传统方法采样的多数数据会被抛弃,那么,为什么还要获取全部数据而不直接获取需要保留的数据呢?Candes和Donoho等人于2004年提出了压缩感知理论。
该理论可以理解为将模拟数据节约地转换成压缩数字形式,避免了资源的浪费。
即,在采样信号的同时就对数据进行适当的压缩,相当于在采样过程中寻找最少的系数来表示信号,并能用适当的重构算法从压缩数据中恢复出原始信号。
压缩感知的主要目标是从少量的非适应线性测量中精确有效地重构信号。
核心概念在于试图从原理上降低对一个信号进行测量的成本。
压缩感知包含了许多重要的数学理论,具有广泛的应用前景,最近几年引起广泛的关注,得到了蓬勃的发展。
2压缩感知原理压缩感知,也被称为压缩传感或压缩采样,是一种利用稀疏的或可压缩的信号进行信号重构的技术。
或者可以说是信号在采样的同时被压缩,从而在很大程度上降低了采样率。
压缩感知跳过了采集N个样本这一步骤,直接获得压缩的信号的表示。
CS理论利用到了许多自然信号在特定的基 上具有紧凑的表示。
即这些信号是“稀疏”的或“可压缩”的。
由于这一特性,压缩感知理论的信号编解码框架和传统的压缩过程大不一样,主要包括信号的稀疏表示、编码测量和重构算法等三个方面。
对于一个实值的有限长一维离散时间信号X ,可以看作为一个N R 空间N ×1的维的列向量,元素为[]n ,n ,=1,2,…N 。
N R 空间的任何信号都可以用N ×1维的基向量{}1i Ni =ψ的线性组合表示。
压缩感知理论(Compressive)

• 设 Φ = ΦΨ ,为了保证少量非相干的投 影包含精确重构信号的足够信息,矩阵 必 Φ ' 须满足受限等距特性(RIP)准则: Φ' • “对于任意具有严格T稀疏的矢量v,矩阵 都能保证如下不等式成立: ' 2 Φv • 2
'
1− ε ≤
v
2 2
≤ 1+ ε
• 式中 ε > 0 ,为限制等容常量”。 • RIP准则的等价情况是CS观测矩阵 Φ和稀 疏基矩阵 Ψ 满足非相干性的要求。相干系 数的定义为:
•
•
•
通过最小化l1范数将信号稀疏表示问题定义成一 类有约束的极值问题,进一步转化为线性规划 问题进行求解 。 (2)贪婪匹配追踪(MP)算法 :从字典中一 个一个挑选向量,每一步都使得信号的逼近更 为优化。 (3)正交匹配追踪(OMP)算法:此算法选取 最佳原子所用的方法和MP算法一样,都是从冗 余字典找出与待分解信号和信号残余最为匹配 的原子。
X = ∑θψ i = ΨΘ i
i =1 N
• {ψ 1 ,ψ 2,...,ψ N } 是变换系数。 Θ 向量中只有k个 非零值,我们就称信号X在稀疏基 Ψ 下是 k-稀疏的。那么,怎样找到或构造适合一类 信号的正交基,以求得信号的最稀疏表示, 这是一个有待进一步研究的问题。 • 常用的稀疏基有:正(余)弦基、小波基、 chirplct基以及curvelet基等。 •
CS理论框图
可压缩信号
稀疏变换
观测得到M维Βιβλιοθήκη 向量重构信号第一:信号的稀疏表示
• 首先,信号X∈RN具有稀疏性或者可压缩性, 所以信号的稀疏表示就成为一个至关重要 的关键问题,直接关系到信号的重构精度。 • 设N时间信号x=[x(1),x(2),…,x(N)]T ∈RN通过 一组基 的线性组合表示: N {ψ i }i=1 •
压缩感知技术综述

压缩感知技术综述摘要:信号采样是模拟的物理世界通向数字的信息世界之必备手段。
多年来,指导信号采样的理论基础一直是著名的Nyquist采样定理,但其产生的大量数据造成了存储空间的浪费。
压缩感知(Compressed Sensing)提出一种新的采样理论,它能够以远低于Nyquist采样速率采样信号。
本文详述了压缩感知的基本理论,着重介绍了信号稀疏变换、观测矩阵设计和重构算法三个方面的最新进展,并介绍了压缩感知的应用及基于压缩感知SAR成像的仿真。
关键词:压缩感知;稀疏表示;观测矩阵;SAR成像;Abstract: Signal sampling is a necessary means of information world physical world to the digital simulation. Over the years, the base theory of signal sampling is the famous Nyquist sampling theorem, but a large amount of data generated by the waste of storage space. Compressed sensing and put forward a new kind of sampling theory, it can be much less than the Nyquist sampling signal sampling rate. This paper introduces the basic theory of compressed sensing, emphatically introduces the new progress in three aspects of signal sparse representation, design of measurement matrix and reconstruction algorithm, and introduces the application of compressed sensing and Simulation of SAR imaging based on Compressive Sensing Keywords: Compressed sensing; Sparse representation; The observation matrix; SAR imaging;0 引言Nyquist采样定理指出,采样速率达到信号带宽的两倍以上时,才能由采样信号精确重建原始信号。
Stomp算法

Stomp 算法匹配追踪算法的计算复杂度高的根本原因在于过完备字典中原子数目太大,而每次匹配选取最佳原子的个数只有一个,这使得整个选取过程中匹配选取的次数过多。
而正交匹配追踪方法利用Gram-Schmidt 正交化过程将投影方向正交化,从而提高了追踪的效率。
但是其正交化过程引入了新的计算开销,特别是对于图像信号,计算量仍然巨大。
2006 年Donoho 进一步提出了分段匹配追踪算法(StOMP ),将OMP 算法进行一定程度的简化,降低了稀疏分解精度,提高了计算速度。
这一算法的本质在于每次匹配追踪时选出的是多个匹配原子而不是单个原子,减少了匹配次数。
设 {}Γ∈=r r g D 是由N >Γ个范数为1的向量所形成的过完备字典。
该字典包含N 个线性无关的向量,这N 个向量构成长度为N 的信号空间N C 的一个基。
设m 为迭代次数。
第一步:令m=0,下标集合φ=m I 。
与匹配追踪算法一样,分段正交匹配追踪算法首先将f 投影到D 一个向量D g r ∈上,并计算出余项f R :f r r Rg g f f +=, (3-19)因f R 与r g 正交,故222,f r R g f f += (3-20) 在选取匹配原子的时候,与匹配追踪算法不同,并不是固定选择一个匹配原子,而是给定一个标准,一次找到多个原子,提高了追踪效率。
因此引入极限因子0t ,找到满足条件原子的下标集合{}Γ∈≥=r t f g i I r ,,:00 (3-21) 在找到这些匹配原子后,利用Gram-Schmidt 正交化过程将这组原子正交化,并定义正交化后的向量为:∑-=∈-=1002,,i p p p p r r i I i u u u g g u i i (3-22)将f 投影到()0I i u i ∈上,得到120,f i I i ii R u u u f f +=∑∈ (3-23) 由1f R 与()01I i u r ∈的正交性得212201,fI i r R u f f +=∑∈ (3-24) 如果满足停止条件ε≤21f R 或者n I >0,迭代结束。
Stomp算法

Stomp 算法匹配追踪算法的计算复杂度高的根本原因在于过完备字典中原子数目太大,而每次匹配选取最佳原子的个数只有一个,这使得整个选取过程中匹配选取的次数过多。
而正交匹配追踪方法利用Gram-Schmidt 正交化过程将投影方向正交化,从而提高了追踪的效率。
但是其正交化过程引入了新的计算开销,特别是对于图像信号,计算量仍然巨大。
2006 年Donoho 进一步提出了分段匹配追踪算法(StOMP ),将OMP 算法进行一定程度的简化,降低了稀疏分解精度,提高了计算速度。
这一算法的本质在于每次匹配追踪时选出的是多个匹配原子而不是单个原子,减少了匹配次数。
设 {}Γ∈=r r g D 是由N >Γ个范数为1的向量所形成的过完备字典。
该字典包含N 个线性无关的向量,这N 个向量构成长度为N 的信号空间N C 的一个基。
设m 为迭代次数。
第一步:令m=0,下标集合φ=m I 。
与匹配追踪算法一样,分段正交匹配追踪算法首先将f 投影到D 一个向量D g r ∈上,并计算出余项f R :f r r Rg g f f +=, (3-19)因f R 与r g 正交,故222,f r R g f f += (3-20) 在选取匹配原子的时候,与匹配追踪算法不同,并不是固定选择一个匹配原子,而是给定一个标准,一次找到多个原子,提高了追踪效率。
因此引入极限因子0t ,找到满足条件原子的下标集合{}Γ∈≥=r t f g i I r ,,:00 (3-21) 在找到这些匹配原子后,利用Gram-Schmidt 正交化过程将这组原子正交化,并定义正交化后的向量为:∑-=∈-=1002,,i p p p p r r i I i u u u g g u i i (3-22)将f 投影到()0I i u i ∈上,得到120,f i I i ii R u u u f f +=∑∈ (3-23) 由1f R 与()01I i u r ∈的正交性得212201,fI i r R u f f +=∑∈ (3-24) 如果满足停止条件ε≤21f R 或者n I >0,迭代结束。
基于量子遗传优化的原子分解算法及其在机械故障诊断中的应用

基于量子遗传优化的原子分解算法及其在机械故障诊断中的应用骆杰;吕勇;易灿灿【摘要】机械设备故障的发生往往伴随着振动现象,通过对故障振动信号进行有效的分析是机械设备故障诊断的关键.最近提出的稀疏分解算法具有多分辨率、稀疏性和冗余的特点,但是也存在着原子库构造困难和分解算法计算量大的问题,为了更好将稀疏分解算法应用于机械故障诊断中,提出在正交匹配追踪算法的基础上,采用具有良好时频特性的Gabor原子,利用量子遗传算法快速求解多参数全局最优解的优点,从振动信号中快速和准确地提取出故障特征信息.通过数值仿真信号分析证明了所提的方法无论在特征提取的准确性上还是减小计算时间上都优于传统的正交匹配追踪算法,另外在轴承故障诊断实际应用中的实例分析中,相比传统的频谱分析方法更能有效地提取出故障特征信息,有效降低了背景噪声和杂质频率的干扰.%The occurrence of mechanical equipment fault is often accompanied by vibration phenomenon.Therefore,the effectiveanalysis of fault vibration signals is the key to the mechanical equipment faultdiagnosis.Although,the new sparse decomposition algorithm has the advantage of mutil-resolution,sparsity and redundancy.In order to better apply the recentlysparse decomposition algorithm to mechanical fault diagnosis,a new method based on orthogonal matching pursuit algorithm is proposea.The Gabor atoms.is introduced which have a good time-frequency characteristic.Meanwhile,the quantum genetic algorithm is utilized due to that it can quickly get the global optimal solution of multiple parameters for rapidly.Thus,the proposed method can accuratelyextracting fault characteristic information from the vibration signal.It is superior to the traditional orthogonal matching pursuit algorithm on the accuracy and reducing the computation time through analyzingoumerical simulatedsignals.The results of application on bearing fault diagnosis show that it is more effective than traditional spectrum analysis method in extracting fault characteristic information and diminishing influence of background noise and unrelated frequency.【期刊名称】《机械设计与制造》【年(卷),期】2017(000)007【总页数】4页(P82-85)【关键词】故障诊断;正交匹配追踪;量子遗传;量子旋转门【作者】骆杰;吕勇;易灿灿【作者单位】武汉科技大学机械自动化学院,湖北武汉430081;武汉科技大学机械自动化学院,湖北武汉430081;武汉科技大学机械自动化学院,湖北武汉430081【正文语种】中文【中图分类】TH16;TH133机械设备在生产过程中故障会导致机器的损坏,进而造成生产中断,甚至导致严重的安全事故的发生。
欠定线性方程

欠定线性方程组的稀疏解Sparse Solution of Underdetermined Linear Equations摘要找出欠定线性方程组的稀疏解,y = Φx NP-hard in general. 此处‘典型’或‘随机’的Φ是稀疏解的近似值,通过使用线性代数的标准操作的定值得出。
我们的建议是,和逐步正交匹配追踪(StOMP),陆续将信号转化为忽略不计的残差。
从初始残差r0 = y开始,在s-th阶段形成‘匹配滤波器’ΦT r s−1,指出所有振幅超过特定临界值的坐标,用已选坐标解决最小平方的问题,并减去最小二乘法拟合,得出一个新的残差。
在经过固定的几个阶段后(例如到10后)停止。
与正交匹配追踪算法(OMP)不同,和逐步正交匹配追踪(StOMP)每个阶段,都有多个系数可以进入的其模型,但在正交匹配追踪算法(OMP)的每个阶段,只有一个系数能够进入;此外,和逐步正交匹配追踪(StOMP)有固定的阶段数(例如,10个阶段),而正交匹配追踪算法(OMP)可以有n个不同的阶段。
就稀疏解而言,StOMP的运行速度要快的多,例如期中的ℓ1最小值以及OMP和其他大规模的问题。
利用相图来比较算法性能分析。
恢复K-稀疏向量(y,Φ)中的x0就是随机的n×N且y = Φx0用图中的一点(n/N, k/n)来表示;值得一提的是,此处的范围为k < n < N。
对于n,相比范围是ℓ1时得到的最小值,StOMP(近似的)正确恢复了y = Φx 中稀疏/不确定的平面的稀疏解。
事实上,比起ℓ1最小化和OMP,StOMP能更好地解决极限欠定问题。
我们严格推导出匹配滤波系数中每个步骤,每个阶段的条件高斯分布,并严谨地为StOMP性能变量建立了大型系统极限。
准确计算出大量样本相位;这些都为StOMP稀疏矢量的近似恢复提供了渐进准确极限所需的样本数量。
通过指出StOMP 在压缩传感,纠错码编码以及超完备表征中能快速有效地找出稀疏解,从而给出数值例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压缩感知重构算法之分段正交匹配追踪(StOMP)分段正交匹配追踪(StagewiseOMP)或者翻译为逐步正交匹配追踪,它是OMP另一种改进算法,每次迭代可以选择多个原子。
此算法的输入参数中没有信号稀疏度K,因此相比于ROMP及CoSaMP有独到的优势。
0、符号说明如下:压缩观测y=Φx,其中y为观测所得向量M×1,x为原信号N×1(M<<N)。
x一般不是稀疏的,但在某个变换域Ψ是稀疏的,即x=Ψθ,其中θ为K稀疏的,即θ只有K个非零项。
此时y=ΦΨθ,令A=ΦΨ,则y=Aθ。
(1)y为观测所得向量,大小为M×1(2)x为原信号,大小为N×1(3)θ为K稀疏的,是信号在x在某变换域的稀疏表示(4)Φ称为观测矩阵、测量矩阵、测量基,大小为M×N(5)Ψ称为变换矩阵、变换基、稀疏矩阵、稀疏基、正交基字典矩阵,大小为N×N(6)A称为测度矩阵、传感矩阵、CS信息算子,大小为M×N上式中,一般有K<<M<<N,后面三个矩阵各个文献的叫法不一,以后我将Φ称为测量矩阵、将Ψ称为稀疏矩阵、将A称为传感矩阵。
注意:这里的稀疏表示模型为x=Ψθ,所以传感矩阵A=ΦΨ;而有些文献中稀疏模型为θ=Ψx,而一般Ψ为Hermite 矩阵(实矩阵时称为正交矩阵),所以Ψ-1=ΨH(实矩阵时为Ψ-1=ΨT),即x=ΨHθ,所以传感矩阵A=ΦΨH,例如沙威的OMP例程中就是如此。
1、StOMP重构算法流程:2、分段正交匹配追踪(StOMP)Matlab代码(CS_StOMP.m)代码参考了文献[4]中的SolveStOMP.m,也可参考文献[5]中的StOMP.m。
其实文献[4]是斯坦福的SparseLab 中的一个函数而已,链接为/,最新版本为2.1,SolveStOMP.m在目录SparseLab21-Core\SparseLab2.1-Core\Solvers里面。
1.function[theta]=CS_StOMP(y,A,S,ts)2.%CS_StOMP Summary ofthisfunctiongoes here3.%Version:1.0 writtenbyjbb0523@2015-04-294.%Detailedexplanationgoeshere5.%y =Phi*x6.% x=Psi*theta7.% y=Phi*Psi*theta8.% 令 A = Phi*Psi, 则y=A*theta9.% S is the maximum number of StOMP iterations to perform10.% ts is the threshold parameter11.% 现在已知y和A,求theta12.% Reference:Donoho D L,Tsaig Y,Drori I,Starck J L.Sparse solution of13.% underdetermined linear equations by stagewise orthogonal matching14.% pursuit[J].IEEE Transactions on Information Theory,2012,58(2):1094—112115. if nargin < 416. ts = 2.5;%ts范围[2,3],默认值为2.517. end18. if nargin < 319. S = 10;%S默认值为1020. end21. [y_rows,y_columns] = size(y);22. if y_rows<y_columns23. y = y';%y should be a column vector24. end25. [M,N] = size(A);%传感矩阵A为M*N矩阵26. theta = zeros(N,1);%用来存储恢复的theta(列向量)27. Pos_theta = [];%用来迭代过程中存储A被选择的列序号28. r_n = y;%初始化残差(residual)为y29. for ss=1:S%最多迭代S次30. product = A'*r_n;%传感矩阵A各列与残差的内积31. sigma = norm(r_n)/sqrt(M);%参见参考文献第3页Remarks(3)32. Js = find(abs(product)>ts*sigma);%选出大于阈值的列33. Is = union(Pos_theta,Js);%Pos_theta与Js并集34. if length(Pos_theta) == length(Is)35. if ss==136. theta_ls = 0;%防止第1次就跳出导致theta_ls无定义37. end38. break;%如果没有新的列被选中则跳出循环39. end40. %At的行数要大于列数,此为最小二乘的基础(列线性无关)41. if length(Is)<=M42. Pos_theta = Is;%更新列序号集合43. At = A(:,Pos_theta);%将A的这几列组成矩阵At44. else%At的列数大于行数,列必为线性相关的,At'*At将不可逆45. if ss==146. theta_ls = 0;%防止第1次就跳出导致theta_ls无定义47. end48. break;%跳出for循环49. end50. %y=At*theta,以下求theta的最小二乘解(Least Square)51. theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解52. %At*theta_ls是y在At列空间上的正交投影53. r_n = y - At*theta_ls;%更新残差54. if norm(r_n)<1e-6%Repeat the steps until r=055. break;%跳出for循环56. end57. end58. theta(Pos_theta)=theta_ls;%恢复出的theta59.end3、StOMP单次重构测试代码以下测试代码基本与OMP单次重构测试代码一样,除了调用CS_StOMP之外,一定要注意这里的测量矩阵Phi =randn(M,N)/sqrt(M),一定一定!!![plain]view plaincopy1.%压缩感知重构算法测试2.clear all;close all;clc;3.M = 64;%观测值个数4.N = 256;%信号x的长度5.K = 12;%信号x的稀疏度6.Index_K = randperm(N);7.x = zeros(N,1);8.x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的,且位置是随机的9.Psi = eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta10.Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵11.A = Phi * Psi;%传感矩阵12.y = Phi * x;%得到观测向量y13.%% 恢复重构信号x14.tic15.theta = CS_StOMP(y,A);16.x_r = Psi * theta;% x=Psi * theta17.toc18.%% 绘图19.figure;20.plot(x_r,'k.-');%绘出x的恢复信号21.hold on;22.plot(x,'r');%绘出原信号x23.hold off;24.legend('Recovery','Original')25.fprintf('\n恢复残差:');26.norm(x_r-x)%恢复残差运行结果如下:(信号为随机生成,所以每次结果均不一样)1)图:2)Command windowsElapsedtime is 0.067904 seconds.恢复残差:ans=6.1267e-0154、门限参数t s、测量数M与重构成功概率关系曲线绘制例程代码因为文献[1]中对门限参数ts给出的是一个取值范围,所以有必要仿真ts取不同值时的重构效果,因此以下的代码虽然是基于OMP相应的测试代码修改的,但相对来说改动较大。
[plain]view plaincopy1.clear all;close all;clc;2.%% 参数配置初始化T = 1000;%对于每组(K,M,N),重复迭代次数4.N = 256;%信号x的长度5.Psi = eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta6.ts_set = 2:0.2:3;7.K_set = [4,12,20,28,36];%信号x的稀疏度集合8.Percentage = zeros(N,length(K_set),length(ts_set));%存储恢复成功概率9.%% 主循环,遍历每组(ts,K,M,N)10.tic11.for tt = 1:length(ts_set)12. ts = ts_set(tt);13. for kk = 1:length(K_set)14. K = K_set(kk);%本次稀疏度15. %M没必要全部遍历,每隔5测试一个就可以了16. M_set=2*K:5:N;17. PercentageK = zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率18. for mm = 1:length(M_set)19. M = M_set(mm);%本次观测值个数20. fprintf('ts=%f,K=%d,M=%d\n',ts,K,M);21. P = 0;22. for cnt = 1:CNT %每个观测值个数均运行CNT次23. Index_K = randperm(N);24. x = zeros(N,1);25. x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的,且位置是随机的26. Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵27. A = Phi * Psi;%传感矩阵28. y = Phi * x;%得到观测向量y29. theta = CS_StOMP(y,A,10,ts);%恢复重构信号theta30. x_r = Psi * theta;% x=Psi * theta31. if norm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功32. P = P + 1;33. end34. end35. PercentageK(mm) = P/CNT*100;%计算恢复概率36. end37. Percentage(1:length(M_set),kk,tt) = PercentageK;38. end39.end40.toc41.save StOMPMtoPercentage1000 %运行一次不容易,把变量全部存储下来42.%% 绘图43.for tt = 1:length(ts_set)44. S = ['-ks';'-ko';'-kd';'-kv';'-k*'];45. figure;46. for kk = 1:length(K_set)47. K = K_set(kk);48. M_set=2*K:5:N;49. L_Mset = length(M_set);50. plot(M_set,Percentage(1:L_Mset,kk,tt),S(kk,:));%绘出x的恢复信号51. hold on;52. end53. hold off;54. xlim([0 256]);55. legend('K=4','K=12','K=20','K=28','K=36');56. xlabel('Number of measurements(M)');57. ylabel('Percentage recovered');58. title(['Percentage of input signals recovered correctly(N=256,ts=',...59. num2str(ts_set(tt)),')(Gaussian)']);60.end61.for kk = 1:length(K_set)62. K = K_set(kk);63. M_set=2*K:5:N;64. L_Mset = length(M_set);65. S = ['-ks';'-ko';'-kd';'-kv';'-k*';'-k+'];66. figure;67. for tt = 1:length(ts_set)68. plot(M_set,Percentage(1:L_Mset,kk,tt),S(tt,:));%绘出x的恢复信号69. hold on;70. end71. hold off;72. xlim([0 256]);73. legend('ts=2.0','ts=2.2','ts=2.4','ts=2.6','ts=2.8','ts=3.0');74. xlabel('Number of measurements(M)');75. ylabel('Percentage recovered');76. title(['Percentage of input signals recovered correctly(N=256,K=',...77. num2str(K),')(Gaussian)']);78.end本程序在联想ThinkPadE430C笔记本(4GBDDR3内存,i5-3210)上运行共耗时4707.513276秒,程序中将所有数据均通过“save StOMPMtoPercentage1000”存储了下来,以后可以再对数据进行分析,只需“loadS tOMPMtoPercentage1000”即可。
