七章回复及再结晶习题答案西北工业大学刘智恩
西北工业大学《材料科学基础》课后题答案

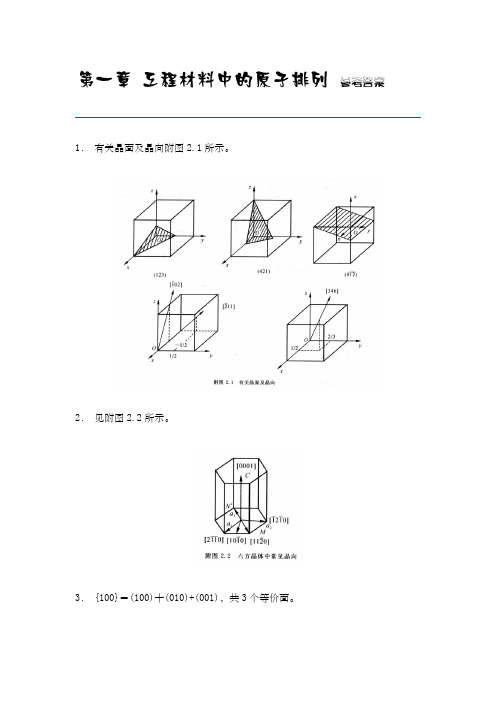
1. 有关晶面及晶向附图2.1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3) 5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
西北工业大学《材料科学基础》课后题答案

1. 有关晶面及晶向附图2.1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3) 5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
西北工业大学《材料科学基础》课后题答案

1. 有关晶面及晶向附图2.1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3) 5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
八章固相反应(西北工业大学-刘智恩)

1.分析固态相变的阻力。
2.分析位错促进形核的主要原因。
—3.下式表示含n 个原子的晶胚形成时所引起系统自由能的变化。
))(/3/2βαλan Es Gv bn G +-∆-=∆式中:∆Gv —— 形成单位体积晶胚时的自由能变化;γα/β —— 界面能;,Es —— 应变能;a 、b —— 系数,其数值由晶胚的形状决定。
试求晶胚为球形时,a 和b 的值。
若∆Gv ,γα/β,Es 均为常数,试导出球状晶核的形核功∆G*。
4.A1-Cu合金的亚平衡相图如图8-5所示,试指出经过固溶处理的合金在T1,T2温度时效时的脱溶顺序;并解释为什么稳定相一般不会首先形成呢。
5.x Cu=的Al-Cu合金(见图4-9),在550℃固熔处理后。
α相中含x Cu =,然后重新加热到100℃,保温一段时间后,析出的θ相遍布整个合金体积。
设θ粒子的平均间距为5 nm,计算:(1) 每立方厘米合金中大约含有多少粒子(2) 假设析出θ后,α相中的x Cu=0,则每个θ粒子中含有多少铜原子(θ相为fcc结构,原子半径为nm){6.连续脱熔和不连续脱熔有何区别试述不连续脱熔的主要特征7.试述Al-Cu合金的脱熔系列及可能出现的脱熔相的基本特征。
为什么脱溶过程会出现过渡相时效的实质是什么8.指出调幅分解的特征,它与形核、长大脱溶方式有何不同【9.试说明脱熔相聚集长大过程中,为什么总是以小球熔解、大球增大方式长大。
10.若固态相变中新相以球状颗粒从母相中析出,设单位体积自由能的变化为108J/m2,比表面能为1J/m2,应变能忽略不计,试求表面能为体积自由能的1%时的新相颗粒直径。
!11.试述无扩散型相变有何特点。
12.若金属B熔入面心立方金属A中,试问合金有序化的成分更可能是A3B还是A2B试用20个A原子和B原子作出原子在面心立方金属(111)面上的排列图形。
13.含碳质量分数w c=及w c=的甲5 mm碳钢试样,都经过860℃加热淬火,试说明淬火后所得到的组织形态、精细结构及成分。
西北工业大学《材料科学基础》课后题答案
1.有关晶面及晶向附图2.1所示。
2.见附图2.2所示。
3.{100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3)5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12.(1)应沿滑移面上、下两部分晶体施加一切应力τ,的方向应与de位错线平行。
(2)在上述切应力作用下,位错线de将向左(或右)移动,即沿着与位错线de垂直的方向(且在滑移面上)移动。
在位错线沿滑移面旋转360°后,在晶体表面沿柏氏矢量方向产生宽度为一个b的台阶。
回复再结晶

习题5:回复和再结晶1. 已知锌单晶的回复激活能为2×104J/mol ,若0℃温度去除25%的加工硬化需要5分钟,试求-20℃温度回复到同样程度所需要的时间。
2. 已知单相黄铜400℃恒温下完成再结晶需要1小时,而350℃恒温时则需要3小时,试求该合金的再结晶激活能。
3. 若某金属的比界面能为0.5J/mol ,若球形晶粒直径为0.2mm 时,试求其晶粒长大的驱动力。
4. 预先经球化退火的1.2%C 钢加热到780℃时,若已知未溶Fe 3C Ⅱ粒子直径为2μm ,试计算此时奥氏体晶粒尺寸(已知Fe 3C 密度为7.6g/cm 3,Fe 的密度为7.8g/cm 3)。
5. 已知黄铜的晶界迁移激活能为73.6J/mol ,当加热至700℃时,试求曲率半径为0.1mm 的晶界的迁移速度。
6. 试比较去应力退火过程与动态回复过程位错运动有何不同?从显微组织上如何区分动、静态回复和动、静态再结晶。
7. 假定以再结晶完成95%作为再结晶完成的标准,则根据约翰逊—梅尔(Johnson—Mehl)方程:3441exp()3V X NG t =-- 其中X V 表示再结晶体积分数,t 表示再结晶时间,导出再结晶后晶粒直径d 与N ,G 的关系为:1/4G d k N ⎛⎫= ⎪⎝⎭习题5答案:1. 解:冷塑性变形金属发生回复时,若回复量(去除25%的加工硬化)一定,回复所需时间t 与回复温度T 间的关系为:ln Q t A RT=+ 设-20℃温度回复到同样程度所需要的时间为t 2,则212111exp t Q t R T T ⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎣⎦已知t 1=5min, T 1=273K ,T 2=253K ,Q =2×104J/mol ,所以421211121011exp 5exp 10min 8.314253273Q t t R T T ⎡⎤⎛⎫⎡⎤⨯⎛⎫==-=⨯-=⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎣⎦2. 解:再结晶进行的速率为e x p ()Q V A Q RT=-再结晶, (为再结晶激活能) 设t 为完成再结晶所需要的时间,则121221122121exp()exp()11ln ln()8.314ln(3/1)76594J/mol 1111623673Q Q A t A t RT RT t Q t R T T R t t Q T T -=-⎛⎫∴=-- ⎪⎝⎭⨯∴===⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭3. 解:设球形晶粒长大的驱动力为ΔP ,已知σ=0.5J/mol ,r =0.1mm =1×10-4m , 则44220.5110P a 110P r σ-⨯∆===⨯⨯ 4.解:根据杠杆定律可得,1.2%C 钢加热到780℃时,Fe 3C Ⅱ的质量百分数为3 1.2%0.94%F e C %100% 4.52%6.69%0.94%-=⨯=-Ⅱ 设Fe 3C Ⅱ粒子的体积分数为f ,则 4.52%7.6100% 4.63%4.52%1 4.52%7.67.8f =⨯=-+ 设奥氏体晶粒的平均直径为D ,则44130μm 33 4.63%r D f ⨯===⨯5.解:设晶界迁移速度为v ,则1141173.6exp()exp()2108.314973m Q dD v K K dt D RT -==∙-=∙-⨯⨯ 6.答:(1)去应力退火过程中,位错通过攀移和滑移重新排列,从高能态转变为低能态;动态回复过程中,则是通过螺位错的交滑移和刃位错的攀移,使异号位错相互抵消,保持位错增值率与位错消失率之间的动态平衡。
西北工业大学材料科学基础04-12年真题答案剖析

2004年西北工业大学硕士研究生入学试题 参考答案一、简答题:(共40分,每小题8分)1、请简述间隙固溶体、间隙相、间隙化合物的异同点?答:相同点:小原子溶入。
不同点:间隙固溶体保持溶剂(大原子)点阵;间隙相、间隙化合物改变了大原子点阵,形成新点阵。
间隙相结构简单;间隙化合物结构复杂。
2、请简述影响扩散的主要因素有哪些。
答:影响扩散的主要因素:(1)温度;(2)晶体结构与类型;(3)晶体缺陷;(4)化学成分。
3、临界晶核的物理意义是什么?形成临界晶核的充分条件是什么?答:临界晶核的物理意义:可以自发长大的最小晶胚(或,半径等于rk 的晶核) 形成临界晶核的充分条件:(1)形成r ≥rk 的晶胚;(2)获得A ≥A*(临界形核功)的形核功。
4、有哪些因素影响形成非晶态金属?为什么?答:液态金属的粘度:粘度越大原子扩散越困难,易于保留液态金属结构。
冷却速度;冷却速度越快,原子重新排列时间越断,越容易保留液态金属结构。
5、合金强化途径有哪些?各有什么特点?答:细晶强化、固溶强化、复相强化、弥散强化(时效强化)加工硬化。
二、计算、作图题:(共60分,每小题12分)1、求]111[和]120[两晶向所决定的晶面,并绘图表示出来。
答:设所求的晶面指数为(h k l ) 则)112(0211:2111:1011::=----=l k h2、氧化镁(MgO )具有NaCl 型结构,即具有O2-离子的面心立方结构。
问:(1)若其离子半径+2Mg r =0.066nm ,-2O r =0.140nm ,则其原子堆积密度为多少? (2)如果+2Mg r /-2O r =0.41,则原子堆积密度是否改变?答:(1)点阵常数nm r r a O Mg 412.0)(222=+=-+堆积密度73.04)(43322=⨯+=-+a r r P O Mg f π(2)堆积密度会改变,因为Pf 与两异号离子半径的比值有关。
3、已知液态纯镍在 1.013×105 Pa (1大气压),过冷度为319 K 时发生均匀形核,设临界晶核半径为1nm ,纯镍熔点为1726 K ,熔化热ΔHm=18075J/mol ,摩尔体积Vs =6.6cm3/mol ,试计算纯镍的液-固界面能和临界形核功。
西北工业大学材料科学基础课后题答案

1.有关晶面及晶向附图2.1所示。
2.见附图2.2所示。
3.{100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3)5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12.(1)应沿滑移面上、下两部分晶体施加一切应力τ,的方向应与de位错线平行。
(2)在上述切应力作用下,位错线de将向左(或右)移动,即沿着与位错线de垂直的方向(且在滑移面上)移动。
在位错线沿滑移面旋转360°后,在晶体表面沿柏氏矢量方向产生宽度为一个b的台阶。
西北工业大学材料科学基础练习题

1. 作图表示立方晶体的晶面及晶向。
2. 在六方晶体中,绘出以下常见晶向等。
3. 写出立方晶体中晶面族{100},{110},{111},{112}等所包括的等价晶面。
4. 镁的原子堆积密度和所有hcp 金属一样,为0.74。
试求镁单位晶胞的体积。
已知Mg 的密度,相对原子质量为24.31,原子半径r=0.161nm 。
5. 当CN=6时离子半径为0.097nm ,试问: 1) 当CN=4时,其半径为多少?2) 当CN=8时,其半径为多少?6. 试问:在铜(fcc,a=0.361nm )的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少?7. 镍为面心立方结构,其原子半径为。
试确定在镍的(100),(110)及(111)平面上1中各有多少个原子。
8. 石英的密度为2.65。
试问: 1) 1中有多少个硅原子(与氧原子)?2) 当硅与氧的半径分别为0.038nm 与0.114nm 时,其堆积密度为多少(假设原子是球形的)?9. 在800℃时个原子中有一个原子具有足够能量可在固体内移动,而在900℃时个原子中则只有一个原子,试求其激活能(J/原子)。
10. 若将一块铁加热至850℃,然后快速冷却到20℃。
试计算处理前后空位数应增加多少倍(设铁中形成一摩尔空位所需要的能量为104600J)。
()()()421,210,123[][][]346,112,021[][][][][]0121,0211,0110,0112,00013Mg/m 74.1=m g ρ+Na nm 1246.0=Ni r 2mm ()2SiO 3Mg/m 3m 101091011. 设图1-18所示的立方晶体的滑移面ABCD 平行于晶体的上、下底面。
若该滑移面上有一正方形位错环,如果位错环的各段分别与滑移面各边平行,其柏氏矢量b ∥AB 。
1) 有人认为“此位错环运动移出晶体后,滑移面上产生的滑移台阶应为4个b ,试问这种看法是否正确?为什么?2) 指出位错环上各段位错线的类型,并画出位错运动出晶体后,滑移方向及滑移量。
西北工业大学《材料科学基础》课后题答案

1. 有关晶面及晶向附图2.1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3) 5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
西北工业大学《材料科学基础》课后题答案
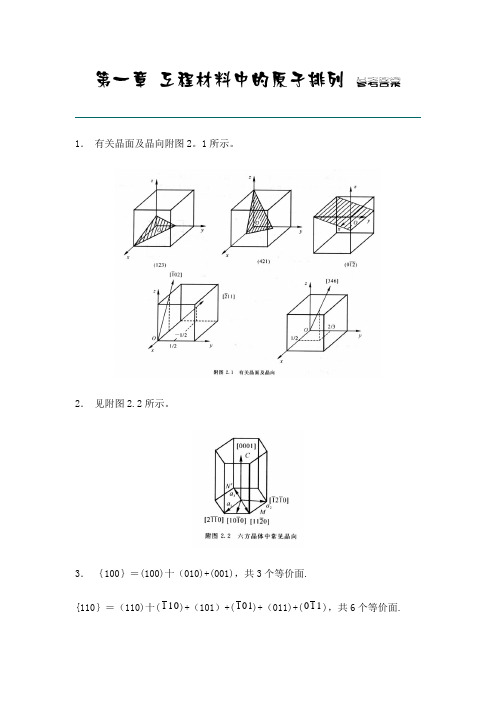
1. 有关晶面及晶向附图2。
1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面.{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面.{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1。
4×10—28m 3) 5. (1)0.088 nm;(2)0。
100 nm.6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3。
50×106个原子/mm 。
7. 1。
6l ×l013个原子/mm 2;1。
14X1013个原子/mm 2;1。
86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0。
4×10-18/个原子。
10. 1.06×1014倍.11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离.(2) A'B'为右螺型位错,C'D'为左螺型位错;B’C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2。
3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
七章 回复与再结晶习题答案(西北工业大学 刘智恩)

1.设计一种实验方法,确定在一定温度( T )下再结晶形核率N和长大线速度G (若N和G都随时间而变)。
2.金属铸件能否通过再结晶退火来细化晶粒?3.固态下无相变的金属及合金,如不重熔,能否改变其晶粒大小?用什么方法可以改变?4.说明金属在冷变形、回复、再结晶及晶粒长大各阶段晶体缺陷的行为与表现,并说明各阶段促使这些晶体缺陷运动的驱动力是什么。
5.将一锲型铜片置于间距恒定的两轧辊间轧制,如图7—4所示。
(1) 画出此铜片经完全再结晶后晶粒大小沿片长方向变化的示意图;(2) 如果在较低温度退火,何处先发生再结晶?为什么?6.图7—5示出。
—黄铜在再结晶终了的晶粒尺寸和再结晶前的冷加工量之间的关系。
图中曲线表明,三种不同的退火温度对晶粒大小影响不大。
这一现象与通常所说的“退火温度越高,退火后晶粒越大”是否有矛盾?该如何解释?7.假定再结晶温度被定义为在1 h 内完成95%再结晶的温度,按阿累尼乌斯(Arrhenius)方程,N =N 0exp(RT Q n -),G =G 0exp(RT Q g -)可以知道,再结晶温度将是G 和向的函数。
(1) 确定再结晶温度与G 0,N 0,Q g ,Q n 的函数关系;(2) 说明N 0,G 0,Q g ,Q 0的意义及其影响因素。
8.为细化某纯铝件晶粒,将其冷变形5%后于650℃退火1 h ,组织反而粗化;增大冷变形量至80%,再于650℃退火1 h ,仍然得到粗大晶粒。
试分析其原因,指出上述工艺不合理处,并制定一种合理的晶粒细化工艺。
9.冷拉铜导线在用作架空导线时(要求一定的强度)和电灯花导线(要求韧性好)时,应分别采用什么样的最终热处理工艺才合适?10.试比较去应力退火过程与动态回复过程位错运动有何不同。
从显微组织上如何区分动、静态回复和动、静态再结晶?11.某低碳钢零件要求各向同性,但在热加工后形成比较明显的带状组织。
请提出几种具体方法来减轻或消除在热加工中形成带状组织的因素。
【基础】材料科学基础作业题及答案西北工业大学

【关键字】基础第4章——三元合金相图习题及答案12.图4-120为Pb-Sn-Zn三元相图液面投影图。
(1)在图上标出合金X(wPb=0.75,wSn=0.15,wZn=0.10)的位置,合金Y(wPb=0.50,wSn=0.30,wZn=0.20)的位置及合金Z(wPb=0.10,wSn=0.10,wZn=0.80)的位置。
(2)若将2kgX,4kgY及6kgZ混熔成合金W,指出W成分点位置。
(3)若有合金X,问需要配何种成分的合金才能混合成合金Y。
解:(1)(2)W合金的成分:wPb=(0.75×2+0.50×4+0.10×6)/(2+4+6)=0.342wSn=(0.15×2+0.30×4+0.10×6)/(2+4+6)=0.175wZn=(0.10×2+0.20×4+0.80×6)/(2+4+6)=0.483(3)需要合金6-3=合金A,其成分为:wPb=(0.50×6-0.75×3)/3=0.25wSn=(0.30×6-0.15×3)/3=0.45wZn=(0.20×6-0.10×3)/3=0.314.试分析图4-96中所示①,②,③,④和⑤区内合金的结晶过程,冷却曲线及组织变化示意图,并在图上标出各相成分变化的路线。
解:15.试分析图4-102所示中Ⅰ,Ⅱ,Ⅲ,Ⅳ和Ⅴ区内合金的结晶过程,冷却曲线及组织组成物。
解:16.请在图4-113所示中指出合金X(wCu=0.15,wMg=0.05)及合金Y(wCu=wMg=0.20)的成分点、初生相及开始凝固温度;并根据液相单变量线的走向判断所有四相平衡转变的类型。
解:成分点见图。
合金X的初生相为α,合金Y的初生相为S。
合金X的开始凝固温度稍低于。
合金Y的开始凝固温度稍高于。
在所示的成分范围内,公有4个液相单变量线的交叉点,它们代表4个四相平衡反应。
西北工业大学《材料科学基础》课后题答案

1. 有关晶面及晶向附图2。
1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面.{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面.{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1。
4×10—28m 3) 5. (1)0.088 nm;(2)0。
100 nm.6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3。
50×106个原子/mm 。
7. 1。
6l ×l013个原子/mm 2;1。
14X1013个原子/mm 2;1。
86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0。
4×10-18/个原子。
10. 1.06×1014倍.11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离.(2) A'B'为右螺型位错,C'D'为左螺型位错;B’C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2。
3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
西南工业大学材料科学与基础第三版(刘智恩)习题解析

西南⼯业⼤学材料科学与基础第三版(刘智恩)习题解析第⼀章原⼦排列1. 作图表⽰⽴⽅晶系中的(123),(012),(421)晶⾯和[102],[211],[346]晶向.附图1-1 有关晶⾯及晶向2. 分别计算⾯⼼⽴⽅结构与体⼼⽴⽅结构的{100},{110}和{111}晶⾯族的⾯间距, 并指出⾯间距最⼤的晶⾯(设两种结构的点阵常数均为a).解由⾯⼼⽴⽅和体⼼⽴⽅结构中晶⾯间的⼏何关系, 可求得不同晶⾯族中的⾯间距如附表1-1所⽰.附表1-1 ⽴⽅晶系中的晶⾯间距显然, FCC中{111}晶⾯的⾯间距最⼤, ⽽BCC中{110}晶⾯的⾯间距最⼤.注意: 对于晶⾯间距的计算, 不能简单地使⽤公式, 应考虑组成复合点阵时, 晶⾯层数会增加.3. 分别计算fcc和bcc中的{100},{110}和{111}晶⾯族的原⼦⾯密度和<100>,<110>和<111>晶向族的原⼦线密度, 并指出两种结构的差别. (设两种结构的点阵常数均为a)解原⼦的⾯密度是指单位晶⾯内的原⼦数; 原⼦的线密度是指晶⾯上单位长度所包含的原⼦数. 据此可求得原⼦的⾯密度和线密度如附表1-2所⽰.附表1-2 ⽴⽅晶系中原⼦的⾯密度和线密度可见, 在BCC 中, 原⼦密度最⼤的晶⾯为{110}, 原⼦密度最⼤的晶向为<111>; 在FCC 中, 原⼦密度最⼤的晶⾯为{111}, 原⼦密度最⼤的晶向为<110>. 4. 在(0110)晶⾯上绘出[2113]晶向. 解详见附图1-2.附图1-2 六⽅晶系中的晶向5. 在⼀个简单⽴⽅⼆维晶体中, 画出⼀个正刃型位错和⼀个负刃型位错. 试求: (1) ⽤柏⽒回路求出正、负刃型位错的柏⽒⽮量.(2) 若将正、负刃型位错反向时, 说明其柏⽒⽮量是否也随之反向.(3) 具体写出该柏⽒⽮量的⽅向和⼤⼩.(4) 求出此两位错的柏⽒⽮量和.解正负刃型位错⽰意图见附图1-3(a)和附图1-4(a).(1) 正负刃型位错的柏⽒⽮量见附图1-3(b)和附图1-4(b).(2) 显然, 若正、负刃型位错线反向, 则其柏⽒⽮量也随之反向.(3) 假设⼆维平⾯位于YOZ坐标⾯, ⽔平⽅向为Y轴, 则图⽰正、负刃型位错⽅向分别为[010]和[010], ⼤⼩均为⼀个原⼦间距(即点阵常数a).(4) 上述两位错的柏⽒⽮量⼤⼩相等, ⽅向相反, 故其⽮量和等于0.6. 设图1-72所⽰⽴⽅晶体的滑移⾯ABCD平⾏于晶体的上下底⾯, 该滑移⾯上有⼀正⽅形位错环. 如果位错环的各段分别与滑移⾯各边平⾏, 其柏⽒⽮量b // AB, 试解答:(1) 有⼈认为“此位错环运动离开晶体后, 滑移⾯上产⽣的滑移台阶应为4个b”, 这种说法是否正确? 为什么?(2) 指出位错环上各段位错线的类型, 并画出位错移出晶体后, 晶体的外形、滑移⽅向和滑移量. (设位错环线的⽅向为顺时针⽅向)图1-72 滑移⾯上的正⽅形位错环附图1-5 位错环移出晶体引起的滑移解 (1) 这种看法不正确. 在位错环运动移出晶体后, 滑移⾯上下两部分晶体相对移动的距离是由其柏⽒⽮量决定的. 位错环的柏⽒⽮量为b, 故其相对滑移了⼀个b 的距离.(2) A ′B ′为右螺型位错, C ′D ′为左螺型位错, B ′C ′为正刃型位错, D ′A ′为负刃型位错. 位错运动移出晶体后滑移⽅向及滑移量见附图1-5.7. 设⾯⼼⽴⽅晶体中的(111)晶⾯为滑移⾯, 位错滑移后的滑移⽮量为[110]2a .(1) 在晶胞中画出此柏⽒⽮量b 的⽅向并计算出其⼤⼩.(2) 在晶胞中画出引起该滑移的刃型位错和螺型位错的位错线⽅向, 并写出此⼆位错线的晶向指数.解 (1) 柏⽒⽮量等于滑移⽮量, 因此柏⽒⽮量的⽅向为[110], /2.(2) 刃型位错与柏⽒⽮量垂直, 螺型位错与柏⽒⽮量平⾏, 晶向指数分别为[112]和[110], 详见附图1-6.附图1-6 位错线与其柏⽒⽮量、滑移⽮量 8. 若⾯⼼⽴⽅晶体中有[101]2a b =的单位位错及[121]6a b =的不全位错, 此⼆位错相遇后产⽣位错反应.(1) 此反应能否进⾏? 为什么?(2) 写出合成位错的柏⽒⽮量, 并说明合成位错的性质. 解 (1) 能够进⾏. 因为既满⾜⼏何条件:[111]3a b b ==∑∑后前, ⼜满⾜能量条件: .22222133b ab a=>=∑∑后前.(2)[111]3a b =合, 该位错为弗兰克不全位错.9. 已知柏⽒⽮量的⼤⼩为b = 0.25nm, 如果对称倾侧晶界的取向差θ = 1° 和10°, 求晶界上位错之间的距离. 从计算结果可得到什么结论? 解根据bD θ≈, 得到θ = 1°,10° 时, D ≈14.3nm, 1.43nm. 由此可知, θ = 10° 时位错之间仅隔5~6个原⼦间距, 位错密度太⼤, 表明位错模型已经不适⽤了. 第⼆章固体中的相结构1. 已知Cd, In, Sn, Sb 等元素在Ag 中的固熔度极限(摩尔分数)分别为0.435, 0.210, 0.130, 0.078; 它们的原⼦直径分别为0.3042 nm, 0.314 nm, 0.316 nm, 0.3228 nm; Ag 的原⼦直径为0.2883 nm. 试分析其固熔度极限差异的原因, 并计算它们在固熔度极限时的电⼦浓度.答: 在原⼦尺⼨因素相近的情况下, 熔质元素在⼀价贵⾦属中的固熔度(摩尔分数)受原⼦价因素的影响较⼤, 即电⼦浓度e/a 是决定固熔度(摩尔分数)的⼀个重要因素, ⽽且电⼦浓度存在⼀个极限值(约为1.4). 电⼦浓度可⽤公式A B B B (1)c Z x Z x =-+ 计算. 式中, ZA, ZB 分别为A, B 组元的价电⼦数; xB 为B 组元的摩尔分数. 因此, 随着熔质元素价电⼦数的增加, 极限固熔度会越来越⼩.Cd, In, Sn, Sb 等元素与Ag 的原⼦直径相差不超过15%(最⼩的Cd 为5.5%, 最⼤的Sb 为11.96%), 满⾜尺⼨相近原则, 这些元素的原⼦价分别为2, 3, 4, 5价, Ag 为1价, 据此推断它们的固熔度极限越来越⼩, 实际情况正好反映了这⼀规律; 根据上⾯的公式可以计算出它们在固熔度(摩尔分数)极限时的电⼦浓度分别为1.435, 1.420, 1.390, 1.312.2. 碳可以熔⼊铁中⽽形成间隙固熔体, 试分析是α-Fe 还是γ-Fe 能熔⼊较多的碳. 答: α-Fe 为体⼼⽴⽅结构, 致密度为0.68; γ-Fe 为⾯⼼⽴⽅结构, 致密度为0.74. 显然, α-Fe中的间隙总体积⾼于γ-Fe, 但由于α-Fe的间隙数量多, 单个间隙半径却较⼩, 熔⼊碳原⼦将会产⽣较⼤的畸变, 因此, 碳在γ-Fe中的固熔度较α-Fe的⼤. 3. 为什么只有置换固熔体的两个组元之间才能⽆限互熔, ⽽间隙固熔体则不能? 答: 这是因为形成固熔体时, 熔质原⼦的熔⼊会使熔剂结构产⽣点阵畸变, 从⽽使体系能量升⾼. 熔质原⼦与熔剂原⼦尺⼨相差越⼤, 点阵畸变的程度也越⼤, 则畸变能越⾼, 结构的稳定性越低, 熔解度越⼩. ⼀般来说, 间隙固熔体中熔质原⼦引起的点阵畸变较⼤, 故不能⽆限互熔, 只能有限熔解.第三章凝固1. 分析纯⾦属⽣长形态与温度梯度的关系.答: 纯⾦属⽣长形态是指晶体宏观长⼤时固-液界⾯的形貌. 界⾯形貌取决于界⾯前沿液相中的温度梯度.(1) 平⾯状长⼤: 当液相具有正温度梯度时, 晶体以平直界⾯⽅式推移长⼤. 此时, 界⾯上任何偶然的、⼩的凸起深⼊液相时, 都会使其过冷度减⼩, 长⼤速率降低或停⽌长⼤, ⽽被周围部分赶上, 因⽽能保持平直界⾯的推移. 长⼤过程中晶体沿平⾏温度梯度的⽅向⽣长, 或沿散热的反⽅向⽣长, ⽽其它⽅向的⽣长则受到限制.(2) 树枝状长⼤: 当液相具有负温度梯度时, 晶体将以树枝状⽅式⽣长. 此时, 界⾯上偶然的凸起深⼊液相时, 由于过冷度的增⼤, 长⼤速率越来越⼤; ⽽它本⾝⽣长时⼜要释放结晶潜热, 不利于近旁的晶体⽣长, 只能在较远处形成另⼀凸起. 这就形成了枝晶的⼀次轴, 在⼀次轴成长变粗的同时, 由于释放潜热使晶枝侧旁液体中也呈现负温度梯度, 于是在⼀次轴上⼜会长出⼩枝来, 称为⼆次轴, 在⼆次轴上⼜长出三次轴……由此⽽形成树枝状⾻架, 故称为树枝晶(简称枝晶).2. 简述纯⾦属晶体长⼤机制及其与固-液界⾯微观结构的关系.答: 晶体长⼤机制是指晶体微观长⼤⽅式, 即液相原⼦添加到固相的⽅式, 它与固-液界⾯的微观结构有关.(1) 垂直长⼤⽅式: 具有粗糙界⾯的物质, 因界⾯上约有50%的原⼦位置空着, 这些空位都可以接受原⼦, 故液相原⼦可以进⼊空位, 与晶体连接, 界⾯沿其法线⽅向垂直推移, 呈连续式长⼤.(2) 横向(台阶)长⼤⽅式: 包括⼆维晶核台阶长⼤机制和晶体缺陷台阶长⼤机制, 具有光滑界⾯的晶体长⼤往往采取该⽅式. ⼆维晶核模式, 认为其⽣长主要是利⽤系统的能量起伏, 使液相原⼦在界⾯上通过均匀形核形成⼀个原⼦厚度的⼆维薄层状稳定的原⼦集团, 然后依靠其周围台阶填充原⼦, 使⼆维晶核横向长⼤, 在该层填满后, 则在新的界⾯上形成新的⼆维晶核, 继续填满, 如此反复进⾏.晶体缺陷⽅式, 认为晶体⽣长是利⽤晶体缺陷存在的永不消失的台阶(如螺型位错的台阶或挛晶的沟槽)长⼤的. 第四章相图1. 在Al-Mg 合⾦中, xMg 为0.15, 计算该合⾦中镁的wMg 为多少.解设Al 的相对原⼦量为MAl, 镁的相对原⼦量为MMg, 按1mol Al-Mg 合⾦计算, 则镁的质量分数可表⽰为M g M gM g A l A lM g M g100%x Mw x Mx M=+.将xMg = 0.15, xAl = 0.85, MMg = 24, MAl = 27代⼊上式中, 得到wMg = 13.56%.2. 根据图4-117所⽰⼆元共晶相图, 试完成:(1) 分析合⾦I, II 的结晶过程, 并画出冷却曲线.(2) 说明室温下合⾦I, II 的相和组织是什么, 并计算出相和组织组成物的相对量.(3) 如果希望得到共晶组织加上相对量为5%的β初的合⾦, 求该合⾦的成分.图4-117 ⼆元共晶相图附图4-1 合⾦I 的冷却曲线附图4-2 合⾦II 的冷却曲线解 (1) 合⾦I 的冷却曲线参见附图4-1, 其结晶过程如下:1以上, 合⾦处于液相;1~2时, 发⽣匀晶转变L →α, 即从液相L 中析出固熔体α, L 和α的成分沿液相线和固相线变化, 达到2时, 凝固过程结束;2时, 为α相;2~3时, 发⽣脱熔转变, α→βII.合⾦II 的冷却曲线参见附图4-2, 其结晶过程如下:1以上, 处于均匀液相;1~2时, 进⾏匀晶转变L →β;2时, 两相平衡共存, 0.50.9L β;2~2时,剩余液相发⽣共晶转变0.50.20.9L βα+;2~3时, 发⽣脱熔转变α→βII.(2) 室温下, 合⾦I 的相组成物为α + β, 组织组成物为α + βII.相组成物相对量计算如下:αβ0.900.20100%82%0.900.050.200.05100%18%0.900.05w w -=?=--==-组织组成物的相对量与相的⼀致.室温下, 合⾦II 的相组成物为α + β, 组织组成物为β初 + (α+β).相组成物相对量计算如下:αβ0.900.80100%12%0.900.050.800.05100%88%0.900.05w w -=?=--==-组织组成物相对量计算如下:β(α+β)0.800.50100%75%0.900.500.900.80100%25%0.900.50w w -==--==-初(3) 设合⾦的成分为wB = x, 由题意知该合⾦为过共晶成分, 于是有β0.50100%5%0.900.50x w -==-初所以, x = 0.52, 即该合⾦的成分为wB = 0.52.3. 计算wC 为0.04的铁碳合⾦按亚稳态冷却到室温后组织中的珠光体、⼆次渗碳体和莱⽒体的相对量, 并计算组成物珠光体中渗碳体和铁素体及莱⽒体中⼆次渗碳体、共晶渗碳体与共析渗碳体的相对量.解根据Fe-Fe3C相图, wC = 4%的铁碳合⾦为亚共晶铸铁, 室温下平衡组织为P + Fe3CII + Ld′, 其中P和Fe3CII 系由初⽣奥⽒体转变⽽来, 莱⽒体则由共晶成分的液相转变⽽成, 因此莱⽒体可由杠杆定律直接计算, ⽽珠光体和⼆次渗碳体则可通过两次使⽤杠杆定律间接计算出来.Ld′相对量: d L4 2.11100%86.3% 4.3 2.11w'-=?=-.Fe3CII 相对量: 3IIFe C4.34 2.110.77100% 3.1% 4.3 2.11 6.690.77w--=??=--.P相对量:P4.34 6.69 2.11100%10.6% 4.3 2.11 6.690.77w--=??=--.珠光体中渗碳体和铁素体的相对量的计算则以共析成分点作为⽀点, 以wC = 0.001%和wC = 6.69%为端点使⽤杠杆定律计算并与上⾯计算得到的珠光体相对量级联得到.P中F相对量: F P6.690.77100%9.38% 6.690.001w w -=??=-.P中Fe3C相对量: 3Fe C10.6%9.38% 1.22%w=-=.⾄于莱⽒体中共晶渗碳体、⼆次渗碳体及共析渗碳体的相对量的计算, 也需采取杠杆定律的级联⽅式, 但必须注意⼀点, 共晶渗碳体在共晶转变线处计算, ⽽⼆次渗碳体及共析渗碳体则在共析转变线处计算.Ld′中共晶渗碳体相对量: dC m L4.3 2.11100%41.27% 6.69 2.11w w'-=??=-共晶Ld′中⼆次渗碳体相对量: dC m L6.69 4.3 2.110.77100%10.2% 6.69 2.11 6.690.77w w'--==--I ILd′中共析渗碳体相对量:dC m L6.69 4.3 6.69 2.110.770.0218100% 3.9% 6.69 2.11 6.690.77 6.690.0218w w'---==---共析4. 根据下列数据绘制Au-V⼆元相图. 已知⾦和钒的熔点分别为1064℃和1920℃.⾦与钒可形成中间相β(AuV3); 钒在⾦中的固熔体为α, 其室温下的熔解度为wV = 0.19; ⾦在钒中的固熔体为γ, 其室温下的熔解度为wAu = 0.25. 合⾦系中有两个包晶转变,即1400V V V 1522V V V (1) β(0.4)L(0.25)α(0.27)(2) γ(0.52)L(0.345)α(0.45)w w w w w w =+===+== ℃℃解根据已知数据绘制的Au-V ⼆元相图参见附图4-3.附图4-3 Au-V ⼆元相图第五章材料中的扩散1. 设有⼀条直径为3cm 的厚壁管道, 被厚度为0.001cm 的铁膜隔开, 通过输⼊氮⽓以保持在膜⽚⼀边氮⽓浓度为1000 mol/m3; 膜⽚另⼀边氮⽓浓度为100 mol/m3. 若氮在铁中700℃时的扩散系数为4×10-7 cm2 /s, 试计算通过铁膜⽚的氮原⼦总数. 解设铁膜⽚左右两边的氮⽓浓度分别为c1, c2, 则铁膜⽚处浓度梯度为7421510010009.010 m ol /m110c c c c xxx--??-≈===- 根据扩散第⼀定律计算出氮⽓扩散通量为722732410(10)(9.01)3.61mc J D x---=-=--?=于是, 单位时间通过铁膜⽚的氮⽓量为3-22-63.610(310)2.5410m o l/s4J A π-=??=?最终得到单位时间通过铁膜⽚的氮原⼦总数为-623A()2.54106.021023.0610 sN JA N =?==第六章塑性变形1. 铜单晶体拉伸时, 若⼒轴为 [001] ⽅向, 临界分切应⼒为0.64 MPa, 问需要多⼤的拉伸应⼒才能使晶体开始塑性变形?解铜为⾯⼼⽴⽅⾦属, 其滑移系为 {111}<110>, 4个 {111} ⾯构成⼀个⼋⾯体, 详见教材P219中的图6-12.当拉⼒轴为 [001] ⽅向时, 所有滑移⾯与⼒轴间的夹⾓相同, 且每个滑移⾯上的三个滑移⽅向中有两个与⼒轴的夹⾓相同, 另⼀个为硬取向(λ = 90°). 于是, 取滑移系(111)[101]进⾏计算.ksc o s c o s c o s c o s 0.64 1.57 M P a.m mλ?λτσ========?=即⾄少需要1.57 MPa 的拉伸应⼒才能使晶体产⽣塑性变形.2. 什么是滑移、滑移线、滑移带和滑移系? 作图表⽰α-Fe, Al, Mg 中的最重要滑移系. 那种晶体的塑性最好, 为什么?答: 滑移是晶体在切应⼒作⽤下⼀部分相对于另⼀部分沿⼀定的晶⾯和晶向所作的平⾏移动; 晶体的滑移是不均匀的, 滑移部分与未滑移部分晶体结构相同. 滑移后在晶体表⾯留下台阶, 这就是滑移线的本质. 相互平⾏的⼀系列滑移线构成所谓滑移带. 晶体发⽣滑移时, 某⼀滑移⾯及其上的⼀个滑移⽅向就构成了⼀个滑移系.附图6-1 三种晶体点阵的主要滑移系α-Fe具有⽴⽅体⼼结构, 主要滑移系可表⽰为{110}<111>, 共有6×2 = 12个; Al 具有⾯⼼⽴⽅结构, 其滑移系可表⽰为{111}<110>, 共有4×3 = 12个; Mg具有密排六⽅结构,主要滑移系可表⽰为{0001}1120<>, 共有1×3 = 3个. 晶体的塑性与其滑移系的数量有直接关系, 滑移系越多, 塑性越好; 滑移系数量相同时, ⼜受滑移⽅向影响, 滑移⽅向多者塑性较好, 因此, 对于α-Fe, Al, Mg三种⾦属, Al的塑性最好, Mg 的最差, α-Fe居中. 三种典型结构晶体的重要滑移系如附图6-1所⽰.3. 什么是临界分切应⼒? 影响临界分切应⼒的主要因素是什么? 单晶体的屈服强度与外⼒轴⽅向有关吗? 为什么?答: 滑移系开动所需的作⽤于滑移⾯上、沿滑移⽅向的最⼩分切应⼒称为临界分切应⼒.临界分切应⼒τk的⼤⼩主要取决于⾦属的本性, 与外⼒⽆关. 当条件⼀定时, 各种晶体的临界分切应⼒各有其定值. 但它是⼀个组织敏感参数,⾦属的纯度、变形速度和温度、⾦属的加⼯和热处理状态都对它有很⼤影响.如前所述, 在⼀定条件下, 单晶体的临界分切应⼒保持为定值, 则根据分切应⼒与外加轴向应⼒的关系: σs = τk / m, m为取向因⼦, 反映了外⼒轴与滑移系之间的位向关系, 因此, 单晶体的屈服强度与外⼒轴⽅向关系密切. m越⼤, 则屈服强度越⼩, 越有利于滑移.4. 孪⽣与滑移主要异同点是什么? 为什么在⼀般条件下进⾏塑性变形时锌中容易出现挛晶, ⽽纯铁中容易出现滑移带?答: 孪⽣与滑移的异同点如附表6-1所⽰.附表6-1 晶体滑移与孪⽣的⽐较锌为密排六⽅结构⾦属, 主要滑移系仅3个, 因此塑性较差, 滑移困难, 往往发⽣孪⽣变形, 容易出现挛晶; 纯铁为体⼼⽴⽅结构⾦属, 滑移系较多, 共有48个, 其中主要滑移系有12个, 因此塑性较好, 往往发⽣滑移变形, 容易出现滑移带. 第七章回复与再结晶1. 已知锌单晶体的回复激活能为8.37×104 J/mol, 将冷变形的锌单晶体在-50 ℃进⾏回复处理, 如去除加⼯硬化效应的25% 需要17 d, 问若在5 min 内达到同样效果, 需将温度提⾼多少摄⽒度?解根据回复动⼒学, 采⽤两个不同温度将同⼀冷变形⾦属的加⼯硬化效应回复到同样程度, 回复时间、温度满⾜下述关系:122111e x p t Q t R T T ??=-- ? ?整理后得到221111lnT t R T Qt =+.将41211223 K ,/5/(172460),8.3710 J/m o l, 8.314 J/(m o l K )4896T t t Q R ==??==?=?代⼊上式得到2274.7 KT=.因此, 需将温度提⾼21274.722351.7 TT T ?=-=-=℃.2. 纯铝在553 ℃和627 ℃等温退⽕⾄完成再结晶分别需要40 h 和1 h, 试求此材料的再结晶激活能.解再结晶速率v 再与温度T 的关系符合阿累尼乌斯(Arrhenius)公式, 即exp()Q v A R T=-再其中, Q 为再结晶激活能, R 为⽓体常数.如果在两个不同温度T1, T2进⾏等温退⽕,欲产⽣同样程度的再结晶所需时间分别为t1, t2, 则122112122111ex p [()]ln (/)t Q t RT T R T T t t Q T T =--=- 依题意, 有T1 = 553 + 273 = 826 K, T2 = 627 + 273 = 900 K, t1 = 40 h, t2 = 1 h, 则58.314826900ln(40/1)3.0810J/m ol900826Q =-3. 说明⾦属在冷变形、回复、再结晶及晶粒长⼤各阶段的显微组织、机械性能特点与主要区别.答: ⾦属在冷变形、回复、再结晶及晶粒长⼤各阶段的显微组织、机械性能特点与主要区别详见附表7-1.附表7-1 ⾦属在冷变形、回复、再结晶及晶粒长⼤各阶段的显微组织、机械性能。
西北工业大学《材料科学基础》课后题

1. 有关晶面及晶向附图2.1所示。
2. 见附图2.2所示。
3. {100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3) 5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de 位错线平行。
(2)在上述切应力作用下,位错线de 将向左(或右)移动,即沿着与位错线de 垂直的方向(且在滑移面上)移动。
西北工业大学材料科学基础课后题答案

1.有关晶面及晶向附图2.1所示。
2.见附图2.2所示。
3.{100}=(100)十(010)+(001),共3个等价面。
{110}=(110)十(101)+(101)+(011)+(011)+(110),共6个等价面。
{111}=(111)+(111)+(111)+(111),共4个等价面。
)121()112()112()211()112()121()211()121()211()211()121()112(}112{+++++++++++=共12个等价面。
4. 单位晶胞的体积为V Cu =0.14 nm 3(或1.4×10-28m 3)5. (1)0.088 nm ;(2)0.100 nm 。
6. Cu 原子的线密度为2.77×106个原子/mm 。
Fe 原子的线密度为3.50×106个原子/mm 。
7. 1.6l ×l013个原子/mm 2;1.14X1013个原子/mm 2;1.86×1013个原子/mm 2。
8. (1) 5.29×1028个矽原子/m 3; (2) 0.33。
9. 9. 0.4×10-18/个原子。
10. 1.06×1014倍。
11. (1) 这种看法不正确。
在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。
位错环的柏氏矢量为b ,故其相对滑移了一个b 的距离。
(2) A'B'为右螺型位错,C'D'为左螺型位错;B'C'为正刃型位错,D'A'为负刃型位错。
位错运动移出晶体后滑移方向及滑移量如附图2.3所示。
12.(1)应沿滑移面上、下两部分晶体施加一切应力τ,的方向应与de位错线平行。
(2)在上述切应力作用下,位错线de将向左(或右)移动,即沿着与位错线de垂直的方向(且在滑移面上)移动。
在位错线沿滑移面旋转360°后,在晶体表面沿柏氏矢量方向产生宽度为一个b的台阶。
金属学与热处理课后习题答案

第七章金属及合金的回复和再结晶7-1 用冷拔铜丝线制作导线,冷拔之后应如何如理,为什么答:应采取回复退火去应力退火处理:即将冷变形金属加热到再结晶温度以下某一温度,并保温足够时间,然后缓慢冷却到室温的热处理工艺;原因:铜丝冷拔属于再结晶温度以下的冷变形加工,冷塑性变形会使铜丝产生加工硬化和残留内应力,该残留内应力的存在容易导致铜丝在使用过程中断裂;因此,应当采用去应力退火使冷拔铜丝在基本上保持加工硬化的条件下降低其内应力主要是第一类内应力,改善其塑性和韧性,提高其在使用过程的安全性;7-2 一块厚纯金属板经冷弯并再结晶退火后,试画出截面上的显微组织示意图;答:解答此题就是画出金属冷变形后晶粒回复、再结晶和晶粒长大过程示意图可参考教材P195,图7-17-3 已知W、Fe、Cu的熔点分别为3399℃、1538℃和1083℃,试估算其再结晶温度;答:再结晶温度:通常把经过严重冷变形变形度在70%以上的金属,在约1h的保温时间内能够完成超过95%再结晶转变量的温度作为再结晶温度;≈δTm,对于工业1、金属的最低再结晶温度与其熔点之间存在一经验关系式:T再纯金属来说:δ值为,取计算;2、应当指出,为了消除冷塑性变形加工硬化现象,再结晶退火温度通常要比其最低再结晶温度高出100-200℃;=,可得:如上所述取T再W=3399×=℃再=1538×=℃Fe再=1083×=℃Cu再7-4 说明以下概念的本质区别:1、一次再结晶和二次在结晶;2、再结晶时晶核长大和再结晶后的晶粒长大;答:1、一次再结晶和二次在结晶;定义一次再结晶:冷变形后的金属加热到一定温度,保温足够时间后,在原来的变形组织中产生了无畸变的新的等轴晶粒,位错密度显着下降,性能发生显着变化恢复到冷变形前的水平,称为一次再结晶;它的实质是新的晶粒形核、长大的过程;二次再结晶:经过剧烈冷变形的某些金属材料,在较高温度下退火时,会出现反常的晶粒长大现象,即少数晶粒具有特别大的长大能力,逐步吞食掉周围的小晶粒,其最终尺寸超过原始晶粒的几十倍或上百倍,比临界变形后的再结晶晶粒还要粗大得多,这个过程称为二次再结晶;二次再结晶并不是晶粒重新形核和长大的过程,它是以一次再结晶后的某些特殊晶粒作为基础而异常长大,严格来说它是特殊条件下的晶粒长大过程,并非是再结晶过程;本质区别:是否有新的形核晶粒;2、再结晶时晶核长大和再结晶后的晶粒长大;定义再结晶晶核长大:是指再结晶晶核形成后长大至再结晶初始晶粒的过程;其长大驱动力是新晶粒与周围变形基体的畸变能差,促使晶核界面向畸变区域推进,界面移动的方向,也就是晶粒长大的方向总是远离界面曲率中心,直至所有畸变晶粒被新的无畸变晶粒代替;再结晶后的晶粒长大:是指再结晶晶核长大成再结晶初始晶粒后,当温度继续升高或延长保温时间,晶粒仍然继续长大的过程;此时,晶粒长大的驱动力是晶粒长大前后总的界面能的差,界面移动的方向,也就是晶粒长大的方向都朝向晶界的曲率中心,直至晶界变成平面状,达到界面能最低的稳定状态;本质区别:1、长大驱动力不同2、长大方向不同,即晶界的移动方向不同;7-5 分析回复和再结晶阶段空位与位错的变化及其对性能的影响;答:回复阶段:回复:是指冷塑性变形的金属在加热时,在光学显微组织发生改变前即再结晶晶粒形成前所产生的某些亚结构和性能的变化过程;空位和位错的变化及对性能的影响:回复过程中,空位和位错发生运动,从而改变了他们的数量和组态;低温回复时,主要涉及空位的运动;空位可以移至表面、晶界或位错处消失,也可以聚集形成空位对、空位群,还可以与间隙原子相互作用而消失,总之空位运动的结果使空位密度大大减小;电阻率对空位密度比较敏感,因此其数值会有显着下降;而力学性能对空位的变化不敏感,没有变化;中温回复时,主要涉及位错的运动;由于位错滑移会导致同一滑移面上异号位错合并而相互抵消,位错密度略有下降,但降低幅度不大,力学性能变化不大;高温回复时,主要涉及位错的运动;位错不但可以滑移、而且可以攀移,发生多边化,使错密度有所降低,降低系统部分内应力,从而使硬度、强度略有下降,塑性、韧性得到改善;综上,回复过程可以使冷塑性变形的金属在基本保持加工硬化的状态下降低其内应力主要是第一类内应力,减轻工件的翘曲和变形,降低电阻率,提高材料的耐蚀性并改善其塑性和韧性,提高工件使用时的安全性;再结晶阶段:再结晶:冷变形后的金属加热到一定温度,保温足够时间后,在原来的变形组织中产生了无畸变的新的等轴晶粒,位错密度显着下降,性能也发生显着变化并恢复到冷变形前的水平;空位和位错的变化及对性能的影响:再结晶阶段主要是位错发生滑移、攀移和多变化,新的无畸变晶粒形成,位错密度显着下降,因塑性变形而造成的内应力可完全被消除,促使硬度和强度显着下降,塑性和韧性得到明显提高;7-6 何谓临界变形度在工业生产中有何实际意义;答:临界变形度:金属在冷塑性变形时,当变形度达到某一数值一般金属均在2%-10%范围内时,再结晶后的晶粒变得特别粗大;这是由于此时的变形度不大,晶核长大线速度和形核率的比值很大,因此得到特别粗大的晶粒;把对应得到特别粗大晶粒的变形度称为临界变形度;实际意义:通常,粗大的晶粒对金属的力学性能十分不能,降低力学性能指标,因此在实际生产时,应当避免在临界变形度范围内进行压力加工;但是,有时为了某种特殊目的,需要得到粗晶粒钢时,例如用于制造电机或变压器的硅钢来说,晶粒越粗大越好磁滞损耗小,效应高,,可以利用这种现象,制取粗晶粒甚至单晶;7-7 一块纯锡板被枪弹击穿,经再结晶退火后,弹孔周围的晶粒大小有何特征,并说明原因;答:弹孔周围晶粒大小特征:晶粒大小随距弹孔的距离产生梯度变化,即距离弹孔距离越近晶粒越细,距离越远晶粒越大,并且在某一距离处变形量处于临界变形量范围内,出现特别粗大晶粒组织;原因:1、锡板被枪弹击穿产生的弹孔相当于弹孔处产生了剧烈的冷塑性变形,且距离弹孔越近则变形越剧烈;2、对冷塑性变形的金属进行再结晶退火,则冷变形的晶粒必然要发生再结晶,且再结晶后的晶粒大小与变形度密切相关,这是因为随着变形度的增加,形变储存能增加,再结晶驱动力增加,形核率N和晶粒长大线速度G同时增加,但G/N 的比值减小,使再结晶的晶粒随变形度增加而变细;3、然而,当变形度在某一临界变形度范围内一般金属在2%-10%范围内,由于变形度不大,G/N的比值很大,使再结晶的晶粒特别粗大;7-8 某厂对高锰钢制碎矿机颚板进行固溶处理时,经1100℃加热后,用冷拔钢丝绳吊挂,由起重吊车送往淬火水槽;行至途中,钢丝绳突然断裂;这条钢丝绳是新的,事先经过检查,并无瑕疵;试分析钢丝绳断裂原因;答:原因:1、按题中所述钢丝绳的质量没有问题,那么钢丝绳发生断裂则必然使是由于所吊颚板重力对钢丝绳产生的应力超过了钢丝绳的抗拉强度造成的;在吊运过程中颚板对钢丝绳产生的应力没有变化,那么发生变化的则必然是钢丝绳的强度;2、由题述,该钢丝绳是冷拔而成,及结果冷塑性变形而成,必然产生了加工硬化现象;由于颚板经过1100加热固溶处理,所以在吊运过程中,高温颚板对冷拔钢丝绳起到了加热作用,当钢丝绳温度超过其再结晶温度时,则会发生再结晶现象,导致钢丝绳强度显着下降,致使颚板重力对钢丝绳产生的应力超过了钢丝绳的强度,导致钢丝绳断裂;7-9 设有一楔形板坯结果冷轧后得到相同厚度的板材,然后进行再结晶退火,试问该板材的晶粒大小是否均匀答:不均匀原因:1、对冷塑性变形的金属进行再结晶退火,则冷变形的晶粒必然要发生再结晶,且再结晶后的晶粒大小与变形度密切相关,这是因为随着变形度的增加,形变储存能增加,再结晶驱动力增加,形核率N和晶粒长大线速度G同时增加,但G/N的比值减小,使再结晶的晶粒随变形度增加而变细;2、此外,当变形度在临界变形度范围内一般金属在2%-10%范围内,由于变形度不大,G/N的比值很大,使再结晶的晶粒特别粗大;3、由题述,是由厚度不一的楔形板冷变形成相同厚度的板材,则板材的不同位置的变形度必然不同,所以再结晶后的晶粒大小也必然不同;7-10 金属材料在热加工时为了获得细小晶粒组织,应该注意一些什么问题答:热加工是在高于再结晶温度以上的塑性变形过程,塑性变形引起的加工硬化和回复再结晶引起的软化几乎同时进行;所以,在热加工时为了获得细小晶粒我觉得应该注意以下几点:1、变形程度;变形度越大则再结晶晶粒的尺寸越小,同时要避开临界变形度范围,防止产生粗大晶粒;2、热加工的温度;即再结晶温度,再结晶温度越高,再结晶的晶粒越大,而且易于引起二次再结晶,得到异常粗大的晶粒组织;3、变形速度;增大变形速度,可推迟再结晶,并提高再结晶转变速度,细化晶粒;4、热加工后的冷却;冷却速度过慢,会造成晶粒粗大;5、原始晶粒的大小;这是因为当变形度一定时,材料的原始晶粒越细,则再结晶后的晶粒越细;6、在金属材料中加入适量的Al、Ti、V、Nb等碳、氮化物形成元素,析出弥散的第二相质点,可以有效地阻止高温下晶粒的长大;7-11 为获得细小的晶粒组织,应根据什么原则制订塑性变形及退火工艺答:塑性变形原则:增大变形度,避开临界变形度范围,保证变形均匀性;退火工艺原则:降低再结晶退火温度,缩短再结晶退火保温时间;。
结晶学基础第七章习题答案

《结晶学基础》第七章习题答案7001单晶:一个晶体能基本上被一个空间点阵的单位矢量所贯穿。
多晶:包含许多颗晶粒,这些晶粒可能为同一品种,也可能不同品种,由于各晶粒在空间取向可能不同,不能被同一点阵的单位矢量贯穿。
7002(D)7004简单立方; Cs+和Cl-; 4C37005(1) 立方F(2) A 和B(3) 4 个(4) 4 组(5) 3a(6) a/270074n个A, 8n个B, n为自然数。
7010d111= 249 pmd211= 176 pmd100= 432 pm7011六方; D3h70127013依次为立方,四方,四方,正交,六方。
7014立方P,立方I,立方F; 四方P,四方I。
7015旋转轴,镜面,对称中心,反轴; 旋转轴,镜面,对称中心,反轴,点阵,螺旋轴,滑移面;n=1,2,3,4,6; 32个; 七个晶系; 14种空间点阵型式; 230个空间群。
7016(1) 四方晶系(2) 四方I(3) D4(4) a=b≠c, α=β=γ=90°7017(1) 单斜晶系,单斜P(2) C2h(3) C2, m, i7018(2a,3b,c):(326);(a,b,c):(111);(6a,3b,3c):(122);(2a,-3b,-3c):(322)。
7019C1,C2,C3,C4,C6; I1=i,I2=m,I4。
7020立方晶系:四个按立方体对角线安放的三重轴; 单斜晶系:一个二重轴或一个对称面。
7021正交晶系和四方晶系 C 和 P C 2(3), m (3), i 和 I 4, C 2(2), m (2)。
702232 个; 230 个 7023四方 I ; 四方 P 7025T , T h ,T d ,O , O h 群 7026(B) 7027D 2h ———mm m 222C 3v -——3mD 2d ———42m T d -——43m 7028 x ,y +21,z 。
《材料科学基础》课后习题(西工大版)

第一章1. 作图表示立方晶体的()()()421,210,123晶面及[][][]346,112,021晶向。
2. 在六方晶体中,绘出以下常见晶向[][][][][]0121,0211,0110,0112,0001等。
3. 写出立方晶体中晶面族{100},{110},{111},{112}等所包括的等价晶面。
4. 镁的原子堆积密度和所有hcp 金属一样,为0.74。
试求镁单位晶胞的体积。
已知Mg 的密度3Mg/m 74.1=mg ρ,相对原子质量为24.31,原子半径r=0.161nm 。
5. 当CN=6时+Na 离子半径为0.097nm ,试问:1) 当CN=4时,其半径为多少?2) 当CN=8时,其半径为多少?6. 试问:在铜(fcc,a=0.361nm )的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少?7. 镍为面心立方结构,其原子半径为nm 1246.0=Ni r 。
试确定在镍的(100),(110)及(111)平面上12mm 中各有多少个原子。
8. 石英()2SiO 的密度为2.653Mg/m 。
试问:1) 13m 中有多少个硅原子(与氧原子)?2) 当硅与氧的半径分别为0.038nm 与0.114nm 时,其堆积密度为多少(假设原子是球形的)?9. 在800℃时1010个原子中有一个原子具有足够能量可在固体内移动,而在900℃时910个原子中则只有一个原子,试求其激活能(J/原子)。
10. 若将一块铁加热至850℃,然后快速冷却到20℃。
试计算处理前后空位数应增加多少倍(设铁中形成一摩尔空位所需要的能量为104600J )。
11. 设图1-18所示的立方晶体的滑移面ABCD 平行于晶体的上、下底面。
若该滑移面上有一正方形位错环,如果位错环的各段分别与滑移面各边平行,其柏氏矢量b ∥AB 。
1) 有人认为“此位错环运动移出晶体后,滑移面上产生的滑移台阶应为4个b ,试问这种看法是否正确?为什么?2) 指出位错环上各段位错线的类型,并画出位错运动出晶体后,滑移方向及滑移量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.设计一种实验方法,确定在一定温度( T )下再结晶形核率N和长大线速度G (若N和G都随时间而变)。
2.金属铸件能否通过再结晶退火来细化晶粒?3.固态下无相变的金属及合金,如不重熔,能否改变其晶粒大小?用什么方法可以改变?4.说明金属在冷变形、回复、再结晶及晶粒长大各阶段晶体缺陷的行为与表现,并说明各阶段促使这些晶体缺陷运动的驱动力是什么。
5.将一锲型铜片置于间距恒定的两轧辊间轧制,如图7—4所示。
(1) 画出此铜片经完全再结晶后晶粒大小沿片长方向变化的示意图;(2) 如果在较低温度退火,何处先发生再结晶?为什么?6.图7—5示出。
—黄铜在再结晶终了的晶粒尺寸和再结晶前的冷加工量之间的关系。
图中曲线表明,三种不同的退火温度对晶粒大小影响不大。
这一现象与通常所说的“退火温度越高,退火后晶粒越大”是否有矛盾?该如何解释?7.假定再结晶温度被定义为在1 h 完成95%再结晶的温度,按阿累尼乌斯(Arrhenius)方程,N =N 0exp(RT Q n -),G =G 0exp(RT Q g -)可以知道,再结晶温度将是G 和向的函数。
(1) 确定再结晶温度与G 0,N 0,Q g ,Q n 的函数关系;(2) 说明N 0,G 0,Q g ,Q 0的意义及其影响因素。
8.为细化某纯铝件晶粒,将其冷变形5%后于650℃退火1 h ,组织反而粗化;增大冷变形量至80%,再于650℃退火1 h ,仍然得到粗大晶粒。
试分析其原因,指出上述工艺不合理处,并制定一种合理的晶粒细化工艺。
9.冷拉铜导线在用作架空导线时(要求一定的强度)和电灯花导线(要求韧性好)时,应分别采用什么样的最终热处理工艺才合适?10.试比较去应力退火过程与动态回复过程位错运动有何不同。
从显微组织上如何区分动、静态回复和动、静态再结晶?11.某低碳钢零件要求各向同性,但在热加工后形成比较明显的带状组织。
请提出几种具体方法来减轻或消除在热加工中形成带状组织的因素。
12.为何金属材料经热加工后机械性能较铸造状态为佳?13.灯泡中的钨丝在非常高的温度下工作,故会发生显著的晶粒长大。
当形成横跨灯丝的大晶粒时,灯丝在某些情况下就变得很脆,并会在因加热与冷却时的热膨胀所造成的应力下发生破断。
试找出一种能延长钨丝寿命的方法。
14.Fe-Si钢(Wsi为0.03)中,测量得到MnS粒子的直径为0.4m,每1 mm2的粒子数为2×105个。
计算MnS对这种钢正常热处理时奥氏体晶粒长大的影响(即计算奥氏体晶粒尺寸)。
15.判断下列看法是否正确。
(1) 采用适当的再结晶退火,可以细化金属铸件的晶粒。
(2) 动态再结晶仅发生在热变形状态,因此,室温下变形的金属不会发生动态再结晶。
(3) 多边化使分散分布的位错集中在一起形成位错墙,因位错应力场的叠加,使点阵畸变增大。
(4) 凡是经过冷变形后再结晶退火的金属,晶粒都可得到细化。
(5) 某铝合金的再结晶温度为320℃,说明此合金在320℃以下只能发生回复,而在320℃以上一定发生再结晶。
(6) 20#钢的熔点比纯铁的低,故其再结晶温度也比纯铁的低。
(7) 回复、再结晶及晶粒长大三个过程均是形核及核长大过程,其驱动力均为储存能。
(8) 金属的变形量越大,越容易出现晶界弓出形核机制的再结晶方式。
(9) 晶粒正常长大是大晶粒吞食小晶粒,反常长大是小晶粒吞食大晶粒。
(10) 合金中的第二相粒子一般可阻碍再结晶,但促进晶粒长大。
(11) 再结晶织构是再结晶过程中被保留下来的变形织构。
(12) 当变形量较大、变形较均匀时,再结晶后晶粒易发生正常长大,反之易发生反常长大。
(13) 再结晶是形核—长大过程,所以也是一个相变过程。
<<<<返回察看答案>>>>返回课程>>>>进入讨论区>>>>本站点的和所有权属于王永欣有关此站点的问题请向主讲教师发请用1024×768的分辨率浏览本站所有页面答案1. 可用金相法求再结晶形核率N和长大线速度G。
具体操作:(1) 测定N:把一批经大变形量变形后的试样加热到一定温度(丁)后保温,每隔一定时间t,取出一个试样淬火,把做成的金相样品在显微镜下观察,数得再结晶核心的个数N,得到一组数据(数个)后作N—t图,在N—t曲线上每点的斜率便为此材料在温度丁下保温不同时间时的再结晶形核率N。
(2) 测定G:将(1)中淬火后的一组试样进行金相观察,量每个试样(代表不同保温时间)中最大晶核的线尺寸D,作D—t图,在D—t曲线上每点的斜率便为了温度下保温不同时间时的长大线速度G。
2. 再结晶退火必须用于经冷塑性变形加工的材料,其目的是改善冷变形后材料的组织和性能。
再结晶退火的温度较低,一般都在临界点以下。
若对铸件采用再结晶退火,其组织不会发生相变,也没有形成新晶核的驱动力(如冷变形储存能等),所以不会形成新晶粒,也就不能细化晶粒。
3. 能。
可经过冷变形而后进行再结晶退火的方法。
4. 答案如附表2.5所示。
附表2.5 冷变形金属加热时晶体缺陷的行为5. (1)铜片经完全再结晶后晶粒大小沿片长方向变化示意图如附图2.22所示。
由于铜片宽度不同,退火后晶粒大小也不同。
最窄的一端基本无变形,退火后仍保持原始晶粒尺寸;在较宽处,处于临界变形围,再结晶后晶粒粗大;随宽度增大,变形度增大,退火后晶粒变细,最后达到稳定值。
在最宽处,变形量很大,在局部地区形成变形织构,退火后形成异常大晶粒。
(2)变形越大,冷变形储存能越高,越容易再结晶。
因此,在较低温度退火,在较宽处先发生再结晶。
6. 再结晶终了的晶粒尺寸是指再结晶刚完成但未发生长大时的晶粒尺寸。
若以再结晶晶粒中心点之间的平均距离d 表征再结晶的晶粒大小,则d 与再结晶形核率N 及长大线速度之间有如下近似关系:41][N G k d = 且)exp( )exp(00RT Q G G RT Q N N n n -=-=,由于Qn 与Qg 几乎相等,故退火温度对G /N 比值的影响微弱,即晶粒大小是退火温度的弱函数。
故图中曲线中再结晶终了的晶粒尺寸与退火温度关系不大。
再结晶完成以后,若继续保温,会发生晶粒长大的过程。
对这一过程而言,退火温度越高,(保温时间相同时)退火后晶粒越大。
这是因为晶粒长大过程是通过大角度晶界的移动来进行的。
温度越高,晶界移动的激活能就越低,晶界平均迁移率就越高,晶粒长大速率就越快,在相同保温时间下,退火后的晶粒越粗大,这与前段的分析并不矛盾。
8. 前种工艺,由于铝件变形处于临界变形度下,故退火时可形成个别再结晶核心,最终晶粒极为粗大,而后种工艺,是由于进行再结晶退火时的温度选择不合理(温度过高),若按T再=0.4T 估算,则T再=100℃,故再结晶温度不超过200℃为宜。
由于熔采用630℃退火1 h,故晶粒仍然粗大。
综上分析,在80%变形量条件下,采用150℃退火1 h,则可使其晶粒细化。
9. 前者采用去应力退火(低温退火);后者采用再结晶退火(高温退火)。
10. 去应力退火过程中,位错通过攀移和滑移重新排列,从高能态转变为低能态;动态回复过程中,则是通过螺位错的交滑移和刃位错的攀移,使异号位错相互抵消,保持位错增殖率与位错消失率之间的动态平衡。
从显微组织上观察,静态回复时可见到清晰的亚晶界,静态再结晶时形成等轴晶粒;而动态回复时形成胞状亚结构,动态再结晶时等轴晶中又形成位错缠结胞,比静态再结晶晶粒要细。
11. 一是不在两相区变形;二是减少夹杂元素含量;三是采用高温扩散退火,消除元素偏析。
对已出现带状组织的材料,在单相区加热、正火处理,则可予以消除或改善。
12. 金属材料在热加工过程中经历了动态变形和动态回复及再结晶过程,柱状晶区和粗等轴晶区消失了,代之以较细小的等轴晶粒;原铸锭中许多分散缩孔、微裂纹等由于机械焊合作用而消失,显微偏析也由于压缩和扩散得到一定程度的减弱,故使材料的致密性和力学性能(特别是塑性、韧性)提高。
13. 可以在钨丝中形成弥散、颗粒状的第二相(如ThO 2)以限制晶粒长大。
因为若ThO 2的体积分数为φ,半径为r 时,晶粒的极限尺寸)cos 1(34αϕ+=rR (α为接触角);若选择合适的φ和r ,使R 尽可能小,即晶粒不再长大。
由于晶粒细化将使灯丝脆性大大下降而不易破断,从而有效地延长其寿命。
15.(1)不对。
对于冷变形(较大变形量)后的金属,才能通过适当的再结晶退火细化晶粒。
(2) 不对。
有些金属的再结晶温度低于室温,因此在室温下的变形也是热变形,也会发生动态再结晶。
(3) 不对。
多边化过程中,空位浓度下降、位错重新组合,致使异号位错互相抵消,位错密度下降,使点阵畸变减轻。
(4) 不对。
如果在临界变形度下变形的金属,再结晶退火后,晶粒反而粗化。
(5) 不对。
再结晶不是相变。
因此,它可以在一个较宽的温度围变化。
(6) 不对。
微量熔质原子的存在(20#钢中WC =0.002),会阻碍金属的再结晶,从而提高其再结晶温度。
(7) 不对。
只有再结晶过程才是形核及核长大过程,其驱动力是储存能。
(8) 不对。
金属的冷变形度较小时,相邻晶粒中才易于出现变形不均匀的情况,即位错密度不同,越容易出现晶界弓出形核机制。
(9) 不对。
晶粒正常长大,是在界面曲率作用下发生的均匀长大;反常长大才是大晶粒吞食小晶粒的不均匀长大。
(10) 不对。
合金中的第二相粒子一般可阻碍再结晶,也会阻止晶粒长大。
(11) 不对。
再结晶织构是冷变形金属在再结晶(一次,二次)过程中形成的织构。
它是在形变织构的基础上形成的,有两种情况,一是保持原有形变织构,二是原有形变织构消失,而代之以新的再结晶织构。
(12) 不对。
正常晶粒长大是在再结晶完成后继续加热或保温过程中,晶粒发生均匀长大的过程,而反常晶粒长大是在一定条件下(即再结晶后的晶粒稳定、存在少数有利长大的晶粒和高温加热),继晶粒正常长大后发生的晶粒不均匀长大过程。
(13) 不对。
再结晶虽然是形核—长大过程,但晶体点阵类型并未改变,故不是相变过程。
