Matlab实验指导书(实验六)
实验六 matlab采样定理的建模和验证
页眉内容
实验六
题目:采样定理的建模和验证
实验目的:通过建模与仿真验证采样定理,理解采样定理的物理实质实验要求:学习和回顾采样定理内容,对采样定理作建模和仿真
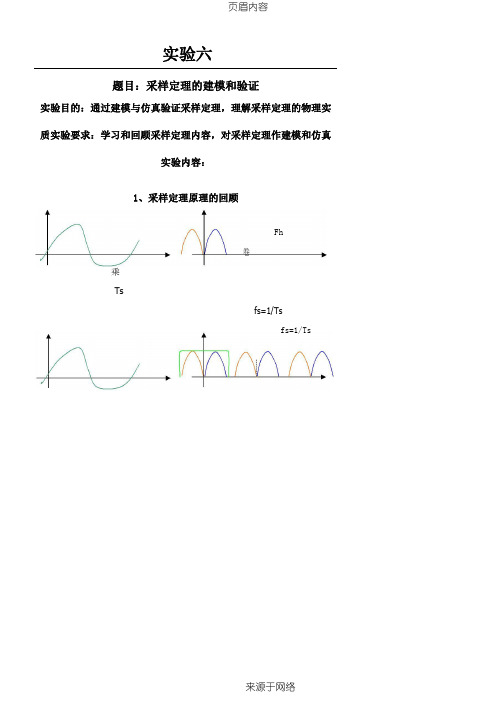
实验内容:
卷
乘
fs=1/Ts
2、建模参数要求:
设计模型,验证采样定理.
设基带波形频谱在 0Hz~200Hz 内. Fh=200Hz(信号最高频率),采样率就应该大于 400Hz 。
用窄脉冲采样,要求窄脉冲宽度是采样周期的 1/10。
从而得到系统仿真步长: 小于等于 1/4000,仿真系统的仿真步长取 1/4000。
采样器用乘法器实现. 而恢复时用低通滤波器实现. 低通滤波器的带宽等于信
号最高频率 Fh,即等于 200Hz.
4、修改基带信号最高频率,如最高频率为200Hz、250Hz 等等,观察采样前后以及恢复的
波形和频谱。
请用实验方法得到频谱混叠后的频谱图和相应的波形。
5. 将被采样信号修改为正弦波、三角波和方波,观察采样前后和恢复非波形和频谱。
实验报告内容和要求:(!!注意每部分得分情况!!)
1.建立采样和恢复模型,说明关键模块的参数设置(30分)
仿真模型建立:
参数设置:
信源与滤波器参数:
2.修改采样率,如采样率为150Hz,200Hz、300Hz等等,观察采样前后以及恢复的波形和频谱。
请用实验方法得到频谱混叠后的频谱图和相应的波形。
(40分)
150Hz:
200Hz:
300Hz:。
matlab实验六

实验六M-文件结构与编写、函数文件格式、编写与调用、程序结构与流程控制一、实验目的:Matlab文件类型及其编写、程序结构、流程控制认识二、实验原理:1、建立M文件将多个可执行的系统命令,用文本编辑器编辑后并存放在后缀为 .m 的文件中,若在MATLAB命令窗口中输入该m-文件的文件名(不跟后缀.m!),即可依次执行该文件中的多个命令。
这个后缀为.m的文件,也称为Matlab的命令文件(Script File)。
注意:文件存放路径必须在Matlab能搜索的范围内。
2、建立函数文件对于一些特殊用户函数,系统提供了一个用于创建用户函数的命令function,以备用户随时调用。
(1).格式:function [输出变量列表]=fun_name(输入变量列表)用户自定义的函数体(2).函数文件名为:fun_name,注意:保存时文件名与函数名最好相同;(3).存储路径:最好在系统的搜索路径上。
(4). 调用方法:输出参量=fun_name (输入变量)例1:计算s = n!,在文本编辑器中输入:function s=pp(n);s=1;for i=1:ns=s*i;ends;在MATLAB命令窗口中输入:s=pp(5)结果为s = 1202、无条件循环当需要无条件重复执行某些命令时,可以使用for循环:for 循环变量t=表达式1 : 达式2 : 表达式3语句体end说明:表达式1为循环初值,表达式2为步长,表达式3为循环终值;当表达式2省略时则默认步长为1;for语句允许嵌套。
例2:如:矩阵输入程序m=input('矩阵行数:m=');n=input('矩阵列数:n=');for i=1:mfor j=1:ndisp(['输入第',num2str(i),'行,第', num2str(j),'列元素'])A(i, j) = input ('')endend生成3×4阶的Hiltber矩阵。
实验六 MATLAB句柄绘图和GUI界面设计

西北农林科技大学实验报告学院名称:理学院专业年级:姓名:学号:课程:数学软件实验报告日期:2014年11月22日实验六MATLAB的句柄绘图与GUI界面设计一、实验目的MATLAB语言的句柄绘图可以对图形的各基本对象进行更为细腻的修饰,能产生更为复杂的图形,而且为动态图形的制作奠定了基础。
本次实验的目的是了解图形的基本结构,掌握图形对象之间的关系,熟悉图形对象属性的获取、设置与修改。
并能初步使用MATLAB 的GUI界面设计进行界面的设计,为将来进行软件开发打好基础。
二.实验要求MATLAB的底层图形修饰方法十分的丰富,通过本次实验,要求能体会句柄图形的概念,熟悉根屏幕、图形窗口、界面控制、界面菜单、轴、线、面、字、块、像等基本图形对象的创建和修改,熟练掌握基本图形对象的属性获取、设置与修改,会利用对象属性修改图形,会创建与修改界面控制与界面菜单。
能根据需要使用消息对话框、警告对话框、输入对话框、提示对话框、列表对话框、进度指示条等。
能初步设计出自己较为满意的GUI图形用户界面。
三.实验内容一、句柄图形的概念句柄图形(Handle Graphics):是一种面向对象的绘图系统。
该系统提供创建计算机图形所必须的各种软件。
它所支持的指令,可直接创建线、文字、网线、面以及图形用户界面。
在MATLAB中的图形系统中,所有的图形操作都是针对图形对象而言的,每个对象从创建时起就被赋予了唯一的标识,这种标识就是该图像的句柄。
1.图形对象MATLAB的图形对象包括计算机屏幕、图形窗口、坐标轴、用户菜单、用户控件、曲线、曲面、文字、图像、光源、区域块和方框等。
系统将每一个对象按树型结构组织起来。
每个具体图形不必包含每个对象,但每个图形必须具备根屏幕和图形窗口。
2.图形对象句柄MATLAB在创建每一个图形对象时,都为该对象分配唯一的一个值,称其为图形对象句柄(Handle)。
句柄是图形对象的唯一标识符,不同对象的句柄不可能重复和混淆。
Matlab实验报告六(三次样条与分段线性插值)范文

本题是给出粗略等分点让你插入更多点用双线性插值法来作出更清晰的山区地貌图。
2.问题求解
x=0:400:2800;
y=0:400:2400;
z=[1430 1450 1470 1320 1280 1200 1080 940;
1450 1480 1500 1550 1510 1430 1300 1200;
2.分段线性插值与计算量与n无关;n越大,误差越小.
3.三次样条插值比分段线性插值更光滑。
4.‘linear’:分段线性插值;‘spline’:三次样条值。
【实验环境】
MatlabR2010b
二、实验内容
问题1对函数 ,x[-5,5],分别用分段线性插值和三次样条插值作插值(其中插值节点不少于20),并分别作出每种插值方法的误差曲线.
本次实验因为是我们课本没有的内容,心理上给了我很大的压力,幸好我们还能根据老师的课件以及例题去掌握这次实验所需要的各种插值法,但结果还好,两道题都做出来了。
plot(x,y,'*',x1,yl,'r',x1,y2,'b')
y0=1./(1+x1.^2);
y3=yl-y0;
y4=ys-y0;
holdon
plot(x1,y3,'y',x1,y4,'g')
3.结果
4误。
问题2山区地貌图在某山区(平面区域(0,2800)(0,2400)内,单位:米)测得一些地点的高程(单位:米)如表1,试作出该山区的地貌图.
1.分析问题
本题先取出少量的插值节点并作出图形,再用分段线性插值法和三次样条插值法做出更精确的图形,最后在作出误差曲线。
matlab实验六报告

实验六MATLAB数据可视化实验者:祝松年级:机设092 学号:09405701002一、实验目的掌握 MATLAB 二维、三维图形绘制,掌握图形属性的设置和图形修饰;掌握图像文件的读取和显示。
二、实验内容(1) 二维图形绘制。
(2) 三维曲线和三维曲面绘制。
(3) 图像文件的读取和显示。
三、实验步骤1 .二维图形绘制(1) 二维图形绘制主要使用函数 plot 。
>>clear all;>> x=linspace(0,2*pi,100);>> y1=sin(x);>> plot(x,y)>> hold on % 保持原有的图形>> y2=cos(x)>> plot(x,y)注: hold on 用于保持图形窗口中原有的图形, hold off 解除保持。
(2) 函数 plot 的参数也可以是矩阵。
>>close all % 关闭所有图形窗口>>x=linspace(0,2*pi,100);>> y1=sin(x);>> y2=cos(x);>> A=[y1 ; y2]'; % 把矩阵转置>> B=[x ; x]'>> plot(B,A)(3) 选用绘图线形和颜色。
>> close all % 关闭所有图形窗口>> plot(x,y1,'g+',x,y2, 'r:')>> grid on % 添加网格线(4) 添加文字标注。
>> title(' 正弦曲线和余弦曲线 ')>> ylabel(' 幅度 ')>> xlabel(' 时间 ')>> legend('sin(x)', 'cos(x)')>> gtext('\leftarrowsinx') % 可用鼠标选择标注的位置,%\leftarrow 产生左箭头,‘\’为转义符(5) 修改坐标轴范围。
MATLAB实验指导书(附答案)

MATLAB基础实验指导书漳州师范学院物电系2010年10月目录实验一MATLAB环境的熟悉与基本运算 (2)实验二MATLAB数值运算 (8)实验三MATLAB语言的程序设计 (12)实验四MATLAB的图形绘制 (16)实验五采用SIMULINK的系统仿真 (20)实验六MATLAB在电路中的应用 (25)实验七MATLAB在信号与系统中的应用 (27)实验八MATLAB在控制理论中的应用 (29)实验一 MATLAB环境的熟悉与基本运算一、实验目的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识:1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质内涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
Matlab实验报告六(三次样条与分段线性插值)

实验名称插值与拟合
所属课程数学软件与实验
实验类型综合型实验
专业信息与计算科学
班级
学号
姓名
指导教师
一、实验概述
【实验目的】
学会在matlab环境下使用几种不同的插值法和拟合两种方法构造函数依据已经知道的某些特殊点来推测实际问题中需要知道但又不便于测量出来的量。
【实验原理】
1.z=interp2(x0,y0,z0,x,y,’method’): 要求x0,y0单调;x, y可取为矩阵, 或x取行向量, y取为列向量, x,y的值分别不能超出x0,y0的范围。
2.分段线性插值与计算量与n无关;n越大, 误差越小.
3.三次样条插值比分段线性插值更光滑。
4.‘linear’ : 分段线性插值;‘spline’ : 三次样条
二、实验内容
问题1 对函数, x([-5,5], 分别用分段线性插值和三次样条插值作插值(其中插值节点不少于20), 并分别作出每种插值方法的误差曲线.
1180 1320 1450 1420 1400 1300 700 900];
mesh(x,y,z)
xi=0:20:2800;
yi=0:20:2400;
zi=interp2(x,y,z,xi',yi,'cubic');
mesh(xi,yi,zi)
3.结果
4.结论及分析
通过实验,结果正确,分析无误。
三、实验小结
1270 1500 1200 1100 1350 1450 1200 1150
1230 1390 1500 1500 1400 900 1100 1060
1180 1320 1450 1420 1400 1300 700 900
实验六、利用MATLAB计算复变函数在孤立奇点处的留数及进行复积分

实验六、利用MATLAB 计算复变函数在孤立奇点处的留数及进行复积分计算一、本实验教学的作用:熟悉MATLAB 基本命令与操作,利用MATLAB 计算复变函数在孤立奇点处的留数;利用MATLAB 计算围线积分。
通过实验具体操作,培养学生综合实践能力。
二、本实验教学目的及学生能力标准:会利用MATLAB 计算复变函数在孤立奇点处的留数;会利用MATLAB 计算围线积分。
三、实验内容:四、相关知识1.在孤立起点处的留数----通过求极限的方法计算留数假设已知奇点α和重数m 则用下面的MATLAB 语句求出相应的留数B=limit(F*(z-α),z, α) 单奇点B=limit(F*(z-α)*m ,z,m -1)/prod(1:m-1),z,α m 重奇点例1 计算z e z z z z f 23)3cos()1(1)(-+-=π在孤立起点处的留数 解 函数)(z f 在0=z 是三重奇点,在1=z 是简单奇点>>syms z>>f=cos(z+pi/3)*exp(-2*z)/z^3*(z-1);>>limit(diff(f*z^3,z,2)/prod(1;2),z,0);>> limit((f*(z-1),z,1)ans=-1/4-1/2*3^(1/2)1/2*exp(-2)*cos(1)-1/2*3^(1/2)*exp(-2)*sin(1)学生练习1 计算z e z z z z f 23)3sin()1(1)(-+-=π在孤立起点处的留数 提示 函数)(z f 在0=z 是三重奇点,在1=z 是简单奇点>>syms z;>>f=sin(z+pi/3)*exp(-2*z)/z^3*(z-1);>>limit(diff(f*z^3,z,2)/prod(1;2),z,0);>> limit((f*(z-1),z,1)ans=-1/4*3^(1/2)+1/2-1/2*exp(-2)*sin(1)+1/2*3^(1/2)*exp(-2)*cos(1)例2 计算3542)(zz i z z f ++=在孤立起点处的留数 解 函数)(z f 在0=z 是三重奇点,在i i z 2,2-=是简单奇点>>syms z;>>f= (z+2*i3) /z^5+z^3);>>limit(diff(f*z^3,z,2)/prod(1;2),z,0);>> limit((f*(z-2*i),z,2i)>> limit((f*(z+2*i),z,-2i)ans=i/8-i/8例3 计算函数1)(2-=z e z f z在∞=z 处的留数 解 函数)(z f 在扩充复平面有三个极点:∞-=,1,1z>>syms z>>z1=exp(z)/(z^2-1);>>B1=limit(z1*(z-1),z,1)>>B2=limit(z1*(z+1),z,-1)>>B=B1+B2ansB1=1/2*exp(1)B2=-1/2*exp(-1)B=1/2*exp(1)-1/2*expp(-1)学生练习2 计算函数4sin )(zz z z f +=在0=z 处的留数 提示 函数)(z f 在0=z 是四重奇点>>syms z;>>f= (sin(z)+z)/z^4;>>limit(diff(f*z^4,z,3)/prod(1;3),z,0);ans=-1/6学生练习3 计算下列函数在奇点处的留数:(1) z z z 212-+ (2)14-z z 解 在Matlab 命令窗口键入:>> [r1,p1,k1]=residue([1,1],[1,-2,0])r1 =1.5000-0.5000p1 =2k1 =[ ]>> [r2,p2,k2]=residue([1 0],[1 0 0 0 -1])r2 =0.25000.2500-0.2500 + 0.0000i-0.2500 - 0.0000ip2 =-1.00001.00000.0000 + 1.0000i0.0000 - 1.0000ik2 =[ ]反之:>> [B,A]=residue([0.2500 0.2500 -0.2500 -0.2500],[-1 1 i -i],[])B =0 0 1 0A =1 0 0 0 -12.求积分2.1 非闭合路径的积分非闭合路径的积分,用函数int 求解,方法同微积分部分的积分。
MATLAB程序设计实验指导书

MATLAB程序设计实验指导书MATLAB是集数值计算、符号运算及图形处理等强大功能于一体的科学计算语言。
作为强大的科学计算平台,它几乎能满足所有的计算需求。
在美国及其他发达国家的理工科院校里,MATLAB已经作为一门必修的课程;在科研院所、大型公司或企业的工程计算部门,MATLAB也是最普遍的计算工具之一。
有鉴于此,我院开设了《MATLAB程序设计》这门课程,它需要一定的理论基础,同时又具有很强的实践性。
如何加强理论课程的学习、加深学生对本课程中的基本理论知识及基本方法的理解,如何培养学生实践动手能力是教学的当务之急。
而MATLAB程序设计实验课程就是一种重要的教学手段和途径。
实验将MATLAB程序设计的基本方法灵活地运用在数学、电路等课程中,重点突出,内容丰富。
同时,注重理论分析与实际动手相结合,以理论指导实践,以实践验证基本原理,旨在提高学生分析问题、解决问题的能力及动手能力,使学生进一步巩固基本理论知识,建立比较全面的MATLAB程序设计的概念。
实验注意事项1、实验系统接通电源前请确保电源插座接地良好。
2、完成实验后请确保关闭电脑电源及插座电源。
实验一 矩阵及其运算一、实验目的1、熟悉MATLAB 工作环境2、掌握矩阵和数组的创建、寻访和运算 二、实验内容验证欧姆定律:iur ,其中i u r , ,分别是电阻(欧姆)、电压(伏特)、电流(安培)。
已知u=[0.89, 1.20, 3.09, 4.27, 3.62, 7.71, 8.99, 7.92, 9.70, 10.41],i=[0.028, 0.040, 0.100, 0.145, 0.118, 0.258, 0.299, 0.257, 0.308, 0.345]。
三、实验器材PC 机 (装有 MA TLAB 软件 ) 1台 四、实验原理 4.1 Desktop 简介MATLAB R2006a 版的Desktop 操作桌面,是一个高度集成的MATLAB 工作界面。
matlab实验六
自动控制原理课程验证性实验报告
实验名称
六、基于matlab控制系统的根轨迹及其性能分析
实验时间
年日
学生姓名
牛景坤
实验地点
同组人员
专业班级
电技1001B
1、实验目的:
1、熟练掌握使用MATLAB绘制控制系统零极点图和根轨迹图的方法
2、学会分析控制系统根轨迹的一般规律
3、利用根轨迹图进行系统性能分析
2)在根轨迹图上标注分离点和临街开环增益对应的点,显示相关的性能指标。
3)在根轨迹图上各区段取点,使用rlocfind()命令分别在ζ=0,0.25,0.7,1,1.2处,得到相应的开环增益K和闭环极点r,由这两组参量写出系统闭环传递函数,分别绘制其对应系统的阶跃响应曲线,记录系统性能指标,并比较分析。将数据填入实验数据记录表格中
6)偶极子及其处理。如果零、极点之间的距离比它们本身的模值小一个数量级,则她们就构成偶极子。原理原点的偶极子其影响可忽略,反之必须考虑。
7)主导极点。在S平面上,最靠近虚轴而附近又无闭环零点的一些闭环极点,对系统性能影响最大,成为主导极点。凡是比主导极点的实部打3-6倍以上的其他闭环零、极点,其影响课忽略
(4)研究闭环零点、极点对系统性能的影响
范例4.3已知一负反馈系统的开环传递函数为G(s)H(s)=k(s+3)/s(s+2)
(1)绘制其根轨迹图,确定根轨迹分离点及相应增益K,临界增益K
(2)确定系统呈现欠阻尼状态的开环增益范围。
解:当系统呈现欠阻尼状态时,对应的闭环极点应该处于实轴上的两分离点之间的根轨迹上,从根轨迹图上可以测到欠阻尼状态时的开环增益范围为0.539<k<7.45
Matlab实验指导书河北大学(郑晓昆)

Matlab实验指导书河北大学电子信息工程学院2004年1月目录MATLAB实验教学计划 (2)实验一MATLAB基本操作 (3)实验二MATLAB图形系统 (5)实验三MATLAB程序设计 (6)实验四MATLAB基本应用领域 (7)实验五设计性综合实验1---数字信道编译码 (14)实验六设计性综合实验2---fir滤波器设计 (16)MATLAB实验教学计划指导教师:郑晓昆薛文玲王竹毅学时数:12学时周4学时2次实验,共3周6次实验,第7—9教学周,每次实验2学时所用仪器设备:MATLAB7.0实验软件系统实验指导书:Matlab实验指导书自编实验参考书:<MATLAB7.X程序设计语言>, 楼顺天等编著,西安电子科大出版社,06年5月第二版实验项目:A, MATLAB基本操作内容:矩阵操作,基本数学函数,逻辑函数操作等;要求:循序渐进完成P83练习题1—10B, MATLAB图形系统内容:图形绘制,图形标注,对数和极坐标,坐标轴控制,颜色控制等要求:循序渐进完成P146练习题1—10C, MATLAB程序设计内容:脚本script和函数function认识,流程控制,参数交互输入,基本程序设计技巧练习,程序调试DEBUG等要求:循序渐进完成P184练习题1—10D, MATLAB基本应用领域内容:线性代数,多项式与内插,曲线拟合,数据分析与统计,泛函基础等要求:循序渐进完成P146练习题1—4,6—19E, 设计性综合实验----数字信道编译码内容:1数字通信系统信道编码AMI编译码2数字通信系统信道编码HDB3编译码F,设计性综合实验----fir滤波器设计内容:设计一个由县冲击相应数字滤波器FIR是该滤波器能够滤出规定频率以上的信号,而该频率以下的信号不受影响。
实验一MATLAB基本操作实验目的熟悉MATLAB的使用方法及特点;学会建立MATLAB搜索路径;熟悉MATLAB工作空间、MATLAB集成环境、命令窗口;掌握MATLAB的通用命令、管理命令和函数、管理变量和工作空间的使用方法;掌握MATLAB基本操作及矩阵基础知识,包括:输入矩阵、矩阵的转置、矩阵元素求和、矩阵下际、矩阵连接、矩阵行列删除、矩阵产生和操作、逻辑和关系运算、操作符和特殊字符、基本矩阵和矩阵操作、基本矩阵和阵列;掌握特殊变量和常数;掌握基本数学函数。
《MATLAB程序设计》实验指导书

三、
实验仪器和设备
1、 计算机一台。 2、 MATLAB7.0 以上集成环境。
四、
预习要求
2
《MATLAB 程序设计》实验指导书
1、 复习 MATLAB 的启动与Байду номын сангаас出,熟悉 MATLAB 运行环境。 2、 复习 MATLAB 中矩阵的生成以及矩阵运算的基本原理。
五、
实验内容及步骤
实验内容:
1、 求下列表达式的值 1) z1
5
《MATLAB 程序设计》实验指导书
2) 函数调用 函数文件编制好后,就可调用函数进行计算了。函数调用的一般格式为 [输出实参表]=函数名(输入实参表) 注意:函数调用时各实参出现的顺序、个数,应与函数定义时形参的顺序、个 数一致,否则会出错。函数调用时,实参先传递给形参,然后再执行函数功能。 5、 选择结构 1) if 语句 a) 单分支 if 语句 if 条件 语句块 end b) 双分支 if 语句 if 条件 语句块 1 else 语句块 2 end c) 多分支 if 语句 if 条件 1 语句块 1 elseif 条件 2 语句块 2 …… elseif 条件 n 语句块 n else 语句块 n+1 end 2) switch 语句 switch 表达式 case 结果表 1 语句块 1 case 结果表 2 语句块 2 ……
二、
实验原理
1、 M 文件 用 MATLAB 语言编写的程序,称为 M 文件,它们的扩展名均为.m。M 文件根据 调用方式的不同分为两类,命令文件(Script file)和函数文件(Function file) 。 2、 建立新的 M 文件 启动 MATLAB 文本编辑器有 3 种方法: 1) 单击工具栏上的“New M-File”命令按钮。 2) 从 MATLAB 主窗口的“File”菜单中选择“New”菜单项,再选择“M-file”命令。 3) 在 MATLAB 命令窗口输入命令“edit”。 3、 打开已有的 M 文件 1) 在当前目录窗口选中要打开的 M 文件,双击鼠标左键。 2) 单击 MATLAB 主窗口工具栏上的“Open File”命令按钮,再从弹出的对话框中 选择所需打开的 M 文件。 3) 从 MATLAB 主窗口的“File”菜单中选择“Open”命令,在“Open”对话框中选中 所需打开的文件。 4) 在 MATLAB 命令窗口输入命令“edit 文件名” 。 4、 函数文件 1) 函数文件的基本结构 函数文件由 function 语句引导,其基本结构为: function 输出形参表=函数名(输入形参表) 注释说明部分 函数体语句 注意:函数名的命名规则与变量名相同。当输出形参多于一个时,应用方括号 括起来。
MATLAB实验报告实验六

MATLAB实验报告实验六实验六1.x=linspace(0,2*pi,101);y=(0.5+3*sin(x)./(1+x.^2));plot(x,y)2.x=-pi:pi/100:pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;plot(x,y1,'r:',x,y2,'g-',x,y3,'b--')x=-pi:pi/100:pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;subplot(1,3,1);plot(x,y1,'r:');title('y1=x.^2'); subplot(1,3,2);plot(x,y2,'g-');title('y2=cos(2*x)'); subplot(1,3,3);plot(x,y1,'b--');title('y3=y1.*y2');x=-pi:pi/100:pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;subplot(2,2,1);plot(x,y1,'r:',x,y2,'g-',x,y3,'b--'); subplot(2,2,2);bar(x,y1,'r');title('y1=x^2');subplot(2,2,3);bar(x,y2,'g');title('y2=cos(2*x)');subplot(2,2,4);bar(x,y3,'b');title('y3=y1.*y2');x=-pi:pi/100:pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;subplot(2,2,1);plot(x,y1,'r:',x,y2,'g-',x,y3,'b--'); subplot(2,2,2); stairs(x,y1,'r:');title('y1=x^2');subplot(2,2,3);stairs(x,y2,'g-');title('y2=cos(2*x)');subplot(2,2,4);stairs(x,y3,'b--');title('y3=y1.*y2');x=-pi:pi/100:pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;subplot(2,2,1);plot(x,y1,'r:',x,y2,'g-',x,y3,'b--'); subplot(2,2,2); stem(x,y1,'r:');title('y1=x^2');subplot(2,2,3);stem(x,y2,'g-');title('y2=cos(2*x)');subplot(2,2,4);stem(x,y3,'b--');title('y3=y1.*y2');x=-pi:pi/100:pi;y1=x.^2;y2=cos(2*x);y3=y1.*y2;subplot(2,2,1);plot(x,y1,'r:',x,y2,'g-',x,y3,'b--'); subplot(2,2,2);fill(x,y1,'r:');title('y1=x^2');subplot(2,2,3);fill(x,y2,'g-');title('y2=cos(2*x)');subplot(2,2,4);fill(x,y3,'b--');title('y3=y1.*y2');3.x=-5:0.01:5;y=(x+sqrt(pi))./(exp(2)).*(x<=0)+0.5*log(x+sqrt(1+x.*x)).*(x>0); plot(x,y4.theta=0:pi/100:2*pi; a=input('请输⼊a:');b=input('请输⼊b:');n=input('请输⼊n:'); rho=a*sin(b+n*theta); polar(theta,rho,'g')a=b=n=2a=b=2,n=4a=n=2,b=4a=4,b=n=2采⽤控制变量法的办法,固定两个参数,变动第三个参数观察输出图象的变化。
MATLAB-第六次实验

x、y、z 都是矩阵时,plot3 命令的使用
[X,Y]=meshgrid(-pi:0.1:pi); Z=sin(X)+cos(Y); plot3(X,Y,Z)
MATLAB基础
5.4 三维图形绘制与复数的图形绘制
g.绘制三维圆柱曲面命令cylinder
cylinder命令中,柱面的轴线定义为 z 轴,只要给出母线的描述就可完成一个柱面。 调用格式为: [X,Y,Z] = cylinder(R,N); [X,Y,Z] = cylinder(R):缺省值 N=20; [X,Y,Z] = cylinder:缺省值 N=20,R=[1,1]。 R:是一描述柱面母线的向量; N:是旋转柱面上的分割线条数;
MATLAB基础
已知系统传递函数
n Y(S) 100 G(S) 2 2 X(S) S 10 S 100 S 2 n S n 2
2
,其中:
0.5 n 10rad / s
在输入信号x(t)=1(即单位阶跃信号),要求建立M文件,画出输出 信号y(t)(即单位阶跃响应)的图象, MATLAB程序如下: G=tf([100],[1,10,100]); %得到传递函数G(S) t=0:0.05:3; %时间t设在0—3秒间,运算间隔0.05秒 y=step(G,t); %得到单位阶跃响应y(t) plot(t,y,'-k'); %绘制出y(t) 图象 xlabel('t'); %横坐标轴标号为t ylabel('y(t)'); %纵坐标轴标号为y(t) grid %绘制出栅格以便于读取数值
MATLAB基础
计算积分
7
int(f,v,a,b): 计算定积分 int(f,a,b): 计算关于默认变量的定积分 int(f,v): 计算不定积分 int(f): 计算关于默认变量的不定积分
软件技术(MATLAB)实验手册

实验课需要我们干什么?一、实验课前的知识点预习。
二、准备实验课要演练的例题。
三、实验课后的总结。
MA TLAB实验一MA TLAB软件环境一、实验目标1.熟悉MA TLAB软件的运行环境以及界面构成。
2.熟悉MA TLAB环境中命令窗口的基本操作。
3.熟悉变量的相关操作。
4.熟悉MA TLAB中基本运算函数。
二、实验内容及要求1.运行MA TLAB软件,观察MA TLAB的界面组成。
并了解各个部分的功能。
(标题栏+菜单栏+工具栏+命令窗口+历史命令窗口+当前目录窗口+工作空间)。
2.命令窗口主要用于进行MA TLAB的各种命令操作。
在该窗口中,可以运行MA TLAB的指令、函数、表达式以及显示除了图形外的所有运行结果。
3.变量的赋值以及引用。
4.MA TLAB基本运算函数的演练。
三、实验步骤(略)四、训练习题1.书上所有例题和课后习题。
2.ppt上的学生演练习题。
五、测试习题1.x=2;MA TLAB实验二深入学习MA TLAB环境设置一、实验目标1.熟悉MA TLAB软件环境设置(包括搜索路径和工作空间等设置)。
2.熟悉变量的存储与读取操作。
3.熟悉.m文件。
二、实验内容及要求1.查找和设置搜索路径,并且测试。
2.在工作空间中对变量进行各种操作。
3.使用save和load命令存储与读取变量。
4.区分.m文件中的命令文件和函数文件。
三、实验步骤(略)四、训练习题1.如何设置和更改matlab的初始化当前目录?2.演练课本中对应章节的例子。
3.独立完成课堂布置的实验作业:add.m 和diaoyongjiafa.m文件。
4.测试并体验.m文件的两大分类的区别和相似。
发现并解决.m文件中的若干问题(函数文件中是否可以定义多个函数?主函数子函数可以互相调用么?外部函数可以调用子函数么?子函数可以调用其他函数么?)。
五、测试习题1.精度计算的问题。
看如下的代码,分析:x=0;for n=1:82x=x+0.01endx==0.82MA TLAB实验三MA TLAB编程基础一、实验目标2.熟悉MA TLAB三大程序结构。
《MATLAB仿真技术》实验指导书2016附问题详解

实验项目及学时安排实验一 MATLAB环境的熟悉与基本运算 2学时实验二 MATLAB数值计算实验 2学时实验三 MATLAB数组应用实验 2学时实验四 MATLAB符号计算实验 2学时实验五 MATLAB的图形绘制实验 2学时实验六 MATLAB的程序设计实验 2学时实验七 MATLAB工具箱Simulink的应用实验 2学时实验八 MATLAB图形用户接口GUI的应用实验 2学时实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、 exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
福州大学MATLAB基础实验指导书

实验一 MATLAB 基础知识一、实验目的1.熟练掌握Matlab 的启动与退出;2. 熟悉Matalb 的命令窗口,常用命令和帮助系统;3. 熟悉Matalb 的数据类型;4. 熟悉Matlab 的基本矩阵操作,运算符和字符串处理二、实验设备1.方正电脑 2.MATLAB 软件三、实验内容1. 已知矩阵A=[3 4 -1 1 -9 10;6 5 0 7 4 -16;1 -4 7 -1 6 -8;2 -4 5 -6 12 -8;-3 6 -7 8 -1 1;8 -4 9 1 3 0] 写出完成下列操作的命令:(1) 将矩阵A 的第2-5行中第1,3,5列元素赋给矩阵B ; (2) 删除矩阵A 的第7号元素; (3) 将矩阵A 的每个元素加上30; (4) 求矩阵A 的大小和维数;(5) 将矩阵A 的右下角3*2矩阵构成矩阵C ; (6) 输出[-5,5]范围内的所有元素; 2. 设x=-74o ,y=27 o ,22的值。
3. 当a 取,,,…,,,时,求0.3sin(0.3)ae a -+在各点的函数值。
4. 已知3542126734457,2874879015930A B -⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦求下列表达式的值:(1) A*B 和A.*B (2) A^3和A.^3 (3) A/B 和B\A(4) [A,B]和[A([1,3]);B^2]5. 设a=1+2i,b=-3+4i,6ic e π=,求abc a b++的值。
实验二 MATLAB 程序设计1.学会编写简单函数m 文件,调用及调试函数m 文件; 2.学会MATLAB 的简单程序编写。
二、实验设备1.方正电脑 2.MATLAB 软件三、实验内容1.从键盘输入一个4位整数,按如下规则加密后输出。
加密规则:每位数字都加上7,然后用和除以10的余数取代该数字;然后将第1位数与第3位数交换,第2位数与第4位数交换。
2. 硅谷公司员工的工资计算方法如下:(1) 工作时数超过120h 者,超过部分加发15%; (2) 工作时数低于60h 者,扣发700元; (3) 其余按每小时84元计发。
matlab实验 三维画图

实验(六)项目名称:三维绘图一、实验目的:熟悉MATLAB中几个常用的绘图命令,掌握集中常见三维图形的画法。
二、实验原理三维绘图命令:Plot(X,Y,Z)//曲线;mesh(X,Y,Z)//网状;surf(X,Y,Z)//表面;contour(X,Y,Z)//等高线。
三、实验环境1.硬件:PC机2. 软件:Windows操作系统、matlab2015四、实验内容、步骤以及结果4.1.1实验要求:用plot函数画出的三维曲线。
4.1.2实验步骤(1)启动matlab,新建一个M文件;(2)输入程序,如图1;(3)保存文件;(4)编译源程序,观察屏幕上显示的编译信息,修改出现的错误,直到编译成功;图1:plot函数画三维曲线4.1.3运行结果如下:图2:三维曲线4.2.1实验要求:用mesh函数画出的三维网状图。
4.2.2实验步骤(5)启动matlab,新建一个M文件;(6)输入程序,如图3;(7)保存文件;(8)编译源程序,查看运行结果,如图4。
图3:mesh函数画三维网状图图4:运行结果4.3.1实验要求:用surf函数画出的三维表面图。
4.3.2实验步骤(9)启动matlab,新建一个M文件;(10)输入程序,如图5;(11)保存文件;(12)编译源程序,查看运行结果,如图6。
图5:surf函数画三维表面图图6:运行结果4.3.1实验要求:用contour函数画出的等高线图。
4.3.2实验步骤(13)启动matlab,新建一个M文件;(14)输入程序,如图7;(15)保存文件;(16)编译源程序,查看运行结果,如图8。
图7:contour函数画等高线图8:运行结果五、实验总结MATLAB具有强大的图形功能,能够将它们直观的表现出来,解决很多的问题。
MATLAB实验六(精品)

第二节 逐点比较法逐点比较法的基本原理是,在刀具按要求轨迹运动加工零件轮廓的过程中,不断比较刀具与被加工零件轮廓之间的相对位置,并根据比较结果决定下一步的进给方向,使刀具沿着坐标轴向减小偏差的方向进给,且只有一个方向的进给。
也就是说,逐点比较法每一步均要比较加工点瞬时坐标与规定零件轮廓之间的距离,依此决定下一步的走向,如果加工点走到轮廓外面去了,则下一步要朝着轮廓内部走;如果加工点处在轮廓的内部, 则下一步要向轮廓外面走,以缩小偏差,周而复始,直至全部结束,从而获得一个非常接近于数控加工程序规定轮廓的刀具中心轨迹。
逐点比较法既可实现直线插补,也可实现圆弧插补。
其特点是运算简单直观,插补过程的最大误差不超过一个脉冲当量,输出脉冲均匀,而且输出脉冲速度变化小,调节方便,但不易实现两坐标以上的联动插补。
因此,在两坐标数控机床中应用较为普遍。
一般来讲,逐点比较法插补过程每一步都要经过如图3-1所示的四个工作节拍:(1)偏差判别 判别刀具当前位置相对于给定轮廓的偏差情况,即通过偏差值符号确定加工点处在理想轮廓的哪一侧,并以此决定刀具进给方向。
(2)坐标进给 根据偏差判别结果,控制相应坐标轴进给一步,使加工点向理想轮廓靠拢,从而减小其间的偏差。
(3)偏差计算 刀具进给一步后,针对新的加工点计算出能反映其偏离理想轮廓的新偏差,为下一步偏差判别提供依据。
(4)终点判别 每进给一步后都要判别刀具是否达到被加工零件轮廓的终点,若到达了则结束插补,否则继续重复上述四个节拍的工作,直至终点为止。
一、逐点比较法I 象限直线插补(一)基本原理设第一象限直线OE ,起点为坐标原点O(0,0),终点为E (X e ,Y e ),另有一个动点为N (X i ,Y i ),如图3-2所示。
其中,各个坐标值均是以脉冲当量为单位的整数,以便于后面的推导与讲解,并且在脉冲增量式插补算法中都是这样约定的。
ee i i X Y X Y = (3-1a ) 即 X e Y i —X i Y e =0 (3-1b ) 当动点N 处于直线OE 的下方N ′处时,直线N O '的斜率小于直线OE 的斜率,从而有ii X Y <e e X Y (3-2a )即 X e Y i —X i Y e <0 (3-2b ) 当动点N 处于直线OE 的上方N ″处时,直线N O ''的斜率大于直线OE 的斜率,从而有ee i i X Y X Y > (3-3a ) 即 X e Y i —X i Y e >0 (3-3b ) 由上述关系可以看出,表达式(X e Y i —X i Y e )的符号就能反映出动点N 相对直线OE 的偏离情况,为此取偏差函数F 为F =X e Y i —X i Y e (3-4)根据上述过程可以概括出如下关系:当F =0时,动点N (X i ,Y i )正好处在直线OE 上;当F >0时,动点N (X i ,Y i )落在直线OE 上方区域;当F <0时,动点N (X i ,Y i )落在直线OE 下方区域。
Matlab实验指导书(1-10完整)

1.初次接触 Matlab 应该注意函数表达式的文本式描述。 2.在使用图形函数计算器 funtool 时,注意观察 1 号和 2 号窗口中函数的图形。
四、实验报告要求
1.针对图形函数计算器 funtool,对每一类型计算记录其中一个图形的曲线。 2.书写实验报告时要结构合理,层次分明,在分析描述的时候,需要注意语言的
⎪⎪⎨⎪−x12+x11+4
x2 x2
− 7x3 − 7x3
−15x4 + 12 x4
− 6x5 = 294 − x5 = −441
⎪⎩6x1 +11x2 +11x3 − 9x4 −13x5 = 103
3.用网孔电流法求如下电路的各支路电流。
Ia
Ib
Id
Ic
60Ω
20Ω
40Ω
40Ω
50V
10V
40V
流畅。
《Matlab 语言及其在电子信息科学中的应用》实验指导书
许钢 编
3
实验二:M 文件和 Mat 文件操作
一、实验目的
1.定制自己的工作环境。 2.编写简单的 M 文件。 3.保存内存工作区中的变量到.mat 文件。 4.学会只用 Matlab 帮助。
二、实验内容
1.使用 format 命令和 File|Peferences 菜单定制自己的工作环境。 2.编写如下 M 文件,试调整参数 a 的大小,观察并记录 y1、y2 的波形特征。
《Matlab 语言及其在电子信息科学中的应用》实验指导书
许钢 编
4.用结点电压法求如下电路的结点电压 un1、un2。
① + u2 - ②
2kΩ
10A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB实验指导书编著:李新平二零零八年三月十四日实验六、数据插值和数据拟合6.1 实验目的1)掌握用 MA TLAB 计算拉格朗日、分段线性、三次样条三种插值的方法,改变节点 的数目,对三种插值结果进行初步分析。
2)掌握用 MA TLAB 进行多项式最小二乘拟合,会选择合适的函数及转化为线性函数。
3)通过实例学习用数据插值和数据拟合解决实际问题。
6.2 分段线性插值设给定一元未知函数 ) (x f y = 的 1 + n 个结点的数据 b x x a n = < < = L 0 对应的函数 值 n y y , , 0 L ,根据这些结点数据求其余 ) ( i j x j ¹ 点的函数值 j y ,可将相邻两个节点之间用 直线连接起来,如此形成的一条折线(见右图)构成的分段线性函数 ) (x I n 来近似表示未知函 数 ) (x f ,从而解决该插值问题的方法就称为分段线性插值。
可用如下公式表示:)( ) ( ) ( 0x f x l y x I nj j j n » = å = 其余, 0 , , ) ( 1111 1 1+ + + - - - £ £ - - £ £ - - ï ï îï ï íì= j j j j j jj j j j j x x x x x x x x x x x x x x x l 可用 MA TLAB 命令 y=interp1(x0,y0,x)来实现, 其中参数 x0 为给定结点数据的横坐标向 量,参数 y0 为 x0 对应的函数值,参数 x 为要未知结点的横坐标向量,函数返回值 y 为参数 x 根据分段线性插值得到的函数值。
【例】插值求在[0,15]区间内步长为 0.1 的机床加工数据:>>x0=[0 3 5 7 9 11 12 13 14 15]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];>>x=0:0.1:15; % 插值点>>y=inpert1(x0, y0, x) % 插值求得函数值6.3 拉格朗日插值设未知函数 ) (x g y = 是n 次多项式,给定该n 次多项式 1 + n 个结点的数据 ),, {( i i y x , } , , 0 n i L = 根据这些结点数据求其余 ) ( i j x j ¹ 点的函数值 j y ,可考虑如下构造:) ( ) () ( 0 x g x l y x L ni i i n » = å = )( ) )( ( ) ( )( ) )( ( ) ( ) (1 1 0 1 1 0 n i i i i i i n i i i x x x x x x x x x x x x x x x x x l - - - - - - - - = + - + - L L L L 来近似表示n 次多项式 ) (x g ,从而解决该插值问题的方法就称为拉格朗日插值。
用 MATLAB 进行拉格朗日插值,要编写拉格朗日插值函数 m 文件,如 lagr1.m ,其函 数调用形式为 y=lagr1(x0,y0,x),其参数形式和函数返回值与分段线性插值相同。
【例】插值求在[0,15]区间内步长为 0.1 的机床加工数据:>>x0=[0 3 5 7 9 11 12 13 14 15]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];>>x=0:0.1:15; % 插值点>>y=lagr1(x0, y0, x) % 插值求得函数值6.4 三次样条插值设给定一元未知函数 ) (x h y = 的 1 + n 个结点的数据 } , , 0 ), , {( n i y x i i L = ,根据这些结 点数据求其余 ) ( i j x j ¹ 点的函数值 j y ,可考虑做如下近似构造 ) ( ) ( x h x S » :(1) 在每个小区间 ] , [ 1 i i x x - 上都是 3 次多项式, 即 i i i i i d x c x b x a x s + + + = 23) ( ; (2) i i y x S = ) ( , n i , ,0L = ; (3) ) (x S 在 n x x x £ £ 0 上的二阶导数连续, 即 ) ( ) ( 1 i i i i x s x s + = , ) ( ' ) ( ' 1 i i i i x s x s + = ,)( " ) ( " 1 i i i i x s x s + = ; 在 MA TLAB 中可以采用函数 y=interp1(x0,y0,x,’spline’)或 y=spline(x0,y0,x)来实现, 参数 形式和函数返回值跟分段线性插值和拉格朗日插值相同。
【例】插值求在[0,15]区间内步长为 0.1 的机床加工数据:>>x0=[0 3 5 7 9 11 12 13 14 15]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6]; >>x=0:0.1:15; % 插值点>>y=interp1(x0, y0, x,’spline’) % 或 y=spline(x0, y0, x)6.5 多项式最小二乘数拟合为了估计指定函数(如 x a a y 1 0 + = , 22 1 0 x a x a a y + + = , xa a y 1 0 += , xa e a y 1 0 = 等) 函数的参数, 从而确定该函数, 即作参数估计求得该函数, 可用先将以上函数转化了以 1 0 ,a a 为自变量的线性函数,再将给定的 1 + n 个结点数据 } , , 0 ),, {( n i y x i i L = 代入线性函数,求解非齐次线性方程组 Y XA = ,使距离 i d 的平方和最小的解 Ta a A ) , ( 1 0 = 即为所求参数。
该 方法就称为线性最小二乘拟合。
在 MA TLAB 中可用函数 aa=ployfit(x,y,n)来求得参数a , 从而实现线性最小二乘拟合(当 然也可以实现多项式函数拟合),其中参数 x 为给定结点数据的横坐标向量,y 为对应的纵 坐标向量,n 为多项式的次数(如线性拟合则 n 为 1,二次多项式拟合为 2 等),函数返回值 aa 为拟合的多项式系数。
在求得多项式系数后,为了求得多项式的值,可用 MA TLAB 函数 y=polyval(aa,x)求得 系数为 aa 的多项式在指定点 x 的函数值 y 。
【例】用多项式最小二乘拟合求电阻R 与温度t 之间的关系 b at R + = : >>t=[20.5 32.5 51 73 95.7]; r=[765 826 873 942 1032]; >>aa=polyfit(t,r ,1); % 插值点>>a=aa(1) % 插值求得一次项系数 a=3.3940 >>b=aa(2) % 插值求得常数项系数 b=702.4918 >>y=polyval(aa,t) >>plot(t,r ,’k+’, t,y,’r’)【上机练习】1.编制计算拉格朗日插值的函数 m 文件 lagr1.m 。
2.选择一些函数,在 n 个节点上(n 不要太大,如 5~11)用拉格朗日、分段线性、三次样条 三种插值方法,计算 m 个插值点的函数值(m 要适中,如 50~100)。
通过数值和图形输出, 将三种插值结果与精确值进行比较。
适当增加 n ,再作比较,由此作初步分析。
下列函 数供选择参考:(1) 1 1 , 1 2£ £ - - = x x y ;(2) 22 , 2£ £ - = - x ey x 3.用 x y = 在 x =0, 1, 4, 9, 16 产生 5个节点函数值 5 2 1 , , , y y y L 。
用不同的节点构造插值 公式来计算 5 = x 处的插值(如用 5 2 4 1 5 1 ~ ; ~ ; ~ y y y y y y 等),与精确值比较并分析。
4.下表给出的 x , y 数据位于机翼断面的轮廓线上,y 1 和 y 2 分别对应轮廓的上下线。
假设 需要得到x 坐标每改变 0.1时的 y 坐标。
试完成加工所需数据,并画出曲线。
x 0 3 5 7 9 11 12 13 14 15 y 1 0 1.8 2.2 2.7 3.0 3.1 2.9 2.5 2.0 1.6 y 21.21.72.02.12.01.81.21.01.65.对以下数据分别作二次和三次多项式拟合,求得多项式系数,并画出图形。
x 2 4 5 6 7 8 10 12 14 16 y6.48.49.289.59.79.8610.210.410.510.66.根据以下数据,确定1790~1900 年美国人口的指数增长模型 rte x t x 0) ( = 中的人口年增长 率r 和初始人口数 0 x 。
t 1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900 x3.95.37.29.612.917.123.231.438.650.262.976.0附 lagr1.m 文件内容如下, 请仔细读懂各语句含义。
