材料力学习题02扭转.doc
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-扭转(圣才出品)

(1)一般矩形截面( h 10) b
分布特点:周边各点切应力与周边相切,没有垂直于周边的切应力分量,顶点处切应力 等于零,切应力变化情况如图 3-3(a)所示。
横截面上的最大切应力 max 发生在长边中点处
短边上切应力最大值发生在中点处
矩形截面扭转时,相对扭转角
7 / 44
;R 为弹簧圈平均半径, 。
6 / 44
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、非圆截面杆扭转的概念 1.基本概念 (1)翘曲:扭转变形后杆的横截面不再保持为平面的现象。 (2)自由扭转:等直杆两端受扭转力偶作用,且翘曲不受任何限制的扭转。 变形和受力特点:各横截面的翘曲程度相同,纵向纤维的长度无变化;横截面上只有切 应力。 (3)约束扭转:等直杆两端受扭转力偶作用,且翘曲受到限制的扭转。 变形和受力特点:各横截面的翘曲程度不同,相邻两截面间纵向纤维的长度改变;横截 面上有切应力和正应力。
WP
=
D3 16
式中, = d 。 D
上述公式只适用于等直杆和线弹性范围。 (2)强度条件 对于等直杆
对于变截面杆件需综合考虑 T 和 Wt,以求得切应力的最大值。
强度条件的应用:
①强度校核
Tmax [ ] Wt
4 / 44
圣才电子书
②截面选择
十万种考研考证电子书、题库视频学习平台
G
=
E
2(1+
)
4.剪切应变能
在应力小于剪切比例极限的情况下,单位体积内的剪切应变能密度为
=
1 2
=
2 2G , v
= 1 2
上述公式主要用于线弹性范围内纯剪切应力状态下剪切应变能密度的计算。
材料力学-扭转-计算公式及例题

求 AB段Mn(1-1剖面)
K N·m 4.50 背向剖切面为正
求 BC段Mn(2-2剖
面) K N·m
-4.50
求 CD段Mn(3-3剖面)
K N·m -1.50
D>=103mm
已知 CD段Mn(3-3剖面)
K N·m -1.5
求
IP m4 1.19E-05
求 φB-A
° 0.216
求 ΦC-B
K N·m
K N·m
K N·m
K N·m
数值
0.62
2.05
1.43
0.62
横截面上的力偶矩的方向,为外力偶矩(如T1,T2,T3)指向剖切面为负,背向剖切面为正
校核AC段 的强度(实
数据状态
代号
单位
数值 校核DB段 的强度(实
数据状态
代号
单位
已知 d1 mm 40
已知 d2 mm
已知 Mn(AC) K N·m 0.62
°/m
m4
1.05E+01 5.00E-01 1.50E-08
,试设 计截面的内
求 D0 mm 63.38
求 d mm 60.44
求 A1/A2
mm 0.51
d2=70mm。 。材料的许用切应 轴的强度和刚度。
。材料的许用切应 轴的强度和刚度。
求 CD段Mn(2-2剖面)
K N·m 0.62 背向剖切面为正
° -0.270
求 φD-C
° -0.108
强度计算 序号
名称
代号
单位
max
M n max Wp
[ ]
1
横截面上的最大扭 矩
Mn max
材料力学复习题第三章 扭 转

第三章 扭 转一、判断题1.圆杆受扭时,杆内各点均处于纯剪切状态。
( ) 2.非圆截面杆不能应用圆杆扭转切应力公式,是因为非圆截面杆扭转时“平面假设”不能成立。
( ) 3.当剪应力超过材料的剪切比例极限时,剪应力互等定律亦成立。
( ) 4.一点处两个相交面上的剪应力大小相等,方向指向(或背离)该两个面的交线。
( ) 5.直径和长度相同,材料不同的两根轴,受相同的扭转力偶矩作用,它们的最大剪应力和最大扭转角都相同。
6. 杆件受扭时,横截面上最大切应力发生在距截面形心最远处。
( )7. 薄壁圆管和空心圆管的扭转切应力公式完全一样。
( )8. 圆杆扭转变形实质上是剪切变形。
( )9. 横截面的角点处的切应力必为零。
( ) 1.√ 2.√ 3.√ 4.× 5.× 6.×(非圆截面) 7.× 8.√ 9.× 二、单项选择题1. 图示圆轴曲面C 左、右两侧的扭矩MC+和M C-的( )。
A .大小相等,正负号相同;B .大小不等,正负号相同; C .大小不等,正负号不同;D .大小相等,正负号不同。
2. 直径为D 的实心圆轴,两端受扭转力矩作用。
轴内最大剪应力τ,若轴的直径改为D/2,则轴内的最大剪应力变为( )。
A .2τ; B .τ; C . 8τ; D .16τ。
3. 阶梯圆轴的最大切应力发生在( )。
A .扭矩最大的截面;B .直径最小的截面;C .单位长度扭转角最大的截面;D .不能确定。
4.空心圆轴的外径为D ,内径为d,α=d/D 。
其抗扭截面系数为( )。
A .()απ-=1163D W P ;B 。
()23116απ-=D W P ;C 。
()33116απ-=D W PD .()43116απ-=D WP5.扭转的切应力公式ρτρPPI M =适用于( )杆件。
A .任意截面; B .任意实心截面;C .任意材料的圆截面; D .线弹性材料的圆面。
材料力学-第四章 扭转_2

T
T 6b 3T TS 2 2 2 2 4G 4G ( 2b ) 8Gb 3
1 2b 2
1 4b 2 2 2 3
结论 若将开口件加工为闭口件,将极大地提高构件的扭转
强度和刚度。
本 章 作 业
4-5,4-10, 4-13,4-29 4-16, 4-17 , 4-19 4-21(c),4-23 4-32,4-34
max
T h b2 T [ ] 2 0.246 2b b
取 b = 45 mm。
6 T 3 10 b 3 3 44.3 0.492[ ] 0.492 70
由 h / b = 2 查表得 = 0.229
T 3 10 6 2 1 2 10 m G 2b b 3 80 103 0.229 2 454
闭口薄壁杆件切应力分析
F
dx dx
x
0
1 1dx 2 2 dx 0
1
1
2
x
2
1 1 2 2
dFS ds
Const
dT ds
T ds ds 2
S S
闭口薄壁杆件切应力
ds dFS
例 正方形截面轴两端承受转矩而产生自由扭转。在强度相同
长度相等的条件下计算圆轴与正方形截面轴的重量比。
转矩 T 在矩形边中点引起最大切应力。 max 由正方形 h / b = 1
T h b2
3
查表得 = 0.208
圆轴
max
T [ ] 3 0.208b
16T d π[ ]
2.约束扭转
材料力学习题册答案-第3章 扭转

第三章扭转一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)For personal use only in study and research; not for commercial use4.圆杆扭转变形实质上是剪切变形。
(×)5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)7.切应力互等定理仅适用于纯剪切情况。
(×)8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)10.受扭圆轴的最大切应力只出现在横截面上。
(×)11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√)12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( × )二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )A τ;B ατ;C 零;D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D ) A 扭矩最大的截面; B 直径最小的截面; C 单位长度扭转角最大的截面; D 不能确定。
《材料力学》扭转习题解

第三章扭转习题解[习题3-1] 一传动轴作匀速转动, 转速n = 200r/min ,轴上装有五个轮子,主动轮 II 输入 的功率为60 kW ,从动轮,I ,山,IV ,V 依次输出18 kW ,12 kW ,22 kW 和8kW 。
试 作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩)T e = 9.55 血n外力偶矩计算(kW 换算成kN.m )题目编号 轮子编号轮子作用功率(kW )转速r/mi nTe (kN.m ) 习题3-1I 从动轮 18 200 0.859II主动轮 60 200 2.865III从动轮 12 200 0.573IV从动轮 22 200 1.051V从动轮82000.382(2)作扭矩图。
用 595[习题3-2] —钻探机的功率为l0kW ,转速n = 180r/min 。
钻杆钻入土层的深度I = 40m 。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度 图。
资料个人收集整理,勿做商业用途 解:(1)求分布力偶的集度= 9.549x® =0.5305(kN m)180M e 0.5305 m = --- = ------l 40= 0.0133(kN /m)设钻杆轴为x 轴, 则:Z M x =0ml =Me1 4325A1 2 0055 1m 3.5 mLSC.3SZm ,并作钻杆的扭矩M e =9.549 丛n L7S mT 图(kN.m)(2)作钻杆的扭矩图T(x) = —mx =—牛X =-0.0133x 。
x<^[0,40] T(0) =0 ;T(40) = M e = —0.5 305kN m) 扭矩图如图所示。
[习题3-3]圆轴的直径d =50mm ,转速为120r/min 。
若该轴横截面上的最大切应力等于 60 MPa ,试问所传递的功率为多大? 资料个人收集整理,勿做商业用途 解:(1)计算圆形截面的抗扭截面模量: 1 3 W p =—血3 P16(2 )计算扭矩1 3 3 = 16®4159 倔=24544(mm ) 2= 60N / mm23T =60N/mm x 24544mm =1472640N ・mm = 1.473(kN ・m)(3)计算所传递的功率T = M e =9.549山=1.473(kN -m)n N k =1.473x120/9.549 =18.5(kW)[习题3-4]空心钢轴的外径 D = 100mm ,内径d =50mm 。
材料力学 扭转(2)
1
M d n1 dx 1 GIp
2
M d n2 dx 2 GI p
M n1 d 因 M n1 M n 2 故 max 1 GI p dx max
max
180 N m 180 0.43 ( ) / m [ ] (80109 Pa)(3.0 105 10-12 m 4 ) π
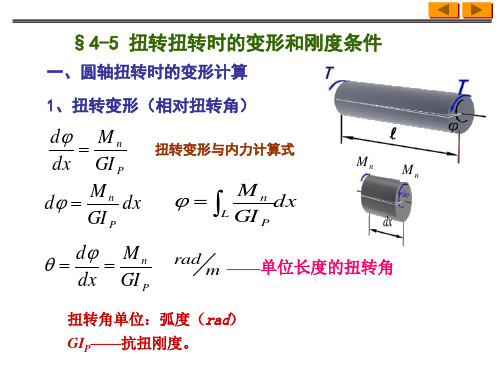
§4-5 扭转扭转时的变形和刚度条件
一、圆轴扭转时的变形计算 1、扭转变形(相对扭转角)
d M n dx GI P Mn d dx GI P d M n dx GI P
扭转变形与内力计算式
Mn Mn
Mn L dx GI P
rad m ——单位长度的扭转角
扭转角单位:弧度(rad) GIP——抗扭刚度。
2.绘扭矩图
7640 N m
3.直径d1的选取 按强度条件
d1
A M e1
( )
M e2
d 2 M e3
C
max
3
16M n 3 d1
3
B
4580 N m
16M n d1 π[ ]
16 7640 π 70 106
82.2 103 m 82.2mm
n
3)等直圆杆受分布扭矩 t 作用,t 的单位为 N m m。
从中取 dx 段,dx 段两相邻截面的扭转角为:
M n x dx AB 截面相对扭转角为: l d l GI p
M n x dx d GI p
4)变截面圆杆,A、B 两端直径 分别为 d1、d2 。
解: 1.外力
P M e1 9549 1 n
材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:(A) 21α-; (B)(C); (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:7. 图示圆轴料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D重量比21W W 9. 想弹塑性材料, 等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的 倍。
10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 为由实验测定的已知常数,试证明该轴的扭转切应力计算公式为:1/e (31)/2π()23m 1mm mM m d ρρτ+=+s /3证:几何方面 d d xρϕγρ= 物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰1//221/0d 2πd d m d mC x ϕρρ+⎛⎫= ⎪⎝⎭⎰(31)/1/()d 22π(31)d m mmd C m x mϕ+⎛⎫= ⎪+⎝⎭1/e (31)/(31)d d 2π()2mm m M m d x Cm ϕ++⋅⎛⎫=⎪⎝⎭⋅ 所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。
电气工程师-公共基础-材料力学-扭转

电气工程师-公共基础-材料力学-扭转[单选题]1.已知实心圆轴按强度条件可承担的最大扭矩为T,若改变该轴的直径,使其横截面积增加1倍。
则可承担的最大扭矩为()。
[2019年真(江南博哥)题]A.B.2TC.D.4T正确答案:C参考解析:扭转剪应力公式为:。
式中,Wp为抗扭截面系数,且。
当横截面面积增加一倍时,直径变为原来的倍。
根据扭转剪应力公式,当最大剪应力不变时,直径变为原来的倍时,可承受的最大扭矩为。
[单选题]2.圆轴直径为d,剪切弹性模量为G,在外力作用下发生扭转变形,现测得单位长度扭转角为θ,圆轴的最大切应力是()。
[2013、2010年真题]A.τ=(16θG)/(πd3)B.τ=(θGπd3)/16C.τ=θGdD.τ=θGd/2正确答案:D参考解析:由公式θ=T/(GIp)得:T=θGIp。
其中,Ip=(d/2)·Wp。
则最大切应力τ=T/Wp=GθIp/Wp=θGd/2。
[单选题]3.在一套传动系统中,有多根圆轴,假设所有圆轴传递的功率相同,转速不同。
该系统的圆轴转速与其扭矩的关系是()。
[2016、2014年真题]A.转速快的轴扭矩大B.转速慢的轴扭矩大C.全部轴的扭矩相同D.无法确定正确答案:B参考解析:根据公式T=9550P/n可知,在功率相同的情况下转速慢的轴扭矩大。
式中,T为扭矩(N·m);P为功率(kW);n为转速(r/min);9550为常系数。
[单选题]4.图5-3-1所示两根圆轴,横截面面积相同,但分别为实心圆和空心圆。
在相同的扭矩T作用下,两轴最大切应力的关系是()。
[2013年真题]图5-3-1A.τa<τbB.τa=τbC.τa>τbD.不能确定正确答案:C参考解析:设d1为实心圆直径,D2为空心圆截面外径,d2为空心圆截面内径,α2=d2/D2。
由最大切应力公式τmax=T/WP,由两轴截面面积相等得:πd12/4=πD22(1-α22)/4,即:实心圆截面的抗扭截面系数WPa=πd13/16;空心圆截面的WPb=πD23(1-α24)/16,因此两轴的抗扭截面系数之比为:故τa>τb。
材料力学 扭转 计算公式及例题
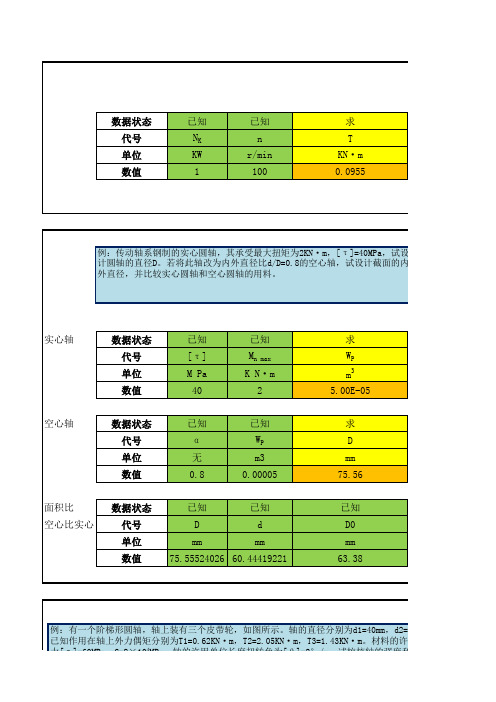
Ip
m4
0.1
求
Ip m4
4.00E-02
求
Ip m4
1.00E-01
求
WP m3
1.99E-01
求
WP m3
1.00E-01 求 d mm
1.01E+03 求 d mm
1.00E+03
数据状态 代号 单位 数值
数据状态 代号 单位 数值
已知 φ ° 1 已知 θ °/m 2
已知
求
代号 θmax
Ip Mn max
G [θ]
单位 °/m
m4 N·m Pa °/m
序号 1 2 3
名称 外力偶矩
功率 转速
代号 T NK n
序号
1 2 3
名称
横截面上的最大扭矩 抗扭截面模量 材料许用切应力
代号 圆轴扭转时的强度条件
Mn max WP
[τ]
序号
名称
强度计算
代号
1
横截面上的最大扭矩
2
Wp
πD3 16
公 圆式柱 公圆式柱 形, 形,
求
WP
m3
1.00E-01 求 d mm
1.01E+03 求 d mm
1.00E+03
公式
圆柱形,实心
Ip
πD 4 32
Wp
πD3 16
公式
公式
圆柱形,空心
圆柱形,薄壁
I
p
π(D4 32
d4)
πD4(1- 32
4)
Ip 2πr03t
Wp
πD3
已知 Mn(AC) K N·m 1.43
已知 G MPa
材料力学 扭转 题目+详解

3-2. 作出图示各杆的扭矩图。
解: (a)(1)用截面法求内力截面1-1eeXMT T Mm-=∴=--=∑110截面2-2eeeXMT T MMm20022-=∴=---=∑(2)画扭矩图(b )(1)用截面法求内力截面1-1eeXMT T Mm-=∴=+=∑110截面2-2(a)2xeeeXMT T MMm203 022=∴=+-=∑(2)画扭矩图(c )(1)用截面法求内力截面1-1kNT T mX30030 011-=∴=--=∑截面2-2kNT T mX1003020 012-=∴=--=∑截面3-3kNT T mX50302015 033=∴=--+=∑截面4-4kNT T mX15030201510 044=∴=--++=∑(2)画扭矩图T 4 4T(kNm)x3-8. 阶梯形圆轴直径分别为d 1=40mm ,d 2=70mm ,轴上装有三个皮带轮。
已知由轮3输入的功率为N 3=30kW,轮1输出的功率为N 1=13kW ,轴作匀速转动,转速n=200 r/min ,材料的许用剪应力[τ]=60MPa ,G=80GPa ,许用扭转角[θ]=2o /m 。
试校核轴的强度和刚度。
解:(1)计算外力扭矩NmnN MNmn N M4.143220030954995497.62020013954995493311=⨯===⨯==(2)计算内力扭矩NmMT Nm M T 4.14327.620332121====--(3)计算抗扭截面模量36322363111031.67161056.1216md πWm d πW t t --⨯==⨯==(4)强度校核MPaWT τMPaWT τt t 28.2142.492322max 1211max ====--强度足够。
(5)刚度校核][/77.1180211max θm πGIT θoop=⨯=-刚度足够。
2163d πR Md oo==3-19. 钻头简化成直径为20mm 的圆截面杆,在头部受均布阻抗扭矩m 的作用,许用剪应力为[τ]=70MPa 。
材料力学_扭转

2
A1 =
πD12
4
= 2122mm 2
因此在承载能力相同的条件下,使用空心轴比较节约材料,比较经济. 因此在承载能力相同的条件下,使用空心轴比较节约材料,比较经济.
3.4 圆轴扭转时的变形 刚度条件
一,扭转变形 圆轴扭转的变形用相对扭转角度量
d T = dx GI p
d =
T dx GI p
Tdx l GI p Tl = GI p
用截面法计算各段轴内的扭矩
T = MB = 1637Nm 1 T2 = MB MC = 3274Nm T3 = MD = 2183Nm
根据扭矩方程画扭矩图 从图上可看出,最大扭矩发生在 段内各截面 从图上可看出,最大扭矩发生在CA段内各截面 扭矩方程
1637
3274 ( Nm )
Tmax = 3274Nm
例: 某传动轴,用45号钢无缝钢管制成,其外径D =66mm,壁厚 t=5 某传动轴, 45号钢无缝钢管制成,其外径 =66 , =5mm,使用时 , 号钢无缝钢管制成 =5 最大扭矩为T =1500N.m,试校核此轴的强度.已知[τ]=60 最大扭矩为 =1500 ,试校核此轴的强度.已知[ ]=60MPa.若此轴改为实心轴, .若此轴改为实心轴, 并要求强度仍与原空心轴相当, 为多少? 并要求强度仍与原空心轴相当,则实心轴的直径 D1为多少? 解:计算传动轴的抗扭截面模量
Ip R
=
πD / 32
4
D/2
=
πD
3
16
空心圆截面: 空心圆截面:
Ip = ∫
D/2
d /2
2πρ 3dρ =
α =d/D πD 4 πd 4 πD 4
32 32 = 32
材料力学习题扭转知识分享

材料力学习题扭转扭转基本概念题一、选择题(如果题目有5个备选答案,选出2~5个正确答案,有4个备选答案选出一个正确答案。
)1.图示传动轴,主动轮A的输入功率为P A = 50 kW,从动轮B,C,D,E 的输出功率分别为P B = 20 kW,P C = 5 kW,P D = 10 kW,P E = 15 kW。
则轴上T出现在( )。
最大扭矩maxA.BA段B.AC段C.CD段D.DE段题1图2.图示单元体的应力状态中属正确的纯剪切状态的是()。
题2图3.上题图示单元体的应力状态中属正确的是()。
4.下列关于剪应力互等定理的论述中正确的是()。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C . 剪应力互等定理适用于各种受力杆件D .剪应力互等定理仅适用于弹性范围E .剪应力互等定理与材料的性能无关 5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是( )。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D 时,设轴内的最大剪应力为τ,若轴的直径改为2D ,其它条件不变,则轴内的最大剪应力变为( )。
A .τ8B .τC .τ16D .16τ7. 受扭空心圆轴(D d =α),在横截面积相等的条件下,下列承载能力最大的轴是( )。
A .0=α(实心轴)B .5.0=αC .6.0=αD .8.0=α8. 扭转应力公式ρτρpI T =的适用范围是( )。
A .各种等截面直杆 B .实心或空心圆截面直杆C .矩形截面直杆D .弹性变形E .弹性非弹性范围9. 直径为D 的实心圆轴,最大的容许扭矩为T ,若将轴的横截面积增加一倍,则其最大容许扭矩为( )。
A .T 2B .T 2C .T 22D .T 410. 材料相同的两根圆轴,一根为实心,直径为1D ;另一根为空心,内径为2d ,外径为2D ,α=22D d 。
若两轴横截面上的扭矩T ,和最大剪应力m ax τ均相同,则两轴外径之比21D D 为( )。
材料力学扭转实验【范本模板】

§1-2 扭转实验一、实验目的1、测定低碳钢的剪切屈服点τs,抗扭强度τb。
2、测定铜棒的抗扭强度τb.3、比较低碳钢和铜棒在扭转时的变形和破坏特征。
二、设备及试样1、伺服电机控制扭转试验机(自行改造).2、0.02mm游标卡尺。
3、低碳钢φ10圆试件一根,画有两圈圆周线和一根轴向线。
4、铜棒铁φ10圆试件一根。
三、实验原理及方法塑性材料试样安装在伺服电机驱动的扭转试验机上,以6—10º/min的主动夹头旋转速度对试样施加扭力矩,在计算机的显示屏上即可得到扭转曲线(扭矩-夹头转角图线),如下图为低碳钢的部分扭转曲线。
试样变形先是弹性性的,在弹性阶段,扭矩与扭转角成线性关系。
弹性变形到一定程度试样会出现屈服。
扭转曲线扭矩首次下降前的最大扭矩为上屈服扭矩T su;屈服段中最小扭矩为下屈服扭矩T sl,通常把下屈服扭矩对应的应力值作为材料的屈服极限τs,即:τs=τsl= T sl/W。
当试样扭断时,得到最大扭矩T b,则其抗扭强度为τb= T b/W式中W为抗扭截面模量,对实心圆截面有W=πd03/16。
铸铁为脆性材料,无屈服现象,扭矩-夹头转角图线如左图,故当其扭转试样破断时,测得最大扭矩T b,则其抗扭强度为:τb= T b/W四、实验步骤1、测量试样原始尺寸分别在标距两端及中部三个位置上测量的直径,用最小直径计算抗扭截面模量.2、安装试样并保持试样轴线与扭转试验机转动中心一致。
3、低碳钢扭转破坏试验,观察线弹性阶段、屈服阶段的力学现象,记录上、下屈服点扭矩值,试样扭断后,记录最大扭矩值,观察断口特征。
4、铜棒扭转破坏试验,试样扭断后,记录最大扭矩值,观察断口特征。
五、实验数据处理1、试样直径的测量与测量工具的精度一致。
2、抗扭截面模量取4位有效数字。
3、力学性能指标数值的修约要求同拉伸实验。
六、思考题1、低碳钢扭转时圆周线和轴向线如何变化?与扭转平面假设是否相符?2、如用木材或竹材制成纤维平行于轴线的圆截面试样,受扭时它们将按怎样的方式破坏?3、根据低碳钢和铜棒的破口特征,分析两种材料扭转破坏的原因?1、比较低碳钢拉伸和扭转实验,从进入塑性变形阶段到破坏的全过程,两者变形有何明显的区别?。
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
3
A.max1max2B.max1max2
2
1
C.max1max2
4
3
D.max1max2
8
- 2 -
题12图题13图
12.在图示的圆轴中,AB段的相对扭转角
1和BC段的相对扭转角2的关系是
()。
8
A.12B.21
3
16
C.21
3
4
D.21
3
13.在上题图示圆轴左段实心,右段空心,其中右段和左段的最大剪应力
计算题
1.内、外直径分别为d和D的空心轴,其横截面的极惯性矩为
4d4
D
Ip,抗
3232
扭截面系数为
3d
3
D
Wt。以上算式是否正确?何故?
1616
题1图
- 4 -
应力();单位长度扭转角(),总相对扭转角()。
6.外径为D,内径为d=0.5D的空心圆轴,两端受扭转外力偶矩m作用时,轴内最大
剪应力为。若轴的外径不变,内径改为d0.8D,则轴内的最大剪应力变为()。
7.扭转应力公式
T
I
p
适用()或()截面直杆。
8.材料相同的两根圆轴,一根为实心轴,直径为
D;另一根为空心轴,内径d2,外
1
径为
D,
2
d
2
D
2
。若两轴横截面上的扭矩T和最大剪应
max均相同,则两轴的横截面积
之比
A
1
Aቤተ መጻሕፍቲ ባይዱ
2
()。
9.一受扭空心圆轴,其内外径之比
d
D
。轴内最大剪应力为max,这时横截面上
内圆周处的剪应力()。
10.矩形截面杆受扭时,横截面上的最大剪应力出现在();
的点在()和()处。
11.矩形截面杆受扭时,横截面上边缘各点的剪应力方向()。
D.剪应力互等定理仅适用于弹性范围
E.剪应力互等定理与材料的性能无关
5.图示受扭圆轴,其横截面上的剪应力分布图正确的是()。
- 1 -
题5图
6.实心圆轴,两端受扭转外力偶作用。直径为D时,设轴内的最大剪应力为,若轴
的直径改为D2,其它条件不变,则轴内的最大剪应力变为()。
A.8B.8C.16D.16
二、判断题(正确的打“√”,错的打“×”)
1.受扭圆轴(实心或空心)横截面上的最小剪应力一定等于零。()
2.当材料和横截面积相同时,空心圆轴的抗扭承载能力大于实心圆轴。()
3.在扭转外力偶矩作用处,扭矩图发生突变。()
4.材料和外圆半径相同时,空心圆轴的抗扭强度大于实心圆轴。()
5.受扭圆轴横截面上,半径相同的点的剪应力大小也相同。()
()。
A.BA段B.AC段C.CD段D.DE段
题1图
2.图示单元体的应力状态中属正确的纯剪切状态的是()。
题2图
3.上题图示单元体的应力状态中属正确的是()。
4.下列关于剪应力互等定理的论述中正确的是()。
A.剪应力互等定理是由平衡
B.剪应力互等定理仅适用于纯剪切的情况
C.剪应力互等定理适用于各种受力杆件
其最大容许扭矩为()。
A.2TB.2TC.22TD.4T
10.材料相同的两根圆轴,一根为实心,直径为
D;另一根为空心,内径为d2,外径
1
为
d
2
D,
2
D
2
。若两轴横截面上的扭矩T,和最大剪应力
max均相同,则两轴外径之比
D
1
D
2
为()。
A.
3
1B.
4
1C.
(1D.3)
3)
13
(1
4)1
3
11.阶梯圆轴及其受力如图所示,其中AB段的最大剪应力max1与BC段的最大剪应力
6.空心和实心圆轴横截面积相同时,空心圆轴的Ip和Wt值较大。()
三、填空题
1.受扭构件所受的外力偶矩的作用面与杆轴线()。
2.受扭圆轴的横截面的内力是(),应力是()。
3.实心圆轴横截面上()处剪应力最大,中心处剪应力()。
- 3 -
4.公式
Tl
GI
p
适用于();式中GIp是(),它反映
了()。
5.在弹性范围内,若只将等截面圆轴的长度增大一倍,其它条件不变,则圆轴的最大
7.受扭空心圆轴(dD),在横截面积相等的条件下,下列承载能力最大的轴是
()。
A.0(实心轴)B.0.5C.0.6D.0.8
8.扭转应力公式
T
I
p
的适用范围是()。
A.各种等截面直杆B.实心或空心圆截面直杆
C.矩形截面直杆D.弹性变形E.弹性非弹性范围
9.直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则
max和
右
max之比max右max左()。
左
A.3B.16 / 5C.6D.24 / 7
14.在上题图示圆轴中,右段的相对扭转角
右和左段的相对扭转角左的比
右()。
左
A.8/5B.16/5C.3/2D.24
15.受扭圆轴的强度条件和刚度条件均与()有关。
A.材料性质B.扭矩大小C.扭矩转向
D.圆轴的长度E.圆轴横截面尺寸
扭转
基本概念题
一、选择题(如果题目有5个备选答案,选出2~5个正确答案,有4个备选答案选出
一个正确答案。)
1.图示传动轴,主动轮A的输入功率为PA= 50 kW,从动轮B,C,D,E的输出功率
分别为PB= 20 kW,PC= 5 kW,PD= 10 kW,PE= 15 kW。则轴上最大扭矩
T出现在
max
