考研数学函数图像大全
函数图像总结

函数图像总结函数图像是指函数在直角坐标系中的图形表示。
通过观察函数图像,可以了解函数的基本特征和性质。
下面我将对常见的函数图像进行总结。
一、一次函数图像:一次函数的一般形式为y = kx + b,其中k为斜率,b为截距。
当k>0时,函数图像呈现正斜率,向右上方倾斜;当k<0时,函数图像呈现负斜率,向右下方倾斜;当k=0时,函数图像为水平直线;当b>0时,函数图像在y轴上方截距b的位置;当b<0时,函数图像在y轴下方截距-b的位置。
二、二次函数图像:二次函数的一般形式为y = ax^2 + bx + c,其中a决定了函数的开口方向和开口大小,b决定了函数图像的对称轴位置,c决定了函数图像与y轴的交点。
当a>0时,函数图像向上开口;当a<0时,函数图像向下开口;当b=0时,函数图像的对称轴为y轴;当b>0时,函数图像的对称轴在原点的右侧;当b<0时,函数图像的对称轴在原点的左侧。
三、指数函数图像:指数函数的一般形式为y = a^x,其中a为底数。
当底数a>1时,函数图像呈现增长趋势,向上凸起;当0<a<1时,函数图像呈现递减趋势,向下凹陷;当a=1时,函数图像为水平直线。
四、对数函数图像:对数函数的一般形式为y = loga(x),其中a为底数。
当底数a>1时,函数图像呈现增长趋势,向右上方倾斜;当0<a<1时,函数图像呈现递减趋势,向右下方倾斜;当a=1时,函数图像为y轴。
五、三角函数图像:常见的三角函数包括正弦函数、余弦函数、正切函数等。
正弦函数的图像呈现周期性的波形,振动范围在[-1,1]之间;余弦函数的图像也呈现周期性的波形,振动范围也在[-1,1]之间;正切函数的图像在某些点上发生突变,振动范围在整个坐标轴上。
总结以上几种函数图像,可以根据函数的数学表达式和特点来推测图像的形状和性质,进而帮助解决与函数相关的问题。
函数图像总结

函数图像总结函数图像是数学中的重要概念,它反映了数学函数在坐标系中的表现形式。
通过观察函数图像,我们可以了解函数的性质、特征以及与其他函数的关系。
本文将对常见的函数图像进行总结,以便读者更好地理解和掌握函数的图像特点。
一、线性函数图像线性函数是最简单也是最容易理解的函数之一。
它的图像即一条直线。
线性函数的一般形式为:y = kx + b,其中k和b为常数。
当k大于0时,直线是向上倾斜的,当k小于0时,直线是向下倾斜的。
b则表示直线与y轴的交点,称为截距。
通过改变k和b的取值,我们可以观察到直线的斜率和截距对图像的影响。
二、二次函数图像二次函数的一般形式为:y = ax² + bx + c,其中a、b、c为常数且a ≠ 0。
二次函数的图像通常是一个抛物线。
抛物线的开口方向由a的正负决定,当a大于0时,抛物线开口向上;当a小于0时,抛物线开口向下。
同时,b和c的取值也会对抛物线的位置产生影响。
通过调整a、b、c的值,我们可以观察到抛物线的顶点、焦点以及与x轴和y轴的交点等特征。
三、指数函数图像指数函数的一般形式为:y = aⁿ,其中a为常数且a > 0,n为自变量。
指数函数图像的特点是随着自变量的增大,函数值呈现出迅速增长或迅速衰减的趋势。
当a大于1时,指数函数图像是递增的;当a位于0和1之间时,指数函数图像是递减的。
指数函数还可以通过调整a的值来改变函数增长或衰减的速度。
四、对数函数图像对数函数的一般形式为:y = logₐx,其中a为底数,x为自变量。
对数函数图像的特点是随着自变量的增大,函数值的增长速度逐渐减缓。
当底数a大于1时,对数函数图像是递增的;当底数a位于0和1之间时,对数函数图像是递减的。
不同底数的对数函数之间在图像形状上有所差异,但都满足递增或递减的特点。
五、三角函数图像三角函数包括正弦函数、余弦函数和正切函数等。
它们的图像都是一条曲线,周期性地在坐标轴上反复出现。
考研高等数学常用公式以及函数图像

考研高等数学常用公式及函数图象导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:函数 角A sincos tg ctg -α -sinα cosα -tgα -ctgα 90°-α cosα sinαctgαtgα 90°+α cosα -sinα -ctgα -tgα 180°-α si nα-cosα -tgα-ctgα 180°+α -sinα -cosα tgα ctgα 270°-α -cosα -sinα ctgα tgα 270°+α -cosα sinα -ctgα -tgα360°-α -sinα cosα -tgα -ctgα 360°+αsinαcosαtgαctgα·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
考研数学函数图像大全

函数图形基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)等价无穷小(x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)。
函数图像总结

函数图像总结函数图像总结函数图像总结一基本函数图像1y=kx(x≠0)2y=kx+b(k≠0)3y4yax2bxc(a0)5yxa6yxk(k0)xk(k0)7yax(a 0,a1)x8ylogax(a0,a1)二抽象图像平移f(x)f(x+1)f(x)f(x-1)f(x)f(x)+1f(x)f(x)-1f(x)f(2x)f(x)2f(x) f(x)f(2x+2)y=f(-x)变成y=f(-x+2)练习:cosxcos2xcos2xcos(2x+4)cosxcos2x+4三图像的变换1f(x)f(|x|)保留y轴右边的,左边关于右边y轴对称2f(x)|f(x)|保留x轴上方的,下方关于x轴对称3f(x)f(-x)y轴对称4f(x)-f(x)x轴对称5f(x)-f(-x)原点对称6f(x)f(|x+1|)先根据1方法变成f(|x|),在向左平移一个单位得到f(|x+1|)7f(x)f(|x|+1)先向左平移一个单位得到f(x+1),再根据1方法变成f(|x|+1)8f(x)与f1(x)的图象关于直线yx对称联想点(x,y),(y,x)9f(x)与f(2ax)的图象关于点(a,0)对称egf(x)= 2x与g(x)=-2x关于对称一、函数yf(x)与函数yf(x)的图象关系函数yf(x)的图象是由yf(x)的图象经沿y轴翻折180°而得到的(即关于y轴对称)。
注意它与函数yf(x)满足f(x)f(x)的图象是不同的,前者代表两个函数,后者表示函数yf(x)本身是关于y轴对称的。
(二)伸缩变换及其应用:函数yaf(bx)的图像可以看作是由函数yf(x)的图像先将横坐标伸长(|b|<1)或缩短(|b|>1)到原来的1倍,再把纵坐标伸长(|a|>1)或缩短(|a|<1)到原来的|a|倍即可得到。
如:|b|1的图像x1要求:1会画y=|x+1|y=-2会画f(x)=lg|x|以及f(x)=|lgx|3会画f(x)=|lg|x+1||以及f(x)=x2-4|x|+5f(x)=|x2-2x-3|二1由图像可知f(x+1)为偶函数对称轴为2由图像可知f(x+1)为奇函数关于点(,)对称Eg、对a,bR,记max{a,b}=(A)0(B) a,ab,函数f(x)=max{|x+1|,|x-2|}(xR)的最小值是b,a<b13(C)(D)3901(选讲)1、yf(x)绕原点顺时针方向旋转;yf(x)12、yf(x);yf (x)绕原点逆时针方向旋转9000yQP(a,b)(yf(x)yQ1xP1(b,a)(yf1(x))P(a,b)(yf(x)0P1(b,a)1(yf(x))0(乙)x(甲)(图五)0说明:关于绕原点旋转180的变换实际上就是关于原点对称的问题。
考研数学涉及的全部函数

考研数学涉及的全部函数
1 指数函数yy=aa xx、对数函数yy=log aa xx(会图像)
2 yy=sin xx、yy=cos xx、yy=tan xx、yy=cot xx及其反三角函数(掌
握图像与性质)yy=sec xx、yy=csc xx(了解)
3 复合函数:yy=ff[φφ(xx)]⇒求导法则
4反函数(求导法则)
5分段函数(求导):接头点处的导数用导数定义求,非接头点处的导
数用公式和法则求
6 符号函数:yy=sgn xx注意:yy=|xx|与yy=xx.sgn xx
7 幂指数函数(求导公式与求极限):yy=uu(xx)vv(xx)(1)求导公式:yy′=uu(xx)vv(xx).[vv(xx).ln uu(xx)]′
(2)lim
xx→xx0ff(xx)gg(xx)(共三种类型)
8 取整函数:yy=[xx](不超过xx的最大整数)
注:lim
xx→0+[xx]=0lim xx→0−[xx]=−1⇒lim xx→0[xx]不存在
9 最大值与最小值函数:
mmaaxx{uu,vv}=uu+vv+|uu−vv|2 min{uu,vv}=uu+vv−|uu−vv|2
思考:最大值和最小值的和及乘积各是什么?
xx aa(4个求导公式)(第二章)10.变限积分函数FF(xx)=∫ff(tt)ⅆtt
11.隐函数:(求导方法)分析法、公式法、全微分法
12 参数方程所确定的函数(数学一、数学二)
xx00、ff(xx)、ff′(xx)三个函数
【说明】:比较FF(xx)=∫ff(tt)ⅆtt
函数模块:三要素⇒四大性质⇒常考的函数⇒建立函数模型
(应用题)。
(完整)(考研高数)基本初等函数图像与性质

(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n 时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n均为奇数时,跟原点对称。
4.当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y , 余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数 反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数xy arctan=,),(+∞-∞∈x,)2,2(ππ-∈y,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ :捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔IotaΚκ:喀帕Kappa ∧λ:拉姆达LambdaΜμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:fai PhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
常用函数图像

常用函数图像函数图像在数学中非常重要,它们可以用来表达函数之间的关系和函数的性质。
常用的函数图像有抛物线、幂函数和三角函数图像。
抛物线图像包括标准抛物线、以及二次抛物线、三次抛物线等多种形式。
标准抛物线的图像表示为 y = x2。
物线图像可以用来表示多种概念,例如,爱心图像、球形曲面、重力势能曲线等。
幂函数图像用来表示一个变量的变化与另一个变量的变化的关系。
它的图像表示为 y = xn,其中 n一个正整数,可以更改它的值,用来表示不同的变化关系。
例如,y = x2图像用来表示立方体的面积;y = x3图像用来表示一个立方体的体积。
三角函数图像是非常常用的一种函数图像,它们可以用来描述物体在不同时刻,在不同方向上的运动轨迹。
常用的三角函数图像有正弦函数图像、余弦函数图像和正切函数图像。
其中,正弦函数图像表示为 y = sinx,主要用来表示振动的运动,例如,钟表的指针的运动;余弦函数图像表示为 y = cosx,主要用来表示循环运动,例如,行星的运动;正切函数图像表示为 y = tanx,主要用来表示直线运动,例如,小船在江河中发生的运动。
除了抛物线、幂函数和三角函数图像之外,还有其他一些常用的函数图像,例如指数函数图像、对数函数图像等。
指数函数图像表示为 y = ax,其中 a一个正数,当 a于任意大于 0数时,指数函数图像的曲线都是一条水平较大的弧线;对数函数图像表示为 y = logax,其中 a一个正数,曲线变形很大,它的曲线以 x为轴心,从右往左发散,当 x得较大值时,可以看到曲线趋于水平轴。
以上就是常用函数图像的简单介绍,通过不同的函数图像,可以描述不同的概念,也可以用来表示函数之间的关系,进而正确地求解数学问题。
考研高等数学常用公式以及函数图像

考研高等数学常用公式及函数图象导数公式:基本积分表:三角函数的有理式积分:ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限: 三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(μμμ·倍角公式: ·半角公式: ·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+= ·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式: 中值定理与导数应用: 曲率:定积分的近似计算: 定积分应用相关公式: 空间解析几何和向量代数: 多元函数微分法及应用 微分法在几何上的应用:),,(),,(),,(30))(,,())(,,())(,,(2)},,(),,,(),,,({1),,(0),,(},,{,0),,(0),,(0))(())(())(()()()(),,()()()(000000000000000000000000000000000000000000000000000z y x F z z z y x F y y z y x F x x z z z y x F y y z y x F x x z y x F z y x F z y x F z y x F n z y x M z y x F G G F F G G F F G G F F T z y x G z y x F z z t y y t x x t M t z z t y y t x x z y x M t z t y t x z y x z y x z y x yx y x x z x z z y z y -=-=-=-+-+-==⎪⎩⎪⎨⎧====-'+-'+-''-='-='-⎪⎩⎪⎨⎧===、过此点的法线方程::、过此点的切平面方程、过此点的法向量:,则:上一点曲面则切向量若空间曲线方程为:处的法平面方程:在点处的切线方程:在点空间曲线ϖϖωψϕωψϕωψϕ方向导数与梯度:上的投影。
函数图像总结

函数图像总结函数图像总结函数图像是数学中的一个重要概念,它是一种以数学函数为基础的图形表达方式。
通过对函数的定义域和值域的探究,可以得出函数的图像特征。
本文将对常见的函数图像进行总结和解析,并通过Markdown文本格式输出。
直线函数直线函数是最简单的一类函数图像,表达式为 $y = kx + b$,其中 $k$ 是斜率,$b$ 是 $y$ 轴的截距。
直线函数的图像特征如下:- 斜率 $k$ 表示了直线的倾斜程度,当 $k>0$ 时,直线向右上方倾斜;当$k<0$ 时,直线向右下方倾斜;当 $k=0$ 时,直线水平。
- 截距 $b$ 表示了直线与 $y$ 轴的交点位置。
当 $b>0$ 时,直线在 $y$ 轴的上方交点;当 $b<0$ 时,直线在 $y$ 轴的下方交点;当 $b=0$ 时,直线经过原点。
平方函数平方函数是一类二次函数图像,表达式为 $y = ax^2 + bx + c$,其中 $a$、$b$、$c$ 是常数。
平方函数的图像特征如下:- 平方函数的图像一般呈现 U 形,称为抛物线。
- 当 $a>0$ 时,抛物线开口朝上;当 $a<0$ 时,抛物线开口朝下。
- 抛物线在 $x = -\\frac{b}{2a}$ 处达到极值,当 $a>0$ 时,极小值;当 $a<0$ 时,极大值。
- 抛物线与 $y$ 轴的交点为 $c$。
- 抛物线的轴对称线为 $x = -\\frac{b}{2a}$。
开方函数开方函数是一类具有根号形式的函数图像,表达式为 $y = \\sqrt{x}$。
开方函数的图像特征如下:- 开方函数在定义域内,即 $x \\geq 0$ 范围内有定义。
- 开方函数的图像为一条右上方向的曲线。
- 开方函数的图像在原点处有切线,斜率为 $1$。
- 开方函数在 $x = 0$ 处为最小值点。
正弦函数正弦函数是一类周期性的函数图像,表达式为 $y = a\\sin(bx+c)$,其中 $a$、$b$、$c$ 是常数。
五种基本函数图像和性质

五种基本函数图像和性质1、幂函数形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
(1)图像几个常见的幂函数图像:注:画幂函数图像时,先画第一象限的部分,在根据函数奇偶性完成整个图像。
(2)性质:•幕函数的图像最多只能同时出现在两个象限,且不经过第四象限;如图与坐标轴相交,则交点一定是坐标原点•所有幕函数在(0,+00)上都有定义,并且图像都经过点(1,1)。
•当a≤-1且a为奇数时,函数在第一、第三象限为减函数•当a≤-1且a为偶数时,函数在第二象限为增函数•当a=0且x不为0时,函数图象平行于x轴且y=1、但不过(0,1)•当a=1时,函数图像为过(0,0),(1,1)且关于原点对称的射线•当0<a<1时,函数是增函数•当a≥1且a为奇数时,函数是奇函数•当a≥1且a为偶数时,函数是偶函数(3)规律:把a看成分数•当分母为偶数时,函数为非奇非偶函数,图像只在第一象限•当分母为奇数时,分子为偶数,函数为偶函数,图像在一、二象限,图像关于Y轴对称•当分母为奇数时,分子为奇数,函数为奇函数,图像在一、三象限,图像关于原点对称2、指数函数函数y=a^x(a>0且a≠1)叫做指数函数,自变量x叫做指数,a叫做底数函数的定义域是R.(1)图像(2)性质•指数函数y=a^x(a>0且a≠1)的函数值恒大于零,定义域为R,值域为(0,+00)•指数函数y=a^x(a>0且a≠1)的图像经过点(0,1)•指数函数y=a^x(a>1)在R上递增,指数函数y=a^x(0 <a< 1)在R上递减•函数总是在某一个方向上无限趋向于X轴,并且永不相交。
•函数总是通过(0,1)这点,(若 ,则函数定过点(0,1+b))•指数函数无界•指数函数是非奇非偶函数•指数函数具有反函数,其反函数是对数函数3、对数函数一般地,函数y=logaX(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
(完整版)数学函数图像大全2
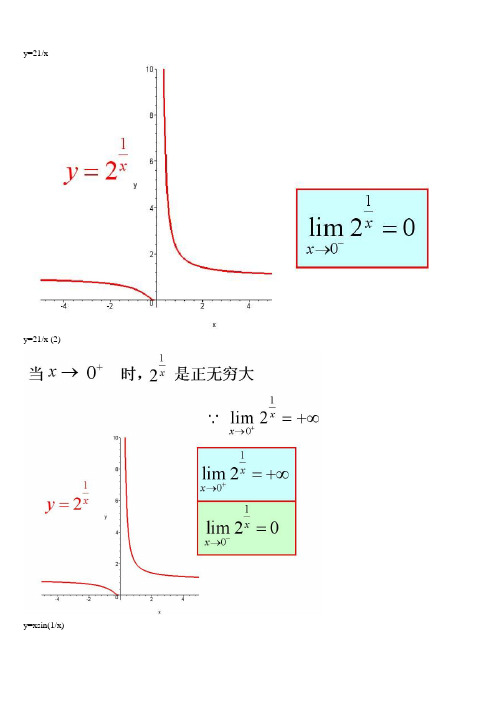
y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xarctanx等价于x1-cosx等价于x^2/2数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$$tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式4.2 和差化积公式。
