蒋立源编译原理 第三版 第三章 习题与答案(修改后)
编译原理_第三版_课后答案

{2,3,5,7,9,10} {2,4,5,7,8,10} {2,4,5,7,8,10} {11} {6} ห้องสมุดไป่ตู้ {2,5,7,8,10} φ φ
{2,3,5,7,10} {2,3,5,7,9,10} φ φ
{11} {11} φ φ S
{6} {6} φ φ
3: 5: 6: S a b S S A a b A a A S b A
文法: (1) 最左推导: 最右推导: (2) (((a,a),^,(a)),a) (((S,a),^,(a)),a) (((T,a),^,(a)),a) (((T,S),^,(a)),a) (((T),^,(a)),a)
((S,^,(a)),a) ((T,^,(a)),a) ((T,S,(a)),a) ((T,(a)),a) ((T,(S)),a) ((T,(T)),a) ((T,S),a) ((T),a) (S,a) (T,S) (T) S “移进-归约”过程: 步骤 栈 输入串 动作 0 # (((a,a),^,(a)),a)# 预备 1 #( ((a,a),^,(a)),a)# 进 2 #(( (a,a),^,(a)),a)# 进 3 #((( a,a),^,(a)),a)# 进 4 #(((a ,a),^,(a)),a)# 进 5 #(((S ,a),^,(a)),a)# 归 6 #(((T ,a),^,(a)),a)# 归 7 #(((T, a),^,(a)),a)# 进 8 #(((T,a ),^,(a)),a)# 进 9 #(((T,S ),^,(a)),a)# 归 10 #(((T ),^,(a)),a)# 归 11 #(((T) ,^,(a)),a)# 进 12 #((S ,^,(a)),a)# 归 13 #((T ,^,(a)),a)# 归 14 #((T, ^,(a)),a)# 进 15 #((T,^ ,(a)),a)# 进 16 #((T,S ,(a)),a)# 归 17 #((T ,(a)),a)# 归 18 #((T, (a)),a)# 进 19 #((T,( a)),a)# 进 20 #((T,(a )),a)# 进 21 #((T,(S )),a)# 归 22 #((T,(T )),a)# 归
蒋立源编译原理 第三版 第三章 习题与答案(修改后)

第3章习题3-1 试构造一右线性文法,使得它与如下得文法等价S→AB A→UT U→aU|a D→bT|b B→cB|c 并根据所得得右线性文法,构造出相应得状态转换图。
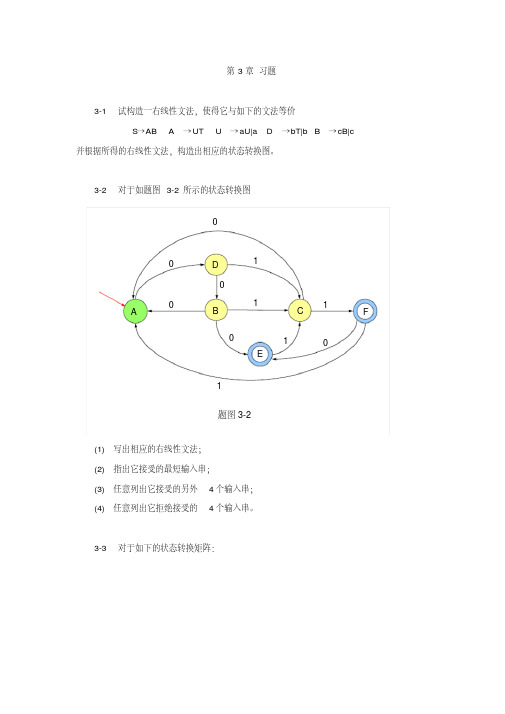
3-2 对于如题图3-2所示得状态转换图(1) 写出相应得右线性文法;(2) 指出它接受得最短输入串;(3) 任意列出它接受得另外4个输入串;(4) 任意列出它拒绝接受得4个输入串。
3-3 对于如下得状态转换矩阵:(1) 分别画出相应得状态转换图;(2) 写出相应得3型文法;(3) 用自然语言描述它们所识别得输入串得特征。
3-4 将如下得NFA确定化与最小化:3-5 将如题图3-5所示得具有ε动作得NFA确定化。
题图3-5 具有ε动作得NFA3-6 设有文法G[S]:S→aA A→aA|bB B→bB|cC|c C→cC|c 试用正规式描述它所产生得语言。
3-7 分别构造与如下正规式相应得NFA。
(1) ((0* |1)(1* 0))*(2) b|a(aa*b)*b3-8 构造与正规式(a|b)*(aa|bb)(a|b)*相应得DFA。
第3章习题答案3-1 解:根据文法知其产生得语言就是:L[G]={a m b n c i| m,n,i≧1}可以构造与原文法等价得右线性文法:S→aA A→aA|bB B→bB|cC|c C→cC|c 其状态转换图如下:3-2 解:(1) 其对应得右线性文法就是G[A]:A →0D B→0A|1C C→0A|1F|1D→0B|1C E→0B|1C F→1A|0E|0(2) 最短输入串为011(3) 任意接受得四个输入串为:0110,0011,000011,00110(4) 任意拒绝接受得输入串为:0111,1011,1100,10013-3 解:(1) 相应得状态转换图为:(2) 相应得3型文法为:(ⅰ) S→aA|bS A→aA|bB|b B→aB|bB|a|b(ⅱ) S→aA|bB|a A→bA|aC|a|b B→aB|bC|b C→aC|bC|a|b(ⅲ) S→aA|bB|b A→aB|bA|a B→aB|bB|a|b(ⅳ) S→bS|aA A→aC|bB|a B→aB|bC|b C→aC|bC|a|b(3) 用自然语言描述得输入串得特征为:(ⅰ) 以任意个(包括0个)b开头,中间有任意个(大于1)a,跟一个b,还可以有一个由a,b组成得任意字符串。
《编译原理》课后习题答案第三章第3章文法和语言第1

《编译原理》课后习题答案第三章第3 章文法和语言第1 题文法G=({A,B,S},{a,b,c},P,S)其中P 为:S→Ac|aBA→abB→bc写出L(G[S])的全部元素。
答案:L(G[S])={abc}第2 题文法G[N]为:N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?答案:G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D或者:允许0 开头的非负整数?第3题为只包含数字、加号和减号的表达式,例如9-2+5,3-1,7等构造一个文法。
答案:G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第4 题已知文法G[Z]:Z→aZb|ab写出L(G[Z])的全部元素。
盛威网()专业的计算机学习网站 1《编译原理》课后习题答案第三章答案:Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={anbn|n>=1}第5 题写一文法,使其语言是偶正整数的集合。
要求:(1) 允许0 打头;(2)不允许0 打头。
答案:(1)允许0 开头的偶正整数集合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许0 开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第6 题已知文法G:<表达式>::=<项>|<表达式>+<项><项>::=<因子>|<项>*<因子><因子>::=(<表达式>)|i试给出下述表达式的推导及语法树。
(5)i+(i+i)(6)i+i*i盛威网()专业的计算机学习网站 2 《编译原理》课后习题答案第三章答案:<表达式><表达式> + <项><因子><表达式><表达式> + <项><因子>i<项><因子>i<项><因子>i( )(5) <表达式>=><表达式>+<项>=><表达式>+<因子>=><表达式>+(<表达式>)=><表达式>+(<表达式>+<项>)=><表达式>+(<表达式>+<因子>)=><表达式>+(<表达式>+i)=><表达式>+(<项>+i)=><表达式>+(<因子>+i)=><表达式>+(i+i)=><项>+(i+i)=><因子>+(i+i)=>i+(i+i)<表达式><表达式> + <项><项> * <因子><因子> i<项><因子>ii(6) <表达式>=><表达式>+<项>=><表达式>+<项>*<因子>=><表达式>+<项>*i=><表达式>+<因子>*i=><表达式>+i*i=><项>+i*i=><因子>+i*i=>i+i*i盛威网()专业的计算机学习网站 3《编译原理》课后习题答案第三章第7 题证明下述文法G[〈表达式〉]是二义的。
编译原理3答案

编译原理3答案【篇一:编译原理试题及答案3】填空题:1、编译方式与解释方式的根本区别在于(是否生成目标代码)。
2、对编译程序而言,输入数据是(源程序),输出结果是(目标程序)。
3、如果编译程序生成的目标程序是机器代码程序,则源程序的执行分为两大阶段:(编译阶段)和(运行阶段)。
4、如果编译程序生成的目标程序是汇编语言程序,则源程序的执行分成三个阶段:(编译阶段)、(汇编阶段)和(运行阶段)。
5、自顶向下语法分析方法会遇到的主要问题有(回溯)和((左递归带来的)无限循环)。
6、ll(k)分析法中,第一个l的含义是(从左到右进行分析),第二个l的含义是(每次进行最左推导),“k”的含义是(向输入串中查看k个输入符号)。
7、ll(1)分析法中,第一个l的含义是(从左到右进行分析),第二个l的含义是(每次进行最左推导),“1”的含义是(向输入串中查看1个输入符号)。
8、自顶向下语法分析方法的基本思想是:从(识别符号)出发,不断建立(直接推导),试图构造一个推导序列,最终由它推导出与输入符号相同的(符号串)。
9、自底向上语法分析方法的基本思想是:从待输入的符号串开始,利用文法的规则步步向上进行(直接归约),试图(归约)到文法的(识别符号|开始符号)。
10、lr(0)分析法的名字中,“l”的含义是(从左到右进行分析),“r”的含义是(采用最右推导的逆过程---最左归约),“0”的含义是(向貌似句柄的符号串后查看0个输入符号)。
11、lr(1)分析法的名字中,“l”的含义是(从左到右进行分析),“r”的含义是(采用最右推导的逆过程---最左归约),“1”的含义是(向貌似句柄的符号串后查看1个输入符号)。
12、slr(1)分析法的名字中,“s”的含义是(简单的),“l”的含义是(从左到右进行分析),“r”的含义是(采用最右推导的逆过程---最左归约),“1”的含义是(向貌似句柄的符号串后查看1个输入符号)。
13、在编译过程中,常见的中间语言形式有(逆波兰表示)、(三元式)、(四元式)和(树形表示)。
编译原理第三版课后习题答案

编译原理第三版课后习题答案编译原理是计算机科学中的一门重要课程,它研究的是如何将高级程序语言转换为机器语言的过程。
而《编译原理》第三版是目前被广泛采用的教材之一。
在学习过程中,课后习题是巩固知识、提高能力的重要环节。
本文将为读者提供《编译原理》第三版课后习题的答案,希望能够帮助读者更好地理解和掌握这门课程。
第一章:引论习题1.1:编译器和解释器有什么区别?答案:编译器将整个源程序转换为目标代码,然后一次性执行目标代码;而解释器则逐行解释源程序,并即时执行。
习题1.2:编译器的主要任务是什么?答案:编译器的主要任务是将高级程序语言转换为目标代码,包括词法分析、语法分析、语义分析、中间代码生成、代码优化和目标代码生成等过程。
第二章:词法分析习题2.1:什么是词法分析?答案:词法分析是将源程序中的字符序列划分为有意义的词素(token)序列的过程。
习题2.2:请给出识别下列词素的正则表达式:(1)整数:[0-9]+(2)浮点数:[0-9]+\.[0-9]+(3)标识符:[a-zA-Z_][a-zA-Z_0-9]*第三章:语法分析习题3.1:什么是语法分析?答案:语法分析是将词法分析得到的词素序列转换为语法树的过程。
习题3.2:请给出下列文法的FIRST集和FOLLOW集:S -> aAbA -> cA | ε答案:FIRST(S) = {a}FIRST(A) = {c, ε}FOLLOW(S) = {$}FOLLOW(A) = {b}第四章:语义分析习题4.1:什么是语义分析?答案:语义分析是对源程序进行静态和动态语义检查的过程。
习题4.2:请给出下列文法的语义动作:S -> if E then S1 else S2答案:1. 计算E的值2. 如果E的值为真,则执行S1;否则执行S2。
第五章:中间代码生成习题5.1:什么是中间代码?答案:中间代码是一种介于源代码和目标代码之间的表示形式,它将源代码转换为一种更容易进行优化和转换的形式。
编译原理第三版答案

编译原理第三版答案第一章答案1.问题:什么是编译器?答案:编译器是一种将源程序转换为目标程序的软件工具。
它负责对源代码进行词法分析、语法分析、语义分析和代码生成等一系列操作,最终生成可执行的目标程序。
2.问题:编译器的主要任务是什么?答案:编译器的主要任务是将高级语言程序转换为能被计算机硬件执行的机器码。
它包括了对源代码进行词法分析、语法分析、语义分析、中间代码生成、代码优化和目标代码生成等过程。
3.问题:编译器的工作过程是什么?答案:编译器的工作过程分为多个阶段。
首先是词法分析,将源代码拆分成一个个的词法单元。
然后是语法分析,根据语法规则构建语法树。
接着是语义分析,对语法树进行检查,确保程序的语义正确。
之后是中间代码生成和优化,将语法树转换为更加高效的中间代码。
最后是目标代码生成,将中间代码转换为特定的目标机器代码。
4.问题:编译器的优化技术有哪些?答案:编译器的优化技术包括了常量折叠、公共子表达式消除、循环优化、函数内联和代码重排等。
这些技术可以提高程序的执行效率和优化代码的空间利用率。
5.问题:编译器的应用领域有哪些?答案:编译器广泛应用于软件开发领域。
它们被用于将高级语言转换为目标机器码,用于开发操作系统、编程语言和应用软件等。
第二章答案1.问题:什么是有限自动机(DFA)?答案:有限自动机是一种表示有限状态和状态之间转换关系的模型。
它可以根据输入字符进行状态转换,最终决定是否接受某个字符串。
2.问题:有限自动机的主要组成部分是什么?答案:有限自动机主要由状态集合、输入字符集、转移函数、初始状态和接受状态集合组成。
3.问题:什么是正则表达式?答案:正则表达式是一种用于描述字符串模式的表达式。
它由普通字符和特殊字符组成,可以用于匹配符合条件的字符串。
4.问题:正则表达式的常用操作符有哪些?答案:正则表达式的常用操作符包括了字面量字符、字符类、重复操作符、选择操作符和位置操作符等。
5.问题:正则表达式如何转换为有限自动机?答案:正则表达式可以通过字面化、连接、选择和闭包等操作转换为等价的有限自动机。
(完整版)编译原理课后答案(第三版蒋立源康慕宁编)

编译原理课后答案(第三版蒋立源康慕宁编)第一章习题解答1解:源程序是指以某种程序设计语言所编写的程序。
目标程序是指编译程序(或解释程序)将源程序处理加工而得的另一种语言(目标语言)的程序。
翻译程序是将某种语言翻译成另一种语言的程序的统称。
编译程序与解释程序均为翻译程序,但二者工作方法不同。
解释程序的特点是并不先将高级语言程序全部翻译成机器代码,而是每读入一条高级语言程序语句,就用解释程序将其翻译成一段机器指令并执行之,然后再读入下一条语句继续进行解释、执行,如此反复。
即边解释边执行,翻译所得的指令序列并不保存。
编译程序的特点是先将高级语言程序翻译成机器语言程序,将其保存到指定的空间中,在用户需要时再执行之。
即先翻译、后执行。
2解:一般说来,编译程序主要由词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、代码优化程序、目标代码生成程序、信息表管理程序、错误检查处理程序组成。
3解:C语言的关键字有:auto break case char const continue default do double else enum extern float for goto if int long register return short signed sizeof static struct switch typedef union unsigned void volatile while。
上述关键字在C语言中均为保留字。
4解:C语言中括号有三种:{},[],()。
其中,{}用于语句括号;[]用于数组;()用于函数(定义与调用)及表达式运算(改变运算顺序)。
C语言中无END关键字。
逗号在C语言中被视为分隔符和运算符,作为优先级最低的运算符,运算结果为逗号表达式最右侧子表达式的值(如:(a,b,c,d)的值为d)。
5略第二章习题解答1.(1)答:26*26=676(2)答:26*10=260(3)答:{a,b,c,...,z,a0,a1,...,a9,aa,...,az,...,zz,a00,a01,...,zzz},共26+26*36+26*36*36=34658个2.构造产生下列语言的文法(1){anbn|n≥0}解:对应文法为G(S) = ({S},{a,b},{ S→ε| aSb },S)(2){anbmcp|n,m,p≥0}解:对应文法为G(S) = ({S,X,Y},{a,b,c},{S→aS|X,X→bX|Y,Y→cY|ε},S)(3){an # bn|n≥0}∪{cn # dn|n≥0}解:对应文法为G(S) = ({S,X,Y},{a,b,c,d,#}, {S→X, S→Y,X→aXb|#,Y→cYd|# },S)(4){w#wr# | w?{0,1}*,wr是w的逆序排列}解:G(S) = ({S,W,R},{0,1,#}, {S→W#, W→0W0|1W1|# },S)(5)任何不是以0打头的所有奇整数所组成的集合解:G(S) = ({S,A,B,I,J},{-,0,1,2,3,4,5,6,7,8,9},{S→J|IBJ,B→0B|IB|e, I→J|2|4|6|8, Jà1|3|5|7|9}, S)(6)所有偶数个0和偶数个1所组成的符号串集合解:对应文法为S→0A|1B|e,A→0S|1C B→0C|1S C→1A|0B3.描述语言特点(1)S→10S0S→aAA→bAA→a解:本文法构成的语言集为:L(G)={(10)nabma0n|n, m≥0}。
编译原理_第三版_课后答案

编译原理_第三版_课后答案编译原理课后题答案第二章P36-6(1)是0~9组成的数字串⑵最左推导:N= ND= NDD= NDDD = DDDD = ODDD = O1DD= 012D= 0127N= ND 二DD 二3D二34N= ND 二NDD = DDD = 5DD = 56D二568最右推导:N 二ND 二N7二ND7二N27二ND27二N127二D127二0127 N = ND = N4= D4= 34N= ND 二N8= ND8二N68二D68二568P36-7G(S)编译原理第三版课后答案O > 1|3|5|7|9N > 2|4|6|8|0D 、0|NS > 0|A0A > AD|NP36-8文法:E T T E +T|E —TT t F T* F|T/ FF > (E)|i最左推导:E = E T= T T=F T = i T = i T * F = i F * F = i i * F = i i*iE = T= T*F 二 F * F = i* F 二i *( E)二i*( E T)二i *( T T)二i *( F T) =i *( i T)二i*(i F)= i*( i i)最右推导:E= E T= E T*F= E T*i= E F*i= E i*i= T i*i= F i*i= i i*iE= T= F*T= F * F= F*( E)= F *( E T)= F *( E F)= F *( E i)=F*( T i)= F*( F i)= F*( i i)= i*(i i)/********************************P36-11*****************P36-9句子iiiei 有两个语法树:S 二 iSeS 二 iSei 二 iiSei = iiiei S= iS = iiSeS = iiSei = iiieiP36-10/**************S > TS |T T > (S)|()***************ii+i+ii-i-iii+i*i***************P36-11L1:S > ACA r aAb | abC r cC | ;L2:S > ABA》aA| ;B r bBc|bcL3:S > ABA—:aAb | ;B = aBb | ;L4:S > A| BA—;0A1| ;B-1B0| A***************/第三章习题参考答案P64 - 7(1)编译原理第三版课后答案1(01)*101(1)1101确定化:1001111最小化:{0,1,2,3,4,5},{6}{0,123,4,5}。
蒋立源编译原理第三版第三章习题与答案(修改后)
3-1 试构造一右线性文法,使得它与如下的文法等价 S→AB A → UT U → aU|a D →bT|b B → cB|c
并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图 3-2 所示的状态转换图 0
0 0 A
D
1
0 1
B
C1
F
0
1
0
E
1 题图 3-2
(1) 写出相应的右线性文法; (2) 指出它接受的最短输入串; (3) 任意列出它接受的另外 4 个输入串; (4) 任意列出它拒绝接受的 4 个输入串。
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(3) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(3) 之 (a) 所示, 给各状态重新命名,即令:
[S]=1, [A]=2, [S,B]=3 且由于 3 的组成中含有 M的终态 B,故 3 为 DFAM′的终态。于是,所构造之 DFAM′的 状态转换矩阵和状态转换图如答案图 3-4-(3) 之(b) 及(c) 所示。
π0:{1,2}, {3}
( ⅱ) 为得到下一分划,考察子集 {1,2} 。因为
{2} b ={3}
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(4) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(4) 之 (a) 所示, 给各状态重新命名,即令:
编译原理第三版课后习题答案

目录P36-6 (2)P36-7 (2)P36-8 (2)P36-9 (3)P36-10 (3)P36-11 (3)P64–7 (4)P64–8 (5)P64–12 (5)P64–14 (7)P81–1 (8)P81–2 (9)P81–3 (12)P133–1 (12)P133–2 (12)P133–3 (14)P134–5 (15)P164–5 (19)P164–7 (19)P217–1 (19)P217–3 (20)P218–4 (20)P218–5 (21)P218–6 (22)P218–7 (22)P219–12 (22)P270–9 (24)P36-6(1)L G ()1是0~9组成的数字串(2)最左推导:N ND NDD NDDD DDDD DDD DD D N ND DD D N ND NDD DDD DD D ⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒0010120127334556568最右推导:N ND N ND N ND N D N ND N D N ND N ND N D ⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒77272712712701274434886868568P36-7G(S)O N O D N S O AO A AD N→→→→→1357924680|||||||||||P36-8文法:E T E T E T TF T F T F F E i→+-→→|||*|/()| 最左推导:E E T T TF T i T i T F i F F i i F i i i E T T F F F i F i E i E T i T T i F T i i T i i F i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+********()*()*()*()*()*()*()最右推导:E E T E TF E T i E F i E i i T i i F i i i i i E T F T F F F E F E T F E F F E i F T i F F i F i i i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+⇒+**********()*()*()*()*()*()*()*()语法树:/********************************EE FTE +T F F T +iiiEEFTE-T F F T -iiiEEFT+T F FTiii*i+i+ii-i-ii+i*i*****************/P36-9句子iiiei 有两个语法树:S iSeS iSei iiSei iiiei S iS iiSeS iiSei iiiei ⇒⇒⇒⇒⇒⇒⇒⇒P36-10/**************)(|)(|S T TTS S →→***************/P36-11/*************** L1:ε||cC C ab aAb A AC S →→→ L2:bcbBc B aA A AB S ||→→→εL3:εε||aBb B aAb A AB S →→→ L4:AB B A A B A S |01|10|→→→ε ***************/第三章习题参考答案P64–7(1)确定化:最小化:{,,,,,},{}{,,,,,}{,,}{,,,,,}{,,,}{,,,,},{},{}{,,,,}{,,}{,,,},{},{},{}{,,,}{,01234560123451350123451246012345601234135012345601231010==== 3012312401234560110112233234012345610101}{,,,}{,,}{,},{,}{},{},{}{,}{}{,}{,}{,}{}{,}{}{},{},{,},{},{},{}=====P64–8(1)01)0|1(*(2))5|0(|)5|0()9|8|7|6|5|4|3|2|1|0)(9|8|7|6|5|4|3|2|1(*(3)******)110|0(01|)110|0(10P64–12(a)确定化:给状态编号:最小化:{,},{,}{,}{}{,}{}{,}{,}{,}{}{,},{},{}012301101223032330123a ba b ====(b)已经确定化了,进行最小化最小化:{{,}, {,,,}}012345011012423451305234523452410243535353524012435011012424{,}{}{,}{,}{,,,}{,,,}{,,,}{,,,}{,}{,}{,}{,}{,}{,}{,}{,}{{,},{,},{,}}{,}{}{,}{,}{,}a b a b a b a b a b a =============={,}{,}{,}{,}{,}{,}{,}10243535353524 b a baP64–14(2):给状态编号:最小化:{,},{,}{,}{}{,}{}{,}{,}{,}{}{,},{},{}0123011012231323301230101====第四章P81–1(1) 按照T,S 的顺序消除左递归ε|,)(||^)(T S T TS T T a S S G '→''→→' 递归子程序: procedure S; beginif sym='a' or sym='^' then abvance else if sym='('then beginadvance;T;if sym=')' then advance;else error;endelse errorend;procedure T;beginS;'Tend;procedure 'T;beginif sym=','then beginadvance;S;'Tendend;其中:sym:是输入串指针IP所指的符号advance:是把IP调至下一个输入符号error:是出错诊察程序(2)FIRST(S)={a,^,(}FIRST(T)={a,^,(}FIRST('T)={,,ε}FOLLOW(S)={),,,#}FOLLOW(T)={)}FOLLOW('T)={)}预测分析表是LL(1)文法P81–2文法:|^||)(|*||b a E P F F F P F T T T F T E E E T E →'→''→→''→+→''→εεε(1)FIRST(E)={(,a,b,^} FIRST(E')={+,ε} FIRST(T)={(,a,b,^} FIRST(T')={(,a,b,^,ε} FIRST(F)={(,a,b,^} FIRST(F')={*,ε} FIRST(P)={(,a,b,^} FOLLOW(E)={#,)} FOLLOW(E')={#,)} FOLLOW(T)={+,),#} FOLLOW(T')={+,),#}FOLLOW(F)={(,a,b,^,+,),#} FOLLOW(F')={(,a,b,^,+,),#} FOLLOW(P)={*,(,a,b,^,+,),#} (2)考虑下列产生式:'→+'→'→'→E E T T F F P E a b ||*|()|^||εεεFIRST(+E)∩FIRST(ε)={+}∩{ε}=φ FIRST(+E)∩FOLLOW(E')={+}∩{#,)}=φ FIRST(T)∩FIRST(ε)={(,a,b,^}∩{ε}=φ FIRST(T)∩FOLLOW(T')={(,a,b,^}∩{+,),#}=φ FIRST(*F')∩FIRST(ε)={*}∩{ε}=φFIRST(*F')∩FOLLOW(F')={*}∩{(,a,b,^,+,),#}=φ FIRST((E))∩FIRST(a) ∩FIRST(b) ∩FIRST(^)=φ 所以,该文法式LL(1)文法.(4)procedure E;beginif sym='(' or sym='a' or sym='b' or sym='^' then begin T; E' endelse errorendprocedure E';beginif sym='+'then begin advance; E endelse if sym<>')' and sym<>'#' then error endprocedure T;beginif sym='(' or sym='a' or sym='b' or sym='^' then begin F; T' endelse errorendprocedure T';beginif sym='(' or sym='a' or sym='b' or sym='^' then Telse if sym='*' then errorendprocedure F;beginif sym='(' or sym='a' or sym='b' or sym='^' then begin P; F' endelse errorendprocedure F';beginif sym='*'then begin advance; F' endendprocedure P;beginif sym='a' or sym='b' or sym='^'then advanceelse if sym='(' thenbeginadvance; E;if sym=')' then advance else error endelse errorend;P81–3/***************(1) 是,满足三个条件。
编译原理_第三版_课后答案

P133–3
(1) FIRSTVT(S)={a,^,(} FIRSTVT(T)={,,a,^,(} LASTVT(S)={a,^,)} LASTVT(T)={,,a,^,)} (2) a ^ ( ) a ^ ( ) < < < > > = >
, > > < >
, < < < > > 是算符文法,并且是算符优先文法 (3)优先函数 a f g 4 5 ^ 4 5 ( 2 5 ) 4 2 , 4 3
^
#
P (4) procedure E; begin if sym='(' or sym='a' or sym='b' or sym='^' then begin T; E' end else error end procedure E'; begin if sym='+' then begin advance; E end else if sym<>')' and sym<>'#' then error end procedure T; begin if sym='(' or sym='a' or sym='b' or sym='^' then begin F; T' end else error end procedure T'; begin if sym='(' or sym='a' or sym='b' or sym='^' then T else if sym='*' then error end procedure F; begin if sym='(' or sym='a' or sym='b' or sym='^' then begin P; F' end else error end procedure F'; begin if sym='*' then begin advance; F' end end
编译原理 第3章习题解答
第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA 确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉 〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉 〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉 〈字母〉→a ∣b 〈数字〉→1∣2试写出相应的有限自动机和状态图。
3.9 图3.29所示的是一个NDFSA A ,试构造一个正规文法G ,使得L(G)= L(A)。
编译原理第三版课后答案

编译 原理 课后题答案第二章P36-6(1)L ( G 1 )是0~9 构成的数字串(2)最左推导 :N ND NDD NDDD DDDD0DDD01DD012D 0127N ND DD 3D34NNDNDDDDD5DD56D568最右推导 :N ND N 7 ND 7 N 27 ND 27N 127D1270127NND N 4 D 4 34N NDN 8ND 8N 68D68 568P36-7G(S)O 1|3|5|7|9N 2|4|6|8|O D0|NS O| AO A AD | NP36-8文法:E T| E T|E TT F |T * F |T / F F ( E)|i最左推导 :E E T T TF Ti Ti T * Fi F * F i i * F i i * i ETT * F F * F i * F i *( E ) i *( ET)i *( T T )i *( FT )i *( i T )i *( i F )i *( ii )最右推导 :E E T E T *F E T * i E F * i E i * i T i * i F i * i i i * iE TF * T F * F F *( E) F *( E T) F *( E F ) F *( E i )F *( T i ) F *( F i ) F *( i i ) i *( i i )语法树: /********************************EE+TE+T FT F iF iii+i+i*****************/P36-9句子 iiiei有两个语法树:S iSeS iSei iiSei iiiei S iS iiSeS iiSei iiieiE EE+T E-T T T*FE-T F F F iT F i i iF iii-i-i i+i*iP36-10/**************S TS | T T( S) | ( )***************/P36-11/*************** L1:S ACA aAb | ab C cC |L2:S ABA aA |B bBc | bcL3:S ABA aAb | BaBb |L4:S A | BA0 A1|B 1B0 | A***************/第三章习题参照答案P64–7(1)1(01|) * 101X Y1101X12345Y1确立化:01 {X}φ{1,2,3}φφφ{1,2,3}{2,3}{2,3,4}{2,3}{2,3}{2,3,4}{2,3,4}{2,3,5}{2,3,4}{2,3,5}{2,3}{2,3,4,Y}{2,3,4,Y}{2,3,5}{2,3,4,}10230011010145111最小化:{ 0,1,2,3,4,5},{ 6}{ 0,1,2,3,4,5} 0{1,3,5}{ 0,1,2,3,4,5} 1{1,2,4,6} { 0,1,2,3,4},{ 5},{ 6}{ 0,1,2,3,4} 0{1,3,5}{ 0,1,2,3},{ 4},{ 5},{ 6}{ 0,1,2,3} 0{1,3}{0,1,2,3} 1{12,,4}{ 0,1},{2,3}{ 4},{ 5},{6}{ 0,1} 0{1}{ 0,1} 1{1,2}{ 2,3} 0{ 3}{ 2,3} 1{4}{ 0},{ 1},{ 2,3},{ 4},{ 5},{ 6}1020010011341116 5P64–8(1)(1 | 0)* 01(2)(1 | 2 | 3| 4 | 5 | 6 | 7 | 8 | 9)(0 |1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9)* (0 | 5) | (0 | 5) (3)0*1( 0 | 10* 1) * |1* 0( 0 |10* 1) *P64–12(a)aa,b01a确立化:a b{0}{0,1}{1}{0,1}{0,1}{1}{1}{0}φφφφ给状态编号:a b012112203333 aa01a b b bb23a最小化:{ 0,1},{2,3}{ 0,1} a{1}{0,1} b{ 2}{ 2,3} a{ 0,3}{ 2,3} b{ 3}{ 0,1},{2},{3}a ab b012ab(b)b b a023a baa bb1a5a a4已经确立化了 ,进行最小化最小化:{{ , }, {,,,}}0 1 2 3 4 5{ 0,1} a{1}{ 0,1} b{ 2,4}{ 2, 3,4,5} a{ 1, 3, 0, 5}{ 2,3,4,5} b{ 2,3,4,5} { 2, 4} a{ 1, 0}{2,4} b{ 3,5}{ 3, 5} a{ 3,5}{ 3,5} b{ 2, 4}{{ 0,1},{ 2, 4},{ 3,5}}{ 0,1} a{1}{ 0,1} b{ 2,4}{ 2, 4} a{ 1, 0}{2,4} b{ 3,5}{ 3, 5} a{ 3,5}{ 3,5} b{ 2, 4}b b a012a baP64–14(1)0101(2):X( 010|)*Y21X1Y确立化:01 {X,1,Y}{1,Y}{2}{1,Y}{1,Y}{2}{2}{1,Y}φφφφ给状态编号:01 01211221333311011123最小化:{ 0,1},{ 2, 3}{ 0,1} 0{1}{ 0,1} 1{2}{ 2,3} 0{1,3}{ 2,3} 1{3}{ 0,1},{ 2},{ 3}111013第四章P81–1(1)依据 T,S 的次序除去左递归G (S)S a |^| (T )T STT, ST |递归子程序:procedure S;beginif sym='a' or sym='^'then abvanceelse if sym='('then beginadvance;T;if sym=')' then advance;else error;endelse errorend;procedure T;beginS; Tend;procedure T ;beginif sym=','then beginadvance;S; Tendend;此中 :sym: 是输入串指针IP 所指的符号advance: 是把 IP 调至下一个输入符号error:是犯错诊察程序(2)FIRST(S)={a,^,(}FIRST(T)={a,^,(}FIRST( T )={,,}FOLLOW(S)={),,,#}FOLLOW(T)={)}FOLLOW(T )={)}展望剖析表a^(),# S S a S ^S (T)T T ST T ST T STT T T, ST是LL(1) 文法P81–2文法:E TEE E |T FTT T |FPFF* F |P( E) | a | b |^(1)FIRST(E)={(,a,b,^}FIRST(E')={+,ε }FIRST(T)={(,a,b,^}FIRST(T')={(,a,b,^,ε }FIRST(F)={(,a,b,^}FIRST(F')={*,ε }FIRST(P)={(,a,b,^}FOLLOW(E)={#,)}FOLLOW(E')={#,)}FOLLOW(T)={+,),#}FOLLOW(T')={+,),#}FOLLOW(F)={(,a,b,^,+,),#}FOLLOW(F')={(,a,b,^,+,),#}FOLLOW(P)={*,(,a,b,^,+,),#}(2)考虑以下产生式:E E|T T|F* F |P( E )|^| a|bFIRST(+E) ∩ FIRST( ε )={+}∩{ ε }= φFIRST(+E) ∩ FOLLOW(E')={+} ∩ {#,)}=φFIRST(T)∩FIRST( ε)={(,a,b,^}∩ { ε}= φFIRST(T)∩FOLLOW(T')={(,a,b,^}∩ {+,),#}=φFIRST(*F')∩ FIRST(ε )={*}∩ {ε }=φFIRST(*F')∩ FOLLOW(F')={*}∩ {(,a,b,^,+,),#}= FIRST((E)) ∩ FIRST(a)∩ FIRST(b)∩FIRST(^)=所以 , 该文法式LL(1) 文法 .φφ(3)+*()a b^#E E TE 'E TE ' E TE ' E TE 'E'E E E E T T FT T FT T FT T FTT' FF' P T T T T T T T T T T TF PF F PF F PF F PFF F* F F F F F F FP( E )P a P b P^(4)procedure E;beginif sym='(' or sym='a' or sym='b' or sym='^' then begin T; E' endelse errorendprocedure E';beginif sym='+'then begin advance; E endelse if sym<>')' and sym<>'#' then error endprocedure T;beginif sym='(' or sym='a' or sym='b' or sym='^' then begin F; T' endelse errorendprocedure T';beginif sym='(' or sym='a' or sym='b' or sym='^' then Telse if sym='*' then errorendprocedure F;beginif sym='(' or sym='a' or sym='b' or sym='^' then begin P; F' endelse errorendprocedure F';beginif sym='*'then begin advance; F' endendprocedure P;beginif sym='a' or sym='b' or sym='^'then advanceelse if sym='(' thenbeginadvance; E;if sym=')' then advanceelse errorendelse errorend;P81–3/***************(1)是,知足三个条件。
编译原理(第3版)课本习题答案

第二章 高级语言及其语法描述6.(1)L (G 6)={0,1,2,......,9}+(2)最左推导:N=>ND=>NDD=>NDDD=>DDDD=>0DDD=>01DD=>012D=>0127 N=>ND=>DD=>3D=>34N=>ND=>NDD=>DDD=>5DD=>56D=>568 最右推导:N=>ND =>N7=>ND7=>N27=>ND27=>N127=>D127=>0127 N=>ND=>N4=>D4=>34N=>ND=>N8=>ND8=>N68=>D68=>5687.【答案】G:S →ABC | AC | CA →1|2|3|4|5|6|7|8|9B →BB|0|1|2|3|4|5|6|7|8|9C →1|3|5|7|98.(1)最左推导:E=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*iE=>T=>T*F=>F*F=>i*F=>i*(E)=>i*(E+T)=>i*(T+T)=>i*(F+T)=>i*(i+T)=>i*(i+F)=>i*(i+i) 最右推导:E=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i=>i+i*iE=>T=>T*F=>T*(E)=>T*(E+T)=>T*(E+F)=>T*(E+i)=>T*(T+i)=>T*(F+i)=>T*(i+i)=>F*(i+i)=>i*(i+i) (2)9.证明:该文法存在一个句子iiiei 有两棵不同语法分析树,如下所示,因此该文法是二义的。
编译原理第3章习题及答案(文法和语言)

17.教材3.14题
18.教材3.16题
习题 第3章 文法和语言 参考答案
1.写一文法,使其语言是偶整数集合。
解:允许以0打头
G:N→+A|-A|A
A→DA|E
D→0|1|2|3|4|5|6|7|8|9
E→0|2|4|6|8
2.写一文法,使其语言是偶整数集合,但不允许由0打头。
Q→b
A→aAQBR|a
R→c
11.已知C语言的下标变量形如:
a[E][E]…[E]
按第10题要求的文法G2的形式写出下标变量文法。
解:G:S→aA
A→[EB
B→]A
B→]
12.设有文法G1:S → aBcA
S → aBdB
A → bA
A → aB
B → BdBຫໍສະໝຸດ → a将其改写成文法G2,使得对每个非终结符均无两个不同规则能导出相同的终结开头符。
解:二义性文法G:S→aS|Sa|a
∵句子aa存在两棵语法树:
∴G是二义性文法。
17.教材3.14题
解:(1) G1:S→CD (2) G2:S→1S0|A (3) G3:S→0S0|aSa|a
C→aCb|A→0A1|
D→aDb|
18.教材3.16题
解:(1) G1:A→aA|(2) G2:A→aA|aB (3) G3:A→aA|bB|cC|
A → a
将其改写成以下形式的文法G2,每条规则形如:
V → pX1X2…Xn
或V → q
其中V和Xi为非终结符,p和q为终结符。
11.已知C语言的下标变量形如:
a[E][E]…[E]
按第10题要求的文法G2的形式写出下标变量文法。
《编译原理》蒋立源课后答案【khdaw_lxywyl】

www.khd课后a答w案.网com
课后答案网
最右推导: <程序>T<分程序>T<标号>:<分程序> T<标号>:<标号>:<分程序> T<标号>:<标号>:<无标号分程序> T<标号>:<标号>:<分程序首部>;<复合尾部> T<标号>:<标号>:<分程序首部>;<语句>;<复合尾部> T<标号>:<标号>:<分程序首部>;<语句>;<语句>;end T<标号>:<标号>:<分程序首部>;<语句>;s;end T<标号>:<标号>:<分程序首部>;s;s;end T<标号>:<标号>:<分程序首部>;说明;s;s;end T<标号>:<标号>:<分程序首部>;d;s;s;end T<标号>:<标号>:begin 说明;d;s;s;end T<标号>:<标号>:begin d;d;s;s;end T<标号>: L:begin d;d;s;s;end TL:L:begin d;d;s;s;end (2)句子 L:L:begin d;d;s;s end 的相应语法树是:
第二章 习题解答
1.(1)答:26*26=676
(2)答:26*10=260
(3)答:{a,b,c,...,z,a0,a1,...,a9,aa,...,az,...,zz,a00,a01,...,zzz}, 共 26+26*36+26*36*36=34658 个
编译原理_第三版_课后答案

1 0 a b (b) b 0 3 2 a a a b 5 4 1 a 已经确定化了,进行最小化 最小化: b 0 2 1 a a b b a a b a b b a
P64–14
(1) 1 0 0 1
0 (2):
Y X 2 0 1 Y 1 X 0 确定化: 0 {X,1,Y} {1,Y} {2} φ 给状态编号: 0 1 2 3 0 1 0 {1,Y} {1,Y} {1,Y} φ 0 1 1 1 3 1 {2} {2} φ φ 1 2 2 3 3
P36-10
/************** ***************/
P36-11
/*************** L1: L2: L3: L4: ***************/
第三章习题参考答案 P64–7
(1)
X Y 0 X 1 2 3 4 Y 5 1 1 1 确定化: 0 {X} φ {1,2,3} {2,3} {2,3,4} {2,3,5} {2,3,4,Y} φ φ {2,3} {2,3} {2,3,5} {2,3} {2,3,5} 0 1 3 2 0 1 {1,2,3} φ {2,3,4} {2,3,4} {2,3,4} {2,3,4,Y} {2,3,4,} 1 0
动
进 进 归
进
归
P134–5
(1)
0. 4. 8. (2) 1
1. 5. 9. 6. 10.
2. 11.
3. 7.
S 9 8 7 S a 11 10 0
A
4 3 2 A d 5 6 确定化: S {0,2,5,7,10} {1,2,5,7,8,10} {2,3,5,7,10} {2,5,7,8,10} {1,2,5,7,8,10} {2,5,7,8,10} {2,4,5,7,8,10} {2,5,7,8,10} A {2,3,5,7,10} {2,3,5,7,9,10} {2,3,5,7,10} {2,3,5,7,9,10} a {11} {11} {11} {11} b {6} {6} {6} {6} S
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章习题3-1 试构造一右线性文法,使得它与如下的文法等价S→AB A→UT U→aU|a D→bT|b B→cB|c 并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图3-2所示的状态转换图(1) 写出相应的右线性文法;(2) 指出它接受的最短输入串;(3) 任意列出它接受的另外4个输入串;(4) 任意列出它拒绝接受的4个输入串。
3-3 对于如下的状态转换矩阵:(1) 分别画出相应的状态转换图;(2) 写出相应的3型文法;(3) 用自然语言描述它们所识别的输入串的特征。
3-4 将如下的NFA确定化和最小化:3-5 将如题图3-5所示的具有ε动作的NFA确定化。
题图3-5 具有ε动作的NFA3-6 设有文法G[S]:S→aA A→aA|bB B→bB|cC|c C→cC|c 试用正规式描述它所产生的语言。
3-7 分别构造与如下正规式相应的NFA。
(1) ((0* |1)(1* 0))*(2) b|a(aa*b)*b3-8 构造与正规式(a|b)*(aa|bb)(a|b)*相应的DFA。
第3章习题答案3-1 解:根据文法知其产生的语言是:L[G]={a m b n c i| m,n,i≧1}可以构造与原文法等价的右线性文法:S→aA A→aA|bB B→bB|cC|c C→cC|c 其状态转换图如下:3-2 解:(1) 其对应的右线性文法是G[A]:A →0D B→0A|1C C→0A|1F|1D→0B|1C E→0B|1C F→1A|0E|0(2) 最短输入串为011(3) 任意接受的四个输入串为:0110,0011,000011,00110(4) 任意拒绝接受的输入串为:0111,1011,1100,10013-3 解:(1) 相应的状态转换图为:(2) 相应的3型文法为:(ⅰ) S→aA|bS A→aA|bB|b B→aB|bB|a|b(ⅱ) S→aA|bB|a A→bA|aC|a|b B→aB|bC|b C→aC|bC|a|b(ⅲ) S→aA|bB|b A→aB|bA|a B→aB|bB|a|b(ⅳ) S→bS|aA A→aC|bB|a B→aB|bC|b C→aC|bC|a|b(3) 用自然语言描述的输入串的特征为:(ⅰ) 以任意个(包括0个)b开头,中间有任意个(大于1)a,跟一个b,还可以有一个由a,b组成的任意字符串。
(ⅱ) 以a打头,中间有任意个(包括0个)b,再跟a,最后由一个a,b所组成的任意串结尾;或者以b打头,中间有任意个(包括0个)a,再跟b,最后由一个a,b所组成的任意串结尾。
(ⅲ) 以a打头,后跟任意个(包括0个)b ,再跟a,最后由一个a,b所组成的任意串结尾;或者以b打头,由一个a,b所组成的任意串结尾。
(ⅳ) 以任意个(包括0个)b开头,中间跟aa,最后由一个a,b所组成的任意串结尾;或者以任意个(包括0个)b开头,中间跟ab后,再接任意个(包括0个)a,再接b,最后由一个a,b所组成的任意串结尾。
3-4 解:(1) 将NFA M确定化后得DFA M′,其状态转换矩阵如答案图3-4-(1)之(a)所示,给各状态重新命名,即令:[S]=1, [S,A]=2, [A,B]=3, [B]=4且由于3及4的组成中均含有M的终态B,故3和4组成了DFA M′的终态集Z′。
于是,所构造之DFA M′的状态转换矩阵和状态转换图如答案图3-4-(1)之(b)及(c)所示。
现将DFA M′最小化:(ⅰ)初始分划由两个子集组成,即π0:{1,2}, {3,4}(ⅱ)为得到下一分划,考察子集{1,2}。
因为{2}b ={3}⊂{3,4}但 {1}b =∅故1和2可区分,于是便得到下一分划π1: {1}, {2}, {3,4}(ⅲ)又因π1≠π0 ,再考虑{3,4},因为{3}b ={3}⊂{3,4}而 {4}b =∅故3和4可区分,从而又得到π2: {1}, {2}, {3}, {4}此时子集已全部分裂,故最小化的过程宣告结束,M′即为状态数最小的DFA。
(2) 将NFA M确定化后得DFA M′,其状态转换矩阵如答案图3-4-(2)之(a)所示,给各状态重新命名,即令:[S]=1, [A]=2, [B,C]=3且由于3的组成中含有M的终态C,故3为DFA M′的终态。
于是,所构造之DFA M′的状态转换矩阵和状态转换图如答案图3-4-(2)之(b)及(c)所示。
现将DFA M′最小化:(ⅰ)初始分划由两个子集组成,即π0:{1,2}, {3}(ⅱ)为得到下一分划,考察子集{1,2}。
因为{2}b ={2}⊂{1,2}但 {1}b =∅故1和2可区分,于是便得到下一分划π1: {1}, {2}, {3}此时子集已全部分裂,故最小化的过程宣告结束,M′即为状态数最小的DFA。
(3) 将NFA M确定化后得DFA M′,其状态转换矩阵如答案图3-4-(3)之(a)所示,给各状态重新命名,即令:[S]=1, [A]=2, [S,B]=3且由于3的组成中含有M的终态B,故3为DFA M′的终态。
于是,所构造之DFA M′的状态转换矩阵和状态转换图如答案图3-4-(3)之(b)及(c)所示。
现将DFA M′最小化:(ⅰ)初始分划由两个子集组成,即π0:{1,2}, {3}(ⅱ)为得到下一分划,考察子集{1,2}。
因为{2}b ={3}但 {1}b =故1和2可区分,于是便得到下一分划π1: {1}, {2}, {3}此时子集已全部分裂,故最小化的过程宣告结束,M′即为状态数最小的DFA。
(4) 将NFA M确定化后得DFA M′,其状态转换矩阵如答案图3-4-(4)之(a)所示,给各状态重新命名,即令:[A]=1, [B,C]=2, [B]=3, [C]=4且由于2和4的组成中含有M的终态C,故2和4组成了DFA M′的终态集Z′。
于是,所构造之DFA M′的状态转换矩阵和状态转换图如答案图3-4-(4)之(b)及(c)所示。
现将DFA M′最小化:(ⅰ)初始分划由两个子集组成,即π0:{1,3}, {2,4}(ⅱ)为得到下一分划,考察子集{1,3}。
因为{1}a ={2}⊂{2,4}但 {3}a ={1}⊂{1,3}故1和3可区分,于是便得到下一分划π1: {1}, {3}, {2,4}(ⅲ)又因π1≠π0,再考虑{2,4},因为{2}a ={4}a ={1}, {2}b ={4}b ={4}所以2和4不可区分,故子集{S,B}已不能再分裂。
此时π 2 =π 1 ,子集分裂的过程宣告结束。
(ⅳ) 现选择状态2作为{2,4}的代表,将状态4从状态转换图中删去,并将原来引至4的矢线都引至2,这样,我们就得到了最小化后的DFA M〞如答案图3-4-(4)之(d)所示。
3-5 解:(1) 将具有ε动作的NFA M确定化后得DFA M′,其状态转换矩阵如答案图3-5-(1)之(a)所示,给各状态重新命名,即令:[S,B,C]=1, [A]=2, [B,C] =3, [C]=4且由于1,3和4的组成中均含有M的终态C,故1,3和4组成了DFA M′的终态集Z′。
于是,所构造之DFA M′的状态转换矩阵和状态转换图如答案图3-5-(1)之(b)及(c)所示。
(2) 将具有ε动作的NFA M确定化后得DFA M′,其状态转换矩阵如答案图3-5-(2)之(a)所示,给各状态重新命名,即令:[S]=1, [Z]=2, [R,U] =3, [S,X]=4,[R,U,Y]=5, [S,U,X]=6, [S,Z]=7, [R,U,Y,Z]=8且由于2,7和8的组成中均含有M的终态Z,故2,7和8组成了DFA M′的终态集Z′。
于是,所构造之DFA M′的状态转换矩阵和状态转换图如答案图3-5-(2)之(b)及(c)所示。
3-6 解:首先将文法写成方程组:S=aA (1)A=aA+bB (2)B=bB+cC+c (3)C=cC+c (4) 将(4)代入(3),得:B=bB+C (5) 由论断3.1,方程(4)的解为:C=c*c将上式代入(5),得:B=bB+c*c由论断3.1,得:B=b*c*c将上式代入(2),得:A=aA+b*bc*c由论断3.1,得:A=a*b*bc*c将上式代入(1),得:S=a*ab*bc*c即文法所产生的语言可用正规式a*ab*bc*c表示。
3-7 解:(1) 构造与正规式((0* |1)(1* 0))*相应的NFA的步骤如答案图3-7-(1)所示:(2) 构造与正规式 b|a(aa*b)*b 相应的NFA的步骤如答案图3-7-(2)所示:答案图3-7-(2) 正规式 b|a(aa*b)*b 的NFA 3-8 解:首先,构造与正规式(a|b)*(aa|bb)(a|b)*相应的NFA M,其构造步骤如答案图3-8(a)所示:其次,将答案图3-8(a)所示的具有ε动作的NFA M确定化后得到DFA M′,其状态转换矩阵如答案图3-8(b)所示,给各状态重新命名,即令:[S,3,1]=S, [3,1,5]=A, [3,1,6] =B, [3,1,5,2,4,Z]=C,[3,1,6,2,4,Z]=D, [3,1,6,4,Z]=E, [3,1,5,4,Z]=F且由于C,D,E和F的组成中均含有NFA M的终态Z,故C,D,E和F组成了DFA M′的终态集Z′。
于是,将NFA M确定化后所得DFA M′的状态转换矩阵和状态转换图如答案图3-8(c)及(d)所示。
(e) 对DFA M′最小化后所得的DFA M〞的状态转换图答案图3-8最后,将所得DFA M′最小化:(ⅰ)初始分划由两个子集组成,即π0:{S,A,B}, {C,D,E,F}(ⅱ)为得到下一分划,考察子集{S,A,B}。
因为{S,B}a ={A}⊂{S,A,B}但 {A}a ={C}⊂{C,D,E,F}故S,B和A可区分,于是便得到下一分划π1: {S,B}, {A}, {C,D,E,F}(ⅲ)因π 1 ≠π0 ,考虑{S,B},因为{S}b ={B}⊂{S,B}但 {B}b ={D}⊂{C,D,E,F}故S和B可区分,于是便得到下一分划π2: {S}, {B}, {A}, {C,D,E,F}(ⅳ) 又因π 2 ≠π 1 ,再考虑{C,D,E,F},因为{C}a ={F}a ={C}, {C}b ={F}b ={E}所以C和F等价;同理可得D和E等价。
又因为{C}a ={C}, {D}a ={F},{C}b ={E}, {D}b ={D}而C和F等价,D和E等价,所以C和D也等价,故C,D,E,F这4个状态等价。
此时π 3 =π 2 ,子集分裂的过程宣告结束。
(ⅴ)现选择状态C作为{C,D,E,F}的代表,将状态D,E,F从状态转换图中删去,并将原来引至D,E,F的矢线都引至C,这样,我们就得到了最小化后的DFA M〞如答案图3-8(e)所示,此DFA M〞即为所求的与正规式(a|b)*(aa|bb)(a|b)*相应的DFA。
