试验设计与数据处理(第二版)课后习题答案.(1)
最新试验设计与数据处理课后答案

试验设计与数据处理》第三章:统计推断3- 13解:取假设HO : u1-u2w 0和假设H1: u1-u2 > 0用sas 分析结果如下:Sample StatisticsGroupNMeanStd. Dev.Std. Errorx8 0.231875 0.0146 0.0051 y100.20970.00970.0031Hypothesis TestNull hypothesis:Mean 1 - Mean 2 = 0Alternative:Mean 1 - Mean 2 A= 0If Varianees Aret statistie DfPr > tEqual3.878 16 0.0013 Not Equal3.70411.670.0032由此可见p 值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中 由 3 个字母组成的词的比例均值差异显著。
3-14解:用sas 分析如下: Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1 Alternative:Varia nee 1 / Varia nee 2 A = 1- Degrees of Freedom -FNumer. Denom.Pr > F第四章:方差分析和协方差分析4- 1 解:Sas 分析结果如下:Dependent Variable: ySum ofSouree DF Squares Mean Square F Value Pr > F Model 41480.823000370.20575040.88<.00012.27 7 由p 值为0.2501 > 0.05 (显著性水平) 9 0.2501,所以接受原假设, 两方差无显著差异Source DF Type I SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n627.000000004.500000000.830.5684Source DF Type III SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n 627.000000004.500000000.830.5684由结果可知, 在不同浓度下得率有显著差异, 在不同温度下得率差异不明显, 交 互作用的效应不显著。
试验设计与数据处理Experimentdesignanddataprocessing回归分析

(j=1,2,…,m) • 多元线性回归方程:
yˆ a b1x1 b2 x2 ... bm xm
偏回归系数:
b1,b2,...,bm
16
第17页/共28页
(2)回归系数的确定
• 根据最小二乘法原理 :求偏差平方和最小时的回归系 数
• -1≤r≤1 • r=±1:x与y有精确的线性关系
y
y
r=1
r=-1
x
x
8
第9页/共28页
• r<0:x与y负线性相关(negative linear correlation) • r>0:x与y正线性相关(positive linear correlation)
y y
0<r<1
-1<r<0
x
i 1
jk
25
第26页/共28页
4.5 Excel在回归分析中的应用
4.5.1 “规划求解”在回归分析中应用
• 解方程组 • 最优化
4.5.2 Excel内置函数在回归分析中应用 4.5.3 Excel图表功能在回归分析中的应用 4.5.4 分析工具库在回归分析中应用
26
第27页/共28页
感谢您的观看!
x
9
第10页/共28页
r=0
r=0
y y
x
x
• r≈0时 ,x与y没有线性关系 ,但可能存在其它类型关 系
• 相关系数r越接近1,x与y的线性相关程度越高 • 试验次数越少 , r越接近1
10
第11页/共28页
③相关系数检验 • 对于给定的显著性水平α,
查相关系数临界值rmin
实验设计与数据处理第五章例题及课后习题答案

习题5.1、
优选过程:
1、首先在试验范围0.618处做第一个实验,这一点的温度为:x1=340+(420-340)×
0.618=389.44.
2、在这点的对称点,即0.382处做一个实验,这一点的温度为:x2=420-(420-340)×0.618=370.56.
3、比较两次的实验结果,发现第一点比第二点的合成率高,故舍去370.56以下部分,在
370.56-420之间,找x1的对称点:x3=420-(420-370.56)×0.618=389.44608.
4、比较两次的实验结果,发现第一点比第三点的合成率高,故舍去389.44608以下部分,
在389.44608-420之间,找x1的对称:x4=420-(420-389.44608)×0.618=401.11767744. 5、比较两次的实验结果,得到最佳点为401.1177。
习题5.2、
优选过程:
1、首先在试验范围3/5处做第一个实验,这一点加入的白砂糖桶数为:
x1=3+3/5*(8-3)=6桶
2、在这点的对称点,即2/5处做一个实验,这一点加入的白砂糖桶数为:
x2=8-3/5*(8-3)=5桶
3、比较两次的实验结果,发现第一点比第二点的实验结果好,故舍去5以下的部分,在5-8之间,找x1的堆成点
习题5.3
目标函数。
实验设计与数据处理课后答案

《试验设计与数据处理》专业:机械工程班级:机械11级专硕学号:S110805035 姓名:赵龙第三章:统计推断3-13 解:取假设H0:u1-u2≤0和假设H1:u1-u2>0用sas分析结果如下:Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
3-14 解:用sas分析如下:Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1Alternative: Variance 1 / Variance 2 ^= 1- Degrees of Freedom -F Numer. Denom. Pr > F----------------------------------------------2.27 7 9 0.2501由p值为0.2501>0.05(显著性水平),所以接受原假设,两方差无显著差异第四章:方差分析和协方差分析4-1 解:Sas分析结果如下:Dependent Variable: ySum ofSource DF Squares Mean Square F Value Pr > FModel 4 1480.823000 370.205750 40.88 <.0001Error 15 135.822500 9.054833Corrected Total 19 1616.645500R-Square Coeff Var Root MSE y Mean0.915985 13.12023 3.009125 22.93500Source DF Anova SS Mean Square F Value Pr > Fc 4 1480.823000 370.205750 40.88 <.0001由结果可知,p值小于0.001,故可认为在水平a=0.05下,这些百分比的均值有显著差异。
实验设计与数据处理(第二版部分答案)

试验设计与数据处理学院班级学号学生指导老师第一章 4、 相故100g 中维生素C 的质量围为:。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则2)、1mm 的汞柱代表的大气压为0.133KPa , 所以3)、1mm 则:6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 20.002136667总体方差σ20.001780556|||69.947|7.747 6.06d x =-=>算术平均误差△0.038333333极差R 0.117、S₁²=3.733,S₂²=2.303F=S₁²/S₂²=3.733/2.303=1.62123而F 0.975(9.9)=0.248386,F0.025(9.9)=4.025994所以F 0.975(9.9)< F <F0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
分析人员A 分析人员B8 7.5 样本方差1 3.7333338 7.5 样本方差2 2.30277810 4.5 Fa值0.248386 4.02599410 4 F值 1.621236 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量1 变量2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量1 变量2平均0.025684615 2.291111111方差0.000005861 0.031611111观测值13 9df 12 8F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349.检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
试验设计与数据处理课后习题

试验设计与数据处理课后习题试验设计与数据处理课后习题第三章3-7分别使用金球和铂球测定引力常数(单位:)1. 用金球测定观察值为 6.683,6.681, 6.676, 6.678, 6.679, 6.6722. 用铂球测定观察值为 6.661, 6.661,6.667, 6.667, 6.664设测定值总体为N(u,)试就1,2两种情况求u的置信度为0.9的置信区间,并求的置信度为0.9的置信区间。
用sas分析结果如下:第一组:第二组:3-13下表分别给出两个文学家马克吐温的8篇小品文以及斯诺特格拉斯的10篇小品文中由3个字母组成的词的比例:马克吐温: 0.225 0.262 0.217 0.240 0.230 0.229 0.235 0.217斯诺特格拉斯:0.209 0.205 0.196 0.210 0.202 0.207 0.224 0.223 0.220 0.201设两组数据分别来自正态总体,且两个总体方差相等,两个样本相互独立,问两个作家所写的小品文中包含由3个字母组成的词的比例是否有显著差异(a 0.05)取假设H0:u1-u2≤0和假设H1:u1-u2>0用sas分析结果如下:Sample StatisticsGroup N Mean Std. Dev. Std. Errorx 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 0Alternative: Mean 1 - Mean 2 ^ 0If Variances Are t statistic Df Pr tEqual 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
实验设计与数据处理(第二版部分答案)教学内容

实验设计与数据处理(第二版部分答案)试验设计与数据处理学院班级学号学生姓名指导老师第一章4、相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为:18.2±0.0182mg 。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则 max 0.2 1.5%0.003330.3758R x MPa KPax E x ∆=⨯==∆=== 2)、1mm 的汞柱代表的大气压为0.133KPa , 所以max 20.1330.1331.6625108R x KPax E x -∆=∆===⨯ 3)、1mm 水柱代表的大气压为gh ρ,其中29.8/g m s = 则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667总体方差σ20.001780556算术平均误差△ 0.038333333 极差R 0.117、S ₁²=3.733,S ₂²=2.303F =S ₁²/ S ₂²=3.733/2.303=1.62123而F 0.975 (9.9)=0.248386,F 0.025(9.9)=4.025994 所以F 0.975 (9.9)< F <F 0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
分析人员A分析人员B8 7.5 样本方差1 3.733333 8 7.5 样本方差2 2.302778 10 4.5 Fa 值 0.248386 4.025994104F 值1.62123|||69.947|7.747 6.06p pd x =-=>6 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 df 12 8 F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349. 检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
实验设计与数据处理习题答案完整版

部分习题答案习题三1、62621086.6S 104.1ˆ002.74ˆ--⨯=⨯=σ=μ2、λ的极大似然估计和矩估计量均为x =λˆ 3、5、 6、(1)(5.608, 6.392) (2)(5.558, 6.442) 7、(1)(6.675, 6.681), (6.8×10-6, 6.8×10-5) (2)(6.61, 6.667), (3.8×10-6, 5.06×10-5) 8、σ已知6.239;σ未知6.356 9、4.052610、接受H O 11、认为不合格 12、认为显著大于10 13、拒绝H O 19、接受H O习题四1、差异显著;2、只有浓度的影响是显著的.习题五1、 填料A 用量范围可能选低了.2、培烧温度与三氧化铝两个因素用量范围可能偏低.习题六1、(2)xy5503.129584.13ˆ+= (4)(11.82,13.28)(5)(19.66,20.18) 2、xy05886.06287.24ˆ+= 3、(2))17.14,29.13)(3(,988.0104.0ˆx y+-=4、x0867318.0e 4556.32y ˆ-=5、2020381.00086.10333.19ˆx x y-+= 6、(1)31321x15.1x 575.09.9yˆ)2(x 15.1x 55.0x 575.09.9yˆ++=+++=习题七1、218.079.1419.300ˆz z y+-= 2、)1(21-=n c 212211,n n n b n n n a +=+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-+-⎪⎭⎫⎝⎛-+⨯+⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-++=-625.1589625.1102879.11025.105613.0625.160073.0263.2ˆ332z z z z y3、 4、 5、 6、 最优工艺条件 7、 最优凝固条件 即 8、.078.1=γ习题八习题九(1) E(5, , 0) (2)(i)扩大反射)1(>α;(ii)内收缩)0(<α;(iii )反射收缩)10(<α<;(3)B(2,4,3),A '(1.5,3,3.5),D '(2.5,2.5,2.5),C '(3,3.5,2)习题十1、 A 3B 3C 32、A 2B 3CD3、最优工艺条件x 1=-0.076,x 2=-0.118,即z 1=3. 848,z 2=0. 753,9.37ˆ=y4、 最优适宜条件 x 1=-0.0135, x 2=0.2557,x 3=-0.3364, 即z 1=6.4865, z 2=112.7865,z 3=0.3318.习题十一1、3.3962、3.54, 3.463、 5、6、 7、有系统误差2221212122212121z 9.21z 676.0z z 469.4z 465.50z 566.8572.2x504.3x 704.2xx 575.3x 1.1x 833.0838.37yˆ---++=-----=323121232221321x x 3.5x x 35.2x x 78.2x 38.3x 8.2x 1.3x 95.0x 388.0x 163.04.37y ˆ---------=.nσ.T2l g⎪⎭⎫⎝⎛σ+⎪⎭⎫⎝⎛σ≈σ.VMVV,VW W M σ+σ+σ≈σ-=.z 0019.0z 0148.0z 1388.0z 1269.06250.47yˆ4321--++=.z z 2.2z 15.058.125y ˆ321+++-=.z 0201.0z 00225.0z 00184.0z 000885.0114.0y ˆ4321-+--=,x 041.0x 023.0.x x 002.0x 052.0x 017.0351.0yˆ22212121--+++=.371.0yˆ,576.8z ,9.119z ,644.0x ,398.0x 2121=====即xx 02.0xx 025.0x025.0x475.0x 400.0218.89yˆ-+-++=,x 896.0x947.0x 399.0x x 375.023222132---+,0735.0x ,261.0x,483.0x 321===.38.89yˆ,02.6z ,13.4z ,42.17z 321====3108、无系统误差 9、是异常数据.习题十二1、543.02、(1)0.695 (2) (3)0.4253、(1)(2)2.98; (3) 0.898;4、(-1.28, -0.255, 0.675, 1.645)习题十四(1)一般; 2.5888(介于良与一般之间);(2)68.2245分.习题十五1、{}{}6,5,4,3,2,12、{}{}6,5,4,3,2,1习题十六2、ρ︒复相关系数上的投影在是其中与;),,,(L ˆ,)ˆ(*p *2*1***o*x x x y y y y⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=16.0431.06.0165.0431.065.01R )10.1,10.1,27.0,55.0,37.1,55.0(x)28.1,91.0,18.0,18.0,91.0,28.1(x ---=---=参考文献[1] Andenson T W. An Introduction to Multivariate StatisticalAnalysis. znd ed . New york: Wiley, 1984[2] 费荣昌试验设计与数据处理,4(1997)[3] 方开泰实用多元统计分析,上海:华东师范大学出版社,1989[4] 盛骤等概率论与数理统计,北京:高等教育出版社,1989[5] 朱道元等多元统计分析与软件SAS,南京:东南大学出版社,1999[6] 彭昭英SAS系统应用开发指南,北京:北京希望电子出版社,2000[7] 邓勃分析测试数据的统计处理方法,北京:清华大学出版社,1995[8] 中国现场统计会三次设计组,正交法和三次设计,北京:科学出版社,1985[9] 张尧庭、方开泰多元统计分析引论,北京:科学出版社,1983[10] 上海师范大学数学系回归分析及其试验设计,上海:上海教育出版社,1978[11] 韦博成、鲁国斌统计诊断引论,南京:东南大学出版社,1991[12] 张明淳工程矩阵理论,南京:东南大学出版社,1995[13] 赵德齐模糊数学,北京:中央民族大学出版社,1995[14] 胡永宏、贺思辉综合评价方法,北京:科学出版社,2000[15] 张崇甫等统计分析方法及其应用,重庆:重庆大学出版社,1995[16] 蒋尔雄等线性代数,北京:人民教育出版社,1978[17]王松桂线性模型的理论及其应用,合肥:安徽教育出版社,1987。
实验设计与数据处理 第二版 第1章 误差分析

n
n
试验次数为有限次时,样本标准差:
s
d
i 1
n
2 i
n 1
( xi x)
i 1
n
2
n 1
2 x ( x ) i /n i 1 2 i i 1
n
n
n 1
表示试验值的精密度,标准差↓,试验数据精密度↑
1.3 试验数据误差的来源及分类
1.3.1 随机误差 (random error )
(3)精密度判断
①极差(range)
R xmax xmin
②标准差(standard error)
n n
R↓,精密度↑
( xi x)
i 1
2
n
2 x ( x ) i /n i 1 2 i i 1
n
n
2 x ( x ) i /n i 1 2 i i 1 n n
1.3.3 过失误差 (mistake )
(1)又称粗大误差,定义: 一种显然与事实不符的误差
(2)产生的原因:
实验人员粗心大意造成 (3)特点:
可以完全避免 没有一定的规律
误差的定义及表示法
表示形式
误差
性质特点
绝对 误差
相对 误差
系统 误差
随机 误差
粗大 误差
1.4 试验数据的精准度
1.4.1 精密度(precision)
(b)
(c)
弹着点集中靶心。相 当于系统误差与随机 误差均小,即正确度、 精密度都高,从而准 确度亦高。
弹着点集中,但偏向 一方,命中率不高。 相当于系统误差大而 随机误差小,即精密 度高,正确度低。
实验与数据处理习题及解答.docx

1.在^xcel中用AVERAGE函数计算平均值,用STEDV函数计算标准偏差,得到结果如表1所示。
表1该污水厂进、出水水质标准偏差及平均值COD SS 氨氮进水出水进水出水进水出水标准偏差102.70497 5.6417987 40.44311 2.2590321 7.7226061 1.1480863 平均值368.39 42.05 243.39 16.65 33.77 1.85图1该污水厂进、出水水质示意图2.在excel中作图如下:(1)加药量(mg/L)加药量(mg/L)图6加药量与浊度去除率、总磷去除率、总氮去除率、COD 去除率的关系图3. (1)图2总磷随加药质的变化关系图 图3余浊随加药质的变化关系图5075 100125150加药量(mg/L)5075100125150加药量(mg/L)图4总氮随加药■的变化关系图 图5 COD 随加药■的变化关系图(8)瓣泰2 0164 2108 6 4 (T/SUONH50 49 485756554 3 2 155 5 5 (q/SUIQooo o Oo o o o O图7进水量Q 与SVI 关系图10.015.020.025.030.035.0水温(笆)图8水温与SVI 关系图0.0010.00 20.00 30.00 40.00 50.00 60.00 70.00SV30 (%)图9 SV30与SVI 关系图0.00 20.0025.00 45.00 2(10(1HUM Hloo O oo O O.O.O. 8 6 430.0035.00 40.00 进水流量Q (万m3/d)50.00II)2((T /SUI0.002.004.006.00 8.0010.0012.00MLSS (g/L)图10 MLSS 与SVI 关系图(2) 用excel 中correl 函数求出相关系数r,再根据0V|rl<l,存在一定线性关系:①0 VlrlVO.3,微弱相关;②0.3VIHV0.5,低度相关;③0.5<lrl<0.8,显著相关;④0.8 <lrlVl,高度相关。
实验设计与数据处理第一章例题及课后习题(附答案)

1、 根据三组数据的绝对误差计算权重:12322211110000,25,400000.010.20.005w w w ====== 因为123::400:1:1600w w w = 所以1.54400 1.71 1.53716001.53840011600pH ⨯+⨯+⨯==++2、 因为量程较大的分度值也较大,用量程大的测量数值较小的物理量会造成很大的系统误差。
3.、含量的相对误差为0.2g ,所以相对误差为:0.20.99790525.3Rx E x ∆===。
4、 相对误差18.20.1%0.0182x mg mg ∆=⨯= 故100g 中维生素C 的质量范围为:18.2±0.0182。
5、1)、压力表的精度为1.5级,量程为0.2,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1的汞柱代表的大气压为0.133,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1水柱代表的大气压为gh ρ,其中29.8/g m s =则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯6、样本测定值算术平均值 3.421666667 3.48 几何平均值 3.421406894 3.37 调和平均值 3.421147559 3.47 标准差s 0.046224092 3.38 标准差 0.04219663 3.4 样本方差 0.002136667 3.43 总体方差0.001780556 算住平均误差 0.038333333极差 0.117、依题意,检测两个分析人员测定铁的精密度是否有显著性差异,用F双侧检验。
根据试验值计算出两个人的方差及F值:221221223.733, 2.3033.7331.621232.303s s s F s ===== 而0.9750.025(9,9)0.248386,(9,9) 4.025994F F ==, 所以0.9750.025(9,9)(9,9)F F F <<两个人的测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
试验设计与建模 第二章课后作业答案
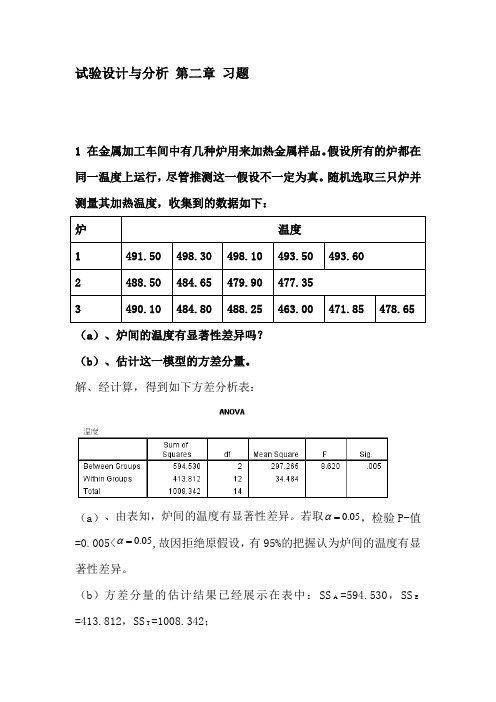
试验设计与分析 第二章 习题1 在金属加工车间中有几种炉用来加热金属样品。
假设所有的炉都在同一温度上运行,尽管推测这一假设不一定为真。
随机选取三只炉并测量其加热温度,收集到的数据如下: 炉 温度1 491.50 498.30 498.10 493.50 493.602 488.50 484.65 479.90 477.353490.10 484.80 488.25 463.00 471.85 478.65(a )、炉间的温度有显著性差异吗? (b )、估计这一模型的方差分量。
解、经计算,得到如下方差分析表:(a )、由表知,炉间的温度有显著性差异。
若取05.0=α,检验P-值=0.005<05.0=α,故因拒绝原假设,有95%的把握认为炉间的温度有显著性差异。
(b )方差分量的估计结果已经展示在表中:SS A =594.530,SS E =413.812,SS T =1008.342;2 纺织厂有很多织布机,设每台织布机每分钟织出同样多的布,为了研究这一假设,随机选取5台织布机并测定它们在不同时间的产量,得出下述数据: 织布机 产量(lb/min) 1 14 14.1 14.2 14 14.1 2 13.9 13.8 13.9 14 143 14.1 14.2 14.1 14 13.9 4 13.6 13.8 14 13.9 13.75 13.813.613.913.814(a )说明为什么这是一种随机效应实验。
这些织布机的产量相等吗?(b )估计织布机间的变异性。
(c )估计实验的误差方差。
(d )给)222σσσττ+(找一个95%的置信区间。
解、(a )因为5台织布机是随机选取的,所以是一种随机效应实验; 经计算,得如下方差分析表:①原假设:H0:织布机不影响产量;H1:织布机影响产量; ②构造统计量:77.5==EMS MS F 处理; ③选定显著性水平:05.0=α;④决策:对于05.0=α,P-值为0.003<05.0=α,故拒绝原假设H0,接受备择假设H1,有95%的把握认为织布机影响产量。
试验设计与数据处理-李云雁-全套323页

1.1.2 平均值(mean)
(1)算术平均值(arithmetic mean)
s——合并标准差:
s (n1 1)s12 (n2 1)s22 n1 n2 2
两组数据的精密度或方差有显著差异时 t x1 x2 s12 s22 n1 n2
服从t分布,其自由度为:
df
(s12 n1 s22 n2 )2 (s12 n1)2 (s22 n2 )2
2
(n1 1) (n2 1)
② t检验
双侧检验 :
若 t t
2
则可判断两平均值无显著差异,否则就有显著差异
1.4.2 正确度(correctness)
(1)含义:反映系统误差的大小 (2)正确度与精密度的关系:
(a)
(b)
(c)
精密度高并不意味着正确度也高
精密度不好,但当试验次数相当多时,有时也会得到 好的正确度
1.4.3 准确度(accuracy)
(1)含义: 反映了系统误差和随机误差的综合 表示了试验结果与真值的一致程度 (2)三者关系 无系统误差的试验
(2)产生的原因: 偶然因素 (3)特点:具有统计规律 小误差比大误差出现机会多 正、负误差出现的次数近似相等 当试验次数足够多时,误差的平均值趋向于零 可以通过增加试验次数减小随机误差 随机误差不可完全避免的
1.3.2 系统误差(systematic error)
(1)定义: 一定试验条件下,由某个或某些因素按照某一 确定的规律起作用而形成的误差
最新实验设计与数据处理(第二版部分答案)

试验设计与数据处理学院班级学号学生姓名指导老师第一章4、 相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为:18.2±0.0182mg 。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1mm 的汞柱代表的大气压为0.133KPa ,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1mm 水柱代表的大气压为gh ρ,其中29.8/g m s = 则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667总体方差σ2 0.001780556算术平均误差△ 0.038333333 极差R 0.117、S ₁²=3.733,S ₂²=2.303F =S ₁²/ S ₂²=3.733/2.303=1.62123而F 0.975 (9.9)=0.248386,F 0.025(9.9)=4.025994 所以F 0.975 (9.9)< F <F 0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
|||69.947|7.747 6.06p p d x =-=>分析人员A 分析人员B8 7.5 样本方差1 3.7333338 7.5 样本方差2 2.30277810 4.5 Fa值0.248386 4.02599410 4 F值 1.621236 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111方差0.000005861 0.031611111观测值13 9假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均 0.025684615 2.291111111 方差 0.0000058610.031611111观测值 13 9 df 128F0.000185422P(F<=f) 单尾 0F 单尾临界0.3510539349. 检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
《实验设计与数据处理》试题

《实验设计与数据处理》试题
注意:
⑴以下题目均选自教材《试验设计与数据处理》(第二版) ,李云雁胡传荣编著,化学工业出版社,2008.7
⑵试题答卷应在课程结束后2周内(2014年5月4日之前)交到曲江校区
教9楼6层622室。
如果有电子版,请发送到邮箱:zhangdsxaut@
1.P41页习题第8题、第9题任选一题。
2.P41页习题第10题。
3.P66页习题第3题、第4题任选一题。
4.P67页习题第5题、第6题任选一题。
5.P81页习题第1题。
6.P81页习题第2题。
7.P112页、113页习题第1题、第2题任选一题。
8.P113页习题第3题、第4题任选一题。
9.P123页习题第1题、第2题任选一题。
10.P123页习题第5题。
11.P160页习题第2题、第3题任选一题。
12.P160页习题第5题、第6题任选一题。
13.P161页习题第8题。
14.P170页习题第1题、第2题任选一题。
实验设计与大数据处理(第二版部分问题详解)

试验设计与数据处理学院班级学号学生姓名指导老师第一章4、 相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为:18.2±0.0182mg 。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1mm 的汞柱代表的大气压为0.133KPa ,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1mm 水柱代表的大气压为gh ρ,其中29.8/g m s = 则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667 总体方差σ2 0.001780556 算术平均误差△ 0.038333333 极差R 0.117、S ₁²=3.733,S ₂²=2.303F =S ₁²/ S ₂²=3.733/2.303=1.62123而F 0.975 (9.9)=0.248386,F 0.025(9.9)=4.025994 所以F 0.975 (9.9)< F <F 0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
|||69.947|7.747 6.06p p d x =-=>分析人员A 分析人员B8 7.5 样本方差1 3.7333338 7.5 样本方差2 2.30277810 4.5 Fa值0.248386 4.02599410 4 F值 1.621236 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111方差0.000005861 0.031611111观测值13 9假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均 0.025684615 2.291111111 方差 0.000005861 0.031611111 观测值 13 9 df 12 8 F 0.000185422 P(F<=f) 单尾 0 F 单尾临界 0.3510539349. 检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
试验设计与数据处理——第1章误差分析

(df1 , df 2 ) F F (df1 , df 2 )
2
则判断两方差无显著差异,否则有显著差异
单侧(尾)检验(one-sided/tailed test) :
左侧(尾)检验 :
若 F F(1 ) (df1, df2 )
则判断该方差1比方差2无显著减小,否则有显著减小
第1章 试验数据的误差分析
误差分析(error analysis) :对原始数据的可靠性进 行客观的评定 误差(error) :试验中获得的试验值与它的客观真实 值在数值上的不一致 试验结果都具有误差,误差自始至终存在于一切科学 实验过程中 客观真实值——真值
1.1 真值与平均值
1.2 误差的基本概念
1.2.1 绝对误差(absolute error)
(1)定义
绝对误差=试验值-真值 或
x x xt
(2)说明 真值未知,绝对误差也未知
可以估计出绝对误差的范围:
或
x x xt x max
xt x x max
绝对误差限或绝对误差上界
x ER x
或
x ER x
可以估计出相对误差的大小范围:
ER
x x xt xt
相对误差限或相对误差上界
max
∴
x xt (1 ER )
相对误差常常表示为百分数(%)或千分数(‰)
1.2.3 算术平均误差 (average discrepancy)
定义式:
② t检验
双侧检验 : 若 t t
2 s2 ,则 都服从正态分布,样本方差分别为 s 和
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题答案 2.1
λ
0.0415
Re
17500
0.0355 0.0336 0.0312 0.0302 0.0289 0.0277 25500 29700 37600 42400 50900 61800
1000000
关系曲线
Re
10000
0.01
0.1
λ
2.2
x
1
y
8
115.9295
df
MS
F P-value F crit
3 25.61517 10.4862 0.000466 3.238872
16 2.44275
19
3.2
乙炔流量 /
(L/min ) 1 1.5 2 2.5
方差分 析:无重 复双因素 分析
SUMMARY 行1 行2 行3 行4
列1 列2 列3 列4 列5
17
浓度与沸点温度之间的关系
系列1
22
27
32
c/%
i
总和 平均
x
y
xi2
yi2
xiyi
1 19.6
105.4 384.16 11109.16 2065.84
2 20.5
106 420.25 11236 2173
3 22.3
107.2 497.29 11491.84 2390.56
4 25.1
108.9 630.01 11859.21 2733.39
NKA-Ⅱ
17.77 1.87 13.71 0.55 13.33 3.67
吸附量/(mg/g)
20 18 16 14 12 10 8 6 4
4
2
0 DA-201 NKA-9
AB-8 D-4006 D-101 树脂型号
S-8 NKA-Ⅱ
2.5
植物油 甲 花生油 棉子油 蓖麻油 菜籽油
凝固点/℃ 乙
2.9 -6.3 -0.1 5.3
空气流量/(L/min)
8 81.1 81.4
75 60.4
9 81.5 81.8 76.1 67.9
10 80.3 79.4 75.4 68.7
11 80 79.1 75.4 69.8
观测数
求和 平均 方差
5 399.9 79.98 3.137
5 397.6 79.52 5.507
5 372.7 74.54 4.528
标准误差 0.029578
观测值
6
方差分析
回归分析 残差
df 1 4
c/℃
10 100
系列1 1000
总计
5
Coeffici
ents
Intercep
t
-8.1419
X
Variable
1
3.887206
T/K
SUMMARY OUTPUT
回归统计
Multiple
R
0.987714594
R Square 0.97558012
方差分析
差异源 样本 列 交互 内部
SS 4.371666667
50.43 2.355 0.42
总计
57.57666667
df
MS
F P-value F crit
2 2.185833 31.22619 0.000673 5.143253
1 50.43 720.4286 1.77E-07 5.987378
行 列 误差
总计
SS 537.6375
35.473 75.155
648.2655
df
MS
F P-value F crit
3 179.2125 28.61486 9.44E-06 3.490295
4 8.86825 1.415994 0.287422 3.259167
12 6.262917
19
3.3
铝材材质 去离子水
1
0.638080517 0.006347 100.5283 1.85E-09 0.621764 0.654397
4.2
T/K
c/%
273 283 293
313 333
353
lnT
lnc
20 2.436163 1.30103 25 2.451786 1.39794 31 2.466868 1.491362
14 1008
1016
14
72
7.1
14 1008
1006
14 73.3
8.8
14 1026.2
993
14 73.3
6.8
14 1026.2
1004
14 73.3
8.1
14 1026.2
967
14 73.3
7.1
14 1026.2
999
14 73.3
6.1
14 1026.2
992
14 74.3
7.8
3.5 -6.2 0.5
5
凝固点/℃
两个产地几种植物油的凝固点数据图
6
5
4
3.5 2.9
3
5.3 5
2
1
0.5
0
-0.ቤተ መጻሕፍቲ ባይዱ 甲
-1
花生油
棉子油
蓖麻油
菜籽油
乙
-2
-3
-4
-5
-6
-7
-6.3-6.2
植物油
2.6
合成表面活性 润滑油 肥皂及洗
应用领域 橡胶工业 剂
(脂) 涤剂 金属皂 其他
比例/%
18
11
9.5
8.1
ph值
30 25 20 15 10
5 0
0
发酵时间与PH值及残糖量的关系图
5 发酵时间/d
6.1 6 5.9 5.8 5.7 5.6 5.5 5.4 5.3 5.2 10
残糖量 PH值
2.4
树脂型号 DA-201 NKA-9
吸附量
/(mg/g)
17.14
AB-8 D-4006 D-101 S-8
5 0.016197 0.003239
6 32.75429
Lower Upper
Coefficients 标准误差 t Stat P-value 95%
95%
Intercep
t
92.91137938 0.156271 594.5544 2.55E-13 92.50967 93.31309
X
Variable
72
7.1
15 1080
979
15
72
8.1
15 1080
988
15
72
6.1
15 1080
968
15
73
8.1
15 1095
940
15
73
7.1
15 1095
29.1 27.9 24.2 31.7
观测数
求和 平均 方差
5 136.6 27.32 2.672
5 147.8 29.56 2.143
5 132.2 26.44 3.298
5 157.3 31.46 1.658
27.2 29.6 26.5 32.8
方差分析 差异源
组间 组内
总计
SS 76.8455 39.084
5
23
21
22
比例/%
比例/%
22
18
21
23
橡胶工业
合成表面活性剂
11
润滑油(脂)
肥皂及洗涤剂
5
金属皂
其他
3.1
第三章习题答案 3.1
颜色 橘黄色 粉色 绿色 无色
方差分 析:单因 素方差分 析
SUMMARY 组
行1 行2 行3 行4
26.5 31.2 27.9 30.8
销售额/万元 28.7 25.1 28.3 30.8 25.1 28.5 29.6 32.4
34 2.495544 1.531479 46 2.522444 1.662758
58 2.547775 1.763428
某物质的溶解度与绝对温度之间的关系
100
SUMMARY OUTPUT
回归统计
Multiple
R
0.987715
R Square 0.97558
Adjusted
R Square 0.969475
14 1040.2
980
14
74
7.1
14 1036
980
14
74
6.1
14 1036
984
14
74
7.1
14 1036
965
15
71
6.1
15 1065
1006
15
71
9.1
15 1065
988
15
72
7.1
15 1080
984
15
72
9.1
15 1080
967
15
72
8.1
15 1080
987
15
4.4
试验号 T/℃ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Na2O(x1) siO2(x2) CaO(x3)/
/%
/%
%
X1=x1 X2=x1x2
1029
14
72
9.1
14 1008
1011
14
72
8.1
