电路分析答案第三章演示教学
电路分析基础第3章

于一个电流源is和多个正电阻组成的电路,有: |ik/is|≤1 式中ik为任一支路电流。
作业: 3-5
3-6
3-11
3-15
2、网络函数 网络函数:对单一激励的线性时不变电路指定响应与激励之比定义为
网络函数。记为:H
H=响应/激励
策动点函数:响应与激励在同一端口,称为策动点函数 转移函数:响应与激励不在同一端口,称为转移函数
由于响应和激励都可以是电流或电压,可以在同一端口或在不同端口,所以网络 函数可分为六种情况。如表3-1所示(P91)。 响应 策动点函数 电流 电压 电流 转移函数 电压 电流 电压 激励 电压 电流 电压 电流 电流 电压 名称及专用符号 策动点电导Gi 策动点电阻Ri 转移电导GT 转移电阻RT 转移电流比Hi 转移电压比Hu
R2
R1 u ' o is1 Ro R1 R 2 Ro
is1
R1
R0
由图(b),运用分流公式后,可求得:
is 2
R2
R2 u ' ' o is 2 Ro R1 R 2 Ro
R1
R0
由图(c),运用分压公式可得:
R1 R 2 u ' ' ' o us R1 R 2 Ro
即:由两个激励所产生的响应,表示为每一激励单独作用时所产生的响应之和
上述特性,在电路理论中称之为“叠加性”。同理,该电路中的其它
电流或电压对us和is的响应,也都存在类似的线性关系。
例3—3:利用叠加定理求解图中电路的电压。
is 2
is1
R1
R 2 R0
us
解:绘出每一独立源单独作用时的电路图,如图(a),(b),(c)所示。 由图(a) ,运用分流公式可求得:
大学物理电路分析精品课程 第三章 电路的一般分析方法

I S I4 I1 0
I
1
I3
I2
0
I
4
I3
I5
0
U 4 U S1 U 3 U1 0 U1 U 2 U 0 U 3 U S1 U 5 U S 2 U 2 0
I1R1 U1
I I
2 3
R2 R3
U2 U3
I
4
R4
U4
I 5 R5 U 5
支路电流法(1B法)
1) U 2
2
添加以下方程:
2U 23 2(U 2 U 3 ) 4U 43 4(U 4 U 3 ) U1 U 4
例题3——割集分析法
5 + 19V - 2
I1 +
30V _
4A 1.5I1
4
+ 25V
_
选树如图所示,则只需要对2、4支路 (树支)所决定的基本割集列写方程即可
(5 2 4) I1 (2 4) 4 4 1.5I1 30 25 19
I S
U4 R4
U1 R1
0
UR11
U3 R3
U2 R2
0
U
4
U3
U5
0
R4 R3 R5
3-3 节点法与割集法
一、节点法
1 .方法
任选电路中某一节点为参考节点, 其他节点与此参考节点间的电压称为 “节点电压”。节点法是以节点电压作 为独立变量,对各个独立节点列写KCL 电流方程,得到含(n-1)个变量的(n-1)个 独立电流方程,从而求解电路中待求量。
第三章 电路的一般分析方法
❖重点 1、支路法 2、节点法 3、网孔法
❖难点 1、改 拓扑术语
支路 节点 回路 网孔 基本回路 割集 基本割集
电路分析基础答案周围版第三章
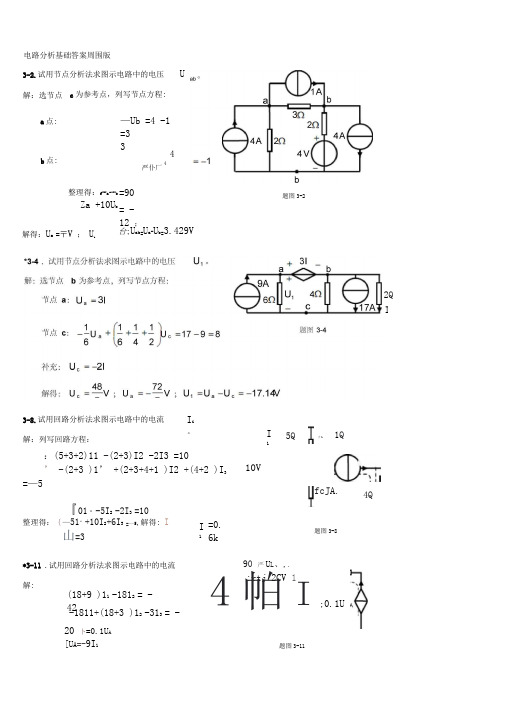
电路分析基础答案周围版 3-2.试用节点分析法求图示电路中的电压 U解:选节点 c 为参考点,列写节点方程: a 点: b 点: 题图3-2—Ub =4 -1 =33 4 严仆厂4整理得:f 25U a-10U b Z a +10U b =90 = -12 ; 2Q I3-8.试用回路分析法求图示电路中的电流 I i 。
解得:U a =〒V ; U b 台;U ab=U a-U b=3.429V 解:列写回路方程: :(5+3+2)11 -(2+3)I2 -2I3 =10 ’ -(2+3 )1’ +(2+3+4+1 )I2 +(4+2 )I 3 =—5 10VI15Q才11Q4Q『01“ -5I 2 -2I 3 =10 整理得:{—51" +10I 2+6I 3 =—5,解得: I山=3 I 1 =0. 6k *3-11 .试用回路分析法求图示电路中的电流 解: (18+9 )11 -1812 = -42-1811+(18+3 )12 -313 = -20 卜=0.1U A [U A =-9I 1fcJ A .题图3-890 严U L 、,.:rtj 2CV 14帕I;0.1U题图3-11将问题的条件代入有: 1.6=0.3X3+0.2I S 2 — 0.1整理得:严叽二7,解得:|17I 3+21I 2 =-20*3-14 .试用叠加定理求图示电路中的电流2; +4+31; +5U x =0 U x =-2I X设电流源单独作用,电路简化成题图 3-14(2)所示(1欧姆电阻被等效去掉),选下节点为参考节点,列写节点方程:依据叠加定理有:l x =m4A0.6 * +2k 2 +k 3 0.7 評 +k 2 +k 3 0.9 =2k 1+2k 2+k 3k^ -0.1,故:l 3 =0.31 S1 +0.2I S 2-0.1,2QU x题图3-14X5U x3Q1Q-2A题图 3-14 (2)题图3-14解:设电压源单独作用,电路简化成题图 3-14( 1)所示,列写方程:「(2+少=2+晋U x =2(2-ix )解得:I X*3-17 . N 为线性网络,IS1=1A , IS2=2A 时,I 3 =0.6A ; IS1=2A , IS2=1A时,I 3=0.7A ; IS1=2A ,IS2=2A 时, I 3=0.9A ; I S1 =3A ,IS2=?A 时, l 3=1.6A ?题图3-17解:设 I 3为响应,有:I 3 =kJ S18A解得:将已知条件代入以上方程有:解得:K =0.3, k 2 =0.2 ,由此可得:I S2 = 4 A3-21 .电路如图示,用戴维南定理求图中电流 I 。
电路分析基础(英文版)课后答案第三章

0 = ¡26i1 ¡ 90i2 + 124i3
[a] Solving, i1 = 5 A; therefore the 80 V source is delivering 400 W to the circuit.
[b] Solving, i3 = 2:5 A; therefore p8− = (6:25)(8) = 50 W
v1 + v1 ¡ v2 = 4:5
1
8
53
54 CHAPTER 3. Techniques of Circuit Analysis
v2 + v2 ¡ v1 + v2 ¡ 30 = 0
12 8
4
Solving, v1 = 6 V v2 = 18 V Thus, i = (v1 ¡ v2)=8 = ¡1:5 A v = v2 + 2i = 15 V
DE 3.8 Use the lower node as the reference node. Let v1 = node voltage across the 7.5 − resistor and v2 = node voltage across the 2.5 − resistor. Place the dependent voltage source inside a supernode between the node voltages v and v2. The node voltage equations are
3
Techniques of Circuit Analysis
Drill Exercises
DE 3.1 [a] 11,8 resistors, 2 independent sources, 1 dependent source
电路分析试题及答案(第三章)

相量图形:1、下图中,R 1=6Ω,L=0.3H ,R 2=6.25Ω,C=0.012F,u (t)=)10cos(210t ,求稳态电流i 1、i 2和i 3,并画出电路的相量图。
解:V U0010∠= R 2和C 的并联阻抗Z 1= R 2//(1/j ωC )=(4-j3)Ω, 输入阻抗 Z = R 1+j ωL +Z 1 =10Ω,则:A Z U I 0010110010∠=∠== A R Z I I 0211287.368.0-∠== A U C j I 02313.536.0∠== ω 所以:A t i )10cos(21=A t i )87.3610cos(28.02ο-= A t i )13.5310cos(26.02ο+=相量图见上右图2、下图所示电路,A 、B 间的阻抗模值Z 为5k Ω,电源角频率ω=1000rad/s ,为使1U 超前2U 300,求R 和C 的值。
解:从AB 端看进去的阻抗为Cj R Z ω1+=, I213其模值为:Ω=+=k CR Z 5)1(22ω (1) 而2U /1U =)arctan()(112CR CR ωω-∠+由于1U 超前2U 300,所以ωCR =tan300=31 (2)联列(1)、(2)两式得R =2.5k Ω,C =0.231μF3、测量阻抗Z 的电路如下图所示。
已知R=20Ω,R 2=6.5Ω,在工频(f =50Hz)下,当调节触点c 使R ac =5Ω时,电压表的读数最小,其值为30V ,此时电源电压为100V 。
试求Z 及其组成的元件的参数值。
(注意:调节触点c ,只能改变cd U 的实部,电压表读数最小,也就是使实部为零,cd U 为纯虚数,即cdU =±j30V)解:UZR R U R R U ac cd++-=22调节触点c ,只能改变cd U 的实部,其值最小,也就是使实部为零,cd U 为纯虚数,即cdU =±j30V , 因此上式可表示为:±j 30=-25+(100⨯6.5)/(6.5+Z ) 解得:Z=(4.15±j 12.79)Ω 故:R Z =4.15ΩL =40.7mHC =249μF4、电路如下图所示,已知f =1kHz ,U =10V ,U 1=4V ,U 2=8V 。
电路分析第三章答案
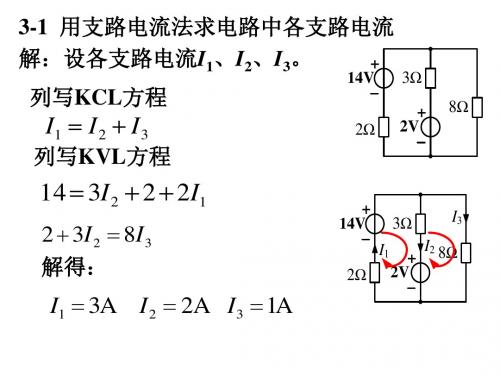
uS1 I1R1 I 2 R2 uS 2 uS 2 I 4 R4 I 3 R3 I 2 R2 I 3 R3 I 5 R5 ri3
附加方程:
I 3 iS
3-4 电路如图,列写支路电流方程 设电流I1、I2、I3、I4、I5、I6、U5 uS2 R + 列写节点①②③的KCL方程 I2 2 3 I1 I 2 I 5 I 5 I 6 I 4 ① I5 R5 ② iS5 + uS4
p1 4i 2W 8V电压源的功率: p2 8I1 28W
4V电压源的功率:
受控源的功率: p2 U n3 2i1 4W
3-16 用节点分析法,求图 示电路中的电压U1和电流I 解:(1)给节点编号, 以节点④为参考节点,列 写节点方程。
U n1 0.5U1 U n1 U n 2 (1 2) 0.5I 2U n1 U n3 (1 2) 0.5I 2
R3 R 3
3-13 列写图示电路的节点电压方程 解:给节点编号,以节点 4A ③为参考节点,列写节点 ① 方程。 + 1Ω
10V 2A
② + 3V 1Ω
+ 5V ③
2Ω
U n1 (1 0.5) U n 2
Un2 5
10 24 2
3-14 列写图示电路的节点电压方程 解:给节点编号,以节点 4Ω ③为参考节点,列写节点 ① 2Ω ② 方程。 + 2A +
I6
I 2 I3 I6
列写回路1、2、3的 KVL方程
I1 + + U5 − R1 U1 R42 − I4 1 + + uS1 βU1
电路分析基础习题第三章答案(史健芳)教程文件

电路分析基础习题第三章答案(史健芳)第3章3.1 选择题1.必须设立电路参考点后才能求解电路的方法是( C )。
A.支路电流法B.回路电流法C.节点电压法D.2b法2.对于一个具有n个结点、b条支路的电路,他的KVL独立方程数为( B )个。
A.n-1 B.b-n+1 C.b-nD.b-n-13.对于一个具有n个结点、b条支路的电路列写结点电压方程,需要列写( C )。
A.(n-1)个KVL方程B.(b-n+1)个KCL方程C.(n-1)个KCL方程D.(b-n-1)个KCL方程4.对于结点电压法中的无伴电压源,下列叙述中,( A )是错误的。
A.可利用电源等效变换转化为电流源后,再列写结点电压方程B.可选择该无伴电压源的负极性端为参考结点,则该无伴电压源正极性端对应的结点电压为已知,可少列一个方程C.可添加流过该无伴电压源电流这一新的未知量,只需多列一个该无伴电压源电压与结点电压之间关系的辅助方程即可D.无伴受控电压源可先当作独立电压源处理,列写结点电压方程,再添加用结点电压表示控制量的补充方程5.对于回路电流法中的电流源,下列叙述中,( D )是错误的。
A.对于有伴电流源,可利用电源等效变换转化为电压源后,再列写回路电流方程B.对于无伴电流源,可选择合适的回路,使只有一个回路电流流过该无伴电流源,则该回路电流为已知,可少列一个方程C.对于无伴电流源,可添加该无伴电流源两端电压这一新的未知量,只需多列一个无伴电流源电流与回路电流之间关系的辅助方程即可D.电流源两端的电压通常为零6.对于含有受控源的电路,下列叙述中,( D )是错误的。
A.受控源可先当作独立电源处理,列写电路方程B.在结点电压法中,当受控源的控制量不是结点电压时,需要添加用结点电压表示控制量的补充方程C.在回路电流法中,当受控源的控制量不是回路电流时,需要添加用回路电流表示控制量的补充方程D.若采用回路电流法,对列写的方程进行化简,在最终的表达式中互阻始终是相等的,即:R ij=R ji3.2 填空题1.对于具有n个结点b条支路的电路,可列出 n-1 个独立的KCL方程,可列出 b-n+1 个独立的KVL方程。
李瀚荪《电路分析基础》(第4版)课后习题详解-第3章 叠加方法与网络函数【圣才出品】
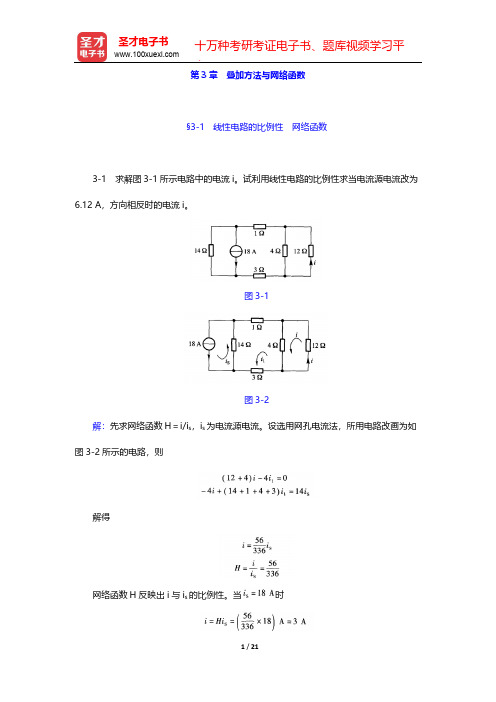
时,uX 是多少?(2)若所示网
络 N 含有一个电源,当
时,uX=-40V;所有(1)年的数据仍有效。求:当
Байду номын сангаас
时,uX 是多少?
图 3-14 解: (1)设 iS1=1 A 能产生 uX 为 a,而 iS2=1A 能产生 uX 为 b,则可列出方程
解得
则
(2)设当 N 内含电源
能产生 uX 为 c,则可列出方程
3-5 电路如图 3-6 所示,试求转移电阻
已知 g=2S。
图 3-6 解:为找到 U0 和 is 的关系,只要列出节点方程
整理得
所以
§3-2 叠加原理 3-6 电路如图 3-7 所示,用叠加原理求 iX。
图 3-7
5 / 21
圣才电子书
十万种考研考证电子书、题库视频学习平 台
所以 (2)应用线性电路的比例性
3-3 (1)求图 3-4(a)所示网络的转移电压比
,设所有电阻均为 1Ω。
(2)某同学认为图 3-4(a)所示网络可看成是网络级联而成,若以
2 / 21
分别表示
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 k 节网络的输入和输出,则
解得
网络函数 H 反映出 i 与 is 的比例性。当
时
1 / 21
圣才电子书
当
时
十万种考研考证电子书、题库视频学习平 台
3-2 电路如图 3-3 所示,(1)若
u2。
10V,求 u2。
,求 i1 及 us;(2)若 10V,求
图 3-3 解: (1)应从输出端向输人端计算,标出节点编号,应用分压、分流关系可得
电路与模拟电子技术基础(第2版)第3章正弦稳态电路的分析习题解答..

第3章 正弦稳态电路的分析习题解答3.1 已知正弦电压,当时,。
求出有效值、频率、()V 314sin 10θ-=t u 0=t V 5=u 周期和初相,并画波形图。
解 有效值为 V07.7210==U ;Hz 502314==πf s 02.01==f T 将 , 代入,有 ,求得初相。
波形图如下0=t V 5=u )sin(105θ-=︒-=30θ3.2 正弦电流的波形如图3.1所示,写出瞬时值表达式。
i图3.1 习题3.2波形图解 从波形见,电流的最大值是,设的瞬时值表达式为i A 20i A π2sin 20⎪⎭⎫ ⎝⎛+=θt T i 当 时,,所以 ,求得或 。
0=t A =10i θsin 2010=︒=30θ6π=θ当 时,,所以 ,求得 。
s 2=t A =20i ⎪⎭⎫ ⎝⎛+⨯=6π2π2sin 2020Ts 12=T 所以 。
A ⎪⎭⎫ ⎝⎛︒+=306πsin 20t i 3.3正弦电流,。
求相位差,说明超前滞()A 120 3cos 51︒-=t i A )45 3sin(2︒+=t i 后关系。
解 若令参考正弦量初相位为零,则的初相位,而初相位1i ︒-=︒-︒=30120901θ2i,其相位差 , 所以滞后于 角,或︒=452θ︒-=︒-︒-=-=75453021θθϕ1i 2i ︒75超前 角。
2i 1i ︒753.4 正弦电流和电压分别为(1)V)60 4sin(23o 1+=t u (2)V)75 4cos(52︒-=t u (3)A)90 4sin(2o 1+-=t i (4) V)45 4cos(252︒+-=t i 写出有效值相量,画出相量图。
解 (1) ,相量图如图(1)V 6031︒∠=∙U (2) V)15 4sin(5)75 4cos(52︒+=︒-=t t u 有效值相量为 ,相量图如图(2)V 15252︒∠=∙U (3) ()()A90 4sin 290 4sin 21︒-=︒+-=t t i 有效值相量为 ,相量图如图(3)A 9021︒-∠=∙I (4) ()()A45 4sin 2545 4cos 252︒-=︒+-=t t i 有效值相量为 ,相量图如图(4)A 4552︒-∠=∙I3.5 图3.2中,已知,,求。
电路分析 第3章 习题与解答
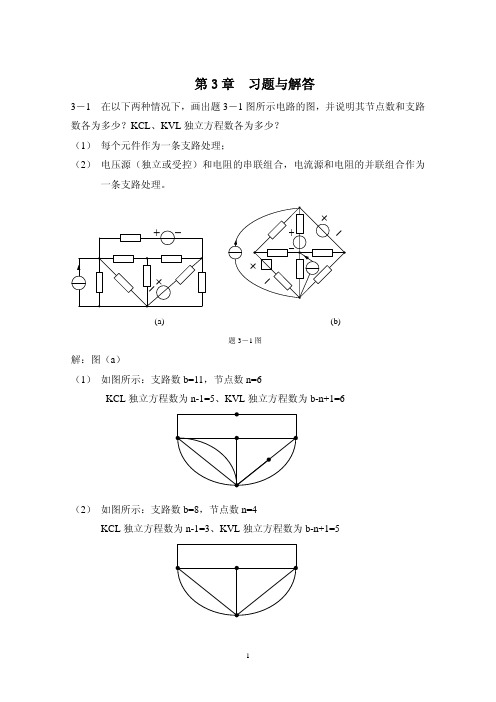
列回路方程如下:
回路 l1
(2 3 5)il1 3il2 3il3 2il3 10
回路 l2
il2 3
回路 l3
(1 2 3 4)il3 3il1 2il1 3il2 il2 5
联立求解得 il1 0.6A il2 3A
il3 1A
KCL 独立方程数为 n-1=6、KVL 独立方程数为 b-n+1=6
(2) 如图所示:支路数=9,节点数=5 KCL 独立方程数为 n-1=4、KVL 独立方程数为 b-n+1=5
3-2 试画出题 3-2 图所示四点全图的全部树。
解:
题 3-2 图
2
3-3 如题 3-3 图所示的有向图,在以下两种情况下列出独立的 KVL 方程。 (1) 任选一树并确定其基本回路组作为独立回路; (2) 选网孔作为独立回路。 1
第 3 章 习题与解答
3-1 在以下两种情况下,画出题 3-1 图所示电路的图,并说明其节点数和支路 数各为多少?KCL、KVL 独立方程数各为多少? (1) 每个元件作为一条支路处理; (2) 电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为
一条支路处理。
U1 32(il1 il2 ) 8V (2)电路的图为
il 3
il1
il 2
列回路电流方程如下:
回路 l1
il1 3.5
回路 l2
(20 4 2 35)il2 (2 4)il1 20il3 0
回路 l3
(20 20)il3 20il2 20il1 0.5UY
电路分析第3章作业参考答案

第3章电路等效及电路定理P3-2 电路如图P3-2所示,应用叠加定理计算电流x i ,并计算Ω10电阻吸收的功率。
图P3-2 图1 图2解:1)15V 单独作用,如图1示 2)4A 单独作用,如图2示A i x 6.0401040401040101215'=+⨯+⨯+= A i x 92.14401101121101''-=⨯++-= 3)共同作用 A i i i x xx 32.1)92.1(6.0'''-=-+=+= 4)10Ω电阻的功率:W R i p x4.1710)32.1(22=⨯-==P3-5 用叠加定理求如图P3-5所示电路的电压x u 。
4Ω4Ω4Ω图P3-5 图1 图2解:1)10V 单独作用,如图1示由KVL 得:04)5(21010''''=++⨯++-x x x xi i i i ,得:A i x 38.0135'==,V i u xx 8.310''== 2)2A 单独作用,如图2示由KVL 得:0)2(4)52(210''''''''=++++⨯+x x x xi i i i ,得:A i x 46.0136''-=-=,V i u xx 6.410''''-== 3)共同作用 V u u u x x 2.1)6.4(8.3'''-=-+=+=P3-9 求图P3-9所示电路的输入电阻in R 。
(分别用电源法和伏安法)图P3-9 图1 图2解:1)电源法:设端口处电压和电流如图1所示:由25Ω电阻VCR得:)5.1(25IIiu-+⨯= 1)控制量:50uI= 2)联立两个方程:iu3100=,因此输入电阻:Ω===3.333100iuRin2)伏安法:端口处电压和电流如图2所示,设控制量AI1=,则:VIu5050==,AIIui5.15.125=-+=,因此输入电阻:Ω===3.335.150iuRinP3-11电路如图P3-11所示,利用电源变换求i。
电路分析基础第三章讲解

IC
CUC
UC 1
UC XC
安
C
徽 职
11
X C C 2fC
业 技
XC称为容抗, 单位为Ω。
术 电流和电压之间的相位关系为正交,即电流超前电压
学
院
ui uC
iC
2
i
u
2
0
t
第三章 正弦交流电路
2.电压与电流的相量关系
安
uC UCm sin(t u )
URIR T
(T
0)
URIR
P
URIR
I
2 R
R
U
2 R
R
第三章 正弦交流电路
p u,i p
安 徽 职
P
Pm=UmIm
P=
1 2
Pm=UI
业
0
t
技
i
术
u
学
电阻元件的功率曲线图
院
例: 一只功率为100W,额定电压为220V 的电烙铁, 接在380V的交流电源上, 问此时它接受的功率为多少? 若接到110V的交流电源上, 它的功率又为多少?
. jt
第三章 正弦交流电路
正弦量的有效值用复数的模表示,
正弦量的初相用复数的幅角来表示。
安 徽 职
该方法为相量表示法。 表示为:
业
.
技 术
I Ie j(ti ) I i
学
院 注:正弦量与相量一一对应。
2、相量图
相量图就是把正弦量的相量画在复平面上。
第三章 正弦交流电路
学
院
同频率正弦量的几种相位关系:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由电流源 单独作用, 电流源 单独作用。
根据分流关系,有:
因而有:
故得:
3.7如题3.7图所示电路,当 分别为1Ω、2Ω和5Ω时,求其上电流 分别为多少?
解:将电流源变换为电压源形式,再根据
叠加原理,有:
整理可得:
当 时,有:
当 时,有:
当 时,有:
3.8如题3.8图所示电路,N为不含独立源的线性电路,已知输出电压 ;若在输出端接上5Ω电阻,则 。问在输出端接3Ω电阻时,输出电压 与输入电压 的关系如何?
有 ②
联解①式和②式,可得:
因而有:
当 , 时,可得
3.13如题3.13图所示电路,已知 ,求电阻R。
解:从电阻R两端进行戴文宁等效,其
开路电压为:
等效电阻为:
则可得:
解得:
3.14如题3.14图所示电路,N为含有独立源的线性电阻电路。已知当 时其上获得最大功率为1W,求N的戴维宁等效电路。
解:将电路等效为如图所示,根据功率
可获得最大功率,为:
3.16如题3.16图所示电路, 、 均未知,已知当 时电流 。若 可任意改变,问 等于多大时其上获得最大功率,并求出该最大功率。
解:从 两端进行戴文宁等效
可知
又有 代入已知数据
可得:
根据最大功率传输定理,有
当 时可获得最大功率
为
3.17如题3.17图所示电路,N为含独立源的线性电阻电路。已知当受控电流源系数 时,电压 ;当 时,电压 。求 为何值时外部电路从N获得最大功率,并求出该功率。
解:根据戴文宁等效电路,端口
电压、电流的约束关系为:
当 时,有
当 时,有
3.12如题3.12图所示线性时不变电阻电路,已知当 、 时,电流 ;当 、 时,电流 ;问当 、 时,电流 为多少?
解:从负载两端进行诺顿等效,根据线性
电路的齐次性,等效电流源为:
则有:
式
单独作用时,有:
根据叠加定理可得:
3.3如题3.3图所示电路,求电压 。如独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,电压 变为多少?
解:根据KVL列一个回路
两个电压源支路可列方程:
由此可得:
代入上式得:
若独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,由上式可知:
3.10求如题3.10图所示各电路ab端的戴维宁等效电路和诺顿等效电路。
解:对图(a)电路进行诺顿等效,求ab两端的短路电流,如图可知:
而
可得:
求电压源短路时,ab两端的等效电阻:
对图(b)电路进行戴文宁等效,
3.11如题3.11(a)图所示线性有源二端电路N,其伏安关系如题3.11(b)图所示。试求它的戴维宁等效电路。
解:设电源 和 对电流 的贡献为 ,
根据线性电路的叠加定理,有:
其中 为开关外接电源的作用。
开关S在位置1时,有
此时可将 视为0
开关S在位置2时,有
由上可解得:
当S在位置3时, ,则有:
3.6如题3.6图所示电路,若 ,求电阻 的值。
解:运用置换定理将电路变为如下图所示。
根据叠加定理电压 可看成电流源 和 共同
最大传输定理,有:
可解得:
又有:
u为 两端的开路电压,可解得:
根据等效电路可知:
解得: 或
3.15如题3.15图所示电路, 可任意改变,问 等于多大时其上获得最大功率,并求出该最大功率。
解:对 两端进行戴文宁等效,首先
求开路电压 ,有:
而
解得 可得:
再求等效电阻 ,如右图所示,有:
而此时
解得
故得
根据最大功率传输定理,当 时,
解:从输出端进行戴文宁等效,有
当 时, ,可得
当 时, ,代入上式可求得:
因此,当 时,有
3.9如题3.9图所示电路,当R=12Ω时其上电流为I。若要求I增至原来值的3倍,而电路中除R外的其他部分均不变,则此时的电阻R为多少?
解:从R两端进行戴文宁等效,可得等效
电源 ,等效电阻
根据等效电路,当 有
而 ,若 ,则有:
结合上面电阻 欧姆定律,有
因而可得
根据给出的已知条件,由电路可知
代入上式,有
解得
3.19如题3.19图所示电路中 仅由线性电阻组成,当 端接电压源 时[如图(a)],测得 、 ;若 接 电阻, 端接电压源 时[如图(b)],求电流 。
解:应用互易定理求解,互易后要保持拓扑结构不变,将图(a)变为如下的电路图(c),并联一个 的电阻不影响电流 ,由置换定理将图(c)电路变为图(d)电路。
解:设两组条件分别对应两个电路:其中第一组条件对应图(a),第二组条件对应图(b)。求解变为对图(b)的电路,当 、 、 时,求
设 中有k个电阻,对图(a),第j个电阻上的电压、电流分别为 和 ;对图(b),第j个电阻上的电压、电流分别为 和 。根据欧姆定律,有
图(a)与图(b)具有相同的拓扑结构,根据特勒根定理,有
解:将电路N进行戴文宁等效,并将受控源
转换为电压源形式,有
得:
又有: 得:
可得:
将 , ; , 代入,有
和
联立求解可得:
再求电路N的等效电阻 ,用外加电压、电流法,有
可求得:
当 时可获得最大功率,则有:
解得:
最大功率为:
3.18如题3.18图所示电路, 仅由线性电阻组成。已知当 、 时, 、 ;当 、 时, ,求此时的 。
显然有:
图(b)电路可以看成图(e)电路,
所以图(e)电路是图(d)电路的互易
电路。根据互易定理形式三,有:
解得:
可得:
3.20如题3.20图所示电路,已知二端电路N端子上的电压电流关系为 ,试求 、 和 。
解:对连接电路N的外电路进行戴文宁
等效,可知等效电阻为
开路电压为(根据叠加定理):
解得
有:
3.4如题3.4图所示电路,N为不含独立源的线性电路。已知:当 、 时, ;当 、 时, ;求当 、 时的电压 。
解:根据线性电路的叠加定理,有:
将已知数据代入,有:
联立解得:
因而有: 将 、 代入
可得:
3.5如题3.5图所示电路,已知当开关S在位置1时,I=40mA;当S在位置2时,I=-60mA;求当S在位置3时的I值。
电路分析答案第三章
第三章习题
3.1如题3.1图所示梯形电路。
⑴已知 ,求 、 和 。
⑵已知 ,求 、 和 。
⑶已知 ,求 和 。
解:根据线性电路的性质,设:
令: 可推出
因而可得:
1当 时,有:
2当 时,有:
3当 时,有:
3.2如题3.2图所示电路,已知 , ,用叠加定理求电路 。
解: 单独作用时,有:
