第六章 Logistic回归
《Logistic回归》课件

公式
f(x)=1/(1+e^-x)其中,x是一个实数,源自表示 自然对数的底数。特点
• 输出范围在0-1之间,代 表了一个概率值;
• 函数有单峰性,中心对 称,可以确定最大值和
• 最在小输值入;接近0时函数近 似于线性函数。
应用场景:二元Logistic回归
乳腺癌预测
贷款审核
二元Logistic回归被广泛应用于医 学界用于识别患有乳腺癌的女性。
数据预处理
4
的潜在关系和规律。
对需要进行缩放、归一化、标准化等处
理的变量进行预处理。
5
模型拟合
将数据划分训练集和测试集,通过模型 对训练集进行拟合,并评估模型预测能 力。
模型评估方法
混淆矩阵
将预测结果与真实结果进行比对,计算假正率、假负率、真正率和真负率等指标。
ROC曲线
通过绘制真正率与假正率的曲线,评估模型的预测能力。
AUC指标
ROC曲线下的面积就是AUC,AUC越大说明模型预测结果越准确。
常见模型优化方法
1 数据增强
通过合成数据或者样本扩 增等方法,增加数据量, 提高模型泛化性能。
2 特征选择
选择对于问题最重要的变 量,避免过拟合。
3 模型集成
通过结合多个模型的结果, 提高整体预测能力。
应用探索:Logistic回归的扩展
2 作用
通过逻辑函数将线性变量转化为概率值,从 而进行二元分类。
3 优点
简单易懂、易于解释和使用,对于大规模数 据集有效率。
4 缺点
只适用于二元分类问题,并且在分类较为复 杂的非线性问题上表现较差。
sigmoid函数
介绍
sigmoid函数是Logistic回归模 型中核心的激活函数,将输入 值映射到0-1的概率分布区间内。
logistic回归

b'j 来计算标准化回归系数
,式中bj是我们通常所指的回
3 1.8138
归参数,即偏回归系数;Sj为第j自变量的标准差;S是
logistic随机变量分布函数的标准差,为 /
每个参数的以e为底的指数就是每个自变量对应的优势比( odds
ratio,OR),即 ORj=exp(bj),ORj值的100(1-α)%可信区间为: exp[bj±1.96 SE(bj)] (16-7)
自变量 (x)
累计发病率P(%)
Logit值
2.3 2.6 2.8 2.9 3.0 3.08
0.1537 0.3829 0.6383 0.7779 0.8519 0.8519
-1.71 -0.48 0.57 1.25 1.75 1.75
Logit=Ln[p/(1-p)]
剂量与效应关系的“S”型曲线
线的形状与方向。随着X的增加,正β值对应的曲线呈上升趋势(见图
16-1),负β值对应的曲线是下降趋势。β=0时,S形曲线变成水平直 线,表示π与自变量X无关;β的绝对值增加,曲线形状逐渐陡峭;β的 绝对值减少,曲线形状逐渐平坦。 当预报概率π为0.5时,由式(16-2)可得对应的X=-β0/β,实例有X =-(-1.4351)/1.6582=0.8655。此X值有时被称为中效水平 (median effective level,EL50),代表了二种结局出现的概率各为 50
logistics回归的原理

logistics回归的原理
Logistic回归是一种用于解决二元分类问题的机器学习算法。
它基于逻辑函数(也称为sigmoid函数)的概念,并通过最大
似然估计来确定模型参数。
Logistic回归的原理可以概括为以下步骤:
1. 数据准备:收集并准备训练数据集,包括输入特征(自变量)和对应的类别标签(因变量)。
2. 特征缩放:对输入特征进行缩放,以确保它们在相似的范围内。
3. 参数初始化:初始化模型的权重和截距。
4. Sigmoid函数:定义Sigmoid函数,它将输入转换为0到1
之间的概率值。
5. 模型训练:使用最大似然估计法来最小化损失函数,以找到最佳模型参数。
通常使用梯度下降等优化算法来实现。
6. 模型预测:使用训练得到的模型参数,对新的输入样本进行预测。
根据预测概率值,可以将样本分类为两个类别之一。
Logistic回归的核心思想是通过sigmoid函数将线性回归模型
的输出映射到概率。
它假设数据服从伯努利分布,并对给定输入特征的条件下属于某个类别的概率进行建模。
通过最大似然估计,可以找到最优的模型参数,使得预测的概率尽可能接近真实标签的概率。
总结起来,Logistic回归的原理是利用最大似然估计来建模分
类问题中的概率,并使用sigmoid函数将线性模型的输出映射到概率范围内。
6.1第六章回归分析

变量之间的联系
确定型的关系:指某一个或某几个现象的变动必然会 引起另一个现象确定的变动,他们之间的关系可以使 用数学函数式确切地表达出来,即y=f(x)。当知道x的 数值时,就可以计算出确切的y值来。如圆的周长与 半径的关系:周长=2πr。 非确定关系:例如,在发育阶段,随年龄的增长,人 的身高会增加。但不能根据年龄找到确定的身高,即 不能得出11岁儿童身高一定就是1米40公分。年龄与 身高的关系不能用一般的函数关系来表达。研究变量 之间既存在又不确定的相互关系及其密切程度的分析 称为相关分析。
(3)方差齐性检验
方差齐性是指残差的分布是常数,与预测变量或 因变量无关。即残差应随机的分布在一条穿过0点 的水平直线的两侧。在实际应用中,一般是绘制 因变量预测值与学生残差(或标准化残差)的散 点图。在线性回归Plots对话框中的源变量表中,选 择SRESID或ZRESID(学生氏残差或标准化残差) 做Y轴;选择ZPRED(标准化预测值)做X轴就 可以在执行后的输出信息中显示检验方差齐性的 散点图。
要认真检查数据的合理性。
2、选择自变量和因变量
3、选择回归分析方法
Enter选项,强行进入 法,即所选择的自变量 全部进人回归模型,该
选项是默认方式。
Remove选项,消去法, 建立的回归方程时,根
据设定的条件剔除部分
自变量。
选择回归分析方法
Forward选项,向前选择 法,根据在option对话框中 所设定的判据,从无自变 量开始。在拟合过程中, 对被选择的自变量进行方 差分析,每次加入一个F值 最大的变量,直至所有符 合判据的变量都进入模型 为止。第一个引入归模型 的变量应该与因变量间相 关系数绝对值最大。
得到它们的均方。
logistic 回归函数

logistic 回归函数Logistic回归函数是一种常用的分类算法,它可以根据输入变量的线性组合来预测二元分类的概率。
在本文中,我们将介绍Logistic 回归函数的原理、应用场景以及如何使用Python来实现。
让我们来了解一下Logistic回归函数的原理。
Logistic回归函数可以看作是在线性回归模型的基础上加上了一个非线性的映射函数,该映射函数被称为Logistic函数或Sigmoid函数。
Logistic函数的表达式为:$$f(x) = \frac{1}{1+e^{-x}}$$其中,x为输入变量的线性组合。
Logistic函数的特点是将输入的实数映射到了(0,1)的区间内,这个区间可以看作是一个概率的范围。
当x趋向于正无穷时,f(x)趋向于1;当x趋向于负无穷时,f(x)趋向于0。
因此,我们可以将f(x)看作是预测样本属于某个类别的概率。
Logistic回归函数的应用场景非常广泛。
一般来说,当我们需要对一个样本进行分类,并且样本的特征是连续的或者离散的,都可以考虑使用Logistic回归函数。
例如,我们可以使用Logistic回归函数来预测用户点击广告的概率,或者预测某个疾病的患病概率等等。
接下来,让我们通过一个具体的例子来演示如何使用Python来实现Logistic回归函数。
假设我们有一个数据集,其中包含了一些患有某种疾病的人的年龄和血压信息,我们的目标是根据这些信息来判断一个人是否患有该疾病。
首先,我们需要导入必要的库和加载数据集:```import numpy as npimport pandas as pdimport matplotlib.pyplot as pltdata = pd.read_csv('data.csv')```接下来,我们需要对数据进行预处理,包括数据清洗、特征选择和数据划分等步骤。
然后,我们可以使用sklearn库中的LogisticRegression类来构建Logistic回归模型,并进行训练和预测:```from sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import train_test_split# 特征选择X = data[['age', 'blood_pressure']]y = data['disease']# 数据划分X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 构建模型model = LogisticRegression()# 模型训练model.fit(X_train, y_train)# 模型预测y_pred = model.predict(X_test)```我们可以使用一些评估指标来评估模型的性能,例如准确率、精确率、召回率和F1值等:```from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score# 计算准确率accuracy = accuracy_score(y_test, y_pred)# 计算精确率precision = precision_score(y_test, y_pred)# 计算召回率recall = recall_score(y_test, y_pred)# 计算F1值f1 = f1_score(y_test, y_pred)```通过以上步骤,我们就可以完成Logistic回归函数的实现和模型评估。
第6章逻辑斯蒂回归模型

–其中probit变换是将概率变换为标准正态分布的 z −值, 形式为:
Logistic回归模型
–双对数变换的形式为:
f ( p ) = ln(− ln(1 − p ))
• 以上变换中以logit变换应最为广泛。 • 假设响应变量Y是二分变量,令 p = P(Y = 1) ,影响Y 的因素有k个 x1 ,L xk ,则称:
β • 其中, 0 , β1 ,L , β k 是待估参数。根据上式可以得到 优势的值: p β + β x +L+ β x
1− p
=e
0
1 1
k k
• 可以看出,参数 βi是控制其它 x 时 xi 每增加一个 单位对优势产生的乘积效应。 • 概率p的值: e β + β x +L+ β x
p=
0 1 1 k k
含有名义数据的logit
• 前例中的协变量为定量数据,logistic回归模型的 协变量可以是定性名义数据。这就需要对名义数 据进行赋值。 • 通常某个名义数据有k个状态,则定义个变量 M 1 ,L , M k −1 代表前面的k-1状态,最后令k-1变量均 为0或-1来代表第k个状态。 • 如婚姻状况有四种状态:未婚、有配偶、丧偶和 离婚,则可以定义三个指示变量M1、M2、M3, 用(1,0,0)、 (0,1,0) 、(0,0,1) 、(0,0,0)或(-1,-1,-1) 来对以上四种状态赋值。
G 2 = −2 ∑ 观测值[ln(观测值/拟合值)]
• 卡方的df应等于观测的组数与模型参数的差,较小的统计量的 值和较大的P-值说明模型拟合不错。 • 当至多只有几个解释变量且这些解释变量为属性变量,并且所 有的单元频数不少于5时,以上统计量近似服从卡方分布。
统计学原理第六章专题 logistic回归
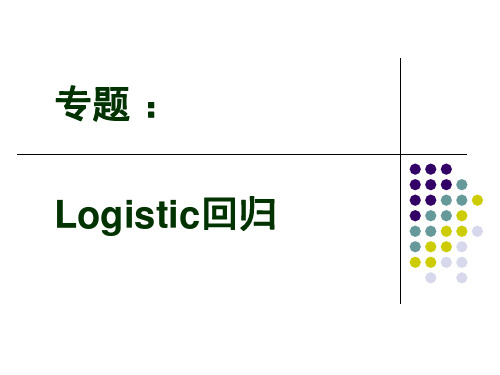
logit P为优比之对数(log odds)
logit
P
ˆ
ln
1
P P
Logistic回归分析
一般地,拟合回归模型时,是要建立属性变 量(因变量)取某种状态的概率pi关于自变量的 关系式.自变量若也是属性的变量,应先把它数 量化.比如自变量x取k种不同的状态,引入k-1个 标识变量zi(i=1,...,k-1)作为自变量.其中
变量名
WEIGHT SEX MONTH/t MAGE FAGE YC
CC ZRLC RGLC MSB MSA FSB FSA MDB FDB MDA JWBS ET XZLC PX RGZ JSCS
取值
1=体重<2500g,0=体重>=2500 1=男,0=女 1月~12月 岁
岁
1=第1次,2=第2次,…
Logistic回归分析
Logistic回归分析--优比率
在这两种情况下,Y=1发生的优比率(Odds
exp( ) Ratio)为 exp(0 1)
exp( 0 )
1
当得到Logistic回归的回归系数估计b后,就可
得到关于Y=1发生优比率的估计值:
优比率=exp(b).
此例的优比率为1.549,表示利用拟合的回归式 预测女性购买100元以上商品的优比为男性的 1.549倍.
Logistic回归分析
Logit 函数 :Y=Logit(p) 的图形如下(随p
由0变到1,Y的值由-∞单调上升到∞) :
Logistic回归分析
当p在(0,1)中变化时,logit(p)就在(-∞,∞)中变 化。利用logit变换可将属性变量取某个值的概 率p的logit变换表示为自变量的线性函数,即
logistic回归原理

logistic回归原理
Logistic回归,又称为逻辑回归,是一种广泛应用的机器学习算法,主要用于分类问题。
它将一个数值变量预测为两个或多个二元变量值之一,例如:通过观察一个变量,我们可以预测另一个变量为正类/负类。
Logistic回归是一种函数拟合技术,它可以根据给定的输入数据,建立一个模型以预测数据的输出值。
它使用一个逻辑函数(也称为S形函数)来将连续的输入变量映射到二元类别输出中,形成一个只具有两个类别的模型。
Logistic回归的基本原理是,我们根据输入特征(例如年龄、性别、学历等)来预测输出(例如好/坏借款人)。
在Logistic回归模型中,输入特征是一个变量,而输出是一个二元变量,即只有两个值-0或1。
为了使Logistic回归模型正确地对数据进行建模,需要在训练阶段对参数进行估计。
估计的方式多种多样,但最常用的是最大似然估计(MLE)。
在MLE中,我们根据给定的训练数据找到最可能产生该数据的参数,也就是找到能够最好地拟合训练数据的参数。
一旦参数被估计出来,就可以使用该模型来预测新数据。
预测时,通常使用两个概念来描述预测:概率和似然估计。
概率表示新数据属于某个类别的可能性,即预测出的结果是0还是1的概率。
而似然估计则表示特定参数的可信度,即该参数产生观测数据的可能性。
总之,Logistic回归是一种广泛应用于分类问题的机器学习算
法,它将一个数值变量预测为两个或多个二元变量值之一。
它使用一个函数来将连续的输入变量映射到二元类别输出中,以预测数据的输出值。
在Logistic回归模型中,我们使用最大似然估计来估计参数,以及概率和似然估计来预测新数据。
Logistic 回归
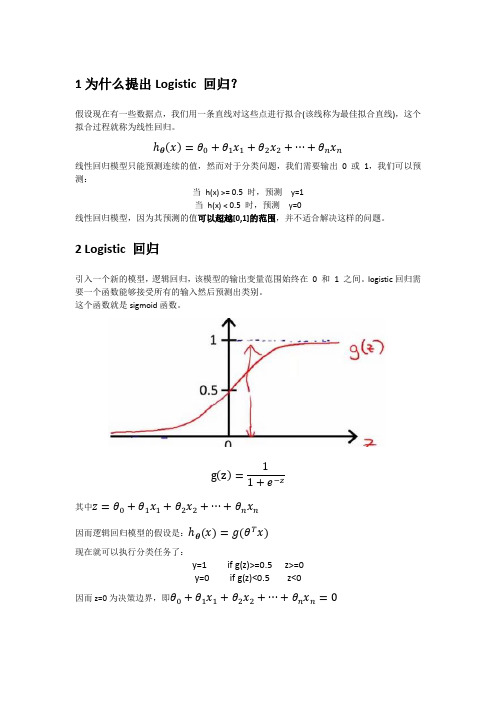
1为什么提出Logistic 回归?假设现在有一些数据点,我们用一条直线对这些点进行拟合(该线称为最佳拟合直线),这个拟合过程就称为线性回归。
θx=θ0+θ1x1+θ2x2+⋯+θn x n线性回归模型只能预测连续的值,然而对于分类问题,我们需要输出0 或1,我们可以预测:当h(x)>= 0.5 时,预测y=1当h(x)< 0.5 时,预测y=0线性回归模型,因为其预测的值可以超越[0,1]的范围,并不适合解决这样的问题。
2Logistic 回归引入一个新的模型,逻辑回归,该模型的输出变量范围始终在0 和 1 之间。
logistic回归需要一个函数能够接受所有的输入然后预测出类别。
这个函数就是sigmoid函数。
g z=1−z其中z=θ0+θ1x1+θ2x2+⋯+θn x n因而逻辑回归模型的假设是: θx=g(θT x)现在就可以执行分类任务了:y=1 if g(z)>=0.5 z>=0y=0 if g(z)<0.5 z<0因而z=0为决策边界,即θ0+θ1x1+θ2x2+⋯+θn x n=03损失函数对于线性回归模型,我们定义的损失函数是所有数据误差的平方和。
但是当我们把logistic 拟合函数的 θx带入损失函数中,发现损失函数变成一个非凸函数。
具有多个极小值,这将影响梯度下降算法寻找全局最小值,如下图左端所示。
因而我们需要定义新的损失函数,使得带入 θx的损失函数变为凸函数。
cost( θx ,y)=−log θx if y=1−log (1− θx) if y=0这样构建的cost( θx ,y)函数的特点是:当实际的y=1 且 θx也为1 时误差为0,当y=1 但 θx不为1 时误差随着 θx的变小而变大;当实际的y=0 且 θx也为0 时代价为0,当y=0 但 θx不为0 时误差随着 θx的变大而变大.最后损失函数为:Jθ=1m−y i log θ x i−1−y i log(1− θ x i) mi=1在得到这样一个损失函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。
logistic回归

比较
以上三种方法中,在多数情况下,似然比 检验是最有效的检验,记分检验一般与它相 一致。但两者计算量均较大;
Wald检验主要用于对单个回归系数的检验, 但是Wald检验未考虑各因素间的综合作用, 比较保守,在因素间有共线性存在时,结果不 像其它两者可靠。
Logistic回归
一般过程
Logistic回归
统计学概念
队列研究 病例对照研究 危险度 相对危险度(RR) 比数比或优势比(OR)
队列研究
也称前瞻性研究、随访研究等。是一种由因及果的 研究,在研究开始时,根据以往有无暴露经历,将研 究人群分为暴露人群和非暴露人群,在一定时期内, 随访观察和比较两组人群的发病率或死亡率。如果两 组人群发病率或死亡率差别有统计学意义,则认为暴 露和疾病间存在联系。
Logistic回归
ROC曲线
涵义与起源
ROC【receiver(relative) operating characteristic的缩
写,译为“接受者工作特征”】
ROC曲线研究历史
1950’s
雷达信号观测能力评价
1960’s中期
实验心理学、心理物理学
1970’s末与1980’s初 诊断医学
ROC曲线
对照
Logistic回归
比数比
是否暴露 暴露组 未暴露组 合计
病例 a c a+c
对照 b d b+d
合计 a+b(n1) c+d(n2) n
比数比(odds ratio、OR):病例对照研究中表示疾病与暴露间
联系强度的指标,也称比值比。
比数(odds):发生率与未发生率之比。即阳性率/阴性率。
logistic回归法

logistic回归法Logistic回归法是一种常用的分类算法,广泛应用于各个领域。
它通过构建一个逻辑回归模型来预测某个事件发生的概率。
本文将介绍Logistic回归法的原理、应用场景以及优缺点。
一、Logistic回归法的原理Logistic回归法是基于线性回归的一种分类算法,它使用sigmoid 函数将线性回归的结果映射到[0,1]之间。
sigmoid函数的公式为:$$f(x) = \frac{1}{1+e^{-x}}$$其中,x为线性回归的结果。
通过这个映射,我们可以将线性回归的结果解释为某个事件发生的概率。
二、Logistic回归法的应用场景Logistic回归法常用于二分类问题,如预测某个疾病的发生与否、判断邮件是否为垃圾邮件等。
它也可以通过一些改进来应用于多分类问题。
在实际应用中,Logistic回归法非常灵活,可以根据需要选择不同的特征和参数,以达到更好的分类效果。
同时,它对特征的要求相对较低,可以处理连续型和离散型的特征,也可以处理缺失值。
三、Logistic回归法的优缺点1. 优点:- 计算简单、效率高:Logistic回归法的计算量相对较小,算法迭代速度快,适用于大规模数据集。
- 解释性强:Logistic回归模型可以得到各个特征的权重,从而可以解释每个特征对结果的影响程度。
- 可以处理离散型和连续型特征:Logistic回归法不对特征的分布做出假设,可以处理各种类型的特征。
- 可以处理缺失值:Logistic回归法可以通过插补等方法处理缺失值,不需要将含有缺失值的样本剔除。
2. 缺点:- 容易出现欠拟合或过拟合:当特征过多或特征与目标变量之间存在非线性关系时,Logistic回归模型容易出现欠拟合或过拟合问题。
- 对异常值敏感:Logistic回归模型对异常值比较敏感,可能会对模型造成较大的干扰。
- 线性关系假设:Logistic回归模型假设特征与目标变量之间的关系是线性的,如果实际情况并非线性关系,模型的预测效果可能较差。
《logistic回归》课件

易于理解和实现: 由于基于逻辑函数,模型输出结 果易于解释,且实现简单。
Logistic回归的优势与不足
• 稳定性好: 在数据量较小或特征维度较高 时,Logistic回归的预测结果相对稳定。
Logistic回归的优势与不足
01
不足:
02
对数据预处理要求高: 需要对输入数据进行标准化或归一化处理,以 避免特征间的尺度差异对模型的影响。
模型假设
01
线性关系
因变量与自变量之间存在线性关系 。
无自相关
因变量与自变量之间不存在自相关 。
03
02
无多重共线性
自变量之间不存在多重共线性,即 自变量之间相互独立。
随机误差项
误差项是独立的,且服从二项分布 。
04
模型参数求解
最大似然估计法
通过最大化似然函数来求解模型参数。
梯度下降法
通过最小化损失函数来求解模型参数。
特征选择与降维
在处理大数据集时,特征选择和降维是提高模 型性能和可解释性的重要手段。
通过使用诸如逐步回归、LASSO回归等方法, 可以自动选择对模型贡献最大的特征,从而减 少特征数量并提高模型的泛化能力。
降维技术如主成分分析(PCA)可以将高维特 征转换为低维特征,简化数据结构并揭示数据 中的潜在模式。
迭代法
通过迭代的方式逐步逼近最优解。
牛顿法
利用牛顿迭代公式求解模型参数。
模型评估指标
准确率
正确预测的样本数占总样本数的比例 。
精度
预测为正例的样本中实际为正例的比 例。
召回率
实际为正例的样本中被预测为正例的 比例。
F1分数
精度和召回率的调和平均数,用于综 合评估模型性能。
LOGISTIC回归

一、回归分析的分类logistic回归(logistic regression)是研究因变量为二分类或多分类观察结果与影响因素(自变量)之间关系的一种多变量分析方法,属概率型非线性回归。
根据1个因变量与多个因变量之分,有以下区分:①一个因变量y:I连续形因变量(y)——线性回归分析II分类型因变量(y)——Logistic 回归分析III 生存时间因变量(y)——生存风险回归分析IV时间序列因变量(y)——时间序列分析②多个因变量(y1,y2,……yn):I 路径分析II 结构方程模型分析在流行病学研究中,常需要分析疾病与各种危险因素间的定量关系,同时为了能真实反映暴露因素与观察结果间的关系,需要控制混杂因素的影响。
(1)Mantel-Haenszel分层分析:适用于样本量大、分析因素较少的情况。
当分层较多时,由于要求各格子中例数不能太少,所需样本较大,往往难以做到;当混杂因素较多时,分层数也呈几何倍数增长,这将导致部分层中某个格子的频数为零,无法利用其信息。
(2)线性回归分析:由于因变量是分类变量,不能满足其正态性要求;有些自变量对因变量的影响并非线性。
(3)logistic回归:不仅适用于病因学分析,也可用于其他方面的研究,研究某个二分类(或无序及有序多分类)目标变量与有关因素的关系。
二、logistic回归分析(一)logistic回归的分类(1)二分类资料logistic回归:因变量为两分类变量的资料,可用非条件logistic回归和条件logistic回归进行分析。
非条件logistic回归多用于非配比病例-对照研究或队列研究资料,条件logistic回归多用于配对或配比资料。
(2)多分类资料logistic回归:因变量为多项分类的资料,可用多项分类logistic回归模型或有序分类logistic回归模型进行分析。
队列研究(cohort study):也称前瞻性研究、随访研究等。
是一种由因及果的研究,在研究开始时,根据以往有无暴露经历,将研究人群分为暴露人群和非暴露人群,在一定时期内,随访观察和比较两组人群的发病率或死亡率。
logistics回归解释

logistics回归解释Logistic回归是统计学中一个常用的分类算法,用于预测二元变量的结果。
例如,它可以用于预测一个人是否喜欢某个产品,或是否患有某种疾病。
Logistic回归的本质是一种线性模型,它通过将自变量的线性组合(在这里通常指特征值)传递到logistic函数中来预测响应变量。
这个函数的输出可以被解释为响应变量是二元的概率。
logistic函数(也称为逻辑斯蒂函数)将线性组合作为输入,并将其“挤压”到介于0和1之间的范围内,它的输出值表示响应变量是1的概率:$$ f(\mathrm{x}) = \frac{1}{1+\mathrm{e}^{-\mathrm{x}}} $$其中x是自变量的线性组合,它的定义可以写成:$$ \mathrm{x} = w_0 + w_1x_1 + w_2x_2 + ... + w_px_p $$其中,w是每个特征的权重,x是每个特征值。
这个方程中的第一个项(w0)是截距项,它确保对于所有的特征值为0的情况下,响应变量的概率为基本值。
当w0+w1x1+w2x2+...wp> 0时,logistic函数的输出为1,并且响应变量被预测为阳性(即响应变量等于1)。
反之,如果w0+w1x1+w2x2+...wp< 0,算法将预测响应变量等于0。
在训练Logistic回归模型时,我们需要确定每个特征的重要程度,以及最佳的随机误差项权重。
我们可以使用最大似然估计(MLE)算法来解决这个问题。
该算法将基于样本数据,逐步调整其参数,直到达到接近最佳拟合的状态。
总之,Logistic回归是一种流行的分类算法,可以处理许多不同的问题,例如预测身患某种疾病的人数,或预测客户对一种产品的反应。
它的输出值可以转化为比率或概率,这使得它非常灵活和可解释。
logistic回归分析.

取 “-”,则xj增大,则xj 增大,则P减小, 即抑制阳性结果的发生,为“保护因素”。
(2)大小 :∣ j1 ∣越大,则xj 对结果的影响也就越大。
Logistic回归分析
3.OR值的计算和意义
影响因素由X▲ 变化到X* 时,有 :
m
ln OR
ˆ
j
(
x
*
j
x
j
)
j 1
(1)对多指标的共同效应进行评价:
m
ˆ ˆ j x*j
OR
p* / q* p / q
e j1
m
ˆ
ˆ
j
x
j
e j1
m
ˆ
j
(
x*j
x
j
)
OR e j1
若OR&水平,
即“不利因素”占主导地位;
若OR<1,则处于X*水平下的阳性结果发生风险要低于X▲水平,
Logistic回归分析
数学模型:
e 1X1 2 X 2 m X m p 1 e 1X1 2 X 2 m X m
Logistic回归分析
一、基本思想
用模型去描述实际资料时,须使 得理论结果与实际结果尽可能的一致。
Logistic回归分析
二、基本原理
Logistic回归分析
三、基本方法
最大似然函数法
四、参数解释
1. 偏回归系数j 的意义
与指标的计量单位有关,从而无实际 的解释意义。
Logistic回归分析
消除xj量纲的影响
2.标准化偏回归系数j1的意义
xij
xij x sj
j
(1)符号:取 “+”,则xj 增大,则P增大,即促进阳性 结果的发生,为“不利因素”;
logistic回归 原理

logistic回归原理Logistic回归是一种常用的分类算法,它基于Logistic函数进行建模,用于解决二分类问题。
本文将介绍Logistic回归的原理及其应用。
一、Logistic回归原理Logistic回归是一种广义线性模型,它的目标是通过对数据进行拟合,得到一个能够将输入数据映射到0和1之间的函数,从而进行分类。
其基本思想是通过线性回归模型的预测结果,经过一个Logistic函数(也称为Sigmoid函数)进行转换,将预测结果限制在0和1之间。
Logistic函数的定义如下:$$f(x) = \frac{1}{1+e^{-x}}$$其中,$e$是自然对数的底数,$x$是输入值。
Logistic函数的特点是在$x$接近正负无穷时,函数值趋近于1和0,而在$x=0$时,函数值为0.5。
这样,我们可以将Logistic函数的输出视为样本属于正类的概率。
而Logistic回归模型的表达式为:$$h_{\theta}(x) = f(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}}$$其中,$h_{\theta}(x)$表示预测值,$\theta$表示模型参数,$x$表示输入特征。
二、Logistic回归的应用Logistic回归广泛应用于二分类问题,例如垃圾邮件分类、疾病诊断、信用评估等。
下面以垃圾邮件分类为例,介绍Logistic回归的应用过程。
1. 数据预处理需要对邮件数据进行预处理。
包括去除HTML标签、提取文本特征、分词等操作。
将每封邮件表示为一个向量,向量的每个元素表示对应词汇是否出现。
2. 特征工程在特征工程中,可以通过选择合适的特征、进行特征组合等方式,提取更有用的特征。
例如,可以统计邮件中出现的特定词汇的频率,或者使用TF-IDF等方法进行特征提取。
3. 模型训练在模型训练阶段,需要将数据集划分为训练集和测试集。
通过最大似然估计或梯度下降等方法,求解模型参数$\theta$,得到训练好的Logistic回归模型。
第6章逻辑斯蒂回归模型

Logistic回归模型
多元logistic模型参数的估计 –采用极大似然估计方法 –假设n次观测中,对应( xi1 , , xik ) 的观测有 ni 个, 其中观测值为1的有 ri 个,观测值为0的有 ni ri 个,则参数β 0 , β1 , , β k 的似然函数:
probit[π ( x)] = α + β x
–其中probit变换是将概率变换为标准正态分布的 z 值, 形式为:
Logistic回归模型
–双对变换的形式为:
f ( p ) = ln( ln(1 p ))
以上变换中以logit变换应最为广泛. 假设响应变量Y是二分变量,令 p = P(Y = 1) ,影响Y 的因素有k个 x1 , xk ,则称:
p ln = 11.536 + 0.124 A + 0.711M 1 0.423M 2 + 0.021M 3 1 p
含有有序数据的logit
Logit模型的协变量也可以是有序数据 对有序数据的赋值可以按顺序用数0,1,2,3,4分别 表示 【例5.8】某地某年各类文化程度的死亡人数见表 5.33,试建立logit模型. 建立死亡率关于年龄和文化程度的logit模型
Logistic回归的推断
效应的置信区间 –指的是参数的置信区间估计 –一般可以采用 β ± zα /2 ( SE ) 的区间形式 β –通过上述区间端点的指数变换得到 e 的区间, 它是 x 每增加1个单位对优势的乘积效应 –当n很小或拟合概率趋近0或1时,可以采用似 然比检验来构造区间,该区间包含所有使原假 设成立的可能值 –通常可以借助软件得到这种区间
前例中的协变量为定量数据,logistic回归模型的 协变量可以是定性名义数据.这就需要对名义数 据进行赋值. 通常某个名义数据有k个状态,则定义个变量 M 1 , , M k 1 代表前面的k-1状态,最后令k-1变量均 为0或-1来代表第k个状态. 如婚姻状况有四种状态:未婚,有配偶,丧偶和 离婚,则可以定义三个指示变量M1,M2,M3, 用(1,0,0), (0,1,0) ,(0,0,1) ,(0,0,0)或(-1,-1,-1) 来对以上四种状态赋值.
logistic回归模型系数估计原理

logistic回归模型系数估计原理
Logistic回归是一种广义线性回归(generalized linear model),与多重线性回归有很多相似之处。
它的模型通过找到一个函数来确定某件事情发生的概率。
具体来说,如果直接将线性回归的模型应用到Logistic回归中,会导致方程两边的取值区间不同,并且普遍存在非直线关系。
因为Logistic回归中的因变量是二分类变量,某个概率作为方程的因变量估计值取值范围为0-1,但方程右边取值范围是无穷大或者无穷小。
所以,Logistic回归在回归模型的基础上进行了改进。
如果L是logistic函数,就是logistic回归;如果L是多项式函数,则是多项式回归。
这种通过引入logistic函数调整因变量的值,以解决线性回归方程左右取值范围不同的问题。
如需了解更多关于logistic回归模型系数估计原理的相关知识,可以查阅统计学或计量经济学专业书籍,也可咨询相关专业人士。
Logistic_回归分析作业答案[3页]
![Logistic_回归分析作业答案[3页]](https://img.taocdn.com/s3/m/bfd1a26871fe910ef02df8a6.png)
第六章 Logistic回归练习题 (操作部分:部分参考答案)1. 下面问题的数据来自“ch6-logistic_exercise”,数据包含受访者的人口学特征、劳动经济特征、流动身份。
数据的变量及其定义如下:变量名变量的定义age 年龄,连续测量degree 受教育程度:1=未上过学;2=小学;3=初中;4=高中;5=大专;6=大学;7=研究生girl 性别:1=女性;0=男性hanzu 民族:1=汉族;0=少数民族hetong 劳动合同:1=固定合同;2=非固定合同;3=无合同income 月收入ldhour 每周劳动时间married 婚姻状态:1=在婚;0=其他(未婚、离异、再婚、丧偶,等)migtype4 流动身份:1=本地市民;2=城-城流动人口;3=乡-城流动人口pid IDss_jobloss 失业保险:1=有;0=无ss_yanglao 养老保险:1=有;1=无这里的研究问题是,流动人口与流入地居民在社会保障、劳动保护和居住环境等方面是否存在显著差别。
流动人口被区分为城-城流动人口(即具有城镇户籍、但离开户籍地半年以上之人)和乡-城流动人口(即具有农村户籍、且离开户籍地半年以上之人)。
因此,样本包含三类人群:本地市民、城-城流动人口、乡-城流动人口及相应特征。
说明:(1)你需要对数据进行一些必要的处理,才能正确回答研究问题;(2)将变量hetong的缺失数据作为一个类别;(3)将degree合并为四类:<=小学,初中、高中、>高中. use "D:\course\integration of theory andmethod\8_ordered\chapter8-logistic_exercise.dta", clear*重新三个社会保障变量. gen ss_jobl=ss_jobloss==1. gen ss_ylao=ss_yanglao==1. gen ss_yili=ss_yiliao ==1*重新code受教育程度. recode degree (1/2=1) (3=2) (4=3)(5/7=4)*将劳动合同的缺失作为一个分类. recode hetong (.=4)请基于该数据,完成以下练习,输出odds ratio的分析结果:其一,运用二分类Logistic模型,探讨流动人口的社会保障机会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优化算法简介
逻辑斯谛回归模型、最大熵模型学习归结为以似然函数 为目标函数的最优化问题,通常通过迭代算法求解,它 是光滑的凸函数,因此多种最优化的方法都适用。 常用的方法有: 改进的迭代尺度法 梯度下降法 牛顿法 拟牛顿法
梯度下降法
梯度下降法(gradient descent) 最速下降法(steepest descent) 梯度下降法是一种迭代算法.选取适当的初值x(0),不断 迭代,更新x的值,进行目标函数的极小化,直到收敛。 由于负梯度方向是使函数值下降最快的方向,在迭代的 每一步,以负梯度方向更新x的值,从而达到减少函数 值的目的.
袁春 清华大学深圳研究生院 李航 华为诺亚方舟实验室
目录
1. 逻辑斯蒂回归模型 2. 最大熵模型 3. 模型学习的最优化方法
一、逻辑斯蒂回归
逻辑斯蒂分布 二项逻辑斯蒂回归 似然函数 模型参数估计 多项logistic回归
回归
面积 销售价钱 (m^2) (万元) 123 150 87 102 … 250 320 160 220 …
牛顿法
(B.8)
牛顿法
算法步骤:
求逆
拟牛顿法
考虑用一个n阶矩阵Gk=G(x(k))来近似代替
拟牛顿条件: 由:
拟牛顿法
如果Hk是正定的, Hk-1也是正定的,那么可以保证牛顿 法搜索方向Pk是下降方向,因为搜索方向 由B.8得: 由B.2得:
将Gk作为
的近似
,拟牛顿条件
最优化原始问题 到 对偶问题:
最大熵模型的学习
最优化原始问题 到 对偶问题:
L(P,w)是P的凸函数,解的等价性(证明部分在SVM部 分介绍) 先求极小化问题:
是w的函数,
最大熵模型的学习
求L(P,w)对P(y|x)的偏导数:
得:最大熵模型的学习由 Nhomakorabea 得:(6.22) 规范化因子: 模型 就是最大熵模型 求解对偶问题外部的极大化问题: (6.23)
回归
回归:广义线性模型(generalized linear model) 分类:根据因变量的不同 连续:多重线性回归 二项分布:logistic回归 poisson分布:poisson回归 负二项分布:负二项回归
逻辑斯蒂分布
Logistic distribution 设X是连续随机变量,X服从Logistic distribution, 分布函数: 密度函数: μ为位置参数,γ大于0为形状参数,(μ,1/2)中心对称
多项logistic回归
设Y的取值集合为
多项logistic回归模型
二、最大熵模型
最大熵原理 最大熵模型的定义 最大熵模型的学习 极大似然估计
最大熵原理
最大熵模型(Maximum Entropy Model)由最大熵原理推 导实现。 最大熵原理: 学习概率模型时,在所有可能的概率模型(分布)中,熵 最大的模型是最好的模型,表述为在满足约束条件的模 型集合中选取熵最大的模型。 假设离散随机变量X的概率分布是P(X), 熵: 且: |X|是X的取值个数,X均匀分布时右边等号成立。
梯度下降法
假设f(x)具有一阶连续偏导数的函数: 一阶泰勒展开: f(x)在x(k)的梯度值:
负梯度方向:
无约束最优化问题
牛顿法(Newton method) 拟牛顿法(quasi Newton method) 有收敛速度快的优点. 牛顿法是迭代算法,每一步需要求解目标函数的海赛矩 阵的逆矩阵,计算比较复杂。 拟牛顿法通过正定矩阵近似海赛矩阵的逆矩阵或海赛矩 阵,简化了这一计算过程。
拟牛顿法
最大熵模型:
目标函数:
梯度:
Q&A?
BFGS(Broyden-Fletcher-GoldfarbShanno)算法
可以考虑用Gk逼近海赛矩阵的逆矩阵H-1,也可以考虑 用Bk逼近海赛矩阵H, 这时,相应的拟牛顿条件是: 用同样的方法得到另一迭代公式.首先令
考虑使Pk和Qk满足: Bk+1的迭代公式:
B.30
改进的迭代尺度法
拟牛顿法
在每次迭代中可以选择更新矩阵
Broyden类优化算法: DFP(Davidon-Fletcher-Powell)算法(DFP algorithm) BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法(BFGS algorithm) Broyden类算法(Broyden's algorithm)
Sigmoid:
双曲正切函数(tanh)
Sigmoid function: def sigmoid(inX): return 1.0/(1+exp(-inX))
二项逻辑斯蒂回归
Binomial logistic regression model 由条件概率P(Y|X)表示的分类模型 形式化为logistic distribution X取实数,Y取值1,0
的期望值:
特征函数f(x,y)关于模型P(Y|X)与经验分布 值:
的期望
如果模型能够获取训练数据中的信息,那么就可以假设 这两个期望值相等,即
假设有n个特征函数:
最大熵模型的定义
定义: 假设满足所有约束条件的模型集合为:
定义在条件概率分布P(Y|X)上的条件熵:
则模型集合C中条件熵H(P)最大的模型称为最大熵模型
极大似然估计
而:
极大似然估计
最大熵模型与逻辑斯谛回归模型有类似的形式,它们又 称为对数线性模型(log linear model). 模型学习就是在 给定的训练数据条件下对模型进行极大似然估计或正则 化的极大似然估计。
三、模型学习的最优化算法
最优化算法简介 梯度下降法 无约束最优化问题 - 牛顿法、拟牛顿法、DFP算法、 BFGS算法
二项逻辑斯蒂回归
事件的几率odds:事件发生与事件不发生的概率之比 为
称为事件的发生比(the odds of experiencing an event), 对数几率:
对逻辑斯蒂回归:
似然函数
logistic分类器是由一组权值系数组成的,最关键的问题就 是如何获取这组权值,通过极大似然函数估计获得,并且 Y ~ f( x ; w ) 似然函数是统计模型中参数的函数。给定输出x时,关于参 数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X 的概率:L(θ|x)=P(X=x|θ) 似然函数的重要性不是它的取值,而是当参数变化时概率 密度函数到底是变大还是变小。 极大似然函数:似然函数取得最大值表示相应的参数能够 使得统计模型最为合理
牛顿法
无约束最优化问题:
假设f(x)具有二阶连续偏导数,若第k次迭代值为x(k), 则可将f(x)在x(k)附近进行二阶泰勒展开: B.2
是f(x)的梯度向量在x(k)的值 是f(x)的海塞矩阵 在点x(k)的值
牛顿法
函数f(x)有极值的必要条件是:在极值点处一阶导数为o, 即梯度向量为o. 特别是当H(x(k))是正定矩阵时,函数f(x)的极值为极小 值. 利用条件: 设迭代从x(k)开始,求目标函数的极小点,
似然函数
那么对于上述m个观测事件,设
其联合概率密度函数,即似然函数为:
目标:求出使这一似然函数的值最大的参数估,w1,w2,…,wn, 使得L(w)取得 最大值。 对L(w)取对数:
模型参数估计
对数似然函数
对L(w)求极大值,得到w的估计值。 通常采用梯度下降法及拟牛顿法,学到的模型:
改进的迭代尺度法
利用
改进的迭代尺度法
于是有 如果能找到适当的δ使下界A(δ|w)提高,那么对数似然 函数也会提高。 δ是一个向量,含多个变量,一次只优化一个变量δi 引进一个量f#(x,y), fi(x,y)是二值函数, f#(x,y)表示所有特征在(x,y)出现的 次数。
改进的迭代尺度法
例子:
假设随机变量X有5个取值{A,B,C,D,E},估计各个值的概 率。 解:满足
P(A)+P(B)+P(C)+P(D)+P(E)=1
等概率估计: 加入一些先验:
于是:
例子:
假设随机变量X有5个取值{A,B,C,D,E},估计各个值的概 率。 解:满足
P(A)+P(B)+P(C)+P(D)+P(E)=1
等概率估计: 加入一些先验:
于是:
再加入约束:
最大熵原理
X和Y分别是输入和输出的集合,这个模型表示的是对 于给定的输入X,以条件概率P(Y|X)输出Y. 给定数据集: 联合分布P(Y|X)的经验分布,边缘分布P(X)的经验分布:
特征函数:
最大熵原理
特征函数f(x,y)关于经验分布
最大熵模型的学习
最大熵模型的学习可以形式化为约束最优化问题。 对于给定的数据集以及特征函数:fi(x,y) 最大熵模型的学习等价于约束最优化问题:
最大熵模型的学习
这里,将约束最优化的原始问题转换为无约束最优化的 对偶问题,通过求解对偶问题求解原始间题: 引进拉格朗日乘子,定义拉格朗日函数:
改进的迭代尺度法(improved iterative scaling,IIS) 由最大熵模型
对数似然函数
求对数似然函数的极大值 IIS思路:假设 希望找到一个新的参数向 量 ,使得模型的对数似然函数值 增大,如果有参数向量更新方法,那么就可以重复使用 这一方法,直至找到对数似然函数的最大值。
利用指数函数的凸性,以及
根据Jensen不等式:
改进的迭代尺度法
于是得到
是对数似然函数改变量的一个新的下界 对δi 求偏导:
令偏导数为0,得到:
依次对δi 解方程。
改进的迭代尺度法
算法 输入:特征函数f1,f2…fn;经验分布 输出:最优参数wi*;最优模型Pw*
