matlab(计算方法的MATLAB实现)
matlab实现数值计算功能源程序(个人整理)

matlab数值计算功能1,基础运算(1)多项式的创建与表达将多项式(x-6)(x-3)(x-8)表示为系数形式a=[6 3 8] % 写成根矢量pa=poly(a)% 求出系数矢量ppa=poly2sym(pa,'x') % 表示成符号形式ezplot(ppa,[-50,50])求3介方阵A的特征多项式a=[6 2 4;7 5 6;1 3 6 ];pa=poly(a)% 写出系数矢量ppa=poly2sym(pa) %表示成符号形式ezplot(ppa,[-50,50]) % 绘图求x^3-6x^2-72x-27的根。
a=[1,-6,-72,-85]; % 写出多项式系数矢量r=roots(a) % 求多项式的根(2)多项式的乘除运算c=conv(a,b) %乘法[q,r]=deconv(c,a)% 除法求a(s)=s^2+2s+3乘以b(s)=4s^2+5s+6的乘积a=[1 2 3]b=[4 5 6] % 写出系数矢量c=conv(a,b)c=poly2sym(c,'s') % 写成符号形式的多项式展开(s^2+2s+2)(s+4)(s+1)并验证结果被(s+4),(s+3)除后的结果。
c=conv([1,2,2],conv([1,4],[1,1]))cs=poly2sym(c,'s')c=[1 7 16 18 8][q1,r1]=deconv(c,[1,4])[q2,r2]=deconv(c,[1,3])cc=conv(q2,[1,3])test=((c-r2)==cc)其他常用的多项式运算命令pa=polyval(p,s) % 按数组规则计算给定s时多项式的值pm=polyvalm(p,s)% 按矩阵规则计算给定s时多项式的值[r,p,k]=residue(b,a) % 部分分式展开,b,a分别是分子,分母多项式系数矢量。
r,p,k分别是留数,极点和值项矢量。
Matlab中的并行计算方法介绍

Matlab中的并行计算方法介绍引言Matlab作为一种功能强大的科学计算工具,在各个领域的应用都不可忽视。
但是,随着数据规模的增加和计算复杂度的提升,单机计算已经无法满足研究者和工程师的需求。
这就需要使用并行计算的方法来实现更高效的计算。
本文将介绍一些常用的Matlab中的并行计算方法,包括如何使用Parallel Computing Toolbox中的函数、Parallel Computing Toolbox中的工具以及Parallel Computing Toolbox结合其他工具一起使用的方法。
一、Parallel Computing Toolbox函数的使用Parallel Computing Toolbox是Matlab中用于进行并行计算的工具箱,它提供了一系列方便易用的函数来实现并行计算。
其中主要的函数包括parfor、parpool和spmd。
1. parfor函数parfor函数是Matlab中用于实现循环并行计算的函数。
它可以将一个循环分解成多个子任务,并在多个处理器上同时执行这些子任务,从而大大提高计算效率。
使用parfor函数的方法如下所示:```matlabparfor i = 1:N% 子任务的计算过程end```在这个例子中,N表示循环的迭代次数。
使用parfor函数的时候,需要注意以下几点:- 子任务之间的计算不能相互依赖,也就是说每个子任务之间不存在数据的读取和写入操作。
- 子任务的计算过程尽量保持相对独立,避免不必要的数据交互。
2. parpool函数parpool函数用于创建一个并行计算的池子,其中包含多个工作进程。
使用这些工作进程可以实现对大规模计算任务的分布式处理。
使用parpool函数的方法如下所示:```matlabparpool('local', N)```在这个例子中,N表示要创建的工作进程的数量。
使用parpool函数的时候,需要注意以下几点:- 工作进程的数量应根据实际情况进行调整,以保证计算效率和资源的合理利用。
Matlab(R2009a版)-第8讲 计算方法的MATLAB实现

2019/2/16 1
课程主要内容
• • • • • • • • • • 第1章 MATLAB简介 第2章 数值运算 第3章 单元数组和结构 计 第8章 计算方法的MATLAB实现 第9章 优化设计 第10章 SIMULINK仿真初探
16
2019/2/16
• 对角变换
• U=diag(x)返回矩阵x主对角线上的元素,返回结 果是一列向量形式; • U=diag(x,k)返回第k条对角线上的元素值。 • 当x为向量时生成矩阵。
2019/2/16
17
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> diag(a) • ans = • • • 12 3 1
12x1 3x2 3x3 15 18x1 3x2 x3 15 x x x 6 1 2 3
2019/2/16
9
程序实例
• • • • • • • • • • • • >> a=[12 -3 3;-18 3 -1;1 1 1]; >> b=[15;-15;6]; >> x1=a\b x1 = 1.0000 2.0000 3.0000 >> x2=inv(a)*b x2 = 1 2 3
2019/2/16
14
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> tril(a) • ans = • • • 12 0 0 -18 3 0 1 1 1
2019/2/16
15
程序实例
• • • • • • • • • • >> tril(a,1) ans = 12 -3 0 -18 3 -1 1 1 1 >> tril(a,-1) ans = 0 0 0 -18 0 0 1 1 0
matlab function实现pi运算

matlab function实现pi运算如何用Matlab实现pi的计算在科学计算中,π(pi)是一个非常重要的数学常数。
它代表了一个圆的周长与其直径之间的比例关系。
不同的领域,如数学、物理、工程等,经常需要使用到π。
Matlab是一款功能强大的科学计算软件,我们可以利用其编程能力来实现π的计算。
本文将一步一步地介绍如何使用Matlab来编写一个计算π的函数。
步骤一:了解π的计算方法计算π的方法有很多种,其中一种著名的方法是蒙特卡洛方法。
该方法基于随机抽样,利用圆的特性进行估算。
我们首先在一个正方形内随机生成大量的点,然后计算这些点落在圆内的比例。
通过该比例乘以正方形的面积,我们就可以估算出圆的面积,从而得到π的近似值。
步骤二:编写Matlab函数首先,我们需要定义一个函数来实现π的计算。
打开Matlab编辑器,并创建一个新的函数文件pi_calculation.m。
接下来,我们将在函数内部编写代码。
步骤三:生成随机点我们可以使用Matlab的rand函数来生成随机的x和y坐标。
由于我们只需要在正方形内生成点,所以我们可以将随机数限制在[0,1]之间。
为了方便起见,我们可以一次性生成大量的点,而不是逐个生成。
matlabfunction pi_value = pi_calculation(num_points)% Generate random pointspoints = rand(num_points, 2);end步骤四:计算落在圆内的点接下来,我们需要判断这些随机生成的点是否落在圆内。
根据圆的特性,我们可以通过判断点到原点的距离是否小于半径来判断点是否在圆内。
matlab% Count points inside the circlecount_inside = sum(points(:, 1).^2 + points(:, 2).^2 < 1);步骤五:计算π的近似值通过计算落在圆内的点的个数,我们可以得到圆的面积的近似值。
matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码二分法(Bisection Method)是一种寻找函数零点的数值计算方法。
该方法的基本思想是:首先确定一个区间[a, b],使得函数在这个区间的两个端点处的函数值异号,然后将区间逐步缩小,直到找到一个区间[a', b'],使得函数在这个区间的中点处的函数值接近于零。
以下是使用MATLAB实现二分法的示例代码:```matlabfunction [x, iter] = bisection(f, a, b, tol)fa = f(a);fb = f(b);if sign(fa) == sign(fb)error('The function has the same sign at the endpoints of the interval');enditer = 0;while (b - a) / 2 > tolc=(a+b)/2;fc = f(c);if fc == 0break;endif sign(fc) == sign(fa)a=c;fa = fc;elseb=c;fb = fc;enditer = iter + 1;endx=(a+b)/2;end```牛顿法(Newton's Method)是一种用于寻找函数零点的数值计算方法。
该方法的基本思想是:通过迭代来逼近函数的零点,每次迭代通过函数的切线来确定下一个近似值,直到满足收敛条件。
以下是使用MATLAB实现牛顿法的示例代码:```matlabfunction [x, iter] = newton(f, df, x0, tol)iter = 0;while abs(f(x0)) > tolx0 = x0 - f(x0) / df(x0);iter = iter + 1;endx=x0;end```黄金分割法(Golden Section Method)是一种用于寻找函数极值点的数值计算方法。
Matlab实现潮流计算程序

程序代码如下:111111.%读入数据clcclearfilename='123.txt';a=textread(filename)n=a(1,1);pinghengjd=a(1,2);phjddianya=a(1,3);jingdu=a(1,4);b=zeros(1,9);j1=0;[m1,n1]=size(a);for i1=1:m1if a(i1,1)==0j1=j1+1;b(j1)=i1;endendb;%矩阵分块a1=a(b(1)+1:b(2)-b(1)+1,1:n1);a2=a(b(2)+1:b(3)-1,1:n1);a3=a(b(3)+1:b(4)-1,1:n1);a4=a(b(4)+1:b(5)-1,1:n1);a5=a(b(5)+1:b(6)-1,1:n1);%设置初值vcz=1;dcz=0;kmax=20;k1=0;%求节点导纳矩阵a11=zeros(4,6);for i0=1:3for j0=1:6a11(i0,j0)=a1(i0,j0);a11(4,j0)=a2(1,j0);endenda11;linei=a11(1:4,2);linej=a11(1:4,3);liner=a11(1:4,4);linex=a11(1:4,5);lineb=a11(1:4,6);branchi=0;branchj=0;branchb=0;G=zeros(4,4);B=zeros(4,4);for k=1:4i2=linei(k,1);j2=linej(k,1);r=liner(k,1);x=linex(k,1);b=0;GIJ=r/(r*r+x*x);BIJ=-x/(r*r+x*x);if k>=4 & lineb(k)~=0k0=lineb(k);G(i2,j2)=-GIJ/k0;G(j2,i2)=G(i2,j2);B(i2,j2)=-BIJ/k0;B(j2,i2)=B(i2,j2);G(i2,i2)=G(i2,i2)+GIJ/k0/k0; B(i2,i2)=B(i2,i2)+BIJ/k0/k0;elseG(j2,i2)=-GIJ;G(i2,j2)=G(j2,i2);B(j2,i2)=-BIJ;B(i2,j2)=B(j2,i2);G(i2,i2)=G(i2,i2)+GIJ;b=lineb(k);B(i2,i2)=B(i2,i2)+BIJ+b;endG(j2,j2)=G(j2,j2)+GIJ;B(j2,j2)=B(j2,j2)+BIJ+b;endG;B;B=B.*i;Yf=G+BY=abs(Yf);alf=angle(Yf);%赋Jacobian矩阵参数P=zeros(n,1);Q=zeros(n,1);Pd=zeros(1,n);Qd=zeros(1,n);dP=zeros(1,n);dQ=zeros(1,n);PG=a4(:,3);PD=a4(:,5);QG=a4(:,4);QD=a4(:,6);i8=a4(:,2);for j8=1:length(i8)P(i8(j8))=PG(i8(j8))-PD(i8(j8));Q(i8(j8))=QG(i8(j8))-QD(i8(j8));enddelt=zeros(n,1);V=ones(n,1);V(3)=1.10;V(4)=1.05;ddelt=zeros(n,1);dV=zeros(n,1);A=zeros(2*n,2*n);B=zeros(2*n,1);Jacobian=Jaco(V,delt,n,Y,alf)%求取矩阵功率for j5=1:kmaxdisp(['第' int2str(j5) '次计算结果'])if k>=kmaxbreakendfor i10=1:4Pd(i10)=0;Qd(i10)=0;for j10=1:nPd(i10)=Pd(i10)+V(i10)*Y(i10,j10)*V(j10)*cos(d elt(i10)-delt(j10)-alf(i10,j10));Qd(i10)=Qd(i10)+V(i10)*Y(i10,j10)*V(j10)*sin(d elt(i10)-delt(j10)-alf(i10,j10));endendfor i4=1:3dP(i4)=P(i4)-Pd(i4);endfor j4=1:2dQ(j4)=Q(j4)-Qd(j4);endA=Jaco(V,delt,n,Y,alf)for i14=1:nB(i14*2-1)=-dP(i14);B(i14*2)=-dQ(i14);endif max(abs(B))>jingduX=A\B;for i16=1:nddelt(i16)=X(2*i16-1);dV(i16)=X(2*i16)*V(i16);endV=V+dVdelt=delt+ddeltelsebreakenddisp('----------------')end%流氓算法% for ii=1:2% V(ii)=V(ii)+dV(ii);% end% V222222.function A=Jaco(V,delt,n,Y,alf)%计算Jacobian矩阵for i7=1:nHd1(i7)=0;Jd1(i7)=0;for j7=1:nHd1(i7)=Hd1(i7)+V(i7)*Y(i7,j7)*V(j7)*sin(delt(i7)-delt(j7)-alf(i7,j7));Jd1(i7)=Jd1(i7)+V(i7)*Y(i7,j7)*V(j7)*cos(delt(i7)-delt(j7)-alf(i7,j7));endendfor i6=1:nfor j6=1:nif i6~=j6H(i6,j6)=-V(i6)*Y(i6,j6)*V(j6)*sin(delt(i6)-delt(j6)-alf(i6,j6));N(i6,j6)=-V(i6)*Y(i6,j6)*V(j6)*cos(delt(i6)-delt(j6)-alf(i6,j6));J(i6,j6)=-N(i6,j6);L(i6,j6)=H(i6,j6);elseH(i6,i6)=Hd1(i6)-V(i6)*Y(i6,i6)*V(i6)*sin(delt(i6)-delt(j6)-alf(i6,j6));J(i6,j6)=-Jd1(i6)+V(i6)*Y(i6,j6)*V(j6)*cos(delt(i6)-delt(j6)-alf(i6,j6));N(i6,j6)=-Jd1(i6)-V(i6)*Y(i6,i6)*V(i6)*cos(alf(i6,i6));L(i6,i6)=-Hd1(i6)+V(i6)*Y(i6,i6)*V(i6)*sin(alf(i6,i6));endendend%修正Jacobian矩阵for j9=3for i9=1:nN(i9,j9)=0;L(i9,j9)=0;J(j9,i9)=0;L(j9,i9)=0;endendL(j9,j9)=1;for j9=4for i9=1:nH(i9,j9)=0;N(i9,j9)=0;J(i9,j9)=0;L(i9,j9)=0;H(j9,i9)=0;N(j9,i9)=0;J(j9,i9)=0;L(j9,i9)=0;endendH(j9,j9)=1;L(j9,j9)=1;%Jaco=[H N;J L];%Jaco=zeros(2*n,2*n);for i11=1:nfor j11=1:nJaco(2*i11-1,2*j11-1)=H(i11,j11); Jaco(2*i11-1,2*j11)=N(i11,j11); Jaco(2*i11,2*j11-1)=J(i11,j11);Jaco(2*i11,2*j11)=L(i11,j11);endendA=Jaco;33333.数据:4 4 1.05 0.000011 12 0.1 0.40 0.015282 1 4 0.12 0.50 0.019203 24 0.08 0.40 0.014131 1 3 0 0.3 0.909090911 1 0 0 0.30 0.182 2 0 0 0.55 0.133 3 0.5 0 0 01 3 1.10 0 0。
matlab圆周率

matlab圆周率计算方法及实现Matlab是一种强大的数学软件,可以用它来进行各种复杂的计算和数据分析。
其中,计算圆周率也是Matlab中常见的问题之一。
本文将介绍几种常见的计算圆周率的方法,并提供相应的Matlab代码实现。
一、Leibniz公式Leibniz公式是一种最简单的计算圆周率的方法。
该公式由德国数学家莱布尼兹在17世纪提出,其基本思想是利用无穷级数逼近圆周率。
具体公式如下:$\pi=4\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1}$根据该公式,我们可以编写如下代码:function pi = leibniz(n)pi = 0;for i = 0:npi = pi + (-1)^i/(2*i+1);endpi = 4*pi;end其中,n为迭代次数。
二、Monte Carlo方法Monte Carlo方法是一种随机模拟方法,可以用于估计各种复杂问题的解。
在计算圆周率时,我们可以利用Monte Carlo方法来模拟投掷点落在圆内或者圆外的概率,并通过比值来估计圆周率。
具体实现过程如下:- 在一个正方形内随机生成n个点;- 统计落在圆内的点的个数m;- 通过比值$\frac{m}{n}$来估计圆周率,即$\pi\approx4\frac{m}{n}$。
根据该方法,我们可以编写如下代码:function pi = monte_carlo(n)x = rand(1,n);y = rand(1,n);d = sqrt(x.^2 + y.^2);m = sum(d <= 1);pi = 4*m/n;end其中,n为生成点的个数。
三、Bailey-Borwein-Plouffe公式Bailey-Borwein-Plouffe公式是一种快速计算圆周率的方法。
该公式由Jonathan M. Borwein、Peter B. Borwein和Simon Plouffe在1995年提出,其基本思想是利用二进制数位上的特殊性质来逼近圆周率。
计算方法matlab实验报告

计算方法matlab实验报告计算方法MATLAB实验报告引言:计算方法是一门研究如何用计算机来解决数学问题的学科。
在计算方法的学习过程中,MATLAB作为一种强大的数值计算软件,被广泛应用于科学计算、工程计算、数据分析等领域。
本实验报告将介绍在计算方法课程中使用MATLAB 进行的实验内容和实验结果。
一、二分法求方程根在数值计算中,求解非线性方程是一个常见的问题。
二分法是一种简单而有效的求解非线性方程根的方法。
在MATLAB中,可以通过编写函数和使用循环结构来实现二分法求解方程根。
实验步骤:1. 编写函数f(x),表示待求解的非线性方程。
2. 设定初始区间[a, b],满足f(a) * f(b) < 0。
3. 利用二分法迭代求解方程根,直到满足精度要求或迭代次数达到预设值。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个非线性方程的根。
例如,对于方程f(x) = x^3 - 2x - 5,我们通过二分法迭代了5次,得到了方程的一个根x ≈ 2.0946。
二、高斯消元法解线性方程组线性方程组的求解是计算方法中的重要内容之一。
高斯消元法是一种常用的求解线性方程组的方法,它通过矩阵变换将线性方程组化为上三角矩阵,从而简化求解过程。
在MATLAB中,可以利用矩阵运算和循环结构来实现高斯消元法。
实验步骤:1. 构建线性方程组的系数矩阵A和常数向量b。
2. 利用高斯消元法将系数矩阵A化为上三角矩阵U,并相应地对常数向量b进行变换。
3. 利用回代法求解上三角矩阵U,得到线性方程组的解向量x。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个线性方程组。
例如,对于线性方程组:2x + 3y - z = 13x - 2y + 2z = -3-x + y + 3z = 7经过高斯消元法的计算,我们得到了方程组的解x = 1,y = -2,z = 3。
三、数值积分方法数值积分是计算方法中的重要内容之一,它用于计算函数在给定区间上的定积分。
最优化计算方法及其matlab程序实现

最优化计算方法及其matlab程序实现最优化计算是一种通过寻找最佳解决方案来解决问题的方法。
在许多实际问题中,我们希望找到使某个目标函数达到最大或最小值的变量取值。
最优化计算可以应用于各种领域,如工程、经济、物理等。
在最优化计算中,我们首先需要定义一个目标函数,它描述了我们要优化的问题。
目标函数可以是线性的也可以是非线性的,具体取决于问题的性质。
然后,我们需要确定变量的取值范围和约束条件。
最后,我们使用最优化算法来搜索最佳解。
常用的最优化算法包括梯度下降法、牛顿法、拟牛顿法等。
这些算法基于不同的原理和策略,在不同的问题中表现出不同的性能。
选择合适的最优化算法对于获得高效的求解结果非常重要。
接下来,我们将介绍如何使用Matlab编写程序来实现最优化计算方法。
Matlab是一种功能强大的数值计算和编程环境,它提供了丰富的工具箱和函数来支持最优化计算。
我们需要定义目标函数。
在Matlab中,我们可以使用函数句柄来表示目标函数。
例如,假设我们要最小化一个简单的二次函数f(x) = x^2,我们可以定义一个函数句柄如下:```matlabf = @(x) x^2;```然后,我们可以使用Matlab提供的最优化函数来搜索最佳解。
例如,使用fminsearch函数来实现梯度下降法:```matlabx0 = 1; % 初始值x = fminsearch(f, x0);```在上述代码中,x0是变量的初始值,fminsearch函数将根据梯度下降法来搜索最佳解,并将结果存储在变量x中。
除了梯度下降法,Matlab还提供了其他常用的最优化函数,如fminunc、fmincon等。
这些函数具有不同的功能和参数,可以根据具体的问题选择合适的函数来求解。
除了单变量最优化,Matlab还支持多变量最优化。
在多变量最优化中,目标函数和约束条件可以是多元函数。
我们可以使用Matlab 提供的向量和矩阵来表示多变量的取值和约束条件。
MATLAB计算方法与实现
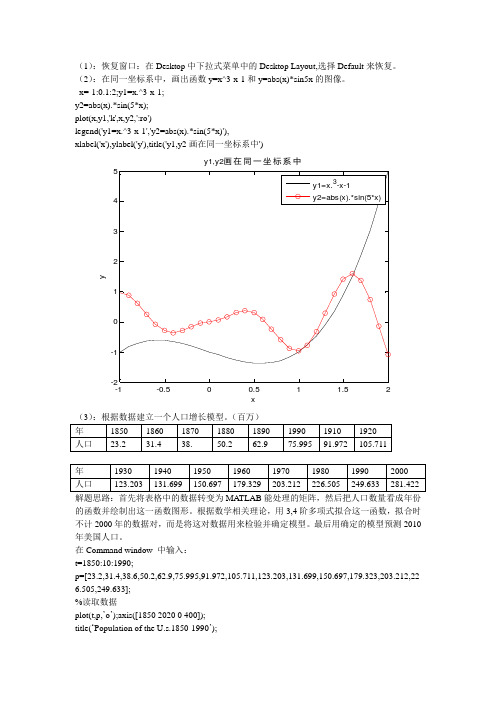
(1):恢复窗口:在Desktop 中下拉式菜单中的Desktop Layout,选择Default 来恢复。
(2):在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x 的图像。
x=-1:0.1:2;y1=x.^3-x-1; y2=abs(x).*sin(5*x); plot(x,y1,'k',x,y2,':ro')legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')-1-0.500.51 1.52xyy1,y2画在同一坐标系中(3):根据数据建立一个人口增长模型。
(百万)的函数并绘制出这一函数图形。
根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。
最后用确定的模型预测2010年美国人口。
在Command window 中输入: t=1850:10:1990;p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633]; %读取数据plot(t,p,’o ’);axis([1850 2020 0 400]); title(‘Population of the U.s.1850-1990’);ylabel(‘Millions ’);%绘制出数据的函数图形并加以修饰f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2 v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值 abs(v-251.422) %计算两个模型与2000年人口数的绝对误差。
特征选择特征提取MATLAB算法实现

特征选择特征提取MATLAB算法实现特征选择和特征提取是模式识别和机器学习中非常重要的步骤,它们用于从原始数据中提取出最具有代表性和区分性的特征,以便用于模型训练和预测。
MATLAB提供了许多算法和函数来实现特征选择和特征提取。
特征选择是从原始特征集中选择一些最有用的特征子集,以降低特征维数和计算复杂度,并且提高模型的性能和泛化能力。
以下是几种常见的特征选择算法的MATLAB实现:1.相关系数法相关系数法用于选择和目标变量最相关的特征。
该方法计算每个特征与目标变量之间的相关系数,并选择具有最高相关系数的特征。
MATLAB 提供了corrcoef函数来计算相关性,并选择相关系数最高的特征。
2.基于信息熵的特征选择基于信息熵的特征选择方法使用信息熵来衡量特征与目标变量之间的相关性。
该方法计算每个特征的信息熵,并选择具有最低信息熵的特征。
MATLAB提供了entropy函数来计算信息熵,并选择信息熵最低的特征。
3.基于卡方检验的特征选择基于卡方检验的特征选择方法使用卡方统计量来衡量特征与目标变量之间的相关性。
该方法计算每个特征的卡方值,并选择具有最高卡方值的特征。
MATLAB提供了chi2test函数来计算卡方值,并选择卡方值最高的特征。
特征提取是从原始数据中提取出新的、更具代表性和区分性的特征。
以下是几种常见的特征提取算法的MATLAB实现:1.主成分分析(PCA)主成分分析是一种常用的特征提取方法,它通过线性变换将原始数据映射到一个新的坐标系中,使得新的特征能够最大程度地解释原始数据的方差。
MATLAB提供了pca函数来进行主成分分析。
2.线性判别分析(LDA)线性判别分析是一种常用的特征提取方法,它寻找投影矩阵,使得在这个投影下不同类别之间的距离最大化,同一类别之间的距离最小化。
MATLAB提供了lda函数来进行线性判别分析。
3.独立成分分析(ICA)独立成分分析是一种用于提取独立信号的方法,它假设观测信号是由多个独立信号的混合而成,并通过反演混合过程来重构独立信号。
matlab单个矩阵的每个元素进行计算方法

matlab单个矩阵的每个元素进行计算方法在MATLAB中,可以使用多种方法对单个矩阵的每个元素进行计算。
下面将介绍一些常见的方法。
1. 使用循环:使用for循环可以遍历矩阵的每个元素,并对其进行计算。
例如,假设我们有一个矩阵A,我们希望将其每个元素都平方,并保存到另一个矩阵B 中。
可以使用以下代码实现:```matlabA = [1 2; 3 4];B = zeros(size(A)); % 创建一个与A相同大小的全零矩阵for i = 1:size(A, 1) % 遍历行for j = 1:size(A, 2) % 遍历列B(i, j) = A(i, j)^2; % 对每个元素进行平方操作endenddisp(B);```2. 利用向量化操作:MATLAB是一种向量化操作非常高效的语言,使用向量化操作可以大大提高计算的效率。
对于单个矩阵的每个元素计算,可以直接对整个矩阵进行操作,而无需循环。
例如,我们仍然使用矩阵A,将其每个元素平方,并保存到矩阵B中,可以使用以下代码实现:```matlabA = [1 2; 3 4];B = A.^2; % 对矩阵A的每个元素进行平方操作disp(B);```3. 使用MATLAB函数:MATLAB提供了许多功能强大的函数来进行矩阵运算。
这些函数可以直接对单个矩阵的每个元素进行计算。
例如,如果我们希望计算矩阵A中每个元素的绝对值,可以使用abs函数:```matlabA = [1 -2; -3 4];B = abs(A); % 对矩阵A的每个元素取绝对值disp(B);```总结:MATLAB提供了多种方法来对单个矩阵的每个元素进行计算。
使用循环、向量化操作或利用MATLAB函数,可以根据具体的需求选择适合的方法来处理矩阵数据。
matlab幂法求特征值和特征向量方法实现和函数表示

matlab幂法求特征值和特征向量方法实现和函数表示1. 引言在数值分析中,求解特征值和特征向量是一项重要而且经常出现的任务。
特征值和特征向量在矩阵和线性代数中有着广泛的应用,涉及到许多领域,如机器学习、信号处理、结构动力学等。
在matlab中,幂法是一种常用的求解特征值和特征向量的方法,同时也有对应的函数可以实现这一过程。
2. 幂法的原理幂法是一种迭代方法,它利用矩阵的特征值和特征向量的性质,通过不断地迭代计算,逼近矩阵的主特征值和对应的特征向量。
具体来说,假设A是一个n阶矩阵,它的特征值λ1>λ2≥...≥λn,并且对应着线性无关的特征向量v1,v2,...,vn。
如果选择一个任意的非零初始向量x0,并进行以下迭代计算:```x(k+1) = Ax(k) / ||Ax(k)||```其中,||.||表示向量的模长。
不断迭代计算后,x(k)将收敛到矩阵A的主特征向量v1上,并且相应的特征值即为A的主特征值λ1。
3. matlab实现幂法求解特征值和特征向量在matlab中,幂法的实现也非常简单。
可以使用自带的eig函数,该函数可以直接求解矩阵的特征值和特征向量。
使用方法如下:```[V,D] = eig(A)```其中,A为待求解的矩阵,V为特征向量矩阵,D为特征值矩阵。
利用eig函数,即可一步到位地求解矩阵的特征值和特征向量,非常简单方便。
4. 函数表示幂法求解特征值和特征向量的过程可以表示为一个matlab函数。
通过封装相关的迭代算法和收敛判据,可以方便地实现幂法的函数表示。
可以定义一个名为powerMethod的函数:```matlabfunction [lambda, v] = powerMethod(A, x0, maxIter, tol)% 初始化k = 1;x = x0;% 迭代计算while k <= maxItery = A * x;lambda = norm(y, inf);x = y / lambda;% 检查收敛性if norm(A * x - lambda * x) < tolbreak;endk = k + 1;endv = x;end```利用这个函数,就可以自己实现幂法求解特征值和特征向量的过程。
数值计算方法实验指导(Matlab版)

《数值计算方法》实验指导(Matlab版)学院数学与统计学学院计算方法课程组《数值计算方法》实验1报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验1 算法设计原则验证(之相近数相减、大数吃小数和简化计算步骤) 2. 实验题目(1) 取1610=z ,计算z z -+1和)1/(1z z ++,验证两个相近的数相减会造成有效数字的损失.(2) 按不同顺序求一个较大的数(123)与1000个较小的数(15310-⨯)的和,验证大数吃小数的现象.(3) 分别用直接法和九韶算法计算多项式n n n n a x a x a x a x P ++++=--1110)(在x =1.00037处的值.验证简化计算步骤能减少运算时间.对于第(3)题中的多项式P (x ),直接逐项计算需要2112)1(+=+++-+n n n 次乘法和n 次加法,使用九韶算法n n a x a x a x a x a x P ++++=-)))((()(1210则只需要n 次乘法和n 次加法. 3. 实验目的验证数值算法需遵循的若干规则. 4. 基础理论设计数值算法时,应避免两个相近的数相减、防止大数吃小数、简化计算步骤减少运算次数以减少运算时间并降低舍入误差的积累.两相近的数相减会损失有效数字的个数,用一个大数依次加小数,小数会被大数吃掉,乘法运算次数太多会增加运算时间. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab6. 实验过程(1) 直接计算并比较;(2) 法1:大数逐个加1000个小数,法2:先把1000个小数相加再与大数加; (3) 将由高次项到低次项的系数保存到数组A[n]中,其中n 为多项式次数.7. 结果与分析 (1) 计算的z z -+1= ,)1/(1z z ++.分析:(2) 123逐次加1000个6310-⨯的和是 ,先将1000个6310-⨯相加,再用这个和与123相加得.分析:(3) 计算次的多项式:直接计算的结果是,用时;用九韶算法计算的结果是,用时.分析:8. 附录:程序清单(1) 两个相近的数相减.%*************************************************************%* 程序名:ex1_1.m *%* 程序功能:验证两个相近的数相减会损失有效数字个数 *%*************************************************************z=1e16;x,y======================================================================(2) 大数吃小数%*************************************************************%* 程序名:ex1_2.m *%* 程序功能:验证大数吃小数的现象. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数z=123; % 大数t=3e-15; % 小数x=z; % 大数依次加小数% 重复1000次给x中加上ty=0; % 先累加小数% 重复1000次给y中加上ty=z + y; % 再加到大数x,y======================================================================(3) 九韶算法%*************************************************************%* 程序名:ex1_3.m *%* 程序功能:验证九韶算法可节省运行时间. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数A=[8,4,-1,-3,6,5,3,2,1,3,2,-1,4,3,1,-2,4,6,8,9,50,-80,12,35,7,-6,42,5,6,23,74,6 5,55,80,78,77,98,56];A(10001)=0; % 扩展到10001项,后面的都是分量0% A为多项式系数,从高次项到低次项x=1.00037;n=9000; % n为多项式次数% 直接计算begintime=clock; % 开始执行的时间 % 求x的i次幂% 累加多项式的i次项endtime=clock; % 完毕执行的时间time1=etime(endtime,begintime); % 运行时间disp('直接计算');disp(['p(',num2str(x),')=',num2str(p)]);disp([' 运行时间: ',num2str(time1),'秒']);% 九韶算法计算begintime=clock; % 开始执行的时间% 累加九韶算法中的一项endtime=clock; % 完毕执行的时间time2=etime(endtime,begintime); % 运行时间disp(' ');disp('九韶算法计算');disp(['p(',num2str(x),')=',num2str(p)]);disp([' 运行时间: ',num2str(time2),'秒']);《数值计算方法》实验1报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验1 算法设计原则验证(之数值稳定性) 2. 实验题目 计算定积分⎰==-1110,1,0,d n x e xI x nn ,分别用教材例1-7推导出的算法A 和B ,其中:算法A :⎩⎨⎧≈-=-6321.0101I nI I n n 算法B :⎪⎩⎪⎨⎧≈-=-0)1(1101I I nI n n 验证算法不稳定时误差会扩大.3. 实验目的验证数值算法需遵循的若干规则. 4. 基础理论设计数值算法时,应采用数值稳定性好的算法.数值稳定的算法,误差不会放大,甚至会缩小;而数值不稳定的算法会放大误差. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab6. 实验过程分别用数组IA[ ]和IB[ ]保存两种算法计算的结果. 7. 结果与分析 运行结果:(或拷屏)8. 附录:程序清单%*************************************************************%* 程序名:ex1_4.m *%* 程序功能:验证数值稳定性算法可控制误差. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数I=[0.856, 0.144, 0.712, 0.865, ...0.538, 0.308, 0.154, 0.938, ...0.492, 0.662, 0.843];% 保留14位小数的精确值, …是Matlab中的续行符% 算法AIA(1) = 0.6321; % Matlab下标从1开始,所以要用IA(n+1)表示原问题中的I(n)% 算法Bdisp('n 算法A 算法B 精确值');for n=1:11fprintf('%2d %14.6f %14.6f %14.6f\n',n-1,IA(n),IB(n),I(n));end% n显示为2位整数, 其它显示为14位其中小数点后显示6位的小数《数值计算方法》实验1报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验1 算法设计原则(除数绝对值不能太小) 2. 实验题目将线性方程组增广矩阵利用初等行变换可化为⎪⎪⎭⎫⎝⎛→-⎪⎪⎭⎫ ⎝⎛→-⎪⎪⎭⎫ ⎝⎛''0'0''02221112'12221121112222211121122121121b a b a r r b a b a a r r b a a b a a a a a a由此可解得'/',/'22221111a b x a b x ==.分别解增广矩阵为161011212-⎛⎫ ⎪⎝⎭和162121011-⎛⎫⎪⎝⎭的方程组,验证除数绝对值远小于被除数绝对值的除法会导致结果失真. 3. 实验目的验证数值算法需遵循的若干规则. 4. 基础理论设计数值算法时,应避免除数绝对值远小于被除数绝对值的除法,否则绝对误差会被放大,使结果失真. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab6. 实验过程用二维数组A 和B 存放方程组的增广矩阵,利用题目所给初等行变换求解方程组. 7. 结果与分析第1种顺序的方程组的解为x =,y =;第2种顺序的方程组的解为x =,y =. 分析:8. 附录:程序清单%************************************************************* %* 程 序 名:ex1_5.m * %* 程序功能:验证除数的绝对值太小可能会放大误差. * %*************************************************************clc;A=[1e-16, 1, 1; 2, 1, 2];B=[2, 1, 2; 1e-16, 1, 1]; % 增广矩阵% 方程组A% m = - a_{21}/a_{11} 是第2行加第1行的倍数% 消去a_{21}% m = - a_{12}/a_{22} 是第1行加第2行的倍数% 消去a_{12}, 系数矩阵成对角线% 未知数x1的值% 未知数x2的值disp(['方程组A的解: x1=',num2str(A(1,3)),', x2=',num2str(A(2,3))]); disp(' ');% 方程组B% m = - b_{21}/b_{11} 是第2行加第1行的倍数% 消去b_{21}% m = - b_{12}/b_{22} 是第1行加第2行的倍数% 消去b_{12}, 系数矩阵成对角线% 未知数x1的值% 未知数x2的值disp(['方程组B的解: x1=',num2str(B(1,3)),', x2=',num2str(B(2,3))]);《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之简单迭代法) 2. 实验题目用简单迭代法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的掌握非线性方程的简单迭代法. 4. 基础理论简单迭代法:将方程0)(=x f 改写成等价形式)(x x ϕ=,从初值0x 开始,使用迭代公式)(1k k x x ϕ=+可以得到一个数列,若该数列收敛,则其极限即为原方程的解.取数列中适当的项可作为近似解. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之Newton 迭代法) 2. 实验题目用Newton 迭代法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的掌握求解非线性方程的Newton 迭代法. 4. 基础理论Newton 迭代法:解方程0)(=x f 的Newton 迭代公式为)(')(1k k k k x f x f x x -=+.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之对分区间法) 2. 实验题目用对分区间法求方程310x x --=在区间[1, 1.5]的一个实根,取绝对误差限为410-. 3. 实验目的掌握求解非线性方程的对分区间法. 4. 基础理论对分区间法:取[a ,b ]的中点p ,若f (p ) ≈ 0或b – a < ε,则p 为方程0)(=x f 的近似解;若f (a ) f (p ) < 0,则说明根在区间取[a ,p ]中;否则,根在区间取[p ,b ]中.将新的有根区间记为 [a 1,b 1],对该区间不断重复上述步骤,即可得到方程的近似根. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程用宏定义函数f (x );为了循环方便,得到的新的有根区间始终用[a ,b ]表示;由于新的有根区间可能仍以a 为左端点,这样会反复使用函数值f (a ),为减少运算次数,将这个函数值保存在一个变量fa 中;同样在判断新的有根区间时用到函数值f (p ),若新的有根区间以p 为左端点,则下一次用到的f (a )实际上就是现在的f (p ),为减少运算次数,将这个函数值保存在一个变量fp 中.算法的伪代码描述:Input :区间端点a ,b ;精度要求(即误差限)ε;函数f (x );最大对分次数N Output :近似解或失败信息7. 结果与分析8. 附录:程序清单说明: 源程序中带有数字的空行,对应着算法描述中的行号%**********************************************************%* 程序名:Bisection.m *%* 程序功能:使用二分法求解非线性方程. *%**********************************************************f=inline('x^3-x-1'); % 定义函数f(x)a=input('有根区间左端点: a=');b=input('右端点:b=');epsilon=input('误差限:epsilona=');N=input('最大对分次数: N=');1 % 对分次数计数器n置12 % 左端点的函数值给变量fafprintf('\n k p f(p) a(k) f(a(k))'); fprintf(' b(k) b-a\n');% 显示表头fprintf('%2d%36.6f%12.6f%12.6f%12.6f\n',0,a,fa,b,b-a);% 占2位其中0位小数显示步数0, 共12位其中小数6位显示各值3% while n≤ N 4 % 取区间中点p5% 求p 点函数值给变量fpfprintf('%2d%12.6f%12.6f',n,p,fp); % 输出迭代过程中的中点信息p 和f(p)6 % 如果f(p)=0或b-a 的一半小于误差限εfprintf('\n\n 近似解为:%f\n',p);% 则输出近似根p (7)return;% 并完毕程序 (7)89 % 计数器加110% 若f(a)与f(p)同号11% 则取右半区间为新的求根区间, 即a 取作p 12 % 保存新区间左端点的函数值 13% 否则14 % 左半区间为新的求根区间, 即b 取作p 15fprintf('%12.6f%12.6f%12.6f%12.6f\n',a,fa,b,b-a); %显示新区间端点与左端函数值、区间长度 16fprintf('\n\n 经过%d 次迭代后未达到精度要求.\n',N); % 输出错误信息(行17)《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之Aitken-Steffensen 加速法) 2. 实验题目用Aitken-Steffensen 加速法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的熟悉求解非线性方程的Aitken-Steffensen 加速法. 4. 基础理论将方程0)(=x f 改写成等价形式)(x x ϕ=,得到从初值0x 开始的迭代公式)(1k k x x ϕ=+后,基于迭代公式)(1k k x x ϕ=+的Aitken-Steffensen 加速法是通过“迭代-再迭代-加速”完成迭代的,具体过程为kk k k k k k k k k k x y z z y x x y z x y +---===+2)(),(),(21ϕϕ. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程为了验证Aitken-Steffensen 加速法可以把一些不收敛的迭代加速成迭代收敛,我们使用将方程组变形为31021x x -=,取迭代函数31021)(x x -=ϕ,并利用宏定义出迭代函数.由于不用保存迭代过程,所以用x0表示初值同时也存放前一步迭代的值,y 和z 是迭代过程中产生的y k 和z k ,x 存放新迭代的结果.算法的伪代码描述:Input :初值x 0;精度要求(即误差限)ε;迭代函数φ(x );最大迭代次数N7. 结果与分析8. 附录:程序清单%************************************************************* %* 程 序 名:Aitken_Steffensen.m * %* 程序功能:用Aitken-Steffensen 加速法求方程. * %************************************************************* clc;clear all;phi=inline('0.5 * sqrt( 10 - x^3)'); % 迭代函数x0=input('初值: x0 = ');epsilon=input('误差限: epsilon='); N=input('最大迭代次数: N=');disp(' n 迭代中间值y(n-1) 再迭代结构z(n-1) 加速后的近似值x(n)'); fprintf('%2d%54.6f\n',0,x0);% 占2位整数显示步数0, 为了对齐, 占54位小数6位显示x01 % n 是计数器2 % while n<=Ny= 3 ; % 迭代 z= 3 ; % 再迭代 x= 3 ; % 加速% x0初值与前一步的近似值, y 和z 是中间变量, x 是下一步的近似值fprintf('%2d%18.6f%18.6f%18.6f\n',n,y,z,x);%显示中间值和迭代近似值6 % 如果与上一步近似解差的绝对值不超过误差限 fprintf('\n\n 近似解 x≈x(%d)≈%f \n',n,x);% 则输出近似根 (7), 可简略为: fprintf('\n\n 近似解 x=%f',x); return; % 并完毕程序(7) 8 % 相当于endif9 % 计数器加110 % 新近似值x 作为下一次迭代的初值 11fprintf('\n 迭代%d 次还不满足误差要求.\n\n',N); %输出错误信息(12)《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之Newton 下山法) 2. 实验题目用Newton 下山法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的熟悉非线性方程的Newton 下山法. 4. 基础理论Newton 下山法:Newton 下山法公式为)(')(1k k kk k x f x f x x λ-=+,使|)(||)(|1k k x f x f <+,其中10≤<k λ.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程定义函数f(x)和df(x),其中df(x)是f(x)的导函数.每步迭代时先取下山因子为1,尝试迭代,判断尝试结果是否满足下山因子,若满足则作为这步的迭代结果;否则将下山因子减半,然后再尝试.为防止当前的x k 是极小值点,附近不会有满足下述条件的其它点,使尝试陷入死循环,同时计算机中能表示出的浮点数也有下界,因此我们设置了最大尝试次数.当超过最大尝试次数时,不再进行下山尝试.由于反复尝试迭代且要判断下山条件,所以f (x 0)和f ‘(x 0)会反复使用,为避免重复计算浪费运行时间,将这两个值分别保存在变量fx0和dfx0.而尝试产生的节点,判断下山条件时要用到它的函数值,若尝试成功,这个点会作为下一步的初值再使用,所以把该点的函数值也保存在变量fx 中.算法的伪代码描述:Input :初值x 0;精度要求(即误差限)ε;函数与其导函数f (x )和f’(x);最大迭代次数N ;K 下山尝试最大次数Output :近似解或失败信息7. 结果与分析8. 附录:程序清单%*************************************************************%* 程序名:NewtonDownhill.m *%* 程序功能:用Newton下山法求解非线性方程. *%*************************************************************clc;clear all;f=inline('x^3-x-1'); % 函数f(x)df=inline('3*x^2-1'); % 函数f(x)的导函数x0=input('初值: x0 = ');epsilon=input('误差限: epsilon=');N=input('最大迭代次数: N=');K=input('最大下山尝试次数: K=');1 % 迭代次数计数器2 % 存x0点函数值fprintf('\n\n n x(n) f(x(n))\n'); % 显示表头fprintf('%2d%14.6f%14.6f\n',0,x0,fx0); % 2位整数显示0, 共14位小数6位显示x0和fx03 % while n≤ Ndisp(''); % 换行显示下山尝试过程的表头disp(' 下山因子尝试x(n) 对应f(x(n)) 满足下山条件');disp('');4 % 存x0点导数值, 每次下山尝试不用重新计算ifdfx0==0 % 导数为0不能迭代disp(‘无法进行Newton迭代’);return;endlambda=1.0; % 下山因子从1开始尝试k=1; % k下山尝试次数计数器while k<=K % 下山最多尝试K次% 下山公式fx=f(x); % 函数值fprintf('%22.6f%14.6f%14.6f',lambda,x,fx); % 显示尝试结果if (abs(fx)<abs(fx0)) % 判断是否满足下山条件fprintf(' 满足\n');break; % 是, 则退出下山尝试的循环elsefprintf(' 不满足\n');endlambda=lambda/2; % 不是, 则下山因子减半k=k+1; % 计数器加1endif k>Kfprintf('\n 下山条件无法满足, 迭代失败.\n\n');return;endfprintf('%2d%14.6f%14.6f\n',n,x,fx);% 2位整数显示步数n, 共14位小数6位显示下步迭代结果22 % 达到精度要求否fprintf('\n\n 方程的近似解为: x≈%f\n\n',x); % (23)return; % 达到, 则显示结果并完毕程序(23) end % (24)% 用x0,fx0存放前一步的近似值和它的函数值, 进行循环迭代25262728fprintf('\n 迭代%d次还不满足误差要求.\n\n',N);《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之弦截法) 2. 实验题目用弦截法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-. 3. 实验目的熟悉非线性方程的弦截法. 4. 基础理论将Newton 迭代法中的导数用差商代替,得到弦截法(或叫正割法)公式)()()(111k k k k k k k x f x f x f x x x x --+---=.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程不保存迭代过程,所以始终以x 0和x 1分别存放x k -1和x k ,而x 存放新产生的迭代值x k +1,这样,下一次迭代时需要把上一步的x 1(即x k )赋值于x 0(做新的x k -1).这些点的函数值会重复用到,在迭代公式中也要用到,上一步的x 1作为下一步的x 0也会再一次用它的函数值,为减少重新计算该点函数值的运行时间,将x 1点的函数值保存在变量fx1中.算法的伪代码描述:Input :初值x 0,x 1;精度要求(即误差限)ε;函数f (x );最大迭代次数N7. 结果与分析8. 附录:程序清单%*************************************************************%* 程序名:SecantMethod.m *%* 程序功能:用弦截法求解非线性方程. *%*************************************************************clc;clear all;f=inline('2*x^3-5*x-1'); % 函数f(x)x0=input('第一初值: x0 = ');x1=input('第二初值: x1 = ');epsilon=input('误差限: epsilon=');N=input('最大迭代次数: N=');fprintf('\n n x(n)\n'); % 显示表头fprintf('%2d%14.6f\n', 0, x0); % 占2位显示步数0, 共14位其中小数6位显示x0fprintf('%2d%14.6f\n', 1, x1); % 占2位显示步数1, 共14位其中小数6位显示x11 % 存x0点函数值2 % 存x1点函数值3 % 迭代计数器4 % while n≤ N% 弦截法公式fprintf('%2d%14.6f\n', n, x); %显示迭代过程6 % 达到精度要求否fprintf('\n\n 方程的近似解为: x≈%f\n\n', x);return; % 达到, 则显示结果并完毕程序89 % 原x1做x0为前两步的近似值10 % 现x做x1为一两步的近似值11 % x0点函数值12 % 计算x1点函数值, 为下一次循环13 % 计数器加1 14fprintf('\n 迭代%d 次还不满足误差要求.\n\n',N);《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之Gauss 消去法) 2. 实验题目用Gauss 消去法求解线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x . 3. 实验目的掌握解线性方程组的Gauss 消去法. 4. 基础理论Gauss 消去法是通过对增广矩阵的初等行变换,将方程组变成上三角方程组,然后通过回代,从后到前依次求出各未知数.Gauss 消去法的第k 步(1≤k≤n -1)消元:若0≠kk a ,则依次将增广矩阵第k 行的kk ik a a /-倍加到第i 行(k+1≤i≤n),将第k 列对角线下的元素都化成0.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之Gauss 列主元消去法) 2. 实验题目用Gauss 列主元消去法求解线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x . 3. 实验目的掌握解线性方程组的Gauss 列主元消去法. 4. 基础理论Gauss 列主元消去法也是通过对增广矩阵的初等行变换,将方程组变成上三角方程组,然后通过回代,从后到前依次求出各未知数.Gauss 列主元消去法的第k 步(1≤k≤n -1)消元:先在nk k k kk a a a ,,,,1 +中找绝对值最大的,将它所在的行与第k 行交换,然后将第k 行的kk ik a a /-倍加到第i 行(k+1≤i≤n),将第k 列对角线下的元素都化成0. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之Doolittle 分解) 2. 实验题目对矩阵A 进行Doolittle 分解,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A .3. 实验目的掌握矩阵的Doolittle 分解. 4. 基础理论矩阵的Doolittle 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个单位下三角矩阵和一个上三角矩阵的乘积.若设⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n n n u u u u u u u u u u U l l ll l l L000000,1010010001333223221131211321323121则可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=+=-=∑∑-=-=1111,,2,1,/)(,,1,,k t kk tk it ik ik k r rj kr kj kj nk k i u u l a l nk k j u l a u其中k = 1,2,…,n .5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程(1)按计算公式依次计算一行u 同时计算一列l ;(2)因为计算完u ij (或l ij )后,a ij 就不再使用,为节省存储空间,将计算的u ij (和l ij )仍存放在矩阵A 中的相应位置;(3)使用L 矩阵和U 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值.L 对角线上的元素为1,上三角部分为0,下三角部分为A 中对应的元素;U 的下三角部分为0,上三角部分为A 中对应的元素.算法的伪代码描述: Input :阶数n ;矩阵A7. 结果与分析8. 附录:程序清单%****************************************************% 程序名: Doolittle.m *% 程序功能: 矩阵LU分解中的Doolittle分解. *%****************************************************clc;clear all;n=4; % 矩阵阶数A=[6 2 1 -1;2 4 1 0; 1 1 4 -1; -1 0 -1 3]disp('A=');disp(A);% LU分解(Doolittle分解)for k=1:n% 计算矩阵U的元素u_{kj}% (可参照下面l_{ik}的公式填写)% 计算矩阵L的元素l_{ik}% L 在A 下三角, U 在上三角(对角线为1) enddisp('分解结果:'); disp('L='); for i=1:n for j=1:nif i>j % 在下三角部分, 则取A 对于的元素显示 fprintf(' %8.4f',A(i,j));elseif i==j % 在对角线上, 则显示1 fprintf(' %8d',1);else % 在上三角部分, 则显示0 fprintf(' %8d',0); end endfprintf('\n'); % 换行 enddisp('U='); for i=1:n for j=1:nif i<=j % 在上三角部分或对角线上, 则取A 对于的元素显示 fprintf(' %8.4f',A(i,j));else % 在下三角部分, 则显示0 fprintf(' %8d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之LU 分解法) 2. 实验题目用LU 分解(Doolittle 分解)法求解线性方程组⎪⎩⎪⎨⎧=++=++=++104615631552162321321321x x x x x x x x x 3. 实验目的熟悉解线性方程组LU 分解法.4. 基础理论若将矩阵A 进行了Doolittle 分解,A = LU ,则解方程组b x A=可以分解求解两个三角方程组b y L=和y x U =.它们都可直接代入求解,其中b y L=的代入公式为∑-==-=11,,2,1,k j j kj k k n k y l b y而y x U=的代入公式为∑+=-=-=nk j kk j kjk k n n k u x uy x 11,,1,,/)( .5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程(1)Doolittle 分解过程依次计算一行u 同时计算一列l 完成,并将计算的u ij (和l ij )仍存放在矩阵A 中的相应位置;(2)求解方程组的代入公式中用到的u ij 和l ij 都直接在A 的相应位置取值即可. 算法的伪代码描述:Input :阶数n ;矩阵A ;常数项向量b7. 结果与分析8. 附录:程序清单%**************************************************** % 程序名: LinearSystemByLU.m *% 程序功能: 利用LU分解(Doolittle分解)解方程组. *%****************************************************clc;clear all;n=3; % 矩阵阶数A=[1 2 6; 2 5 15; 6 15 46];b=[1;3;10];% LU分解(Doolittle分解)for k=1:n% 计算矩阵U的元素u_{kj}% (可参照下面l_{ik}的公式填写)% 计算矩阵L的元素l_{ik}% L在A下三角, U在上三角(对角线为1) endfor k=1:n % 用代入法求解下三角方程组Ly=by(k)=b(k);3 %∑-==-=11,,2,1,kjj kjk knkylby33enddisp('方程组Ly=b的解:y=');disp(y');for k=n:-1:1 % 回代求解上三角方程组Ux=y x(k)=y(k);6 %∑+=-=-=nkjj kjk knnkxuyx11,,1,,666 enddisp('原方程组的解:x='); disp(x');《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X成绩:1. 实验名称实验3 解线性方程组的直接法(之Cholesky 分解) 2. 实验题目对矩阵A 进行Cholesky 分解,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A . 3. 实验目的理解矩阵的Cholesky 分解. 4. 基础理论矩阵的Cholesky 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个下三角矩阵L 和L 转置的乘积,即A =LL T,其中L 各元素可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=-=∑∑-=-=11112,,2,1,/)(k t kktk it ik ik k r kr kk kk nk k i l l l a l l a l其中k = 1,2,…,n .5. 实验环境操作系统:Windows xp ; 程序设计语言:VC++ 6. 实验过程(1)按计算公式依次先计算一列对角线上的元素l kk ,再计算这列其他元素l ik ,且对称位置的元素也取同一个值;(2)因为计算完l ij 后,a ij 就不再使用,为节省存储空间,将计算的l ij 仍存放在矩阵A 中的相应位置;(3)使用L 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值.L 上三角部分为0,对角线和下三角部分为A 中对应的元素.算法的伪代码描述:Input :阶数n ;矩阵AOutput :矩阵L (合并存储在数组A 中)行号 伪代码注释1 for k ← 1 to n2∑-=-=112k r krkk kk l a l3 for i ← k to n4 ∑-=-=11/)(k t kk tk it ik ik l l l a l计算结果存放在a ij5 endfor6 endfor7return L输出L7. 结果与分析8. 附录:程序清单%************************************************************* %* 程 序 名:Cholesky.m * %* 程序功能:对称正定矩阵的Cholesky 分解. * %*************************************************************n=4; % 矩阵阶数 A=[6,2,1,-1; 2,4,1,0; 1,1,4,-1; -1,0,-1,3];disp('A ='); for i=1:n for j=1:nfprintf('%10.4f',A(i,j)); % 共占14位endfprintf('\n');% 一行完毕换行end% Cholesky 分解 for k=1:n % 计算对角线上的l _{kk}% 计算其他的l _{ik} % 和l _{ki}end % L 在A 下三角, L^T 在上三角disp('分解结果:'); disp('L='); for i=1:n for j=1:n if i>=j % 在下三角部分或对角线上, 则取A 对于的元素显示fprintf('%10.4f',A(i,j));else % 在上三角部分, 则显示0 fprintf('%10d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X成绩:1. 实验名称实验3 解线性方程组的直接法(之改进的Cholesky 分解) 2. 实验题目对矩阵A 进行改进的Cholesky 分解,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A .3. 实验目的理解矩阵改进的Cholesky 分解. 4. 基础理论矩阵的改进的Cholesky 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个单位下三角矩阵L 和对角矩阵D 与L 转置的乘积,即A =LDL T,其中L 和D 各元素可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=-=∑∑-=-=11112,,2,1,/)(k t k kt it t ik ik k r kr r kk k nk k i d l l d a l l d a d其中k = 1,2,…,n .5. 实验环境操作系统:Windows xp ; 程序设计语言:VC++ 6. 实验过程(1)按计算公式依次先计算D 的一个元素d k ,再计算L 中这列的元素l ik ,且对称位置的元素也取同一个值;(2)因为计算完d k 和l ij 后,a kk 或a ij 就不再使用,为节省存储空间,将计算的a kk 或l ij 仍存放在矩阵A 中的相应位置;(3)使用L 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值.L 对角线和上三角部分为0,下三角部分为A 中对应的元素;D 对角线为A 中对应的元素,其余都是0.算法的伪代码描述: Input :阶数n ;矩阵AOutput :矩阵L (合并存储在数组A 中)7. 结果与分析8. 附录:程序清单%************************************************************* %* 程 序 名:ImprovedCholesky.m * %* 程序功能:对称正定矩阵的改进的Cholesky 分解. * %*************************************************************n=4; % 矩阵阶数A=[6,2,1,-1; 2,4,1,0; 1,1,4,-1; -1,0,-1,3];disp('A =');for i=1:nfor j=1:nfprintf('%10.4f',A(i,j)); % 共占14位endfprintf('\n'); % 一行完毕换行end% Cholesky分解for k=1:n% 计算D对角线上的u_{kk}% 计算L的元素l_{ik}% 和L转置的元素l_{ki} end % L在A下三角, D在对角线disp('分解结果:');disp('L=');for i=1:nfor j=1:nif i>j % 在下三角部分, 则取A对于的元素显示fprintf('%10.4f',A(i,j));elseif i==j % 在对角线上, 则显示1fprintf('%10d',1);else % 在上三角部分, 则显示0fprintf('%10d',0);endendfprintf('\n'); % 换行enddisp('D='); for i=1:n for j=1:n if i==j % 在对角线上, 则取A 对于的元素显示fprintf('%10.4f',A(i,j));else % 其余显示0fprintf('%10d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之追赶法) 2. 实验题目用追赶法求解线性方程组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----101053001210023100124321x x x x 3. 实验目的熟悉解线性方程组的追赶法. 4. 基础理论对于系数矩阵为三对角矩阵的方程组,其Crout 分解可分解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=------11111211122111122211n n nn n n nn n n t t t s a s a s a s b a c b a c b a c b A这样,解方程组可以由如下2步完成:“追”:,,,3,2,/)(,,/,/,1111111111n i s y a f y t a b s s c t s f y b s i i i i i i i i i i i i =-=-====-----其中:Tn f f ),,(1 为方程组的常数项,n t 没用;“赶”:.1,,2,1,,1 --=-==+n n i x t y x y x i i i i n n5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程在“追”的过程中,向量s 和y 都有n 个元素,t 只有n -1个元素,又1s 和1y 的计算公式与其它i s 和i y 不同,所以先单独计算1s 和1y ,然后在一个n -1次循环中,求其它i s 和i y 以与i t .由于在“追”的过程中,i b ,i c 和i f 在分别计算完对应的i s ,i t 和i y 后就不再使用,所以借用数组b ,c 和f 存储向量s ,t 和y ;同样在“赶”的过程中,i y 在计算完对应的i x 后就不再使用,所以再一次借用数组f 存储向量x .追赶法算法的伪代码描述:Input :阶数n ;三对角矩阵的三条对角线向量a ,b ,c ,常数项向量f Output :方程组的解x改进的追赶法算法的伪代码描述:Input :阶数n ;三对角矩阵的三条对角线向量a ,b ,c ,常数项向量f Output :方程组的解x7. 结果与分析8. 附录:程序清单%*************************************************************%* 程序名:ChaseAfter.m *%* 程序功能:用追赶法求解三对角线性方程组. *%*************************************************************clc;clear all;n=4;a=[0,-1,-1,-3];b=[2, 3, 2, 5];c=[-1, -2, -1, 0];f=[0, 1, 0, 1];% "追"s(1) = b(1);y(1) = f(1); % 先单独求s_1和y_1 for k = 1 : n-1% 再求t_i(i=1,2,…,n-1)% s_i(i=2,3,…,n)% y_i(i=2,3,…,n)end% "赶"x(n) = y(n); % 先单独求x_nfor k = n-1 : -1 : 1% 再求x_i(i=n-1,n-2, (1)endx=x' % 输出解向量-------------------------------------------------------------------------------------------------------------------改进的程序:%*************************************************************%* 程序名:ChaseAfter.m *%* 程序功能:用追赶法求解三对角线性方程组. *%*************************************************************clc;clear all;n=4;a=[0,-1,-1,-3];b=[2, 3, 2, 5];c=[-1, -2, -1, 0];f=[0, 1, 0, 1];% "追"% b(1)=b(1); % s_1仍在b_1中,不用重新计算y(1)=f(1)/b(1); % 先单独y_1for k=1:n-1% 再求t_i(i=1,2,…,n-1)% s_i(i=2,3,…,n)% y_i(i=2,3,…,n)end% "赶"% f(n)=f(n); % x_n等于y_n仍在f_n中for k=n-1:-1:1% 再求x_i(i=n-1,n-2, (1)endx=f' % 输出解向量《数值计算方法》实验4报告班级:20##级####x班学号:20##2409####:##X 成绩:1. 实验名称实验4 解线性方程组的迭代法(之Jacobi迭代)2. 实验题目用Jacobi迭代法求解线性方程组1231231232251223x x x x x x x x x +-=⎧⎪++=⎪⎨++=⎪⎪⎩任取3. 实验目的掌握解线性方程组的Jacobi 迭代法. 4. 基础理论将第i (n i ≤≤1)个方程i n in i i b x a x a x a =+++ 2211移项后得到等价方程ii n in i i i i i i i i i a x a x a x a x a b x /)(11,11,11------=++--便可构造出Jacobi 迭代公式,1,0,/)()()(11,)(11,)(11)1(=------=++--+k a x a x a x a x a b x ii k n in k i i i k i i i k i i k i . 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验4报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验4 解线性方程组的迭代法(之Gauss-Seidel 迭代) 2. 实验题目用Gauss-Seidel 迭代法求解线性方程组。
在MATLAB中使用并行计算的方法

在MATLAB中使用并行计算的方法随着计算机的普及和性能的提高,我们可以利用并行计算的方法来加速计算任务。
MATLAB作为一种广泛使用的数值计算环境,也提供了一些并行计算的方法来提高计算效率。
在本文中,我们将介绍如何在MATLAB中使用并行计算的方法,以及一些相关技巧和注意事项。
一、什么是并行计算并行计算是指将一个大任务分解为多个小任务,并同时运行这些小任务以提高计算速度的方法。
在单核处理器时代,我们只能依次执行任务,而在多核处理器或者分布式计算环境下,我们可以同时执行多个任务,从而提高计算效率。
在MATLAB中,我们可以利用并行计算工具箱(Parallel Computing Toolbox)来实现并行计算。
这个工具箱提供了一些函数和工具,可以帮助我们将任务分解为多个小任务,并将其分配到多个处理核心或者多台计算机上进行计算。
二、使用并行计算的好处使用并行计算的好处是显而易见的。
通过将任务分解为多个小任务,并同时运行这些小任务,我们可以大幅度提高计算速度,从而节省时间和资源。
这对于需要处理大量数据或者复杂计算的任务尤为重要。
此外,使用并行计算还可以提高代码的可扩展性和灵活性。
通过将任务分解为多个小任务,我们可以更好地利用计算资源,提高代码的并行性和并行效率。
这意味着我们可以轻松地将代码应用于不同规模的问题,并随着问题规模的增大而提高计算效率。
三、在MATLAB中,我们可以使用并行计算工具箱提供的函数和工具来实现并行计算。
以下是一些常用的方法:1. 使用parfor循环:parfor循环是MATLAB中的一个特殊的循环语句,用于并行执行循环体内的代码。
parfor循环与普通的for循环类似,但是它会将循环中的迭代任务分配到多个处理核心或者多台计算机上进行并行计算。
我们可以使用parfor循环来并行处理数组、矩阵等数据结构,从而提高计算效率。
2. 使用spmd语句:spmd语句是MATLAB中的一个特殊的语句,用于并行执行任务。
编程MATLAB程序实现复化梯形和辛普森数值积分

编程MATLAB程序实现复化梯形和辛普森数值积分MATLAB是一种高级编程语言和计算环境,适用于各种科学和工程应用。
在MATLAB中,可以使用数值积分的方法来近似计算函数的定积分。
本文将介绍如何使用MATLAB编程实现复化梯形和辛普森数值积分。
首先,我们来介绍复化梯形法。
复化梯形法是一种基本的积分数值方法,它将定积分区间等分为若干个小的子区间,然后在每个子区间上应用梯形公式进行近似计算。
下面是复化梯形法的MATLAB代码:``` matlabh=(b-a)/N;x=a:h:b;y=f(x);I = h * (sum(y) - (y(1) + y(end)) / 2);end```在上述代码中,`f`是积分的函数,`a`和`b`是积分的上下限,`N`是子区间的数量。
首先,我们计算出每个子区间的步长`h`,然后生成一个数组`x`,其中包含了每个子区间的起始点和终止点。
接下来,根据积分函数`f`计算出在每个子区间上的函数值,并将这些函数值存储在数组`y`中。
最后,使用梯形公式计算出近似积分结果`I`。
下面是使用复化梯形法进行数值积分的示例:``` matlaba=0;b = pi;N=100;disp(I);```接下来,我们来介绍辛普森法。
辛普森法是一种更精确的数值积分方法,它将定积分区间等分为若干个小的子区间,然后在每个子区间上应用辛普森公式进行近似计算。
下面是辛普森法的MATLAB代码:``` matlabh=(b-a)/(2*N);x=a:h:b;y=f(x);I = h / 3 * (y(1) + y(end) + 4 * sum(y(2:2:end-1)) + 2 * sum(y(3:2:end-2)));end```在上述代码中,`f`是积分的函数,`a`和`b`是积分的上下限,`N`是子区间的数量。
首先,我们计算出每个子区间的步长`h`,然后生成一个数组`x`,其中包含了每个子区间的起始点和终止点。
matlab 点到线段最短距离

matlab 点到线段最短距离(原创版)目录一、引言二、点到线段的距离计算方法1.计算点到线段的垂足2.计算点到线段的两个端点的距离3.计算最短距离三、MATLAB 实现点到线段最短距离的函数四、结论正文一、引言在几何学中,点到线段的距离问题是一个基本问题。
在 MATLAB 中,我们可以通过编程实现点到线段的最短距离的计算。
本文将从点到线段的距离计算方法入手,介绍如何在 MATLAB 中实现点到线段最短距离的函数,并举例说明其应用。
二、点到线段的距离计算方法点到线段的距离计算方法可以分为以下几个步骤:1.计算点到线段的垂足:假设点 P(x0, y0, z0) 到线段 AB 的两个端点 A(x1, y1, z1) 和 B(x2, y2, z2),首先我们需要计算点 P 到线段 AB 的垂足 H。
可以通过计算向量 PA 和向量 PB 的点积来找到垂足H,公式为:HP·AB = 0,其中 AB = (x2 - x1, y2 - y1, z2 - z1) 是线段 AB 的方向向量。
解这个方程组,可以得到垂足 H 的坐标。
2.计算点到线段的两个端点的距离:计算点 P 到线段 AB 的两个端点 A 和 B 的距离,分别为 PA 和 PB。
3.计算最短距离:最短距离就是 PA 和 PB 中的较小值。
三、MATLAB 实现点到线段最短距离的函数在 MATLAB 中,我们可以通过编写一个函数来实现点到线段最短距离的计算。
以下是一个简单的示例:```matlabfunction dist = pointToLineSegment(P, A, B)% P: 点的坐标 (x0, y0, z0)% A: 线段的一个端点的坐标 (x1, y1, z1)% B: 线段的另一个端点的坐标 (x2, y2, z2)% 计算向量PA = P - A;PB = P - B;% 计算点到线段的两个端点的距离PA_norm = norm(PA);PB_norm = norm(PB);% 计算最短距离dist = min(PA_norm, PB_norm);end```四、结论通过以上分析和示例,我们可以看到在 MATLAB 中,可以通过编写函数实现点到线段最短距离的计算。
实验一信号基本运算的MATLAB实现

实验一信号基本运算的MATLAB实现MATLAB是一种用于数值计算和数据可视化的高级编程语言和环境。
它提供了丰富的函数和工具箱来处理信号。
在MATLAB中,我们可以进行一系列信号的基本运算,包括信号的加法、乘法、平移、取反等。
下面将介绍几种常见的信号基本运算的MATLAB实现方法。
1.信号的加法:信号的加法可以使用MATLAB的"+"操作符来实现。
例如,我们有两个信号x1和x2,它们的采样点分别存储在向量x1和x2中,我们可以使用以下代码将它们相加,并将结果存储在向量y中:```matlabx1=[1,2,3];x2=[4,5,6];y=x1+x2;disp(y); % 输出结果:5 7 9```2.信号的乘法:信号的乘法可以使用MATLAB的"\*"操作符来实现。
与信号的加法类似,我们可以将要相乘的信号存储在向量中,并使用"\*"操作符进行乘法运算。
例如,两个信号x1和x2的乘积可以用以下代码实现:```matlabx1=[1,2,3];x2=[4,5,6];y=x1.*x2;disp(y); % 输出结果:4 10 18```3.信号的平移:信号的平移是将信号在时间上移动一定的步长。
在MATLAB中,我们可以使用向量索引来实现信号的平移。
例如,我们有一个信号x,要将其向右平移3个单位,可以使用以下代码实现:```matlabx=[1,2,3,4,5];shift = 3;y = [zeros(1, shift), x];disp(y); % 输出结果:0 0 0 1 2 3 4 5```在上述代码中,我们使用了`zeros`函数生成了一个长度为平移步长的零向量,并将其与信号x进行拼接。
4.信号的取反:信号的取反是将信号的每个采样点的值取相反数。
在MATLAB中,我们可以使用"-"操作符来实现信号的取反。
例如,我们有一个信号x,要将其取反,可以使用以下代码实现:```matlabx=[1,-2,3,-4,5];y=-x;disp(y); % 输出结果:-1 2 -3 4 -5```在上述代码中,我们使用了"-"操作符来实现信号的取反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 2、线性方程组求解中的变换
• 上三角变换 • U=triu(x)返回矩阵x的上三角部分; • U=triu(x,k)返回第k条对角线以上部分的元
素。
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> triu(a) • ans =
• • •
12 0 0 -3 3 3 -1 0 1
• Gauss-Saidel迭代法 • 编写gauss函数,并使之计算 • >> a=[10 -2 -1;-2 10 -1;-1 -2 5]; • >> b=[3 15 10]'; • >> s=gauss(a,b,[0 0 0]',eps) •s= • 1 • 2 • 3
• • • • • • • • • • • • • • • • • • • • •
许误差 if nargin==1 eps=1.0e-6; elseif nargin<1 error return end xx=fx(x);%第一次迭代 while norm(xx-x)>=eps x=xx; xx=fx(x); end s=xx; return
• function y=fx(x) • y(1)=0.1*(x(1)*x(1)+x(2)*x(2)+8); • %y(1)=x(1)*x(1)+x(2)*x(2)-10*x(1)+8; • y(2)=0.1*(x(1)*x(2)*x(2)+x(1)+8); • %y(2)=x(1)*x(2)*x(2)+x(1)-10*x(2)+8; • y=[y(1) y(2)];
• ans = •
1 1
• • • • • • • • • • • • • • • • • • • • •
function s=newtoniterate(x,eps) %newton迭代法解非线性方程组,x为迭代初值,eps为允许误差 if nargin==1 eps=1.0e-6; elseif nargin<1 error return end x1=fx1(x);%非线性方程组 x2=-dfx1(x);%非线性方程组导数 x3=inv(x2); x0=x3*x1'; while norm(x0)>=eps x=x0'+x; x1=fx1(x); x2=-dfx1(x); x3=inv(x2); x0=x3*x1'; end s=x0'+x; return
• Newton迭代法 • 用newton迭代法求解下面的方程组
x1 10 x1 x2 8 0 2 x1 x2 x1 10 x2 8 0
2 2
• 首先,编写上述非线性方程组的M文件
fx1.m • 然后,编写上述非线性方程组导数的M文件 dfx1.m • >> newtoniterate([0 0])
function s=gauss(a,b,x0,eps) %gauss-seidel迭代法皆线性方程组 %a为系数矩阵,b为方程组ax=b中的右边的矩阵b,x0为迭代初值 if nargin==3 eps=1.0e-6; elseif nargin<3 error return end L=tril(a,-1);%求出严格下三角矩阵 D=diag(diag(a));%求出对角矩阵 U=triu(a,1);%求出严格上三角矩阵 C=inv(D+L); B=-C*U; f=C*b; s=B*x0+f; while norm(s-x0)>=eps x0=s; s=B*x0+f; end return
-18 1
• 下三角变换 • U=tril(x)返回矩阵x的下三角部分; • U=tril(x,k)返回第k条对角线以上下部分的元
素。
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> tril(a)
• ans =
• • •
12 -18 1
0 3 1
0 0 1
• >> tril(a,1) • ans =
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> diag(a)
• ans =
• • •
12 3 1
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> diag(a,1)
• ans =
• •
-3 -1
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> diag(a,-1) • ans = • •
MATLAB 7.0从入 门到精通
主要讲述内容
• 第1章 MATLAB简介 • 第2章 数值运算 • 第3章 单元数组和结构 • 第4章 字符串 • 第5章 符号运算 • 第6章 MATLAB绘图基础 • 第7章 程序设计 • 第8章 计算方法的MATLAB实现 • 第9章 优化设计 • 第10章 Simulink仿真初探
• function y=fx1(x) • y(1)=x(1)*x(1)-10*x(1)+x(2)*x(2)+8; • y(2)=x(1)*x(2)*x(2)-10*x(2)+x(1)+8; • y=[y(1) y(2)];
• function y=dfx1(x) • y(1)=2*x(1)-10; • y(2)=2*x(2); • y(3)=x(2)*x(2)+1; • y(4)=2*x(1)*x(2)-10; • y=[y(1) y(2);y(3) y(4)];
• 8.3 非线性方程组数值解法
• 与线性方程组的求解一样,非线性方程组的
求解也是应用很广泛的课题。一般情况,非 线性方程组的数据值解法主要采用迭代法来 求解。比较常用的迭代法主要有不动点迭代 法、Newton迭代法、拟Newton迭代法等几 种方法。
• 不动点迭代 • 编写不动点迭代函数,并使之计算 • 用不动点迭代法求解下面的方程组
• Method可取如下的值: • ‘nearest’最近插值 • ‘linear’线性插值 • ‘spline’三次样条插值 • ‘cubic’三次插值 • Method默认值为线性插值,上述插值要求
向量x单调。
• >> x=[1 2 4 6 8 9 10 13 15 16]; • >> y=[5 7 8 10 13 14 15 17 19 20]; • >> x1=[1.2 2.1 3]; • >> y1=interp1(x,y,x1) • y1 = •
• 1、一维线性插值
• 8.4 插值与拟合
• yi=interp1(x,y,xi)返回在插值向量xi处的函数
向量yi,它是根据向量x和y插值而来。如y是矩 阵,则对y每一列进行插值,如xi中元素不在x 内,返回NaN。 • yi=interp1(y,xi)省略x,表示x=1:N,此时N为 向量y的长度或为矩阵y的行数。 • yi=interp1(x,y,xi,’method’)表示用method指定 的插值方法进行插值。
• >> triu(a,1)
• ans =
• • •
0 0 0 -3 0 0 3 -1 0
• >> triu(a,-1)
• ans = • • •
12 -18 0 -3 3 1 3 -1 1
• 对角变换 • U=diag(x)返回矩阵x主对角线上的元素,返
回结果是一列向量形式; • U=diag(x,k)返回第k条对角线上的元素值。 • 当x为向量时生成矩阵。
5.4000 7.0500 7.5000
• >> x=[1 2 4 6 8 9 10 13 15 16]; • >> y=[5 7 8 10 13 14 15 17 19 20]; • >> x1=[1.2 2.1 3]; • >> y1=interp1(x,y,x1,'nearest')
must differ in sign.
• 1、直接解法
• 8.2 线性方程组数值解法
• A*X=B • X=A\B或x=inv(A)*B • 例: • 12x(1)-3x(2)+3x(3)=15 • -18x(1)+3x(2)-x(3)=-15 • X(1)+x(2)+x(3)=6
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> b=[15;-15;6]; • >> x=a\b •x= • 1.0000 • 2.0000 • 3.0000 • >> inv(a)*b • ans = • 1 • 2 • 3
• • •
12 -18 1
-3 3 1
0 -1 1
• >> tril(a,-1) • ans =
• • •
0 -18 1
0 0 1
0 0 0
• 3、迭代解法
• 迭代解法非常适用于求解大型稀疏系数矩阵的
方程组,在线性方程组常用的迭代解法主要有 Jacobi迭代法、Gauss-Seidel迭代法。
• Jacobi迭代法 • 编写jacobi函数,并使之计算 • >> a=[10 -2 -1;-2 10 -1;-1 -2 5]; • >> b=[3 15 10]'; • >> s=jacobi(a,b,[0 0 0]',eps) •s= • 1 • 2 • 3
• • • • • • • • • • • • • • • • • • • • •
