小学六年级-分数乘法-思维导图
六年级数学上册思维导图

认识圆
第 五 单 元
Hale Waihona Puke 扇形圆求一个数比另一个数 多(或少)百分之几 求比一个数多(或少) 求常见的百分率 百分之几的数是多少
用百分数解决 百分数的意义 和写法.. 问题..
百分数和分数、
小数的互化
第六单元
百分 数
节约用水
扇形统计图 条形统计图
统 计 图
第 七 单 元
折线统计图
数与形
数 学 广 角
全 册 教 材 安 排
内容结构
2.位置 与方向
5.圆
统计与 概率 7.扇形 统计图
4.比
3.分数 数与代数 除法 1.分数 乘法
图形与几何
六 年 级 上 册
综合与 实践
8.数学广角 确定起跑线 节约用水
分数乘 整数 分数乘 分数
乘法运算 定律推广 到分数
求一个数的 几分之几是 多少的问题
求比一个数多(少) 几分之几的数是多 少的问题
分 数 乘 法
第一单元
位置
与方向
(第二单元)
已知一个数的 几分之几是多 少求这个数的 问题
已知比一个数多 (少)几分之几 是多少求这个数 的问题
分数除法 的意义 计算方 法
解决问题
倒数的认识
分数除法
混合运算
分 数 除 法
第三单元
求一个 数的倒 数
比的基本性质
认识比
比的应用
比
第四单元
圆的周长
圆的面积
第 八 单 元
小学六年级 分数乘法 思维导图(2020年整理).pdf

1计算方法:通过三种运算定律(乘法交换律、乘法结合律、乘法分配率)来使计算时可以约分,这样计算数据较小,更加简便、快捷。
计算方法:计算前可画图和写等量关系式,以方便理清思路。
例1 分数乘整数 例题: ×3 == =计算方法:用分子乘整数的积分作分子,分母不变。
能约分的先约分,再计算。
例2 分数乘分数 例题: × ==计算方法: 用分子相乘的积做分子,用分母相乘的积做分母。
注意:有时需约分,但不能在原题上约,需再写一遍,然后约分。
例3 分数乘小数 例题: ×2.4=计算方法: 1、把2.4化成分数计算;2、把3/4化成小数计算;3、2.4和分母约分后再计算。
注意:有时分数化不成有限小数,所以第2种方法有时不能用。
例4 乘法运算定律交换定律例题: 23 ×14 ×3 = 23 ×3×14 = 2×14 = 12结合定律例题:13 ×95 ×59 = 13 ×(95 ×59 ) = 13 ×1 = 13分配定律例题:57 + 57 ×6 = 57 ×(1+6) = 57 ×7 = 5计算方法:有单位时,可以采用数量法或分率法。
但分率法求分率时不能带任何单位。
例 5 一个数的几分之几的几分之几例题:480×12 ×14 =60例6 一个数比另一个数多(少)几分之几。
例题:噪音为80分贝,绿化造林降低1/8,绿化后为多少分贝。
80×(1 - 18 )=80×78 =70(分贝)或者:80-80×18 =80-10=70(分贝)。
六年级数学上册思维导图知识树
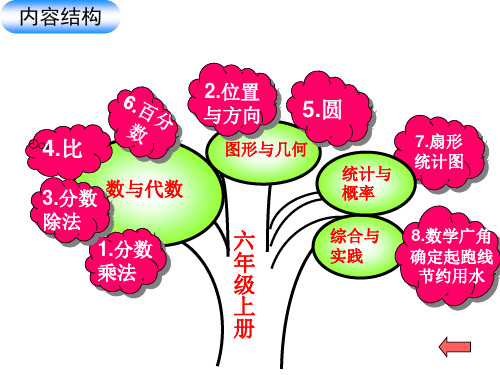
求一个数比另一个数
多(或少)百分之几
求常见的百分率
求比一个数多(或少) 百分之几的数是多少
用百分数解决
百分数的意义 和写法
问题
百分数和分数、 小数的互化
第六单元
百分 数
节约用水
扇形统计图
条形统计图
折线统计图
统第
计
七 单
图元
数与形
数 学
第 八
广单
角元
内容结构
4.比
3.分数 数与代数 除法
1.分数 乘法
2.位置 与方向
5.圆
图形与几何
统计与 概率
六
综合与
年
实践
级
上
册
7.扇形 统计图
8.数学广角 确定起跑线 节约用水
分数乘 整数
分数乘 分数
求一个数的 几分之几是 多少的问题
求比一个数多(少) 推广
到分数
分 数 乘 法
第一单元
位置
与方向
(第二单元)
已知一个数的 几分之几是多 少求这个数的
问题
已知比一个数多 (少)几分之几 是多少求这个数
的问题
分数除法 的意义
解决问题
计算方
法
分数除法
倒数的认识
分
数
混合运算
除
法
第三单元
求一个 数的倒
数
比的基本性质
认识比 比的应用
比
第四单元
圆的周长 圆的面积
认识圆
扇形
第 五 单 元
人教版小学数学六年级上册第一单元分数乘法知识点汇总思维导图
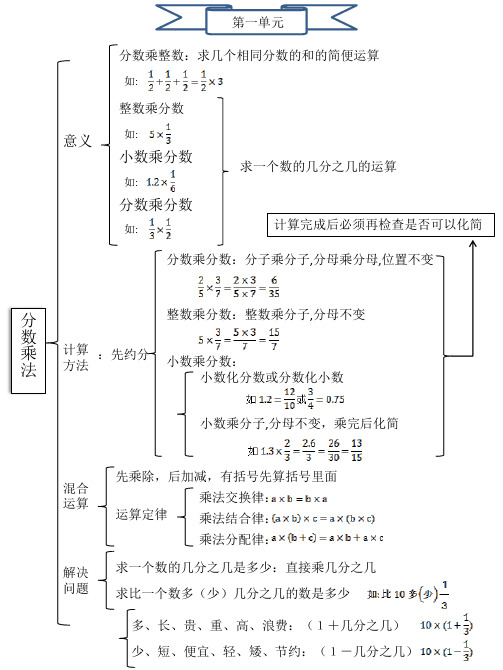
混合 运算
解决 问题
先乘除,后加减,有括号先算括号里面
运算定律
乘法交换律: 乘法结合律:
乘法分配律:
求一个数的几分之几是多少:直接乘几分之几
求比一个数多(少)几分之几的数是多少
多、长、贵、重、高、浪费:(1+几分之几) 少、短、便宜、轻、矮、节约:(1-几分之几)
意义
第一单元
分数乘整数:求几个相同分数的和的简便运算
Байду номын сангаас
如:
整数乘分数
如:
小数乘分数
如:
分数乘分数
如:
求一个数的几分之几的运算 计算完成后必须再检查是否可以化简
分数乘分数:分子乘分子,分母乘分母,位置不变
分
整数乘分数:整数乘分子,分母不变
数
乘 法
计算 :先约分 方法
小数乘分数:
小数化分数或分数化小数
小数乘分子,分母不变,乘完后化简
人教版六年级数学上册 第一单元 分数乘法 思维导图(高清版)
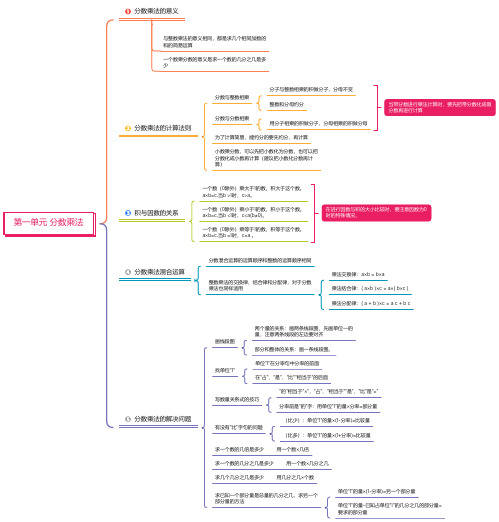
第一单元 分数乘法分数乘法的意义 分数乘法的计算法则 积与因数的关系 分数乘法混合运算 与整数乘法的意义相同,都是求几个相同加数的 和的简易运算 一个数乘分数的意义是求一个数的几分之几是多少 分数与整数相乘分数与分数相乘 分子与整数相乘的积做分子,分母不变 整数和分母约分 用分子相乘的积做分子,分母相乘的积做分母 为了计算简易,能约分的要先约分,再计算 小数乘分数,可以先把小数化为分数,也可以把 分数化成小数再计算(建议把小数化分数再计 算) 当带分数进行乘法计算时,要先把带分数化成假 分数再进行计算 一个数(0除外)乘大于1的数,积大于这个数。
a ×b=c,当b >1时,c>a 。
一个数(0除外)乘小于1的数,积小于这个数。
a ×b=c,当b <1时,c<a(b≠0)。
一个数(0除外)乘等于1的数,积等于这个数。
a ×b=c,当b =1时,c=a 。
在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
分数混合运算的运算顺序和整数的运算顺序相同整数乘法的交换律、结合律和分配律,对于分数 乘法也同样适用 乘法交换律:a×b = b×a乘法结合律:( a×b )×c = a×( b×c )乘法分配律:( a + b )×c = a c + b c分数乘法的解决问题 画线段图找单位“1”写数量关系式的技巧“的”相当于“×”,“占”、“相当于”“是”、“比”是“=”分率前是“的”字:用单位“1”的量×分率=部分量 两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐部分和整体的关系:画一条线段图。
单位“1”在分率句中分率的前面在“占”、“是”、“比”“相当于”的后面有没有“比”字句的问题(比少):单位“1”的量×(1-分率)=比较量(比多):单位“1”的量×(1+分率)=比较量求一个数的几倍是多少 求一个数的几分之几是多少 用一个数×几分之几求几个几分之几是多少 用几分之几×个数求已知一个部分量是总量的几分之几,求另一个 部分量的方法 单位“1”的量×(1-分率)=另一个部分量 单位“1”的量-已知占单位“1”的几分之几的部分量=要求的部分量 用一个数×几倍。
第1讲 分数乘法-六年级上册数学讲义(含答案)
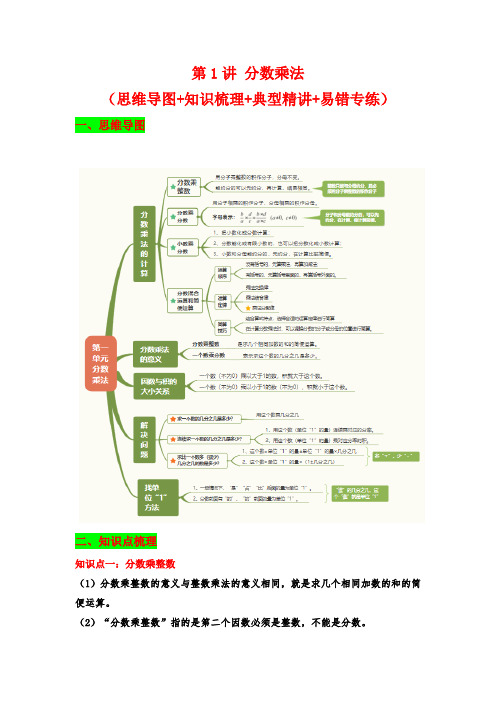
第1讲分数乘法(思维导图+知识梳理+典型精讲+易错专练)一、思维导图二、知识点梳理知识点一:分数乘整数(1)分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
(2)“分数乘整数”指的是第二个因数必须是整数,不能是分数。
分数乘整数,就是用分子乘整数作分子,分母不变。
(3)能约分的可以先约分,再计算,这样可以简便些。
(4)一个数乘分数的意义:就是求一个数的几分之几是多少。
“一个数乘分数”指的是第二个因数必须是分数,不能是整数。
知识点二:分数与分数1、分数乘分数用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)(1)如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
(2)分数化简的方法是:分子、分母同时除以它们的最大公因数。
(3)在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)。
(4)分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
知识点三:积与因数的关系1、一个数(0除外)乘大于1的数,积大于这个数。
a×b=c,当b >1时,c>a。
2、一个数(0除外)乘小于1的数,积小于这个数。
a×b=c,当b <1时,c<a(b ≠0)。
3、一个数(0除外)乘等于1的数,积等于这个数。
a×b=c,当b =1时,c=a 。
在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
知识点四:分数乘法混合运算1、分数合运算顺序:(与整数相同),先乘、除后加、减,有括号的先算括号里面的。
2、整数乘法运算定律对分数乘法同样适用;运算定律可以使一些计算简便。
乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:a×(b±c)=a×b±a×c知识点五:用分数乘法解决问题1、求一个数的几分之几是多少?用单位“1”的量与分数相乘。
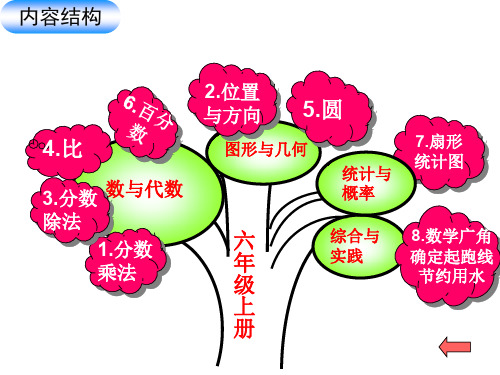
六年级数学上册知识点思维导图
求一个数比另一个数
多(或少)百分之几
求常见的百分率
求比一个数多(或少) 百分之几的数是多少
用百分数解决
百分数的意义 和写法
问题
百分数和分数、 小数的互化
第六单元
百分 数
节约用水
扇形统计图
条形统计图
折线统计图
统第
计
七 单
图元
数与形
数 学
第 八
广单
角元
第一单元
位置
与方向
(第二单元)
已知一个数的 几分之几是多 少求这个数的
问题
已知比一个数多 (少)几分之几 是多少求这个数
的问题
分数除法 的意义
解决问题
计算方
法
分数除法
倒数的认识
分
数
混合运算
除
法
第三单元
求一个 数的倒
数
比的基本性质
认识比 比的应用
比
第四单元
圆的周长 圆的面积
认识圆
扇形
第 五 单 元
内容结构
4.比
3.分数 数与代数 除法
1.分数 乘法
2.位置 与方向
5.圆
图形与几何
统计与 概率六综合与年实践级
上
册
7.扇形 统计图
8.数学广角 确定起跑线 节约用水
分数乘 整数
分数乘 分数
求一个数的 几分之几是 多少的问题
求比一个数多(少) 几分之几的数是多
少的问题
乘法运算 定律推广
到分数
分 数 乘 法
第1讲 分数乘法-六年级上册数学精品课件(教学目标+思维导图+知识梳理+典例精讲)人教版(含答案)

教学目标
本章节教学分目标 一、分数乘整数 1、在学生已有的分数加法及分数基本意义的基础上,结合生活实例,通过对分数连加算 式的研究,使学生理解分数乘整数的意义,掌握分数乘整数的计算方法,能够应用分数 乘整数的计算法则,比较熟练地进行计算。 2、通过观察比较,指导学生通过体验,归纳分数乘整数的计算法则,培养学生的抽象概 括能力。 3、引导学生探求知识的内在联系,激发学生学习兴趣。通过演示,使学生初步感悟算理, 并在这过程中感悟到数学知识的魅力,领略到美。
典例精讲
考点一:分数乘整数 【典型一】甲数比乙数少 ,乙数是50,甲数是多少,列式正确的是( )。 A. 50÷(1+ ) B. 50÷(1- ) C. 50×(1+ ) D. 50×(1- ) 【分析】甲数=乙数×(1-甲数比乙数少几分之几),据此列式作答即可。 【解答】解:列式正确的是:50×(1- )。 故答案为:D。
教学目标
本章节教学分目标 四、分数混合运算 1、理解整数乘法运算定律对于分数乘法同样适用。 2、能应用这些定律进行一些简便计算。 3、熟练掌握运算定律,灵活、准确、合理地进行计算,进一步培养、发展观察推理能力。 五、用分数乘法解决问题 1、使学生理解和掌握连续求一个数的几分之几是多少的问题的数量关系,掌握分数连乘 法的计算方法,并能正确计算。 2、让学生在“用数学”活动中,学会收集、选择和加工信息,在共同探讨中培养学生的 合作意识以及分析问题、解决问题的能力。
【分析】根据一个数乘分数的意义进行计算画图。 【解答】
典例精讲
考点三:分数混合运算
【典型一】奶牛场每头奶牛平均日产牛奶 1 t,42头奶牛100天可产奶多少吨? 50
பைடு நூலகம்
42100 1 50
人教版小学数学六年级下册1-6单元知识点思维导图

人教版小学数学六年级下册16单元知识点思维导图一、数与代数1. 分数分数的意义和性质分数加减法分数乘除法分数混合运算2. 小数小数的意义和性质小数加减法小数乘除法小数混合运算3. 比和比例比的意义和性质比例的意义和性质比例尺比例应用题二、空间与图形1. 角角的度量角的分类角的画法2. 三角形三角形的性质三角形的分类三角形的画法3. 四边形四边形的性质四边形的分类四边形的画法4. 圆圆的性质圆的画法圆的周长和面积三、统计与概率1. 数据的收集和整理调查法抽样调查数据整理2. 数据的表示条形统计图折线统计图扇形统计图3. 数据的分析平均数中位数众数4. 概率概率的定义概率的计算概率应用题四、实践与综合应用1. 实践活动数学游戏数学实验数学探究2. 综合应用解决实际问题的能力综合应用题数学建模人教版小学数学六年级下册16单元知识点思维导图一、数与代数1. 分数分数的意义和性质分数表示部分与整体的关系分数的分子和分母分数的基本性质分数加减法同分母分数的加减法异分母分数的加减法分数加减法的应用分数乘除法分数乘法的意义和计算方法分数除法的意义和计算方法分数乘除法的应用分数混合运算分数混合运算的顺序分数混合运算的技巧分数混合运算的应用2. 小数小数的意义和性质小数表示部分与整体的关系小数的整数部分和小数部分小数的基本性质小数加减法小数点对齐的加减法小数加减法的应用小数乘除法小数乘法的意义和计算方法小数除法的意义和计算方法小数乘除法的应用小数混合运算小数混合运算的顺序小数混合运算的技巧小数混合运算的应用3. 比和比例比的意义和性质比表示两个数的关系比的基本性质比例的意义和性质比例表示两个比的关系比例的基本性质比例尺比例尺的定义比例尺的应用比例应用题比例问题的解决方法比例问题的应用二、空间与图形1. 角角的度量角的定义角的度量单位角的分类锐角、直角、钝角、周角角的画法角的画法步骤角的画法应用2. 三角形三角形的性质三角形的边和角的关系三角形的分类三角形的分类按边分类:等边三角形、等腰三角形、不等边三角形按角分类:锐角三角形、直角三角形、钝角三角形三角形的画法三角形的画法步骤三角形的画法应用3. 四边形四边形的性质四边形的边和角的关系四边形的分类四边形的分类按边分类:等边四边形、等腰四边形、不等边四边形按角分类:锐角四边形、直角四边形、钝角四边形四边形的画法四边形的画法步骤四边形的画法应用4. 圆圆的性质圆的定义圆的基本性质圆的画法圆规的使用方法圆的画法应用圆的周长和面积圆的周长公式圆的面积公式三、统计与概率1. 数据的收集和整理调查法调查问卷的设计调查数据的收集抽样调查抽样调查的方法抽样调查的应用数据整理数据的排序数据的分组2. 数据的表示条形统计图条形统计图的制作条形统计图的应用折线统计图折线统计图的制作折线统计图的应用扇形统计图扇形统计图的制作扇形统计图的应用3. 数据的分析平均数平均数的计算方法平均数的应用中位数中位数的计算方法中位数的应用众数众数的计算方法众数的应用4. 概率概率的定义概率的计算方法概率的表示概率的计算概率的基本公式概率的计算应用概率应用题概率问题的解决方法概率问题的应用四、实践与综合应用1. 实践活动数学游戏数学游戏的设计数学游戏的规则数学实验数学实验的设计数学实验的操作数学探究数学探究的主题数学探究的方法2. 综合应用解决实际问题的能力实际问题的分析实际问题的解决综合应用题综合应用题的类型综合应用题的解答数学建模数学建模的意义数学建模的方法人教版小学数学六年级下册16单元知识点思维导图一、数与代数1. 分数分数的意义和性质分数表示部分与整体的关系分数的分子和分母分数的基本性质分数加减法同分母分数的加减法异分母分数的加减法分数加减法的应用分数乘除法分数乘法的意义和计算方法分数除法的意义和计算方法分数乘除法的应用分数混合运算分数混合运算的顺序分数混合运算的技巧分数混合运算的应用2. 小数小数的意义和性质小数表示部分与整体的关系小数的整数部分和小数部分小数的基本性质小数加减法小数点对齐的加减法小数加减法的应用小数乘除法小数乘法的意义和计算方法小数除法的意义和计算方法小数乘除法的应用小数混合运算小数混合运算的顺序小数混合运算的技巧小数混合运算的应用3. 比和比例比的意义和性质比表示两个数的关系比的基本性质比例的意义和性质比例表示两个比的关系比例的基本性质比例尺比例尺的定义比例尺的应用比例应用题比例问题的解决方法比例问题的应用二、空间与图形1. 角角的度量角的定义角的度量单位角的分类锐角、直角、钝角、周角角的画法角的画法步骤角的画法应用2. 三角形三角形的性质三角形的边和角的关系三角形的分类三角形的分类按边分类:等边三角形、等腰三角形、不等边三角形按角分类:锐角三角形、直角三角形、钝角三角形三角形的画法三角形的画法步骤三角形的画法应用3. 四边形四边形的性质四边形的边和角的关系四边形的分类四边形的分类按边分类:等边四边形、等腰四边形、不等边四边形按角分类:锐角四边形、直角四边形、钝角四边形四边形的画法四边形的画法步骤四边形的画法应用4. 圆圆的性质圆的定义圆的基本性质圆的画法圆规的使用方法圆的画法应用圆的周长和面积圆的周长公式圆的面积公式三、统计与概率1. 数据的收集和整理调查法调查问卷的设计调查数据的收集抽样调查抽样调查的方法抽样调查的应用数据整理数据的排序数据的分组2. 数据的表示条形统计图条形统计图的制作条形统计图的应用折线统计图折线统计图的制作折线统计图的应用扇形统计图扇形统计图的制作扇形统计图的应用3. 数据的分析平均数平均数的计算方法平均数的应用中位数中位数的计算方法中位数的应用众数众数的计算方法众数的应用4. 概率概率的定义概率的计算方法概率的表示概率的计算概率的基本公式概率的计算应用概率应用题概率问题的解决方法概率问题的应用四、实践与综合应用1. 实践活动数学游戏数学游戏的设计数学游戏的规则数学实验数学实验的设计数学实验的操作数学探究数学探究的主题数学探究的方法2. 综合应用解决实际问题的能力实际问题的分析实际问题的解决综合应用题综合应用题的类型综合应用题的解答数学建模数学建模的意义数学建模的方法。
第2讲 分数乘法+知识梳理

第2讲分数乘法(思维导图+知识梳理+典型精讲+易错专练)一、思维导图二、知识点梳理知识点一:分数与整数的乘法(一)分数与整数相乘的意义和计算方法1.整数乘法的意义。
求几个相同加数的和的简便运算。
2.(1)分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数的和的简便运算。
(2)分数与整数相乘的计算方法:用分数的分子和整数相乘的积作分子,分母不变。
能约分的要先约分,再计算。
(二)求一个数的几分之几是多少1.求一个数的几分之几是多少,用乘法计算。
2.求比一个数多(少)几分之几的部分是多少解决求比一个数多(少)几分之几的部分是多少的问题,关键是找准单位“1”的量,单位“1”的量×比一个数多(少)的几分之几=比一个数多(少)的几分之几的量。
知识点二:分数与分数的乘法(一)分数乘分数的意义和计算方法1.分数乘分数的意义就是求一个数的几分之几是多少。
2.分数和分数相乘,用分子相乘的积作分子,分母相乘的积作分母。
能约分的要先约分,再计算。
3.整数可以看成分母是1的分数,所以分数与整数相乘,也可以看成是分数与分数相乘,即分数与分数相乘的计算方法适用于分数与整数相乘。
(二)连续求一个数的几分之几是多少的解题方法及分数连乘的计算方法1.连续求一个数的几分之几是多少的解题方法:先求出中间的间接量,再求出最后要求的量。
2.分数连乘的计算方法:分子和分子相乘的积作分子,分母和分母相乘的积作分母。
能约分的要先约分,再计算。
知识点三:倒数(一)倒数的意义及求法1.意义:乘积是1的两个数互为倒数。
2.理解“互为倒数”。
“互为倒数”是对两个数来说的,它们是相互依存的,不能单独说某个数是倒数。
3.求一个数的倒数的方法。
(1)求真分数、假分数的倒数,可以直接调换这个分数的分子、分母的位置。
(2)求一个整数(0除外)的倒数,先把整数看作分母是1的假分数,再调换这个分数分子、分母的位置。
(3)求小数的倒数,先把小数化成最简分数,再调换分子、分母的位置,也可以根据倒数的意义来找。
小学六年级-分数乘法-思维导图【模板范本】
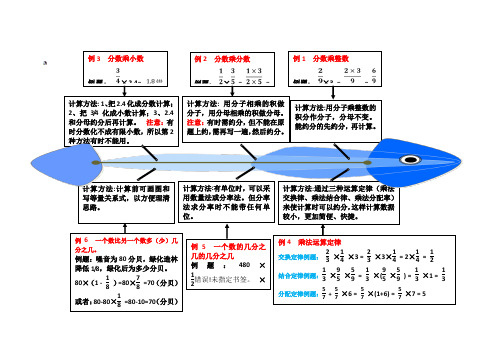
计算方法:通过三种运算定律(乘法交换律、乘法结合律、乘法分配率)来使计算时可以约分,这样计算数据较小,更加简便、快捷。
计算方法:计算前可画图和写等量关系式,以方便理清思路。
例1 分数乘整数 例题: ×3 ==计算方法:用分子乘整数的积分作分子,分母不变。
能约分的先约分,再计算。
例2 分数乘分数例题: × ==计算方法: 用分子相乘的积做分子,用分母相乘的积做分母。
注意:有时需约分,但不能在原题上约,需再写一遍,然后约分。
例3 分数乘小数例题: ×2.4=错计算方法: 1、把2.4化成分数计算; 2、把3/4化成小数计算;3、2.4和分母约分后再计算。
注意:有时分数化不成有限小数,所以第2种方法有时不能用。
例4 乘法运算定律交换定律例题: 23 ×14 ×3 = 23 ×3×14 = 2×14 = 12结合定律例题:13 ×95 ×59 = 13 ×(95 ×59 ) = 13 ×1 = 13分配定律例题:57 + 57 ×6 = 57 ×(1+6) = 57 ×7 = 5计算方法:有单位时,可以采用数量法或分率法。
但分率法求分率时不能带任何单位。
例 5 一个数的几分之几的几分之几例题:480×12错误!未指定书签。
×例6 一个数比另一个数多(少)几分之几。
例题:噪音为80分贝,绿化造林降低1/8,绿化后为多少分贝。
80×(1 - 18 )=80×78 =70(分贝)或者:80-80×18 =80-10=70(分贝)。
六年级数学第一单元分数乘法知识结构图
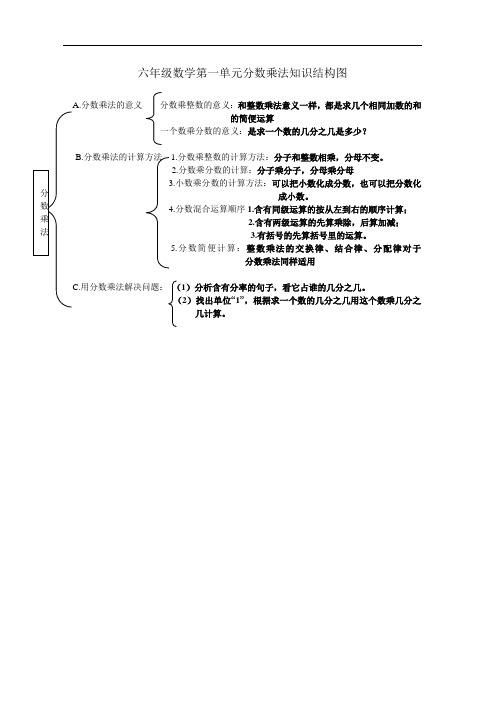
六年级数学第一单元分数乘法知识结构图
分数乘法的意义分数乘整数的意义:和整数乘法意义一样,都是求几个相同加数的和
的简便运算
一个数乘分数的意义:是求一个数的几分之几是多少?
B.分数乘法的计算方法 1.分数乘整数的计算方法:分子和整数相乘,分母不变。
2.分数乘分数的计算:分子乘分子,分母乘分母
3.小数乘分数的计算方法:可以把小数化成分数,也可以把分数化
成小数。
4.分数混合运算顺序1.含有同级运算的按从左到右的顺序计算;
2.含有两级运算的先算乘除,后算加减;
3.有括号的先算括号里的运算。
5.分数简便计算:整数乘法的交换律、结合律、分配律对于
分数乘法同样适用
用分数乘法解决问题:(1)分析含有分率的句子,看它占谁的几分之几。
(2)找出单位“1”,根据求一个数的几分之几用这个数乘几分之
几计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算方法:通过三种运算定律(乘法交换律、乘法结合律、乘法分配率)来使计算时可以约分,这样计算数据较小,更加简便、快捷。
计算方法:计算前可画图和
写等量关系式,以方便理清思路。
例1 分数乘整数 例题: ×3 =
= =
计算方法:用分子乘整数
的积分作分子,分母不变。
能约分的先约分,再计算。
例2 分数乘分数 例题: × =
=
计算方法: 用分子相乘的积做
分子,用分母相乘的积做分母。
注意:有时需约分,但不能在原
题上约,需再写一遍,然后约分。
例3 分数乘小数 例题: ×2.4=
计算方法: 1、把2.4化成分数计
算; 2、把3/4化成小数计算;3、2.4和分母约分后再计算。
注意:有时分数化不成有限小数,所以第2种方法有时不能用。
例4 乘法运算定律
交换定律例题: 2
3 ×1
4 ×3 = 23 ×3×14 = 2×14 = 12
结合定律例题:13 ×95 ×59 = 13 ×(95 ×59 ) = 13 ×1 = 1
3
计算方法:有单位时,可以采用数量法或分率法。
但分率法求分率时不能带任何单位。
例 5 一个数的几分之
几的几分之几
例题:480×12 ×1
4
=60
例6 一个数比另一个数多(少)几分之几。
例题:噪音为80分贝,绿化造林降低1/8,绿化后为多少分贝。
80×(1 - 18 )=80×7
8 =70(分
贝)。
