隐圆模型(解析版)
2024年中考复习-专题13隐圆问题3种模型(解析版)

专题13隐圆问题3种模型通用的解题思路:隐圆一般有如下呈现方式:(1)定点定长:当遇到同一个端点出发的等长线段时,通常以这个端点为圆心,等线段长为半径构造辅助圆;(2)定弦定角:当遇到动点对定点对定线段所张的角为定值时,通常把张角转化为圆周角构造辅助圆。
当遇到直角时,通常以斜边为直径构造辅助圆。
(3)四点共圆:对角互补的四边形的四个顶点共圆。
隐圆常与线段最值结合考查。
类型1:定点定长1.(2023•新城区校级三模)圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.(1)已知:如图1,OA OB OC∠=︒,则ACB∠=AOB==,请利用圆规画出过A、B.C三点的圆.若7035︒.如图,Rt ABCAB=.∠=︒,2BCA∆中,90∠=︒,30ABC(2)已知,如图2.点P为AC边的中点,将AC沿BA方向平移2个单位长度,点A、P、C的对应点分别为点D、E、F,求四边形BDFC的面积和BEA∠的大小.(3)如图3,将AC边沿BC方向平移a个单位至DF,是否存在这样的a,使得直线DF上有一点Q,满足45∠=︒且此时四边形BADF的面积最大?若存在,求出四边形BADF面积的最大值及平移距离a,BQA若不存在,说明理由.【分析】(1)利用圆的定义知A,B,C三点共圆,再利用圆周角定理求解.(2)根据图形的平移性质,判定平移后图形形状,继而确定面积的计算方式和方法,角度问题也迎刃而解.(3)因角度不变,借助圆周角定点在圆周上运动时角度不变的思想,判断出D点能够向右移动的最大距离,求出四边形的最大面积.【解答】(1)以O 为圆心,OA 为半径作辅助圆,如图,,70AOB ∠=︒ ,35ACB ∴∠=︒,故答案为35︒.(2)连接PB ,PE ,如图,,Rt ABC ∆中,90ABC ∠=︒,30BCA ∠=︒,2AB =.4AC ∴=,60BAC ∠=︒,BC =.P 为Rt ABC ∆斜边AC 中点,122BP AC ∴==,线段AC 平移到DF 之后,2AB AD PE ===,2BP AE ==,∴四边形ABPE 为菱形,60BAC ∠=︒ ,30BEA ∴∠=︒,//CF BD ,且90ABC ∠=︒,∴四边形BDFC 为直角梯形,11()622S BD CF BC ∴=+⨯=⨯⨯=(3)如图所示,以AB 为斜边在AB 的右侧作等腰直角三角形OAB ,以O 为圆心,OA 为半径作O ,当AC 边沿BC 方向平移a 个单位至DF 时,满足45BQA ∠=︒且此时四边形BADF 的面积最大,∴直线DF 与O 相切于点Q ,连接OQ 交AD 于G ,过点O 作OH AD ⊥于H ,则90AHO OHG DQG ∠=∠=∠=︒,45OAH ∠=︒,30GDQ ∠=︒,90ABC ∠=︒ ,30BCA ∠=︒,2AB =,BC ∴=OA OB OQ ===1AH OH ∴==,33HG =,233OG =,3GQ ∴=,23DG GQ ==-,11AD AH HG GD ∴=++=++,1a ∴=+,此时直角梯形ABFD 的最大面积为:11()112222S BF AD AB =⨯+⨯=⨯++-++⨯=+.【点评】本题主要考查图形的平移,圆心角,圆周角之间的关系,解题的关键是数形结合,找到极值点求解.2.(2024•兰州模拟)综合与实践【问题情境】在数学综合实践课上,“希望小组”的同学们以三角形为背景,探究图形变化过程中的几何问题,如图,在ABC ∆中,AB AC =,90BAC ∠=︒,点D 为平面内一点(点A ,B ,D 三点不共线),AE 为ABD ∆的中线.【初步尝试】(1)如图1,小林同学发现:延长AE 至点M ,使得ME AE =,连接DM .始终存在以下两个结论,请你在①,②中挑选一个进行证明:①DM AC =;②180MDA DAB ∠+∠=︒;【类比探究】(2)如图2,将AD 绕点A 顺时针旋转90︒得到AF ,连接CF .小斌同学沿着小林同学的思考进一步探究后发现:12AE CF =,请你帮他证明;【拓展延伸】(3)如图3,在(2)的条件下,王老师提出新的探究方向:点D 在以点A 为圆心,AD 为半径的圆上运动()AD AB >,直线AE 与直线CF 相交于点G ,连接BG ,在点D 的运动过程中BG 存在最大值.若4AB =,请直接写出BG的最大值.【分析】(1)利用SAS 证明ABE MDE ∆≅∆,可得AB DM =,再结合AB AC =,即可证得DM AC =;由全等三角形性质可得BAE DME ∠=∠,再运用平行线的判定和性质即可证得180MDA DAB ∠+∠=︒;(2)延长AE 至点M ,使得ME AE =,连接DM .利用SAS 证得ACF DMA ∆≅∆,可得CF AM =,再由12AE AM =,可证得12AE CF =;(3)延长DA 至M ,使AM AD =,设AM 交CF 于N ,连接BM 交CF 于K ,取AC 中点P ,连接GP ,可证得()ACF ABM SAS ∆≅∆,利用三角形中位线定理可得//AE BM ,即//AG BM ,利用直角三角形性质可得11222GP AC AB ===,得出点G 在以P 为圆心,2为半径的P 上运动,连接BP 并延长交P 于G ',可得BG '的长为BG 的最大值,再运用勾股定理即可求得答案.【解答】(1)证明:①AE 为ABD ∆的中线,BE DE ∴=,在ABE ∆和MDE ∆中,BE DE AEB MED AE ME =⎧⎪∠=∠⎨⎪=⎩,()ABE MDE SAS ∴∆≅∆,AB DM ∴=,AB AC = ,DM AC ∴=;②由①知ABE MDE ∆≅∆,BAE DME ∴∠=∠,//AB DM ∴,180MDA DAB ∴∠+∠=︒;(2)证明:延长AE 至点M ,使得ME AE =,连接DM.由旋转得:AF AD =,90DAF ∠=︒,90BAC ∠=︒ ,360DAF BAC BAD CAF ∠+∠+∠+∠=︒,180BAD CAF ∴∠+∠=︒,由(1)②得:180MDA DAB ∠+∠=︒,DM AB AC ==,CAF MDA ∴∠=∠,在ACF ∆和DMA ∆中,AF AD CAF MDA AC DM =⎧⎪∠=∠⎨⎪=⎩,()ACF DMA SAS ∴∆≅∆,CF AM ∴=,12AE AM = ,12AE CF ∴=;(3)如图3,延长DA 至M ,使AM AD =,设AM 交CF 于N ,连接BM 交CF 于K ,取AC 中点P ,连接GP ,由旋转得:AF AD =,90DAF ∠=︒,AF AM ∴=,1809090MAF ∠=︒-︒=︒,90BAC ∠=︒ ,MAF CAM BAC CAM ∴∠+∠=∠+∠,即CAF BAM ∠=∠,在ACF ∆和ABM ∆中,AC AB CAF BAM AF AM =⎧⎪∠=∠⎨⎪=⎩,()ACF ABM SAS ∴∆≅∆,AFC AMB ∴∠=∠,即AFN KMN ∠=∠,ANF KNM ∠=∠ ,90FAN MKN ∴∠=∠=︒,BM CF ∴⊥,E 、A 分别是DB 、DM 的中点,AE ∴是BDM ∆的中位线,//AE BM ∴,即//AG BM ,AG CF ∴⊥,90AGC ∴∠=︒,点P 是AC 的中点,11222GP AC AB ∴===,∴点G 在以P 为圆心,2为半径的P 上运动,连接BP 并延长交P 于G ',BG ∴'的长为BG 的最大值,在Rt ABP ∆中,BP ==2BG BP PG ∴'=+'=+,BG ∴的最大值为2+.【点评】本题是几何综合题,考查了三角形的全等的性质与判定,两直线垂直的判定,三角形中位线定理,勾股定理,圆的性质,熟练掌握全等三角形的判定定理是解决本题的关键.3.(2022•番禺区二模)已知抛物线23(0)2y ax bx a =+->与x 轴交于点A ,B 两点,OA OB <,4AB =.其顶点C 的横坐标为1-.(1)求该抛物线的解析式;(2)设点D 在抛物线第一象限的图象上,DE AC ⊥垂足为E ,//DF y 轴交直线AC 于点F ,当DEF ∆面积等于4时,求点D 的坐标;(3)在(2)的条件下,点M 是抛物线上的一点,M 点从点B 运动到达点C ,FM FN ⊥交直线BD 于点N ,延长MF 与线段DE 的延长线交于点H ,点P 为N ,F ,H 三点构成的三角形的外心,求点P 经过的路线长.【分析】(1)利用对称性,求得A 和B 的坐标,然后用待定系数法求得抛物线的解析式;(2)证明CGA ∆和DEF ∆都为等腰直角三角形,利用等面积法求得4DF =,再求得直线AC 的解析式为1y x =-,设点D 的坐标,得到点F 的坐标,然后求解即可;(3)先求得45BDF ∠=︒,推出点P 的运动路径时11H N 的中点绕点F 逆时针旋转90︒得到2N H 的中点之间的弧长,证明四边形2DN FE 为正方形,即可求解.【解答】解:(1) 点A ,点B 两点关于直线1x =-对称,4AB =,(1,0)A ∴,(3,0)B -,代入232y ax bx =+-得,30239302a b a b ⎧+-=⎪⎪⎨⎪--=⎪⎩,解得:121a b ⎧=⎪⎨⎪=⎩,∴抛物线的解析式为21322y x x =+-.(2)如图1所示://DF y 轴//GC ,GCA DFE ∴∠=∠,抛物线的解析式为22131(1)2222y x x x =+-=+-,∴顶点(1,2)C --,(1,0)A ,2AG ∴=,2CG =,CGA ∴∆为等腰直角三角形,45GCA DFE ∴∠=∠=︒,DE AC ⊥ ,DEF ∴∆为等腰直角三角形,DE EF ∴=,DF =,142DEF S DE EF ∆=⋅= ,DE ∴=,4DF ∴==,设直线AC 的解析式为y kx b =+,则02k b k b +=⎧⎨-+=-⎩,解得:11k b =⎧⎨=-⎩,∴直线AC 的解析式为1y x =-,设点213(,22D x x x +-,则(,1)F x x -,221311(1)42222DF x x x x ∴=+---=-=,解得:3x =或3x =-(舍),(3,6)D ∴,(3,2)F .(3)如图2所示,NFH ∆ 是直角三角形,NFH ∴∆的外心是斜边NH 的中点,当点M 位于点B 时,△11N FH ,其外心是斜边11H N 的中点,当点M 位于点C 时,得△2N FE ,其外心是斜边22N H 的中点,即2N E 的中点,(3,6)D ,(3,0)B -,33tan 16BDF +∴∠==,45BDF ∴∠=︒,由(2)得,45FDE ∠=︒,45DBA BAC ∴∠=∠=︒,//BD AC ∴,FN BD ∴⊥,DF ∴平分BDE ∠,90BDE ∠=︒,∴点D ,N ,F ,H 四点共圆,∴点P 在线段DF 的垂直平分线上,即点P 在2N E 上运动,即点P 的运动轨迹是一条线段.2290DN F N DH DHF ∠=∠=∠=︒ ,2FN FE =,∴四边形2DN FE 为正方形,此时点P 在DF 上,且2EP =;当点M 与点C 重合时,此时点P 在DF 上,即为2P ,且222FP EP ==,由题意,224BN BD DN =-=,BF =2N F =,21//FN DH ,2BFN ∴∆∽△1BH D ,∴21BN BF BD BH =,解得1FH =,1FP ∴=,由勾股定理可得:121P P =,即点P 的运动轨迹长为1.【点评】本题主要考查二次函数的综合问题,包括待定系数法确定函数解析式,三角形外接圆的性质,弧长公式,勾股定理,三角函数解直角三角形等,理解题意,作出相应辅助线是解题的关键.4.(2021•红谷滩区校级模拟)(1)学习心得:小刚同学在学习完“圆”这一章内容后,感觉到有一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在ABC=,求BDC∆外一点,且AD AC∠的度数.若∆中,AB AC=,80BAC∠=︒,D是ABC以点A 为圆心,AB 为半径作辅助圆A ,则点C 、D 必在A 上,BAC ∠是A 的圆心角,而BDC ∠是圆周角,从而可容易得到BDC ∠=40︒.(2)问题解决:如图,在四边形ABCD 中,90BAD BCD ∠=∠=︒,25BDC ∠=︒,求BAC ∠的度数.(3)问题拓展:抛物线21(1)34y x =--+与y 轴交于点A ,顶点为B ,对称轴BC 与x 轴交于点C ,点P 在抛物线上,直线//PQ BC 交x 轴于点Q ,连接BQ .①若含45︒角的直线三角板如图所示放置,其中,一个顶点与C 重合,直角顶点D 在BQ 上,另一顶点E 在PQ 上,求Q 的坐标;②若含30︒角的直角三角板一个顶点与点C 重合,直角顶点D 在BQ 上,另一个顶点E 在PQ 上,点D 与点B ,点Q 不重合,求点P 的坐标.【分析】(1)利用同弦所对的圆周角是所对圆心角的一半求解.(2)由A 、B 、C 、D 共圆,得出BDC BAC ∠=∠,(3)①先求出抛物线顶点的坐标,再由点D 、C 、Q 、E 共圆,得出45CQB OED ∠=∠=︒,求出CQ ,再求点Q 的坐标.②分两种情况,Ⅰ、当30︒的角的顶点与点C 重合时,Ⅱ、当60︒的角的顶点与点C 重合时,运用点D 、C 、Q 、E 共圆,求出CQ 即点P 的横坐标,再代入抛物线求出点P 的纵坐标,即可求出点P 的坐标.【解答】解:(1)AB AC = ,AD AC =,∴以点A 为圆心,点B 、C 、D 必在A 上,BAC ∠ 是A 的圆心角,而BDC ∠是圆周角,1402BDC BAC ∴∠=∠=︒,(2)如图2,90BAD BCD ∠=∠=︒ ,∴点A 、B 、C 、D 共圆,BDC BAC ∴∠=∠,25BDC ∠=︒ ,25BAC ∴∠=︒,(3)①如图3点B 为抛物线21(1)34y x =--+的顶点,∴点B 的坐标为(1,3),45︒ 角的直角三角板如图所示放置,其中,一个顶点与C 重合,直角顶点D 在BQ 上,另一顶点E 在PQ 上,∴点D 、C 、Q 、E 共圆,45CQB CED ∴∠=∠=︒,3CQ BC ∴==,4OQ ∴=,∴点Q 的坐标为(4,0),②如图4,Ⅰ、当30︒的角的顶点与点C 重合时,直角三角板30︒角的顶点与点C 重合,直角顶点D 在BQ 上,另一个顶点E 在PQ 上∴点D 、C 、Q 、E 共圆,60CQB CED ∴∠=∠=︒,3CQ BC ∴==1OQ ∴=+,∴把1+代入21(1)34y x =--+得94y =,∴点P 的坐标是(1+94Ⅱ、如图5,当60︒的角的顶点与点C 重合时,直角三角板60︒角的顶点与点C 重合,直角顶点D 在BQ 上,另一个顶点E 在PQ 上∴点D 、C 、Q 、E 共圆,30CQB CED ∴∠=∠=︒,CQ ∴==,1OQ ∴=+∴把1+21(1)34y x =--+得154y =-,∴点P 的坐标是(1+,154-综上所述,点P 的坐标是(1+94或(1+15)4-.【点评】本题主要考查了圆的综合题,解题的关键就是运用同弦对的圆周角相等.类型2:定弦定角1.(2022•雁塔区校级三模)问题提出(1)如图①,已知ABC ∆为边长为2的等边三角形,则ABC ∆的面积为问题探究(2)如图②,在ABC ∆中,已知120BAC ∠=︒,BC =,求ABC ∆的最大面积;问题解决(3)如图③,某校学生礼堂的平面示意为矩形ABCD ,其宽20AB =米,长24BC =米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面CD 上安装一台摄像头M 进行观测,并且要求能观测到礼堂前端墙面AB 区域,同时为了观测效果达到最佳,还需要从点M 出发的观测角45AMB ∠=︒,请你通过所学知识进行分析,在墙面CD 区域上是否存在点M 满足要求?若存在,求出MC 的长度;若不存在,请说明理由.【分析】(1)作AD BC ⊥于D ,由勾股定理求出AD 的长,即可求出面积;(2)作ABC ∆的外接圆O ,可知点A 在 BC上运动,当A O BC '⊥时,ABC ∆的面积最大,求出A H '的长,从而得出答案;(3)以AB 为边,在矩形ABCD 的内部作一个等腰直角三角形AOB ,且90AOB ∠=︒,过O 作HG AB ⊥于H ,交CD 于G ,利用等腰直角三角形的性质求出OA ,OG 的长,则以O 为圆心,OA 为半径的圆与CD 相交,从而O 上存在点M ,满足45AMB ∠=︒,此时满足条件的有两个点M ,过1M 作1M F AB ⊥于F ,作1EO M F ⊥于E ,连接OF ,利用勾股定理求出OE 的长,从而解决问题.【解答】解:(1)作AD BC ⊥于D ,ABC ∆ 是边长为2的等边三角形,1BD ∴=,AD ∴==ABC ∴∆的面积为122⨯=;(2)作ABC ∆的外接圆O ,120BAC ∠=︒ ,BC =,∴点A 在 BC上运动,当A O BC '⊥时,ABC ∆的面积最大,60BOA '∴∠=︒,33BH CH ==,3OH ∴=,6OB =,633A H OA OH ''∴=-=-=,ABC ∴∆的最大面积为133932⨯=(3)存在,以AB 为边,在矩形ABCD 的内部作一个等腰直角三角形AOB ,且90AOB ∠=︒,过O 作HG AB ⊥于H ,交CD 于G ,20AB = 米,10AH OH ∴==米,2OA =米,24BC = 米,14OG ∴=米,10214> ,∴以O 为圆心,OA 为半径的圆与CD 相交,O ∴ 上存在点M ,满足45AMB ∠=︒,此时满足条件的有两个点M ,过1M 作1M F AB ⊥于F ,作1EO M F ⊥于E ,连接OF ,10EF OH ∴==米,1102OM =114EM ∴=米,22112OE OM M E ∴-=米,18CM BF ∴==米,同理210212CM BH OE =+=+=(米),MC ∴的长度为8米或12米.【点评】本题是四边形综合题,主要考查了等边三角形的性质,矩形的性质,等腰直角三角形的性质,勾股定理,垂径定理等知识,熟练掌握定角定边的基本模型是解题的关键.2.(2023•灞桥区校级模拟)问题提出:(1)如图①,ABC ∆为等腰三角形,120C ∠=︒,8AC BC ==,D 是AB 上一点,且CD 平分ABC ∆的面积,则线段CD 的长度为4.问题探究:(2)如图②,ABC ∆中,120C ∠=︒,10AB =,试分析和判断ABC ∆的面积是否存在最大值,若存在,求出这个最大值;若不存在,请说明理由.问题解决:(3)如图③,2023年第九届丝绸之路国际电影开幕式在西安曲江竞技中心举行,主办方要在会场旁规划一个四边形花圃ABCD ,满足600BC =米,300CD =米,60C ∠=︒,60A ∠=︒,主办方打算过BC 的中点M 点(入口)修建一条径直的通道ME (宽度忽略不计)其中点E (出口)为四边形ABCD 边上一点,通道ME 把四边形ABCD 分成面积相等并且尽可能大的两部分,分别规划成不同品种的花圃以供影迷休闲观赏.问是否存在满足上述条件的通道ME ?若存在,请求出点A 距出口的距离AE 的长;若不存在,请说明理由.【分析】(1)由题意可知,CD 是ABC ∆的中线,利用等腰三角形的性质推出CD AB ⊥,利用三角函数求解即可解决问题;(2)当ABC ∆的AB 边上的高CD 最大时,三角形ABC 的面积最大,即CD 过圆心O ,连接AO .求出CD 的最大值即可得出答案;(3)连接DM ,BD .首先证明90BDC ∠=︒,求出BD ,推出BDC ∆的面积是定值,要使得四边形ABCD 的面积最大,只要ABD ∆的面积最大即可,因为BD 为定值,A ∠为定角60=︒,推出当ABD ∆是等边三角形时,求出四边形ABCD 的面积最大值,然后再求出90MDE ∠=︒,构建方程解决问题即可.【解答】解:(1)如图①,CD 平分ABC ∆的面积,AD DB ∴=,8AC BC == ,CD AB ∴⊥,1602ACD BCD ACB ∠=∠=∠=︒,cos 8cos 604CD AC ACD ∴=∠=︒=,CD ∴的长度为4,故答案为:4;(2)存在.如图②,10AB = ,120ACB ∠=︒都是定值,∴点C 在AB 上,并且当点C 在 AB 的中点时,ABC ∆的面积最大;连接OC 交AB 于点D ,则CD AB ⊥,152AD BD AB ===,1602ACD ACB ∠=∠=︒,∴tan AD ACD CD ∠=,53tan 603AD CD ==︒,∴125323ABC S AB CD ∆=⋅=,答:ABC ∆(3)存在.如图③,连接DM ,BD ,M 是BC 的中点,13002CM BC ∴==,CM CD ∴=,又60C ∠=︒ ,CMD ∴∆是等边三角形,60MDC CMD ∴∠=∠=︒,CM DM BM ==,30CBD MDB ∴∠=∠=︒,90BDC ∴∠=︒,tan 60BD CD ∴=⋅︒=米,在ABD ∆中,BD =60A ∠=︒为定值,由(2)可知当AB AD =时,即ABD ∆为等边三角形时ABD ∆的面积最大,此时也为四边形ABCD 的最大值(BDC ∆的面积不变),21330024max BDC BDA S S S ∆∆=+=⨯⨯=;ABD ∆ 是等边三角形,60ADB ∴∠=︒,90ADM ADB BDM ∴∠=∠+∠=︒,由12EMD CDM max S S S ∆∆+=,得:21130030022DE ⨯+=⨯解得:DE =,AE AD DE ∴=-==),答:点A 距出口的距离AE 的长为米.【点评】本题是圆的综合题,考查了勾股定理,垂径定理,解直角三角形,等边三角形的判定和性质等知识,解题的关键是理解题意构造辅助圆,灵活运用所学知识解决问题,难度较大,属于中考压轴题.3.(2023•柯城区校级一模)如图,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该直角坐标系内的一个动点.(1)使30APB ∠=︒的点P 有无数个;(2)若点P 在y 轴上,且30APB ∠=︒,求满足条件的点P 的坐标;(3)当点P 在y 轴上移动时,APB ∠是否有最大值?若有,求点P 的坐标,并说明此时APB ∠最大的理由;若没有,也请说明理由.【分析】(1)已知点A 、点B 是定点,要使30APB ∠=︒,只需点P 在过点A 、点B 的圆上,且弧AB 所对的圆心角为60︒即可,显然符合条件的点P 有无数个.(2)结合(1)中的分析可知:当点P 在y 轴的正半轴上时,点P 是(1)中的圆与y 轴的交点,借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点P 的坐标;当点P 在y 轴的负半轴上时,同理可求出符合条件的点P 的坐标.(3)由三角形外角的性质可证得:在同圆或等圆中,同弧所对的圆周角大于同弧所对的圆外角.要APB ∠最大,只需构造过点A 、点B 且与y 轴相切的圆,切点就是使得APB ∠最大的点P ,然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题.【解答】解:(1)以AB 为边,在第一象限内作等边三角形ABC ,以点C 为圆心,AC 为半径作C ,交y 轴于点1P 、2P .在优弧1APB 上任取一点P ,如图1,则11603022APB ACB ∠=∠=⨯︒=︒.∴使30APB ∠=︒的点P 有无数个.故答案为:无数.(2)①当点P 在y 轴的正半轴上时,过点C 作CG AB ⊥,垂足为G ,如图1.点(1,0)A ,点(5,0)B ,1OA ∴=,5OB =.4AB ∴=.点C 为圆心,CG AB ⊥,122AG BG AB ∴===.3OG OA AG ∴=+=.ABC ∆ 是等边三角形,4AC BC AB ∴===.CG ∴===∴点C 的坐标为(3,.过点C 作CD y ⊥轴,垂足为D ,连接2CP ,如图1,点C 的坐标为(3,,3CD ∴=,OD =1P 、2P 是C 与y 轴的交点,1230APB AP B ∴∠=∠=︒.24CP CA == ,3CD =,2DP ∴== 点C 为圆心,12CD PP ⊥,12PD P D ∴==2(0P ∴,-.1(0P ,+.②当点P 在y 轴的负半轴上时,同理可得:3(0,P -.4(0,P -.综上所述:满足条件的点P 的坐标有:(0,-、(0,、(0,--、(0,-+.(3)当过点A 、B 的E 与y 轴相切于点P 时,APB ∠最大.理由:可证:APB AEH ∠=∠,当APB ∠最大时,AEH ∠最大.由2sin AEH AE∠=得:当AE 最小即PE 最小时,AEH ∠最大.所以当圆与y 轴相切时,APB ∠最大.①当点P 在y 轴的正半轴上时,连接EA ,作EH x ⊥轴,垂足为H ,如图2.E 与y 轴相切于点P ,PE OP ∴⊥.EH AB ⊥ ,OP OH ⊥,90EPO POH EHO ∴∠=∠=∠=︒.∴四边形OPEH 是矩形.OP EH ∴=,3PE OH ==.3EA ∴=.90EHA ∠=︒ ,2AH =,3EA =,EH ∴===OP ∴P ∴.②当点P 在y 轴的负半轴上时,同理可得:(0,P .理由:①若点P 在y 轴的正半轴上,在y 轴的正半轴上任取一点M (不与点P 重合),连接MA ,MB ,交E 于点N ,连接NA ,如图2所示.ANB ∠ 是AMN ∆的外角,ANB AMB ∴∠>∠.APB ANB ∠=∠ ,APB AMB ∴∠>∠.②若点P 在y 轴的负半轴上,同理可证得:APB AMB ∠>∠.综上所述:当点P 在y 轴上移动时,APB ∠有最大值,此时点P 的坐标为和(0,.【点评】本题考查了垂径定理、圆周角定理、勾股定理、等边三角形的性质、矩形的判定与性质,切线的性质、三角形外角性质等知识,综合性强.同时也考查了创造性思维,有一定的难度.构造辅助圆是解决本题关键.类型3:四点共圆1.(2022•中原区校级模拟)阅读下列材料,并完成相应的任务.西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线).某数学兴趣小组的同学们尝试证明该定理.如图(1),已知ABC∆内接于O,点P在O上(不与点A,B,C重合),过点P分别作AB,BC,AC的垂线,垂足分别为点D,E,F.求证:点D,E,F在同一条直线上.如下是他们的证明过程(不完整):如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF,则12EQ FQ PC PQ CQ====,(依据1)点E,F,P,C四点共圆,180FCP FEP∴∠+∠=︒.(依据2)又180ACP ABP∠+∠=︒,FEP ABP∴∠=∠.同上可得点B,D,P,E四点共圆,⋯⋯任务:(1)填空:①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半;②依据2指的是.(2)请将证明过程补充完整.(3)善于思考的小虎发现当点P是 BC的中点时,BD CF=,请你利用图(2)证明该结论的正确性.【分析】(1)利用直角直角三角形斜边上的中线的性质和圆内接四边形对角互补即可;(2)利用直角三角形斜边上中线的性质证明点E,F,P,C和点B,D,P,E四点分别共圆,再说明180FEP DEP∠+∠=︒,可证明结论;(3)连接PA,PB,PC,利用HL证明Rt PBD Rt PCF∆≅∆,从而得出结论.【解答】(1)解:①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半,②依据2指的是圆内接四边形对角互补,故答案为:①直角三角形斜边上的中线等于斜边的一半;②圆内接四边形对角互补;(2)解:如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF,则12EQ FQ PC PQ CQ ====,∴点E,F,P,C四点共圆,180FCP FEP∴∠+∠=︒,又180ACP ABP∠+∠=︒,FEP ABP∴∠=∠,同上可得点B,D,P,E四点共圆,DBP DEP∴∠=∠,180ABP DBP∠+∠=︒,180FEP DEP∴∠+∠=︒,∴点D,E,F在同一直线上;(3)证明:如图,连接PA,PB,PC,点P 是 BC的中点,∴ BPPC =,BP PC ∴=,PAD PAC ∠=∠,又PD AD ⊥ ,PF AC ⊥,PD PF ∴=,Rt PBD Rt PCF(HL)∴∆≅∆,BD CF ∴=.【点评】本题主要考查了四点共圆,以及圆内接四边形的性质,角平分线的性质,全等三角形的判定与性质等知识,证明Rt PBD Rt PCF ∆≅∆是解题的关键.2.(2021•哈尔滨模拟)(1)【学习心得】于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在ABC ∆中,AB AC =,90BAC ∠=︒,D 是ABC ∆外一点,且AD AC =,求BDC ∠的度数.若以点A 为圆心,AB 为半径作辅助A ,则点C 、D 必在A 上,BAC ∠是A 的圆心角,而BDC ∠是圆周角,从而可容易得到BDC ∠=45︒.(2)【问题解决】如图2,在四边形ABCD 中,90BAD BCD ∠=∠=︒,25BDC ∠=︒,求BAC ∠的度数.(3)【问题拓展】如图3,如图,E ,F 是正方形ABCD 的边AD 上两个动点,满足AE DF =.连接CF 交BD 于点G ,连接BE 交AG 于点H .若正方形的边长为2,则线段DH 长度的最小值是.【分析】(1)利用同弦所对的圆周角是所对圆心角的一半求解.(2)由A 、B 、C 、D 共圆,得出BDC BAC ∠=∠,(3)根据正方形的性质可得AB AD CD ==,BAD CDA ∠=∠,ADG CDG ∠=∠,然后利用“边角边”证明ABE ∆和DCF ∆全等,根据全等三角形对应角相等可得12∠=∠,利用“SAS ”证明ADG ∆和CDG ∆全等,根据全等三角形对应角相等可得23∠=∠,从而得到13∠=∠,然后求出90AHB ∠=︒,取AB 的中点O ,连接OH 、OD ,根据直角三角形斜边上的中线等于斜边的一半可得112OH AB ==,利用勾股定理列式求出OD ,然后根据三角形的三边关系可知当O 、D 、H 三点共线时,DH 的长度最小.【解答】解:(1)如图1,AB AC = ,AD AC =,∴以点A 为圆心,AB 为半径作圆A ,点B 、C 、D 必在A 上,BAC ∠ 是A 的圆心角,而BDC ∠是圆周角,1452BDC BAC ∴∠=∠=︒,故答案为:45;(2)如图2,取BD 的中点O ,连接AO 、CO .90BAD BCD ∠=∠=︒ ,∴点A 、B 、C 、D 共圆,BDC BAC ∴∠=∠,25BDC ∠=︒ ,25BAC ∴∠=︒,(3)如图3,在正方形ABCD 中,AB AD CD ==,BAD CDA ∠=∠,ADG CDG ∠=∠,在ABE ∆和DCF ∆中,AB CD BAD CDA AE DF =⎧⎪∠=∠⎨⎪=⎩,()ABE DCF SAS ∴∆≅∆,12∴∠=∠,在ADG ∆和CDG ∆中,AD CD ADG CDG DG DG =⎧⎪∠=∠⎨⎪=⎩,()ADG CDG SAS ∴∆≅∆,23∴∠=∠,13∴∠=∠,390BAH BAD ∠+∠=∠=︒ ,190BAH ∴∠+∠=︒,1809090AHB ∴∠=︒-︒=︒,取AB 的中点O ,连接OH 、OD ,则112OH AO AB ===,在Rt AOD ∆中,OD ===,根据三角形的三边关系,OH DH OD +>,∴当O 、D 、H 三点共线时,DH 的长度最小,最小值1OD OH =-=.(解法二:可以理解为点H 是在Rt AHB ∆,AB 直径的半圆 AB 上运动当O 、H 、D 三点共线时,DH 长度最小)1-.【点评】本题主要考查了圆的综合题,需要掌握垂径定理、圆周角定理、等腰直角三角形的性质以及勾股定理等知识,难度偏大,解题时,注意辅助线的作法.3.(2022•潢川县校级一模)如图1,点B 在直线l 上,过点B 构建等腰直角三角形ABC ,使90BAC ∠=︒,且AB AC =,过点C 作CD ⊥直线l 于点D ,连接AD .(1)小亮在研究这个图形时发现,90BAC BDC ∠=∠=︒,点A ,D 应该在以BC 为直径的圆上,则ADB ∠的度数为45︒,将射线AD 顺时针旋转90︒交直线l 于点E ,可求出线段AD ,BD ,CD 的数量关系为;(2)小亮将等腰直角三角形ABC 绕点B 在平面内旋转,当旋转到图2位置时,线段AD ,BD ,CD 的数量关系是否变化,请说明理由;(3)在旋转过程中,若CD 长为1,当ABD ∆面积取得最大值时,请直接写AD 的长.【分析】(1)由90BAC ∠=︒,且AB AC =,可得45ACB ABC ∠=∠=︒,由90BAC BDC ∠=∠=︒,推出A 、B 、C 、D 四点共圆,所以45ADB ACB ∠=∠=︒;由题意知EAB DAC ∆≅∆,所以BE CD =,由AE AD =,90EAD ∠=︒,可知ADE ∆是等腰直角三角形,推出2CD DB EB BD DE +=+==;(2)如图2,将AD 绕点A 顺时针旋转90︒交直线l 于点E .易证()EAB DAC SAS ∆≅∆,则BE CD =,由AE AD =,90EAD ∠=︒,所以ADE ∆是等腰直角三角形,则2DE =,由BD CD BD BE DE -=-=,推出BD CD-=;(3)当点D在线段AB的垂直平分线上且在AB的左侧时,ABD∆的面积最大.【解答】解:(1)①如图,在图1中.=,,且AB AC∠=︒90BACACB ABC∴∠=∠=︒,45,∠=∠=︒90BAC BDC∴、B、C、D四点共圆,A∴∠=∠=︒;45ADB ACB②由题意可知,90∠=∠=︒,EAD BAC∴∠=∠,EAB DAC又AE AD=,AB AC=,EAB DAC SAS∴∆≅∆,()∴=,BE CD,90AE AD=∠=︒,EAD∴∆是等腰直角三角形,ADE∴=,DE,+=+=CD DB EB BD DE∴+=;CD DB故答案为45︒,CD DB+=;(2)线段AD,BD,CD的数量关系会变化,数量关系为BD CD-=.理由如下:如图2,将AD绕点A顺时针旋转90︒交直线l于点E.则90∠=∠=︒,DAE CAB∴∠=∠,DAC EAB又AD AE=,AC AB=,EAB DAC SAS∴∆≅∆,()∴=,BE CD,90AE AD=∠=︒,EAD∴∆是等腰直角三角形,ADE∴=,2DE,-=-=BD CD BD BE DE∴-=;2BD CD(3)由(2)知,CDA BEA∆≅∆,∴∠=∠,CDA AEB,∠=︒DEA45∴∠=︒-︒=︒,AEB18045135∴∠=∠=︒,135CDA AEB∴∠+∠=︒+︒=︒,13545180CDA ABC∴、B、C、D四点共圆,A于是作A、B、C、D外接圆O,如图,当点D在线段AB的垂直平分线上且在AB的左侧时,DG经过圆心,此时DG最长,因此ABD∆的面积最大.作DG AB ⊥,则DG 平分ADB ∠,DB DA =,在DA 上截取一点H ,使得1CD DH ==,45ADB ACB ∠=∠=︒ ,22.5GDB ∴∠=︒,67.5DBG ∠=︒,67.54522.5DBC ∴∠=︒-︒=︒,4522.522.5HCB DHC HBC ∠=∠-∠=︒-︒=︒,HCB HBC ∴∠=∠,HB CH ∴==,1AD BD DH BH ∴==+=.【点评】本题考查三角形综合题、等腰直角三角形的性质和判定、全等三角形的判定和性质、圆等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用辅助圆解决问题,属于中考压轴题.。
隐圆模型---定弦定角【模型专题】(含答案解析)

∴∠CED=∠CEB=90°,
∴点E在以BC为直径的⊙Q上,
∵BC=4,
∴QC=QE=2,
当点Q、E、A共线时AE最小,
∵AC=10,
∴AQ= = ,
∴AE=AQ−QE= ,
∴AE的最小值为 ,
故答案为 .
【点睛】本题考查了圆周角定理和勾股定理,解决本题的关键是确定E点运动的规律,从而把问题转化为圆外一点到圆上一点的最短距离问题.
【结论3】如图所示,在 中,A,B均为定点,点P为平面内一动点,且 (或 ),则点P在以 为底,以 为腰构造 等腰 (或 )的顶点C(或 )为圆心的圆上运动.
【解题技巧】
构造隐圆
圆形中一般求一个定点到一动点线段长度的最小值问题的时候一般涉及定弦定角问题.
定弦定角解决问题的步骤:
(1)让动点动一下,观察另一个动点的运动轨迹,发现另一个动点的运动轨迹为一段弧
【答案】 ﹣2
【解析】
【详解】试题分析:如图,连接BO′、BC.在点D移动的过程中,点E在以AC为直径的圆上运动,当O′、E、B共线时,BE的值最小,最小值为O′B- O′E,利用勾股定理求出B O′即可解决问题.
点睛:本题主要考查的就是直角三角形的勾股定理以及圆的基本性质的问题,本题有一定的难度.解决本题的关键问题就是找出点E所运动的轨迹是什么,然后根据两点之间线段最短以及直角三角形的勾股定理进行求解得出答案.同学们对于解决动点问题时,首先要找出运动轨迹,然后根据题意得出最短距离.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
【分析】(1)如图①,先作等边三角形 ,再以点 为圆心, 为半径作 ,则 与矩形 的边 , 的交点 , 即是使 的所有点 ;
圆中的重要几何模型-隐圆模型(解析版)精选全文完整版

圆中的重要几何模型-隐圆模型隐圆是各地中考选择题和填空题、甚至解答题中常考题,题目常以动态问题出现,有点、线的运动,或者图形的折叠、旋转等,大部分学生拿到题基本没有思路,更谈不上如何解答。
隐圆常见的有以下四种形式,动点定长、定弦对直角、定弦对定角、四点共圆(对角互补或等弦对等角),上述四种动态问题的轨迹是圆。
题目具体表现为折叠问题、旋转问题、角度不变问题等,此类问题综合性强,隐蔽性强,很容易造成同学们的丢分。
本专题就隐圆模型的相关问题进行梳理及对应试题分析,方便掌握。
模型1、动点定长模型(圆的定义)若P为动点,但AB=AC=AP,则B、C、P三点共圆,A圆心,AB半径圆的定义:平面内到定点的距离等于定值的所有点构成的集合.寻找隐圆技巧:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧.例1.(2020·四川中考真题)已知:等腰直角三角形ABC的腰长为4,点M在斜边AB上,点P为该平面内一动点,且满足PC=2,则PM的最小值为()A.2B.22-2C.22+2D.22【答案】B【分析】根据等腰直角三角形的性质得到斜边AB=42,由已知条件得到点P在以C为圆心,PC为半径的圆上,当点P在斜边AB的中线上时,PM的值最小,于是得到结论.【详解】解:∵等腰直角三角形ABC的腰长为4,∴斜边AB=42,∵点P为该平面内一动点,且满足PC=2,∴点P在以C为圆心,PC为半径的圆上,当点P在斜边AB的中线上时,PM的值最小,∵△ABC是等腰直角三角形,∴CM=12AB=22,∵PC=2,∴PM=CM-CP=22-2,故选:B.【点睛】本题考查线段最小值问题,涉及等腰三角形的性质和点到圆的距离,解题的关键是能够画出图形找到取最小值的状态然后求解.例2.(2020·江苏连云港市·中考真题)如图,在平面直角坐标系xOy中,半径为2的eO与x轴的正半轴交于点A,点B是eO上一动点,点C为弦AB的中点,直线y=34x-3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为.【答案】2【分析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE 的面积最小.【详解】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x-3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),∴OD=4,OE=3,∴DE=OE2+OD2=32+42=5,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴MNOE=DMDE,∴MN3=35,∴MN=95,当点C与C′重合时,△C′DE的面积最小,△C′DE的面积最小值=12×5×95-1,故答案为2.【点睛】本题考查三角形的中位线定理,三角形的面积,一次函数的性质等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.例3.(2022·北京市·九年级专题练习)如图,四边形ABCD中,AE、AF分别是BC,CD的中垂线,∠EAF=80°,∠CBD=30°,则∠ABC=,∠ADC=.【答案】 40°; 60°【分析】连接AC,根据线段垂直平分线的性质可得AB=AC=AD,从而得到B、C、D在以A为圆心,AB为半径的圆上,根据圆周角定理可得∠DAC=2∠DBC=60°,再由等腰三角形的性质可得∠DAF=∠CAF=30°,即可求解.【详解】解:连接AC,∵AE、AF分别是BC、CD的中垂线,∴AB=AC=AD,∴B、C、D在以A为圆心,AB为半径的圆上,∵∠CBD=30°,∴∠DAC=2∠DBC=60°,∵AF⊥CD,CF=DF,∴∠DAF=∠CAF=30°,∴∠ADC=60°,∵AB=AC,BE=CE,∴∠BAE=∠CAE,又∵∠EAC=∠EAF-∠CAF=80°-30°=50°,∴∠ABC=∠ACE=90°-50°=40°.故答案为:40°,60°.【点睛】本题主要考查了圆周角定理,线段垂直平分线的性质,等腰三角形的性质,根据题意得到B、C、D在以A为圆心,AB为半径的圆上是解题的关键.例4.(2022·广东·汕头市一模)如图,在△ABC中,∠C=90°,AC=8,AB=10,D是AC上一点,且CD =3,E是BC边上一点,将△DCE沿DE折叠,使点C落在点F处,连接BF,则BF的最小值为.【答案】35-3##-3+35【分析】先由折叠判断出F的运动轨迹是为以D为圆心,CD的长度为半径的圆,当B、D、F共线且F在B、D之间时BF最小,根据勾股定理及圆的性质求出此时BD、BF的长度即可.【详解】解:由折叠知,F点的运动轨迹为:以D为圆心,CD的长度为半径的圆,如图所示,可知,当点B、D、F共线,且F在B、D之间时,BF取最小值,∵∠C=90°,AC=8,AB=10,∴BC=6,在Rt△BCD中,由勾股定理得:BD=CD2+BC2=32+62=35,∴BF=BD-DF=35-3,故答案为:35-3.【点睛】本题考查了折叠的性质、圆的性质、勾股定理解直角三角形的知识,该题涉及的最值问题属于中考常考题型,根据折叠确定出F点运动轨迹是解题关键.模型2、定边对直角模型(直角对直径)固定线段AB 所对动角∠C 恒为90°,则A 、B 、C 三点共圆,AB 为直径寻找隐圆技巧:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.例1.(2022·湖北·武汉九年级阶段练习)如图,AB 是⊙O 的直径,AB =4,C 为AB的三等分点(更靠近A 点),点P 是⊙O 上一个动点,取弦AP 的中点D ,则线段CD 的最大值为.【答案】3+1【分析】如图,连接OD ,OC ,首先证明点D 的运动轨迹为以AO 为直径的⊙K ,连接CK ,当点D 在CK 的延长线上时,CD 的值最大,利用勾股定理求出CK 即可解决问题.【详解】解:如图,连接OD ,OC ,∵AD =DP ,∴OD ⊥PA ,∴∠ADO =90°,∴点D 的运动轨迹为以AO 为直径的⊙K ,连接CK ,AC ,当点D 在CK 的延长线上时,CD 的值最大,∵C 为AB的三等分点,∴∠AOC =60°,∴△AOC 是等边三角形,∴CK ⊥OA ,在Rt △OCK 中,∵∠COA =60°,OC =2,OK =1,∴CK =OC 2-OK 2=3,∵DK =12OA =1,∴CD =3+1,∴CD 的最大值为3+1,故答案为:3+1.【点睛】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识,解题的关键是正确寻找点D 的运动轨迹,学会构造辅助圆解决问题.例2.(2022·山东泰安·中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52B.125C.13-32D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的园上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的园上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.例3.(2022·内蒙古·中考真题)如图,⊙O 是△ABC 的外接圆,AC 为直径,若AB =23,BC =3,点P 从B 点出发,在△ABC 内运动且始终保持∠CBP =∠BAP ,当C ,P 两点距离最小时,动点P 的运动路径长为.【答案】33π.【分析】根据题中的条件可先确定点P 的运动轨迹,然后根据三角形三边关系确定CP 的长最小时点P 的位置,进而求出点P 的运动路径长.【详解】解:∵AC 为⊙O 的直径,∴∠ABC =90°.∴∠ABP +∠PBC =90°.∵∠PAB =∠PBC ,∴∠PAB +∠ABP =90°.∴∠APB =90°.∴点P 在以AB 为直径的圆上运动,且在△ABC 的内部,如图,记以AB 为直径的圆的圆心为O 1,连接O 1C 交⊙O 1于点P ,连接O 1P ,CP .∵CP ≥O 1C -O 1P ,∴当点O 1,P ,C 三点共线时,即点P 在点P 处时,CP 有最小值,∵AB =23∴O 1B =3在Rt ΔBCO 1中,tan ∠BO 1C =BC O 1B =33= 3.∴∠BO1C =60°.∴BP =60π×3180=33π.∴.C ,P 两点距离最小时,点P 的运动路径长为33π.【点睛】本题主要考查了直径所对圆周角是直角,弧长公式,由锐角正切值求角度,确定点P 的路径是解答本题的关键.模型3、定边对定角模型(定弦定角模型)固定线段AB 所对同侧动角∠P =∠C ,则A 、B 、C 、P 四点共圆根据圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角都相.寻找隐圆技巧:AB 为定值,∠P 为定角,则P 点轨迹是一个圆.例1.(2021·广东·中考真题)在△ABC 中,∠ABC =90°,AB =2,BC =3.点D 为平面上一个动点,∠ADB =45°,则线段CD 长度的最小值为.【答案】5-2【分析】由已知∠ADB =45°,AB =2,根据定角定弦,可作出辅助圆,由同弧所对的圆周角等于圆心角的一半可知,点D 在以O 为圆心OB 为半径的圆上,线段CD 长度的最小值为CO -OD .【详解】如图:以12AB 为半径作圆,过圆心O 作ON ⊥AB ,OM⊥BC ,以O 为圆心OB 为半径作圆,则点D 在圆O 上,∵∠ADB =45°∴∠AOB =90°∵AB =2AN =BN =1∴AO =12+12=2∵ON =OM =12AB =1,BC =3∴OC =12+(3-1)2=5∴CO -OD =5-2线段CD 长度的最小值为:5-2.故答案为:5-2.【点睛】本题考查了圆周角与圆心角的关系,圆外一点到圆上的线段最短距离,勾股定理,正确的作出图形是解题的关键.例2.(2022·浙江湖州·中考真题)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD 中,M ,N 分别是AB ,BC 上的格点,BM =4,BN =2.若点P 是这个网格图形中的格点,连接PM ,PN ,则所有满足∠MPN =45°的△PMN 中,边PM 的长的最大值是()A.42B.6C.210D.35【答案】C 【分析】根据同弧所对的圆周角等于所对圆心角的一半,过点M 、N 作以点O 为圆心,∠MON =90°的圆,则点P 在所作的圆上,观察圆O 所经过的格点,找出到点M 距离最大的点即可求出.【详解】作线段MN 中点Q ,作MN 的垂直平分线OQ ,并使OQ =12MN ,以O 为圆心,OM 为半径作圆,如图,因为OQ 为MN 垂直平分线且OQ =12MN ,所以OQ =MQ =NQ ,∴∠OMQ =∠ONQ =45°,∴∠MON =90°,所以弦MN 所对的圆O 的圆周角为45°,所以点P 在圆O 上,PM 为圆O 的弦,通过图像可知,当点P 在P 位置时,恰好过格点且P M 经过圆心O ,所以此时P M 最大,等于圆O 的直径,∵BM =4,BN =2,∴MN =22+42=25,∴MQ =OQ =5,∴OM =2MQ =2×5=10,∴P M =2OM =210,故选C .【点睛】此题考查了圆的相关知识,熟练掌握同弧所对的圆周角相等、直径是圆上最大的弦,会灵活用已知圆心角和弦作圆是解题的关键.例3.(2022·广西贵港·中考真题)如图,在边长为1的菱形ABCD 中,∠ABC =60°,动点E 在AB 边上(与点A 、B 均不重合),点F 在对角线AC 上,CE 与BF 相交于点G ,连接AG ,DF ,若AF =BE ,则下列结论错误的是()A.DF =CEB.∠BGC =120°C.AF 2=EG ⋅ECD.AG 的最小值为223【答案】D 【分析】先证明△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,得DF =CE ,判断A 项答案正确,由∠GCB +∠GBC =60゜,得∠BGC =120゜,判断B 项答案正确,证△BEG ∽△CEB 得BE GE=CE BE ,即可判断C 项答案正确,由∠BGC =120°,BC =1,得点G 在以线段BC 为弦的弧BC 上,易得当点G 在等边△ABC 的内心处时,AG 取最小值,由勾股定理求得AG =33,即可判断D 项错误.【详解】解:∵四边形ABCD 是菱形,∠ABC =60°,∴AB =AD =BC =CD ,∠BAC =∠DAC =12∠BAD =12×(180°-∠ABC )=60°=∠ABC ,∴△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,∴DF =CE ,故A 项答案正确,∠ABF =∠BCE ,∵∠ABC =∠ABF +∠CBF =60゜,∴∠GCB +∠GBC =60゜,∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜,故B 项答案正确,∵∠ABF =∠BCE ,∠BEG =∠CEB ,∴△BEG ∽△CEB ,∴BE GE=CE BE ,∴BE 2=GE ∙CE ,∵AF =BE ,∴AF 2=GE ∙CE ,故C 项答案正确,∵∠BGC =120°,BC =1,点G 在以线段BC 为弦的弧BC 上,∴当点G 在等边△ABC 的内心处时,AG 取最小值,如下图,∵△ABC 是等边三角形,BC =1,∴BF ⊥AC ,AF =12AC =12,∠GAF =30゜,∴AG =2GF ,AG 2=GF 2+AF 2,∴AG 2=12AG 2+12 2,解得AG =33,故D 项错误,故应选:D 【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理,熟练掌握菱形的性质是解题的关键.模型4、四点共圆模型(对角互补模型与等弦对等角)1)若平面上A 、B 、C 、D 四个点满足∠ABC +∠ADC =180°,则A 、B 、C 、D 四点共圆.条件:1)四边形对角互补;2)四边形外角等于内对角.2)若平面上A、B、C、D四个点满足∠ADB=∠ACB,则A、B、C、D四点共圆.条件:线段同侧张角相等.例1.(2022·广东·九年级专题练习)如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD =2,E是AC的中点,连接DE,则线段DE长度的最小值为.【答案】3-1【分析】先判断出四边形ABCD是圆内接四边形,得到∠ACD=∠ABD=30°,根据题意知点E在以FG为直径的⊙P上,连接PD交⊙P于点E,此时DE长度取得最小值,证明∠APD=90°,利用含30度角的直角三角形的性质求解即可.【详解】解:∵∠BAD=∠BCD=90°,∴四边形ABCD是圆内接四边形,∴∠ACD=∠ABD=30°,∴∠ADB=60°,∵AD=2,∴BD=2AD=4,分别取AB、AD的中点F、G,并连接FG,EF,EG,∵E是AC的中点,∴EF∥BC,EG∥CD,∴∠AEF=∠ACB,∠AEG=∠ACD,∴∠AEF+∠AEG=∠ACB+∠ACD=90°,即∠FEG=90°,∴点E在以FG为直径的⊙P上,如图:当点E恰好在线段PD上,此时DE的长度取得最小值,连接PA,BD=2,∴∵F、G分别是AB、AD的中点∴FG∥BD,FG=12∠ADB=∠AGF=60°,∵PA=PG,∴△APG是等边三角形,∴∠APG=60°,∵PG=GD=GA,且∠AGF=60°,∴∠GPD=∠GDP=30°,∴∠APD=90°,∴PD=AD2-PA2=22-12=3,∴DE长度的最小值为(3-1).故答案为:(3-1).【点睛】本题考查了圆周角定理,圆内接四边形的性质,等边三角形的判定和性质,含30度角的直角三角形的性质,得到点E 在以FG 为直径的⊙P 上是解题的关键.例2.(2022陕西中考模拟)如图,在等边△ABC 中,AB =6,点P 为AB 上一动点,PD ⊥BC 于点D ,PE ⊥AC 于点E ,则DE 的最小值为.【答案】92【详解】如解图,∵∠PEC =∠PDC =90°,故四边形PDCE 对角互补,故P 、D 、C 、E 四点共圆,∠EOD =2∠ECD =120°,故ED =3R ,要使得DE 最小,则要使圆的半径R 最小,故直径PC 最小,当CP ⊥AB 时,PC 最短为33,故R =332,故DE =3R =3×332=92.例3.(2022江苏九年级期末)如图,在Rt △ABC 中,∠ACB =90°,BC =3,AC =4,点P 为平面内一点,且∠CPB =∠A ,过C 作CQ ⊥CP 交PB 的延长线于点Q ,则CQ 的最大值为()A.175B.154C.455D.655【答案】B【分析】根据题意可得A 、B 、C 、P 四点共圆,由AA 定理判定三角形相似,由此得到CQ 的值与PC 有关,当PC 最大时CQ 即取最大值.【详解】解:∵在Rt △ABC 中,∠ACB =90°,∠CPB =∠A ,BC =3,AC =4∴A 、B 、C 、P 四点共圆,AB 为圆的直径,AB =BC 2+AC 2=5∵CQ ⊥CP ∴∠ACB =∠PCQ =90°∴△ABC ∽△PQC∴AC BC =PC CQ ,43=PC CQ,即CQ =34PC ∴当PC 取得最大值时,CQ 即为最大值∴当PC =AB =5时,CQ 取得最大值为154故选:B .【点睛】本题考查相似三角形的判定和性质以及四点共圆,掌握同圆或等圆中,同弧所对的圆周角相等确定四点共圆,利用相似三角形性质得到线段间等量关系是解题关键.课后专项训练例4.(2022·江苏无锡·中考真题)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.【答案】 80 4-3##-3+4【分析】利用SAS证明△BDC≌△AEC,得到∠DBC=∠EAC=20°,据此可求得∠BAF的度数;利用全等三角形的性质可求得∠AFB=60°,推出A、B、C、F四个点在同一个圆上,当BF是圆C的切线时,即当CD⊥BF时,∠FBC最大,则∠FBA最小,此时线段AF长度有最小值,据此求解即可.【详解】解:∵△ABC和△DCE都是等边三角形,∴AC=BC,DC=EC,∠BAC=∠ACB=∠DCE =60°,∴∠DCB+∠ACD=∠ECA+∠ACD=60°,即∠DCB=∠ECA,在△BCD和△ACE中,CD=CE∠BCD=∠ACE BC=AC,∴△ACE≌△BCD(SAS),∴∠EAC=∠DBC,∵∠DBC=20°,∴∠EAC=20°,∴∠BAF=∠BAC+∠EAC=80°;设BF与AC相交于点H,如图:∵△ACE≌△BCD∴AE=BD,∠EAC=∠DBC,且∠AHF=∠BHC,∴∠AFB=∠ACB=60°,∴A、B、C、F四个点在同一个圆上,∵点D在以C为圆心,3为半径的圆上,当BF是圆C的切线时,即当CD⊥BF时,∠FBC最大,则∠FBA最小,∴此时线段AF长度有最小值,在Rt△BCD中,BC=5,CD=3,∴BD=52-32=4,即AE=4,∴∠FDE=180°-90°-60°=30°,∵∠AFB=60°,∴∠FDE=∠FED=30°,∴FD=FE,过点F作FG⊥DE于点G,∴DG=GE=32,∴FE=DF=DGcos30°=3,∴AF=AE-FE=4-3,故答案为:80;4-3.【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.例5.(2021·湖北鄂州·中考真题)如图,Rt △ABC 中,∠ACB =90°,AC =23,BC =3.点P 为ΔABC 内一点,且满足PA 2+PC 2=AC 2.当PB 的长度最小时,ΔACP 的面积是()A.3B.33C.334D.332【答案】D 【分析】由题意知∠APC =90°,又AC 长度一定,则点P 的运动轨迹是以AC 中点O 为圆心,12AC 长为半径的圆弧,所以当B 、P 、O 三点共线时,BP 最短;在Rt ΔBCO 中,利用勾股定理可求BO 的长,并得到点P 是BO 的中点,由线段长度即可得到ΔPCO 是等边三角形,利用特殊Rt ΔAPC 三边关系即可求解.【详解】解:∵PA 2+PC 2=AC 2∴∠APC =90°取AC 中点O ,∴AO =PO =CO =12AC 点P 的轨迹为以O 为圆心,12AC 长为半径的圆弧上由题意知:当B 、P 、O 三点共线时,BP 最短∵CO =12AC =12×23=3,BC =3∴BO =BC 2+CO 2=23∴BP =BO -PO =3∴点P 是BO 的中点∴在Rt ΔBCO 中,CP =12BO =3=PO ∴ΔPCO 是等边三角形∴∠ACP =60°∴在Rt ΔAPC 中,AP =CP ×tan60°=3∴S ΔAPC =12AP ×CP =3×32=332.【点睛】本题主要考察动点的线段最值问题、点与圆的位置关系和隐形圆问题,属于动态几何综合题型,中档难度.解题的关键是找到动点P 的运动轨迹,即隐形圆.例6.(2020·西藏中考真题)如图,在矩形ABCD 中,E 为AB 的中点,P 为BC 边上的任意一点,把沿PE 折叠,得到,连接CF .若AB =10,BC =12,则CF 的最小值为.【答案】8【分析】点F 在以E 为圆心、EA 为半径的圆上运动,当E 、F 、C 共线时时,此时FC 的值最小,根据勾股定理求出CE ,再根据折叠的性质得到BE =EF =5即可.【详解】如图所示,点F 在以E 为圆心EA 为半径的圆上运动,当E 、F 、C 共线时时,此时CF 的值最小,根据折叠的性质,△EBP ≌△EFP ,∴EF ⊥PF ,EB =EF ,∵E 是AB 边的中点,AB =10,∴AE =EF =5,∵AD =BC =12,∴CE ===13,∴CF =CE -EF =13-5=8.故答案为8.【点睛】本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,灵活应用相关知识是解答本题的关键.例7.(2022·北京·清华附中九年级阶段练习)如图,四边形ABCD 中,DA =DB =DC ,∠BDC =72°,则∠BAC 的度数为.【答案】36°##36度【分析】根据题意可得A ,B ,C 三点在以D 为圆心DA 为半径的圆上,根据圆周角定理即可求解.【详解】解:如图,∵DA =DB =DC ,∴A ,B ,C 三点在以D 为圆心DA 为半径的圆上,∵∠BDC =72°,CB =CB ∴∠BAC =12∠BDC =36°.故答案为:36°.【点睛】本题考查了圆周角定理,掌握圆周角定理是解题的关键.例8.(2022·河北·唐山九年级阶段练习)如图所示,在四边形ABCD 中,AB =AC =AD ,∠BAC =26°,∠CAD =74°,则∠BCD =°,∠DBC °.【答案】 130 37【分析】根据题意可得点B,C,D在以A为圆心的圆上,根据圆周角定理求得∠BDC,∠DBC,根据三角形内角和定理求得∠BCD.【详解】∵AB=AC=AD,∴点B,C,D在以A为圆心的圆上,∵∠BAC=26°∴∠BDC=12∠BAC=13°,∵∠CAD=74°,∴∠DBC=12∠CAD=37°.∴∠BCD=180-∠DBC-∠BDC=180°-13°-37°=130°故答案为:130,37【点睛】此题考查了圆周角定理,三角形内角和定理,综合运用以上知识是解题的关键.例9.(2022·安徽蚌埠·一模)如图,Rt△ABC中,AB⊥BC,AB=8,BC=6,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为()A.325B.2C.213-6D.213-4【答案】D【分析】结合题意推导得∠APB=90°,取AB的中点O,以点O为圆心,AB为直径作圆,连接OP;根据直角三角形斜边中线的性质,得OP=OA=OB=12AB=4;根据圆的对称性,得点P在以AB为直径的⊙O上,根据两点之间直线段最短的性质,得当点O、点P、点C三点共线时,PC最小;根据勾股定理的性质计算得OC,通过线段和差计算即可得到答案.【详解】∵∠ABC=90°,∴∠ABP+∠PBC=90°,∵∠PAB=∠PBC,∴∠BAP+∠ABP=90°,∴∠APB=90°,取AB的中点O,以点O为圆心,AB为直径作圆,连接OP,∴OP=OA=OB=12AB=4∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,当点O、点P、点C三点共线时,PC最小在Rt△BCO中,∵∠OBC=90°,BC=6,OB=4,∴OC=BO2+BC2=42+62=213,∴PC=OC-OP=213-4∴PC最小值为213-4故选:D.【点睛】本题考查了两点之间直线段最短、圆、勾股定理、直角三角形斜边中线的知识;解题的关键是熟练掌握圆的对称性、两点之间直线段最短、直角三角形斜边中线的性质,从而完成求解.例10.(2022·成都市·九年级专题练习)如图,在Rt ΔABC 中,∠ACB =Rt ∠,AC =8cm ,BC =3cm .D 是BC 边上的一个动点,连接AD ,过点C 作CE ⊥AD 于E ,连接BE ,在点D 变化的过程中,线段BE 的最小值是()A.1B.3C.2D.5【答案】A 【分析】由∠AEC =90°知,点E 在以AC 为直径的⊙M 的CN 上(不含点C 、可含点N ),从而得BE最短时,即为连接BM 与⊙M 的交点(图中点E ′点),BE 长度的最小值BE ′=BM -ME ′.【详解】如图,由题意知,∠AEC =90°,∴E 在以AC 为直径的⊙M 的CN上(不含点C 、可含点N ),∴BE 最短时,即为连接BM 与⊙M 的交点(图中点E ′点),在Rt ΔBCM 中,BC =3cm ,CM =12AC =4cm ,则BM =BC 2+CM 2=5cm .∵ME ′=MC =4cm ,∴BE 长度的最小值BE ′=BM -ME ′=1cm ,故选:A .【点睛】本题主要考查了勾股定理,圆周角定理,三角形的三边关系等知识点,难度偏大,解题时,注意辅助线的作法.例11.(2022·广东·九年级课时练习)如图,△ACB 中,CA =CB =4,∠ACB =90°,点P 为CA 上的动点,连BP ,过点A 作AM ⊥BP 于M .当点P 从点C 运动到点A 时,线段BM 的中点N 运动的路径长为()A.22πB.2πC.3πD.2π【答案】A【详解】解:设AB 的中点为Q ,连接NQ ,如图所示:∵N 为BM 的中点,Q 为AB 的中点,∴NQ 为△BAM 的中位线,∵AM ⊥BP ,∴QN ⊥BN ,∴∠QNB =90°,∴点N 的路径是以QB 的中点O 为圆心,14AB 长为半径的圆交CB 于D 的QD,∵CA =CB =4,∠ACB =90°,∴AB =2CA =42,∠QBD =45°,∴∠DOQ =90°,∴QD 为⊙O 的14周长,∴线段BM 的中点N 运动的路径长为:90π×14×42180=22π,故选:A .例12.(2022·全国·九年级专题练习)如图,在△ABC 中,∠ACB =90°,AC =BC ,AB =4cm ,CD 是中线,点E 、F 同时从点D 出发,以相同的速度分别沿DC 、DB 方向移动,当点E 到达点C 时,运动停止,直线AE 分别与CF 、BC 相交于G 、H ,则在点E 、F 移动过程中,点G 移动路线的长度为()A.2B.πC.2πD.22π【答案】D【详解】解:如图,∵CA =CB ,∠ACB =90°,AD =DB ,∴CD ⊥AB ,∴∠ADE =∠CDF =90°,CD =AD =DB ,在△ADE 和△CDF 中AD =CD∠ADE =∠CDF DE =DF,∴△ADE ≌△CDF (SAS ),∴∠DAE =∠DCF ,∵∠AED =∠CEG ,∴∠ADE =∠CGE =90°,∴A 、C 、G 、D 四点共圆,∴点G 的运动轨迹为弧CD ,∵AB =4,AB =2AC ,∴AC =22,∴OA =OC =2,∵DA =DC ,OA =OC ,∴DO ⊥AC ,∴∠DOC =90°,∴点G 的运动轨迹的长为90π×2180=22π.故选:D .例13.(2022·山西·九年级课时练习)如图,在等腰Rt ∆ABC 中,AC =BC =42,点P 在以斜边AB 为直径的半圆上,M 为PC 的中点.当点P 沿半圆从点A 运动至点B 时,点M 运动的路径长是()A.22π+4B.2πC.42+2D.4π【答案】B 【详解】分析:取AB 的中点O 、AC 的中点E 、BC 的中点F ,连结OC 、OP 、OM 、OE 、OF 、EF ,如图,利用等腰直角三角形的性质得到AB =2BC =8,则OC =12AB =4,OP =12AB =4,再根据等腰三角形的性质得OM ⊥PC ,则∠CMO =90°,于是根据圆周角定理得到点M 在以OC 为直径的圆上,由于点P 点在A 点时,M 点在E 点;点P 点在B 点时,M 点在F 点,则利用四边形CEOF 为正方得到EF =OC =4,所以M 点的路径为以EF 为直径的半圆,然后根据圆的周长公式计算点M 运动的路径长.详解:取AB 的中点O 、AC 的中点E 、BC 的中点F ,连结OC 、OP 、OM 、OE 、OF 、EF ,如图,∵在等腰Rt △ABC 中,AC =BC =42,∴AB =2BC =8,∴OC =12AB =4,OP =12AB =4. ∵M 为PC 的中点,∴OM ⊥PC ,∴∠CMO =90°,∴点M 在以OC为直径的圆上,点P 点在A 点时,M 点在E 点;点P 点在B 点时,M 点在F 点,易得四边形CEOF 为正方形,EF =OC =4,∴M 点运动的路径为以EF 为直径的半圆,∴点M 运动的路径长=12•4π=2π. 故选B .点睛:本题考查了轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用等腰三角形的性质和圆周角定理确定M 点的轨迹为以EF 为直径的半圆.例14.(2022·山东·烟台九年级期中)如图,平面直角坐标系中,点A 、B 坐标分别为(3,0)、(0,4),点C 是x 轴正半轴上一点,连接BC .过点A 垂直于AB 的直线与过点C 垂直于BC 的直线交于点D ,连接BD ,则sin ∠BDC 的值是.【答案】45【分析】根据图形的特点证明∠BDC =∠BAO ,故可出sin ∠BDC 的值.【详解】∵BA ⊥AD ,BC ⊥CD ∴∠BAD =∠BCD =90°∴A 、B 、C 、D 四点共圆∴∠BDA =∠BCA∵∠BDA +∠DBA =∠BCA +∠CBO =90°∴∠DBA =∠CBO∴∠DBA -∠CBA =∠CBO -∠CBA 即∠DBC =∠ABO又∠DBC +∠BDC =∠ABO +∠BAO =90°∴∠BDC =∠BAO∵点A 、B 坐标分别为(3,0)、(0,4),∴BO =4,OA =3,AB =42+32=5∴sin ∠BAO =BO AB=45∴sin ∠BDC =45故答案为:45.【点睛】此题主要考查三角函数的求解,解题的关键是熟知四点共圆的性质、勾股定理及三角函数的求解方法.例15.(2022·湖北·九年级期中)如图,△ABC 中,AC =BC =6,∠ACB =90°,若D 是与点C 在直线AB 异侧的一个动点,且∠ADB =45°,则CD 的最大值为.【答案】62+6##6+62【分析】以AB 为底边,在AB 的下方作等腰三角形AOB ,则OA =AC =6,根据∠ADB =45°,点与圆的位置关系可知,点D 在以O 为圆心,6为半径的圆上运动,当CD 过圆心时,CD 最大,根据OA =AC =6,∠CAO =90°,利用勾股定理可求出CO 的长,即可得.【详解】解:如图所示,以AB 为底边,在AB 的下方作等腰三角形AOB ,则OA =AC =6,∵∠ADB =45°,∴点D 在以O 为圆心,6为半径的圆上运动,当CD 过圆心时,CD 最大,∵OA =AC =6,∠CAO =90°,∴CO =62+62=62,∴CD 的最大值为:62+6,故答案为:62+6.【点睛】本题考查了等腰直角三角形的性质,圆周角定理,勾股定理,解题的关键是理解题意,掌握这些知识点.例16.(2022·浙江·九年级专题练习)如图,AB 是Rt △ABC 和Rt △ABD 的公共斜边,AC =BC ,∠BAD =32°,E 是AB 的中点,联结DE 、CE 、CD ,那么∠ECD =°.【答案】13【分析】先证明A 、C 、B 、D 四点共圆,得到∠DCB 与∠BAD 的是同弧所对的圆周角的关系,得到∠DCB 的度数,再证∠ECB =45°,得出结论.【详解】解:∵AB 是Rt △ABC 和Rt △ABD 的公共斜边,E 是AB 中点,∴AE =EB =EC =ED ,∴A 、C 、B 、D 在以E 为圆心的圆上,∵∠BAD =32°,∴∠DCB =∠BAD =32°,又∵AC =BC ,E 是Rt △ABC 的中点,∴∠ECB =45°,∴∠ECD =∠ECB -∠DCB =13°.故答案为:13.【点睛】本题考查直角三角形的性质、等腰三角形性质、圆周角定理和四点共圆问题,综合性较强.例17.(2022·黑龙江·九年级阶段练习)如图,等边△ABC 中,D 在BC 上,E 在AC 上,BD =CE ,连BE 、AD 交于F ,T 在EF 上,且DT =CE ,AF =50,TE =16,则FT =.【答案】17【分析】用“SAS ”可判定△ABD ≌△BCE ,得到∠AFE =60°,延长FE 至点G ,使得FG =FA ,连AG ,AT ,得到△AFG 是等边三角形,证明A 、B 、D 、T 四点共圆,设法证明△FAT ≌△GAE (ASA ),即可求得答案.【详解】∵△ABC 为等边三角形,∴AB =AC =BC ,∠ABD =∠BCE =60°,在△ABD 和△BCE 中,AB =BC∠ABD =∠BCE =60°BD =CE,∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,∵∠ADC =∠CBE +∠BFD =∠BAD +∠B ,∴∠BFD =∠B =∠AFE =60°;延长FE 至点G ,使得FG =FA ,连AG ,AT ,∵∠AFE =60°,∴△AFG 是等边三角形,∴AG =AF =FG =50,∠AGF =∠FAG =60°,∵∠BAF +∠EAF =∠CAG +∠EAF =60°,∴∠BAF =∠CAG ,∵DT =CE ,∴∠DBT =∠BTD ,∵∠BAD =∠CBE ,∴∠BAD =∠BTD ,∴A 、B 、D 、T 四点共圆,∴∠BAD =∠DAT ,∴∠FAT =∠GAE ,在△FAT 和△GAE 中,∠FAT =∠GAEAF =AG ∠AFG =∠AGF =60°,∴△FAT ≌△GAE (ASA ),∴FT =GE ,∵FG =50,TE =16,∴FT =12(FG -TE )=17.故答案为:17.【点睛】本题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,圆周角定理等,作出辅助线,判断出△FAT ≌△GAE 是解本题的关键.例18.(2020·四川成都·二模)如图,在矩形ABCD 中,AB =9,AD =6,点O 为对角线AC 的中点,点E 在DC 的延长线上且CE =1.5,连接OE ,过点O 作OF ⊥OE 交CB 延长线于点F ,连接FE 并延长交AC 的延长线于点G ,则FG OG=.【答案】455【分析】作OM ⊥CD 于M ,ON ⊥BC 于N ,根据三角形中位线定理分别求出OM 、ON ,根据勾股定理求出OE ,根据相似三角形的性质求出FN ,得到FC 的长,证明△GFC ∽△GOE ,根据相似三角形的性质列出比例式,代入计算得到答案.【详解】解:作OM ⊥CD 于M ,ON ⊥BC 于N ,∵四边形ABCD 为矩形,∴∠D =90°,∠ABC =90°,∴OM ∥AD ,ON ∥AB ,∵点O 为AC 的中点∴OM =12AD =3,ON =12AB =4.5,CM =4.5,CN =3,∵CE =1.5,∴ME =CM +CE =6在Rt △OME 中,OE =OM 2+ME 2=32+62=35,∵∠MON =90°,∠EOF =90°,∴∠MOE +∠NOE =∠NOF +∠NOE =90°,∴∠MOE =∠NOF ,又∠OME =∠ONF =90°,∴△OME ∽△ONF ,∴OM ON=ME FN ,即34.5=6FN ,解得,FN =9,∴FC =FN +NC =12,∵∠FOE =∠FCE =90°,∴F 、O 、C 、E 四点共圆,∴∠GFC =∠GOE ,又∠G =∠G ,∴△GFC ∽△GOE ,∴FG OG =FC OE =1235=455,故答案为:455.【点睛】本题考查了矩形的性质、相似三角形的判定和性质、圆周角定理的应用,掌握相似三角形的判定定理和性质定理是解题的关键.例19.(2022·成都市锦江区嘉祥外国语学校九年级阶段练习)如图,在△ABC 中,AC =6,BC =83,∠ACB =60°,过点A 作BC 的平行线l ,P 为直线l 上一动点,⊙O 为△APC 的外接圆,直线BP 交⊙O 于E 点,则AE 的最小值为.【答案】2【分析】如图,连接CE .首先证明∠BEC =120°,根据定弦定角,可得点E 在以M 为圆心,MB 为半径的BC 上运动,连接MA 交BC 于E ′,此时AE ′的值最小.【详解】解:如图,连接CE .∵AP ∥BC ,∴∠PAC =∠ACB =60°,∴∠CEP =∠CAP=60°,∴∠BEC =120°,∵BC =83,为定值,则点E 的运动轨迹为一段圆弧如图,点E 在以M 为圆心,MB 为半径的BC 上运动,过点M 作MN ⊥BC∴⊙M 中优弧BC 度数为2∠BEC =240°,则劣弧BC 度数为120°∴△BMC 是等腰三角形,∠BMC =120°,∵∠BCM =30°,BC =83,MB =MC∴BN =BM 2-MN 2==3MN =12BC =43∴MB =MC =8,∴连接MA 交BC 于E ′,此时AE ′的值。
隐圆模型(解析版)

隐圆模型(解析版)隐圆模型触发隐圆模型的类型1.动点定长模型:如果P是动点,但AB=AC=AP,则B、C、P三点共圆,以A为圆心,AB为半径。
2.直角圆周角模型:固定线段AB所对动角∠XXX为90°,则A、B、C三点共圆,以AB为直径。
3.定弦定角模型:固定线段AB所对动角∠P为定值,则点P运动轨迹为过A、B、C三点的圆。
原理:在圆A中,AB=AC=AP。
常常通过全等或相似证明出定长。
4.四点共圆模型①:如果动角∠A+动角∠C=180°,则A、B、C、D四点共圆。
原理:圆内接四边形对角互补。
注意:点A与点C在线段AB异侧。
5.四点共圆模型②:固定线段AB所对同侧动角∠P=∠C,则A、B、C、P四点共圆。
原理:弦AB所对同侧圆XXX相等。
注意:点P与点C需在线段AB同侧。
圆中旋转最值问题条件:线段AB绕点O旋转一周,点M是线段AB上的一动点,点C是定点。
1.求CM最小值与最大值。
2.求线段AB扫过的面积。
3.求△XXX的最大值与最小值。
作法:建立三个同心圆,作OM⊥AB,B、A、M运动路径分别为大圆、中圆、小圆。
结论:① CM1最小,CM3最大。
②线段AB扫过面积为大圆与小圆组成的圆环面积。
③△ABC最小值以AB为底,CM1为高;最大值以AB 为底,CM2为高。
典题探究例题1:在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△XXX沿MN所在直线翻折得到△A`MN,连接A`C,则A`C长度的最小值是多少?分析:考虑△XXX沿MN所在直线翻折得到△A’MN,可得MA’=MA=1,所以A’轨迹是以M点为圆心,MA为半径的圆弧。
连接CM,与圆的交点即为所求的A’,此时A’C的值最小。
构造直角△MHC,勾股定理求CM,再减去A’M即可,答案为7-1.注:删除了明显有问题的段落,对每段话进行了小幅度改写,使其更加简洁明了。
题目格式已经整理好了,以下是改写后的文章:在直角三角形ABC中,角C为90度,AC等于6,BC等于8.点F在边AC上,且CF等于2.点E为边BC上的动点。
初三隐圆问题的4种模型

初三隐圆问题的4种模型咱来唠唠初三隐圆问题的那四种模型哈。
一、定点定长模型你就想象有这么一个点,它像个圆心一样,然后有个固定的长度,就好比是这个圆的半径。
不管这个点怎么动来动去,只要到某个点的距离始终是这个固定长度,那这些点就能构成一个隐圆。
比如说,一个点A到另一个点B的距离始终是5厘米,那点A运动的轨迹就是一个以B为圆心、5厘米为半径的圆,只不过这个圆有时候不是明明白白画出来给你的,得你自己去发现,这就是定点定长模型的隐圆啦。
二、定弦定角模型这个就像是有一根固定的弦,就像琴弦一样,在这根弦的同侧,有一个固定大小的角。
你想啊,不管这个角的顶点在弦的同侧怎么挪,只要这个角的大小不变,那这个顶点的运动轨迹就是一个圆。
比如说,有一条线段AB,然后在AB同侧有个角∠C,∠C始终是30°,那点C就会在一个隐圆上运动。
就好比是这个角被这根弦给“牵制”着,只能在特定的圆上活动,这就是定弦定角模型的妙处。
三、直角对直径模型这个就特别有趣啦。
你知道圆的直径所对的圆周角是直角吧?反过来,如果有一个直角,它的顶点在运动,但是这个直角的两条边分别经过两个定点,那这个直角顶点的运动轨迹就是一个圆,而且这个圆的直径就是这两个定点所连成的线段。
就好像这个直角被这两个定点“绑架”了,只能在以这两点连线为直径的圆上晃悠,这就是直角对直径模型的隐圆,发现这个模型就像发现了一个隐藏的小秘密一样。
四、四点共圆模型这个模型呢,就是有四个点,这四个点要是满足一些特殊的条件,那它们就在同一个圆上。
比如说,如果四边形的对角互补,那这个四边形的四个顶点就在同一个圆上。
就好像这四个点商量好了似的,它们之间有着一种神秘的联系,让它们能够共同在一个隐圆上存在。
还有一种情况就是,如果一个四边形的一个外角等于它的内对角,那这四个点也共圆。
这就像是这四个点之间有一种默契,按照一种特殊的规则就可以确定它们在一个隐圆上啦。
专题16 构造辅助圆(隐圆)解题的几种常见模型-2023年中考数学二轮复习核心考点拓展训练(解析版)

专题16 构造辅助圆(隐圆)解题的几种常见模型(解析版)类型一定点定长模型典例1(威海中考)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )A.68°B.88°C.90°D.112°思路引领:如图,作辅助圆;首先运用圆周角定理证明∠CAD=2∠CBD,∠BAC=2∠BDC,结合已知条件∠CBD=2∠BDC,得到∠CAD=2∠BAC,即可解决问题.解:如图,∵AB=AC=AD,∴点B、C、D在以点A为圆心,以AB的长为半径的圆上;∵∠CBD=2∠BDC,∠CAD=2∠CBD,∠BAC=2∠BDC,∴∠CAD=2∠BAC,而∠BAC=44°,∴∠CAD=88°,故选:B.总结提升:该题主要考查了圆周角定理及其推论等几何知识点及其应用问题;解题的方法是作辅助圆,将分散的条件集中;解题的关键是灵活运用圆周角定理及其推论等几何知识点来分析、判断、推理或解答.针对训练1.(苏州期中)如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD2的值为( )A.14B.15C.18D.12思路引领:作AM⊥BC于点M,AN⊥BD于点N,根据题给条件及等腰三角形的性质证明△ABN≌△BAM,继而求出AN的值,在Rt△ABN中,利用勾股定理求解即可.解:作AM⊥BC于点M,AN⊥BD于点N,∵AC=AB,∴△ABC为等腰三角形,∴AM也是△ABC的中线和角平分线(三线合一),∴∠CAM=∠BAM,∴△ABM≌△ACM,∵AB∥CD,AC=AD,∴∠ADC=∠ACD=∠CAB,∵∠ADB=∠ABD=∠CDB,∴∠ADB=12∠ADC=∠MAB,∴∠MAB=∠DBA,又∵AB=AB,∴△ABN≌△BAM(AAS),∴AN=12BC=12,∵AB=2,∴BN2=AB2﹣AN2=15 4,∴BD2=4BN2=15.故选:B.总结提升:本题考查了梯形的知识,同时涉及了等腰三角形的性质和勾股定理的知识,难度适中,解题关键是正确作出辅助线.2.(2021春•牧野区校级期中)如图,在矩形ABCD中,E为AB的中点,P为BC边上的任意一点,把△PBE 沿PE折叠,得到△PFE,连接CF.若AB=10,BC=12,当CF取最小值时,BP的值等于 .思路引领:点F在以E为圆心EA为半径的圆上运动,当E、F、C共线时时,此时FC的值最小,根据勾股定理求出CE,根据折叠的性质可知BE=EF=5,即可求出CF,再利用勾股定理即可解决问题.解:如图所示,点F在以E为圆心EA为半径的圆上运动,当E、F、C共线时时,此时CF的值最小,根据折叠的性质,△EBP≌△EFP,∴EF⊥PF,EB=EF,∵E是AB边的中点,AB=10,∴AE=EF=5,∵AD=BC=12,∴CE=BE2+BC2=13,∴CF=CE﹣EF=13﹣5=8.由折叠可知:FP=BP,∴CP=BC﹣BP=12﹣BP,在Rt△CFP中,根据勾股定理得:CF2+FP2=CP2,∴82+BP2=(12﹣BP)2,解得BP=10 3.故答案为:10 3.总结提升:本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,熟练掌握折叠的性质是解题的关键.类型二对角互补模型典例2 (2018•汉阳区模拟)如图,在菱形ABCD中,点P是BC边上一动点,P和C不重合,连接AP,AP 的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )A.变大B.先变大后变小C.先变小后变大D.不变思路引领:连接AC交BD于O,连接EO、AG,根据菱形的性质得出∠AOB=90°,AO=CO,求出A、E、G、O四点共圆,得出∠PAG=∠EOB,∠APG=∠PAG,求出∠APG=∠EOB=∠DBC,即可求出答案.解:连接AC交BD于O,连接EO、AG,∵四边形ABCD是菱形,∴∠AOB=90°,∵EG是AP的垂直平分线,∴AG=PG,∠AEG=∠AOB=90°,∴A、E、G、O四点共圆,∴∠PAG=∠EOB,∠APG=∠PAG,∴∠EOG=∠APG,∵四边形ABCD是菱形,∴OA=OC,∵AE=PE,∴OE∥BC,∴∠EOB =∠DBC =12∠ABC ,∵菱形ABCD 固定,∴∠ABC 的度数固定,即∠APG 的度数不变,故选:D .总结提升:本题考查了菱形的性质,线段垂直平分线性质,圆内接四边形性质等知识点,能正确作出辅助线是解此题的关键.变式训练1.(2018•碑林区校级一模)如图,在△ABC 中,∠ACB =120°,AC =BC =2,D 是AB 边上的动点,连接CD ,将△BCD 绕点C 沿顺时针旋转至△ACE ,连接DE ,则△ADE 面积的最大值= .思路引领:设BD 为a ,表示线段AE ,AD ,用a 表示△ADE 的面积表达式,从而利用二次函数的极值属性求出极值.解:设BD 为a∵∠ACB =120°,AC =BC =2∴AB =23∴AD =23―a∵AE =BD ,∠B =∠CAE =30°,BC =AC∴△BDC ≌△AEC (SAS )作EF ⊥AB ,垂足为F在Rt △AEF 中∠FAE =60°,AE =BD =a∴AF =12a ,EF =123a ∴△ADE 的面积=12×(23―a)×123a =―34a 2+32a 即当a =3,△ADE 的面积有最大值为343故答案为343总结提升:本题考查了数形结合的数学思想,将几何问题转化为函数问题,利用函数关系式获得极值.2.(2020•淮阴区模拟)在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2,O为AC的中点,过O作OE⊥OF,OE、OF分别交射线AB,BC于E、F,则EF的最小值为 .思路引领:首先过点O分别作OM⊥AB于M,ON⊥BC于N,易证四边形OMBN为矩形,则OM∥BC,ON∥AB,由直角三角形中30°角性质,可得AC的长,进而求得BC长.又O为AC中点,可求得OM 与ON的长,由勾股定理可得MN的长.又由垂线段最短,可得当OE与OM重合,OF与ON重合时,EF最短.得解.解:∵∠ABC=90°,∠ACB=30°,AB=2.∴AC=2AB=4.过点O分别作OM⊥AB于M,ON⊥BC于N.∵∠B=90°,∴四边形OMBN为矩形,∴OM∥BC,ON∥AB.∴△AOM∽△ACB,△CON∽△CAB,∴OM:CB=OA:CA,ON:AB=OC:AC.∵O为AC中点,则OB=12AC=2=MN,由垂线段最短,可得当OE与OM重合,OF与ON重合时,EF最短.∴EF的最小值为2.故答案为:2.总结提升:本题考查了矩形的判定和性质,相似三角形的判定与性质,勾股定理以及垂线段最短的知识,难度适中,注意数形结合思想的运用.3.如图,在平面直角坐标系xOy中,A(0,2),点P在直线y=33x上,连接AP,过点P作PQ⊥AP,交x轴于点Q,连接AQ.求∠QAP的度数.思路引领:分点P在第三象限、点P在第一象限的线段OH上、点P在第一象限的线段OH的延长线上三种情况,用四点共圆求解.解:①当点P在第三象限时,如图2,由∠QPA=∠QOA=90°,可得Q、P、O、A四点共圆,∴∠PAQ=∠POQ=30°;②当点P在第一象限的线段OH上时,如图3,由∠QPA=∠QOA=90°可得Q、P、O、A四点共圆,∴∠PAQ+∠POQ=180°,又此时∠POQ=150°,∴∠PAQ=180°﹣∠POQ=30°;③当点P在第一象限的线段OH的延长线上时,由∠QPA=∠QOA=90°可得∠APQ+∠AOQ=180°,∴Q、P、O、A四点共圆,∴∠PAQ=∠POQ=30°.总结提升:本题为一次函数综合题,涉及到四点共圆、等腰三角形性质,分类讨论求解是解决此题关键.类型三定边定角模型(1)定边对直角典例3东西湖区模拟)如图,已知A(2,6)、B(8,﹣2),C为坐标轴上一点,且△ABC是直角三角形,则满足条件的C点有( )个.A.6B.7C.8D.9思路引领:过点A作AB的垂线,交x轴于点C1,交y轴于点C2;过点B作AB的垂线,交x轴于点C3,交y轴于点C4;根据直径所对的圆周角为直角,以AB为直径作圆,根据A和B的坐标求出AB的长度,即为圆的直径,可得出半径的长,进而判断得出圆与y轴相切,可得出圆与y轴有1个交点,与x 轴交于2点.所以满足条件的点共有7个.解:分三种情况考虑:①当A为直角顶点时,过A作AC⊥AB,交x轴于点C1,交y轴于点C2,此时满足题意的点为C1,C2;②当B为直角顶点时,过B作BC⊥AB,交x轴于点C3,交y轴于点C4,此时满足题意的点为C3,C4;③当C为直角顶点时,以AB为直径作圆,由A(2,6)、B(8,﹣2),可得此圆与y轴相切,则此圆与y轴有1个交点,与x轴有2个交点,分别为C5,C6,C7.综上,所有满足题意的C有7个.故选:B.总结提升:此题考查了圆周角定理,直角三角形以及坐标与图形性质,利用了分类讨论及数形结合的思想.注意:若△ABC是直角三角形,则它的任意一个顶点都有可能为直角顶点.针对训练1.(2021•内乡县一模)(1)【学习心得】于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC 是圆周角,从而可容易得到∠BDC= °.(2)【问题解决】如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.(3)【问题拓展】如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 5―1 .思路引领:(1)利用同弦所对的圆周角是所对圆心角的一半求解.(2)由A、B、C、D共圆,得出∠BDC=∠BAC,(3)根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG 全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=12AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.解:(1)如图1,∵AB=AC,AD=AC,∴以点A为圆心,AB为半径作圆A,点B、C、D必在⊙A上,∵∠BAC是⊙A的圆心角,而∠BDC是圆周角,∴∠BDC=12∠BAC=45°,故答案是:45;(2)如图2,取BD的中点O,连接AO、CO.∵∠BAD=∠BCD=90°,∴点A、B、C、D共圆,∴∠BDC=∠BAC,∵∠BDC=25°,∴∠BAC=25°,(3)如图3,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,AB=CD∠BAD=∠CDAAE=DF,∴△ABE≌△DCF(SAS),∴∠1=∠2,在△ADG和△CDG中,AD=CD∠ADG=∠CDGDG=DG,∴△ADG≌△CDG(SAS),∴∠2=∠3,∴∠1=∠3,∵∠BAH+∠3=∠BAD=90°,∴∠1+∠BAH=90°,∴∠AHB=180°﹣90°=90°,取AB的中点O,连接OH、OD,则OH=AO=12AB=1,在Rt△AOD中,OD=AO2+AD2=12+22=5,根据三角形的三边关系,OH+DH>OD,∴当O、D、H三点共线时,DH的长度最小,最小值=OD﹣OH=5―1.(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆AB上运动当O、H、D三点共线时,DH长度最小)故答案为:5―1.总结提升:本题主要考查了圆的综合题,需要掌握垂径定理、圆周角定理、等腰直角三角形的性质以及勾股定理等知识,难度偏大,解题时,注意辅助线的作法.(2)定边对定角典例4(2021秋•如皋市期中)如图,△ABC 为等边三角形,AB =3.若P 为△ABC 内一动点,且满足∠PAB =∠ACP ,则线段PB 长度的最小值为( )A .1.5B .3C .433D .2思路引领:由等边三角形的性质得出∠ABC =∠BAC =60°,AC =AB =3,求出∠APC =120°,当O 、P 、B 共线时,PB 长度最小,由等边三角形的性质得出AD =CD =12AC =32,∠PAC =∠ACP =30°,求出PD 和BD 的长,可得PB 的长,即可得出答案.解:∵△ABC 是等边三角形,∴∠ABC =∠BAC =60°,AC =AB =3,∵∠PAB =∠ACP ,∴∠PAC +∠ACP =60°,∴∠APC =120°,∴点P 的运动轨迹是AC ,设AC 所在圆的圆心为O ,当O 、P 、B 共线时,PB 长度最小,设OB 交AC 于D ,如图所示:此时PA=PC,OB⊥AC,则AD=CD=12AC=32,∠PAC=∠ACP=30°,∠ABD=12∠ABC=30°,∴PD=32,BD=332,∴PB=BD﹣PD=332―32=3.故选:B.总结提升:本题考查了等边三角形的性质、等腰三角形的性质、三角形内角和定理、勾股定理等知识;作辅助线构建圆是解决问题的关键.典例5(2021秋•白云区期中)在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并证明;(3)若点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求∠BEC的度数.思路引领:(1)在四边形ABCD中,由四边形内角和定理即可得出结果;(2)以BD为边向下作等边△BDQ,连接CQ,由等边三角形的性质得出∠DBQ=60°,BD=BQ,证出∠ABD=∠CBQ,证明△ABD≌△CBQ,得出AD=CQ,∠A=∠BCQ,证出∠DCQ=90°,再由勾股定理即可得出结论;(3)根据旋转的性质作辅助线,构建全等三角形,利用勾股定理的逆定理和等边三角形的判定和性质可得结论.解:(1)在四边形ABCD中,∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠D=30°,∴∠A+∠C=360°﹣60°﹣30°=270°;(2)结论:CD2+AD2=BD2,理由:以BD为边向下作等边△BDQ,连接CQ,则∠DBQ=60°,BD=BQ,∵∠ABC=∠DBQ=60°,∴∠ABD=∠CBQ,在△ABD和△CBQ中,AB=BC∠ABD=∠CBQ,BD=BQ∴△ABD≌△CBQ(SAS),∴AD=CQ,∠A=∠BCQ,∴∠A+∠BCD=∠BCQ+∠BCD=270°,∴∠DCQ=90°,∴CD2+CQ2=DQ2,∵CQ=AD,DQ=BD,∴CD2+AD2=BD2;(3)如图2,∵AB=BC,∠ABC=60°,∴将△ABE绕点B顺时针旋转60°得到△CBE',∴△ABE≌△CBE,∴BE=BE',AE=CE',∠EBE'=60°,∴△EBE'是等边三角形,∴EE'=BE,∠BEE'=60°,∵AE2=BE2+CE2,∴CE'2=E'E2+CE2,∴∠CEE'=90°,∵∠BEE'=60°,∴∠BEC=60°+90°=150°.总结提升:本题是四边形的综合题,考查了四边形内角和定理、等边三角形的判定和性质、勾股定理以及逆定理、全等三角形的判定与性质、解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.针对训练1.(广州中考)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.思路引领:(1)利用四边形内角和定理计算即可;(2)连接BD.以BD为边向下作等边三角形△BDQ.想办法证明△DCQ是直角三角形即可解决问题;(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.想办法证明∠BEC=150°即可解决问题;解:(1)如图1中,在四边形ABCD中,∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠D=30°,∴∠A+∠C=360°﹣60°﹣30°=270°.(2)如图2中,结论:DB2=DA2+DC2.理由:连接BD.以BD为边向下作等边三角形△BDQ.∵∠ABC=∠DBQ=60°,∴∠ABD=∠CBQ,∵AB=BC,DB=BQ,∴△ABD≌△CBQ(SAS),∴AD=CQ,∠A=∠BCQ,∵∠A+∠BCD=∠BCQ+∠BCD=270°,∴∠DCQ=90°,∴DQ2=DC2+CQ2,∵CQ=DA,DQ=DB,∴DB2=DA2+DC2.(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.则△AER是等边三角形,∵EA2=EB2+EC2,EA=RE,EC=RB,∴RE2=RB2+EB2,∴∠EBR=90°,∴∠RAE+∠RBE=150°,∴∠ARB+∠AEB=∠AEC+∠AEB=210°,∴∠BEC=150°,∴点E的运动轨迹在O为圆心的圆上,在⊙O上取一点K,连接KB,KC,OB,OC,∵∠K+∠BEC=180°,∴∠K=30°,∠BOC=60°,∵OB=OC,∴△OBC是等边三角形,∴OB=OC=BC=1,∴点E的运动路径=60⋅π⋅1180=π3.总结提升:本题考查四边形综合题、等边三角形的判定和性质、勾股定理以及逆定理、弧长公式等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题2.如图,在△ABC中,∠C=120°,则△ABC所在的平面上是否存在点M,使△ABM的面积等于△ABC 的面积,且∠AMB=60°?若存在,画出该点的位置,若不存在,请说明理由.思路引领:构造等边三角形ABE,作等边△ABE的外接圆⊙O,过点C作AB的平行线交⊙O于点M1和M2,由同底等高三角形面积相等可知△ABM1和△ABM2的面积与△ABC的面积相等,由同弧所对的圆周角相等可知∠AM1B=∠AM2B=∠E=60°,故M1和M2是符合题意的点,分别作M1和M2关于AB 的对称点M3和M4也符合题意.解:存在点M,如图,构造等边三角形ABE,作等边△ABE的外接圆⊙O,过点C作AB的平行线交⊙O于点M1和M2,∴∠AM1B=∠AM2B=∠E=60°,∵M1M2∥AB,∴S△ABM1=S△ABM2=S△ABC,∴M1和M2是符合题意的点,分别作M1和M2关于AB的对称点M3和M4,则点M3和M4也符合题意,故符合题意的点有4个,分别为M1、M2、M3和M4.总结提升:本题考查了三角形的综合知识,掌握圆周角定理和同底等高三角形面积相等是解决问题的关键.。
隐圆模型---四点共圆【模型专题】(含答案解析)

,
是等边三角形
为等边三角形
,
,且 ,
(2)如图,过点 作 ,交 的延长线于点 ,
,
,
,
,
,且 ,
点 是 中点
(3)如图,连接 ,
是等边三角形,
点 ,点 ,点 ,点 四点在以 为直径的圆上,
最大为直径,
即最大值为1
【点睛】本题是三角形的综合题,考查了等边三角形的性质,旋转的性质,全等三角形的判定与性质,圆的性质等知识,熟练掌握这些知识并灵活运用是关键.
四点共圆
【模型讲解】
如图①பைடு நூலகம்②,Rt△ABC和Rt△ABD共斜边,取AB 中点O,根据直角三角形斜边上的中线等于斜边的一半,可得:OC=OD=OA=OB,∴A、B、C、D四点共圆.即共斜边的两个直角三角形,直角顶点在斜边同侧或异侧,都可得到四点共圆.得到四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,这是证明角度相等重要的途径之一.
【详解】过点O作OM⊥AB于点M,作ON⊥BC于点N,
∵∠ABC=90°,
∴四边形OMBN是矩形,
∴OM∥BC,ON∥AB,
∴△AOM∽△ACB,△CON∽△CAB,
∴OM:BC=OA:AC,ON:AB=OC:AC,
∵O为AC的中点,
∴OM= BC= ×8=4,ON= AB= ×6=3,
∴MN= =5,
∴HC=OD,DH=OA,
又∵BO=AO,
∴HO=DH+DO=OB+CH,
而CH=OQ,HO=CQ,
∴CQ=OB+OQ=BQ,
∴∠CBQ=45°,
又∵CH∥BA,
最值模型之隐圆模型(解析版)

最值模型之隐圆模型模型一隐圆之定点定长型1、借助“隐圆”解决几何最值问题的理论依据有两个:①定圆的所有弦中,直径最长;②圆外一点与圆心的连线上,该点和此直线与圆的近交点距离最短、远交点距离最长.2、圆外的定点A与圆上动点B的距离AB的最值问题:当A、B、O三点共线时,AB有最大值或最小值。
如图2,AB最大值=OA+半径;如图3,AB最小值=OA-半径;定长模型(共顶点的三条等线段)若P为动点,但AB=AC=AP原理:圆A中,AB=AC=AP则B、C、P三点共圆,A圆心,AB半径备注:常转全等或相似证明出定长例题解析1如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A`MN,连接A`C,则A`C长度的最小值是.【分析】考虑△AMN沿MN所在直线翻折得到△A'MN,可得MA'=MA=1,所以A'轨迹是以M点为圆心,MA为半径的圆弧.连接CM,与圆的交点即为所求的A',此时A'C的值最小.构造直角△MHC,勾股定理求CM,再减去A'M即可,答案为7-1.2如图,在矩形ABCD中,AB=2,AD=7,动点P在矩形的边上沿B→C→D→A运动.当点P不与点A、B重合时,将△ABP沿AP对折,得到△AB P,连接CB ,则在点P的运动过程中,线段CB 的最小值为.【答案】11-2【思路点拨】根据折叠的性质得出B 在A为圆心,2为半径的弧上运动,进而分类讨论当点P在BC上时,当点P在DC上时,当P在AD上时,即可求解.【详解】解:∵在矩形ABCD中,AB=2,AD=7,∴BC=AD=7,AC=BC2+AB2=7+4=11,如图所示,当点P在BC上时,∵AB =AB=2∴B 在A为圆心,2为半径的弧上运动,当A,B ,C三点共线时,CB 最短,此时CB =AC-AB =11-2,当点P在DC上时,如图所示,此时CB >11-2当P在AD上时,如图所示,此时CB >11-2综上所述,CB 的最小值为11-2变式训练1如图,在矩形ABCD中,AB=2,AD=3,点E,F分别为AD、DC边上的点,且EF=2,G为EF的中点,P为BC边上一动点,则PA+PG的最小值为?【答案】4【简析】简单:G的运动轨迹为圆,求AP+PG典型的“将军饮马”问题,故做A关于BC的对称点A',则AP+PG=A P+PG,当A'、P、G三点共线时,最短,又因为A 为固定点,G在圆上运动,可知当A'、G、D三点共线时,此时A'G最短,为4动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是.【分析】考虑到将△FCE沿EF翻折得到△FPE,可得P点轨迹是以F点为圆心,FC为半径的圆弧.过F 点作FH⊥AB,与圆的交点即为所求P点,此时点P到AB的距离最小.由相似先求FH,再减去FP,即可得到PH.答案为1.2.3如图,点A,B的坐标分别为A(6,0),B(0,6),C为坐标平面内一点,BC=22,M为线段AC的中点,连接OM,当OM取最大值时,点M的坐标为.【答案】4,4【详解】解:如图,∵点C为坐标平面内一点,BC=22,∴C在⊙B上,且半径为22,在x轴上取OD=OA=6,连接CD,∵AM=CM,OD=OA,∴OM是△ACD的中位线,∴OM=1CD,2∴即当OM最大时,CD最大,而D,B,C三点共线时,即当C在DB的延长线上时,OM最大,∵OB=OD=6,∠BOD=90°,∴BD=62,∴CD=62+22=82,且C(2,8),∴OM=1CD=42,即OM的最大值为42,2∵M是AC的中点,则M(4,4),故答案为:(4,4).4如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF.当GF最小时,AE的长是.【答案】55-5【详解】解:①分析所求线段GF端点:G是定点、F是动点;②动点F的轨迹:正方形ABCD的边长为10,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,则BF=BA=10,因此动点轨迹是以B为圆心,BA=10为半径的圆周上,如图所示:③最值模型为点圆模型;④GF最小值对应的线段为GB-10;⑤求线段长,连接GB,如图所示:在RtΔBCG中,∠C=90°,正方形ABCD的边长为10,点G是边CD的中点,则CG=5,BC=10,根据勾股定理可得BG=CG2+BC2=52+102=55,当G、F、B三点共线时,GF最小为55-10,接下来,求AE的长:连接EG,如图所示根据翻折可知EF=EA,∠EFB=∠EAB=90°,设AE=x,则根据等面积法可知S正方形=SΔEDG+SΔBCG+SΔBAE+SΔBEG,即100=12DE⋅DG+12BC⋅CG+12AB⋅AE+12BG⋅EF=1 2510-x+5×10+10x+55x整理得5+1x=20,解得x=AE=205+1=205-15+15-1=55-55如图,在矩形ABCD中,AB=3,AD=4,E、F分别是边AD、BC上的动点,且CF=2AE,连接EF,将四边形ABFE沿EF翻折,点A、B的对应点分别为A'、B',连接A'D,则A'D的最小值为.【答案】73-5 3提示:连接AC交EF于点O,连接OA'、OD,作OH⊥AD于H则△AOE∽△COF∵CF=2AE,∴CO=2AO,∴A'O=AO=13AC=53∴AH=45AO=43,OH=35AO=1∴DH=AD-AH=4-43=83,OD=OH2+DH2=733∴A'D≥OD-OA'=73-5 3模型二隐圆之定长定角型(1)直角圆周角模型固定线段AB所对动角∠C恒为90°原理:圆O中,圆周角为90°所对弦是直径则A、B、C三点共圆,AB为直径备注:常通过互余转换等证明出动角恒为直角解题技巧:若定角为90°,取定长AB的中点O为圆心,AB的一半为半径画辅助圆。
隐圆模型(解析版).doc

隐圆模型(解析版).doc一. 前言隐圆模型(Hidden Circle Model)是指在机器学习领域中,对于给定的样本数据集,利用隐圆模型来优化求解目标函数的优化算法。
隐圆模型在实际应用中广泛被用于回归分析、聚类分析、异常检测等众多领域中。
相比于传统的模型,隐圆模型结构简单、运算效率高、收敛速度快等优点,深受学术界和工业界的欢迎。
二. 原理在隐圆模型中,首先需要定义一个圆心向量、一个半径向量和一个权重向量,用于描述隐含的模式特征。
具体地,圆心向量指的是样本数据的中心点,半径向量是样本点到圆心点的欧几里得距离,权重向量是样本特征的权重,用于描述样本点的特征对结果的影响程度。
在隐圆模型中,采用的是最小二乘法,即通过最小化误差平方和,来计算权重向量和半径向量。
在求解过程中,还需要使用迭代算法来更新权重向量和半径向量,以达到最优化的目标。
三. 算法流程1. 初始化:定义圆心向量、半径向量和权重向量的初值。
2. 迭代计算:根据误差平方和的最小化目标函数,通过梯度下降法,更新权重向量和半径向量的值。
3. 模型验证:通过验证样本数据的误差值,来判断隐圆模型的准确性和可靠性。
四. 优化算法在隐圆模型中,为了提高模型的精度和稳定性,可以采用如下的优化算法:1. 学习率优化:学习率指的是在梯度下降法中,每次迭代中更新权重向量和半径向量的步长。
为了保持稳定性,需要适当调整学习率,可以通过加入动量因子来解决。
2. 损失函数优化:为了避免在梯度下降中出现局部最优解的情况,可以采用正则化技术来调节权重向量,通过调整损失函数的惩罚系数来提高模型的泛化能力。
3. 数据预处理:在输入数据中存在异常值、缺失值等情况时,需要进行数据预处理,可以通过归一化、标准化等技术来提高数据质量和模型精度。
五. 应用案例1. 回归分析:隐圆模型可以用于拟合非线性回归模型,通过精细的权重调整和半径变化,来准确预测结果。
2. 聚类分析:隐圆模型可以将样本数据分为不同的簇,通过最小化误差平方和和不同类别之间的距离,来优化聚类结果。
定点定长隐圆模型讲解

定点定长隐圆模型讲解
哎呀呀!什么是定点定长隐圆模型呀?这听起来可真神秘!
就好像我们在玩捉迷藏,那个隐藏起来的圆就是我们要找的小伙伴。
想象一下,在一个大大的数学世界里,有一些点和线段,它们好像在悄悄地说着什么秘密。
比如说,有一个固定的点,还有一条长度不变的线段。
这就好像我们在操场上,有一个小朋友站在那里不动,手里拿着一根不会变长也不会变短的跳绳。
假如有另外一个小朋友,他的脚必须要和那个站着不动的小朋友的脚连着,而且手里还要拿着跳绳的另一头。
那这个拿着跳绳另一头的小朋友能跑到哪儿去呢?
这时候你是不是在想,他不就只能围着那个固定的小朋友,以跳绳的长度为半径跑圈圈嘛!没错,这就是定点定长隐圆模型啦!
老师在讲这个的时候,好多同学都皱着眉头,一脸的困惑。
“这到底是怎么回事呀?”“怎么这么难理解!” 我心里也在嘀咕:“这也太奇怪了吧,怎么能想到是个圆呢?” 可是老师不慌不忙地给我们举了好多例子。
老师说:“就像一只小狗被拴在柱子上,绳子的长度不变,小狗能跑的范围不就是一个圆嘛!” 同学们一听,恍然大悟,“哦,原来是这样啊!” 我也拍了一下脑袋,“我怎么没想到呢!”
再比如,有一辆车从一个固定的地方出发,它的天线长度一直不变,那车开着开着,天线扫过的轨迹不也是一个圆嘛!
经过老师这么一讲,我们好像慢慢明白了这个神奇的定点定长隐圆模型。
我觉得呀,数学有时候就像一个魔法世界,充满了各种奇妙的东西等着我们去发现。
这个定点定长隐圆模型虽然一开始让人摸不着头脑,但是只要我们认真去想,去琢磨,就能揭开它神秘的面纱。
所以,同学们,不要害怕数学里的这些难题,只要我们用心,就能找到答案!。
巧用隐圆 妙解最值(解析版)

巧用隐圆妙解最值模型背诵隐圆一:定弦定角,隐圆正好。
AB的长度固定不变(定弦),∠ABC=α不变(定角)。
这样的图形就是我们所谓的“定弦定角模型”。
隐圆一特殊:若∠ACB=90°,则AB为三点所在圆的直径。
(可以解决动点轨迹。
)隐圆二:等弦对等角,隐圆可以找。
(可以利用四点共圆证相似,角相等)若∠ADC=∠ABC,则A,B,C,D四点共圆。
在半角模型中,证四点共圆,主要利用了这类隐圆.隐圆二特殊.若∠ABC=∠ADC=90°,则A,B,C,D四点共圆,且AC为直径。
隐圆三:对角互补,四点共圆.若∠ADC+∠ABC=180°,则A,B,C,D四点共圆。
隐圆三特殊:若∠ABC=∠ADC=90°,则A,B,C,D四点共圆,且AC为直径。
隐圆四:定点定长,隐圆必现。
CA=CB=CP隐圆五、瓜豆原理之种圆得圆。
若Q为AP的中点,当P沿⊙O运动一周,则Q的运动轨迹为以AO中点M为圆心的圆。
(P为“主动点”,点Q为“从动点。
)典例分析如图1-1,点P(3,4),圆P半径为2,A(2.8,0),B(5.6,0),点M是圆P上的动点,点C是MB的中点,则AC的最小值是_______.【点睛】图1-2,M点为主动点,C点为从动点,B点为定点.考虑C是BM中点,可知C点轨迹:取BP中点O,以O为圆心,OC为半径作圆,即为点C轨迹.图1-3:当A、C、O三点共线且点C在线段OA上时,AC取到最小值,根据B、P坐标求O,利用两点间距离公式求得OA,再减去OC即可.实战训练一.选择题(共8小题)1.如图,在Rt△ABC中,∠C=90°且AB=10,点P为△ABC的内心,点O为AB边中点,将BO绕点B顺时针旋转90°得到线段BD,连接DP,则DP长的最小值为()A.55-52B.52C.35-32 D.52-52试题分析:在AB的下方作等腰直角三角形AKB,使得∠AKB=90°,AK=BK.连接DK,PK,过点K作KT⊥DB交DB的延长线于点T.判断出点P的运动轨迹,求出DK,PK,可得结论.答案详解:解:在AB的下方作等腰直角三角形AKB,使得∠AKB=90°,AK=BK.连接DK,PK,过点K作KT⊥DB交DB的延长线于点T.∵点P是△ACB的内心,∠C=90°,∴∠PAB=12∠CAB,∠PBA=12∠ABC,∴∠PAB +∠PBA =12(∠CAB +∠CBA )=45°,∴∠APB =180°-45°=135°,∴点P 在以K 为圆心,KA 为半径的圆上运动,∵AB =10,AK =BK ,∠AKB =90°,∴AK =BK =KP =52,∠ABK =45°,∵∠ABT =90°,∴∠KBT =45°,∴KT =BT =5,∵OA =OB =BD =5,∴DT =10,∴DK =DT 2+KT 2=55,∴DP ≥DK -PK =55-52,∴DP 的最小值为55-52.所以选:A .2.已知抛物线y =-316(x -1)(x -9)与x 轴交于A ,B 两点,对称轴与x 轴交于点D ,点C 为抛物线的顶点,以C 点为圆心的⊙C 半径为2,点G 为⊙C 上一动点,点P 为AG 的中点,则DP 的最大值与最小值和为()A.72B.23C.412D.5试题分析:P 为AG 中点,D 为AB 中点,所以PD 是△ABG 的中位线,则DP =12BG ,当BG 最大时,则DP 最大.由圆的性质可知,当G 、C 、B 三点共线时,BG 最大或最小.答案详解:解:如图,连接BG .因为P 为AG 中点,D 为AB 中点,所以PD 是△ABG 的中位线,则DP =12BG ,当BG 最大时,则DP 最大.由圆的性质可知,当G 、C 、B 三点共线时,BG 最大.∵C (5,3),B (9,0),∴BC =32+42=5,∴BG 的最大值为2+5=7,BG 的最小值=5-2=3,∴DP 的最大值为72.DP 的最小值为32,∴DP 的最大值与最小值的和为5.所以选:D .3.如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一点,连接PA,PC,PD,若PA⊥PD,则PC的最小值为()A.213-4B.210-3C.2D.4试题分析:由PA⊥PD可得点P在以AD中点O为圆心AD为直径的圆上,连接CO交圆于一点即为最短距离点,即可得到答案.答案详解:解:∵PA⊥PD,∴点P在以AD中点O为圆心AD为直径的圆上,如图所示,∴连接CO交圆于一点即为最短距离点P,如图所示,∵AB=4,BC=6,∴OD=3,DC=4,根据勾股定理可得,OC=32+42=5,∴CP=5-3=2,所以选:C.4.如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点M,则线段MC的最小值为()A.2B.5C.3D.102试题分析:当A,M,C三点共线时,线段CM的长度最小,求出此时CM的长度即可.答案详解:解:连接AM,∵点B和M关于AP对称,∴AB=AM=3,∴M在以A为圆心,3为半径的圆上,∴当A,M,C三点共线时,CM最短,∵AC=32+42=5,AM=AB=3,∴CM=5-3=2,所以选:A.5.如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连接AP,取AP中点Q,连接CQ,则线段CQ的最大值为()A.3B.1+6C.1+32D.1+7试题分析:如图,连接OQ,作CH⊥AB于H.首先证明点Q的运动轨迹为以AO为直径的⊙K,连接CK,当点Q在CK的延长线上时,CQ的值最大,利用勾股定理求出CK即可解决问题;答案详解:解:如图,连接OQ,作CH⊥AB于H.∵AQ=QP,∴OQ⊥PA,∴∠AQO=90°,∴点Q的运动轨迹为以AO为直径的⊙K,连接CK,当点Q在CK的延长线上时,CQ的值最大(也可以通过CQ≤QK+CK求解)在Rt△OCH中,∵∠COH=60°,OC=2,OC=1,CH=3,∴OH=12在Rt△CKH中,CK=(3)2+22=7,∴CQ的最大值为1+7,所以选:D.6.如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点E、F移动过程中,点G移动路线的长度为()A.2B.πC.2πD.22π试题分析:由△ADE ≌△CDF ,推出∠DAE =∠DCF ,因为∠AED =∠CEG ,推出∠ADE =∠CGE =90°,推出A 、C 、G 、D 四点共圆,推出点G 的运动轨迹为弧CD ,利用弧长公式计算即可.答案详解:解:如图,∵CA =CB ,∠ACB =90°,AD =DB ,∴CD ⊥AB ,∴∠ADE =∠CDF =90°,CD =AD =DB ,在△ADE 和△CDF 中,AD =CD ∠ADE =∠CDF DE =DF,∴△ADE ≌△CDF (SAS ),∴∠DAE =∠DCF ,∵∠AED =∠CEG ,∴∠ADE =∠CGE =90°,∴A 、C 、G 、D 四点共圆,∴点G 的运动轨迹为弧CD ,∵AB =4,AB =2AC ,∴AC =22,∴OA =OC =2,∵DA =DC ,OA =OC ,∴DO ⊥AC ,∴∠DOC =90°,∴点G 的运动轨迹的长为90π×2180=22π.所以选:D .7.如图,在△ABC 中,∠ABC =90°,AB =8,BC =12,D 为AC 边上的一个动点,连接BD ,E 为BD 上的一个动点,连接AE ,CE ,当∠ABD =∠BCE 时,线段AE 的最小值是()A.3B.4C.5D.6试题分析:如图,取BC 的中点T ,连接AT ,ET .首先证明∠CEB =90°,求出AT ,ET ,根据AE ≥AT -ET ,可得结论.答案详解:解:如图,取BC 的中点T ,连接AT ,ET .∵∠ABC =90°,∴∠ABD +∠CBD =90°,∵∠ABD =∠BCE ,∴∠CBD +∠BCE =90°,∴∠CEB =90°,∵CT =TB =6,∴ET =12BC =6,AT =AB 2+BT 2=82+62=10,∵AE ≥AT -ET ,∴AE ≥4,∴AE 的最小值为4,所以选:B .8.如图,已知在矩形ABCD 中,AB =1,BC =3,点P 是AD 边上的一个动点,连接BP ,点C 关于直线BP 的对称点为C 1,当点P 运动时,点C 1也随之运动.若点P 从点A 运动到点D ,则线段CC 1扫过的区域的面积是()A.πB.π+334C.332D.2π试题分析:由临界状态确定出C 1的运动路径,明确点P 从点A 运动到点D ,则线段CC 1扫过的区域为:扇形BC 'C ''和△BCC '',再分别计算两部分面积即可.答案详解:解:如图,当P 与A 重合时,点C 关于BP 的对称点为C ′,当P 与D 重合时,点C 关于BP 的对称点为C ″,∴点P 从点A 运动到点D ,则线段CC 1扫过的区域为:扇形BC 'C ''和△BCC '',在△BCD 中,∵∠BCD =90°,BC =3,CD =1,∴tan ∠DBC =13=33,∴∠DBC =30°,∴∠CBC ″=60°,∵BC =BC '',∴△BCC ''为等边三角形,∴S 扇形BC ′C ″=120×π×(3)2360=π,作C ''F ⊥BC 于F ,∵△BCC ''为等边三角形,∴BF=12BC=32,∴C''F=tan60°×32=32,∴S△BCC''=12×3×32=334,∴线段CC1扫过的区域的面积为:π+334.所以选:B.二.填空题(共12小题)9.如图,等边三角形ABC和等边三角形ADE,点N,点M分别为BC,DE的中点,AB=6,AD=4,△ADE绕点A旋转过程中,MN的最大值为 53 .试题分析:分析题意可知,点M是在以AM为半径,点A为圆心的圆上运动,连接AN,AM,以AM 为半径,点A为圆心作圆,反向延长AN与圆交于点M′,以此得到M、A、N三点共线时,MN的值最大,再根据勾股定理分别算出AM、AN的值,则MN的最大值M′N=AN+AM′=AN+AM.答案详解:解:连接AN,AM,以AM为半径,点A为圆心作圆,反向延长AN与圆交于点M′,如图,∵△ADE绕点A旋转,∴点M是在以AM为半径,点A为圆心的圆上运动,∵AM+AN≥MN,∴当点M旋转到M′,即M、A、N三点共线时,MN的值最大,最大为M′N,∵△ABC和△ADE都是等边三角形,点N,点M分别为BC,DE的中点,AB=6,AD=4,∴AN⊥BC,AM⊥DE,BN=3,DM=2,在Rt△ABN中,由勾股定理得AN=AB2-BN2=33,在Rt△ADM中,由勾股定理得AM=AD2-DM2=23,根据旋转的性质得,AM′=AM=23,∴M′N=AN+AM′=53,即MN的最大值为53.所以答案是:53.10.如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为 210 .试题分析:如图,作点D关于直线BC的对称点K,连接MK,以AB为直径作⊙J,取CD的中点H,连接JH交⊙J于点T.由题意,点P的运动轨迹是AT,当点P运动到点T时,且点M在KT上时,DM+MP=KM+MP的值最小,最小值为KT的长.答案详解:解:如图,作点D关于直线BC的对称点K,连接MK,以AB为直径作⊙J,取CD的中点H,连接JH交⊙J于点T.∵点E与点F的速度相同.∴AE=DF,∵四边形ABCD为正方形,∴∠BAE=∠ADF,AB=AD,∴△ABE≌△DAF(SAS),∴∠ABE=∠DAF,∵∠DAF+∠PAB=90°,∴∠ABE+∠PAB=90°,∴点P在以AB为直径的圆上,圆心为点J,由题意,点P的运动轨迹是AT,当点P运动到点T时,且点M在KT上时,DM+MP=KM+MP 的值最小,最小值为KT的长.在Rt△THK中,TH=2,HK=6,∴TK=TH2+KH2=22+62=210,∴DM+MP的最小值为210,所以答案是:210.11.如图,在锐角三角形ABC中,BC=8,sin A=45,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 28825 .试题分析:画出△ABC的外接圆⊙O,连接OB,利用定角对定边可知点A在优弧BC上运动,当A'O⊥BC时,△A'BC的面积最大,求出△ABC的最大面积,再利用三角函数求出AM的长度,利用相似三角形的面积比等于相似比的平方可得答案.答案详解:解:画出△ABC的外接圆⊙O,连接OB,∵BC=8,sin A=45,∴点A 在优弧BC 上运动,当A 'O ⊥BC 时,△A 'BC 的面积最大,∴BH =4,∵∠BOH =∠BAC ,∴BO =5,OH =3,∴AH =8,cos ∠BOH =35,∴S △ABC 最大为12×8×8=32,∵CM ⊥AB ,∴cos ∠MAC =AMAC=35,∵AB =AC ,AM =AN ,∠MAN =∠BAC ,∴△AMN ∽△ABC ,∴S △AMN S △ABC =AM AB2,∴S △AMN 32=925,∴S △AMN =28825,所以答案是:28825.12.在△ABC 中,AB =4,∠C =45°,则2AC +BC 的最大值为410 .试题分析:过点B 作BD ⊥AC 于点D ,则△BCD 为等腰直角三角形,设BD =CD =a ,延长AC 至点F ,使得CF =a ,则可求出tan ∠AFB ,作△ABF 的外接圆⊙O ,过点O 作OE ⊥AB 于点E ,则AE =12AB =2,∠AOE =∠AFB ,则可利用tan ∠AOE 求出OE 、OA ,最后利用三角形三边关系即可求出2AC +BC 的最大值为2(OA +OF ),计算即可.答案详解:解:过点B 作BD ⊥AC 于点D ,∵∠C =45°,∴△BCD 为等腰直角三角形,∴BD =CD ,设BD =CD =a ,延长AC 至点F ,使得CF =a ,∵tan ∠AFB =a 2a =12,作△ABF 的外接圆⊙O ,过点O 作OE ⊥AB 于点E ,则AE =12AB =2,∠AOE =∠AFB ,∴tan ∠AOE =12,∴OE =4,OA =22+42=25,∴2AC+BC=2AC+22BC=2(AC+CF)=2AF≤2(OA+OF),∴2AC+BC的最大值为2×45=410.所以答案是:410.13.如图,四边形ABCD中,AB=AC=AD,∠CBD=15°,BD=3AB,则∠BDC=45°.试题分析:过点A作AM⊥BD于M.分别求出∠ADC,∠ADB,可得结论.答案详解:解:过点A作AM⊥BD于M.∵AB=AC=AD,∴∠CAD=2∠CBD=30°,∴∠ADC=∠ACD=75°,∵AB=AD,AM⊥BD,∴BM=DM,∵BD=3AB,∴BMAB =32,∴cos∠ABM=32,∴∠ABM=∠ADB=30°,∴∠BDC=∠ADC-∠ADB=45°.所以答案是:45°.14.如图,等边△ABC中,AB=6,点D、点E分别在BC和AC上,且BD=CE,连接AD、BE交于点F,则CF的最小值为23 .试题分析:首先证明∠AFB=120°,推出点F的运动轨迹是O为圆心,OA为半径的弧上运动(∠AOB=120°,OA=23),连接OC交⊙O于N,当点F与N重合时,CF的值最小.答案详解:解:如图,∵△ABC是等边三角形,∴AB=BC=AC,∠ABC=∠BAC=∠BCE=60°,∵BD=CE,∴△ABD≌△BCE(SAS)∴∠BAD=∠CBE,又∵∠AFE=∠BAD+∠ABE,∴∠AFE=∠CBE+∠ABE=∠ABC,∴∠AFE=60°,∴∠AFB =120°,∴点F 的运动轨迹是O 为圆心,OA 为半径的弧上运动(∠AOB =120°,OA =23),连接OC 交⊙O 于N ,当点F 与N 重合时,CF 的值最小,最小值=OC -ON =43-23=23.所以答案是23.15.如图,正方形ABCD 中,AB =2,动点E 从点A 出发向点D 运动,同时动点F 从点D 出发向点C 运动,点E 、F 运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF 、BE 相交于点P ,M 是线段BC 上任意一点,则MD +MP 的最小值为 10 .试题分析:首先作出点D 关于BC 的对称点D ′从而可知当点P 、M 、D ′在一条直线上时,路径最短,当点E 与点D 重合,点F 与点C 重合时,PG 和GD ′均最短,即PD ′最短,然后由正方形的性质和轴对称图形的性质可知:PG =1,GD ′=3,最后由勾股定理即可求得PD ′的长,从而可求得MD +MP 的最小值.答案详解:解:如图作点D 关于BC 的对称点D ′,连接PD ′,由轴对称的性质可知:MD =D ′M ,CD =CD ′=2∴PM +DM =PM +MD ′=PD ′过点P 作PE 垂直DC ,垂足为G ,易证AF ⊥BE ,故可知P 的轨迹为以AB 为直径的四分之一圆弧上,当点E 与点D 重合,点F 与点C 重合时,PG 和GD ′均最短,∴此时,PD ′最短.∵四边形ABCD 为正方形,∴PG =12AD =1,GC =12DC =1.∴GD ′=3.在Rt △PGD ′中,由勾股定理得:PD ′=PG 2+GD '2=12+32=10.所以答案是:10.16.如图,Rt △ABC 中,∠ACB =90°,∠CAB =60°,AB =4,点P 是BC 边上的动点,过点C 作直线AP 的垂线,垂足为Q ,当点P 从点C 运动到点B 时,点Q 的运动路径长为 23π .试题分析:由AQ⊥CQ,推出∠AQC=90°,可知当点P从点C运动到点B时,点Q的运动的轨迹是以AC为直径的半圆上,延长即可解决问题.答案详解:解:∵AQ⊥CQ,∴∠AQC=90°,∴当点P从点C运动到点B时,点Q的运动的轨迹是以AC为直径的半圆上,路径是120度的弧长,在Rt△ABC中,∵AB=4,∠B=30°,∴AC=12AB=2,∴点Q的运动路径长为120⋅π⋅1180=23π17.如图,在平面直角坐标系中,有一条长为10的线段AB,其端点A、点B分别在y轴、x轴上滑动,点C为以AB为直径的⊙D上一点(C始终在第一象限),且tan∠BAC=12.则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为20-65 .试题分析:如图1中,作射线OC.首先证明点C在射线OC上运动,∠COB=∠CAB=定值,求出三种特殊位置OC的值即可解决问题;答案详解:解:如图1中,作射线OC.∵tan∠BAC=12,∴∠CAB是定值,∵∠COB=∠CAB,∴∠COB是定值,∴点C在射线OC上运动.如图2中,当线段AB在y轴上时,设OC1=k,A1C1=2k,则有:k2+4k2=102,∴k=25∴OC1=25,如图2中,四边形A2OB2C2是矩形时,OC2=AB=10,此时OC2的值最大,当线段AB在x轴上时,同法可得OC3=45,观察图形可知,点C的运动轨迹是C1→C2→C3,∴点C的运动路径为:(10-25)+(10-45)=20-65,所以答案是20-65.18.如图,等边△ABC的边长为6,D为BC边上的中点,P为直线BC上方的一个动点,且满足∠PAD=∠PDB,则线段CP长的最大值为 37+332.试题分析:首先证明点P在以AD为直径的⊙O上,连接OC,延长CO交⊙O于点P,此时PC最大,利用勾股定理求出OC即可解决问题.答案详解:解:∵等边△ABC的边长为6,D为BC边上的中点,∴∠ADB=90°,∴∠ADP+∠PDB=90°,∵∠PAD=∠PDB∴∠DAP+∠ADP=90°,∴∠APD=90°,∴点P在以AD为直径的⊙O上,连接OC,延长CO交⊙O于点P,此时PC最大,在Rt△CDO中,∵∠ODC=90°,DC=12BC=3,OD=12AD=332,∴OC=OD2+CD2=372,∴PC=OC+OP=372+332=37+332.∴CP长的最大值为37+332.所以答案是37+332.19.在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为 5-2 .试题分析:根据∠ADB=45°,AB=2,作△ABD的外接圆O,连接OC,当O、D、C三点共线时,CD的值最小.将问题转化为点圆最值.可证得△AOB为等腰直角三角形,OB=OA=2,同样可证△OBE也为等腰直角三角形,OE=BE=1,由勾股定理可求得OC的长为5,最后CD最小值为OC-OD=5-2.答案详解:解:如图所示.∵∠ADB=45°,AB=2,作△ABD的外接圆O(因求CD最小值,故圆心O在AB的右侧),连接OC,当O、D、C三点共线时,CD的值最小.∵∠ADB=45°,∴∠AOB=90°,∴△AOB为等腰直角三角形,∴AO=BO=sin45°×AB=2.∵∠OBA=45°,∠ABC=90°,∴∠OBE=45°,作OE⊥BC于点E,∴△OBE为等腰直角三角形.∴OE=BE=sin45°•OB=1,∴CE=BC-BE=3-1=2,在Rt△OEC中,OC=OE2+CE2=1+4=5.当O、D、C三点共线时,CD最小为CD=OC-OD=5-2.所以答案是:5-2.20.如图,在矩形ABCD中,AB=1,AD=3,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为 3-π3 .试题分析:由矩形的性质求出∠ABQ=120°,由矩形的性质和轴对称性可知,△BOQ≌△DOC,根据S阴影部分=S四边形ABQD-S扇形ABQ=2S△ABD-S扇形ABQ可求出答案.答案详解:解:∵当点P从点A运动到点D时,PQ=PA,∴点Q运动轨迹是圆弧,如图,阴影部分的面积即为线段PQ在平面内扫过的面积,∵矩形ABCD中,AB=1,AD=3,∴∠ABC=∠BAC=∠C=∠Q=90°.∴∠ADB=∠DBC=∠ODB=∠OBQ=30°,∴∠ABQ=120°,由矩形的性质和轴对称性可知,△BOQ≌△DOC,S△ABD=S△BQD,∴S阴影部分=S四边形ABQD-S扇形ABQ=2S△ABD-S扇形ABQ,=S矩形ABCD -S扇形ABQ=1×3-120π×12360=3-π3.所以答案是:3-π3.三.解答题(共3小题)21.圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.(1)已知:如图1,OA=OB=OC,请利用圆规画出过A、B.C三点的圆.若∠AOB=70°,则∠ACB=35°.如图,Rt△ABC中,∠ABC=90°,∠BCA=30°,AB=2.(2)已知,如图2.点P为AC边的中点,将AC沿BA方向平移2个单位长度,点A、P、C的对应点分别为点D、E、F,求四边形BDFC的面积和∠BEA的大小.(3)如图3,将AC边沿BC方向平移a个单位至DF,是否存在这样的a,使得直线DF上有一点Q,满足∠BQA=45°且此时四边形BADF的面积最大?若存在,求出四边形BADF面积的最大值及平移距离a,若不存在,说明理由.试题分析:(1)利用圆的定义知A,B,C三点共圆,再利用圆周角定理求解.(2)根据图形的平移性质,判定平移后图形形状,继而确定面积的计算方式和方法,角度问题也迎刃而解.(3)因角度不变,借助圆周角定点在圆周上运动时角度不变的思想,判断出D点能够向右移动的最大距离,求出四边形的最大面积.答案详解:(1)以O为圆心,OA为半径作辅助圆,如图,∵∠AOB=70°,∴∠ACB=35°,所以答案是35°.(2)连接PB,PE,如图,,Rt△ABC中,∠ABC=90°,∠BCA=30°,AB=2.∴AC=4,∠BAC=60°,BC=23.∵P为Rt△ABC斜边AC中点,∴BP=12AC=2,线段AC平移到DF之后,AB=AD=PE=2,BP=AE=2,∴四边形ABPE为菱形,∵∠BAC=60°,∴∠BEA=30°,∵CF∥BD,且∠ABC=90°,∴四边形BDFC为直角梯形,∴S=12(BD+CF)×BC=12×6×23=63,(3)如图所示,当AC边沿BC方向平移2个单位至DF时,满足∠BQA=45°且此时四边形BADF的面积最大,此时直角梯形ABFD的最大面积为,S=12×(BF+AQ)×AB=12×(23+2+2)×2=4+23.22.阅读下列材料,回答问题.材料:求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型,此类题型试题有时出题者将圆隐藏,故又称为“隐圆问题”.解决这类问题,关键是要找到动点的运动轨迹,即该动点是绕哪一个定点旋转,且能保持旋转半径不变.从而找到动点所在的隐藏圆,进而转换成圆外一点到圆心的距离减半径,求得最小值.解决问题:(1)如图①,圆O的半径为1,圆外一点A到圆心的距离为3,圆上一动点B,当A、O、B满足条件点B在线段AO上时,AB有最小值为2.(2)如图②,等腰△ABC两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到BC的距离最小值为2.(3)如图③,OA⊥OB,P、Q分别是射线OA、OB上两个动点,C是线段PQ的中点,且PQ=4,则在线段PQ滑动的过程中,求点C运动形成的路径长,并说明理由.(4)如图④,在矩形ABCD中,AB=4,AD=8,点E是AB中点,点F是BC上一点,把△BEF沿着EF翻折,点B落在点B'处,求DB'的最小值,并说明理由.(5)如图⑤,在△ABC中,AB=10,AC=8,BC=6,以边AB中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,求PQ长的最小值,并说明理由.试题分析:(1)如图①,连接OA,OB,OA,由三角形的三边关系可得AB≤AO-BO,则当点B在线段AO上时,AB有最小值=3-1=2;(2)如图②中,过点A作AH⊥BC于H,交⊙A于P,此时点P到BC的距离最小.(3)利用直角三角形斜边中线的性质,的长OC=2,再利用弧长公式求解即可.(4)如图④中,连接DE,DB′.利用勾股定理求出DE,根据DB′≥DE-EB′,可得DB′≥217-2,由此可得结论.(5)当O、Q、P三点共线且OP⊥BC时,PQ有最小值,设AC与圆的切点为D,连接OD,分别利用三角形中位线定理可求得OD和OP的长,则可求得PQ的最小值.答案详解:解:(1)如图①,连接OA,OB,OA,在△ABO中,AB≤AO-BO,当点B在线段AO上时,AB有最小值=3-1=2,所以答案是:点B在线段AO上,2.(2)如图②中,过点A作AH⊥BC于H,交⊙A于P,此时点P到BC的距离最小.∵AB=AC=5,AH⊥BC,BC=3,∴BH=CH=12∴AH=AB2-BH2=52-32=4,∵PA=2,∴PH=AH-AP=2,∴圆上动点P到BC的距离最小值为2,所以答案是:2.(3)如图③中,连接OC.∵∠POQ=90°,PQ=4,PC=CQ,PQ=2,∴OC=12∴点C的运动轨迹是圆弧,运动路径的长=90⋅π⋅2=π.180(4)如图④中,连接DE,DB′.∵四边形ABCD是矩形,∴∠A=90°,∵AE=EB=2,AD=8,∴DE=AE2+AD2=22+82=217,∵BE=EB′=2,∴DB′≥DE-EB′,∴DB′≥217-2,∴DB′的最小值为217-2.(5)当O、Q、P三点共线且OP⊥BC时,PQ有最小值,设AC与圆的切点为D,连接OD,如图⑤中,∵AC为圆的切线,∴OD⊥AC,∵AC=8,BC=6,AB=10,∴AC2+BC2=AB2,∴∠ACB=90°,∴OD ∥BC ,且O 为AB 中点,∴OD 为△ABC 的中位线,∴OD =12BC =3,同理可得PO =12AC =4,∴PQ =OP -OQ =4-3=1,∴PQ 的最小值为1.23.在矩形ABCD 中,BC =3CD ,点E 、F 分别是边AD 、BC 上的动点,且AE =CF ,连接EF ,将矩形ABCD 沿EF 折叠,点C 落在点G 处,点D 落在点H 处.(1)如图1,当EH 与线段BC 交于点P 时,求证:PE =PF ;(2)如图2,当点P 在线段CB 的延长线上时,GH 交AB 于点M ,求证:点M 在线段EF 的垂直平分线上;(3)当AB =5时,在点E 由点A 移动到AD 中点的过程中,计算出点G 运动的路线长.试题分析:(1)欲证明PE =PF ,只要证明∠PEF =∠PFE .(2)连接AC 交EF 于O ,连接PM ,PO .首先证明P ,M ,O 共线,再利用等腰三角形的三线合一的性质解决问题即可.(3)如图3中,由题意,点E 由点A 移动到AD 中点的过程中,点G 运动的路径是图中弧BC .利用弧长公式,解决问题即可.答案详解:(1)证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠DEF =∠EFB ,由翻折变换可知,∠DEF =∠PEF ,∴∠PEF =∠PFE ,∴PE =PF .(2)证明:如图2中,连接AC 交EF 于O ,连接PM ,PO .∵AE ∥CF ,∴∠EAO =∠FCO ,∵AE =CF ,∠AOE =∠COF ,∴△AEO ≌△CFO (AAS ),∴OE =OF ,∵PE =PF ,∴PO 平分∠EPF ,∵AD =BC ,AE =FC ,∴ED =BF ,由折叠的性质可知ED =EH ,所以BF =EH ,∴PE -EH =PF -BF ,∴PB =PH ,∵∠PHM =∠PBM =90°,PM =PM ,∴Rt △PMH ≌Rt △PMB (HL ),∴PM 平分∠EPF ,∴P .M ,O 共线,∵PO ⊥EF ,OE =OF ,∴点M 在线段EF 的垂直平分线上.(3)如图3中,由题意,点E 由点A 移动到AD 中点的过程中,点G 运动的路径是图中弧BC .在Rt △BCD 中,tan ∠CBD =CD BC=33,∴∠CBD =30°,∴∠ABO =∠OAB =60°,∴△AOB 是等边三角形,∴OA =OD =OB =OC =AB =5,∠BOC =120°,∴点G 运动的路径的长=120⋅π⋅5180=103π.所以答案是:103π.。
2024专题4.1隐圆模型 课件(共23张PPT)-中考数学二轮复习必会几何模型剖析(全国通用)

为__________.
6.如图,四边形ABCD中,AB=AC=AD=2,BC=1,AB∥CD,则BD=____.
15 定点定长型
P1
C
A
B
P2
B
C
D
A
E
强化训练
“隐圆”模型
提升能力
7.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,连接EF.
求证:∠AEF=∠C.
点M和N分别从点B、C同时出发,以相同的速度沿BC、CA运动.连
4 3
接AM和BN,交于点P,则PC长的最小值为____.
3
A
P
B
M
D
N
C
知识归纳
定边对定角---直径对直角
考点3-2
模型分析
C
图
形 A
B
条
AB为定线段(即直径),线段AB外一点C与A,B两
件
端形成的张角为直角(即∠ACB=90º),
四点共圆-对角互补
D
A
C
E
B
针对训练
四点共圆
考点3-3
2.如图,△ABD,△AEC都是等腰三角形,AB=AD,AE=AC,AC>AB
∠BAD=∠EAC=α,连接CD,BE交于点P,连接AP.
A
(1)求∠BPD的度数(用含α的代数式表示);
(2)求证:∠APD=∠ABD.
(3)PA平分∠DPE.
(1)(2)利用四点共圆求解
2
(1)在旋转过程中,BD的最小值为_____;
⌒
(2)当α=30º,试判断BD与CD的位置关系,并给予证明;
(3)当C、D、B在同一直线上时,求BC的长。
模型23 隐圆系列之点圆最值模型(解析版)-中考数学解题大招复习讲义

模型介绍平面内一定的D和⓪O上动点M的连线中,当连线过圆心O时,线段DM有最大值和最小值。
分以下情况讨论:(设OD=d,⓪O的半径为r)点D在⓪O外时,d>r,如图:①当D、M、O三点共线时,线段DM出现最值,DM的最大值为d+r,DM的最小值为d-r;②当点D在⓪O上时,d=r,如图:当D、O、M三点共线时,线段DM有最值;DM最大值为d+r,DM最小值为d-r=0(即点D与点M重合)③当点D在⓪O内时,d<r,如图当点D、O、M三点共线时,DM有最值;DM最大值为d+r,DM最小值为|d-r|=r-d;点圆最值:平面内一定点到圆上一点的距离的最值问题.方法:求出该定点到圆心的距离d,则最大值为d+r,最小值为|d-r|例题精讲【例1】.如图,在长方形纸片ABCD中,AB=4,AD=6.点E是AB的中点,点F是AD边上的一个动点.将△AEF沿EF所在直线翻折,得到△GEF.则GC长的最小值是()A.B.C.2D.2解:以点E为圆心,AE长度为半径作圆,连接CE,当点G在线段CE上时,GC的长取最小值,如图所示根据折叠可知:GE=AE=AB=2.在Rt△BCE中,BE=AB=2,BC=6,∠B=90°,∴CE==2,∴GC的最小值=CE﹣GE=2﹣2.故选:A.变式训练【变式1-1】.如图,在平行四边形ABCD中,AB=6,AD=2,∠A=45°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.解:如图,连接MC;过点M作ME⊥CD,交CD的延长线于点E.∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC=2,CD=AB=6,∵点M为AD的中点,∠A=45°,∴DM=MA=,∠MDE=∠A=45°,∴ME=DE=DM=1,∴CE=CD+DE=6+1=7,由勾股定理得:CM2=ME2+CE2,∴CM==5;由翻折变换的性质得:MA′=MA=,点A′在以M为圆心,为半径的圆上显然,当折线MA′C与线段MC重合时,线段A′C的长度最短,此时A′C=MC﹣MA′=5﹣=4,故答案为4.【变式1-2】.如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=,则点F与点C的最小距离为.解:如图取AB的中点G,连接FG.FC.GC.∵∠EAF=90°,tan∠AEF=,∴=,∵AB=6,AG=GB,∴AG=GB=3,∵AD=9,∴==,∴=,∵四边形ABCD是矩形,∴∠BAD=∠B=∠EAF=90°,∴∠FAG=∠EAD,∴△FAG∽△EAD,∴FG:DE=AF:AE=1:3,∵DE=3,∴FG=1,∴点F的运动轨迹是以G为圆心1为半径的圆,∵GC==3,∴FC≥GC﹣FG,∴FC≥3﹣1,∴CF的最小值为3﹣1.故答案为3﹣1.【例2】.如图,△ABC中,AB=AC,BC=24,AD⊥BC于点D,AD=5,P是半径为3的⊙A上一动点,连结PC,若E PC的中点,连结DE,则DE长的最大值为_______解:如图,连接PB,∵AB=AC,AD⊥BC,∴CD=DB=BC=12,∵点E为AC的中点,∴DE是△PBC的中位线,∴DE=PB,∴当PB取最大值时,DE的长最∵P是半径为3的⊙A上一动点,∴当PB过圆心A时,PB最大,∵BD=12,AD=5,∴AB=,∵⊙A的半径为3,∴PB的最大值为13+3=16,∴DE长的最大值为8,故选:A.变式训练【变式2-1】.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE⊥AF于E,在点F变化的过程中,线段DE的最小值是.解:如图,∵BE⊥AF于E,∴E在以AB为直径圆心为O的圆上,∴当O、E、D三点共线的时候线段DE最小,∵AB=2,四边形ABCD为正方形,∴AO=1=OE,AD=2,∴OD==,∴段DE最小值为OD﹣OF=﹣1.故答案为:﹣1.【变式2-2】.如图,AB是⊙O的直径,点C在半圆的中点,且BC=4cm,点D是上的一个动点,连接BD,过C点作CH⊥BD于H,连接AH,在点D的运动过程中,AH 长度的最小值是.解:连接AC,取BC的中点T,连接AT,TH.∵AB是直径,∴∠ACB=90°,∵点C在半圆的中点,∴=,∴AC=CB=4,∵CT=TB=2,∴AT===2,∵CH⊥BD,∴∠CHB=90°,∴点H在以BC为直径的圆上运动,∵CT=TB,∴HT=BC=2,∵AH≥AT﹣HT=2﹣2,∴AH的最小值为2﹣2,故答案为:2﹣2.1.如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为()A.B.C.﹣D.﹣2解:如图,取AD的中点O,连接OB,OM.∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC=4,∴∠BAP+∠DAM=90°,∵∠ADM=∠BAP,∴∠ADM+∠DAM=90°,∴∠AMD=90°,∵AO=OD=2,∴OM=AD=2,∴点M在以O为圆心,2为半径的⊙O上,∵OB===,∴BM≥OB﹣OM=﹣2,∴BM的最小值为﹣2.故选:D.2.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为()A.1.5B.C.D.2解:∵△ABC是等边三角形,∴∠ABC=∠BAC=60°,AC=AB=3,∵∠PAB=∠ACP,∴∠PAC+∠ACP=60°,∴∠APC=120°,∴点P的运动轨迹是,设所在圆的圆心为O,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:此时PA=PC,OB⊥AC,则AD=CD=AC=,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,∴PD=,BD=,∴PB=BD﹣PD=﹣=.故选:B.3.如图,在Rt△ABC中,∠ACB=90°,AB=2,点D为线段AB的中点,将线段BC绕点B顺时针旋转90°,得到线段BE,连接DE,则DE最大值是.解:如图,将线段BD绕点B顺时针旋转90°,得到线段BP,连接PE,PD,则DB=PB,∠DBP=90°,∵将线段BC绕点B顺时针旋转90°,得到线段BE,∴BC=BE,∠CBE=90°,∴∠CBD=∠EBP,∴△CBD≌△EBP(SAS),∴PE=DC,∵在Rt△ABC中,∠ACB=90°,AB=2,点D为线段AB的中点,∴DB=CD=AB=1,∴PE=1,PB=1,∴DP=,∵PD+PE≥DE,∴DE≤+1,∴DE最大值为+1,故答案为:+1.4.如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点P,则∠APD的度数为90°;连接CP,线段CP的最小值为﹣1.解:∵四边形ABCD是正方形,∴AD=CD,∠ADE=∠DCF=90°,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS),∴∠DAE=∠CDF,∵∠CDF+∠ADF=∠ADC=90°,∴∠ADF+∠DAE=90°,∴∠APD=90°,取AD的中点O,连接OP,则OP=AD=×2=1(不变),根据两点之间线段最短得C、P、O三点共线时线段CP的值最小,在Rt△COD中,根据勾股定理得,CO===,所以,CP=CO﹣OP=﹣1.故答案为:90°,﹣1.5.如图,在△ABC中,∠BAC=90°,AC=8,BC=10,AD是BC边上的高,E、F分别为边DC,DA上的动点,且DE:DF=4:3,射线AE与BF相交于点M,若连接CM,则线段CM的最小值为.解:如图1,连接EF,并延长EF交边AB于点G,∵在△ABC中,∠BAC=90°,AC=8,BC=10,∴,∴AC:AB=4:3,∴AC:AB=DE:DF=4:3,∴,∵∠BAC=∠FDE=90°,∴△BAC∽△FDE,∴∠GBE=∠DFE,∵AD是BC边上的高,∴AD⊥BC,∴∠DFE+∠DEF=90°,∴∠GBE+∠DEF=90°,∴∠BGE=90°,∴EG是△ABE的高,∵AD是△ABE的BE边上的高,∴BM是△ABE的AE边上的高,∴BM⊥AM,∴∠AMB=90°,∴点M在线段AB为直径的上,如图2,作以线段AB为直径的,取圆心O,连接OC交于点N,则当点O、M、C 三点共线时,线段CM的最小值,如图3,∵AB=6,点O是圆心,∴OA=ON=3,∵∠BAC=90°,AC=8,∴,∴线段CM的最小值即,故答案为:.6.如图,直角梯形ABCD中,AB∥DC,∠B=90°,AB=1,BC=2,CD=3,以B为圆心,半径为1的弧交BC于M,E是线段CD上一动点,EG⊥AD,垂足为G,F是弧AM 上一动点,则EG+EF的最小值为.解:作AH⊥CD于点H是矩形.DH=CD﹣AB=3﹣1=2,AH=BC=2.则AH=DH,△ADH是等腰直角三角形.则∠ADC=45°.延长BC到M使CM=BC=2,作MN⊥AD于点N,交CD于点K.则当E到K时,EG+EF 取得最小值.∵∠ADC=90°,MN⊥AD,∴△DNK是等腰直角三角形,∠NKD=∠CKM=45°,同理△CMK是等腰直角三角形.则CK=CM=2,KM=CM=2,∴DK=CD﹣CK=3﹣2=1,∴NK=DK=.则MN=MK+NK=2+=,则EG+EF的最小值是﹣1=.故答案是:.7.如图,在△ABC中,∠ACB=90°,AB=4,点O是AB的中点,以BC为直角边向外作等腰Rt△BCD,连接OD,当OD取最大值时,则∠ODB的度数是.解:如图,将△ODB绕点B逆时针旋转90°,得到△ECB,连接CO,EO,∵将△ODB绕点B逆时针旋转90°,得到△ECB,∴OB=BE,OD=CE,∠BCE=∠BDO,∠OBE=90°∵CE≤OC+OE∴当点O在CE上时,CE有最大值,即OD取最大值,∵BE=OB,∠ABE=90°∴∠BOE=45°∵点O是AB中点,∠ACB=90°∴CO=BO∴∠ECB=∠CBO,∵∠EOB=∠ECB+∠OBC=45°∴∠ECB=22.5°=∠BDO故答案为:22.5°8.如图,正方形ABCD的边长为2,点E为正方形外一个动点,∠AED=45°,P为AB中点,线段PE的最大值是.解:如图,若点E在正方形右侧,连接AC,BD交于点O,连接PO,EO,∵∠AED=45°,∠ACD=45°,∴A,C,E,D四点共圆,∵正方形ABCD的边长为2,∴OE=OD=BD=,∵P为AB的中点,O是BD的中点,∴OP=AD=,∵PE≤OP+OE=+,∴当点O在线段PE上时,PE=OP+OE=+,即线段PE的最大值为+,如图,点E在正方形ABCD上方,作斜边为AD的等腰直角△AOD,∠AOD=90°,则点E在以O为圆心,OA为半径的圆上,∴当点P,点O,点E共线时,PE的值最大,过点O作ON⊥AB,交BA延长线于点N,∵AD=2,AO=DO,∠AOD=90°∴AO=,∠OAD=45°,∵ON⊥AB,AD⊥AB∴∠NAO=∠NOA=45°∴AN=NO=∴PO===∴PE最大值为+>+,故答案为:+9.如图,在矩形ABCD中,AB=4,BC=6.(1)如图①,点E是AB的中点,点F是BC边上一点,将△BEF沿EF折叠,点B的对应点为点P,求CP的最小值;(2)如图②,若点P是矩形ABCD内部一点,且∠BPC=90°,求PD取得最小值时,BP的长;(3)如图③,若点P是矩形ABCD内部一点,且∠PAD+∠PBC=60°,求AP+BP的最大值.解:(1)如图1,∵点E是AB的中点,∴BE=AB=2,由折叠知,PE=BE=2,∴点P是在以E为圆心,2为半径的半圆上运动,当点E,P,C共线时,CP最小,∵四边形ABCD时矩形,∴∠ABC=90°,∴CE===2,=CP′=CE﹣EP′=2﹣2;∴CP最小(2)如图2,∵∠BPC=90°,∴点P在以BC为直径的半圆O上运动,当点D,P,O共线时,PD最小,在Rt△COD中,CD=4,OC=BC=3,∴OD=5,∴P′D=OD﹣OP′=5﹣3=2,作P′Q⊥BC于Q,∵∠OQP′=∠BCD=90°,∠COD为公共角,∴△OQP′∽△OCD,∴,∴,∴OQ=,QP′=,在Rt△BQP′中,QP′=,BQ=OB+OQ=3+=,∴BP′==,∴当PD取得最小值时,BP的长为:;(3)如图3,∵四边形ABCD是矩形,∴∠CAB=∠BAD=90°,∴∠CAB+∠BAD=180°,∵∠PAD+∠PBC=60°,∴(∠CAB+∠BAD)﹣(∠PAD+∠PBC)=120°,∴∠PAB+∠PBA=120°,在△ABP中,∠APB=180°﹣120°=60°,延长BP至E,使PE=PA,∴∠E=∠PAE,∵∠E+∠PAE=∠APB=60°,∴∠E=30°,在AB的右侧作等边三角形ABO,以O为圆心,AB为半径作圆O,则点E优弧AEC上运动,当BE为直径时,即点P在点O处时,AP+BP最大,最大为直径BE′=2AB=8.10.如图,已知四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G为FC的中点,连接GD,ED.(1)如图①,当点E在AB边上时,请直接写出DE,DG的数量关系;(2)如图②,将图①中的△AEF绕点A逆时针旋转,其他条件不变.①探究(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;②若AD=4,AE=1,求DG的最大值和最小值.解:(1)DE=DG,理由如下:如图①,连接EG,延长EG交BC的延长线于M,连接DM.∵四边形ABCD是正方形,∴AD=CD,∠B=∠ADC=∠DAE=∠DCB=∠DCM=90°,∵∠AEF=∠B=90°,∴EF∥CM,∴∠CMG=∠FEG,∵∠CGM=∠EGF,GC=GF,∴△CMG≌△FEG(AAS),∴EF=CM,GM=GE,∵AE=EF,∴AE=CM,∴△DCM≌△DAE(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∴DG⊥EM,DG=GE=GM,∴△EGD是等腰直角三角形,∴DE=DG.(2)①结论成立,理由如下:如图②,连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R.∵EG=GM,FG=GC,∠EGF=∠CGM,∴△CGM≌△FGE(SAS),∴CM=EF,∠CMG=∠GEF,∴CM∥ER,∴∠DCM=∠ERC,∵∠AER+∠ADR=180°,∴∠EAD+∠ERD=180°,∵∠ERD+∠ERC=180°,∴∠DCM=∠EAD,∵AE=EF,∴AE=CM,∴△DAE≌△DCM(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∵EG=GM,∴DG=EG=GM,∴△EDG是等腰直角三角形,∴DE=DG;②∵AE=1,△AEF绕点A旋转,∴点E在以点A为圆心,1为半径的圆A上运动,如图③,当点A、E、D三点共线,且点E在点A的左侧时,DE最大,此时DE=AD+AE=4+1=5,由①可知,DE=DG,∴DG=DE=,即DG的最大值为;如图④,当点A、E、D三点共线,且点E在点A的右侧时,DE最小,此时DE=AD﹣AE=4﹣1=3,由①可知,DE=DG,∴DG=DE=,即DG的最小值为;综上所述,DG的最大值为,最小值为.11.(1)如图1,A、B是⨀O上的两个点,点P在⨀O上,且△APB是直角三角形,⨀O 的半径为1①请在图1中画出点P的位置;②当AB=1时,∠APB=30°;(2)如图2,⨀O的半径为5,A、B为⨀O外固定两点(O、A、B三点不在同一直线上),且OA=9,P为⊙O上的一个动点(点P不在直线AB上),以PA和AB为作平行四边形PABC,求BC的最小值并确定此时点P的位置;(3)如图3,A、B是⊙O上的两个点,过A点作射线AM⊥AB,AM交⨀O于点C,若AB=3,AC=4,点D是平面内的一个动点,且CD=2,E为BD的中点,在D的运动过程中,求线段AE长度的最大值与最小值.解:(1)①如图1,△APB、△AP′B是直角三角形;②在Rt△APB中,AB=AP,∴∠APB=30°,故答案为:30;(2)四边形PABC是平行四边形,∴BC=AP,∴BC的最小值即AP的最小值,∵当P为OA与⊙O的交点时,AP最小,∴AP的最小值为9﹣5=4,即BC的最小值为4;(3)连接BC,∵AM⊥AB,∴∠CAB=90°,∴BC是⊙O的直径,∵点D是平面内的一个动点,且CD=2,∴点D的运动路径为以C为圆心,以2为半径的圆,在直角△ABC中,BC===5,∵O是直角△ABC斜边BC上的中点,∴AO=BC=,∵E是BD的中点,O是BC的中点∴OE=CD=1,∴AE的最小值是AO﹣OE=,最大值是AO+OE=.12.【问题提出】(1)如图①,四边形ABCD为正方形,以BC边为直径在BC上方作半圆O,P是上一点,若AB=6,则DP的最小值为3﹣3;【问题探究】(2)如图②,在Rt△ABC中,∠ACB=90°,BC=4,AC=3,CD是中线,将△ACD 沿CD折叠,得到△ECD,点A的对应点为E,连接AE,求AE的长;【问题解决】(3)如图③是一块矩形ABCD的场地,AB=300m,AD=600m,D为场地的出人口,点E在AD边上,且AE=400m.按照规划,要在矩形内修建一个小型观光台P,且满足∠APE=90°,在BC上修建休息亭M,并要在观光台P、休息台M以及出入口D之间规划道路PM,DM,为了节约成本,要使得线段PM,DM之和最短,试求PM+DM的最小值,并说明理由.(道路的宽度忽略不计)解:(1)如图1,连接OD,交⊙O于点P,则DP最小,∵四边形ABCD是正方形,∴∠BCD=90°,CD=BC=AB=3,在Rt△COD中,OC==3,CD=6,∴OD==3,∴DP=OD﹣OP=3﹣3,故答案为:3﹣3;(2)设CD,AE交于点F,∵∠ACB=90°,AC=3,BC=4,∴AB=5,由折叠得:AE=2AF,CD⊥AE,∵∠ACB=90°,CD是中线,∴AD=CD,∴∠ACD=∠CAD,∵∠AFC=∠ACB=90°,∴△ACF∽△BAC,∴,∴=,∴AF=,∴AE=2AF=;(3)如图2,∵∠APE=90°,∴点P在以AE为直径的⊙O上运动,作点D关于BC的对称点G,连接OG,交BC于M,交⊙O于P,则PM+DM最小,最小值为PG的长,∵四边形ABCD是矩形,∴CG=CD=AB=300,∠ADC=90°,在Rt△ODG中,DG=CD+CG=600,OD=AD﹣OA=600﹣200=400,∴OG===200,∴PG=OG﹣OP=200﹣200,∴PM+DM的最小值为:200﹣200.。
备考2024年中考数学专题突破(全国通用) 八种隐圆类最值问题(解析版)

2023 年湖北省鄂州市中考数学真题 2023·邵阳市中考真题 2023·广西南宁市二模 2022·辽宁抚顺·中考真题 2022·长春·中考真题 题型二 直角的对边是直径 2023·菏泽市中考真题 2022·通辽·中考真题 2023·汕头市金平区一模 2023·广州市天河区三模 2022·成都市成华区二诊 题型三 对角互补得圆 2023 年·广元市一模 题型四 定弦定角得圆 2023·成都市新都区二模 2023·成都市金牛区二模 2023·达州·中考真题 题型五 四点共圆 题型六 相切时取到最值 2023·随州市中考真题 2022·江苏无锡·中考真题 2022 扬州中考真题 题型七 定角定高面积最小、周长最小问题 题型八 米勒角(最大张角)模型 徐州中考
问题解决
资料整理
证明:在直线 l 上任取一点 Q(不与 P 点重合),连接 AQ、BQ,∠AQB 即为圆 O 的圆外角 ∴∠APB>∠AQB,∠APB 最大 ∴当圆与直线 l 相切时,∠APB 最大
资料整理
题型一 定点定长得圆
1.如图,在矩形 ABCD 中,已知 AB=3,BC=4,点 P 是 BC 边上一动点(点 P 不与 B,C 重合),连接 AP,作点 B 关于直线 AP 的对称点 M,则线段 MC 的最小值为( )
六、定角定高(探照灯模型) 什么叫定角定高,如右图,直线 BC 外一点 A,A 到直线 BC 距离为定值(定高),∠BAC 为定角。则 △ABC 的面积有最小值。又因为,像探照灯一样所以也叫探照灯模型。
A
O B DC
问题解决:如果顶角和高,都为定值,那么三角形 ABC 的外接圆的大小,也就是半径,是会随着 A 点 的运动而发生变化的。从而弦 BC 的长也会发生变化,它会有一个最小值,由于它的高 AD 是定值,因 此三角形 ABC 的面积就有一个最小值。
隐形圆(模型梳理与题型分类)(解析版)

隐形圆(4大模型与6类题型)第一部分【模型梳理与题型目录】隐形圆模型是初中数学中的重要知识点,常用于解决一些看似没有直接使用圆的知识但实际上需要运用圆的性质来解决的问题,隐形圆常常用于解决最值问题.本专题梳理了隐形圆四大模型,供大家参考使用.【模型1】 定点定长模型【模型分析】(1)出现共端点、等线段时,可以利用圆的定义构造辅助圆;(2)如图1,若OA=OB =OC,则A、B、C在以O为圆心,OA为半径的圆上.由圆周角定理可得:∠ABC= 1∠AOC,∠ACB=12∠AOB,∠BAC=12∠BOC.2图1【模型2】 90°圆周角模型【模型分析】如图2,在△ABC中,∠C=90°,点C为动点,则点C的轨迹是以AB为直径的⊙O (不包含A、B两点).注:作出辅助圆是关键,计算时结合求点圆、线圆、最值等方法进行相关计算.图2应用:常用于解决直角三角形中动点的轨迹问题。
【模型3】 定弦定角模型【模型分析】固定的线段只要对应固定的角度,那么这个角的顶点轨迹为圆的一部分.如图①,在⊙O中,若弦AB长度固定,则弦AB所对的圆周角都相等;(注意:弦AB所对的劣弧(AB)上也有圆周角,需要根据题目灵活运用)如图②,若有一固定线段AB及线段AB所对的∠C大小固定,根据圆的知识可知点C不唯一.当∠C<90°时,点C在优弧上运动;当∠C=90°时,点C在半圆上运动,且线段AB是⊙O的直径;当∠C >90°时,点C在劣弧上运动.【模型4】四点共圆模型【模型分析】在四边形ABCD中,若∠A+∠C=1800,则A、B、C、D在圆O上,称之为A、B、C、D四点共圆.图3应用:常用于解决四点共圆的问题,如角度相等、线段最值等问题.【题型1】定点定长模型......................................................3;【模型2】 90°圆周角模型...................................................6;【题型3】定弦定角模型.....................................................11;【题型4】四点共圆模型.....................................................15;【题型5】直通中考.........................................................20;【题型6】拓展延伸.........................................................23.第二部分【题型展示与方法点拨】【题型1】 定点定长模型1.(23-24九年级上·福建福州·期末)如图,在等边△ABC中,AB=4,D,E分别是边AB,BC上的动点(不与△ABC的顶点重合),连接AE,CD相交于点F,连接BF,若∠BDF+∠BEF=180°,则BF的最小值为.【答案】433/433【分析】根据等边三角形的性质,结合∠BDF +∠BEF =180°,得到∠DFE =120°,对顶角相等,得到∠AFC =120°,进而得到点F 在以O 为圆心,OA 的长为半径,且∠AOC =120°的圆弧上运动,连接OA ,OC ,OB ,OF ,则:OA =OC =OF ,BF ≥OB -OF ,证明△AOB ≌△COB ,得到△AOB 为含30度角的直角三角形,进行求解即可.解:∵等边△ABC ,∴∠ABC =60°,AB =BC ,∵∠BDF +∠BEF =180°,∴∠DFE +∠ABC =360°-∠BDF +∠BEF =180°,∴∠DFE =120°,∴∠AFC =120°,∴点F 在以O 为圆心,OA 的长为半径,且∠AOC =120°的圆弧上运动,如图,连接OA ,OC ,OB ,OF ,则:OA =OC =OF ,BF ≥OB -OF ,∵AB =BC ,OB =OB ,OA =OC ,∴△AOB ≌△COB ,∴∠ABO =∠CBO =12∠ABC =30°,∠AOB =∠BOC =12∠AOC =60°,∴∠BAO =90°,∴BO =2AO ,AB =3AO =4,∴AO =433,∴BO =2OA =833,OF =AO =433,∴BF ≤433,即:BF 的最小值为:433;故答案为:433.【点拨】本题考查等边三角形的性质,含30度角的直角三角形,勾股定理,全等三角形的判定和性质,求圆外一点到圆上一点的最值,解题的关键是确定点F 的运动轨迹.2.(24-25九年级上·全国·课后作业)如图,P 是边长为1的正方形ABCD 内的一个动点,且满足∠PBC +∠PDC =45°,则CP 的最小值是()A.2-2B.12C.22D.2-1【答案】D【分析】本题考查了正方形的性质、等腰直角三角形的性质、勾股定理、圆周角定理,在凹四边形BCDP中,求出∠BPD=135°,得点P在运动过程中,使得∠BPD=135°,即点P在正方形ABCD内,以A为圆心,AB长为半径的圆弧上,如解图,连接AP,AC,当A、P、C三点共线时,CP取得最小值,最小值为AC-AP,求出AC和AP的长度,即可得到结果,解本题的关键是证明∠BPD是定值,从而得到点P的轨迹.解:∵四边形ABCD是正方形,∴∠BCD=90°,在凹四边形BCDP中,∵∠BCD=90°,∠PBC+∠PDC=45°,∴∠BPC+∠CPD=360°-∠BCD-(∠PBC+∠PDC)=225°,∴∠BPD=360°-(∠BPC+∠CPD)始终为135°,得点P在运动过程中,使得∠BPD=135°,即点P在正方形ABCD内,以A为圆心,AB长为半径的圆弧上,如解图,连接AP,AC,,由解图可得AP+CP≥AC,当A、P、C三点共线时,CP取得最小值,最小值为AC-AP,在Rt△ABC中,∵AB=BC=1,∴AC=AB2+BC2=2,∵AP=AB=1,∴CP最小=AC-AP=2-1,故选:D.3.(24-25九年级上·江苏宿迁)如图,在矩形ABCD中,AB=6,BC=8,点E、F分别是边AB、BC上的动点,且EF=4,点G是EF的中点,AG、CG,则四边形AGCD面积的最小值为()A.30B.32C.35D.38【答案】D【分析】首先连接AC,BG,证明G在以B为圆心,2为半径的圆弧上,过B作BH⊥AC于H,当G在BH 上时,△ACG面积取最小值,此时四边形AGCD面积取最小值,再进一步解答即可.解:连接AC,BG,∵矩形ABCD,∴∠ABC=90°,S矩形=48,∵EF=4,G为EF的中点,∴BG=12EF=2,∴G在以B为圆心,2为半径的圆弧上,过B作BH⊥AC于H,当G在BH上时,△ACG面积取最小值,此时四边形AGCD面积取最小值,四边形AGCD面积=三角形ACG面积+三角形ACD面积,即四边形AGCD面积=三角形ACG面积+24.设圆弧交BH于G ,此时四边形AGCD面积取最小值,由勾股定理得:AC=62+82=10,∵1 2AC⋅BH=12AB⋅BC,∴BH=4.8,∴G H=2.8,即四边形AGCD面积的最小值=12×10×2.8+24=38.故选:D.【点拨】本题考查了勾股定理及矩形中的与动点相关的最值问题,圆的确定,解题的关键是利用直角三角形斜边的直线等于斜边的一半确定出G点的运动轨迹.【题型2】 90°圆周角模型4.(2024·湖南娄底·一模)如图,正方形ABCD的边长为a,点E、F分别在BC、CD上,且BE=CF,AE与BF相交于点G,连接CG,则CG的最小值为.【答案】5-1 a2【分析】本题考查了正方形的性质,圆周角定理,勾股定理,以及全等三角形的判定与性质,熟练掌握90°的圆周角所对的弦是直径是解答本题的关键.通过证明△ABE ≌△BCF SAS ,可证∠AGB =90°,则点G 在以AB 为直径的一段弧上运动,当点G 在OC 与弧的交点处时,CG 最短,然后根据勾股定理求出OC 的长即可求解.解:∵四边形ABCD 是正方形,∴∠ABC =∠BCF =90°,AB =BC =a ,∴在△ABE 和△BCF 中,AB =BC∠ABC =∠BCFBE =CF∴△ABE ≌△BCF SAS ,∴∠BAE =∠CBF ,∵∠ABF +∠CBF =90°,∴∠ABF +∠BAE =90°,∴∠AGB =90°,∴点G 在以AB 为直径的一段弧上运动,设AB 的中点为O ,则当点G 在OC 与弧的交点处时,CG 最短,∵AB =a ,∴OB =OG =a 2,∴OC =a 2 2+a 2=52a ,∴CG=OC -OG =5-1 a 2,故答案为:5-1 a 2.5.(23-24九年级下·山东日照)如图,已知正方形ABCD 的边长为2,点F 是正方形内一点,连接CF ,DF ,且∠ADF =∠DCF ,点E 是AD 边上一动点,连接EB ,EF ,则EB +EF 长度的最小值为()A.13-1B.10-1C.10D.5+1【答案】A【分析】根据正方形的性质得到∠ADC=90°,推出∠DFC=90°,得到点F在以CD为直径的半圆上移动,如图,设CD的中点为O,正方形ABCD关于直线AD对称的正方形ADC B ,则点B 的对应点是B,连接B O交AD于E,交半圆O于F,线段B F的长即为EB+EF的长度最小值,根据勾股定理即可得到结论.解:∵四边形ABCD是正方形,∴∠ADC=90°,∴∠ADF+∠CDF=90°,∵∠ADF=∠DCF,∴∠DCF+∠CDF=90°,∴∠DFC=90°,∴点F在以CD为直径的半圆上移动,如图,设CD的中点为O,正方形ABCD关于直线AD对称的正方形ADC B ,则点B 的对应点是B,连接B O交AD于E,交半圆O于F,线段B F的长即为EB+EF的长度最小值,OF=1,∵∠C =90°,B C =C D =CD=2,∴OC =3,∴OB =B C 2+OC 2=13,∴B F=13-1,∴FD+FE的长度最小值为13-1,故选:A.【点拨】此题考查了正方形的性质,圆周角定理,轴对称的性质,点的运动轨迹,勾股定理,最小值问题,正确理解点的运动轨迹是解题的关键.6.(24-25九年级上·广东深圳·开学考试)如图,E,F是正方形ABCD的边AD上两个动点,满足AE= DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为1,则线段DH长度的最小值是()A.52-1 B.5-12C.52D.5-1【答案】B【分析】由SAS可判定△ABE≌△DCF,由全等三角形的性质得∠ABE=∠DCF,同理可证∠DCG=∠DAG,由角的和差得∠AHB=90°,取AB的中点O,连接OH,H的运动轨迹为以O为圆心,OH=1 2AB=12为半径的半圆,当O、H、D三点共线时,DH最小,即可求解.解:∵四边形ABCD是正方形,∴AB=AD=CD=1,∠BAE=∠CDF=90°,∠ADG=∠CDG,∵∠BAH+∠DAG=90°,在△ABE和△DCF中,AB=CD∠BAE=∠CDFAE=DF,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,在△ADG和△CDG中,AD=CD∠ADG=∠CDGDG=DG,∴△ADG≌△CDG(SAS),∴∠DCG=∠DAG,∴∠ABE=∠DAG,∴∠ABE+∠BAH=90°,∴∠AHB=90°,如下图,取AB的中点O,连接OH,∴OA=12,∴H的运动轨迹为以O为圆心,OH=12AB=12为半径的半圆,如图,当O、H、D三点共线时,DH最小,∴OD=OA2+AD2=122+12=52,∴DH=OD-OH=52-1 2=5-12;故选:B.【点拨】本题考查了正方形的性质,全等三角形的判定及性质,勾股定理,直角三角形的特征,圆外一点到圆上任一点距离的最值等;能找出动点的运动轨迹及取得最小值的条件,熟练利用勾股定咯求解是解题的关键.【题型3】 定弦定角模型7.(22-23九年级上·江苏南京·阶段练习)如图,CD是△ABC的高,若AB=2,∠ACB=45°,则CD长的最大值为()A.1+2B.4-2C.2D.4【答案】A【分析】在AB上方作以AB为斜边的等腰直角三角形△AOB,根据“定线段对定角度”确定点C在以O为圆心,OA长为半径的圆上运动,当CD经过圆心时CD最长,再计算即可.解:在AB上方作以AB为斜边的等腰直角三角形△AOB,∵∠ACB=45°∴点C在以O为圆心,OA长为半径的圆上运动,∵AB=2,∴OA=OC=2,当CD经过圆心时CD最长∵CD是△ABC的高,∴AD=BD=OD=1AB=12此时CD=OC+OD=2+1,故选:A.【点拨】本题考查几何最值问题,解题的关键是确定点C在以O为圆心,OA长为半径的圆上运动.8.(20-21九年级上·江苏无锡·期末)如图,在平面直角坐标系中,动点A、B分别在x轴上和函数y=x的图象上,AB=4,CB⊥AB,BC=2,则OC的最大值为()A.22+2B.22+4C.25D.25+2【答案】A【分析】根据y=x与x轴的夹角为45°,以AB为斜边作等腰直角三角形,连接AD,CD,OD,则∠DBC= 45°,根据勾股定理求得DB的长,进而证明△DCB是直角三角形,求得DC的长,根据OD+DC≥OC,即可求得OC的最大值解:如图,以AB为斜边作等腰直角三角形,连接AD,CD,OD,∵y=x与x轴的夹角为45°,∴∠AOB=45°=1∠ADB2∴A,O,B在⊙D上,∵AB=4,∠ADB=90°,∴BD=AD=22,∴∠ABD=45°∵BC⊥AB∴∠CBA=90°∴∠CBD=45°∴△BCD中BC=2,BD=22,∠CBD=45°过点C作CE⊥BD于点E,如图则BE=CE=2=DE∴CD=CB=2∵OD+DC≥OC∴当O,D,C三点共线时,OC取得最大值,最大值为OD+DC=DB+DC=22+2故选A【点拨】本题主要考查了勾股定理,同弧所对的圆周角等于圆心角的一半,找到⊙D是解决本题的关键.9.(19-20九年级上·浙江宁波·期末)如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为()A.0.5B.2-1C.2-2D.13【答案】C 【分析】先计算出∠PBC +∠PCB =45°,则∠BPC =135°,利用圆周角定理可判断点P 在以BC 为弦的⊙O 上,如图,连接OA 交BC 于P ′,作BC 所对的圆周角∠BQC ,利用圆周角定理计算出∠BOC =90°,从而得到△OBC 为等腰直角三角形,四边形ABOC 为正方形,所以OA =BC =2,OB =2,根据三角形三边关系得到AP ≥OA -OP (当且仅当A 、P 、O 共线时取等号,即P 点在P ′位置),于是得到AP 的最小值.解:解:∵△ABC 为等腰直角三角形,∴∠ACB =45°,即∠PCB +∠PCA =45°,∵∠PBC =∠PCA ,∴∠PBC +∠PCB =45°,∴∠BPC =135°,∴点P 在以BC 为弦的⊙O 上,如图,连接OA 交BC于P ′,作BC 所对的圆周角∠BQC ,则∠BCQ =180°-∠BPC =45°,∴∠BOC =2∠BQC =90°,∴△OBC 为等腰直角三角形,∴四边形ABOC 为正方形,∴OA =BC =2,∴OB =22BC =2,∵AP ≥OA -OP (当且仅当A 、P 、O 共线时取等号,即P 点在P ′位置),∴AP 的最小值为2-2.故选:C .【点拨】本题考查了圆周角定理及等腰直角三角形的性质.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.【题型4】四点共圆模型10.(22-23九年级上·黑龙江哈尔滨·阶段练习)如图,在四边形ABCD 中,∠ABC =∠D =90°,连接AC ,点F 为边CD 上一点,连接BF 交AC 于点E ,AB =AE ,∠FGC +∠FBG =90°,∠BFG +2∠GFC =180°,若AD =722,BG =4,则CG 的长为.【答案】8【分析】延长BA 与CD 的延长线相交于点H ,证明∠FGC =∠ABF ,∠GFC =∠BFD ,由三角形内角和定理得到∠H=∠ACB,BH=BC,进一步得到∠H=∠DAH=45°,则AD=DH=722,由勾股定理得到AH=AD2+DH2=7,证明点C、G、E、F四点共圆,如图,连接EG,证明CE=CG,设CE=CG=x,则BH=BC=4+x,AE=AB=x-3,AC=2x-3,由勾股定理得AB2+BC2=AC2,即x-32+x+42 =2x-32,解方程即可得到答案.解:延长BA与CD的延长线相交于点H,∵∠FGC+∠FBG=90°,∠FBG+∠ABF=∠ABC=90°∴∠FGC=∠ABF,∵∠BFG+2∠GFC=180°,∠BFG+∠BFD+∠CFG=180°,∴2∠GFC=∠BFD+∠CFG,∴∠GFC=∠BFD,∵∠H+∠ABF+∠BFD=180°=∠ACB+∠FGC+∠GFC,∴∠H=∠ACB,∵∠ABC=90°,∴∠H=∠ACB=45°,BH=BC,∵∠ADH=90°,∴∠H=∠DAH=45°,∴AD=DH=722,∴AH=AD2+DH2=7,∵AB=AE,∴∠ABE=∠AEB,∵∠FGC=∠ABE,∠CEF=∠AEB,∴∠FGC=∠CEF,∴点C、G、E、F四点共圆,如图,连接EG,∴∠GFC=∠CEG,∠BFD=∠CGE,∵∠GFC=∠BFD,∴∠CGE=∠CEG,∴CE=CG,设CE=CG=x,则BH=BC=BG+CG=4+x,∴AE=AB=BH-AH=x+4-7=x-3,∴AC=AE+CE=x-3+x=2x-3,由勾股定理得,AB2+BC2=AC2,∴x-32+x+42=2x-32,解得x=-1(不合题意,舍去)或x=8,∴CG=8,故答案为:8【点拨】此题考查了等腰直角三角形的判定和性质、勾股定理、等腰三角形的判定和性质、四点共圆、圆周角定理、圆内接四边形的性质、解一元二次方程等知识,关键在于等腰直角三角形的判定和性质与证明四点共圆.11.(24-25九年级上·江苏宿迁·阶段练习)如图,等边三角形ABC中,AB=5,P为AB边上一动点,PD⊥BC ,PE ⊥AC ,垂足分别为D ,E 则DE 的最小值为.【答案】154【分析】如图,连接PC ,取CP 的中点O ,连接OE ,OD ,过点O 作OH ⊥DE 于H ,首先证明△ODE 是顶角为120°的等腰三角形,当OE 的值最小时,DE 的值最小,即可求出PC 的最小值.解:如图,连接PC ,取CP 的中点O ,连接OE ,OD ,过点O 作OH ⊥DE 于H ,∵△ABC 是等边三角形,∴∠ACB =60°,AB =BC =AC =5,∵PD ⊥BC ,PE ⊥AC ,∴∠PEC =∠PDC =90°,∵OP =OC ,∴OE =OP =OC =OD ,∴C 、D 、P 、E 四点共圆,∴∠EOD =2∠ECD =120°,∴当OE 的值最小时,DE 的值最小,根据垂线段最短可得,当CP ⊥AB 时,PC =532,此时OE 最小,OE =534,∵OE =OD ,OH ⊥DE ,∴DH =EH ,∠DOH =∠EOH =60°,∴∠OEH =30°,∴OH =12OE =538,∴DH =EH =OE 2-OH 2=158,∴DE =2DH =154,∴DE 的值最小为154,故答案为:154.【点拨】本题考查了四点共圆、垂线段最短、圆周角定理、含30°角的直角三角形的性质、等腰直角三角形的判定与性质等知识;正确判断当CP ⊥AB 时OE 最小是解题的关键.12.(23-24九年级下·江苏南京·阶段练习)如图,在△ABC 中,∠ACB =90°,AC =BC =2,点P 是射线AB 上一动点,∠CPD =90°,且PC =PD ,连接AD 、CD ,则AD +CD 的最小值是.【答案】25【分析】取AC中点H,连接DH交AB于点G,连接BD,PH,当DH⊥AC时,DH有最小值,此时易得△ACD是等腰三角形,推出AD=CD,即AD,CD有最小值,则AD+CD有最小值,此时根据∠AHD=∠CHD=∠ACB=90°,推出DH∥BC,设CD中点为O,根据∠CHD=∠CPD=90°,易得点C,H,P,D在以点O为圆心CD为直径的圆上,易得∠CHP+∠PDC=180°,由∠ABC=45°,易得此时点B在圆O上,进而推出∠CBD+∠CPD=180°,则∠CBD=90°,得到四边形BCHD是矩形,即HD=BC=2,利用勾股定理即可计算出CD的最小值,进而得出结果.解:取AC中点H,连接DH交AB于点G,连接BD,PH,当DH⊥AC时,DH有最小值,∵点H是AC中点,DH⊥AC,∴△ACD是等腰三角形,∴AD=CD,∵AH,CH是定值,DH有最小值时,即AD,CD有最小值,则AD+CD有最小值,∵∠AHD=∠CHD=∠ACB=90°,∴DH∥BC,设CD中点为O,∵∠CHD=∠CPD=90°,∴点C,H,P,D在以点O为圆心CD为直径的圆上,∴∠CHP+∠PDC=180°,∵∠ABC=45°,∴此时点B在圆O上,∴∠CBD+∠CPD=180°,∴∠CBD=90°,∵DH∥BC,∴四边形BCHD是矩形,∴HD=BC=2,∵HC=1AC=1,2在Rt△CHD中,∴CD=CH2+HD2=5,∴AD+CD的最小值为2CD=25,故答案为:25.【点拨】本题考查勾股定理求最短距离,圆周角定理,四点共圆,等腰三角形的判定与性质,矩形的判定与性质,正确作出辅助线,证明四点共圆是解题的关键.第三部分【中考链接与拓展延伸】1、直通中考1.(2023·山东泰安·中考真题)如图,在平面直角坐标系中,Rt △AOB 的一条直角边OB 在x 轴上,点A 的坐标为(-6,4);Rt △COD 中,∠COD =90°,OD =43,∠D =30°,连接BC ,点M 是BC 中点,连接AM .将Rt △COD 以点O 为旋转中心按顺时针方向旋转,在旋转过程中,线段AM 的最小值是()A.3B.62-4C.213-2D.2【答案】A【分析】如图所示,延长BA 到E ,使得AE =AB ,连接OE ,CE ,根据点A 的坐标为(-6,4)得到BE =8,再证明AM 是△BCE 的中位线,得到AM =12CE ;解Rt △COD 得到OC =4,进一步求出点C 在以O 为圆心,半径为4的圆上运动,则当点M 在线段OE 上时,CE 有最小值,即此时AM 有最小值,据此求出CE 的最小值,即可得到答案.解:如图所示,延长BA 到E ,使得AE =AB ,连接OE ,CE ,∵Rt △AOB 的一条直角边OB 在x 轴上,点A 的坐标为(-6,4),∴AB =4,OB =6,∴AE =AB =4,∴BE =8,∵点M 为BC 中点,点A 为BE 中点,∴AM 是△BCE 的中位线,∴AM =12CE ;在Rt △COD 中,∠COD =90°,OD =43,∠D =30°,∴OC =33OD =4,∵将Rt △COD 以点O 为旋转中心按顺时针方向旋转,∴点C 在以O 为圆心,半径为4的圆上运动,∴当点M 在线段OE 上时,CE 有最小值,即此时AM 有最小值,∵OE =BE 2+OB 2=10,∴CE 的最小值为10-4=6,∴AM 的最小值为3,故选A .【点拨】本题主要考查了一点到圆上一点的最值问题,勾股定理,三角形中位线定理,坐标与图形,含30度角的直角三角形的性质等等,正确作出辅助线是解题的关键.2.(2022·广西柳州·中考真题)如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为.【答案】25-2【分析】如图,由EG=2,确定E在以G为圆心,半径为2的圆上运动,连接AE,再证明△ADE≌△CDF (SAS),可得AE=CF,可得当A,E,G三点共线时,AE最短,则CF最短,再利用勾股定理可得答案.解:如图,由EG=2,可得E在以G为圆心,半径为2的圆上运动,连接AE,∵正方形ABCD,∴AD=CD,∠ADC=90°,∴∠ADC=∠EDF=90°,∴∠ADE=∠CDF,∵DE=DF,∴△ADE≌△CDF(SAS),∴AE=CF,∴当A,E,G三点共线时,AE最短,则CF最短,∵G位BC中点,BC=AB=4,∴BG=2,此时AG=BG2+AB2=22+42=25,此时AE=25-2,所以CF的最小值为:25-2.故答案为:25-2【点拨】本题考查的是正方形的性质,圆的基本性质,勾股定理的应用,二次根式的化简,熟练的利用圆的基本性质求解线段的最小值是解本题的关键.2、拓展延伸3.(2022·辽宁抚顺·中考真题)如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF.当GF最小时,AE的长是.【答案】55-5【分析】根据动点最值问题的求解步骤:①分析所求线段端点(谁动谁定);②动点轨迹;③最值模型(比如将军饮马模型);④定线段;⑤求线段长(勾股定理、相似或三角函数),结合题意求解即可得到结论.解:①分析所求线段GF端点:G是定点、F是动点;②动点F的轨迹:正方形ABCD的边长为10,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,则BF=BA=10,因此动点轨迹是以B为圆心,BA=10为半径的圆周上,如图所示:③最值模型为点圆模型;④GF最小值对应的线段为GB-10;⑤求线段长,连接GB,如图所示:在RtΔBCG中,∠C=90°,正方形ABCD的边长为10,点G是边CD的中点,则CG=5,BC=10,根据勾股定理可得BG=CG2+BC2=52+102=55,当G、F、B三点共线时,GF最小为55-10,接下来,求AE的长:连接EG,如图所示根据翻折可知EF=EA,∠EFB=∠EAB=90°,设AE=x,则根据等面积法可知S=S+S+SΔBAE+SΔBEG,即100=12DE⋅DG+12BC⋅CG+12AB⋅AE+12BG⋅EF=1 2510-x+5×10+10x+55x整理得5+1x=20,解得x=AE=205+1=205-15+15-1=55-5,故答案为:55-5.【点拨】本题考查动点最值下求线段长,涉及到动点最值问题的求解方法步骤,熟练掌握动点最值问题的相关模型是解决问题的关键.4.(2024·内蒙古兴安盟·二模)如图,在正方形ABCD中,点M,N分别为AB,BC上的动点,且AM= BN,DM,AN交于点E,点F为AB的中点,点P为BC上一个动点,连接PE,PF,若AB=4,则PE +PF的最小值为.【答案】210-2【分析】证明△DAM≌△ABN SAS,则∠ADM=∠BAN,∠AED=90°,如图,取AD的中点O,则E在以O为圆心,AD为直径的圆上运动,作F关于BC对称的点F ,连接PF ,连接OF 交⊙O于E ,则PF = PF,由PE+PF=PE+PF ,可知当O、E 、P、F 四点共线时,PE+PF最小为E F ,由勾股定理得,OF =AF 2+OA2=210,根据E F =OF -OE ,求解作答即可.解:∵正方形ABCD,∴AD=AB,∠DAM=∠ABN=90°,又∵AM=BN,∴△DAM≌△ABN SAS,∴∠ADM=∠BAN,∴∠ADM+∠DAE=∠BAN+∠DAE=90°,∴∠AED=90°,如图,取AD的中点O,则E在以O为圆心,AD为直径的圆上运动,作F关于BC对称的点F ,连接PF ,连接OF 交⊙O于E ,∴PF =PF,∴PE+PF=PE+PF ,∴当O、E 、P、F 四点共线时,PE+PF最小为E F ,由勾股定理得,OF =AF 2+OA2=62+22=210,∴E F =OF -OE =210-2,故答案为:210-2.【点拨】本题考查了正方形的性质,全等三角形的判定与性质,90°圆周角所对的弦为直径,轴对称的性质,勾股定理等知识.熟练掌握正方形的性质,全等三角形的判定与性质,90°圆周角所对的弦为直径,轴对称的性质,勾股定理是解题的关键.。
专题11 圆的最值问题(隐圆模型)(解析版)-2024年常考压轴题攻略(9年级上册人教版)
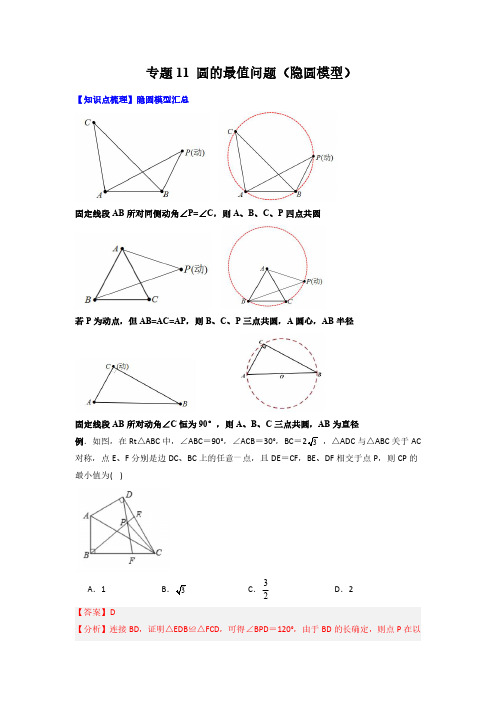
专题11圆的最值问题(隐圆模型)【知识点梳理】隐圆模型汇总固定线段AB所对同侧动角∠P=∠C,则A、B、C、P四点共圆若P为动点,但AB=AC=AP,则B、C、P三点共圆,A圆心,AB半径固定线段AB所对动角∠C恒为90°,则A、B、C三点共圆,AB为直径A.1B.作正方形ABCD关于直线BC对称的正方形则点D的对应点是F,连接FO交BC于P,交半圆O于=,根据对称性有:PD PF+=+,则有:PE PD PE PF+的长度最小值,则线段EF的长即为PE PD【答案】634-【分析】取AD 的中点O ,连接OF BC ⊥于F ,交CD 于G 取AD 的中点O ,连接OM ,过点于F ,交CD 于G ,则OM ME + AB CD ,60DAB ∠= ,AD ∴120ADC ∠=︒,AD CD =,【答案】3∴BD=2,∴11 2BD=.D运动的一个动点,联结EF,将AEF沿EF折叠,点A落在点G处,在运动的过程中,点G运动的路径长为()A.23πB C.3πD.1【答案】A【详解】解:∵点E 为AB 中点,点F 为AD 边上从A 到D 运动的一个动点,联结EF ,将AEF 沿EF 折叠,∴AE EB EG ==,∴G 点在以E 为圆心,AE 长为半径的圆上运动.当F 与D 点重合时,如图,则G 点运动的路径为 AG .∵AB =2,点E 为AB 中点,∴112AE AB ==,∵矩形ABCD ,∴90EAD ∠=︒,∵1AE =,AD =90EAD ∠=︒,∴tan AD AED AE∠==60AED ∠=︒.∵将AEF 沿EF 折叠,∴60DEG AED ∠=∠=︒,∴120AEG ∠=︒,∵1AE =,∴120223603AG AE ππ=⨯⨯=.故选:A .3.如图,在Rt ABC 中,90ACB ∠=︒,5AC =,12BC =,D 是以点A 为圆心,3为半径的圆上一点,连接BD ,M 是BD 的中点,则线段CM 长度的最小值为()A .3B .4C .5D .6【答案】C 【详解】作AB 的中点E ,连接EM 、CE 、AD ,则有AD =3,∵∠ACB =90°,即在Rt ABC 中,13AB ==,∵E 是Rt ABC 斜边AB 上的中点,∴11322CE AB ==,∵M 是BD 的中点,E 是AB 的中点,∴1322ME AD ==,∴在CEM 中,1331332222CM -+<<,即58CM <<;当C 、M 、E 三点共线时有133822CM +==或者133522CM -==;即58CM ≤≤,∴CM 最小值为5,故选:C .【答案】21022-【分析】由题意可知,AGB ∠圆周角45APB ∠=︒的圆上,(要使。
隐圆模型(解析版)

隐圆模型(解析版)隐圆模型(解析版)隐圆模型是一种常见的数学模型,用于描述在给定的数据集中存在一个或多个圆形结构的情况。
它被广泛应用于图像分析、模式识别和计算机视觉等领域。
本文将详细介绍隐圆模型的基本原理、应用案例以及解析方法。
一、隐圆模型的基本原理隐圆模型是一种统计模型,它假设数据集中存在一个或多个未知的圆形结构。
每个圆由其圆心位置和半径大小来定义。
在隐圆模型中,圆心位置和半径大小被视为模型参数,需要通过对数据集进行观察和分析来估计。
隐圆模型的基本原理可以通过以下步骤来描述:1. 数据预处理:首先,对输入的数据集进行预处理,包括去除噪声、归一化等操作,以提高模型的准确性和鲁棒性。
2. 圆心估计:通过对数据集进行分析,通过最大似然估计或其他方法来估计圆心位置。
常用的方法包括迭代算法、数学优化等。
3. 半径估计:在估计了圆心位置之后,通过计算每个数据点到圆心的距离,并进行合适的求解方法,例如最小二乘法,来估计圆的半径大小。
4. 圆形结构检测:在估计了圆心位置和半径大小之后,可以通过定义适当的判定条件来检测是否存在圆形结构。
例如,可以通过计算数据点到估计的圆心的距离,判断是否接近估计的半径大小。
二、隐圆模型的应用案例隐圆模型在许多领域都有广泛的应用。
以下是一些常见的应用案例:1. 图像分析:隐圆模型可以应用于图像分析领域,如圆形目标的检测、图像边缘提取等。
通过在图像中检测和估计圆的参数,可以实现图像中圆形结构的自动识别和分析。
2. 模式识别:在模式识别任务中,隐圆模型可以用于描述和识别具有圆形特征的模式。
例如,可以利用隐圆模型来识别和跟踪运动中的圆形目标。
3. 计算机视觉:在计算机视觉领域,隐圆模型可以应用于物体检测、跟踪和分割等任务。
通过对图像中的圆形结构进行建模和分析,可以实现对图像中对象的自动识别和定位。
三、隐圆模型的解析方法隐圆模型的解析方法主要基于数学分析和优化算法。
以下是一些常见的解析方法:1. 最小二乘法:最小二乘法是一种经典的数学分析方法,可用于估计圆心位置和半径大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
隐圆模型【点睛1】触发隐圆模型的类型(1)动点定长模型若P为动点,但AB=AC=AP 原理:圆A中,AB=AC=AP则B、C、P三点共圆,A圆心,AB半径备注:常转全等或相似证明出定长(2)直角圆周角模型固定线段AB所对动角∠C恒为90°原理:圆O中,圆周角为90°所对弦是直径则A、B、C三点共圆,AB为直径备注:常通过互余转换等证明出动角恒为直角(3)定弦定角模型固定线段AB所对动角∠P为定值原理:弦AB所对同侧圆周角恒相等则点P运动轨迹为过A、B、C三点的圆备注:点P在优弧、劣弧上运动皆可(4)四点共圆模型①若动角∠A+动角∠C=180° 原理:圆内接四边形对角互补则A 、B 、C 、D 四点共圆 备注:点A 与点C 在线段AB 异侧(5)四点共圆模型②固定线段AB 所对同侧动角∠P=∠C 原理:弦AB 所对同侧圆周角恒相等 则A 、B 、C 、P 四点共圆 备注:点P 与点C 需在线段AB 同侧【点睛2】圆中旋转最值问题条件:线段AB 绕点O 旋转一周,点M 是线段AB 上的一动点,点C 是定点 (1)求CM 最小值与最大值 (2)求线段AB 扫过的面积 (3)求ABC S △最大值与最小值作法:如图建立三个同心圆,作OM ⊥AB ,B 、A 、M 运动路径分别为大圆、中圆、小圆 结论:①CM 1最小,CM 3最大②线段AB 扫过面积为大圆与小圆组成的圆环面积③ABC S △最小值以AB 为底,CM 1为高;最大值以AB 为底,CM 2为高典题探究 启迪思维 探究重点例题1. 如图,在边长为2的菱形ABCD 中,∠A =60°,M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在直线翻折得到△A `MN ,连接A `C ,则A `C 长度的最小值是__________.A'N MA BCD【分析】考虑△AMN 沿MN 所在直线翻折得到△A ’MN ,可得MA ’=MA =1,所以A ’轨迹是以M 点为圆心,MA 为半径的圆弧.连接CM ,与圆的交点即为所求的A ’,此时A ’C 的值最小.构造直角△MHC ,勾股定理求CM ,再减去A ’M .A'N MA BCDDC BA MN A'H A'N MA BCD变式练习>>>1.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,点F 在边AC 上,并且CF =2,点E 为边BC 上的动点,将△CEF 沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是__________.ABCEFP【分析】考虑到将△FCE 沿EF 翻折得到△FPE ,可得P 点轨迹是以F 点为圆心,FC 为半径的圆弧.过F 点作FH ⊥AB ,与圆的交点即为所求P 点,此时点P 到AB 的距离最小.由相似先求FH ,再减去FP ,即可得到PH .答案为1.2.ABCEFPB例题2. 如图,已知圆C 的半径为3,圆外一定点O 满足OC =5,点P 为圆C 上一动点,经过点O 的直线l 上有两点A 、B ,且OA =OB ,∠APB =90°,l 不经过点C ,则AB 的最小值为________.l【分析】连接OP ,根据△APB 为直角三角形且O 是斜边AB 中点,可得OP 是AB 的一半,若AB 最小,则OP 最小即可.连接OC ,与圆C 交点即为所求点P ,此时OP 最小,AB 也取到最小值.答案为4.ll变式练习>>>2.如图,矩形ABCD 中,AB =4,BC =8,P 、Q 分别是直线BC 、AB 上的两个动点,AE =2,△AEQ 沿EQ 翻折形成△FEQ ,连接PF 、PD ,则PF +PD 的最小值是_________.Q ABC DEFP答案为8.【分析】F 点轨迹是以E 点为圆心,EA 为半径的圆,作点D 关于BC 对称点D ’,连接PD ’,PF +PD 化为PF +PD ’.连接ED ’,与圆的交点为所求F 点,与BC 交点为所求P 点,勾股定理先求ED ‘,再减去EF 即可.D'PFE D CBAQ例题3. 如图,E 、F 是正方形ABCD 的边AD 上的两个动点,满足AE =DF ,连接CF 交BD 于点G ,连接BE 交AG 于点H ,若正方形边长为2,则线段DH 长度的最小值是________.HGAB CDEF【分析】根据条件可知:∠DAG =∠DCG =∠ABE ,易证AG ⊥BE ,即∠AHB =90°,所以H 点轨迹是以AB 为直径的圆弧当D 、H 、O 共线时,DH1αααHGABCDE F变式练习>>>3.如图,Rt △ABC 中,AB ⊥BC ,AB =8,BC =4,P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值是_________.PABC答案为4【分析】∵∠PBC +∠PBA =90°,∠PBC =∠P AB ,∴∠P AB +∠PBA =90°,∴∠APB =90°, ∴P 点轨迹是以AB 为直径的圆弧.当O 、P 、C 共线时,CP 取到最小值,勾股定理先求OC ,再减去OP 即可.例题4. 如图,在Rt △ABC 中,∠ACB =90°,BC =4,AC =10,点D 是AC 上的一个动点,以CD 为直径作圆O ,连接BD 交圆O 于点E ,则AE 的最小值为_________.B【分析】连接CE ,由于CD 为直径,故∠CED =90°,考虑到CD 是动线段,故可以将此题看成定线段CB 对直角∠CEB .取CB 中点M ,所以E 点轨迹是以M 为圆心、CB 为直径的圆弧.连接AM ,与圆弧交点即为所求E 点,此时AE值最小,22AE AM EM =-==.BB变式练习>>>4.如图,正方形ABCD 的边长为4,动点E 、F 分别从点A 、C 同时出发,以相同的速度分别沿AB 、CD 向终点B 、D 移动,当点E 到达点B 时,运动停止,过点B 作直线EF 的垂线BG ,垂足为点G ,连接AG ,则AG 长的最小值为 .GF EDCB A【分析】首先考虑整个问题中的不变量,仅有AE =CF ,BG ⊥EF ,但∠BGE 所对的BE 边是不确定的. 重点放在AE =CF ,可得EF 必过正方形中心O 点,连接BD ,与EF 交点即为O 点.∠BGO 为直角且BO 边为定直线,故G 点轨迹是以BO 为直径的圆.记BO 中点为M 点,当A 、G 、M 共线时,AG 取到最小值,利用Rt △AOM 勾股定理先求AM ,再减去GMAB CDEF G例题5. 如图,等边△ABC 边长为2,E 、F 分别是BC 、CA 上两个动点,且BE =CF ,连接AE 、BF ,交点为P 点,则CP 的最小值为________.EFCBAP【分析】由BE =CF 可推得△ABE ≌△BCF ,所以∠APF =60°,但∠APF 所对的边AF 是变化的.所以考虑∠APB =120°,其对边AB 是定值.所以如图所示,P 点轨迹是以点O 为圆心的圆弧.(构造OA =OB 且∠AOB =120°) 当O 、P 、C 共线时,可得CP 的最小值,利用Rt △OBC 勾股定理求得OC ,再减去OP 即可.60°EF CBAP 120°EF CBAP 120°MOP ABCF E120°变式练习>>>5.在△ABC 中,AB =4,∠C =60°,∠A >∠B ,则BC 的长的取值范围是________. 【分析】先作图,如下4ABC 60°答案为:8343BC <≤条件不多,但已经很明显,AB 是定值,∠C =60°,即定边对定角.故点C 的轨迹是以点O 为圆心的圆弧.(作AO =BO 且∠AOB =120°)题意要求∠A >∠B ,即BC >AC ,故点C 的轨迹如下图.当BC 为直径时,BC 取到最大值为833,考虑∠A 为△ABC 中最大角,故BC 为最长边,BC >AB =4.无最小值. O 120°60°C BAABC 60°120°O O 120°CBAO 120°CBA例题6. 如图,ABCD 为正方形,O 为AC 、BD 的交点,△DCE 为Rt △,∠CED =90°,∠DCE =30°,若OE =,则正方形的面积为( )A .5B .4C .3D .2【解答】解:如图,过点O 作OM ⊥CE 于M ,作ON ⊥DE 交ED 的延长线于N , ∵∠CED =90°,∴四边形OMEN 是矩形, ∴∠MON =90°,∵∠COM +∠DOM =∠DON +∠DOM , ∴∠COM =∠DON , ∵四边形ABCD 是正方形,∴OC =OD ,在△COM 和△DON 中,∴△COM ≌△DON (AAS ), ∴OM =ON ,∴四边形OMEN 是正方形, 设正方形ABCD 的边长为2a , ∵∠DCE =30°,∠CED =90° ∴DE =a ,CE =a , 亦可按隐圆模型解答设DN =x ,x +DE =CE ﹣x ,解得:x =, ∴NE =x +a =,∵OE =NE , ∴=•, ∴a =1, ∴S 正方形ABCD =4 故选:B .变式练习>>>6.如图, BE ,CF 为△ABC 的高,且交于点H ,连接AH 并延长交于BC 于点D ,求证:AD ⊥BC.DHEFABC例题7. 如图,在四边形ABCD中,∠BCD=90°,AC为对角线,过点D作DF⊥AB,垂足为E,交CB延长线于点F,若AC=CF,∠CAD=∠CFD,DF﹣AD=2,AB=6,则ED的长为.【解答】解:∵∠CAD=∠CFD,∴点A,F,C,D四点共圆,∴∠F AD+∠DCF=180°,∠F AC=∠FDC,∵∠DCF=90°,∴∠F AD=90°,∵AC=FC,∴∠F AC=∠AFC,∵DF⊥AB,∴∠ABF+∠BFE=∠CDF+∠BFE=90°,∴∠ABF=∠CDF,∴∠AFB=∠ABF,∴AF=AB=6,∵DF﹣AD=2,∴DF=AD+2,∵DF2=AF2+AD2,∴(2+AD)2=62+AD2,解得:AD=8,∴DF=10,∵∠F AD=90°,AE⊥DF,∴△ADE∽△DAF,∴=,∴DE===,故答案为:.变式练习>>>7.(1)如图1,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外角平分线于点F,求证:FE=DE.(2)如图2,正方形ABCD,∠EAF=45°,当点E,F分别在对角线BD、边CD上,若FC=6,则BE的长为3.图1 图2证明:(1)如图,连接DB、DF.∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,∴∠CBF=45°,∠DBC=45°,∴∠DBF=90°.又∵∠DEF=90°,∴D、E、B、F四点共圆.∴∠DFE=∠DBE=45°(同弧所对的圆周角相等).∴△DEF是等腰直角三角形.∴FE=DE.(2)解:作△ADF的外接圆⊙O,连接EF、EC,过点E分别作EM⊥CD于M,EN⊥BC于N(如图)∵∠ADF=90°,∴AF为⊙O直径,∵BD为正方形ABCD对角线,∴∠EDF=∠EAF=45°,∴点E在⊙O上,∴∠AEF=90°,∴△AEF为等腰直角三角形,∴AE=EF,在△ABE与△CBE中,∴△ABE≌△CBE(SAS),∴AE=CE,∴CE=EF,∵EM⊥CF,CF=6,∴CM=CF=3,∵EN⊥BC,∠NCM=90°,∴四边形CMEN是矩形,∴EN=CM=3,∵∠EBN=45°,∴BE=EN=3,故答案为:3.例题8. 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.[解析]如图,过点B作BD⊥AC,D为垂足,因为△ABC为锐角三角形,所以点D在线段AC上,在Rt△BCD中,BD=BC×sin45°=;①当P在AC上运动与AB垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=﹣2;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=2+5=7.变式练习>>>8.如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.【分析】考虑l是经过点P的直线,且△ABC沿直线l折叠,所以B’轨迹是以点P为圆心,PB为半径的圆弧.考虑△ACB’面积最大,因为AC是定值,只需B’到AC距离最大即可.过P作作PH⊥AC交AC于H 点,与圆的交点即为所求B’点,先求HB’,再求面积.答案为24.达标检测 领悟提升 强化落实1. 如图, AB 是半圆O 的直径,点C 在半圆O 上,AB =10,AC =8.D 是弧BC 上的一个动点,连接AD ,过点C 作CE ⊥AD 于E ,连接BE .在点D 移动的过程中,BE 的最小值为 .OEDCBA答案为:2134【分析】E 是动点,E 点由点C 向AD 作垂线得来,∠AEC =90°,且AC 是一条定线段,所以E 点轨迹是以AC 为直径的圆弧.当B 、E 、M 共线时,BE 取到最小值.连接BC ,勾股定理求BM ,再减去EM 即可.MOEDCBAABCEOM2. 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,∠AEB =90°,AC 、BD 交于O .已知AE 、BE 的长分别为3,5,求三角形OBE 的面积.O ADE3. 如图,正方形ABCD 的边长是4,点E 是AD 边上一动点,连接BE ,过点A 作AF ⊥BE 于点F ,点P 是AD 边上另一动点,则PC +PF 的最小值为________.ABCDE FP答案为:2【分析】∠AFB =90°且AB 是定线段,故F 点轨迹是以AB 中点O 为圆心、AB 为直径的圆.考虑PC +PF 是折线段,作点C 关于AD 的对称点C ’,化PC +PF 为PC ’+PF ,当C ’、P 、F 、O 共线时,取到最小值.4. 如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AB =4,D 是BC 上一动点,CE ⊥AD 于E ,EF ⊥AB 交BC 于点F ,则CF 的最大值是_________.F EDCBA【分析】∠AEC =90°且AC 为定值,故E 点轨迹是以AC 为直径的圆弧.考虑EF ⊥AB ,且E 点在圆上,故当EF 与圆相切的时候,CF 取到最大值.连接OF ,易证△OCF ≌△OEF ,∠COF =30°,故CF 可求.答案为3BBB5. 如图,△ABC 为等边三角形,AB =3,若P 为△ABC 内一动点,且满足∠P AB =∠ACP ,则线段PB 长度的最小值为_________.ABCP答案为36. 如图,AB 是半圆O 的直径,点C 在半圆O 上,AB =5cm ,AC =4cm .D 是弧BC 上的一个动点(含端点B ,不含端点C ),连接AD ,过点C 作CE ⊥AD 于E ,连接BE ,在点D 移动的过程中,BE 的取值范围是﹣2≤BE <3 .【解答】解:如图, 由题意知,∠AEC =90°, ∴E 在以AC 为直径的⊙M 的上(不含点C 、可含点N ),∴BE 最短时,即为连接BM 与⊙M 的交点(图中点E ′点), ∵AB =5,AC =4, ∴BC =3,CM =2, 则BM ===,∴BE 长度的最小值BE ′=BM ﹣ME ′=﹣2, BE 最长时,即E 与C 重合,∵BC =3,且点E 与点C 不重合, ∴BE <3, 综上,﹣2≤BE <3, 故答案为:﹣2≤BE <3. 7. 在Rt △ABC 中,∠C =90°,AC =10,BC =12,点D 为线段BC 上一动点.以CD 为⊙O 直径,作AD 交⊙O 于点E ,连BE ,则BE 的最小值为 8 .【解答】解:解:如图,连接CE,∴∠CED=∠CEA=90°,∴点E在以AC为直径的⊙Q上,∵AC=10,∴QC=QE=5,当点Q、E、B共线时BE最小,∵BC=12,∴QB==13,∴BE=QB﹣QE=8,∴BE的最小值为8,故答案为8.8. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为2﹣2.【解答】解:连结AE,如图1,∵∠BAC=90°,AB=AC,BC=,∴AB=AC=4,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的⊙O上,∵⊙O的半径为2,∴当点O、E、C共线时,CE最小,如图2,在Rt△AOC中,∵OA=2,AC=4,∴OC==2,∴CE=OC﹣OE=2﹣2,即线段CE长度的最小值为2﹣2.故答案为2﹣2.9. 如图,在矩形ABCD中,已知AB=4,BC=8,点O、P分别是边AB、AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是2﹣2.【解答】解:如图,连接EO、PO、OC.∵四边形ABCD是矩形,∴∠B=∠OAP=90°,在Rt△OBC中,BC=8,OB=2,∴OC==2,在Rt△AOP中,OA=2,P A=4,∴OP==2,∵OE=OC=2,PE≥OE﹣OP,∴PE的最小值为2﹣2.故答案为2﹣2.10. 如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.【解答】解:∵四边形ABCD是矩形,∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得,AC=5,∵AB=3,AE=2,∴点F在BC上的任何位置时,点G始终在AC的下方,设点G到AC的距离为h,∵S四边形AGCD=S△ACD+S△ACG=AD×CD+AC×h=×4×3+×5×h=h+6,∴要四边形AGCD的面积最小,即:h最小,∵点G是以点E为圆心,BE=1为半径的圆上在矩形ABCD内部的一部分点,∴EG⊥AC时,h最小,即点E,点G,点H共线.由折叠知∠EGF=∠ABC=90°,延长EG交AC于H,则EH⊥AC,在Rt△ABC中,sin∠BAC=,在Rt△AEH中,AE=2,sin∠BAC=,∴EH=AE=,∴h=EH﹣EG=﹣1=,∴S四边形AGCD最小=h+6=+6=.故答案为:.。
