(完整版)2017年高考理科数学试题及答案-全国卷3,推荐文档
2017理数全国三卷及答案
绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A.3B.3C.3D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP =λAB +μAD ,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。
2017年全国统一高考数学试卷(理科)(新课标ⅲ)及参考答案
16. (5 分)a,b 为空间中两条互相垂直的直线,等腰直角三角形 ABC 的直角边 AC 所在直线与 a,b 都垂直,斜边 AB 以直线 AC 为旋转轴旋转,有下列结论: ①当直线 AB 与 a 成 60°角时,AB 与 b 成 30°角; ②当直线 AB 与 a 成 60°角时,AB 与 b 成 60°角; ③直线 AB 与 a 所成角的最小值为 45°; ④直线 AB 与 a 所成角的最小值为 60°; 其中正确的是 . (填写所有正确结论的编号)
不低于 25,需求量为 500 瓶;如果最高气温位于区间[20,25) ,需求量为 300 瓶;如果最高气温低于 20,需求量为 200 瓶.为了确定六月份的订购计划,统 计了前三年六月份各天的最高气温数据,得下面的频数分布表: 最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40) 天数 2 16 36 25 7 4
20. (12 分)已知抛物线 C:y2=2x,过点(2,0)的直线 l 交 C 与 A,B 两点, 圆 M 是以线段 AB 为直径的圆. (1)证明:坐标原点 O 在圆 M 上; (2)设圆 M 过点 P(4,﹣2) ,求直线 l 与圆 M 的方程. 21. (12 分)已知函数 f(x)=x﹣1﹣alnx. (1)若 f(x)≥0,求 a 的值; (2)设 m 为整数,且对于任意正整数 n, (1 + ) (1+ m 的最小值. )…(1+ )<m,求
2017 年全国统一高考数学试卷(理科) (新课标Ⅲ)
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选 项中,只有一项是符合题目要求的。 1. (5 分)已知集合 A={(x,y)|x2+y2=1},B={(x,y)|y=x},则 A∩B 中元素 的个数为( A.3 B.2 ) C.1 D.0 )
2017年高考真题——理科数学(全国Ⅲ卷)含答案
绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
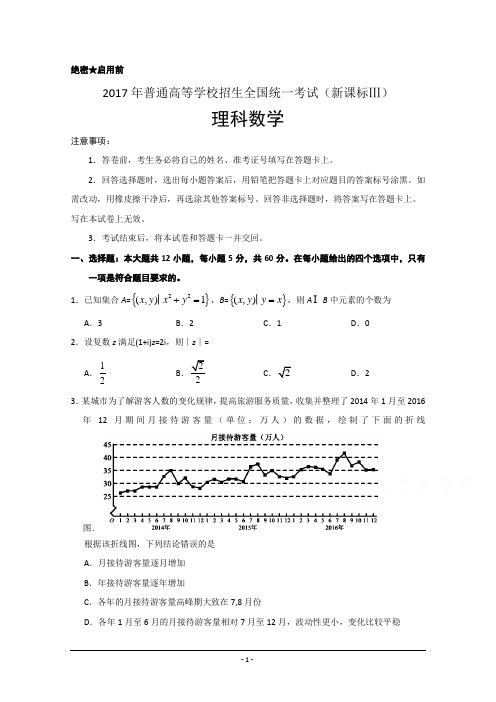
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .12B C D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为ABC.3D .1311.已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP=λAB +μAD,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。
(word完整版)2017全国三卷理科数学高考真题及答案,推荐文档
2017年普通高等学校招生全国统一考试(新课标山)理科数学、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
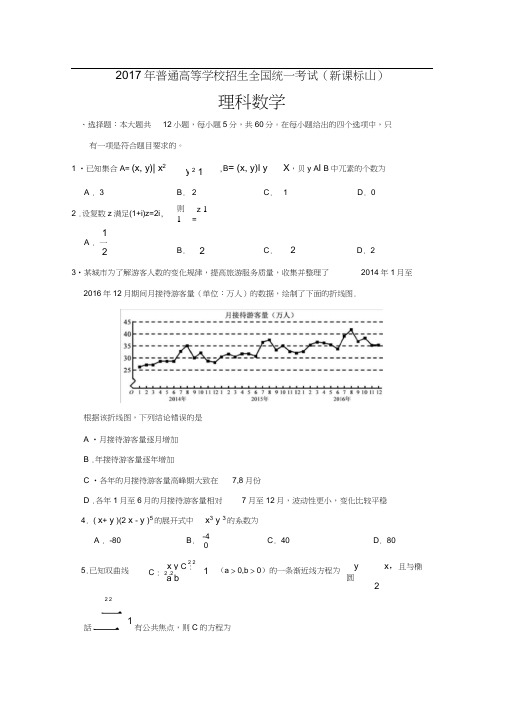
1 •已知集合A= (x, y)| x2y21,B= (x, y)l y X,贝y A l B中兀素的个数为A . 3B. 2C. 1 D. 02 .设复数z满足(1+i)z=2i, 则1z 1=1A . 一2B. 2C. 2 D. 23•某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A •月接待游客量逐月增加B .年接待游客量逐年增加C •各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4. ( x+ y )(2 x - y )5的展开式中x3 y 3的系数为A . -80B. -4C. 40D. 805.已知双曲线2 2x y C :C : 2 .2a b1(a > 0,b > 0)的一条渐近线方程为y x,且与椭圆22 2話二1有公共焦点,则C的方程为体积为3 nnnA . nB .C .D .—4 2 49.等差数列a n 的首项为1,公差不为0 .若a 2, a 3, a 6成等比数列,则a n 前6项的和A . -24B . -3C . 3D . 82 2x y10 .已知椭圆 C :二 2 1 , ( a>b>0)的左、右顶点分别为 A 1, A 2,且以线段 A 1A 2为a b直径的圆与直线 bx ay 2ab 0相切,则C 的离心率为.3-1A .BC .D .33 3 32 2xy ’A .12 2x y ’ B .12x C.—52 x D.— 42y- i 36.设函数则下列结论错A • f(x)的一个周期为-2 B . y=f(x)的图像关于直线 8x=- 3对称C . f(x+n 的一个零点为x=—6D . f(x)在(一,n 单调递减22的同一个球的球面上,则该圆柱的N 的最小值为11 .已知函数f(x)2x 2x a(ex1e % 1)有唯一零点,则 a=11 1A .B.-C.-D . 1232uur12.在矩形ABC D中,AB=1 ,AD=2,动点P 在以点 C 为圆心且与 BD 相切的圆上.若APuuu uuurAB +AD , 则 +的最大值为A . 3B . 2 2C . 5D . 2二、 填空题:本题共 4小题,每小题5分,共20分。
2017年全国卷3高考理科数学含答案详解

2017年全国卷3高考理科数学含答案详解绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={}22x y y x│,则A I B(,)=│,B={}+=(,)1x y x y中元素的个数为A.3 B.2 C.1 D.0 2.设复数z满足(1+i)z=2i,则∣z∣=A.12B.2C.2D.23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.学#科&网根据该折线图,下列结论错误的是A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月份D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(x+y)(2x-y)5的展开式中x3y3的系数为A.-80 B.-40 C.40D.805.已知双曲线C :22221x y a b -= (a >0,b>0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4 C .π2 D .π49.等差数列{}na 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}na 前6项的和为 A .-24 B .-3 C .3 D .810.已知椭圆C :22221x y a b +=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A 6B 3C .23D .1311.已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP u u u r =λAB u u u r +μAD u u u r ,则λ+μ的最大值为A .3B .2C 5D .2二、填空题:本题共4小题,每小题5分,共20分。
2017全国三卷理科数学高考真题及答案
2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为5y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6πD .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A 6B 3C .23D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A.12-B.13C.12D.112.在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若AP=λAB+μAD,则λ+μ的最大值为A.3 B.CD.2二、填空题:本题共4小题,每小题5分,共20分。
2017全国三卷理科数学高考真题及答案

2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6πD .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A.12-B.13C.12D.112.在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若AP=λAB+μAD,则λ+μ的最大值为A.3 B.CD.2二、填空题:本题共4小题,每小题5分,共20分。
2017年全国卷3高考理科数学含答案详解

绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .12B .2C D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.学#科&网根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b-= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为?2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为 A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为AB C D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP =λAB +μAD ,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。
2017年高考理科数学全国卷3及答案解析
数学试卷 第1页(共18页) 数学试卷 第2页(共18页)绝密★启用前2017年普通高等学校招生全国统一考试(全国卷Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}22(,)1A x y x y =+=│,{}(,)B x y y x ==│,则A B 中元素的个数( )A.3B.2C.1D.0 2.设复数z 满足()1i z 2i +=,则z =( )A.12D.23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月份D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.()()5+y 2y x x -的展开式中33y x 的系数为( )A.-80B.-40C.40D.805.已知双曲线2222:1x y C a b-=()00>>a b ,的一条渐近线方程为y x =,且与椭圆221123x y+=有公共焦点,则C 的方程为( ) A.221810x y -= B.22145x y -= C.22154x y -= D.22143x y -= 6.设函数()π3cos ⎛⎫=+ ⎪⎝⎭f x x ,则下列结论错误的是( )A.()f x 的一个周期为2π-B.()f x 的图像关于直线8π=3x 对称 C.()π+f x 的一个零点为π6=x D.()f x 在(π2,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A.5B.4C.3D.28.已知圆柱的高为1,它的两个底面的圆周在直径2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π49.等差数列{}n a 的首项为1,公差不为0.若236a a a ,,成等比数列,则{}n a 前6项的和为 ( ) A.24-B.3-C.3D.810.已知椭圆C :22221x y a b+=()0a b >>的左、右顶点分别为1A ,2A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第3页(共18页) 数学试卷 第4页(共18页)D.1311.已知函数211()2(e e )--+=-++x x f x x x a 有唯一零点,则a = ( )A.12-B.13C.12D.112.在矩形ABCD 中,12AB AD ==,,动点P 在以点C 为圆心且与BD 相切的圆上.若AP=AB+AD λμ,则λμ+的最大值为( )A.3D.2二、填空题:本题共4小题,每小题5分,共20分.13.若x ,y 满足约束条件y 0,20,0,x x y y -≥⎧⎪+-≤⎨⎪≥⎩则z 34x y =-的最小值为 .14.设等比数列{}n a 满足1213–1,3a a a a +==--,则4=a . 15.设函数1,0,()2,0,xx x f x x +≤⎧=⎨>⎩则满足1()()12f x f x +->的x 的取值范围是 .16.ab ,为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a b ,都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与a 成60︒角时,AB 与b 成30︒角; ②当直线AB 与a 成60︒角时,AB 与b 成60︒角; ③直线AB 与a 所成角的最小值为45︒; ④直线AB 与a 所成角的最大值为60︒.其中正确的是 .(填写所有正确结论的编号)三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)ABC △的内角A B C ,,的对边分别为a b c ,,,已知sin 0=A A,a ,2b =.(1)求c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD △的面积.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:(1)求六月份这种酸奶一天的需求量X (单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量n (单位:瓶)为多少时,Y 的数学期望达到最大值?19.(12分)如图,四面体ABCD 中,ABC △是正三角形,ACD △是直角三角形,.ABD CBD AB BD ∠=∠=,(1)证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角––D AE C 的余弦值.数学试卷 第5页(共18页) 数学试卷 第6页(共18页)20.(12分)已知抛物线C :22y x =,过点(2,0)的直线l 交C 与,A B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,-2),求直线l 与圆M 的方程.21.(12分)已知函数1(n )l =--f x a x x . (1)若()0f x ≥,求a 的值;(2)设m 为整数,且对于任意正整数n ,21111+1+1+222n m ⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭<,求m 的最小值.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线1l 的参数方程为2+,,x t y kt =⎧⎨=⎩(t 为参数),直线2l 的参数方程为2,,x m my k =-+⎧⎪⎨=⎪⎩(m 为参数).设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设3l :()cos si n ρθθ+,M 为3l 与C 的交点,求M 的极径.23.[选修4-5:不等式选讲](10分)已知函数12f x x x =+--(). (1)求不等式1f x ≥()的解集;(2)若不等式2– f x x x m ≥+()的解集非空,求m 的取值范围.2017年普通高等学校招生全国统一考试(全国卷Ⅲ)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共18页) 数学试卷 第8页(共18页)AB 中元素的个数为()1i -,所以3.【答案】A【解析】根据折线图可知,2014年8月到9月、2014年10月到11月等月接待游客量都是减少,所以A 错误. 4.【答案】C【解析】当第一个括号内取x 时,第二个括号内要取含23x y 的项,即()()23352C x y -,当第一个括号内取y 时,第二个括号内要取含32x y 的项,即()()32252C x y -,所以33x y 的系数为()23325522108440C C ⨯-⨯=⨯-=.5.【答案】B【解析】根据双曲线C 的渐近线方程为2y x =,可知2b a = ①,又椭圆221123x y +=的焦点坐标为(3,0)和(3-,0),所以229a b += ②,根据①②可知224,5a b ==,所以选B. 6.【答案】D【解析】根据函数解析式可知函数()f x 的最小正周期为2π ,所以函数的一个周期为π2-,A 正确;当8ππ,3π33=+=x x ,所以πcos 13⎛⎫+=- ⎪⎝⎭x ,所以B 正确;()4cos cos 33ππππ⎛⎫⎛⎫+=++=+ ⎪ ⎪⎝⎭⎝⎭f x x x ,当π6=x 时,4π3π32+=x ,所以()π0+=f x ,所以C 正确;函数()πcos 3⎛⎫=+ ⎪⎝⎭f x x 在(π2,23π)上单调递减;(23π,π)上单调递增,故D 不正确.所以选D . 7.【答案】D【解析】010*******,100911001090,13S M t S M t =+==-==-===,,>;, ,90<91,输出S ,此时,3t =不满足t N ≤,所以输入的正整数N 的最小值为2,故选D. 8.【答案】B【解析】设圆柱的底面半径为r ,则22213=1=24r ⎛⎫-⎪⎝⎭,所以,圆柱的体积33=π1=π44⨯V ,故选B. 9.【答案】A【解析】设等差数列n a 的公差为d ,因为236,,a a a 成等比数列,所以2263a a a =,即()()()211152a d a d a d ++=+,又11a =,所以220d d +=,又0,d ≠则2d =-,所以6159a a d =+=-,所以n a 的前6项的和6196242S -=⨯=-,故选A. 10.【答案】A以线段12A A 为直径的圆的方程为222x y a +=,由原点到直线20bx ay ab -+=的距离==d a ,得223a b =,所以C 的离心率3e ==.11.【答案】C【解析】由()()2112x x f x x x a e e --+=-++,得()()()()()(221212112122224422x x x x x f x x x a e e x x x a e e x x a e --+-----⎡⎤-=---++=-++++=-+⎣⎦,所以()()2f x f x -=,即1x =为()f x 图像的对称轴.由题意()f x 有唯一零点,所以()f x 的零点只能为1x =,即()()2111111210f a e e --+=-⨯++=,解得12a =.故选C. 12.【答案】A【解析】以A 为坐标原点,AB AD ,所在直线分别为x ,y 轴建立如图所示的平面直角坐标系,则A (0,0),B (1,0),C (1,2),D (0,2),可得直线BD 的方程为220x y +-=,点C 到直线BD =,圆C :数学试卷 第9页(共18页) 数学试卷 第10页(共18页)()()224125x y -+-=,因为P 在圆C 上,所以P(1cos 5θ+,25θ+)(1,0)AB =,(0,2)AD =,(,2)AP AB AD λμλμ=+=,所以122{θλθμ==()22sin 3λμθθθα+==++≤,tan 2α=,选A.13.【答案】1-【解析】作出约束条件表示的可行域如图中阴影部分所示,作出直线:340l x y -=,平移直线l ,当直线34z x y =-经过点A (1,1)时,z 取得最小值,最小值为341-=-.14.【答案】8-【解析】设等比数列{}n a 的公比为q ,则121(1)1a a a q +=+=-,2131(1)3a a a q -=-=-,两式相除,得21113q q +=-,解得12,1q a =-=,所以3418a a q ==-.15.【答案】∞1(-,+)4【解析】当0x >,()=21xf x >恒成立,当102x ->,即12x >时,121()=212x f x -->,当102x -≤,即102x ≤<时,111()=222f x x -+>,则不等式1()()12f x f x +->恒成立.当0x ≤时,113()()121222+-=+++=+f x f x x x x >,所以104x -≤<.综上所述,x 的取值范围是(14-,+∞).16.【答案】②③【解析】由题意知,,,a b AC 三条直线两两相互垂直,画出图形如图.不妨设图中所示正方体的棱长为1,则1,AC AB ==AB 以直线AC 为旋转轴旋转,则A点保持不变,B 点的运动轨迹是以C 为圆心,l 为半径的圆.数学试卷 第11页(共18页) 数学试卷 第12页(共18页)以C 为坐标原点,以CD 的方向为x 轴正方向,CB 方向为y 轴正方向,CA 的方向为z 轴正方向建立空间直角坐标系.则D (1,0,0),A (0,0,1), 直线a 的单位方向向量(0,1,0), 1.a a == B 点起始坐标为(0,1,0), 直线b 的单位方向向量b (1,0,0), 1.b == 设B 点在运动过程中的坐标B'(cos ,sin ,0)θθ, 其中θ为'CB 与CD 的夹角,[0,2)θπ∈.那么AB'在运动过程中的向量'(cos ,sin ,1),'2AB AB θθ=-=.设直线AB'与a 所成的夹角为[0,2],απ∈(cos ,sin ,1)(0,1,0)cos a ABθθαθ-⋅==∈ 故[,],42ππα∈所以③正确,④错误. 设直线AB'与b 所成的夹角为β,则[0,2],βπ∈'b cos 'AB b AB β⋅=(cos ,sin ,1)(1,0,0)'b AB θθ-⋅=.θ 当'AB 与a 成60︒角时,=3πα,1sin=322πθα因为22sin+cos =1,θθ所以cos =2θ 所以1cos =.2βθ 因为[0,2],βπ∈所以=3πβ,此时'AB 与b 成60︒角.所以②正确,①错误.三、解答题17.【答案】解:(1)由已知得tan =A 所以2π3A=. 在ABC 中,由余弦定理得22π2844cos3=+-c c ,即2+224=0c c -. 解得c 6=-,(舍去),c =4(2)由题设可得π=2∠CAD ,所以π6∠=∠-∠=BAD BAC CAD .故ABD 面积与ACD 面积的比值为1πsin 26112AB AD AC AD= 又ABC 的面积为142sin 2BAC ⨯⨯∠=所以ABD ∆【解析】(1))先求出角A ,再根据余弦定理求出c 即可;(2)根据ABD ,ACD ,ABC 的面积之间的关系求解即可.18.【答案】解:(1)由题意知,X所有的可能取值为200,300,500,由表格数据知()2162000.290P X +===,数学试卷 第13页(共18页) 数学试卷 第14页(共18页)()363000.490P X ===,()25745000.490P X ++===. 因此X 的分布列为(2200,因此只需考虑200500n ≤≤当300500n ≤≤时,若最高气温不低于25,则642Y n n n =-=;若最高气温位于区间[)20,,25,则63002300412002;Y n n n =⨯+--=-() 若最高气温低于20,则6200220048002;Y n n n =⨯+--=-() 因此()20.4120020.480020.26400.4.EY n n n n =⨯+-⨯+-⨯=-() 当200300n <≤时,若最高气温不低于20,则642;Y n n n =-=若最高气温低于20,则6200220048002;Y n n n =⨯+--=-() 因此()()20.40.480020.2160 1.2.EY n n n =⨯++-⨯=+ 所以300n =时,Y 的数学期望达到最大值,最大值为520元.【解析】(1)根据表格提供的数据进行分类求解即可;(2)根据分布列得到关于利润的函数表达式,进而求解最值. 19.解:(1)由题设可得,,ABD CBD ∆≅∆从而AD DC =. 又ACD ∆是直角三角形,所以0=90ACD ∠.取AC 的中点O ,连接,,DO BO 则,.DO AC DO AO ⊥= 又由于ABC ∆是正三角形,故BO AC ⊥. 所以DOB ∠为二面角D AC B --的平面角. 在Rt AOB ∆中,222BO AO AB +=.又AB BD =,所以222222BO DO BO AO AB BD +=+==,故0∠DOB=90.所以平面ACD ⊥平面ABC .(2)由题设及(1)知,OA,OB,OD 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA为单位长,建立如图所示的空间直角坐标系O xyz -,则-(1,0,0),(0(1,0,0),(0,0,1)A B C D .由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得102E ⎛⎫ ⎪ ⎪⎝⎭,,故()()11,0,1,2,0,0,1,2AD AC AE ⎛⎫=-=-=- ⎪ ⎪⎝⎭设()=x,y,z n 是平面DAE 的法向量,则0AD AE ⎧=⎪⎨=⎪⎩,,n n即01022x z x y z .-+=⎧⎪⎨-++=⎪⎩,可取113=,⎛⎫⎪ ⎪⎝⎭n .设m 是平面AEC 的法向量,则0,0,AC AE ⎧=⎪⎨=⎪⎩m m 同理可得(01,=-m .则77cos ,==n m n m n m . 所以二面角D AE C --.数学试卷 第15页(共18页) 数学试卷 第16页(共18页)【解析】(1)通过题目中的边角关系证明线线垂直,进而得二面角D AC B --的平面角为DOB ∠,最后利用勾股定理的逆定理得 90DOB ∠=︒,从而得证;(2)根据(1)中得到的垂直关系,建立空间直角坐标系计算即可. 20.【答案】解:(1)设()()11222A x ,y ,B x ,y ,l :x my .=+ 由222x my y x=+⎧⎨=⎩,可得212240则4y my ,y y --==-.又221212==22y y x ,x ,故()21212==44y y x x . 因此OA 的斜率与OB 的斜率之积为12124==14y y x x --,所以OA OB ⊥. 故坐标原点O 在圆M 上.(2)由(1)可得()2121212+=2+=++4=24y y m,x x m y y m +. 故圆心M 的坐标为()2+2,m m ,圆M 的半径r =由于圆M 过点42P -(,),因此0AP BP = ,故()()()()121244220x x y y --+++=,即()()121212124+2200x x x x y y y y -++++= 由(1)可得1212=-4,=4y y x x , 所以2210m m --=,解得11或2m m ==-. 当1m =时,直线l 的方程为20x y --=,圆心M 的坐标为(3,1),圆M 的半径为,圆M 的方程为()()223110x y -+-=.当12m =-时,直线l 的方程为240x y +-=,圆心M 的坐标为91,-42⎛⎫⎪⎝⎭,圆M 的半径为4,圆M 的方程为229185++4216x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭.【解析】(1)设出l 的方程,通过联立方程,证明直线OA 与OB 的斜率之积为1-即可; (2)根据(1)的结论及P 点的坐标即可求解直线与圆的方程. 21.【答案】解:(1)()f x 的定义域为()0,+∞.①若0a ≤,因为11=-+2<022f a ln ⎛⎫⎪⎝⎭,所以不满足题意; ②若>0a ,由()1a x a f 'x x x-=-=知,当()0x ,a ∈时,()<0f 'x ;当(),+x a ∈∞时,()>0f 'x ,所以()f x 在()0,a 单调递减,在(),+a ∞单调递增,故x a =是()f x 在()0,+x ∈∞的唯一最小值点.由于()10f =,所以当且仅当1a =时,()0f x ≥. 故1a =.(2)由(1)知当()1,+x ∈∞时,1>0x ln x --. 令1=1+2n x 得111+<22n n ln ⎛⎫ ⎪⎝⎭,从而 2211111111++1+++1+<+++=1-<12222222n n n ln ln ln ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故21111+1+1+<222n e ⎛⎫⎛⎫⎛⎫⋅⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭而231111+1+1+>2222⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭,所以m 的最小值为3. 【解析】(1)通过求函数的导数,对函数的单调性进行研究,求解函数最小值点即可;(2)将问题转化为“和”式不等式,根据数列求和公式求解即可.数学试卷 第17页(共18页) 数学试卷 第18页(共18页)22.【答案】(1)消去参数t 得1l 的普通方程()12l :y k x =-;消去参数m 得2l 的普通方程()212l :y x k=+.设,P x y (),由题设得()()212y k x y x k ⎧=-⎪⎨=+⎪⎩,消去k 得()2240x y y -=≠. 所以C 的普通方程为()2240x y y -=≠. (2)C 的极坐标方程为()()222cossin 40<<2ππ-=≠,.联立()()222cossin 4cos +sin-2=0⎧-=⎪⎨⎪⎩得()cossin =2cos +sin -.故1tan 3=-,从而2291cos =,sin =1010.代入()222cos-sin =4得2=5,所以交点M .【解析】(1)先将两条直线的参数方程化为普通方程,联立,消去k 即可得所求曲线C的普通方程;(2)先将(1)中求得的曲线C 的普通方程化为极坐标方程,再与3l 的极坐标方程联立,求出M 的极径即可.23.【答案】解:(1)()31211232,x f x x ,x ,x .--⎧⎪=--≤≤⎨⎪⎩<,,> 当<1x -时,()1f x ≥无解;当12x -≤≤时,由()1f x ≥得,211x -≥,解得12x ≤≤ 当>2x 时,由()1f x ≥解得>2x . 所以()1f x ≥的解集为{}1x x ≥.(2)由()2f x x x m ≥-+得212m x x x x ≤+---+,而22212+1+235=+2454x x x x x x x xx ,+---+≤--+⎛⎫-- ⎪⎝⎭≤且当32x =时,2512=4x x x x +---+. 故m 的取值范围为5-,4⎛⎤∞ ⎥⎝⎦.【解析】(1)直接分段讨论即可解决问题;(2)先分离出参数m ,再将问题转化为最值问题,进而求解参数的取值范围.。
2017年高考真题——理科数学(全国Ⅲ卷) Word版含解析

2017年普通高等学校招生全国统一考试(全国)理科数学(试题及答案解析)一、选择题:(本题共12小题,每小题5分,共60分)1.已知集合{}22(,)1A x y x y =+=,{}(,)B x y y x ==,则A B I 中元素的个数为()A .3B .2C .1D .0 【答案】B【解析】A 表示圆221x y +=上所有点的集合,B 表示直线y x =上所有点的集合,故A B I 表示两直线与圆的交点,由图可知交点的个数为2,即A B I 元素的个数为2,故选B.2.设复数z 满足(1i)2i z +=,则z =() A .12B 2C 2D .2【答案】C【解析】由题,()()()2i 1i 2i 2i 2i 11i 1i 1i 2z -+====+++-,则22112z =+ C.3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.2014年 2015年 2016年根据该折线图,下列结论错误的是() A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 【答案】A【解析】由题图可知,2014年8月到9月的月接待游客量在减少,则A 选项错误,故选A.4.5()(2)x y x y +-的展开式中33x y 的系数为()A .-80B .-40C .40D .80 【答案】C【解析】由二项式定理可得,原式展开中含33x y 的项为()()()()2332233355C 2C 240x x y y x y x y ⋅-+⋅-=,则33x y 的系数为40,故选C.5.已知双曲线22221x y C a b -=:(0a >,0b >)的一条渐近线方程为5y =,且与椭圆221123x y +=有公共焦点.则C 的方程为() A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -=【答案】B【解析】∵双曲线的一条渐近线方程为5y x =,则5b a =又∵椭圆221123x y +=与双曲线有公共焦点,易知3c =,则2229a b c +==② 由①②解得2,5a b ==,则双曲线C 的方程为22145x y -=,故选B.6.设函数π()cos()3f x x =+,则下列结论错误的是()A .()f x 的一个周期为2π-B .()y f x =的图像关于直线8π3x =对称 C .()f x π+的一个零点为π6x =D .()f x 在π(,π)2单调递减【答案】D【解析】函数()πcos 3f x x ⎛⎫=+ ⎪⎝⎭的图象可由cos y x =向左平移π3个单位得到,如图可知,()f x 在π,π2⎛⎫⎪⎝⎭上先递减后递增,D 选项错误,故选D.π23π53-π36πg x y O 7.执行右图的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为()A .5B .4C .3D .2 【答案】D【解析】程序运行过程如下表所示:S M初始状态0 100 1 第1次循环结束100 10- 2 第2次循环结束90 1 3 此时9091S =<首次满足条件,程序需在3t =时跳出循环,即2N =为满足条件的最小值,故选D.8.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .3π4C .π2D .π4【答案】B【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径221312r ⎛⎫=-= ⎪⎝⎭,则圆柱体体积23ππ4V r h ==,故选B.9.等差数列{}n a 的首项为1,公差不为0.若2a ,3a ,6a 成等比数列,则{}n a 前6项的和为()A .24-B .3-C .3D .8 【答案】A【解析】∵{}n a 为等差数列,且236,,a a a 成等比数列,设公差为. 则2326a a a =⋅,即()()()211125a d a d a d +=++ 又∵11a =,代入上式可得220d d += 又∵0d ≠,则2d =-∴()61656561622422S a d ⨯⨯=+=⨯+⨯-=-,故选A.10.已知椭圆2222:1x y C a b+=(0a b >>)的左、右顶点分别为1A ,2A ,且以线段1A 2A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为() ABCD .13【答案】A【解析】∵以12A A 为直径为圆与直线20bx ay ab -+=相切,∴圆心到直线距离等于半径,∴d a == 又∵0,0a b >>,则上式可化简为223a b =∵222b ac =-,可得()2223a a c =-,即2223c a =∴c e a == A11.已知函数211()2(e e )x x f x x x a --+=-++有唯一零点,则a =()A .1-2B .13C .12D .1【答案】C【解析】由条件,211()2(e e )x x f x x x a --+=-++,得:221(2)1211211(2)(2)2(2)(e e )4442(e e )2(e e )x x x x x x f x x x a x x x a x x a ----+----+-=---++=-+-+++=-++∴(2)()f x f x -=,即1x =为()f x 的对称轴, 由题意,()f x 有唯一零点, ∴()f x 的零点只能为1x =, 即21111(1)121(e e )0f a --+=-⋅++=,解得12a =.12.在矩形ABCD 中,1AB =,2AD =,动点P 在以点C 为圆心且与BD 相切的圆上.若AP AB AD λμ=+u u u r u u u r u u u r,则λμ+的最大值为() A .3 B. CD .2【答案】A【解析】由题意,画出右图.设BD 与C e 切于点E ,连接CE . 以A 为原点,AD 为轴正半轴, AB 为轴正半轴建立直角坐标系, 则C 点坐标为(2,1). ∵||1CD =,||2BC =.∴BD = ∵BD 切C e 于点E . ∴CE ⊥BD .∴CE 是Rt BCD △中斜边BD 上的高.12||||22||||||BCD BC CD S EC BD BD ⋅⋅⋅====△即C e. ∵P 在C e 上.∴P 点的轨迹方程为224(2)(1)5x y -+-=. 设P 点坐标00(,)x y ,可以设出P 点坐标满足的参数方程如下:0021x y θθ⎧=+⎪⎪⎨⎪=+⎪⎩ 而00(,)AP x y =u u u r ,(0,1)AB =u u u r ,(2,0)AD =u u u r. ∵(0,1)(2,0)(2,)AP AB AD λμλμμλ=+=+=u u u r u u u r u u u r∴0112x μθ==+,01y λθ==. 两式相加得:112)2sin()3λμθθθϕθϕ+=++=+=++≤(其中sin ϕ=,cos ϕ当且仅当π2π2k θϕ=+-,k ∈Z 时,λμ+取得最大值3.()A O DxyB P gCE二、填空题:(本题共4小题,每小题5分,共20分)13.若x ,y 满足约束条件0,20,0,-⎧⎪+-⎨⎪⎩x y x y y ≥≤≥则34z x y =-的最小值为________.【答案】1-【解析】由题,画出可行域如图:目标函数为34z x y =-,则直线344zy x =-纵截距越大,值越小. 由图可知:在()1,1A 处取最小值,故min 31411z =⨯-⨯=-.14.设等比数列{}n a 满足121a a +=-,133a a -=-,则4a =________. 【答案】8-【解析】{}n a Q 为等比数列,设公比为.121313a a a a +=-⎧⎨-=-⎩,即1121113a a q a a q +=-⎧⎪⎨-=-⎪⎩①②, 显然1q ≠,10a ≠,②①得13q -=,即2q =-,代入①式可得11a =, ()3341128a a q ∴==⨯-=-.15.设函数1,0,()2,0,+⎧=⎨>⎩xx x f x x ≤则满足1()()12f x f x +->的x 的取值范围是________. 【答案】1,4⎛⎫-+∞ ⎪⎝⎭【解析】()1,02 ,0+⎧=⎨>⎩Q x x x f x x ≤,()112f x f x ⎛⎫+-> ⎪⎝⎭,即()112f x f x ⎛⎫->- ⎪⎝⎭由图象变换可画出12y f x ⎛⎫=- ⎪⎝⎭与()1y f x =-的图象如下:1)2-)由图可知,满足()112f x f x ⎛⎫->- ⎪⎝⎭的解为1,4⎛⎫-+∞ ⎪⎝⎭.16.,为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与,都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与成60︒角时,AB 与成30︒角; ②当直线AB 与成60︒角时,AB 与成60︒角; ③直线AB 与所成角的最小值为45︒; ④直线AB 与所成角的最大值为60︒.其中正确的是________(填写所有正确结论的编号) 【答案】②③【解析】由题意知,a b AC 、、三条直线两两相互垂直,画出图形如图.不妨设图中所示正方体边长为1, 故||1AC =,2AB =,斜边AB 以直线AC 为旋转轴旋转,则A 点保持不变, B 点的运动轨迹是以C 为圆心,1为半径的圆.以C 为坐标原点,以CD u u u r 为轴正方向,CB u u u r为轴正方向, CA u u u r为轴正方向建立空间直角坐标系. 则(1,0,0)D ,(0,0,1)A ,直线的方向单位向量(0,1,0)a =r ,||1a =r. B 点起始坐标为(0,1,0),直线的方向单位向量(1,0,0)b =r,||1b =r .设B 点在运动过程中的坐标(cos ,sin ,0)B θθ', 其中为B C '与CD 的夹角,[0,2π)θ∈.那么'AB 在运动过程中的向量(cos ,sin ,1)AB θθ'=--u u u r ,||2AB '=u u u r .设AB 'u u u r 与所成夹角为π[0,]2α∈,则(cos ,sin ,1)(0,1,0)22cos |sin |[0,]a AB θθαθ--⋅==∈'r u u u r. 故ππ[,]42α∈,所以③正确,④错误.设AB 'u u u r 与所成夹角为π[0,]2β∈,cos (cos ,sin ,1)(1,0,0)2|cos |AB bb AB b AB βθθθ'⋅='-⋅='=u u u r r r u u u rr u u u r .当AB 'u u u r 与夹角为60︒时,即π3α=,12sin 2cos 2cos 232πθα====. ∵22cos sin 1θθ+=,∴|cos |θ.∴1cos |cos |2βθ=.∵π[0,]2β∈.∴π=3β,此时AB 'u u u r 与夹角为60︒.∴②正确,①错误.三、解答题:(共70分.第17-20题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答) (一)必考题:共60分. 17.(12分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 0A A =,a =,2b =.(1)求c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD △的面积.【解析】(1)由sin 0A A =得π2sin 03A ⎛⎫+= ⎪⎝⎭,即()ππ3A k k +=∈Z ,又()0,πA ∈,∴ππ3A +=,得2π3A =.由余弦定理2222cos a b c bc A =+-⋅.又∵12,cos 2a b A ===-代入并整理得()2125c +=,故4c =.(2)∵2,4AC BC AB ===,由余弦定理222cos 2a b c C ab +-=∵AC AD ⊥,即ACD △为直角三角形,则cos AC CD C =⋅,得CD =由勾股定理AD =又2π3A =,则2πππ326DAB ∠=-=, 1πsin 26ABDS AD AB =⋅⋅△18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[)2025,,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数(1)求六月份这种酸奶一天的需求量X (单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为Y (单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时,Y 的数学期望达到最大值? 【解析】⑴易知需求量可取200,300,500()21612003035P X +===⨯()3623003035P X ===⨯()257425003035P X ++===⨯.⑵①当200n ≤时:,此时max 400Y =,当200n =时取到.②当200300n <≤时:()()4122002200255Y n n =⋅+⨯+-⋅-⎡⎤⎣⎦ 880026800555n n n -+=+= 此时max 520Y =,当300n =时取到. ③当300500n <≤时,()()()()12220022002300230022555Y n n n =⨯+-⋅-+⨯+-⋅-+⋅⋅⎡⎤⎡⎤⎣⎦⎣⎦ 320025n -=此时520Y <.④当500n ≥时,易知一定小于③的情况. 综上所述:当300n =时,取到最大值为520.19.(12分)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形.ABD CBD ??,AB BD =.(1)证明:平面ACD ^平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分.求二面角D AE C --的余弦值.【解析】⑴取AC 中点为O ,连接BO ,DO ; ABC ∆Q 为等边三角形 ∴BO AC ⊥ ∴AB BC =AB BC BD BDABD DBC =⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. ∴AD CD =,即ACD ∆为等腰直角三角形,ADC ∠ 为直角又O 为底边AC 中点DA B C ED A BC EO∴DO AC ⊥令AB a =,则AB AC BC BD a ====易得:2OD a =,OB = ∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥ OD AC OD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩I 平面平面OD ABC ∴⊥平面 又∵OD ADC ⊂平面由面面垂直的判定定理可得ADC ABC ⊥平面平面 ⑵由题意可知V V D ACE B ACE --= 即B ,D 到平面ACE 的距离相等 即E 为BD 中点以O 为原点,OA u u u r 为轴正方向,OB u u u r为轴正方向,OD u u u r为轴正方向,设AC a =,建立空间直角坐标系,则()0,0,0O ,,0,02a A ⎛⎫ ⎪⎝⎭,0,0,2a D ⎛⎫ ⎪⎝⎭,,0B ⎛⎫ ⎪ ⎪⎝⎭,,4a E ⎛⎫ ⎪ ⎪⎝⎭易得:,24a a AE ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,0,22a a AD ⎛⎫=- ⎪⎝⎭u u u r ,,0,02a OA ⎛⎫= ⎪⎝⎭u u u r 设平面AED 的法向量为1n u u r ,平面AEC 的法向量为2n u u r,则1100AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u r u u u r u u r,解得1n =u u r 2200AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u r u u u r u u r,解得(20,1,n =u u r 若二面角D AE C --为,易知为锐角,则1212cos n n n n θ⋅==⋅u u r u u r uu r u u r20.(12分)已知抛物线2:2C y x =,过点(2,0)的直线交C 于A ,B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,2-),求直线与圆M 的方程.【解析】⑴显然,当直线斜率为时,直线与抛物线交于一点,不符合题意.设:2l x my =+,11(,)A x y ,22(,)B x y ,联立:222y xx my ⎧=⎨=+⎩得2240y my --=,2416m ∆=+恒大于,122y y m +=,124y y =-. 1212OA OB x x y y ⋅=+uu r uu u r12(2)(2)my my =++21212(1)2()4m y y m y y =++++24(1)2(2)4m m m =-+++0= ∴OA OB ⊥u u r u u u r,即O 在圆M 上.⑵若圆M 过点P ,则0AP BP ⋅=uu u r uu r1212(4)(4)(2)(2)0x x y y --+++= 1212(2)(2)(2)(2)0my my y y --+++=21212(1)(22)()80m y y m y y +--++=化简得2210m m --=解得12m =-或①当12m =-时,:240l x y +-=圆心为00(,)Q x y ,120122y y y +==-,0019224x y =-+=,半径||r OQ =则圆229185:()()4216M x y -++=②当1m =时,:20l x y --=圆心为00(,)Q x y ,12012y y y +==,0023x y =+=,半径||r OQ ==则圆22:(3)(1)10M x y -+-=21.(12分)已知函数()1ln f x x a x =--.(1)若()0f x ≥,求的值;(2)设m 为整数,且对于任意正整数,2111(1)(1)(1)222nm ++鬃?<,求m 的最小值. 【解析】⑴ ()1ln f x x a x =--,0x >则()1a x af x x x-'=-=,且(1)0f =当0a ≤时,()0f x '>,()f x 在()0+∞,上单调增,所以01x <<时,()0f x <,不满足题意; 当0a >时,当0x a <<时,()0f x '<,则()f x 在(0,)a 上单调递减; 当x a >时,()0f x '>,则()f x 在(,)a +∞上单调递增.①若1a <,()f x 在(,1)a 上单调递增∴当(,1)x a ∈时()(1)0f x f <=矛盾 ②若1a >,()f x 在(1,)a 上单调递减∴当(1,)x a ∈时()(1)0f x f <=矛盾 ③若1a =,()f x 在(0,1)上单调递减,在(1,)+∞上单调递增∴()(1)0f x f =≥满足题意综上所述1a =.⑵ 当1a =时()1ln 0f x x x =--≥即ln 1x x -≤则有ln(1)x x +≤当且仅当0x =时等号成立∴11ln(1)22k k+<,*k ∈N 一方面:221111111ln(1)ln(1)...ln(1) (112222222)n n n ++++++<+++=-<,即2111(1)(1)...(1)e 222n +++<.另一方面:223111111135(1)(1)...(1)(1)(1)(1)222222264n +++>+++=>当3n ≥时,2111(1)(1)...(1)(2,e)222n +++∈∵*m ∈N ,2111(1)(1)...(1)222n m +++<,∴m 的最小值为.22.选修4-4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线的参数方程为,,x t y kt =2+⎧⎨=⎩(t 为参数),直线l 2的参数方程为,,x m my k =-2+⎧⎪⎨=⎪⎩(m 为参数),设与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C . (1)写出C 的普通方程:(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设:(cos sin )l ρθθ3+0,M 为与C 的交点,求M 的极径. 【解析】⑴将参数方程转化为一般方程()1:2l y k x =- ……①()21:2l y x k=+ ……②①②消可得:224x y -=即P 的轨迹方程为224x y -=; ⑵将参数方程转化为一般方程3:0l x y +-= ……③ 联立曲线C和224x y x y ⎧+⎪⎨-=⎪⎩解得x y ⎧=⎪⎪⎨⎪=⎪⎩ 由cos sin x y ρθρθ=⎧⎨=⎩解得ρ即M.23.选修4-5:不等式选讲](10分)已知函数()||||f x x x =+1--2. (1)求不等式()f x ≥1的解集;(2)若不等式()f x x x m 2≥-+的解集非空,求m 的取值范围.【解析】⑴()|1||2|f x x x =+--可等价为()3,121,123,2--⎧⎪=--<<⎨⎪⎩x f x x x x ≤≥.由()1f x ≥可得:①当1-x ≤时显然不满足题意;②当12x -<<时,211-x ≥,解得1x ≥;③当2x ≥时,()31=f x ≥恒成立.综上,()1f x ≥的解集为{}|1x x ≥.⑵不等式()2-+f x x x m ≥等价为()2-+f x x x m ≥,令()()2g x f x x x =-+,则()g x m ≥解集非空只需要()max ⎡⎤⎣⎦g x m ≥.而()2223,131,123,2⎧-+--⎪=-+--<<⎨⎪-++⎩x x x g x x x x x x x ≤≥.①当1-x ≤时,()()max 13115g x g =-=---=-⎡⎤⎣⎦;②当12x -<<时,()2max3335312224g x g ⎛⎫⎛⎫==-+⋅-=⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭; ③当2x ≥时,()()2max 22231g x g ==-++=⎡⎤⎣⎦. 综上,()max 54g x =⎡⎤⎣⎦,故54m ≤.。
(完整版)2017年全国三卷理科数学高考真题及答案解析,推荐文档

2016年普通高等学校招生全国统一考试理科数学一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合S ={}{}(x 2)(x 3)0,T 0S x x x =--≥=I >P ,则S I T =(A) [2,3] (B)(-∞ ,2]U [3,+∞) (C) [3,+∞) (D)(0,2]U [3,+∞) (2)若z=1+2i ,则41izz =- (A)1 (B) -1 (C) i (D)-i(3)已知向量12(,)22BA =uu v ,31(,),22BC =uu u v 则∠ABC= (A)300(B) 450(C) 600(D)1200(4)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中A 点表示十月的平均最高气温约为150C ,B 点表示四月的平均最低气温约为50C 。
下面叙述不正确的是(A) 各月的平均最低气温都在00C 以上(B) 七月的平均温差比一月的平均温差大(C) 三月和十一月的平均最高气温基本相同(D) 平均气温高于200C 的月份有5个(5)若3tan 4α=,则2cos 2sin 2αα+= (A)6425 (B) 4825 (C) 1 (D)1625(6)已知432a =,344b =,1325c =,则(A )b a c << (B )a b c <<(C )b c a <<(D )c a b << (7)执行下图的程序框图,如果输入的a =4,b =6,那么输出的n =(A )3 (B )4 (C )5 (D )6(8)在ABC △中,π4B =,BC 边上的高等于13BC ,则cos A = (A )310 (B )10(C )10-(D )310- (9)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )18365+ (B )54185+(C )90 (D )81(10) 在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球,若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是 (A )4π (B )92π(C )6π(D )323π(11)已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,A ,B 分别为C 的左,右顶点.P 为C上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为 (A )13(B )12(C )23(D )34(12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意2k m ≤,12,,,k a a a L 中0的个数不少于1的个数.若m =4,则不同的“规范01数列”共有 (A )18个 (B )16个 (C )14个 (D )12个二、填空题:本大题共3小题,每小题5分(13)若x ,y 满足约束条件错误!未找到引用源。
2017全国三卷理科数学高考真题及答案(最新整理)

2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A =,B =,则A B 中元素的个数为{}22(,)1x y x y +=│{}(,)x y y x =│ A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .B C D .2123.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A .月接待游客量逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(+)(2-)5的展开式中33的系数为x y x y x y A .-80B .-40C .40D .805.已知双曲线C : (a >0,b >0)的一条渐近线方程为,且与椭圆22221x y a b -=y x =有公共焦点,则C 的方程为221123x y +=A .B .C .D .221810x y -=22145x y -=22154x y -=22143x y -=6.设函数f (x )=cos(x +),则下列结论错误的是3πA .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =对称83πC .f (x +π)的一个零点为x =D .f (x )在(,π)单调递减6π2π7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .B .C .D .π3π4π2π49.等差数列的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则前6项的和{}n a {}n a 为A .-24B .-3C .3D .810.已知椭圆C :,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为22221x y a b+=直径的圆与直线相切,则C 的离心率为20bx ay ab -+=A B C D .1311.已知函数有唯一零点,则a =211()2()x x f x x x a e e --+=-++A .B .C .D .112-131212.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若=AP+,则+的最大值为λAB μADλμA .3B.CD .2二、填空题:本题共4小题,每小题5分,共20分。
2017年全国统一高考数学试卷与参考答案(理科)(全国新课标III)

2017 年全国统一高考数学试卷(理科)(全国新课标III )一、选择题:本题共12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5 分)已知集合 A={ (x,y)|x2+y 2=1} , B={ (x, y)|y=x} ,则 A∩B中元素的个数为()A.3 B.2 C.1 D.02.(5 分)设复数 z 满足( 1+i) z=2i,则 |z|=()A.B.C.D.23.(5 分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年 1 月至 2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7, 8 月D.各年 1 月至 6 月的月接待游客量相对于7 月至 12 月,波动性更小,变化比较平稳4.(5 分)(x+y)(2x﹣ y)5的展开式中的x3y3系数为()A.﹣80B.﹣ 40C.40 D.805.(5 分)已知双曲线 C:﹣=1 (a>0,b>0)的一条渐近线方程为 y=x,且与椭圆+ =1 有公共焦点,则 C 的方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=16.(5 分)设函数 f( x) =cos(x+),则下列结论错误的是()A .f( x)的一个周期为﹣ 2πB. y=f (x)的图象关于直线x=对称C. f( x+π)的一个零点为x=D.f( x)在(,π)单调递减7.(5 分)执行如图的程序框图,为使输出S 的值小于 91,则输入的正整数N 的最小值为()A.5 B.4 C.3 D.28.(5 分)已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为()A .πB.C.D.9.(5 分)等差数列 {a n} 的首项为 1,公差不为 0.若 a2,a3,a6成等比数列,则{a n} 前 6 项的和为()A.﹣24B.﹣ 3 C.3 D.810.( 5 分)已知椭圆C:=1(a>b>0)的左、右顶点分别为 A 1,A 2,且以线段 A 1A 2为直径的圆与直线 bx﹣ay+2ab=0 相切,则 C 的离心率为()A.B.C.D.11.( 5 分)已知函数2x﹣ 1﹣ x+1)有唯一零点,则 a=()f(x)=x ﹣ 2x+a(e+eA .﹣B.C.D.112.( 5 分)在矩形 ABCD 中, AB=1 , AD=2 ,动点 P 在以点 C 为圆心且与 BD 相切的圆上.若=λ +μ,则λ+μ的最大值为()A.3 B.2 C.D.2二、填空题 :本题共 4 小题,每小题 5 分,共 20 分。
2017全国三卷理科数学高考真题及答案

2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A.12-B.13C.12D.112.在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若AP=λAB+μAD,则λ+μ的最大值为A.3 B.CD.2二、填空题:本题共4小题,每小题5分,共20分。
2017年高考理科数学全国3卷(附答案)

学校:____________________ _______年_______班 姓名:____________________ 学号:________ - - - - - - - - 密封线 - - - - - - - - - 密封线 - - - - - - - - -绝密★启用前2017年普通高等学校招生全国统一考试理科数学 全国III 卷(全卷共11页)(适用地区:云南、广西、贵州、四川)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答案卡一并交回。
一、 选择题:本题共12小题,每小题5分,共60分。
在每个小题给出的四个选项中, 只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A .月接待游客量逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80 B .-40 C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -=C .22154x y -=D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6πD .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x ya b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为ABC.3D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP =λ AB +μAD ,则λ+μ的最大值为 A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
25 B = {(x , y ) y = x } AB - y - y - y - y 2017年普通高等学校招生全国统一考试(全国3卷)理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
A = {(x , y ) x 2 + y 2 = 1}1. 已知集合 ,,则 中元素的个数为 A .3B .2C .1D .02.设复数 z 满足(1+ i )z = 2i ,则| z |=1A. 22 B. 2C. D .23. 某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加 C .各年的月接待游客量高峰期大致在7,8月D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(x + y )(2x - y )5 的展开式中 x 3 y 3 的系数为()A .-80B .-40C .40D .80C : x 2 y 21(a 0, b 0) y = x x 2 y 2 - = > > + = 1 5.已知双曲线 a 2 b 2的一条渐近线方程为 2 ,且与椭圆12 3 有公共焦点.则C 的方程为()22 = 1 2 2 = 1 2 2= 12 2= 1 A . 8 10B. 4 5C. 5 4D. 4 3f (x ) = cos(x +)6.设函数3 ,则下列结论错误的是() xx x x52A. f (x ) 的一个周期为-2x =B. y = f (x ) 的图像关于直线x =8 3 对称f (x +)6f (x )( 2 ,)C.的一个零点为D .在 单调递减7. 执行右图的程序框图,为使输出 S 的值小于91,则输入的正整小值为 A .5 B .4 C .3 D .28. 已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球则该圆柱的体积为()数 N 的最的球面上,A.3 B. 4C. 2D . 49. 等差数列{a n }的首项为1,公差不为0.若 a 2 , a 3 , a 6 成等比数列,则{a n }前6项的和为A .-24B .-3C .3D .8x 2 y 210. 已知椭圆 C : + = 1 a 2 b 2 ( a > b > 0 )的左、右顶点分别为 A 1, A 2 ,且以线段 A 1A 2为直径的圆与直线bx - ay + 2ab = 0 相切,则C 的离心率为()6A. 33 B. 3C. 31 D. 311. 已知函数 f (x ) = x 2 - 2x + a (e x -1 + e -x +1) 有唯一零点,则 a = ()- 1 A. 2 1 B. 3 1 C. 2 D .1 12.在矩形 ABCD 中, AB = 1, AD = 2 ,动点 P 在以点C 为圆心且与 BD 相切的圆上.若AP = AB + AD ,则+ 的最大值为 A .3B . 2C .D .2二、填空题:(本题共4小题,每小题5分,共20分)⎧x - y ≥ 0, ⎪x + y - 2 ≤ 0, x , y ⎪⎨ y ≥ 0 z = 3x - 4 y 13.若 满足约束条件⎩ 则 的最小值为.214.设等比数列{a n }满足a 1 + a 2 = -1, a 1 - a 3 = -3 ,则 a 4 = .f (x ) = ⎧x +1, x ≤ 0,1 15. 设函数 ⎩⎨2x ,x > 0则满足 f (x ) + f (x - ) > 12 的 x 的取值范围是 .16.a ,b 为空间中两条互相垂直的直线,等腰直角三角形 ABC 的直角边 AC 所在直线与 a , b 都垂直,斜边AB 以直线 AC 为旋转轴旋转,有下列结论: ①当直线 AB 与 a 成60 角时, AB 与b 成30 角; ②当直线 AB 与 a 成60 角时, AB 与b 成60 角; ③直线 AB 与 a 所成角的最小值为45 ; ④直线 AB 与 a 所成角的最大值为60 . 其中正确的是(填写所有正确结论的编号)三、解答题:(共70分.第17-20题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答) (一)必考题:共60分. 17.(12分)∆ABC 的c 内角 A , B , C 的对边分别为 a , b , c ,已知sin A + cos A = 0, a = 2 7, b = 2(1) 求; (2) 设 D 为 BC 边上一点,且 AD ⊥ AC ,求△ABD 的面积.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20, 25) ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表: 最高气温 [10 ,15) [15 ,20) [20 ,25) [25 ,30) [30 ,35) [35 ,40) 天数216362574(1) 求六月份这种酸奶一天的需求量 X (单位:瓶)的分布列;(2) 设六月份一天销售这种酸奶的利润为Y (单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时, Y 的数学期望达到最大值?19.(12分)如图,四面体 ABCD 中, △ABC 是正三角形,△ACD 是直角三角形. ÐABD = ÐCBD , AB = BD .(1) 证明:平面 ACD ^ 平面 ABC ; (2) 过 AC 的平面交 BD 于点 E ,若平面 AEC 把四面体3 DCEBA2 ⎨ ABCD 分成体积相等的两部分.求二面角 D - AE - C 的余弦值.20.(12分)已知抛物线C : y 2= 2x ,过点(2,0)的直线l 交C 于 A , B 两点,圆 M 是以线段 AB 为直径的圆.(1) 证明:坐标原点O 在圆 M 上;(2) 设圆 M 过点 P (4,- 2 ),求直线l 与圆 M 的方程.21.(12分)已知函数 f (x ) = x - 1 - a ln x .(1) 若f (x ) ≥ 0 ,求 a 的值;1 1 1+ )( 1+ ) ×××( 1+ ) < m(2) 设 m 为整数,且对于任意正整数 n , 2 22 2n,求m 的最小值. (二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)xOy l ⎧x = 2 + t , y = kt l在直角坐标系 中,直线 1 的参数方程为⎩ ⎧x = -2 + m , ⎨ y = m (t 为参数),直线 2 的参数方程为 ⎪ k( m 为参数),设l 1 与l 2 的交点为 P ,当 k 变化时, P 的轨迹为曲线C .(1) 写出C 的普通方程:(2) 以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3 : (cos + sin ) - = 0 ,M 为l 3 与C 的交点,求 M 的极径.23.[选修4-5:不等式选讲](10分) 已知函数 f (x ) =| x +1| - | x - 2 | .(1) 求不等式f (x ) ≥1的解集;(2) 若不等式f (x ) ≥ x 2- x + m 的解集非空,求 m 的取值范围. ( 13 32017年普通高等学校招生全国统一考试(全国3)理科数学参考答案一、选择题1.B 2.C 3.A 4.C 5.B 6.D7.D8.B9.A10.A 11.C 12.A二、填空题13. -1 三、解答题17.解:14.-8 15.(- 1, +∞) 4A =216.②③(1) 由已知可得tan A = -,所以328 = 4 + c 2 - 4c cos2在∆ABC 中,由余弦定理得 解得c = -6 (舍去), c = 4∠CAD =3 ,即c 2 + 2c - 24 = 0∠BAD = ∠BAC - ∠CAD =(2) 由题设可得2 ,所以 6 1 AB AD sin故∆ABD面积与∆ACD 2面积的比值为 1 AC AD 26 = 1 1⨯ 4 ⨯ 2 sin ∠BAC = 2又∆ABC 的面积为 2 ,所以∆ABD 的面积为18. 解:(1) 由题意知, X 所有可能取值为200,300,500,由表格数据知P (X = 200)= 2 + 16= 0.2 90 因此 X 的分布列为:P (X = 300)= 36 = 0.4 , 90 , P (X = 500)=25 + 7 + 4 = 0.4 90 .(2) 200,因此只需考虑200≤ n ≤ 500 当300 ≤ n ≤ 500 时,若最高气温不低于25,则Y = 6n - 4n = 2n ;3X 200 300 500 P0.20.40.43 z DC EOyBA x若最高气温位于区间[20,25),则Y = 6 ⨯ 300 + 2(n - 300) - 4n = 1200 - 2n ; 若最高气温低于20,则Y = 6 ⨯ 200 + 2(n - 200) - 4n = 800 - 2n因 此 EY = 2n ⨯ 0.4 + (1200 - 2n ) ⨯ 0.4 + (800 - 2n ) ⨯ 0.2 = 640 - 0.4n 当200 ≤ n < 300 时,若最高气温不低于20,则Y = 6n - 4n = 2n ;若最高气温低于20,则Y = 6 ⨯ 200 + 2(n - 200) - 4n = 800 - 2n 因 此 EY = 2n ⨯(0.4 + 0.4) + (800 - 2n ) ⨯ 0.2 = 160 +1.2n 所以 n = 300 时, Y 的数学期望达到最大值,最大值为520元。
19. 解:(1) 由题设可得, ∆ABD ≅ ∆CBD ,从而 AD = DC又∆ACD 是直角三角形,所以∠ADC = 90 取 AC 的中点O ,连结 DO , BO , 则 DO ⊥ AC , DO = AO又由于∆ABC 是正三角形,故 BO ⊥ AC 所以∠DOB 为二面角 D - AC - B 的平面角在 Rt ∆AOB 中 ,BO 2 + AO 2 = AB 2又 AB = BD ,所以BO 2 + DO 2 = BO 2 + AO 2 = AB 2 = BD 2 ,故∠DOB = 90 所以平面 ACD ⊥ 平面 ABCOA , OB , OD(2) 由题设及(1)知,两两垂直,以O 为坐标原点, OA 的方向为 x 轴正方向, | OA | 为单 位长,建立如图所示的空间直角坐标系O - xyz ,则A (1, 0, 0),B (0, 3, 0),C (-1, 0, 0),D (0, 0,1)由题设知,四面体 ABCE 的体积为四面体1ABCD 的体积的 2 ,从而 E 到平面 ABC 的距离1为 D 到平面 ABC 的距离的 2 ,即 E 为 DB 的中1 E (0, , )点,得2 2 ,故3 1AD = (-1, 0,1), AC = (-2, 0, 0), AE = (-1, , )2 2DCEOBA7设 n = (x , y , z )是平面DAE的法向量,则 ⎪⎨m ⋅ A C = 0, ⎩ m ⋅AE = 0 同理可取 m = (0, -1, 3)cos < n , m >= n m =则| n || m | 7 所以二面角 D - AE - C 的余弦值为 720. 解:(1)设 A (x 1 , y 1 ), B (x 2 , y 2 ), l : x = my + 2⎧x = my + 2, ⎨y 2 = 2xy 2 - 2my - 4 = 0由⎩可得,则y 1 y 2 = -4y 2 y 2 ( y y )2x 1 = 1 , x 2 = 2 又2 2 x 1 x 2 = 1 2 = 4,故 4 y 1 y 2 -4因此OA 的斜率与OB 的斜率之积为故坐标原点O 在圆 M 上 = = -1x 1 x 2 4 ,所以OA ⊥ OBy + y = 2m , x + x = m ( y + y ) + 4 = 2m 2 + 4(2)由(1)可得 121212故圆心 M 的坐标为(m 2+2, m ) ,圆 M 的半径 r = (m 2 +2)2 + m 2 P (4, -2)由于圆 M 过点 ,因此AP ⋅ BP = 0 , 故(x 1 - 4)(x 2 - 4) + ( y 1 + 2)( y 2 + 2) = 0 , 即 x 1 x 2 - 4(x 1 + x 2 ) + y 1 y 2 + 2( y 2 + y 2 ) + 20 = 0 由(1)可得 y 1 y 2 = -4, x 1 x 2 = 4所以2m 2- m -1 = 0 ,解得 m = 1或m = - 12 当 m = 1时,直线l 的方程为 x - y -1 = 0 ,圆心 M 的坐标为(3,1) ,圆 M 的半径为方程为(x - 3)2 + ( y -1)2= 10,圆 M 的m = - 19 1 85 2l 2x + y - 4 = 0M( 4 , - 2)M4当 时,直线 的方程为,圆心的坐标为,圆的半径为,(x - 9 )2 + ( y + 1 )2 = 85圆 M 的方程为21. 解:4 2 16 7102 (1) f (x ) 的定义域为(0, +∞)f ( 1 ) = - 1 + a ln 2 < 0① 若a ≤ 0 ,因为 2 2 ,所以不满足题意; f '(x ) = 1- a = x - a② 若 a > 0 ,由x x 知,当 x ∈(0, a ) 时, f '(x ) < 0 ;当 x ∈(a , +∞) 时, f '(x ) > 0 。
