2018北京各区初中数学二模分类汇编27号题及答案

合集下载

北京市2018年中考数学二模试题汇编(20份)

代几综合题2018昌平二模28.在平面直角坐标系xOy 中，对于任意三点A 、B 、C 我们给出如下定义：“横长”a ：三点中横坐标的最大值与最小值的差，“纵长”b ：三点中纵坐标的最大值与最小值的差，若三点的横长与纵长相等，我们称这三点为正方点.例如：点A (2-,0) ，点 B (1,1) ，点 C (1-, 2-)，则A 、B 、C 三点的 “横长”a =|1(2)--|=3，A 、B 、C 三点的“纵长”b =|1(2)--|=3. 因为a =b ，所以A 、B 、C 三点为正方点.（1）在点R (3，5) ，S (3，2-) ，T (4-，3-)中，与点A 、B 为正方点的是；（2）点P (0，t )为y 轴上一动点，若A ，B ，P 三点为正方点，t 的值为；（3）已知点D (1，0).①平面直角坐标系中的点E 满足以下条件：点A ，D ，E 三点为正方点，在图中画出所有符合条件的点E 组成的图形； ②若直线l ：12y x m =+上存在点N ，使得A ，D ，N 三点为正方点，直接写出m 的取值范围．y xxy yx2018朝阳二模28. 对于平面直角坐标系xOy 中的点P 和直线m ，给出如下定义：若存在一点P ，使得点P 到直线m 的距离等于，则称P 为直线m 的平行点．（1）当直线m 的表达式为y =x 时， ①在点P 1（1，1），P 2（0，2），P 3（22-，22）中，直线m 的平行点是； ②⊙O 的半径为10，点Q 在⊙O 上，若点Q 为直线m 的平行点，求点Q 的坐标. （2）点A 的坐标为（n ，0），⊙A 半径等于1，若⊙A 上存在直线x y 3=的平行点，直接写出n 的取值范围．2018东城二模28. 研究发现，抛物线214y x =上的点到点F (0，1)的距离与到直线l ：1y =-的距离相等.如图1所示，若点P 是抛物线214y x =上任意一点，PH ⊥l 于点H ，则PH PF =.基于上述发现，对于平面直角坐标系x O y 中的点M ，记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ，称d 为点M 关于抛物线214y x =的关联距离；当24d ≤≤时，称点M 为抛物线214y x =的关联点.（1）在点1(20)M ，，2(12)M ，，3(45)M ，，4(04)M -，中，抛物线214y x =的关联点是______ ；（2）如图2，在矩形ABCD 中，点(1)A t ，，点(13)C t +， ①若t =4，点M 在矩形ABCD 上，求点M 关于抛物线214y x =的关联距离d 的取值范围；②若矩形ABCD 上的所有点都是抛物线214y x =的关联点，则t 的取值范围是__________.2018房山二模28. 已知点P，Q为平面直角坐标系xOy中不重合的两点，以点P为圆心且经过点Q作⊙P，则称点Q为⊙P的“关联点”，⊙P为点Q的“关联圆”.（1）已知⊙O的半径为1，在点E（1，1），F（－12，32），M（0，－1）中，⊙O的“关联点”为；（2）若点P（2，0），点Q（3，n），⊙Q为点P的“关联圆”，且⊙Q的半径为 5 ，求n的值；（3）已知点D（0，2），点H（m，2），⊙D是点H的“关联圆”，直线443y x=-+与x轴，y轴分别交于点A，B. 若线段AB上存在⊙D的“关联点”，求m的取值范围.2018丰台二模28．在平面直角坐标系xOy 中，将任意两点()11,y x P 与()22y x Q ，之间的“直距”定义为：2121y y x x D PQ -+-=.例如：点M （1，2-），点N （3，5-），则132(5)5MN D =-+---=. 已知点A (1，0)、点B (-1，4).（1）则_______=AO D ，_______=BO D ；（2）如果直线AB 上存在点C ，使得CO D 为2，请你求出点C 的坐标；（3）如果⊙B 的半径为3，点E 为⊙B 上一点，请你直接写出EO D 的取值范围.2018海淀二模28．对某一个函数给出如下定义：若存在实数k ，对于函数图象上横坐标之差为1的任意两点1(,)a b ，2(1,)a b +，21b b k -≥都成立，则称这个函数是限减函数，在所有满足条件的k 中，其最大值称为这个函数的限减系数．例如，函数2y x =-+，当x 取值a 和1a +时，函数值分别为12b a =-+，21b a =-+，故211b b k -=-≥，因此函数2y x =-+是限减函数，它的限减系数为1-．（1）写出函数21y x =-的限减系数；（2）0m >，已知1y x=（1,0x m x -≤≤≠）是限减函数，且限减系数4k =，求m 的取值范围．（3）已知函数2y x =-的图象上一点P ，过点P 作直线l 垂直于y 轴，将函数2y x =-的图象在点P 右侧的部分关于直线l 翻折，其余部分保持不变，得到一个新函数的图象，如果这个新函数是限减函数，且限减系数1k ≥-，直接写出P 点横坐标n 的取值范围．2018平谷二模28．对于平面直角坐标系xOy 中的点P 和⊙M ，给出如下定义：若⊙M 上存在两个点A ，B ，使AB =2PM ，则称点P 为⊙M 的“美好点”．（1）当⊙M 半径为2，点M 和点O 重合时，○1点()120P -，，()211P ，，()322P ，中，⊙O 的“美好点”是； ○2点P 为直线y=x+b 上一动点，点P 为⊙O 的“美好点”，求b 的取值范围；（2）点M 为直线y=x 上一动点，以2为半径作⊙M ，点P 为直线y =4上一动点，点P 为⊙M 的“美好点”，求点M 的横坐标m 的取值范围．2018石景山二模28．在平面直角坐标系xOy 中，对于任意点P ，给出如下定义：若⊙P 的半径为1，则称⊙P 为点P 的“伴随圆”．（1）已知，点()1,0P ，①点1,2A ⎛⎝⎭在点P 的“伴随圆” （填“上”或“内”或“外”）； ②点()1,0B -在点P 的“伴随圆” （填“上”或“内”或“外”）；（2）若点P 在x 轴上，且点P 的“伴随圆”与直线x y 33=相切，求点P 的坐标；（3）已知直线2+=x y 与x 、y 轴分别交于点A ，B ，直线2-=x y 与x 、y 轴分别交于点C ，D ，点P 在四边形ABCD 的边上并沿DA CD BC AB →→→的方向移动，直接写出点P 的“伴随圆”经过的平面区域的面积．2018西城二模28. 对于平面直角坐标系xOy 中的点(,)Q x y （x ≠0），将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”，记作Q L .如(1,2)Q -的“理想值”221Q L ==--. （1）①若点(1,)Q a 在直线4y x =-上，则点Q 的“理想值”Q L 等于_________；②如图，C ，⊙C 的半径为1. 若点Q 在⊙C 上，则点Q 的“理想值”Q L 的取值范围是 .（2）点D 在直线+3y =上，⊙D 的半径为1，点Q 在⊙D 上运动时都有0≤L Q ，求点D 的横坐标D x 的取值范围；（3）(2,)M m （m ＞0），Q 是以r 为半径的⊙M 上任意一点，当0≤L Q ≤件的最大圆，并直接写出相应的半径r 的值.（要求画图位置准确，但不必尺规作图）2018怀柔二模28. A 为⊙C 上一点，过点A 作弦AB ，取弦AB 上一点P ，若满足131<≤ABAP ，则称P 为点A 关于⊙C 的黄金点．已知⊙C 的半径为3，点A 的坐标为（1，0）． (1)当点C 的坐标为（4，0）时，①在点D （3，0），E （4，1），F （7，0）中，点A 关于⊙C 的黄金点是； ②直线3333-=x y 上存在点A 关于⊙C 的黄金点P ，求点P 的横坐标的取值范围； (2)若y 轴上存在．．点A 关于⊙C 的黄金点，直接写出点C 横坐标的取值范围．2018门头沟二模28.在平面直角坐标系xOy中的某圆上，有弦MN，取MN的中点P，我们规定:点P到某点（直”表示.线）的距离叫做“弦中距”，用符号“d中以(3,0)W-为圆心，半径为2的圆上.（1）已知弦MN长度为2.①如图1：当MN∥x轴时，直接写出到原点O的d的长度；中的取值范围.②如果MN在圆上运动时，在图2中画出示意图，并直接写出到点O的d中（2）已知点(5,0)y x=-，求到直线2=-的dy xM-,点N为⊙W上的一动点，有直线2中备用图2018顺义二模28．已知边长为2a 的正方形ABCD ，对角线AC 、BD 交于点Q ，对于平面内的点P 与正方形ABCD ，给出如下定义：如果a ≤PQ，则称点P 为正方形ABCD 的“关联点”．在平面直角坐标系xOy 中，若A (-1，1)，B (-1，-1)，C (1，-1)，D (1，1) ．（1）在11(,0)2-P，21(2P，3P 中，正方形ABCD 的“关联点”有；（2）已知点E 的横坐标是m ，若点E在直线=y 上，并且E 是正方形ABCD 的“关联点”，求m 的取值范围；（3）若将正方形ABCD 沿x 轴平移，设该正方形对角线交点Q 的横坐标是n ，直线1=+y 与x 轴、y 轴分别相交于M 、N 两点．如果线段MN 上的每一个点都是正方形ABCD 的“关联点”，求n 的取值范围．代数综合题2018昌平二模26.在平面直角坐标系xOy 中，抛物线223(0)y ax ax a a =--≠，与x 轴交于A 、B 两点(点A 在点B 的左侧)．（1）求点A 和点B 的坐标；（2）若点P （m ，n ）是抛物线上的一点，过点P 作x 轴的垂线，垂足为点D ．①在0a >的条件下，当22m -≤≤时，n 的取值范围是45n -≤≤，求抛物线的表达式； ②若D 点坐标（4，0），当PD AD >时，求a 的取值范围.2018朝阳二模26.已知二次函数)0(222≠--=a ax ax y ．（1）该二次函数图象的对称轴是直线；（2）若该二次函数的图象开口向上，当-1≤x ≤5时，函数图象的最高点为M ，最低点为N ，点M 的纵坐标为211，求点M 和点N 的坐标；（3）对于该二次函数图象上的两点A （x 1，y 1），B （x 2，y 2），设t ≤ x 1 ≤ t +1，当x 2≥3时，均有y 1 ≥ y 2，请结合图象，直接写出t 的取值范围．2018东城二模26．在平面直角坐标系xOy 中，抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ，．（1）求该抛物线的表达式；（2）求直线AB 关于x 轴的对称直线的表达式；（3）点P 是x 轴上的动点，过点P 作垂直于x 轴的直线l ，直线l 与该抛物线交于点M ，与直线AB 交于点N ．当PM PN ＜时，求点P 的横坐标P x 的取值范围．2018房山二模26. 在平面直角坐标系xOy 中，二次函数2y ax bx c =++（0a ≠）的图象经过A （0，4），B （2，0），C （－2，0）三点.（1）求二次函数的表达式；（2）在x 轴上有一点D （－4，0），将二次函数的图象沿射线DA 方向平移，使图象再次经过点B .①求平移后图象顶点E 的坐标；②直接写出此二次函数的图象在A ，B 两点之间（含A ，B 两点）的曲线部分在平移过程中所扫过的面积.2018丰台二模26．在平面直角坐标系xOy 中，二次函数22y x hx h =-+的图象的顶点为点D ．（1）当1h =-时，求点D 的坐标；（2）当1x ≤≤≤1-≤1时，求函数的最小值m ．（用含h 的代数式表示m ）2018海淀二模26．在平面直角坐标系xOy 中，已知点(3,1)A -，(1,1)B -，(,)C m n ，其中1n >，以点,,A B C 为顶点的平行四边形有三个，记第四个顶点分别为123,,D D D ，如图所示.（1）若1,3m n =-=，则点123,,D D D 的坐标分别是（），（），（）；（2）是否存在点C ，使得点123,,,,A B D D D 在同一条抛物线上？若存在，求出点C 的坐标；若不存在，说明理由.2018平谷二模26．在平面直角坐标系中，点D 是抛物线223y ax ax a =--()0a >的顶点，抛物线与x轴交于点A ，B （点A 在点B 的左侧）．（1）求点A ，B 的坐标；（2）若M 为对称轴与x 轴交点，且DM =2AM ，求抛物线表达式；（3）当30°<∠ADM <45°时，求a 的取值范围．2018石景山二26．在平面直角坐标系xOy 中，抛物线()240y ax x c a =++≠经过点()34,A -和()02,B ．（1）求抛物线的表达式和顶点坐标；（2）将抛物线在A 、B 之间的部分记为图象M （含A 、B 两点）．将图象M 沿直线3x =翻折，得到图象N ．若过点()94,C 的直线y kx b =+与图象M 、图象N 都相交，且只有两个交点，求b 的取值范围．2018西城二模26. 抛物线M ：241y ax ax a =-+- (a ≠0)与x 轴交于A ，B 两点（点A 在点B 左侧），抛物线的顶点为D .（1）抛物线M 的对称轴是直线____________；（2）当AB =2时，求抛物线M 的函数表达式；（3）在（2）的条件下，直线l ：y kx b =+(k ≠0)经过抛物线的顶点D ，直线y n =与抛物线M 有两个公共点，它们的横坐标分别记为1x ，2x ，直线y n =与直线l 的交点的横坐标记为3x （30x >），若当2-≤n ≤1-时，总有13320x x x x ->->，请结合函数的图象，直接写出k 的取值范围.2018怀柔二模26.在平面直角坐标系xOy 中，二次函数C 1：()332--+=x m mx y （m ＞0）的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C . (1)求点A 和点C 的坐标； (2)当AB =4时，①求二次函数C 1的表达式；②在抛物线的对称轴上是否存在点D ，使△DAC 的周长最小，若存在，求出点D 的坐标，若不存在，请说明理由；(3)将(2)中抛物线C 1向上平移n 个单位，得到抛物线C 2，若当0≤x ≤25时，抛物线C 2与x 轴只有一个公共点，结合函数图象，求出n 的取值范围.2018门头沟二模26.在平面直角坐标系xOy 中，有一抛物线其表达式为222y x mx m =-+. （1）当该抛物线过原点时，求m 的值；（2）坐标系内有一矩形OABC ,其中(4,0)A 、(4,2)B . ①直接写出C 点坐标；②如果抛物线222y x mx m =-+与该矩形有2个交点，求m 的取值范围.x2018顺义二模26．在平面直角坐标系中，二次函数221y x ax a =+++的图象经过点 M （2，-3）．（1）求二次函数的表达式；（2）若一次函数(0)y kx b k =+≠的图象与二次函数221y x ax a =+++的图象经过x 轴上同一点，探究实数k ，b 满足的关系式；（3）将二次函数221y x ax a =+++的图象向右平移2个单位，若点P （x 0，m ）和Q （2，n ）在平移后的图象上，且m >n ，结合图象求x 0的取值范围．反比例综合题2018昌平二模22.如图，在平面直角坐标系xOy 中，一次函数+(0)y ax b a =≠与反比例函数ky k x=≠（0）的图象交于点A （4，1）和B （1-，n ）．（1）求n 的值和直线+y ax b =的表达式；（2）根据这两个函数的图象，直接写出不等式0kax b x+-<的解集．x2018朝阳二模21. 如图，在平面直角坐标系xOy 中，直线61+=x k y 与函数)0(2>=x xk y 的图象的两个交点分别为A （1，5），B . （1）求21,k k 的值；（2）过点P （n ，0）作x 轴的垂线，与直线61+=x k y 和函数)0(2>=x xk y 的图象的交点分别为点M ，N ，当点M 在点N 下方时，写出n 的取值范围.2018东城二模22. 已知函数1y x =的图象与函数()0y kx k =≠的图象交于点(),P m n .（1）若2m n =，求k 的值和点P 的坐标；（2）当m n ≤时，结合函数图象，直接写出实数k 的取值范围.2018房山二模22. 如图，在平面直角坐标系xOy 中，直线y kx m =+与双曲线2y x=-相交于点A （m ，2）．（1）求直线y kx m =+的表达式；（2）直线y kx m =+与双曲线2y x=-的另一个交点为B ，点P 为x 轴上一点，若AB BP =，直接写出P 点坐标．2018丰台二模22．在平面直角坐标系xOy 中，直线l ：21(0)y mx m m =-+≠. （1）判断直线l 是否经过点M （2，1），并说明理由；（2）直线l 与反比例函数ky x=的图象的交点分别为点M ，N ，当OM =ON 时，直接写出点N 的坐标.2018海淀二模22．已知直线l 过点(2,2)P ，且与函数(0)ky x x=>的图象相交于,A B 两点，与x 轴、y 轴分别交于点,C D ，如图所示，四边形,ONAE OFBM 均为矩形，且矩形OFBM 的面积为3. （1）求k 的值；（2）当点B 的横坐标为3时，求直线l 的解析式及线段BC 的长；（3）如图是小芳同学对线段,AD BC 的长度关系的思考示意图.记点B 的横坐标为s ，已知当23s <<时，线段BC 的长随s 的增大而减小，请你参考小芳的示意图判断：当3s ≥时，线段BC 的长随s 的增大而 . （填“增大”、“减小”或“不变”）2018平谷二模21．如图，在平面直角坐标系xOy 中，函数()0ky k x=≠的图象与直线y =x －2交于点A （a ，1）．（1）求a ，k 的值；（2）已知点P （m ，0）（1≤m < 4），过点P 作平行于y 轴的直线，交直线y =x －2于点M （x 1，y 1），交函数()0ky k x=≠的图象于点N （x 1，y 2），结合函数的图象，直接写出12y y -的取值范围．2018石景山二模22．在平面直角坐标系xOy 中，直线1:2l y x b =-+与x 轴，y 轴分别交于点1(,0)2A ，B ，与反比例函数图象的一个交点为(),3M a . （1）求反比例函数的表达式；（2）设直线2:2l y x m =-+与x 轴，y 轴分别交于点C ,D ,且3OCD OAB S S ∆∆=，直接写出m 的值 .2018西城二模23. 如图，在平面直角坐标系xOy 中，函数my x=（0x <）的图象经过点(4,)A n -，AB ⊥x 轴于点B ，点C 与点A 关于原点O 对称， CD ⊥x 轴于点D ，△ABD 的面积为8.（1）求m ，n 的值；（2）若直线y kx b =+（k ≠0）经过点C ，且与x 轴，y 轴的交点分别为点E ，F ，当2CF CE =时，求点F 的坐标．2018怀柔二模23.在平面直角坐标系xOy 中，直线y =kx +b （k ≠0）与双曲线)0(≠=m xmy 相交于A ，B 两点，A 点坐标为（-3，2），B 点坐标为（n ，-3）. (1)求一次函数和反比例函数表达式；(2)如果点P 是x 轴上一点，且△ABP 的面积是5，直接写出点P 的坐标.2018门头沟二模20. 如图，在平面直角坐标系xOy 中，一次函数y x =与反比例函数ky x=（k ≠0）的图象相交于点(2,2)M . （1）求k 的值；（2）点(0,)P a 是y 轴上一点，过点P 且平行于x 轴的直线分别与一次函数y x =、反比例函数ky x=的图象相交于点1(,)A x b 、2(,)B x b ，当12x x <时，画出示意图并直接写出a 的取值范围.2018顺义二模20．如图，在平面直角坐标系xOy 中，函数ky x=（x >0）的图象与直线21y x =+交于点A （1，m ）．（1）求k 、m 的值；（2）已知点P （n ，0）（n ≥1），过点P 作平行于y 轴的直线，交直线21y x =+于点B ，交函数ky x=（x >0）的图象于点C ．横、纵坐标都是整数的点叫做整点． ①当3n =时，求线段AB 上的整点个数； ②若ky x=（x >0）的图象在点A 、C 之间的部分与线段AB 、BC 所围成的区域内（包括边界）恰有5个整点，直接写出n 的取值范围．函数操作题2018昌平二模25．有这样一个问题：探究函数3126y x x =-的图象与性质.小彤根据学习函数的经验，对函数3126y x x =-的图象与性质进行了探究.下面是小彤探究的过程，请补充完整：（1）求m 的值为；（2）如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；（3）方程31226x x -=-实数根的个数为；（4）观察图象，写出该函数的一条性质；（5）在第（2）问的平面直角坐标系中画出直线12y x =，根据图象写出方程311262x x x -=的一个正数根约为（精确到0.1）.2018朝阳二模25. 在数学活动课上，老师提出了一个问题：把一副三角尺如图1摆放，直角三角尺的两条直角边分别垂直或平行，60°角的顶点在另一个三角尺的斜边上移动，在这个运动过程中，有哪些变量，能研究它们之间的关系吗？小林选择了其中一对变量，根据学习函数的经验，对它们之间的关系进行了探究．下面是小林的探究过程，请补充完整：（1）画出几何图形，明确条件和探究对象；如图2，在Rt △ABC 中，∠C =90°，AC =BC =6cm ，D 是线段AB 上一动点，射线DE ⊥BC 于点E ，∠EDF = °，射线DF 与射线AC 交于点F ．设B ，E 两点间的距离为x cm ，E ，F 两点间的距离为y cm ．图1 图2（说明：补全表格时相关数据保留一位小数）（3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（4）结合画出的函数图象，解决问题：当△DEF为等边三角形时，BE的长度约为 cm.2018东城二模25. 小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园，妈妈问九年级的小强至少需要几米长的竹篱笆（不考虑接缝）.小强根据他学习函数的经验做了如下的探究. 下面是小强的探究过程，请补充完整：建立函数模型：设矩形小花园的一边长为x米，篱笆长为y米.则y关于x的函数表达式为 ;列表（相关数据保留一位小数）：根据函数的表达式，得到了x与y的几组值，如下表：描点、画函数图象：如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；观察分析、得出结论：根据以上信息可得，当x = 时，y 有最小值. 由此，小强确定篱笆长至少为米.2018房山二模25. 有这样一个问题：探究函数3126y x x =-的图象与性质．小东根据学习函数的经验，对函数3126y x x =-的图象与性质进行了探究.下面是小东的探究过程，请补充完整：（1）函数3126y x x =-的自变量x 的取值范围是 ; (2) 下表是y 与x 的几组对应值则m的值为；(3) 如下图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；（4）观察图象，写出该函数的两条性质．2018丰台二模25．数学活动课上，老师提出问题：如图，有一张长4dm，宽3dm的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大.下面是探究过程，请补充完整：Array（1）设小正方形的边长为x dm，体积为y dm3，根据长方体的体积公式得到y和x的关系式：；（2）确定自变量x的取值范围是；（3）列出y与x的几组对应值.（说明：表格中相关数值保留一位小数）（4）在下面的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm时，盒子的体积最大，最大值约为 dm3.2018海淀二模25．小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。

2018北京13区初三二模数学分类汇编--第27题

(2018海淀二模)27．在平面直角坐标系xOy 中，抛物线224y mx m m x -++=与y 轴交于点A （0,3），与x 轴交于点B ，C （点B 在点C 左侧）.（1）求该抛物线的表达式及点B ，C 的坐标；（2）抛物线的对称轴与x 轴交于点D ，若直线y kx b =+经过点D 和点E (1,2)--，求直线DE 的表达式；（3）在（2）的条件下，已知点P （t ，0），过点P 作垂直于x 轴的直线交抛物线于点M ，交直线DE 于点N ，若点M 和点N 中至少有一个点在x 轴下方，直接写出t 的取值范围．（2018东城二模）27．在平面直角坐标系中，抛物线2+3y ax bx =+()0≠a 与x 轴交于点A （-3,0）、B （1,0）两点， D 是抛物线顶点，E 是对称轴与x 轴的交点. (1)求抛物线的解析式;(2)若点F 和点D 关于x 轴对称, 点P 是x 轴上的一个动点，过点P 作PQ ∥OF 交抛物线于点Q ，是否存在以点O ,F ,P ,Q 为顶点的平行四边形？若存在，求出点P 坐标;若不存在，请说明理由.（2018西城二模）27．已知一次函数1y k x b =+（k ≠0）的图象经过(2,0)，(4,1)两点，二次函数 2224y x a x =-+（其中a ＞2）．（1）求一次函数的表达式及二次函数图象的顶点坐标（用含a 的代数式表示）；（2）利用函数图象解决下列问题：①若25=a ，求当10y >且2y ≤0时，自变量x 的取值范围；xy()–5–4–3–2–112345–5–4–3–2–112345o②如果满足10y >且2y ≤0时的自变量x的取值范围内恰有一个整数，直接写出a 的取值范围．（2018朝阳二模）27. 已知：关于x 的一元二次方程22(1)20(0)a x a x a a --+-=>．（1）求证：方程有两个不相等的实数根；（2）设方程的两个实数根分别为1x ，2x （其中1x ＞2x ）．若y 是关于a 的函数，且21y ax x =+，求这个函数的表达式；（3）在（2）的条件下，结合函数的图象回答：若使231y a ≤-+，则自变量a 的取值范围为．（2018丰台二模）27．在平面直角坐标系xOy 中，抛物线21y ax bx =++经过(13)A ，，(21)B ，两点.（1）求抛物线及直线AB 的解析式；（2）点C 在抛物线上，且点C 的横坐标为3．将抛物线在点A ，C 之间的部分（包含点A ，C ）记为图象G ，如果图象G 沿y 轴向上平移t （0t >）个单位后与直线 AB 只有一个公共点，求t 的取值范围．75676544123123321213xOy（2018顺义二模）27．已知关于x 的方程()2230x m x m +-+-=．（1）求证：方程()2230x m x m +-+-=总有两个实数根；（2）求证：抛物线()223y x m x m =+-+-总过x 轴上的一个定点；（3）在平面直角坐标系xOy 中，若（2）中的“定点”记作A ，抛物线()223y x m x m =+-+-与x 轴的另一个交点为B ，与y 轴交于点C ，且△OBC 的面积小于或等于8，求m 的取值范围．（2018平谷二模） 27．如图，在平面直角坐标系中，点 A (5,0)，B (3,2)，点C 在线段OA 上，BC =BA ，点Q 是线段BC 上一个动点，点P 的坐标是(0,3)，直线PQ 的解析式为y=kx+b (k ≠0)，且与x 轴交于点D ．（1）求点C 的坐标及b 的值；（2）求k 的取值范围；（3）当k 为取值范围内的最大整数时，过点B作BE ∥x 轴，交PQ 于点E ，若抛物线y=ax 2﹣5ax (a ≠0)的顶点在四边形ABED 的内部，求a 的取值范围．（2018门头沟二模）xyOyx D P BA O C QxyO27．在平面直角坐标系xOy 中，抛物线214y x bx c =-++经过点A （4，0）和B （0，2）．（1）求该抛物线的表达式；（2）在（1）的条件下，如果该抛物线的顶点为C ，点B 关于抛物线对称轴对称的点为D ，求直线CD 的表达式；（3）在（2）的条件下，记该抛物线在点A ，B 之间的部分（含点A ，B ）为图象G ，如果图象G 向上平移m （m ＞0）个单位后与直线CD 只有一个公共点，请结合函数的图象，直接写出m 的取值范围．（2018房山二模）27.已知关于x 的一元二次方程()23130kx k x +++= (k ≠0).（1）求证：无论k 取何值，方程总有两个实数根；（2）点()()120,0A x B x ，、在抛物线()2313y kx k x =+++上，其中12x x ＜0＜，且12x x 、和k 均为整数，求A ，B 两点的坐标及k 的值；（3）设（2）中所求抛物线与y 轴交于点C ，问该抛物线上是否存在点E ，使得ABEABCS S=，若存在，求出E 点坐标，若不存在，说明理由.（2018昌平二模）yx11O27．已知抛物线2y ax bx c =++经过原点O 及点A （-4，0）和点B （-6，3）．（1）求抛物线的解析式以及顶点坐标；（2）如图1，将直线2y x =沿y 轴向下平移后与（1）中所求抛物线只有一个交点C ，平移后的直线与y 轴交于点D ，求直线CD 的解析式；（3）如图2，将（1）中所求抛物线向上平移4个单位得到新抛物线，请直接写出新抛物线上到直线CD 距离最短的点的坐标及该最短距离．yx图1BACD Oyx图2CD O（2018通州二模）27．已知关于x 的方程mx 2－(3m －1)x +2m －2=0（1）求证：无论m 取任何实数时，方程恒有实数根．（2）若关于x 的二次函数y = mx 2－(3m －1)x +2m －2的图象与x 轴两交点间的距离为2时，求二次函数的表达式．。

2018年北京市西城区中考二模数学试卷附答案

北京市西城区2018年九年级模拟测试2分）第1-8题均有四个选项，符合题意的选项只有一个.1. 如图所示，a ∥b ，直线a 与直线b 之间的距离是A ．线段PA 的长度 B ．线段PB 的长度C ．线段PC 的长度D ．线段CD 的长度2. 将某不等式组的解集1-≤x <3表示在数轴上，下列表示正确的是3. 下列运算中，正确的是A ．22456x x x +=B ．326x x x ⋅=C ． 236()x x =D ．33()xy xy =4.下列实数中，在2和3之间的是A ． πB ．π2-C ．325D ．3285. 一副直角三角板如图放置，其中∠C =∠DFE = 90︒，∠A = 45︒， ∠E = 60︒，点F 在CB 的延长线上.若DE ∥CF ，则∠BDF 等于A ．35︒ B ．30︒ C ．25︒D ．15︒6. 中国古代在利用“计里画方”（比例缩放和直角坐标网格体系）的方法制作地图时，会利用测杆、水准仪和照板来测量距离．在如图所示的测量距离AB 的示意图中，记照板“内芯”的高度为 EF . 观测者的眼睛（图中用点C 表示）与BF 在同一水平线上，则下列结论中，正确的是A ．B ．EF CFAB FB =EF CFAB CB =C ．D ．CE CFCA FB=CE CFEA CB=7. 在一次男子马拉松长跑比赛中，随机抽取了10名选手，记录他们的成绩（所用的时间）如下：A ．这组样本数据的平均数超过130B ．这组样本数据的中位数是147C ．在这次比赛中，估计成绩为130 min 的选手的成绩会比平均成绩差D ．在这次比赛中，估计成绩为142 min 的选手，会比一半以上的选手成绩要好 8．如图1所示，甲、乙两车沿直路同向行驶，车速分别为20 m/s 和v (m/s)，起初甲车在乙车前a (m)处，两车同时出发，当乙车追上甲车时，两车都停止行驶．设x (s)后两车相距y(m)，y 与x 的函数关系如图2所示．有以下结论：①图1中a 的值为500；②乙车的速度为35 m/s ；③图1中线段EF 应表示为；5005x +④图2中函数图象与x 轴交点的横坐标为100．其中所有的正确结论是A ．①④B ．②③C ．①②④D ．①③④二、填空题（本题共16分，每小题2分）9.有意义，那么x 的取值范围是．10.不透明袋子中装有5个红色球和3个蓝色球，这些球除了颜色外没有其他差别.从袋子中随机摸出一个球，摸出蓝色球的概率为．11. 如图，等边三角形ABC 内接于⊙O ，若⊙O 的半径为2，则图中阴影部分的面积等于．12.某校“百变魔方”社团为组织同学们参加学校科技节的“最强大脑”大赛，准备购买A ，B 两款魔方.社长发现若购买2个A 款魔方和6个B 款魔方共需170元，购买3个A 款魔方和购买8个B 款魔方所需费用相同. 求每款魔方的单价.设A 款魔方的单价为x 元，B 款魔方的单价为y 元，依题意可列方程组为.13. 如图，在矩形ABCD 中，顺次连接矩形四边的中点得到四边形EFGH .若AB=8，AD=6，则四边形EFGH 的周长等于．A 款B 款14.在平面直角坐标系xOy 中，将抛物线平移后得到抛物线.请你写出一种平移23(2)1y x =+-232y x =+方法. 答：.15. 如图，AB 为⊙O 的直径，AC 与⊙O 相切于点A ，弦BD ∥OC .若，则∠DOC=．36C ∠=︒︒16. 我们知道：四边形具有不稳定性.如图，在平面直角坐标系xOy 中，矩形ABCD 的边AB 在x 轴上，(3,0)A -，(4,0)B ，边AD 长为5. 现固定边AB ，“推”矩形使点D 落在y 轴的正半轴上（落点记为D '），相应地，点C 的对应点C '的坐标为.三、解答题（本题共68分，第17~21题每小题5分，第22、23题每小题6分，第24题5分，第25、26题每小题6分，第27、28题每小题7分）17．计算：．06cos6027(π2)32︒+---18．解方程：.1322x x x+=--19. 如图，在四边形ABCD 中，E 为AB 的中点，DE ⊥AB 于点E ，，，BC= AD ，求∠C 的度数．66A ∠=︒90ABC ∠=︒20.先化简，再求值：，其中．2569122x x x x -+⎛⎫-÷⎪++⎝⎭5x =-21.如图，在Rt △ABC 中，，CD ⊥AB 于点D ，90ACB ∠=︒BE ⊥AB 于点B ，BE=CD ，连接CE ，DE ．（1）求证：四边形CDBE 为矩形；（2）若AC =2，，求DE 的长．1tan 2ACD ∠=22.阅读下列材料：材料一：早在2011年9月25日，北京故宫博物院就开始尝试网络预售门票，2011年全年网络售票仅占1.68%.2012年至2014年，全年网络售票占比都在2%左右.2015年全年网络售票占17.33%，2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日，首次实现全部网上售票.与此同时，网络购票也采用了“人性化”的服务方式，为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后，在北京故宫博物院的精细化管理下，观众可以更自主地安排自己的行程计划，获得更美好的文化空间和参观体验.材料二：以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.年度20132014201520162017参观人数（人次）7 450 0007 630 0007 290 0007 550 0008 060 000年增长率（%）38.72.4-4.53.66.8他还注意到了如下的一则新闻：2018年3月8日，中国国家博物馆官方微博发文，宣布取消纸质门票，观众持身份证预约即可参观. 国博正在建设智慧国家博物馆，同时馆方工作人员担心的是：“虽然有故宫免（纸质）票的经验在前，但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票，他遵守预约的程度是不一样的.但（国博）免费就有可能约了不来，挤占资源，所以难度其实不一样.” 尽管如此，国博仍将积极采取技术和服务升级，希望带给观众一个更完美的体验方式.根据以上信息解决下列问题：（1）补全以下两个统计图；（2）请你预估2018年中国国家博物馆的参观人数，并说明你的预估理由.23. 如图，在平面直角坐标系xOy 中，函数（）的图象经过点，AB ⊥x 轴于点B ，点C my x=0x <(4,)A n -与点A 关于原点O 对称， CD ⊥x 轴于点D ，△ABD 的面积为8.（1）求m ，n 的值；（2）若直线（k ≠0）经过点C ，且与x 轴，y 轴的交点分别为点E ，F ，当时，y kx b =+2CF CE =求点F 的坐标．24．如图，AB 是⊙O 的直径，C 是圆上一点，弦CD ⊥AB 于点E ，且DC=AD ．过点A 作⊙O 的切线，过点C 作DA 的平行线，两直线交于点F ，FC 的延长线交AB 的延长线于点G .（1）求证：FG 与⊙O 相切；（2）连接EF ，求的值.tan EFC25.阅读下面材料：已知：如图，在正方形ABCD 中，边.1AB a 按照以下操作步骤，可以从该正方形开始，构造一系列的正方形，它们之间的边满足一定的关系，并且一个比一个小.请解决以下问题：（1）完成表格中的填空：① ；② ； ③ ；④ ；（2）根据以上第三步、第四步的作法画出第三个正方形CHIJ （不要求尺规作图）.26. 抛物线M ： (a ≠0)与x 轴交于A ，B 两点（点A 在点B 左侧），抛物线的顶点为D .241y ax ax a =-+-（1）抛物线M 的对称轴是直线____________；（2）当AB =2时，求抛物线M 的函数表达式；（3）在（2）的条件下，直线l ：(k ≠0)经过抛物线的顶点D ，直线与抛物线M 有两个y kx b =+y n =公共点，它们的横坐标分别记为，，直线与直线l 的交点的横坐标记为3x （30x >），1x 2x y n =若当2-≤n ≤1-时，总有，请结合函数的图象，直接写出k 的取值范围.13320x x x x ->->27. 如图1，在等边三角形ABC中，CD为中线，点Q在线段CD上运动，将线段QA绕点Q顺时针旋转，使得点A的对应点E落在射线BC上，连接BQ，设∠DAQ=α（0°＜α＜60°且α≠30°）.（1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE（用含α的式子表示）；②探究线段CE，AC，CQ之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE，AC，CQ之间的数量关系.图1 备用图28. 对于平面直角坐标系xOy 中的点（x ≠0），将它的纵坐标y 与横坐标x 的比称为点Q 的“理想(,)Q x y yx值”，记作.如的“理想值”.Q L (1,2)Q -221Q L ==--（1）①若点在直线上，则点Q 的“理想值”等于_________；(1,)Q a 4y x =-Q L ②如图，，⊙C 的半径为1. 若点Q 在⊙C 上，则点Q 的“理想值”的取值范围是.3,1)C Q L （2）点D 在直线上，⊙D 的半径为1，点Q 在⊙D 上运动时都有3+3y =0≤L Q ，求点D 的横坐标的取值范围；3D x （3）（m ＞0），Q 是以r 为半径的⊙M 上任意一点，当0≤L Q ≤(2,)M m 22圆，并直接写出相应的半径r 的值.（要求画图位置准确，但不必尺规作图）北京市西城区2018年九年级模拟测试数学试卷答案及评分标准2018.5一、选择题（本题共16分，每小题2分）题号12345678答案ABCCDBCA二、填空题（本题共16分，每小题2分）9. x ≤2． 10. 38． 11. 4π3.12. 26170,38.x y x y +=⎧⎨=⎩13. 20.14.答案不唯一，例如，将抛物线23(2)1y x =+-先向右平移2个单位长度，再向上平移3个单位长度得到抛物线.232y x =+15. 54． 16. (7,4)．三、解答题（本题共68分，第17~21题每小题5分，第22、23题每小题6分，第24题5分，第25、26题每小题6分，第27、28题每小题7分）17.解： 06cos6027(π2)32︒--- ……………………………………………………… 4分16331(23)2=⨯-+-333123=-+-+． ……………………………………………………………………………5分223=-18．解方程：1322x x x+=--.解：去分母，得13(2)x x -=-．……………………………………………………… 1分去括号，得136x x -=-． ……………………………………………………… 2分移项，得 361x x -=-．合并同类项，得 25x =．………………………………………………………… 3分系数化为1，得52x =．…………………………………………………………… 4分经检验，原方程的解为52x =．……………………………………………………5分19. 解：如图1，连接BD .∵ E 为AB 的中点，DE ⊥AB 于点E ，∴ AD= BD ， …………………………………………… 1分∴ 1A ∠=∠．∵ 66A ∠=︒，∴ 166∠=︒．………………………………………………2分∵ 90ABC ∠=︒，∴ 2124ABC ∠=∠-∠=︒． …………………………… 3分∵ AD=BC ，∴ BD=BC ．…………………………………………………………………………4分∴ 3C ∠=∠．∴． …………………………………………………… 5分1802==782C ︒-∠∠︒20.解： 2569122x x x x -+⎛⎫-÷⎪++⎝⎭2322(3)x x x x -+=⨯+- ………………………………………………………………… 3分13x =-．……………………………………………………………………………… 4分当5x =-时，原式18=-．……………………………………………………………5分21. （1）证明：如图2.∵ CD ⊥AB 于点D ，BE ⊥AB 于点B ，∴ ．90CDA DBE ∠=∠=︒∴ CD ∥BE ．………………………………… 1分又∵ BE=CD ，图1∴ 四边形CDBE 为平行四边形．……………2分又∵，90DBE ∠=︒∴ 四边形CDBE 为矩形． ……………………………………………… 3分（2）解：∵ 四边形CDBE 为矩形，∴ DE=BC ．………………………………………………………………… 4分∵ 在Rt △ABC 中，90ACB ∠=︒，CD ⊥AB ，可得 1ACD ∠=∠．∵ 1tan 2ACD ∠=，∴ 1tan 1tan 2ACD ∠=∠=．∵ 在Rt △ABC 中，90ACB ∠=︒，AC =2，1tan 12∠=，∴ 4tan 1ACBC ==∠．∴ DE=BC=4．…………………………………………………………… 5分22.解：（1）补全统计图如图3.………………………………………………………………… 4分（2）答案不唯一，预估理由合理，支撑预估数据即可． ……………………… 6分23. 解：（1）如图4.∵ 点A 的坐标为(4,)A n -，点C 与点A 关于原点O 对称，图3∴ 点C 的坐标为(4,)C n -．∵ AB ⊥x 轴于点B ，CD ⊥x 轴于点D ，∴ B ，D 两点的坐标分别为(4,0)B -，(4,0)D ．∵ △ABD 的面积为8，11()8422ABD S AB BD n n =⨯=⨯-⨯=- ，∴ 48n -=．解得 2n =-． …………………………………………………………… 2分∵ 函数my x=（0x <）的图象经过点(4,)A n -，∴ 48m n =-=．…………………………………………………………… 3分（2）由（1）得点C 的坐标为(4,2)C ．① 如图4，当0k <时，设直线y kx b =+与x 轴，y 轴的交点分别为点1E ，1F ．由 CD ⊥x 轴于点D 可得CD ∥1OF ．∴ △1E CD ∽△1E 1F O ．∴1111E CDC OF E F =．∵ 112CF CE =，∴113DC OF =．∴ 136OF DC ==．图4∴ 点1F 的坐标为1(0,6)F ．②如图5，当0k >时，设直线y kx b =+与x 轴，y 轴的交点分别为点2E ，2F ．同理可得CD ∥2OF ，2222E CDC OF E F =．∵ 222CF CE =，∴ 2E 为线段2CF 的中点，222E C E F =．∴ ．22OF DC ==∴ 点2F 的坐标为2(0,2)F -．…………6分综上所述，点F 的坐标为1(0,6)F ，2(0,2)F -．24. （1）证明：如图6，连接OC ，AC .∵ AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∴ CE=DE ，AD=AC .∵ DC=AD ，∴ DC=AD= AC .∴ △ACD 为等边三角形．∴ ∠D =∠DCA=∠DAC =60︒．∴ 11302DCA ∠=∠=︒．∵ FG ∥DA ，∴ ．180DCF D ∠+∠=︒图6图5∴ 180120DCF D ∠=︒-∠=︒．∴ 190OCF DCF ∠=∠-∠=︒．∴ FG ⊥OC ．∴ FG 与⊙O 相切．……………………………………………………… 3分（2）解：如图6，作EH ⊥FG 于点H ．设CE= a ，则DE= a ，AD=2a ．∵ AF 与⊙O 相切，∴ AF ⊥AG ．又∵ DC ⊥AG ，可得AF ∥DC ．又∵ FG ∥DA ，∴ 四边形AFCD 为平行四边形．∵ DC =AD ，AD=2a ，∴ 四边形AFCD 为菱形．∴ AF=FC=AD=2 a ，∠AFC=∠D = 60︒．由（1）得∠DCG= 60︒，，．3sin 60EH CE =⋅︒=1cos602CH CE a=⋅︒=∴．52FH CH CF a=+=∵ 在Rt △EFH 中，∠EHF= 90︒，∴ ． …………………………………… 5分332tan 5aEH EFC FH a ∠===25．解：（1）①斜边和一条直角边分别相等的两个直角三角形全等．………………… 1分②．………………… 2分121)a -③．…………………3分21(21)a -④．……………… 4分11(21)n a -（2）所画正方形CHIJ 见图7.……………………………6分26.解：如图8.（1）2x =.…………………………… 1分（2）∵ 抛物线的对称轴为直线2x =，抛物线M 与x 轴的241y ax ax a =-+-交点为点A ，B （点A 在点B 左侧），AB =2，∴ A ，B 两点的坐标分别为(1,0)A ，(3,0)B .……………………………… 2分∵ 点A 在抛物线M 上，∴ 将(1,0)A 的坐标代入抛物线的函数表达式，得410a a a -+-=.解得 12a =-. ………………………………………………………………… 3分∴ 抛物线M 的函数表达式为. ………………………… 4分213222y x x =-+-（3）. …………………… 6分54k >图727. 解：（1）当0°＜α＜30°时，①画出的图形如图9所示．…………… 1分∵ △ABC 为等边三角形，∴ ∠ABC=60°．∵ CD 为等边三角形的中线，Q 为线段CD 上的点，由等边三角形的对称性得QA=QB ．∵ ∠DAQ =α，∴ ∠ABQ =∠DAQ=α，∠QBE =60°-α．∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得，∴ QE = QA ．∴ QB=QE ．可得 1802BQE QBE ∠=︒-∠．……… 2分1802(60)602αα=︒-︒-=︒+②3CE AC CQ +=．……………………………………………………… 3分证法一：如图10，延长CA 到点F ，使得AF=CE ，连接QF ，作QH ⊥AC 于点H ． ∵ ∠BQE =60°+2α，点E 在BC 上，∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α．图9图8∵ 点F 在CA 的延长线上，∠DAQ =α，∴ ∠QAF =∠BAF +∠DAQ=120°+α．∴ ∠QAF=∠QEC ．又∵ AF =CE ，QA=QE ，∴ △QAF ≌△QEC ．∴ QF=QC ．∵ QH ⊥AC 于点H ，∴ FH=CH ，CF=2CH ．∵ 在等边三角形ABC 中，CD 为中线，点Q 在CD 上，∴ ∠ACQ==30°，12ACB∠即△QCF 为底角为30°的等腰三角形．∴．3cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=∴ ．CE AC AF AC CF +=+=23CH CQ ==即3CE AC CQ +=． ………………………………………… 6分思路二：如图11，延长CB 到点G ，使得BG=CE ，连接QG ，可得△QBG ≌△QEC ，△QCG 为底角为30°的等腰三角形，与证法一同理可得．CE AC BG BC CG +=+=3CQ =图10（2）如图12，当30°＜α＜60°时，3AC CE CQ -=．………………………… 7分28.解：（1）①3-． ………………………………………………………………………… 1分② 0≤3．……………………………………………………………… 2分Q L （2）设直线与x 轴，y 轴的交点分别为点A ，点B ，可得，3+3y =(33,0)A ．(0,3)B ∴ ，，．33OA =3OB =30OAB ∠=︒由0≤3，作直线．Q L 3y x =①如图13，当⊙D 与x 轴相切时，相应的圆心满1D 足题意，其横坐标取到最大值．作轴11D E x ⊥于点，1E 可得∥OB ，．11D E 111D E AE BO AO =∵ ⊙D 的半径为1，∴ ．111D E =∴ ．13AE 1123OE OA AE =-=图12图13∴ ．123D x =②如图14，当⊙D 与直线相切时，3y x =相应的圆心满足题意，其横坐标取到2D 最小值．作轴于点，则⊥OA ．22D E x ⊥2E 22D E 设直线与直线的3y x =3+3y x =交点为F ．可得，OF ⊥AB ．60AOF ∠=︒则．39cos 332AF OA OAF =⋅∠==∵ ⊙D 的半径为1，∴ ．21D F =∴ ．2272AD AF D F =-=∴ ，22cos AE AD OAF =⋅∠73732==．2253OE OA AE =-=∴ 253D x =由①②可得，≤≤．D x 53D x 23………………………………………… 5分图14（3）画图见图15．．…………………………………………… 7分2图15。

2018年北京市西城区初三数学二模试题及答案

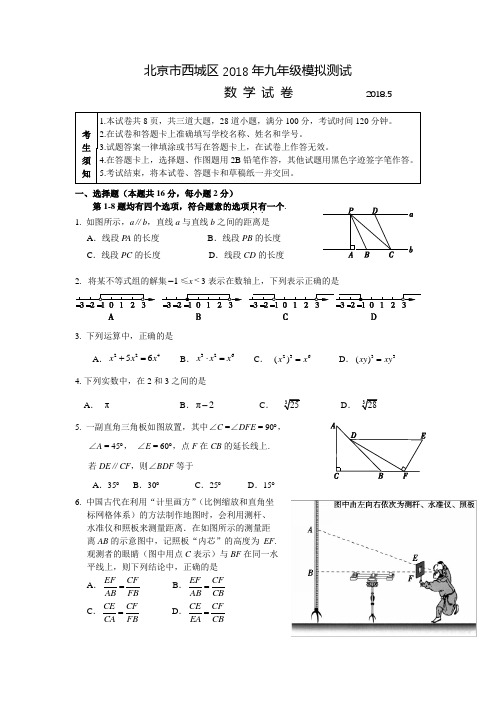
北京市西城区2018年九年级模拟测试数学试卷 2018.5一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有．．一个. 1. 如图所示，a ∥b ，直线a 与直线b 之间的距离是 A ．线段P A 的长度 B ．线段PB 的长度 C ．线段PC 的长度 D ．线段CD 的长度2. 将某不等式组的解集≤x 3表示在数轴上，下列表示正确的是3. 下列运算中，正确的是A ．B ．C ．D ．4.下列实数中，在2和3之间的是A ．B ．C ．D ．5. 一副直角三角板如图放置，其中∠C =∠DFE = 90︒， ∠A = 45︒， ∠E = 60︒，点F 在CB 的延长线上. 若DE ∥CF ，则∠BDF 等于A ．35︒B ．30︒C ．25︒D ．15︒ 6. 中国古代在利用“计里画方”（比例缩放和直角坐标网格体系）的方法制作地图时，会利用测杆、水准仪和照板来测量距离．在如图所示的测量距离AB 的示意图中，记照板“内芯”的高度为 EF . 观测者的眼睛（图中用点C 表示）与BF 在同一水平线上，则下列结论中，正确的是A ．EF CF AB FB = B ．EF CFAB CB=C ．CE CFCA FB = D ．CE CF EA CB=1-<22456x x x +=326x x x ⋅=236()x x =33()xy xy =π π2-7. 在一次男子马拉松长跑比赛中，随机抽取了10名选手，记录他们的成绩（所用的时间）如下：A ．这组样本数据的平均数超过130B ．这组样本数据的中位数是147C ．在这次比赛中，估计成绩为130 min 的选手的成绩会比平均成绩差D ．在这次比赛中，估计成绩为142 min 的选手，会比一半以上的选手成绩要好8．如图1所示，甲、乙两车沿直路同向行驶，车速分别为20 m/s 和v (m/s)，起初甲车在乙车前a (m)处，两车同时出发，当乙车追上甲车时，两车都停止行驶．设x (s)后两车相距y (m)，y 与x 的函数关系如图2所示．有以下结论：①图1中a 的值为500； ②乙车的速度为35 m/s ； ③图1中线段EF 应表示为5005x +；④图2中函数图象与x 轴交点的横坐标为100．其中所有的正确结论是A ．①④B ．②③C ．①②④D ．①③④ 二、填空题（本题共16分，每小题2分）9. 有意义，那么x 的取值范围是．10.不透明袋子中装有5个红色球和3个蓝色球，这些球除了颜色外没有其他差别.从袋子中随机摸出一个球，摸出蓝色球的概率为．11. 如图，等边三角形ABC 内接于⊙O ，若⊙O 的半径为2，则图中阴影部分的面积等于．12.某校“百变魔方”社团为组织同学们参加学校科技节的 “最强大脑”大赛，准备购买A ，B 两款魔方.社长发现若购买2个A 款魔方和6个B 款魔方共需170元，购买 3个A 款魔方和购买8个B 款魔方所需费用相同. 求每款魔方的单价.设A款魔方的单价为x 元，B款魔方的单价为y 元，依题意可列方程组为 .13. 如图，在矩形ABCD 中，顺次连接矩形四边的中点得到四边形EFGH . 若AB=8，AD=6，则四边形EFGH 的周长等于．14.在平面直角坐标系xOy 中，将抛物线23(2)1y x =+-平移后得到抛物线232y x =+.请你写出一种平移方法. 答： .15. 如图，AB 为⊙O 的直径，AC 与⊙O 相切于点A ，弦BD ∥OC .若36C ∠=︒，则∠DOC= ︒．16. 我们知道：四边形具有不稳定性.如图，在平面直角坐标系xOy 中，矩形ABCD 的边AB 在x 轴上，，，边AD 长为5. 现固定边AB ，“推”矩形使点D 落在y 轴的正半轴上（落点记为），相应地，点C 的对应点的坐标为 .三、解答题（本题共68分，第17~21题每小题5分，第22、23题每小题6分，第24题5分，第25、26题每小题6分，第27、28题每小题7分） 17．计算：06cos60(π2)2︒-．18．解方程：1322x x x+=--.19. 如图，在四边形ABCD 中，E 为AB 的中点，DE ⊥AB 于点E ，66A ∠=︒，90ABC ∠=︒，BC= AD ，求∠C 的度数．20.先化简，再求值：2569122x x x x -+⎛⎫-÷⎪++⎝⎭，其中5x =-．21.如图，在Rt △ABC 中，90ACB ∠=︒，CD ⊥AB 于点D ，BE ⊥AB 于点B ，BE=CD ，连接CE ，DE ．（1）求证：四边形CDBE 为矩形；（2）若AC =2，1tan 2ACD ∠=，求DE 的长．(3,0)A -(4,0)B D 'C'22.阅读下列材料：材料一：早在2011年9月25日，北京故宫博物院就开始尝试网络预售门票，2011年全年网络售票仅占1.68%.2012年至2014年，全年网络售票占比都在2%左右.2015年全年网络售票占17.33%，2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日，首次实现全部网上售票.与此同时，网络购票也采用了“人性化”的服务方式，为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后，在北京故宫博物院的精细化管理下，观众可以更自主地安排自己的行程计划，获得更美好的文化空间和参观体验.材料二：以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.他还注意到了如下的一则新闻：2018年3月8日，中国国家博物馆官方微博发文，宣布取消纸质门票，观众持身份证预约即可参观. 国博正在建设智慧国家博物馆，同时馆方工作人员担心的是：“虽然有故宫免（纸质）票的经验在前，但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票，他遵守预约的程度是不一样的.但（国博）免费就有可能约了不来，挤占资源，所以难度其实不一样.”尽管如此，国博仍将积极采取技术和服务升级，希望带给观众一个更完美的体验方式.根据以上信息解决下列问题：（1）补全以下两个统计图；（2）请你预估2018年中国国家博物馆的参观人数，并说明你的预估理由.23.如图，在平面直角坐标系xOy中，函数myx=（0x<）的图象经过点(4,)A n-，AB⊥x轴于点B，点C与点A关于原点O对称，CD⊥x轴于点D，△ABD的面积为8.（1）求m，n的值；（2）若直线y kx b=+（k≠0）经过点C，且与x轴，y轴的交点分别为点E，F，当2CF CE=时，求点F的坐标．24．如图，AB是⊙O的直径，C是圆上一点，弦CD⊥AB于点E，且DC=AD．过点A作⊙O的切线，过点C作DA的平行线，两直线交于点F，FC的延长线交AB的延长线于点G.（1）求证：FG与⊙O相切；（2）连接EF，求tan EFC∠的值.25.阅读下面材料：已知：如图，在正方形ABCD 中，边1AB a .按照以下操作步骤，可以从该正方形开始，构造一系列的正方形，它们之间的边满足一定的关系，并且一个比一个小.请解决以下问题：（1）完成表格中的填空：① ；② ； ③ ；④ ；（2）根据以上第三步、第四步的作法画出第三个正方形CHIJ （不要求尺规作图）.26. 抛物线M ：241y ax ax a =-+- (a ≠0)与x 轴交于A ，B 两点（点A 在点B 左侧），抛物线的顶点为D .（1）抛物线M 的对称轴是直线____________；（2）当AB =2时，求抛物线M 的函数表达式；（3）在（2）的条件下，直线l ：y kx b =+(k ≠0)经过抛物线的顶点D ，直线y n =与抛物线M 有两个公共点，它们的横坐标分别记为1x ，2x ，直线y n =与直线l 的交点的横坐标记为（），若当≤n ≤时，总有13320x x x x ->->，请结合函数的图象，直接写出k 的取值范围.27. 如图1，在等边三角形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A 的对应点E 落在射线BC 上，连接BQ ，设∠DAQ =α （0°＜α＜60°且α≠30°）. （1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE （用含α的式子表示）； ②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE ，AC ，CQ 之间的数量关系.3x 30x >2-1-28. 对于平面直角坐标系xOy 中的点(,)Q x y （x ≠0），将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”，记作Q L .如(1,2)Q -的“理想值”221Q L ==--. （1）①若点(1,)Q a 在直线4y x =-上，则点Q 的“理想值”Q L 等于_________；②如图，C ，⊙C 的半径为1. 若点Q 在⊙C 上，则点Q 的“理想值”QL 的取值范围是 .（2）点D 在直线+3y =上，⊙D 的半径为1，点Q 在⊙D 上运动时都有0≤L Q D 的横坐标D x 的取值范围；（3）(2,)M m （m ＞0），Q 是以r 为半径的⊙M 上任意一点，当0≤L Q ≤满足条件的最大圆，并直接写出相应的半径r 的值.（要求画图位置准确，但不必尺规作图）北京市西城区2018年九年级模拟测试数学试卷答案及评分标准 2018.5二、填空题（本题共16分，每小题2分） 9. x ≤2． 10.． 11. .12.13. 20. 14.答案不唯一，例如，将抛物线先向右平移2个单位长度，再向上平移3个单位长度得到抛物线232y x =+. 15. 54． 16. ．三、解答题（本题共68分，第17~21题每小题5分，第22、23题每小题6分，第24题5分，第25、26题每小题6分，第27、28题每小题7分） 17.解：161(22=⨯-- ……………………………………………………… 4分313=-+-2=-． ……………………………………………………………………………5分18．解方程：. 解：去分母，得．……………………………………………………… 1分去括号，得．……………………………………………………… 2分移项，得．合并同类项，得．………………………………………………………… 3分系数化为1，得．…………………………………………………………… 4分经检验，原方程的解为．……………………………………………………5分19. 解：如图1，连接BD .∵ E 为AB 的中点，DE ⊥AB 于点E ，∴ AD= BD ， ……………… ………… 1分∴ ． ∵ ，∴ ．………………………… ……2分 ∵ ，384π326170,38.x y x y +=⎧⎨=⎩23(2)1y x =+-(7,4)06cos60(π2)2︒-1322x x x+=--13(2)x x -=-136x x -=-361x x -=-25x =52x =52x =1A ∠=∠66A ∠=︒166∠=︒90ABC ∠=︒∴ ． …………………………… 3分 ∵ AD=BC ，∴ BD=BC ．…………………………………………………………………………4分 ∴ ．∴1802==782C ︒-∠∠︒． …………………………………………………… 5分20.解： ………………………………………………………………… 3分．……………………………………………………………………………… 4分当时，原式．……………………………………………………………5分21. （1）证明：如图2.∵ CD ⊥AB 于点D ，BE ⊥AB 于点B ， ∴ 90CDA DBE ∠=∠=︒．∴ CD ∥BE ．………………………………… 1分又∵ BE=CD ，∴ 四边形CDBE 为平行四边形．……………2分又∵90DBE ∠=︒，∴ 四边形CDBE 为矩形． ……………………………………………… 3分（2）解：∵ 四边形CDBE 为矩形，∴ DE=BC ．………………………………………………………………… 4分 ∵ 在Rt △ABC 中，，CD ⊥AB ，可得．∵ ， ∴ ． ∵ 在Rt △ABC 中，，AC =2，， ∴ ． ∴ DE=BC=4．…………………………………………………………… 5分22.解：（1）补全统计图如图3.2124ABC ∠=∠-∠=︒3C ∠=∠2569122x x x x -+⎛⎫-÷⎪++⎝⎭2322(3)x x x x -+=⨯+-13x =-5x =-18=-90ACB ∠=︒1ACD ∠=∠1tan 2ACD ∠=1tan 1tan 2ACD ∠=∠=90ACB ∠=︒1tan 12∠=4tan 1ACBC ==∠图2………………………………………………………………… 4分（2）答案不唯一，预估理由合理，支撑预估数据即可． ……………………… 6分23. 解：（1）如图4.∵ 点A 的坐标为，点C 与点A 关于原点O 对称，∴ 点C 的坐标为．∵ AB ⊥x 轴于点B ，CD ⊥x 轴于点D ，∴ B ，D 两点的坐标分别为，．∵ △ABD 的面积为8，， ∴ ．解得． …………………………………………………………… 2分 ∵ 函数（）的图象经过点， ∴ ． …………… 3分（2）由（1）得点C 的坐标为． ① 如图4，当时，设直线与x 轴，y 轴的交点分别为点，．由 CD ⊥x 轴于点D 可得CD ∥．∴ △CD ∽△O ．∴ ． ∵ ，∴．∴ ． ∴ 点的坐标为．②如图5，当时，设直线与x 轴，y 轴的交点分别为(4,)A n -(4,)C n -(4,0)B -(4,0)D 11()8422ABD S AB BD n n =⨯=⨯-⨯=- 48n -=2n =-m y x=0x <(4,)A n -48m n =-=(4,2)C 0k <y kx b =+1E 1F 1OF 1E 1E 1F 1111E C DC OF E F =112CF CE =113DC OF =136OF DC ==1F 1(0,6)F 0k >y kx b =+图4点，．同理可得CD ∥，． ∵ ，∴ 为线段的中点，．∴ 22OF DC ==．∴ 点的坐标为．…………6分综上所述，点F 的坐标为，．24. （1）证明：如图6，连接OC ，AC .∵ AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∴ CE=DE ，AD=AC .∵ DC=AD ，∴ DC=AD= AC .∴ △ACD 为等边三角形．∴ ∠D =∠DCA=∠DAC =60︒．∴ ． ∵ FG ∥DA ，∴ 180DCF D ∠+∠=︒． ∴ ．∴ ．∴ FG ⊥OC ．∴ FG 与⊙O 相切．……………………………………………………… 3分（2）解：如图6，作EH ⊥FG 于点H ．设CE= a ，则DE= a ，AD=2a ．∵ AF 与⊙O 相切，∴ AF ⊥AG ．又∵ DC ⊥AG ，可得AF ∥DC ．又∵ FG ∥DA ，∴ 四边形AFCD 为平行四边形．∵ DC =AD ，AD=2a ，∴ 四边形AFCD 为菱形．∴ AF=FC=AD=2 a ，∠AFC=∠D = 60︒．由（1）得∠DCG= 60︒，sin60EH CE =⋅︒=，1cos602CH CE a =⋅︒=． ∴52FH CH CF a =+=． ∵ 在Rt △EFH 中，∠EHF= 90︒，∴2tan 52EH EFC FH a ∠===． …………………………………… 5分2E 2F 2OF 2222E C DC OF E F =222CF CE =2E 2CF 222E C E F =2F 2(0,2)F -1(0,6)F 2(0,2)F -11302DCA ∠=∠=︒180120DCF D ∠=︒-∠=︒190OCF DCF ∠=∠-∠=︒图6图525．解：（1）①斜边和一条直角边分别相等的两个直角三角形全等．………………… 1分②11)a ．………………… 2分③211)a ．…………………3分④111)n a -．……………… 4分（2）所画正方形CHIJ 见图7.……………………………6分26.解：如图8.（1）.…………………………… 1分（2）∵ 抛物线241y ax ax a =-+-的对称轴为直线，抛物线M 与x 轴的交点为点A ，B （点A 在点B 左侧），AB =2，∴ A ，B 两点的坐标分别为，.……………………………… 2分∵ 点A 在抛物线M 上，∴ 将的坐标代入抛物线的函数表达式，得.解得 . ………………………………………………………………… 3分 ∴ 抛物线M 的函数表达式为213222y x x =-+-. ………………………… 4分（3）54k >. …………………… 6分27. 解：（1）当0°＜α＜30°时，①画出的图形如图9所示．…………… 1分∵ △ABC 为等边三角形，∴ ∠ABC=60°．∵ CD 为等边三角形的中线，Q 为线段CD上的点，由等边三角形的对称性得QA=QB ．∵ ∠DAQ =α，∴ ∠ABQ =∠DAQ=α，∠QBE =60°-α．2x =2x =(1,0)A (3,0)B (1,0)A 410a a a -+-=12a =-∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得，∴ QE = QA ．∴ QB=QE ．可得 1802(60)602αα=︒-︒-=︒+．……… 2分②．……………………………………………………… 3分证法一：如图10，延长CA 到点F ，使得AF=CE ，连接QF ，作QH ⊥AC于点H ．∵ ∠BQE =60°+2α，点E 在BC 上，∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α．∵ 点F 在CA 的延长线上，∠DAQ =α，∴ ∠QAF =∠BAF +∠DAQ=120°+α．∴ ∠QAF=∠QEC ．又∵ AF =CE ，QA=QE ，∴ △QAF ≌△QEC ．∴ QF=QC ．∵ QH ⊥AC 于点H ，∴ FH=CH ，CF=2CH ．∵ 在等边三角形ABC 中，CD 为中线，点Q 在CD 上，∴ ∠ACQ=12ACB ∠=30°，即△QCF 为底角为30°的等腰三角形． ∴cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=．∴ CE AC AF AC CF +=+=2CH =．即． ………………………………………… 6分思路二：如图11，延长CB 到点G ，使得BG=CE ，连接QG ，可得△QBG ≌△QEC ，△QCG 为底角为30°的等腰三角形，与证法一同理可得CE AC BG BC CG +=+=．1802BQE QBE ∠=︒-∠CE AC +=CE AC +=图10（2）如图12，当30°＜α＜60°时，．………………………… 7分28.解：（1）①． ………………………………………………………………………… 1分② 0≤Q L ……………………………………………………………… 2分（2）设直线+3y =与x 轴，y 轴的交点分别为点A ，点B ，可得A ，(0,3)B ．∴OA =，3OB =，30OAB ∠=︒．由0≤Q L ，作直线y ．①如图13，当⊙D 与x 轴相切时，相应的圆心1D 满足题意，其横坐标取到最大值．作11D E x ⊥轴于点1E ，可得11D E ∥OB ，111D E AE BO AO =． ∵ ⊙D 的半径为1，∴ 111D E=．∴ 1AE11OE OA AE =-=∴ 1D x =②如图14，当⊙D 与直线y 相切时，相应的圆心2D 满足题意，其横坐标取到最小值．AC CE -=3-图11 图12作22D E x ⊥轴于点2E ，则22D E ⊥OA ．设直线y =与直线+3y =的交点为F ．可得60AOF ∠=︒，OF ⊥AB ．则9cos 2AF OA OAF =⋅∠==． ∵ ⊙D 的半径为1，∴ 21D F =．∴ 2272AD AF D F =-=．∴ 22cos AE AD OAF =⋅∠72==，22OE OA AE =-=．∴2D x =．由①②可得，D x的取值范围是≤D x≤．………………………………………… 5分（3）画图见图15．7分。

北京市海淀区2018年中考数学二模试题标准答案

海淀区九年级第二学期期末练习数学参考答案及评分标准2018．5一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分）9．23(1)a + 10．6π 11．412．1213．10010018.752.74x x-= 14．4 15．①直径所对的圆周角为直角②线段垂直平分线上的点与这条线段两个端点的距离相等 16．532m ≤≤三、解答题（本题共68分，第17~22题，每小题5分；第23~26小题，每小题6分；第27~28小题，每小题7分）17.解：原式=414+- 3.18.解：去分母，得63(2)2(2)x x x -+<-. 去括号，得63642x x x --<-. 移项，合并得510x <. 系数化为1，得2x <.不等式的解集在数轴上表示如下：19.证明：∵3AD =，4AE =，5ED =，∴222AD AE ED +=.∴90A ∠=︒. ∴DA AB ⊥. ∵90C ∠=︒. ∴DC BC ⊥.∵BD 平分ABC ∠， ∴DC AD =. ∵3AD =， ∴3CD =.20．（1）证明：依题意，得22[(3)]413(3)m m m ∆=-+-⨯⨯=-.∵2(3)0m -≥， ∴方程总有实数根.(2)解：∵原方程有两个实数根3，m ， ∴取4m =，可使原方程的两个根中只有．．一个根小于4. 注：只要4m ≥均满足题意. 21．（1）解：∵AB ∥CD ， ∴∠ABE =∠EDC . ∵∠BEA =∠DEF ， ∴△ABE ∽△FDE . ∴AB BEDF DE=. ∵E 是BD 的中点， ∴BE =DE . ∴AB =DF .∵F 是CD 的中点， ∴CF =FD . ∴CD =2AB .∵∠ABE =∠EDC ，∠AGB =∠CGD ， ∴△ABG ∽△CDG . ∴12BG AB GD CD ==. （2）证明：∵AB ∥CF ，AB =CF ， ∴四边形ABCF 是平行四边形. ∵CE =BE ，BE =DE ， ∴CE =ED . ∵CF =FD ， ∴EF 垂直平分CD . ∴∠CF A =90°.∴四边形ABCF 是矩形.EGF ABCD22．解：（1）设点B 的坐标为（x ，y ），由题意得：BF y =，BM x =. ∵矩形OMBF 的面积为3， ∴3xy =. ∵B 在双曲线ky x=上， ∴3k =. （2）∵点B 的横坐标为3，点B 在双曲线上， ∴点B 的坐标为（3，1）. 设直线l 的解析式为y ax b =+. ∵直线l 过点(2,2)P ，B （3，1）， ∴22,3 1.a b a b +=⎧⎨+=⎩解得1,4.a b =-⎧⎨=⎩∴直线l 的解析式为4y x =-+. ∵直线l 与x 轴交于点C （4，0），∴BC =.（3）增大23．解：（1）60；（2）连接OD ，∵CD AB ⊥，AB 是O 的直径， ∴CM MD =. ∵M 是OA 的中点， ∴AM MO =.又∵AMC DMO ∠=∠， ∴AMC OMD ≅△△. ∴ACM ODM ∠=∠. ∴CA ∥OD . ∵DE CA ⊥， ∴90E ∠=︒.∴18090ODE E ∠=︒-∠=︒. ∴DE OD ⊥.B∴DE 与⊙O 相切．（3）连接CF ，CN ， ∵OA CD ⊥于M ， ∴M 是CD 中点. ∴NC ND =. ∵45CDF ∠=︒， ∴45NCD NDC ∠=∠=︒. ∴90CND ∠=︒. ∴90CNF ∠=︒.由（1）可知60AOD ∠=︒. ∴1302ACD AOD ∠=∠=︒. 在Rt △CDE 中，90E ∠=︒，30ECD ∠=︒，3DE =， ∴6sin 30DECD ==︒. 在Rt △CND 中，90CND ∠=︒，45CDN ∠=︒，6CD =，∴sin 45CN CD =⋅︒=由（1）知2120CAD OAD ∠=∠=︒， ∴18060CFD CAD ∠=︒-∠=︒.在Rt △CNF 中，90CNF ∠=︒，60CFN ∠=︒，CN =∴tan 60CNFN ==︒24．（1）补充表格：（2）答案不唯一，可参考的答案如下：B甲选手：和乙选手的平均成绩相同，中位数高于乙，打出9环及以上的次数更多，打出7环的次数较少，说明甲选手相比之下发挥更加稳定；乙选手：与甲选手平均成绩相同，打出10环次数和7环次数都比甲多，说明乙射击时起伏更大，但也更容易打出10环的成绩.（2）如图所示：（3）①231w w w <<； ②如上图所示.26．解：（1）1D （-3，3），2D （1，3），3D （-3，-1）（2）不存在.理由如下：假设满足条件的C 点存在，即A ，B ，1D ，2D ，3D 在同一条抛物线上，则线段AB 的垂直平分线2x =-即为这条抛物线的对称轴，而1D ，2D 在直线y n =上，则1D 2D 的中点C 也在抛物线对称轴上，故2m =-，即点C 的坐标为（-2，n ）. 由题意得：1D （-4，n ），2D （0，n ），3D （-2，2n -）.注意到3D 在抛物线的对称轴上，故3D 为抛物线的顶点. 设抛物线的表达式是()222y a x n =++-.当1x =-时，1y =，代入得1a n =-. 所以()()2122y n x n =-++-.令0x =，得()41232y n n n n =-+-=-=，解得1n =，与1n >矛盾. 所以不存在满足条件的C 点.27．（1）DE DF =；（2）解：连接DE ，DF ， ∵△ABC 是等边三角形， ∴60C ∠=︒. ∵DBC α∠=， ∴120BDC α∠=︒-.∵点C 与点F 关于BD 对称，∴120BDF BDC α∠=∠=︒-，DF DC =. ∴1202FDC α∠=︒+. 由（1）知DE DF =.∴F ，E ，C 在以D 为圆心，DC 为半径的圆上. ∴1602FEC FDC ∠=∠=︒+α. （3）BG GF FA =+.理由如下：连接BF ，延长AF ，BD 交于点H ， ∵△ABC 是等边三角形，∴60ABC BAC ∠=∠=︒，AB BC CA ==.GFED CBA∵点C 与点F 关于BD 对称， ∴BF BC =，FBD CBD ∠=∠. ∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=，则602ABF α∠=︒-. ∴60BAF α∠=︒+. ∴FAD α∠=. ∴FAD DBC ∠=∠. 由（2）知60FEC α∠=︒+. ∴60BGE FEC DBC ∠=∠-∠=︒. ∴120FGB ∠=︒，60FGD ∠=︒.四边形AFGB 中，360120AFE FAB ABG FGB ∠=︒-∠-∠-∠=︒. ∴60HFG ∠=︒. ∴△FGH 是等边三角形. ∴FH FG =，60H ∠=︒. ∵CD CE =， ∴DA EB =.在△AHD 与△BGE 中，,,.AHD BGE HAD GBE AD BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△△AHD BGE ≅. ∴BG AH =.∵AH HF FA GF FA =+=+， ∴BG GF FA =+．28．解：（1）函数21y x =-的限减系数是2；（2）若1m >，则10m ->，（1m -，11m -）和（m ，1m）是函数图象上两点，HGFEDCBA11101(1)m m m m -=-<--，与函数的限减系数4k =不符，∴1m ≤．若102m <<，（1t -，11t -）和（t ，1t）是函数图象上横坐标之差为1的任意两点，则0t m <≤，1111(1)t t t t -=---，∵(1)0t t -->，且2211111(1)()()24244t t t m --=--+≤--+<，∴1141t t ->-，与函数的限减系数4k =不符. ∴12m ≥．若112m ≤≤，（1t -，11t -）和（t ，1t）是函数图象上横坐标之差为1的任意两点，则0t m <≤，1111(1)t t t t -=---，∵(1)0t t -->，且2111(1)()244t t t --=--+≤，∴11141(1)t t t t -=≥---，当12t =时，等号成立，故函数的限减系数4k =． ∴m 的取值范围是112m ≤≤．（3）11-n ≤≤．。

2018北京各区初中数学二模分类汇编27号题和答案

2018北京各区初中数学二模分类汇编27号题及答案门头沟 27. 如图，在正方形ABCD 中，连接BD ，点E 为CB 边的延长线上一点，点F 是线段AE 的中点，过点F 作AE 的垂线交BD 于点M ,连接ME 、MC . （1）根据题意补全图形，猜想MEC ∠与MCE ∠的数量关系并证明；（2）连接FB ，判断FB 、FM 之间的数量关系并证明.西城27. 如图1，在等边三角形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A 的对应点E 落在射线BC 上，连接BQ ，设∠DAQ =α （0°＜α＜60°且α≠30°）. （1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE （用含α的式子表示）； ②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE ，AC ，CQ 之间的数量关系.平谷27．正方形ABCD 的对角线AC ，BD 交于点O ，作∠CBD 的角平分线BE ，分别交CD ，OC 于点E ，F ．（1）依据题意，补全图形（用尺规作图，保留作图痕迹）；（2）求证：CE=CF ；（3）求证：DE =2OF ．顺义27．在等边ABC △外侧作直线AM ，点C 关于AM 的对称点为D ，连接BD 交AM于点E ,连接CE ，CD ，AD ．（1）依题意补全图1，并求BEC ∠的度数；（2）如图2 ，当30MAC ∠=︒时，判断线段BE 与DE 之间的数量关系，并加以证明；（3）若0120MAC ︒<∠<︒，当线段2DE BE =时，直接写出MAC ∠的度数．图1MCBA东城27. 如图所示，点P 位于等边ABC △的内部，且∠ACP =∠图2MEDCBACBP ．(1) ∠BPC 的度数为________°；(2) 延长BP 至点D ，使得PD =PC ，连接AD ，CD ．①依题意，补全图形； ②证明：AD +CD =BD ；(3) 在(2)的条件下，若BD 的长为2，求四边形ABCD 的面积．房山27. 已知AC =DC ，AC ⊥DC ，直线MN 经过点A ，作DB ⊥MN ，垂足为B ，连接CB . （1）直接写出∠D 与∠MAC 之间的数量关系;（2）① 如图1，猜想AB ，BD 与BC 之间的数量关系，并说明理由；② 如图2，直接写出AB ，BD 与BC 之间的数量关系；（3）在MN 绕点A 旋转的过程中，当∠BCD =30°，BC 的值.昌平27.如图，在△ABC 中，AB =AC >BC ，BD 是AC 边上的高，点C 关于直线BD 的对称点为点E ，连接BE .图1图2（1） ①依题意补全图形；②若∠BAC =α，求∠DBE 的大小（用含α的式子表示）；（2）若DE =2AE ，点F 是BE 中点，连接AF ，BD =4，求AF 的长.（备用图）海淀27．如图，在等边ABC △中， ,D E 分别是边,AC BC 上的点，且C D C E= ,30DBC ∠<︒ ，点C 与点F 关于BD 对称，连接,AF FE ，FE 交BD 于G .（1）连接,DE DF ，则,D ED F之间的数量关系是；（2）若DBC α∠=，求FEC ∠的大小; （用α的式子表示）（2）用等式表示线段,BG GF 和FA 之间的数量关系，并证明.石景山27．在△ABC 中，∠ABC =90°，AB =BC =4，点M 是线段BC 的中点，点N 在射线MB 上，连接AN ，平移△ABN ，使点N 移动到点M ，得到△DEM （点D 与点A 对应，点E 与点B 对应），DM 交AC 于点P ．（1）若点N 是线段MB 的中点，如图1．① 依题意补全图1；② 求DP 的长；（2）若点N 在线段MB 的延长线上，射线DM 与射线AB 交于点Q ，若MQ =DP ，求D CB A DCB AGFEDCBA怀柔27.在△ABC 中，AB=BC =AC ，点M 为直线BC 上一个动点（不与B ，C 重合），连结AM ，将线段AM 绕点M 顺时针旋转60°，得到线段MN ，连结NC .(1)如果点M 在线段BC 上运动. ①依题意补全图1；②点M 在线段BC 上运动的过程中，∠MCN 的度数是否确定？如果确定，求出∠MCN 的度数；如果不确定，说明理由；(2)如果点M 在线段CB 的延长线上运动，依题意补全图2，在这个过程中，∠MCN 的度数是否确定？如果确定，直接写出∠MCN 的度数；如果不确定，说明理由.朝阳27.如图，在△ABC 中，AB=AC ，∠BAC =90°，M 是BC 的中点，延长AM 到点D ，AE = AD ，∠EAD =90°，CE 交AB 于点F ，CD =DF . （1）∠CAD = 度；（2）求∠CDF 的度数；（3）用等式表示线段CD 和CE 之间的数量关系，并证明.BA AB丰台27．如图，正方形ABCD 中，点E 是BC 边上的一个动点，连接AE ，将线段AE 绕点A 逆时针旋转90°，得到AF ，连接EF ，交对角线BD 于点G ，连接AG ．（1）根据题意补全图形；（2）判定AG 与EF 的位置关系并证明；（3）当AB = 3，BE = 2时，求线段BG 的长．答案门头沟 27．（本小题满分7分）（1）补全图形正确 ……………………………………………1分 MEC ∠=MCE ∠ ………………………………………2分证明：连接AM∵点F 是AE 的中点，FM AE ⊥A B CE D∴MA ME =∵点A 、点C 是关于正方形ABCD 对角线BD 所在直线的对称点 ∴MA MC =………………………………………3分 ∴ME MC =∴MEC ∠=MCE ∠………………………………………4分（2）数量关系：FB FM = ……………………5分 ∵点M 在正方形对角线上，可得MAD MCD △≌△∴MAD ∠=MCD ∠ ∵MEC ∠=MCE ∠∴90MEC MAD DCM MCE ∠+∠=∠+∠=︒ ∵AD CE ∥∴180DAE CEA ∠+∠=︒ ∴90MAE MEA ∠+∠=︒ ∴90AME ∠=︒∴EMA △是等腰直角三角形……………………6分 ∴12FM AE = ∵12FB AE =∴FB FM = ……………………7分西城27. 解：（1）当0°＜α＜30°时，①画出的图形如图9所示．…………… 1分∵ △ABC 为等边三角形，∴ ∠ABC=60°．∵ CD 为等边三角形的中线，Q 为线段CD 上的点，由等边三角形的对称性得QA=QB ． ∵ ∠DAQ =α，∴ ∠ABQ =∠DAQ=α，∠QBE =60°-α．∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得， ∴ QE = QA ．∴ QB=QE ．可得 1802BQE QBE ∠=︒-∠1802(60)602αα=︒-︒-=︒+．……… 2分②CE AC +=．……………………………………………………… 3分图9证法一：如图10，延长CA 到点F ，使得AF=CE ，连接QF ，作QH ⊥AC 于点H ． ∵ ∠BQE =60°+2α，点E 在BC 上，∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α．∵ 点F 在CA 的延长线上，∠DAQ =α， ∴ ∠QAF =∠BAF +∠DAQ=120°+α． ∴ ∠QAF=∠QEC ．又∵ AF =CE ，QA=QE ， ∴ △QAF ≌△QEC ． ∴ QF=QC ．∵ QH ⊥AC 于点H ， ∴ FH=CH ，CF=2CH ．∵ 在等边三角形ABC 中，CD 为中线，点Q 在CD 上，∴ ∠ACQ=12ACB∠=30°，即△QCF 为底角为30°的等腰三角形．∴cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=．∴ CE AC AF AC CF +=+=2CH ==．即CE AC +=． ………………………………………… 6分思路二：如图11，延长CB 到点G ，使得BG=CE ，连接QG ，可得△QBG ≌△QEC ，△QCG 为底角为30°的等腰三角形，与证法一同理可得CE AC BG BC CG +=+=．（2）如图12，当30°＜α＜60°时，AC CE -=．………………………… 7分平谷27．（1）如图 (1)图10图11 图12y yxx E DMCBA（2）证明：∵BE 平分∠CBD ，∴∠CBE =∠DBE ． ························ 2 ∵正方形ABCD 的对角线AC ，BD 交于点O ，∴∠BOC =∠BCD =90°．∵∠CBE +∠CEB =90°， ∠DBE +∠BFO =90°，∴∠CEB =∠BFO ． ························ 3 ∵∠EFC =∠BFO ， ∴∠EFC =∠CEB ．∴CF=CE ． ··························· 4 （3）证明：取BE 的中点M ，连接OM ． ···················· 5 ∵O 为AC 的中点，∴OM ∥DE ， DE =2OM ． ...................... 6 ∴∠OMF =∠CEF ．∵∠OFM =∠EFC =∠CEF ， ∴∠OMF =∠OFM ．∴OF=OM ． ∴DE =2OF ． (7)顺义27．解：（1）补全图形如右图： …………………………………………………… 1分依题意显然可以得出AD =AC ,∠=∠=DAE CAE x ,∠=∠DEM CEM ． ∵等边ABC △，∴AB =AC ，60∠=︒BAC ．∴AB =AD ．∴∠=∠=ABD ADB y ．在△ABD 中，2260180++︒=︒x y ， ∴60+=︒x y ．∴60∠=∠=+=︒DEM CEM x y ．∴60∠=︒BEC ．………………………………………………………… 4分（2）判断：2=BE DE ．证明：∵30MAC ∠=︒，结合（1）中证明过程，显然可以得出30∠=︒ABD , 又∵等边ABC △, ∴60∠=︒ABC ． ∴30∠=︒DBC ．又∵60∠=︒BEC , ∴90∠=︒ECB ． ∴2=BE CE ．∵=CE DE , ∴2=BE DE ．（3）90∠=︒MAC ．………………………………………………………… 7分 4东城 27. 解：(1)120°. ---------------------------------------------------2分(2)①∵如图1所示.②在等边ABC △中，60ACB ∠=︒， ∴60.ACP BCP ∠+∠=︒ ∵=ACP CBP ∠∠，∴60.CBP BCP ∠+∠=︒∴()180120.BPC CBP BCP ∠=︒-∠+∠=︒ ∴18060.CPD BPC ∠=︒-∠=︒ ∵=PD PC ，∴CDP △为等边三角形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=︒， ∴.ACD BCP ∠=∠ 在ACD △和BCP △中，AC BC ACD BCP CD CP =⎧⎪∠=∠⎨⎪=⎩，，， ∴()SAS ACD BCP △≌△. ∴.AD BP = ∴.AD CD BP PD BD +=+=-----------------------------------------------------------------4分（3）如图2，作BM AD ⊥于点M ，BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=︒， ∴=60.ADB CDB ∠∠=︒ ∴=60.ADB CDB ∠∠=︒∴=2BM BN BD == 又由（2）得，=2AD CD BD +=，ABD BCD ABCD S S S ∴△△四边形=+1122AD BMCD BN =+()2AD CD =+22==----------------------------------------------------------7分房山27. 解：（1）相等或互补；………………………………………………2分（注：每个1分）（2）① 猜想：BD +AB =2BC …………………………………………………………3分如图1，在射线AM 上截取AE =BD ，连接CE .又∵∠D =∠EAC ，CD =AC ∴△BCD ≌△ECA ∴BC =EC ,∠BCD =∠ECA ∵AC ⊥CD ∴∠ACD =90° 即∠ACB +∠BCD =90° ∴∠ACB +∠ECA =90° 即∠ECB =90° ∴BE =2BC ∵AE +AB =BE =2BC∴BD +AB =2BC ……………………………………………………………4分 ② AB －BD =2BC ……………………………………………………………5分（3）BC =3+1 或3－1 ……………………………………………………………7分昌平27．如图，在△ABC 中，AB =AC >BC ，BD 是AC 边上的高，点C 关于直线BD 的对称点为点E ，连接BE . （1）①补全图形；②若∠BAC =α，求∠DBE 的大小（用含α的式子表示）；（2）若DE =2AE ，点F 是BE 中点，连接AF ，BD =4，求AF 的长. （1）解：①如图． ……………………… 1分 ②∵ AB =AC ，∠BAC =α，M图1DBAE∴ ∠ABC =∠ACB =90°-12α．∵点C 关于直线BD 的对称点为点E ，BD 是AC 边上的高.∴ BD ⊥CE ，CD =DE ． ∴ BE =BC ．∴ ∠BEC =∠ACB =90°-12α． …………………… 2分 ∴∠DBE =12α．……………… 3分（2）解：作FG ⊥AC 于G ， ∵BD ⊥CE ，∴FG ∥BD∵点F 是BE 中点，∴EG =DG ．∴1FG=BD 2…………4分 ∵DE =2AE ，∴AE =EG =DG ．……………… 5分设AE =EG =DG=x ，则CD =DE=2x ，AC =5x ，∴AB=AC =5x ．∴BD =4x ． ∵BD =4，∴x =1．……………… 6分 ∴AG =2．∵1FG=BD 2=2， ∴AF= 7分海淀 27．（1）DE DF =；（2）解：连接DE ，DF ， ∵△ABC 是等边三角形， ∴60C ∠=︒. ∵DBC α∠=， ∴120BDC α∠=︒-. ∵点C 与点F 关于BD 对称，∴120BDF BDC α∠=∠=︒-，DF DC =. ∴1202FDC α∠=︒+. 由（1）知DE DF =.∴F ，E ，C 在以D 为圆心，DC 为半径的圆上.EABCDFG GFED CBA∴1602FEC FDC ∠=∠=︒+α.（3）BG GF FA =+.理由如下：连接BF ，延长AF ，BD 交于点H ， ∵△ABC 是等边三角形，∴60ABC BAC ∠=∠=︒，AB BC CA ==. ∵点C 与点F 关于BD 对称， ∴BF BC =，FBD CBD ∠=∠. ∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=，则602ABF α∠=︒-. ∴60BAF α∠=︒+. ∴FAD α∠=.∴FAD DBC ∠=∠. 由（2）知60FEC α∠=︒+. ∴60BGE FEC DBC ∠=∠-∠=︒.∴120FGB ∠=︒，60FGD ∠=︒.四边形AFGB 中，360120AFE FAB ABG FGB ∠=︒-∠-∠-∠=︒. ∴60HFG ∠=︒.∴△FGH 是等边三角形. ∴FH FG =，60H ∠=︒. ∵CD CE =， ∴DA EB =.在△AHD 与△BGE 中，,,.AHD BGE HAD GBE AD BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△△AHD BGE ≅.HGFEDCBA∴BG AH=.∵AH HF FA GF FA=+=+，∴BG GF FA=+．石景山27．解：（1）①如图1，补全图形. ………………… 1分②连接AD，如图2.在Rt△ABN中,∵∠B=90°，AB=4，BN=1，∴17=AN.∵线段AN平移得到线段DM，∴DM=AN=17，AD=NM=1，AD∥MC，∴△ADP∽△CMP.∴21==MCADMPDP.∴317=DP.………………… 3分（2）连接NQ，如图3.由平移知：AN∥DM，且AN=DM.∵MQ DP=，∴PQ DM=.∴AN∥PQ，且AN=PQ.∴四边形ANQP是平行四边形.∴NQ∥AP.∴45BQN BAC∠=∠=︒.又∵90NBQ ABC∠=∠=︒，∴BN BQ=.∵AN∥MQ，∴AB NBBQ BM=.又∵M是BC的中点，且4AB BC==∴42NBNB=.∴NB=舍负).∴ME BN==∴2CE= (7)（2）法二，连接AD，如图4.图1图2A B 设CE 长为x ，∵线段AB 移动到得到线段DE ， ∴4+==x BE AD ，AD ∥BM . ∴△ADP ∽△CMP . ∴24xMC AD MP DP +==. ∵MQ =DP ， ∴x xMP DP DP QD MQ 21042++=+=. ∵△QBM ∽△QAD ， ∴xAD BM QD MQ +==42. 解得222-=x .∴222-=CE . ………………… 7分27. (1)①补全图形，如图：…………………………………………….………………….…………………………………1分②点M 在线段BC 上运动的过程中，∠MCN 的度数确定，为120°理由如下：在AB 上取点P ，使得BP=BM ，连结PM ……………………………………………………2分∵BP =BM ，∠B =60º，∴△BPM 是等边三角形. ∴∠BPM =∠BMP =60º. ∴∠APM =120º.∴∠PAM +∠AMP =60º.∴∠PAM +∠AMP +∠BMP =120º.即∠PAM +∠AMB =120º. ∵AB=BC ， ∴AP=MC .∵∠AMN =60º， ∴∠AMB +∠NMC =120º. ∴∠PAM =∠NMC .又∵AM=MN ，∴△APM ≌△NMC .∴∠MCN =∠APM =120º………………5分 (2) 补全图形，如图……………………………………………………………….………………………6分B∠MCN =60º……………………………………………………………….……………………7分朝阳27. 解：（1）45 ……………………………………………………………………………………1分（2）解：如图，连接DB.∵90 AB AC BAC =∠=，°，M 是BC 的中点， ∴∠BAD=∠CAD=45°.∴△BAD ≌△CAD . ………………………………2分 ∴∠DBA =∠DCA ，BD = CD . ∵CD =DF ,∴B D =DF . ………………………………………3分 ∴∠DBA =∠DFB =∠DCA . ∵∠DFB +∠DFA =180°, ∴∠DCA +∠DFA =180°. ∴∠BAC +∠CDF=180°.∠CDF =90°. …………………………………………………………………………4分（3）CE =)1CD . ………………………………………………………………………5分证明：∵90 EAD ∠=°，∴∠EAF =∠DAF =45°. ∵AD =AE ，∴△EAF ≌△DAF . ……………………………………………………………………6分 ∴DF =EF .由②可知，CF . ∴CE =)1C D . ………………………………………………………………7分丰台27．解：（1）图形补全后如图…………………1分（2）结论：AG ⊥EF ． …………………2分证明：连接FD ，过F 点FM ∥BC ，交BD 的延长线于点M ．∵四边形ABCD 是正方形，∴AB=DA=DC=BC ，∠DAB =∠ABE =∠ADC =90°， ∠ADB =∠5=45°．∵线段AE 绕点A 逆时针旋转90°，得到AF ， ∴AE=AF ，∠FAE =90°．∴∠1=∠2．∴△FDA ≌△EBA ． …………………3分∴∠FDA =∠EBA =90°，FD=BE ．∵∠ADC =90°， ∴∠FDA +∠ADC =180°。

北京市东城区2018届中考数学二模试题含答案

北京市东城区 2018届中考数学二模试题学校______________班级______________姓名_____________考号____________一、选择题(本题共16分，每小题2分)下面各题均有四个选项，其中只有一个．．是符合题意的1. 长江经济带覆盖上海、江苏、浙江、安徽、江西、湖北、湖南、重庆、四川、云南、贵州等11省市，面积约2 050 000平方公里，约占全国面积的21% .将2 050 000用科学记数法表示应为 A. 205万 B. 420510⨯ C. 62.0510⨯ D. 72.0510⨯ 2. 在平面直角坐标系xOy 中，函数31y x =+的图象经过A. 第一、二、三象限B. 第一、二、四象限C. 第一、三、四象限D. 第二、三、四象限3. 在圆锥、圆柱、球、正方体这四个几何体中，主视图不可能．．．是多边形的是 A. 圆锥 B. 圆柱 C. 球 D. 正方体4. 七年级1班甲、乙两个小组的14名同学身高（单位：厘米）如下：甲组 158 159 160 160 160 161 169 乙组158159160161161163165以下叙述错误．．的是 A. 甲组同学身高的众数是160 B. 乙组同学身高的中位数是161 C. 甲组同学身高的平均数是161 D. 两组相比，乙组同学身高的方差大 5. 在平面直角坐标系xOy 中，若点()3,4P 在O 内，则O 的半径r 的取值范围是A. 0r ＜＜3B. r ＞4C. 0r ＜＜5D. r ＞56. 如果23510a a +-=，那么代数式()()()5323+232a a a a +--的值是A. 6B. 2C. - 2D. - 67. 在以下三个图形中，根据尺规作图的痕迹，能判断射线AD 平分∠BAC 的是A. 图2B. 图1与图2C. 图1与图3D. 图2与图38. 有一圆形苗圃如图1所示，中间有两条交叉过道AB ，CD ，它们为苗圃O e 的直径，且AB ⊥CD . 入口K 位于»AD 中点，园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为x ，与入口K 的距离为y ，表示y 与x 的函数关系的图象大致如图2所示，则该园丁行进的路线可能是图2A. A →O →DB. C→A→O→ BC. D →O →CD. O→D→B→C 二、填空题(本题共16分，每小题2分) 9．若分式22xx +的值为正，则实数x 的取值范围是__________________. 10．在平面直角坐标系xOy 中，点P 到x 轴的距离为1，到y 轴的距离为2.写出一个．．符合条件的点P 的坐标________________.11. 如图，在△ABC 中，AB =AC ，BC =8. O e 是△ABC 的外接圆，其半径为5. 若点A 在优弧BC 上，则tan ABC ∠的值为_____________.第11题图第15题图 12. 抛物线221y mx mx =++（m 为非零实数）的顶点坐标为_____________.13．自2008年9月南水北调中线京石段应急供水工程通水以来，截至2018年5月8日5 时52分，北京市累计接收河北四库来水和丹江口水库来水达50亿立方米. 已知丹江口水库来水量比河北四库来水量的2倍多1.82亿立方米，求河北四库来水量. 设河北四库来水量为x 亿立方米，依题意，可列一元一次方程为_________ .14. 每年农历五月初五为端午节，中国民间历来有端午节吃粽子、赛龙舟的习俗．某班同学为了更好地了解某社区居民对鲜肉粽、豆沙粽、小枣粽、蛋黄粽的喜爱情况，对该社区居民进行了随机抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．分析图中信息，本次抽样调查中喜爱小枣粽的人数为；若该社区有10 000人，估计爱吃鲜肉粽的人数约为 .15. 如图，在平面直角坐标系xOy 中，点A ，P 分别在x 轴、 y 轴上，30APO ∠=︒ .先将线段PA 沿y 轴翻折得到线段PB ，再将线段PA 绕点P 顺时针旋转30°得到线段PC ，连接BC . 若点A 的坐标为()1,0- ，则线段BC 的长为 . 16. 阅读下列材料：数学课上老师布置一道作图题：小东的作法如下：老师说：“小东的作法是正确的.”请回答：小东的作图依据是 .三、解答题(本题共68分，第17-24题，每小题5分，第25题6分，第26-27，每小题7分，第28题8分)17．计算：()332sin 60+2+12--︒-18．解不等式()()41223x x ---＞，并把它的解集表示在数轴上.19. 如图，在Rt ABC △中，90C ∠=︒，AB 的垂直平分线交AC 于点D ，交AB 于点E .(1)求证：ADE ABC △≌△;(2)当8AC =，6BC =时，求DE 的长.20. 已知关于x 的一元二次方程2610kx x -+=有两个不相等的实数根.(1)求实数k 的取值范围；(2)写出满足条件的k 的最大整数值，并求此时方程的根.21．如图，在菱形ABCD 中，BAD α∠=，点E 在对角线BD 上. 将线段CE 绕点C 顺时针旋转α，得到CF ，连接DF . （1）求证：BE =DF ；（2）连接AC ，若EB =EC ，求证：AC CF ⊥.22. 已知函数1y x=的图象与函数()0y kx k =≠的图象交于点(),P m n . （1）若2m n =，求k 的值和点P 的坐标；（2）当m n ≤时，结合函数图象，直接写出实数k 的取值范围. 23．如图，AB 为O 的直径，直线BM AB ⊥于点B .点C 在O 上，分别连接BC ，AC ，且AC的延长线交BM 于点D .CF 为O 的切线交BM 于点F .（1）求证：CF DF =；（2）连接OF . 若10AB =，6BC =，求线段OF 的长.24．十八大报告首次提出建设生态文明，建设美丽中国. 十九大报告再次明确，到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障，提高森林的数量和质量对生态文明建设非常关键 .截止到2013年，我国已经进行了八次森林资源清查，其中全国和北京的森林面积和森林覆盖率情况如下：表1 全国森林面积和森林覆盖率表2 北京森林面积和森林覆盖率（以上数据来源于中国林业网）请根据以上信息解答下列问题：(1) 从第________次清查开始，北京的森林覆盖率超过全国的森林覆盖率；(2) 补全以下北京森林覆盖率折线统计图，并在图中标明相应数据；(3) 第八次清查的全国森林面积20768.73（万公顷）记为a，全国森林覆盖率21.63%记为b，到2018年第九次森林资源清查时，如果全国森林覆盖率达到27.15%，那么全国森林面积可以达到________万公顷（用含a和b的式子表示）.25. 小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园，妈妈问九年级的小强至少需要几米长的竹篱笆（不考虑接缝）.小强根据他学习函数的经验做了如下的探究. 下面是小强的探究过程，请补充完整：建立函数模型：设矩形小花园的一边长为x 米，篱笆长为y 米.则y 关于x 的函数表达式为 ; 列表（相关数据保留一位小数）：根据函数的表达式，得到了x 与y 的几组值，如下表：描点、画函数图象：如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；观察分析、得出结论：根据以上信息可得，当x = 时，y 有最小值. 由此，小强确定篱笆长至少为米.26．在平面直角坐标系xOy 中，抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ，．（1）求该抛物线的表达式；（2）求直线AB 关于x 轴的对称直线的表达式；（3）点P 是x 轴上的动点，过点P 作垂直于x 轴的直线l ，直线l 与该抛物线交于点M ，与直线AB交于点N ．当PM PN ＜时，求点P 的横坐标P x 的取值范围．27. 如图所示，点P 位于等边ABC △的内部，且∠ACP =∠CBP ． (1) ∠BPC 的度数为________°；(2) 延长BP 至点D ，使得PD =PC ，连接AD ，CD ．①依题意，补全图形； ②证明：AD +CD =BD ；(3) 在(2)的条件下，若BD 的长为2，求四边形ABCD 的面积．28. 研究发现，抛物线214y x =上的点到点F (0，1)的距离与到直线l ：1y =-的距离相等.如图1所示，若点P 是抛物线214y x =上任意一点，PH ⊥l 于点H ，则PH PF =.基于上述发现，对于平面直角坐标系x O y 中的点M ，记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ，称d 为点M 关于抛物线214y x =的关联距离；当24d ≤≤时，称点M 为抛物线214y x =的关联点.（1）在点1(20)M ，，2(12)M ，，3(45)M ，，4(04)M -，中，抛物线214y x =的关联点是______ ；（2）如图2，在矩形ABCD 中，点(1)A t ，，点(13)A t +，C ( t .①若t =4，点M 在矩形ABCD 上，求点M 关于抛物线214y x =的关联距离d 的取值范围； ②若矩形ABCD 上的所有点都是抛物线214y x =的关联点，则t 的取值范围是__________. 东城区2017-2018学年度第二学期初三年级统一测试（二）数学试题卷参考答案及评分标准 2018.5一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题 2分）9. x ＞0 10. ()()()()21212121--，，，-，，，，-（写出一个即可） 11. 2 12. ()1,1m -- 13. ()2 1.8250x x ++= 14. 120 ；3 000 15. 22 16. 三边分别相等的两个三角形全等；全等三角形的对应角相等；两点确定一条直线；内错角相等两直线平行.三、解答题（本题共68分，17-24题，每题5分，第25题6分，26-27题，每小题7分，第28题8分）3=3-232⨯17.解：原式--------------------------------------------------------------------4分-------------------------------------------------------------------------------------------------- 5分 18. 解：移项，得()1213x -＜，去分母，得 23x -＜，移项，得x ＜5.∴不等式组的解集为x ＜5.--------------------------------------------------------------------3分--------------------------------5分 19. 证明：（1） ∵DE 垂直平分AB ,∴ 90AED ∠=︒. ∴AED C ∠=∠. ∵A A ∠=∠， ∴ADE ABC △∽△.--------------------------------------------------------------------2分(2) ABC Rt △中，8AC =，6BC =， ∴10AB =.∵DE 平分AB ， ∴5AE =.∵ADE ABC △∽△，∴DE AEBC AC =. ∴568DE = .∴154DE = . ---------------------------------------------------------------------5分20. 解：（1）依题意，得()20,640k k ≠⎧⎪⎨∆=--⎪⎩＞，解得k k ≠＜9且0.----------------------------------------------------------------------2分(2) ∵k 是小于9的最大整数，∴=8k .此时的方程为28610x x -+=. 解得11=2x ，21=4x . ---------------------------------------------------------------------5分21 . (1) 证明：∵四边形ABCD 是菱形，∴=BC DC ，BAD BCD α==∠∠. ∵ECF α=∠，∴ BCD ECF ∠=∠. ∴=BCE DCF ∠∠.∵线段CF 由线段CE 绕点C 顺时针旋转得到， ∴=CE CF .在BEC △和DFC △中，BC DC BCE DCF CE CF =⎧⎪∠=∠⎨⎪=⎩，，， ∴BEC △≌()SAS DFC △.∴=.BE DF ----------------------------------------------------------------------2分 (2) 解：∵四边形ABCD 是菱形， ∴ACB ACD ∠=∠，AC BD ⊥. ∴+90ACB EBC ∠=︒∠. ∵=EB EC ，∴=EBC BCE ∠∠.由（1）可知，∵=EBC DCF ∠∠，∴+90DCF ACD EBC ACB ∠=∠+∠=︒∠.∴90ACF =︒∠.∴AC CF ⊥. ---------------------------------------------------------------------5分22. 解：（1）12k =，222P ，，或22P ⎛- ⎝⎭，;---------------------------3分 (2) 1k ≥.---------------------------------------------------------------------5分23. （1）证明：∵AB 是O 的直径，∴90ACB ∠=︒.∴90DCB ∠=︒.∴90CDB FBC ∠+∠=︒.∵ AB 是O 的直径，MB AB ⊥， ∴MB 是O 的切线. ∵CF 是O 的切线，∴FC FB =.∴=FCB FBC ∠∠.∵90FCB DCF ∠+∠=︒ ,∴=CDB DCF ∠∠.∴=CF DF . ---------------------------------------------------------------------3分（2）由（1）可知，ABC △是直角三角形，在Rt ABC △中，=10AB ，=6BC ，根据勾股定理求得=8AC .在Rt ABC △和Rt ADB △中，A A ACB ABD ∠=∠⎧⎨∠=∠⎩，， ∴Rt ABC △∽Rt ADB △. ∴AB AC AD AB=.∴10810AD = . ∴252AD =. 由（1）知，∵=CF DF ，=CF BF ，∴=DF BF .∵=AO BO ，∴ OF 是ADB △的中位线. ∴125.24OF AD ==---------------------------------------------------------------------5分 24. 解：(1)四； ---------------------------------------------------------------------1分（2）如图： ---------------------------------------------------------------------3分（3）5432000a b.------------------------------------------------------5分 25. 解：42y x x ⎛⎫=+ ⎪⎝⎭；----------------------------------------------1分 810，； --------------------------------------------------------3分如图； ----------------------------------------------------------4分28，. -----------------------------------------------------------5分26. 解：（1）把点(10)-，和(45)，分别代入23(0)y ax bx a =+-≠，得 0--35164-3a b a b =⎧⎨=+⎩，，解得12a b ==-，． ∴抛物线的表达式为223y x x =--． -------------------------------------------------------------2分（2）设点()45B ，关于x 轴的对称点为B '，则点B '的坐标为()45，-.∴直线AB 关于x 轴的对称直线为直线AB '.设直线AB '的表达式为y mx n =+，把点(10)-，和(45)-，分别代入y mx n =+，得054m n m n =-+⎧⎨-=+⎩，，解得11m n =-=-，．∴直线AB '的表达式为1y x =--．即直线AB 关于x 轴的对称直线的表达式为1y x =--.--------------------------------------4分（3）如图，直线AB '与抛物线223y x x =--交于点C .设直线l 与直线AB '的交点为N '，则 'PN PN =．∵PM PN <，∴'PM PN <.∴点M 在线段'NN 上（不含端点）．∴点M 在抛物线223y x x =--夹在点C 与点B 之间的部分上．联立223y x x =--与1y x =--，可求得点C 的横坐标为2．又点B 的横坐标为4，∴点P 的横坐标P x 的取值范围为24P x <<． --------------------------------------------------7分27. 解：(1)120°.---------------------------------------------------2分(2)①∵如图1所示.②在等边ABC △中，60ACB ∠=︒，∴60.ACP BCP ∠+∠=︒∵=ACP CBP ∠∠，∴60.CBP BCP ∠+∠=︒∴()180120.BPC CBP BCP ∠=︒-∠+∠=︒∴18060.CPD BPC ∠=︒-∠=︒∵=PD PC ，∴CDP △为等边三角形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=︒，∴.ACD BCP ∠=∠在ACD △和BCP △中，AC BC ACD BCP CD CP =⎧⎪∠=∠⎨⎪=⎩，，，∴()SAS ACD BCP △≌△.∴.AD BP =∴.AD CD BP PD BD +=+=-----------------------------------------------------------------4分（3）如图2，作BM AD ⊥于点M ，BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=︒，∴=60.ADB CDB ∠∠=︒∴=60.ADB CDB ∠∠=︒ ∴3= 3.BM BN == 又由（2）得，=2AD CD BD +=，ABD BCD ABCD S S S ∴△△四边形=+1122AD BM CD BN =+)32AD CD =+ 32= 3.=----------------------------------------------------------7分28. (1) 12M M ，； -----------------------------------------------------------------2分（2）①当4t =时，()41A ，，()51B ，，()53C ，，()43D ，，此时矩形ABCD 上的所有点都在抛物线214y x =的下方， ∴.d MF =∴.AF d CF ≤≤∵=4=29AFCF ，∴d 4≤ ---------------------------------------------------------------------------------- 5分t≤② 1. ------------------------------------------------------------------------8分。

2018北京市海淀区中考二模数学试卷(含答案)

海淀区九年级第二学期期末练习数学2018．5学校姓名成绩考生须知1．本试卷共8页，共三道大题，28道小题，满分100分。

考试时间120分钟。

2．在试卷和答题卡上准确填写学校名称、班级和准考证号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5．考试结束，将本试卷、答题卡和草稿纸一并交回。

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．1．若代数式有意义，则实数的取值范围是31x -x A . B. 1x >1x ≥ C.D.1x ≠0x ≠2．如图，圆的弦，，，中最短的是O GH EF CD AB A . B. GH EF C.D. CD AB3．2018年4月18日，被誉为“中国天眼”的FAST 望远镜首次发现的毫秒脉冲星得到国际认证．新发现的脉冲星自转周期为0.00519秒，是至今发现的射电流量最弱的高能毫秒脉冲星之一．将0.00519用科学记数法表示应为A. -25.1910⨯ B. -35.1910⨯ C. -551910⨯ D. -651910⨯4．下列图形能折叠成三棱柱的是ABE DCD 5．如图，直线经过点，，°，°，则等于DE A DE BC ∥=45B ∠1=65∠2∠A ．° 60B ．° 65C ．° 70D ．°756．西周时期，丞相周公旦设置过一种通过测定日影长度来确定时间的仪器，称为圭表．如图是一个根据北京的地理位置设计的圭表，其中，立柱高为．已知，冬至时北京的正午日AC a 光入射角约为°，则立柱根部与圭表的冬至线的距离（即的长）约为ABC ∠26.5BC A ．B ．sin 26.5a ︒tan 26.5a︒C ．D ．cos 26.5a ︒cos 26.5a ︒7．实数在数轴上的对应点的位置如图所示，若，,,a b c a b >则下列结论中一定成立的是A. B ． 0b c +>2a c +<-C.D. 1ba<0abc ≥8．“单词的记忆效率”是指复习一定量的单词，一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中四位同学的单词记忆,,,M N S T 效率与复习的单词个数的情况，则这四位同学在这次单词复习中正确默写出的y x 单词个数最多的是A ．B ．M N c ba 光光光光光光光光光光光光光光光光光光光光光光光光光光EDCB A21C ．D ．S T二、填空题（本题共16分，每小题2分）9．分解因式：．2363a a ++=10．如图，是⊙的直径，是⊙上一点，，，则AB O C O 6OA =30B ∠=︒图中阴影部分的面积为．11．如果，那么代数式的值是．3m n =n m mm n n m⎛⎫-⋅ ⎪-⎝⎭12．如图，四边形与四边形是以为位似中心的位似图形，满足，，，ABCD 1111A B C D O 11=OA A A E F ，1E 分别是，，的中点，则1F AD BC ，11A D 11B C 11=E F EF．13．2017年全球超级计算机500强名单公布，中国超级计算机“神威·太湖之光”和“天河二号”携手夺得前两名．已知“神威·太湖之光”的浮点运算速度是“天河二号”的2.74倍．这两种超级计算机分别进行100亿亿次浮点运算，“神威·太湖之光”的运算时间比“天河二号”少18.75秒，求这两种超级计算机的浮点运算速度．设“天河二号”的浮点运算速度为亿亿次/秒，依题意，可列方程为．x 14．袋子中有20个除颜色外完全相同的小球. 在看不到球的条件下，随机地从袋子中摸出一个球，记录颜色后放回，将球摇匀. 重复上述过程150次后，共摸到红球30次，由此可以估计口袋中的红球个数是__________..BA请回答：在上面的作图过程中，①是直角三角形的依据是；②是等腰三角形的依据是 ABC △ABC △．16．在平面直角坐标系中，点绕坐标原点顺时针旋转后，恰好落在右图中阴影区域（包xOy (2,)A m -O 90︒括边界）内，则的取值范围是.m 三、解答题（本题共68分，第17~22题，每小题5分；第23~26小题，每小题6分；第27~28小题，每小题7分）解答应写出文字说明、演算步骤或证明过程．17．214sin 452)(2--︒+--18．解不等式，并把解集在数轴上表示出来.2223x xx +--<19．如图，四边形中，°，平分，，为上一点，，ABCD 90C ∠=BD ABC ∠3AD =E AB 4AE =，求的长．5ED =CD E DCBA20．关于的一元二次方程.x 2(3)30x m x m -++=（1）求证：方程总有实数根；（2）请给出一个的值，使方程的两个根中只有一个根小于.m 421．如图，在四边形中，，交于，是的中点，连接并延长，交于ABCD AB CD BD AC G E BD AE CD 点，恰好是的中点.F F CD GBC（1）求的值；BGGD（2）若，求证：四边形是矩形.CE EB =ABCF 22．已知直线过点，且与函数的图象l (2,2)P (0)ky x x =>相交于两点，与轴、轴分别交于点，如图,A B x y ,C D 所示，四边形均为矩形，且矩形,ONAE OFBM 的面积为.OFBM 3（1）求的值；k （2）当点的横坐标为时，求直线的解析式及线段的长；B 3l BC （3）如图是小芳同学对线段的长度关系的思考示意图.,AD BC 记点的横坐标为，已知当时，线段的长随的增大而减小，请你参考小芳的示意图判断：B s 23s <<BC s 当时，线段的长随的增大而 . （填“增大”、“减小”或“不变”）3s ≥BC s23．如图，是的直径，是的中点，弦于点，过点作交的延长线AB O M OA CD AB ⊥M D DE CA ⊥CA 于点.E （1）连接，则= ；AD OAD ∠︒（2）求证：与相切；DE O （3）点在上，，交于点.若，求的长.F BC45CDF ∠=︒DF AB N 3DE =FN24．如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.（1）根据折线图把下列表格补充完整；运动员平均数中位数众数甲8.59乙8.5（2）根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.25．小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：收费项目收费标准3公里以内收费13元基本单价 2.3元/公里…………备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。

北京市2018年中考数学二模试题汇编代几综合题

代几综合题2018昌平二模28.在平面直角坐标系中，对于任意三点A 、B 、C 我们给出如xOy 下定义：“横长”a ：三点中横坐标的最大值与最小值的差，“纵长”b ：三点中纵坐标的最大值与最小值的差，若三点的横长与纵长相等，我们称这三点为正方点.例如：点 (,0) ，点 (1,1) ，点 (, )，则、A 2-BC 1-2-A 、三点的 “横长”=||=3，、、三点的“纵B C a 1(2)--A B C 长”=||=3. 因为=，所以、、三点为正方点.b 1(2)--a b A B C （1）在点 (3，5) ，(3，) ， (，)中，与点、R S 2-T 4-3-A 为正方点的是；B （2）点P (0，t )为轴上一动点，若，，三点为正方点，的值为；y A B P t （3）已知点 (1，0).D ①平面直角坐标系中的点满足以下条件：点，，三点为正方点，在图中画出所有符合条件的E A D E 点组成的图形；E ②若直线：上存在点，使得，，三点为正方点，直接写出m 的取值范围． l 12y x m =+N A D N 2018朝阳二模28. 对于平面直角坐标系xOy 中的点P 和直线m ，给出如下定义：若存在一点P ，使得点P 到直线m 的距离等于，则称1P 为直线m 的平行点．（1）当直线m 的表达式为y =x 时，①在点P 1（1，1），P 2（0，），P 3（，）中，直线m 的平行点是；222-22②⊙O 的半径为，点Q 在⊙O 上，若点Q 为直线m 的平行点，求点Q 的坐标.10y xxyyx（2）点A 的坐标为（n ，0），⊙A 半径等于1，若⊙A 上存在直线的平行点，直接写出n 的x y 3=取值范围．2018东城二模28. 研究发现，抛物线上的点到点F (0，1)的距离与到直线l ：的距离相等.如图1所214y x =1y =-示，若点P 是抛物线上任意一点，PH ⊥l 于点H ，则PH PF =.214y x =基于上述发现，对于平面直角坐标系x O y 中的点M ，记点到点的距离与点到点的距离之M P P F 和的最小值为d ，称d 为点M 关于抛物线的关联距离；当时，称点M 为抛物线214y x =24d ≤≤的关联点.214y x=（1）在点，，，中，抛物线的关联点是______ ；1(20)M ，2(12)M ，3(45)M ，4(04)M -，214y x =（2）如图2，在矩形ABCD 中，点，点(1)A t ，(13)C t +，①若t =4，点M 在矩形ABCD 上，求点M 关于抛物线的关联距离d 的取值范围；214y x =②若矩形ABCD 上的所有点都是抛物线的关联点，则t 的取值范围是__________.214y x =2018房山二模28. 已知点P ，Q 为平面直角坐标系xOy 中不重合的两点，以点P 为圆心且经过点Q 作⊙P ，则称点Q 为⊙P 的“关联点”，⊙P 为点Q 的“关联圆”.（1）已知⊙O 的半径为1，在点E （1，1），F （，），M （0，－1）中，⊙O 的“关联点”为－1232；（2）若点P （2，0），点Q （3，n ），⊙Q 为点P 的“关联圆”，且⊙Q 的半径为，求n 的值；5（3）已知点D （0，2），点H （m ，2），⊙D 是点H 的“关联圆”，直线与x 轴，y 轴分别443y x =-+交于点A ，B . 若线段AB 上存在⊙D 的“关联点”，求m 的取值范围.2018丰台二模28．在平面直角坐标系xOy 中，将任意两点与之间的“直距”定义为：()11,y x P ()22y x Q ，.2121y y x x D PQ -+-=例如：点M （1，），点N （3，），则.2-5-132(5)5MN D =-+---=已知点A (1，0)、点B (-1，4).（1）则，；_______=AO D _______=BO D （2）如果直线AB 上存在点C ，使得为2，请你求出点C 的坐标；CO D （3）如果⊙B 的半径为3，点E 为⊙B 上一点，请你直接写出的取值范围.EO D2018海淀二模28．对某一个函数给出如下定义：若存在实数，对于函数图象上横坐标之差为1的任意两点，k 1(,)a b ，都成立，则称这个函数是限减函数，在所有满足条件的中，其最大值称为这2(1,)a b +21b b k -≥k 个函数的限减系数．例如，函数，当取值和时，函数值分别为，2y x =-+x a 1a +12b a =-+，故，因此函数是限减函数，它的限减系数为．21b a =-+211b b k -=-≥2y x =-+1-（1）写出函数的限减系数；21y x =-（2），已知（）是限减函数，且限减系数，求的取值范围．0m >1y x=1,0x m x -≤≤≠4k =m （3）已知函数的图象上一点，过点作直线垂直于轴，将函数的图象在点2y x =-P P l y 2y x =-右侧的部分关于直线翻折，其余部分保持不变，得到一个新函数的图象，如果这个新函数是限减P l 函数，且限减系数，直接写出点横坐标的取值范围．1k ≥-P n2018平谷二模28．对于平面直角坐标系xOy 中的点P 和⊙，给出如下定义：若⊙上存在两个点A ，B ，使M M AB =2PM ，则称点P 为⊙的“美好点”． M （1）当⊙半径为2，点M 和点O 重合时， M 点，，中，⊙的“美好点”是；○1()120P -，()211P ，()322P ，O 点P 为直线y=x+b 上一动点，点P 为⊙○2的“美O 好点”，求b 的取值范围；（2）点M 为直线y=x 上一动点，以2为半径作⊙，M 点P 为直线y =4上一动点，点P 为⊙的M “美好点”，求点M 的横坐标m 的取值范围．442018石景山二模28．在平面直角坐标系中，对于任意点P ，给出如下定义：若⊙P 的半径为1，则称⊙P 为点P 的xOy “伴随圆”．（1）已知，点，()1,0P ①点在点P 的“伴随圆” （填“上”或“内”或“外”）；13,2A ⎛⎝②点在点P 的“伴随圆” （填“上”或“内”或“外”）；()1,0B -（2）若点P 在轴上，且点P 的“伴随圆”与直线相切，求点P 的坐标；x x y 33=（3）已知直线与、轴分别交于点A ，B ，直线与、轴分别交于点C ，D ，点2+=x y x y 2-=x y x y P 在四边形的边上并沿的方向移动，直接写出点P 的“伴随圆”经ABCD DA CD BC AB →→→过的平面区域的面积．2018西城二模28. 对于平面直角坐标系xOy 中的点（x ≠0），将它的纵坐标y 与横坐标x 的比称为点Q (,)Q x y yx的“理想值”，记作.如的“理想值”.Q L (1,2)Q -221Q L ==--（1）①若点在直线上，则点Q 的“理想值”等于_________；(1,)Q a 4y x =-Q L ②如图，，⊙C 的半径为1. 若点Q 在⊙C 上，则点Q 的“理想值”的取值范围是 .(3,1)C Q L （2）点D 在直线上，⊙D 的半径为1，点Q 在⊙D 上运动时都有0≤L Q ，求点D 的3+3y x =3横坐标的取值范围；D x （3）（m ＞0），Q 是以r 为半径的⊙M 上任意一点，当0≤L Q ≤(2,)M m 22圆，并直接写出相应的半径r 的值.（要求画图位置准确，但不必尺规作图）2018怀柔二模28. A 为⊙C 上一点，过点A 作弦AB ，取弦AB 上一点P ，若满足，则称P 为点A 关于131<≤ABAP⊙C 的黄金点．已知⊙C 的半径为3，点A 的坐标为（1，0）．(1)当点C 的坐标为（4，0）时，①在点D （3，0），E （4，1），F （7，0）中，点A 关于⊙C 的黄金点是；②直线上存在点A 关于⊙C 的黄金点P ，求点P 的横坐标的取值范围；3333-=x y (2)若y 轴上存在点A 关于⊙C 的黄金点，直接写出点C 横坐标的取值范围．2018门头沟二模28.在平面直角坐标系xOy 中的某圆上，有弦MN ，取MN 的中点P ，我们规定:点P 到某点（直线）的距离叫做“弦中距”，用符号“”表示.d 中以为圆心，半径为2的圆上.(3,0)W -（1）已知弦MN 长度为2.①如图1：当MN ∥x 轴时，直接写出到原点O 的的长度；d 中 ②如果MN 在圆上运动时，在图2中画出示意图，并直接写出到点O 的的取值范围.d 中（2）已知点,点N 为⊙W 上的一动点，有直线，求到直线的(5,0)M -2y x =-2y x =-d 中备用图2018顺义二模28．已知边长为2a 的正方形ABCD ，对角线AC 、BD 交于点Q ，对于平面内的点P 与正方形ABCD ，给出xyWO如下定义：如果≤，则称点P 为正方形ABCD 的“关联点”．a PQ 在平面直角坐标系xOy 中，若A (-1，1)，B (-1，-1)，C (1，-1)，D (1，1) ．（1）在，，中，正方形ABCD 的“关联点”有；11(,0)2-P 21(2P 3P （2）已知点E 的横坐标是m，若点E 在直线上，并且E 是正方形ABCD 的“关联点”，求m 的=y 取值范围；（3）若将正方形ABCD 沿x 轴平移，设该正方形对角线交点Q 的横坐标是n ，直线与x 轴、1=+y y 轴分别相交于M 、N 两点．如果线段MN 上的每一个点都是正方形ABCD 的“关联点”，求n 的取值范围．y xO。

2018年北京中考二模数学代几综合题汇编

28.在平面直角坐标系xOy 中，对于任意三点A 、B 、C 我们给出如下定义：“横长”a ：三点中横坐标的最大值与最小值的差，“纵长”b ：三点中纵坐标的最大值与最小值的差，若三点的横长与纵长相等，我们称这三点为正方点.例如：点A (2-,0) ，点 B (1,1) ，点 C (1-, 2-)，则A 、B 、C 三点的 “横长”a =|1(2)--|=3，A 、B 、C 三点的“纵长”b=|1(2)--|=3. 因为a =b ，所以A 、B 、C 三点为正方点.（1）在点R (3，5) ，S (3，2-) ，T (4-，3-)中，与点A 、B 为正方点的是；（2）点P (0，t )为y 轴上一动点，若A ，B ，P 三点为正方点，t 的值为；（3）已知点D (1，0).①平面直角坐标系中的点E 满足以下条件：点A ，D ，E 三点为正方点，在图中画出所有符合条件的点E 组成的图形；②若直线l ：12y x m =+上存在点N ，使得A ，D ，N 三点为正方点，直接写出m 的取值范围．y xxyyx28. 对于平面直角坐标系xOy 中的点P 和直线m ，给出如下定义：若存在一点P ，使得点P 到直线m 的距离等于1，则称P 为直线m 的平行点．（1）当直线m 的表达式为y =x 时， ①在点P 1（1，1），P 2（0，2），P 3（22-，22）中，直线m 的平行点是； ②⊙O 的半径为10，点Q 在⊙O 上，若点Q 为直线m 的平行点，求点Q 的坐标. （2）点A 的坐标为（n ，0），⊙A 半径等于1，若⊙A 上存在直线x y 3=的平行点，直接写出n 的取值范围．28. 研究发现，抛物线214y x =上的点到点F (0，1)的距离与到直线l ：1y =-的距离相等.如图1所示，若点P 是抛物线214y x =上任意一点，PH ⊥l 于点H ，则PH PF =.基于上述发现，对于平面直角坐标系x O y 中的点M ，记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ，称d 为点M 关于抛物线214y x =的关联距离；当24d ≤≤时，称点M 为抛物线214y x =的关联点.（1）在点1(20)M ，，2(12)M ，，3(45)M ，，4(04)M -，中，抛物线214y x =的关联点是______ ；（2）如图2，在矩形ABCD 中，点(1)A t ，，点(13)A t +，C ( t . ①若t =4，点M 在矩形ABCD 上，求点M 关于抛物线214y x =的关联距离d 的取值范围；②若矩形ABCD 上的所有点都是抛物线214y x =的关联点，则t 的取值范围是__________.2018房山二模28. 已知点P，Q为平面直角坐标系xOy中不重合的两点，以点P为圆心且经过点Q作⊙P，则称点Q为⊙P的“关联点”，⊙P为点Q的“关联圆”.（1）已知⊙O的半径为1，在点E（1，1），F（－12，32），M（0，－1）中，⊙O的“关联点”为；（2）若点P（2，0），点Q（3，n），⊙Q为点P的“关联圆”，且⊙Q的半径为 5 ，求n 的值；（3）已知点D（0，2），点H（m，2），⊙D是点H的“关联圆”，直线443y x=-+与x轴，y轴分别交于点A，B. 若线段AB上存在⊙D的“关联点”，求m的取值范围.2018丰台二模 28．在平面直角坐标系xOy 中，将任意两点()11,y x P 与()22y x Q ，之间的“直距”定义为：2121y y x x D PQ -+-=.例如：点M （1，2-），点N （3，5-），则132(5)5MN D =-+---=.已知点A (1，0)、点B (-1，4).（1）则_______=AO D ，_______=BO D ；（2）如果直线AB 上存在点C ，使得CO D 为2，请你求出点C 的坐标；（3）如果⊙B 的半径为3，点E 为⊙B 上一点，请你直接写出EO D 的取值范围.2018海淀二模28．对某一个函数给出如下定义：若存在实数k ，对于函数图象上横坐标之差为1的任意两点1(,)a b ，2(1,)a b +，21b b k -≥都成立，则称这个函数是限减函数，在所有满足条件的k 中，其最大值称为这个函数的限减系数．例如，函数2y x =-+，当x 取值a 和1a +时，函数值分别为12b a =-+，21b a =-+，故211b b k -=-≥，因此函数2y x =-+是限减函数，它的限减系数为1-．（1）写出函数21y x =-的限减系数；（2）0m >，已知1y x=（1,0x m x -≤≤≠）是限减函数，且限减系数4k =，求m 的取值范围．（3）已知函数2y x =-的图象上一点P ，过点P 作直线l 垂直于y 轴，将函数2y x =-的图象在点P 右侧的部分关于直线l 翻折，其余部分保持不变，得到一个新函数的图象，如果这个新函数是限减函数，且限减系数1k ≥-，直接写出P 点横坐标n 的取值范围．2018平谷二模28．对于平面直角坐标系xOy 中的点P 和⊙M ，给出如下定义：若⊙M 上存在两个点A ，B ，使AB =2PM ，则称点P 为⊙M 的“美好点”．（1）当⊙M 半径为2，点M 和点O 重合时，○1点()120P -，，()211P ，，()322P ，中，⊙O 的“美好点”是； ○2点P 为直线y=x+b 上一动点，点P 为⊙O 的“美好点”，求b 的取值范围；（2）点M 为直线y=x 上一动点，以2为半径作⊙M ，点P 为直线y =4上一动点，点P 为⊙M 的“美好点”，求点M 的横坐标m 的取值范围．2018石景山二模28．在平面直角坐标系xOy 中，对于任意点P ，给出如下定义：若⊙P 的半径为1，则称⊙P 为点P 的“伴随圆”．（1）已知，点()1,0P ， ①点13,22A ⎛⎫-⎪ ⎪⎝⎭在点P 的“伴随圆” （填“上”或“内”或“外”）； ②点()1,0B -在点P 的“伴随圆” （填“上”或“内”或“外”）；（2）若点P 在x 轴上，且点P 的“伴随圆”与直线x y 33=相切，求点P 的坐标；（3）已知直线2+=x y 与x 、y 轴分别交于点A ，B ，直线2-=x y 与x 、y 轴分别交于点C ，D ，点P 在四边形ABCD 的边上并沿DA CD BC AB →→→的方向移动，直接写出点P 的“伴随圆”经过的平面区域的面积．2018西城二模28. 对于平面直角坐标系xOy 中的点(,)Q x y （x ≠0），将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”，记作Q L .如(1,2)Q -的“理想值”221Q L ==--. （1）①若点(1,)Q a 在直线4y x =-上，则点Q 的“理想值”Q L 等于_________；②如图，C ，⊙C 的半径为1. 若点Q 在⊙C 上，则点Q 的“理想值”Q L 的取值范围是 .（2）点D 在直线+33y x =-上，⊙D 的半径为1，点Q 在⊙D 上运动时都有0≤L Q ，求点D 的横坐标D x 的取值范围；（3）(2,)M m （m ＞0），Q 是以r 为半径的⊙M 上任意一点，当0≤L Q ≤条件的最大圆，并直接写出相应的半径r 的值.（要求画图位置准确，但不必尺规作图）2018怀柔二模28. A 为⊙C 上一点，过点A 作弦AB ，取弦AB 上一点P ，若满足131<≤ABAP ，则称P 为点A 关于⊙C 的黄金点．已知⊙C 的半径为3，点A 的坐标为（1，0）． (1)当点C 的坐标为（4，0）时，①在点D （3，0），E （4，1），F （7，0）中，点A 关于⊙C 的黄金点是； ②直线3333-=x y 上存在点A 关于⊙C 的黄金点P ，求点P 的横坐标的取值范围； (2)若y 轴上存在．．点A 关于⊙C 的黄金点，直接写出点C 横坐标的取值范围．。

2018北京市昌平区二模数学试题(含答案)

收集数据
从八、九两个年级各随机抽取 20 名学生，进行了体质健康测试，测试成绩（百
分制）如下：
八年级
78 86
74
81
75
76
87
70
75
90
75 79
81
70
74
80
86
69
83
77
九年级
93 73
88
81
72
81
94
83
77
83
80 81
70
81
73
78Leabharlann 82807040
整理、描述数据
按如下分数段整理、描述这两组样本数据：
李老师说小丽的作法正确，请你写出她作图的依
据：
．
16. 如图，在圆 O 的内接四边形 ABCD 中，AB=3 ，AD=5，∠
BAD=60°，点 C 为弧 BD 的中点，则 AC 的长是
．
（第 16 题）三、解答题（本题共 12 道小题，共 68 分，第 17-22 题每小题 5 分，第 23-26
其中两条纵向虚线上端的数值分别
是每个年级抽出的 40 名男生身高的平均数，根据统计图提供的信息，
下列结论不合理的是（） A．六年级 40 名男生身高的中位数在第 153~158cm 组
（第 6 题）
B．可以估计该校九年级男生的平均身高比六年级的平均身高高出 18.6cm
C．九年级 40 名男生身高的中位数在第 168~173cm 组
度，小文同学做了如下的探索：根据物理学中光的反射
定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子放在合适的位置，刚好能在

北京市2018年中考数学二模试题汇编代几综合题

代几综合题2018 昌平二模28. 在平面直角坐标系 xOy 中，对于随意三点 A 、B 、 C 我们给出以下 y定义：“横长” ：三点中横坐标的最大值与最小值的差，“纵长”a4 ：三点中纵坐标的最大值与最小值的差，若三点的横长与纵长相等，b3 我们称这三点为正方点 .2比如：点 A ( 2 ,0)，点 B (1,1)，点 C ( 1,2)，则 A 、BA1xB 、C 三点的 “横长” a =| 1 ( 2) |=3 ， A 、 B 、 C 三点的“纵–4–3–2–1 O1 2 3 4–1 长” b =| 1 ( 2) |=3. 由于 a = b ，所以 A 、 B 、 C 三点为正方点 . C–2 –3 （ 1）在点 R (3 ，5)，S (3， 2)，T ( 4， 3 )中，与点 A 、–4B 为正方点的是；（ 2）点 P (0 ， t ) 为 y 轴上一动点，若 A ， B ， P 三点为正方点， t 的值为；（ 3）已知点 D (1 ， 0). ①平面直角坐标系中的点 E 知足以下条件：点 A ， D ， E 三点为正方点，在图中画出全部切合条件的点 E构成的图形；1 m 上存在点 N ，使得 A ， D ， N 三点为正方点，直接写出m 的取值范围．②若直线 l ： yx2y y 5 5 4 4 3 322 A 1A1DxDx–5–4–3–2–1 O 1 2 3 4 5–5–4–3–2–1 O 1 2 3 4 5–1–1 2018 旭日二 –2 –2 –3 –3 模 –4 –4 28. 对于平 –5–5面直角坐标系 xOy 中的点 P 和直线 m ，给出以下定义：若存在一点 P ，使得点 P 到直线 m 的距离等于，则称 P 为直线的平行点．m（ 1）当直线 m 的表达式为 y =x 时，①在点 P 1（ 1， 1）， P 2（ 0， 2 ）， P 3（2，2）中，直线 m 的平行点是；22②⊙ O 的半径为10 ，点 Q 在⊙ O 上，若点 Q 为直线 m 的平行点，求点 Q 的坐标 .（ 2）点A的坐标为（n，0），⊙A半径等于1，若⊙A上存在直线y3x 的平行点，直接写出n 的取值范围．2018 东城二模28. 研究发现，抛物线y 1x2 上的点到点 F ，1)的距离与到直线 l ：y 1的距离相等.如图1所示，4 (01若点 P 是抛物线y x2上随意一点，PH⊥l于点H，则 PF PH .4鉴于上述发现，对于平面直角坐标系xOy 中的点 M，记点M到点P的距离与点P到点F的距离之和的最小值为 d，称 d 为点 M对于抛物线y 1 x2的关系距离；当2≤d≤4 时，称点 M为抛物线y 1 x2的4 4关系点 .（ 1）在点 M 1 (2，0) ， M 2 (1，2) ， M 3 (4，5) ， M 4 (0， 4) 中，抛物线 y1x 2 的关系点是 ______ ；4（ 2）如图 2，在矩形 ABCD 中，点 A(t ，1) ，点 C (t 1，3)①若 t =4，点 M 在矩形 ABCD 上，求点 M 对于抛物线 y 1 x 2 的关系距离 d 的取值范围；4②若矩形 ABCD 上的全部点都是抛物线 y1x 2 的关系点，则 t 的取值范围是 __________.42018 房山二模28. 已知点为平面直角坐标系中不重合的两点，以点 P 为圆心且经过点Q 作⊙ ，则称点为⊙P ，Q xOyP QP的“关系点” ，⊙ P 为点 Q 的“关系圆” .13（ 1）已知⊙ O 的半径为 1，在点 E （ 1，1），F （－ 2， 2 ），M （0，－ 1）中，⊙ O 的“关系点” 为；（ 2）若点 P （2， 0），点 Q （ 3，n ），⊙ Q 为点 P 的“关系圆” ，且⊙ Q 的半径为 5 ，求 n 的值；（ 3）已知点（0， 2），点（，2），⊙ D 是点 H 的“关系圆” ，直线 y44 与 x 轴， y 轴分别交于DH mx3点 A ， B . 若线段 AB 上存在⊙ D 的“关系点” ，求 m 的取值范围 .2018 丰台二模28 ．在平面直角坐标系 xOy 中，将任意两点 P x 1 , y 1 与 Q x 2， y 2 之间的 “ 直距 ” 定义为：DPQx 1 x 2 y 1 y 2 .比如：点（1， 2 ），点（3， 5 ），则 DMN 132( 5) 5.M N已知点 (1 ，0) 、点 (-1 ， 4).AB（ 1）则 D AO _______ ， D BO _______ ；（ 2）假如直线 AB 上存在点 C ，使得 D CO 错误！未找到引用源。