第3章凸轮资料
合集下载
第三章 凸轮机构及其设计

O
等速运动规律 a
o
v
1
2
a
正弦加速度运动规律
五、从动件运动规律(Law of Motion of Follower ) 设计应考虑的问题 (1)应满足机器工作的要求; (2)对于高速凸轮机构,应使凸轮机构具有良好 的运动和动力性能;
(3)设计从动件运动规律时,应考虑到凸轮轮廓
§3-1凸轮机构的应用及分类
3)按从动件的运动形式分: 摆动从动件 (Oscillating Follower)
§3-1凸轮机构的应用及分类
4)按凸轮高副的锁合方式分:力锁合 (Force Closure)
§3-1凸轮机构的应用及分类
4)按凸轮高副的锁合方式分:形锁合(Profile Closure)。
0
/2
0
/2
a
等加速等减速运动规律从动件位移曲线绘制方法一
S
0 1
4
9 4
1
o
1
2
δ1
3
4
5
6Hale Waihona Puke t δ等加速等减速运动规律从动件位移曲线绘制方法二
S
6 5 4 3 2
1
o
1
2
δ1
3
4
5
6
t δ
三、从动件常用运动规律
4'
s
5'
6'
(二)三角函数类基本运动规律 1.余弦加速度运动规律(推程)
的工艺性要好。 从动件动量 mvmax 在选择从动件的运动规律时,除要考虑刚性冲击与柔性 amax 从动件惯性力 ma 冲击外,还应该考虑各种运动规律的速度幅值 vmax 、加速 max 度幅值 amax 及其影响加以分析和比较。 对于重载凸轮机构,应选择 值较小的运动规律; max
第3章 凸轮机构

机械原理—凸轮机构
等宽凸轮机构
凸轮廓线上任意两条 平行切线间的距离都等于 框架内侧的宽度。 框架内侧的宽度。
缺点:从动件的运动规律的选择受到一定的限制, 从动件的运动规律的选择受到一定的限制,
180º 当180º范围内的凸轮廓线根据从动件运动规律确定 后,其余180º内的凸轮廓线必须符合等宽原则 其余180º 180
r = a +l
投影得凸轮廓线B点坐标: 投影得凸轮廓线 点坐标: 点坐标
x = a sin δ − l sin( δ + ϕ + ϕ 0 ) y = a cos δ − l cos( δ + ϕ + ϕ 0 )
r02 = a 2 + l 2 − 2 al cos ϕ 0
a 2 + l 2 − r02 ϕ 0 = arccos 2 al
机械原理—凸轮机构
第3章 凸轮机构
凸轮机构的组成与类型 从动件运动规律设计 凸轮轮廓的设计 凸轮机构基本尺寸的确定 凸轮机构的计算机辅助设计
机械原理—凸轮机构
3.1 凸轮机构的组成与类型 3.1.1 凸轮机构的组成
1 ─凸轮 ─从动件 2 ─从动件 3 ─机架 ─机架
}
高副机构
机械原理—凸轮机构
结束
机械原理—凸轮机构
3.4 凸轮机构基本尺寸的确定
3.4.1 移动滚子从动件盘形凸轮
机械原理—凸轮机构
(1) 压力角与许用值
F' = F cosα F → '' F = F sin α
F < fF → 锁 自 −1 1 即 α > tg : ⇒αmax ≤ [α] f
' ''
凸轮传动
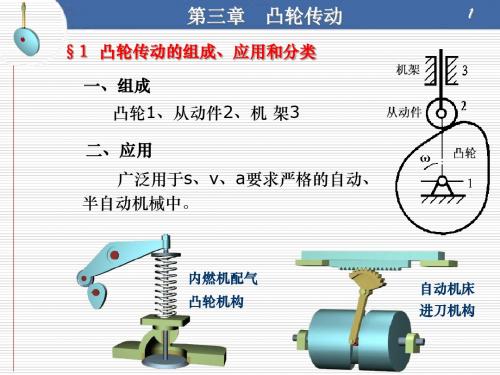
第三章 凸轮传动
6
一般凸轮机构的命名原则:
布置形式+运动形式+推杆形状+凸轮形状
对心直动尖顶推 杆盘形凸轮机构
偏置直动滚子推 杆盘形凸轮机构
摆动平底推杆 盘形凸轮机构
第三章 凸轮传动
§2 从动件的常用运动规律及其选择 设计凸轮传动:
工作要求
从动件运动规律
7 凸轮轮廓曲线
从动件运动:上升——停——下降——停
1、内凹曲线
ρ0——理论轮廓曲线
曲率半径
ρ——实际轮廓曲线
ρ0
曲率半径
ρ
ρ= ρ0+rT
无论rT为多大,都能作出
第三章 凸轮传动
2、外凸曲线 ρ= ρ0-rT
29 ρ0
ρ ρ0
rT<ρ0时,可作出。
rT=ρ0时,尖点,易 磨损——失真。
ρ0
rT>ρ0时,ρ<0,轮廓线交叉,加
工时交叉部分被切掉——失真。
4
s v
c0 c11 c212 (1 c1 2c21)
a 2c212
10 1 2
δt/2
v2
边界条件
0
a2
1 0, s 0, v 0, c0 0, c1 0
1
t
/
2, s
h/
2, c2
2h
t2
0
345
δt
h/2
h
6 δ1 δ1 δ1
1.一次多对项于式多(项n=式1)运:动等规速律运,动其规多律项式中待定系数的数 2.二目要次应求多与来项边确式界定(条。n=件但2)的当:数边等目界加相条速等件与,增等其多减数时速目,运多会动少使规应设律根计据计工算作复 3.五杂次,多加项工式精运度动也规难律以(达n=到5),故通常不宜采用太高次数
第三章 凸轮机构

图3-9 等加速、等减速 运动规律线图
3.2.2.3 简谐运动规律(余弦加速度运动规律)
图3-10 简谐运动线图 当一质点在圆周上作匀速运动时,该点在这个圆的直径上
的投影所构成的运动,称为简谐运动。从动件的位移按简 谐运动变化的运动规律,称为简谐运动规律。 如图3-10所 示,设从动件升程h为直径,其从动件的位移方程为 h (3-4) s (1 cos ) 2 由图3-10可知,当θ=π时,φ=φ0,故θ=πφ/φ0代入上式可导 出从动件推程时简谐运动方程为
单,是凸轮最基本的形式。盘形凸轮分为两种:利用外轮 廓推动从动件运动的称为盘形外轮廓凸轮,如图3-1、图3-2 所示;利用曲线沟槽推动从动件运动的称为盘形槽凸轮, 如图3-4所示。 盘形凸轮作等速回转时,从动件在垂直于凸轮轴线的平面 内运动(往复移动或摆动),因此,盘形凸轮机构属于平面凸 轮机构。由于从动件的行程或摆动太大会引起凸轮径向尺 寸变化过大,不利于机构正常工作。因此,盘形凸轮机构 一般用于从动件行程或摆动较小的场合。
凸轮轮廓,便可得到从动件所需的运动规律。 缺点:凸轮与从动件属高副接触,压强大,易磨损。适用 于传力不大的控制机构和调节机构中。
3.1.2 凸轮机构的类型
3.1.2.1 按凸轮的形状分类
按凸轮的形状可分为盘形凸轮、移动凸轮和柱体凸轮3类。
(1) 盘形凸轮。是一个具有变化半径的圆盘形构件,结构简
图3-10 简谐运动线图
3.余弦加速度运动规律
5 特点: 4 加速度变化连续平缓. 3 始、末点有软性冲击. 2 6
S
7
8 H
d0
1 0
1 V
2
3
4
5
6
7
第3章 凸轮机构

e ω
r0
A O
凸轮曲线组成: 凸轮曲线组成: 基圆--- ---以凸轮轮廓曲 1、基圆---以凸轮轮廓曲 线最小矢径ro为半径所作之圆 线最小矢径ro为半径所作之圆 ro 称为基圆,ro称为基圆半径 称为基圆半径。 称为基圆,ro称为基圆半径。 B 偏置距离e--凸轮回转中心O 偏置距离e--凸轮回转中心 凸轮回转中心O 点到从动件导路之间的距离e 点到从动件导路之间的距离e
D
O
SD
C
Sc
ω
制作: 制作:电子科大机电学院 郭连忠
二、 如图示凸轮机构中,试用图解法在图中标出:
(6)、 (6)、从动件的最大行程 Hmax
C D
O
F
ω
r0
Hmax
制作: 制作:电子科大机电学院 郭连忠
先将导路旋转到B 先将导路旋转到B点。
导路与基圆的交点为B 导路与基圆的交点为B1 圆弧AB 才是尖底A 圆弧AB1才是尖底A实际转过 的圆弧段。 的圆弧段。 ∠AOB1才是凸轮在推程中 实际转过的角度。 实际转过的角度。 故推程角是: 故推程角是: OA与 之间的夹角。 OA与OB1之间的夹角。 制作: 制作:电子科大机电学院 郭连忠
-ω
凸轮转角线: 凸轮转角线: --导路与基圆的交点 --导路与基圆的交点 与回转中心O B1与回转中心O的连线 5、远休止角: 远休止角: BC段为一段圆弧, BC段为一段圆弧,故凸轮 段为一段圆弧 BC段停止不动 段停止不动。 在BC段停止不动。 BC段对应的中心角Φs称 BC段对应的中心角Φs称 段对应的中心角Φs 为远休止角。 为远休止角。 故远休止角是: 故远休止角是: 之间的夹角。 OB1与OC1之间的夹角。
故凸轮的转角是: 故凸轮的转角是:导路与基圆的交点 OA之间的夹角 之间的夹角。 线OA之间的夹角。
凸轮机构运动规律.完美版PPT

当凸轮连续转动时,从动件将重复上述运动过程。
移动凸轮 其凸轮是具有曲线轮廓、作往复直线移动的构件,它可看成是转动轴线位于无穷远处的盘形凸轮。
凸轮机构由凸轮1、从动件2、机架3三个基本构件及锁合装置组成。 用图解法绘制凸轮轮廓曲线的方法;
当凸轮连续转动时,从动件将重复上述运动过程。
从动件的常用运动规律
形锁合凸轮机构 依靠凸轮和从动件几何形状来保证 锁合。
按从动件相对机架的运动方式分为:
移动从动件凸轮机构 摆动从动件凸轮机构 按其从动件导路是否通过凸轮
分为对心移动从动件 偏置移动从动件凸轮机构
40Cr 40-45HRC 20Cr 56-62HRC
从动件的常用运动规律
1.凸轮轮廓曲线与从动件运动规律的关系
第三章凸轮机构运动规律
第三章 凸轮机构
主要内容:
1.凸轮机构的结构、特点、类型及应用; 2.从动件的常用运动规律及其选择; 3.用图解法绘制凸轮轮廓曲线的方法; 4. 凸轮机构的设计。
凸轮机构的应用与分类
1. 组成
凸轮机构由凸轮1、从动件2、 机架3三个基本构件及锁合装 置组成。是一种高副机构。其 中凸轮是一个具有曲线轮廓或 凹槽的构件,通常作连续等速 转动,从动件则在凸轮轮廓的 控制下按预定的运动规律作往 复移动或摆动。
凸轮机构的应用与分类
3. 应用
平面连杆机构虽然应用广泛,但它只能近似地实 现给定的运动规律,且设计比较复杂。当从动件须 精确地按预定运动规律尤其是复杂运动规律工作时, 则常采用凸轮机构。
凸轮机构的应用与分类
4. 类型 按从动件末端形状分:
平底从动件凸轮机构 其从动件端部为一平底。若 不计摩擦,凸轮对从动件的作用力始终垂直于平底, 传力性能良好,且凸轮与平底接触面间易形成润滑 油膜,摩擦磨损小、效率高,故可用于高速,缺点 是不能用于凸轮轮廓有内凹的情况。
机械原理 第3章 凸轮机构
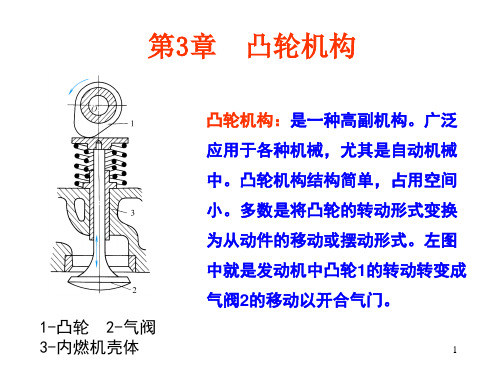
2
26
§3.3 凸轮轮廓曲线的设计 一、凸轮轮廓曲线设计是根据凸轮参数如 基圆半径、推程和推程运动角、回程及回程 运动角、远、近休止角、偏距等参数,用反 转法设计凸轮轮廓曲线。
27
二、1-对心反转图解法设计凸轮廓线,见下图:
28
29
2-偏心反转 图解法设计凸轮轮廓
主要介绍已知从动件运动规律线图设计凸轮轮廓。 一、直动从动件盘形凸轮轮廓的绘制 分别介绍以下两种类型。 1、偏置尖顶直动从动件盘形凸轮 已知从动件位移线图如图3-8 (b)所示,基圆半径 r0,凸轮行程h,推程运动角Φ=1800,休止角 Φs=300,回程角Φ'=900,按图示画出凸轮轮廓线。 作图步骤按反转法如下: 1)将Φ、Φ'各平为4等份,如图(b)中1-1';...8-8'。 并以偏距e和r0画圆,如图(a)所示。基圆与导 路的交点B0(C0)即为从动件的起始点。 2)以OC0为起点,在基圆上平分Φ=180和Φ'=90 分别得C1、C2、C3、和C6、C7、C8各点,并过 C0、C1 . . . 各点向偏距圆作切线,这些切线就是 反转法导路在此点的位置。 3)在各对应的切线上,取C1B1=11' ;C2B2=22' ....得从动件尖顶位置B1、B2、B3... 4)将B0、B1、B2…连接成光滑的曲线就是凸轮 轮廓线(注意:B4、B5是圆弧,B9、B0之间是基 圆) 最后画出图纸进行加工。 30 当e=0时,各切线变成通过O点的射线。
10
一、从动件的运动规律的描述与术语
从动杆位移线图的作图方法及基本名词术语
首先应确认,从动件的运 动规律是由主动件凸轮的轮 廓形状决定的。在图 3-5 中, 回转中心 O 到半径最小点 A 的 K' 圆叫基圆。图 3-5 中凸轮的轮 ϕk 廓规律是,弧 AB 间的半径逐 渐变大,对应的圆心角为 ϕ; 弧 BC 间半径保持不变,对应 K ϕk 的圆心角为 ϕ s ;弧 CD 间半径 逐步变小到基圆半径,对应 的圆心角为 ϕ ' ;弧 DA 间半径 保持基圆半径不变,对应的 圆心角为ϕs'。现凸轮以ω速度 顺时针转动,以 φ=ωt 为横坐 标,从动杆的移动 S为纵坐标, 则从动杆的移动曲线展开图 图3-12:凸轮轮廓与从动件位移线图 如(b)所示。其中: h--升程;ϕ--推程运动角;ϕs--远休止角; ϕ‘--回程运动角;ϕ's--近休止角。这 些角度总和为360˚。从图中可知,当凸轮从A点转过ϕk角到K点时,从动杆升高 到K’点;当凸轮从A点转过ϕ角度,从动杆升高了h到B点。其他各点作图方法 11 一样,然后将各点连成光滑的曲线,就是从杆的位移线图(b).
《机械设计原理》第3章凸轮机构

5’ 3’
1’
12’
13’ 14’
1 3 5 7 8 9 11 13 15
设计:潘存云
设计步骤小结:
①选比例尺μl作基圆rmin。 ②反向等分各运动角。原则是:陡密缓疏。
③确定反转后,从动件尖顶在各等份点的位置。
④将各尖顶点连接成一条光滑曲线。
中南大学专用
作者: 潘存云教授
2.偏置直动尖顶从动件盘形凸轮
回 凸 轮
作者:潘存云教授
优点:只需要设计适当的轮廓曲线,从动件便可获得
任意的运动规律,且结构简单、紧凑、设计方便。
缺点:线接触,容易磨损。
中南大学专用
作者: 潘存云教授
应用实例:
3
线 2 A 设计:潘存云 1
中南大学专用
绕线机构
作者: 潘存云教授
卷带轮
12 1 放 放音 音键 键
设计:潘存云
5
1.等速运动(一次多项式)运动规律 s2
在推程起始点:δ1=0, s2=0
在推程终止点:δ1=δt ,s2=h 代推入程得运: 动方C0=程0:, C1=h/δt
δt
v2
s2 =hδ1/δt
v2 a2
= =
hω1 0
/δt
同理得回程运动方程:
a2 刚性冲击 +∞
s2=h(1-δ1/δh ) v2=-hω1 /δh a =0 2 中南大学专用
5)摆动尖顶从动件盘形凸轮机构
中南大学专用
作者: 潘存云教授
一、凸轮廓线设计方法的基本原理
反转原理:
给整个凸轮机构施以-ω1时,不影响各构件之间
的相对运动,此时,凸轮将静止,而从动件尖顶复合
运动的轨迹即凸轮的轮廓曲线。
0 第3章 (1-4)凸轮机构

1. 根据凸轮的结构确定rb
当凸轮与轴做成一体时:rb r rr (2 ~ 5) mm
当凸轮装在轴上时: rb rn rr (2 ~ 5) mm
r——凸轮轴的半径,mm; rn——凸轮轮毂的半径,mm;一般rn=(1.5~1.7)r; rr——滚子半径,mm; 2. 根据αmax≤[α]确定rb 已知推程运动角、行程和最大压力角,由诺模图求得。
盘形凸轮的结构设计
三、滚子半径的选择 (1)当滚子半径rr<ρ时,实际轮廓的曲率半径ρ'>0,即比
较圆滑;
(2)当滚子半径rr=ρ时, 实际轮廓的曲率半径ρ'=0, 出现尖点; (3)滚子半径rr>ρ时,实 际轮廓的曲率半径ρ'<0,轮 廓线发生叠交,叠交阴影 部分在实际加工过程中将 被切去。工作时,这一部 分的运动规律无法实现, 这种现象称为运动失真。
盘形凸轮的结构设计
Fx F sin
Fy F cos
由上述关系式知,压力角
α愈大,有效分力Fy愈小,有 害分力Fx愈大。当a角大到某
一数值时,必将会出现Fy<Fx 的情况。这时,不论施加多大
的Fn力,都不能使从动件运动, 这种现象称为自锁。因此,为
了保证凸轮机构的正常工作,
必须对凸轮机构的压力角进行
盘形凸轮的结构设计
图解法设计凸轮轮廓曲线时,假设凸轮的基圆半径、滚 子半径等尺寸均为已知。而在实际设计时,则需根据机构的 受力情况,并考虑结构的紧凑性、运动的可靠性等因素,合 理确定这些尺寸。
一、压力角
不考虑从动件与凸轮 接触处的磨擦,凸轮对从 动件的作用力F沿接触点 A的法线n方向,直动从动 杆的速度v沿导路方向。 从动件所受作用力F与受 力点速度ν间所夹的锐角 称为凸轮机构的压力角, 用α表示。
当凸轮与轴做成一体时:rb r rr (2 ~ 5) mm
当凸轮装在轴上时: rb rn rr (2 ~ 5) mm
r——凸轮轴的半径,mm; rn——凸轮轮毂的半径,mm;一般rn=(1.5~1.7)r; rr——滚子半径,mm; 2. 根据αmax≤[α]确定rb 已知推程运动角、行程和最大压力角,由诺模图求得。
盘形凸轮的结构设计
三、滚子半径的选择 (1)当滚子半径rr<ρ时,实际轮廓的曲率半径ρ'>0,即比
较圆滑;
(2)当滚子半径rr=ρ时, 实际轮廓的曲率半径ρ'=0, 出现尖点; (3)滚子半径rr>ρ时,实 际轮廓的曲率半径ρ'<0,轮 廓线发生叠交,叠交阴影 部分在实际加工过程中将 被切去。工作时,这一部 分的运动规律无法实现, 这种现象称为运动失真。
盘形凸轮的结构设计
Fx F sin
Fy F cos
由上述关系式知,压力角
α愈大,有效分力Fy愈小,有 害分力Fx愈大。当a角大到某
一数值时,必将会出现Fy<Fx 的情况。这时,不论施加多大
的Fn力,都不能使从动件运动, 这种现象称为自锁。因此,为
了保证凸轮机构的正常工作,
必须对凸轮机构的压力角进行
盘形凸轮的结构设计
图解法设计凸轮轮廓曲线时,假设凸轮的基圆半径、滚 子半径等尺寸均为已知。而在实际设计时,则需根据机构的 受力情况,并考虑结构的紧凑性、运动的可靠性等因素,合 理确定这些尺寸。
一、压力角
不考虑从动件与凸轮 接触处的磨擦,凸轮对从 动件的作用力F沿接触点 A的法线n方向,直动从动 杆的速度v沿导路方向。 从动件所受作用力F与受 力点速度ν间所夹的锐角 称为凸轮机构的压力角, 用α表示。
第3章 凸轮机构

第三章 凸轮机构
一、凸轮机构的工作过程
1.工作过程: ⑴凸轮转角 ⑵从动件的位移 s ⑶Rb(凸轮轮廓的最短向径)基圆半径 ⑷ h(从动件移动的最大距离)行程 ⑸ 推程 ⑹β1 推程运动角 升高h ⑺β´ 远休止角 ⑻回程 ⑼β2 回程运动角 下降h 不动
⑽β" 近休止角
第三章 凸轮机构
不动
一、凸轮机构的工作过程
第三章 凸轮机构
作业:3-4
第五节 凸轮机构设计中的几个问题
设计凸轮机构,不仅要保证从动件能实现预定的运动规 律,还须使设计的机构传力性能良好,结构紧凑,满足 强度和安装等要求,为此,设计时应注意处理好下述问 题。 设计要求:结构紧凑 传力性能好
Rb、Rr
压力角
一、滚子半径的选择
二、凸轮机构的压力角 三、凸轮基圆半径的确定
机架
第三章 凸轮机构
一、组成、特点及应用
应用 当从动件的位移、速度、加速度必须严格 按照预定规律变化时,常用凸轮机构。
凸轮式间歇运动机构 机床刀架中的 箭杆织机中的
凸轮机构
第六章 第三章 凸轮机构
打纬凸轮机构
一、组成、特点及应用
应用: 送料机构 车床主轴箱
内燃机配气机构
第三章 凸轮机构
录音机卷带机构
⑶注意:
如:
①理论廓线按给定运动规律 绘制Rb在理论廓线上量取 ②实际廓线不等于向径减去滚子半径
③从动件的转动方向
第三章 凸轮机构
3.移动平底从动件盘形凸轮
⑴设计思路: ①平板与导路的交点是尖顶从动件的尖端。 ②任何时刻平板都与廓线相切、与向径垂直,而导路与 向径重合。 ③从动件相对初始位置的移动距 离等于基圆以外到平板之间的 长度。 ⑵设计方法: 在每条向径(反转后的导路)上量取位移得理论廓线 上的点,过这些点作向径的垂线(平板),然后做这 些垂线的包络线(实际廓线)。
机械设计基础第3章凸轮

绘制凸轮轮廓时需要凸轮与图纸相对静止。采用“反转法”。
凸轮廓线设计方法的基本原理----反转原理(动画)
给整个凸轮机构施以-ω 1时,不影响各构件间相对运动, 此时,凸轮将静止,而从动件尖顶复合运动(随机架和导路以 角速度-ω1的绕O点转动;在导路中往复移动)轨迹即凸轮的轮 廓曲线。(下图所示)
几种盘形凸轮轮廓绘制
ω1
rmiDn α v2
OP
s2 s0
S2 + r2min - e2
e C 设计:潘存云
rmin↓ →α↑, 当α max< [α]许用 可增大rmin
n
同理,当导路位于中心左侧时,有:
ds2/dδ 1
偏置尖顶----
lOP =lCP- lOC → lCP = ds2/dδ 1 + e
lCP = (S2+S0 )tgα S0= rmin2-e2
小引起压力角 (α↑)增大。
P点为相对速度瞬心, 于是有:v=lOPω1
→ lOP =v/ω1 = ds2 /dδ 1= lOC + lCP
因lOC = e,所以lCP = ds2/dδ 1- e
n
v2
B
又因lCP = (S2+S0 )tgα,而 S0= r2min-e2
所以tgα =
ds2/dδ 1- e
4、自动送料机构。
2
设计:潘存云
1 3
送料机构
带凹槽凸轮1转动时,通过槽中滚子驱使从动件2往复移动。凸轮每回转一周, 从动件即从储料器中推出一个毛坯,送到加工位。
由所举例子可知:凸轮机构的
1、组成:三个构件:凸轮、从动件(杆件)、机架。
2、作用:将连续回转 => 从动件直线移动或摆动。
凸轮廓线设计方法的基本原理----反转原理(动画)
给整个凸轮机构施以-ω 1时,不影响各构件间相对运动, 此时,凸轮将静止,而从动件尖顶复合运动(随机架和导路以 角速度-ω1的绕O点转动;在导路中往复移动)轨迹即凸轮的轮 廓曲线。(下图所示)
几种盘形凸轮轮廓绘制
ω1
rmiDn α v2
OP
s2 s0
S2 + r2min - e2
e C 设计:潘存云
rmin↓ →α↑, 当α max< [α]许用 可增大rmin
n
同理,当导路位于中心左侧时,有:
ds2/dδ 1
偏置尖顶----
lOP =lCP- lOC → lCP = ds2/dδ 1 + e
lCP = (S2+S0 )tgα S0= rmin2-e2
小引起压力角 (α↑)增大。
P点为相对速度瞬心, 于是有:v=lOPω1
→ lOP =v/ω1 = ds2 /dδ 1= lOC + lCP
因lOC = e,所以lCP = ds2/dδ 1- e
n
v2
B
又因lCP = (S2+S0 )tgα,而 S0= r2min-e2
所以tgα =
ds2/dδ 1- e
4、自动送料机构。
2
设计:潘存云
1 3
送料机构
带凹槽凸轮1转动时,通过槽中滚子驱使从动件2往复移动。凸轮每回转一周, 从动件即从储料器中推出一个毛坯,送到加工位。
由所举例子可知:凸轮机构的
1、组成:三个构件:凸轮、从动件(杆件)、机架。
2、作用:将连续回转 => 从动件直线移动或摆动。
第三章 凸轮机构

尖底从动件
凸轮与从动件之间为滚动摩 擦,因此摩擦磨损较小,可 用于传递较大的动力。
滚子从动件
从动件与凸轮之间易形成 油膜,润滑状况好,受力 平稳,传动效率高,常用 于高速场合。但与之相配 合的凸轮轮廓须全部外凸。
平底从动件
三)、按凸轮与从动件的锁合方式分
锁合:指保持从动件与凸轮之间的高副接触。
从动件常用基本运动规律特性比较 v ma amax 冲击特性 适用范围 运动规律
x (h / F ) (h 2/ F 2 )
等 速 等加速等减速 余弦加速度 正弦加速度
1.0 2.0 1.57 2.00
4.00 4.93 6.28
刚性 柔性 柔性 无
低速轻载 中速轻载 中速中载 高速轻载
第三章
凸轮机构
凸轮机构:是一种高副机构。
广泛应用于各种机械,尤其
是自动机械中。
§31凸轮机构的应用及分类
一、凸轮机构的应用
1、凸轮机构:凸轮是
一个具有曲线轮廓 的构件。含有凸轮 的机构称为凸轮机 构。它由凸轮、从 动件和机架组成。
2、凸轮机构的应用
内燃机配气凸轮机构
进刀凸轮机构
二、凸轮机构的优点:
1
s1
2
1
h
3
e
摆动从动件盘形凸轮机构
已知:= (),rb,L,a, A0
2
1 1 3 2 4 5 6 7 2 3 4 8 5 6 7 8 9
A9 A8
B9
0
B0
C0
B1
C1 1
A1
B2
C2
F S'
O
F
FS
F'
F S'
第三章 凸轮机构

C
机械设计基础——凸轮机构
二、从动件常用运动规律
1 等速运动 2 简谐运动
3 正弦加速度运动
机械设计基础——凸轮机构
1 等速运动——一次多项式运动规律
推程
0≤≤φ
s
Displacement
h
运动方程
位移方程: s hψ /φ 速度方程: v hw /φ 加速度方程:运动过程中 a 0 运动线图 冲击特性:始点、末点刚性冲击 适用场合:低速轻载
机械设计基础——凸轮机构
3-4 图解法设计凸轮轮廓
一、图解法的基本原理 二、作图法设计凸轮廓线
机械设计基础——凸轮机构
一、图解法的基本原理
相对运动原理法(反转法) 对心式: 对整个系统施加-w运动
此时,凸轮保持不动 推杆作复合运动=绕基圆中心 反转运动(-w) +预期运动(s)
-w
A
h
S
w
rb
s'
r
' s
机械设计基础——凸轮机构
一、凸轮机构的运动过程
从动件的运动规律是指从动件的位移、速度、加 速度等随时间t或凸轮转角变化的规律
s
A’ A φs ’ φ h 0
t
φ
推程
D
Φs
远休止
φ’
回程
φs ’
近休止
ψ
r0
φ’ φs
w
B
运动线图: 从动件的位移、速度、加速 度等随时间t或凸轮转角ψ变化关系图
1 按凸轮的形状分
盘形凸轮, 实例
凸轮呈向径变化的盘形
机械设计基础——凸轮机构

3.余弦加速度(简谐运动)规律:
从动件加速度在起点和终点存在有限值O
v
突变,故有柔性冲击;
若从动件作无停歇的升-降-升连续往
0/2 p h /20
复运动,加速度曲线变为连续曲线,可
O
以避免柔性冲击;
a
可适用于高速的场合。
O
0/2 p22 h /202
0/2
机械设计基础
-p22 h /202
0
机械设计基础
直动平底从动件盘形凸轮轮廓的绘制
机械设计基础
直动平底从动件盘形凸轮轮廓的绘制
-
机械设计基础
实际廓线
3.6 凸轮机构设计中应注意的几个问题
(1)滚子半径的选择
设计滚子从动件时若从强度和耐用性考虑,滚子 的半径应取大些。滚子半径取大时,对凸轮的实际轮 廓曲线影响很大,有时甚至使从动件不能完成预期的 运动规律。
机械设计基础
1、图解法的原理 -
-
B1
s
rb
B0 B
e
假想给整个凸轮机构加上 一个与凸轮角速度大小相等 、方向相反的角速度(- ), 凸轮将处于静止状态;机架则 以( - )的角速度围绕凸轮 原来的转动轴线转动;而从动 件一方面随机架转动,另一方 面又按照给定的运动规律相对 机架作往复运动。 ——反转法
机械设计基础
机械设计基础
第三章 凸轮机构
• 学习重点:
1.了解凸轮机构的组成、特点、分类及应用 2.掌握从动件的常用运动规律;了解其冲击特性及应 用
学习难点
凸轮机构运动的实现
机械设计基础
当从动件的位移、速度、加速度必须严格按预 定规律变化,特别是当原动件作连续运动时从动件必 须作间歇运动下,采用凸轮机构设计最为简便
机械原理第3章 凸轮机构(第二版)

二、凸轮机构的分类
1.按凸轮的形状分 (1) 盘形凸轮机构
盘形凸轮是一个具有变化向径的盘形构件,绕固定转轴回转。 它是凸轮的基本型式,应用最为广泛。
(2)移动凸轮机构
移动凸轮相对机架作往复直线运动。 凸轮与从动件的相对运动是平面运动,属于平面凸轮机构。
(3)圆柱凸轮机构
圆柱凸轮是一个在圆柱上开有曲线槽或是在 圆柱端面上作出曲线轮廓的构件。 凸轮与从动件的相对运动是空间运动,属于 空间凸轮机构.
凸轮廓线上任意 两条平行切线间 的距离都等于框 架内侧的宽度。
两滚子中心间 的距离始终保 持不变。
等径凸轮机构
共轭凸轮机构
两滚子中心间的距离 始终保持不变。
主凸轮推动从动件——正行程, 从凸轮推动从动件——反行程。 克服了等宽、等径凸轮的缺点, 结构复杂,制造精度要求高。
从动件的运动规律的选择受到一定的限制,当180º范围内的 凸轮廓线根据从动件运动规律确定后,其余180º内的凸轮廓 线必须符合等宽、等径原则。
2. 按从动件形状及运动形式分
(1)按从动件形状: 尖顶、滚子和平底从动件
尖顶从动件
尖端能以任意复杂的凸轮轮廓保持接触, 从而使从动件实现任意的运动规律。
但尖端处极易磨损,只适用于低速场合。
滚子从动件
凸轮与从动件之间为滚动摩擦, 因此摩擦磨损较小,可用于传递 较大的动力。
平底从动件
从动件与凸轮之间易形成油膜, 润滑状况好,受力平稳,传动效 率高,常用于高速场合。但与之 相配合的凸轮轮廓须全部外凸。
三、 凸轮机构的特点
●运动特点:连续回转 → 往复运动。 ●优点:可精确实现任意运动规律,简单紧凑。 ●缺点:高副,线接触,易磨损,传力不大。 ●应用:传力不大的场合。
机械原理-凸轮

第二节 凸轮机构的传力特性 G
传力特性分析目的 确定构件之间相互的作用力,为 解决磨损及强度尺寸设计提供可靠的 数据。
压力角—不计摩擦时,凸轮对
从动件作用力方向线nn与从动件上 力作用点的速度方向之间所夹的锐 角。
FR2 2
d
vl
F2R1
n
tb
B
t
1 F
n
传力特性分析
Fx 0 F sin( 1) (FR1 FR2 )cos2 0
(二) 组合运动规律
为了克服单一运动规律的某 些缺陷,获得更好的运动和动力 特性,可以把几种运动规律拼接 起来,构成组合运动规律(Law of combined motion)。
组合原则 位移曲线、速度曲线必须连 续,高速凸轮机构加速度曲线也 必须连续。
各段运动规律的位移、速度 和加速度曲线在连接点处其值应 分别相等。
构将产生刚性冲击(Rigid impulse)。等速运动规律适 加速度线图
a
,t
用于低速轻载场合。
,t
⑵ 等加速等减速运动规律 (Law of constant acceleration and deceleration)
推程
前半程
后半程
s
2h
2
2
s
h
2h
2
(
)2
v
4h 2
v
4h 2
(
)
4h 2 a 2
B
远停
h B
远停角s
回程
B0 S
rb
O
S S
360º
,t
回程角
近停
近停角s
S
D
D0
从动件的运动线图(Diagram of motion)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重写加速段推程运动方程为:
s2 =2hδ2 1 /δ2t
v2 =4hω1δ1 /δ2t
a =4hω /δ 湖北工学院专用
2
22 1t
s2
设计:潘存云
1 23 4 5
δt
v2 2hω/δt
h/2
h/2
6 δ1
δ1
a2 4hω2/δ2t
δ1
柔性冲击
作者: 潘存云教授
同理可得回程等加速段的运动方程为:
s2 =h-2hδ21/δ2h v2 =-4hω1δ1/δ2h a2 =-4hω21/δ2h
凸轮转过推程运动角δt-从动件上升h 凸轮转过回程运动角δh-从动件下降h
湖北工学院专用
作者: 潘存云教授
s2 = C0+ C1δ1+ C2δ21+…+Cnδn1 v2 = C1ω+ 2C2ω1δ+…+nCnω1δn-11
a2 = 2 C2ω21+ 6C3ω21δ1…+n(n-1)Cnω21δn-21
湖北工学院专用
作者: 潘存云教授
推程减速上升段边界条件:
中间点:δ1=δt/2,s2=h/2 终止点:δ1=δt ,s2=h,v2=0
求得:C0=-h, C1=4h/δt , C2=-2h/δ2t
减速段推程运动方程为:
s2 v2
==h-4-2hhω(1δ(tδ–t-δδ11))2//δδ22tt
a2 =-4hω21 /δ2t
优点:可精确实现任意运动规律,简单紧凑。 实例 缺点:高副,线接触,易磨损,传力不大。
应用:内燃机 、牙膏生产等自动线、补 鞋机、配钥匙机等。
分类:1)按凸轮形状分:盘形、 移动、 圆柱凸轮 ( 端面 ) 。
2)按推杆形状分:尖顶、 滚子、 特点: 平底从动件。 尖顶--构造简单、易磨损、用于仪表机构; 滚子――磨损小,应用广; 平底――受力好、润滑好,用于高速传动。
湖北工学院专用
作者: 潘存云教授
3).按推杆运动分:直动(对心、偏置)、 摆动
4).按保持接触方式分: 力封闭(重力、弹簧等)
几何形状封闭(凹槽、等宽、等径、主回凸轮)
刀架
o 2
1
内燃机气门机构
湖北工学院专用
机床进给机构
作者: 潘存云教授
凹 槽 凸 轮
等
宽
凸
ቤተ መጻሕፍቲ ባይዱ
W
轮
等
径
r1
凸
主
轮
r2
r1+r2 =const
第3章 凸轮机构
§3-1 凸轮机构的应用和类型 §3-2 从动件的常用运动规律 §3-3 凸轮机构的压力角 §3-4 图解法设计凸轮的轮廓 §3-5 解析法设计凸轮的轮廓
湖北工学院专用
作者: 潘存云教授
§3-1 凸轮机构的应用和类型
结构:三个构件、盘(柱)状曲线轮廓、从动件呈杆状。
作用:将连续回转 => 从动件直线移动或摆动。
回 凸 轮
作者:潘存云教授
优点:只需要设计适当的轮廓曲线,从动件便可获得
任意的运动规律,且结构简单、紧凑、设计方便。
缺点:线接触,容易磨损。
湖北工学院专用
作者: 潘存云教授
应用实例:
3
线 2 A 设计:潘存云 1
湖北工学院专用
绕线机构
作者: 潘存云教授
卷带轮
12 1 放 放音 音键 键
设计:潘存云
s2
h a2
δ1 δt
湖北工学院专用
作者: 潘存云教授
二、三角函数运动规律 1.余弦加速度(简谐)运动规律
5 4
6
s2
推程: s2=h[1-cos(πδ1/δt)]/2
v2 =πhω1sin(πδ1/δt)δ1/2δt a2 =π2hω21 cos(πδ1/δt)/2δ2t
3
2 1
h
设计:潘存云
δ1
1 2 34 5 6
δt v2 Vmax=1.57hω/2δ0
回程等减速段运动方程为:
s2 =2h(δh-δ1)2/δ2h v2 =-4hω1(δh-δ1)/δ2h a2 =4hω21/δ2h
湖北工学院专用
作者: 潘存云教授
3.五次多项式运动规律
位移方程:
s2=10h(δ1/δt)3-15h (δ1/δt)4+6h (δ1/δt)5
无冲击,适用于高速凸轮。
v2
1.等速运动(一次多项式)运动规律 s2
在推程起始点:δ1=0, s2=0
在推程终止点:δ1=δt ,s2=h 代推入程得运: 动方C0=程0:, C1=h/δt
δt
v2
s2 =hδ1/δt
v2 a2
= =
hω1 0
/δt
同理得回程运动方程:
a2 刚性冲击 +∞
s2=h(1-δ1/δh ) v2=-hω1 /δh a =0 2 湖北工学院专用
B’
一、推杆的常用运动规律 名词术语:
基圆、基圆半径、 推程、 推程运动角、远休止角、
h
A D δ’s rmin
o δt δs
δt
δh
ω1
δs 设计:潘存云 B
回程、回 程 运 动 角 、
近休止角、 行程。一个循环
C
t δh δ’s δ1
湖北工学院专用
作者: 潘存云教授
运动规律:推杆在推程或回程时,其位移S2、速度V2、
和加速度a2 随时间t 的变化规律。
S2=S2(t)
V2=V2(t)
a2=a2(t)
形式:多项式、三角函数。
D
B’
A δ’s rmin
s2
h
o
位移曲线
t δt δs δh δ’s δ1
δ 设计:t 潘存云
δh
ω1
δs
B
湖北工学院专用
C
作者: 潘存云教授
一、多项式运动规律
一般表达式:s2=C0+ C1δ1+ C2δ21+…+Cnδn1 (1)
求一阶导数得速度方程:
v2 = ds2/dt = C1ω1+ 2C2ω1δ1+…+nCnω1δn-11
求二阶导数得加速度方程:
a2 =dv2/dt =2 C2ω21+ 6C3ω21δ1…+n(n-1)Cnω21δn-21 其中:δ1-凸轮转角,dδ1/dt=ω1-凸轮角速度,
Ci-待定系数。
边界条件:
5
3
3
摩擦轮
4 4
录音机卷带机构
皮皮带带轮轮
湖北工学院专用
作者: 潘存云教授
2
设计:潘存云
3
湖北工学院专用
1 送料机构
作者: 潘存云教授
§3-2 推杆的运动规律
凸轮机构设计的基本任务: 1)根据工作要求选定凸轮机构的形式;
2)推杆运动规律; 3)合理确定结构尺寸;
4)设计轮廓曲线。
s2
而根据工作要求选定推杆运动规律,是设计凸轮轮廓曲线的前提。
h
δ1
δ1
δ1
-∞
作者: 潘存云教授
2. 等加等减速(二次多项式)运动规律 位移曲线为一抛物线。加、减速各占一半。
推程加速上升段边界条件:
起始点:δ1=0, s2=0, v2=0 中间点:δ1=δt /2,s2=h/2
求得:C0=0, C1=0,C2=2h/δ2t
加速段推程运动方程为:
s2 =2hδ21 /δ2t v2 =4hω1δ1 /δ2t a2 =4hω21 /δ2t
