第七章 平面图形的认识二期末复习课件.ppt
合集下载
《平面图形的认识》复习课件

我们学习过哪些平面图形?
三角形
长方形
正方形
平行四边形
梯形
圆
如果把这些平面图形分成两类,你打算这些平面图形分成两类,你打算怎样分?
三角形 长方形 正方形 平行四边形 梯形
平面图形 都是由线段围成的图形——多边形
圆是曲线图形 圆 多边形包括哪些图形? 多边形包括:三角形、四边形、五边形……
(平行四边形)
(
(
( 长方形 ) ( 正方形 )
等
腰 梯
梯 形
形
)
)
圆
怎样用圆规画圆?
圆心 直径d O
半径
O
直径
O
5厘米,它的面积是( A )平方厘米。
h
四边形
1 2
67 5
4 3
8
2+3 2+6 3+7 6+7
中垂线) 中垂线)
副
三角形
什么是三角形?三角形各部分的名称是什么? 由三条线段首尾相接围成的平面图形叫三角形。
顶点
顶点
边
角边
角
角
边
顶点
由三条线段首尾相接围成的平面图形是什么图形?
三角形
由四条线段首尾相接围成的平面图形是什么图形?
四边形
由五条线段首尾相接围成的平面图形是什么图形?
五边形 由n条线段首尾相接围成的平面图形是什么图形? n边形
锐角三角形 三个锐角
三角形
直角三角形 一个直角
钝角三角形 一个钝角
两边之和大 于第三边
内角和是 180度
等腰三角形 两条边相等,两个底角相等。
等边三角形 三条边相等,三个角相等。
A
A
A A
三角形
长方形
正方形
平行四边形
梯形
圆
如果把这些平面图形分成两类,你打算这些平面图形分成两类,你打算怎样分?
三角形 长方形 正方形 平行四边形 梯形
平面图形 都是由线段围成的图形——多边形
圆是曲线图形 圆 多边形包括哪些图形? 多边形包括:三角形、四边形、五边形……
(平行四边形)
(
(
( 长方形 ) ( 正方形 )
等
腰 梯
梯 形
形
)
)
圆
怎样用圆规画圆?
圆心 直径d O
半径
O
直径
O
5厘米,它的面积是( A )平方厘米。
h
四边形
1 2
67 5
4 3
8
2+3 2+6 3+7 6+7
中垂线) 中垂线)
副
三角形
什么是三角形?三角形各部分的名称是什么? 由三条线段首尾相接围成的平面图形叫三角形。
顶点
顶点
边
角边
角
角
边
顶点
由三条线段首尾相接围成的平面图形是什么图形?
三角形
由四条线段首尾相接围成的平面图形是什么图形?
四边形
由五条线段首尾相接围成的平面图形是什么图形?
五边形 由n条线段首尾相接围成的平面图形是什么图形? n边形
锐角三角形 三个锐角
三角形
直角三角形 一个直角
钝角三角形 一个钝角
两边之和大 于第三边
内角和是 180度
等腰三角形 两条边相等,两个底角相等。
等边三角形 三条边相等,三个角相等。
A
A
A A
平面图形的认识PPT教学课件

A
DE
B
C
1.如图,AD⊥BC,BE⊥AC ,CF⊥AB, 垂足分别为 D、E、F ,则△ABC中 AC 边上的高是( )
A. FC B. BE C. AD D. AE
A F
B
C
D
E
2.如图,在Rt△ABC中,∠ACB=900,CD是 AB 边上的高, AB=5cm,BC=4cm,AC=3cm. (1)求△ ABC的面积; (2)求CD 的长.
复习第七章 平面图形的认识
例1.如图,直线AB∥CD,截线EF 与 AB 、
CD 分别交于 M、N 两点.请你从中选出
两个你认为相等的角
.
A
6
2 3
5
E 1 4
B
C7 8
D
F
例2: 1.如图,AB∥CD,∠ABE=1200,∠ECD=250,
求∠BEC的度数.
A
B
E
C
D
变式训练:如图,AB∥CD,∠A=1300, ∠C=1100,求∠APC.
A D
C
B
夏: 前2070-1600;阳城;禹-桀.
更替 商: 前1600-1046;亳-殷;汤-纣.
夏
周:
前1046-771;镐京;武王-厉王暴政-幽王-西周. 前770-475-256;洛邑;平王-东周-春秋-战国.
商 周 的
目的:巩固奴隶制国家.
井田制 性质:奴隶制土地国有制-经济基础.
政
内容:诸侯受地,交纳贡赋.集体耕作.
面镜m、n之间来回反射,已知∠1=600,
∠2=500。
则∠3= 。
例5.等腰三角形一腰上的中线把这个三角形 的周长分成9cm和15cm两部分,求这个 三角形三边的周长.
DE
B
C
1.如图,AD⊥BC,BE⊥AC ,CF⊥AB, 垂足分别为 D、E、F ,则△ABC中 AC 边上的高是( )
A. FC B. BE C. AD D. AE
A F
B
C
D
E
2.如图,在Rt△ABC中,∠ACB=900,CD是 AB 边上的高, AB=5cm,BC=4cm,AC=3cm. (1)求△ ABC的面积; (2)求CD 的长.
复习第七章 平面图形的认识
例1.如图,直线AB∥CD,截线EF 与 AB 、
CD 分别交于 M、N 两点.请你从中选出
两个你认为相等的角
.
A
6
2 3
5
E 1 4
B
C7 8
D
F
例2: 1.如图,AB∥CD,∠ABE=1200,∠ECD=250,
求∠BEC的度数.
A
B
E
C
D
变式训练:如图,AB∥CD,∠A=1300, ∠C=1100,求∠APC.
A D
C
B
夏: 前2070-1600;阳城;禹-桀.
更替 商: 前1600-1046;亳-殷;汤-纣.
夏
周:
前1046-771;镐京;武王-厉王暴政-幽王-西周. 前770-475-256;洛邑;平王-东周-春秋-战国.
商 周 的
目的:巩固奴隶制国家.
井田制 性质:奴隶制土地国有制-经济基础.
政
内容:诸侯受地,交纳贡赋.集体耕作.
面镜m、n之间来回反射,已知∠1=600,
∠2=500。
则∠3= 。
例5.等腰三角形一腰上的中线把这个三角形 的周长分成9cm和15cm两部分,求这个 三角形三边的周长.
苏科版 第7章平面图形的认识(二) 本章总结提升(共35张PPT)

本章总结提升
【归纳总结】三角形一边上的高垂直于这条边,一角的平分线平 分该角,每一条边上的中线平分这条边和三角形的面积.
谢 谢 观 看!
图形平移时,连接各对应点的线段有什么关系?你T-3,在方格纸中,每个小方格的边长均为 1 个单位
长度,△ABC 的三个顶点和点 P 都在小方格的顶点上.要求:①将 △ABC 平移,使点 P 落在平移后的三角形内部;②平移后的三角形
的顶点在方格的顶点上. 请你在图甲和图乙中分别画出符合要求的一个示意图,并写出平移 的方法.
本章总结提升
模块7 多边形的内角和与外角和
n 边形的 n 个内角之间有怎样的关系?如何推导得出这个结论?n 边 形的外角和与 n 有关吗?
本章总结提升
3 例 8 已知一个多边形的内角和是其外角和的2倍,则这个多边形的
边数是____5____.
3 [解析] 设这个多边形的边数为 n,由题意得(n-2)×180°=2×360°,解 得 n=5.
本章总结提升
【归纳总结】三角形的任意两边之和大于第三边,任意两边之差 小于第三边,通常用此性质来确定第三边长的取值范围.
本章总结提升
模块5 三角形中的三条重要线段
与三角形有关的重要线段有哪些?怎样画出这些线段?这些线段在 三角形中的位置有何特点?
本章总结提升
例 6 如图 7-T-5 所示,AD,AE 分别是△ABC 的高和角平分线,∠B =36°,∠C=76°,求∠DAE 的度数.
本章总结提升
【归纳总结】平移后的图形和原图形的对应线段平行(或在同一 条直线上)且相等.
本章总结提升
模块4 三角形的三边关系
三角形的三边之间有什么关系?得出这个结论的依据是什么?
平面图形的认识(ppt)

学习立体几 何
学习图形的 变换
图形的组合是研究如何将多个图形组合在一起形成更 复杂图形的方法,通过学习图形的组合,可以更深入
地理解图形的构造和应用。
学习图形的 组合
图形的变换是研究图形在平面上如何移动和变换的方 法,通过学习图形的变换,可以更深入地理解图形的 几何性质和应用。
THANKS
感谢观看
边长关系
平面图形中的边长关系是指图形中各 边之间的长度关系。例如,等边三角 形的三条边长度相等,而等腰梯形的 两条腰长度相等。
面积和周长的计算
面积计算
面积是指平面图形所占的面积大小。不同形状的平面图形有不同的面积计算公 式。例如,正方形的面积是边长的平方,而圆的面积是π乘以半径的平方。
周长计算
周长是指平面图形的边界长度。不同形状的平面图形有不同的周长计算公式。 例如,正方形的周长是4乘以边长,而圆的周长是2π乘以半径。
转不变性。
圆形在几何学中具有重要的地位, 是许多定理和公式的核心。
圆形可以用于表示钟表、方向盘、 车轮等物体的外轮廓。
其他平面图形
其他常见的平面图形还包括五边形、六边形、扇形、椭圆等 。
这些图形在日常生活和科学研究中都有广泛的应用,如五角 星、蜂巢等。
03
平面图形的性质和特点
对称性
第一季度
第二季度
平面图形的认识
• 引言 • 平面图形的分类 • 平面图形的性质和特点 • 平面图形在实际生活中的应用 • 总结与展望
01
引言
主题简介
01
平面图形是数学和几何学中的基 本概念,是指二维空间中的图形 。
02
平面图形通常由直线、曲线、多 边形等基本元素构成,具有多种 属性和特征。
苏科版七年级下平面图形的认识(二)复习ppt课件

平行四边形的性质与判定
平行四边形的性质
对边平行、对角相等、对角线互 相平分。
平行四边形的判定
一组对边平行且相等、两组对边 分别平行、两组对角分别相等、 对角线互相平分。
矩形的性质与判定
矩形的性质
四个角都是直角、对角线相等且互相 平分。
矩形的判定
有一个角是直角的平行四边形、有三 个角是直角的四边形。
本章复习重点总结
01
解题方法梳理
02
掌握解决平面图形相关问题的基 本方法和思路,如利用平行线性 质解决角度问题。
学习方法与技巧分享
主动学习
01
实践应用
03
02
积极参与课堂讨论,主动提问,及时解决疑 惑。
04
在生活中寻找平面图形的实例,加深理解 和记忆。
习题巩固
05
06
通过大量习题练习,熟练掌握解题技巧和 方法。
综合较大,涉及平面图形的组合、变换和推理等知识点,旨在培养学生的思维能力和 创新能力。
综合练习题答案与解析
总结词:答案详解
详细描述:提供所有综合练习题的答案,并对每道题的解题思路和步骤进行详细解析,帮助学生理解解题方法和技巧。
综合练习题答案与解析
总结词:答案详解
矩形的性质与判定
矩形的性质
四个角都是直角、对角线相等且互相 平分。
矩形的判定
有一个角是直角的平行四边形、有三 个角是直角的四边形。
菱形的性质与判定
菱形的性质
四边相等、对角线垂直且平分。
菱形的判定
四边相等的四边形、对角线垂直的平行四边形。
菱形的性质与判定
菱形的性质
四边相等、对角线垂直且平分。
菱形的判定
学习方法与技巧分享
总复习——平面图形的认识PPT优秀课件

平面图形的认识总复习思维导图思维导图思维导图思维导图平面图形1
总复习
第一课时:平面.平面图形有哪些特征? 3.图形与图形之间有什么联系?
1. 组内传阅思维导图,边传阅边交流。 2. 互相提出建议,讨论后完善思维导图。 3.各小组合作梳理一个部分的知识。
一个60°的角。
(╳ )
4.平角是一条直线。
()
╳
5. 两条直线不平行就相交。
(╳)
收获与体会
温馨提示:小组合作时间为4分钟。
1. 讲——吐字清晰,声音洪亮! 2. 听——认真倾听,边听边思! 3. 做——听中感悟,补充导图! 4. 问——大胆提问,质疑问难!
判断 。(正确比手势“√”,错误的比手势“╳”)
1. 直线比射线长。
(╳)
2.角的大小与角的两边的长短无关。 ( √ )
3.用一个放大5倍的放大镜看一个12°的角,将看到
总复习
第一课时:平面.平面图形有哪些特征? 3.图形与图形之间有什么联系?
1. 组内传阅思维导图,边传阅边交流。 2. 互相提出建议,讨论后完善思维导图。 3.各小组合作梳理一个部分的知识。
一个60°的角。
(╳ )
4.平角是一条直线。
()
╳
5. 两条直线不平行就相交。
(╳)
收获与体会
温馨提示:小组合作时间为4分钟。
1. 讲——吐字清晰,声音洪亮! 2. 听——认真倾听,边听边思! 3. 做——听中感悟,补充导图! 4. 问——大胆提问,质疑问难!
判断 。(正确比手势“√”,错误的比手势“╳”)
1. 直线比射线长。
(╳)
2.角的大小与角的两边的长短无关。 ( √ )
3.用一个放大5倍的放大镜看一个12°的角,将看到
平面图形的认识整理与复习ppt课件
(2)下图中,有( B )组互相平行的线段,有 ( C )组互相垂直的线段。
A、4 B、12 C、24
采 用 PP管 及 配 件: 根据给 水设计 图配置 好PP管 及配件 ,用管 件在管 材垂直 角切断 管材, 边剪边 旋转, 以保证 切口面 的圆度 ,保持 熔接部 位干净 无污物
7、
如图,从A、B两村各挖一条水渠与运河
回顾与交流
1.分别画出直线、射线和线段,并说一说他们 的联系与区别。
名称
图形
区别
端点个数 能否度量
联系
直线
0 不能度量 都是直的
射线 线段
. ..
1
不能度量 射线、线
段是直线
的一部分
2
能度量
采 用 PP管 及 配 件: 根据给 水设计 图配置 好PP管 及配件 ,用管 件在管 材垂直 角切断 管材, 边剪边 旋转, 以保证 切口面 的圆度 ,保持 熔接部 位干净 无污物
长方形
四 条 边 相 等
正方形
图形
特性
两组对边分别平行且相等
两组对边分别平行且相等 四个角都是直角
两组对边分别平行 四个角都是直角 四条边都相等
采 用 PP管 及 配 件: 根据给 水设计 图配置 好PP管 及配件 ,用管 件在管 材垂直 角切断 管材, 边剪边 旋转, 以保证 切口面 的圆度 ,保持 熔接部 位干净 无污物
按角分 直角三角形
钝角三角形
按边分:等等腰边三三角角形形
平行四边形(长方形、正方形) 梯形
……
图形
……
立体图形
等边三角形 等腰三角形
三角形
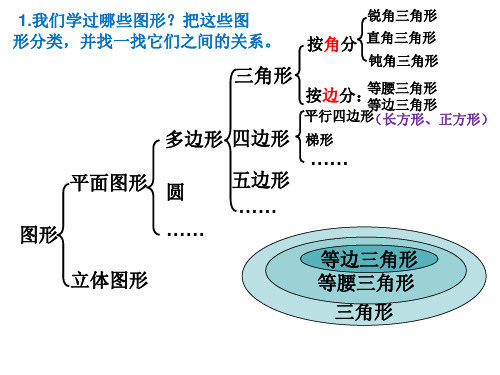
1.我们学过哪些图形?把这些图形 采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在管材垂直角切断管材,边剪边旋转,以保证切口面的圆度,保持熔接部位干净无污物 分类,并找一找它们之间的关系。 按角分
课件认识图形二 认识平面图形 人教新课标(共12张PPT)【实用资料】

有( 3 )个 有( 2 )个 有( 1 )个 有( 2 )个 有( 3 )个
创新微课
认识平面图形
本节小结
1 长方形有四条边,两条长边相等,两条短边相等;
2
正方形的四条边都相等;
3
平行四边形有四条边,相对的边相等;
4
三角形有三条边;
5
圆是由一条曲线围成的。
创新微课
同学,下节再见
每个人都有潜在的能量,只是很容易被习惯所掩盖,被时间所迷离,被惰性所消磨。把命运寄托在自己身上,这是这个世界上最美妙的心思。为此努力,拼搏,不舍昼夜。每个人的内心都充 满了魔鬼,学会控制他。如果你还认为自己还年轻,还可以蹉跎岁月的话,你终将一事无成,老来叹息。在实现理想的路途中,必须排除一切干扰,特别是要看清那些美丽的诱惑。忍一时之 气,免百日之忧信心、毅力、勇气三者具备,则天下没有做不成的事改变自己是自救,影响别人是救人。当你感到无助的时候,还有一种坚实的力量可以依靠,那就是你自己。想过去是杂念, 想未来是妄想,最好把握当下时刻。幸福不在得到多,而在计较少。改变别人,不如先改变自己。一个人能走多远,要看他有谁同行;一个人有多优秀,要看他有谁指点;一个人有多成功, 要看他有谁相伴。同样的一瓶饮料,便利店里2块钱,五星饭店里60块,很多的时候,一个人的价值取决于所在的位置。忙碌是一种幸福,让我们没时间体会痛苦;奔波是一种快乐,让我们真 实地感受生活;疲惫是一种享受,让我们无暇空虚。10、我是世界上独一无二的,我一定会成功!成功者往往有个计划,而失败者往往有个托辞。成功者会说:“我帮你做点什么吧!而失败者 说:那不是我的事。成功三个条件:机会;自己渴望改变并非常努力;贵人相助亿万财富买不到一个好的观念;好的观念却能让你赚到亿万财富。一个讯息从地球这一端到另一端只需要0.05 秒,而一个观念从脑外传到脑里却需要一年,三年甚至十年。要改变命运,先改变观念。人生的成败往往就在于一念之差。鸟无翅膀不能飞,人无志气不成功。成功99%是心志,1%是能力。一 个人不成功是因为两个字——恐惧。一个会向别人学习的人就是一个要成功的人。人要是惧怕痛苦,惧怕种种疾病,惧怕不测的事情,惧怕生命的危险和死亡,他就什么也不能忍受了,人格 的完善是本,财富的确立是末。傲不可长,欲不可纵,乐不可极,志不可满。在人之上,要把人当人;在人之下,要把自己当人。锲而舍之,朽木不折;锲而不舍,金石可镂。真者,精诚之 至也,不精不诚,不能动人。我觉得坦途在前,人又何必因为一点小障碍而不走路呢?对时间的慷慨,成功不是将来才有的,而是从决定去做的那一刻起,持续累积而成。天下之事常成于困 约,而败于奢靡。企业家收获着梦想,又在播种着希望;原来一切辉煌只代表过去,未来永远空白。一个最困苦、最卑贱、最为命运所屈辱的人,只要还抱有希望,便无所怨惧。你生而有翼, 为何一生匍匐前进,形如蝼蚁世界上只有想不通的人,没有走不通的路。世上那有什么成功,那只是努力的另一个代名词罢了。所谓英雄,其实是指那些无论在什么环境下都能够生存下去的 人。微笑不用本钱,但能创造财富。赞美不用花钱,但能产生气力。分享不用过度,但能倍增快乐。微笑向阳,无畏悲伤。我们不知道的事情并不等于没发生,我们不了解的事情并不代表不 存在。我们渴望成功,首先要志在成功。我要让未来的自己为现在的自己感动。想哭就哭,想笑就笑,不要因为世界虚伪,你也变得虚伪了。小鸟眷恋春天,因为它懂得飞翔才是生命的价值。 笑对人生,能穿透迷雾;笑对人生,能坚持到底;笑对人生,能化解危机;笑对人生,能照亮黑暗。学在苦中求,艺在勤中练。不怕学问浅,就怕志气短。一个细节足以改变一生。一切成就 都缘于一个梦想和毫无根据的自信。永远不要嘲笑你的教师无知或者单调,因为有一天当你发现你用瞌睡来嘲弄教师实际上很愚蠢时,你在社会上已经碰了很多钉子了。幽默胜过直白,话少 胜过多言;坦率胜过伪装,自然胜过狡辩;心静何来多梦,苦索不如随缘。有一种落差是,你配不上自己的野心,也辜负了所受的苦难。最可怕的不是有人比你优秀,而是比你优秀的人还比 你更努力。最有希望的成功者,并不是才干出众的人而是那些最善利用每一时机去发掘开拓的人。昨天如影——记住你昨天的挫折和失败的教训;今天如画快乐和幸福的人生要靠你自己去描 绘;明天如梦——珍惜今天,选择好自己的目标,努力地为自己的明天去寻求和拼搏。不曾扬帆,何以至远方。不论你在什么时候开始,重要的是开始之后就不要轻言放弃。不去耕耘,不去播 种,再肥的沃土也长不出庄稼,不去奋斗,不去创造,再美的青春也结不出硕果。不要盘算太多,要顺其自然。该是你的终会得到。成大事不在于力量多少,而在能坚持多久。成为一个成功 者最重要的条件,就是每天精力充沛的努力工作,不虚掷光阴。从未跌倒算不得光彩,每次跌倒后能再战起来才是最大的荣耀。脆弱的心灵创伤太多,追求才是愈合你伤口最好的良药。挫折 经历的太少,所以总是把一些琐碎的小事看得很重。当你知道你不在是你的时候,你才是真正的你!漫无目的的生活就像出海航行而没有指南针。人生多一份感恩,就多一份美化。所有的豪 言都收起来,所有的呐喊都咽下去。成功六机握机当你握着两手沙子时,一定就拿不到地上那颗珍珠了。快乐在满足中求,烦恼多从欲中来。人若有志,万事可为。为明天做准备的最好方法, 就是要集中你所有的智慧,所有的热诚,把今天的事情做得尽善尽美。在茫茫沙漠,唯有前进时的脚步才是希望的象征。在我们了解什么是生命之前,我们已将它消磨了一半。这个世界既不 是有钱人的世界,也不是有权人的世界,它是有心人的世界。这个世界上任何奇迹的产生都是经过千辛万苦的努力而得的,首先承认自己的平凡,然后用千百倍的努力来弥补平凡。真正的导 者,其厉害之处不在于能指挥多少君子,而在于能驾驭多少小人。追逐着鹿的猎人看不到脚下的高山。
六年级下册数学课件2.《平面图形的认识(2)》苏教版PPT课件

4 . 初 步 形成 宽容他 人的良 好品质 。 5 . 通 过 具体 事例体 验宽容 对己对 人带来 的慰藉 。 6. 传统的 节日也 应有时 代的价 值,不 符合时 代需要 的,应 该淘汰 。 7. 生活中 ,伴随 着我们 成长有 许多风 俗,其 中不少 体现了 尊老的 传统美 德。
亲爱的同学们,再见!
周长的计量单位: 厘米 分米 米…(长度单位)
面积的计量单位: 平方厘米 平方分米 平方米…(面积单位)
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
我们学过哪些平面图形的面积公式?这些公式各是怎样推导 的?根据推导的过程进行整理,并与同学交流。
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
6. 求下面各图形中涂色部分的面积。(单位:cm) (4+9)×6÷2 =39(平方厘米) 4×6÷2 =12(平方厘米) 39-12 = 27(平方厘米)
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
深
度
思
考
3、如图,正方形的面积是12平方厘米,求图中外面和 里面两个圆的面积。
内圆半径r的平方=12 ÷4=3
内圆的面积是: 3.14×3=9.42 (平方厘米)
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
怎样计算长方形、正方形和圆的周长?
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
亲爱的同学们,再见!
周长的计量单位: 厘米 分米 米…(长度单位)
面积的计量单位: 平方厘米 平方分米 平方米…(面积单位)
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
我们学过哪些平面图形的面积公式?这些公式各是怎样推导 的?根据推导的过程进行整理,并与同学交流。
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
6. 求下面各图形中涂色部分的面积。(单位:cm) (4+9)×6÷2 =39(平方厘米) 4×6÷2 =12(平方厘米) 39-12 = 27(平方厘米)
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
深
度
思
考
3、如图,正方形的面积是12平方厘米,求图中外面和 里面两个圆的面积。
内圆半径r的平方=12 ÷4=3
内圆的面积是: 3.14×3=9.42 (平方厘米)
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
怎样计算长方形、正方形和圆的周长?
六年级下册数学课件2.《平面图形的 认识(2 )》苏 教版PP T课件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
又∵∠BAC=1800-∠B2-∠C
∴∠DAE==9120(0-∠∠BC--∠12C()1800-∠B-∠C)
• 13、已知如图∠xOy=900,BE是∠ABy的 平分线,BE的反向延长线与∠OAB的平分 线相交于点C,当点A,B分别在射线Ox, Oy上移动时,试问∠ACB的大小是否发生 变化?如果保持不变,请说明理由;如果 随点A,B的移动而变化,请求出变化范围。
1、在△ABC中,
(1)若∠A=400,∠B-∠C=400,
则∠B =_90_0 ∠C=_5_00_
(2)、若∠A= 1 ∠B= 1 ∠C,
2
3
则∠A=_3_00_∠B=_6_00_∠C=_9_00_
• 2、如图,在△ABC中,∠A、∠B的平 • 分线相交于点I,若∠C=700,则∠AIB
=_12_50,若∠AIB=1550,则∠C=_13_00_。 • 3、如图,∠1+∠2+∠3+∠4+∠5=320o ∠6=__40_0 _
7、在△ABC中,如果∠A+∠B=2∠C,
∠A≠∠B,那么( D)
A、∠A、∠B、∠C都不等于600
B、∠A=600
C、∠B=600,
D、∠C=600
9、若一个多边形的内角和是外角和的3.5倍,
则此多边形的边数是( )C
A、7 B、14
C、9
D、18
10、直角三角形两锐角的平分线所交成的角
的度数是( B )
解:延长BP交AC于D
在△ABD中,根据三角形三边关
D
系得AB+AD>BP+PD①
在△PDC中,同理可得 PD+DC>PC②
①+②得: AB+AD+PD+DC>BP+PD+PC
则,AB+AC>BP+PC
26、如图,已知P是 AOB 内一点且
PC OA于C,PD OB于D且EC=FD,
EP=PF,猜想 AOP 和 BOP
的大小关系并说明你的理由。
C
A
E
P
O
D FB
.在如图所示的4×4正方形 网格中, ∠1+∠2+∠3+ ∠4+∠5+∠6+∠7=
6
5
4
7
3
2
1
第13题
如图,三条直线两两相交,写 出图中的同位角、内错角、同旁 内角,并指出它们分别是由哪两 条直线被哪一条直线所截成的。
10 c
1 4111295 8 b
你知道吗? • 2、你知道两直线平行有什么性质吗?
性质1、两直线平行,同位角相等 性质2、两直线平行,内错角相等 性质3、两直线平行,同旁内角互补 性质4、两平行线之间的距离相等 性质5、如果两个角的两边分别平行,
那么这两个角相等或互补。
你知道吗?
• 3、图形的平移 1、图形的平移的要素:方向、距离。 2、图形平移的性质: (1)图形的平移不改变图形的形状与大小, 只改变位置。 (2)图形平移后,对应点的连线平行或在同 一直线上且相等 (3)图形平移后,对应线段平行或在同一直 线上且相等,对应角相等。
A、45o
B、135o
C、45o或135o
Байду номын сангаас
D、以上答案都不对
11、如图,在△ABC中,∠BAC=4∠ABC= 4∠C,BD⊥AC,垂足为D,求∠ABD的度数
解:设∠C=x, 则,∠ABC=x,∠BAC=4x 根据三角形内角和性质: x+x+4x=1800,x=300 即:∠BAC=1200,所以∠BAD=600 又因为:BD⊥AC,即∠D=900 所以:∠ABD=300
第七章 平面图形的认识(二)
复习课
你知道吗? • 1、你知道如何判定两条直线是否平行吗?
方法1、同位角相等,两直线平行 方法2、内错角相等,两直线平行 方法3、同旁内角互补,两直线平行 方法4、在同一平面内,不相交的两条直线 是平行线 方法5、平行于同一条直线的所有直线平行 方法6、垂直于同一条直线的所有直线平行
• 12、在△ABC中,∠B>∠C,AD为∠BAC的平分
线,AE⊥BC,垂足为E,试说明∠DAE=
1(∠B-∠C)
2
解:∵AE⊥BC
∴∠DAE=900-∠ADE
又∵∠ADE=∠C+∠DAC
而AD为∠BAC的平分线
∴∠DAC= 1∠BAC
2
∴∠ADE=∠C+
1
∠BAC
即∠DAE=900-∠2 C- 1 ∠BAC
∠4=∠6,所以∠3=∠5;③因为
解:在△ABC中根据外角的性质, ∠ACB=∠EBA-∠BAC
而BE平分∠yBA,AC平分∠BAO
∴∠EBA= 1 ∠yBA,∠BAC= 1 ∠BAO
2
2
∴∠ACB= 1(∠yBA-∠BAO)
2
在△ABO中,根据外角的性质,得
∠yBA-∠BAO=∠AOB=900
∴∠ACB=450
即∠ACB的大小保持不变,且等于45度。
你知道吗?
• 4、认识三角形
锐角三角形
1、三角形的分类:按按角边分分
直不角等三边角三形角形 等腰三角形
钝角三角形
2、三角形的三条主要线段: (1)角平分线 (2)中线 (3)高
你知道吗?
• 5、三角形的三边之间的关系
三角形的任意一边大于其它两边的差, 小于其它两边的和。
• 6、三角形的三角之间的关系 三角形的三个内角和为1800 • 7、多边形的内角和 n边形的内角和为(n-2)1800 • 8、多边形的外角和 n边形的外角和为3600
4、锐角三角形ABC中,3条高相交于点H, 若∠BAC=700,则∠BHC=__11_00__ 5、已知:三角形的3边长分别为1,x,5,
且x为整数,则x=__5___。
6、如图,∠O的两边被一直线所截,用α和β
的式子
表示∠O的度数为( B )
A、α-β
B、β-α
C、1800-α+β D、1800-α-β
23
6 7a
1.如果两条直线被第三条直线 所截,那么下面的结论:①同位 角相等;②内错角相等;③同旁 内角互补;④一定有内错角.其 中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图,∠a的同旁内 角有 ( )
A.1个 B.2个
a
C.3个 D.4个
3.如图,有下列四个判断:
①因为∠4=∠6,所以∠2=∠5;②因为
• 14、如图,AB∥DC,ED∥BC,AE∥BD, 写出图中与△ABD面积相等的三角形。
解:由DC∥AB得 S△ABD=S△ABC
由AE∥BD得 S△ABD=S△EBD
由ED∥BC得 S△EBD=S△EDC
• 15、如图,P为△ABC内任意一点,试比较 AB+AC与PB+PC的大小,并说明理由。
