五年级数学上册解决问题的策略专项练习
(易错笔记)第7练解决问题的策略应用题常考易错题专项汇编(试题)小学数学五年级上册(苏教版,含答案)

第7练解决问题的策略应用题常考易错题专项汇编(试题)一、应用题1.刘弯小学举行小型运动会,项目只有100米,跳远和跳高三项。
规定:参赛运动员最多可以报三项,那么每一位参赛运动员可以有几种不同的选择方法?(先填表,再解答)答:每一位参赛运动员可以有______种不同的选择方法。
2.小红有下面3张纸币,用这些纸币可以组成多少种不同的币值?写一写。
3.甜甜蛋糕店的面包师制作了30个蛋挞,准备装入盒中售卖。
现有两种包装盒(如图),如果正好全部装完,一共有多少种装法?完成下面表格并回答。
答:一共有()种不同的装法。
4.甲、乙、丙、丁、戊五人见面握手,已知甲握了4次,乙握了3次,丙握了2次,丁握了1次,戊握了几次?5.某信号兵用红、黄、蓝3面旗从上到下挂在旗杆上的三个位置表示不同的信号。
每次可以挂1面、2面或3面,并且不同的顺序、不同的位置表示不同的信号。
3面旗一共可以表示出多少种不同的信号?6.小张有1元、2元、5元的人民币若干张,要拿出10元,可以有多少种拿法?7.一次数学竞赛共有3题,答对一题得40分,答错或不答1题倒扣10分.小华参加了这次数学竞赛.她可能得多少分?(注:最低分为0分)8.妈妈为小红准备的早餐是:一块面包、一盒牛奶、一个鸡蛋,小红要把它们吃完,可以有多少种不同顺序的吃法?9.某快餐店今日快餐种类如下图,小明想选一种荤菜和一种素菜,一共有多少种不同的搭配方法?(先连一连,再回答)10.有足够的2角和5角两种人民币,要拿出5元钱,有多少种不同的拿法?11.小红从家到学校有3条路可走,从学校到少年宫有4条路可走,如果小明从家出发经过学校到少年宫,有几种不同的走法?12.小张、小王、小高、小于、小赵、小李六位同学进行乒乓球比赛,每两人都要赛一场。
现在小张和小王已经赛了5场,小高赛了4场,小于和小赵赛了3场,问:小李赛了几场?13.婷婷要把10个苹果分给2个小朋友,且每人最少分2个苹果,那么婷婷一共有多少种不同的分法?14.甜甜有15根棒棒糖,她要把这些棒棒糖分成3堆,且每堆至少有3根棒棒糖。
五年级数学解决问题的策略(一一列举)

五年级数学解决问题的策略(一一列举)吴海峰1、妈妈为女儿的早餐准备了牛奶、豆浆、高乐高、果珍4种饮料;面包、沙琪玛、蛋糕3种糕点。
女儿选1种饮料和1种糕点,一共有多少种不同的搭配?2、有红、黄、蓝三种颜色的小旗各一面,从中选用1面或2面升上旗杆,分别用来表示一种信号。
一共可以表示多少种不同的信号?3、两个自然数的积是12,这样的算式有多少个?4、两个自然数的和是12,这两个数的乘积可能是多少?5、用20个长为1厘米的小木棒围成一个长方形,共有多少种不同的围法,面积最大的是多少?你发现了什么?6、用20个边长为1厘米的小正方形,拼成一个长方形,有多少种不同的拼法,周长最大是多少?你发现了什么?7、用20米长的栅栏围成一个长方形,其中有一面靠墙,有多少种围法?8、用18根1分米长的小棒围成一个等腰三角形,一共有多少种不同的围法?(小棒全部用完)9、小刚有面值为60分和80分的邮票各两枚,她用这些邮票能付多少种不同的邮资?10、篮球比赛中,如果投中1球得1分、2分或3分,如果投不中,得0分。
小明在一次比赛中,连续投了两个球,请你分析一下,他有多少种得分可能?11、有1克、2克、4克的砝码各一个,选其中的一个或几个,能在天平上直接称出多少种不同的重的物体?12、有4本不同的杂志,最少可订阅1本,最多可订阅4本,一共可以有多少种不同的订法?13、小明准备用8角钱去买练习本,他现有1角、2角、5角的人民币各8张,小明要拿8角钱,有几种拿法?14、有5位同学参加演讲比赛,如果他们要互相握一次手,那么一共要握多少次手?元旦到了他们又互寄贺年卡片,他们共寄了多少张卡片?15、小明、小军、小伟去公园游玩,他们要拍照,一共有多少种不同的拍照方法?16、从5、7、8、三张数字卡片中,选1张、2张或3张,可以摆出多少个不同的自然数?17、有ABCDEF六支球队进行比赛,A赛了5场,B赛了4场,C赛了3场,D赛了2场,E赛了1场,则F赛了多少场?分别是和谁比赛的?18、一次数学竞赛共有4道题,答对一道得4分,答错一题倒扣1分,小明参加了这次数学竞赛,他有可能得多少分?(注最低分为0分,不答视为答错处理)19、从甲地到乙地,中途共经过5个小站,每站都有乘客上下车。
完整)苏教版五年级数学上册解决问题的策略练习题

完整)苏教版五年级数学上册解决问题的策略练习题1、用3、5、8三张卡片组成的所有三位数有多少个。
答:一共有 54 个不同的三位数。
2、用 24 个边长为 1 厘米的正方形摆成的长方形有多少种不同的摆法。
答:一共有 12 种不同的摆法。
3、用 24 根 1 米长的木棒围成长方形羊圈,有多少种不同的围法?其中面积最大是多少平方米。
答:一共有 6 种不同的围法,其中面积最大是36 平方米。
4、平行四边形面积是 24 平方厘米,它的底和高都是整厘米数,有多少种不同的平行四边形。
答:一共有 6 种不同的平行四边形。
5、图1中有()个正方形,图2中有()个长方形。
答:图1中有 9 个正方形,图2中有 10 个长方形。
6、图3,从 A 地去 B 地有()种不同的走法。
(路程最近)答:从 A 地去 B 地有 2 种不同的走法。
(路程最近)7、图4,ABCDE 五个人每两个人通电话一次,一共要通()次,在图中连一连。
答:ABCDE 五个人一共要通 10 次电话。
8、填空:□.□×□=3.6,一共有()个不同的算式。
答:一共有 8 个不同的算式:1.2×3,2.4×1.5,3.6×1,1×3.6,1.5×2.4,3×1.2,1.2×3,2.4×1.5.9、有20 个篮球队进行淘汰赛,进行()场,决出冠军。
答:进行 19 场比赛,决出冠军。
10、一路车每隔 10 分钟发车一次,二路车每隔 8 分钟发车一次,两车 6:00 同时发车,下一次同时发车是几点几分。
答:两车下一次同时发车是 6:40.11、用简便方法计算。
答:略。
12、脱式计算。
答:略。
数学五上第七单元【解决问题的策略 】精华训练题含答案

苏教版小学数学五年级上册第七单元【解决问题的策略】精华篇训练题含答案题号一二三四五总分评分一、单选题1.三张不同颜色的彩纸包语文书、数学书、英语书(每张纸只能包一本书),一共有()种不同的包法。
A. 10B. 12C. 15D. 62.A、B、C、D四个篮球队,每两个队都要比赛一场,到现在为止,A已赛了3场,B 已赛了2场,D 已赛了1场,C已赛了()场。
A. 4B. 3C. 2D. 13.从牌面是2、3、4、5四张扑克牌中任意选出两张求和,得到大小不同的和有()种。
A. 4B. 5C. 6D. 74.把四张扑克牌(如下图)反扣在桌面上,任意摸2张,可能有()种不同的情况。
A. 4B. 5C. 6D. 75.一辆长途汽车往返于A、B两地,沿途要经过C、D二个站。
汽车运输公司要为这辆汽车准备()种车票。
A. 4B. 6C. 8D. 12二、判断题6.用6、0、7这三张数字卡片,一共能组成6个不同的三位数。
()7.从小明、小华、小烨中选出两名中队委,一共有6种不同的选法。
()8.用1、2、3三张数字卡片能组成6个不同的两位数。
()9.从1元和5元的纸币中拿走15元,共有3种不同的拿法。
()10.车站有客车和货车共6辆,客车和货车的辆数可能有5种情况。
()三、填空题11.6个图形排在一起,如图,如果把形状相同的图形挨在一起,可以有________种排法。
12.四位同学一起去山西省图书馆看书,见面后每两人握一次手,他们一共握了次手。
13.2019年12月16日,正式投人运营的盐城高铁站总建筑面积为323549平方米,改写成用“万”作单位的数是________万平方米,再保留整数大约是________万平方米。
盐城到淮安的高铁,中途会在建湖、阜宁2个车站停靠,往返需要准备________种不同的车票。
14.甲、乙、丙、丁四队进行篮球比赛,如果每两队之间都要比赛一场,一共要比赛________场,如果采用淘汰赛制(每比赛一场就淘汰一支队伍),那么只要比赛________场就能赛出冠军。
苏教版2022-2023学年小学数学五年级上册期末真题专项练习(解决问题的策略)含解析

苏教版2022-2023学年小学数学五年级上册期末真题专项练习(解决问题的策略)一、选择题1.(2022·江苏·五年级)不计算,请你根据规律选出得数。
6.6 6.744.22⨯=⨯=6.6666.7444.2226.6666×6666.7=()A.4444.2222B.4444.2222C.44444.22222 2.(2021·安徽滁州·六年级期末)六年级8个班进行男子三人制篮球赛,如果首轮(8进4)进行淘汰赛,次轮进行循环赛,最后产生冠军,一共要比赛()场。
A.7B.8C.9D.10 3.(2020·河南新乡·五年级期中)毛毛有7.8元钱,给玲玲2.3元钱,两人的钱数就相等,玲玲原有()元钱。
A.5.5元B.2.3元C.3.2元4.(2022·江苏徐州·五年级期末)小红和小力各有8、2、5三张数字卡片,每人拿出1张,一共有()种不同的拿法。
A.9种B.6种C.5种5.(2021·安徽六安·三年级期末)笑笑的衣柜里有2件上衣和3条裤子,若1件上衣和1条裤子搭配成一套衣服,有()种不同的搭配方法。
A.4B.5C.66.(2022·辽宁·三年级)用30根1米长的木条围成一个长方形菜地,有()不同的围法,面积最大是()。
A.7种;56平方米B.6种;56平方米C.6种;58平方米D.7种;58平方米7.(2022·江苏淮安·五年级期末)小宁从家到少年宫(如图),如果只允许向东或向北走,一共有()种不同的路线。
A.4B.5C.6D.7 8.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学五年级期末)把16分成两个单数的和,一共有()中不同的分法。
(两个加数相同的,算一种分法)A.3B.4C.5D.6二、填空题9.(2022·江苏·南京市江北新区浦口实验小学浦园路分校五年级期末)江北新区有32支小学男子足球队参加比赛,比赛采取淘汰制进行。
五年级上册数学专项练习解决问题的策略 苏教版

五年级上册数学专项练习解决问题的策略苏教版
第 2 页
第 3 页
发车的时间是几时?
1路车6:
00
6:
15
6:
30
2路车6:
10
6:
30
5.小王、小李和小华是好朋友,春节前,他们每两人之间互相寄一张贺卡,一共要寄多少张贺卡?
6.一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6环。
小明投中2次,可能得多少环?
7.用2、4、8这三张数字卡片一共能组成多少个不同的三位数?用2、4、0这三张数字卡片呢?
8.小芳有2枚1元的邮票,1枚0.8元的邮票。
用这些邮票能付多少种不同的邮资?
9.到早餐店吃早餐,有包子、油条、馒头三种早点供选择,最少吃一种,最多吃三种,有多
第 4 页
少种不同的选择方法?
10.用36个1平方厘米的正方形拼成长方形(或正方形),有多少种不同的拼法?它们的周长各是多少?算出结果填在表中。
长/厘
米
宽/厘
米
周长/
厘米
11.从红桃4、红桃5、红桃6、红桃7这4张扑克牌中选出2张,有多少种不同的选法?选出的两张扑克牌上数的和,一共有几种?12.如图,小敏从家到学校,只向北或向西走,走到学校,一共有多少种走法?
13.下图中一共有多少个正方形?
第 5 页
14.小华和小丽各有4、6、7三张数字卡片,每人拿出1张,一共有多少种不同的拿法?
第 6 页。
苏教版 五年级上册数学解决问题的策略专项练习

解决问题的策略——假设法一、填空1.如果△+△+△=○,那么○+○+○=()个△,△+△+△+○相当于()个△或者()个○。
2.如果1只兔的重量相当于2只鸡的重量,那么6只鸡相当于()只兔的重量,8只兔的重量相当于()只鸡的重量。
10只鸡和10只兔的总重量相当于()只鸡或()只兔的重量。
3.如果1只小兔的重量相当于一只小狗的1,那么3只小狗的重量相当于()只小兔的重量;8只小兔2和3只小狗的重量相当于()只小狗的重量或者相当于()只小兔的重量。
4.如果1个梨比1个苹果重30克,那么5个梨比5个苹果重()克;如果把一堆水果中的4个苹果看作4个梨,总重要会()(填“增加”或“减少”)()克。
5.某味精厂11月份上旬生产的味精包装成400克一袋,共生产1200袋。
如果包装成100克一袋,那么可生产()袋。
6.一个玻璃杯的价格是一个保温杯的1,王叔叔买了10个玻璃杯和3个保温杯,所花的钱相当于()5个玻璃杯的钱,或()个保温杯的钱。
7.如果4袋味精的质量=2袋盐的质量,1袋盐的质量=1袋面粉的质量,那么一袋面粉的质量等于()4袋味精的质量。
8.2本笔记本的价钱与8本数学本的价钱相等,5本笔记本的价钱等于()本数学本的价钱。
9.商店里一文具组合包括一副尺子和一把圆规,售价3.9元。
其中圆规的价格比尺子贵1.1元,圆规售价()元,尺子售价()元。
10.快餐店里一个汉堡、一杯饮料和两个蛋黄派,一共25元。
汉堡的单价是饮料的3倍,饮料的单价是蛋黄派的2倍,那么,汉堡的单价是()元,蛋黄派的单价是()元。
11.张大爷家养了4头牛和12头猪,如果1头牛的重量相当于3头猪的重,那么这些牛和猪的总重量相当于()头牛的重量,或者相当于()头猪的重量。
12.小明和小华出同样多的钱买一箱苹果,结果小明拿了8千克,小华拿了12千克,这样,小华就要给小明12元,苹果的单价是()元。
13,小汤身上的钱可以买12支铅笔或4 块橡皮,她先买了3支铅笔,剩下的钱可以买橡皮()块。
苏教版数学五年级上册第七单元(解决问题的策略)测试卷1

第七单元解决问题的策略一、填空。
(第2题5分,其余每空2分,共27分)1.从1~12这12个自然数中,每次取两个数,要使它们的和等于13,共有()种不同的取法。
2.下面的数可以写成哪两个自然数的乘积?在括号里填一填。
15=()×()=()×()18=()×()=()×()=()×()3.张军、王明、陈芳3人排成一排照相,一共有()种不同的排法;如果从这三人中每次选2人排在一起照相,一共有()种不同的排法。
4.如图,张大爷准备用20米长的篱笆围一块长方形菜地。
要使长和宽都是整米数,有()种不同的围法,围成菜地的面积最大是()平方米。
5.如图,星期天,小芳从家到图书馆看书。
如果只是向西、向南走,一共有()种不同的路线。
6.从下面的五张数字卡片中选出两张,有()种不同的选法;选出的两张数字卡片上数的和,一共有()种。
7.学校组织了艺术、象棋和体育三个兴趣小组,王芳参加了其中的一个或几个,有()种不同的参加方法。
8.有5个小朋友,如果他们每两人之间互相通一次电话,一共要通()次电话;如果他们每两人之间互相寄一张明信片,一共要寄()张明信片。
二、判断。
(对的画“√”,错的画“×”)(5分)1.用0、4、9这三个数字能组成6个不同的三位数。
()2.4名小朋友每两人互相握一次手,一共握了8次手。
()3.4名小学生下象棋,每两人都要下一局,一共要下8局。
()4.底和高都是整厘米数,面积是12平方厘米的平行四边形有4个。
()5.小明、小刚、小芳三人互相发一份邮件,一共要发3份邮件。
()三、选择。
(将正确答案的序号填在括号里)(10分)1.小林从家经过学校去公园,一共有()条路可以选择。
A.3B.5C.6D.72.购买右面球类,最少购买2种,最多购买3种,有()种不同的购买方法。
A.3B.4C.5D.63.一个音乐钟,每隔一段相等的时间就会发出铃声。
已知上午7:00、7:45、8:30、9:15发出铃声,那么在()也会发出铃声。
五年级数学上册第七单元第1课时解决问题的策略(1)课时作业(含答案)

第七单元解决问题的策略1.解决问题的策略(1)【基础堂堂清】1. 小军有红、黄、蓝3件不同颜色的上衣和蓝、黑2条不同颜色的裤子。
一件上衣搭配一条裤子。
其有多少种不同的搭配方法?(先填表,再回答)上衣颜色裤子颜色2.佳佳的爸爸是火车司机,每工作3天休息1天。
佳佳的妈妈是空中乘务员,每工作1天休息1佳佳周一至周五上学,周六、日休息。
9 月1日(周四)佳佳的爸爸妈妈都开始工作,到这个月10日,哪几天是爸爸的休息日?哪一天三人同时休息?(先在下表里画一画,再回答)周四周五周六周日周一周二周三周四周五周六日期佳佳爸爸妈妈3.田田去文具店买橡皮。
小橡皮每块1元,大橡皮每块2元,她一共买了6块橡皮,所花的钱数有几种情况?4.(开放题)如图,王大爷要用15根1米长的栅栏靠墙(墙足够长)围一个长方形羊圈。
围成的长方形羊圈的长与宽都取整米数,有多少种不同的围法?怎样围羊圈的面积最大?【能力素养练】5.张老师要把42个球装在盒子里,每个小盒子可以装4个,每个大盒子可以装6个。
如果每个盒子都要装满,共有多少种不同的装法?【知识归纳】用一一列举的策略解决实际问题,要做到不重复、不遗漏,同时要对列举出的结果进行比较,做出选择。
参考答案:1.答:一共有6种不同的搭配方法。
2.答:9月4日、8日是爸爸的休息日,9月4日三人同时休息。
3.6x1=6(元)5x1+1x2=7(元)4x1+2x2=8(元)3x1+3x2=9(元)2x1+4x2=10(元)1x1+5x2=11(元)6x2=12(元)答:所花的钱数有7种情况。
4.答:有7种不同的围法,当与墙相对的栅栏长7米时,羊圈的面积最大。
点拨:用一一列举的策略解决。
注意 15 x1 =15 米是长方形三条边的长度和。
5.答:共有4种不同的装法。
解析:用一一列举的方法找出所有答案:7个大盒子;5个大盒子和3个小盒子;3个大盒子和6个小盒子;1个大盒子和9个小盒子。
故共有4种不同的装法。
苏教版小学五年级数学上册《解决问题的策略》测试卷(含答案)

苏教版小学五年级数学上册《解决问题的策略》测试卷(含答案)第七单元测试卷一、填空题。
1.到某早餐店吃早餐,有包子、烧卖、烧饼三种早点供选择。
最少吃一种,最多吃两种,有(4)种不同的选择方法。
2.五年级5个班举行篮球比赛,每两个班都要比赛一场,一共需要比赛(10)场。
3.有红、黄、绿三种颜色的小旗各一面,从中选用一面或两面升上旗杆,分别用来表示一种信号。
一共可以表示(4)种不同的信号。
4.一种面包有2块装和3块装两种不同规格的包装。
妈妈要购买18块面包,一共有(7)种不同的选择方法。
5.新客站是1路和2路公交车的起始站,1路车每隔10分钟发一辆,2路车每隔15分钟发一辆,1路车和2路车都是早晨7:00发车,这两路车再次同时发车是(7:30)。
二、选择题。
(把正确答案的序号填在括号里)1.用2、4、6这三个数,一共可以组成(C)个不同的两位数。
A.2B.4C.6D.72.旅游团19人到旅馆住宿,住3人间和2人间(每个房间不能有空床位),共有(D)种不同的安排。
A.2B.3C.4D.53.盒子里装有1~6六张数字卡片各两张,每次摸出两张卡片,两个数字的和不可能是(A)。
A.12B.10C.2D.14.有1克、2克、5克的砝码各一个,选其中的一个或几个,能在天平上称出(C)种不同质量的物体。
A.4B.5C.6D.7三、先将下面的表格填写完,再回答问题。
五(1)班第1小组有3名男生和3名女生,老师打算从中选出1名男生和1名女生担任星期一的值日班长,一共有(9)种不同的选法。
3名男生用甲、乙、丙代替,3名女生用A、B、C代替。
甲甲甲乙乙乙丙丙丙A B C四、计算题。
1.直接写得数。
0.7+0.3=10.52+0.48=12.5-0.5=22.4+0.6=31.8-0.4=1.41-0.65=0.350.97-0.7=0.279.17+1.83=112.用简便方法计算。
5.8+0.98+0.02=6.8 8.53-(0.89+2.53)=5.11 3.85+0.9-0.85=3.9 21.7-2.8-7.2=11.7 12.4-7.65+7.69=12.44 9.9+0.1-0.9+0.1=9.2五、解决问题。
苏教版五年级上册数学第七单元《解决问题的策略》单元测试卷(含答案)

苏教版五年级上册数学第七单元《解决问题的策略》单元测试卷(含答案)一、填空。
(每空3 分,共33 分)1.一列从上海开往南京的特快列车,途中要停靠3 个站,铁路部门要为这列车准备( )种不同的单程车票。
2.周末,小芳一家想去壶口瀑布、云丘山、洪洞大槐树观光游玩,他们一共有( )种不同的游玩顺序。
3.2022 年4 月1 日是星期五,则2022 年5 月1 日是星期( )。
4.若每两人要握手1 次,则5 人共需握手( )次。
5.丽丽要用20 根同样长的火柴摆一个长方形或正方形,她有( )种不同的摆法。
6.一只蚂蚁在如图所示的平面上爬行,如果只能向右或向上爬行,从A点爬行到B 点有( )种不同的路线。
7.从1 ~ 10 这10 个数中,每次取两个数使它们的和大于10,一共有( )种不同的取法。
8.小刚是2014 年出生的,那年是马年,当小刚10 周岁时他的属相是( ),这一年是( )年。
(填十二生肖)9.小红说:“我比你小。
”小丽说:“咱俩的年龄都超过了5 岁,且和是14 岁。
”小红( )岁,小丽( )岁。
二、选择。
(将正确答案的字母填在括号里)(每小题2 分,共18 分)1.用0、3、8 三个数字可以组成( )个不同的三位数。
A.4 B.5 C.6 D.72.明星小学每天8:00 上课,每节课40 分钟,课间休息10 分钟,上午共上4 节课,上课、下课都会响铃,在下面的时刻中,会响铃的是( )。
A.9:10 B.10:00 C.10:30 D.11:003.右图中一共有( )个正方形。
A.16 B.30C.17 D.214.红红想从书法小组、象棋小组、音乐小组、美术小组4 个兴趣小组中选择2 个报名参加,她有( )种不同的选择。
A.6 B.9 C.12 D.115.新华小学红领巾广播站有3 个女播音员和3 个男播音员,每天必须安排一男一女两个播音员,一天共有( )种不同的安排方法。
A.12 B.11 C.9 D.66.学校组织篮球比赛,五年级一共有5 个班参加。
五年级数学(上册)解决问题的策略(列举)练习(3)

五年级数学(上册)解决问题的策略(列举)练习(3)班级姓名成绩
1.小明玩投靶游戏,打靶纸上共有三个圈,投中内圈得10环,投中中
圈得8环,投中外圈得6环。
他共投了3次,他可能得到哪几种环数?
2.从红桃4、红桃5、红桃6、红桃7这4张扑克牌中选出2张,有多少
种不同的选法?选出的两张扑克牌上数的和,一共有几种?
3.有6支篮球队参加篮球比赛,如果每两支球队要赛一场,那么一共要
赛()场。
4.甲、乙、丙、丁和小强进行围棋比赛,每两人之间都比一盘,甲已经
比了4盘,乙比了3盘,丙比了1盘,丁比了2盘,小强比了多少盘?分别是和谁比的?
5.袋子里有红球、黄球、蓝球各两个,小红从袋子里任取两个球,一共
有多少种不同的取法?
6.一辆火车往返于A、B两地,沿途经过C、D、E、F四个站,需要准备多少种不同的车票?
7.从甲地到乙地,中途共有5个小站,每站都有乘客上下车,一辆汽车往返于甲乙两地,需要准备多少种不同的车票?
8.两个自然数相乘,积是48的乘法算式有()个。
9.两个自然数的和是12,那么这两个自然数的积可能是多少?。
苏教版五年级上册数学《解决问题的策略》练习附答案

苏教版五上《解决问题的策略》练习附答案1、丹丹的家和学校位置如下图。
上学了,丹丹要去学校。
如果只允许向东走或向北走,一共有多少种不同的路线?2、用20根1厘米的小棒围成一个长方形,有多少种分发?怎么分的?怎样分长方形的面积最大?3、明明、冬冬和艳艳初次见面,他们每两个人要握一次手,一共要握多少次?4、用1、8、9三张数字卡片可以组成多少个三位数?不可以重复使用。
5、两个自然数相乘,积是48的乘法算式有多少个?参考答案:1、152、5 种边长分别为1 9,2 8,3 7,4 6,5 5 长和宽相等面积最大3、34、65、5《解决问题的策略》习题1、直接写得数。
0.35×100=85÷10=1.3+0.7=3.2-2.8=27÷0.3=0.3×0.04=2、周五放学后,冬冬和明明相约回家拿玩具一起玩耍,冬冬有4个玩具,明明有5个玩具,如果他们每人只带1个,一共有多少种不同的可能?3、用24个边长1厘米的正方形拼成长方形,有多少种不同的拼法?4、下图中有多少个正方形和三角形?参考答案:1、0.35×100=35 85÷10=8.5 1.3+0.7=23.2-2.8=0.4 27÷0.3=90 0.3×0.04=0.0122、203、44、5个正方形和10个三角形《解决问题的策略》习题31、选择题。
(1)芳芳、欢欢、笑笑、乐乐四位同学进行乒乓球友谊赛,每两人都要比赛一场,一共要比赛()场。
A.4B.6C.8(2)王明给在外地工作的爸爸寄一封挂号信,需要贴2元的邮票。
如果只有5角、2角和1角三种面值的邮票,一共有()种不同的贴法。
A.29B.12C.15(3)从0、5、7三个数字中选出1个、2个或3个数字进行组合,可以得到()个不同的数。
A.11B.9C.102、用1元、5元和10元的人民币各一张,能组成多少种不同数额不同的人民币?3、用16根长度是1分米的小棒围成长方形或正方形,有多少种不同的围法?它们的面积各是多少?摆一摆,算出不同的结果填在下表中。
人教版2022-2023学年小学数学五年级上册专项提升练习(解决问题的策略)含解析

人教版2022-2023学年小学数学五年级上册专项提升练习(解决问题的策略)一、选择题1.书架上有4本不同的故事书和3本不同的科技书,小明从中取出故事书和科技书各1本,有()种不同的取法。
A.7B.4C.3D.122.用0、3、7各一个可以组成()个不同的三位数。
A.3B.4C.63.有1元、2元、5元和10元人民币各1张,任意取2张,可以有()种不同的取法。
A.4B.6C.10D.144.某小学2017年9月3日正式上课,这一天是星期一,星期六和星期天不上课,那么这个月该小学一共上了()天课。
A.19B.20C.21D.225.用栅栏围成一个长12米宽4米的长方形苗圃,如果不增加栅栏,要使面积扩大的方法是()。
A.减长增宽B.增长减宽C.不可能D.增长增宽6.一根铁丝长18厘米,把它围成长和宽都是整数厘米的长方形,围成的长方形面积最大是()平方厘米。
A.14B.18C.20D.247.芳芳和玲玲玩游戏。
每人每次出1,2,3三个数字中的一个。
如果两人出的数字相加。
和是奇数就算芳芳赢,和是偶数就算玲玲赢。
那么芳芳赢的可能性与玲玲相比、结果怎样?()A.比玲玲小B.比玲玲大C.和玲玲相等D.无法确定谁赢的可能性大8.4个素菜和2个荤菜要配成一荤一素,一共有()种不同的配菜方法。
A.8B.6C.10二、填空题9.用2张10元、2张20元的钞票,可以组成()种不同的钱数。
10.小明口渴了,有果汁、可乐、矿泉水三种饮料选择。
最少选一种,最多选两种,有()种不同的选择方法。
11.小红用0、7、5这三张数字卡片,可以摆出()个不同的三位数。
其中最大的与最小的相差()。
12.有5支球队参加比赛,如果每两支球队比赛一场,那么一共要比赛()场。
13.一列火车在淮安、南通两个城市之间运行,沿途停靠盐城、海安、东台这三个站。
一共要为这列火车准备()种不同的火车票。
14.三位同学进行100米赛跑,比赛结果可能会有()种不同的情况(三个同学的名次不并列);如果他们三位同学进行乒兵球比赛,每两人都要比赛一场,一共要赛()场。
(完整)苏教版五年级数学上册解决问题的策略练习题
苏教版五年级数学上册解决问题的策略练习题
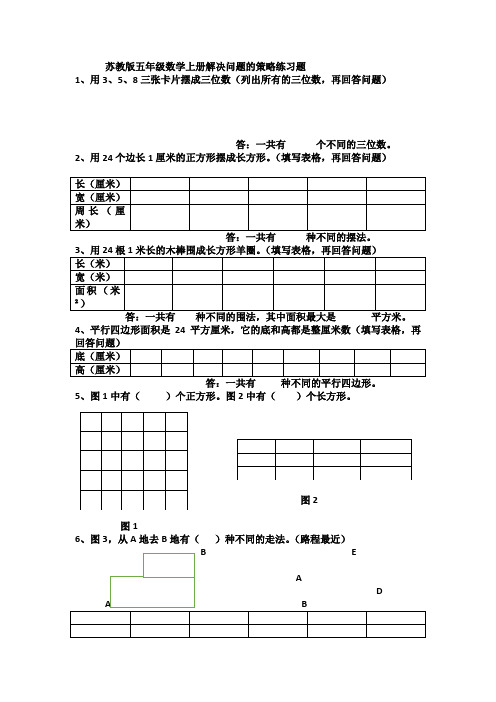
1、用3、5、8三张卡片摆成三位数(列出所有的三位数,再回答问题)
答:一共有 个不同的三位数。
2、用24个边长1厘米的正方形摆成长方形。
(填写表格,再回答问题)
4、平行四边形面积是24平方厘米,它的底和高都是整厘米数(填写表格,再
5、图1中有( )个正方形。
图2中有( )个长方形。
图2
图1
6、图3,从A 地去B 地有( )种不同的走法。
(路程最近)
B E
A
D
C
图3 图4
7、图4,ABCDE五个人每两个人通电话一次,一共要通()次,在图中连一连。
8、□.□×□=3.6,一共有()个不同的算式(列出所有的算式)
9、有20个篮球队进行淘汰赛,进行()场,决出冠军。
10、一路车每隔10分钟发车一次,2路车每隔8分钟发车一次,两车6:00同时
2.4×10.1 0.25×4.4
3.75—1.63—1.37 5.4÷1.2
3.5×0.65+0.35×3.5 1.25×9.7—1.25×1.7 2.5×1.6×1.25
12、脱式计算
10.8﹣0.8÷(0.35+0.05)8×[1÷(2.3﹣2.25) 5.4÷[0.51÷(1.2﹣1.03)] [(8.1﹣5.6)×0.9﹣1.05]÷0.04 5.4÷[2.5×(3.7﹣2.9)]。
苏教版 五年级上册数学解决问题的策略专项练习

解决问题的策略——假设法一、填空1.如果△+△+△=○,那么○+○+○=()个△,△+△+△+○相当于()个△或者()个○。
2.如果1只兔的重量相当于2只鸡的重量,那么6只鸡相当于()只兔的重量,8只兔的重量相当于()只鸡的重量。
10只鸡和10只兔的总重量相当于()只鸡或()只兔的重量。
3.如果1只小兔的重量相当于一只小狗的1,那么3只小狗的重量相当于()只小兔的重量;8只小兔2和3只小狗的重量相当于()只小狗的重量或者相当于()只小兔的重量。
4.如果1个梨比1个苹果重30克,那么5个梨比5个苹果重()克;如果把一堆水果中的4个苹果看作4个梨,总重要会()(填“增加”或“减少”)()克。
5.某味精厂11月份上旬生产的味精包装成400克一袋,共生产1200袋。
如果包装成100克一袋,那么可生产()袋。
6.一个玻璃杯的价格是一个保温杯的1,王叔叔买了10个玻璃杯和3个保温杯,所花的钱相当于()5个玻璃杯的钱,或()个保温杯的钱。
7.如果4袋味精的质量=2袋盐的质量,1袋盐的质量=1袋面粉的质量,那么一袋面粉的质量等于()4袋味精的质量。
8.2本笔记本的价钱与8本数学本的价钱相等,5本笔记本的价钱等于()本数学本的价钱。
9.商店里一文具组合包括一副尺子和一把圆规,售价3.9元。
其中圆规的价格比尺子贵1.1元,圆规售价()元,尺子售价()元。
10.快餐店里一个汉堡、一杯饮料和两个蛋黄派,一共25元。
汉堡的单价是饮料的3倍,饮料的单价是蛋黄派的2倍,那么,汉堡的单价是()元,蛋黄派的单价是()元。
11.张大爷家养了4头牛和12头猪,如果1头牛的重量相当于3头猪的重,那么这些牛和猪的总重量相当于()头牛的重量,或者相当于()头猪的重量。
12.小明和小华出同样多的钱买一箱苹果,结果小明拿了8千克,小华拿了12千克,这样,小华就要给小明12元,苹果的单价是()元。
13,小汤身上的钱可以买12支铅笔或4 块橡皮,她先买了3支铅笔,剩下的钱可以买橡皮()块。
苏教版五年级数学上册解决问题的策略练习题及答案1

解决问题的策略(1)物以类聚,人以群分。
《易经》如海学校陈泽学开心预习新课,轻松搞定基础。
1. 红领巾广播站有2名男播音员和3名女播音员,每次必须安排一男一女,一共有多少种不同的安排方法?(先填好表,再算出有多少种安排法。
)重难疑点,一网打尽。
2. 小红用20根1分米长的小棒,围成一个长方形,有多少种不同的围法?(1)用列表的方法把长和宽列举出来。
(2)算出围成的每个长方形的面积,并比较它们的长、宽和面积,你有什么发现?3.到早餐店吃早餐,有包子、油条、馒头三种早点供选择,最少吃一种,最多吃三种,有多少种不同的选择方法?源于教材、宽于教材、拓展探究显身手。
4. 周长是50米的长方形,当长是16米时,宽是( )米,面积是( )平方米;当宽是5米时,长是( )米,面积是( )平方米。
5. 用36个1平方厘米的小正方形拼成长方形,有多少种不同的拼法?它们的周长各是多少?拼一拼,算出结果,填在下面的表中。
6 解决问题的策略第1课时1. 表略6种2. 略3. 7种提示:分别为:①包子;②油条;③馒头;④包子、油条;⑤包子、馒头;⑥油条、馒头;⑦包子、油条、馒头。
4. 9 144 20 1005. 略【素材积累】从诞生的那一刻起,我们就像一支离弦的箭,嗖嗖地直向着生命的终点射去。
但我们无论怎样地气喘吁吁疾步如飞,也赶不上岁月那轻捷的步履。
她无声无息波澜不惊地带走纷沓的人群,卷走一个又一个朝代,不在世界的任何一个角落停留,也不在心的重重羁绊前稍一驻足。
无论历经了多少沧海桑田的变迁,她永远年轻、纯洁、轻盈、清澈如初。
时光不老人易老。
穿行在一片又一片洁白的日子里,我们可曾朝涂曦霞,暮染烟岚,在她的脉络里注进拼搏的汗水,把每一页洁白的日子都涂成一幅斑斓的图画,剪成一贴丰满的记忆?穿行在一片又一片洁白的日子里,我们可曾删繁就简,除去芜杂的枝蔓,抖落发黄的往事,省略多余的情节,向着既定的目标轻装向前。
苏教版小学五年级数学上册第7单元解决问题的策略单元测试题(附答案)

苏教版小学五年级数学上册第7章解决问题的策略单元测试题一.选择题(共10小题,满分20分,每小题2分)1.(2分)小强观察一个建筑物模型(由若干个相同的小正方体拼成),分别从前面,右面,上面观察,看到的图案如图所示,那么该模型共由()个小正方体拼成.A.8B.9C.10D.112.(2分)10张连号的世博园如愿券,张老师一家人要拿3张连号的,共有()种不同的拿法.A.6B.7C.83.(2分)如图,五个正方形重叠,连结点正好是正方形的中点,正方形的边长都是a,如图的周长是()A.24a B.18a C.14a D.12a.4.(2分)在下面的数表中,每次框出2个数,一共有()种不同的和.2345678910111213A.12B.11C.10D.95.(2分)有15个连续的自然数,每次用长方形框出4个连续的自然数,一共有()种不同的框法.A.10B.11C.126.(2分)在下面的月历卡中,用“十”字形框5个数,共可以框出()个不同的和.A.14B.15C.10D.117.(2分)用形如的框在图中去框,一共有()种不同的框法.A.12B.18C.248.(2分)如图,每次框出连续的3个数,共可得到()个不同的和.A.27B.28C.29D.309.(2分)在表方框里的两个数的和是3.移动这个方框,可以使每次框出的两个数的和各不相同.一共可以得到()个不同的和.12345678910 A.3B.40C.10D.910.(2分)在百数表中,用三连方(如图)盖住了三个数字,这三个数字之和可能是()A.69B.100C.105D.130二.填空题(共9小题,满分12分)11.(1分)如图是某年某月的月历,认真观察阴影部分五个数的关系.想一想:如果像这种形式的五个数的和为105,则中间的那个数是.12.(1分)在如图中,每次框出连续4个自然数,共可得到个不同的和.13.(2分)如图是2013年8月的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数.框出的3个数和最大的是,一共可以框出种不同的和.14.(1分)在1、2、3、4、5、6、7、8中,每次选出4个连续的数求和,一共可以有种不同的和.15.(1分)如图是一条带花的彩带.如果剪3朵花连在一起的彩带,一共有不同的剪法.16.(2分)如图是小林卧室一面墙上贴的瓷砖,中间块组成了一个图案.在保持组合图案不变的情况下,有种不同贴法.17.(1分)今年“国庆七日长假”,明明想参加“西湖两日游”,哪两日去呢,他共有不同的选择.18.(2分)在下表中每次框出2个相邻的数,一共可以得到个不同的和;如果每次框出3个相邻的数,一共可以得到个不同的和.12345678910 19.(1分)下面一排圆圈共有15个,如果要给相邻的4个涂上红色.一共有种不同的涂法.三.操作题(共6小题,满分30分,每小题5分)20.(5分)如图是2010年5月的台历.(1)小明的爸爸每上4天班休息一天,妈妈却是上3天班休息一天,5月2日爸爸、妈妈都在家休息,下一次他们同时在家休息是星期.(2)算一算,上表中被阴影覆盖的5个数的和与中间的数有什么关系?(计算后再说明)(3)如果框出的5个数的和是75,那么这5个数分别是多少,在图中框出来.(4)一共可以框出个不同的和.21.(5分)如图是2008年1月的月历表,表中用“十”字框每次框出5个数(不能少框).(1)用“十”字框任意框几次,框中5个数的和是正中间一个数的倍.(2)如果“十”字框正中间一个数为x,5个数的和为90,那么x的值是.22.(5分)下面的每一个图形都是由中的两个构成的.观察各个图形,根据图下表示的数,找出规律,画出表示31的图形.23.(5分)根据前三幅图的变化规律画出第四幅图.24.(5分)算一算,框一框.(1)用长方形在上面的月历卡上框出三个数,使这三个数的和等于48.(2)用正方形框出9个数,使这九个数的和等于99.25.(5分)(1)图是2008年10的月历卡,用形如的长方形去框月历卡里的日期数,每次同时框出3个数,框出的3个数的和最大是,最小是,一共可以框出种不同的和.(2)请你用框出和是87的3个数.四.解答题(共7小题,满分38分)26.(5分)将1﹣1001的自然数按如表方式排列,用一个方框框出九个数,要使这九个数的和等于2007或2008,你能否办到?如果你能请分别写出这个方框中的最大数和最小数.A当这九个数的和是2007时,能否办到,如果能方框中最大数是,最小数是;B当这九个数的和是2008时,能否办到,如果能方框中最大数是?最小数是?27.(5分)日历的规律:认真观察如图阴影方框中正中间的数与其他4个数的关系.(1)中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是,下面的数是.(2)方框中5个数之和与该方框中间的数有什幺关系?(3)当5个数的和是80时,中间的数是多少?28.(5分)仔细观察如图,任意框出四个数,请将表格中其余三个数用含有字母的式子表示出来.如果框出的四个数的和是84,那么这四个数分别是多少?29.(6分)表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.(1)你能发现每次框出的5个数的和与中间数有什么关系吗?(2)如果框出5个数的和要是375,应该怎么框?(先在图中框一框,并在下面用文字说明)(3)能框出和是295的5个数吗?为什么?(4)一共可以框出多少个大小不同的和?30.(5分)下表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同.(1)一共可以框出多少个不同的和?(2)能框出和是64的三个数吗?为什么?31.(6分)探索与实践:认真观察月历表的规律,如图阴影方框中正中间的数与其他四个数的关系.(1)正中间的数是y,左边的数是,右边的数是,上面的数是,下面的数是.(2)方框中5个数之和与该方框正中间的数有什么关系?(3)当5个数的和是115时,正中间的数是.32.(6分)如图是一张4×4的方格图,它由16个小正方形组成,每个小正方形里都写了一个数.(1)在这个方格图上框出形,那么框出的4个数的和一共有多少种?其中和最大是多少?最小呢?(2)在这个方格图上框出形,那么框出的5个数的和一共有多少种?每5个数的和一定是15的倍数吗?为什么?参考答案与试题解析一.选择题(共10小题,满分20分,每小题2分)1.解:通过观察与想象知道该模型共由9个小正方体拼成.即3+2+1+1+2=9(个).故选:B.2.解:给这10张如愿券编号为1~10,只有第9、10号不能放在开头,所以一共有:10﹣2=8(种);答:共有8种不同的拿法.故选:C.3.解:3a+3a+2a×3=12a,答:这个图形的周长是12a.故选:D.4.解:数字数:13﹣2+1=12(个)不同的和数:12﹣2+1=11(个)答:一共有11种不同的和.故选:B.5.解:相邻的4个数有15﹣4+1=12种情况,则有12种不同的和,即一共有12种不同的框法.故选:C.6.解:观察图形可知:中间数只能在第二、三、四行,而且中间数的上下左右必须有数,那么:第二行的中间数可以是:8,9,10,11;第三行的中间数可以是:14,15,16,17,18;第四行的中间数可以是:21;一共有4+5+1=10(个);有10个不同的中间数,就有10个不同的和.故选:C.7.解:由分析得出:不同的框法有:6×4=24(种).答:一共有24种不同的框法.故选:C.8.解:31﹣2=29(个).答:共可得到29个不同的和.故选:C.9.解:10﹣1=9(中);答:一共可以得到9个不同的和.故选:D.10.解:根据题干分析可得:14+23+32=69答:这三个数字之和可能是69.故选:A.二.填空题(共9小题,满分12分)11.解:因为像这种形式五个数的和是105,那么五个数的和是中间的数的5倍,所以中间的数是:105÷5=21,即中间的那个数是21.故答案为:21.12.解:40﹣2+1﹣3=39﹣3=36故共可得到36个不同的和.故答案为:36.13.解:29+30+31=59+31=901+5×4=21(种)答:框出的3个数和最大的是90,一共可以框出21种不同的和.故答案为:90,21.14.解:依次选出4个连续的数可以为:1、2、3、4;2、3、4、5;3、4、5、6;4、5、6、7;5、6、7、8.所以每次选出4个连续的数求和,一共可以有5种不同的和.故答案为:5.15.解:8﹣2=6(种)答:一共有6种不同的剪法.故答案为:6种.16.解:贴法如下图:(11﹣3+1)×(6﹣2+1)=9×5=45(种)答:在保持组合图案不变的情况下,有45种不同的贴法.故答案为:6,45.17.解:明明可以选择以下的两天去旅游:10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日;共6种选择.故答案为:6种.18.解:根据题干分析可得:(1)如果每次框出2个数,可以得到9个不同的和.(2)如果每次框出3个数,可以得到8个不同的和.故答案为:9,8.19.解:15﹣4+1=12(种);答:一共有12种不同的涂法.故答案为:12.三.操作题(共6小题,满分30分,每小题5分)20.解:(1)5和4是互质数,所以5和4的最小公倍数是:5×4=20,所以5月2日,他们同时休息,那么下一次他们同时休息是:2+20=22,即5月22日,星期六;(2)上表中被阴影覆盖的5个数和是:11+17+18+19+25=90;90÷18=5,所以这5个数的和是中间的数的5倍;(3)因为这5个数的和是中间的数的5倍,所以中间数是75÷5=15,则框出的5个数为:8、14、15、16、22;如图:(4)1+5×2=11(个)所以,一共可以框出11个不同的和.故答案为:六、11.21.解:(1)1+7+8+9+15=40=8×52+8+9+10+16=45=9×53+9+10+11+17=50=10×5所以可得:框出的5个数的和是中间数的5倍.(2)90÷5=18答:x的值是18;故答案为:5,18.22.解:31由圆和平行四边形组成,且圆大,平行四边形小,如图:23.解:根据图形的旋转规律,如图:24.解:(1)48÷3=16,这三个数分别是15、16、17(用红色长方形框出).(2)99÷3÷3=11,即这九个数中间的一个数是11,这九个分别是:3、4、5、10、11、12、17、18、19(用绿色正方形框出).25.解:(1)29+30+31=901+2+3=62+5+5+5+4=21(种)答:框出的3个数和最大的是90,最小是6,一共可以框出21种不同的和.(2)87÷3=29,中间的数是29,前一个数是28,后一个数是30,所以:故答案为:90,6,21.四.解答题(共7小题,满分38分)26.解:设方框内最小的数(左上角)为a,则框内的九个数可分别表示为:a,a+1,a+2,a+7,a+7+1,a+7+2,a+7×2,a+7×2+1,a+7×2+2.它们的和是9a+7×3+7×2×3+(1+2)×3=9×(a+8).由于总和9×(a+8)是9的倍数,所以总和是2008不可能,只可能是2007.当方框内9个数的和是2007时,框内的最小数是2007÷9﹣8=215,最大数是215+7×2+2=231;答:方框中的最大数是231,最小数是215.故答案为:231,215.27.解:(1)由分析得出:中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是x﹣7,下面的数是x+7;(2)左边五个数的和是:7+13+14+15+21=70,70是中间的数14的5倍;右边五个数的和是:4+10+11+12+18=55,55是中间的数11的5倍;所以得出:方框中5个数之和是该方框中间的数的5倍;(3)中间的数都是:80÷5=16.答:中间的数是16.故答案为:(1)x﹣7;x+7;(2)方框中5个数之和是该方框中间的数的5倍;(3)中间的数是16.28.解:因为17+18+24+25=84,所以这四个数分别是17、18、24、25.29.解:(1)通过每次框出的5个数,发现:115÷23=5倍,所以5个数之和正好是中间数的5倍;(2)375÷5=75,框出的5个数的中间的数是75,所以框法为:(3)295÷5=59因为59在所给表的最右边,不能被框为中间的数,所以,不能框出和是295的5个数;(4)根据所给框的例子,知道23、25、27、29、31、33、35、37、及它们对应的下两行的数,都可以被框为中间的数,所以,一共可以框出大小不同的和的个数:8×3=24(个).答:一共可以框出24个大小不同的和.30.解:(1)1﹣29共有15个数字,每次框出3个数字,一共有15﹣2=13(种)框法,所以有13个不同的和.答:一共可以框出13个不同的和.(2)由题意可知框出的三个数的和是3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数.答:不能框出和是64的三个数.因为框出的三个数的和是3的倍数,因为64不是3的倍,所以不能框出和是64的三个是.31.解:(1)由分析得出:中间数是x,则左边的数是x﹣1,右边的数是x+1,上面的数是x﹣7,下面的数是x+7;(2)左边五个数的和是:7+13+14+15+21=70,70是中间的数14的5倍;右边五个数的和是:4+10+11+12+18=55,55是中间的数11的5倍;所以得出:方框中5个数之和是该方框中间的数的5倍答:方框中5个数之和是该方框中间的数的5倍.(3)中间的数都是:115÷5=23.答:当5个数的和是115时,正中间的数是23.故答案为:(1)y﹣1,y+1,y﹣7;y+7.32.解:(1)竖着有3种框法,横着有2种框法,一共有3×2=6种,即出的4个数的和一共有6种;最大是30+42+45+48=165最小是3+15+18+21=57(2)横着有2种框法,竖着也有2种框法,一共有2×2=4种框法,框出的5个数的和一共有4种;根据框中心数与周围数的关系,可得和是中心数的5倍,中心的数18、21、30、33都是3的整数倍,5×3=15,所以每5个数的和一定是15的倍数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学(上册)解决问题的策略(列举)练习
1.王大叔用20根1米长的木条围成一个长方形(或正方形)羊圈,有多少种不同的围
2.一个音乐钟,每隔一段相等的时间就发出铃声。
已经知道上午8:00、8:40、9:20、10:00发出铃声,那么下面哪些时刻也发出铃声?
11:00 12:00 13:20 14:20
3.两个自然数相乘,积是24的乘法算式有多少个?
4.公交公司是1路和2路公交车的起始站。
早上6时整1路车开始发车,以后每隔15分钟发一辆车,6时10分2路车开始发车,以后每隔20分钟发一辆车。
这两路车第二
5.小王、小李和小华是好朋友,春节前,他们每两人之间互相寄一张贺卡,一共要寄多少张贺卡?
6.一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6环。
小明投中2次,可能得多少环?
7.用2、4、8这三张数字卡片一共能组成多少个不同的三位数?用2、4、0这三张数字卡片呢?
8.小芳有2枚1元的邮票,1枚0.8元的邮票。
用这些邮票能付多少种不同的邮资?
9.到早餐店吃早餐,有包子、油条、馒头三种早点供选择,最少吃一种,最多吃三种,有多少种不同的选择方法?
10.用36个1平方厘米的正方形拼成长方形(或正方形),有多少种不同的拼法?它们的周长各是多少?算出结果填在表中。
长/厘米
宽/厘米
周长/厘米
11.从红桃4、红桃5、红桃6、红桃7这4张扑克牌中选出2张,有多少种不同的选法?选出的两张扑克牌上数的和,一共有几种?
12.如图,小敏从家到学校,只向北或向西走,
走到学校,一共有多少种走法?
13.下图中一共有多少个正方形?
14.小华和小丽各有每人拿出1张,一共有多少种不同的拿法?。
