《概率论与数理统计》习题答案(复旦大学出版社)第三章
概率论与数理统计(第三版)第三章课后答案
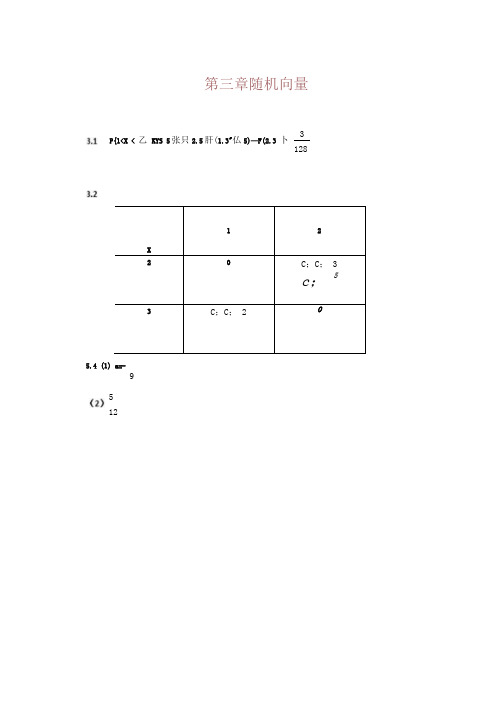
第三章随机向量X122C ;C ; 3c ; 53C ;C ; 25.4 (1) a=-95 12P{1<X < 乙 KYS 5张只2.5肝(1.3"仏5)—F(2.3 卜3 128<3)P{(X.r)eD}=f^『*6*必"制:[(6-〉”-討疗&T:(护-®+5討詁(护3+5”)|:=諾=善3.5 K: (1)y)工J: J:01 皿=f eP寸"血=(-<- UXr^ IS)=(1 -0X1 - 严)<2>P(rsx)= f:\f*如2严创;『dy =「2严(-八Qdx =J; 2宀(i十肚.j:(2宀》女肚=(・严3.6H: PC^ + JSa3.9B : x 術加HK 昨通»斤(0为:饴X>1 或xvOirL /(xj) = Op斤0) = [4.8>・(2-如=4 83[2*4门:*8川卜2》+黑计Zr(x) = O y > 或 <00<><1A(x) = f>.8y(2 “妙=2 妒(2-纠;=2*(2-x)©SOSxMl 时,/t (x) = | 4.8y(2-x>A =2 4y :(2-x)|r =2 4工(2・兀)3・7參见课本后面P227的答案3.8 f x (x) = J :/(x, >•>” J:訊如扌吟|:■专厶ox J :討法訐£ 'X0SXS2AW= 2* 0苴它/iO)h3>20<> <1 0其它Zr(x)h [(沖0<x<l=V2工+3°"幻3其它0 其它0<> <23 60< v<2其它 b 其它Y的血利K率密度跚齐3为:® 当或<0时尸/(x f>) = 0, /}(>) = 0②当0 Sg 时,力3 = f 4.8>(2-x>ft = 4 8>[2x-lr]|; = 4.8口1 卜2)+ £y2] =2.4>(3-4y+>:)MO (1〉券见课本石面P227的答案3 J2聲见课本后面P228的答案313 (1) 6x(17 0<x<l 0 其它0^x<l其它0<y<l其它311參见课本后面P228的答案【3+卸对TO<x<irt, A(x)>o2 5 X 她缘分布 1 0.15 0.250350.75 30.050.18 0.02 0.2S布0.2 0.430.371由表格可知 P{X-l;Y-2b0.29/:P{X.l}P{Y-2)-0.3225对于0<y<2时,/;(i)>0?0<x<l6x 2+ln0<x<lTT3 6 0 ■其它o+y其它-3-咖2卄犒h=2<+兰30 »JiX X故p^X=x)P{Y=y)所以X与Y不独立由鮭僚件P {X二工;丫二)[} "{工=卫尸{ Y=y)则P{X =2;K=2} = P{X = 2}P{Y = 2}P(X=2;r = 3) = P{X= 2}P{Y = 3}y;P{x=?}=iCO""30<x<2, 时,几(力齐(>)=4冷—/(兀“当x>2或x<OH,当)〉1 或y<o时,A(x)/iO) = o=/(x?j) 所以,x与Y之硼互独立・(訐(2〉衽3・9中,f x(x) =‘2.4三(2-力»0<x<l其它A(J)=2.4r(3-4v +y2)b 0^ v<l 其它3.16 B (J 在 3.8 中f x M= 2Io OSxS2其它AO) = <3y2 0<j ^16其它Xr(或40)二2・4疋(2-力2・4丿(3-4,+护)“・7&?(2-如3-令+小*/Uy),所以x与丫之冋不相5独NJ.17 解:二严=xe »)=匸心) f t(0=.匚fg 沁二 f* xe'(妇c以詁;芦希Z (x)/ o)=xe詁孑=fg >')故x与Y相歹檢立J・18聲见课本后面P228的答案。
概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
最新概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
《概率论与数理统计》习题及答案第三章

《概率论与数理统计》习题及答案第 三 章1.掷一枚非均质的硬币,出现正面的概率为p (01)p <<,若以X 表示直至掷到正、反面都出现时为止所需投掷次数,求X 的分布列。
解 ()X k =表示事件:前1k -次出现正面,第k 次出现反面,或前1k -次出现反面,第k 次出现正面,所以11()(1)(1),2,3,.k k P X k p p p p k --==-+-=2.袋中有b 个黑球a 个白球,从袋中任意取出r 个球,求r 个球中黑球个数X 的分布列。
解 从a b +个球中任取r 个球共有ra b C +种取法,r 个球中有k 个黑球的取法有kr kb aC C -,所以X 的分布列为()k r kb ara bC C P X k C -+==,max(0,),max(0,)1,,min(,)k r a r a b r =--+,此乃因为,如果r a <,则r 个球中可以全是白球,没有黑球,即0k =;如果r a >则r 个球中至少有r a -个黑球,此时k 应从r a -开始。
3.一实习生用一台机器接连生产了三个同种零件,第i 个零件是不合格品的概率1(1,2,3)1i p i i ==+,以X 表示三个零件中合格品的个数,求X 的分布列。
解 设i A =‘第i 个零件是合格品’1,2,3i =。
则1231111(0)()23424P X P A A A ===⋅⋅=, 123123123(1)()P X P A A A A A A A A A ==++123123123()()()P A A A P A A A P A A A =++111121113623423423424=⋅⋅+⋅⋅+⋅⋅=, 123123123(2)()P X P A A A A A A A A A ==++123123123()()()P A A A P A A A P A A A =++1211131231123423423424=⋅⋅+⋅⋅⋅+⋅⋅=,1231236(3)()23424P X P A A A ===⋅⋅=. 即X 的分布列为01231611624242424XP. 4.一汽车沿一街道行驶,需通过三个设有红绿信号灯的路口,每个信号灯为红或绿与其他信号灯为红或绿相互独立,且每一信号灯红绿两种信号显示的概率均为12,以X 表示该汽车首次遇到红灯前已通过的路口的个数,求X 的概率分布。
(完整版)概率论与数理统计习题答案详解版(廖茂新复旦版)

概率论与数理统计习题答案详解版(廖茂新复旦版)习题一1. 设A,B,C 为三个事件,用A,B,C 的运算式表示下列事件:(1)A 发生而B与 C 都不发生;(2)A,B,C 至少有一个事件发生;(3)A,B,C 至少有两个事件发生;(4)A,B,C 恰好有两个事件发生;(5)A,B至少有一个发生而 C 不发生;(6)A,B,C 都不发生.解:(1)A BC或 A B C或 A (B∪C).(2)A∪B∪C.(3)(AB)∪(AC)∪(BC).(4)(AB C )∪(AC B )∪(BC A).(5)(A∪B)C.(6) A B C 或ABC.2. 对于任意事件A,B,C,证明下列关系式:(1)(A+B)(A+B )( A + B)( A + B )= ;(2)AB+A B +A B+A B AB= AB;(3)A-(B+C)= (A-B)-C. 证明:略.3.设A,B为两事件,P(A)=0.5,P(B)=0.3,P(AB)=0.1,求:(1)A发生但B不发生的概率;(2)A,B 都不发生的概率;(3)至少有一个事件不发生的概率.解(1)P(A B )=P(A-B)=P(A-AB)=P(A)-P(AB)=0.4;(2) P(AB)=P( A B)=1-P(A∪B)=1-0.7=0.3;(3) P(A∪B)=P(AB )=1-P(AB)=1-0.1=0.9.4.调查某单位得知。
购买空调的占15%,购买电脑占12%,购买DVD 的占20%;其中购买空调与电脑占6%,购买空调与DVD占10%,购买电脑和DVD占5%,三种电器都购买占2%。
求下列事件的概率。
(1)至少购买一种电器的;(2)至多购买一种电器的;(3)三种电器都没购买的.解:(1)0.28, (2)0.83, (3)0.725.10 把钥匙中有 3 把能打开门,今任意取两把,求能打开门的概率。
解:8/156. 任意将10 本书放在书架上。
其中有两套书,一套 3 本,另一套4 本。
概率论与数理统计 修订版 (韩旭里 谢永钦 著)课后习题答案 复旦大学出版社

概率论与数理统计习题及答案习题一1. 略.见教材习题参考答案.2.设A ,B ,C 为三个事件,试用A ,B ,C 的运算关系式表示下列事件:(1)A 发生,B ,C 都不发生;(2)A 与B 发生,C 不发生;(3)A ,B ,C 都发生;(4)A ,B ,C 至少有一个发生;(5)A ,B ,C 都不发生;(6)A ,B ,C 不都发生;(7)A ,B ,C 至多有2个发生;(8)A ,B ,C 至少有2个发生.【解】(1)A (2)AB (3)ABC BC C (4)A ∪B ∪C =C ∪B ∪A ∪BC ∪A C ∪AB ∪ABC =AB A C BC A B C ABC(5)=(6)ABC A B C∪∪ABC (7)BC ∪A C ∪AB ∪C ∪A ∪B ∪==∪∪A B C AB BC A C ABC ABC A B C(8)AB ∪BC ∪CA =AB ∪A C ∪BC ∪ABC C B A 3. 略.见教材习题参考答案4.设A ,B 为随机事件,且P (A )=0.7,P (A −B )=0.3,求P ().AB 【解】P ()=1−P (AB )=1−[P (A )−P (A −B )]AB =1−[0.7−0.3]=0.65.设A ,B 是两事件,且P (A )=0.6,P (B )=0.7,求:(1)在什么条件下P (AB )取到最大值?(2)在什么条件下P (AB )取到最小值? 【解】(1)当AB =A 时,P (AB )取到最大值为0.6.(2)当A ∪B =Ω时,P (AB )取到最小值为0.3.6.设A ,B ,C 为三事件,且P (A )=P (B )=1/4,P (C )=1/3且P (AB )=P (BC )=0,P (AC )=1/12,求A ,B ,C 至少有一事件发生的概率.【解】P (A ∪B ∪C )=P (A )+P (B )+P (C )−P (AB )−P (BC )−P (AC )+P (ABC )=++−=141413112347. 从52张扑克牌中任意取出13张,问有5张黑桃,3张红心,3张方块,2张梅花的概率是多少?【解】p =5332131313131352C C C C /C 8. 对一个五人学习小组考虑生日问题:(1)求五个人的生日都在星期日的概率;(2)求五个人的生日都不在星期日的概率;(3)求五个人的生日不都在星期日的概率.【解】(1)设A 1={五个人的生日都在星期日},基本事件总数为75,有利事件仅1个,故P (A 1)==()5(亦可用独立性求解,下同)51717(2)设A 2={五个人生日都不在星期日},有利事件数为65,故P (A 2)==()5556767(3)设A 3={五个人的生日不都在星期日}P (A 3)=1−P (A 1)=1−()5179. 略.见教材习题参考答案.10.一批产品共N 件,其中M 件正品.从中随机地取出n 件(n <N ).试求其中恰有m 件(m ≤M )正品(记为A )的概率.如果:(1)n 件是同时取出的;(2)n 件是无放回逐件取出的;(3)n 件是有放回逐件取出的.【解】(1)P (A )=C C /C m n m n M N M N−−(2)由于是无放回逐件取出,可用排列法计算.样本点总数有种,n 次抽取中有mP n N 次为正品的组合数为种.对于固定的一种正品与次品的抽取次序,从M 件正C m n 品中取m 件的排列数有种,从N −M 件次品中取n −m 件的排列数为种,P m M P n m N M −−故P (A )=C P P P m m n m n M N M n N−−由于无放回逐渐抽取也可以看成一次取出,故上述概率也可写成P (A )=C C C m n m M N M n N−−可以看出,用第二种方法简便得多.(3)由于是有放回的抽取,每次都有N 种取法,故所有可能的取法总数为N n 种,n次抽取中有m 次为正品的组合数为种,对于固定的一种正、次品的抽取次序,C m n m 次取得正品,都有M 种取法,共有M m 种取法,n −m 次取得次品,每次都有N −M种取法,共有(N −M )n −m 种取法,故()C ()/m m n m nn P A M N M N −=−此题也可用贝努里概型,共做了n 重贝努里试验,每次取得正品的概率为,则取得M Nm 件正品的概率为()C 1m n mm n M M P A N N −⎛⎞⎛⎞=−⎜⎟⎜⎟⎝⎠⎝⎠11. 略.见教材习题参考答案.12. 50只铆钉随机地取来用在10个部件上,其中有3个铆钉强度太弱.每个部件用3只铆钉.若将3只强度太弱的铆钉都装在一个部件上,则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少?【解】设A ={发生一个部件强度太弱}133103501()C C /C 1960P A ==13. 一个袋内装有大小相同的7个球,其中4个是白球,3个是黑球,从中一次抽取3个,计算至少有两个是白球的概率.【解】设A i ={恰有i 个白球}(i =2,3),显然A 2与A 3互斥.213434233377C C C 184(),()C 35C 35P A P A ====故232322()()()35P A A P A P A =+=∪14. 有甲、乙两批种子,发芽率分别为0.8和0.7,在两批种子中各随机取一粒,求:(1)两粒都发芽的概率;(2)至少有一粒发芽的概率;(3)恰有一粒发芽的概率.【解】设A i ={第i 批种子中的一粒发芽},(i =1,2)(1)1212()()()0.70.80.56P A A P A P A ==×=(2)12()0.70.80.70.80.94P A A =+−×=∪(3)2112()0.80.30.20.70.38P A A A A =×+×=∪15. 掷一枚均匀硬币直到出现3次正面才停止.(1)问正好在第6次停止的概率;(2)问正好在第6次停止的情况下,第5次也是出现正面的概率.【解】(1)(2)223151115()()22232p C ==1342111C ()()22245/325p ==16. 甲、乙两个篮球运动员,投篮命中率分别为0.7及0.6,每人各投了3次,求二人进球数相等的概率.【解】设A i ={甲进i 球},i =0,1,2,3,B i ={乙进i 球},i =0,1,2,3,则33312123330()(0.3)(0.4)C 0.7(0.3)C 0.6(0.4)i i i P A B ==+××+∪22223333C (0.7)0.3C (0.6)0.4+(0.7)(0.6)×=0.3207617. 从5双不同的鞋子中任取4只,求这4只鞋子中至少有两只鞋子配成一双的概率.【解】4111152222410C C C C C 131C 21p =−=18. 某地某天下雪的概率为0.3,下雨的概率为0.5,既下雪又下雨的概率为0.1,求:(1)在下雨条件下下雪的概率;(2)这天下雨或下雪的概率.【解】设A ={下雨},B ={下雪}.(1)()0.1()0.2()0.5P AB p B A P A ===(2)()()()()0.30.50.10.7p A B P A P B P AB =+−=+−=∪19. 已知一个家庭有3个小孩,且其中一个为女孩,求至少有一个男孩的概率(小孩为男为女是等可能的).【解】设A ={其中一个为女孩},B ={至少有一个男孩},样本点总数为23=8,故()6/86()()7/87P AB P B A P A ===或在缩减样本空间中求,此时样本点总数为7.6()7P B A =20. 已知5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是男人的概率(假设男人和女人各占人数的一半).【解】设A ={此人是男人},B ={此人是色盲},则由贝叶斯公式()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+0.50.05200.50.050.50.002521×==×+×21. 两人约定上午9∶00~10∶00在公园会面,求一人要等另一人半小时以上的概率.题21图题22图【解】设两人到达时刻为x,y,则0≤x,y≤60.事件“一人要等另一人半小时以上”等价于|x−y|>30.如图阴影部分所示.22301604P==22. 从(0,1)中随机地取两个数,求:(1)两个数之和小于的概率;65(2)两个数之积小于的概率.14【解】设两数为x,y,则0<x,y<1.(1)x+y<.6511441725510.68125p=−==(2)xy=<.141111244111d d ln242xp x y⎛⎞=−=+⎜⎟⎝⎠∫∫23. 设P()=0.3,P(B)=0.4,P(A)=0.5,求P(B|A∪)A B B【解】()()()()()()()()P AB P A P ABP B A BP A B P A P B P AB−==+−∪∪课后答案网:。
《概率论与数理统计答案》第三章

习题参考答案与提示
第三章 随机变量的数字特征习题参考答案与提示
1.设随机变量 X 的概率分布为
X
-3 0.1
0 0.2
1 0.3
5 0.4
pk 试求 EX 。
答案与提示: EX = 2 。 2.已知随机变量 X 的分布列为
X
0 0.1
1
p
2 0.4
3 0.2
Pk
答案与提示:(1)由归一性, p = 0.3 ; (2) EX = 1.7 ; (3) DX = 0.81 3.已知随机变量 X 的分布列为
后
答
D X −Y = 1−
26.设灯管使用寿命 X 服从指数分布,已知其平均使用寿命为 3000 小时,现有
—5—
案
若一周 5 个工作日里无故障可获利 10 万元,发生一次故障仍获利 5 万元,发生二次2π网
。
ww w
3 ; 2
.k
hd a
EZ =
1 , DZ = 3 ; 2
w. c
解:(1)由数学期望、方差的性质及相关系数的定义( ρ XY =
第三章
习题参考答案与提示
求:(1) Y = 2 X 的数学期望;(2) Y = e −2 X 的数学期望。 答案与提示:(1) EY = E 2 X = 2 ;(2) EY = Ee −2 X = 1/ 3 。
1 11.试证明事件在一次试验中发生的次数的方差不超过 。 4
答案与提示:事件在 n 次独立重复试验中发生的次数服从参数为 n , p 的二项分 布 B ( n, p ) ,当然在一次试验中发生的次数应服从 B (1, p ) ,即为(0-1)分布。
f ( x) = 1 − x− β e 2α
概率论与数理统计第三章课后习题及参考答案

概率论与数理统计第三章课后习题及参考答案1.设二维随机变量),(Y X 只能取下列数组中的值:)0,0(,)1,1(-,31,1(-及)0,2(,且取这几组值的概率依次为61,31,121和125,求二维随机变量),(Y X 的联合分布律.解:由二维离散型随机变量分布律的定义知,),(Y X 的联合分布律为2.某高校学生会有8名委员,其中来自理科的2名,来自工科和文科的各3名.现从8名委员中随机地指定3名担任学生会主席.设X ,Y 分别为主席来自理科、工科的人数,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:(1)由题意,X 的可能取值为0,1,2,Y 的可能取值为0,1,2,3,则561)0,0(3833====C C Y X P ,569)1,0(381323====C C C Y X P ,569)2,0(382313====C C C Y X P ,561)3,0(3833====C C Y X P ,283)0,1(382312====C C C Y X P ,289)1,1(38131312====C C C C Y X P ,283)2,1(382312====C C C Y X P ,0)3,1(===Y X P ,563)0,2(381322====C C C Y X P ,563)1,2(381322====C C C Y X P ,0)2,2(===Y X P ,0)3,2(===Y X P .),(Y X 的联合分布律为:(2)X 的边缘分布律为X 012P1452815283Y 的边缘分布律为Y 0123P285281528155613.设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其他.,0,42,20),6(),(y x y x k y x f 求:(1)常数k ;(2))3,1(<<Y X P ;(3))5.1(<Y P ;(4))4(≤+Y X P .解:方法1:(1)⎰⎰⎰⎰--==+∞∞-+∞∞-422d d )6(d d ),(1yx y x k y x y x f ⎰--=42202d |)216(y yx x x k k y y k 8d )210(42=-=⎰,∴81=k .(2)⎰⎰∞-∞-=<<31d d ),()3,1(y x y x f Y X P ⎰⎰--=32102d d )216(yx yx x x ⎰--=32102d |)216(81y yx x x 83|)21211(81322=-=y y .(3)),5.1()5.1(+∞<<=<Y X P X P ⎰⎰+∞∞-∞---=5.1d d )6(81yx y x ⎰⎰--=425.10d d )6(81y x y x y yx x x d )216(81422⎰--=3227|)43863(81422=-=y y .(4)⎰⎰≤+=≤+4d d ),()4(y x y x y x f Y X P ⎰⎰---=2042d )6(d 81x y y x x ⎰+-⋅=202d )812(2181x x x 32|)31412(1612032=+-=x x x .方法2:(1)同方法1.(2)20<<x ,42<<y 时,⎰⎰∞-∞-=yxv u v u f y x F d d ),(),(⎰⎰--=y xv u v u 20d d )6(81⎰--=y xv uv u u 202d |)216(81⎰--=y v xv x x 22d )216(81y xv v x xv 222|)21216(81--=)1021216(81222x xy y x xy +---=,其他,0),,(=y x F ,∴⎪⎩⎪⎨⎧<<<<+---=其他.,0,42,20),1021216(81),(222y x x x xy y x xy y x F 83)3,1()3,1(==<<F Y X P .(3))42,5.1(),5.1()5.1(<<<=+∞<<=<Y X P Y X P X P )2,5.1()4,5.1(<<-<<=Y X P Y X P 3227)2,5.1()4,5.1(=-=F F .(4)同方法1.4.设随机变量),(Y X 的概率密度为⎩⎨⎧>>=--其他.,0,0,0,e ),(2y x A y x f y x 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)⎰⎰⎰⎰+∞+∞--+∞∞-+∞∞-==02d d e d d ),(1yx A y x y x f y x ⎰⎰+∞+∞--=002d e d e y x A y x2|)e 21(|)e (020A A y x =-⋅-=∞+-∞+-,∴2=A .(2)0>x ,0>y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰--=yxv u vu 02d d e 2yv x u 020|)e 21(|)e (2---⋅-=)e 1)(e 1(2y x ----=,其他,0),(=y x F ,∴⎩⎨⎧>>--=--其他.,0,0,0),e 1)(e 1(),(2y x y x F y x .5.设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=其他.,0,10,10,),(y x Axy y x f 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)2121d d d d ),(11010⋅⋅===⎰⎰⎰⎰+∞∞-+∞∞-A y y x x A y x y x f ,∴4=A .(2)10≤≤x ,10≤≤y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰=yxv u uv 0d d 4220202||y x v u yx =⋅=,10≤≤x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4xv u uv 210202||x v u x =⋅=,10≤≤y ,1>x 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4yu v uv 202102||y v u y =⋅=,1>x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=101d d 4v u uv 1||102102=⋅=v u,其他,0),(=y x F ,∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>≤≤>>≤≤≤≤≤≤=其他.,0,1,1,1,10,1,,1,10,,10,10,),(2222y x y x y y x x y x y x y x F .6.把一枚均匀硬币掷3次,设X 为3次抛掷中正面出现的次数,Y 表示3次抛掷中正面出现次数与反面出现次数之差的绝对值,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:由题意知,X 的可能取值为0,1,2,3;Y 的可能取值为1,3.易知0)1,0(===Y X P ,81)3,0(===Y X P ,83)1,1(===Y X P ,0)3,1(===Y X P 83)1,2(===Y X P ,0)3,2(===Y X P ,0)1,3(===Y X P ,81)3,3(===Y X P 故),(Y X 得联合分布律和边缘分布律为:7.在汽车厂,一辆汽车有两道工序是由机器人完成的:一是紧固3只螺栓;二是焊接2处焊点,以X 表示由机器人紧固的螺栓紧固得不牢的数目,以Y 表示由机器人焊接的不良焊点的数目,且),(Y X 具有联合分布律如下表:求:(1)在1=Y 的条件下,X 的条件分布律;(2)在2=X 的条件下,Y 的条件分布律.解:(1)因为)3,3()1,2()1,1()1,0()1(==+==+==+====Y X P Y X P Y X P Y X P Y P 08.0002.0008.001.006.0=+++=,所以43)1()1,0()1|0(=======Y P Y X P Y X P ,81)1()1,1()1|1(=======Y P Y X P Y X P ,101)1()1,2()1|2(=======Y P Y X P Y X P ,401)1()1,3()1|3(=======Y P Y X P Y X P ,故在1=Y 的条件下,X 的条件分布律为X 0123P4381101401(2)因为)2,2()1,2()0,2()2(==+==+====Y X P Y X P Y X P X P 032.0004.0008.002.0=++=,所以85)2()0,2()2,0(=======X P Y X P X Y P ,4)2()1,2()2,1(=======X P Y X P X Y P ,81)2()2,2()2,2(=======X P Y X P X Y P ,故在2=X 的条件下,Y 的分布律为:Y 012P8541818.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=+-其他.,0,0,0,e ),()2(y x c y x f y x 求:(1)常数c ;(2)X 的边缘概率密度函数;(3))2(<+Y X P ;(4)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)⎰⎰⎰⎰+∞+∞+-+∞∞-+∞∞-==0)2(d d e d d ),(1yx c y x y x f y x⎰⎰+∞+∞--=002d e d ey x c y x2|)e (|)e 21(002c c y x =-⋅-=∞+-∞+-,∴2=c .(2)0>x 时,⎰+∞∞-=y y x f x f X d ),()(⎰+∞+-=0)2(d e 2y y x x y x 202e 2|)e (e 2-+∞--=-=,0≤x 时,0)(=x f X ,∴⎩⎨⎧≤>=-.0,0,0,e 2)(2x x x f x X ,同理⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)⎰⎰<+=<+2d d ),()2(y x y x y x f Y X P ⎰⎰---=2202d d e 2xy x yx 422202e e 21d e d e 2-----+-==⎰⎰xy x y x .(4)由条件概率密度公式,得,当0>y 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e 2,0,0,e e 2)(),()|(22|x x y f y x f y x f xy y x Y Y X ,0≤y 时,0)|(|=y x f Y X ,所以⎩⎨⎧>>=-其他.,0,0,0,e 2)|(2|y x y x f x Y X ;同理,当0>x 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e ,0,0,2e e 2)(),()|(22|y y x f y x f x y f yx y x X X Y 0≤x 时,0)|(|=x y f X Y ,所以⎩⎨⎧>>=-其他.,0,0,0,e )|(|y x x y f y X Y .9.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<=其他.,0,0,10,3),(x y x x y x f求:(1)关于X 、Y 的边缘概率密度函数;(2)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)10<<x 时,⎰+∞∞-=y y x f x f X d ),()(203d 3x y x x==⎰,其他,0)(=x f X ,∴⎩⎨⎧<<=其他.,0,10,3)(2x x x f X ,密度函数的非零区域为}1,10|),{(}0,10|),{(<<<<=<<<<x y y y x x y x y x ,∴10<<y 时,⎰+∞∞-=x y x f y f Y d ),()()1(23d 321y x x y-==⎰,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<-=其他.,0,10),1(23)(2y y y f Y .(2)当10<<y 时,有⎪⎩⎪⎨⎧<<-=⎪⎪⎩⎪⎪⎨⎧<<-==其他.其他.,0,1,12,0,1,)1(233)(),()|(22|x y y x x y y xy f y x f y x f Y Y X ,其他,0)|(|=y x f Y X ,故⎪⎩⎪⎨⎧<<<<-=其他.,0,10,1,12)|(2|y x y y xy x f Y X .当10<<x 时,有⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==其他.其他.,0,0,1,0,0,33)(),()|(2|x y x x y x x x f y x f x y f X X Y ,其他,0)|(|=x y f X Y ,故⎪⎩⎪⎨⎧<<<<=其他.,0,10,0,1)|(|x x y x x y f X Y .10.设条件密度函数为⎪⎩⎪⎨⎧<<<=其他.,0,10,3)|(32|y x yx y x f Y X Y 的概率密度函数为⎩⎨⎧<<=其他.,0,10,5)(4y y y f Y 求21(>X P .解:⎩⎨⎧<<<==其他.,0,10,15)|()(),(2|y x y x y x f y f y x f Y X Y ,则6447d )(215d d 15d d ),(21(121421211221=-===>⎰⎰⎰⎰⎰>x x x x y y x y x y x f X P xx .11.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<<<+=其他.,0,20,10,3),(2y x xyx y x f 求:(1)),(Y X 的边缘概率密度;(2)X 与Y 是否独立;(3))),((D Y X P ∈,其中D 为曲线22x y =与x y 2=所围区域.解:(1)10<<x 时,x x y xy x y y x f x f X 322d )3(d ),()(222+=+==⎰⎰+∞∞-,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<+=其他.,0,10,322)(2x x x x f X ,20<<y 时,⎰+∞∞-=x y x f y f Y d ),()(316)d 3(12+=+=⎰y x xy x ,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<+=其他.,0,20,316)(y y y f Y .(2)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(3)}22,10|),{(2x y x x y x D ≤≤<<=,∴⎰⎰+=∈102222d d )3()),((x xx y xy x D Y X P 457d )32238(10543=--=⎰x x x x .12.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=-其他.,0,0,0,e )1(),(2y x y x y x f x试讨论X ,Y 的独立性.解:当0>x 时,xx x X x yx y y x y y x f x f -∞+-∞+-∞+∞-=+-=+==⎰⎰e |11e d )1(e d ),()(002,当0≤x 时,0)(=x f X ,故⎩⎨⎧≤>=-.0,0,0,e )(x x x x f x X ,同理,可得⎪⎩⎪⎨⎧≤>+=.0,0,0,)1(1)(2y y y y f Y ,因为)()(),(y f x f y x f Y X =,所以X 与Y 相互独立.13.设随机变量),(Y X 在区域}|),{(a y x y x g ≤+=上服从均匀分布,求X 与Y 的边缘概率密度,并判断X 与Y 是否相互独立.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其他.,0,,21),(2a y x a y x f ,当0<<-x a 时,有)(1d 21d ),()(2)(2x a ay a y y x f x f xa x a X +===⎰⎰++-+∞∞-,当a x <≤0时,有)(1d 21d ),()(2)(2x a a y a y y x f x f x a x a X -===⎰⎰---+∞∞-,当a x ≥时,0d ),()(==⎰+∞∞-y y x f x f X ,故⎪⎩⎪⎨⎧≥<-=.a x a x x a a x f X ,0,),(1)(2,同理,由轮换对称性,可得⎪⎩⎪⎨⎧≥<-=.a y a y y a a y f Y ,0,),(1)(2,显然)()(),(y f x f y x f Y X ≠,所以X 与Y 不相互独立.14.设X 和Y 时两个相互独立的随机变量,X 在)1,0(上服从均匀分布,Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY (1)求X 和Y 的联合概率密度;(2)设含有a 的二次方程为022=++Y aX a ,试求a 有实根的概率.解:(1)由题可知X 的概率密度函数为⎩⎨⎧<<=其他.,0,10,1)(x x f X ,因为X 与Y 相互独立,所以),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧><<==-其他.,0,0,10,e 21)()(),(2y x y f x f y x f yY X ,(2)题设方程有实根等价于}|),{(2X Y Y X ≤,记为D ,即}|),{(2X Y Y X D ≤=,设=A {a 有实根},则⎰⎰=∈=Dy x y x f D Y X P A P d d ),()),(()(⎰⎰⎰---==1021002d )e 1(d d e 2122xx y x x y⎰--=102d e12x x ⎰--=12e 21212x x ππππ23413.01)]0()1([21-=Φ-Φ-=.15.设i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,求行列式4321X X X X X =的分布律.解:由i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,易知41X X ~)84.0,16.0(b ,32X X ~)84.0,16.0(b .因为1X ,2X ,3X ,4X 相互独立,所以41X X 与32X X 也相互独立,又32414321X X X X X X X X X -==,则X 的所有可能取值为1-,0,1,有)1()0()1,0()1(32413241======-=X X P X X P X X X X P X P 1344.016.084.0=⨯=,)1,1()0,0()0(32413241==+====X X X X P X X X X P X P )1()1()0()0(32413241==+===X X P X X P X X P X X P 7312.016.016.084.084.0=⨯+⨯=,)0()1()0,1()1(32413241=======X X P X X P X X X X P X P 1344.084.016.0=⨯=,故X 的分布律为X 1-01P1344.07312.01344.016.设二维随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-其他.,0,0,0,e 2),()2(y x y x f y x 求Y X Z 2+=的分布函数及概率密度函数.解:0≤z 时,若0≤x ,则0),(=y x f ;若0>x ,则0<-=x z y ,也有0),(=y x f ,即0≤z 时,0),(=y x f ,此时,0d d ),()2()()(2==≤+=≤=⎰⎰≤+zy x Z y x y x f z Y X P z Z P z F .0>z 时,若0≤x ,则0),(=y x f ;只有当z x ≤<0且02>-=xz y 时,0),(≠y x f ,此时,⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 2d d ),()2()()(⎰⎰-+-=zx z y x y x 020)2(d e 2d z z z ----=e e 1.综上⎩⎨⎧≤>--=--.0,0,0,e e 1)(z z z z F z z Z ,所以⎩⎨⎧≤<='=-.0,0,0,e )()(z z z z F z f z Z Z .17.设X ,Y 是相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤=其他.,0,10,1)(x x f X ,⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y 求Y X Z +=的概率密度.解:0<z 时,若0<x ,则0)(=x f X ;若0≥x ,则0<-=x z y ,0)(=-x z f Y ,即0<z 时,0)()(=-x z f x f Y X ,此时,0d )()()(=-=⎰+∞∞-x x z f x f z f Y X Z .10≤≤z 时,若0<x ,则0)(=x f X ;只有当z x ≤≤0且0>-=x z y 时0)()(≠-x z f x f Y X ,此时,z zx z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e 1d e d )()()(0)(.1>z 时,若0<x ,0)(=x f X ;若1>x ,0)(=x f X ;若10≤≤x ,则0>-=x z y ,此时,0)()(≠-x z f x f Y X ,z x z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e )1e (d e d )()()(1)(.综上,⎪⎩⎪⎨⎧<>-≤≤-=--.0,0,1,e )1e (,10,e 1)(z z z z f z z Z .18.设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=+-其他.,0,0,0,e)(21),()(y x y x y x f y x (1)X 和Y 是否相互独立?(2)求Y X Z +=的概率密度.解:(1)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(2)0≤z 时,若0≤x ,则0)(=x f X ;若0>x ,则0<-=x z y ,0),(=y x f ,此时,0d ),()(=-=⎰+∞∞-x x z x f z f Z .0≥z 时,若0≤x ,则0)(=x f X ;只有当z x <<0且0>-=x z y 时0),(≠y x f ,此时,⎰+∞∞--=x x z x f z f Z d ),()(⎰+-+=zy x x y x 0)(d e )(21⎰-=z z x z 0d e 21z z -=e 212,所以⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2z z z z f zZ .19.设X 和Y 时相互独立的随机变量,它们都服从正态分布),0(2σN .证明:随机变量22Y X Z +=具有概率密度函数⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.解:因为X 与Y 相互独立,均服从正态分布),0(2σN ,所以其联合密度函数为2222)(2e 121),(σσπy x y xf +-⋅=,(+∞<<∞-y x ,)当0≥z 时,有⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 22d d ),()()()(22⎰⎰≤++-⋅=zy x y x y x 22222d e 1212)(2σσπ⎰⎰-⋅=πσθσπ2022d ed 12122zr r r ⎰-=zr r r 022d e122σσ,此时,2222e)(σσz Z z z f -=;当0<z 时,=≤+}{22z Y X ∅,所以0)()()(22=≤+=≤=z Y X P z Z P z F Z ,此时,0)(=z f Z ,综上,⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.20.设),(Y X 在矩形区域}10,10|),{(≤≤≤≤=y x Y X G 上服从均匀分布,求},min{Y X Z =的概率密度.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他.,0,20,10,21),(y x y x f ,易证,X ~]1,0[U ,Y ~]2,0[U ,且X 与Y 相互独立,⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(x x x x x F X ,⎪⎪⎩⎪⎪⎨⎧≥<≤<=.2,1,20,2,0,0)(y y yy y F Y ,可得)](1)][(1[1)(z F z F z F Y X Z ---=)()()()(z F z F z F z F Y X Y X -+=⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.1,1,10,223,0,02z z z z z ,求导,得⎪⎩⎪⎨⎧<<-=其他.,0,10,23)(z z z f Z .21.设随机变量),(Y X 的概率密度为⎩⎨⎧+∞<<<<=+-其他.,0,0,10,e ),()(y x b y x f y x (1)试确定常数b ;(2)求边缘概率密度)(x f X 及)(y f Y ;(3)求函数},max{Y X U =的分布函数.解:(1)⎰⎰⎰⎰+∞+-+∞∞-+∞∞-==01)(d d e d d ),(1yx b y x y x f y x ⎰⎰+∞--=10d e d e y x b y x)e 1(|)e(|)e (10102-+∞---=-⋅=b b y x ,∴1e11--=b .(2)10<<x 时,1)(1e1e d e e 11d ),()(--∞++--∞+∞--=-==⎰⎰x y x X y y y x f x f ,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<-=--其他.,0,10,e 1e )(1x x f xX ,0>y 时,⎰+∞∞-=x y x f y f Y d ),()(yy x x -+--=-=⎰e d e e 1110)(1,0≤y 时,0)(=y f Y ,∴⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)0≤x 时,0)(=x F X ,10<<x 时,101e1e 1d e 1e d )()(----∞---=-==⎰⎰xxt xX X t t t f x F ,1≥x 时,1)(=x F X ,∴⎪⎪⎩⎪⎪⎨⎧≥<<--≤=--.1,1,10,e 1e1,0,0)(1x x x x F x X ;0≤y 时,0)(=y F Y ,0>y 时,y yv y Y Y v v v f y F --∞--===⎰⎰e 1d e d )()(0,∴⎩⎨⎧≤>-=-.0,0,0,e 1)(y y y F y Y ,故有)()()(y F x F u F Y X U =⎪⎪⎩⎪⎪⎨⎧≥-<≤--<=---.1,e 1,10,e 1e1,0,01u u u uu .。
概率论与数理统计复旦大学出版社第三章课后答案

概率论与数理统计 习题三 答案1.将一硬币抛掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律. 【解】X 的可能取值为:0,1,2,3;Y 的可能取值为:0,1.X 和Y 的联合分布律如下表:222⨯⨯222⨯⨯2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X 表示取到黑球的只数,以Y 表示取到红球的只数.求X 和Y 的联合分布律. 【解】X 的可能取值为:0,1,2,3;Y 的可能取值为:0,1,2.324C 35= 324C 35= 3224C 35= 113224C C 12C 35= 1324C 2C 35= 224C 35= 213224C C 6C 35= 2324C 3C 35=3.设二维随机变量(,)X Y 的联合分布函数为ππsin sin ,0,0(,)220,x y x y F x y ⎧≤≤≤≤⎪=⎨⎪⎩ 其它求二维随机变量(,)X Y 在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,40πππy x 内的概率. 【解】如图πππ{0,}(3.2)463P X Y <≤<≤公式ππππππ(,)(,)(0,)(0,)434636F F F F --+ππππππsin sin sin sin sin0sin sin0sin4346362(31).4=--+=-题3图说明:也可先求出密度函数,再求概率。
4.设随机变量(,)X Y的分布密度(34)e,0,0(,)0,x yA x yf x y-+⎧>>=⎨⎩ 其他求:(1)常数A;(2)随机变量(,)X Y的分布函数;(3)P{0≤X<1,0≤Y<2}.【解】(1)由-(34)00(,)d d e d d112x yAf x y x y A x y+∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得A=12(2)由定义,有(,)(,)d dy xF x y f u v u v-∞-∞=⎰⎰(34)340012e d d(1e)(1e)0,0,0,0,y y u vx yu v y x-+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3) {01,02}P X Y≤<≤<12(34)3800{01,02}12e d d(1e)(1e)0.9499.x yP X Yx y-+--=<≤<≤==--≈⎰⎰5.设随机变量(,)X Y的概率密度为(6),02,24(,)0,k x y x yf x y--<<<<⎧=⎨⎩ 其它(1)确定常数k;(2)求P{X<1,Y<3};【解】(1) 由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故 18k =(2) 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰ (3) 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=⎰⎰⎰⎰如图1.542127d (6)d .832x x y y =--=⎰⎰(4) 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83xx x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量,X 在(0,0.2)上服从均匀分布,Y 的密度函数为55e ,0,()0,.y Y y f y -⎧>=⎨⎩其它求:(1) X 与Y 的联合分布密度;(2) {}P Y X ≤.题6图【解】(1) 因X 在(0,0.2)上服从均匀分布,所以X 的概率密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其它 而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其它 所以(,),()*()X Y f x y X Y f x f y 独立5515e 25e ,00.2,00.20,y yx y --⎧⨯=<<>⎪=⎨⎪⎩ 其它(2) 5()(,)d d 25ed d yy xDP Y X f x y x y x y -≤≤=⎰⎰⎰⎰如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.x y x x y x-==-+≈⎰⎰⎰7.设二维随机变量(,)X Y 的联合分布函数为42(1e )(1e ),0,0,(,)0,.x y x y F x y --⎧-->>=⎨⎩其他 求(X ,Y )的联合分布密度.【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y -+⎧>>∂==⎨∂∂⎩其他.8.设二维随机变量(,)X Y 的概率密度为4.8(2),01,0,(,)0,.y x x y x f x y -≤≤≤≤⎧=⎨⎩其他 求边缘概率密度.【解】X 的边缘概率密度为()(,)d X f x f x y y +∞-∞=⎰x204.8(2)d 2.4(2),01y x y x x x ⎧-=-≤≤⎪=⎨⎪⎩⎰ 0, 其它 Y 的边缘概率密度为()(,)d Y f y f x y x+∞-∞=⎰12y4.8(2)d 2.4(34),01y x x y y y y ⎧-=-+≤≤⎪=⎨⎪⎩⎰ 0, 其它题8图 题9图9.设二维随机变量(,)X Y 的概率密度为e ,0(,)0y x yf x y -⎧<<=⎨⎩, 其它求边缘概率密度.【解】X 的边缘概率密度为()(,)d X f x f x y y +∞-∞=⎰e d e ,00,y x x y x +∞--⎧=>⎪=⎨⎪⎩⎰ 其它Y 的边缘概率密度为()(,)d Y f y f x y x +∞-∞=⎰0e d e ,00,yy x x y y --⎧=>⎪=⎨⎪⎩⎰ 其它题10图10.设二维随机变量(,)X Y 的概率密度为22,1(,)0cx y x y f x y ⎧≤≤=⎨⎩, 其它(1) 试确定常数c ; (2) 求边缘概率密度. 【解】(1)(,)d d (,)d d Df x y x y f x y x y+∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c ==⎰⎰ 得214c =. (2) ()(,)d X f x f x y y +∞-∞=⎰212242121=(1),11480,x x ydy x x x ⎧--≤≤⎪=⎨⎪⎩⎰ 其它()(,)d Y f y f x y x +∞-∞=⎰522217d ,01420,y y x y x y y -⎧=≤≤⎪=⎨⎪⎩⎰ 其它 11.设随机变量(,)X Y 的概率密度为1,,01(,)0,y x x f x y ⎧<<<⎪=⎨⎪⎩ 其它求条件概率密度()Y X f y x ,()X Y f x y .题11图【解】()(,)d X f x f x y y +∞-∞=⎰1d 2,01,0,.xx y x x -⎧=<<⎪=⎨⎪⎩⎰其他111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y -+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他所以|1,||1,(,)(|)2()0,.Y X X y x f x y f y x xf x ⎧<<⎪==⎨⎪⎩其他|1, 1,1(,)1(|),1,()10,.X Y Y y x y f x y f x y y x f y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他 12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X ,最大的号码为Y .(1) 求X 与Y 的联合概率分布;(2) X 与Y 是否相互独立? 【解】(1) X 的可能取值为:1,2,3;Y 的可能取值为3,4,5. X 与Y 的联合分布律及边缘分布律如下表:3 4 5{}i P X x =13511C 10= 3522C 10= 3533C 10= 610 23511C 10= 3522C 10= 310 3 02511C 10= 110{}i P Y y =110 310610(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠=== 故X 与Y 不独立13.设二维随机变量(,)X Y 的联合分布律为 2 5 80.4 0.80.15 0.30 0.35 0.05 0.12 0.032 5 8 P {Y=y i }0.4 0.15 0.30 0.35 0.8 0.80.05 0.12 0.03 0.2{}i P X x =0.20.420.38YXXY XY(2) 因{2}{0.4}0.20.8P X P Y ===⨯0.160.15(2,0.4),P X Y =≠===故X 与Y 不独立.14.设X 与Y 是两个相互独立的随机变量,X 在(0,1)上服从均匀分布,Y 的概率密度为/21e ,0,()20,.y Y y f y -⎧>⎪=⎨⎪⎩其他(1)求X 和Y 的联合概率密度;(2) 设含有a 的二次方程为a 2+2Xa +Y =0,试求a 有实根的概率.【解】(1) 因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩独立其他题14图(2) 方程220a Xa Y ++=有实根的条件是2(2)40X Y ∆=-≥即 2X Y ≥, 从而方程有实根的概率为:22{}(,)d d x yP X Y f x y x y ≥≥=⎰⎰22211/2200121d e d 1e d 212d 12[(1)(0)]20.1445.xx y x x y xx πππ---==-==-Φ-Φ=⎰⎰⎰ 15.设X 和Y 分别表示两个不同电子器件的寿命(以小时计),并设X 和Y 相互独立,且服从同一分布,其概率密度为f (x )=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求/Z X Y =的概率密度.【解】因为X 和Y 相互独立,所以X 与Y 的联合概率密度为62210,1000,1000(,)0,x y f x y x y ⎧>>⎪=⎨⎪⎩ 其它如图,Z 的分布函数(){}{}Z XF z P Z z P z Y=≤=≤ (1) 当z ≤0时,()0Z F z =(2) 当0<z <1时,(这时当x =1000时,y =1000z)(如图a) 3366102222101010()(,)d d d d d d yz Z zx x y y zzF z f x y x y x y y x x y x y +∞≥≥===⎰⎰⎰⎰⎰⎰ 33610231010=d 2z zy yzy +∞⎛⎫-= ⎪⎝⎭⎰题15图(3) 当z ≥1时,(这时当y =103时,x =103z )(如图b )3366222210101010()(,)d d d d d d zy Z xx y y zzF z f x y x y x y y x x yx y +∞≥≥===⎰⎰⎰⎰⎰⎰ 336231010101=d 12y yzy z +∞⎛⎫-=- ⎪⎝⎭⎰即 11,1,2(),01,20,.Z z z zF z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 16.设某种型号的电子管的寿命(以小时计)近似地服从N (160,202)分布.随机地选取4 只,求其中没有一只寿命小于180的概率.【解】设取到的四只电子元件寿命为i X (i =1,2,3,4),则2~(160,20)i X N ,从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥之间独立34{180}{180}P X P X ≥≥ 1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ== 17.设X ,Y 是相互独立的随机变量,其分布律分别为()(),0,1,2,3,P X k p k k === ()(),0,1,2,3,P Y r q r r ===证明随机变量Z =X +Y 的分布律为()()()ik P Z i p k q i k ===-∑,i =0,1,2,….【证明】因X 和Y 所有可能值都是非负整数,所以 {}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==于是{}{,}ik P Z i P X k Y i k =====-∑,{}{}ik X Y P X k P Y i k ===-∑相互独立0()()ik p k q i k ==-∑18.设X ,Y 是相互独立的随机变量,它们都服从参数为n ,p 的二项分布.证明Z =X +Y 服从参数为2n ,p 的二项分布.【证明】方法一:X +Y 可能取值为0,1,2,…,2n .{}{,}ki P X Y k P X i Y k i =+====-∑002200(){}2)ki ki n i k i n k ii kk n k k n ki ki P X i P Y k i n n p q p qi k i n n n p qp q i k i k n m m n i k i k =---+=--=====-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭+⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭∑∑∑∑(提示:组合计数公式方法二:参见第四章。
概率论与数理统计课后习题答案(复旦大学 韩旭里)

(7) A BC∪A B C∪AB C ∪ AB C∪A BC ∪ A B C ∪ ABC = ABC = A ∪ B ∪ C (8) AB∪BC∪CA=AB C ∪A B C∪ A BC∪ABC 3. 略.见教材习题参考答案 4.设 A,B 为随机事件,且 P(A)=0.7,P(A− B)=0.3,求 P( AB ). P(AB)=1− [P(A)− P(A− B)] 【解】 P( AB )=1− =1− [0.7− 0.3]=0.6 5.设 A,B 是两事件,且 P(A)=0.6,P(B)=0.7,求: (1) 在什么条件下 P(AB)取到最大值? (2) 在什么条件下 P(AB)取到最小值? 【解】(1) 当 AB=A 时,P(AB)取到最大值为 0.6. (2) 当 A∪B=Ω 时,P(AB)取到最小值为 0.3. 6.设 A,B,C 为三事件,且 P(A)=P(B)=1/4,P(C)=1/3 且
=0.32076 17.从 5 双不同的鞋子中任取 4 只,求这 4 只鞋子中至少有两只鞋子配成一双的概率. 【解】
p = 1−
4 1 1 1 1 C5 C2 C 2C 2 C2 13 = 4 C10 21
18. 某地某天下雪的概率为 0.3,下雨的概率为 0.5,既下雪又下雨的概率为 0.1,求: (1) 在下雨条件下下雪的概率;(2) 这天下雨或下雪的概率. 【解】 设 A={下雨},B={下雪}. (1) p ( B A) =
第 1 页 共 105 页
1
P(AB)=P(BC)=0,P(AC)=1/12,求 A,B,C 至少有一事件发生的概率. P(AB)− P(BC)− P(AC)+P(ABC) 【解】 P(A∪B∪C)=P(A)+P(B)+P(C)− =
概率论与数理统计第三章课后习题答案

概率论与数理统计第三章课后习题答案习题二1■将一硬币抛掷二次,以X表示在二次中出现正面的次数,以Y表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X和丫的联合分布律.【解】X和丫的联合分布律如表:2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X表示取到黑球的只数,以Y表示取到红球的只数.求X和Y的联合分布律.【解】X和丫的联合分布律如表:3•设二维随机变量(X, F)的联合分布函数为求二维随机变量(x, y)在长方形域内的概率.4 6 3J【解】如图叫眈怎<今空^求:(1)常数/;F (x, y)sin xsiny,0,0"岁詣其他.・Tt ■兀・兀■兀=sin —_sin ——sin —_sin ——4 3 4 6二#(dl).斗sin OLfeinK ■八■兀—+sinIksin —3 6JT7说明:也可先求出密度函数,再求概率。
4•设随机变量(X, Y)的分布密度f(兀,y)j e-(3.r+4y)x >0, y >0, 其他.(2) 随机变量(X, Y)的分布函数;(3) P{0 «1, 0之<2}.【解】(1)由 f(x,y)dxdy° °Ae(3x4y)dxdy £ 1得A = 12(2) 由定义,有y xF (x, y)f (u, v)dudvy y(3u 4v)12e dudvo o0,(3) P{0 X 1,0 Y 2}P{0 X 1,0 Y 2}5. 设随机变量(X, Y )的概率密度为(1 e 3x )(1 e 4y ) y 0,x 0,0,其他212e (3x 04y)dxdy(1 e 3)(1 e 8)0.9499.f(x ,y)=k(6 x y), 0,x 2,2 y 4,其他.(1)确定常数k ;(2)求 P{X v 1, Y v 3};(3)求 P{X<1.5};(4)求 P{X+Y W 4}.【解】(1)由性质有2 4f(x, y)dxdy ° 2 k(6 x y)dydx 8k 1,31-k(6 x y)dydx86.设X和丫是两个相互独立的随机变量,X在(0,0.2)上服从均匀分布,Y的密度函数为求:(1) X与Y的联合分布密度;(2)P{YN}.(2) P{X 1,Y 3} f (x, y)dydx(3)P{X(4)P{X1.5}x 1.5f (x, y)dxdy 如图 a f (x,y)dxdy1.5 4 10 dx -(6 x y)dy82732Y 4}Xf (x, y)dxdy如图 b f (x,y)dxdy(61 ) y)f Y( y)5e5y, y 0,0, 其他.【解】(1)因X 在(0, 0.2) 上服从均匀分布,所以X 的密度函数为f x (X)10 x 0.2,0.2,0,其他.而f/y)5e 5y , y 0,0,其他.所以f (x, y)X,丫独立 fx(x)gf Y (y)⑵ P(Y X) f (x, y)dxdy 如图 25e 5y dxdyy xD丄 0.2 5e 5y0,25e 5y, 0 x 0.2且 y 0, 0, 其他•0.2 0dx25e -5ydy0.2 5x0 ( 5e5)dx■1=e 0.3679.7.设二维随机变量(X, Y )的联合分布函数为F ( x ,y )(1 e 4x)(1 e 2y), x 0,y 0,0,其他.求(X ,Y )的联合分布密度2[解] f(x,y)x y8e(4x 2y), x 0,y 0,0, 其他.8.设二维随机变量(X, Y )的概率密度为f (x, y)=4.8y(2 x), 0 0,x 1,0 y x,其他.求边缘概率密度.【解】f x(x) f (x,y)dyx0 4.8y(2x)dy0,2.4X2(2 x), 0 x 1,0, 其他.f y(y) f (x,y)dx1=y4-8y(2x)dx 2.4y(3 4y y2), 0 y 1,0, 其他.,题8图9.设二维随机变量题9图X, Y)的概率密度为f (x, y) e y, 0 x y,0, 其他.求边缘概率密度.【解】f x(X) f (x, y)d yx0,e y dy xe , x 0,0, 其他.f Y(y) f (x,y)dxy e y dx0,ye x, y 0,0, 其他.y\i■v=xw p题10图10.设二维随机变量(X, Y)2f (x, y)= J试确定常数c;求边缘概率密度的概率密度为x2y 1,其他.(1)(2)【解】(1)f (x, y)dxdy如图Df (x,y)dxdy1 12-1dx x2cx ydy4c211.214f x(X) f(x,y)dy1 212 , xydyx 40, 212。
概率论与数理统计课程第三章练习题及解答

第三章 多维随机变量及其分布一、判断题(在每题后的括号中 对的打“√”错的打“×” )1、若X ,Y 均服从正态分布,则(X ,Y )服从二维正态分布 ( × )2、随机变量(X ,Y )的概率密度为22,1(,)0,k x y f x y ⎧+≤=⎨⎩其它,则π1=k (√ )3、有限个相互独立的正态随机变量的线性组合仍然服从正态分布。
(√) 二、单选题1、随机变量X ,Y 相互独立且~(0,1)X N ,~(1,1)Y N ,则下列各式成立的是( B )A .21}0{=≤+Y X P ; B .21}1{=+≤Y X P ; C .21}0{=≥+Y X P ; D .-≤=1{1}2P X Y 。
分析 因X ,Y 相互独立,它们又都服从正态分布,因此X +Y 与X -Y 也都服从正态分布,且(1,2)X Y N + ,(1,2)X Y N --,由于1{1}(0)2P X Y +≤=Φ=Φ=,选B2、设随机变量21,X X 的分布律为:101111424iX p- i =1,2且满足1}0{21==X X P ,则==}{21X X P ( A )A .0;B .41;C .21; D .1。
分析 从1}0{21==X X P ,可知12{0}0P X X ≠=,即12121212{1,1}{1,1}{1,1}{1,1}0P X X P X X P X X P X X =-=-==-====-==== 根据联合分布与边缘分布的关系,求出21,X X 的联合概率分布12121212{}{1,1}{0,0}{1,1}0P X X P X X P X X P X X ===-=-+==+===,选A 3、设随机变量X ,Y 相互独立且同分布:1{1}{1}2P X P Y =-==-=,1{1}{1}2P X P Y ====,则下列各式成立的是( A )A .1{}2P X Y ==; B .{}1P X Y ==; C .1{0}4P X Y +==; D .1{1}4P XY ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题三1.将一硬币抛掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表:2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X 表示取到黑球的只数,以Y 表示取到红球的只数.求X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表:3.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎪⎩⎪⎨⎧≤≤≤≤.,020,20,sin sin 其他ππy x y x求二维随机变量(X ,Y )在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,40πππy x 内的概率. 【解】如图πππ{0,}(3.2)463P X Y <≤<≤公式 ππππππ(,)(,)(0,)(0,)434636F F F F --+ππππππsin sinsinsinsin 0sinsin 0sin4346361).4=--+=题3图说明:也可先求出密度函数,再求概率。
4.设随机变量(X ,Y )的分布密度f (x ,y )=⎩⎨⎧>>+-.,0,0,0,)43(其他y x A y x e求:(1) 常数A ;(2) 随机变量(X ,Y )的分布函数;(3) P {0≤X <1,0≤Y <2}.【解】(1) 由-(34)(,)d d ed d 112x y A f x y x y A x y +∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得 A =12(2) 由定义,有(,)(,)d dy x F x y f u v u v -∞-∞=⎰⎰(34)340012e d d (1e )(1e )0,0,0,0,y y u v x y u vy x -+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3) {01,02}P X Y ≤<≤<12(34)38{01,02}12ed d (1e )(1e )0.9499.x y P X Y x y -+--=<≤<≤==--≈⎰⎰5.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<--.,0,42,20),6(其他y x y x k(1) 确定常数k ; (2) 求P {X <1,Y <3};(3) 求P {X <1.5}; (4) 求P {X +Y ≤4}. 【解】(1) 由性质有2402(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故 18R =(2) 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰(3) 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=⎰⎰⎰⎰如图1.5402127d (6)d .832x x y y =--=⎰⎰(4) 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83x x x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量,X 在(0,0.2)上服从均匀分布,Y 的密度函数为f Y (y )=⎩⎨⎧>-.,0,0,55其他y y e求:(1) X 与Y 的联合分布密度;(2) P {Y ≤X }.题6图【解】(1) 因X 在(0,0.2)上服从均匀分布,所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其他所以(,),()()X Yf x y X Y f x f y 独立 5515e 25e ,00.20,0.20,0,yy x y --⎧⎧⨯<<>⎪==⎨⎨⎩⎪⎩且其他.(2) 5()(,)d d 25ed d yy xDP Y X f x y x y x y -≤≤=⎰⎰⎰⎰如图0.20.2-55-1d 25ed (5e5)d =e0.3679.xyx x y x-==-+≈⎰⎰⎰7.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎩⎨⎧>>----.,0,0,0),1)(1(24其他y x y x e e求(X ,Y )的联合分布密度. 【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y-+⎧>>∂==⎨∂∂⎩其他.8.设二维随机变量(X ,Y )的概率密度为f (x ,y )= 4.8(2),01,0,0,.y x x y x -≤≤≤≤⎧⎨⎩其他求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰x 24.8(2)d 2.4(2),01,=0,.0,y x y x x x ⎧⎧--≤≤⎪=⎨⎨⎩⎪⎩⎰其他()(,)d Y f y f x y x+∞-∞=⎰12y4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ⎧-⎧-+≤≤⎪=⎨⎨⎩⎪⎩⎰其他题8图 题9图9.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<-.,0,0,其他e y x y求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰e d e ,0,=0,.0,y x x y x +∞--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他()(,)d Y f y f x y x +∞-∞=⎰0e d e ,0,=0,.0,y y x x y y --⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他题10图10.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧≤≤.,0,1,22其他y x y cx(1) 试确定常数c ; (2) 求边缘概率密度. 【解】(1)(,)d d (,)d d Df x y x y f x y x y +∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c ==⎰⎰得 214c =.(2) ()(,)d X f x f x y y +∞-∞=⎰212422121(1),11,d 840,0,.x x x x x y y ⎧⎧--≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他()(,)d Y f y f x y x +∞-∞=⎰5227d ,01,20,0, .x y x y y ⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩其他11.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<.,0,10,,1其他x x y求条件概率密度f Y |X (y |x ),f X |Y (x |y ).题11图【解】()(,)d X f x f x y y +∞-∞=⎰1d 2,010,.x x y x x -⎧=<<⎪=⎨⎪⎩⎰其他111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y -+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他 所以|1,||1,(,)(|)2()0,.Y XX y x f x y f y x xf x ⎧<<⎪==⎨⎪⎩其他|1, 1,1(,)1(|),1,()10,.X Y Y yx y f x y f x y y x f y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他 12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X ,最大的号码为Y . (1) 求X 与Y 的联合概率分布; (2) X 与Y 是否相互独立? 【解】(1) X 与Y 的联合分布律如下表(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠===故X 与Y 不独立(2) X 与Y 是否相互独立?【解】(1)X 和Y 的边缘分布如下表(2) 因{2}{0.4}0.20.8P X P Y ===⨯ 0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.14.设X 和Y 是两个相互独立的随机变量,X 在(0,1)上服从均匀分布,Y 的概率密度为f Y (y )=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e(1)求X 和Y 的联合概率密度; (2) 设含有a 的二次方程为a 2+2Xa +Y =0,试求a 有实根的概率.【解】(1) 因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩独立其他题14图(2) 方程220a Xa Y ++=有实根的条件是2(2)40X Y ∆=-≥故 X 2≥Y , 从而方程有实根的概率为:22{}(,)d d x yP XY f x y x y ≥≥=⎰⎰21/21d ed 21(1)(0)]0.1445.x y x y-==-Φ-Φ=⎰⎰15.设X 和Y 分别表示两个不同电子器件的寿命(以小时计),并设X 和Y 相互独立,且服从同一分布,其概率密度为f (x )=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}Z X F z P Z z P z Y =≤=≤(1) 当z ≤0时,()0Z F z =(2) 当0<z <1时,(这时当x =1000时,y =1000z )(如图a)3366102222101010()d d d d yzZ zx y zF z x y y x x yx y+∞≥==⎰⎰⎰⎰33610231010=d 2zzy yzy +∞⎛⎫-= ⎪⎝⎭⎰题15图(3) 当z ≥1时,(这时当y =103时,x =103z )(如图b )3366222210101010()d d d d zyZ x y zF z x y y x x yx y+∞≥==⎰⎰⎰⎰336231010101=d 12y yzy z +∞⎛⎫-=- ⎪⎝⎭⎰即 11,1,2(),01,20,.Z z z zf z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 16.设某种型号的电子管的寿命(以小时计)近似地服从N (160,202)分布.随机地选取4 只,求其中没有一只寿命小于180的概率.【解】设这四只寿命为X i (i =1,2,3,4),则X i ~N (160,202),从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥ 之间独立34{180}{180}P X P X ≥≥ 1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ== 17.设X ,Y 是相互独立的随机变量,其分布律分别为P {X =k }=p (k ),k =0,1,2,…,P {Y =r }=q (r ),r =0,1,2,….证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(,i =0,1,2,….【证明】因X 和Y 所有可能值都是非负整数,所以 {}{}Z i X Y i ==+= {0,}{1,1}{,X Y i X Y i X i Y =====-==于是0{}{,},ik P Z i P X k Y i k X Y =====-∑相互独立{}{}ik P X k P Y i k===-∑ 0()()ik p k q i k==-∑18.设X ,Y 是相互独立的随机变量,它们都服从参数为n ,p 的二项分布.证明Z =X +Y 服从参数为2n ,p 的二项分布.【证明】方法一:X +Y 可能取值为0,1,2,…,2n .{}{,}ki P X Y k P Xi Y k i =+====-∑0022(){}2ki ki n i ki nkii kk n ki k n kP X i P Y k in n p q p qi k i n n p q i k i n p qk =---+=-=-===-⎛⎫⎛⎫=⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫=⎪ ⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭∑∑∑方法二:设μ1,μ2,…,μn ;μ1′,μ2′,…,μn ′均服从两点分布(参数为p ),则X =μ1+μ2+…+μn ,Y =μ1′+μ2′+…+μn ′,X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以,X +Y 服从参数为(2n ,p )的二项分布.(2) 求V =max (X ,Y )的分布律; (3) 求U =min (X ,Y )的分布律; (4) 求W =X +Y 的分布律. 【解】(1){2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑ {3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑ (2){}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i =====<+≤=1{,}{,},i ik k P Xi Y k P Xk Y i -=====+==∑∑ 0,1,2,3,4i =所以V 的分布律为(3) {}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k ik i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑0,1,2,3i = 于是20.雷达的圆形屏幕半径为R ,设目标出现点(X ,Y )在屏幕上服从均匀分布. (1) 求P {Y >0|Y >X };(2) 设M =max{X ,Y },求P {M >0}.题20图【解】因(X ,Y )的联合概率密度为22221,,(,)π0,.x y R f x y R ⎧+≤⎪=⎨⎪⎩其他(1){0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=>0(,)d(,)dy y xy xf x y f x y σσ>>>=⎰⎰⎰⎰π2π/405π42π/41d d π1d d πR R r rRr rRθθ=⎰⎰⎰⎰3/83;1/24== (2) {0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=-≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=-≤≤=-=-=⎰⎰21.设平面区域D 由曲线y =1/x 及直线y =0,x =1,x=e 2所围成,二维随机变量(X ,Y )在区域D 上服从均匀分布,求(X ,Y )关于X 的边缘概率密度在x =2处的值为多少?题21图【解】区域D 的面积为 22ee 0111d ln 2.S x xx===⎰(X ,Y )的联合密度函数为211,1e ,0,(,)20,.x y f x y x ⎧≤≤<≤⎪=⎨⎪⎩其他(X ,Y )关于X 的边缘密度函数为1/2011d ,1e ,()220,.x X y x f x x⎧=≤≤⎪=⎨⎪⎩⎰其他所以1(2).4X f =22.设随机变量X 和Y 相互独立,下表列出了二维随机变量(X ,Y )联合分布律及关于X 和【解】因21{}{,}j j i j i P Y y P P Xx Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+== 从而11111{,}.6824P X x Y y ===-=而X 与Y 独立,故{}{}{,}i j i i P X x P Y y P X x Y y ===== , 从而11111{}{,}.624P X x P X x Y y =⨯====即:1111{}/.2464P X x ===又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+== 即1,3111{},4248P X x Y y =++==从而131{,}.12P X x Y y ===同理21{},2P Y y ==223{,}8P X x Y y ===又31{}1j j P Y y ===∑,故3111{}1623P Y y ==--=.同理23{}.4P X x ==从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====-===-=故23.设某班车起点站上客人数X 服从参数为λ(λ>0)的泊松分布,每位乘客在中途下车的概率为p (0<p <1),且中途下车与否相互独立,以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率;(2)二维随机变量(X ,Y )的概率分布.【解】(1) {|}C (1),0,0,1,2,m m n mn P Y m X n p p m n n -===-≤≤= .(2) {,}{}{|}P X n Y m P X n P Y m X n ======eC (1),,0,1,2,.!m mnmnnpp n m n n n λλ--=-≤≤= 24.设随机变量X 和Y 独立,其中X 的概率分布为X ~⎪⎪⎭⎫⎝⎛7.03.021,而Y 的概率密度为f (y ),求随机变量U =X +Y 的概率密度g (u ).【解】设F (y )是Y 的分布函数,则由全概率公式,知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|P Y u X P Y u X =≤-=+≤-=由于X 和Y 独立,可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(F u F u =-+-由此,得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u '''==-+-0.3(1)0.7(f u f u =-+-25. 25. 设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,求P {max{X ,Y }≤1}.解:因为随即变量服从[0,3]上的均匀分布,于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩ 1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩因为X ,Y 相互独立,所以1, 03,03,(,)90, 0,0,3, 3. x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩推得 1{m a x {,}1}9P XY ≤=. 26. 设二维随机变量(X ,Y )的概率分布为其中a ,(1)a,b,c的值;(2)Z的概率分布;(3)P{X=Z}.解(1) 由概率分布的性质知,a+b+c+0.6=1 即a+b+c = 0.4. 由()0.2E X=-,可得0.1a c-+=-.再由{0,0}0.1 {00}0.5{0}0.5P X Y a bP Y XP X a b≤≤++≤≤===≤++,得0.3a b+=.解以上关于a,b,c的三个方程得0.2,0.1,0.1a b c===.(2) Z的可能取值为-2,-1,0,1,2,{2}{1,1}0.2P Z P X Y=-==-=-=,{1}{1,0}{0,1}0.1P Z P X Y P X Y=-==-=+==-=,{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y===-=+==+==-=,{1}{1,0}{0,1}0.3P Z P X Y P X Y====+===,{2}{1,1}0.1P Z P X Y=====,即Z的概率分布为(3) {}{0}0.10.20.10.10.20.4P X Z P Y b====++=++=.。
