高层建筑结构随机振动的最优阻尼器控制策略_彭勇波

合集下载

磁流变阻尼器对建筑结构地震响应半主动控制分析

模型及剪切型最优控制（ｌｐｄＯｔａＣｎｏ）Ｃｉｅ — ｐｍｌｏｔ１算法对建筑结构地震响应进行了半主动控制分析研究，ｐｉｒ并
且与结构被动控制的效果进行了对比。研究结论：Ｅ —ｃｎｒ地震激励作用下，在Ｉｅｔｏ被动控制和半主动控制对结构地震响应的水平位移与速度产
Ｍａｎｔ — ｈｏｏｉａａｅａｅｂｅｐｌｄｉｏｔｏｆｔｅｖｂａｉｎｏｉｉｓｃｕｅｉｏｅｇｏｎｒｓｗｔｇｅｏ— ｒｅｌｇｃｄｍｐｒｈｖｅｎａｐｉｎｃｎｒｌｏｈｉｒｔｆｃｖｌｔｔｒｎｆｒｉｎｃｕｔｉｉａｌｓｅｏｒｕｅｈｐｒｃｃｉｖｍｅｔｈｒｈｒｔｅｒｔａｎｌｓｓａｄｔｓｒｏｅｆｒｔｅｅｒｑａｅｒｓｏｓｆｂｉｉｇｓｒｃｕｅｅｆｔａｈｅｅｎ．Ｔｅｆｔｅｏｅｉｌａａｙｅｅｔａｅｄｎｏｈａｔｕｋｅｐｎｅｏｕｌｎｔｔｒｅｕｈｃｎｓｈｄｕｂｇｅ — ｒｅｌｇｃａｐｒｆｒｈｕｐｓｆｉｅｉｇｔｅａｐｉａｉｎｏｇｅ — ｒｅｌｇｃａｅｏｓｃｉｎｙｍａｔ — ｈｏｏｉａｄｎｌｍｅｅｐｒｏｅｏｄｎｎｐｌｔｆｍａｎｔ — ｈｏｏｉａｄｍｐｒｉｃｎｔｔ．ｏｔｗｈｃｏｌｎｕｒｏ
ｌｎｔｆｉｏ，ｎｅｉｔｆｙｎｅａｄｆｉｉｏｉ）ｉｐｔｕｒｎａｄｆｑｅｃｆｉｐｅｈｒｏｉｍｔｎｅｇｏｓｎｉｎｒａｅｏｌｄｒｎｕｄｖｃｓｙ，ｎｕｒｔｎｅｕｎｙｏｍｌａｍｎｃｏｉｈｐｔｄｍｅｒｃｉｌｓｔｃｅｒｓｏ

底层大空间高层建筑自由振动的实用计算方法

底层大空间高层建筑自由振动的实用计算方法
汪梦甫
【期刊名称】《地震学刊》
【年(卷),期】1995(000)001
【摘要】以连杆节间为界，按弹性支座上的Ｔｉｍｏｓｈｅｎｋｏ悬臂梁建立剪力墙部分的振动方程，按一般框架建立框架部分的振动方程。

根据力、变形协调条件，形成底层大空间高层建筑结构的自由振动，并据此计算其自由振动。

【总页数】6页(P12-17)
【作者】汪梦甫
【作者单位】无
【正文语种】中文
【中图分类】TU973.31
【相关文献】
1.底层大空间高层建筑地震反应的混合控制研究 [J], 祁皑;刘季
2.底层大空间高位转换高层建筑振动台试验研究 [J], 马玉宏;崔杰;黄襄云;陈建秋;任珉;魏陆顺;谭平
3.底层大空间高层结构自由振动的实用计算方法 [J], 王兰生
4.底层大空间记层结构自由振动的模态综合解法 [J], 汪梦甫
5.含壁式框架的底层大空间高层建筑中落地剪力墙合理数量的确定方法 [J], 沈蒲生;廖志
因版权原因，仅展示原文概要，查看原文内容请购买。

大型超高层建筑的随机风振响应分析

收稿日期： 2009 － 02 － 17. 基金项目：国家自然科学基金资助项目（ 50608021 ）；高等学校博士学科点专项科研基金资助项目（ 20061078001 ） . 作者简介：卜国雄（ 1981 —），男，博士研究生；周福霖（ 1939 —），男，博士生导师，中国工程院院士.
［ 6］
｛ y（ t）｝ = ［｛ u（ t）｝ = Φ］
u j ｛｝ j . ∑ j =1
（6）
式中： q 为所选取的振型数； u j 为第 j 阶振型的广义位移. 根据规范，一般取 Davenport 脉动风速谱作为激励谱 S ff ，其不随高度变化. 当知道了结构各点高度处的平均风速 V j ，风荷载体型系数 Us 及迎风面面积 A j 后，就可以得出自荷载谱： S PP = UsV j A j S ff . （7）如果考虑各随机激励之间的相关性，则引入相关系数 ρ ，便可形成荷载功率谱矩阵 S PP （ ω） . S PP （ ω）为非负的 Hermite 矩阵，显然，因此可以对其进行 LDL 分解 S PP （ ω） = LDL * . D，则有：对角矩阵. 取 d = 槡 S PP （ ω） = L ·d·d·L * = （ Ld） 2 ，（ 9 ）所以，构造的 n 个（原来荷载列向量的个数）虚拟激励向量为｛ x （ t ）｝ = L · d · e i ωt . 于是求得结构的虚拟位移
（8）
D 为实式中：L 为对角元素均为 1 的下三角矩阵，
1
随机响应虚拟激励法的原理
虚拟激励法
［ 9］
的基本思想是当线性系统受到功率谱密度为 S xx （ ω）的平稳随机激励 x（ t）时，对应响应 y 的功率谱 S yy （ ω）可表示为 S yy （ ω） = | H | 2 S xx （ ω） . （1）式中： H 为频率响应函数. 即当随机激励被单位 i t 简谐激励 e ω 代替时，相应的简谐响应为 y = He . 则若在激励 e 了一虚拟激励：

地震下结构振动的最优控制算法模型比较与改进

地震下结构振动的最优控制算法模型比较与改进
杜永峰;李慧
【期刊名称】《世界地震工程》
【年(卷),期】2005(21)3
【摘要】模拟地震激励输入结构的过程,将控制目标函数化解到每个时间步长上。

用激励所产生的脉冲响应重新构造控制目标函数,直接从泛函变分出发,推导出了一种改进的最优控制算法,并用状态转移的数值方法加以实现。

从概念上讲,本算法是一种更为合理的结构最优控制算法。

算例表明,在相同控制能量下,本算法能更有效地削减响应峰值,且稳定性良好。

【总页数】7页(P57-63)
【关键词】结构动力反应;控制算法;智能隔震;最优控制;地震工程
【作者】杜永峰;李慧
【作者单位】兰州理工大学防震减灾研究所
【正文语种】中文
【中图分类】TU435
【相关文献】
1.多维地震作用下隔震桥梁地震反应(Ⅰ)——模型结构振动台试验 [J], 韩强;杜修力;刘晶波;刘文光
2.地震作用下结构振动瞬时最优控制的一种改进算法 [J], 杜永峰;刘彦辉;李慧
3.地震作用下结构振动最优控制的一种一般算法 [J], 杜永峰;李慧;赵国藩
4.结构振动序列最优控制算法及其Simulink仿真实现 [J], 孙玉萍;曹志峰;杜永峰;李慧
5.地震动作用下的结构瞬时开闭环最优控制算法 [J], 任晓崧;徐植信
因版权原因，仅展示原文概要，查看原文内容请购买。

带五种被动阻尼器的高层建筑侧移—扭转下随机风振响应的解析法

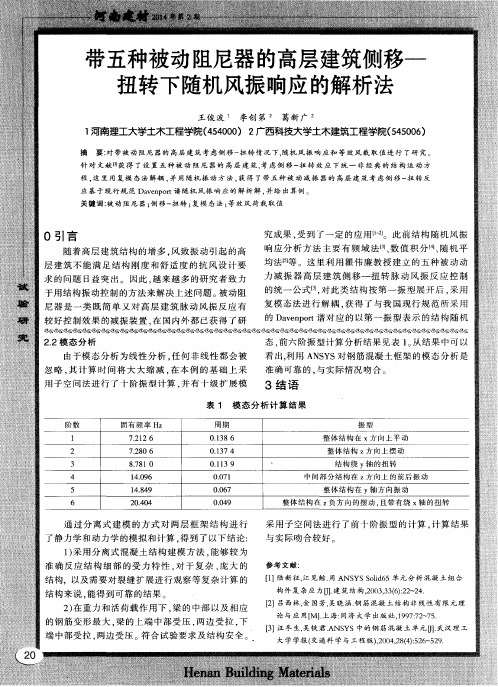
通过分பைடு நூலகம்离式建模的方式对两层框架结构进行
采用子空间法进行了前十阶振型的计算，计算结果与实际吻合较好。
参考文献：
了静力学和动力学的模拟和计算，得到了以下结论：１）采用分离式混凝土结构建模方法，能够较为准确反应结构细部的受力特性，对于复杂、庞大的
论与应用［Ｍ】．上海：同济大学出版社，１９９７：７２￣７５．
【３】汪冬生，吴铁君．ＡＮＳＹＳ中的钢筋混凝土单元Ｕ１．武汉理工
大学学报（交通科学与工程版），２００４，２８（４）：５２６－５２９．
针对文献ｌ引获得了设置五种被动阻尼器的高层建筑，考虑侧移一扭转效应下统一非经典的结构运动方程，这里用复模态法解耦，并用随机振动方法，获得了带五种被动减振器的高层建筑考虑侧移一扭转反应基于现行规范Ｄａｖｅｎｐｏｒｔ谱随机风振响应的解析解，并给出算例。
结构，以及需要对裂缝扩展进行观察等复杂计算的结构来说，能得到可靠的结果。
２）在重力和活荷载作用下。梁的中部以及相应的钢筋变形最大．梁的上端中部受压，两边受拉，下端中部受拉，两边受压。符合试验要求及结构安全。

振动控制-主动、半主动

目录0．前言 (1)0．1 结构振动控制研究与应用概况 (1)1．结构振动主动控制、半主动控制 (2)2．结构振动控制分类 (3)3．各类控制系统构造及性能 (4)3．1 结构振动主动控制概述 (4)3．1．1 主动控制控制原理 (5)3．1．2 加力方式及加力位置 (7)3．1．3 控制装置 (8)3．2 结构振动半主动控制概述 (8)4．结构振动主动控制、半主动控制算法 (11)4．1 主动控制算法 (12)4．1．2 几种算法的简单介绍 (13)4．2 半主动控制算法 (21)4．3 智能控制算法 (22)5．结构主动、半主动控制系统分析方法及设计方法 (24)5．1 主动控制系统的最优控制力设计与分析 (25)5．1．1 主动控制系统的最优控制力设计 (25)5．1．2 主动最优控制力和受控反应特征分析 (26)5．2 结构主动变阻尼和智能阻尼控制系统的最优控制力设计与分析 (30)5．2．1半主动最优控制力设计 (31)5．2．2系统反应分析 (36)5．3 结构主动变刚度控制系统的最优控制力设计与分析 (37)5．3．1主动变刚度最优控制力设计 (37)5．3．2系统反应分析 (40)6．结构振动主动控制、半主动控制系统的工程应用 (41)6．1 AMD控制系统的工程应用 (41)6．2 结构主动变刚度控制系统的工程应用 (41)6．3 结构主动变阻尼控制系统的工程应用 (42)6．4 其他结构振动控制系统的工程应用 (42)7．研究展望 (43)7．1 结构振动主动控制、半主动控制的研究与发展方向 (43)7．2 结构振动控制的有待研究的问题 (43)8．结语 (43)参考文献 (44)主动控制、半主动控制综述0．前言0．1 结构振动控制研究与应用概况结构振动控制技术与传统的依靠结构自身强度、刚度和延性来抵抗地震作用的做法不同，通过在结构中安装各种控制装置，从而达到减小结构地震反应、保障结构地震安全的目的。

建筑结构地震响应的MR阻尼器PID半主动控制

建筑结构地震响应的MR阻尼器PID半主动控制
肖跃彬
【期刊名称】《山西建筑》
【年(卷),期】2009(035)035
【摘要】根据建筑结构的特点进行了结构上的简化计算,并采用了磁流变(MR)阻尼器的Bingham模型及PID半主动控制算法对建筑结构地震响应进行了半主动控制分析研究,并且与结构被动控制的效果进行了对比,数值结果表明:在EI-centro地震激励作用下,被动控制和半主动控制对结构地震响应的水平位移与速度取得了不同的控制效果;对结构的位移及速度的控制效果,MR半主动控制均明显的优于被动控制.
【总页数】2页(P47-48)
【作者】肖跃彬
【作者单位】江西华杰建筑设计有限公司,江西,南昌,330000
【正文语种】中文
【中图分类】TU352
【相关文献】
1.基于SDMR阻尼器的建筑结构半主动控制研究 [J], 于国军;孙虎;苏波;操礼林
2.磁流变阻尼器对建筑结构地震响应半主动控制分析 [J], 陈水生;李锦华
3.基于SDMR阻尼器的建筑结构半主动控制研究 [J], 于国军;孙虎;苏波;操礼林;
4.ER/MR智能阻尼器耦联的带裙房高层建筑结构地震反应的半主动控制 [J], 瞿伟
廉;王军武;徐幼麟;陈朝晖
5.建筑结构地震响应半主动控制的遗传-模糊算法 [J], 汪权;王建国
因版权原因，仅展示原文概要，查看原文内容请购买。

建筑结构振动控制技术考核试卷

D.所有类型的建筑结构
10.以下哪些是隔震技术的主要目标？（）
A.减少地震作用下的结构响应
B.防止结构产生共振
C.提高结构的自振频率
D.降低结构的阻尼比
11.建筑结构振动控制中的混合控制策略可能包括以下哪些组合？（）
A.主动控制与被动控制
B.隔震与减震
C.结构控制与非结构控制
D.预防性控制与修复性控制
A.传感器技术
B.无人机监测
C.结构健康监测系统
D.人工巡检
15.建筑结构振动控制中的模态分析主要包括以下哪些内容？（）
A.振型分析
B.阻尼分析
C.动力特性分析
D.地震响应分析
16.以下哪些因素会影响建筑结构振动控制系统的设计？（）
A.建筑物用途
B.建筑物地理位置
C.建筑物结构类型
D.建筑物成本预算
15.以下哪种材料常用于建筑结构振动控制的摩擦阻尼器？（）
A.钢材
B.橡胶
C.铅
D.水泥
16.在调谐质量阻尼器（TMD）的设计中，质量比通常定义为多少？（）
A.质量与结构总质量的比值
B.质量与结构基础质量的比值
C.质量与结构顶部质量的比值
D.质量与结构底部质量的比值
17.以下哪种现象可能导致建筑结构振动控制系统的失效？（）
17.建筑结构振动控制技术中，被动控制系统的优点包括哪些？（）
A.不需要外部能源
B.成本较低
C.维护简单
D.控制效果稳定
18.以下哪些控制算法可以用于建筑结构振动控制？（）
A.线性二次型最优控制算法
B.模糊控制算法
C.遗传算法
D. PID控制算法
19.建筑结构振动控制中，隔震技术主要包括以下哪些类型？（）

超高层建筑结构风致振动的动力参数敏感性研究

超高层建筑结构风致振动的动力参数敏感性研究徐安;石碧青;赵若红;张志华【摘要】以广州珠江城为例,分析了超高层建筑结构风致振动对于阻尼比和峰值因子取值的敏感性.结果表明:一方面,结构的顶部加速度响应及基底倾覆弯矩响应均随阻尼比的增长呈负指数衰减规律,极端情况下,阻尼比取0.01的加速度响应计算结果比阻尼比取0.04的工况大100%以上;另一方面,由横风向涡激振动引起的基底倾覆弯矩响应对阻尼比的敏感性远大于由顺风向湍流引起的基底倾覆弯矩响应.分析认为:这是由于顺风向湍流引起的基底倾覆弯矩响应很大一部分由平均风荷载贡献,而该部分在计算过程中是按照静力荷载施加在结构上的,不受阻尼比取值的影响.在不利风向角工况下,峰值因子取值在2.5～3.5的范围内变化时,加速度响应及基底倾覆弯矩的变化幅度基本在20%以内.【期刊名称】《广州大学学报（自然科学版）》【年(卷),期】2011(010)001【总页数】6页(P54-59)【关键词】高层建筑;风洞试验;动力参数;随机振动【作者】徐安;石碧青;赵若红;张志华【作者单位】广州大学广州大学-淡江大学工程结构灾害与控制联合研究中心,广东,广州,510006;汕头大学土木工程系,广东,汕头,515063;广州大学广州大学-淡江大学工程结构灾害与控制联合研究中心,广东,广州,510006;广州大学广州大学-淡江大学工程结构灾害与控制联合研究中心,广东,广州,510006【正文语种】中文【中图分类】TU973.32;TU317.2风荷载是超高层建筑结构水平控制荷载之一.在进行结构设计前，通常需要进行风洞测压试验获取作用在结构上的脉动风荷载，进一步结合结构有限元模态分析所得到的动力参数进行风振响应计算.显然，结构的响应是由风荷载和结构动力参数共同决定的［1－3］.风荷载一般取决于风环境及结构外形，如果忽略风场与建筑物的流固耦合效应，在建筑设计方案确定后，风荷载就已确定.结构动力参数则包括结构的固有频率、振型和阻尼比.其中固有频率和振型一般直接采用有限元模型的模态分析结果，阻尼比的取值成为风振响应分析中动力参数取值的关键问题［4］. 一般而言，在结构风致响应计算过程中都采用常阻尼比假设，对于不同的实际项目，取值区间大致在0.01 ～0.04 之间［5－6］.实际采用的取值只能根据建筑物高度、主要结构形式、整体刚度等要素采用经验估计的方式来确定.而不同的取值对结构响应计算结果则存在一定影响，因而在结构设计时，对阻尼比取值的确定常需要经过反复讨论.此外，峰值因子的取值对结构响应计算结果也有着一定影响.峰值因子实际上只是结构响应计算参数而非动力参数，但其取值一般采用经验方式取2.5～3.5之间的某个常数，或者是按照 Davenport一次穿越理论自动计算峰值因子［7］.因而峰值因子的取值方式在一定程度上类似于阻尼比的取值，即根据经验确定，不同的风工程研究人员取值不一定完全一致，这或许将导致计算结果的差异［8］.以广州珠江新城CBD区域的标志性建筑珠江城为工程案例，研究了高层建筑风振响应的2个主要参考量:结构顶部加速度及基底倾覆弯矩对于阻尼比和峰值因子取值的敏感性，所得结果可供其他类似结构风振响应分析参考.珠江城项目地下5层，地上71层，±0.000 m以上，总高度309.6 m.外围由周边钢柱和钢梁组成，内部为钢筋混凝土核心筒.第23～27层和第49～53层在核心筒东西两侧安装风力发电机，由于这个独特的设计，整个结构的传力在这2个部位发生了一定的改变.位于第23～27和第49～53层的外伸及带状桁架，把外围周边4根大柱与内部钢筋混凝土巨型核心筒剪力墙系统，以及由端部斜支撑连接起来的组合钢柱相连接，共同组成了整体结构的主要抗侧力系统，抵抗水平风载及水平地震作用，其中外伸桁架在水平荷载的传递方面扮演了重要角色.珠江城外观效果如图1所示.本项目的模态参数采用结构设计单位所提供的结果，前3阶自振周期分别为6.855 s、5.522 s和3.875 s.下文将对峰值加速度、基底弯矩响应2个重要指标对应于不同阻尼比及峰值因子取值所得到的计算结果进行比较分析.本项目的风洞试验及风振响应计算采用图2所示的坐标系，风向角以X轴为方向顺时针转动.测压模型用有机玻璃材料制成，模型的几何缩尺比为1∶400.根据建筑的体型和试验要求，在模型表面布置了15个测点层共367个测压点.地貌类型按C类考虑，地貌指数为0.22，试验以36个风向角在湍流边界层来流条件中进行，如图3所示.风洞试验采样频率312.5 Hz，采样帧数为20 480.由于峰值因子取值对计算结果有较为直接的影响，此处考察2种峰值因子取值的工况.图4为峰值因子取g=2.5时，对应不同的结构自振周期的顶部最大峰值加速度随阻尼比的变化曲线，其中，T0表示设计院提供的结构自振周期工况;1.1表示将结构各阶自振周期放大1.1倍的工况，其余类推.峰值基底弯矩分50 a和100 a重现期2种情况，由于结构特征的缘故，珠江城基本是受Mx(绕X轴的基底弯矩)控制的.根据不同参数的各种风向角试验结果，发现Mx的最大值出现在180度和280度风向角，前者本质是横风向的涡激振动效应，后者则是顺风向湍流引起的.图5～6给出这2个风向角的分析结果.由图4可见，结构顶部加速度响应随阻尼比的增加而单调递减，衰减规律接近于负指数函数.实际上，在超高层建筑风振分析的实际工程应用中，关于阻尼比的取值存在一定争议，超高层建筑物阻尼比受到主体结构，填充墙等非结构构件以及装饰装修等因素的影响，其合理取值在建筑物尚未建成之前是难以确定的.部分超高层建筑在进行风振响应分析时，其阻尼比取为0.04，根据上述研究结果，如果其实际阻尼比为0.01，则其实际加速度响应将比采用0.04阻尼比计算结果大100%以上.图5～6显示了180度和280度风向角下基底倾覆弯矩对于阻尼比的敏感性.如前所述，180度风向角下的倾覆弯矩Mx主要是由横风向涡激振动引起的，而280度风向角下的倾覆弯矩Mx主要是由顺风向湍流引起的.结果显示，它们对于阻尼比的敏感性是不同的.在180度风向角下，阻尼比取0.04时所得到的倾覆弯矩Mx 比阻尼比取0.01时下降了接近50%，而在280度风向角工况下，阻尼比取0.04时所得到的倾覆弯矩My比阻尼比取0.01时下降了约20%.这说明，横风向涡激振动引起的倾覆弯矩对于阻尼比的敏感性远大于顺风向湍流.上述分析中，峰值因子均取2.5，在实际工程中也有采用Davenport一次穿越理论确定峰值因子的案例.随机荷载或响应x(t)的峰值或等效值通常采用下式计算: 其中和σx分别为均值和均方根值;g为峰值因子，可用Davenport基于一次穿越理论提出的表达式估算:其中，v是平均循环比率;T为观察时间，可视为基本风压的取值时距即10 min，平均循环比率v取决于荷载的功率谱S(n)，其关系为其中，n是脉动频率，视不同结构和风速;g值的范围可能会在3.0～3.5之间.按上述公式自动计算峰值因子g时，不同自振周期工况结构顶部最大峰值加速度随阻尼比的变化曲线，见图7.由图7～9可见，在取峰值因子按式(1)～(3)计算时，结构顶部加速度响应和基底弯矩响应随阻尼比的变化规律与峰值因子取2.5时类似，但由于按式(1)～(3)计算的峰值因子比2.5大，因此得到的加速度响应和基底倾覆弯矩响应值也就更大.峰值因子是风振响应分析中除结构阻尼比外另一个取值具有一定不确定性的量，下面考察不同峰值因子取值对结构风振响应的影响.共计算了4种峰值因子取值情况的顶部加速度响应和基底弯矩响应，即 g=2.5，3.0，3.5 和用式(1) ～ (3)自动计算g值.图10列出了对于不同峰值因子取值情况得到的顶部峰值加速度和基底峰值弯矩Mx随风向角的变化曲线，自振周期不作改变.由图10(a)、(b)可见，不论是何种峰值因子取值情况，结构顶部峰值加速度均没有超过有关规范的限定值.这表明在现有的结构参数下，舒适度可以满足要求.2.0%阻尼比和1.5%阻尼比2种工况下，对应于不同峰值因子取值，加速度响应随风向角变化的趋势是类似的.由图示可见，自动计算峰值因子的加速度响应结果基本处于峰值因子取3.0和3.5的对应的计算结果之间，而峰值因子取2.5的结果比自动计算结果小约20% ～30%.峰值因子取值对基底倾覆弯矩的影响与对加速度的影响是类似的.按照Davenport 一次穿越理论自动计算峰值因子所得到的弯矩响应结果处于峰值因子取3和3.5所得结果之间.图10、图11显示在加速度和倾覆弯矩最大的极限风向角下，不同的风致因子取值对计算结果的影响基本在20%以内.以珠江城为案例，进行了刚性模型多点同步测压风洞试验，采用不同的阻尼比和峰值因子取值计算了结构顶部加速度响应以及基底倾覆弯矩响应，得到了以下基本结论:①结构顶部加速度及基底倾覆弯矩均随着结构阻尼比的增大呈近似指数律衰减规律;②阻尼比取0.04时的顶部峰值加速度响应比取0.01时降低50%左右，这表明，顶部加速度响应的计算结果对阻尼比是比较敏感的;③横风向涡激振动引起的基底倾覆弯矩与顺风向湍流引起的涡激振动对于阻尼比取值的敏感性是不同的，前者对于阻尼比取值的敏感性远大于后者，分析认为，这是由于顺风向湍流引起的基底倾覆弯矩响应很大一部分由平均风荷载贡献，而该部分在计算过程中是按照静力荷载施加在结构上的，不受阻尼比取值的影响;④在通常的峰值因子取值范围内(g=2.5～3.5)，不利风向角下的顶部加速度响应及基底倾覆弯矩响应的计算结果相对误差在20%以内.一些学者对于超高层建筑结构风致振动现场实测的相关研究结果表明，其阻尼比并非常数，而是一个与振幅呈非线性关系的量，由于目前进行现场实测的案例仍然是非常有限的，关于阻尼比合理取值的问题仍有待深入研究.【相关文献】［1］ XIE Zhuang-ning，FANG Xiao-dan，NI Zheng-hua，et al.Study of wind effects of Guangzhou West Tower［J］.Journal of Building Structures，2009，30(1):107-114.(in Chinese)［2］ SHIBi-qing，XIE Zhuang-ning，NI Zheng-hua.Study of wind effects of Guangzhou West Tower using high-frequence-force balance method［J］.China Civil Engineering Journal，2008，41(2):42-48.(in Chinese)［3］ JIXue-pei，XIE Zhuang-ning，LIXiao-kang.An experimental study on the wind induced response and aerodynamic damping of Guangzhou West Tower［J］.China Civil Engineering Journal，2009，42(7):59-64.(in Chinese)［4］ WU JR，LIU P F，LIQ S.Effects of nonlinear damping and time constant on wind-induced responses of a 79-story tall building［J］.Computers ＆ Structures.2007，85:1014-1021.［5］ XU Y L，CHEN SW，ZHANG R C.Modal identification of DiWang Building under typhoon York using the Hilbert-Huang transform method［J］.The Structural Design of Tall and Special Building，2003(12):21-47.［6］ LIQ S，WU JR.Time-frequency analysis of wind characteristics and wind-induced responses of a super tall building during a typhoon［C］∥ Proceedings of the Sixth Asia-Pacific Conference on Wind Engineering，Seoul，2005:1321-1336.［7］ SOLARIG，PICARDO G.Probabilistic 3-D turbulence for gust buffeting of structures ［J］.Probabilistic Engineering Mechanics，2001(16):73-86.［8］ JEARY A P.Establishing non-linear damping characteristics of structures from non-stationary time-histories［J］.The Structural Engineer，1992，70:61-66.参考文献:［1］谢壮宁，方小丹，倪振华，等.广州西塔风效应研究［J］.建筑结构学报，2009，30(1):107-114.［2］石碧清，谢壮宁，倪振华.用高频底座力天平研究广州西塔的风效应［J］.土木工程学报，2008，41(2):42-48.［3］嵇学培，谢壮宁，李小康.广州西塔风致响应和气动阻尼特性的试验研究［J］.土木工程学报，2009，42(7):59-64.【责任编辑:刘少华】。

高层建筑地震反应的TLD振动控制

高层建筑地震反应的TLD振动控制
陈招平;董平;黄丽婷
【期刊名称】《建筑科学与工程学报》
【年(卷),期】2008(025)001
【摘要】利用调谐液体阻尼器(Tuned Liquid Damper,TLD)对高层建筑地震反应进行振动控制研究.根据Fujino等提出的矩形TLD减振基本原理,建立了TLD中液体动水压力的控制方程,并采用有限差分法对矩形浅水TLD液体动水压力进行数值模拟,然后根据1栋91.0 m的高层建筑实际情况提出几种TLD设计方案,分别对其进行TLD-结构地震作用下的动力分析,比较几种方案的减振效果,确定最佳方案及具体的结构振动控制设计.结果表明,TLD系统对高层建筑地震作用下的加速度反应和位移反应均具有比较好的控制效果.
【总页数】5页(P122-126)
【作者】陈招平;董平;黄丽婷
【作者单位】华中科技大学,土木工程与力学学院,湖北,武汉,430074;华中科技大学,土木工程与力学学院,湖北,武汉,430074;华中科技大学,土木工程与力学学院,湖北,武汉,430074
【正文语种】中文
【中图分类】TU311.3
【相关文献】
1.用多重TLD减小高层建筑地震反应的控制研究 [J], 石艳妮;贾影
2.高层建筑地震反应多重TLD控制研究 [J], 李承;李忠献
3.高层建筑地震反应最优多重TLD控制 [J], 李忠献;王森林;姜忻良
4.矩形TLD在结构振动控制中的性能试验研究 [J], 董平;陈招平
5.不同参数对TLD振动控制作用的影响 [J], 贾影;赵林;余枫
因版权原因，仅展示原文概要，查看原文内容请购买。

带五种被动阻尼器的高层建筑侧移——扭转下随机风振响应的解析法

带五种被动阻尼器的高层建筑侧移——扭转下随机风振响应
的解析法
王俊波;李创第;葛新广
【期刊名称】《河南建材》
【年(卷),期】2014(000)002
【摘要】对带被动阻尼器的高层建筑考虑侧移-扭转情况下,随机风振响应和等效风载取值进行了研究.针对文献[3]获得了设置五种被动阻尼器的高层建筑,考虑侧移-扭转效应下统一非经典的结构运动方程,这里用复模态法解耦,并用随机振动方法,获得了带五种被动减振器的高层建筑考虑侧移-扭转反应基于现行规范Davenport谱随机风振响应的解析解,并给出算例.
【总页数】6页(P20-25)
【作者】王俊波;李创第;葛新广
【作者单位】河南理工大学土木工程学院 454000;广西科技大学土木建筑工程学院 545006;广西科技大学土木建筑工程学院 545006
【正文语种】中文
【相关文献】
1.带Maxwell阻尼器的高层建筑结构基于Davenport谱随机风振响应的解析解法[J], 王俊波;范国辉;余强;苏永章
2.带粘弹性阻尼器的多高层建筑基于Davenport谱随机风振响应的精确解法 [J], 邹奕男;罗臻
3.广义Maxwell阻尼器高层结构随机风振响应解析法 [J], 李创第;王磊石;邹万杰;
葛新广;李暾
4.带粘滞阻尼器结构随机风振响应分析 [J], 高传友; 王俊波
5.可调液体—质量阻尼器对高层建筑侧移—扭转风振响应的控制 [J], 梁枢果因版权原因，仅展示原文概要，查看原文内容请购买。

高层建筑结构设计中的隔震减震措施

高层建筑结构设计中的隔震减震措施摘要：在我国经济高速发展的背景下，城市建筑的高度也在不断增加，这给我国的建筑抗震减震工作带来了极大挑战。

本文从隔震减震支座、建筑设施的走向、高层建筑结构选择三个角度，阐述了当前高层建筑中存在的有关隔震减震性能的设计问题，并对此提出了相应的解决措施，在保证建筑效率的前提下，全面提升高层建筑的隔震减震设计质量，从而提高我国高层建筑的安全性和稳定性。

关键词：高层建筑；隔震减震；结构设计；策略分析多年来，我国地震带附近地区地震频繁，这给我国经济和人民生活带来了极大冲击。

所以，如何有效进行建筑，尤其是高层建筑的防震减震工作成为我国建筑行业关注的焦点。

《建设工程抗震管理条例》中明确要求高烈度地区、地震重点监视防御区的八大类建筑应当充分应用减隔振技术，以保障居民的生命安全。

随着我国建筑水平的提高，抗震隔震技术也越来越成熟，以从多个角度、多种途径达到提高建筑抗震减震工作质量的目的。

1.高层建筑结构的隔震减震设计中存在的问题1.1隔震减震支座总体来看，防震支架的设计会受到防震墙的影响，在进行隔震减震墙的设计时，必须遵循分散的设计原则，不能在建筑物的四周设置隔震减震墙，这样不仅会增加地震墙的倾倒力，还会对隔震支座的性能造成一定影响。

在荷载较大的部位，必须设置抗震缓冲支架，并与相应的支撑装置一起提高整体质量，使各项减震措施的效果最大化，确保其能够提高建筑的质量[1]。

1.2建筑设施的走向地震是由地壳运动引起的一种比较普遍的自然现象。

因此，在进行高层建筑的结构设计时，一定要重视对当地地质构造的分析，因为一旦发生地震，将会影响到房屋和设备的正常使用，进一步导致房屋倒塌。

在地震发生时，必须正确地调整地震中建筑的振动方向，并根据建筑物的实际地质和水文情况，使建筑物的结构与震源方向保持垂直，而不能与震源水平。

这主要是由于建筑物的朝向与地震方向平行，会增加建筑物坍塌的危险，而维持竖直关系的建筑物则不太可能发生坍塌。

结构阻尼比对超高层建筑顺风向风振响应的影响

d o i :10.3963/j.i s s n .1674-6066.2024.01.023结构阻尼比对超高层建筑顺风向风振响应的影响郭小飞1,2,袁哲峰1,2,王瑞1,2,牛方义1,2(1.中国建筑科学研究院有限公司,北京100013;2.建研院检测中心有限公司,北京100013)摘要: 以某超高层建筑结构为工程研究背景,主要研究了阻尼比对风振响应(基底剪力㊁楼层位移㊁加速度)的影响,结果表明:阻尼比较大时,其对结构顺风向的风振响应影响较小;随着阻尼比的增加,风振响应(基底剪力㊁楼层位移)最大值减小幅度较大,而均方根值和平均值减小幅度较小,几乎无太大变化;随着阻尼比的增加,顶层加速度最大值㊁最小值和均方根值变化量比较大,而平均值几乎无变化㊂关键词: 风振系数; 阻尼比; 超高层建筑; 风振响应I n f l u e n c e o f S t r u c t u r a lD a m p i n g Ra t i o o n W i n d w a r dV ib r a t i o n R e s p o n s e o f S u p e rT a l l B u i l d i n gs G U OX i a o -f e i 1,2,Y U A N Z h e -f e n g 1,2,WA N GR u i 1,2,N I UF a n g -yi 1,2(1.C h i n aA c a d e m y o fB u i l d i n g R e s e a r c hC o ,L t d ,B e i j i n g 100013,C h i n a ;2.C A B RT e s t i n g C e n t e rC o ,L t d ,B e i j i n g 100013,C h i n a )A b s t r a c t : T a k i n g a s u p e r h i g h -r i s e b u i l d i n g s t r u c t u r e a s t h e e n g i n e e r i n g r e s e a r c hb a c k g r o u n d ,t h e i n f l u e n c e o f d a m p -i n g r a t i oo nw i n d i n d u c e dv i b r a t i o nr e s p o n s e (b a s es h e a r f o r c e ,f l o o rd i s p l a c e m e n t ,a c c e l e r a t i o n )w a sm a i n l y s t u d i e d .T h e r e s u l t s a r e a s f o l l o w s .W h e n t h ed a m p i n g r a t i o i s l a r g e ,i t s i m p a c t o nt h ew i n d -i n d u c e dv i b r a t i o nr e s po n s eo f t h e s t r u c t u r e i n t h e d o w n w i n dd i r e c t i o n i s r e l a t i v e l y s m a l l .A s t h e d a m p i n g r a t i o i n c r e a s e s ,t h em a x i m u mv a l u e o fw i n d i n -d u c e d r e s p o n s e (b a s e s h e a r f o r c e ,f l o o r d i s p l a c e m e n t )d e c r e a s e s s i g n i f i c a n t l y ,w h i l e t h e r o o tm e a n s q u a r e v a l u e a n d a v -e r a g e v a l u e d e c r e a s e s l i g h t l y ,w i t ha l m o s tn os i g n i f i c a n t c h a n g e .A s t h ed a m p i n g r a t i o i n c r e a s e s ,t h e m a x i m u m ,m i n i -m u m ,a n d r o o tm e a n s q u a r e v a l u e s o f t h e t o p -l e v e l a c c e l e r a t i o n c h a n g e s i g n i f i c a n t l y ,w h i l e t h e a v e r a g e v a l u e r e m a i n s a l -m o s t u n c h a n ge d .K e y wo r d s : w i n dv i b r a t i o n c o e f f i c i e n t ; d a m p i n g r a t i o ; s u p e r t a l l b u i l d i n g s ; w i n d i n d u c e dv i b r a t i o n r e s p o n s e 收稿日期:2023-08-30.基金项目:中国建筑科学研究院有限公司青年基金项目(20230112331030034).作者简介:郭小飞(1995-),工程师.E -m a i l :838208250@q q.c o m 结构阻尼比是用来表示结构阻尼的大小,是用于结构在振动过程中能量耗散的基本术语[1]㊂阻尼比是超高层建筑结构风振响应分析中所要考虑的重要参数,直接决定着风荷载及风振系数的取值,进而会影响到超高层建筑结构的工程总造价㊂因此,论文研究阻尼比对超高层建筑结构的风振系数㊁基底剪力㊁加速度㊁位移等影响,为工程结构设计和规范的修正提供有效参考价值㊂限于篇幅,D a v e n po r t 脉动风速谱对应的风荷载时程数据和工程概况参见论文‘基于线性滤波法的超高层建筑脉动风速时程模拟“[2]㊂1 风振系数分析方法风荷载是高层建筑结构㊁高耸结构以及大跨度空间网壳结构设计时主要考虑的水平荷载之一㊂而在实际的抗风设计研究中,常常运用风振系数来表示㊂常用的风振系数分析方法有两种形式,分别为荷载风振系数和位移风振系数㊂荷载风振系数为结构节点的静力风荷载及脉动风荷载的总和与静力风荷载的比值;位移风振系数为结构节点的静力风荷载和脉动风荷载产生的位移总和与静力风荷载产生的位移的比值[3]㊂采用规范[4]给出的荷载风振系数进行研究,公式为79建材世界 2024年第45卷第1期β(z )=F k (z )+F d (z )F k(z )(1)式中,F k (z )为顺风向单位高度静力风荷载(k N /m ),可由式(2)得出㊂F k (z )=w 0μs μz (z )B (2)式中,F d (z )为顺风向单位高度动力风荷载(k N /m ),可由式(3)计算㊂F d (z )=m (z )(2πn i )2φi (z )g σy i (z )(3)式中,m (z )为单位高度质量;n i 为第i 阶频率;φi (z )为第i 阶振型;g 为峰值因子;σy i (z )为第i 阶振型z 高度处的位移均方根㊂我国规范对体型规则的建筑结构且其仅仅考虑一阶振型,风振简化计算公式为[4]β(z )=1+ξ1η1φ1(z )μz (z )(4)式中,ξ1为脉动增大系数;η1为脉动影响系数㊂2 结构阻尼比对风振系数影响公式结构阻尼比对建筑结构的影响作用主要体现在建筑结构的风致振动中,风振响应分析方法有频域法和时域法㊂在实际的工程结构设计时,为使工程师能够方便应用,我国‘建筑结构荷载规范“(G B 50009 2012)[4]采用等效静力风荷载来计算结构的风致响应㊂下面将根据第一节介绍的内容对规范给出的风振系数公式进行推导,并详细介绍阻尼比对风振系数的影响㊂由式(3)可知,σq1为顺风向一阶广义位移均方根,当假设相干函数与频率没有关系时,可由式(5)计算σq 1=2w 0I 10B μs ω21mˑʏB 0ʏB 0c o h xx 1,x ()2d x 1d x2ʏHϕ21()z d z ˑʏ¥H j i ()w 2w 41S f (w )d w ˑʏHʏH 0[μz (z 1)ϕ1(z 1)I -z (z 1)μz (z 2)ϕ1(z 2)I -z (z 2[])w h z z 1,z ()2d z 1d z 2(5) 将风振响应近似取为准静态的背景分量及窄带共振响应分量之和㊂则式(5)与频率有关的积分项可近似表示为ʏ¥0H q 1i ()w 2w 41S f ()w dw ʈ1+R 2(6) 而式(5)中与频率无关的积分项乘以ϕ1(z )/μz (z )后以背景分量因子表示为B z =ʏHʏH 0[μz (z 1)ϕ1(z 1)I -z (z 1)μz (z 2)ϕ1(z 2)I -z (z 2[])w h z (z 1,z 2)d z 1d z 2ʏH 0ϕ21(z )d zˑʏB 0ʏB0c o h x (x 1,x 2)d x 1d x 2ˑϕ1(z )μz (z )(7) 将式(2)㊁式(3)㊁式(5)~式(7)代入式(1),就可以得到我国‘建筑荷载规范“[3]给出的风振系数计算表达式为βz =1+2g Ι10B z1+R 2(8)式中,脉动风荷载共振分量因子R 可由式(9)计算㊂R =πf 1S f (f 1)4ξ1(9)式中,S f 为归一化风速谱,采用D a v e n p o r t 教授建议的经典风速功率谱公式,则S f (f )=2x 23f (1+x 2)43(10) 由式(9)和式(10)就可以得到规范共振因子表达式89建材世界 2024年第45卷第1期R =π6ξ1x 21(1+x 21)43(11)x 1=30f 1k wω0 , x 1>5(12)式中,f 1为结构的第一阶自振频率(H z );k w 为地面粗糙度修正系数;ξ1为结构阻尼比㊂由式(8)可以看出,阻尼比对风振系数的影响体现在共振风量因子上,并且阻尼比ξ1取值越小,风振系数公式中的共振响应因子R 会越大,也就意味着风振系数βz 越大,进而会导致计算风荷载越大㊂3 阻尼比对风振系数的影响在进行超高层建筑结构风振响应分析过程中,阻尼比是一个不确定但又非常重要的因素㊂对于一般的钢筋混凝土结构或钢结构,阻尼比一般取值为0.01~0.05之间,为了精确地分析阻尼比对风振系数的影响,该文选择阻尼比为0.01㊁0.02㊁0.03㊁0.04㊁0.05㊁0.07㊁0.1进行分析㊂图1分别给出了第100层㊁第89层及第77层风振系数随着结构阻尼比的变化规律曲线㊂由此可以看出,随着阻尼比的增加荷载风振系数逐渐变小,并且变化规律渐渐趋于平缓,在结构阻尼比小于0.05时荷载风振系数缓慢变小,而在结构阻尼比大于0.05时荷载风振系数几乎无变化,这说明阻尼比较大时对结构顺风向的风振响应影响比较小㊂4 阻尼比对基底剪力的影响为了更好地了解阻尼比对建筑结构风荷载效应的影响,表1给出了不同阻尼比下结构的基底剪力最大值㊁平均值和均方根值㊂由此可以看出,整体上结构的基底剪力最大值㊁平均值和均方根值随着阻尼比的增大而减小,且结构基底剪力最大值随着阻尼比的增加减小幅度较大,而平均值和均方根值减小幅度较小,几乎无变化㊂当阻尼比从0.01增加到0.02,基底剪力最大值减小了12.69%,均方根减小了0.80%㊂当阻尼比由0.02增加到0.03,基底剪力最大值减小了4.96%,均方根减小了0.30%㊂当阻尼比由0.03增加到0.04,基底剪力最大值减小了2.77%,均方根减小了0.12%㊂当阻尼比由0.04增加到0.05时,基底剪力最大值减小了1.45%,均方根减小了0.06%㊂当阻尼比由0.05增加到0.07时,基底剪力最大值减小了2.06%,均方根减小了0.06%㊂当阻尼比由0.07增加到0.1时,基底剪力最大值减小了1.70%,均方根减小了0.04%㊂表1 不同阻尼比对基底剪力影响/k N阻尼比最大值平均值均方根值阻尼比最大值平均值均方根值0.0154786.5234012.8334631.530.0543562.6234011.0434191.250.0247832.1634012.6334355.800.0742665.1334010.7634170.730.0345461.6134012.1134253.140.141940.6834010.4734156.360.0444201.7834011.6034212.085 阻尼比对位移的影响图2给出了部分楼层位移最大值随阻尼比的变化规律㊂图3给出了部分楼层位移均方根值随阻尼比的变化规律㊂图4给出了部分楼层位移平均值随阻尼比的变化规律㊂由图可知,60层㊁69层㊁78层㊁90层和100层的楼层位移最大值㊁均方根值和平均值随着阻尼比的变化规律基本一致,随着阻尼比的增加楼层位移最大值减小幅度较大,而均方根值和平均值减小幅度较小,几乎无太大变化,尤其是阻尼比大于0.03时㊂当阻尼比由0.01增加到0.02,100层的楼层位移最大值减小了8.73%,均方根值减小了0.28%㊂当阻尼比由99建材世界 2024年第45卷第1期0.02增加到0.03,100层的楼层位移最大值减小了5.80%,均方根值减小了1.37%㊂当阻尼比由0.03增加到0.04,100层的楼层位移最大值减小了3.31%,均方根值减小了0.19%㊂当阻尼比由0.04增加到0.05,100层的楼层位移最大值减小了2.16%,均方根值减小了0.09%㊂当阻尼比由0.05增加到0.07,100层的楼层位移最大值减小了2.54%,均方根值减小了0.09%㊂当阻尼比由0.07增加到0.1,100层的楼层位移最大值减小了1.82%,均方根值减小了0.06%㊂6 阻尼比对加速度的影响表2给出了顶层加速度最大值㊁最小值㊁平均值和均方根值随阻尼比的变化规律㊂由此可知,随着阻尼比的增大,顶层加速度最大值㊁最小值和均方根值变化量比较大,而平均值几乎无变化㊂当阻尼比从0.01增加到0.02,顶层加速度最大值减小了33.85%,最小值增大了33.87%,均方根减小了15.36%㊂当阻尼比从0.02增加到0.03,顶层加速度最大值减小了21.06%,最小值增大了22.52%,均方根减小了28.17%㊂当阻尼比从0.03增加到0.04,顶层加速度最大值减小了15.72%,最小值增大了16.39%,均方根减小了13.34%㊂当阻尼比从0.04增加到0.05,顶层加速度最大值减小了12.02%,最小值增大了12.67%,均方根减小了10.38%㊂当阻尼比从0.05增加到0.07,顶层加速度最大值减小了8.48%,最小值增大了16.59%,均方根减小了15.08%㊂当阻尼比从0.07增加到0.1,顶层加速度最大值减小了8.51%,最小值增大了13.47%,均方根减小了15.73%㊂表2 阻尼比对顶层加速度的影响/(mm ㊃s-2)阻尼比最大值最小值平均值均方根值阻尼比最大值最小值平均值均方根值0.01122.09-109.410.0338.210.0547.27-40.930.0218.040.0280.76-72.350.0332.340.0743.26-34.140.0215.320.0363.75-56.060.0323.230.139.58-29.540.0112.910.0453.73-46.870.0220.137 结语阻尼比较大时对结构顺风向的风振响应影响较小㊂随着阻尼比的增加风振响应(基底剪力㊁楼层位移)最大值减小幅度较大,而均方根值和平均值减小幅度较小,几乎无太大变化㊂随着阻尼比的增加顶层加速度最大值㊁最小值和均方根值变化量比较大,而平均值几乎无变化㊂参考文献[1] 金虎.X 型超高层建筑三维风荷载与风致响应研究[D ].杭州:浙江大学,2008.[2] 常乐,郭小飞.基于线性滤波法的超高层建筑脉动风速时程模拟[J ].工程质量,2020,38(11):76-81.[3] 毛贵牛.高层建筑结构风振时程分析方法研究[D ].广州:华南理工大学,2010.[4] G B50009 2012,建筑结构荷载规范[S ].北京:中国建筑工业出版社,2012.01建材世界 2024年第45卷第1期。

五种被动动力减振器对高层建筑脉动风振反应控制的实用设计方法

五种被动动力减振器对高层建筑脉动风振反应控制的实用设计方法高层建筑在面对脉动风振反应时，需要采用被动动力减振器来控制结构的振动。

被动动力减振器是一种通过结构振动的能量转移来减少结构振动的装置。

本文将介绍五种被动动力减振器的实用设计方法，以帮助工程师在高层建筑设计中更好地控制脉动风振反应。

1. 液体阻尼器液体阻尼器是一种通过液体的黏性阻力来减少结构振动的装置。

液体阻尼器的设计需要考虑液体的黏性、密度和容积等因素。

在高层建筑中，液体阻尼器通常被安装在结构的顶部或底部，以减少结构的水平振动。

2. 摆式质量阻尼器摆式质量阻尼器是一种通过质量的振动来减少结构振动的装置。

摆式质量阻尼器的设计需要考虑质量的大小、摆的长度和摆的摆动角度等因素。

在高层建筑中，摆式质量阻尼器通常被安装在结构的顶部或底部，以减少结构的水平振动。

3. 弹簧质量阻尼器弹簧质量阻尼器是一种通过弹簧的振动来减少结构振动的装置。

弹簧质量阻尼器的设计需要考虑弹簧的刚度、质量的大小和弹簧的振动频率等因素。

在高层建筑中，弹簧质量阻尼器通常被安装在结构的顶部或底部，以减少结构的垂直振动。

4. 液体弹簧阻尼器液体弹簧阻尼器是一种通过液体和弹簧的振动来减少结构振动的装置。

液体弹簧阻尼器的设计需要考虑液体的黏性、弹簧的刚度和质量的大小等因素。

在高层建筑中，液体弹簧阻尼器通常被安装在结构的顶部或底部，以减少结构的水平振动。

5. 液体摆式质量阻尼器液体摆式质量阻尼器是一种通过液体和质量的振动来减少结构振动的装置。

液体摆式质量阻尼器的设计需要考虑液体的黏性、质量的大小和摆的长度等因素。

在高层建筑中，液体摆式质量阻尼器通常被安装在结构的顶部或底部，以减少结构的水平振动。

在实际设计中，需要根据具体的工程情况选择合适的被动动力减振器，并进行合理的设计和安装。

同时，还需要进行模拟分析和实验验证，以确保被动动力减振器的有效性和可靠性。

通过合理的设计和选择，被动动力减振器可以有效地控制高层建筑的脉动风振反应，提高结构的安全性和舒适性。

钢结构建筑设计中的振动控制研究

2019-2020年高中物理第五章曲线运动第七节生活中的圆周运动预习导航
学案新人教版必修
2．向心力的来源
(1)若转弯时内外轨一样高，则由外轨对轮缘的弹力提供向心力，这样，铁轨和车轮极易受损。

(2)内外轨有高度差。

依据转弯半径和速度，适当选择内外轨的高度差，使转弯时所需的向心力由支持力和重力的合力来提供。

二、拱形桥
1．向心力的来源：汽车以速度v 过半径R 的凸形(或凹形)桥时受力如图所示，在最高点(或最低点)处，由重力和支持力的合力提供向心力。

2．在凸形桥上，速度越大，F N 越小，向心力越大；
3．在凹形桥上，速度越大，F N 越大，向心力越大。

三、航天器中的失重现象
1．航天器在近地轨道的运动：
(1)对于航天器，重力充当向心力，满足的关系为mg ＝m v 2R
，航天器的速度v ＝gR 。

(2)对于航天员，由重力和座椅的支持力提供向心力，满足的关系为mg －F N ＝mv 2R
，由此可得F N ＝0，航天员处于失重状态，对座椅无压力。

2．对失重现象的认识：航天器内的任何物体都处于完全失重状态，但并不是物体不受重力。

正因为受到重力作用才使航天器连同其中的乘员环绕地球转动。

四、离心运动
1．定义：物体沿切线飞出或做逐渐远离圆心的运动。

2．原因：向心力突然消失或合外力不足以提供所需的向心力。

3．应用：洗衣机的脱水桶，XXX 无缝钢管、水泥管道、水泥电线杆等。

工程结构随机地震响应分析的大质量扩阶解法

工程结构随机地震响应分析的大质量扩阶解法曹春青【摘要】为简化求解平稳过滤白噪声地震动激励下工程结构动力响应的求解公式,提出一种大质量扩阶解法,将输入简化为白噪声模型.结合复振型分解理论,即可基于白噪声过程激励下单自由度结构动力响应的求解公式获得结构在复杂地震动作用下的随机动力响应,并指出该方法可避免繁琐的积分运算,求解速度快,值得推广应用.【期刊名称】《山西建筑》【年(卷),期】2011(037)017【总页数】3页(P51-53)【关键词】结构工程;扩阶;大质量;地震响应;随机分析【作者】曹春青【作者单位】中铁电气化局集团北京建筑工程有限公司,北京,100000【正文语种】中文【中图分类】TU311.3在平稳白噪声过程激励下，工程结构的线性动力响应的功率谱和方差通常都能求得解析解。

不过，对于一些其他常用的复杂平稳随机过程，求解过程将非常复杂，大多数情况下甚至很难得到解析解。

不过，当随机过程的功率谱可以由白噪声过程过滤得到时，则有可能通过扩展结构系统自由度阶数而降低求解积分运算的难度。

方同曾提出一种扩阶解法求解平稳过滤白噪声过程激励下结构的随机响应［1，2］，该方法将过滤层在白噪声激励下的动力平衡方程与上部结构在过滤层相应的输出结果激励下的方程联立起来，组成一个在白噪声过程激励下的扩阶系统。

由于此扩阶系统中上部结构受到过滤层的作用，但过滤层不接受上部的反馈作用，所以扩阶系统的参数矩阵是非对称的，扩阶系统也仅仅是形式上的联立，并不对应任何实际的物理模型，本文称之为“数学扩阶解法”。

一些学者在随机振动问题的研究中采用了类似的方法：姚昌仁等人采用扩阶解法研究有色噪声激励下结构随机响应的灵敏度问题［3］、侯志强等人采用此法计算有色噪声激励下的迟滞系统的随机响应［4］、李创第和李暾等人采用此法研究建筑结构调频减振［5，6］和隔震问题［7］、吴存利、冷小磊和方同采用此法研究TMD减震问题［8］。

由于数学扩阶解法形成的扩阶矩阵是非对称的，因而需要求解左、右特征向量，本文提出一种大质量扩阶解法，可以避免该问题。

结构地震反应性态的物理随机最优控制

结构地震反应性态的物理随机最优控制
彭勇波;李杰
【期刊名称】《防灾减灾工程学报》
【年(卷),期】2011(31)5
【摘要】本研究发展了结构地震反应性态的随机最优控制理论和方法。

这一研究建立在物理随机系统思想的新理论框架下,突破了以I^to随机微分方程描述动力系统的经典随机最优控制的藩篱。

提出了基于系统二阶统计量评价、单目标超越概率和多目标能量均衡的控制器参数设计准则,以及基于概率可控指标的控制器位置设计准则,并将它们统一为物理随机最优控制的广义最优控制律。

数值算例分析表明,本文发展的物理随机最优控制方法能够实现结构地震反应性态的精细化控制。

【总页数】7页(P483-489)
【作者】彭勇波;李杰
【作者单位】同济大学土木工程防灾国家重点实验室
【正文语种】中文
【中图分类】O232;TB114.2
【相关文献】
1.8度区框-剪结构中框架在罕遇地震下的反应性态
2.结构地震反应随机最优控制的多目标概率准则研究
3.地震激励下20层钢结构基准模型的非线性随机最优控制
4.基于随机地震响应的大跨隔震结构性态设计方法
5.基于随机地震动模型的结构随机地震反应谱及其应用
因版权原因，仅展示原文概要，查看原文内容请购买。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

与被动控制相关的结构控制算法主要涉及获得最大控制效益的阻尼器的最优布置和参数优化。然而，由于作用于工程结构的动力荷载，如地震、强风、海浪等在时间、空间和大小上往往具有明显的随机性，按传统确定性结构控制算法很难实现结构反应性态的精细化控制。而依赖于状态方程描述和 It 微积
引言
为增强工程结构抵御灾害性荷载的能力，早在一百多年前，人们就尝试将基础隔震原理运用到了结构抗震设计中。而直至 20 世纪 70 年代初，结构控制概念的提出，结构减震或振动控制理论和技术在工程实践中才得到广泛关注和迅速发展。根据控制系统实
基金项目: 国家自然科学基金( 50621062、51108344 ) 、上海市浦江人才计划( 11PJ1409300) 和土木工程防灾国家重点实验室探索性研究课题( SLDRCE11-B-04)
DOI:10.15951/j.tmgcxb.2012.s2.021
第 45 卷增刊 2 2012 年
土木程学报
CHINA CIVIL ENGINEERING JOURNAL
Vol． 45 2012
高层建筑结构随机振动的最优阻尼器控制策略
彭勇波李杰
( 同济大学，上海 200092)
摘要: 提出考虑阻尼器布置与阻尼器参数同步优化的高层建筑结构随机最优控制方法。为有效地寻找每个序列工况的阻尼器最优拓扑和阻尼器最优参数，分别定义了基于超越概率的层可控指标梯度最小准则和能量均衡最优准则。上述控制准则内蕴了系统安全性、系统服务性、系统舒适性、阻尼器工作性以及它们之间的均衡。以随机地震动作用下十层剪切型框架结构的黏滞阻尼器最优控制为例进行分析，结果表明，采用该方法可以以最小的投资获得最大的控制效益，受控后结构反应沿层分布较受控前更均匀、能达到所期望的结构性态。关键词: 最优阻尼器控制; 层可控指标梯度; 能量均衡; 超越概率; 随机地震动中图分类号: O232 TB114． 2 文献标识码: A 文章编号: 1000-131X( 2012) S2-0168-04
Optimal damping control scheme for random vibration of high-rising building structures
Peng Yongbo Li Jie
( Tongji University，Shanghai 200092，China)
Abstract: An integrated scheme for optimization design of damper placement and parameters of passively controlled structures is proposed in the present paper． The scheme features the simultaneous consideration of optimal control force and optimal device placement． Two control criteria with a minimum storey controllability index gradient and an optimal energy trade-off are defined，respectively，to efficiently search for the optimal topology and optimal parameters of dampers． The control criteria both hinge on the exceedance probability that indicates system safety， system serviceability，system comfort，damper workability，and their trade-off． The resolution procedure of the integrated scheme is detailed，and a numerical example is investigated involving a randomly base-excited ten-storey shear frame equipped with viscoelastic dampers． Numerical results reveal that the proposed integrated scheme can gain the maximum control effectiveness with the minimum control cost． The controlled system response is significantly reduced and becomes smoother along the height of the structure，which results in a more desirable structural performance． Keywords: optimal damping control; storey controllability index gradient; energy trade-off; exceedance probability; stochastic ground motions E-mail: lijie@ tongji． edu． cn
作者简介: 彭勇波，博士，讲师收稿日期: 2012-05-30
施过程中是否需要提供外加能源及所需能源功率大小，结构控制一般可以分为被动控制、主动控制、半主动控制与混合控制等类型［1］。被动控制是指在结构上附加隔震或耗能减震装置以增加结构阻尼、刚度和强度特性，一般不需要外加能源。由于其设计相对简单、在工程中易于实现，且能满足系统稳定性要求，近年来其研究与应用较为广泛［2］。