小学三年级数学之巧求周长
三年级上册数学巧求图形周长

1、在一条长25厘米的线段上画大小两个正方形(如图)大正方形的周长比小正方形的周长多20厘米,求大小两个正方形的周长各是多少厘米?25×4=100(厘米)(100+20)÷2=60(厘米)60-20=40(厘米)答:大正方形的周长是60厘米,小正方形的周长是40厘米。
2、有一个长方形花坛,长和宽分别增加8米,面积增加了224平方米。
问原来这个花坛的周长是多少米?解:(224-8×8)÷8=20(米)20×2=40(米)答:原来这个花坛的周长是40米。
3、计算下面图形的周长。
(单位:厘米)(30+20)×2+13×2=126(厘米)4、求下面图形的周长。
(每个正方形的顶点恰好在另一个正方形的中心)(单位:分米)0084×3×4=48(分米)5、如下图ABCD是正方形,DH=7厘米,FB=8厘米,求长方形EFGH的周长。
(7+8)×2=30(厘米)6、用5个边长为1厘米的正方形纸片, 拼成下面各种图形.周长最长的是哪一个?周长最长的是D7、在一条长32厘米的线段上画大小两个正方形(如图)大正方形的周长比小正方形的周长多24厘米,求大小两个正方形的周长各是多少厘米?大:(32×4+24)÷2=76(厘米)小:76-24=52(厘米)8、一个长方形,如果它的长边和宽边分别增加6厘米,那么面积则增加156平方厘米。
求这个长方形的周长是多少厘米?(156-6×6)÷6×2=40(厘米)9、有一个正方形,它的一条边长增加了8厘米,另一条边长增加了3厘米,面积就比原来多310平方厘米。
这个正方形原来的周长是多少厘米?(310-8×3)÷(8+3)×2=52(厘米)10、有一块长方形广告牌,它的长边和宽边分别增加了4厘米,它的面积增加了820平方厘米。
最新小学三年级巧求周长(一)
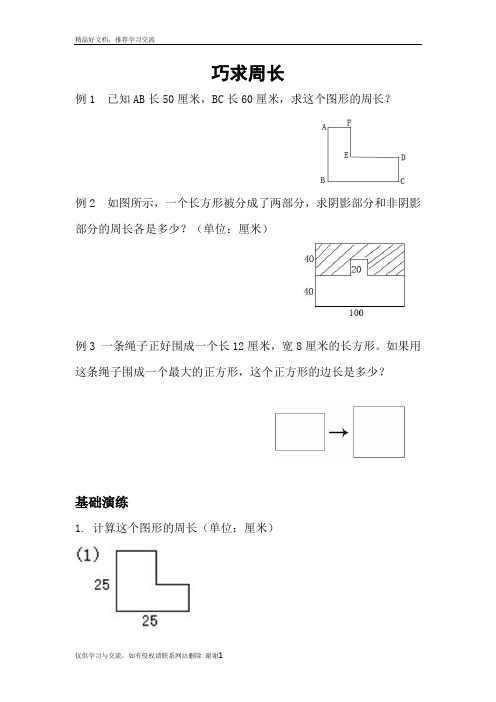
巧求周长例1 已知AB长50厘米,BC长60厘米,求这个图形的周长?例2 如图所示,一个长方形被分成了两部分,求阴影部分和非阴影部分的周长各是多少?(单位:厘米)例3 一条绳子正好围成一个长12厘米,宽8厘米的长方形。
如果用这条绳子围成一个最大的正方形,这个正方形的边长是多少?基础演练1.计算这个图形的周长(单位:厘米)(2)(3)(4)(5)(6)两个正方形拼起来周长计算;30cm 30cm1cm(7)两个长方形拼成正方形周长计算:8cm 8cm初三学化学元素周期表时背的口诀主要背前20种元素:氢氦锂铍硼H He Li Be B碳氮氧氟氖 C N O F Ne钠镁铝硅磷Na Mg Al Si P硫氯氩钾钙S Cl Ar K Ca锌铁锰钡碘Zn Fe Mn Ba I铜汞银铂金Cu Hg Ag Pt Au第一周期:氢氦---- 侵害第二周期:锂铍硼碳氮氧氟氖---- 鲤皮捧碳蛋养福奶第三周期:钠镁铝硅磷硫氯氩---- 那美女桂林留绿牙(那美女鬼流露绿牙)第四周期:钾钙钪钛钒铬锰---- 嫁改康太反革命铁钴镍铜锌镓锗---- 铁姑捏痛新嫁者砷硒溴氪---- 生气休克第五周期:铷锶钇锆铌---- 如此一告你钼锝钌---- 不得了铑钯银镉铟锡锑---- 老把银哥印西堤碲碘氙---- 地点仙第六周期:铯钡镧铪----(彩)色贝(壳)蓝(色)河钽钨铼锇---- 但(见)乌(鸦)(引)来鹅铱铂金汞砣铅---- 一白巾供它牵铋钋砹氡---- 必不爱冬(天)第七周期:钫镭锕---- 很简单了~就是---- 防雷啊!化合价:一价请驴脚拿银,(一价氢氯钾钠银)二价羊盖美背心。
(二价氧钙镁钡锌)一价钾钠氢氯银二价氧钙钡镁锌三铝四硅五价磷二三铁、二四碳一至五价都有氮铜汞二价最常见正一铜氢钾钠银正二铜镁钙钡锌三铝四硅四六硫二四五氮三五磷一五七氯二三铁二四六七锰为正碳有正四与正二再把负价牢记心负一溴碘与氟氯负二氧硫三氮磷初中常见原子团化合价口决:负一硝酸氢氧根,负二硫酸碳酸根,还有负三磷酸根,只有铵根是正一。
苏教版三年级上册数学长方形和正方形巧求周长二

长方形和正方形巧求周长二
例1.把一张长18厘米,宽10厘米的长方形纸,剪开成两个完全相等的小长方形,每个小长方形的周长是多少厘米?
试一试:
1.把一张长8厘米,宽6厘米的纸,剪开成两个完全相等的小长方形,每个小长方形的周长是多少厘米?
2.将一张长12厘米,宽9厘米的纸,剪成3个形状大小完全相同的小长方形,每个小长方形的周长是多少厘米?
3.将一个长为10分米,宽6分米的长方形如下图剪成6个完全一样的小长方形,这6个小长方形周长之和比原来的长方形周长增加了多少分米?
10分米
例2.一根铁丝长18分米,把它折成一个长5分米的长方形,这个长方形的宽是多少分米?
试一试:
1.一根铁丝长24分米,把它折成一个长10分米的长方形,这个长方形的宽是多少分米?
2.把一根长122厘米的铁丝围成一个长方形,接头处重合2厘米,要使长方形的宽是10厘米,长方形的长应是多少厘米?
3.把一根长150厘米的铁丝围成一个长方形,接头处重合2厘米,要使长比宽多16厘米,长和宽各是多少厘米?
例3.一张长方形的纸长30厘米,宽16厘米,先剪下一个最大的正方形,再从余下的纸片中剪下一个最大的正方形,最后余下的长方形周长是多少?
试一试:
1.一张长方形纸,长18厘米,宽15厘米,从中剪下一个最大的正方形,余下的长方形周长是多少厘米?
2.一张长方形纸,长32厘米,宽18厘米,从中剪下一个最大的正方形,再从余下的纸片中剪下一个最大的正方形,最后余下的长方形周长是多少厘米?
3.一张长方形纸宽2分米,长是宽的2倍多1分米,从中剪下一个最大的正方形,再从余下的纸片中剪一个最大的正方形,最后余下的长方形周长是多少分米?。
周长—巧求周长(教案)-三年级上册数学人教版

教案:周长—巧求周长教学目标:1. 知识与技能:使学生理解和掌握周长的概念,能够正确计算给定图形的周长。
2. 过程与方法:通过观察、操作、实验等教学活动,培养学生动手操作能力和解决问题的能力。
3. 情感态度与价值观:激发学生对数学学习的兴趣,培养学生合作学习的精神。
教学内容:1. 周长的概念:围成封闭图形一周的长度叫做图形的周长。
2. 常见图形的周长计算方法:正方形、长方形、圆形等。
3. 巧求周长的方法:利用图形的性质和规律,简化周长的计算过程。
教学重点与难点:1. 教学重点:使学生掌握周长的概念,能够正确计算给定图形的周长。
2. 教学难点:理解并运用巧求周长的方法,简化计算过程。
教具与学具准备:1. 教具:周长相关的课件、图片、模型等。
2. 学具:直尺、圆规、计算器等。
教学过程:1. 导入:通过图片或实物,引导学生观察并思考周长的概念。
2. 新课:讲解周长的定义,介绍常见图形的周长计算方法。
4. 活动二:学生分组实践,计算给定图形的周长,验证巧求周长的方法。
6. 作业布置:布置相关的练习题,巩固所学知识。
板书设计:1. 周长的概念2. 常见图形的周长计算方法3. 巧求周长的方法作业设计:1. 基础题:计算给定图形的周长。
2. 提高题:运用巧求周长的方法,解决实际问题。
课后反思:本节课通过观察、操作、实验等教学活动,使学生理解和掌握了周长的概念,能够正确计算给定图形的周长。
同时,通过分组讨论和实践,培养了学生动手操作能力和解决问题的能力。
在教学过程中,教师应注重激发学生的学习兴趣,引导学生主动参与教学活动,培养学生的合作学习精神。
在课后作业设计方面,应注重巩固所学知识,提高学生的计算能力和解决问题的能力。
总体来说,本节课教学效果良好,达到了预期的教学目标。
但在教学过程中,教师还需进一步关注学生的学习情况,及时调整教学策略,提高教学效果。
重点关注的细节:巧求周长的方法1. 巧求周长的方法:(1)利用图形的性质:对于一些具有特殊性质的图形,如正方形、长方形、圆形等,可以利用它们的性质简化周长的计算过程。
巧求周长(三四年级通用版)

巧求周长例题精讲基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积. 基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长. 常用方法:对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解. ?转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.~在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢对称、旋转、平移这几种几何变换就是解决这类面积问题的手段. 平移:在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.割补:割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变. )旋转:在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.对称:平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.代换:在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力. 【例 1】 求图中所有线段的总长(单位:厘米)34ED C【解析】 要注意到,题目所求的是图中所有线段的总长,而图中的线段,并不仅仅是A 、BC 、CD 、DE 四段,还包括AC 、BE 等等,因此不能简单地将图中标示的线段长度进行求和.同时应该注意到,A ;BE,等等.因此,为了计算图中所有线段的总长,需要先计算AB 、BC 、CD 、DE 这四条线段分别被累加了几次. 这里,可以按照每条线段分别是由几部分组成的加以讨论:由1段组成的线段共有4条,即AB 、BC 、CD 、DE ,而求和过程中AB 、BC 、CD 、DE 这四条线段各被累加了1次. ,类似地考虑到,由2段组成的线段共有3条,求和过程中AB 、DE 各被累加了1次,BC 、CD 各被累加了2次.由3段组成的线段共有2条,求和过程中AB 、DE 各被累加了1次,BC 、CD 各被累加了2次.由4段组成的线段只有AE ,其中AB 、BC 、CD 、DE 各被计算了1次. 综上所述,AB 、DE 各被计算了4次,BC 、CD 各被计算了6次. 因而图中所有线段的总长度为:【例 2】 如图所示,一个大长方形被三条线段分成了四个小长方形,各条线段长度见图(单位:厘米).求:图中所有长方形的周长之和.21342【解析】 类似于上题,题目中所说的长方形,并不只包括最小的几个长方形,因此需要先求出每条线段在求和过程中被累加了多少次. %因为没从大长方形的长上找到一条线段,就能对应地找到大长方形内的一个长方形,所以可以利用上一个问题的结论来解决这个问题.当然,要考虑到,每个长方形都有两条长和两条宽,因此计算过程中应该注意不要漏算.先考虑大长方形的长上各边:应用上一道题目的结论,每条边上长为4、3、1、2的线段分别被计算了4、6、6、4次. 然后再考虑大长方形的宽:因为共有4+个长方形,所以长度为2的宽被计算了10⨯次. 故总周长可以用下式计算得到:2.【例 3】 如图,正方形的边长为4,被分割成如下12个小长方形,求这12个小长方形的所有周长之和.【解析】 4445256⨯+⨯⨯=.【巩固】(“希望杯”第一试)如右图,正方形ABCD 的边长是6厘米,过正方形内的任意两点画直线,可把正方形分成9个小长方形。
三年级巧求周长完

第35周巧求周长(一)举一反三11. 下图是一个楼梯的侧面,如果在阶梯上铺地毯,要计算地毯的长度,可以怎样测量?2. 如下图所示,小明和小玲同时从学校走到少儿书店,小明沿A 路线行走,路线行走,小玲沿小玲沿B 路线行走,他们俩一共走了多少米?行走,他们俩一共走了多少米?3. 下图是由6个面积为1平方厘米的小正方形拼成的图形,它的周长是多少厘米?平方厘米的小正方形拼成的图形,它的周长是多少厘米?举一反三21.下图是由5个边长为3厘米的正方形组成的图形,求此图形的周长。
厘米的正方形组成的图形,求此图形的周长。
学校学校 B A 110米 200米 少儿书店少儿书店2.下图是由6个边长为2厘米的正方形组成的图形,求此图形的周长。
厘米的正方形组成的图形,求此图形的周长。
举一反三3 1.把两个大小相同的正方形拼成一个长方形后,这个长方形的周长比原来两个正方形的周长厘米,原来一个正方形的周长是多少厘米?的和减少了10厘米,原来一个正方形的周长是多少厘米?2.把一个正方形剪成两个大小相同的长方形后,两个长方形周长的和比原来正方形的周长增加了28分米,原来正方形的周长是多少分米?分米,原来正方形的周长是多少分米?3.把边长是48厘米的正方形剪成三个同样大小的长方形。
每个长方形的周长是多少厘米?厘米的正方形剪成三个同样大小的长方形。
每个长方形的周长是多少厘米? 举一反三4 1.把16个边长为3厘米的小正方形拼成一个大正方形。
这个拼成的大正方形周长是多少厘米?米?2.把6个边长为4厘米的小正方形如下图拼成一个长方形。
这个长方形的周长是多少厘米?这个长方形的周长是多少厘米?3.把6个长为3厘米,宽为2厘米的小正方形如下图拼成一个大长方形。
这个大长方形的周长是多少厘米?周长是多少厘米?举一反三5 1.讲一张边长为12厘米的正方形纸,剪成4个完全一样的小正方形,那么这4个小正方形周长之和比原来的大正方形的周长增加了多少厘米?周长之和比原来的大正方形的周长增加了多少厘米?2.把一个边长为20厘米的正方形,如下图剪成6个完全一样的小长方形,这6个小长方形周长的和与原来的正方形的周长相比增加了多少厘米?周长的和与原来的正方形的周长相比增加了多少厘米?3.将一个长为8分米、宽为6分米的长方形如下图剪成6个完全一样的小长方形,这6个小长方形周长之和比原来长方形的周长增加了多少分米?小长方形周长之和比原来长方形的周长增加了多少分米?第36周巧求周长(二)举一反三11.如右图所示,已知大长方形的周长为38厘米,阴影部分为正方形。
小学三年级巧求周长练习及答案【三篇】

【导语】芬芳袭⼈花枝俏,喜⽓盈门捷报到。
⼼花怒放看通知,梦想实现今⽇事,喜笑颜开忆往昔,勤学苦读最美丽。
在学习中学会复习,在运⽤中培养能⼒,在总结中不断提⾼。
以下是为⼤家整理的《⼩学三年级巧求周长练习及答案【三篇】》供您查阅。
【第⼀篇】
5个同样⼤⼩的⼩长⽅形拼成了⼀个⼤长⽅形,已知⼩长⽅形的长是12厘⽶,求⼤长⽅形的周长。
【第⼆篇】
“⽤四个完全相同的边长分别为5、12、13的直⾓三⾓形拼成了⼀个”风车“,求这个风车的周长.
【第三篇】
有⼀块长⽅形的玻璃,从长边截去20厘⽶宽的⼀块后,剩下的玻璃正好是块正⽅形,它的周长是160厘⽶。
原来长⽅形玻璃的周长和⾯积各是多少?
解答:周长:200厘⽶,160÷4=40(厘⽶);(40+20)×2+40×2=200(厘⽶);⾯积:2400平⽅厘⽶,(40+20)×40=2400(平⽅厘⽶)。
“。
三年级 第15讲 巧求周长

(3)一只蜗牛沿枯藤爬行分钟爬1分米.10分钟才爬了枯藤的一半.问枯 藤有多长?
【例 3】
【例3】有5 张长2厘米、宽 1厘米的长方形硬纸片,用它们拼成一个 大的长方形.这个大长方形的周长最少是多少厘米?
小学三年级奥数
——某某某老师
第15讲 巧求周长 感谢您下载魔方网平台上提供的PPT作品,为了您和魔方网以及原创作者的利益,请勿复制、传播、销售,否则将承担法律责任!魔方网将对作品进行维权,按照传播下载次数进行十倍的索取赔偿!
i魔方123
第15讲—巧求周长
➢ 巧求周长: 什么是周长? 一个图形的周长是指围成它的所有线段的长度的总和。分 为规则不规则。 常见规则的图形长方形和正方形。 它们的周长计算如下: 长方形的周长=(长+宽)× 2 正方形的周长=边长×4
●●●● 随 堂 练 习 3
(1)在例3 中,大长方形的周长最多 是多少厘米?
(2)△ A B C 及正方形B C E D 组 成下图.△ A B C是边长为2cm的正 三角形.求图形的周长.
(3)求下图所示图形的周长.
【例 4】
【例4】求图15 - 3 的周长.(单位:分米)
●●●● 随 堂 练 习 4
第15讲—巧求周长
➢ 复杂不规则图形的周长
【例 1】
【例1】用16个边长为2 厘米的小正方形拼成一个大正方形.大正方 形的周长是多少?
●●●● 随 堂 练 习 1
(1)用 9个边长为3厘米的小正方形拼成一个大正方形.大正方形的周 长是多少?
(2)长为12分米、宽为4分米的三个长方形拼成一个正方形.正方形 的周长和面积各是多少?
小学三年级奥数课件:巧求周长

什么布切不断?
答案:瀑布
一只蚂蚁居然从四川爬到了上海,可能吗? 答案:地图上爬
什么牛不会吃草Leabharlann 答案:蜗牛周长公式:正方形的周长= 边长×4 长方形的周长=(长+宽)×2
不规则图形的周长
【精讲1】、有两个相同的长方形,长7厘米,宽5厘米,把他
们按下图的样子重叠在一起,这个图形的周长是多少厘米?
8、用24个边长是1厘米的正方形拼成一个长方形, 这个长方形的周长是多少厘米?
(1+24)×2=50(厘米) (2+12)×2=28(厘米) (3+8)×2=22(厘米) (4+6)×2=20(厘米) 答:这个长方形的周长可能是 50、28、22、20厘米。
9、把边长是9厘米的正方形剪成三个同 样大小的长方形,算一算每个长方形的 周长是多少厘米?
【思路导航】根据长方形的周长是正方形的2倍,可以 求出:
(1)正方形的周长:4×4=16(厘米) (2)长方形的周长:16×2=32(厘米) (3)长方形的长:32÷2-4=12(厘米)
4×4×2÷2-4=12(厘米)
答:长方形的长是12厘米。
【精讲9】如图,三个同样大小的长方形正好拼成一个 正方形,正方形的周长是48厘米。求每个长方形的周 长?
2×4=8厘米,宽为有2个小正方形的边长,宽为2×2=4厘米, 所以这个图形的周长为:
(2×4+2×2)×2=24(厘米)
答:这个图形的周长是24厘米。
【精讲4】一个正方形,边长是5厘米,将9个这样的 正方形如图所示拼成一个大正方形,问拼成的这个大 正方形的周长是多少?
【思路导航】从图可以看出,9个小正方 形共有3排,每排由3个小正方形组成。 已知小正方的边长是5厘米,所以大正方 形的边长就为5×3=15厘米
三年级数学巧求周长

大家看这样的图形,你能求出它的周长不?下面由启灵教育杜老师帮你解密。
用它们可以解决许多直角多边形(所有的角都是直角的多边形)的周长问题。
这是因为直角多边形总可以分割成若干个正方形或长方形。
下边就让我带着大家一起走进求周长的奥秘吧。
先看例题:例1一个苗圃园(如左下图),周边和中间有一些路供人行走(图中线段表示“路”),几个小朋友在里面观赏时发现:从A处出发,在速度一样的情况下,只要是按“向右”、“向上”方向走,几个人分头走不同的路线,总会同时达到B处。
你知道其中的道理吗?分析与解:如右上图所示,将各个交点标上字母。
由A处到B处,按“向右”、“向上”方向走,只有下面六条路线:(1)A→C→D→E→B;(2)A→C→O→E→B;(3)A→C→O→F→B;(4)A→H→G→F→B;(5)A→H→O→E→B;(6)A→H→O→F→B。
因为A→C与H→O,G→F的路程一样长,所以可以把它们都换成A→C;同理,将O→E,F →B都换成C→D;将A→H,C→O都换成D→E;将H→G,O→F都换成E→B。
这样换过之后,就得到六条路线的长度都与第(1)条路线相同,而第(1)条路线的长“AD+DB”就是长方形的“长+宽”,也就是说,每条路线的长度都是“长+宽”。
路程、速度都相同,当然到达B处的时间就相同了。
例2计算下列图形的周长(单位:厘米)。
解:(1)将图中右上缺角处的线段分别向上、向右平行移动到虚线处(见左下图),这样正好移补成一个正方形,所以它的周长为25×4=100(厘米)。
(2)与(1)类似,可以移补成一个长方形,周长为(10+15)×2=50(厘米)。
1.下图是一个方形螺线。
已知两相邻平行线之间的距离均为1厘米,求螺线的总长度。
2.右图是某小学教学楼的平面示意图,设计者在图上只标明了三条线段的长度(单位:米)。
请你算出它的周长。
周长—巧求周长(教案)-三年级上册数学 人教版

教案:周长—巧求周长教学目标:1. 让学生理解周长的概念,知道周长是围成封闭图形的所有边的总长度。
2. 培养学生运用测量工具测量图形周长的能力。
3. 引导学生发现并掌握巧求周长的方法,提高解决问题的能力。
教学重点:1. 周长的概念及测量方法。
2. 巧求周长的方法。
教学难点:1. 周长概念的建立。
2. 巧求周长的方法。
教学准备:1. 课件或黑板。
2. 测量工具(如直尺、卷尺等)。
3. 图形卡片。
教学过程:一、导入(5分钟)1. 利用课件或黑板展示各种图形,引导学生观察并说出图形的名称。
2. 提问:这些图形有什么共同特点?引导学生发现图形都是由线段围成的。
二、探究周长的概念(10分钟)1. 引导学生观察图形,提出问题:这些图形的边有什么特点?2. 学生回答:图形的边都是直线。
3. 提问:如果我们要计算这些图形的边长总和,应该怎么计算呢?4. 学生回答:将所有边的长度相加。
5. 总结:将图形的所有边的长度相加,得到的结果就是图形的周长。
三、测量周长(10分钟)1. 分组活动:每组发一张图形卡片,要求学生用测量工具测量图形的周长。
2. 学生操作,教师巡回指导。
3. 各组汇报测量结果,教师点评并总结测量方法。
四、巧求周长(10分钟)1. 出示课件或黑板上的图形,引导学生观察并思考:这些图形的周长有什么规律?2. 学生回答:正方形的周长等于边长乘以4,长方形的周长等于长和宽的和乘以2。
3. 教师总结:正方形和长方形的周长可以通过简单的计算得到,这就是巧求周长的方法。
五、巩固练习(15分钟)1. 出示课件或黑板上的练习题,要求学生独立完成。
2. 学生完成后,教师点评并解答疑问。
六、总结(5分钟)1. 提问:今天我们学习了什么内容?学生回答:周长的概念、测量周长的方法以及巧求周长的方法。
2. 教师总结:周长是围成封闭图形的所有边的总长度,我们可以通过测量工具测量周长,也可以通过巧求周长的方法快速计算正方形和长方形的周长。
小学三年级下册逻辑思维 第十一讲 巧求周长(二)

小学三年级下册逻辑思维第十一讲巧求周长(二)【一】把长14厘米的铁丝围成一个长方形,要使长6厘米,宽是多少厘米?练习1、已知这个长方形的周长是28厘米,宽是4厘米,求长方形的长是多少?2、绕一个长方形球场跑一圈是78米,球场宽是13米,这个球场的长是多?【二】把32厘米的铁丝围成一个长方形,要使长比宽长4厘米,长和宽各是多少厘米?练习1、已知这个长方形的周长是28厘米,宽比长少4厘米,求长方形的长和宽各是多少厘米?2、绕一个长方形球场跑三圈是300米,长比宽多10米,这个球场的长是多少米?【三】把长40厘米的铁丝围成一个长方形,接头处重合2厘米,要使长比宽多5厘米,长和宽各是多少厘米?练习1、如图,已知这个长方形的周长是26厘米,空白部分为正方形。
求长方形的长和宽。
2、陈亮家给长方形的院子装上了篱笆墙,由于门宽1米,所以篱笆共长17米,而这个长方形的长是宽的2倍,长和宽各多少米?【四】一根铁丝长86厘米,围成一个边长为6厘米的正方形,余下的铁丝围成一个长为22厘米的长方形,这个长方形的宽是多少厘米?练习1、一根彩带长90厘米,围成一个边长为10厘米的正方形,余下的彩带围成一个宽为8厘米的长方形,这个长方形的长是多少?2、一根绳子长40厘米,围成一个长7厘米,宽5厘米的长方形,余下的围成一个正方形,这个正方形边长是多少厘米?【五】一个长方形的周长是正方形的2倍,正方形的边长与长方形的宽都为3分米,长方形的长是多少分米?练习1、一个长方形的周长是正方形的3倍,正方形的边长与长方形的宽都为5厘米,长方形的长是多少厘米?2、一根绳子,恰好可围成边长9厘米的正方形,如果把它围成一个宽为7厘米的长方形,这个长方形的长应是多少厘米?【六】三个同样大小的长方形正好拼成一个正方形,正方形的周长是36厘米,求每个长方形的周长。
练习1、四个同样大小的长方形正好拼成一个正方形,正方形的周长为64厘米,求每个长方形周长是多少?2、六个同样大小的长方形正好排成一个如下图的正方形,正方形周长为24厘米,每个长方形的周长是多少?【七】一张长方形的纸,长是25厘米,宽是16厘米,先剪下一个最大的正方形,再从余下的纸片中,再剪下一个最大的正方形,最后余下的长方形周长是多少?练习1、一张长为17厘米,宽为12厘米的长方形纸,若剪下一个最大的正方形,余下的长方形纸片的周长是多少?2、一张长方形纸,长为90厘米,宽为60厘米,先剪下一个最大的正方形,再从余下的纸片中,又剪一个最大的正方形,最后余下的长方形周长是多少?课外作业1、绕一个长方形球场跑一圈是400米,球场宽是80米,这个球场的长是多少米?2、已知一个长方形的周长是60厘米,宽比长少10厘米,求长方形的长和宽各是多少?3、一个周长为24厘米的正方形,从中间剪开成为两个大小相同的长方形,这两个长方形周长共多少厘米?4、一根铁丝围成一个边长为7厘米的正方形,余下的正好围成一个长为6厘米、宽为2厘米的长方形,这根铁丝长多少厘米?5、一张长方形纸,长7分米,宽5分米,剪下一个最大的正方形后,余下的长方形纸周长是多少?6、明明用三个同样大小的长方形拼成一个大长方形,已知大长方形的周长是30厘米,长是宽的4倍,求小长方形的周长。
小学三年级《巧求周长》奥数教案

师:同学们,我们都学过周长了是吗?生:是。
师:那什么叫做周长呢?生:绕封闭图形一周的长度我们叫周长。
师:很好。
看来同学们是真正用心在学习,记忆力也非常好。
那现在我们看到例题一的第一个图形。
这个图形我们知道所有线段的长度吗?生:不知道。
师:对,但是我们能不能用已知的线段长来求出图形的周长呢?生:……师:我们都学过图形的平移,对不对?生:对。
师:那我们能不能把这道题中的某一条或者某几条线段进行平移,得到一个我们能立刻算出周长的图形呢?同学们想想看,移移看。
生:可以!师:哦,来说说看。
生:这里有三层,我们把下面两层的宽度向上移到和最上层同样高的地方,把每层的高度向右移到和最左侧高度一致的地方。
师:大家听清楚了吗?生:没有。
师:好的,那老师老帮助这位同学把图形的平移画出来。
(通过PPT的演示)现在大家清楚怎么移动了吗?生:清楚了。
师:好的,那同学们请看,现在我们看到的图形是什么?生:是长方形。
师:对,我们知道长方形的长了吗?生:知道,是120厘米。
师:没错,那我们知道长方形的宽了吗?生:不知道,但是我们能把它算出来。
师:那我们怎么算呢?生:12+24+48=84(厘米)。
师:非常好。
那我们现在周长是不是可以算了?生:没错。
师:周长是?生:(120+84)×2=408(厘米)。
师:非常棒!师:解决了第一小题,我们来看一看第二小题。
这道题目能不能跟第一小题一样,我们进行平移?生:可以。
师:那请同学们先试试看。
把尝试的结果告诉老师。
生:可以平移,但是有线段多出来。
师:哦,多出来,哪条线段多出来了?生:是10厘米的,多了两条。
师:那我们算周长的时候该怎么办呢?生:把多出来的也加进去。
师:非常好,我们不能落下每一条线段。
所以最后的答案是?生:(50+35)×2+10×2=190(厘米)师:非常棒,看来同学们掌握的都很不错,观察的也很仔细。
那么我们就开始做练习,熟能生巧,我们不仅要会做,还要做得快、做得正确。
三年级数学-巧求周长和巧求面积

巧求周长【知识要点】通过前面的学习,同学们已经知道围成一个图形所有边的长度总和,叫做这个图形的周长。
上册课本中我们接触了用平移法求一些不规则图形的周长,本节课我们【典型例题】例1. 一张长方形纸,长28厘米,宽15厘米,剪下一个最大的正方形后,余下的长方形纸周长是多少?例2.从一个长为100厘米的长方形中截去一个最大正方形,求剩下的长方形的周长是多少?练一练1如图,已知这个长方形的周长为38厘米,阴影部分为正方形,求长方形的长和宽。
例3.如图,一个正方形被分成3个大小、形状完全一样的长方形。
每个小长方形的周长都是32厘米,求这个正方形的周长。
练一练2一个正方形分成三个相同的长方形(如图),一个长方形的周长是64 厘米,正方形的面积是多少平方厘米?例4.如图,四个同样的长方形和一个小正方形拼成一个大正方形,大正方形的面积是100平方米,小正方形的面积是36平方米,求每个小长方形的周长。
练一练3明明用学具盒里的三个同样大小的长方形拼成一个大长方形,已知大长方形的周长是60厘米,长是宽的4倍,求小长方形的周长?※例5.如下图,在长方形ABCD中,EFGH是正方形,已知AF=10㎝,HC=7㎝,则长方形ABCD的周长是多少?能力训练1. 求图(1),图(2)的周长?(单位:分米)2. 下图已知a=18cm、b=16cm、e=6cm。
求图形的周长。
3.一个周长为20厘米的正方形,从中间剪开成为两个大小相等的长方形,这两个长方形周长共多少厘米?4. 两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了6厘米。
原来每个正方形的周长是多少厘米?5.长方形的长是50厘米,截去一个最大的正方形后,余下一个长方形,这个长方形的周长是多少厘米?6.一张长方形纸,长为32厘米,宽为15厘米,先剪下一个最大的正方形,再从余下的纸片中,又剪一个最大的的正方形,最后余下的长方形周长是多少?7.一根铁丝长80厘米,围成一个边长为8厘米的正方形,余下的铁丝围成一个长为14厘米的长方形,这个长方形的宽为多少厘米?8. 6张同样大小的正方形纸重叠着,每个正方形的边长都是2厘米,重叠部分的边长为原来每个正方形边长的一半。
(完整版)小学数学三年级奥数巧求周长

巧求周长(一)同学们都知道长方形的周长=(长+宽)×2,我们把长方形的周长用 C 表示,长用 a 表示,宽用 b 表示,长方形的周长用字母表示。
正方形的周长=边长×4,用C 表示正方形的周长, a 表示边长,正方形的周长用字母表示。
运用上边两个公式能够求出标准的长方形和正方形的周长。
今日我们要进一步学习运用长方形和正方形周长计算公式巧求周长,培育同学们灵巧应用知识的能力。
(一)典型例题例 1. 下列图是一块近似长方形的麦地,这块麦地的周长是多少?例 2. 下列图是一个楼梯的侧剖图面,已知每步台阶宽 3 分米,高 2 分米,问这个楼梯侧面周长是多少米?例 3. 王爷爷用篱笆在一面靠墙的地方围一个长方形的菜园,这些篱笆长30 米,假如这个长方形菜园长18 米,宽应当是多少?例 4. 用两个长和宽分别是9 分米、 7 分米的长方形,拼成一个大的长方形,拼成后的长方形周长最长是()分米,最短是()米。
例 5. 街心花园有一块草坪(以下列图),在草坪周围从某极点开始每 2 米种一棵月季花,一共能够种多少棵月季花?(二)试一试,独立达成1.一个长方形边长 6 分米,把它均匀分红 3 个小长方形,求每个小长方形的周长和面积各是多少?2. 下列图是一个餐厅室的平面图,准备从头装饰。
每一米长的墙壁需用50 元壁纸,10 元钱的胶。
请你估算一下,装饰墙壁约需资料费多少元?3. 用 9 个边长 2 厘米的小正方形摆成下列图形状,它的周长是__________ 厘米。
4. 下列图正方形被切割成4 个长方形,每个长方形的周长都是20 厘米,求这个正方形的周长?。
巧求周长(三四年级通用版)

巧求周长(三四年级通用版)work Information Technology Company.2020YEAR巧求周长例题精讲基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积.基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长.常用方法:对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.平移:在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.割补:割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.旋转:在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.对称:平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.代换:在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 求图中所有线段的总长(单位:厘米) 4E D C B A【解析】 要注意到,题目所求的是图中所有线段的总长,而图中的线段,并不仅仅是、、、四段,还包括、等等,因此不能简单地将图中标示的线段长度进行求和.同时应该注意到,;,等等.因此,为了计算图中所有线段的总长,需要先计算AB 、BC 、CD 、DE 这四条线段分别被累加了几次.这里,可以按照每条线段分别是由几部分组成的加以讨论:由1段组成的线段共有4条,即AB 、BC 、CD 、DE ,而求和过程中AB 、BC 、CD 、DE 这四条线段各被累加了1次.类似地考虑到,由2段组成的线段共有3条,求和过程中AB 、DE 各被累加了1次,BC 、CD 各被累加了2次.由3段组成的线段共有2条,求和过程中AB 、DE 各被累加了1次,BC 、CD 各被累加了2次.由4段组成的线段只有AE ,其中AB 、BC 、CD 、DE 各被计算了1次.综上所述,AB 、DE 各被计算了4次,BC 、CD 各被计算了6次.因而图中所有线段的总长度为: 4【例 2】 如图所示,一个大长方形被三条线段分成了四个小长方形,各条线段长度见图(单位:厘米).求:图中所有长方形的周长之和.21342【解析】 类似于上题,题目中所说的长方形,并不只包括最小的几个长方形,因此需要先求出每条线段在求和过程中被累加了多少次.因为没从大长方形的长上找到一条线段,就能对应地找到大长方形内的一个长方形,所以可以利用上一个问题的结论来解决这个问题.当然,要考虑到,每个长方形都有两条长和两条宽,因此计算过程中应该注意不要漏算.先考虑大长方形的长上各边:应用上一道题目的结论,每条边上长为4、3、1、2的线段分别被计算了4、6、6、4次.然后再考虑大长方形的宽:因为共有个长方形,所以长度为2的宽被计算了次.故总周长可以用下式计算得到:.【例3】 如图,正方形的边长为4,被分割成如下12个小长方形,求这12个小长方形的所有周长之和.【解析】 4445256⨯+⨯⨯=.【巩固】(“希望杯”第一试)如右图,正方形ABCD 的边长是6厘米,过正方形内的任意两点画直线,可把正方形分成9个小长方形。
小学三年级数学巧求图形的周长

巧求图形的周长正方形周长=边长×4,长方形周长=(长+宽)×2=长×2+宽×2这两个计算公式看起来十分简单,但用途却十分广泛。
利用它们可以巧求一些复杂图形的周长。
解决这类问题主要从两方面入手:1、对于一些运用拼和剪来构造新图形的问题,我们常常要画图帮助理解,仔细分析,思考怎样从已知条件中找到求周长所要的条件或找到新图形周长与原来图形周长间的关系,再求出它的周长。
2、对于一些不规则的比较复杂的图形,求它们的周长,往往要运用“平移、转化”等方法把问题转化成长方形或正方形的周长。
在转化过程中要抓住“变”与“不变”两个部分,而且不能遗漏掉某些线段的长度。
例1、用3个周长是15厘米的正方形拼成一个长方形,求所拼成的长方形的周长。
分析与解答:请你画图后再思考解答。
试一试1、用3个周长是17厘米的正方形拼成一个长方形,求所拼成的长方形的周长。
例2、一张长方形纸长是32厘米,宽20厘米,先剪下一个最大的正方形纸片,再从余下的纸片中又剪下一个最大的正方形,最后剩下的长方形纸片的周长是多少厘米?分析与解答:先画图,然后想一想,第一次剪的正方形的边长是多少,第二次剪的正方形的边长是多少。
试一试2、在一个长是24厘米,宽15厘米长方形纸中,先剪下一个最大的正方形纸片,再从余下的纸片中又剪下一个最大的正方形,最后剩下的长方形纸片的周长是多少厘米?例3、计算下列图形(左图)的周长(单位:厘米)。
252532分析与解答:将图中右上缺角处的线段分别向上、向右平行移动,这样正好移补成一个正方形。
试一试3、如上右图是一个楼梯的侧剖图。
已知每步台阶宽3分米,高2分米。
求这个楼梯侧面的周长是多少米?例4、求下面图(1)的周长(单位:厘米)。
分析与解答:求这个图形的周长,我们也同样采用转化的方法,想一想,可以转化成什么图形,转化后图形的周长与原来图形周长之间有什么样的关系,可以怎样求原图的周长。
试一试4、求上图(2)的周长。
小学三年级数学教案巧求周长(一)

2 巧求周长(一)学习目标:1、理解掌握周长的意义,学会用平移等方法求出不规则图形的周长,渗透转化的数学思想。
2、初步了解图形拼接和切割后,新图形周长的变化规律,能灵活运用长方形和正方形的周长计算公式解决相关问题。
3、体会数学与生活的密切联系,培养动手操作能力和解决问题的能力。
教学重点:把不规则图形通过平移割补等方法变成规则的图形求出周长。
教学难点:1、掌握计算不规则图形的周长的方法2、初步了解图形拼接和切割后,新图形周长的变化规律教学过程:一、情景体验师:同学们,你们知道什么是平面图形的周长吗?(封闭图形一周的长度就是它的周长)师:你会求哪些图形的周长呢?师引导学生得出:正方形周长=边长×边长长方形周长=(长+宽)×2师:今天早晨,朋朋和爸爸沿着公园的小池塘跑步,跑了几圈后,朋朋问爸爸:“我们跑一圈有多少米啊?”爸爸摸着朋朋的脑袋说:“跑一圈的路程就是小池塘的周长。
”朋朋疑惑地说“我只会求长方形和正方形的周长,但我们跑的路线既不是长方形,也不是正方形,该怎样算呢?”(老师作图,学生思考)师:现在只知道80米和60米这两条线段的长度,这个图形的周长容易求出来吗?生:不容易师:为什么?生:因为这个图形既不是长方形,也不是正方形,不能直接用公式求。
师:对,我们前面学过的长方形、正方形都是规则图形,这个图形是我们学过的规则图形吗?生:是不规则的图形师:那该如何求它的周长呢?今天我们就一起来探究不规则图形的周长的求法。
板书:巧求周长。
朋朋沿着如下图所示的小路跑步,跑一圈的路程是多少呢?(单位:米)师:想一想,该怎样计算这个图形的周长呢?(学生分组讨论)生:我发现右上角缺了一个小长方形,补上之后就变成一个大长方形,大长方形的周长跟原图形的周长相等。
师:大家同意他(她)的说法吗?(学生讨论,得出结果:同意)师:你是怎么发现大长方形的周长跟原图形的周长是相等的呢?生:因为小长方形的两条长和两条宽是相等的师:很好!跟原图形相比,就相当于将原图形中的两条线段进行平移,变成一个规则的长方形(课件展示动画)师:平移后线段的长短有没有改变?生:没有师:对,所以对于不规则的图形,我们可以通过平移的方法转化成规则的图形再来求周长,请自主完成计算过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 如何运用长方形、正方形周长计算 公式,巧妙地求一些复杂图形的周 长呢?
• 平移
• 分割
例1
• 下图是一个楼梯的侧面图,求此图形的周长。
2米
3米
3+2=5(米) 5×2=10(米)
试一试1:
• 下图是一个楼梯的侧面,如果在阶梯上铺地毯, 要计算地毯的长度,可以怎样测量?
10÷2=5(厘米)
4 × 5=20(厘米)
答:原来一个正方形的周 长是20厘米。
例2
• 下图是由6个边长2厘米的正方形拼 成的,这个图形的周长是多少厘米?
长:2×4=8(厘米) 宽:2×2=4(厘米)
(8+4)×2=24(厘米) 答:这个图形的周长是24厘米。
试一试2:
• 右图是由5个边长为3厘米的正方形 组成的图形,求此图形的周长。
长:3×3=9(厘米) 宽:3×3=9(厘米)
9×4=36(厘米) 答:这个图形的周长是36厘米。
例3
• 两个大小相同的正方形拼成一个长方形后, 周长比原来两个正方形周长的和减少了6厘 米。原来一个正方形的周长是多少厘米?
边长:6÷2=3(厘米) 周长:3 ×4=1相同的正方形拼成一个长方形 后,周长比原来两个正方形的周长和减少 10厘米。原来一个正方形的周长是多少?
