制药化工原理课后习题答案
制药化工原理习题答案

制药化工原理习题答案【篇一:制药工程化工原理期中考试答案】__…__…__…__…:号…学… 线_…__…__…__…__…__…__…_:名封姓…… _…__…__…__…__…_:密.级…班… …__…__…__…__…:系…院….… …新乡学院2013 ― 2014 学年度第二学期《化工原理》期中试卷课程归属部门:化学与化工学院试卷适用范围:2012级制药工程专业考试形式:开卷考试时间:110 分钟一、(每空1分,共30分)1.液柱压差计是基于流体静力学原理的测压装置,用u形管压差计测压时,若一端与大气相通,则读数r表示的是表压或真空度。
2. 若离心泵入口真空表读数为700mmhg,当地大气压为760mmhg,则输送42℃水时(饱和蒸汽压为8.2kpa)泵内会发生汽蚀现象。
(会,不会)3.牛顿粘性定律的表达式为f??adudy,该式应用条件是流体作层流流动。
4.一转子流量计,当通过水流量为1 m3/h时,测得该流量计进、出间压强降为20pa,当流量增大为2 m3/h时,相应的压强降。
5.往复压缩机的实际工作循环包括:压缩、排气、、四个过程。
6.启动时需要关闭出口阀门的液体输送泵是。
7.离心泵说明书中所标的汽蚀余量越大,说明其抗汽蚀能力。
8.安装在管路上的离心泵,其他条件不变,所送液体温度降低,泵发生汽蚀的可能性低,若供液槽液面上方的压强降低,泵发生汽蚀的可能性增大;若所送液体密度增大,泵发生汽蚀的可能性增大。
9.由三支管组成的并联管路,各支管的管长和摩擦系数相等,管径比为1:2:3,则三支管的流量比为1::243。
10.已知某油品在圆管中定态流动,其re=1000。
已测得管中心处的点速度为0.5m/s,则此管截面上的平均速度为 0.25m/s。
若油品流量增加一倍,则通过每米直管的压头损失为原损失的 2 倍。
11.往复泵流量调节的方法有:、 12.当要求气体的压缩比p2p?1时,宜采用多级压缩。
制药化工原理课后习题答案

制药化工原理课后习题答案The latest revision on November 22, 2020绪论2.解:∴2321001325.1mJmNmNatmL⨯=⋅⋅⋅⋅⋅⋅-∴21001325.1JatmL⨯=⋅以J·mol-1·K-1表示R的值R =××102 J﹒mol-1﹒K-1= J﹒mol-1﹒K-1第一章流体流动1.表压=-真空度=-×104Pa绝压=×104 Pa2.解:设右侧水面到B′点高为h3,根据流体静力学基本方程可知PB=PB′则ρ油gh2=ρ水gh3h=h1+h3=892mm3.解:正U型管水银压差计由图可知 PA =P1+(x+R1)ρ水gP B =P 2+x ρ水g∵P 1-P 2=∴P A -P B =+ρ水gR 1又有P A =P C P C = P B +ρHg gR 1∴ρHg gR 1=+ρ水gR 1∴mm m s m m kg R 00.200200.081.9)100013600( 2.472kPa231==⋅⨯⋅-=--倒U 型压差计 设右侧管内水银高度为M∵指示流体为空气∴P C =P DP 1=P C +ρ水g(R 2+M) P 2=P D +ρ水gM∴mm m sm m kg R 0.2522520.081.91000 2.472kPa232==⋅⨯⋅=- 4.(1)P B =-(表)(2)R ′=7.解:由公式AVsu =可得 Vs=uA=u πd 2/4=×π××2)2×10-6=×10-3m 3/sWs=Vs ρ=×10-3×1840=s8.解:由题可知:1—1′截面:P 1=×105Pa u=0以2—2′截面为基准水平面∴z 1=3m2—2′截面:设管内流速为u z 2=03—3′截面:u, z 3=3m4—4′截面:u, z 4=3+=5—5′截面:u, z 5=3m6—6′截面:u, z 6=2m, P 6=×105Pa根据伯努利方程:We=0, ∑h f =0有ρ++=ρ+62611P 2u gz P gz∵P 1=P 6 ∴u 2/2=g(z 1-z 6)=有ρρ222112P u gz P gz ++=+×3+×105/1000=+P 2/1000∴P 2=×105Pa×105/1000=+P 3/1000∴P 3=×105Pa×3+×105/1000=×++P 4/1000∴P 4=×105Pa∴P 5=×105Pa9. (1)u=s V h =h(2)Δz=解:ηNeN =Ne=We ﹒Ws取釜内液面为1—1′截面,高位槽内液面为2—2′截面根据伯努利方程:f h Pu gz We u P gz ∑+++=+++ρρ22222111221—1′截面:z 1=0, P 1=-×104(表压), u 1=02—2′截面:z 2=15m, P 2=0(表压), AWsu ρ=2A=πd 2/4=×π×[(76-4×2)×10-3]2=×10-3m 2∴s m h m u /46.1/3.524710501063.3102342==⨯⨯⨯=- 173740106105046.11068Re 43=⨯⨯⨯⨯==--μρdu >4000 湍流又ε/d=×10-3/68×10-3=×10-3查图得λ=查表1—3得,ξ全开闸阀= ξ半开截止阀= ξ90°标准弯头= ξ进= ξ出=1∴h f ′=++3×+×2=kg∴∑h f =+=kgWe=kgNe=×2×104/3600=N==12.解:1—1′:高位槽液面 2—2′:出口管内侧列伯努利方程 f h Pu gz We u P gz ∑+++=+++ρρ2222211122z 2=0, z 1=4m, P 1=P 2=0(表), u 1=0, We=0∴∑hf +u22/2=4g∑hf = hf+hf′查表1—3得,ξ半开截止阀= ξ90°标准弯头=hf ′=∑ξ﹒u22/2=++×u22/2=×u22/2∴gdu4)75.10201(222=++λ化简得(400λ+×u22/2=20℃时μ水=λ=f(Re)=f(u2) 需试差321075.49Re⨯==uduμρ假设 u0 Re λ→ u0 01.0=dε766307960082588∴截止阀半开时该输水系统的u=sVs=uA=×π×=s∴Vs=h第二章 流体输送设备1、解:分别取离心泵的进、出口截面为1-1′截面和2-2′截面,由伯努力方程得:其中,12Z Z -= m ;41109.1⨯-=p Pa(表压);52107.4⨯=p Pa(表压);21u u =;21,-f H =0;20℃时水的密度3m kg 2.998-⋅=ρ。
化工原理课后习题答案上下册(钟理版)

第一章 流体流动习题解答1-1 已知甲城市的大气压为760mmHg ,乙城市的大气压为750mmHg 。
某反应器在甲地操作时要求其真空表读数为600mmHg ,若把该反应器放在乙地操作时,要维持与甲地操作相同的绝对压,真空表的读数应为多少,分别用mmHg 和Pa 表示。
[590mmHg, 7.86×104Pa]解:P (甲绝对)=760-600=160mmHg 750-160=590mmHg=7.86×104Pa1-2用水银压强计如图测量容器内水面上方压力P 0,测压点位于水面以下0.2m 处,测压点与U 形管内水银界面的垂直距离为0.3m ,水银压强计的读数R =300mm ,试求 (1)容器内压强P 0为多少?(2)若容器内表压增加一倍,压差计的读数R 为多少?习题1-2 附图[(1) 3.51×104N ⋅m -2 (表压); (2)0.554m] 解:1. 根据静压强分布规律 P A =P 0+g ρHP B =ρ,gR因等高面就是等压面,故P A = P BP 0=ρ,gR -ρgH =13600×9.81×0.3-1000×9.81(0.2+0.3)=3.51×104N/㎡ (表压) 2. 设P 0加倍后,压差计的读数增为R ,=R +△R ,容器内水面与水银分界面的垂直距离相应增为H ,=H +2R∆。
同理, ''''''02R p gR gH gR g R gH gρρρρρρ∆=-=+∆--000p g g p p 0.254m g g 10009.81g g 136009.812R H R ρρρρρρ⨯∆⨯⨯,,,4,,-(-)- 3.5110====---220.30.2540.554m R R R ∆,=+=+=1-3单杯式水银压强计如图的液杯直径D =100mm ,细管直径d =8mm 。
制药化工原理课后习题答案新编

绪论2.解:∴2321001325.1m J m N m N atm L ⨯=⋅⋅⋅⋅⋅⋅-∴21001325.1J atm L ⨯=⋅以J ·mol -1·K -1表示R 的值R =××102 J ﹒mol -1﹒K -1= J ﹒mol -1﹒K -1第一章 流体流动1. 表压=-真空度=-×104Pa 绝压=×104 Pa2.解:设右侧水面到B ′点高为h 3,根据流体静力学基本方程可知P B =P B ′ 则ρ油gh 2=ρ水gh 3h=h 1+h 3=892mm3.解:正U 型管水银压差计 由图可知 P A =P 1+(x +R 1)ρ水gP B =P 2+x ρ水g ∵P 1-P 2= ∴P A -P B =+ρ水gR 1又有P A =P C P C = P B +ρHg gR 1∴ρHg gR 1=+ρ水gR 1∴mm m s m m kg R 00.200200.081.9)100013600( 2.472kPa231==⋅⨯⋅-=--倒U 型压差计 设右侧管内水银高度为M∵指示流体为空气∴P C =P D P 1=P C +ρ水g(R 2+M) P 2=P D +ρ水gM∴mm m s m m kg R 0.2522520.081.91000 2.472kPa232==⋅⨯⋅=-4.(1)P B =-(表) (2)R ′=0.178m 7.解:由公式AVsu =可得 Vs=uA=u πd 2/4=×π××2)2×10-6=×10-3m 3/sWs=Vs ρ=×10-3×1840=2.89kg/s8.解:由题可知:1—1′截面:P 1=×105Pa u=0以2—2′截面为基准水平面∴z 1=3m2—2′截面:设管内流速为u z 2=0 3—3′截面:u, z 3=3m 4—4′截面:u, z 4=3+=3.5m 5—5′截面:u, z 5=3m6—6′截面:u, z 6=2m, P 6=×105Pa 根据伯努利方程:We=0, ∑h f =0有ρ++=ρ+62611P 2u gz P gz∵P 1=P 6 ∴u 2/2=g(z 1-z 6)=有ρρ222112P u gz P gz ++=+×3+×105/1000=+P 2/1000∴P 2=×105Pa ×105/1000=+P 3/1000∴P 3=×105Pa×3+×105/1000=×++P 4/1000∴P 4=×105Pa ∴P 5=×105Pa9. (1)u=1.55m/s V h =10.95m 3/h (2)Δz=2.86m 解:ηNeN =Ne=We ﹒Ws取釜内液面为1—1′截面,高位槽内液面为2—2′截面根据伯努利方程:f h Pu gz We u P gz ∑+++=+++ρρ22222111221—1′截面:z 1=0, P 1=-×104(表压), u 1=0 2—2′截面:z 2=15m, P 2=0(表压), AWsu ρ=2 A=πd 2/4=×π×[(76-4×2)×10-3]2=×10-3m 2∴s m h m u /46.1/3.524710501063.3102342==⨯⨯⨯=- 173740106105046.11068Re 43=⨯⨯⨯⨯==--μρdu >4000 湍流 又ε/d=×10-3/68×10-3=×10-3查图得λ=查表1—3得,ξ全开闸阀= ξ半开截止阀= ξ90°标准弯头= ξ进= ξ出=1∴h f ′=++3×+×2=kg∴∑h f =+=kgWe=kg Ne=×2×104/3600=N==12.解:1—1′:高位槽液面 2—2′:出口管内侧列伯努利方程 f h Pu gz We u P gz ∑+++=+++ρρ2222211122z 2=0, z 1=4m, P 1=P 2=0(表), u 1=0, We=0∴∑h f +u 22/2=4g ∑h f = h f +h f ′查表1—3得,ξ半开截止阀= ξ90°标准弯头= h f ′=∑ξ﹒u 22/2=++ ×u 22/2=×u 22/2∴g du 4)75.10201(222=++λ化简得(400λ+×u 22/2=20℃时μ水=λ=f(Re)=f(u 2) 需试差 321075.49Re ⨯==u du μρ假设 u 0 Re λ → u 001.0=dε76630 79600 82588∴截止阀半开时该输水系统的u 0=1.66m/sVs=uA=×π×=0.00326m 3/s∴Vs=11.73m 3/h第二章 流体输送设备1、解:分别取离心泵的进、出口截面为1-1′截面和2-2′截面,由伯努力方程得: 其中,12Z Z -=0.4 m ;41109.1⨯-=p Pa(表压);52107.4⨯=p Pa(表压);21u u =;21,-f H =0;20℃时水的密度3m kg 2.998-⋅=ρ。
制药化工原理课后习题答案

绪论2.解:∴2321001325.1m J m N m N atm L ⨯=⋅⋅⋅⋅⋅⋅- ∴21001325.1J atm L ⨯=⋅以J ·mol -1·K -1表示R 的值R =0.08206×1.01325×102 J ﹒mol -1﹒K -1=8.315 J ﹒mol -1﹒K -1第一章 流体流动1. 表压=-真空度=-4.8×104Pa 绝压=5.3×104 Pa2.解:设右侧水面到B ′点高为h 3,根据流体静力学基本方程可知P B =P B ′ 则ρ油gh 2=ρ水gh 3h=h 1+h 3=892mm3.解:正U 型管水银压差计 由图可知 P A =P 1+(x +R 1)ρ水gP B =P 2+x ρ水g∵P 1-P 2=2.472kPa ∴P A -P B =2.472kP A +ρ水gR 1 又有P A =P C P C = P B +ρHg gR 1∴ρHg gR 1=2.472kPa +ρ水gR 1∴mm m s m m kg R 00.200200.081.9)100013600( 2.472kPa231==⋅⨯⋅-=--倒U 型压差计 设右侧管内水银高度为M∵指示流体为空气∴P C =P DP 1=P C +ρ水g(R 2+M) P 2=P D +ρ水gM∴mm m s m m kg R 0.2522520.081.91000 2.472kPa232==⋅⨯⋅=-4.(1)P B =-845.9Pa(表) (2)R ′=0.178m 7.解:由公式AVsu =可得 Vs=uA=u πd 2/4=0.8×π×(57-3.5×2)2×10-6=1.57×10-3m 3/sWs=Vs ρ=1.57×10-3×1840=2.89kg/s8.解:由题可知:1—1′截面:P 1=1.013×105Pa u=0以2—2′截面为基准水平面∴z 1=3m2—2′截面:设管内流速为u z 2=0 3—3′截面:u, z 3=3m4—4′截面:u, z 4=3+0.5=3.5m 5—5′截面:u, z 5=3m6—6′截面:u, z 6=2m, P 6=1.013×105Pa 根据伯努利方程:We=0, ∑h f =0有ρ++=ρ+62611P 2u gz P gz∵P 1=P 6 ∴u 2/2=g(z 1-z 6)=9.8有ρρ222112P u gz P gz ++=+9.8×3+1.013×105/1000=9.8+P 2/1000∴P 2=1.209×105Pa 1.013×105/1000=9.8+P 3/1000∴P 3=0.915×105Pa9.8×3+1.013×105/1000=9.8×3.5+9.8+P 4/1000∴P 4=0.866×105Pa ∴P 5=0.915×105Pa9. (1)u=1.55m/s V h =10.95m 3/h (2)Δz=2.86m 解:ηNeN =Ne=We ﹒Ws取釜内液面为1—1′截面,高位槽内液面为2—2′截面根据伯努利方程:f h Pu gz We u P gz ∑+++=+++ρρ22222111221—1′截面:z 1=0, P 1=-2.5×104(表压), u 1=0 2—2′截面:z 2=15m, P 2=0(表压), AWsu ρ=2 A=πd 2/4=0.25×π×[(76-4×2)×10-3]2=3.63×10-3m 2∴s m h m u /46.1/3.524710501063.3102342==⨯⨯⨯=- 173740106105046.11068Re 43=⨯⨯⨯⨯==--μρdu >4000 湍流又ε/d =0.3×10-3/68×10-3=4.41×10-3 查图得λ=0.029 查表1—3得,ξ全开闸阀=0.17 ξ半开截止阀=9.5 ξ90°标准弯头=0.75 ξ进=0.5 ξ出=1∴h f ′=(0.17+9.5+3×0.75+1.5)×1.462/2=14.2J/kg∴∑h f =22.7+14.2=36.9J/kgWe =208.87J/kgNe =208.87×2×104/3600=1.16kWN=1.16/0.7=1.66kW12.解:1—1′:高位槽液面 2—2′:出口管内侧列伯努利方程 f h Pu gz We u P gz ∑+++=+++ρρ2222211122z 2=0, z 1=4m, P 1=P 2=0(表), u 1=0, We=0∴∑h f +u 22/2=4g ∑h f = h f +h f ′查表1—3得,ξ半开截止阀=9.5 ξ90°标准弯头=0.75h f ′=∑ξ﹒u 22/2=(9.5+0.75+0.5) ×u 22/2=10.75×u 22/2∴g du 4)75.10201(222=++λ化简得(400λ+11.75)×u 22/2=39.220℃时μ水=1.005λ=f(Re)=f(u 2) 需试差 321075.49Re ⨯==u du μρ假设 u 0 Re λ → u 0 01.0=dε1.5 76630 0.039 1.66 1.6 79600 0.039 1.66 1.66 82588 0.0388 1.66 ∴截止阀半开时该输水系统的u 0=1.66m/sVs=uA=1.66×0.25π×0.052=0.00326m 3/s∴Vs=11.73m 3/h第二章 流体输送设备1、解:分别取离心泵的进、出口截面为1-1′截面和2-2′截面,由伯努力方程得: 其中,12Z Z -=0.4 m ;41109.1⨯-=p Pa(表压);52107.4⨯=p Pa(表压);21u u =;21,-f H =0;20℃时水的密度3m kg 2.998-⋅=ρ。
化工原理课后习题答案第七章吸收习题解答

化工原理课后习题答案第七章吸收习题解答(总18页)-本页仅作为预览文档封面,使用时请删除本页-第七章 吸 收7-1 总压 kPa ,温度25℃时,1000克水中含二氧化硫50克,在此浓度范围内亨利定律适用,通过实验测定其亨利系数E 为 MPa , 试求该溶液上方二氧化硫的平衡分压和相平衡常数m 。
(溶液密度近似取为1000kg/m 3)解:溶质在液相中的摩尔分数:50640.01391000501864x ==+ 二氧化硫的平衡分压:*34.13100.0139kPa=57.41kPa p Ex ==⨯⨯相平衡常数:634.1310Pa40.77101.310PaE m P ⨯===⨯7-2 在逆流喷淋填料塔中用水进行硫化氢气体的吸收,含硫化氢的混合气进口浓度为5%(质量分数),求填料塔出口水溶液中硫化氢的最大浓度。
已知塔内温度为20℃,压强为×105 Pa ,亨利系数E 为。
解:相平衡常数为:6548.910321.711.5210E m P ⨯===⨯ 硫化氢的混合气进口摩尔浓度:15340.04305953429y ==+若填料塔出口水溶液中硫化氢达最大浓度,在出口处气液相达平衡,即:41max 0.0430 1.3410321.71y x m -===⨯7-3 分析下列过程是吸收过程还是解吸过程,计算其推动力的大小,并在x - y 图上表示。
(1)含NO 2 (摩尔分率)的水溶液和含NO 2 (摩尔分率) 的混合气接触,总压为,T=15℃,已知15℃时,NO 2水溶液的亨利系数E =×102 kPa ;(2)气液组成及温度同(1),总压达200kPa (绝对压强)。
解:(1)相平衡常数为:5131 1.6810Pa1.658101.310Pa E m P ⨯===⨯ *1 1.6580.0030.00498y m x ==⨯=由于 *y y >,所以该过程是吸收过程。
天津大学版 化工原理下册课后答案

第七章传质与分离过程概论1.在吸收塔中用水吸收混于空气中的氨。
已知入塔混合气中氨含量为 5.5%(质量分数,下同),吸收后出塔气体中氨含量为0.2%,试计算进、出塔气体中氨的摩尔比、。
解:先计算进、出塔气体中氨的摩尔分数和。
进、出塔气体中氨的摩尔比、为由计算可知,当混合物中某组分的摩尔分数很小时,摩尔比近似等于摩尔分数。
2. 试证明由组分A和B组成的双组分混合物系统,下列关系式成立:(1)(2)解:(1)由于故(2)故3. 在直径为0.012 m、长度为0.35 m的圆管中,CO气体通过N2进行稳态分子扩散。
管内N2的温度为373 K,总压为101.3 kPa,管两端CO的分压分别为70.0 kPa和7.0 kPa,试计算CO的扩散通量。
解:设 A-CO; B-N2查附录一得4. 在总压为101.3 kPa,温度为273 K下,组分A自气相主体通过厚度为0.015 m的气膜扩散到催化剂表面,发生瞬态化学反应。
生成的气体B离开催化剂表面通过气膜向气相主体扩散。
已知气膜的气相主体一侧组分A的分压为22.5 kPa,组分A在组分B中的扩散系数为1.85×10-5 m2/s。
试计算组分A和组分B的传质通量和。
解:由化学计量式可得代入式(7-25),得分离变量,并积分得5. 在温度为278 K的条件下,令某有机溶剂与氨水接触,该有机溶剂与水不互溶。
氨自水相向有机相扩散。
在两相界面处,水相中的氨维持平衡组成,其值为0.022(摩尔分数,下同),该处溶液的密度为998.2 kg/m3;在离界面5 mm的水相中,氨的组成为0.085,该处溶液的密度为997.0 kg/m3。
278 K时氨在水中的扩散系数为1.24×10–9 m2/s。
试计算稳态扩散下氨的传质通量。
解:设 A-NH3;B-H2O离界面5 mm处为点1、两相界面处为点2,则氨的摩尔分数为,点1、点2处溶液的平均摩尔质量为溶液的平均总物质的量浓度为故氨的摩尔通量为6. 试用式(7-41)估算在105.5 kPa、288 K条件下,氢气(A)在甲烷(B)中的扩散系数。
化工原理第三版(陈敏恒)上、下册课后思考题答案(精心整理版)

化工原理第三版(陈敏恒)上、下册课后思考题答案(精心整理版)第一章流体流动1、什么是连续性假定?质点的含义是什么?有什么条件?连续性假设:假定流体是由大量质点组成的,彼此间没有间隙,完全充满所占空间的连续介质。
质点指的是一个含有大量分子的流体微团,其尺寸远小于设备尺寸,但比分子自由程却要大得多。
2、描述流体运动的拉格朗日法和欧拉法有什么不同点?拉格朗日法描述的是同一质点在不同时刻的状态;欧拉法描述的是空间各点的状态及其与时间的关系。
3、粘性的物理本质是什么?为什么温度上升,气体粘度上升,而液体粘度下降?粘性的物理本质是分子间的引力和分子的运动与碰撞。
通常气体的粘度随温度上升而增大,因为气体分子间距离较大,以分子的热运动为主,温度上升,热运动加剧,粘度上升。
液体的粘度随温度增加而减小,因为液体分子间距离较小,以分子间的引力为主,温度上升,分子间的引力下降,粘度下降。
4、静压强有什么特性?①静止流体中,任意界面上只受到大小相等、方向相反、垂直于作用面的压力;②作用于某一点不同方向上的静压强在数值上是相等的;③压强各向传递。
7、为什么高烟囱比低烟囱拔烟效果好?由静力学方程可以导出,所以H增加,压差增加,拔风量大。
8、什么叫均匀分布?什么叫均匀流段?均匀分布指速度分布大小均匀;均匀流段指速度方向平行、无迁移加速度。
9、伯努利方程的应用条件有哪些?重力场下、不可压缩、理想流体作定态流动,流体微元与其它微元或环境没有能量交换时,同一流线上的流体间能量的关系。
12、层流与湍流的本质区别是什么?区别是否存在流体速度u、压强p的脉动性,即是否存在流体质点的脉动性。
13、雷诺数的物理意义是什么?物理意义是它表征了流动流体惯性力与粘性力之比。
14、何谓泊谡叶方程?其应用条件有哪些?应用条件:不可压缩流体在直圆管中作定态层流流动时的阻力损失计算。
15、何谓水力光滑管?何谓完全湍流粗糙管?当壁面凸出物低于层流内层厚度,体现不出粗糙度过对阻力损失的影响时,称为水力光滑管。
化工原理上册课后习题及答案

化⼯原理上册课后习题及答案第⼀章:流体流动⼆、本章思考题1-1 何谓理想流体?实际流体与理想流体有何区别?如何体现在伯努利⽅程上?1-2 何谓绝对压⼒、表压和真空度?表压与绝对压⼒、⼤⽓压⼒之间有什么关系?真空度与绝对压⼒、⼤⽓压⼒有什么关系?1-3 流体静⼒学⽅程式有⼏种表达形式?它们都能说明什么问题?应⽤静⼒学⽅程分析问题时如何确定等压⾯?1-4 如何利⽤柏努利⽅程测量等直径管的机械能损失?测量什么量?如何计算?在机械能损失时,直管⽔平安装与垂直安装所得结果是否相同? 1-5 如何判断管路系统中流体流动的⽅向?1-6何谓流体的层流流动与湍流流动?如何判断流体的流动是层流还是湍流?1-7 ⼀定质量流量的⽔在⼀定内径的圆管中稳定流动,当⽔温升⾼时,Re 将如何变化? 1-8 何谓⽜顿粘性定律?流体粘性的本质是什么? 1-9 何谓层流底层?其厚度与哪些因素有关?1-10摩擦系数λ与雷诺数Re 及相对粗糙度d / 的关联图分为4个区域。
每个区域中,λ与哪些因素有关?哪个区域的流体摩擦损失fh 与流速u 的⼀次⽅成正⽐?哪个区域的fh 与2u 成正⽐?光滑管流动时的摩擦损失fh 与u 的⼏次⽅成正⽐?1-11管壁粗糙度对湍流流动时的摩擦阻⼒损失有何影响?何谓流体的光滑管流动? 1-12 在⽤⽪托测速管测量管内流体的平均流速时,需要测量管中哪⼀点的流体流速,然后如何计算平均流速?三、本章例题例1-1 如本题附图所⽰,⽤开⼝液柱压差计测量敞⼝贮槽中油品排放量。
已知贮槽直径D 为3m ,油品密度为900kg/m3。
压差计右侧⽔银⾯上灌有槽内的油品,其⾼度为h1。
已测得当压差计上指⽰剂读数为R1时,贮槽内油⾯与左侧⽔银⾯间的垂直距离为H1。
试计算当右侧⽀管内油⾯向下移动30mm 后,贮槽中排放出油品的质量。
解:本题只要求出压差计油⾯向下移动30mm 时,贮槽内油⾯相应下移的⾼度,即可求出排放量。
⾸先应了解槽内液⾯下降后压差计中指⽰剂读数的变化情况,然后再寻求压差计中油⾯下移⾼度与槽内油⾯下移⾼度间的关系。
制药工程原理课后习题答案(可编辑)

制药工程原理课后习题答案习题与思考题第二章液体搅拌第三章流体输送设备【例2-1】离心泵特性曲线的测定附图为测定离心泵特性曲线的实验装置,实验中已测出如下一组数据:泵进口处真空表读数p12.67×104Pa真空度泵出口处压强表读数p22.55×105Pa表压泵的流量Q12.5×10-3m3/s功率表测得电动机所消耗功率为6.2kW吸入管直径d180mm压出管直径d260mm两测压点间垂直距离Z2-Z10.5m泵由电动机直接带动,传动效率可视为1,电动机的效率为0.93实验介质为20℃的清水试计算在此流量下泵的压头H、轴功率N和效率η。
解:(1)泵的压头在真空表及压强表所在截面1-1与2-2间列柏努利方程:式中 Z2-Z10.5mp1-2.67×104Pa(表压)p22.55×105Pa(表压)u1u2两测压口间的管路很短,其间阻力损失可忽略不计,故H0.5+29.88mH2O(2)泵的轴功率功率表测得功率为电动机的输入功率,电动机本身消耗一部分功率,其效率为0.93,于是电动机的输出功率(等于泵的轴功率)为:N6.2×0.935.77kW(3)泵的效率在实验中,如果改变出口阀门的开度,测出不同流量下的有关数据,计算出相应的H、N和η值,并将这些数据绘于坐标纸上,即得该泵在固定转速下的特性曲线。
【例2-2】将20℃的清水从贮水池送至水塔,已知塔内水面高于贮水池水面13m。
水塔及贮水池水面恒定不变,且均与大气相通。
输水管为φ140×4.5mm的钢管,总长为200m(包括局部阻力的当量长度)。
现拟选用4B20型水泵,当转速为2900r/min时,其特性曲线见附图,试分别求泵在运转时的流量、轴功率及效率。
摩擦系数λ可按0.02计算。
解:求泵运转时的流量、轴功率及效率,实际上是求泵的工作点。
即应先根据本题的管路特性在附图上标绘出管路特性曲线。
化工原理课后习题答案详解第四章

第四章多组分系统热力学4.1有溶剂A与溶质B形成一定组成的溶液。
此溶液中B的浓度为c B,质量摩尔浓度为b B,此溶液的密度为。
以M A,M B分别代表溶剂和溶质的摩尔质量,若溶液的组成用B的摩尔分数x B表示时,试导出x B与c B,x B与b B之间的关系。
解:根据各组成表示的定义4.2D-果糖溶于水(A)中形成的某溶液,质量分数,此溶液在20 ︒C时的密度。
求:此溶液中D-果糖的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:质量分数的定义为4.3在25 ︒C,1 kg水(A)中溶有醋酸(B),当醋酸的质量摩尔浓度b B介于和之间时,溶液的总体积。
求:(1)把水(A)和醋酸(B)的偏摩尔体积分别表示成b B的函数关系。
(2)时水和醋酸的偏摩尔体积。
解:根据定义当时4.460 ︒C时甲醇的饱和蒸气压是84.4 kPa,乙醇的饱和蒸气压是47.0 kPa。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %,求60 ︒C 时此混合物的平衡蒸气组成,以摩尔分数表示。
解:质量分数与摩尔分数的关系为求得甲醇的摩尔分数为根据Raoult定律4.580 ︒C是纯苯的蒸气压为100 kPa,纯甲苯的蒸气压为38.7 kPa。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物,80 ︒C时气相中苯的摩尔分数,求液相的组成。
解:根据Raoult定律4.6在18 ︒C,气体压力101.352 kPa下,1 dm3的水中能溶解O2 0.045 g,能溶解N2 0.02 g。
现将 1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾,赶出所溶解的O2和N2,并干燥之,求此干燥气体在101.325 kPa,18 ︒C下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为:,解:显然问题的关键是求出O2和N2的Henry常数。
18 ︒C,气体压力101.352 kPa下,O2和N2的质量摩尔浓度分别为这里假定了溶有气体的水的密度为(无限稀溶液)。
制药工程 化工原理 习题集
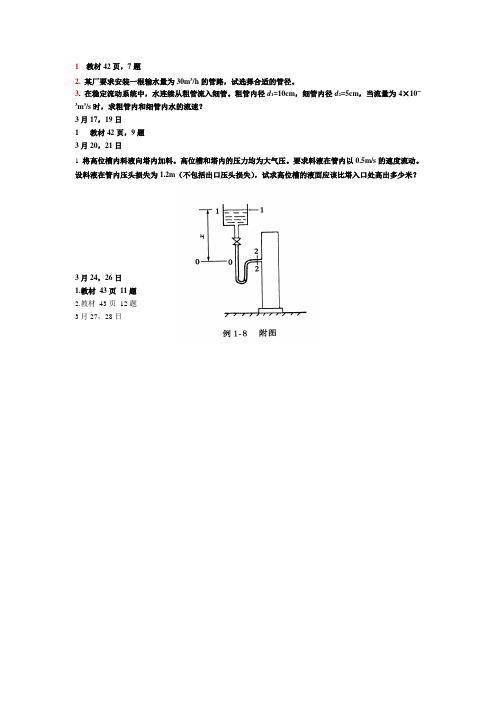
1教材42页,7题2.某厂要求安装一根输水量为30m3/h的管路,试选择合适的管径。
3. 在稳定流动系统中,水连续从粗管流入细管。
粗管内径d1=10cm,细管内径d2=5cm,当流量为4×10-3m3/s时,求粗管内和细管内水的流速?3月17,19日1教材42页,9题3月20,21日1 将高位槽内料液向塔内加料。
高位槽和塔内的压力均为大气压。
要求料液在管内以0.5m/s的速度流动。
设料液在管内压头损失为1.2m(不包括出口压头损失),试求高位槽的液面应该比塔入口处高出多少米?3月24,26日1.教材43页11题2.教材43页12题3月27,28日1.55kw3月31,2日离心泵特性曲线的测定附图为测定离心泵特性曲线的实验装置,实验中已测出如下一组数据:泵进口处真空表读数p1=2.67×104Pa(真空度),泵出口处压强表读数p2=2.55×105Pa(表压),泵的流量Q=12.5×10-3m3/s,功率表测得电动机所消耗功率为6.2kW,吸入管直径d1=80mm,压出管直径d2=60mm,两测压点间垂直距离Z2-Z1=0.5m,泵由电动机直接带动,传动效率可视为1,电动机的效率为0.93,实验介质为20℃的清水,两测压口间的管路很短,其间阻力损失可忽略不计试计算在此流量下泵的压头H、轴功率N和效率η。
浙5-1红砖平壁墙,厚度500mm,内侧温度200℃,外侧30℃,设红砖的平均热导率可取为0.57Wm-1℃-1,试求:(1)传导热通量q(2)距离内侧350mm出的温度t ANJUCT4-3:在外径为140mm的蒸气管道外包扎保温材料,以减少热损失。
蒸气管外壁温度为390℃,保温层外表面温度不大于40℃。
保温材料的λ与t的关系为λ=0.1+0.0002t(t的单位为℃,λ的单位为W/(m·℃))。
若要求每米管长的热损失Q/L不大于450W/m,试求保温层的厚度以及保温层中温度分布。
《化工原理》上册(第二版)各章节课后习题答案

22 δ= 10mm ; Qmax = 11.3KW 23 R = 6.3×10-3m2·℃/W
24 n = 31 ; L = 1.65m
25 L = 9.53m
26 qm = 4.0kg/s ; A = 7.14m2
27 qm2
=
10.9kg/s
;
n
=
36
;
L
=
2.06m
;
q, m1
= 2.24kg/s
第六章 传热 1 δ1 = 0.22m ; δ2Байду номын сангаас= 0.1m 2 t1 = 800℃
第 7 页,共 10 页
《化工原理》上册(第二版)各章节课后习题答案
3 t1 = 405℃ 4 δ = 50mm 5 (λ’-λ)/ λ = -19.7﹪ 6略 7 Q,/Q = 1.64 λ小的放内层 8 a = 330W/m2*℃ 9 a = 252.5W/ m2*℃ 10 q = 3.69kw/m2 11 q1/q2 =1 12 w = 3.72×10-3kg/s ; w’= 7.51×10-3kg/s 13 Tg = 312℃ 14 Tw = 746K 15 τ = 3.3hr 16 εA = 0.48 ; εB = 0.40 17 略
第二章 流体输送机械
化工原理课后题答案

化工原理课后题答案1. 请解释化学反应速率的概念,并列举影响化学反应速率的因素。
化学反应速率是指单位时间内反应物消耗或生成物产生的量。
影响化学反应速率的因素包括温度、浓度、压力、催化剂等。
温度升高会加快分子的运动速度,增加碰撞频率和能量,从而提高反应速率。
浓度的增加会增加反应物分子之间的碰撞频率,也会提高反应速率。
压力的增加对气相反应有影响,因为增加压力会使气体分子的密度增加,碰撞频率增加,反应速率也会增加。
催化剂是一种可以改变反应速率但本身不参与反应的物质,可以提高反应速率,降低活化能,加速反应的进行。
2. 请说明化学平衡的概念,并列举影响化学平衡的因素。
化学平衡是指在封闭容器中,当化学反应达到一定条件时,反应物和生成物的浓度不再发生变化的状态。
影响化学平衡的因素包括温度、压力、浓度、催化剂等。
温度的变化会影响平衡位置,对吸热反应和放热反应的影响不同。
压力的增加对气相反应有影响,根据Le Chatelier原理,增加压力会使平衡位置移向摩尔数较少的一侧。
浓度的变化也会影响平衡位置,增加某一种物质的浓度会使平衡位置移向另一侧。
催化剂可以影响反应速率,但不影响平衡位置。
3. 请解释原子结构中原子核的构成和特点。
原子核由质子和中子组成,质子带正电荷,中子不带电荷。
原子核的直径约为10^-15米,占据整个原子体积的极小部分,但质子和中子的质量占据了原子质量的绝大部分。
原子核带正电荷,因此原子核周围围绕着带负电的电子云,形成了原子的结构。
4. 请解释化学键的概念,并列举化学键的种类。
化学键是指原子之间通过共用电子或者电子转移而形成的连接。
化学键的种类包括离子键、共价键、金属键等。
离子键是通过正负电荷之间的静电作用形成的化学键,通常是金属和非金属之间的化合物。
共价键是通过原子之间共用电子而形成的化学键,常见于非金属之间的化合物。
金属键是金属原子之间通过电子海模型相互连接而形成的化学键。
5. 请解释化学反应的热力学基本概念,并列举热力学基本定律。
制药化工原理

制药化工原理[填空题]1用离心泵在两个敞口容器间输送液体。
若维持两容器的液面高度不变,则当输送管道上的阀门关小后,管路总阻力将()。
参考答案:不变[填空题]2空塔速度等于()体积流量除以()所得的流速。
参考答案:流体;塔截面积[填空题]3气体的粘度随温度升高而(),水的粘度随温度升高而()。
参考答案:增大;减小[填空题]4已知旋风分离器的平均旋转半径为0.5m,气体的切向进口速度为20m/s,则该分离器的分离因数为(g=10)()。
参考答案:80[单项选择题]5、下面对双膜理论描述不正确的是()A.气液接触时,气液间存在气膜和液膜B.气膜与液膜间存在一个相界面C.气液界面上气液相互平衡,界面上存在一定的阻力D.溶质的浓度梯度全部集中在气膜和液膜上参考答案:C[单项选择题]6、下面哪种干燥方法不同于其他干燥方法()A.加热面传热干燥B.对流干燥C.冷冻升华干燥D.红外线干参考答案:C[单项选择题]7、下面对泵流量调节叙述不正确的是()。
A.可通过改变阀门开度调节往复泵流量B.通过改变阀门开度可调节离心泵流量C.通过改变转速调节离心泵流量D.可通过旁路调节来改变流量参考答案:A[单项选择题]8、在下面溶液中,亨利定律可适用的是()。
A.高温低浓度易溶性气体B.总压为10MPa的难溶性混合气体C.分压为1MPa的难溶性气体D.低温高浓度的易溶性气体参考答案:A[单项选择题]9、圆形直管内流动的流体,湍流时雷诺数是()。
A.Re>40000B.Re>4000C.Re=2000-4000D.Re<2000参考答案:A[填空题]10板框过滤机的洗涤速率为最终过滤速率的()。
参考答案:1/4[填空题]11流体在外径为30cm、内径为20cm的环形管道内流动,则该环形管道的当量直径为()。
参考答案:10cm[填空题]12根据水分与物料结合的状况不同,物料中所含水分分为()和()。
参考答案:结合水;非结合水[单项选择题]13、冷热水通过间壁换热器换热,热水进口温度为90℃,出口温度为50℃,冷水进口温度为15℃,出口温度为53℃,冷热水的流量相同,且假定冷热水的物性为相同,则热损失占传热量的()。
化工原理第二版杨祖荣主编课后习题答案

2 0.785d 2
m s 2 = 16470kg/h
=
9 / 3600 0.785 × 0.05 2
= 1.27m/s
或:
u 2 = u1 (
d1 2 68 ) = 0.69( ) 2 = 1.27 m/s d2 50
G 2 = u 2 ⋅ ρ = 1.27 × 1830 = 2324.1kg/(m 2 ⋅ s)
p1 − p 2 ≈ Rgρ 0
用双液体 U 管压差计测量时,有
p1 − p 2 = R ' g ( ρ A − ρ C )
因为所测压力差相同,联立以上二式,可得放大倍数
ρ0 R' 1000 = = = 14.3 R ρ A − ρ C 920 − 850
此时双液体 U 管的读数为
R ' = 14.3R = 14.3 × 12 = 171.6mm
9.图示为汽液直接混合式冷凝器,水蒸气与冷水相遇被冷凝为 水,并沿气压管流至地沟排出。现已知真空表的读数为 78kPa,求气 压管中水上升的高度 h。 解:
p + ρgh = p a
题9
附图
3
水柱高度
h=
pa − p 78 × 10 3 = 3 = 7.95m ρg 10 × 9.81
10.硫酸流经由大小管组成的串联管路,其尺寸分别为φ76×4mm和φ57×3.5mm。已 知硫酸的密度为 1830 kg/m3,体积流量为 9m3/h,试分别计算硫酸在大管和小管中的(1)质 量流量; (2)平均流速; (3)质量流速。 解: (1) 大管: φ76 × 4mm
p = p0 + ρgΔz = p1 + ρgh
∴ Δz = p1 + ρgh − p 0 p − p0 (58 − 42) × 10 3 = 1 +h= + 0.55 = 2.36m ρg ρg 900 × 9.81
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
制药化工原理课后习题答案绪论2.解:∴∴以J ·mol -1·K -1表示R 的值R =0.08206×1.01325×102 J ﹒mol -1﹒K -1=8.315 J ﹒mol -1﹒K -1第一章 流体流动1.表压=-真空度=-4.8×104Pa 绝压=5.3×104 Pa2.解:设右侧水面到B ′点高为h 3,根据流体静力学基本方程可知P B =P B ′则ρ油gh 2=ρ水gh 3h=h 1+h 3=892mm3.解:正U 型管水银压差计由图可知 P A =P 1+(x +R 1)ρ水gP B =P 2+x ρ水g ∵P 1-P 2=2.472kPa ∴P A -P B =2.472kP A +ρ水gR 1又有P A =P C P C = P B +ρHg gR 1∴ρHg gR 1=2.472kPa +ρ水gR 1∴倒U 型压差计 设右侧管内水银高度为M∵指示流体为空气∴P C =P DP 1=P C +ρ水g(R 2+M) P 2=P D +ρ水gM∴4.(1)P B =-845.9Pa(表)51001325.1Paatm⨯=1mN Pa2=⋅-1m N J =⋅3310m L -=2321001325.1m J m N m N atm L ⨯=⋅⋅⋅⋅⋅⋅-21001325.1J atm L ⨯=⋅mmm kg mm m kg h 4921000600820h 3323=⋅⨯⋅==--水油ρρmmm s m m kg R 00.200200.081.9)100013600( 2.472kPa231==⋅⨯⋅-=--mmm s m m kg R 0.2522520.081.91000 2.472kPa232==⋅⨯⋅=-(2)R ′=0.178m 7.解:由公式可得Vs=uA=u πd 2/4=0.8×π×(57-3.5×2)2×10-6=1.57×10-3m 3/sWs=Vs ρ=1.57×10-3×1840=2.89kg/s8.解:由题可知:1—1′截面:P 1=1.013×105Pa u=0以2—2′截面为基准水平面∴z 1=3m2—2′截面:设管内流速为u z 2=03—3′截面:u, z 3=3m4—4′截面:u, z 4=3+0.5=3.5m 5—5′截面:u, z 5=3m6—6′截面:u, z 6=2m, P 6=1.013×105Pa 根据伯努利方程:We=0, ∑h f =0有∵P 1=P 6 ∴u 2/2=g(z 1-z 6)=9.8有9.8×3+1.013×105/1000=9.8+P 2/1000∴P 2=1.209×105Pa1.013×105/1000=9.8+P 3/1000∴P 3=0.915×105Pa9.8×3+1.013×105/1000=9.8×3.5+9.8+P 4/1000∴P 4=0.866×105Pa∴P 5=0.915×105Pa9. (1)u=1.55m/s V h =10.95m 3/h (2)Δz=2.86mAVsu =s m kg u AWsG ⋅=⨯===2/147218408.0ρρ++=ρ+62611P 2u gz P gz ρρ222112P u gz P gz ++=+ρρ323112P u gz P gz ++=+ρρ424112P u gz P gz ++=+ρρ525112P u gz P gz ++=+解:Ne=We ﹒Ws取釜内液面为1—1′截面,高位槽内液面为2—2′截面根据伯努利方程:1—1′截面:z 1=0, P 1=-2.5×104(表压), u 1=02—2′截面:z 2=15m, P 2=0(表压), A=πd 2/4=0.25×π×[(76-4×2)×10-3]2=3.63×10-3m 2∴>4000 湍流又ε/d =0.3×10-3/68×10-3=4.41×10-3查图得λ=0.029查表1—3得,ξ全开闸阀=0.17 ξ半开截止阀=9.5 ξ90°标准弯头=0.75 ξ进=0.5 ξ出=1∴h f ′=(0.17+9.5+3×0.75+1.5)×1.462/2=14.2J/kg∴∑h f =22.7+14.2=36.9J/kgWe =208.87J/kgNe =208.87×2×104/3600=1.16kWN=1.16/0.7=1.66kW12.解:1—1′:高位槽液面2—2′:出口管内侧列伯努利方程 z 2=0, z 1=4m, P 1=P 2=0(表), u 1=0, We=0∴∑h f +u 22/2=4g ∑h f = h f +h f ′查表1—3得,ξ半开截止阀=9.5 ξ90°标准弯头=0.75h f ′=∑ξ﹒u 22/2=(9.5+0.75+0.5) ×u 22/2=10.75×u 22/2ηNeN =fh Pu gz We u P gz ∑+++=+++ρρ2222211122AWsu ρ=2sm h m u /46.1/3.524710501063.3102342==⨯⨯⨯=-173740106105046.11068Re 43=⨯⨯⨯⨯==--μρdu kgJ u d l h f /7.22246.1068.050029.0222=⨯⨯=⋅=λ9.36246.1151050105.224++=+⨯-g We fh Pu gz We u P gz ∑+++=+++ρρ222221112222u d l h f ⋅=λ∴化简得(400λ+11.75)×u 22/2=39.220℃时μ水=1.005λ=f(Re)=f(u 2) 需试差 假设 u 0Reλ → u 01.5 76630 0.039 1.661.6 79600 0.039 1.661.66 82588 0.03881.66∴截止阀半开时该输水系统的u 0=1.66m/sVs=uA=1.66×0.25π×0.052=0.00326m 3/s∴Vs=11.73m 3/h第二章 流体输送设备1、解:分别取离心泵的进、出口截面为1-1′截面和2-2′截面,由伯努力方程得:其中,=0.4 m ;Pa(表压);Pa(表压);;=0;20℃时水的密度。
m3、解:(1)20℃时:由附录2及附录7知,水的密度,饱和蒸气压Pa 。
m(2)85℃时:由附录2及附录7知,水的密度,饱和蒸气压Pa 。
g du 4)75.10201(222=++λ321075.49Re ⨯==u du μρ01.0=dε21,2222211122-+++=+++f H gu ρg p Z H g u ρg p Z 21,212212122-+-+-+-=⇒f H gu u ρg p p Z Z H 12Z Z -41109.1⨯-=p 52107.4⨯=p 21u u =21,-f H 3m kg 2.998-⋅=ρ34.500081.92.998109.1107.44.045=++⨯⨯+⨯+=⇒H kW7.13W 1037.170.0360081.92.9987034.504e=⨯=⨯⨯⨯⨯===⇒ηρηgHQ N N 10,v0g ----=f H h ρgp p H ∆3m kg 2.998-⋅=ρ4v 102335.0⨯=p 28.45.2381.92.998102335.01081.944g =--⨯⨯-⨯=⇒H 3m kg 6.968-⋅=ρ5v 105788.0⨯=pm4、解:=-2.21m<-1.5m故该泵不能正常工作。
6、解:=17 m 由于输送介质为水,结合和m ,查附录21选IS100-80-125型泵,主要性能参数为:,m,,,kW故泵实际运行时的轴功率为kW ,其中因阀门调节所多消耗的功率为第四章 沉降与过滤2、解:设颗粒沉降位于层流区,故核算流型故假设成立,即颗粒沉降位于层流区。
因此,可完全除去的最小颗粒直径为。
3、解:在操作温度下,气体量=5538.527.15.2381.96.968105788.01081.954g -=--⨯⨯-⨯=⇒H 10,v0g ----=f H h ρgp p H ∆6.15.381.95301045.6106.655--⨯⨯-⨯=21,21221212e 2-+-+-+-=f H gu u ρg p p Z Z H 81.91000109.600104⨯⨯+++=13e h m 100-⋅=Q 17e =H 13h m 100-⋅=Q 20=H 1min r 2900-⋅=n 78.0=η0.7=N 0.7=N kW 05.1W 104878.0360081.91000100)1720(==⨯⨯⨯⨯-==ηρ∆∆g HQ N tcS bLu V = 1S tc s m 025.04036003600-⋅=⨯==⇒bL V u μρρ18)(s 2c tc gd u -=m1075.181.9)06.13000(025.010218)(1855s tc c --⨯=⨯-⨯⨯⨯=-=⇒g u d ρρμ2023.010206.1025.01075.1e 55tc c t <=⨯⨯⨯⨯==--μρu d R m1075.15-⨯13S s m 54.127342727336002160-⋅=+⨯=V 13h m -⋅设8颗粒沉降位于层流区,则由 层(需50块隔板)m 核算流型故假设成立,得降尘室内隔板间距和层数分别为0.082m 和51层。
注:此题原始数据有点问题。
在该组数据下,气流在降尘室内已达到湍流。
5、解:根据恒压过滤方程得;由下式可算得,15min 收集到的总滤液量,即故再过5min 所得的滤液量=0.47 L6、解:(1)过滤面积滤框总容积滤饼充满滤框时滤液体积过滤终了时恒压过滤方程μm 13526s 2c tc s m 101.4104.31881.9)5.04000()108(18)(----⋅⨯=⨯⨯⨯-⨯⨯=-=μρρg d u tc S NbLu V =51101.41.48.154.13tc S ≈⨯⨯⨯==⇒-bLu V N 082.0512.4===⇒N H h 2108.4104.35.0101.4108e 4536tc c t <⨯=⨯⨯⨯⨯⨯==----μρu d R τ2e 22KA V V V =+⎪⎩⎪⎨⎧⨯⨯⨯=⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯----6010)1.0()106.1(2)106.1(605)1.0()101(2)101(23e 2323e 23K V K V 34e m 107-⨯=⇒V 127s m 108--⋅⨯=K 6015)1.0()108()107(22742⨯⨯⨯⨯=⨯⨯⨯+--V V 33m 1007.2-⨯=⇒V 3333m 1047.0106.11007.2---⨯=⨯-⨯=V ∆22m86.4938281.0=⨯⨯=A 32m 623.038025.081=⨯⨯=3m 79.708.0623.0==V 23m m 156.086.4979.7-⋅===A V q τK q q q =+e 22τ52105156.001.02156.0-⨯=⨯⨯+⇒(2)洗涤时间=416 s(3)(4)由于,故。
