2011年广东省肇庆初中毕业生学业考试试题及答案(word版,答案扫描)

合集下载

肇庆市中考物理试卷及答案

肇庆市2011年初中毕业生学业考试物理试卷注意事项：1．本试卷共6页，共26题．考试时间90分钟，满分100分．2．做1～10题时请用2B 铅笔将答题卡上对应题号的选项涂黑．如需改动，用橡皮擦干净后，再选涂其它选项．3．做11～26题时，请用黑色字迹的钢笔或签字笔解答，不准使用铅笔和涂改液．请将解答写在答题卡上对应题号后的相应位置上．如需改动，先划掉原来的解答，再写上新的解答．不按以上要求的作答无效．4．考生必须保持答题卡的整洁．考试结束后，将本试卷和答题卡一并交回．一、本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个是正确的，请用2B 铅笔将答题卡上对应题号的选项涂黑．1．用二胡、吉它、笛子三种乐器演奏同一首曲子，我们在隔壁房间仍能分辨出是哪种乐器演奏的，这主要是依据声音的:（ B ）A ．音调B ．音色C ．音速D ．响度2．下列实例中，为了减少摩擦的是：（ A ）A ．给自行车轴加润滑油B ．拔河时用力握住绳子C ．拧矿泉水瓶盖时，往往在手与瓶盖之间垫上一块布D ．为了擦净玻璃上的污渍，要用力压抹布3．下列四幅图中，符合安全用电的是:（ C ）4．下列说法，正确的是：（ C ）A ．汽车开过乡间公路，路面扬起灰尘，这些灰尘是由分子运动引起的B ．分别滴在热水和冷水中的墨水，它们的扩散速度相同C ．10mL 酒精和10mL 水混和后的总体积小于20mL ，这是由于分子间有空隙D ．水、水蒸气、冰三种物态分子间的距离都是相同的5．几种燃料的密度见下表．三辆完全相同的油罐车，分别盛满这三种燃料，下列说法正确的是：（ A ）A ．甲车最重B ．乙车最重C ．丙车最重D ．三车重量相同6．借助简单机械将重物提升，若不计滑轮重量及摩擦，以下装置最火线零线火线零线火线零线火线零线 AB 火线零线省力的是：（ D ）7向左运动；（ B A C 8．小明同学在平面镜中的像是下图中的：（ D ） 9．如右图所示，以下四种措施不能．．是：（ C ） A ．将条形磁铁向下插入线圈B ．将条形磁铁从线圈中抽出C ．让条形磁铁静止在线圈中D ．条形磁铁静止而将线圈向上移动 10．小汽车在高速公路上正常行驶，它的速度最接近：（ B ）A ．3m/sB ．30m/sC ．300m/sD ．3000m/s二、本题共10小题，每小题3分，共30分．请在答题卡上对应位置作答，不要求写出计算过程.11．2011年春季，我国长江中下游流域发生大面积旱情．抗旱指挥部采用人工降雨缓解旱情．人工降雨时，飞机将干冰撒入高空的冷云层中，干冰很快从固态升华成气态，并从周围空气吸收（选填“吸收”或“放出”）大量的热，于是高空中的部分水蒸气凝华成小冰粒，这些小冰粒在下降过程中，遇到暖气流就熔化为雨点并降落到地面．（第一空和第三空选填物态变化的名称）12．有一种材料，它的导电性介于导体和绝缘体之间，这种材料称为半导体材料，电脑的微处理器就是由成千上万个这种材料制成的元件组成；某些材料在特定温度下，电阻接近于零，这种材料物理学上称之为超导材料，此处的特定温度通常很低（选填“很高”、“接近常温”或“很低”）．13．1kg 的水温度升高1℃，需吸收4.2×103 J 的热量．相同质量的水和砂石，若吸收或放出同样多热量，温度变化较大的是沙石，据此可解释沙漠地区的昼夜温差较沿海地区的要大．（选填“大”或“小”）14．用电磁波传递电视信号的大致过程如下：①用摄像机拍摄画面和录音；②制作电视节目；③发射电视节目的视频和音频信号；④接收并还原电磁波的图像和声音信息．下列四幅图中对应③的是图 B ，对应④的是图 D ．电磁波能否在真空中传播能．（选填“能”或“不能”）A BC D（丙）A B C D B C C （甲）15．停止蹬车后，行驶在水平路面上的自行车仍继续向前运动一段距离，这是因为自行车具有惯性，自行车最后还会停下来，这是因为它受到阻力（摩擦力）的缘故．若路面光滑，自行车将一直做匀速直线运动，牛顿曾对此做过研究，并总结出牛顿第一定律．16．如右图所示，用电吹风吹机翼模型，机翼模型上升．图中A 、B 、C 三点，气体流速最快的是 B ，气体压强最大的是 A ．若增大风力，机翼模型获得的升力将增大（选填“增大”、“减小”或“不变”）．17．如下图所示，调节蜡烛、凸透镜和光屏的位置，都能得到清晰的像，其中在光屏上成倒立缩小实像的是图 B ，在光屏上成倒立放大实像的是图 A ，成虚像的是图 C ．18．手机传递信息的电磁波频率有f 1和f 2=1800MHz ，与这两个频率相对应的电磁波波长及波速分别是λ1、v 1和λ2、v 2，则λ1 > λ2，v 1 = v 2（以上两空选填“＞”、“=”或“＜”）；除手机外，人们还发明了许多利用电磁波来传递信息的设备，如电视塔． 19．如右图所示，请在图上标出通电螺线管周围a 、b 、c 三点小磁针静止时的N 极（用字母N 表示）．20．取大气压强值为1.0×105Pa ，若一只手掌的面积为0.01m 2，则手掌承受的大气压力是103 N ．在海拔2km 以内，每升高10m ，大气压约减少111Pa ，若某处气压计示数是91120Pa ，则该处海拔是 800 m ，该处水的沸点 < 100℃（选填“＞”、“=”或“＜”）．三、实验探究题．本题共3小题，共20分．请在答题卡上对应位置作答.21．（6分）（1）如图（甲）所示，木块的长度是 3.70----3.79 cm ．（2）如（乙）所示，物体 1.5 N ，该物体受到力是 0.6 N ．（3）的质量是 53.2 g ．（4）如图（丁）所示，室温是22．（7分）果，探装入两个瓶中，一个放在水中，一个放在空气中，其件均相cb a同，如下图所示．实验时他们每隔一定时间记录一次甲、乙两温度计的示数，如下表所示：（1 （2间变化化的图（3 （4快慢前（5明用“冷却速度”来表示物体冷却快慢，“冷却速度”可以定义为：1千克物体，单位时间内冷却的温度叫做冷却速度．23．（7分）如下图所示，在探究电流做功与哪些因素有关的实验中，小电动机通过细线将砝码吊起．（1）请将滑动变阻器接入电路中（要求连线不得交叉）（2）若不计摩擦及损耗，则电流通过小电动机所做的功，与小电动机对）电流表和电压表的读数如图（甲）机两端的电压是 4 V ，电功率P 电）若砝码的重力是10N ，小电动机在P =0.8W ；）P 电与P 的大小关系是P 电 = P (原因可能是测量时间不准确．（写出一条理由即可）四、综合能力题．本题共3小题，共20分．请在答题卡上对应位置作答．24．（6分）如右图所示，电阻R 两端的电压U =6V ，流过电阻R 的电流I =0.5A ．通过计算求：（1）电阻R 的阻值； 12（2）电阻R 在1min 内产生的热量是多少焦? 18025．（7分）2011年3月11日，日本东北部海域发生里氏9.0级强震并引发海啸，造成重大人员伤亡和财产损失．地震发生后，地震波在地球内部以大约6.5km/s 的速度传播．地震引发的海啸最高达到24m ．海啸造成日本福岛第一核电站发生严重核泄漏事故．根据以上材料，回答下列问题：（1）本次地震中，某一地震台距震源130km ，则地震发生 20 s 后，该地震台接收到由震源传来的地震波；（2）如下图（甲）所示，海啸发生时，A 点的压强由于海啸增加了 2.4×105 pa ．已知海水的密度ρ=1.03×103kg/m 3，g 取10N/kg ．（3）如下图（乙）所示，核反应堆工作时，将铀核裂变释放的核能转化为蒸汽的内能，然后将高温高压的蒸汽通入涡轮机中，驱动涡轮机转动，使蒸汽的内能转化为涡轮机能，并带动发电机，使机械能能转化成电能．分）随着低碳理念的普及，学校科技小组的同学拟设计一种以太阳能电池驱动提供150W 的电功率．拟设计的太阳能汽车质量是500kg ，它在平直路面上最快每秒可行驶15m ，行驶过程中所受的平均阻力是车重的0.02倍．该汽车的驱动电机能够将90%的电功率转化为牵引汽车前进的机械功率．若该车在平直路面上以最高速度行驶，试通过计算回答下列问题（g 取10N/kg ）：（1）驱动电机提供的推力是多少牛？ 100N （2）驱动电机提供的机械功率是多少瓦？1500W（3）该车的太阳能电池板面积约为多大？（计算结果小数点后保留一位数字）11.1 （甲）（乙）。

广东省肇庆市2011年中考化学试题(word版含答案)

肇庆市2011年初中毕业生学业考试化学试卷注意事项：1．全卷共6页。

考试时间90分钟，满分100分。

2．答卷前，务必用黑色字迹的钢笔或签字笔将自己的准考证号和姓名填写在答题卡对应位置上，并用2B铅笔将试室号和座位号涂黑。

3．请将选择题的答案用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦擦干净后，再选涂其他答案。

4．非选择题必须用黑色字迹的钢笔或签字笔在答题卡上指定区域作答；如需改动，先在原来的答案上划一横线，然后在旁边空位处重新写。

不准．．使用铅笔和涂改液。

5．可能用到的相对原子质量：H-1 C-12 O-16 Mg-24 Cl-35.5K-39 Fe-56 Zn-65 Ag-108一、选择题（本题有14小题，每题2分，共28分。

每小题只有一个选项符合题意）1．下列变化属于化学变化的是A．干冰升华B．火柴梗被折断C．玻璃破碎D．木柴燃烧2．下列说法正确的是A．天燃气是可再生的能源B．吃海产品有利于碘的摄取C．“白色污染”就是指白颜色的垃圾D．摄入太多的脂肪会使人变胖，所以脂肪对人体有害3．下列做法中正确的是A．点燃可燃性气体前都必须验纯B．蒸发溶液时，在蒸发皿下垫石棉网C．用湿润的pH试纸粗略测定稀醋酸的pHD．用托盘天平称量时，左盘放砝码右盘放药品4．下列实验操作不正确．．．的是A．倾倒液体B．检查气密性C．稀释浓硫酸D．取用固体5．日本福岛核电站泄漏危机，部分民众曾抢购碘盐，其实，正常食用量不能预防核辐射，碘盐是在食盐中添加碘酸钾（KIO3）。

钾元素化合价为+1，碘元素的化合价为A．+3 B．+4 C．+5 D．+66．下列关于石油的说法正确的是A．石油的蕴藏量是无限的B．石油是“清洁燃料”C．石油主要由多种有机物组成D．石油除了作燃料，不能再开发利用了7．化学与生活密切相关，生活中的下列做法不合理．．．的是A．高楼发生火灾，乘电梯逃生B．用白醋除水壶中的水垢C．家用电器着火，应先切断电源再用干粉灭火器灭火D．用燃烧法区分羊毛纤维和合成纤维8．临近中考，家长为了给学生增加营养，制定了如下食谱：主食馒头、米饭副食红烧牛肉、清蒸西江鱼饮料酸牛奶、白开水用你所学的知识，建议家长增加的食物是A．炒鸡蛋B．蒸猪排骨C．炖豆腐D．炒瓜苗9．燃煤发电厂利用反应2SO2+2CaCO3+X=2CaSO4+2CO2来减少SO2的排放，其中X的化学式为A．O2B．CO C．CO2D．H210．我国“十二五”规化对“低碳经济”给予政策支持，实现“低碳经济”的一种策略是节能。

2011年广东省初中毕业生学业考试数学(附答案)(高清扫描版)

一、2011年广东省初中毕业生学业考试数学参考答案一、1-5、DBACB二、6、-27、___ x ≥2__8、___12__9、__25º__ 10、2561 三、11、原式=-6 12、x ≥3 13、由△ADF ≌△CB E ，得AF =C E ，故得：AE=CF14、（1）⊙P 与⊙P 1外切。

（2）∏-215、（1）c ＞ 21 （2）顺次经过三、二、一象限。

因为：k ＞0，b=1＞0四、16、解：设该品牌饮料一箱有x 瓶，依题意，得6.032626=+-x x 化简，得013032=-+x x解得 131-=x (不合，舍去)，102=x经检验：10=x 符合题意答：略.17、略解：AD=25(3+1)≈68.3m18、（1）“班里学生的作息时间”是总体（2）略（3）10%19、略解：（1）∠BDF =90º；（2）AB=BD ×sin60°=6.五、20、略解：(1)64，8，15；（2）n 2-2n+2，n 2，(2n-1);（3）第n 行各数之和：)12)(1()12(222222-+-=-⨯++-n n n n n n n 21、略解：（1）、△HAB △HGA ；（2）、由△AGC ∽△HAB ，得AC/HB=GC/AB ，即9/y=x/9，故y=81/x (0<x<29)（3）因为：∠GAH = 45①当∠GAH = 45°是等腰三角形.的底角时，如图（1）：可知CG =x =29/2 ②当∠GAH = 45°是等腰三角形.的顶角时, 如图（2）：由△HGA ∽△HAB 知：HB= AB=9，也可知BG=HC ，可得：CG =x =18-29图（1）B （D ）A FE G（H ） C图（2） 22、略解：（1）易知A(0,1)，B(3,2.5)，可得直线AB 的解析式为y =121+x （2） )30(41545)121(14174522≤≤+-=+-++-=-==t t t t t t MP NP MN s （3）若四边形BCMN 为平行四边形，则有MN =BC ，此时，有25415452=+-t t ，解得11=t ，22=t 所以当t =1或2时，四边形BCMN 为平行四边形.①当t =1时，23=MP ，4=NP ，故25=-=MP NP MN , 又在Rt △MPC 中，2522=+=PC MP MC ，故MN =MC ，此时四边形BCMN 为菱形②当t =2时，2=MP ，29=NP ，故25=-=MP NP MN , 又在Rt △MPC 中，522=+=PC MP MC ，故MN ≠MC ，此时四边形BCMN 不是菱形. B（D ）A F E G HC。

2011年广东省初中毕业生学业考试

2011年中考数学模拟试题（一）参考答案一、1. A 2.B 3.C 4.B 5.A二、6. 7.26×1010元 7.5,021==x x 8.2.5 9.[]2)1()1(1100x x ++++=50010. 217三、11.解：原式=3+（-3）-2×21+1…………5分 =0………………6分12．解：)(2222y x y xy x y x -+-+……………1分 =)()(22y x y x y x --+……………3分 =yx y x -+2……………4分当03=-y x 时，y x 3=…………5分原式=272736==-+y y y y y x ……………6分 13．解：①………2分②………4分路线长：π2……6分14.(1)证明：连结DE ，BE …………1分∵AB 是直径∴BE ⊥AC …………2分∵D 是BC 的中点∴DE=DB∴∠DBE=∠DEB 又0E=0B ∴∠0BE=∠0EB∴∠DBE+∠OBE=∠DEB+∠OEB即∠ABD=∠OED 但∠ABC=900，∴∠OED=900∴DE 是⊙O 的切线…………4分(2) ∵AC=346)32(2222=+=+BC AB∴BE=334632=⋅=⋅AC BC AB ∴AE=391222=-=-BE AB ………………6分15．解：(1) ∵OA=OB=OD=1，∴点A 、B 、D 的坐标分别为A(-1，0)，B(0，1)，D(1，0)．………3分(2) ∵点A 、B 在一次函数y=kx+b(k ≠0)的图象上，∴⎩⎨⎧==⎩⎨⎧==+-11,10b k b b k 解得∴一次函数的解析式为y=x+1．…………………………4分∵点C 在一次函数y=x+l 的图象上，且CD ⊥x 轴．∴点C 的坐标为(1，2)．……………………………………5分又∵点C 在反比例函数)0(≠=m xm y 的图象上，m=2． ∴反比例函数的解析式为xy 2=……………6分四、1，1），（2，2），（3，3）共3种，P （两数差为0）=41123=…………4分（2）不公平，改为小明每次得1分，小华每次得3分。

2011年广东省初中毕业生学业考试

2011年广东省初中毕业生学业考试语文说明：1．全卷共6页，满分120分。

考试用时120分钟。

2．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和准考证号、试室号、座位号填写在答题卡上。

3．答题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目的指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．本试卷设有附加题，共10分，考生可答可不答；该题得分作为补偿分计入总分，但全卷最后得分不得超过120分。

5．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、基础（25分）1．根据课文默写古诗文。

（10分）(1)子日：“口口口口口，可以为师矣。

”（《论语》）（1分）(2)了却君王天下事，口口口口口口口。

口口口口口！（辛弃疾《破阵子》）（2分）(3)香远益清，亭亭净植，口口口口口口口口口。

（周敦颐《爱莲说》）（1分）(4)王安石《登飞来峰》中的诗句“口口口口口口口，口口口口口口口”与杜甫的“会当凌绝顶，一览众山小”有异曲同工之妙。

（2分）(5)默写韦应物的《滁州西涧》。

（4分）口口口口口口口，口口口口口口口。

口口口口口口口，口口口口口口口。

2．根据拼音写出相应的词语。

（4分）(1)如果我能kuān shù人，体谅人——我都得感谢我的慈母。

(2)惜秦皇汉武，略输文采；唐宗宋祖，稍逊féng sāo。

(3)有一位长期以来xiān wéi rén zhī的科学家：邓稼先。

(4)对于叔叔回国这桩shí ná jiǔ wěn的事，大家还拟定了上千种计划。

3．下列对病句的修改不正确的一项是( )（3分）A．“拾荒老娘”于化玲，9年来孤身一人在城市独自拾荒，供儿子读书。

（删除“独自”）B．他的晚年，仍然精力充沛，充满创作激情，留下了许多优秀作品。

（把“他的晚年”改为“晚年的他”）C．由于长江流域连续干旱，导致洞庭湖、鄱阳湖水面大面积缩小，给人们的生产和生活带来很大影响。

广东省肇庆市2011年中考历史真题试题

肇庆市2011年初中毕业生学业考试历史（共55分）第一部分选择题（共30分）六.选择题：在每小题列出的四个选项中，只有一项最符合题目要求，请将正确答案的选项涂到答题卡上。

（本大题共15小题，每小题2分，共30分。

）①承认土地私有，允许买卖；②奖励耕战；③根据军功授予爵位和田宅；④建立县制A.①②③④B.①②③C.②③D.①④“焚书坑儒”，而西汉则实行“罢黜百家，独尊儒术”，两者的根本目的是A.压制知识分子B.加强君主专制统治C.推行法家思想D.有区别地对待知识文化——货币，这些出土文物说明了大食金币波斯萨珊银币东罗马金币A.唐代没有统一的货币B.中国古代金币、银币流通时间长范围广C.唐代中外贸易十分繁盛D.证明唐代日本、新罗与中国交往密切24.右图是1785年的广州十三行，是清政府唯一特许经营管理对外贸易的机构。

此种情况反映了这个时期清朝“闭关锁国”政策25.“舟师识地理，夜则观星，昼则观日，阴晦则观指南针。

”这说明，中国古代四大发明之一的指南针，对于古人在哪一方面的活动有着重大的意义？26．“《辛丑条约》的签定，使中国完全沦为半殖民地半封建社会”，主要是指A.冲击了中国自给自足的自然经济B.帝国主义直接统治中国人民C.赔款数额巨大，增加了人民的沉重负担D.清政府完全成为列强统治中国的工具27.阅读下面民国时期中国民族工业发展变化统计表。

中国民族工业出现这种变化的主要原因是年份拥有厂家拥有资本工人人数1913 689家33亿元27万多1920 1795家50亿元55万多A.新中国成立B.“三大改造”完成C.土地改革完成D.“一五”计划完成别行政区的区徽。

关于两个区徽所包含的历史意义表述不．正确的是C.“一国两制”的实施是成功的D.“一国两制”有利于推进祖国的统一30.新中国成立后相当长的一个时期内，人们要凭粮票才能购买到粮食。

1990年，广东省宣布终止粮票的流通，1993年全国终止粮票的流通。

对此理解不．正确的是“希腊内部的极盛时期”，主要是指伯里克利统治时期—16世纪，欧洲出现了一股倡导人文精神的文化运动。

2011年广东省中考数学试卷及答案(WORD版)

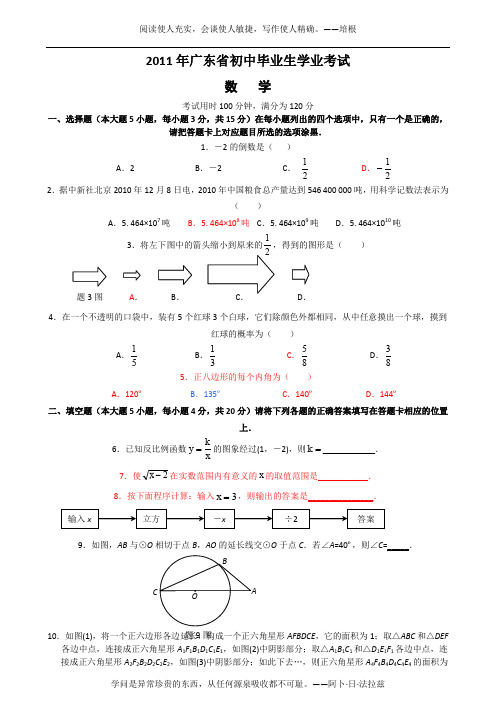
2011年广东省初中毕业生学业考试数学考试用时100分钟，满分为120分一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．－2的倒数是（）A ．2B ．－2C ． 21D ．21- 2．据中新社北京2010年12月8日电，2010年中国粮食总产量达到546 400 000吨，用科学记数法表示为（）A ．5.464×107吨B ．5.464×108吨C ．5.464×109吨D ．5.464×1010吨3．将左下图中的箭头缩小到原来的1，得到的图形是（） 4．在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（）A ．51B ．31C ．85D ．83 5．正八边形的每个内角为（）A ．120ºB ．135ºC ．140ºD ．144º二、填空题（本大题5小题，每小题4分，共20分）请将下列各题的正确答案填写在答题卡相应的位置上．6．已知反比例函数xk y =的图象经过(1，－2)，则=k ____________． 7．使2-x 在实数范围内有意义的x 的取值范围是______ _____．8．按下面程序计算：输入3=x ，则输出的答案是_______________．9．如图，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ．若∠A =40º，则∠C =_____．10．如图(1)，将一个正六边形各边延长，构成一个正六角星形AFBDCE ，它的面积为1；取△ABC 和△DEF各边中点，连接成正六角星形A 1F 1B 1D 1C 1E 1，如图(2)中阴影部分；取△A 1B 1C 1和△D 1E 1F 1各边中点，连接成正六角星形A 2F 2B 2D 2C 2E 2，如图(3)中阴影部分；如此下去…，则正六角星形A 4F 4B 4D 4C 4E 4的面积为A ．B ． D ．题3图题9图 BC O A_________________．三、解答题（一）（本大题5小题，每小题6分，共30分）11．计算：20245sin 18)12011(-︒+-．12．解不等式组：⎩⎨⎧-≤-->+128,312x x x ，并把解集在数轴上表示出来．13．已知：如图，E 14．如图，在平面直角坐标系中，点P 的坐标为（－4，0），⊙P 的半径为2，将⊙P 沿x 轴向右平移4个单位长度得⊙P 1．（1）画出⊙P 1，并直接判断⊙P 与⊙P 1的位置关系；（2）设⊙P 1与x 轴正半轴，y 轴正半轴的交点分别为A ，B ，求劣弧AB 与弦AB 围成的图形的面积（结果保留π）．15．已知抛物线c x x y ++=221与x 轴没有交点．（1）求c 的取值范围；（2）试确定直线1+=cx y 经过的象限，并说明理由．四、解答题（二）（本大题4小题，每小题7分，共28分）16．某品牌瓶装饮料每箱价格26元．某商店对该瓶装饮料进行“买一送三”促销活动，若整箱购买，则题13图 B C DA F E 题14图题10图（1） E E C E 题10图（2）题10图（3）买一箱送三瓶，这相当于每瓶比原价便宜了0.6元．问该品牌饮料一箱有多少瓶？17．如图，小明家在A 处，门前有一口池塘，隔着池塘有一条公路l ，AB 是A 到l 的小路. 现新修一条路AC 到公路l . 小明测量出∠ACD =30º，∠ABD =45º，BC =50m . 请你帮小明计算他家到公路l 的距离AD 的长度（精确到0.1m ；参考数据：414.12≈，732.13≈）.18．李老师为了解班里学生的作息时间表，调查了班上50名学生上学路上花费的时间，他发现学生所花时间都少于50分钟，然后将调查数据整理，作出如下频数分布直方图的一部分（每组数据含最小值不含最大值）．请根据该频数分布直方图，回答下列问题：（1）此次调查的总体是什么？（2）补全频数分布直方图；（3）该班学生上学路上花费时间在30分钟以上（含30分钟）的人数占全班人数的百分比是多少？19．如图，直角梯形纸片ABCD 中，AD //BC ，∠A =90º，∠C =30º．折叠纸片使BC 经过点D ，点C 落在点E处，BF 是折痕，且BF =CF =8．（1）求∠BDF 的度数；（2）求AB 的长．五、解答题（三）（本大题3小题，每小题9分，共27分）20．如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答．12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 2526 27 28 29 30 31 32 33 34 35 36…………………………（1）表中第8行的最后一个数是______________，它是自然数_____________的平方，第8行共有____________个数；（2）用含n 的代数式表示：第n 行的第一个数是___________________，最后一个数是________________，第n 行共有_______________个数；第17题图 ) 题19图 B CED AF 题18图（3）求第n 行各数之和．21．如图（1），△ABC 与△EFD 为等腰直角三角形，AC 与DE 重合，AB =AC =EF =9，∠BAC =∠DEF =90º，固定△ABC ，将△DEF 绕点A 顺时针旋转，当DF 边与AB 边重合时，旋转中止．现不考虑旋转开始和结束时重合的情况，设DE ，DF (或它们的延长线)分别交BC (或它的延长线) 于G ，H 点，如图(2)（1）问：始终与△AGC 相似的三角形有及；（2）设CG =x ，BH =y ，求y 关于x 的函数关系式（只要求根据图(2)的情形说明理由）（3）问：当x 为何值时，△AGH 是等腰三角形.22．如图，抛物线1417452++-=x y 与y 轴交于A 点，过点A 的直线与抛物线交于另一点B ，过点B 作BC ⊥x （1（2）动点P 在线段OC 点M ，交抛物线于点N . 设点P 移动的时间为t 出t （3）设在（2）的条件下（不考虑点P 与点O BCMN 为平行四边形？问对于所求的t 2011一、1-5、DBACB二、6、-27、___ x ≥2__8、___12__9、__25º__ 10、2561 三、11、原式=-6 12、x ≥3 13、由△ADF ≌△CB E ，得AF =C E ，故得：AE=CF14、（1）⊙P 与⊙P 1外切。

2011年广东省肇庆市中考政治试卷及答案

肇庆市2011年初中毕业生学业考试思想品德（共65分）一、选择题：在下列每小题的四个选项中，只有一项是最符合题意的。

本大题共16小题，每小题2分，共32分。

1.2011年7月1日是中国共产党成立周年。

A．70 B．80 C．90 D．1002．中央农村工作会议2010年12月21日至22日在北京举行。

会议提出2011年“三农”工作的首要任务是A．稳定农村土地承包关系 B．稳定发展粮食生产C．增强农村发展活力 D．大兴水利强基础3．2010年11月12日，第届亚运会在隆重开幕。

国务院总理温家宝出席开幕式并宣布本届运动会开幕。

A．十五上海 B．十五广州 C．十六上海 D．十六广州4．如果在江河湖泊发现有人溺水，我们中学生A．应该马上下水救人 B．要量力而行，不要贸然下水C．如果是陌生人就不冒险救助 D．珍惜自己的生命，谁都不救助5．大凡获得成功的人，都是多年如一日，专心致志，坚忍不拔的人。

这表明磨砺坚强意志要A．持之以恒，善始善终 B．培养良好的学习习惯C．从小培养自己具有坚强的意志 D．明确提出自强进取的任务6．小丽在日记里写道：“李明成绩好、长得帅，很受女同学的欢迎。

可我一看到他和别的女生在一起就莫名其妙的生气。

我只对他一个人好也希望他只对我好。

”小丽A．这样想是很自然的，不必大惊小怪B．可以想办法让李明只对她一个人好C．不懂得用恰当的方式和男生交往D．可以想办法阻止别的女生和李明交往7．少年张晓，四岁丧父，母亲病重卧床，自小他挑起家庭重担，克服常人难以想象的困难，精心侍奉瘫痪在床的母亲。

这启示我们A．挫折普遍存在，谁也逃避不了 B．一个人不经历挫折，就难以成才C．挫折造成的影响都是积极的 D．要采取积极的态度面对挫折8．近年来，我国市场相继出现了“苏丹红”“三聚氰胺”“瘦肉精”“塑化剂”等食品安全事件。

对此，我们认为①有关经营者侵犯了消费者的安全保障权②受害的消费者可以通过多种合法途径维权③有关经营者侵犯了消费者的公平交易权④有关经营者侵犯了消费者的自主选择权A．①②③ B．①②④ C．①③④ D．②③④9.九（3）班值日生小雨和小萌为了去看自己偶像的演唱会，没有打扫课室就走了。

广东肇庆中考数学试题解析版

专题：探究型。
分析：先根据二次函数的解析式判断出函数的开口方向，再由其顶点式求出其最值即可．
解答：解：∵ 二次函教 y=x2+2x﹣5 中 a=1＞0，
∴ 此函数有最小值，
∴ y 最小=
=﹣6．
故选 D．
点评：本题考查的是二次函数的最值问题，即二次函数 y=ax2+bx+c（a≠0）中，当 a＞0 时，函数有最小值
=32（吨）．
9、（2011•肇庆）已知正六边形的边心距为，则它的周长是（）
A、6
B、12 C、
D、
考点：正多边形和圆。
专题：计算题。
分析：设正六边形的中心是 O，一边是 AB，过 O 作 OG⊥AB 与 G，在直角△ OAG 中，根据三角函数即可求
得边长 AB，从而求出周长．
解答：解：如图，在 Rt△ AOG 中，OG= ，∠ AOG=30°，
分析：根据圆内接四边形的对角互补得到 ∠ BAD+∠ BCD=180°，而 ∠ BCD 与 ∠ DEC 为邻补角，得到 ∠ DCE=∠ BAD=105°．解答：解：∵ 四边形 ABCD 是圆内接四边形， ∴ ∠ BAD+∠ BCD=180°，而∠ BCD+∠ DEC=180°， ∴ ∠ DCE=∠ BAD，而∠ BAD=105°， ∴ ∠ DCE=105°．故选 B．点评：本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了邻补角的定义以及等角的补
故选 B
点评：掌握好关于点对称的规律，此种类型题难度不大，注意细心．
7、（2011•肇庆）如图，四边形 ABCD 是圆内接四边形，E 是 BC 延长线上一点，若∠ BAD=105°，则∠ DCE

肇庆市2011年中考数学试题及答案(word版)

肇庆市2011年初中毕业生学业考试数学试题说明：全卷共4页，考试时间为100分钟，满分120分．一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的4个选项中，只有一项是符合题目要求的．） 1．21的倒数是 A .2 B . 2- C .21 D . 21- 2．我国第六次人口普查的结果表明，目前肇庆市的人口约为4050000人，这个数用科学记数法表示是A.410405⨯ B.5105.40⨯ C. 61005.4⨯ D. 71005.4⨯ 3．如图1是一个几何体的实物图，则其主视图是4．方程组⎩⎨⎧=+=-422y x y x 的解是A ．⎩⎨⎧==21y xB ．⎩⎨⎧==13y xC ．⎩⎨⎧-==20y xD ．⎩⎨⎧==02y x5．如图2，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F ，AC = 4，CE = 6，BD = 3，则BF =A. 7B. 7.5C. 8D. 8.56．点M （2-，1）关于x 轴对称的点的坐标是A. （2-，1-）B. （2，1）C.（2，1-）D. （1，2-） 7．如图3，四边形ABCD 是圆内接四边形，E 是BC 延长线上一点，若∠BAD =105°，则∠DCE 的大小是A. 115°B. 105°C. 100°D. 95°8．某住宅小区六月份1日至5日每天用水量变化情况如图4所示，那么这5天平均每天的图1DCBAAD 3032 3634 用水量/吨 · ···a b cA B C DEF m n图2用水量是A ．30吨B ．31吨C ．32吨D ．33吨 9．已知正六边形的边心距为3，则它的周长是A ．6B ．12C ．36D ．312 10．二次函数522-+=x x y 有A. 最大值5-B. 最小值5-C. 最大值6-D. 最小值6- 二、填空题（本大题共5小题，每小题3分，共15分．） 11．化简：12 = ▲ ．12．下列数据5，3，6，7，6，3，3，4，7，3，6的众数是 ▲ ． 13．在直角三角形ABC 中，∠C = 90°，BC = 12，AC = 9，则AB = ▲ ． 14．已知两圆的半径分别为1和3，若两圆相切，则两圆的圆心距为 ▲ ．15．如图5所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n （n 是大于0的整数）个图形需要黑色棋子的个数是 ▲ ．三、解答题（本大题共10小题，共75分．解答应写出文字说明，证明过程或演算步骤．） 16．（本小题满分6分）计算：︒-+-60cos 292117．（本小题满分6分）解不等式组:⎩⎨⎧<+<-5263x x第1个图形第2个图形第3个图形第4个图形图518．（本小题满分6分）如图6是一个转盘,转盘分成8个相同的扇形,颜色分为红、绿、黄三种．指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形）．求下列事件的概率：（1）指针指向红色；（2）指针指向黄色或绿色．19．（本小题满分7分）先化简，再求值：)211(342--⋅--a a a ，其中3-=a ．20．（本小题满分7分）如图7，在正方形ABCD 中，E 为对角线AC 上一点，连接EB 、ED ．（1）求证：△BEC ≌△DEC ；（2）延长BE 交AD 于点F ，若∠DEB = 140︒，求∠AFE 的度数．21．（本小题满分7分）肇庆市某施工队负责修建1800米的绿道，为了尽量减少施工对周边环境的影响，实际工作效率比原计划提高了20%，结果提前两天完成．求原计划平均每天修绿道的长度． 22．（本小题满分8分）如图8，矩形ABCD 的对角线相交于点O ，DE ∥AC ，CE ∥BD ．（1）求证：四边形OCED 是菱形；（2）若∠ACB =30︒，菱形OCED 的面积为38，求AC 的长．23．（本小题满分8分）如图9，一次函数b x y +=的图象经过点B （1-，0），且与反比例函数xky =（k 为ABCDEF图7yAAB CDEO图8∙黄黄黄红红绿绿绿图6不等于0的常数）的图象在第一象限交于点A （1，n ）．求：（1）一次函数和反比例函数的解析式；（2）当61≤≤x 时，反比例函数y 的取值范围．24．（本小题满分10分）已知：如图10，∆ABC 内接于⊙O ，AB 为直径，∠CBA 的平分线交AC 于点F ，交 ⊙O 于点D ，DE ⊥AB 于点E ，且交AC 于点P ，连结AD ．（1）求证：∠DAC =∠DBA ；（2）求证：P 是线段AF 的中点；（3）若⊙O 的半径为5，AF = 215，求tan ∠ABF 的值．25．（本小题满分10分）已知抛物线2243m mx x y -+=（m >0）与x 轴交于A 、B 两点．（1）求证：抛物线的对称轴在y 轴的左侧；（2）若3211=-OA OB （O 是坐标原点），求抛物线的解析式；（3）设抛物线与y 轴交于点C ，若∆ABC 是直角三角形，求∆ABC 的面积．∙ A BC DE OF P图10肇庆市2011年初中毕业生学业考试数学试题参考答案和评分标准一、选择题（本大题共10小题，每小题3分，共30分.）题号 12345678910答案A C C DB A BC B D二、填空题（本大题共5小题，每小题3分，共15分.）题号 1112 13 14 15答案323154或2)2(+n n三、解答题（本大题共10小题，共75分.）16.（本小题满分6分）解：原式=212321⨯-+ （3分） = 127- （5分）= 25（6分）17.（本小题满分6分）解：解不等式63<-x 得2->x （2分）解不等式52<+x 得3<x （4分） ∴原不等式组的解集是：32<<-x （6分） 18.（本小题满分6分）解：按颜色把8个扇形分为红1、红2、绿1、绿2、绿3、黄1、黄2、黄3，所有可能结果的总数为8. （1分）（1）指针指向红色的结果有2个， ∴ P (指针指向红色)=4182= （3分）（2）指针指向黄色或绿色的结果有3+3 = 6个，∴ P (指针指向黄色或绿色)4386== （6分） 19.（本小题满分7分）解:)211(342--⋅--a a a =)2122(3)2)(2(----⋅--+a a a a a a （3分） =233)2)(2(--⋅--+a a a a a （4分）=2+a （5分）当3-=a 时，原式=2+a =123-=+- （7分）20.（本小题满分7分）解：（1）证明：∵四边形ABCD 是正方形 ∴CD=CB ，（1分） ∵AC 是正方形的对角线 ∴∠DCA=∠BCA （2分）又 CE = CE ∴△BEC ≌△DEC （4分）（2）∵∠DEB = 140︒由△BEC ≌△DEC 可得∠DEC =∠BEC=140︒÷2=70︒，（5分） ∴∠AEF =∠BEC=70︒，（6分）又∵AC 是正方形的对角线， ∠DAB=90︒ ∴∠DAC =∠BAC=90︒÷2=45︒，在△AEF 中，∠AFE=180︒— 70︒— 45︒=65︒ （7分） 21.（本小题满分7分）解：设原计划平均每天修绿道x 米，依题意得2%)201(18001800=+-xx （3分）解这个方程得：150=x （米）（5分）经检验，150=x 是这个分式方程的解，∴这个方程的解是150=x （6分）答：原计划平均每天修绿道150米．（7分） 22.（本小题满分8分）解：（1）证明：∵DE ∥OC ，CE ∥OD ，∴四边形OCED 是平行四边形．（1分） ∵四边形ABCD 是矩形 ∴ AO=OC=BO=OD （3分） ∴四边形OCED 是菱形．（4分）（2）∵∠ACB=30° ∴∠DCO = 90°— 30°= 60° 又∵OD= OC ， ∴△OCD 是等边三角形（5分）过D 作DF ⊥OC 于F ，则CF=21OC ，设CF=x ，则OC= 2x ，AC=4x 在Rt △DFC 中，tan 60°=FCDF∴DF=FC ⋅ tan 60°x 3= （6分）A BC DEO 图 F由已知菱形OCED 的面积为38得OC ⋅ DF=38，即3832=⋅x x （7分），解得 x =2， ∴ AC=4⨯2=8 （8分）23.（本小题满分8分）解：（1）将点B （1-，0）代入b x y +=得：b +-=10 ∴b=1. （2分）∴一次函数的解析式是1+=x y （3分）∵点A （1，n ）在一次函数1+=x y 的图象上，将点A （1，n ）代入1+=x y 得：n =1+1，∴n =2 （4分）即点A 的坐标为（1，2），代入xky =得：12k =，解得：2=k （5分）∴反比例函数的解析式是xy 2= （6分）（2）对于反比例函数xy 2=，当0>x 时，y 随x 的增大而减少，而当1=x 时，2=y ；当6=x 时，31=y （7分）∴当61≤≤x 时，反比例函数y 的取值范围是231≤≤y （8分）24.（本小题满分10分）（1）∵BD 平分∠CBA ，∴∠CBD=∠DBA∵∠DAC 与∠CBD 都是弧CD 所对的圆周角，∴∠DAC =∠CBD （1分） ∴∠DAC =∠DBA （2分）（2）∵AB 为直径，∴∠ADB=90° （3分）又∵DE ⊥AB 于点E ，∴∠DEB=90° ∴∠ADE +∠EDB=∠ABD +∠EDB=90° ∴∠ADE=∠ABD=∠DAP （4分） ∴PD=PA （5分）又∵∠DFA +∠DAC=∠ADE +∠PD F=90°且∠ADE=∠DAC∴∠PDF=∠PFD （6分） ∴PD=PF ∴PA= PF 即P 是线段AF 的中点（7分）（3）∵∠DAF =∠DBA ，∠ADB=∠FDA=90°∴△FDA ∽△ADB （8分）∴ABAFDB AD = （9分） ∴在Rt △ABD 中，tan ∠ABD=4310215===AB AF DB AD ，即tan ∠ABF=43 （10分）25.（本小题满分10分）（1）证明：∵m >0 ∴022<-=-=ma b x （1分） ∴抛物线的对称轴在y 轴的左侧（2分）（2）解：设抛物线与x 轴交点坐标为A （1x ，0），B （2x ，0），则021<-=+m x x ，043221<-=⋅m x x ， ∴1x 与2x 异号（3分）又3211=-OA OB 0> ∴OB OA > 由（1）知：抛物线的对称轴在y 轴的左侧 ∴01<x ，02>x ∴11x x OA -==,2x OB = （4分）代入3211=-OA OB 得：3211111212=+=--x x x x 即322121=⋅+x x x x ，从而32432=--m m ，解得：2=m （5分）∴抛物线的解析式是322-+=x x y （6分）（3）[解法一]：当0=x 时，243m y -= ∴抛物线与y 轴交点坐标为C （0，243m -）∵∆ABC 是直角三角形，且只能有AC ⊥BC ，又OC ⊥AB ，∴∠CAB= 90°— ∠A BC ，∠BCO= 90°— ∠ABC ，∴∠CAB =∠BCO∴Rt △AOC ∽Rt △COB ，（7分）∴OC AO OB OC =，即OB OA OC ⋅=2∴212243x x m ⋅-=-即2443169m m = 解得：332=m （8分）此时243m -=1)332(432-=- ，∴点C 的坐标为（0，—1）∴OC=1 又222212212124)43(4)(4)()(m m m x x x x x x =-⋅--=⋅-+=- （9分）∵m >0，∴m x x 212=- 即AB=m 2 ∴∆ABC 的面积=21⋅AB ⋅OC=21⨯m 2⨯1=332（10分）[解法二]：略解: 当0=x 时，243m y -= ∴点C （0，243m -）∵∆ABC 是直角三角形 ∴222BC AC AB += （7分）∴2221221)43()(m x x x -+=-2222)43(m x -++ （8分）∴421892m x x =⋅- ∴ 4289)43(2m m =-- 解得： 332=m （9分）∴332432214*********=⨯⨯=-⋅-=⋅⨯=∆m m m x x OC AB S ABC （10分）[注：以上的解答题若用了不同的解法，可按评分标准中相对应的步骤给分]。

2011年广东省初中毕业生学业考试

A D CB 机密★启用前2011年广东省初中毕业生学业考试数学试卷（6月押题卷）说明：1．全卷共6页，考试用时100分钟，满分为120分。

2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、试室号、座位号。

用2B 铅笔把对应该号码的标号涂黑。

3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上。

4．非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

5．考生务必保持答题卡的整洁。

考试结束时，将试卷和答题卡一并交回。

一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑。

1、－2的倒数是（）A 、2B 、－2C 、21D 、－212．日本东部大地震造成日本国内经济损失约2350亿美元，其中2350亿保留两个有效数字用科学记数法表示为( )A ．2.3×1011B ．2.35×1011C ．2.4×1011D ．0.24×10123.在下列图形中，即是轴对称图形，又是中心对称图形的是（） 4．如图是一个正方体的平面展开图，则这个正方体 “美”字所在面的对面标的字是（） A ．让 B ．生 C ．活 D ．更5. 某市某一周的最高气温统计如下表：则这组数据的中位数与众数分别是（） A ．27，28B ．27.5，28C ．28，27D ．26.5，27二、填空题（本大题5小题，每小题4分，共20分）请将下列各题的正确答案填写在答题卡相应的位置上。

6、函数y=11-x 自变量x 的取值范围是。

7．分解因式：324b b a -= ．8.一个十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒．当你抬头看信号灯时，是绿灯的概率是．9、反比例函数y=x k 32-的图象在每个象限内，y 随x 的增大而增大，则K 的取值范围是。

2011年广东省初中毕业生学业考试物理试卷及答案(试题word版答案扫描)

2011年广东省初中毕业生学业考试物理试卷及答案说明：1．全卷共6页，满分为100分，考试用时为80分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、试室号、座位号．用2B铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4．非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、单项选择题(本大题7小题，每小题3分，共21分)在每小题列出的四个选项中。

只有一个是正确的。

请把答题卡上对应题目所选的选项涂黑。

1．坐在高速行驶火车上的乘客，我们说他静止是以下列哪个物体为参照物的A．火车车厢B．铁轨C．迎面开来的火车D．车厢里走动的乘务员2．关于惯性，下列说法中正确的是A．静止的物体没有惯性B．运动物体的惯性比静止时大C．航天员在空间站中失去惯性D．物体在任何情况下都有惯性和L2组成并联电路，应3．如图1所示，要使灯泡LA．只闭合S2B．只闭合S3C．只闭合S1和S3D．只闭合S2和S34．如图2所示的光路图中，能正确表示光从空气射人水中时发生的反射和折射现象是5．以下四个措施中：①马路旁的房子的窗户采用双层玻璃；②城市禁止机动车鸣喇叭；③马路两旁植树；④高架道路两侧设隔音板墙。

对控制噪音污染有作用的是A．①②B．②④C．①②④D．①②③④6．关于静止在水平地面上的物体，以下叙述中的两个力属于一对平衡力的是A．地球对物体的吸引力与物体对地球的吸引力B．地面对物体的支持力与物体的重力C．物体对地面的压力与地面对物体的支持力D．物体对地面的压力与物体的重力7．如图3所示，电源电压保持不变，闭合开关，将滑动变阻器的滑片向右滑动时，则A．通过灯L的电流变小，变阻器两端的电压变小B．通过灯L的电流变大，变阻器两端的电压变大C．灯L两端的电压变小，通过变阻器的电流变小D．灯L两端的电压变大，通过变阻器的电流变小二、填空题（本大题7小题，每空1分，共21分）8．硅、锗等半导体材料的导电能力比铜、铁等金属的导电能力____(选填“强”或“弱”)。

广东肇庆-解析版

初中毕业学业考试试卷( 重点卷)一、选择题（本大题共l0小题，每小题3分，共30分）1、（2011•肇庆）的倒数是（）A、2B、﹣2C、﹣D、考点：倒数。

专题：计算题。

分析：根据倒数的定义即可解答．解答：解：的倒数是2．故选A．点评：本题主要考查了倒数的定义，正确理解定义是解题的关键．2、（2011•肇庆）我国第六欢人口普查的结果表明，目前肇庆市的人口约为4050000人，这个数用科学记教法表示为（）A、405×104B、40.5×105C、4.05×106D、4.05×107考点：科学记数法—表示较大的数。

分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：4 050 000=4.05×106，故选：C．点评：此题主要考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3、（2011•肇庆）如图是一个几何体的实物图，则其主视图是（）A、B、C、D、考点：简单组合体的三视图。

分析：找到从正面看所得到的图形即可．解答：解：从正面看可得到一个矩形和一个下底和矩形相邻的梯形的组合图，故选C．点评：本题考查了三视图的知识，主视图是从物体的正面看得到的视图．4、（2011•肇庆）方程组的解是（）A、B、C、D、考点：解二元一次方程组。

专题：计算题。

分析：此题运用加减消元法解方程组，由①+②先求出x，再代入求出y．解答：解：，①+②得：3x=6，x=2，把x=2代入①得：y=0，∴，故选：D．点评：此题考查的知识点是接二元一次方程组，关键是先用加减消元法求出x．5、（2011•肇庆）如图，已知直线a∥b∥c，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F，AC=4，CE=6，BD=3，则BF=（）A、7B、7.5C、8D、8.5考点：平行线分线段成比例。