解应用题口诀
一年级应用题技巧口诀

看关键字:“一共”、“总共”、“合计”、“原来”等字眼通常代表使用加法。
而“还剩”、“多多少”、“少多少”、“贵多少”、“谁比谁多”、“谁比谁少”、“哪个多”、“哪个少”等则通常使用减法。
钟表问题:一年级的应用题中,关于钟表的问题是常见的。
孩子们需要掌握钟表上的整点和半点,以及时针和分针的关系。
口诀如下:
大数记心里,小数上下加减。
加法:大数记心里,小数往上数,如4+2= 把4记在心里,往上数两个数,5、6,之后得出结果4+2=6。
减法:大数记在心里,小数往下数,如6-3= 把6记在心里,往下数三个数,5、4、3,之后得出结果6-3=3。
应用题口诀顺口溜大全

应用题口诀顺口溜大全
以下是一份应用题口诀顺口溜大全的范例,仅供参考:
1. 读题三遍,题意自明。
单位换算,计算准确。
一加一减,计算无误。
分子分母,先约后算。
多个条件,逐一分析。
缺条件时,尽量猜测。
常见数量,提前列出。
画图分析,直观明了。
复杂问题,分解解决。
多个问题,逐一解答。
思路清晰,步骤明确。
看表先标,数据清楚。
统计图表,先看后算。
2. 和差问题:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
3. 鸡兔同笼问题:假设全是鸡,假设全是兔;多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
4. 浓度问题:加水先求糖,糖完求糖水;糖水减糖水,便是加糖量。
加糖浓化:加糖先求水,水完求糖水;糖水减糖水,求出便解题。
5. 路程问题:相遇那一刻,路程全走过;除以速度和,就把时间得。
追及问题:慢鸟要先飞,快的随后追;先走的路程,除以速度差,时间就求对。
6. 和比问题:家要众人合,分家有原则;分母比数和,分子自己的。
这些口诀顺口溜有助于孩子们更好地理解和解决数学应用题。
小学典型应用题解题口诀

小学典型应用题解题口诀路程问题(相遇)【口诀】:相遇那一刻,路程全走过。
除以速度和,就把时间得。
举例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所以相遇的时间就为120÷60=2(小时)路程问题(追及)【口诀】:慢鸟要先飞,快的随后追。
先走的路程,除以速度差,时间就求对。
举例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?先走的路程,为3×2=6(千米)速度的差,为6-3=3(千米/小时)。
所以追上的时间为:6÷3=2(小时)鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
举例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36×2)÷(4-2)=24求鸡时,假设全是兔,则鸡数=(4×36-120)÷(4-2)=12和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
举例:已知两数和是10,差是2,求这两个数。
按口诀,大数=(10+2)÷2=6,小数=(10-2)÷2=4浓度问题(加水稀释)【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加水量。
举例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20×15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)浓度问题(加糖浓化)【口诀】:加糖先求水,水完求糖水。
四年级应用题公式大全口诀

四年级应用题公式大全口诀以下是四年级应用题公式大全口诀:一、求平均数公式1. 求平均数:总数÷份数=平均数2. 求某项平均值:某项数÷项数=平均值3. 求某项最大或最小值:某项数×(最大值 - 最小值)÷项数=最大或最小值二、倍数关系公式1. 两个数是倍数关系:如果一个数是另一个数的倍数,那么这两个数就叫倍数关系。
2. 求倍数关系:被倍数÷倍数=求倍数关系3. 解决倍数关系应用题的基本步骤:(1) 分析题意,明确两个数是倍数关系;(2) 确定被倍数,计算倍数关系;(3) 根据倍数关系,列出算式,求出解答;(4) 检查解答是否合理,是否符合题意。
三、时间、速度、路程公式1. 相遇问题:速度和×相遇时间=总路程2. 追及问题:速度差×追及时间=总路程3. 过桥问题:路程÷桥长=速度4. 时间=路程÷速度5. 速度=时间÷路程四、三角形面积公式1. 已知三角形底和高,求面积:三角形面积=底×高÷22. 已知三角形两边和其中一边对角线,求面积:三角形面积=两边对角线乘积的一半3. 已知三角形三边长度,求面积:三角形面积=底×高÷2五、分数应用题公式1. 求出总数和份数,然后求出一份数:总数÷份数=一份数2. 已知总数和份数,求出一份数:一份数×份数=总数3. 解决分数应用题的基本步骤:(1) 分析题意,明确题意涉及的分数关系;(2) 确定已知条件和问题,并列出分数关系式;(3) 计算问题所要求的分数,并解应用题;(4) 检查答案是否合理,是否符合题意。
以上是四年级应用题公式大全口诀的详细内容,希望能为小学生提供帮助。
数学口诀好东东

数学口诀好东东解一元一次方程的口诀:去分母,去括号,移项要变号,合并同类项,系数变为1(幺)。
列方程解应用题的步骤:析题意,狠抓等量关系;设未知,方程根据题意;解方程,检验作答完毕。
一元二次方程求根公式:分母是2a,分子含-b,正负根号下,判别式占据。
去括号与添括号法则:负变正不变,要变全部变。
有理数加法法则:同号不变值相加,异号取大值相减。
因式分解的公式:平方差,平方差,两数和乘两数差;平方和,二倍积,和差平方要对齐。
**注:两个数的平方和加上这两个数的积的2倍,等于这两个数的和的平方。
两个数的平方和减去这两个数的积的2倍,等于这两个数的差的平方。
“十字相乘法”:首尾分解,交叉相乘,求和试中判断对数式的正负:同正异负平面几何题怎样添加辅助线辅助线,如何添,找出规律凭经验。
题中有角平分线,可向两边作垂线。
线段垂直平分线,可向两端把线连。
三角形中两中点,连结则成中位线。
三角形中有中线,延长中线同样长。
成比例,证相似,经常要作平行线。
作线原则有一条,证题线段别割断。
圆外若有一切线,切点圆心把线连。
如果两圆内外切,经过切点作切线。
两圆相交于两点,一般作它公共弦。
是直径,成半圆,想做直角把线连。
作等角,添个圆,证明题目少困难。
辅助线,是虚线,画图注意勿改变。
完全平方公式:首平方,尾平方,首尾二倍中间放。
绝对值不等式的解集若|x|>a,则x>a或x<-a若|x|<a,则-a<x<a口诀:“大于取两边,小于取中间”。
合并同类项口诀不能忘系数相加减字母不变样分式不等式------移项,通分,化简,等价;分母不等于0。
2、合并同类项法则合并同类项,法则不能忘;只求系数代数和,字母、指数不变样。
3、分解因式歌首先提取公因式,然后考虑用公式。
十字相乘试一试,分组分得要合适。
四种方法反复试,分解完成连乘式4、一元一次不等式组的四种情况大大取较大,小小取较小,小大,大小中间找,小小,大大解不了。
5、角的集合数学里面角很多,组成一个大集合。
小学典型应用题解题口诀+公示表

路程问题(相遇)【口诀】:相遇那一刻,路程全走过。
除以速度和,就把时间得。
举例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所以相遇的时间就为120÷60=2(小时)路程问题(追及)【口诀】:慢鸟要先飞,快的随后追。
先走的路程,除以速度差,时间就求对。
举例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?先走的路程,为3×2=6(千米)速度的差,为6-3=3(千米/小时)。
所以追上的时间为:6÷3=2(小时)鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
举例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36×2)÷(4-2)=24求鸡时,假设全是兔,则鸡数=(4×36-120)÷(4-2)=12和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
举例:已知两数和是10,差是2,求这两个数。
按口诀,大数=(10+2)÷2=6,小数=(10-2)÷2=4浓度问题(加水稀释)【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加水量。
举例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20×15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)浓度问题(加糖浓化)【口诀】:加糖先求水,水完求糖水。
一年级数学应用题口诀公式

一年级数学应用题口诀公式一年级数学应用题口诀公式
一、加减口诀公式
加法的口诀公式:
相同的数字相加,结果直接相加;
不同的数字相加,先找大数,再数小数。
减法的口诀公式:
减法是找差,较小数减大数;
借位见零,个位减个位。
二、乘除口诀公式
乘法的口诀公式:
个位相乘、十位分开算;
十位相乘、再相加;
再加上千位,算完了。
除法的口诀公式:
除法是找商,除数放前面;
被除数减除数,商若为负数;
余数放一边,整除不现。
三、面积和周长口诀公式
矩形的面积公式:
长乘宽,结果明;
周长才用长宽加,边长加一倍。
正方形的面积公式:
边长乘以边长,结果响亮;
周长计算方法同矩形不两样。
圆形的面积公式:
半径乘半径乘π,结果够大;
周长就是半径乘以二π。
四、时钟口诀公式
一小时有60分钟,乘以分针和时针;
每小时有12个刻度,乘以时针和分钟。
五、计算口诀公式
加减乘除顺序记清楚,按顺序一步步走;
括号表达式最先算,先算括号再算其他。
总结:
数学应用题要求我们灵活运用口诀公式,在解题过程中记住这些技巧。
加减要注意数字的相加和借位,乘除要按照乘法口诀和除法口诀计算,面积和周长要根据图形的特点运用相应的公式,时钟口诀是帮助我们
计算时间的好方法,最后,计算过程中要按照正确的顺序进行,准确解决问题。
只要我们掌握了这些口诀公式,数学应用题就不再难题。
小学典型应用题解题口诀

小学典型应用题解题口诀路程问题(相遇)【口诀】:相遇那一刻,路程全走过。
除以速度和,就把时间得。
举例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所以相遇的时间就为120÷60=2(小时)路程问题(追及)【口诀】:慢鸟要先飞,快的随后追。
先走的路程,除以速度差,时间就求对。
举例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?先走的路程,为3×2=6(千米)速度的差,为6-3=3(千米/小时)。
所以追上的时间为:6÷3=2(小时)鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
举例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36×2)÷(4-2)=24求鸡时,假设全是兔,则鸡数=(4×36-120)÷(4-2)=12和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
举例:已知两数和是10,差是2,求这两个数。
按口诀,大数=(10+2)÷2=6,小数=(10-2)÷2=4浓度问题(加水稀释)【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加水量。
举例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20×15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)浓度问题(加糖浓化)【口诀】:加糖先求水,水完求糖水。
【免费】小学三年级数学“典型应用题”解题口诀(名校版)

小学三年级数学“典型应用题”解题口诀(名校版)路程问题(相遇)【口诀】:相遇那一刻,路程全走过。
除以速度和,就把时间得。
举例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所以相遇的时间就为120÷60=2(小时)路程问题(追及)【口诀】:慢鸟要先飞,快的随后追。
先走的路程,除以速度差,时间就求对。
举例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?先走的路程,为3×2=6(千米)速度的差,为6-3=3(千米/小时)。
所以追上的时间为:6÷3=2(小时)鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
举例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36×2)÷(4-2)=24 求鸡时,假设全是兔,则鸡数=(4×36-120)÷(4-2)=12和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
举例:已知两数和是10,差是2,求这两个数。
按口诀,大数=(10+2)÷2=6,小数=(10-2)÷2=4浓度问题(加水稀释)【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加水量。
举例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20×15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)浓度问题(加糖浓化)【口诀】:加糖先求水,水完求糖水。
五年级应用题必背口诀

五年级应用题必背口诀摘要:一、口诀背景- 适用年级- 为什么需要背诵二、口诀内容1.加法2.减法3.乘法4.除法三、口诀背诵方法1.分阶段学习2.结合实际应用题3.创造记忆口诀四、口诀在实际应用中的意义1.提高解题速度2.加深对数学概念的理解3.培养学习兴趣正文:一、口诀背景对于即将进入五年级的同学们来说,掌握一些基本的应用题解题技巧是至关重要的。
应用题是数学学习中的一个重要环节,通过解答应用题,同学们可以巩固所学的数学知识,培养逻辑思维能力。
而应用题必背口诀,则是帮助同学们更好地掌握解题技巧的有效方法。
二、口诀内容1.加法加法口诀主要包括:“同号相加,异号相减;正负号看清楚,答案就在你眼前。
”通过这句口诀,同学们可以迅速判断两个数相加后的结果是正还是负。
2.减法减法口诀:“减法想加法,轻松解答;正负号别搞错,计算才能正确。
”这句口诀提醒同学们,在解答减法题目时,可以先将减法转化为加法,再按照加法口诀进行计算。
3.乘法乘法口诀:“乘法交换律,因数位置调换;乘法结合律,因数分组计算。
”掌握乘法交换律和结合律,可以让同学们在计算乘法题目时更加灵活。
4.除法除法口诀:“除法想乘法,商和被除数相乘;余数别忘记,答案才能完整。
”这句口诀教导同学们,在解答除法题目时,可以通过转换思维,将除法转化为乘法进行计算。
三、口诀背诵方法1.分阶段学习在背诵口诀时,同学们可以根据自己的学习进度,分阶段进行。
例如,先掌握加法和减法口诀,再逐步学习乘法和除法口诀。
2.结合实际应用题为了更好地理解和记忆口诀,同学们可以多做一些实际应用题。
在解答过程中,尝试运用口诀进行计算,加深对口诀的理解。
3.创造记忆口诀除了背诵现有的口诀外,同学们还可以尝试自己创造一些记忆口诀。
这样既能让学习过程更加有趣,也能帮助同学们更好地记忆口诀。
四、口诀在实际应用中的意义1.提高解题速度熟练掌握口诀后,同学们在解答应用题时可以迅速找到解题方法,提高解题速度。
分数应用题解题技巧及口诀

分数应用题解题技巧及口诀
1. 哎呀呀,遇到分数应用题先别慌!咱要找关键量呀!就像找宝藏一样,找到了关键量,问题就好解决啦!比如说,有一道题说小明吃了一堆苹果的$\frac{1}{3}$,那这“$\frac{1}{3}$”就是个关键呀,咱得围绕它来解题呀!明白不?
2. 嘿!遇到那种问整体是多少的,就得用除法啦!这就好比是要把一块大饼还原成整个的呀!比如题目说知道了部分是多少,又知道占整体的几分之几,那赶紧用部分除以所占比例,整体不就出来啦!能懂不?
3. 哇塞,有的时候可以画图呀!把分数的关系用图表示出来,一下子就清楚啦,就跟地图让人看懂路线一样呢!像有个题是说甲占乙的几分之几,那画个图,甲乙的关系不就明明白白啦!是不是很神奇呀?
4. 记住咯,看到增加或减少的分数,得小心啦!可不能马虎哟!这就像是走钢丝,得步步谨慎!比如说题目说某东西增加了$\frac{1}{4}$,那咱就得把原来的看作单位“1”,然后再计算呀!对不?
5. 哈哈,分数应用题里的单位“1”很重要呀!就像游戏里的老大一样!一
旦确定了单位“1”,就像找到了方向啦!比如人家问你某东西占谁的几分
之几,那赶紧找到那个“1”呀!这不难吧?
6. 哎呀呀,咱还得学会灵活转化呀!分数可以变来变去的呢,就像孙悟空七十二变一样!例如知道了甲是乙的几分之几,那乙是甲的几分之几不也就可以算出来啦!是不是很有意思呀?
我的观点结论:只要掌握了这些技巧和口诀,分数应用题就没那么可怕啦,咱都能轻松应对!。
小学数学13种典型应用题解析与掌握的口诀
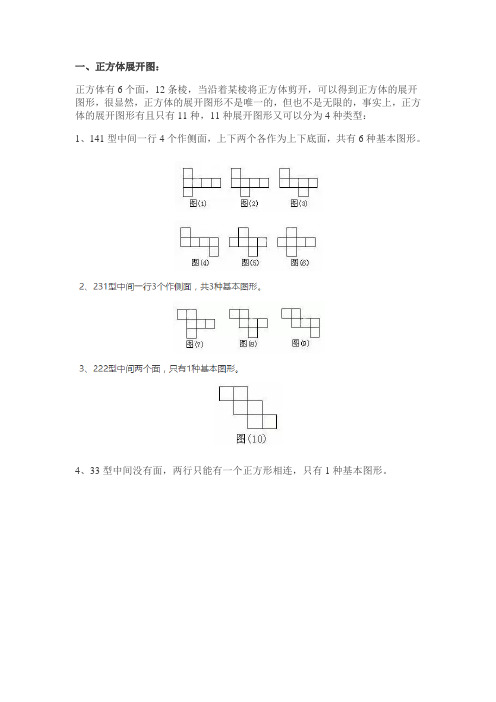
一、正方体展开图:正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:1、141型中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
4、33型中间没有面,两行只能有一个正方形相连,只有1种基本图形。
二、和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。
三、鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24求鸡时,假设全是兔,则鸡数=(4X36-120)/(4-2)=12四、浓度问题(1)加水稀释【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)(2)加糖浓化【口诀】:加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X(1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)五、路程问题(1)相遇问题【口诀】:相遇那一刻,路程全走过。
一年级应用题口诀顺口溜

一年级应用题口诀顺口溜一年级应用题排队口诀如下:
1、两个有几加自己(+1)。
2、两个第几减自己(-1)。
3、一个有几,一个第几,不加不减正常算。
公式口诀:
前+后+1=一共。
前+后-1=一共。
前+后=一共。
“排队问题”的三种常见题型总结:
第一种:前面有几人,后面有几人,一共有多少人?
例题:前面有4人,后面有2人,一共有多少人?
列式:4+2+1=7(人)。
口诀:前+后+1=一共。
第二种:从前面数排第几,从后面数排第几,一共有多少人?例题:从前面数排第5,从后面数排第4,一共有多少人?
列式:5+4 -1 = 8(人)。
口诀:前+后-1=一共。
第三种:从前往后数排第几,后面还有几人,一共有多少人?例题:从前往后数排第4,后面还有6人,一共有多少人?
列式:4+6 = 10(人)。
口诀:前+后=一共。
二年级应用题口诀14句

二年级应用题口诀14句二年级的应用题目,常常令孩子们感到头疼和困惑。
实际上,只需要掌握一些基本方法和技巧,就能轻松解决这些问题。
下面,就让我们一步步地学习“二年级应用题口诀14句”。
第一句:“找关键词”,通常情况下,应用题目中会出现一些明显的关键词,比如“共有”、“剩余”、“每个”等等,这些关键词往往是解题的关键。
第二句:“找出题人想考察的知识点”,有些应用题目是为了考察孩子们的应用能力,而有些应用题目则是为了考察孩子们对于某个具体概念的理解程度。
第三句:“认真观察数据”,在解题过程中,一定要认真观察题目中的各种数据,根据这些数据进行计算和分析。
第四句:“转换数据”,有时候,题目中给出的数据不是直接可用的,需要进行一些必要的转换,才能进行计算和分析。
第五句:“画图辅助”,在解决一些比较复杂的应用题目时,可以通过画图来辅助计算和分析,以便更好地理解题意。
第六句:“分类讨论”,在某些应用题目中,可以根据不同情况进行分类讨论,以便更好地解决问题。
第七句:“抽象问题”,有些应用题目较为抽象,需要通过抽象问题的方式来进行分析和计算,从而得出答案。
第八句:“列式运算”,很多应用题目需要进行列式运算才能得出答案,因此,在解题过程中要熟练掌握各种列式运算的方法。
第九句:“找规律”,有些应用题目中存在一定的规律性,可以通过发现规律来简化计算和解决问题。
第十句:“逐步推导”,在解决某些复杂的应用题目时,可以逐步推导出较为简单的公式和表达式,以便更好地计算和分析。
第十一句:“备选答案”,在进行计算和分析时,可以预先列出备选答案,从而更好地判断正确答案的范围。
第十二句:“检验答案”,解题过程中在得出答案之后,一定要进行必要的检验,以免出现计算错误等情况。
第十三句:“复盘总结”,在解决一些较难的应用题目之后,可以进行复盘总结,以便更好地掌握解题方法和技巧。
第十四句:“勤于练习”,只有在日常生活中多做应用题目,才能更好地掌握解题方法和技巧,从而轻松应对各种考试和竞赛。
【免费】小学三年级数学“典型应用题”解题口诀(名校版)

小学三年级数学“典型应用题”解题口诀(名校版)路程问题(相遇)【口诀】:相遇那一刻,路程全走过。
除以速度和,就把时间得。
举例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所以相遇的时间就为120÷60=2(小时)路程问题(追及)【口诀】:慢鸟要先飞,快的随后追。
先走的路程,除以速度差,时间就求对。
举例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?先走的路程,为3×2=6(千米)速度的差,为6-3=3(千米/小时)。
所以追上的时间为:6÷3=2(小时)鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
举例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36×2)÷(4-2)=24 求鸡时,假设全是兔,则鸡数=(4×36-120)÷(4-2)=12和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
举例:已知两数和是10,差是2,求这两个数。
按口诀,大数=(10+2)÷2=6,小数=(10-2)÷2=4浓度问题(加水稀释)【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加水量。
举例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20×15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)浓度问题(加糖浓化)【口诀】:加糖先求水,水完求糖水。
应用题必背口诀幼儿园

应用题必背口诀幼儿园1.乘法口诀儿歌一只青蛙一张嘴,两只眼睛四条腿。
两只青蛙两张嘴,四只眼睛八条腿。
三只青蛙三张嘴,六只眼睛十二条腿。
四只青蛙四张嘴,扑嗵扑嗵跳下水。
2.一个数除几位数儿歌先看被除数最高位,高位不够多一位除到被除数哪一位,商就写在哪一位,不够商1就写0,商中头尾算数位,余数要比除数小,这样运算才算对。
3.小数加减法儿歌计算小数加减法,关键对齐小数点,用0补齐末位,便可进行加减。
小数大小比较儿歌(自编)小数大小比较很容易,先把他们都竖起,小数点,数位要对起,然后再把他们比。
首先比较最高位,最高位相同下位比。
至到最后分高低,哪个高来哪个大。
牢记在心不忘记。
除法是小数的除法除法是小数,移位要记住。
移动小数点,使它变整数,除数移几位,被除数同样多,数位如不够,添0来补位。
4.四则混合运算儿歌通览全题定方案,细看是否能简便;从左到右脱式算,先乘除来后加减;括号依次小中大,先算里面后外面;横式计算竖检验,一步一查是关键5.解应用题儿歌题目读几遍,从中找关键;先看求什么,再去找条件;合理列算式,仔细来计算;一题求多解,单位莫遗忘;结果要验算,最后写答案。
长度、面积、体积、容积的认识长度一条线,面积一大片;体积占空间,容积算里面。
6.四舍五入法儿歌四舍五入方法好,近似数来有法找;取到哪位看下位,再同5字作比较;是5大5前进1,小于5的全舍掉;等号换成约等号,使人一看就明白。
7.鸡兔同笼问题的解法鸡有两只脚,兔有四只脚。
先数头和身。
再按鸡分脚。
8.运算顺序歌诀打竹板,连天,各位同学听我言。
今天不把别的表,四则运算聊一聊,混合试题要计算,明确顺序是关键。
同级运算最好办,从左到右依次算。
两级运算都出现,先算乘除后加减。
遇到括号怎么办?小括号里算在先,中括号里后边算,次序千万不能乱,每算一步都检验,又对又快喜心间。
