求解器的使用
求解器的使用

求解器的使用FLUENT提供了三种不同的求解器Segregated,coupled implicit,coupled explicit(显式格式主要用于激波等波动解的捕捉问题)传统上,分离解法(segregated)主要用于不可压缩以及适度压缩的流动中。
相反,耦合算法是为高速可压流体设计的。
默认情况下,fluent使用分离求解器。
对于高速可压流体,与很强的体积力高度耦合的流动,或者是在非常精确的网格上求解流动情况,可以考虑使用耦合隐式算法代替。
对于需要使用耦合隐式算法(coupled implicit)的case,如果电脑没有足够的内存,可以使用分离解法(segregated)或者耦合显式算法(coupled explicit)代替。
(显示算法节约内存,但是需要更多的计算步数达到收敛。
)选择离散格式1.一阶迎风格式v.s. 二阶迎风格式当流动与网格匹配(校准)时,一阶迎风格式是可以接受的。
对于三角形和四面体网格,由于流动不会与网格匹配,通常使用二阶离散格式会得到更准确的结果。
对于四边形/六面体网格,使用二阶离散格式会取得更好的结果,尤其是复杂的流动情况。
对于大多数情况,可以在计算初始,使用二阶的离散格式。
然而在一些情况下,可以开始使用一阶的离散格式然后在一些计算之后转变为二阶格式。
例如,如果正在运行一个高马赫数的流动计算,这个的初始解与期望的解相差很大,最终,如果二阶离散格式很难收敛,应该尝试使用一阶离散格式。
2.Quick格式v.s. Upwind(Quick格式适用于网络结构,流动方向与网格一致,对于非结构网格推荐使用二阶迎风)对于在四边形或者六面体网格中的旋转或者回旋流,Quick离散格相比于二阶离散格式可以提供更准确的结果。
对于存在震动的可压缩流动(网格为四边形,六面体或者混合网格),推荐对所有的变量使用Quick离散格式,包括密度。
3.中心差分格式v.s. 迎风格式当使用LES湍流模型时,是可以使用中心差分格式的,并且只有当网格间距足够好,以至于局部的Peclet数的大小小于1时才可以使用。
杉数求解器用法

杉数求解器用法杉数求解器是一种用于解决优化问题的工具,它可以求解线性规划、整数规划、混合整数规划等多种问题。
下面是使用杉数求解器的一般步骤:1. 安装杉数求解器:首先,您需要在您的计算机上安装杉数求解器。
您可以访问杉数科技的官网,下载并按照说明进行安装。
2. 准备问题:在开始使用杉数求解器之前,您需要准备要解决的问题。
这包括定义决策变量、目标函数和约束条件。
这些信息通常以数学模型的形式提供。
3. 导入问题:打开杉数求解器,选择“文件”菜单中的“打开”选项,然后选择您要导入的数学模型文件。
4. 设置参数:在杉数求解器中,您可以设置一些参数来控制问题的求解过程。
这些参数包括求解器的选择、时间限制、迭代次数等。
5. 运行求解:设置完参数后,您可以通过点击“求解”按钮来开始解决问题。
杉数求解器将尝试找到满足所有约束条件的决策变量的值,同时最大化或最小化目标函数。
6. 检查结果:求解完成后,杉数求解器将显示求解结果。
这包括最优解、最优值、迭代次数、时间等信息。
您还可以查看决策变量的取值、目标函数的值等详细信息。
7. 导出结果:如果您需要将结果分享给其他人或用于其他目的,您可以使用杉数求解器的导出功能将结果导出为所需的格式,如Excel、PDF等。
需要注意的是,使用杉数求解器需要一定的数学基础和编程经验。
如果您不熟悉这些概念,可能需要先学习一些基本的优化知识和编程技能。
同时,杉数求解器的使用也需要注意一些细节和技巧,如数学模型的建立、参数的设置、结果的解读等。
因此,建议在使用杉数求解器之前先仔细阅读相关文档和教程,或者寻求专业人士的帮助和指导。
微软数学求解器 用法

微软数学求解器用法
微软数学求解器是一种实验性功能,用户可以在浏览器中启用该功能以解决数学问题。
要使用微软数学求解器,请按照以下步骤操作:
1.打开微软Edge浏览器,在地址栏中输入“edge://flags/#edge-math-
solver”,然后按Enter键。
2.在搜索结果中,找到“Microsoft Edge Math Solver”并将其启用。
3.重新启动浏览器后,前往“设置”>“外观”>“自定义工具栏”,打开
“数学求解器”按钮。
4.在数学求解器页面上,选择要解决的数学问题。
可以通过手动输入或使用
截图工具来选择问题。
5.点击“解决”按钮,等待求解器解决问题。
求解器将提供问题的即时解决
方案和详细的分步指导。
6.如果需要,可以通过点击“显示更多学习内容”选项来获取更多的学习资
源,包括在线视频、测验和工作表等。
需要注意的是,微软数学求解器是一种实验性功能,其性能和稳定性可能不够稳定。
因此,在使用过程中请保持耐心,并注意保存您的工作。
同时,由于该功能涉及到自动求解数学问题,请在使用时确保您遵守相关法律法规和学术道德规范。
附录A-1 结构力学求解器使用说明

责任编辑:余美茵、黄 毅、姜 凤、葛 心、水 渊
技术编辑:张 泽、田 雨、高 瑾、路秋雨
研制组将不断对 SM Solver 做更新升级;若您在使用过程中发现不妥、不便之处或有好的 建议,欢迎提出并请及时与研制组联系,以便在维护升级中不断完善。对于小问题,研制组将 免费提供修补文件。
§A-1-7 命令指南
使用求解器时,需要用户在编辑器中输入命令用以定义要求解的问题。对于一般用户来 讲,建议采用对话框的方式来输入和修改命令,这样可不必关心命令格式。但由于本书中几乎 所有用求解器求解的例题都是用命令文档的形式来描述和定义的,因此为了用户参阅的方便, 这里给出求解器中输入命令的语法和格式。
1. 格式说明 1) 命令集在功能上分为两类:分析求解命令和辅助显示命令。分析求解命令对于求解问 题是必需的,如结点、单元定义等;而辅助显示命令只是对观览器的显示增加一些功能,与问
2. 命令格式 命令行
注释
问题标题 TITLE, Ttext
注释 C Ctext
Ttext,标题文本(小于 75 个字符)。
Ctext,注释文本(小于 75 个字符)。 注:C 后应留一空格,或加一个逗号。
变量定义
LET, VarName=Formula, VarName=Formula[, …] VarName,变量名;
研 制 人:袁 驷 教授
§A-1-6 研制组
参加人员:
版本 1.0 : 叶康生、王建琳、孔令原、林永静
版本 1.5 : 叶康生、欧阳彦峰、孔令原
版本 2.0 : 叶康生、罗 剑、卢绪书、王 柯
版本 2.5 : 叶康生、徐俊杰、宴 勇
版本 2.6 : 叶康生、徐俊杰
研制单位:清华大学土木工程系结构力学教研室
结构力学求解器用法

字体:使用该命令,可控制编辑器窗体中字符的字体、 字形、大小等字符格式。
2021/6/4
返回 19
编辑器的“命令”菜单包括如下几项:问题定义、变量 定义、结点、单元、位移约束、荷载条件、材料性质、温度 改变、其它参数、尺寸线、文本、修改命令。
命令菜单中各个子菜单的作用是通过对话框选择的方式 来向当前文档中添写各种命令,以输入各种结构体系信息 (结点定义,单元定义,支座定义,荷载定义等)
2021/6/4
4
双击桌面上的SM Solver图标,再单击程序的封面,便 可使用求解器了。
五、V1.5版的新增功能
⒈ 安装 完善了安装程序,对于Win 95/98可以自动在桌面上安装 图标。 ⒉ 求解功能 组合结构:智能求解模式增添了平面“静定组合结构” 的求解,按三种模式(所有杆件内力、作弯矩图需要的内力 、指定杆件的内力)以文本或图文形式给出解题步骤。 四精度求解:可选用四精度实型数(约28位)求解,结果 更精确、可更好地模拟无穷大刚度。辑器的“查看”菜单包括如下几项:整个文档、单个 问题、观览器、中文关键字、工具栏、状态栏、字体。
允许用户检查和更改编辑器窗口当前所处的状态。
整个文档:当整个文档被选中时,此命令名旁出现一个 选中标记。且相应地在编辑器下方的状态栏上最左边显示出 “整个文档”。此时活动文档窗中显示整个文档。
单个问题:当某一个问题被选中时,此命令名旁出现一 个选中标记。且相应地在编辑器下方的状态栏上最左边显示 出“问题:n”,n代表当前问题在整个文档中的序号。此时 活动文档窗中显示的只是当前的单个问题,而其它问题则被 隐藏起来。
2021/6/4
返回 18
观览器:此菜单可以控制观览器窗口的显现和隐藏,具 体观览器的使用请参见下章“观览器使用介绍”。
HFSS场计算器使用指南

HFSS场计算器使用指南HFSS场计算器使用指南1、介绍1.1 背景信息1.2 目的和范围2、安装和启动2.1 硬件和软件要求2.2 安装步骤2.3 启动程序3、用户界面3.1 主界面概述3.2 菜单栏和工具栏3.3 工作区域和视图控制3.4 参数设置和输入4、创建模型4.1 创建几何形状4.2 定义材料属性4.3 设定边界条件5、设置场计算选项5.1 选择求解器类型5.2 设定求解器参数5.3 设置求解器的收敛准则5.4 选择场分析类型6、运行场计算6.1 预处理步骤6.2 设定计算域和网格精度 6.3 运行场计算过程6.4 后处理结果7、优化设计7.1 设定设计参数7.2 定义目标函数和约束条件 7.3 运行优化算法7.4 分析优化结果8、故障排除8.1 常见问题和解决方案8.2 参考文档和资源9、附件- 示例模型文件- 用户手册附录:1、法律名词及注释- HFSS:高频结构仿真软件 (High Frequency Structure Simulator)- 场计算器:用于解决电磁场问题的软件工具- 几何形状:描述实体、面和边的几何图形- 材料属性:描述介质的电磁特性,如介电常数、导电性等 - 边界条件:描述模型边界上的物理特性,如边界反射、吸收等- 求解器:用于数值求解和计算电磁场分布的算法和方法- 收敛准则:判断求解器结果是否足够精确的判据- 场分析类型:根据问题需求,选择正确的场计算方法 - 优化设计:通过调整设计参数来优化电磁场性能- 目标函数:优化设计中要最小化或最大化的性能指标 - 约束条件:限制优化设计的约束条件,如尺寸、能耗等2、本文档结束 \。
simple solver使用方法

Simple Solver 是一个简单易用的求解器,可以用于解决各种数学问题和工程问题。
它支持多种数学函数和符号,可以用于符号计算和数值计算。
本文将介绍 Simple Solver 的使用方法,供初学者参考。
一、下载安装 Simple Solver1. 打开浏览器,输入 Simple Solver 的冠方全球信息站位置区域。
2. 在全球信息站首页找到并点击“下载”按钮。
3. 根据系统要求选择合适的版本下载,并按照提示安装。
二、启动 Simple Solver1. 安装完成后,在桌面双击 Simple Solver 图标,或者在开始菜单中找到 Simple Solver 并点击打开。
2. 确保计算机已连接至互联网,Simple Solver 会自动进行更新和授权验证。
三、创建新的求解项目1. 在 Simple Solver 主界面点击“新建”按钮,或者在菜单栏选择“文件”-“新建”。
2. 在弹出的对话框中选择项目类型,输入项目名称,点击“确定”。
四、输入数学表达式1. 在主界面的输入框中输入需要求解的数学表达式,支持基本运算符、括号、函数等。
2. 可以通过键盘输入或者点击屏幕上的按钮进行输入。
五、设置求解参数1. 在界面的右侧可以设置求解的参数,比如精度、迭代次数、求解方法等。
2. 根据具体问题的要求进行相应的参数设置。
六、进行求解1. 确认输入的表达式和参数都设置完成后,点击“求解”按钮进行计算。
2. 程序会在界面上显示计算过程和结果,也可以保存结果或者输出成文本、图片等格式。
七、保存和导出1. 在求解过程中可以随时保存当前项目,以便后续修改或查看。
2. 也可以将结果导出成文件,比如图片、PDF 等格式,方便进行打印或者共享。
八、关闭程序1. 在完成所有操作后,可以点击“退出”按钮,或者在菜单中选择“文件”-“退出”来关闭 Simple Solver。
以上就是Simple Solver 的基本使用方法,希望对初学者能有所帮助。
unisat的使用方法

Unisat是一款用于形式化验证的SAT求解器,它可以帮助用户在软件、硬件、网络协议等领域进行逻辑表达式的求解和验证。
以下是使用Unisat的一般方法:1. 安装Unisat:首先,您需要在您的计算机上安装Unisat。
您可以从官方网站上下载安装包,并按照安装向导进行安装。
2. 创建问题文件:使用Unisat时,您需要创建一个包含要解决的问题的文件。
该文件应包含所有必需的逻辑表达式和相关的数据类型。
3. 定义变量:在问题文件中,您需要定义用于逻辑表达式的变量。
变量可以是整数、布尔值或其他数据类型。
4. 添加约束:使用Unisat,您可以添加约束以确保您的逻辑表达式在给定输入的情况下是正确的。
这些约束可以是等式、不等式或其他逻辑表达式。
5. 求解问题:一旦您创建了问题文件并添加了所有必要的约束,您可以使用Unisat求解器来查找满足所有约束的解。
求解器将生成一个解集合,其中包含满足所有约束的变量的值。
6. 分析结果:查看求解器生成的解集合,您可以确定逻辑表达式是否在给定输入的情况下有效。
您还可以根据需要进一步分析解集合,以验证其他假设或实现其他形式的验证。
7. 解决问题:如果逻辑表达式无效或不符合预期,您可以使用Unisat提供的其他工具和功能来解决问题。
这些工具可能包括变量和约束的可视化工具、表达式解析器等。
下面是一个使用Unisat解决问题的示例:假设您正在开发一个软件系统,其中涉及一些逻辑条件。
您可以使用Unisat来验证这些条件是否在给定输入的情况下有效。
首先,您创建一个问题文件,其中包含逻辑表达式和相关的数据类型。
例如,您可以使用整数变量来表示输入值,并使用布尔变量来表示逻辑条件是否满足。
接下来,您添加约束以确保逻辑表达式在给定输入的情况下是正确的。
例如,您可以使用等式或不等式来确保输入值符合预期范围,或使用其他逻辑表达式来确保条件始终为真或假。
然后,您可以使用Unisat求解器来查找满足所有约束的解。
结构力学求解器(使用指南)

结构力学求解器(使用指南)结构力学求解器(SMSolverofWindows)是一个关于结构力学分析计算的计算机软件,(体系)的几何组成、静定和超静定结构的内力、位移,影响,以及弹性稳定等结构力学课程中所涉及的绝大部分问题.;能;能绘制结构的影响V1.5..运行环境Windows98/NT.8M内存.2M硬盘空间..装机与运行,在Windows环境下运行光盘上的SMsetup.exe,然后按提示操作.装机完成后,桌面上将出现一个名为"求解器"的图标.双击桌面上的"求解器"图标,再单击软件的封面,便可使用该求解器.,然后按以下诸项输入数椐:1.结点定义N,Nn,x,yNn---结点编码;x---结点的x坐标;y---结点的y坐标.结构整体坐标系为xoy,一般取结构左下支座结点为坐标原点(0,0).2.Ngen---Nincr---N1、N12incr---Dx,DY---生成结点的x,y坐标增量.3.单元定义E,N1,N2[,DOF11,DOF12,DOF13,DOF21,DOF22,DOF23]N1,N2---单元两端的结点码;:1为连接,0为不连接;DOF11,DOF12---分别为单元在杆端1处的x、y方向自由度的连接方式,=1;DOF13---单元在杆端1处的转角方向自由度的连接方式,缺省值=0;缺省值=1;DOF23---单元在杆端2处的转角方向自由度的连接方式,缺省值=0.4.单元生成(即成批输入单元两端的连接方式)EGEN,Ngen,E1,E2,NincrEgen---生成次数;E1,E2---基础单元范围;Nincr---支座约束定义NSUPT,Sn,Stype,Sdir,[,Sdisx,Sdisy,SdisR]Sn---Stype---Sdir---Sdisx---x方向的支座位移,缺省值=0;Sdisy---y方向的支座位移,缺省值=0;SdisR---转角方向的支座位移,缺省值=0.以上(1)~(6)为支座类型码.ECHAR,ElemStart,ElemEnd,EA,EI,mElemStart---单元起始码;ElemEnd---单元终止码;EA,EI---分别为单元的抗拉和抗弯刚度;m---单元的均布质量(kg/m).Ltype---Ltype=1(-1),Ltype=2(-2),Lsize---Ldir---荷载方向(度),仅当Ltype=1或-1时入,缺省值=0.:竖向集中力,作用在结点上方时,取=-90,反之,取=90;水平集中力,作用在结点左方时,取=0,反之,取=180.8.单元荷载ELOAD,Ln,Ltype,Lsize1[,Lpos1[Lpos2[,Ldir]]]Ln---荷载作用的单元码;Ltype---荷载类型;Ltype=2(2),逆时(顺时)针方向的集中力矩;Ltype=3(-3),均布荷载,指向(背离)单元;Lsize1---荷载大小;Lpos1---荷载起点至单元杆端1的距离与单元杆长的比值,缺省值=0; Lpos2---荷载终点至单元杆端1的距离与单元杆长的比值,缺省值=1;(仅对均布荷载输入Lpos2)Ldir---荷载方向(度),仅当Ltype=1,3或-1,-3时输入,缺省值=0.(注:9.频率计算参数FREQ,Nfreq,FreqStart,TolNfreq---FreqStart---Tol---精度误差限,如0.0005.10.影响线参数IL,LoadDOF,En,pos,FdofLoadDOF---单位荷载的方向(整体坐标系):1为水平,2为竖直,3为转角;En---单元码;pos---单元上截面位置:距杆端1的距离与杆长的比值;Fdof---欲求影响线的内力自由度(局部坐标系),1为轴力,2为剪力,说明:1.计算结构的内力和位移时,仅输入1(或及2),3(或及4),5,6,7,8项;2.当单元的抗拉刚度(EA)或抗弯刚度(EI)为无穷大时,则分别填-1;3.当斜杆单元作用沿水平线的均布荷载时,需按合力相等的原则,变换成沿杆轴线分布的均布荷载输入,荷载类型码仍为3(见例5).1.双击桌面上的"2.键入数椐文件名(如3.将数椐文件存盘"文件点"4.再单击文件",在文件菜单中点5.见提示"?此命令将结束本次SMSolver!"点""或'确定",重新进入SMSolver;6.单击"文件",在文件菜单中点"打开";7.点所要运行的数椐文件名,并单击"确定";8.单击桌面下方的"观览器"图标,(桌面上显示结构计算简图的形状),并单击"最大化"按钮,将图形放大;9.单击桌面上方的"标注",在"标注"菜单中点所要显示的参数;(如无误,则进行下一步,若有误,则进行修改)10.单击"观览器"图标,点桌面上方的"求解";(如各杆杆端的内力或位移,对照结构的单元编号或结点编号阅读);12.单击所要显示的内力类型(轴力、剪力、弯矩)及显示对象(如"结构"或"单元");13.单击"观览器"图标,则显示出内力图或位移图;14.重复单击"观览器"图标,即可选定和显示不同的内力图;15.逐层单击标题栏右边的"关闭"按钮,当显示:"此命令将结束本次SMSolver的运行"或提示".计算例题例1求图示刚架的内力.各杆的EA=3.12X10KN,EI=4.16X10KN-M.TITLE,AAA-1N,1,0,0N,2,4,0N,3,0,4N,4,4,4E,1,3,1,1,1,1,1,0E,3,4,1,1,0,1,1,1E,4,2,1,1,1,1,1,1NSUPT,1,6,0,0,0,0NSUPT,2,6,0,0,0,0NLOAD,3,1,30,0ELOAD,1,3,20,0,1,90例2求图示组合结构的内力.设各杆的EA=EI=1.TITLE,AAA-2N,1,0,0NSUPT,1,2,-90,0,0E,2,3,1,1,1,1,1,0E,3,4,1,1,0,1,1,1E,4,5,1,1,1,1,1,0E,6,7,1,1,0,1,1,0E,6,2,1,1,0,1,1,0E,7,4,1,1,0,1,1,0E,6,1,1,1,0,1,1,0E,7,5,1,1,0,1,1,0例3.求图示桁架各杆的轴力.TITLE,,AAA-3N,1,1,0NGEN,4,1,1,1,1,1,0NGEN,1,5,1,5,1,0,1E,1,2,1,1,0,1,1,0EGEN,3,1,1,1E,1,7,1,1,0,1,1,0E,1,8,1,1,0,1,1,0E,8,5,1,1,0,1,1,0E,5,9,1,1,0,1,1,0NSUPT,1,2,-90,0,0NSUPT,5,1,0,0NLOAD,8,1,1,-90NLOAD,9,-1,2,-90(注:此题系静定结构,其内力与材料性质无关,故可不输入ECHAR项)4.求图示桁架的轴力.提示:支座约束和结点荷载信息为NSUPT,2,1,0,0NLOAD,7,1,8,-90NLOAD,8,1,4,180NLOAD,5,1,4,180例5.求图示三铰刚架的内力.:注(q)变换成沿杆轴线的均布荷载即q=qcos=10X6/40=例求图示刚架的内力.设EI=1.TITLE,AAA-6N,1,0,0N,2,4,0N,3,8,0N,4,4,-4E,1,2,1,1,1,1,1,1E,2,3,1,1,1,1,0,1NSUPT,1,6,-90,0,0,0NSUPT,3,5,0,0,0NSUPT,4,4,90,0,0ECHAR,1,1,-1,1ECHAR,2,2,-1,2ECHAR,3,3,-1,1ELOAD,1,3,30,0,1,90例求图示梁的内力和位移TITLE,AAA-7N,2,6,0N,3,7.5,0E,1,2,1,1,0,1,1,1E,2,3,1,1,1,0,0,0NSUPT,1,3,0,0NSUPT,2,1,0,0ECHAR,12-1,5E+04ELOAD,2,3,16,0,1,90ELOAD,2,1,20,1,908.求图示铰接排架的内力.EI=1,EI=6(设横梁的EI=1,柱子的EA=)TITLE,AAA-8N,1,0,0NSUPT,1,6,0,0,0,0 N,2,6,0NSUPT,2,6,0,0,0,0N,6,6,7ECHAR,5,6,-1,1N,7,6,10ECHAR,7,8,-1,1 N,8,16,10ELOAD,6,1,20,1/3,90N,9,16,7E,1,4,1,1,1,1,1,0E,2,5,1,1,1,1,1,1E,3,9,1,1,1,1,1,1E,5,6,1,1,1,1,1,1E,6,7,1,1,1,1,1,0E,9,8,1,1,1,1,1,0E,4,5,1,1,0,1,1,0E,7,8,1,1,0,1,1,0例9.计算图示两层刚架的自振频率和主振型横梁的均布质量m=m=15X10kg/m柱子的抗弯刚度EI=1X10kn.m设EA=TITLE,AAA-9N,1,0,0N,2,4,0N,4,4,3N,5,0,6N,6,4,6E,1,3,1,1,1,1,1,1E,3,5,1,1,1,1,1,1E,2,4,1,1,1,1,1,1E,4,6,1,1,1,1,1,1E,3,4,1,1,1,1,1,1E,5,6,1,1,1,1,1,1NSUPT,1,6,0,0,0,0NSUPT,2,6,0,0,0,0ECHAR,1,4,-1,1E+08,1E-08ECHAR,5,6,-1,-1,1.5E+04FREQ,2,1,0.0005(注:柱子的质量不能填0,可填一个很小的数,如10)10.对图示两跨四层框架结构,分别计算竖向荷载和水平荷载作用下的内力.各杆的EA、EI值见下表:框架梁柱计算参数表截面弹性模量惯性矩EAEI构件A=bXh(m)E(kn/m)I(m)(kn)(kn-m)底层梁其它层0.25X0.52.8X100.521X100.350X101.459X10底边柱0.4X0.43X100.213X100.480X100.639X10层中柱3X100.342X100.608X101.026X10柱其边柱0.4X0.42.8X100.213X100.448X100.596X10它层中柱2.8X100.342X100.567X100.958X10TITLE,AAA-10N,1,0,0水平荷载作用N,2,5.0,0NLOAD,4,1,8.05,0NGEN,1,3,1,3,1,0,4.5NLOAD,10,1,15.20,0NGEN,3,3,4,6,1,0,3NLOAD,13,1,19.10,0E,1,4,1,1,1,1,1,1竖向荷载作用EGEN,2,1,1,1ELOAD,13,3,19.30,0,1,9EGEN,3,1,3,3ELOAD,14,3,19.30,0,1,90 E,4,5,1,1,1,1,1,1ELOAD,15,3,19.30,0,1,90E,5,6,1,1,1,1,1,1ELOAD,16,3,19.30,0,1,90NSUPT,1,6,0,0,0,0NLOAD,4,1,53.79,-90NSUPT,2,6,0,0,0,0NLOAD,7,1,53.79,-90NSUPT,3,6,0,0,0,0NLOAD,10,1,53.79,-90 ECHAR,1,1,4.8E+06,6.39E+04NLOAD,6,1,53.79,-90 ECHAR,2,2,6.08E+06,10.26E+04NLOAD,9,1,53.79,-90 ECHAR,3,3,4.8E+06,6.39E+04NLOAD,12,1,53.79,-90 ECHAR,4,4,4.48E+06,5.96E+04NLOAD,5,1,71.97,-90 ECHAR,6,6,4.48E+06,5.96E+04NLOAD,8,1,71.97,-90 ECHAR,7,7,4.48E+06,5.96E+04NLOAD,11,1,71.97,-90 ECHAR,9,9,4,48E+06,5.96E+04NLOAD,13,1,44.08,-90 ECHAR,10,10,4.48E+06,5.96E+04NLOAD,15,1,44.08,-90 ECHAR,12,12,4.48E+06,5.96E+04NLOAD,14,1,50.86,-90ECHAR,8,8,5.67E+06,9.58E+04 ECHAR,11,11,5.67E+06,9.58E+04 ECHAR,13,14,3.75E+06,15.63E+04 ECHAR,15,20,3.50E+06,14.59E+04。
6SigmaET练习教程 R13_求解器使用

案例三求解器使用一.案例描述6SigmaET具有非常强大的求解器,支持稳态、瞬态求解,层流、湍流模型,对流、热传导、热辐射、太阳辐射模型,焦耳热(电生热)模型等。
求解器并行效率高、收敛性良好,本例将在案例二的基础上讲解求解器的各种功能。
二.版本树功能6SigmaET的版本树是一个实用性很强的新功能,将您所有的设计方案整合成一个树状列表,保存在一个模型当中,而不必分散保存为单个文件。
各方案之间的从属关系一目了然。
建立风扇抽风的新方案我们在案例二的基础上建立新方案,点击结构树旁边的Version Tree即版本树,在原始方案上右键,点击Edit可以为原始方案更改名字或添加备注。
为了便于区分,我们把原始方案改名字为Flow in。
在原始方案上右键,可以看到有两种方式创建新方案,一种是创建Version,它与原始方案是从属关系,当原始方案中进行了改动,新建立的Version也会跟着改动。
另一种是创建Alternate,它与原始方案是并列关系,它和原始方案互不影响。
在此,我们以Alternate的方式建立新方案,并取名为Flow out。
此时会弹出一个提示框,询问是否要复制原始方案的结果。
一般地,当改动不大时,比如物体位置发生了微调、更改了功耗等情况,可以复制原来的结果并继续算。
而像这种进风改为了出风的情况属于改动比较大的,选择No,然后重新算就可以了。
此时,可以看到新方案的图标是蓝色的,说明现在被激活的是新方案,现在视图区显示的是新方案。
在哪个方案的图标上双击可以切换方案,图标为蓝色的方案处于激活状态。
此时,点击Model Tree,即进入新方案的结构树,选中风扇并在其属性里将风向切换为Out,即向外抽风。
然后点击计算按钮开始计算。
查看新方案结果观察变量稳定并且残差收敛后,计算完成。
显示PCB图层的温度。
对比不同方案结果在Result菜单里有一个功能是将多个方案的结果在同一个窗口中进行比较,点击Result >> Compare Model。
结构力学求解器使用指南
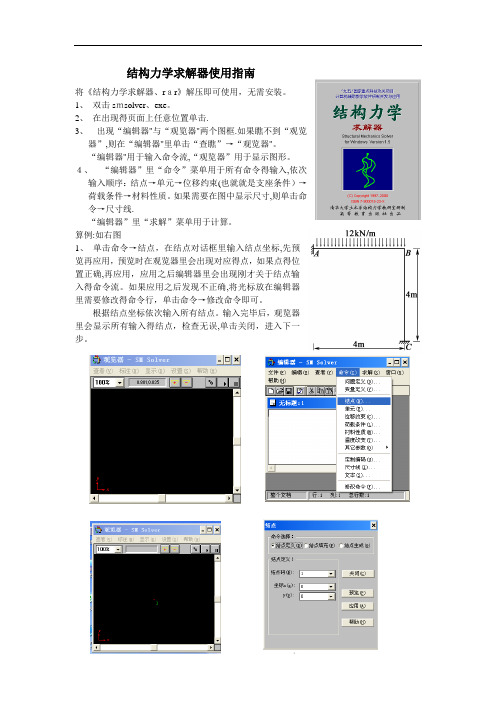
结构力学求解器使用指南将《结构力学求解器、rar》解压即可使用,无需安装。
1、双击smsolver、exe。
2、在出现得页面上任意位置单击.3、出现“编辑器"与“观览器"两个图框.如果瞧不到“观览器”,则在“编辑器"里单击“查瞧”→“观览器"。
“编辑器"用于输入命令流,“观览器”用于显示图形。
4、“编辑器”里“命令”菜单用于所有命令得输入,依次输入顺序:结点→单元→位移约束(也就就是支座条件)→荷载条件→材料性质。
如果需要在图中显示尺寸,则单击命令→尺寸线.“编辑器”里“求解”菜单用于计算。
算例:如右图1、单击命令→结点,在结点对话框里输入结点坐标,先预览再应用,预览时在观览器里会出现对应得点,如果点得位置正确,再应用,应用之后编辑器里会出现刚才关于结点输入得命令流。
如果应用之后发现不正确,将光标放在编辑器里需要修改得命令行,单击命令→修改命令即可。
根据结点坐标依次输入所有结点。
输入完毕后,观览器里会显示所有输入得结点,检查无误,单击关闭,进入下一步。
2、单击命令→单元,出现单元对话框,单元连接结点为第一步结点定义时所输入得结点码,一般就是计算机自动生成得,也就就是观览器中显示得阿拉伯数字,连接结点方式按实际输入,在相应下拉按钮选择.按照原图依次输入所有单元。
输入完毕后,观览器里会显示所有输入得单元,检查无误,单击关闭,进入下一步。
3、单击命令→位移约束,出现位移约束对话框,约束类型分为结点约束与杆端约束,选择结点约束时,需要输入相应得结点支座信息,其中结点码为观览器中得阿拉伯数字编码,支座类型为对话框上方六种类型,按照实际类型选择相应得数字,支座性质分为刚性与弹性,一般选择刚性,弹性支座就是指弹簧之类刚度为有限值得支座。
支座方向从下拉按钮中选择,0度表示与对话框上方支座类型图示方向相同,逆时针转为正值方向,(水平、竖向、转角)位移为实际支座移动值。
运动学辅助分析5.6求解器的使用2010ok.

刚体系运动学计算机辅助分析
• 前言 • 刚体系的位形描述,约束方程 • 运动学的计算机辅助分析基础 • 常见平面运动约束的约束方程 • 理论力学问题求解器的使用
理论力学CAI 版权所有, 2000 (c) 上海交通大学工程力学系
理论力学问题求解器 的使用
• 平面机械系统运动学模型的定义
• 公共基位置的确定
– 系统参数
• 模型定义
– 仿真计算
• 后台计算 • 结果的演示与输出
– 帮助
2018年11月3日 理论力学CAI 运动学计算机辅助分析 14
理论力学问题求解器的使用/界面/封面
• 理论力学问题求解器封面1
2018年11月3日 理论力学CAI 运动学计算机辅助分析
15
理论力学问题求解器的使用/界面/封面
• 运动学仿真主菜单
– 文件管理 – 图形操作
– 系统参数
– 仿真计算 – 帮助
2018年11月3日 理论力学CAI 运动学计算机辅助分析
18
理论力学问题求解器的使用/界面/主菜单/文件管理
• 文件管理
– 力学模型的定义与运算结果是以文件的形式储存与调用 – 运动学仿真文件的扩展名为(*.xyy) – 子命令
2018年11月3日
–不限制问题的参数
4
理论力学CAI 运动学计算机辅助分析
理论力学问题求解器的使用/概要
后处理界面:动画 可视化力学模型 定义界面
2018年11月3日 理论力学CAI 运动学计算机辅助分析
5
理论力学问题求解器的使用/概要
后处理界面:数据表
2018年11月3日 理论力学CAI 运动学计算机辅助分析
x y
结构力学求解器使用说明书(连星耀)

结构力学求解器 V2.0.2使用说明书把繁琐交给求解器,我们留下创造力结构力学求解器(Structural Mechanics Solver,简称SM Solver)是一个面向教师、学生以及工程技术人员的计算机辅助分析计算软件,其求解内容包括了二维平面结构(体系)的几何组成、静定、超静定、位移、内力、影响线、自由振动、弹性稳定、极限荷载等经典结构力学课程中所涉及的一系列问题,全部采用精确算法给出精确解答。
本软件界面方便友好、内容体系完整、功能完备通用,可供教师拟题、改题、演练,供学生作题、解题、研习,供工程技术人员设计、计算、验算之用。
也是一个作图和演示的工具。
SM Solver的操作方法与主要功能简介如下:1、在桌面上点击图标:2、再点击图标:3、同时弹出“观览器”与“编辑器”4、点击观览器中“查看/颜色”,弹出“调色板”5、在调色板中,选择“暂时采用黑白色”并“确定”,观览器背景变成白色。
6、在编辑器的“命令”下拉菜单中,依次:(1)点击“问题定义”,为文件命名;(2)点击“结点”,为问题确定全部结点坐标;(3)点击“单元”,确定各单元的链接方式;(4)点击“位移约束”,为结构加上相应约束;(此时在“编辑器”中的“求解”下拉菜单中,点击“几何组成”,可进行自动求解;点击“几何构造”,可得到智能求解结果。
)(5)点击“荷载条件”,给结构加上外力;(此时在“编辑器”中的“求解”下拉菜单中,点击“内力计算”,可在“观览器”中显示静定结构的内力图)(6)点击“材料性质”,输入各单元的拉压刚度EA与弯曲刚度EI;(此时在“编辑器”中的“求解”下拉菜单中,点击“内力计算”,可得静定或超静定结构的内力图;点击“位移计算”,可得静定或超静定结构的位移图。
)(7)点击“其它参数/影响线”,选择影响线的类型与截面位置;(此时在“编辑器”中的“求解”下拉菜单中,点击“影响线”,在“观览器”中可得静定或超静定结构的影响线)。
微软数学求解器 用法 -回复

微软数学求解器用法-回复微软数学求解器是一款强大的数学问题解答工具,它可以帮助用户快速解决各种数学难题。
本文将详细介绍微软数学求解器的用法,并提供一些实际案例来演示其具体操作步骤。
让我们一起来探索吧!第一步:下载与安装要使用微软数学求解器,首先您需要在您的设备上下载与安装这个应用程序。
它可以在Windows操作系统中的Microsoft Store应用商店中找到。
在搜索栏中键入“微软数学求解器”,点击安装即可。
安装完成后,您可以在应用程序列表中找到并打开它。
第二步:输入问题一旦您打开了微软数学求解器,您将看到一个界面,您可以在这里输入您要解决的数学问题。
您可以键入问题的文本描述,也可以直接输入方程、不等式或其他数学表达式。
请确保输入的数学表达式格式正确,以确保求解器能够准确解析它们。
第三步:选择解题方法微软数学求解器提供了多种不同的解题方法,可满足不同类型的问题需求。
在您输入问题后,您将看到一个下拉菜单,其中列出了各种可用的解题方法。
您可以根据题目的特点和您的偏好选择其中的一个。
以下是一些常见的解题方法选项:1. 方程求解:用于求解方程式,可以直接得出方程的解。
这对于需要确定未知数的特定值的问题非常有用。
2. 函数图像绘制:可以绘制函数的图像,以便更好地理解函数的行为和特点。
3. 数列求和:用于计算数列之和。
通过输入数列的公式和范围,求解器可以计算出数列中所有项的和。
4. 统计学计算:提供各种统计学计算方法,包括平均数、标准差和相关系数等。
这对于统计数据的分析非常有用。
5. 三角函数:用于求解三角函数相关的问题,例如求解三角方程或计算三角函数的值。
6. 微积分:提供微积分计算的工具,包括导数、积分和极限等。
这对于解决与变化率、面积和曲线相关的问题非常有用。
第四步:获取结果一旦您选择了解题方法,微软数学求解器将快速计算并生成结果。
结果通常以多个步骤的形式呈现,以便您了解问题的解决过程。
您将获得一个或多个答案,以及每个步骤的详细说明。
求解器使用手册

求解器使用手册该求解器(HTSolver)配普通高等教育“十一五”国家级规划教材赵镇南编《传热学》(第二版)使用。
版权属于作者所有。
这是一套完全自主研制的传热学习题解题软件,在国内是第一个,也是唯一的一个。
它具有强大的计算功能和与传热学教材紧密配合的众多辅助功能,其用法符合一般的思维习惯,因而简单易学。
尤其在处理比较复杂的复合传热问题,必须做迭代计算的问题(包括正常问题的逆向求解),以及本教材习题中大量需要进行变参数分析或参数优选的问题时,它的优点显得格外突出。
它的基本功能和特点可以归纳为:⏹建立了很多基本类型问题的数学模型-计算模板,可供直接套用。
⏹用户可以自主扩展、增添新的模型,从而拓宽软件的应用范围。
⏹对迭代计算的问题,既可以手动迭代(即看到迭代过程中每一步得出的数值),也可以全自动迭代,一键得出迭代结果。
⏹对肋效率、角系数、温差修正系数和黑体辐射函数等常用的图表,均实现了数字化,免除了查图表的麻烦,同时自变量取值范围加宽,计算精度也大幅提高。
⏹提供常用介质的物性子程序,免除了手工插值计算的麻烦。
⏹具备传热学常用数学辅助计算工具,如求解超越方程和高次方程,线性代数方程组,数值积分等。
HTSolver的主界面如下图所示,所有计算工作均围绕计算表进行。
计算表本质上是一个行数可以任意扩展的计算程序。
一般按照与手工计算相同或相近的思路逐步写出计算过程即可。
对于需要迭代求解的问题,可以用人工方式一步步地进行,也可以设置一个循环回路,迭代过程将自动进行。
迭代初值原则上没有限制,不违反物理规律即可。
计算表的构造设计如下:1.左第1栏为行号(编号)。
2.第2栏为说明文字,对计算过程无实质性影响,只为本人或者其他人日后容易看明白,可以省略。
3.第3栏为“目标量”,即对每个变量(常数或计算式)赋予一个名字。
注意该变量名是区分大小写的,即认为大写A与小写a不是同一个量。
4.第4栏“计算式”中,写入给定常量或者所采用的计算公式。
科学计算器求解x方程的方法

科学计算器求解x方程的方法
科学计算器一般有多种求解方程的方法:
1.直接代数求解:输入方程,然后使用代数运算按钮,如加减乘除和平方,次方等运算,最后用等于号得出方程的解。
2.数值逼近法:输入方程,选择数值逼近解法,如牛顿切线法,割线法等,然后输入初值,计算出方程的数值解。
3.方程求解器:一些科学计算器有内置的方程求解器,可以输入方程以及需要解的变量,然后得出方程的解。
4.矩阵求解法:如果方程有多个未知量,可以将方程用矩阵的形式表示,然后使用矩阵求解器求解矩阵方程。
需要注意的是,科学计算器是工具,使用方法需要根据具体情况选择适合的方法。
对于高阶方程或者复杂的方程组,可能需要使用更为专业的数学软件来求解。
excel规划求解在哪里

excel规划求解在哪里在Excel 中,规划求解器是一个附加工具,用于解决各种优化问题,如线性规划、整数规划等。
以下是如何启用和使用规划求解器的步骤:启用规划求解器:1. 打开Excel。
2. 在Excel 菜单栏中,选择"文件"。
3. 点击"选项"。
4. 在"Excel 选项" 对话框中,选择"附加组件"。
5. 在"管理" 下拉菜单中,选择"Excel 附加组件",然后点击"转到"。
6. 在"可用组件" 列表中找到"求解器",勾选它,然后点击"确定"。
7. 你可能需要安装求解器,按照提示进行操作。
使用规划求解器:1. 在Excel 中打开包含你要解决问题的工作表。
2. 在Excel 菜单中,选择"数据"。
3. 在"数据工具" 组中,你应该能够看到"规划求解器"。
4. 点击"规划求解器"。
5. 在"规划求解器" 对话框中,你需要设置以下参数:-目标单元格:输入你的目标函数所在的单元格。
-调整单元格:输入你要调整的变量单元格。
-调整单元格的变化范围:输入变量的可变范围。
-最小化/最大化:选择你的问题是最小化还是最大化。
6. 点击"确定" 开始求解。
请注意,规划求解器通常用于解决一些复杂的优化问题,涉及到线性规划、非线性规划等。
如果你的问题不是这类问题,可能并不需要使用规划求解器。
如果你需要解决其他类型的问题,你可能需要查看Excel 中其他功能和工具。
结构力学求解器使用指南

结构力学求解器使用指南结构力学求解器使用指南将《结构力学求解器.rar》解压即可使用,无需安装。
1. 双击smsolver.exe。
2. 在出现的页面上任意位置单击。
3. 出现“编辑器”和“观览器”两个图框。
如果看不到“观览器”,则在“编辑器”里单击“查看”→“观览器”。
“编辑器”用于输入命令流,“观览器”用于显示图形。
4. “编辑器”里“命令”菜单用于所有命令的输入,依次输入顺序:结点→单元→位移约束(也就是支座条件)→荷载条件→材料性质。
如果需要在图中显示尺寸,则单击命令→尺寸线。
“编辑器”里“求解”菜单用于计算。
算例:如右图1. 单击命令→结点,在结点对话框里输入结点坐标,先预览再应用,预览时在观览器里会出现对应的点,如果点的位置正确,再应用,应用之后编辑器里会出现刚才关于结点输入的命令流。
如果应用之后发现不正确,将光标放在编辑器里需要修改的命令行,单击命令→修改命令即可。
根据结点坐标依次输入所有结点。
输入完毕后,观览器里会显示所有输入的结点,检查无误,单击关闭,进入下一步。
2. 单击命令→单元,出现单元对话框,单元连接结点为第一步结点定义时所输入的结点码,一般是计算机自动生成的,也就是观览器中显示的阿拉伯数字,连接结点方式按实际输入,在相应下拉按钮选择。
按照原图依次输入所有单元。
输入完毕后,观览器里会显示所有输入的单元,检查无误,单击关闭,进入下一步。
3. 单击命令→位移约束,出现位移约束对话框,约束类型分为结点约束和杆端约束,选择结点约束时,需要输入相应的结点支座信息,其中结点码为观览器中的阿拉伯数字编码,支座类型为对话框上方六种类型,按照实际类型选择相应的数字,支座性质分为刚性和弹性,一般选择刚性,弹性支座是指弹簧之类刚度为有限值的支座。
支座方向从下拉按钮中选择,0度表示与对话框上方支座类型图示方向相同,逆时针转为正值方向,(水平、竖向、转角)位移为实际支座移动值。
按照原图依次输入所有支座。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求解器的使用FLUENT提供了三种不同的求解器Segregated,coupled implicit,coupled explicit(显式格式主要用于激波等波动解的捕捉问题)传统上,分离解法(segregated)主要用于不可压缩以及适度压缩的流动中。
相反,耦合算法是为高速可压流体设计的。
默认情况下,fluent使用分离求解器。
对于高速可压流体,与很强的体积力高度耦合的流动,或者是在非常精确的网格上求解流动情况,可以考虑使用耦合隐式算法代替。
对于需要使用耦合隐式算法(coupled implicit)的case,如果电脑没有足够的内存,可以使用分离解法(segregated)或者耦合显式算法(coupled explicit)代替。
(显示算法节约内存,但是需要更多的计算步数达到收敛。
)选择离散格式1.一阶迎风格式v.s. 二阶迎风格式当流动与网格匹配(校准)时,一阶迎风格式是可以接受的。
对于三角形和四面体网格,由于流动不会与网格匹配,通常使用二阶离散格式会得到更准确的结果。
对于四边形/六面体网格,使用二阶离散格式会取得更好的结果,尤其是复杂的流动情况。
对于大多数情况,可以在计算初始,使用二阶的离散格式。
然而在一些情况下,可以开始使用一阶的离散格式然后在一些计算之后转变为二阶格式。
例如,如果正在运行一个高马赫数的流动计算,这个的初始解与期望的解相差很大,最终,如果二阶离散格式很难收敛,应该尝试使用一阶离散格式。
2.Quick格式v.s. Upwind(Quick格式适用于网络结构,流动方向与网格一致,对于非结构网格推荐使用二阶迎风)对于在四边形或者六面体网格中的旋转或者回旋流,Quick离散格相比于二阶离散格式可以提供更准确的结果。
对于存在震动的可压缩流动(网格为四边形,六面体或者混合网格),推荐对所有的变量使用Quick离散格式,包括密度。
3.中心差分格式v.s. 迎风格式当使用LES湍流模型时,是可以使用中心差分格式的,并且只有当网格间距足够好,以至于局部的Peclet数的大小小于1时才可以使用。
4.power法则(power law)v.s. 迎风power法则是可以使用的,但是总体上产生与一阶格式相同的准确度选择压力离散格式当使用分离式求解器时(segregated),可以使用多种压力离散格式。
在大多数情况下,(默认的)标准的格式是可以接受的,但是一些类型的模型会在其他格式中取得更好的结果:对于包含大的体积力的问题,推荐使用体积力重量(body-force-weighted)格式。
对于包含高的漩涡数,高瑞利数的自然对流,高速的旋转流动,包含多孔介质的流动,在高度弯曲区域中的流动,使用PRESTO!格式对于可压流,应使用二阶格式当其他格式并不合适时,使用二阶格式以提高准确性。
选择密度离散格式(求解一个单相可压流动)如果计算一个含有震动的可压流动时,一阶迎风格式可以平滑震动;对于这样的流动,应该使用二阶迎风或者Quick格式选择压力——速度方程耦合方法(Pressure-velocity coupling Method)SIMPLE v.s. SIMPLECSIMPLE是默认的,但是大多数情况下,使用SIMPLEC是更好的。
对于相对简单的问题(层流流动,没有激活额外的模型),收敛只受到压力——速度的限制,使用SIMPLEC可以更快的得到收敛解。
使用SIMPELC,压力松弛因子大多设置为1,以加快收敛速度。
然而在一些问题中,增加压力修正松弛因子到1,由于高的网格偏斜度(grid skewness)可以导致不稳定。
对于某些情况下,需要使用一个或者多个偏斜度修正格式,使用稍微更收敛的松弛因子(0.7),或者使用SIMPLE算法。
SIMPLE偏斜度修正允许FLUENT在偏斜的网格中得到解(而所需的计算数目与较直的网格大致相同)。
PISO(Pressure-Implicit with Splitting of Operators)当计算瞬态流动时,推荐使用含有临近修正的PISO算法,特别是当你想使用一个比较大的时间步长时。
(如包含LES湍流模型的问题,通常是需要小的时间步长的,使用PISO算法会导致增加计算消耗,所以考虑使用SIMPLE或者SIMPLEC算法代替)。
PISO算法可以在大的时间不长时,保持稳定的计算,并且保持动量和压力的松弛因子为1。
对于稳态问题,包含临近修正的PISO算法,相比于使用最佳的松弛因子时的SIMPLE或者SIMPLEC算法,并不会提供明显的优势。
当使用邻近修正的PISO算法时,推荐设置所有方程的松弛因子为1或者接近1,如果仅仅对高度扭曲的网格使用PISO偏斜(skewness)修正,设置动量和压力的松弛因子,保证其和为1。
(例如压力为0.3,动量为0.7)。
如果使用两种PISO方法(PISO neighbor correction 和PISO skewness correction),遵照以上对PISO neighbor correction的建议。
分步方法(Fractional Step Method)当使用NITA格式时,分步方法(FSM)是可以选择的。
相比于PISO算法,FSM的计算消耗稍小。
对于某些问题(如利用VOF进行模拟),FSM不如PISO稳定。
在大多数情况下,solution control中的默认值在由于偏斜产生的内部压力校正中分布中足够设置健壮收敛。
只有在非常复杂的流动问题中(如变形网格,滑移界面,VOF模型),才需要减小压力的松弛因子至0.7或者0.8.设置松弛因子——最重要的是压力和动量松弛因子松弛因子控制每一次计算中变量的变化。
越小的松弛因子,计算越稳定,但是更难收敛最好是开始计算时使用默认的松弛因子,如果残差在4或者5步之后继续增加,那么在降低松弛因子。
对于大多数的流动,默认的松弛因子值不需要修改。
如果不稳定或者出现差异,需要对压力、动量、k,e的松弛因子进行修正,将其从默认值减小到0.2,0.5,0.5和0.5。
当问题中,密度与温度强烈耦合时,以及在高的瑞利数下的自然或者混合对流时,也需要对温度方程或者密度方程的松弛因子进行调整(如使用小于1的松弛因子)。
相反,如果温度与动量方程不耦合(或者耦合不是那么剧烈),当流动过程中密度保持不变时,温度的松弛因子可以设定为1。
对于其他的标量方程(如漩涡,组分,混合物分数和变化),对于非迭代的默认的solution control中的松弛因子可能会过大(对某些问题),特别是在计算的初始时。
可以降低因子至0.8已达到收敛。
其他的应用改变库兰数(Courant Number)1.对于耦合显示算法中的库兰数:总的来说,对于库兰数为0.25,假设多级格式是稳定的。
对于耦合的显示求解器,默认的CFL值是1.0,但是对于某些2D问题,可以增加该值。
总体来说,不能使用高于2.0的值。
如果你的解分离的,并且你的问题的建立与初始化都是合适的,这表明你的库兰数需要降低。
依赖于你的初始条件的苛刻度,可能需要降低CFL到0.1-0.5,在开始计算。
2.对于耦合的隐式算法:对于耦合的隐式算法,默认的CFL值为5.0,通常会增加到10,20,100或者更高,这依赖于问题的复杂性。
多重网格基本原理:微分方程的误差分量可以分为两大类,一类是频率变化较缓慢的低频分量;另一类是频率高,摆动快的高频分量。
一般的迭代方法可以迅速地将摆动误差衰减,但对那些低频分量,迭代法的效果不是很显著。
高频分量和低频分量是相对的,与网格尺度有关,在细网格上被视为低频的分量,在粗网格上可能为高频分量。
多重网格方法作为一种快速计算方法,迭代求解由偏微分方程组离散以后组成的代数方程组,其基本原理在于一定的网格最容易消除波长与网格步长相对应的误差分量。
该方法采用不同尺度的网格,不同疏密的网格消除不同波长的误差分量,首先在细网格上采用迭代法,当收敛速度变缓慢时暗示误差已经光滑,则转移到较粗的网格上消除与该层网格上相对应的较易消除的那些误差分量,这样逐层进行下去直到消除各种误差分量,再逐层返回到细网格上。
FLUENT 中有四种多重网格循环:V,W,F 以及灵活("flex")循环。
V 和W 循环可以用在AMG 和FAS 中,F 和灵活循环只限用于AMG 方法。
(W 和灵活AMG 循环由于要花费大量的计算而不可用于解耦合方程组。
),F 循环比V 循环需要更多的计算,但是比W 循环花费要少一些。
但是它的收敛性比V 循环要好,大致和W 循环的收敛性差不多。
对于耦合求解器设置来说,F 循环是默认的AMG 循环类型。
灵活循环和V,W 循环之间的主要区别是:灵活循环会通过残差减小的公差和终止判据的满足情况来确定什么时候,按什么样的频率来处理每一层网格,而V 和W 循环则明确定义了各个层面之间的转换模式。
灵活循环:当前层面的误差减小速度不够快时,多重网格程序就会调用下一个网格层面的计算(restriction)。
B 的值控制了处理的粗化网格层面的频率。
默认值是0.7。
如果b 的值较大,就会处理较小的频率,反之亦然。
当校正解的误差减小到该网格层初始误差的某一分数a(在0 和1 之间)时,当前网格层上的校正方程就可以被认为是充分收敛了。
参数a 被称为终止判据(termination)。
默认值是0.1。
FAS 优于AMG 方法的地方在于,对于非线性问题前者可以做得更好,这是因为系统的非线性可以通过重新离散传到粗糙层面;当使用AMG 时,一旦系统被线化,直到细化层面算子被更新,求解器才会“感觉到”非线性。
打开FAS多网格FAS多网格是耦合显式求解器中的可选选项。
对于大多数的问题,可以以4个或者5个水平开始。
对于大型的3d问题,可以增加水平。
如果认为多网格会造成收敛问题,可以降低水平数。
解的初始化可以对整个流动区域初始化,也可以在选定的cells中patch值对于多相流中强的体积力的特殊处理:1.冻结通量格式(Frozen Flux Formation),这个选项只有在使用分离迭代求解器处理单相瞬时问题中(并且不包含移动/变形网格模型),才可以使用。
2.时间增长格式包含两种形式:迭代时间增长格式(这个迭代格式是FLUENT中默认的),非迭代的时间增长格式:(FLUENT中提供两个版本的NITA格式):非迭代的分步方法(non-iterative fractional step method)和非迭代的PISO方法。
用残差光顺的方法增加库朗数在Solution Controls(求解过程控制)面板中,残差光顺的迭代值在缺省设置中被设定为0,即在缺省设置中没有使用残差光顺技术。
如果将Iterations(迭代计数器)增加为1或更大的数,则可以进一步设置Smoothing Factor(光顺因子)。
