2020年考研数学函数图像大全
经典数学函数图像大全
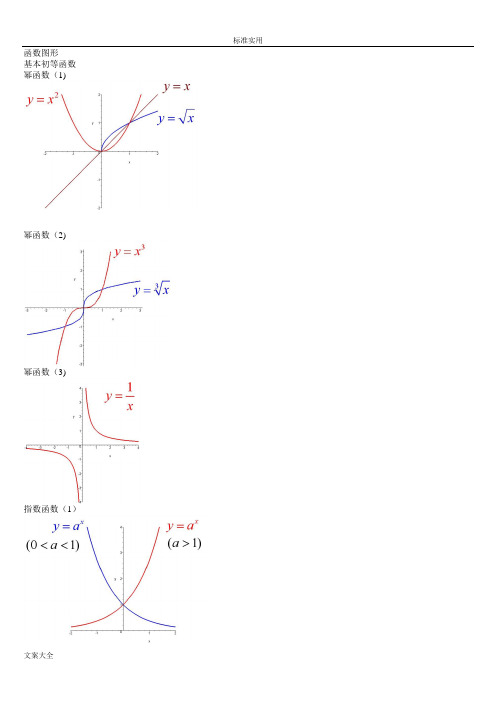
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
经典数学函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
2020年(考研高数)基本初等函数图像与性质
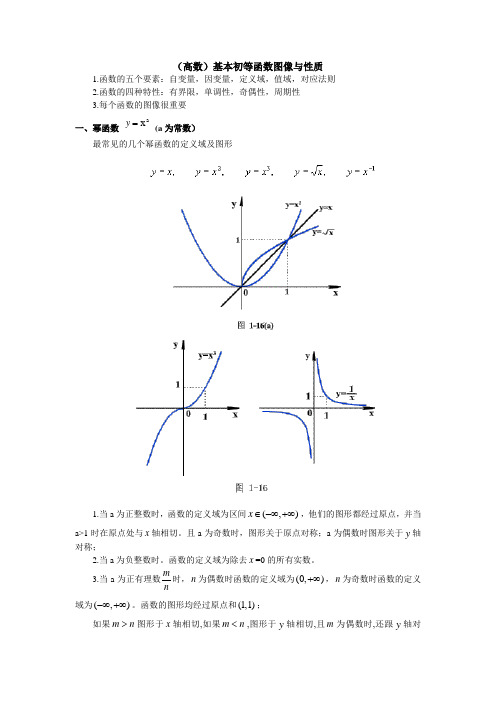
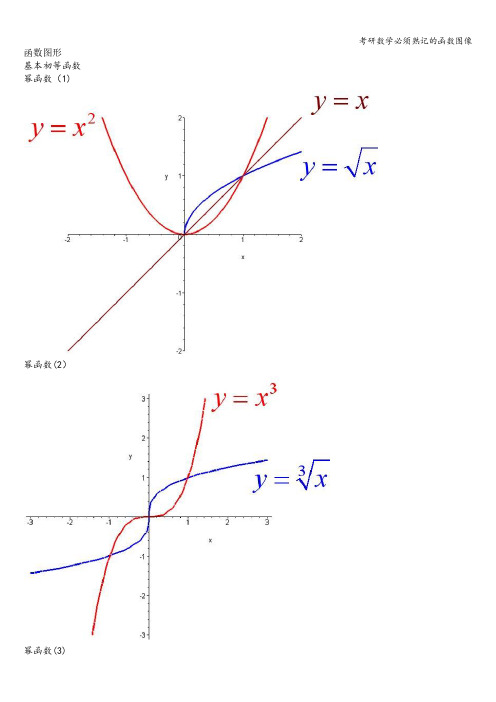
(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n 时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n均为奇数时,跟原点对称。
4.当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y , 余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数 反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数xy arctan=,),(+∞-∞∈x,)2,2(ππ-∈y,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ :捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔IotaΚκ:喀帕Kappa ∧λ:拉姆达LambdaΜμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron ∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:fai PhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
考研数学函数图像大全

函数图形基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)等价无穷小(x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)。
(整理)考研数学函数图像大全
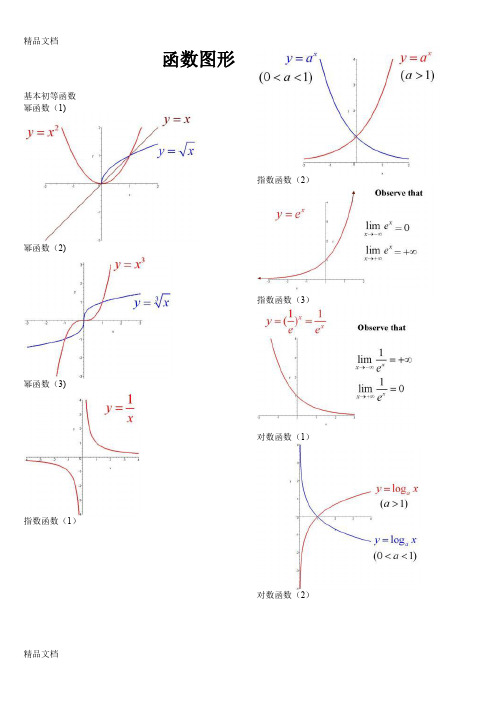
函数图形基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)等价无穷小(x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1) 夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2)。
经典数学函数图像大全-数学函数图像-函数图像全
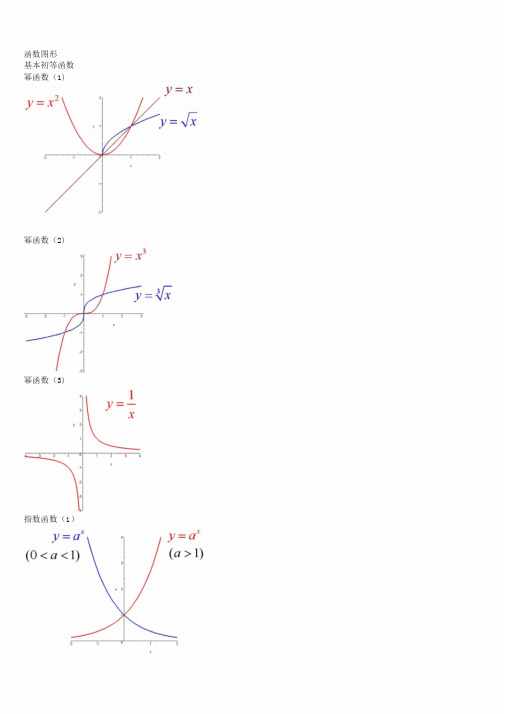
函数图形基本初等函数幂函数(1)幂函数(2) 幂函数(3) 指数函数(1)指数函数(3)对数函数(1)对数函数(2)三角函数(2)三角函数(3)三角函数(4)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(5)反三角函数(6)反三角函数(7)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(6)y=sin(1/x)(1) y=sin(1/x)(2)WOIRD格式y=[1/x](2 )y=sin(1/x)(3)y=sin(1/x)(4)y=[1/x](1)y=21/xy=21/x(2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx(x->∞)绝对值函数y=|x| 符号函数y=sgnx 取整函数y=[x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1)(局部保号性) 极限的性质(2)(局部保号性)极限的性质(3)(不等式性质) 极限的性质(4)(局部有界性) 极限的性质(5)(局部有界性)两个重要极限y=sinx/x(1)y=sinx/x(2)limsinx/x的一般形式y=(1+1/x)^x(1)y=(1+1/x)^x(2)lim(1+1/x)^x的一般形式(1) lim(1+1/x)^x的一般形式(2) lim(1+1/x)^x的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线WOIRD格式y=(x+1)/(x-1)数列的夹逼性(1) y=sinx/x(x->∞)数列的夹逼性(2) 夹逼定理(1)夹逼定理(2)。
考研数学必须熟记的函数图像
考研数学必须熟记的函数图像函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6) y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4) y = [1/x](1)y = [1/x](2) y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x—〉∞)绝对值函数 y = |x|符号函数 y = sgnx 取整函数 y= [x]极限的几何解释(1)极限的几何解释 (2)极限的几何解释 (3)极限的性质(1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2) limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于x tanx等价于xarctanx等价于x1-cosx等价于x^2/2 sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x—〉∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性 (2)。
经典数学函数图像(大全)

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线,其一般形式为 y = mx + b,其中 m是斜率,b 是 y 轴截距。
当 m > 0 时,直线向上倾斜;当 m < 0 时,直线向下倾斜。
2. 二次函数图像二次函数图像是一个抛物线,其一般形式为 y = ax^2 + bx + c,其中 a、b、c 是常数。
当 a > 0 时,抛物线开口向上;当 a < 0 时,抛物线开口向下。
3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。
正弦函数图像是一条波动曲线,余弦函数图像与正弦函数图像相似,但相位差为π/2。
正切函数图像是一条周期性振荡的曲线。
4. 指数函数图像指数函数图像是一条上升或下降的曲线,其一般形式为 y = a^x,其中 a 是底数,x 是指数。
当 a > 1 时,曲线上升;当 0 < a < 1 时,曲线下降。
5. 对数函数图像对数函数图像是一条上升或下降的曲线,其一般形式为 y =log_a(x),其中 a 是底数,x 是真数。
当 a > 1 时,曲线上升;当0 < a < 1 时,曲线下降。
6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线,而双曲正切函数图像是一条周期性振荡的曲线。
7. 幂函数图像幂函数图像是一条上升或下降的曲线,其一般形式为 y = x^n,其中 n 是指数。
当 n > 0 时,曲线上升;当 n < 0 时,曲线下降。
8. 反比例函数图像反比例函数图像是一条双曲线,其一般形式为 y = k/x,其中 k是常数。
当 k > 0 时,曲线位于第一和第三象限;当 k < 0 时,曲线位于第二和第四象限。
经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数,包括反正弦函数、反余弦函数和反正切函数。
考研数学函数图像大全
y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于x1-cosx等价于x^2/2数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$$tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:正弦函数∙余弦函数∙正切函数∙余切函数∙正割函数∙余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:∙正弦函数∙余弦函数∙正切函数∙余切函数∙正割函数∙余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式4.2 和差化积公式。
十二种基本函数的图像

十二种基本函数的图像
十二种基本函数的图像
y=(x的绝对值+/-一个数字)的图像:v字形上下移动(上加下减);
y=(x+/-一个数)的绝对值的图像:v字形左右移动(左加右减);
y=(x^2)+/-一个数:抛物线上下移动(上加下减);
y=(x+/-一个数)^2:抛物线左右移动(左加右减);
y=根号下x的图像:关于x^2的图像以直线Y=x对称(只有第一象限);y=根号下(x+/-一个数):同上图左右移动(左加右减);
y=(根号下x)+/-一个数(2种):同上图上下移动(上加下减);
y=x^3的图像:关于原点对称的图像;
y=x^3(+/-一个数)的图像:y=x^3的图像上下移动(上加下减);
y=(x+/-一个数)^3的图像:y=x^3的图像左右移动(左加右减);
移动的距离为+/-一个数的单位长度。
扩展资料:
基本函数(初等函数)是由常函数、幂函数、指数函数、对数函数、三角函数和反三角函数经过有限次的有理运算(加、减、乘、除、有限次乘方、有限次开方)及有限次函数复合所产生、并且在定义域上能用一个方程式表示的函数。
一般来说,分段函数不是初等函数,因为在这些分段函数的定义域上不能用一个解析式表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y = [1/x](2)
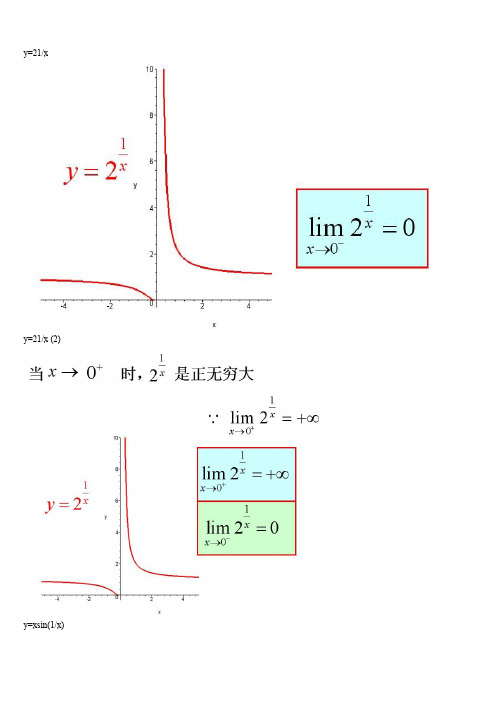
y=21/x
y=21/x (2)
y=xsin(1/x)
y=arctan(1/x)
y=e1/x
y=sinx (x->∞)
绝对值函数y = |x|
符号函数y = sgnx
取整函数y= [x]
极限的几何解释(1)
极限的几何解释(2)
极限的几何解释(3)
极限的性质(1) (局部保号性)
极限的的性质(4) (局部有界性)
极限的性质(5) (局部有界性)
两个重要极限
y=sinx/x (1)
y=sinx/x (2)
limsinx/x的一般形式
y=(1+1/x)^x (1)
y=(1+1/x)^x (2)
lim(1+1/x)^x的一般形式(1)
基本初等函数
幂函数(1)
幂函数(2)
幂函数(3)
指数函数(1)
指数函数(2)
指数函数(3)
对数函数(1)
对数函数(2)
三角函数(1)
三角函数(2)
三角函数(3)
三角函数(4)
三角函数(5)
反三角函数(1)
反三角函数(2)
反三角函数(3)
反三角函数(4)
反三角函数(5)
反三角函数(6)
反三角函数(7)
y=sinx/x (x->∞)
夹逼定理(1)
夹逼定理(2)
数列的夹逼性(1)
数列的夹逼性(2)
lim(1+1/x)^x的一般形式(2)
lim(1+1/x)^x的一般形式(3)
等价无穷小(x->0)
sinx等价于x
arcsinx等价于x
tanx等价于x
arctanx等价于x
1-cosx等价于x^2/2
sinx等价于x
数列的极限的几何解释
海涅定理
渐近线
水平渐近线
铅直渐近线
y=(x+1)/(x-1)
反三角函数(8)
双曲函数(1)
双曲函数(2)
双曲函数(3)
双曲函数(4)
双曲函数(5)
双曲函数(6)
双曲函数(7)
反双曲函数(1)
反双曲函数(2)
反双曲函数(3)
反双曲函数(4)
反双曲函数(5)
反双曲函数(6)
y=sin(1/x) (1)
y=sin(1/x) (2)
y=sin(1/x) (3)
y=sin(1/x) (4)
