电力系统分析作业——电网节点导纳矩阵的计算机形成
14节点导纳矩阵

14节点导纳矩阵14节点导纳矩阵是描述电力系统中节点之间相互连接关系的一种数学工具。
本文将介绍14节点导纳矩阵的构成和作用,以及如何利用导纳矩阵进行电力系统分析。
导纳矩阵是描述电力系统中节点之间导纳关系的一种矩阵形式。
它由14行14列组成,每个元素表示对应节点之间的导纳值。
导纳是指电路元件对电流的响应程度,是电路的重要参数之一。
14节点导纳矩阵的构成是基于电力系统的拓扑结构和电路元件的导纳值。
拓扑结构描述了电力系统中各节点之间的连接关系,而电路元件的导纳值则代表了电路元件对电流的响应程度。
在14节点导纳矩阵中,对角线元素表示各节点的自导纳值,非对角线元素表示各节点之间的互导纳值。
自导纳值可以理解为节点本身的电流响应能力,而互导纳值则表示节点之间的电流传输能力。
利用14节点导纳矩阵可以进行电力系统的各种分析。
例如,可以通过求解导纳矩阵的特征值和特征向量来判断电力系统的稳定性。
特征值表示系统的固有频率,特征向量则表示系统的振荡模式。
导纳矩阵还可以用于计算电力系统中节点之间的电压和电流分布。
通过对导纳矩阵进行运算,可以得到各节点的电压和电流值,从而了解电力系统的工作状态。
除了稳定性分析和电压电流计算,导纳矩阵还可以用于故障分析和电力系统的优化设计。
在发生故障时,可以通过修改导纳矩阵中对应元素的值来模拟故障情况,并分析故障对电力系统的影响。
在电力系统的优化设计中,可以通过调整导纳矩阵中的元素值来改变电力系统的结构和参数,以达到提高电力系统效率和可靠性的目的。
14节点导纳矩阵是描述电力系统中节点之间导纳关系的重要工具。
它可以用于电力系统的稳定性分析、电压电流计算、故障分析和优化设计等方面。
通过对导纳矩阵的分析和运算,可以更好地了解和优化电力系统的工作状态。
3.3复杂电力网潮流计算的计算机解法

3.3复杂电力网潮流计算的计算机解法3.3.1 导纳矩阵的形成1.自导纳节点i的自导纳,亦称输入导纳,在数值上等于在节点i施加单位电压,其他节点全部接地时,经节点i注入网络的电流。
主对角线元素,更具体地说,就等于与节点连接的所有支路导纳的和。
2.互导纳节点i、j间的互导纳,在数值上等于在节点i施加单位电压,其他节点全部接地时,经节点j注入网络的电流。
非对角线元素。
更具体地说,是连接节点j和节点i支路的导纳之和再加上负号而得。
3.导钠矩阵的特点:(1)因为,导纳矩阵Y是对称矩阵;(2)导纳矩阵是稀疏矩阵,每一非对角元素是节点i和j间支路导纳的负值,当i和j间没有直接相连的支路时,即为零,根据一般电力系统的特点,每一节点平均与3-5个相邻节点有直接联系,所以导纳矩阵是一高度稀疏的矩阵;(3)导纳矩阵能从系统网络接线图直观地求出。
4.节点导纳矩阵的修改(1)从原有网络引出一支路,同时增加一节点,设i为原有网络结点,j为新增节点,新增支路ij的导纳为y ij。
如图3-17(a)所示。
因新增一节点,新的节点导纳阵需增加一阶。
且新增对角元Y jj=y ij,新增非对角元Y ij=Y ji=-y ij,同时对原阵中的对角元Y ii进行修改,增加ΔY ii=y ij。
(2)在原有网络节点i、j间增加一支路。
如图3-17(b)所示。
设在节点i增加一条支路,由于没有增加节点数,节点导纳矩阵Y阶次不变,节点的自导纳Y ii、Y jj和互导纳Y ij分别变化量为(3-57)图 3-17 网络接线的变化图(a)网络引出一支路,(b)节点间增加一支路,(c)节点间切除一支路,(d)节点间导纳改变(3)在原有网络节点i、j间切除一支路。
如图3-17(c)所示。
设在节点i切除一条支路,由于没有增加节点数,节点导纳矩阵Y阶次不变,节点的自导纳Y ii、Y jj和互导纳Y ij分别发生变化,其变化量为(3-58)(4)原有网络节点i、j间的导纳改变为。
节点导纳矩阵的形成

极坐标形式 Page-132 令:
P i P Gi P Di U i U j Gij cos ij Bij sin ij (4-43a) Qi QGi QDi U i U j Gij sin ij Bij cos ij (4-43b)
——雅克比矩阵对角元素的计算公式
为什么
没有i=j项
为什么 有2倍项
42
雅克比矩阵元素的特点
雅克比矩阵不对称 节点分块雅克比矩阵与节点导纳矩阵具有相同的结构 维数相同,稀疏结构相同(非零元的位置相同)
N11 L11 N n1 H1n 1 J U / U 1n 1 1 H nn n nn
0
f1 x2 f 2 x2 f n x2
0
0
0
0
0
0 0 x 1 f 2 0 ... x2 xn 0 x 0 n f n ... xn 0 f1 ... xn
j 1 j 1 n
Ui ei jfi
25
直角坐标形式:(P-129:式(4-36a),(4-36b)
4.2.1.2 功率方程中变量的分类
n节点系统 2n个 2n个 2n个
给定2n个扰动变量和2n个控制变量,则功率方程组可解吗?
26
4.2.1.2 功率方程中变量的分类 ——变量的约束条件
4.2.1.1 功率方程
——两节点系统功率方程的形成
等式两边取共轭乘电压,则得节点的注入功率方程:
网络的功率损耗等于所有节点注入功率的代数和,则:
电力系统网络矩阵

i
Yii
+
N
YNi
-
节点导纳矩阵表示短路参数。
在网络中节点i 接单位电压源,其余 节点都短路接地,此时流入节点i 的
电流数值上是Yii,流入节点j的电流
数值上是Yij。
注意:只有和节点i有支路相连的节点才有 电流,因此导纳矩阵是稀疏矩阵。节点导 纳矩阵的元素只包含网络的局部信息。
2011-1-1
高等电力网络分析
C2Z(0)C1
yaa1
zaa
za 0 z01z0a
2011-1-1
高等电力网络分析
14
3、追加树支支路
增加新节点q
部i 分 网
络j
a p
q 前 A0
A
A0 0T
ep 1q
后 y0
Y
A0 0T
ep y0
1
ya
0
y0a A0T
yaa
eTp
0 1
整理后可得
Z
Z(0) C2Z(0)
(Yn YpYpp1YpT )Vn In YpYpp1Ip
Y Yn YpYpp1YpT
i p
2011-1-1
j
i
k
j
消去节点p,只需对Y阵
中和p有支路相连的节
点之间的元素进行修正,
k
其他节点之间的元素不
需要修正。
高等电力网络分析
8
4、节点电压给定的情况
Yn YsT
Ys Yss
Vn Vs
部i
分
追加前:
网
a
络j
Y(0) A0z01A0T
追加后: Y A0
辅助矩阵求逆定理
M a
y0
节点导纳矩阵的计算机方法

节点导纳矩阵的计算机方法节点导纳矩阵的计算机方法什么是节点导纳矩阵节点导纳矩阵是在电力系统分析中常用的一种计算方法,用于描述系统中各个节点之间的电流传输关系。
它是一种由复数元素组成的方阵,可以通过矩阵运算来进行电力系统的计算和分析。
节点导纳矩阵的计算方法节点导纳矩阵的计算方法有多种,下面将介绍其中几种常用的方法。
拓扑法拓扑法是一种基于系统拓扑结构的计算方法,先通过系统的线路连接关系构建拓扑图,然后根据拓扑图来计算节点导纳矩阵。
具体步骤如下: 1. 根据系统的线路连接关系构建拓扑图; 2. 根据拓扑图确定系统的节点数和支路数; 3. 根据支路的参数(电阻、电抗)计算节点导纳矩阵的元素; 4. 构建完整的节点导纳矩阵。
潮流法潮流法是一种基于系统潮流计算的方法,通过计算系统中各个节点的电压和电流值来求解节点导纳矩阵。
具体步骤如下: 1. 根据系统的拓扑结构和支路的参数构建节点导纳方程组; 2. 根据节点导纳方程组进行潮流计算,求解各个节点的电压和电流值; 3. 根据节点的电压和电流值计算节点导纳矩阵的元素; 4. 构建完整的节点导纳矩阵。
传递函数法传递函数法是一种基于系统传递函数的计算方法,通过系统的传递函数来计算节点导纳矩阵。
具体步骤如下: 1. 根据系统的拓扑结构和支路的参数构建传递函数; 2. 根据传递函数计算节点导纳矩阵的元素; 3. 构建完整的节点导纳矩阵。
总结节点导纳矩阵的计算方法有拓扑法、潮流法和传递函数法等多种方法,每种方法都有其适用的场景和计算步骤。
在实际应用中,需要根据具体的电力系统分析问题选择合适的计算方法来计算节点导纳矩阵,以实现准确的分析和计算。
频域方法频域方法是一种基于系统频率响应的计算方法,通过系统在不同频率下的响应来计算节点导纳矩阵。
具体步骤如下: 1. 根据系统的拓扑结构和支路的参数构建频域模型; 2. 在不同频率下输入信号,并记录系统的输出响应; 3. 根据输入和输出信号的频域表达式计算节点导纳矩阵的元素; 4. 构建完整的节点导纳矩阵。
大工14秋《电力系统分析》在线作业1答案

大工14秋《电力系统分析》在线作业1
一,单选题
1. 电力线路始末端实际运行电压与线路额定电压的差值称为()。
A. 线损率
B. 电压调整
C. 电压降落
D. 电压偏移
?
正确答案:D
2. 医院属于()负荷。
A. 一级
B. 二级
C. 三级
D. 四级
?
正确答案:A
3. 节点导纳矩阵形成过程中,把变压器采用π形等值电路表示后,下列说法错误的是()。
A. 电网中存在阻抗支路
B. 电网中存在导纳支路
C. 电网中不存在理想变压器
D. 以上说法都不正确
?
正确答案:D
4. 环形网络中的无功功率分点通常是系统()。
A. 电流最低点
B. 电流最高点
C. 电压最低点
D. 电压最高点
?
正确答案:C
5. 功率方程中,每个节点有()个变量。
A. 7
B. 6
C. 5
D. 4
?
正确答案:B。
电力系统分析第一章

y430
4
y320 z34
y430
y340
i
yij = 1 ( k ji zij )
y40
yij 0 =
+ 1 1 = 2 k ji zij k ji zij
k ji − 1 k ji zij
∆Yij = − 1 k ji zij
y ji 0 =
1 − k ji k 2 zij ji
∆Yii =
Y13 = Y31 = Y14 = Y41 = Y15 = Y51 = Y25 = Y52 = Y45 = Y54 = 0
& I i = ( yi 0 + & = YiiU i +
j∈i , j ≠ i
∑
yij 0 + & YijU j
j∈i , j ≠ i
∑
& yij )U i +
j∈i , j ≠ i
1
& I1
y12
2
y23
3
y35
5
y120
y210
& I2
y230 y24 y420
3
y320 y34
& I3
y350
& I5
y530
y240
4 y y & I 4 y40 430 340
5
1
z12 1:k21
2
z23
k35 :1 z35
i
zij 1:k ji 1:k
j j
y230 z24 y240
y240
y420
4 y y & I 4 y40 430 340
Y11 = y120 + y12
电力系统三大计算例题

简单电力系统如图16-8所示,各元件的参数及初始运行情况均按照例16-1和例16-2给定的条件。
假定在输电线路之一的始端发生了两相接地短路,线路两侧开关经0.1s 同时切除,试计算极限切除角lim ⋅c δ,并用分段计算法计算转子摇摆曲线和极限切除时间lim ⋅c t ,判断系统能否保持暂态稳定性。
图 1发电机:S GN =352.5MVA ,P GN =300MW ,V GN =10.5kV ,x d =1.0,x q =0.6, 25.0='d x ,2.0 2=x ,s T JN 8 =。
变压器: 1-T MVA S TN 3601=,14%1=ST V ,242/5.10 1=T k ;2-T 3602MVA S TN =,14% 2=ST V ,110/2202=T k 。
线路: 250km l =,km x L /41.0 Ω=,kV V N 220=。
运行条件: 1150kV V =,MW P 2500=,95.0cos 0=ϕ。
解题思路:mIImIII mII cr mIII cr c P P P P P -δ-δ+δ-δ=δ-⋅0001lim cos cos )(cos (17-6)1. 求对应三种情况的等值电路和等值参数X I X II X III图 22. 对应的功率特性, 得到P mII 和P mIII δ0 和δcr3. 求极限切除角4. 分段法求 δ( t ), 直到δ=δc.lim解:93.2586.055X 19.007.95.105.3522502.0o L 222)(222=⨯===⨯⋅==L I B GN GN B G X V V S S x X 由例16-1的计算已知原始运行参数及网络的参数:P T =P 0=1.0, 54.31,47.1000=='='δδ E (一)计算功角特性(1)正常运行时。
在此情况下可作系统的等值电路,如图2(a)所示。
电力系统分析实验讲义稳态

电力系统分析(上)实验讲义实验一:节电导纳矩阵的形成一.实验目的掌握节点导纳矩阵形成的方法二.实验学时:2学时 三.实验原理与方法n 个独立节点的网络,n 个节点方程 B Y U I =。
式中的B Y 即为节点导纳矩阵。
1.自导纳(0,)j i ii i U j i I Y U =≠⎛⎫= ⎪⎝⎭ 0ii i ij j Y y y =+∑具体说,ii Y 就等于与节点i 相连的所有支路导纳的和。
2.互导纳(0,)j jji iU j i I Y U =≠⎛⎫=⎪⎪⎝⎭ ij ji ij Y Y y ==- 即给节点i 加单位电压,其余节点全部接地,由节点j 注入网络的电流。
节点导纳矩阵的特点: (1) 直观易得阶数:等于除参考节点外的节点数n ;对角元:等于该节点所连导纳的总和;非对角元Yij :等于连接节点i 、j 支路导纳的负值。
(2) 稀疏矩阵,非对角元素中有大量的零元素。
(3) 对称矩阵。
3.非标准变比变压器在包括变压器的输电线路中,变压器线圈匝数比为标准变比时,变压器的高、低压两侧的电压和电流值用线圈匝数比来换算是不成问题的。
但是变压器线圈匝数比为不等于标准变比时需要加以注意。
图中1212,,,U U I I 是按标准变比换算出来的变压器高、低压侧的电压和电流,理想变压器的线圈匝数比k :1表示变压器线圈匝数比对标准变比的比值。
由图可得: 2I1I1’2’12112121T U Z I kU I I k ⎫-=⎪⎬=⎪⎭上面的电压电流关系用π形等值网络表示有两种:对于用导纳表示的π形等值网络,从1-1'端口看进去的节点自导纳为:11(1)T T T Y kY k Y Y =+-=,和k 等于1时相同。
从2-2'端口看进去的节点自导纳为:222(1)T T T Y kY k k Y k Y =+-=,是标准变比时导纳的 k 2倍。
互导纳1221T Y Y kY ==-, 是标准变比时导纳的 k 倍。
潮流计算步骤

潮流计算步骤
潮流计算是电力系统分析中的一种基本计算方法,用于确定电网中的电压分布和功率流动情况。
以下是潮流计算的基本步骤:
1、输入原始数据和信息:包括电网的结构信息、设备参数、负荷和电源的分布及大小等。
2、建立数学模型:根据电路理论和电力系统网络模型,建立描述电力系统中电压、电流和功率关系的数学模型。
3、形成节点导纳矩阵:根据电网结构,形成节点导纳矩阵,用于描述系统中各节点之间的电气联系。
4、确定待求状态变量初值:根据实际情况,为待求的状态变量(如节点电压)设定初值。
5、迭代求解:使用迭代法对数学模型进行求解,逐步更新状态变量的值,直到满足收敛条件为止。
6、计算节点电压:根据迭代求解的结果,计算出各节点的电压值。
7、计算功率分布:根据节点电压和网络参数,计算出各支路的功率流动情况。
8、结果分析:对计算结果进行整理和分析,评估电网的运行状态,为进一步优化和调整提供依据。
需要注意的是,潮流计算的具体步骤可能会因不同的计算方法和电力系统分析软件而有所差异。
在实际应用中,需要根据具体的软件
和要求进行操作。
电力网节点导纳矩阵计算例题与程序
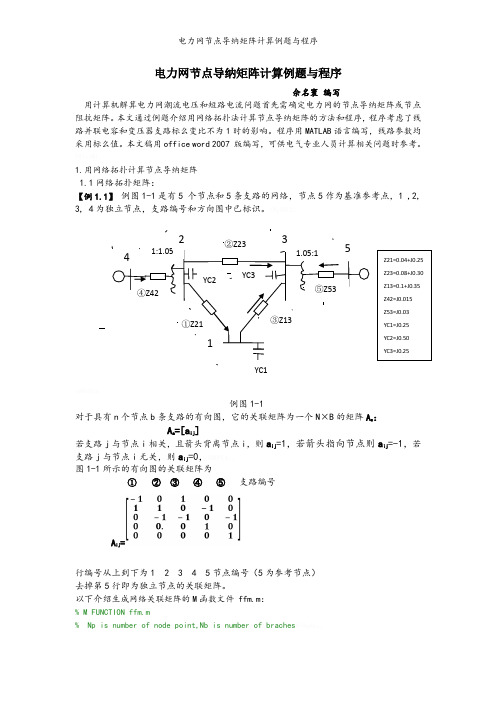
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0,图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1.051.05:142315Z21=0.04+J0.25 Z23=0.08+J0.30 Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25 YC2=J0.50 YC3=J0.25% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
电力系统稳态分析作业题

第四章复杂电力系统的潮流计算一、基本要求掌握电力系统潮流计算的数学模型(节点电压方程)和解算方法;掌握电力网络的节点导纳矩阵;掌握电力系统潮流计算中的功率方程和变量、节点的分类;了解高斯-塞德尔法潮流计算;掌握牛顿-拉夫逊法潮流计算。
二、 重点内容1、 节点导纳矩阵导纳矩阵中的对角元素称为自导纳ii Y ,ii Y 数值上等于与该节点相连的所有支路导纳的总和。
导纳矩阵中的非对角元素称为互导纳ij Y ,ij Y 数值上等于相连节点i 、j 支路导纳的负值,而且ji ij Y Y =,如果节点i 、j 之间无支路相连,则0==ji ij Y Y 。
节点导纳矩阵的特点:(1)节点导纳矩阵是一个n n ⨯阶方阵。
n 为电网的节点数(不包括接地点)。
(2)节点导纳矩阵是一个对称方阵。
(3)节点导纳矩阵具有对角优势,其对角元素绝对值大于非对角元素。
(4)节点导纳矩阵是一个稀疏矩阵,即节点导纳矩阵中有零元素存在。
2、 电力网络功率方程电力网络方程采用节点电压方程:BB B U Y I &&⋅=……………(3-1) 根据节点注入电流和注入功率的关系:*S I U ⎛⎫= ⎪⎝⎭&&,得到以节点注入功率表示的节点电压方程:B B BU Y U S &&⋅=⎥⎦⎤⎢⎣⎡*,将矩阵方程展开为:………………………(3-2)********123123n n n nn n n n n n n S U Y U U Y U U Y U U Y U =++++&&&&L (n 为电网节点数) 展开通式为∑==⋅=n j j j ij i i U Y U S 1**&,其中i 、j = 1、2、……n 。
将有功、无功功率分开,得到以节点注入功率表示的实数方程:⎥⎥⎦⎤⎢⎢⎣⎡⋅=⎥⎥⎦⎤⎢⎢⎣⎡⋅=∑∑====n j j j ij i i n j j j ij i i U Y U Q U Y U P 1**1**Im Re && ……………(3-3)3、 电力网络节点的分类(1)PQ 节点:已知节点的注入功率S P jQ =+,节点的电压向量U &(i i U δ)为待求量;(2)PV 节点:已知节点的注入有功功率P 和电压大小U ,节点注入无功功率Q 和电压相位δ为待求量;(3)平衡节点:已知节点的电压大小U 和电压相位δ,节点注入有功功率P 和无功功率Q 为待求量。
电力系统分析作业——电网节点导纳矩阵的计算机形成

电力系统分析作业——电网节点导纳矩阵的计算机形成编程软件:matlab R2010b程序说明:1.如果已经输入i-j支路的信息,则不可再输入j-i支路的信息。
2.变压器支路的第一个节点编号默认为变压器一次侧,即变压器的等值电路中的阻抗归算侧,亦即变压器非标准变比的1:k中的‘1’。
3.标幺值等值电路中,如果变比为1:1,则默认为线路,因此,变压器的非标准变比不可以是1:1。
5.如果变压器支路也有导纳B不为零,则说明此导纳就是励磁导纳,与线路的导纳B/2不同含义,只算作变压器原边的自导纳。
4.由于程序执行的是复数运算,所以即使实部为零时,也会输出实部‘0’。
程序代码:a=load('data.txt');%从’data.txt’中读入数据[m,n]=size(a);w=1i;u=1;while (u<=m)hnode=a(u,1);enode=a(u,2);z=a(u,3)+a(u,4)*w;b=a(u,5)*w;k=a(u,6);y(hnode,enode)=-1/(k*z);y(enode,hnode)=-1/(k*z);y(hnode,hnode)=y(hnode,hnode)+1/(k*z)+(k-1)/(k*z);y(enode,enode)=y(enode,enode)+1/(k*z)+(1-k)/(k*k*z);if (abs(k-1)<0.0001)%如果为线路y(hnode,hnode)=y(hnode,hnode)+b;y(enode,enode)=y(enode,enode)+b;endif (abs(k-1)>0.0001)%如果为变压器y(hnode,hnode)= y(hnode,hnode)-b;endu=u+1;end[m,n]=size(y);disp(‘Y=’);disp(y(1:m,1:n));clear;算例输入数据:首端编号末端编号电阻电抗电纳/2 变比2 3 0.08 0.30 0.25 14 2 0 0.015 0 1.055 3 0 0.03 0 1.051 2 0.04 0.25 0.25 11 3 0.1 0.35 0 1输出数据:Y=1.3787 - 6.2917i -0.6240 + 3.9002i -0.7547 +2.6415i 0 0 -0.6240 +3.9002i 1.4539 -66.9808i -0.8299 + 3.1120i 0 +63.4921i 0 -0.7547 + 2.6415i -0.8299 + 3.1120i 1.5846 -35.7379i 0 0+31.7460i0 0 +63.4921i 0 0 -66.6667i 0 0 0 0 +31.7460i 0 0 -33.3333i经手算校验,程序结果准确。
电力系统稳态分析实验报告

竭诚为您提供优质文档/双击可除电力系统稳态分析实验报告篇一:南昌大学电力系统分析实验报告3南昌大学实验报告学生姓名:李开卷学号:6100312199专业班级:电力系统124班实验类型:□验证□综合■设计□创新实验日期:12.19实验成绩:一、实验项目名称电力系统故障分析计算二、实验目的:本实验通过对电力系统故障条件下的网络分析计算的计算机程序的编制和调试,获得进行简单不对称故障的计算机程序,使得在网络故障点已知的条件下,故障端口的电气量计算可以自行完成,即根据已知电力系统元件参数及故障点位置由计算程序运行完成该电力系统的故障分析。
通过实验教学加深学生对电力系统故障分析概念的理解,学会运用数学模型进行故障分析,掌握电力系统简单不对称故障的计算过程及其特点,熟悉各种常用应用软件,熟悉硬件设备的使用方法,加强编制调试计算机程序的能力,提高工程计算的能力,学习如何将理论知识和实际工程问题结合起来。
三、实验器材:计算机、软件(已安装,包括各类编程软件c语言、c++、Vb、Vc等、应用软件mATLAb等)、移动存储设备(学生自备,软盘、u盘等)四、实验步骤:编制调试电力系统故障分析的计算机程序。
程序要求根据已知的电力网的数学模型(元件正、负及零序主抗)及故障点位置,完成该电力系统的不对称故障计算,要求计算出故障点的基准相各序分量及其余项故障电压、电流。
1、熟悉电力系统称故障的计算方法,按照计算方法编制程序。
2、将事先编制好的电力系统故障计算的计算程序原代码由自备移动存储设备导入计算机。
3、在相应的编程环境下对程序进行组织调试。
4、应用计算例题验证程序的计算效果。
5、对调试正确的计算程序进行存储、打印。
6、完成本次实验的实验报告。
六、实验项目:如下图已知网络的正序主抗参数和电源的等值电势,输电线路x(0)=3x(1),变压器T-1和T-2为Yn,d接法,T-3为Y,d接法。
分别分析a点发生(b,c)两相短路接地和线路L-1在节点a侧(a)单相断线故障。
电力系统分析大作业matlab三机九节点潮流计算报告

电力系统分析大作业一、设计题目本次设计题目选自课本第五章例5—8,美国西部联合电网WSCC系统的简化三机九节点系统,例题中已经给出了潮流结果,计算结果可以与之对照.取ε=0。
00001 .二、计算步骤第一步,为了方便编程,修改节点的序号,将平衡节点放在最后。
如下图:9第二步,这样得出的系统参数如下表所示:第三步,形成节点导纳矩阵。
第四步,设定初值:;,。
第五步,计算失配功率=0,=—1。
25,=—0.9,=0,=—1,=0,=1。
63,=0。
85;=0。
8614,=—0。
2590,=—0。
0420,=0。
6275,=—0.1710,=0。
7101。
显然,.第六步,形成雅克比矩阵(阶数为14×14)第七步,解修正方程,得到:-0.0371,—0.0668,—0.0628,0。
0732,0。
0191,0。
0422,0。
1726,0。
0908;0.0334,0。
0084,0。
0223,0.0372,0。
0266,0。
0400。
从而—0.0371,-0。
0668,-0。
0628,0。
0732,0。
0191,0。
0422,0.1726,0。
0908;1。
0334,1.0084,1。
0223,1。
0372,1.0266,1。
0400。
然后转入下一次迭代。
经三次迭代后。
迭代过程中节点电压变化情况如下表:迭代收敛后各节点的电压和功率:最后得出迭代收敛后各支路的功率和功率损耗:三、源程序及注释由于计算流程比较简单,所以编写程序过程中没有采用模块化的形式,直接按顺序一步步进行。
disp(’【节点数:】’);[n1]=xlsread(’input。
xls’,'A3:A3')%节点数disp('【支路数:】');[n]=xlsread('input。
xls’,’B3:B3')%支路数disp('【精度:】’);Accuracy=xlsread('input。
电力网节点导纳矩阵计算例题与程序
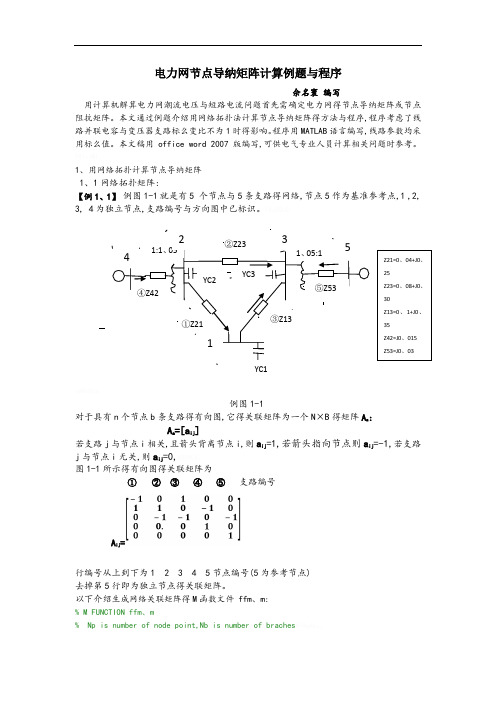
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压与短路电流问题首先需确定电力网得节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵得方法与程序,程序考虑了线路并联电容与变压器支路标么变比不为1时得影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1、用网络拓扑计算节点导纳矩阵 1、1网络拓扑矩阵:【例1、1】 例图1-1就是有5 个节点与5条支路得网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号与方向图中已标识。
例图1-1对于具有n 个节点b 条支路得有向图,它得关联矩阵为一个N ×B 得矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0,图1-1所示得有向图得关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点得关联矩阵。
以下介绍生成网络关联矩阵得M 函数文件 ffm 、m:% M FUNCTION ffm 、m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1、051、05:142315Z21=0、04+J0、25Z23=0、08+J0、30Z13=0、1+J0、35Z42=J0、015 Z53=J0、03% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm、m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij就是相同得。
电力系统分析-电力网络的数学模型

Y12 Y32 Y52
Y13 Y33 Y53
Y14 Y34 Y54
Y22 Y23 Y24 Y42 Y43 Y44
I Y15 U 1 1 Y25 U I 2 2 I Y35 U 3 3 Y45 U 4 I 4 I Y55 U 5 5
Y11 Y 21 Y31 Y41 Y51 Y12 Y32 Y52 Y13 Y33 Y53 Y14 Y34 Y54 Y22 Y23 Y24 Y42 Y43 Y44 I Y15 U 1 1 Y25 U 2 I 2 I Y35 U 3 3 Y45 U 4 I 4 I Y55 U 5 5
i
zij 1:k ji
j j
i
yij 1 ( k ji zij )
y240
y40
y340
yij 0
1 1 2 k ji zij k ji zij
k ji 1 k ji zij
Yij 1 k ji zij
y ji 0
1 k ji k2 ji zij
Yii
k ji 1 k ji zij
1 1 k ji zij zij
Y jj
1 k ji k2 ji zij
1.1节点电压方程与节点导纳矩阵
1
I 1
y12
2
y23
3
y35
5
y120
y210
I 2
y230
y24
y320 y34
I 3
y350
y530
I 5
y240
电力系统计算与仿真分析 第一章 节点网络方程

小结
当电力网络结构或元件参数发生局 部变化时,可以在原有的节点导纳矩 阵基础上进行修改得到新的节点导纳 矩阵。节点导纳矩阵和节点阻抗矩阵 互为逆矩阵。节点网络方程也可以节 点阻抗矩阵形式描述。
感谢聆听!
物理意义:当电网络中节点i接入单 位电压源,其他节点都接地时,自导 纳Yii在数值上等于节点i注入网络的 电流。
一、节点电压方程
节点阻抗矩阵Z: 两边同乘Y-1: 即:
Z Y 1 Y 1YU = Y 1 I
ZI = U
节点网络方程的另一种形式
二、节点导纳矩阵的形成
节点导纳矩阵可以根据降阶节点—支路关联矩阵A(简称关联矩阵)来形成。 对于n个独立节点、b条支路的网络,A的阶次为n×b。
Yii Yii yij yij
Yjj
Yjj
yij
yij
Yij Yji Yij yij yij Yji yij yij
四、小结
本章详细地介绍了以节点导纳矩阵
形式描述的节点网络方程。节点导纳 矩阵Y可以根据关联矩阵A以及支路导 纳所组成的对角矩阵YB形成。关联矩 阵A可以表示节点与支路的联系,矩 阵A反映了电力网络的拓扑约束。矩 阵YB反映了电力网络的支路特性约束
电力系统计算与仿真分析
第一章 节点网络方程
提纲
Outline
一 节点电压方程 二 节点导纳矩阵的形成 三 节点导纳矩阵的修改 四 小结
一、节点电压方程
广泛应用
一、节点电压方程
对于具有n个独立节点的网络,可以列出以下方程:
YY1211UU11
Y12U 2 Y22U 2
Y1kU k Y2kU k
自导纳发Y生 变Y化: y
ii
ii
电力系统分析第4章习题答案

第四章 思考题及习题答案4-1 节点导纳矩阵是如何形成的?各元素的物理意义是什么?节点导纳矩阵有何特点? 答:节点导纳矩阵的对角元素称为自导纳,在数值上等于与该节点相连支路的导纳之和,其物理意义是:在该节点施加单位电压,其他节点全部接地时,由该节点注入网络的电流。
节点导纳矩阵的非对角元素称为互导纳,互导纳在数值上等于节点i 和ji Y j 之间支路导纳的负值,其物理意义是:在节点施加单位电压,其他节点全部接地时,经节点i j 注入网络的电流。
节点导纳矩阵有以下特点:其阶数等于电力网络中除参考节点之外的节点数;是稀疏矩阵;是对称矩阵;易于形成和修改。
4-2 节点阻抗矩阵中各元素的物理意义是什么?它有何特点?答:节点阻抗矩阵的对角元素称为自阻抗,其物理意义是:在该节点注入单位电流,其他节点全部开路时,该节点的电压值。
节点阻抗矩阵的非对角元素称为互阻抗,其物理意义是:互阻抗等于节点i 注入单位电流,其他节点全部开路时,节点ji Z j 的电压值。
节点导纳矩阵有以下特点:其阶数等于电力网络中除参考节点之外的节点数;是满矩阵;是对称矩阵;形成和修改较困难。
4-3 电力系统潮流计算中节点是如何分类的? 答:电力系统进行潮流计算时,节点是可分为三类:(1)PQ 节点:给定节点的有功功率i P 和无功功率,待求节点电压幅值和相位角i Q i U i δ。
(2)PV 节点:给定节点的有功功率i P 和电压幅值,待求无功功率和电压的相位角i U i Q i δ。
(3)平衡节点(V δ节点):给定节点电压幅值和电压相位角,待求节点的注入功率。
4-4 电力系统中变量的约束条件是什么? 答:常用的约束条件有:(1)电压数值的约束:各节点电压幅值应限制在一定的范围之内,即; max .min .i i i U U U ≤≤(2)发电机输出功率的约束:电源节点的有功功率和无功功率应满足和;max .min .Gi Gi Gi P P P ≤≤max .min .Gi Gi Gi Q Q Q ≤≤(3)电压相角的约束:系统中两个节点之间的相位差应满足maxji j i ij δδδδδ−≤−=。
电力网节点导纳矩阵计算例题与程序

电力网节点导纳矩阵计算例题与程序————————————————————————————————作者:————————————————————————————————日期:电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0, 图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m②③①YYY④⑤1:1 1.042315Z21=0.04+J0.25Z23=0.08+J0.30Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电力系统分析作业——电网节点导纳矩阵的计算机形成
编程软件:matlab R2010b
程序说明:
1.如果已经输入i-j支路的信息,则不可再输入j-i支路的信息。
2.变压器支路的第一个节点编号默认为变压器一次侧,即变压器的等值电路中的阻抗归算侧,亦即变压器非标准变比的1:k中的‘1’。
3.标幺值等值电路中,如果变比为1:1,则默认为线路,因此,变压器的非标准变比不可以是1:1。
5.如果变压器支路也有导纳B不为零,则说明此导纳就是励磁导纳,与线路的导纳B/2不同含义,只算作变压器原边的自导纳。
4.由于程序执行的是复数运算,所以即使实部为零时,也会输出实部‘0’。
程序代码:
a=load('data.txt');%从’data.txt’中读入数据
[m,n]=size(a);
w=1i;
u=1;
while (u<=m)
hnode=a(u,1);
enode=a(u,2);
z=a(u,3)+a(u,4)*w;
b=a(u,5)*w;
k=a(u,6);
y(hnode,enode)=-1/(k*z);
y(enode,hnode)=-1/(k*z);
y(hnode,hnode)=y(hnode,hnode)+1/(k*z)+(k-1)/(k*z);
y(enode,enode)=y(enode,enode)+1/(k*z)+(1-k)/(k*k*z);
if (abs(k-1)<0.0001)%如果为线路
y(hnode,hnode)=y(hnode,hnode)+b;
y(enode,enode)=y(enode,enode)+b;
end
if (abs(k-1)>0.0001)%如果为变压器
y(hnode,hnode)= y(hnode,hnode)-b;
end
u=u+1;
end
[m,n]=size(y);
disp(‘Y=’);
disp(y(1:m,1:n));
clear;
算例
输入数据:
首端编号末端编号电阻电抗电纳/2 变比
2 3 0.08 0.30 0.25 1
4 2 0 0.01
5 0 1.05
5 3 0 0.03 0 1.05
1 2 0.04 0.25 0.25 1
1 3 0.1 0.35 0 1
输出数据:
Y=
1.3787 - 6.2917i -0.6240 + 3.9002i -0.7547 +
2.6415i 0 0 -0.6240 +
3.9002i 1.4539 -66.9808i -0.8299 + 3.1120i 0 +63.4921i 0 -0.7547 + 2.6415i -0.8299 + 3.1120i 1.5846 -35.7379i 0 0 +31.7460i 0 0 +63.4921i 0 0 -66.6667i 0 0 0 0 +31.7460i 0 0 -33.3333i 经手算校验,程序结果准确。
