利用MATLAB进行实验数据处理
MATLAB语言及其应用实验报告.doc

MATLAB语言及其应用实验报告.doc一、实验目的1、熟悉MATLAB语言及其基本操作;2、掌握利用MATLAB进行数据分析和可视化的方法;3、掌握MATLAB应用于科学计算的基本方法。
二、实验环境MATLAB R2018a三、实验内容及方法3.1 实验内容1、打开MATLAB环境;2、读入数据文件,并对数据进行分析和处理;3、通过MATLAB绘制图表,对数据进行可视化。
四、实验细节及流程4.1 读入数据文件本实验使用的数据文件为sales.xlsx,其中包括2018年各个季度的销售数据。
首先,通过以下命令导入数据:data=xlsread('sales.xlsx');4.2 数据分析和处理1、计算各季度销售总额通过以下代码计算每个季度的销售额并求和,得到每年的销售总额:Q1=data(:,2);TotalSales=sum([Q1 Q2 Q3 Q4],2);2、计算增长率根据每年的销售总额,计算出每年的增长率。
具体代码如下:GrowthRate(1)=0;for i=2:length(TotalSales)GrowthRate(i)=((TotalSales(i)-TotalSales(i-1))/TotalSales(i-1))*100; endSalesGrowth=[TotalSales GrowthRate];3、计算每个季度的均值和标准差meanQ1=mean(Q1);stdQ1=std(Q1);4、计算出每年第一个季度的销售额所占比例首先,我们将第一个季度的销售额单独提出来,具体代码如下:4.3 数据可视化1、柱形图对于销售总额,使用柱形图进行可视化,具体代码如下:结果如下图所示:图1 销售总额2、线性图3、箱形图boxplot([Q1 Q2 Q3 Q4],{'Q1','Q2','Q3','Q4'});图3 每个季度的销售额4、饼图pie(FirstQSalesRatio(:,1));五、结论本实验通过对销售数据的分析和可视化,得出以下结论:1、2018年销售总额呈逐年上升趋势,其中2017年到2018年的增长率最高;2、每年第一个季度的销售额所占比例在40%至45%之间,与其他季度相比,显著高于其他季度;3、2018年第二季度的销售额经过调整后,表现出了相对较高的波动。
基于matlab的实验报告

基于matlab的实验报告实验报告:基于MATLAB 的实验一、实验目的通过使用MATLAB 软件,掌握如何进行数据分析、图像处理、算法实现等一系列实验操作,提高实验者的实践能力和动手能力。
二、实验原理MATLAB 是一种在科学计算和技术开发领域广泛应用的计算机软件。
它能进行矩阵计算、绘制函数和数据图像、实现算法以及进行数据分析等。
通过掌握MATLAB 的使用,能够快速、高效地解决各种科学和工程问题。
三、实验内容1. 数据分析:使用MATLAB 的数据分析工具进行数据的导入、处理和分析。
2. 图像处理:利用MATLAB 的图像处理工具包对图像进行滤波、增强、分割等操作。
3. 算法实现:使用MATLAB 实现常用的算法,如排序、搜索、图像压缩等。
四、实验步骤1. 数据分析:(1)使用MATLAB 的读取数据函数将数据导入MATLAB 环境中。
(2)利用MATLAB 的数据处理函数进行数据清洗和预处理。
(3)使用MATLAB 的统计工具进行数据分析,如求平均值、标准差等。
(4)利用MATLAB 的绘图函数将分析结果可视化。
2. 图像处理:(1)使用MATLAB 的读取图像函数将图像导入MATLAB 环境中。
(2)利用MATLAB 的图像处理工具包进行滤波操作,如均值滤波、中值滤波等。
(3)使用MATLAB 的图像增强函数对图像进行锐化、变换等操作。
(4)利用MATLAB 的图像分割算法对图像进行分割。
3. 算法实现:(1)使用MATLAB 编写排序算法,如冒泡排序、快速排序等。
(2)使用MATLAB 编写搜索算法,如二分查找、线性搜索等。
(3)使用MATLAB 实现图像压缩算法,如离散余弦变换(DCT)。
五、实验结果实验中,我们使用MATLAB 完成了数据分析、图像处理和算法实现的一系列实验操作。
通过数据分析,我们成功导入了数据并对其进行了清洗和预处理,最后得到了数据的统计结果。
在图像处理方面,我们对图像进行了滤波、增强和分割等操作,最终得到了处理后的图像。
Matlab实验仿真实验数据
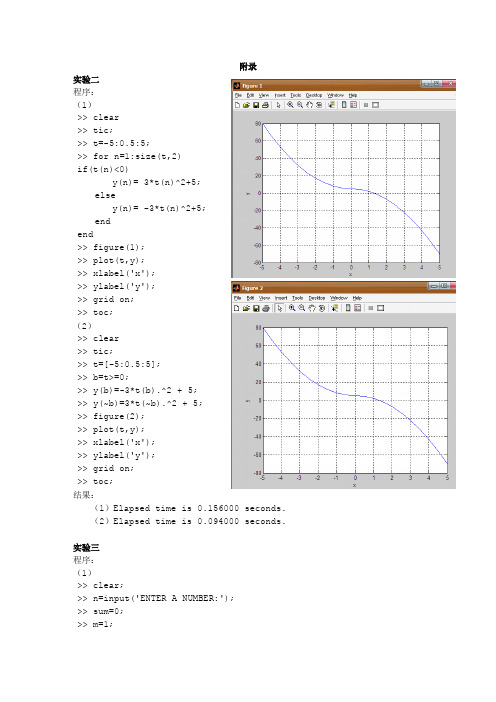
附录实验二程序:(1)>> clear>> tic;>> t=-5:0.5:5;>> for n=1:size(t,2)if(t(n)<0)y(n)= 3*t(n)^2+5;elsey(n)= -3*t(n)^2+5;endend>> figure(1);>> plot(t,y);>> xlabel('x');>> ylabel('y');>> grid on;>> toc;(2)>> clear>> tic;>> t=[-5:0.5:5];>> b=t>=0;>> y(b)=-3*t(b).^2 + 5;>> y(~b)=3*t(~b).^2 + 5;>> figure(2);>> plot(t,y);>> xlabel('x');>> ylabel('y');>> grid on;>> toc;结果:(1)Elapsed time is 0.156000 seconds.(2)Elapsed time is 0.094000 seconds.实验三程序:(1)>> clear;>> n=input('ENTER A NUMBER:');>> sum=0;>> m=1;>> while m<nsum=sum+m;m=m+2;end>> fprintf('The result of all odd numbers within a given number is:%d\n',sum);(2)创建Fib.m文件% 函数功能: 计算斐波那契数列的第 n 个斐波那契数% 文件名: Fib.m% 含有 n 个数的斐波那契数列的定义如下:% f(1) = 1% f(2) = 2% f(n) = f(n-1) + f(n-2)function y=Fib(n);a(1)=1;a(2)=1;i=2;while i<=na(i+1)=a(i-1)+a(i);i=i+1;end;y=a(i);结果:(1)ENTER A NUMBER:6The result of all odd numbers within a given number is:9(2)>> Fib(7)ans =21实验四(1)程序:创建myfun.m文件% 函数功能: 计算x的双曲正弦、双曲余弦和双曲正切,并画出对应的图象。
基于MATLAB的误差数据处理实验报告

结果:
X=
l 1 1.0280 x1 1.015 0.9830 ˆ 1 X l 2 0.985 x2 ( A A) A L l 3 1.0130 1.020 x3 L 5. 一元线性回归分析 l 2 . 016 4 l 1.981 6 5 3.032 l 6
误差理论与数据处理 实验报告
班 学 姓
级 号 名
测控 10-1 13 刘英皓 庄 严
指导老师
2012 年 7 月 5 日
测控 10-3
刘英皓
前言
门捷列夫说:“科学是从测量开始的” 钱学森说:“新技术革命的关键技术是信息技术。信息技术由测量技术、计 算机技术、通讯技术三部分组成。测量技术是关键和基础”。 测量技术是新科技革命的关键部分,科学技术的发展与实验测量密切相关。 在进行实验测量时,产生误差是不可避免的。因此,必须借助误差理论,研究、 估计和判断测量的数据和结果是否精确可靠,并采用正确的数据处理方法,以提 高测量结果的精确程度。 误差理论是我们认识客观规律的有力工具,是工程学科 学生应该掌握的基础知识 。 但是与此同时, 误差理论具有较为繁复的数据处理量, 有时候面对这些数据, 我们也无能为力,习惯采用经验估计去解决现实问题。毋庸置疑,这样做,引入 的误差必然相当大。 MATLB 具有强大的数据处理能力,若是借助 MATLB 处理那些难以处理的 数据,既可以节约时间,又可以提高精确度。本实验的主旨,就是通过使用 MATLAB 处理数据,让我们体会计算机辅助处理数据优点,让我们更直接,更 直观观察结果。
1
测控 10-3
ቤተ መጻሕፍቲ ባይዱ
刘英皓
实验目的:利用
Matlab多次重复实验记录结果,MATLAB数据处理实验记录与总结.doc

Matlab多次重复实验记录结果,MATLAB数据处理实验记录与总结.docMATLAB实验报告学 号实验名称MATLAB数据处理实验实验⽬的掌握⼆维曲线图、三维曲线图、三维曲⾯图的绘制⽅法掌握常⽤统计图的绘制⽅法熟悉三维图形常⽤编辑⽅法了解动画的绘制⽅法实验记录1.离散数据可视化实验:2.⼆维曲线绘制实验:1)Plot⽅法⽤于绘制图像2)Subplot绘制⼦表3)Axis函数表⽰坐标的范围4)Set设置坐标轴系统5)Legend⽤于添加图例或者图表的声明6)xlabel、ylabel、zlabel、⽤于标⽰各个坐标轴的名称7)Title设置图表的标题8)Text添加⽂本,注释坐标系中⼀点9)grid on10)Hold指令的基本格式11)双坐标轴3、三维曲线绘制实验1)plot3函数2)Mesh绘制曲⾯3)Surf函数的使⽤⽅法4)Fplot函数的使⽤⽅法4、统计图绘制实验:1)⾯域图(area)2)直⽅图(bar、barh、bar3、bar3h)3)Pie指令4)散点图(scatter、scatter3、plotmatrix)5、三维图形编辑(精细控制)实验:1)View的⽤法2)Rotate的⽤法3)Colordef指令的使⽤4)Colormap⽅法5)Shading⽅法6)Light⽅法7)Lighting命令8)Material指令9)Surfl指令6、制作动画实验总结1、Matlab绘图的基本步骤:准备图标的数据。
⽤户需要确定图标的绘制范围,制定对应的⾃变量,最后计算相应的函数值。
设置显⽰图表的位置。
在多个⾃读的情况下,需要设置每个⼦图的显⽰位置。
对应命令为subplot。
绘图,并设置相应的参数。
主要命令plot,⽤户可以通过该命令绘制图表,同时为了显⽰⽅便还应该调⽤其他辅助函数设定表的颜⾊,形状等等。
设置坐标轴的属性,添加刻度,和坐标系的分隔等等。
添加表的注释。
如坐标的名称,图例,⽂字说明等等。
MATLAB中的数据处理

四、使用输入函数 对于大量的数据,或者格式更加复杂的数据文件,以上方法就不 太方便,此时针对不同格式的数据文件,可以采用相应的输入函数导 入数据。 1、load 函数 装载 Matlab 格式的数据文件(.mat)和文本格式的定界符为空格的 矩形文件。 例:载入文件“data02.txt”中的数据 2、dlmread 函数 将带有定界字符的 ASCII 数字数据读入矩阵 常用格式: M=dlmread(‘filename’) 是默认定界符。 M=dlmread(‘filename’,delimiter),指定定界符。 M=dlmread(‘filename’,delimiter,R,C),从矩形数据的左上角 R 行、C 列的位置开始读入。 注意:矩形数据的开始位置是 0 行 0 列。 M=dlmread(‘filename’,delimiter,range) ,读取用 range 指定范围的数 据,range=[R1 C1 R2 C2],R1C1 是左上角的行列号,R2C2 是右下角 的行列号;range 也可以用如下表示法:range=’A1..B7’。 例:对于 data02.txt 中的数据 >> dlmread('d:\data\data02.txt') %读全部数据 %Matlab 从文件格式中推断定界符,逗号
num = xlsread(filename, -1) %将在 Excel 窗口打开 filename 文件, 可以交互选择工作区中的数据文件; num = xlsread(filename, sheet) %选择工作表 sheet,默认为第一 个工作表; num = xlsread(filename, range) %指定工作表中的数据范围, 如’A4:B5’ num = xlsread(filename, sheet, range) 例:将电子表格 data01.xls 中的数据载入到 Matlab 工作区 >> xlsread('d:\data\data01')
如何利用Matlab进行模拟和仿真实验

如何利用Matlab进行模拟和仿真实验Matlab是一种功能强大的数学计算和数据可视化软件。
它不仅可以进行数学模拟和仿真实验,还可以处理数据、绘制图表和实施算法。
在工程、物理学、生物学等领域,Matlab被广泛用于解决各种实际问题。
本文将介绍如何利用Matlab进行模拟和仿真实验,并探讨其在实验设计和结果分析中的应用。
一. Matlab的基本功能Matlab具有很多基本功能,如矩阵操作、数值计算、符号计算等。
这些功能使得Matlab成为进行模拟和仿真实验的理想选择。
在Matlab中,可以定义和操作矩阵,进行线性代数运算,如求解方程组、矩阵求逆等。
此外,Matlab还提供了许多内置函数,可以进行数值计算和符号计算,如求解微分方程、积分、数值优化等。
二. 模拟实验的设计在进行模拟实验之前,首先需要设计实验方案。
实验设计包括选择合适的模型和参数设置,确定实验变量和观测指标等。
在Matlab中,可以使用函数或脚本来定义模型和参数,通过修改参数值来观察实验结果的变化。
比如,可以使用Matlab的模型库来选择合适的模型,然后使用函数传入参数值进行求解。
此外,Matlab还提供了绘图功能,可以绘制实验结果的图表,以便更直观地分析数据。
三. 仿真实验的实施在设计好实验方案后,就可以开始进行仿真实验了。
在Matlab中,可以使用已定义的模型和参数进行仿真计算。
可以通过Matlab的编程功能来实现计算过程的自动化。
比如,可以使用循环语句来迭代计算,以观察参数变化对结果的影响。
此外,Matlab还提供了随机数生成和统计分析函数,可以用于生成随机变量和分析实验数据。
四. 实验结果的分析在完成仿真实验后,需要对实验结果进行分析。
Matlab提供了丰富的数据处理和分析工具,可以对实验数据进行统计分析、绘图和可视化展示。
可以使用Matlab的数据处理函数来计算均值、标准差、相关系数等统计指标。
此外,Matlab还可以通过绘图函数来绘制直方图、散点图、线图等图形,以便更好地理解和展示数据。
基于MATLAB实验数据的几种处理方法

模式识别与仿真技术Pattern Recognition and Simulation《自动化技术与应用》2005年第24卷第1期基于MAT LAB实验数据的几种处理方法吴晓光,徐精彩,李树刚,李 华(西安科技大学,陕西 西安 710054)摘要:本文从M AT LAB的工程计算与数据处理能力出发,着重讨论如何运用M AT LAB实现实验数据处理的方法,包括数据拟合、数值插值、数值微商和数值积分,并通过实际应用得出M AT LAB是具有强大数据计算和分析功能的软件,同时将使用者从繁琐的底层编程中解放出来,大大提高工作效率。
关键词:数据处理;M AT LAB;曲线拟合中图分类号:TP27412 文献标识码:B 文章编号:100327241(2005)0120025203Matla b-bas e d Proces sin g Met h o ds of Exp eri m e ntal DataWU Xiao-guang,XU Jing-cai,LI Shu-gang,LI H ua(X i’an University of Science&T echnology,X i’an710054,China)Abstract:Because of the high capability of the engineering calculation and data processing of M AT LAB,the data processing methods suck as data fit2 ting,data interpretation,differential and integral for the experimental data by using M AT LAB are all presented in the paper.K ey w ords:Data processing;M AT LAB;Curve fitting1 引言数据处理是一项复杂、繁琐的事情,随着计算机技术的迅速发展,美国Mathw orks公司于1967年推出了Matrix Laboratory(缩写为M AT LAB)软件包,集应用程序和图形于同一环境[1]。
实验一 数据处理方法的MATLAB实现范文

实验一数据处理方法的MATLAB实现一、实验目的学会在MATLAB环境下对已知的数据进行处理。
二、实验方法1. 求取数据的最大值或最小值。
2. 求取向量的均值、标准方差和中间值。
3.在MATLAB环境下,对已知的数据分别进行曲线拟合和插值。
三、实验设备1.586以上微机,16M以上内存,400M硬盘空间,2X CD-ROM2.MATLAB5.3以上含CONTROL SYSTEM TOOLBOX。
四、实验内容1.在MATLAB环境下,利用MATLAB控制系统工具箱中的函数直接求取数据的最大值或最小值,以及向量的均值、标准方差和中间值。
2.在MATLAB环境下,选择合适的曲线拟合和插值方法,编写程序,对已知的数据分别进行曲线拟合和插值。
五、实验步骤1. 在MATLAB环境下,将已知的数据存到数据文件mydat.mat中。
双击打开Matlab,在命令窗口(command window)中,输入一组数据:实验一数据处理方法的MATLAB实现一、实验目的学会在MATLAB环境下对已知的数据进行处理。
二、实验方法1. 求取数据的最大值或最小值。
2. 求取向量的均值、标准方差和中间值。
3.在MATLAB环境下,对已知的数据分别进行曲线拟合和插值。
三、实验设备1.586以上微机,16M以上内存,400M硬盘空间,2X CD-ROM2.MATLAB5.3以上含CONTROL SYSTEM TOOLBOX。
四、实验内容1.在MATLAB环境下,利用MATLAB控制系统工具箱中的函数直接求取数据的最大值或最小值,以及向量的均值、标准方差和中间值。
2.在MATLAB环境下,选择合适的曲线拟合和插值方法,编写程序,对已知的数据分别进行曲线拟合和插值。
五、实验步骤1. 在MATLAB环境下,将已知的数据存到数据文件mydat.mat中。
双击打开Matlab,在命令窗口(command window)中,输入一组数据:x=[1,4,2,81,23,45]x =1 42 81 23 45单击保存按钮,保存在Matlab指定目录(C:\Program Files\MATLAB71)下,文件名为“mydat.mat”。
matlab数值计算实验报告

matlab数值计算实验报告Matlab数值计算实验报告引言:Matlab是一种广泛应用于科学与工程领域的高级计算机语言和环境,它提供了丰富的函数库和工具箱,方便用户进行数值计算、数据分析和可视化等任务。
本实验报告将介绍我在使用Matlab进行数值计算实验中的一些经验和心得体会。
一、数值计算方法数值计算方法是一种利用数值近似来解决实际问题的方法,它在科学和工程领域具有广泛的应用。
在Matlab中,我们可以利用内置的函数和工具箱来实现各种数值计算方法,例如插值、数值积分、数值微分等。
二、插值方法插值是一种通过已知数据点来推测未知数据点的方法。
在Matlab中,我们可以使用interp1函数来进行插值计算。
例如,我们可以通过已知的一些离散数据点,利用interp1函数来估计其他位置的数值。
这在信号处理、图像处理等领域具有重要的应用。
三、数值积分数值积分是一种通过分割曲线或曲面来近似计算其面积或体积的方法。
在Matlab中,我们可以使用quad函数来进行数值积分计算。
例如,我们可以通过quad函数来计算某个函数在给定区间上的积分值。
这在概率统计、物理学等领域具有广泛的应用。
四、数值微分数值微分是一种通过数值逼近来计算函数导数的方法。
在Matlab中,我们可以使用diff函数来进行数值微分计算。
例如,我们可以通过diff函数来计算某个函数在给定点上的导数值。
这在优化算法、控制系统等领域具有重要的应用。
五、数值求解数值求解是一种通过数值近似来计算方程或方程组的根的方法。
在Matlab中,我们可以使用fsolve函数来进行数值求解计算。
例如,我们可以通过fsolve函数来求解某个非线性方程的根。
这在工程计算、金融分析等领域具有广泛的应用。
六、实验应用在本次实验中,我使用Matlab进行了一些数值计算的应用实验。
例如,我利用插值方法来估计某个信号在给定位置的数值,利用数值积分方法来计算某个曲线下的面积,利用数值微分方法来计算某个函数在给定点的导数值,以及利用数值求解方法来求解某个方程的根。
matlab插值实验报告

matlab插值实验报告Matlab插值实验报告引言:在数学和工程领域中,插值是一种常见的数据处理方法。
它通过已知数据点之间的推断来填补数据的空缺部分,从而获得连续的函数或曲线。
Matlab是一种功能强大的数值计算软件,具备丰富的插值函数和工具包。
本实验旨在通过使用Matlab进行插值实验,探索插值方法的原理和应用。
实验步骤:1. 数据准备首先,我们需要准备一组实验数据。
以一个简单的二维函数为例,我们选择f(x) = sin(x),并在区间[0, 2π]上取若干个等间隔的点作为已知数据点。
2. 线性插值线性插值是插值方法中最简单的一种。
它假设函数在两个已知数据点之间是线性变化的。
在Matlab中,可以使用interp1函数进行线性插值。
我们将已知数据点和插值结果绘制在同一张图上,以比较它们之间的差异。
3. 多项式插值多项式插值是一种常用的插值方法,它通过已知数据点构造一个多项式函数来逼近原始函数。
在Matlab中,polyfit函数可以用来拟合多项式。
我们可以选择不同的多项式次数进行插值,并观察插值结果与原始函数之间的差异。
4. 样条插值样条插值是一种更为精确的插值方法,它通过在每个小区间内构造局部多项式函数来逼近原始函数。
在Matlab中,可以使用spline函数进行样条插值。
我们可以选择不同的插值节点数目,并比较插值结果的平滑程度和逼近效果。
5. 拉格朗日插值拉格朗日插值是一种基于多项式的插值方法,它通过构造插值多项式来逼近原始函数。
在Matlab中,可以使用polyval函数进行拉格朗日插值。
我们可以选择不同的插值节点数目,并观察插值结果与原始函数之间的差异。
实验结果:通过实验,我们得到了不同插值方法的结果,并将其与原始函数进行了比较。
在线性插值中,我们观察到插值结果与原始函数之间存在一定的误差,特别是在函数变化较快的区域。
而多项式插值和样条插值在逼近原始函数方面表现更好,特别是在插值节点数目较多的情况下。
如何用Matlab进行数据分析

如何用Matlab进行数据分析引言:数据分析是一种重要的技能,可以帮助我们从大量的数据中提取有用的信息和洞察力。
在现今信息高度发达的社会中,数据分析在各个领域都发挥着重要作用。
Matlab作为一种功能强大的数学软件,可以帮助我们轻松进行数据分析。
本文将介绍如何使用Matlab进行数据分析的基本方法和技巧。
一、数据准备阶段在进行数据分析之前,首先需要准备好待分析的数据。
数据准备阶段包括以下几个步骤:1. 数据收集:从不同渠道收集数据,可以是实验室实测数据、网络爬虫获取的数据、传感器采集的数据等。
2. 数据预处理:对收集到的原始数据进行清洗和处理,主要包括缺失值处理、异常值处理、重复值处理等。
Matlab提供了丰富的数据处理函数,例如`ismissing`用于判断缺失值、`rmoutliers`用于剔除异常值等。
3. 数据探索:对数据进行初步探索,了解数据的分布、特征等。
Matlab可以通过绘制直方图、散点图、箱线图等可视化方法,帮助我们更加直观地理解数据。
二、数据分析方法数据分析的方法有很多种,选择合适的方法可以提高分析效果和结果可信度。
下面介绍几个常用的数据分析方法:1. 描述统计分析:描述统计分析主要通过计算数据的中心趋势、离散程度、分布形状等指标来描述数据的基本特征。
Matlab提供了众多描述统计函数,例如`mean`计算均值、`std`计算标准差等。
2. 相关性分析:相相关性分析用于研究两个或多个变量之间的关联程度。
Matlab提供了`corrcoef`函数用于计算变量之间的相关系数,并可以通过绘制相关系数矩阵热图的方法直观地展示变量之间的关系。
3. 回归分析:回归分析用于研究一个或多个自变量与因变量之间的关系。
Matlab提供了`regress`函数进行回归分析,并可以通过绘制残差图和回归线来评估回归模型的拟合效果。
4. 聚类分析:聚类分析用于将相似的数据样本归为一类,同时将不相似的样本划分到不同的类别。
实验五 用Matlab数据拟合

2. 已知观测数据点如表所示 x 1.6 2.7 1.3 4.1 3.6 2.3 y 17.7 49 13.1 189.4 110.8 34.5
0.6
4
4.9
409.1
3
65
2.4
36.9
求a, b, c的值, 使得曲线 f(x)=aex+bsin x+c lnx 与已知数据 点在最小二乘意义上充分接近.
例4 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17 求三个参数 a, b, c的值, 使得曲线 f(x)=aex+bx2+cx3 与 已知数据点在最小二乘意义上充分接近.
1.55
500 106
2.47
2. 93
3. 03
2.89
1000 106 1500 106 2000 106 2375 106
3 1.953 103 1.517 103 1.219 10
/ / N / m 2 3.103 103 2.465 103
解: 描出散点图, 在命令窗口输入: t=[0:1:16] y=[30.0 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8 24.0] plot(t,y,'*')
a=polyfit(t,y,1) a= -0.3012 29.3804 hold on
beta
= 3.0022 4.0304 0.9404
Matlab解决弗兰克—赫兹实验的实验数据处理

《数学实验》报告实验名称MATLAB与数学实验_ 学院专业班级姓名学号年月工科物理实验一、【作业题目】弗兰克—赫兹实验的实验数据处理;二、【作业程序】x=0:0.5:53;y=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.001,0.012,0.027,0.051,0.068,0.085,0.095,0.105,0.113,0.121,0.126,0.127,0.128,0.125,0.12,0.111,0.101,0.088,0.075,0.062,0.048,0.037,0.027,0.021,0.019,0.023,0.041,0.074,0.114,0.154,0.183,0.211,0.231,0.242,0.247,0.243,0.234,0.214,0.191,0.158,0.128,0.095,0.078,0.065,0.054,0.047,0. 04,0.039,0.056,0.084,0.148,0.213,0.263,0.313,0.347,0.372,0.388,0.39,0.381,0.364,0.332,0.289,0.252,0.198,0.146,0.102,0.076,0.054,0.045,0.044,0.045,0.066,0.142,0. 221,0.295,0.348,0.405,0.437,0.47,0.492,0.5,0.498,0.483,0.445,0.417,0.356,0.285];p2=polyfit(x,y,2)p7=polyfit(x,y,7)p10=polyfit(x,y,10)p20=polyfit(x,y,20)disp('二次拟合函数'),f2=poly2str(p2,'x')disp('七次拟合函数'),f7=poly2str(p7,'x')disp('十次拟合函数'),f10=poly2str(p10,'x')disp('二十次拟合函数'),f20=poly2str(p20,'x')x1=0:0.5:53;y2=polyval(p2,x1);y7=polyval(p7,x1);y10=polyval(p10,x1);y20=polyval(p20,x1);plot(x,y,'rp',x1,y2,'--',x1,y7,'bd',x1,y10,'y-.',x1,y20,'k-')三、【作业结果】p2 =0.0001 0.0023 0.0025p7 =-0.0000 0.0000 -0.0000 0.0001 -0.0024 0.0230 -0.0854 0.0648p10 =-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0001 -0.0014 0.0112 -0.0458 0.0727 -0.0202p20 =Columns 1 through 130.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0001Columns 14 through 21-0.0012 0.0084 -0.0398 0.1268 -0.2473 0.2547 -0.1007 0.0027二次拟合函数f2 =8.8472e-05 x^2 + 0.0023245 x + 0.0024688七次拟合函数f7 =-2.4449e-10 x^7 + 4.5621e-08 x^6 - 3.3585e-06 x^5 + 0.00012385 x^4- 0.0023934 x^3 + 0.022986 x^2 - 0.085418 x + 0.06481十次拟合函数f10 =-8.8668e-14 x^10 + 2.1806e-11 x^9 - 2.2792e-09 x^8 + 1.3223e-07 x^7- 4.6647e-06 x^6 + 0.00010298 x^5 - 0.0014065 x^4 + 0.011236 x^3- 0.045832 x^2 + 0.072654 x - 0.020234二十次拟合函数f20 =7.7725e-26 x^20 - 4.2453e-23 x^19 + 1.0725e-20 x^18 - 1.6619e-18 x^17+ 1.7666e-16 x^16 - 1.365e-14 x^15 + 7.9243e-13 x^14 - 3.5248e-11 x^13 + 1.2142e-09 x^12 - 3.2533e-08 x^11 + 6.7733e-07 x^10 - 1.0894e-05 x^9 + 0.00013389 x^8 - 0.0012359 x^7 + 0.0083537 x^6 - 0.039837 x^5+ 0.12682 x^4 - 0.24729 x^3 + 0.25467 x^2 - 0.10066 x + 0.0026858四、【作业分析】通过使用Matlab对弗兰克赫兹实验的实验数据处理,可以观察到上图所示的曲线。
基于MATLAB的误差数据处理实验报告

基于MATLAB的误差数据处理实验报告《误差理论与数据处理》实验20121138晋美扎巴·测控三班实验⼀:MATLAB软件基础(⼀)实验⽬的:熟悉MATLAB软件的⽤户环境;了解MATLAB软件的⼀般⽬的命令;掌握MATLAB教组操作与运算函数;掌握MATLAB软件的基本绘图命令;掌握MATLAB语⾔的⼏种循环、条件和开关选择结构。
(⼆)实验内容:1.MATLAB软件的数组处理及运算操作E=eye(3,3);R=rand(3,2);O=zeros(2,3);S=[2,0;0,4];A=[E,R;O,S]B=[E,R+R*S;O,S^2]C=A*A所以B=C,原结论成⽴。
2.直接使⽤MATLAB软件进⾏作图练习(1)t=-1:0.01:1;x=sin(2*pi*t);y=cos(2*pi*10*t);plot(t,x,t,y)xlabel('t');ylabel('函数值')legend('正弦函数','余弦函数')(2)1) x=-10:0.01:10; y=normpdf(x,0,1); plot(x,y)(3)[x,y]=meshgrid(-10:0.05:10);z=sin(pi*sqrt(x.^2+y.^2));mesh(x,y,z);3.⽤MATLAB语⾔编写命令M-⽂件和函数M-⽂件a=input('请输⼊a的值')x0=a./2x1=(x0+a./x0)./2while(abs((x0-x1)>1e-5))x0=x1;x1=(x0+a./x0)./2;enddigits(8)vpa(x1)实验⼆:测量数据的统计分析(⼀)实验⽬的:通过对测量数据进⾏统计分析,学习掌握测量数据统计分析的基本⽅法。
(⼆)实验内容:1.>> x=normrnd(10,5,500,1);>> mu=mean(x)mu =9.7672>> sigma=std(x)sigma =4.8754>> va=var(x)va =23.7697>> hist(x)>> y=normpdf(x,mu,sigma); >> plot(x,y)2. x=-15:0.01:15; y1=normpdf(x,0,1); y2=normpdf(x,0,4); y3=normpdf(x,10,1); plot(x,y1,y2,y3);3.>> x=randn(500,1);>> mu=mean(x);>> va=var(x);>> cs=skewness(x);>> ck=kurtosis(x);>> hist(x);>> sigma=std(x);>> y=normpdf(x,mu,sigma); >> plot(x,y) >> cscs =0.1117>> ckck =3.0089>> mumu =0.0730>> vava=0.99814. >> x=-5:0.1:5; >> y1=tpdf(x,5); >> y2=tpdf(x,10); >> y3=tpdf(x,20); >> z=normpdf(x,0,1); >>plot(x,y1,x,y2,x,y3,x,z)5.>> x=0:0.2:30; >> y1=chi2pdf(x,5); >> y2=chi2pdf(x,10); >> y3=chi2pdf(x,20); >>plot(x,y1,x,y2,x,y3)6.x=0:0.01:10;y1=fpdf(x,4,5);y2=fpdf(x,10,20);y3=fpdf(x,50,50); plot(x,y1,x,y2,x,y3)实验三:等精度和⾮等精度直接测量数据处理(⼀)实验⽬的:通过本实验使学⽣掌握等精度和⾮等精度直接测量数据的基本处理⽅法;学习如何发现和处理测量列中的随机误差、系统误差和粗⼤误差,如何科学地表达测量结果。
matlab上机实验报告ppt

matlab上机实验报告pptMATLAB上机实验报告摘要:本实验报告利用MATLAB软件进行了一系列实验,包括数据处理、图像处理、信号处理等内容。
通过实验,我们掌握了MATLAB软件的基本操作和应用技巧,提高了数据分析和处理的能力。
1. 实验背景MATLAB是一种用于数学计算、数据分析和可视化的高级技术计算语言和交互式环境。
它是工程师和科学家们进行算法开发、数据分析、数据可视化和数值计算的首选工具。
本次实验旨在通过实际操作,掌握MATLAB的基本操作和应用技巧。
2. 实验内容本次实验主要包括以下内容:(1)数据处理:利用MATLAB对一组实验数据进行处理,包括数据的导入、清洗、分析和可视化。
(2)图像处理:利用MATLAB对一幅图像进行处理,包括图像的读取、处理和保存。
(3)信号处理:利用MATLAB对一组信号进行处理,包括信号的生成、滤波和频谱分析。
3. 实验过程(1)数据处理:首先,我们利用MATLAB将实验数据导入到工作空间中,然后对数据进行清洗和分析,最后利用MATLAB绘制出数据的可视化图表。
(2)图像处理:我们利用MATLAB读取一幅图像,并对图像进行处理,比如调整图像的亮度、对比度等参数,最后保存处理后的图像。
(3)信号处理:我们利用MATLAB生成一组信号,并对信号进行滤波处理,然后利用MATLAB进行信号的频谱分析。
4. 实验结果通过本次实验,我们成功地利用MATLAB对实验数据进行了处理和分析,得到了清晰的数据可视化图表;对一幅图像进行了处理,并保存了处理后的图像;对一组信号进行了滤波处理,并进行了频谱分析。
实验结果表明,MATLAB是一款功能强大、灵活多样的工程计算软件,能够满足工程师和科学家们的各种需求。
5. 实验结论本次实验通过MATLAB软件的实际操作,使我们掌握了MATLAB的基本操作和应用技巧,提高了我们的数据分析和处理能力。
同时,也加深了我们对MATLAB软件的理解和认识,为今后的工程计算和科学研究打下了坚实的基础。
matlab 实验报告

matlab 实验报告Matlab实验报告引言:Matlab是一种强大的数值计算和可视化软件,广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一:矩阵运算在这个实验中,我使用Matlab进行了矩阵运算。
首先,我创建了一个3x3的矩阵A和一个3x1的矩阵B,并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*,我得到了一个3x1的结果矩阵C。
接着,我对矩阵C进行了转置操作,得到了一个1x3的矩阵D。
最后,我计算了矩阵C和矩阵D的点积,并将结果输出。
实验二:数据可视化在这个实验中,我使用Matlab进行了数据可视化。
我选择了一组实验数据,包括时间和温度两个变量。
首先,我将数据存储在一个矩阵中,并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着,我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后,我使用Matlab的legend函数添加了图例,以便更好地理解图表。
实验三:数值积分在这个实验中,我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先,我使用Matlab的syms函数定义了符号变量x,并定义了函数f(x)。
接着,我使用Matlab的int函数对函数f(x)进行积分计算,并将结果输出。
为了验证结果的准确性,我还使用了Matlab的diff函数对积分结果进行了求导操作,并与原函数f(x)进行了比较。
实验四:信号处理在这个实验中,我使用Matlab进行了信号处理。
我选择了一个音频文件,并使用Matlab的audioread函数读取了该文件。
接着,我使用Matlab的fft函数对音频信号进行了傅里叶变换,并将结果绘制成频谱图。
为了进一步分析信号的特征,我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察,我可以更好地理解信号的频率和时域特性。
matlab上机实验报告

matlab上机实验报告《Matlab上机实验报告:探索数据分析与图像处理的奇妙世界》摘要:本实验报告基于Matlab平台,探索了数据分析与图像处理的应用。
通过实验,我们发现Matlab具有强大的数据处理和图像处理能力,能够帮助我们快速高效地分析数据和处理图像。
本文将详细介绍实验过程和结果,以及对Matlab在数据分析与图像处理中的应用前景进行探讨。
1. 实验目的本次实验旨在通过Matlab平台进行数据分析与图像处理实验,探索Matlab在这两个领域的应用能力,为学习者提供实践机会,加深对数据分析与图像处理的理解,并为未来的科研工作和工程实践提供技术支持。
2. 实验内容2.1 数据分析我们首先使用Matlab对一组实验数据进行分析,包括数据的可视化、统计特征提取、数据拟合等操作。
通过Matlab强大的数据处理工具,我们可以快速准确地分析数据,提取出其中的规律和特征,为后续的决策和应用提供支持。
2.2 图像处理其次,我们利用Matlab对一组图像进行处理,包括图像的增强、滤波、边缘检测等操作。
通过Matlab丰富的图像处理工具,我们可以对图像进行各种操作,改善图像质量,提取图像特征,甚至实现图像识别和分析。
3. 实验结果在数据分析方面,我们利用Matlab对实验数据进行了可视化展示,并提取了数据的统计特征,得到了数据的分布规律和趋势。
在图像处理方面,我们利用Matlab对图像进行了增强和边缘检测,得到了处理后的图像,观察到了图像质量的改善和边缘特征的提取。
4. 实验结论通过本次实验,我们深刻认识到Matlab在数据分析与图像处理领域的强大能力,能够帮助我们快速高效地分析数据和处理图像,为科研工作和工程实践提供技术支持。
我们相信,在未来的发展中,Matlab将在数据分析与图像处理领域发挥越来越重要的作用。
5. 展望基于本次实验的结果,我们对Matlab在数据分析与图像处理领域的应用前景进行了展望。
我们相信,随着科技的不断发展,Matlab将在数据分析与图像处理领域发挥越来越重要的作用,为人类社会的进步和发展做出更大的贡献。
matlab实验一实验报告

matlab实验一实验报告实验一:Matlab实验报告引言:Matlab是一种强大的数学软件工具,广泛应用于科学计算、数据分析和工程设计等领域。
本实验旨在通过使用Matlab解决实际问题,探索其功能和应用。
一、实验目的本次实验的主要目的是熟悉Matlab的基本操作和常用函数,了解其在科学计算中的应用。
二、实验内容1. 数值计算在Matlab中,我们可以进行各种数值计算,包括基本的加减乘除运算,以及更复杂的矩阵运算和方程求解。
通过编写相应的代码,我们可以实现这些功能。
例如,我们可以使用Matlab计算两个矩阵的乘积,并输出结果。
代码如下:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A * B;disp(C);```2. 数据可视化Matlab还提供了强大的数据可视化功能,可以将数据以图表的形式展示出来,更直观地观察数据的规律和趋势。
例如,我们可以使用Matlab绘制一个简单的折线图,来展示某个物体在不同时间下的位置变化。
代码如下:```matlabt = 0:0.1:10;x = sin(t);plot(t, x);xlabel('Time');ylabel('Position');title('Position vs. Time');```3. 图像处理Matlab还可以进行图像处理,包括图像的读取、处理和保存等操作。
我们可以通过Matlab对图像进行增强、滤波、分割等处理,以及进行图像的压缩和重建。
例如,我们可以使用Matlab读取一张图片,并对其进行灰度化处理。
代码如下:```matlabimg = imread('image.jpg');gray_img = rgb2gray(img);imshow(gray_img);```三、实验结果与分析在本次实验中,我们成功完成了数值计算、数据可视化和图像处理等任务。
基于MATLAB实验数据的几种处理方法

基于MATLAB实验数据的几种处理方法1.数据可视化:MATLAB提供了丰富的绘图函数和工具箱,可以通过绘制柱状图、折线图、散点图等可视化方式来展示实验数据的分布和趋势。
通过数据可视化,可以更直观地观察数据的特征,发现异常值或者趋势,并作为后续数据处理的依据。
2.数据预处理:对实验数据进行预处理可提高后续分析的准确性。
常见的数据预处理方法有:数据清洗(去除异常值、重复值、缺失值)、数据平滑(滤波处理,如移动平均、中值滤波)、数据标准化(归一化、标准化)等。
可以使用MATLAB的内置函数或者工具箱来实现这些数据预处理方法。
3.拟合与回归分析:通过拟合与回归分析,可以建立实验数据的数学模型,用于预测和估计。
MATLAB提供了各种拟合函数和回归分析工具,如线性回归、非线性回归、多项式拟合等。
这些方法可以帮助我们找到最佳的拟合曲线或者回归方程,用于预测未来的数据或者进行参数估计。
4. 数据聚类与分类:聚类与分类是将数据集划分为不同的类别或者簇群,利用相似性或距离度量确定数据之间的关系。
MATLAB提供了多种聚类和分类算法,如K-means聚类、层次聚类、支持向量机(SVM)等。
通过聚类与分类,我们可以发现数据内在的结构与规律,对数据进行分类,提取关键特征。
5.数据频谱分析:频谱分析是研究信号在频域上的特性,对于周期性信号或者周期性成分较强的信号,频谱分析可以揭示其频率分量和相应的能量分布。
MATLAB提供了多种频谱分析方法,如傅里叶变换、功率谱估计等。
通过频谱分析,我们可以对实验数据进行频域特征提取,提供有关信号周期性、频率成分等信息。
6.时间序列分析:时间序列分析是研究时序数据之间的相关性和趋势性的方法。
MATLAB提供了时间序列分析的函数和工具箱,如自相关函数(ACF)、偏自相关函数(PACF)、平稳性检验、ARMA模型等。
通过时间序列分析,可以建立模型预测未来的数据,或者研究数据随时间的变化规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%要内插的数据点为 2.5
y1 =
64
%得到对应 2.5 的值
>> y1=interp1(t,y,[2.5 4.3])
%内插数据点为 2.5,4.3,采用[ ]放入多个内插点
y1 =
64.0000 Байду номын сангаас6.9000
>> y2=interp1(t,y,[2.5 4.3],'cubic')
%以三次方程式对数据点 2.5,4.3 作内插
text(2, 0,'degree 3');
text(2,-1.3,'degree 4');
text(2,-2.6,'degree 5');
hold off
如图则为不同阶数的多项式拟合曲线。
figure4 3~5 阶多项式拟合曲线图
可以看出,次数越高的多项式精度越好。5 次的多项式经过所有的 6 个点。对于这个特殊 的数据集合来说,这个多项式可称为内部插值多项式。
下面我们对这些问题给以介绍并应用 MATLAB 进行处理。
2.多项式插值和拟合:
设 a = x0 < x1 < ⋯ < xn = b ,已知有 n +1对节点 (xi , yi ) , i = 0,1, 2⋯, n ,其中 xi 互不相 同,这些节点 (xi , yi ) , i = 0,1, 2⋯, n 可以看成是由某个函数 y = f (x) 产生的。 f 的解析表达
p=polyfit(x,y,n)
[p,s]=polyfit(x,y,n)
其中,x,y 为已知的数据组,n 为要拟合的多项式的阶次,向量 p 为返回的要拟合的多项式
的系数,向量 s 为调用函数 polyval 获得的错误预估计值。一般来说,多项式拟合中阶数 n 越大,
拟合的的精度就越高。请看下述例子。
p3=polyfit(x,y,3)
p4=polyfit(x,y,4)
p5=polyfit(x,y,5)
%分别求多项式
p3 =
-0.0162 0.0559 -0.0640 2.6681
5
利用 MATLAB 进行实验数据处理
p4 =
-0.0153 0.1067 0.1045 -1.2766 2.7130
设已知数据正确,要求以某种方法描述数据节点之间的关系,从而可以估计别的函数节点的值。 即多项式插值是根据给定的有限个样本点,产生另外的估计点以达到数据更为平滑的效果,这 种技术在信号处理与图像处理上应用广泛。
拟合方法的求解思路与插值不同,在拟合方法中,人们设法找出某条光滑曲线,它最佳地 拟合已知数据,但对经过的已知数据节点个数不作要求。当最佳拟合被解释为在数据节点上的
(1).多项式插值函数
yi = interp1(x,y,xi,method)对应于插值函数 yi = g(xi ) ,其中 x 和 y 是原已知数据的 x、y 值,
xi 是要内插的数据点,method 是插值方法,可以设定的内插方法有:‘nearest’为寻找最近数 据节点,由其得出函数值;‘linear’为线性插值;‘spline’为样条插值函数,在数据节点处光 滑,即左导等于右导;‘cubic’为三次方程式插值。其中‘nearest’执行速度最快,输出结果为 直角转折;‘linear’是默认值,在样本点上斜率变化很大 ;‘spline’最花时间,但输出结果也 最平滑;‘cubic’最占内存,输出结果与‘spline’差不多。如果数据变化较大,以‘spline’函 数内插所形成的曲线最平滑,效果最好。
时间/s
0
1
2
3
4
5
温度/℃
0
20
60
68
77
110
其中温度的数据从 20℃变化到 110℃,如果要分别估计在 t=2.5s 和 t=4.3s 时的温度,可以进行
如下处理:
>> clear
>> t=[0 1 2 3 4 5];y=[0 20 60 68 77 110];
%输入时间,输入温度
y1=interp1(t,y,2.5)
在某个[a,b] 区间上是存在的,但通常只能获取它在[a,b] 上一系列离散节点的值(即观测数
据)。函数在其它 x 点上的取值是未知的,这时只能用一个经验函数 y = g(x) 对真实函数
y = f (x) 作近似。
根据实验数据描述对象的不同,常用来确定经验函数 y = g(x) 的方法有两种:插值和拟合。
yˆi = α0 + α1r1(xi ) +⋯ + αmrm (xi ) , i = 1, 2,⋯, n
这就涉及到一个测量值准确与否的问题。如果测量值是准确的,没有误差,一般用插值;如果 测量值与真实值有误差,一般用曲线拟合。在 MATLAB 中,无论是插值还是拟合,都有相应 的函数来处理。
还有一个问题就是,在工程实践与科学应用中,经常要计算函数的积分与微分。当已知函 数形式来求函数的积分时,理论上可以利用牛顿-莱布尼兹公式来计算。但在实际应用中,经常 接触到的许多函数都找不到其积分函数,或者函数难于用公式表示(如只能用图形或表格绘出), 或者有些函数在用牛顿-莱布尼兹公式求解时非常复杂,有时甚至计算不出来。微分也存在相似 的情况,此时,需考虑这些函数的积分和微分的近似计算。
%由三次方程式插值绘出黑色曲线
>> figure(3)
%创建另一图像(3)
>> plot(xi,y0,'.r');hold on
%做出精确值的图像,用红色的小点表示
>> y3=interp1(x,y,xi,'spline');
%样条插值结果
plot(xi,y3,'og');hold on
%样条插值点的图像,用绿色的圈描出
线性插值也就是分段线性插值,它是将每两个相邻的节点用直线连起来,如此形成的一条 折线就是分段线性插值函数。线性内插是最简单的内插方法,但其适用范围很小;如果原来数
据的函数 f 有极大的变化,则假设其数据点之间为线性变化并不合理。而且线性插值虽然在 n
足够大时精度也相当高,但是折线在各个节点处不光滑,即插值函数在节点处导数不存在,从 而影响了线性插值在需要光滑插值曲线(如机械加工等)的领域中的应用。 三次样条函数其实就是分段三次多项式,它的二阶导数连续,且曲率也连续。三次样条函数记
3.最小二乘法拟合:
多项式拟合函数是最小二乘拟合的一种常用函数形式,我们常说的最小二乘拟合通常是指 最小二乘多项式拟合。比多项式更一般的拟合函数形式为
y = α0 + α1r1(x) +⋯ + αmrm (x)
(1)
其中 r1(x) , r2 (x) ,···, rm (x) 为 m 个函数(多项式拟合中取为幂函数)。假设有 n 组测量 数据 (xi , yi ) , i = 1, 2,⋯, n , n > m ,将它们代入上面设定的拟合函数形式中得到
%做出精确值的图像,用红色的小点表示
>> y1=interp1(x,y,xi);
%线性插值的结果
plot(xi,y1,'*b');hold on
%线性插值点的图像,用蓝色的*描出
>> plot(xi,y1,'-b')
%由线性插值绘出蓝色曲线(结果是好几段折线)
>> figure(2)
%创建另一图像(2)
y2 =
64.6078 83.3720
>> y3=interp1(t,y,[2.5 4.3],'spline')
%以 spline 函数对数据点 2.5,4.3 作内插
y3 =
66.8750 83.7127
(2).多项式拟合函数
MATLAB 的 polyfit 函数提供了从一阶到高阶多项式的拟合,其调用方法有两种
p5 =
0.0055 -0.0729 0.1615 0.7799 -1.9600 2.0000
>> xcurve=-3.5:0.1:7.2;
%生成 x 值
p3curve=polyval(p3,xcurve);
p4curve=polyval(p4,xcurve);
p5curve=polyval(p5,xcurve);
2
利用 MATLAB 进行实验数据处理
最小误差平方和,且所用的曲线限定为多项式时,这种拟合方法相当简捷,称为多项式拟合(也 称曲线拟合)。这在分析实验数据,将实验数据做解析描述时非常有用。
拟合和插值有许多相似之处,但是这两者最大的区别在于拟合要找出一个曲线方程式,而 插值仅是要求出插值数值即可。
下面以一维插值为例进行讨论。一维插值在 MATLAB 中可用多项式插值函数 interp1 来实 现,多项式拟合用 polyfit 来实现。
%计算在这些 x 点的多项式值
plot(xcurve,p3curve,'--',xcurve,p4curve,'-.',xcurve,p5curve,'-',x,y,'.')
>> lx=[-1,1.5];ly=[0,0];hold on;
plot(lx,ly,'--',lx,ly-1.3,'-.',lx,ly-2.6,'-');
作 S(x)(a ≤ x ≤ b) ,要求它满足以下三个条件:
(1) 在每个小区间[ xi−1, xi ](i = 1, 2,⋯, n) 上是三次多项式;
(2) 在 a ≤ x ≤ b 上二阶导数连续;
