偏微分方程数值及matlab实验报告
偏微分方程数值解第三次上机实验报告
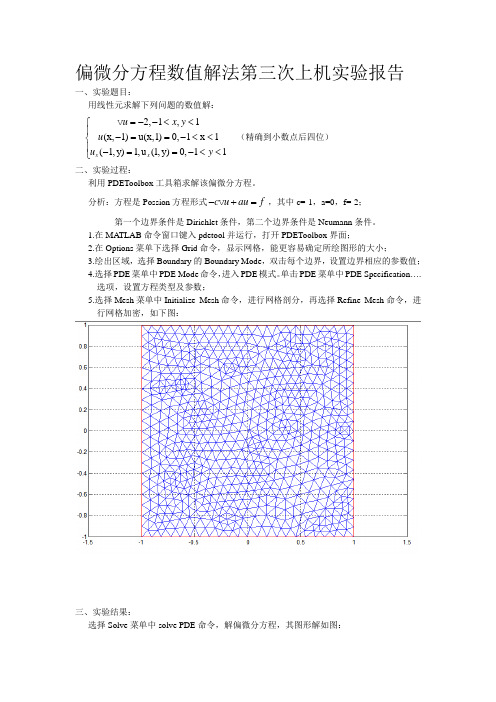
偏微分方程数值解法第三次上机实验报告一、实验题目:用线性元求解下列问题的数值解:2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ (精确到小数点后四位)二、实验过程:利用PDEToolbox 工具箱求解该偏微分方程。
分析:方程是Possion 方程形式c u au f -+=,其中c=-1,a=0,f=-2; 第一个边界条件是Dirichlet 条件,第二个边界条件是Neumann 条件。
1.在MA TLAB 命令窗口键入pdetool 并运行,打开PDEToolbox 界面;2.在Options 菜单下选择Grid 命令,显示网格,能更容易确定所绘图形的大小;3.绘出区域,选择Boundary 的Boundary Mode ,双击每个边界,设置边界相应的参数值;4.选择PDE 菜单中PDE Mode 命令,进入PDE 模式。
单击PDE 菜单中PDE Specification ….选项,设置方程类型及参数;5.选择Mesh 菜单中Initialize Mesh 命令,进行网格剖分,再选择Refine Mesh 命令,进行网格加密,如下图:三、实验结果:选择Solve 菜单中solve PDE 命令,解偏微分方程,其图形解如图:图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh,得到结点xy坐标;选择Solve菜单中的Export Solution…,得到每个节点处的值,输出u,即解的数值。
四、实验总结:通过本次试验,掌握了利用Matlab中的PDE求解工具得到PDE的解的方法,并对偏微分方程的形式有了更多的掌握。
用matlab对微分方程求解实验报告.

o 《高等数学》上机作业(三一、上机目的1、学会用 M a t l a b 求简单微分方程的解析解。
2、学会用 M a t l a b 求微分方程的数值解。
二、上机内容1、求简单微分方程的解析解.2、求微分方程的数值解.3、数学建模实例.4、上机作业. 三、上机作业1. 求微分方程:在初值条件下的特解,并画出解函数的图形. 命令>> y =d s o l v e ('x *D y +y -e x p (x =0','y (1=2*e x p (1','x ' 运行结果:y = 1/x *e x p (x +1/x *e x p (1'xxy y e +-=12(y e =函数图象:2. 求微分方程的特解.22450(00,'(110d y dyy dx dx y y ?+-=???==?命令>> y=dsolve('D2y+4*Dy-5*y=0','y(0=0,Dy(1=10','x' 运行结果:y=10/(exp(1+5*exp(-5*exp(x-10/(exp(1+5*exp(-5*exp(-5*x3. 鱼雷追击问题一敌舰在某海域内沿着正北方向航行时,我方战舰恰好位于敌舰的正西方向 1 公里处.我舰向敌舰发射制导鱼雷,敌舰速度为0.42 公里/分,鱼雷速度为敌舰速度的2倍。
试问敌舰航行多远时将被击中?M文件x0=0; xf=0.9999999999999; [x,y]=ode15s('eq1',[x0 xf],[0 0]; plot(x,y(:,1,'b.'hold on;y=0:0.1:1;plot(1,y, '*'运行结果图像:结论:大概在y=0.67处击中敌方舰艇!(选做一个慢跑者在平面上沿椭圆以恒定的速率v=1跑步,设椭圆方程为:x=10+20cost, y=20+5sint. 突然有一只狗攻击他. 这只狗从原点出发,以恒定速率w跑向慢跑者,狗的运动方向始终指向慢跑者.分别求出w=20,w=5时狗的运动轨迹.W=20M文件代码function dy=eq3(t,ydy=zeros(2,1;dy(1=20*(10+20*cos(t-y(1/sqrt((10+20*cos(t-y(1^2+(2 0+15*sin(t-y(2^2;dy(2=20*(20+15*sin(t-y(2/sqrt((10+20*cos(t-y(1^2+(2 0+15*sin(t-y(2^2;运行命令t0=0;tf=10;[t,y]=ode45('eq3',[t0 tf],[0 0];T=0:0.1:2*pi;X=10+20*cos(T;Y=20+15*sin(T;plot(X,Y,'-'hold onplot(y(:,1,y(:,2,'r*'运行结果:利用二分法更改tf tf=5时tf=2.5时tf=3.15时:所以在t=3.15时刻恰好追上!W=5M文件代码function dy=eq4(t,ydy=zeros(2,1;dy(1=5*(10+20*cos(t-y(1/sqrt((10+20*cos(t-y(1^2+(20 +15*sin(t-y(2^2; dy(2=5*(20+15*sin(t-y(2/sqrt((10+20*cos(t-y(1^2+(20 +15*sin(t-y(2^2; 命令:t0=0;tf=10;[t,y]=ode45('eq4',[t0 tf],[0 0]; T=0:0.1:2*pi;X=10+20*cos(T; Y=20+15*sin(T; plot(X,Y,'-'hold onplot(y(:,1,y(:,2,'*' 运行结果更改tf=20运行结果Tf=40 11所以永远追不上!四、上机心得体会高等数学是工科学生的主干科目,它应用于生产生活的方方面面,通过建模,计算可以求出实际问题的最优化问题!因此我们需要掌握建模和利用专业软件处理实际问题的能力! 12。
(完整版)偏微分方程的MATLAB解法

引言偏微分方程定解问题有着广泛的应用背景。
人们用偏微分方程来描述、解释或者预见各种自然现象,并用于科学和工程技术的各个领域fll。
然而,对于广大应用工作者来说,从偏微分方程模型出发,使用有限元法或有限差分法求解都要耗费很大的工作量,才能得到数值解。
现在,MATLAB PDEToolbox已实现对于空间二维问题高速、准确的求解过程。
偏微分方程如果一个微分方程中出现的未知函数只含一个自变量,这个方程叫做常微分方程,也简称微分方程;如果一个微分方程中出现多元函数的偏导数,或者说如果未知函数和几个变量有关,而且方程中出现未知函数对几个变量的导数,那么这种微分方程就是偏微分方程。
常用的方法有变分法和有限差分法。
变分法是把定解问题转化成变分问题,再求变分问题的近似解;有限差分法是把定解问题转化成代数方程,然后用计算机进行计算;还有一种更有意义的模拟法,它用另一个物理的问题实验研究来代替所研究某个物理问题的定解。
虽然物理现象本质不同,但是抽象地表示在数学上是同一个定解问题,如研究某个不规则形状的物体里的稳定温度分布问题,由于求解比较困难,可作相应的静电场或稳恒电流场实验研究,测定场中各处的电势,从而也解决了所研究的稳定温度场中的温度分布问题。
随着物理科学所研究的现象在广度和深度两方面的扩展,偏微分方程的应用范围更广泛。
从数学自身的角度看,偏微分方程的求解促使数学在函数论、变分法、级数展开、常微分方程、代数、微分几何等各方面进行发展。
从这个角度说,偏微分方程变成了数学的中心。
一、MATLAB方法简介及应用1.1 MATLAB简介MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
1.2 Matlab主要功能数值分析数值和符号计算工程与科学绘图控制系统的设计与仿真数字图像处理数字信号处理通讯系统设计与仿真财务与金融工程1.3 优势特点1) 高效的数值计算及符号计算功能,能使用户从繁杂的数学运算分析中解脱出来;2) 具有完备的图形处理功能,实现计算结果和编程的可视化;3) 友好的用户界面及接近数学表达式的自然化语言,使学者易于学习和掌握;4) 功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。
matlab求微分方程的解 实验报告四
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
matlab求微分方程的解-实验报告四

matlab求微分方程的解-实验报告四《matlab与数学实验》实验报告实验序号:实验四日期: 2015年 5 月 25 日班级132132002姓名彭婉婷学号 1321320057 实验名称求微分方程的解问题背景描述实际应用问题通过数学建模所归纳而得到的方程,绝大多数都是微分方程,另一方面,能够求解的微分方程也是十分有限的,特别是高阶方程和偏微分方程(组).这就要求我们既要研究微分方程(组)的解析解法(精确解),更要研究微分方程(组)的数值解法(近似解).实验目的本实验将主要研究微分方程(组)的数值解法(近似解),重点介绍 Euler 折线法.实验原理与数学模型MATLAB7.11.0主要内容(要点)1. 求微分方程0sin2')1(2=-+-xxyyx的通解.2. 求微分方程xeyyy x sin5'2''=+-的通解.3. 求微分方程组⎪⎪⎩⎪⎪⎨⎧=-+=++yxdtdyyxdtdx在初始条件0|,1|====ttyx下的特解,并画出解函数()y f x=的图形.4. 分别用 ode23、ode45 求上述第 3 题中的微分方程初值问题的数值解(近似解),求解区间为[0,2]t∈.利用画图来比较两种求解器之间的差异.5. 用 Euler 折线法求解微分方程初值问题⎪⎩⎪⎨⎧=-=1)0(,12'32yyxyy的数值解(步长h取0.1),求解范围为区间[0,2].选做:6. 用四阶 Runge-Kutta 法求解微分方程初值问题⎩⎨⎧=-=1)0(,cos'yxeyy x的数值解(步长h取0.1),求解范围为区间[0,3].迭代法实验过程记录(含基本步骤、主要程序清单及异常情况记录等)1.求微分方程0sin2')1(2=-+-xxyyx的通解.程序:clearsyms x yy=dsolve('(x^2-1)*Dy+2*x*y=sin(x)','x') 答案:y =-(C2 + cos(x))/(x^2 - 1)2.求微分方程xeyyy x sin5'2''=+-的通解.程序:clearsyms x yy=dsolve('D2y-2*Dy+5*y=exp(x)*sin(x)','x ')simplyify(x/y)weijiao答案:y =(exp(x)*sin(x))/6 - (sin(3*x)*exp(x))/8 + (sin(5*x)*exp(x))/24 + C4*cos(2*x)*exp(x) + sin(2*x)*exp(x)*(cos(x)/4 - cos(3*x)/12 + 1/6) + C5*sin(2*x)*exp(x)3. 求微分方程组⎪⎪⎩⎪⎪⎨⎧=-+=++00y x dt dy y x dt dx在初始条件0|,1|00====t t y x 下的特解,并画出解函数()y f x =的图形.程序:clearsyms x y t[x,y]=dsolve('Dx+x+y=0','Dy+x-y=0','x(0)=1','y(0)=0','t')ezplot(x,y,[0, 1])(t 的取值,t 是与x,y 相关的,如果不给范围,则会默认为一个较大的区间) simplify(x)simplify(y)答案:x =exp(2^(1/2)*t)/2 + 1/(2*exp(2^(1/2)*t)) - (2^(1/2)*exp(2^(1/2)*t))/4 +2^(1/2)/(4*exp(2^(1/2)*t))y =2^(1/2)/(4*exp(2^(1/2)*t)) -(2^(1/2)*exp(2^(1/2)*t))/4图形:4. 分别用 ode23、ode45 求上述第 3 题中的微分方程初值问题的数值解(近似解),求解区间为t .利用画图来比较两种求解器之间的差异.[0,2]先编写函数文件verderpol.m:clearfunction xprime=verderpol(t,x)xprime=[-x(1)-x(2); x(2)-x(1)];再编写命令文件cleary0=[1;0];[t,x] = ode45('verderpol',[0,2],y0);x1=x(:,1);x2=x(:,2);plot(x1,x2,'b-')hold ony0=[1;0];[t,x]=ode23('verderpol',[0,2],y0);x1=x(:,1);x2=x(:,2);plot(x(:,1),x(:,2),'r-');图形:两种求解器之间的差异:ode45大部分场合的首选算法ode23使用于精度较低的情形但在此题中并没有体现出差异。
matlab数值计算实验报告

matlab数值计算实验报告Matlab数值计算实验报告引言:Matlab是一种广泛应用于科学与工程领域的高级计算机语言和环境,它提供了丰富的函数库和工具箱,方便用户进行数值计算、数据分析和可视化等任务。
本实验报告将介绍我在使用Matlab进行数值计算实验中的一些经验和心得体会。
一、数值计算方法数值计算方法是一种利用数值近似来解决实际问题的方法,它在科学和工程领域具有广泛的应用。
在Matlab中,我们可以利用内置的函数和工具箱来实现各种数值计算方法,例如插值、数值积分、数值微分等。
二、插值方法插值是一种通过已知数据点来推测未知数据点的方法。
在Matlab中,我们可以使用interp1函数来进行插值计算。
例如,我们可以通过已知的一些离散数据点,利用interp1函数来估计其他位置的数值。
这在信号处理、图像处理等领域具有重要的应用。
三、数值积分数值积分是一种通过分割曲线或曲面来近似计算其面积或体积的方法。
在Matlab中,我们可以使用quad函数来进行数值积分计算。
例如,我们可以通过quad函数来计算某个函数在给定区间上的积分值。
这在概率统计、物理学等领域具有广泛的应用。
四、数值微分数值微分是一种通过数值逼近来计算函数导数的方法。
在Matlab中,我们可以使用diff函数来进行数值微分计算。
例如,我们可以通过diff函数来计算某个函数在给定点上的导数值。
这在优化算法、控制系统等领域具有重要的应用。
五、数值求解数值求解是一种通过数值近似来计算方程或方程组的根的方法。
在Matlab中,我们可以使用fsolve函数来进行数值求解计算。
例如,我们可以通过fsolve函数来求解某个非线性方程的根。
这在工程计算、金融分析等领域具有广泛的应用。
六、实验应用在本次实验中,我使用Matlab进行了一些数值计算的应用实验。
例如,我利用插值方法来估计某个信号在给定位置的数值,利用数值积分方法来计算某个曲线下的面积,利用数值微分方法来计算某个函数在给定点的导数值,以及利用数值求解方法来求解某个方程的根。
偏微分方程(PDEs)的MATLAB数值解法

偏微分方程的MATLAB求解精讲©MA TLAB求解微分/偏微分方程,一直是一个头大的问题,两个字,“难过”,由于MA TLAB对LaTeX的支持有限,所有方程必须化成MA TLAB可接受的标准形式,不支持像其他三个数学软件那样直接傻瓜式输入,这个真把人给累坏了!不抱怨了,还是言归正传,回归我们今天的主体吧!MA TLAB提供了两种方法解决PDE问题,一是pdepe()函数,它可以求解一般的PDEs,据用较大的通用性,但只支持命令行形式调用。
二是PDE工具箱,可以求解特殊PDE问题,PDEtool有较大的局限性,比如只能求解二阶PDE问题,并且不能解决偏微分方程组,但是它提供了GUI界面,从繁杂的编程中解脱出来了,同时还可以通过File->Save As直接生成M代码一、一般偏微分方程组(PDEs)的MA TLAB求解 (3)1、pdepe函数说明 (3)2、实例讲解 (4)二、PDEtool求解特殊PDE问题 (6)1、典型偏微分方程的描述 (6)(1)椭圆型 (6)(2)抛物线型 (6)(3)双曲线型 (6)(4)特征值型 (7)2、偏微分方程边界条件的描述 (8)(1)Dirichlet条件 (8)(2)Neumann条件 (8)3、求解实例 (9)一、一般偏微分方程组(PDEs)的MATLAB 求解1、pdepe 函数说明MA TLAB 语言提供了pdepe()函数,可以直接求解一般偏微分方程(组),它的调用格式为sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t)【输入参数】@pdefun :是PDE 的问题描述函数,它必须换成下面的标准形式(,,)[(,,,)](,,,)()m m u u u uc x t x x f x t u s x t u x t x x x−∂∂∂∂∂=+∂∂∂∂∂式1 这样,PDE 就可以编写下面的入口函数 [c,f,s]=pdefun(x,t,u,du)m,x,t 就是对应于(式1)中相关参数,du 是u 的一阶导数,由给定的输入变量即可表示出出c,f,s 这三个函数@pdebc :是PDE 的边界条件描述函数,必须先化为下面的形式(,,)(,,).*(,,,)0up x t u q x t u f x t u x∂+=∂ 于是边值条件可以编写下面函数描述为 [pa,qa,pb,qb]=pdebc(x,t,u,du)其中a 表示下边界,b 表示下边界@pdeic :是PDE 的初值条件,必须化为下面的形式00(,)u x t u =我们使用下面的简单的函数来描述为 u0=pdeic(x)m,x,t :就是对应于(式1)中相关参数【输出参数】sol :是一个三维数组,sol(:,:,i)表示u i 的解,换句话说u k 对应x(i)和t(j)时的解为sol(i,j,k)通过sol ,我们可以使用pdeval()直接计算某个点的函数值2、实例讲解试求解下面的偏微分2111222221220.024()0.17()u u F u u t xu u F u u tx ∂∂=−− ∂∂ ∂∂ =−− ∂∂ 其中, 5.7311.46()x x F x e e −=−,且满足初始条件12(,0)1,(,0)0u x u x ==及边界条件1221(0,)0,(0,)0,(1,)1,(1,)0u ut u t u t t x x∂∂====∂∂【解】(1)对照给出的偏微分方程,根据标注形式,则原方程可以改写为111222120.024()1.*1()0.17u u F u u x u u F u u t t x ∂−−∂∂∂=+ ∂−∂∂∂可见m=0,且1122120.024()1,,1()0.17u F u u x c f s u F u u x ∂−− ∂===∂−∂%% 目标PDE 函数function [c,f,s]=pdefun (x,t,u,du) c=[1;1];f=[0.024*du(1);0.17*du(2)]; temp=u(1)-u(2);s=[-1;1].*(exp(5.73*temp)-exp(-11.46*temp));(2)边界条件改写为12011010.*.*00000u f f u −+=+=下边界上边界%% 边界条件函数function [pa,qa,pb,qb]=pdebc(xa,ua,xb,ub,t) %a 表示下边界,b 表示上边界 pa=[0;ua(2)];qa=[1;0]; pb=[ub(1)-1;0]; qb=[0;1];(3)初值条件改写为1210u u =%% 初值条件函数function u0=pdeic(x) u0=[1;0];(4)最后编写主调函数 clcx=0:0.05:1; t=0:0.05:2; m=0;sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t);figure('numbertitle','off','name','PDE Demo ——by Matlabsky') subplot(211)surf(x,t,sol(:,:,1)) title('The Solution of u_1') xlabel('X') ylabel('T') zlabel('U') subplot(212)surf(x,t,sol(:,:,2)) title('The Solution of u_2') xlabel('X') ylabel('T') zlabel('U')二、PDEtool 求解特殊PDE 问题MATLAB 的偏微分工具箱(PDE toolbox)可以比较规范的求解各种常见的二阶偏微分方程,但是惋惜的是只能求解特殊二阶的PDE 问题,并且不支持偏微分方程组!PDE toolbox 支持命令行形式求解PDE 问题,但是要记住那些命令以及调用形式真的很累人,还好MATLAB 提供了GUI 可视交互界面pdetool ,在pdetool 中可以很方便的求解一个PDE 问题,并且可以帮我们直接生成M 代码(File->Save As)。
偏微分方程解的几道算例(差分、有限元)-含matlab程序(1)

A(i-1,i)=-r; A(i,i-1)=-r; end end u=zeros(N+1,M+1); u(N+1,:)=u1; for k=1:N b=u(N+2-k,2:M)+0.02; u(N+1-k,2:M)=inv(A)*b';%求解迭代方程组 end uT=u(1,:);%0.25时刻的解 %精确解与数值解画图 x1=[0,x,1]; plot(x1,uT,'o') hold u_xt = exp (-pi*pi*T)*sin (pi*x1) + x1.*(1 - x1); plot (x1, u_xt, ' r') e=u_xt-uT; 六点格式 function [e]=six(dx,dt,T) %用六点对称格式求解,dx为x方向步长,dt为t方向步长 % e为误差 M=1/dx; N=T/dt; %得到第一层的值 u1=zeros(1,M+1); x=[1:M-1]*dx; u1([2:M])= sin(pi*x)+x.*(1 - x); %网比 r=dt/dx/dx;r2=2+2*r;r3=2-2*r; %构造三对角矩阵A for i=1:M-1 A(i,i)=r2;
0.0070 0.0027
-0.0097 -0.0037
-0.0013 -0.0005
0.0082 0.0000
-0.0114 0.0000
-0.0015 0.0000
0.0087 -0.0120
-0.0016
注:这里的"误差"=精确解-数值解. 2.精确解与数值解结果图像对比
“向前差分格式”:
偏微分方程数值解上机实验报告(matlab做的)

偏微分方程数值解法上机报告(一)一、实验题目:用Ritz-Galerkin 方法求解边值问题2u '',01(0)0,(1)1u x x u u ⎧-+=<<⎨==⎩的第n 次近似()n u x ,基函数()sin(),1,2,...,i x i x i n ϕπ==.二、实验目的:通过本次上机实验,理解求解初值问题的变分问题的最重要的近似解法——Ritz-Galerkin 方法,以便为学习有限元法打好基础。
此外,要熟悉用Matlab 解决数学问题的基本编程方法,提高运用计算机解决问题的能力。
三、实验代码:n=5;syms x;for i=1:np(i)=sin(i*pi*x);q(i)=-i^2*pi^2*sin(i*pi*x);endfor i=1:nb(i)=2*int(p(i),0,1);for j=1:nA(i,j)=int((-q(j)+p(j))*p(i),0,1);endendt=inv(A)*b'四、运行结果:t=2251799813685248/3059521645650671/pi281474976710656/9481460623939047/pi281474976710656/43582901062631895/pi五、总结:通过本次上机,我了解了Ritz-Galerkin 方程 n j j p f cj p i p a n i i ,...,2,1)),(,())(),((1==∑=,明白了用Ritz-Galerkin 方法解决边值问题的变分问题的基本原理,并接近一步提高自己的编程动手能力,受益匪浅。
偏微分方程数值解法上机报告(二)一、 实验题目:用线性元求下列边值问题的数值解2''2sin ,0142(0)0,'(1)0y y x x y y ππ⎧-+=<<⎪⎨⎪==⎩二、 实验目的:通过本次上机,熟悉和掌握用Galerkin 法观点出发导出的求解处置问题数值解的线性有限元法。
MATLAB中的偏微分方程数值解法

MATLAB中的偏微分方程数值解法偏微分方程(Partial Differential Equations,PDEs)是数学中的重要概念,广泛应用于物理学、工程学、经济学等领域。
解决偏微分方程的精确解往往非常困难,因此数值方法成为求解这类问题的有效途径。
而在MATLAB中,有丰富的数值解法可供选择。
本文将介绍MATLAB中几种常见的偏微分方程数值解法,并通过具体案例加深对其应用的理解。
一、有限差分法(Finite Difference Method)有限差分法是最为经典和常用的偏微分方程数值解法之一。
它将偏微分方程的导数转化为差分方程,通过离散化空间和时间上的变量,将连续问题转化为离散问题。
在MATLAB中,使用有限差分法可以比较容易地实现对偏微分方程的数值求解。
例如,考虑一维热传导方程(Heat Equation):∂u/∂t = k * ∂²u/∂x²其中,u为温度分布随时间和空间的变化,k为热传导系数。
假设初始条件为一段长度为L的棒子上的温度分布,边界条件可以是固定温度、热交换等。
有限差分法可以将空间离散化为N个节点,时间离散化为M个时刻。
我们可以使用中心差分近似来计算二阶空间导数,从而得到以下差分方程:u(i,j+1) = u(i,j) + Δt * (k * (u(i+1,j) - 2 * u(i,j) + u(i-1,j))/Δx²)其中,i表示空间节点,j表示时间步。
Δt和Δx分别为时间和空间步长。
通过逐步迭代更新节点的温度值,我们可以得到整个时间范围内的温度分布。
而MATLAB提供的矩阵计算功能,可以大大简化有限差分法的实现过程。
二、有限元法(Finite Element Method)有限元法是另一种常用的偏微分方程数值解法,特点是适用于复杂的几何形状和边界条件。
它将求解区域离散化为多个小单元,通过构建并求解代数方程组来逼近连续问题。
在MATLAB中,我们可以使用Partial Differential Equation Toolbox提供的函数进行有限元法求解。
偏微分方程数值解实验报告

(2) u
uh H 1 、 u
uh
L2
、
max
0 x1
u - uh
2、用线性元求解下列问题的数值解:
u = -2,-1< x, y < 1, u(x,-1)= u(x,1)= 0,-1< x < 1, ux(-1, y)= 1,ux = 0,-1< y < 1.
精确到小数点后第六位,并画出解曲面。
偏微分方程数值实验报告及算法实现(1)

偏微分方程数值实验报告一实验题目:利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x ex u x -=-实现算法:对于两点边值问题 ,)(,)(,,d 22βα==∈=-b u a u l x f dxu (1) 其中),(b a l =f b a ),(<为],[b a l =上的连续函数,βα,为给定常数.其相应的有限差分法的算法如下:1.对求解区域做网格剖分,得到计算网格.在这里我们对区间l 均匀剖分n 段,每个剖分单元的剖分步长记为na b h -=. 2.对微分方程中的各阶导数进行差分离散,得到差分方程.运用的离散方法有:方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα 方法二:利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈ (2) 将(2)带入(1)可以得到)()()()(2)(211u R x f hx u x u x u i i i i i +=+---+, 其中)(u R i 为无穷小量,这时我们丢弃)(u R i ,则有在i x 处满足的计算公式:1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i , (3) 3.根据边界条件,进行边界处理.由(1)可得βα==n u u ,0 (4)称(3)(4)为逼近(1)的差分方程,并称相应的数值解向量1-n U 为差分解,i u 为)(i x u 的近似值.4.最后求解线性代数方程组,得到数值解向量1-n U .程序代码:第一步:编写有限差分格式相关函数function [ x,U ]=FDld_bvp(N,f,a,b,u)%******************************************************************** %% FD1d_bvp利用中心差分格式求解两点边值问题%参数:% 输入参数:% 整数N,网格节点数,% 函数f(x),计算右端函数f(x);% a,计算区间左端点% b,计算区间右端点% u,真解函数% 输出参数:% 差分解向量U% 均匀剖分区间[a,b],得到网格x(i)=a+(i-1)*(b-a)/(N-1)h=(b-a)/(N-1);x=(a:h:b)';% 创建线性差分方程组系数矩阵c1=-1/h/h;c2=2/h/h+1;g=[c1*ones(1,N-2),0];c=[0,c1*ones(1,N-2)];d=[1,c2*ones(1,N-2),1];A=diag(g,-1)+diag(d)+diag(c,1);% 创建线性差分方程组右端项rhs=f(x);rhs(1)=u(x(1));rhs(N)=u(x(N));% 求解上述代数系统U=A\rhs;endfunction[e0,e1,emax]=FD1d_error(x,U,u_exact)%% FD1d_ERROR 计算有限差分误差% 参数:% 输入参数:% x,网格节点坐标向量% U,网格节点坐标向量上的有限差分数值解向量Ux% u_exact,真解函数% 输出参数:% e0% e1% emaxN=length(x);h=(x(end)-x(1))/(N-1);ue=u_exact(x);%真解在网格点处的值xee=ue-U;e0=h*sum(ee.^2);e1=sum((ee(2:end)-ee(1:end-1)).^2)/h;e1=e1+e0;e0=sqrt(e0);e1=sqrt(e1);emax=max(abs(ue-U));endfunction FD1d_bvp_test%%测试脚本% 初始化相关数据N=[6,11,21,41,81];L=-1;R=1;emax=zeros(5,1);e0=zeros(5,1);e1=zeros(5,1);%%求解并计算误差for i = 1:5[x,U] =FD1d_bvp(N(i),@f ,L,R,@u);[e0(i),e1(i),emax(i)]=FD1d_error(x,U,@u);X{i}=x;UN{i}=U;endue=u(X{5});%% 显示真阶及不同网格剖分下的数值解plot(X{5},ue,'-k*',X{1},UN{1},'-ro',X{2},...UN{2},'-gs',X{3},UN {3},'-bd ',...X{4},UN{4},'-ch ',X{5} , UN {5},'-mx');title('The solution plot');xlabel('x');ylabel ('u');legend('exact','N=6','N =11','N=21','N =41','N =81'); %% 显示误差format shortedisp ('emax e0 e1 ');disp ([ emax , e0 , e1 ]);end第二步:编写方程的右端函数和真解分别保存为m f .和m u . function f=f(x)f=exp(-x.^2).*(4.*x.^4-15.*x.^2+5);endfunction u=u(x)u=exp(-x.^2).*(1-x.^2);end实验结果:在命令窗口输入>> FD1d_bvp_test回车可得运算结果和图像emax e0 e15.8219e-02 5.3470e-02 1.1724e-011.5919e-02 1.2802e-022.9349e-023.9305e-03 3.1663e-03 7.3357e-039.7959e-04 7.8946e-04 1.8338e-032.4471e-04 1.9723e-04 4.5844e-04。
二阶椭圆偏微分方程实例求解(附matlab代码)

《微分方程数值解法》期中作业实验报告二阶椭圆偏微分方程第一边值问题姓名:学号:班级:2013年11月19日二阶椭圆偏微分方程第一边值问题摘要对于解二阶椭圆偏微分方程第一边值问题.课本上已经给出了相应的差分方程。
而留给我的难题就是把差分方程组表示成系数矩阵的形式.以及对系数进行赋值。
解决完这个问题之后.我在利用matlab 解线性方程组时.又出现“out of memory ”的问题。
因为99*99阶的矩阵太大.超出了分配给matlab 的使用内存。
退而求其次.当n=10.h=1/10或n=70.h=1/70时.我都得出了很好的计算结果。
然而在解线性方程组时.无论是LU 分解法或高斯消去法.还是gauseidel 迭代法.都能达到很高的精度。
关键字:二阶椭圆偏微分方程 差分方程 out of memory LU 分解 高斯消去法 gauseidel 迭代法一、题目重述解微分方程:()()2222((,))((,))()(,)()(,)(,)1y x x x y y x y yxxyxye u x y e u x y x y u x y x y u x y u x y y e x e e y x e--+++-+=-++++已知边界:(0,)1,(1,),(,0)1,(,1)y x u y u y e u x u x e ====求数值解, 把区域[0,1][0,1]G =?分成121/100,1/100h h ==.n =100 注:老师你给的题F 好像写错了.应该把22x y y e x e +改成22y x y e x e +。
二、问题分析与模型建立2.1微分方程上的符号说明()()22221y x xy xy y e x e e y x e -++++2.2课本上差分方程的缺陷课本上的差分方程为:举一个例子:当i=2,j=3时.;当i=3,j=3时.。
但是.显然这两个不是同一个数.其大小也不相等。
数值分析matlab实验报告

数值分析matlab实验报告数值分析 Matlab 实验报告一、实验目的数值分析是研究各种数学问题数值解法的学科,Matlab 则是一款功能强大的科学计算软件。
本次实验旨在通过使用 Matlab 解决一系列数值分析问题,加深对数值分析方法的理解和应用能力,掌握数值计算中的误差分析、数值逼近、数值积分与数值微分等基本概念和方法,并培养运用计算机解决实际数学问题的能力。
二、实验内容(一)误差分析在数值计算中,误差是不可避免的。
通过对给定函数进行计算,分析截断误差和舍入误差的影响。
例如,计算函数$f(x) =\sin(x)$在$x = 05$ 附近的值,比较不同精度下的结果差异。
(二)数值逼近1、多项式插值使用拉格朗日插值法和牛顿插值法对给定的数据点进行插值,得到拟合多项式,并分析其误差。
2、曲线拟合采用最小二乘法对给定的数据进行线性和非线性曲线拟合,如多项式曲线拟合和指数曲线拟合。
(三)数值积分1、牛顿柯特斯公式实现梯形公式、辛普森公式和柯特斯公式,计算给定函数在特定区间上的积分值,并分析误差。
2、高斯求积公式使用高斯勒让德求积公式计算积分,比较其精度与牛顿柯特斯公式的差异。
(四)数值微分利用差商公式计算函数的数值导数,分析步长对结果的影响,探讨如何选择合适的步长以提高精度。
三、实验步骤(一)误差分析1、定义函数`compute_sin_error` 来计算不同精度下的正弦函数值和误差。
```matlabfunction value, error = compute_sin_error(x, precision)true_value = sin(x);computed_value = vpa(sin(x), precision);error = abs(true_value computed_value);end```2、在主程序中调用该函数,分别设置不同的精度进行计算和分析。
(二)数值逼近1、拉格朗日插值法```matlabfunction L = lagrange_interpolation(x, y, xi)n = length(x);L = 0;for i = 1:nli = 1;for j = 1:nif j ~= ili = li (xi x(j))/(x(i) x(j));endendL = L + y(i) li;endend```2、牛顿插值法```matlabfunction N = newton_interpolation(x, y, xi)n = length(x);%计算差商表D = zeros(n, n);D(:, 1) = y';for j = 2:nfor i = j:nD(i, j) =(D(i, j 1) D(i 1, j 1))/(x(i) x(i j + 1));endend%计算插值结果N = D(1, 1);term = 1;for i = 2:nterm = term (xi x(i 1));N = N + D(i, i) term;endend```3、曲线拟合```matlab%线性最小二乘拟合p = polyfit(x, y, 1);y_fit_linear = polyval(p, x);%多项式曲线拟合p = polyfit(x, y, n);% n 为多项式的次数y_fit_poly = polyval(p, x);%指数曲线拟合p = fit(x, y, 'exp1');y_fit_exp = p(x);```(三)数值积分1、梯形公式```matlabfunction T = trapezoidal_rule(f, a, b, n)h =(b a) / n;x = a:h:b;y = f(x);T = h ((y(1) + y(end))/ 2 + sum(y(2:end 1)));end```2、辛普森公式```matlabfunction S = simpson_rule(f, a, b, n)if mod(n, 2) ~= 0error('n 必须为偶数');endh =(b a) / n;x = a:h:b;y = f(x);S = h / 3 (y(1) + 4 sum(y(2:2:end 1))+ 2 sum(y(3:2:end 2))+ y(end));end```3、柯特斯公式```matlabfunction C = cotes_rule(f, a, b, n)h =(b a) / n;x = a:h:b;y = f(x);w = 7, 32, 12, 32, 7 / 90;C = h sum(w y);end```4、高斯勒让德求积公式```matlabfunction G = gauss_legendre_integration(f, a, b)x, w = gauss_legendre(5);%选择适当的节点数t =(b a) / 2 x +(a + b) / 2;G =(b a) / 2 sum(w f(t));end```(四)数值微分```matlabfunction dydx = numerical_derivative(f, x, h)dydx =(f(x + h) f(x h))/(2 h);end```四、实验结果与分析(一)误差分析通过不同精度的计算,发现随着精度的提高,误差逐渐减小,但计算时间也相应增加。
偏微分数值解(2,MATLAB求解方法)

初始条件:
u1 ( x,0) 1,
u2 ( x,0) 0
边界条件:
u1 (0, t ) 0, u1 (1, t ) 1 x u2 u2 (0, t ) 0, (1, t ) 0 x
方程来自电动力学中关于电磁场理论的一个 偏微分方程组。
2.1 用偏微分方程工具箱求解微分方程
直接使用图形用户界面( Graphical User Interface,简记作GUI)求解.
图22.1 所讨论定解问题的区域
第三步:选取边界 首先选择Boundary菜单中Boundary Mode命 令,进入边界模式.然后单击Boundary菜单中 Remove All Subdomain Borders选项,从而去掉子 域边界,如图22.2.单击Boundary菜单中Specify Boundary Conditions选项,打开Boundary Conditions对话框,输入边界条件.本例取默认条 件,即将全部边界设为齐次Dirichlet条件,边界显 示为红色.如果想将几何与边界信息存储,可选择 Boundary菜单中的Export Decomposed Geometry,Boundary Cond‟s命令,将它们分别存储 在g、b变量中,并通过MATLAB形成M文件.
第八步:若要画等值线图和矢量场图,单击 Plot 菜单中 Parameter 选项,在 Plot selection 对话框中选中 Contour 和 Arrows 两项.然后单击 Plot 按钮,可显示解的等值 线图和矢量场图,如图 2. 6 所示。
图 2.6 解的等值线图和矢量场图
(1) u1=hyperbolic(u0,ut0,tlist,b,p,e,t,c,a,f,d)
偏微分方程实验报告

Columns 9 through 11
0.4663 0.2451 0.0000
u =
Columns 1 through 8
0 0.2800 0.5325 0.7330 0.8617 0.9060 0.8617 0.7330
end
un=[0 un 0]
e=abs(u-Un)
Un=un;
end
5、实验数据记录与分析
e =
0 0 0 0 0 0 0 0 0 0 0
u =
Columns 1 through 8
0 0.2941 0.5595 0.7701 0.9053 0.9518 0.9053 0.7701
Columns 9 through 11
n=length(t)
Un=sin(pi*x0)
fori=1:n
un=[];
u=[];
forr=1:11
u1=exp(-pi^2*t(i))*sin(pi*x0(r));
u=[u u1];
end
u
forj=2:10
Un1=Un(j)+0.5*(Un(j+1)-2*Un(j)+Un(j-1));
un=[un Un1];
偏微分方程实验报告偏微分方程偏微分方程数值解matlab解偏微分方程偏微分方程pdf椭圆型偏微分方程matlab偏微分方程matlab解偏微分方程组二阶偏微分方程二阶线性偏微分方程
实验名称
抛物型方程的差分格式
实验时间
2014年5月15日
2014年5月29日
2014年6月12日
matlab数值分析实验报告

matlab数值分析实验报告Matlab数值分析实验报告引言数值分析是一门研究利用计算机进行数值计算和模拟的学科,它在科学计算、工程技术和金融等领域有着广泛的应用。
本次实验报告将介绍在Matlab环境下进行的数值分析实验,包括数值微分、数值积分和线性方程组求解等内容。
一、数值微分数值微分是通过数值方法计算函数的导数,常用的数值微分方法有前向差分、后向差分和中心差分。
在Matlab中,可以使用diff函数来计算函数的导数。
例如,对于函数f(x)=x^2,在Matlab中可以使用如下代码进行数值微分的计算:```matlabsyms x;f = x^2;df = diff(f, x);```二、数值积分数值积分是通过数值方法计算函数的定积分,常用的数值积分方法有梯形法则、辛普森法则和龙贝格积分法。
在Matlab中,可以使用trapz、quad和integral等函数来进行数值积分的计算。
例如,对于函数f(x)=sin(x),可以使用如下代码进行数值积分的计算:```matlabx = linspace(0, pi, 100);y = sin(x);integral_value = trapz(x, y);```三、线性方程组求解线性方程组求解是数值分析中的重要问题,常用的求解方法有高斯消元法和LU 分解法。
在Matlab中,可以使用\操作符来求解线性方程组。
例如,对于线性方程组Ax=b,可以使用如下代码进行求解:```matlabA = [1, 2; 3, 4];b = [5; 6];x = A\b;```四、实验结果与分析在本次实验中,我们分别使用Matlab进行了数值微分、数值积分和线性方程组求解的计算。
通过实验结果可以发现,Matlab提供了丰富的数值计算函数和工具,能够方便地进行数值分析的计算和求解。
数值微分的计算结果与解析解相比较,可以发现数值微分的误差随着步长的减小而减小,但是当步长过小时,数值微分的误差会受到舍入误差的影响。
偏微分方程数值解实验报告

偏微分方程数值解上机实验报告(一)实验一一、上机题目:用线性元求解下列边值问题的数值解:-y′′+π24y=π22sinπ2x,0<x<1y(0)=0,y′(1)=0二、实验程序:function S=bzx=fzero(@zfun,1);[t y]=ode45(@odefun,[0 1],[0 x]);S.t=t;S.y=y;plot(t,y)xlabel('x:´从0一直到1')ylabel('y')title('线性元求解边值问题的数值解')function dy=odefun(x,y)dy=[0 0]';dy(1)=y(2);dy(2)=(pi^2)/4*y(1)-((pi^2)/2)*sin(x*pi/2);function z=zfun(x);[t y]=ode45(@odefun,[0 1],[0 x]);z=y(end)-0;三、实验结果:1.以步长h=0.05进行逐步运算,运行上面matlab程序结果如下:2.在0<x<1区间上,随着x 的不断变化,x ,y 之间关系如下图所示:(二)实验二四、 上机题目:求解Helmholtz 方程的边值问题:21u k u -∆-=,于(0,1)*(0,1)Ω=0u =,于1{0,01}{01,1}x y x y Γ==≤≤≤≤= 12{0,01}{01,1}0,{01,0}{1,01}x y x y u x y x y n Γ==≤≤≤≤=∂=Γ=≤≤==≤≤∂于其中k=1,5,10,15,20五、实验程序:(采用有限元方法,这里对[0,1]*[0,1]采用n*n的划分,n为偶数)n=10;a=zeros(n);f=zeros(n);b=zeros(1,n);U=zeros(n,1);u=zeros(n,1);for i=2:na(i-1,i-1)=pi^2/(12*n)+n;a(i-1,i)= pi^2/(24*n)-n;a(i,i-1)= pi^2/(24*n)-n;for j=1:nif j==i-1a(i,j)=a(i,i-1);else if j==ia(i-1,j-1)=2*a(i-1,i-1);else if j==i+1a(i,j)=a(i,i+1);elsea(i,j)=0;endendendendenda(n,n)=pi^2/(12*n)+n;for i=2:nf(i-1,i)=4/pi*cos((i-1)*pi/2/n)-8*n/(pi^2)*sin(i*pi/2/n)+8*n/(pi^2)*s in((i-1)*pi/2/n);endfor i=1:nf(i,i)=-4/pi*cos(i*pi/2/n)+8*n/(pi^2)*sin(i*pi/2/n)-8*n/(pi^2)*sin((i -1)*pi/2/n);end%b(j)=f(i-1,j)+f(i,j)for i=1:(n-1)b(i)=f(i,i)+f(i,i+1);endb(n)=f(n,n);tic;n=20;can=20;s=zeros(n^2,10);h=1/n;st=1/(2*n^2);A=zeros((n+1)^2,(n+1)^2);syms x y;for k=1:1:2*n^2s(k,1)=k;q=fix(k/(2*n));r=mod(k,(2*n));if (r~=0)r=r;else r=2*n;q=q-1;endif (r<=n)s(k,2)=q*(n+1)+r;s(k,3)=q*(n+1)+r+1;s(k,4)=(q+1)*(n+1)+r+1;s(k,5)=(r-1)*h;s(k,6)=q*h;s(k,7)=r*h;s(k,8)=q*h;s(k,9)=r*h;s(k,10)=(q+1)*h;elses(k,2)=q*(n+1)+r-n;s(k,3)=(q+1)*(n+1)+r-n+1;s(k,4)=(q+1)*(n+1)+r-n;s(k,5)=(r-n-1)*h;s(k,6)=q*h;s(k,7)=(r-n)*h;s(k,8)=(q+1)*h;s(k,9)=(r-n-1)*h;s(k,10)=(q+1)*h;endendd=zeros(3,3);B=zeros((n+1)^2,1);b=zeros(3,1);for k=1:1:2*n^2L(1)=(1/(2*st))*((s(k,7)*s(k,10)-s(k,9)*s(k,8))+(s(k,8)-s(k,10))*x+(s(k,9)-s(k,7))*y);L(2)=(1/(2*st))*((s(k,9)*s(k,6)-s(k,5)*s(k,10))+(s(k,10)-s(k,6))*x+(s (k,5)-s(k,9))*y);L(3)=(1/(2*st))*((s(k,5)*s(k,8)-s(k,7)*s(k,6))+(s(k,6)-s(k,8))*x+(s(k ,7)-s(k,5))*y);for i=1:1:3for j=i:3d(i,j)=int(int(((((diff(L(i),x))*(diff(L(j),x)))+((diff(L(i),y))*(dif f(L(j),y))))-((can^2)*L(i)*L(j))),x,0,1),y,0,1);d(j,i)=d(i,j);endendfor i=1:1:3for j=1:1:3A(s(k,(i+1)),s(k,(j+1)))=A(s(k,(i+1)),s(k,(j+1)))+d(i,j);endendfor i=1:1:3b(i)=int(int((L(i)),x,0,1),y,0,1);B(s(k,(i+1)),1)=B(s(k,(i+1)),1)+b(i);endendM=zeros((n+1)^2,n^2);j=n^2;for i=(n^2+n):-1:1if ((mod(i,(n+1)))~=1)M(:,j)=A(:,i);j=j-1;else continueendendpreanswer=M\B;answer=zeros((n+1)^2,1);j=1;for i=1:1:(n^2+n)if ((mod(i,(n+1)))~=1)answer(i)=preanswer(j);j=j+1;else answer(i)=0;endendZ=zeros((n+1),(n+1));for i=1:1:(n+1)^2s=fix(i/(n+1))+1;r=mod(i,(n+1));if(r==0)r=n+1;s=s-1;elseendZ(r,s)=answer(i);end[X,Y]=meshgrid(1:-h:0,0:h:1);surf(X,Y,Z);toc;t=toc;K=a ;B=b';U=inv(K)*Bfor i=1:nu(i,1)=4/(pi^2)*sin(pi*i/n/2);endue=U-u六、实验结果:程序中的变量can为问题中的k,为了方便比较,采用了画图的方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏微分方程数值实验报告八实验题目:利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x e x u x -=-实现算法:对于两点边值问题,)(,)(,,d 22βα==∈=-b u a u l x f dxu(1)其中),(b a l =f b a ),(<为],[b a l =上的连续函数,βα,为给定常数.其相应的有限差分法的算法如下:1.对求解区域做网格剖分,得到计算网格.在这里我们对区间l 均匀剖分n 段,每个剖分单元的剖分步长记为nab h -=.2.对微分方程中的各阶导数进行差分离散,得到差分方程.运用的离散方法有:方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα方法二:利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈(2)将(2)带入(1)可以得到)()()()(2)(211u R x f h x u x u x u i i i i i +=+---+,其中)(u R i 为无穷小量,这时我们丢弃)(u R i ,则有在i x 处满足的计算公式:1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i ,(3)3.根据边界条件,进行边界处理.由(1)可得βα==n u u ,0(4)称(3)(4)为逼近(1)的差分方程,并称相应的数值解向量1-n U 为差分解,i u 为)(i x u 的近似值.4.最后求解线性代数方程组,得到数值解向量1-n U .实验题目:用Lax-Wendroff 格式求解方程:.4sin 1),1(],1,0[,2sin 1)0,(,0),1,0(,02t t u x x x u t x u u x t ππ+=∈+=>∈=- (1) (精确解).2(2sin 1t x u ++=π) 数值边值条件分别为: (a )).(20101n 0nn nu u hu u -+=+τ (b ).1n 0nu u =(c ).02-12111n 0=++++n n u u u请将计算结果与精确解进行比较。
实现算法: 1.网格剖分:对求解区域],0()1,0(G T ⨯=作均匀网格剖分. 节点: ,jh x j = N j ,...,1,0= ,jh t k = M k ,...,1,0= 其中空间和时间步长:.,1MT N h ==τ 2.算法实现将),(1+k i t x u 在节点),(k i t x 处作泰勒级数展开)(][!2][),(),(32221τττO tu t u t x u t x u ki k i k i k i +∂∂+∂∂+=+ (2)考虑在节点),(k j t x 处(1)的微分方程,有:.0=∂∂-∂∂xu a t u .)()(22222x u a t u x a x u a t t u ∂∂=∂∂∂∂-=∂∂-∂∂=∂∂ 将上述两式代入(2)式,得)(][2][),(),(322221τττO xu a x u a t x u t x u ki k i k i k i +∂∂+∂∂-=+对x 的一阶、二阶导数用中心差商代替)())],(),([(21][211h O t x u t x u hx u k i k i k i +-=∂∂-+ )())],(),(2),([(1][211222h O t x u t x u t x u hx u k i k i k i k i ++-=∂∂-+ 代入整理后得到)()()()],(),(2),([2)],(),([2),(),(322211222111τττττO h O h O t x u t x u t x u ha t x u t x u ha t x u t x u k i k i k i k i k i k i k i ++++-+--=-+-++略去误差项,以ki u 代替),(k i t x u ,得到如下差分格式)2(2)(211222111k i k i k i ki k i k ik iu u u ha u u h a u u---+++-+--=ττ (3) (3)式就是Lax-Wendroff 格式,其截断误差为)(22h O +τ,节点如图 令ha r τ||=,就得到(1)式的Lax-Wendroff 格式的公式 )2(2)(2112111k i k i k i ki k i k ik iu u u r u u r u u---+++-+--= (4)(4)式是二阶精度的差分格式.程序代码:function [X,T,U] = advection_fd1d (NS ,NT ,pde,bd) % WAVE_EQUATION_FD1D 利用有限差分方法计算一维双曲线方程 % 输入参数:% NS 整型,空间剖分段数 % NT 整型,时间剖分段数% pde 结构体,带求解的微分方程模型的已知数据, % 如边界、初始、系数和右端项等条件. % bd 数值边值条件 % 输出参数:% X 长度 NS+1 的列向量,空间网格剖分% T 长度 NT+1 的行向量,时间网格剖分% U (NS+1)*(NT+1) 矩阵,U(:,i) 表示第 i 个时间层网格剖分上的数值解[X,h] = (NS);[T,tau] = (NT);N = length(X); M = length(T);U = zeros(N,M);% 初值条件U(:,1) = (X);a = ;r = a*tau/h;% 边值条件if a >= 0 % 左边值条件U(1,:) = (T)elseU(end,:) = (T) %右边值条件endfor i = 2:MU(2:end -1,i) =U(2:end-1,i-1)-r*(U(3:end,i-1)-U(1:end-2,i-1))/2+... r^2*(U(3:end,i-1)-2*U(2:end-1,i-1)+U(1:end-2,i-1))/2;switch (bd)case {'a0'}a0();case {'b'}b();case {'c'}c();otherwisedisp(['Sorry, I do not know your ', bd]);endendfunction a0()U(1,i)=U(1,i-1)-r*(U(2,i-1)-U(1,i-1));endfunction b()U(1,i)=U(2,i-1);endfunction c()U(1,i)=2*U(2,i)-U(3,i);endendfunction pde = model_data ()%MODEL_DATA 数据模型TI = 0;TF = 1;SI = 0;SF = 1;pde = struct('u_exact',@u_exact,'u_initial',@u_initial,...'u_left',@u_left,'u_right',@u_right,'time_grid',...@time_grid,'space_grid',@space_grid,'advection_fd1d_error',@advection_fd1d_error,'a ',-2);function [T,tau] = time_grid(NT)T = linspace(TI,TF,NT+1);tau = (TF-TI)/NT;endfunction [X,h] = space_grid(NS)X = linspace(SI,SF,NS+1)'h = (SF-SI)/NS;endfunction U = u_exact(X,T)[x,t]=meshgrid(X,T);U = 1+sin(2*pi*(x+2*t));endfunction u = u_initial (x)u = 1+sin(2*pi*x);endfunction u = u_right(t)u =1+sin(4*pi*t);endendfunction showsolution (X,T,U)%% SHOWSOLUTION 以二元函数方式显示数值解% 输入参数% X 长度为 NS +1 的列向量,空间网格剖分N% T 长度为 NT +1 的行向量,时间网格剖分M% U N*M 矩阵,U(:,i)表示第i个时间层网格部分上的数值解[x,t] = meshgrid (X,T);mesh (x,t,U');xlabel ('X');ylabel ('T');zlabel ('U(X,T)');endfunction showvarysolution (X,T,U,UE)%% SHOWVARYSOLUTION 显示数值解随着时间的变化% 输入参数% X 长度为 NS +1 的列向量,空间网格剖分N% T 长度为 NT +1 的行向量,时间网格剖分M% U N*M 矩阵,U(:,i)表示第i个时间层网格部分上的数值解M = size (U ,2) ;figurexlabel ('X');ylabel ('U');s = [X(1) ,X(end),min(min(U)),max(max(U))];axis (s);for i = 1:Mplot (X,U(:,i));axis (s);pause ;title ([ 'T=',num2str(T(i)),'时刻的温度分布'])End% 一维双曲线有限差分方法主测试脚本pde=model_data()[X,T,U]=advection_fd1d(100,200,pde,'a');UE=(X,T);showvarysolution(X,T,U,UE);%以随时间变化方式显示数值解showsolution(X,T,U);%以二元函数方式显示数值解[X,T,U]=advection_fd1d(100,200,pde,'b');UE=(X,T);showvarysolution(X,T,U,UE);%以随时间变化方式显示数值解showsolution(X,T,U);%以二元函数方式显示数值解[X,T,U]=advection_fd1d(100,200,pde,'c');UE=(X,T);showvarysolution(X,T,U,UE);%以随时间变化方式显示数值解showsolution(X,T,U);%以二元函数方式显示数值解。
